Логарифмические уравнения
Главный принцип решения логарифмических уравнений состоит в том, чтобы избавиться от этих самых логарифмов:
Если логарифмы обоих чисел по одному и тому же основанию равны, то их подлогарифмические выражения тоже равны:
Также следует помнить основные логарифмические свойства:
Пример 1.
Решите уравнение:
Число 8 обозначает показатель степени, в который нужно возвести основание (2), чтобы получить число (х)
Ответ: x=256..
Пример 2.
Решите уравнение:
Число обозначает показатель степени, в которой нужно возвести основание (3), чтобы получить число (x)
По свойству логарифмов: получаем:
Ответ: x=9.
Пример 3.
Решите уравнение:
Число обозначает показатель степени, в которой нужно возвести основание (3), чтобы получить число
По свойству логарифмов: получаем:
— по Т Виета
Ответ: .
Пример 4.
Решите уравнение:
Воспользуемся формулой :
Приводим к общему знаменателю:
Приводим к общему знаменателю:
Число 3 обозначает показатель степени, в который нужно возвести основание (3), чтобы получить число (х)
Ответ: x=27.
Пример 5.
Решите уравнение:
Приведём логарифмы к общему основанию (5) с помощью формулы
:
Сокращаем:
Раскроем по формуле суммы логарифмов
По свойству логарифмов :
Замена:
Ответ: .
Пример 6.
Решите уравнение:
По формуле преобразуем левую часть:
Число 0 обозначает показатель степени, в который нужно возвести основание (4), чтобы получить число
Вычислим корень из правой и из левой части:
Ответ: .
Пример 7.
Решите уравнение:
Замена:
Обратная замена:
Число -1 обозначает показатель степени, в который нужно возвести основание (10), чтобы получить число (x)
Ответ: .
Пример 8.
Решите уравнение:
О.Д.З:
3) – это условие выполняется при любом x, т.к. число в чётной степени. Остаётся только учесть строгость неравенства:
Если дробь равна 0, значит её числитель равен 0:
Произведение равно 0, когда один из его множителей равен 0:
По О.Д.З нам подходят корни:
Ответ:
Автор статьи: Дьяков Александр Дмитриевич
Редакторы статьи: Гаврилина Анна Викторовна, Агеева Любовь Александровна
Логарифмические уравнения
Факт 1.\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\):\[{\color{blue}{a^t=b \quad\Leftrightarrow\quad \log_a{b}=t}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in \mathbb{R}\).
Примеры:
1) \(\log_24\) – степень, в которую нужно возвести \(2\), чтобы получить \(4\). Следовательно, \(\log_24=2\).
2) \(\log_3\frac13\) – степень, в которую нужно возвести \(3\), чтобы получить \(\dfrac13\). Следовательно, \(\log_3\frac13=-1\). \(\bullet\) Некоторые важные формулы:
(0) при \(a>0, \ a\ne 1, \ b>0\) выполняется основное логарифмическое тождество \[a^{\log_ab}=b\]
(1) при \(a>0,\ a\ne 1\) \[\log_a1=0, \qquad \log_aa=1\]
(2) при \(a>0,\ a\ne 1,\ b>0\) \[\log_{a}{b^m}=
m\log_ab\]
\[\log_{a^n}{b}=\frac 1n\log_ab\]
\[\log_{a^n}{b^m}=\frac mn\log_ab\]
при четных \(m\) и \(n\) и \(a\ne 0,\ a\ne 1,\ b\ne 0\) \[\log_{a^n}{b^m}=\dfrac mn\log_{|a|}{|b|}\]
(3) при \(a>0,\ a\ne 1,\ b>0,\ c>0\) \[b^{\log_ac}=c^{\log_ab}\]
(4) при \(a>0,\ a\ne 1,\ bc>0\) \[\log_a{bc}=\log_a{|b|}+\log_a{|c|} \qquad \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\]
(5) при \(a>0,\ a\ne 1,\ b>0,\ b\ne 1,\ c>0\) \[\log_ab\cdot \log_bc=\log_ac \quad\Leftrightarrow\quad
\log_bc=\dfrac{\log_ac}{\log_ab}\]
\[\log_ab\cdot \log_ba=1 \quad\Leftrightarrow\quad
\log_ba=\dfrac{1}{\log_ab}\]
\(\bullet\) Частный случай формул (2): \[m=\log_a{a^m}\]
С помощью нее нагляднее видно, как заменить число на логарифм по нужному основанию:
\(4=\log_2{2^4}=\log_2{16}\).
\(\bullet\) Формулу (0) удобно использовать, чтобы заменить число на степень с нужным основанием:
\(4=3^{\log_34}\).
\(\bullet\) С помощью формулы \(\log_ba=\dfrac1{\log_ab}\) из (5) можно “менять” основание и аргумент логарифма местами:
\(\log_52=\dfrac1{\log_25}\).
\(\bullet\) Логарифмическое уравнение – уравнение, содержащее переменную \(x\) в основании и/или аргументе логарифма.
Простейшее логарифмическое уравнение:
\[\log_a{f(x)}=\log_a{g(x)} \quad \Leftrightarrow \quad
\begin{cases}
f(x)=g(x)\\
f(x)>0 \ (\text{или }g(x)>0)
\end{cases}\] где \(a>0, a\ne 1\).
Неравенства \(f(x)>0\) и \(g(x)>0\) составляют ОДЗ данного уравнения.
Примеры решения уравнений:
1) Решить уравнение \(\log_{\frac13}(4x+1)=-3\).
Решение.
ОДЗ уравнения: \(4x+1>0\).
Пользуясь определением логарифма, уравнение можно переписать в виде \(\left(\frac13\right)^{-3}=4x+1\). Так как \(\left(\frac13\right)^{-1}=3\), то \(\left(\frac13\right)^{-3}=3^3=27\). Следовательно, получаем уравнение \(27=4x+1\), откуда \(x=6,5\). Данный корень подходит по ОДЗ.
2) Решить уравнение \(\log_{\sqrt5}(2x+15)=4\log_{\sqrt5}2\).
Решение.
ОДЗ уравнения: \(2x+15>0\).
Так как \(m\log_ab=\log_ab^m\), то \(4\log_{\sqrt5}2=\log_{\sqrt5}2^4=\log_{\sqrt5}16\). Следовательно, получаем уравнение \(\log_{\sqrt5}(2x+15)=\log_{\sqrt5}16\). Получили простейшее логарифмические уравнение, которое преобразуется в \(2x+15=16\), откуда \(x=0,5\). Данный корень подходит по ОДЗ.
3) Решить уравнение \(\log_3(2x+1)=\log_3(3-x)+1\).
Решение.
ОДЗ уравнения: \(2x+1>0\) и \(3-x>0\).
Так как \(1=\log_33\), то правая часть равна \(\log_3(3-x)+\log_33=\log_3(3(3-x))\), следовательно, уравнение примет вид \(\log_3(2x+1)=\log_3(9-3x)\). Данное уравнение преобразуется в \(2x+1=9-3x\), откуда \(x=1,6\). Данный корень подходит по ОДЗ.
Факт 2.
\(\bullet\) Объясним, зачем нужны модули в формулах (2) и (4).
1) Рассмотрим частный случай формулы (2) при четном \(m\): \(\log_a{b^m}=m\log_a{|b|}\) на примере.
Рассмотрим: \(\log_3{b^2}=2\log_3{|b|}\).
Зачем модуль? Заметим, что в левую часть равенства можно подставлять вместо \(b\) все числа \(b\ne 0\). Если в правой части не поставить модуль (т.е. \(\log_3b\)), то вместо \(b\) можно подставлять только \(b>0\). Таким образом, теряется часть возможных значений числа \(b\).
2) В формулах (4): \[\log_a{bc}=\log_a{|b|}+\log_a{|c|} \ \ \ \ \ \ \text{и}
\ \ \ \ \ \ \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\] аналогичная причина: в левую часть равенств можно подставлять как одновременно положительные \(b\) и \(c\), так и одновременно отрицательные (так как произведение двух отрицательных чисел является положительным числом). А вот в правые части, если в них убрать модули, отрицательные \(b\) и \(c\) уже подставлять будет нельзя (так как аргумент логарифма – всегда положительное выражение). Таким образом, не поставив модули, мы значительно сузим возможные значения для \(b\) и \(c\).
Пример:
Если не поставить модули, а записать, например, \(\log_2{bc}=\log_2b+\log_2c\), то значения \(b=-1\) и \(c=-1\) не удовлетворяют равенству. Тогда как с модулями числа \(b\) и \(c\) могут одновременно быть отрицательными.
Логарифмические уравнения, формулы и примеры
Определение и формулы логарифмических уравнений
Типы логарифмических уравнений
Тип 1. Простейшим логарифмическим уравнением называется уравнение вида
решение которого (при условии, что )
Тип 2. Уравнения вида .
Такие уравнения эквивалентны системе
Тип 3. Уравнения .
Уравнения такого типа равносильны одной из систем:
или
Из указанных двух систем выбирается та, которая содержит более простое неравенство.
| Понравился сайт? Расскажи друзьям! | |||
Урок-лекция по теме «Логарифмические уравнения. Основные методы их решения»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
В моём календарно-тематическом планировании на тему “Логарифмические уравнения” отводится 3 часа. Я их разбиваю следующим образом:
1 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”. В конце лекции задаю блок уравнений обязательного уровня.
2 урок – решение уравнений различного типа и сложности (это зависит от уровня математической подготовки класса, использую индивидуальный подход).
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
2 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”, но только два метода – на основании определения и потенцирования. Решение уравнений на применение этих методов.
2 урок – лекция “Логарифмические уравнения. Основные методы их решения”, два других метода – подстановки и логарифмирования. Решение уравнений на применение этих методов.
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
Вариант подачи темы зависит от подготовленности класса.
1 урок
Лекция “Логарифмические уравнения. Основные методы их решения”.
Слайд 1.
Эпиграфом своей сегодняшней лекции я привожу слова Ричарда Олдингтона (1892 – 1962гг., английский поэт, прозаик, критик): “Ничему тому, что важно знать, научить нельзя, — всё, что может сделать учитель, это указать дорожки”.
Слайд 2.
А так же – русскую народную пословицу: “Кто говорит – тот сеет, кто слушает – тот собирает”.
В самом начале моей лекции я хотела бы обратить ваше внимание на следующее. При решении логарифмических уравнений применяют преобразования, которые не приводят к потере корней, но могут привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений. Здесь возможны два подхода:
Проверка путём подстановки полученных решений в исходное уравнение.
Нахождение области допустимых значений уравнения (ОДЗ). Тогда корнями могут быть только те числа, которые принадлежат этой области.
В своей лекции я буду использовать оба этих подхода, а ваше право уже самим выбирать, какой лично вам больше нравится. Следует отметить, что при решении логарифмических неравенств возможен только один из них: ОДЗ!
Основные методы решения логарифмических уравнений.
Слайд 3.
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Решение логарифмических уравнений на основании определения логарифма.
Определение логарифма: Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. Т. е.
Таким образом, применяя его к нашей теме, мы получим следующее:
при этом
Пример 1:
Число 16 удовлетворяет ОДЗ, значит 16 – корень исходного уравнения.
Ответ: 16.
Слайд 4.
Пример 2:
Проверка: — верно, значит число 4 – корень исходного уравнения.
Ответ: 4.
Пример 3:
По определению логарифма значит
Ответ:
Слайд 5.
А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид при этом Хочу отметить особо, что рассуждения НЕ ИЗМЕНИЛИСЬ!
Пример 4:
ОДЗ:.
С учётом ОДЗ получим, что решением данного уравнения является число 2.
Ответ: 2.
Как мы видим, наличие выражения с переменной в основании влияет лишь на ОДЗ, а не на ход рассуждений. Кроме того, данное уравнение можно решать, не прибегая к нахождению ОДЗ, а просто в конце выполнить проверку.
Метод потенцирования.
Слайд 6.
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
, где
Пример 5:
Проверка:
— верно.
— не верно.
Значит, только число 1 является решением исходного уравнения.
Ответ:1.
Слайд 7.
Если же в основании – выражение с переменной, то рассуждения не меняем! В этом случае уравнение будет иметь вид
, где
И пример такого уравнения можно разобрать на предыдущем примере 5.
Пример 6:
Проверка:
— верно.
— не верно.
Значит, только число 1 является решением исходного уравнения.Ответ:1.
ОДЗ для данного уравнения выглядит следующим образом:
Мы видим, что в этом уравнении рациональнее выполнить проверку, а не искать ОДЗ. Но ещё раз повторюсь, что при решении неравенств ОДЗ находить придётся ОБЯЗАТЕЛЬНО.
Рассмотрим пример, который, на первый взгляд, не может относиться к данному типу уравнений.
Слайд 8.
Пример7:
Сделаем замену , получим воспользовавшись свойством логарифма (сумма логарифмов равна логарифму произведения подлогарифмических выражений: ), получим уравнение которое в свою очередь замечательно решается методом потенцирования, т.е. А это линейное уравнение, решив которое, получим
Проверка: — верно.
Ответ: 0.
Замечу, что часто перед применением какого-либо метода решений, необходимо преобразовать уравнение, применив различные свойства логарифмов. Предыдущий пример, тому подтверждение.
Метод подстановки.
Слайд 9.
Данный метод мы достаточно часто встречаем в математике, вспомните тригонометрические или показательные уравнения. Поэтому применение его при решении логарифмических уравнений я вам покажу на примере.
Пример 8: .
В этом уравнении рациональней найти ОДЗ:
Пусть , тогда уравнение примет вид
,
Значит или . А это уравнения, которые мы решим, используя определение: 1)
2)
Мы видим, что оба корня удовлетворяют ОДЗ, значит оба числа являются решениями исходного уравнения.
Ответ:
Слайд 10.
Если в основании логарифма лежит выражение с переменной, то уравнение в общем виде будет выглядеть следующим образом:
, где
И опять, вы сами выбираете: ОДЗ или проверка.
Пример 9: .
ОДЗ:
Приведём логарифмы к одному основанию – 7, пользуясь свойством перехода к новому основанию , получим:
, выполним подстановку , получим уравнение
,
Значит,
Оба числа удовлетворяют ОДЗ.
Ответ:
Метод логарифмирования.
Слайд 11.
Данный метод является “обратным” методу потенцирования, т. е. мы от уравнения без логарифмов переходим к уравнению, их содержащему.
, при этом
Этот метод обычно используется, если в уравнении есть показательные функции, логарифмы – в показателе. Рассмотрим этот метод на примере.
Пример 10:
ОДЗ:
Прологарифмируем обе части уравнения по основанию 3:
а теперь воспользуемся свойством логарифмов , получим
Выполним подстановку , получим уравнение
Значит,
Оба числа удовлетворяют ОДЗ.
Ответ: 3, 27.
Этот пример показывает, что при решении логарифмических уравнений, возможна комбинация нескольких методов. А значит необходимо уметь пользоваться каждым из них. Научиться этому – теперь ваша задача.
Слайд 12.
Итак, сегодня мы с вами рассмотрели основные методы решения логарифмических уравнений:
- На основании определения логарифма.
- Метод потенцирования.
- Метод постановки.
- Метод логарифмирования.
Главным, по моему мнению, является метод, основанный на определении логарифма. Практически в каждом их других методов происходит “выход” на него. Кроме того, на примерах мы увидели, что все методы
Лекция по математике тема: «Логарифмические уравнения»
Лекция
Тема: Логарифмические уравнения
План
1. Определение логарифмического уравнения
2. Решение простейших уравнений
3. Потенцирование.
4. Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию.
5. Уравнения вида Alog a f(x) + Blog b g(x) + C = 0.
6. Введение новой переменной
Определение логарифмического уравнения
Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение вида loga x = b (где а>0, и а ≠1).
Функция у=log a x является возрастающей (или убывающей) на промежутке
(0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне) для любого b это уравнение имеет корень, и только один.
Решение простейших уравнений
Простейшими логарифмическими уравнениями будем называть уравнения следующих видов:
log a x = b, a > 0, a 1.
log a f(x) = b, a > 0, a 1.
log f(x) b = c, b > 0.
Эти уравнения решаются на основании определения логарифма:
если logb a = c, то a = bc.
Пример 2.1.
Решение. Область определения уравнения x > 0. По определению логарифма x = 23, x = 8 принадлежит области определения уравнения.
Ответ: x = 8.
Уравнения вида loga f(x) = b, a > 0, a ≠ 1.
Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x). Уравнение равносильно следующей системе

Обычно область определения находится отдельно, и после решения уравнения f(x) = ab проверяется, принадлежат ли его корни области определения уравнения.
Пример 2.2. log3(5х – 1) = 2.
Решение: ОДЗ: 5х – 1 > 0; х > 1/5. log3(5х– 1) = 2, log3(5х – 1) = log332, 5х — 1 =9,
х = 2. Ответ: 2.
Пример 2.3.

Решение. Область определения уравнения находится из неравенства 2х2 – 2х – 1 > 0. Воспользуемся определением логарифма:

Применим правила действий со степенями, получим 2х2 – 2х – 1 = 3. Это уравнение имеет два корня х = –1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х2 – 2х – 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями.
Ответ. х1 = –1, х2 = 2.
Уравнения вида logf(x) b = с, b > 0.
Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе

Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения (f(x))c = b или равносильного уравнения

проверяется, принадлежат ли его корни найденной области.
Пример 2.4. logx–19 = 2.
Решение. Данное уравнение равносильно системе
 Ответ. x = 4.
Ответ. x = 4.
Потенцирование.
Суть метода заключается в переходе от уравнения
log a f(x) = log a g(x) к уравнению f(x) = g(x), которое обычно
не равносильно исходному.
Уравнения вида loga f(x) = loga g(x) , а > 0, а 1.
На основании свойства монотонности логарифмической функции заключаем, что f(x) = g(x).
Переход от уравнения loga f(x) = loga g(x) к уравнению f(x) = g(x) называется потенцированием.
Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении f(x) > 0, g(x) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними.
Пример 3.1 log3 (x2 – 3x – 5) = log3 (7 – 2x).
Решение. Область определения уравнения найдётся из системы неравенств

Потенцируя данное уравнение, получаем х2 – 3х – 5 = 7 – 2х,
х2 – х – 12 = 0, откуда х1 = –3, х2 = 4. Число 4 не удовлетворяет системе неравенств. Ответ. х = –3.
Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию.
Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log a f(x) = log a g(x) используются следующие свойства логарифмов:
logb a + logb c = logb (ac), где a > 0; c > 0; b > 0, b 1,
logb a – logb c = logb (a/c), где a > 0; c > 0; b > 0, b 1,
m logb a = logb a m, где a > 0; b > 0, b 1; mR.
Пример 4. 1. log6 (x – 1) = 2 – log6 (5x + 3).
Решение. Найдём область определения уравнения из системы неравенств

Применяя преобразования, приходим к уравнению
log6 (x – 1) + log6 (5x + 3) = 2,
log6 ((x – 1)(5x + 3)) = 2, далее, потенцированием, к уравнению
(х – 1)(5х + 3) = 36, имеющему два корня х = –2,6; х = 3. Учитывая область определения уравнения, х = 3. Ответ. х = 3.
Пример 4.2. 
Решение. Найдём область определения уравнения, решив неравенство
(3x – 1)(x + 3) > 0 методом интервалов.
Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log5 (x + 3) 2 = 0. По определению логарифма
(х + 3) 2 = 1, х = –4, х = –2. Число х = –2 посторонний корень.
Ответ. х = –4.
Пример 4. 3. log2 (6 – x) = 2log6 x.
Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 – x = x2, откуда х = –3, х = 2. Число х = –3 посторонний корень.
Ответ. х = 2.
Уравнения вида Alog a f(x) + Blog b g(x) + C = 0.
Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы:




Пример 5.1. 
Решение. Область определения уравнения 1 < x < 2. Используя формулу (3), получим 
Так как 3 = log28, то на области определения получим равносильное уравнение (2–x)/(x–1) = 8, откуда x = 10/9. Ответ. x = 10/9.
Пример 5.2. 
Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4). Ответ. х = 6.
Ответ. х = 6.
Пример 5. 3. 
Решение. Область определения уравнения x > –1, x 0. Приведём логарифмы к основанию 3, используя формулу (2). 
Умножим обе части уравнения на log 3(x + 1) 0 и перенесем все слагаемые в левую часть уравнения. Получим (log 3(x + 1)–1)2 = 0, откуда log 3(x + 1) = 1 и
x = 2. Ответ. x = 2..
Введение новой переменной
Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным.


Уравнения вида где a > 0, a 1, A, В, С – действительные числа.
где a > 0, a 1, A, В, С – действительные числа.
Пусть t = loga f(x), tR. Уравнение примет вид t2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.
Пример 6. 1. lg 2 x – lg x – 6 = 0.
Решение. Область определения уравнения – интервал (0; ).Введём новую переменную t = lg x, tR.
Уравнение примет вид t 2 – t – 6 = 0. Его корни t1 = –2, t2 = 3.
Вернёмся к первоначальной переменной lg x = –2 или lg x = 3,
х = 10 –2 или х = 10 3. Оба значения x удовлетворяют области определения данного уравнения (х > 0).Ответ. х = 0,01; х = 1000.
Пример 6. 2. 
Решение. Найдём область определения уравнения

Применив формулу логарифма степени, получим уравнение 
Так как х < 0, то | x | = –x и следовательно 
Введём новую переменную t = log3 (–x), tR. Квадратное уравнение
t 2 – 4t + 4 = 0имеет два равных корня t1,2 = 2. Вернёмся к первоначальной переменной log3 (–x) = 2, отсюда –х = 9, х = –9. Значение неизвестной принадлежит области определения уравнения. Ответ. х = –9.
Уравнения вида  где a > 0, a 1, A, В, С – действительные числа , A0, В0.
где a > 0, a 1, A, В, С – действительные числа , A0, В0.
Уравнения данного вида приводятся к квадратным умножением обеих частей его на loga f(x) 0. Учитывая, что loga f(x) logf(x) a=1
(свойство logb a = 1/ loga b), получим уравнение

Замена loga f(x)=t, tR приводит его к квадратному At2 + Ct + B = 0.
Из уравнений loga f(x)= t1 , logb f(x)= t2 найдем значения x и выберем среди них принадлежащие области определения уравнения: f(x) > 0, f(x) 1.
Пример.6.3 
Решение. Область определения уравнения находим из условий x+2>0, x+2 1, т.е. x >–2, x –1.Умножим обе части уравнения на log5 (x+2) 0, получим
 или, заменив log5 (x+2) = t, придем к квадратному уравнению t 2 – t – 2 = 0, t1 = –1, t2 =2.
или, заменив log5 (x+2) = t, придем к квадратному уравнению t 2 – t – 2 = 0, t1 = –1, t2 =2.
Возвращаемся к первоначальной переменной:
log5 (x+2) = –1, x+2 = 1/5, x = –9/5,
log5 (x+2) = 2, x+2 = 25, x = 23.
Оба корня принадлежат области определения уравнения.
Ответ: x = –9/5, x = 23.
Упражнения для закрепления материала
Решить уравнения
1)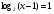 ; 2)
; 2)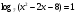 ; 3)
; 3)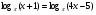 ;
;
4)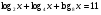 ; 5)
; 5)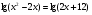 ;
;
Контрольные вопросы
1. Сформулировать определение логарифмического уравнения.
2. Назвать основные методы решения логарифмических уравнений
Литература
1.Ш.А.Алимов, стр.105-111 2 О.Н.Афанасьева, стор.2753-279 3.А.Г.Мерзляк, стор.202-2