Как решать неравенства с двумя модулями – Неравенство с несколькими модулями | Подготовка к ЕГЭ по математике — Детская игровая комната «Волшебный лес»

Posted on 28.01.201922.12.2019 by alexxlab

Содержание

Неравенство с несколькими модулями | Подготовка к ЕГЭ по математике

«Неравенство с двумя модулями. Часть I» смотрим здесь.

Решим неравенство

Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них.

В нашем случае нуль первого модуля – это 4, нули второго подмодульного выражения – это -3 и 2.

Вся числовая ось указанными точками разбивается на 4 промежутка. Нам предстоит поработать с неравенством в каждом из них.

Если у вас возник вопрос, почему, например, в крайнем левом промежутке у нас число -3 не включено, а на следующем включено (аналогично с другими), – ответим на него. На самом деле, – все равно, куда именно вы включите концы промежутков. Лишь бы при склейке все промежутки давали бы нам всю числовую прямую, если мы работаем на R.

Выясним, как распределяются знаки подмодульных выражений на каждом из промежутков.

Начнем с первого подмодульного выражения. Очевидно, что при x>4 знак выражения 4-x – минус, то есть 4-x<0 , а при $x\leq 4$

$4-x\geq0$ .

«Переключателями» же знака второго подмодульного выражения из неравенства являются точки -3 и 2. Если $-3\leq x\leq 2$ , то $x^2+x-6\leq 0,$ при остальных имеем: . Если вам не кажутся очевидными знаки этого подмодульного выражения на указанных промежутках, загляните сюда (метод интервалов).

Мы замечаем, что на двух промежутках (первом и третьем слева) знаки подмодульных выражений распределены одинаково.

Итак, первый случай:

Предстоит решить систему (мы объединили первый и третий промежутки в совокупность):

$\begin{cases} \left[\begin{gathered} x<-3, & 2<x\leq 4; \end{gathered} \right& & 4-x+x^2+x-6\geq 7; \end{cases}$

Во второй строке системы приводим подобные слагаемые и раскладываем на множители:

$\begin{cases} \left[\begin{gathered} x<-3, & 2<x\leq 4; \end{gathered} \right& & (x-3)(x+3)\geq 0; \end{cases}$

Теперь переходим на ось, пересекаем два множества между собой:

$x\in(-\infty;-3)\cup[3;4]$ .

Второй случай:

$\begin{cases} -3\leq x\leq 2,& & 4-x-x^2-x+6\geq 7; \end{cases}$

$\begin{cases} -3\leq x\leq 2,& & x^2+2x-3\leq 0; \end{cases}$

$\begin{cases} -3\leq x\leq 2,& & (x-1)(x+3)\leq 0; \end{cases}$

$x\in[-3;1]$ .

Третий случай:

$\begin{cases} x>4,& & -4+x+x^2+x-6\geq 7; \end{cases}$

$\begin{cases} x>4,& & x^2+2x-17\geq 0; \end{cases}$

$\begin{cases} x>4,& & (x-(-1+3\sqrt2))(x-(-1-3\sqrt2))\geq 0; \end{cases}$

76п

$x\in(4;+\infty)$ .

Нам осталось объединить решения каждого из случаев между собой:

Ответ: $(-\infty;1]\cup[3;+\infty)$

Для тренировки предлагаю Вам решить следующее неравенство:

$(-\infty;1]\cup[3;+\infty)$

Ответ: + показать $\frac{5-\sqrt{41}}{2}\leq x\leq 2$

egemaximum.ru

Неравенства с модулями. Видеоурок. Алгебра 11 Класс

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Неравенства с модулями

Существует несколько определений модуля. Эти определения должны быть равноценны, эквивалентны, т. е. из первого определения следует второе, а из второго первое.

Определение:

Модулем числа t называется само число t, если оно больше нуля, модулем нуля является ноль, и если под модулем отрицательное число, то модуль t равен минус t.

Обычно в задачах под модулем стоит целое выражение, зависящее от х, тогда:

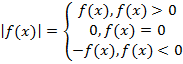
Из вешесказанного следует простое правило: если под модулем стоит положительное число, то модуль можно отбросить. Если же под модулем стоит отрицательное число, то модуль следует отбросить, но поставить знак минус перед всем подмодульным выражением.

Определение:

Модуль числа t – это расстояние от точки t до точки 0.

В частности,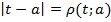

Например:

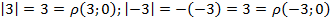
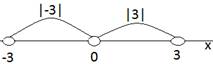
Рис. 1. Модули чисел 3 и -3

Из определения модуля следует основной прием решения задач с модулем, а именно, освободиться от модуля на основе его определения. Поясним на конкретном примере.

Пример 1 – построить график функции:

Согласно определению модуля, рассматриваем два случая:

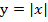
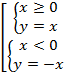
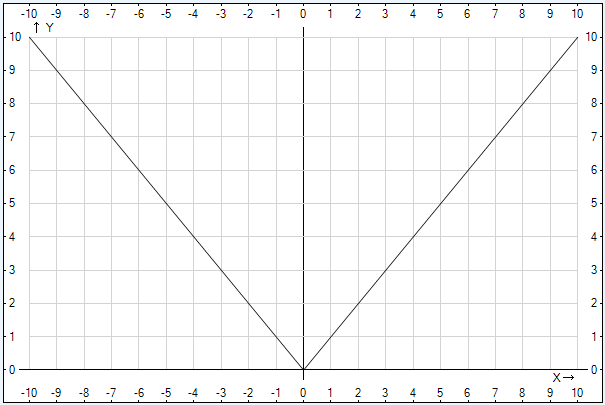
Рис. 2. График функции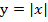

Пример 2 – решить неравенства:

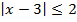
Решим, опираясь на второе определение:

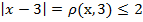
Проиллюстрируем:

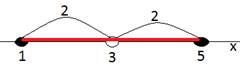
Рис. 3. Решение примера 2.a

Любая точка, не принадлежащая выбранному отрезку, не будет являться решением, так как расстояние от нее до точки 3 будет больше заданного расстояния.

Ответ: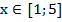

б)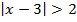

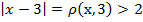
Проиллюстрируем:

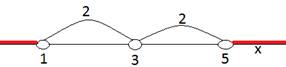
Рис. 4. Решение примера 2.б

Любая точка, не принадлежащая выбранным промежуткам, не будет являться решением, так как расстояние от нее до точки 3 будет меньше заданного расстояния.

Ответ: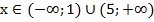

Рассмотрим неравенства вида:

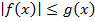
Данное неравенство можно решать двумя способами.

Способ 1 (по определению):

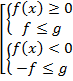
Способ 2:

Строгое доказательство данного способа опустим, приведем и прокомментируем его.

Поясним на графике (рисунок 5)

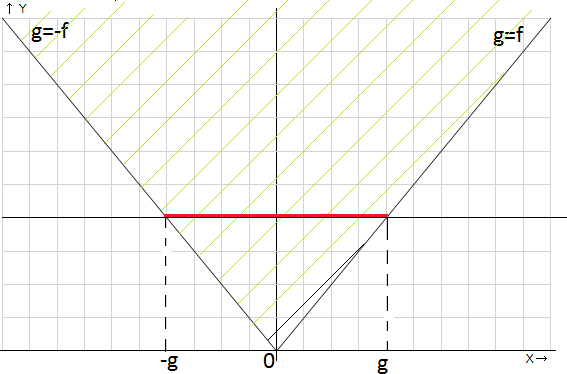
Рис. 5. Пояснительный график

Итак, на рисунке 12.5 изображен график функции . Решения неравенства 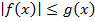заштрихованы зеленым цветом. Если функция g(x) задана как константа, то нас удовлетворит промежуток значений (-g; g) – показано красным.

Рассмотрим следующий тип неравенств с уединенным модулем:

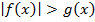
Аналогично предыдущему неравенству, покажем два способа решения.

Способ 1:

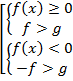
Способ 2:

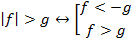
Доказательство данного способа можно получить, продолжив преобразовывать совокупность, полученную в первом способе. Мы проиллюстрируем данный способ решения:

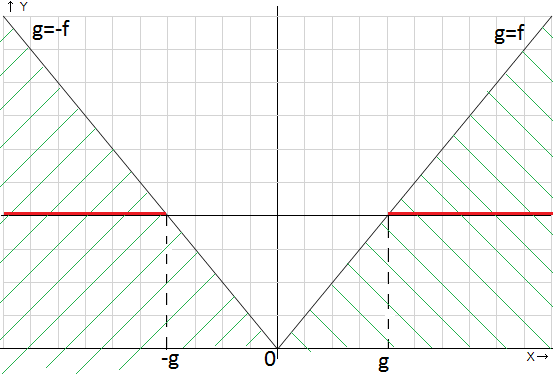
Рис. 6. Пояснительный график

Итак, на рисунке 6 изображен график функции

. Решения неравенства

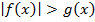заштрихованы зеленым цветом. Если функция g(x) задана как константа, то нас удовлетворят промежутки значений

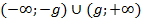– показано красным.

Пример 3 – решить неравенство:

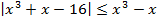
Решаем неравенство вторым способом:

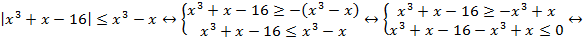
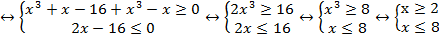
Проиллюстрируем решение системы:

Рис. 7 Решение системы в примере 3

Ответ: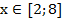

Пример 4 – решить неравенство:

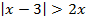
Решаем вторым способом:

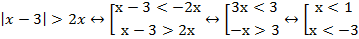
Проиллюстрируем решение совокупности:

Рис. 8. Решение совокупности в примере 4

Ответ:

Неравенства с модулем можно решать методом интервалов.

Пример 5 – решить неравенства:

а)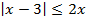

б)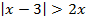

Согласно стандартному алгоритму, рассматриваем функцию, стоящую в левой части, если справа ноль:

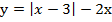
Исследуем функцию. ОДЗ: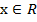

Чтобы найти корни, решим уравнение:

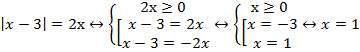
Выделяем интервалы знакопостоянства и определяем знаки функции:

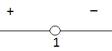
Рис. 9. Интервалы знакопостоянства функции

Ответ: а)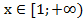; б) ;

Рассмотрим неравенство, в котором сравниваются два модуля.

Пример 6 – решить неравенство:

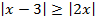
Напомним, что если обе части неравенства положительны, мы имеем право возвести их в квадрат, при этом равносильность не теряется. В данном случае каждый модуль неотрицателен, имеем право возвести в квадрат, при этом модули уничтожатся, согласно свойству ():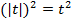

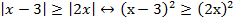
Перенесем все в одну сторону и разложим на множители:

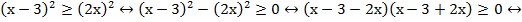
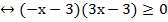
Вынесем из скобок константные множители:

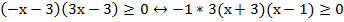
Разделим обе части неравенства на минус три, при этом знак неравенства меняется на противоположный:

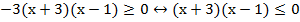
Получено простейшее квадратное неравенство. Парабола, ветви направлены вверх, интересующие нас значения находятся в интервале между корнями.

Ответ: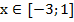

Итак, мы рассмотрели различные типовые неравенства с модулем, привели некоторые схемы решения и решили примеры. Далее перейдем к системам уравнений.

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал естественных наук (Источник).

2. ЕГЭ по математике (Источник).

3. Математика, которая мне нравится (Источник).

Домашнее задание

1. Решить неравенство:

а) ;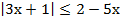

б) ;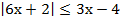

в) ;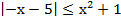

г) ;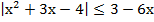

2. Решить неравенство:

а) ;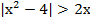

б);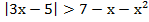

в);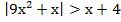

г) ;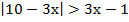

3. Решить неравенство:

а) ;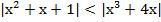

б) ;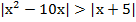

в) ;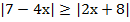

г) ;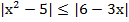

interneturok.ru

Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.

Как решать неравенства с модулем?

Методы решения систем линейных неравенств отличаются от методов решения линейных уравнений тем, что знаки неравенства не позволяют выполнять подстановку, как мы это делаем с уравнениями. Тем не менее, мы решаем по определенной системе. Система линейных неравенств включает в себя несколько выражений, которые при решении могут дать ряд решений.

$|x|$— расстояние на числовой прямой от $0$ до точки $a$.

$|u|=u$ $—>$ $u\geq0$
$|u|=-u$ $—>$ $u\le \: 0$
$|u|=|v|$ $—>$ $v^2=u^2$
$|x|<a $ $—>$ $-a<x<a$ Система
$|x|\le \:a $ $—>$ $-a\le \:x\le \:a$
$|x|> a $ $—>$ $\left[ \begin{gathered} x < -a \\ x >a \\ \end{gathered} \right.$ Совокупность
$|x|\geq a $ $—>$ $\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.$

Пример 1. Решить неравенство $|3+x| \geq|x|$.

Решение. $|3+x| \geq|x|$$—>$ $(3+x)^2\geq x^2$ $—>$ $x^2+6x+9\geq x^2$ $—>$ $6x\geq -9$ $—>$ $x\geq -1,5$

Ответ: $[-1,5; +∞)$

Пример 2. Решить неравенство $\left|3+2x\right|\le \:7$. Система

Решение. $\left|3+2x\right|\le \:7$ $—>$ $3+2x\le \:7$ и $3+2x\ge \:-7$ или $-7\le \:3+2x\le \:7$

$x\le \:2$ и $x\ge \:-5$ $-5\le \:x\le \:2$

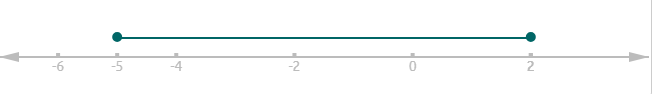
Ответ: [-5;2];

Пример 3. Решить неравенство $\left|3x-5\right|<\:4$

Решение: $-4<3x-5<4$ $—>$ $\frac{1}{3}<x<3$

Ответ: $(\frac{1}{3};3)$;

Пример 4. Решить неравенство $\left|x-8\right|\ge \:\:3$

Решение: Совокупность  $\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.$ $—>$ $\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.$

Ответ: $(+∞;5)⋃ (11;+∞)$

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Неравенства с модулем

Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них.

1) Решение неравенства с помощью геометрического свойства модуля.

Напомню, что такое геометрическое свойство модуля: модуль числа x – это расстояние от начала координат до точки с координатой x.

В ходе решения неравенств этим способом может возникнуть 2 случая:

1. |x| ≤ b, тогда картинка решения выглядит так:

И неравенство с модулем очевидно сводится к системе двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

2. |x| ≥ b, тогда картинка решения выглядит так:

И неравенство с модулем очевидно сводится к совокупности двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

Пример 1.

Решить неравенство |4 – |x|| ≥ 3.

Решение.

Данное неравенство равносильно следующей совокупности:

[4 – |x| ≤ -3
[4 – |x| ≥ 3.

Хочу напомнить принципиальное отличие понятия совокупности от понятия системы. Когда мы ставим знак системы « { », мы подразумеваем, что выполняются и первое и второе неравенства одновременно, то есть мы ищем общие решения двух неравенств. Когда мы ставим знак совокупности « [ », мы подразумеваем, что выполняется или первое неравенство, или второе, то есть мы ищем те значения неизвестного x, которые являются решением либо первого, либо второго неравенства.

Теперь решаем систему.

[-|x| ≤ -7
[-|x| ≥ -1,
[|x| ≥ 7
[|x| ≤ 1.

Решаем отдельно первое неравенство:

[x ≥ 7
[x ≤ -7.

Решаем отдельно второе неравенство:

{x ≥ -1
{x ≤ 1.

Мы получили совокупность, состоящую из подсовокупности и системы. Решением исходного неравенства будут все x, которые удовлетворяют хотя бы одному неравенству из совокупности и каждому из неравенств системы.

Ответ: x € (-∞; -7] U [-1;1] U [7; +∞]

Пример 2.

Решить неравенство ||x+2| – 3| ≤ 2.

Решение.

Данное неравенство равносильно следующей системе.

{|x + 2| – 3 ≥ -2
{|x + 2| – 3 ≤ 2,
{|x + 2| ≥ 1
{|x + 2| ≤ 5.

Решим отдельно первое неравенство системы. Оно эквивалентно следующей совокупности:

[x + 2 ≥ 1
[x + 2 ≤ -1,
[x ≥ -1
[x ≤ -3.

Решим отдельно второе неравенство системы. Оно эквивалентно следующей системе:

{x + 2 ≤ 5
{x + 2 ≥ -5,
{x ≤ 3
{x ≥ -7.

Мы получили систему, состоящую из подсистемы и совокупности. Решением исходного неравенства будут все x, которые являются одновременно решением совокупности и решением подсистемы.

Ответ: х € [-7; -3] U [-1; 3].

2) Решение неравенств, используя определение модуля.

Напомню для начала определение модуля.

|a| = a, если a ≥ 0 и |a| = -a, если a < 0.

Например, |34| = 34, |-21| = -(-21) = 21.

Пример 1.

Решить неравенство 3|x – 1| ≤ x + 3.

Решение.

Используя определение модуля получим две системы:

{x – 1 ≥ 0
{3(x – 1) ≤ x + 3

{x – 1 < 0
{-3(x – 1) ≤ x + 3.

Решая первую вторую системы в отдельности, получим:

{x ≥ 1
{x ≤ 3,

{x < 1
{x ≥ 0.

Решением исходного неравенства будут все решения первой системы и все решения второй системы.

Ответ: x € [0; 3].

3) Решение неравенств методом возведения в квадрат.

Пример 1.

Решить неравенство |x² – 1| < | x² – x + 1|.

Решение.

Возведем обе части неравенства в квадрат. Замечу, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева и справа стоят модули, поэтому мы можем это сделать.

(|x² – 1|)² < (|x² – x + 1|)².

Теперь воспользуемся следующим свойством модуля: (|x|)² = x².

(x² – 1)² < (x² – x + 1)²,

(x² – 1)² – (x² – x + 1)² < 0.

Дальше лучше всего воспользоваться формулой разности квадратов. Можно, конечно и возводить в квадрат левую и правую скобку, но это займет гораздо больше времени.

(x² – 1 – x² + x – 1)( x² – 1 + x² – x + 1) < 0,

(x – 2)(2x² – x) < 0,

x(x – 2)(2x – 1) < 0.

Решаем методом интервалов.

Ответ: x € (-∞; 0) U (1/2; 2)

4) Решение неравенств методом замены переменных.

Пример.

Решить неравенство (2x + 3)² – |2x + 3| ≤ 30.

Решение.

Заметим, что (2x + 3)² = (|2x + 3|)². Тогда получим неравенство

(|2x + 3|)² – |2x + 3| ≤ 30.

Сделаем замену y = |2x + 3|.

Перепишем наше неравенство с учетом замены.

y² – y ≤ 30,

y² – y – 30 ≤ 0.

Разложим квадратный трехчлен, стоящий слева, на множители.

D = 121,

y1 = (1 + 11) / 2,

y2 = (1 – 11) / 2,

y1 = 6,

y2 = -5.

(y – 6)(y + 5) ≤ 0.

Решим методом интервалов и получим:

-5 ≤ y ≤ 6.

Вернемся к замене:

-5 ≤ |2x + 3| ≤ 6.

Данное двойное неравенство равносильно системе неравенств:

{|2x + 3| ≤ 6
{|2x + 3| ≥ -5.

Решим каждое из неравенств в отдельности.

Первое равносильно системе

{2x + 3 ≤ 6
{2x + 3 ≥ -6.

Решим ее.

{x ≤ 1.5
{x ≥ -4.5.

Второе неравенство очевидно выполняется для всех x, так как модуль по определению число положительное. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то решением исходной системы будет решение ее первого двойного неравенства (ведь второе верно для всех x).

Ответ: x € [-4,5; 1,5].

blog.tutoronline.ru

Уравнения и неравенства с модулями

Сегодня порешаем немного заданий с модулями, вспомним, как они раскрываются, будут и уравнения, и неравенства. Поехали…

Задание 1. Решить уравнение: delim{

Совсем простое уравнение. Раскрываем модуль со знаком «плюс» слева от точки 2 и со знаком «минус» – справа, так как в этой точке подмодульное выражение меняет знак с плюса на минус: 2-x=0 , x=2 .

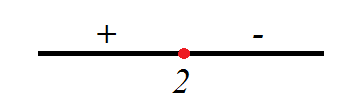Получаем систему:

Решение x=-3 найдено на промежутке , и, соответственно, этому промежутку не принадлежит, поэтому этот корень уравнения посторонний. Ответ: x={1/3}

Задание 2. Решить уравнение: delim{

Приравняем к нулю оба подмодульных выражения, чтобы определить точки перемены их знаков:

Расставляем полученные точки на координатной оси, они нам ее разобьют на три промежутка. Расставляем знаки подмодульных выражений на каждом получившемся промежутке. Это просто сделать, подставив любое число из данного промежутка в модуль и определив, получается положительное число или отрицательное.

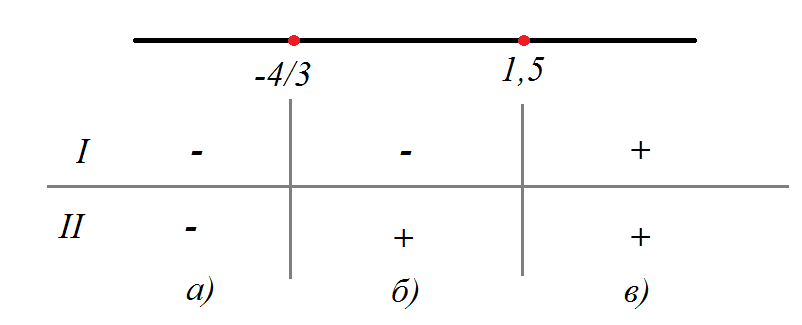
Раскрываем модуль

Теперь видно, с каким знаком надо раскрыть модуль на каждом интервале. Придется решить три уравнения, раскрыв модули с нужными знаками на каждом из них.

Интервал а) – оба модуля раскрываем со знаком «минус»: x= -7

Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»: x= -0,2

Интервал в) – оба модуля раскрываем со знаком «плюс»: x= -7 – эта точка не принадлежит своему интервалу, поэтому этот корень – посторонний. Ответ: x=-7 , x=-0,2

Задание 3. Решить уравнение: delim{

Решать можно либо графическим способом, либо постепенно раскрывая модули снаружи, как будто снимая листья с кочана капусты. Мы сделаем и тем способом, и другим. Сначала – аналитически (то есть раздевая капусту), снимаем первый модуль:

Раскрываем второй модуль:

Раскрываем третий модуль:

Теперь решим графически. Построим сначала прямую 4-x :

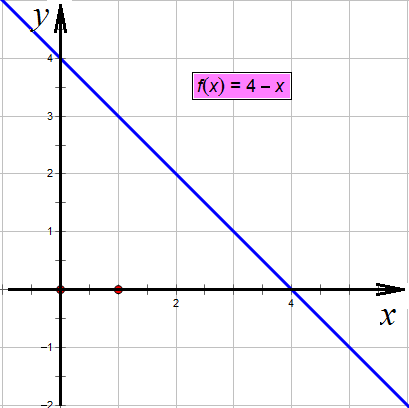
Построение прямой

Теперь «наденем» на нее модуль, то есть отразим всю ее часть, что оказалась ниже оси х, вверх: delim{

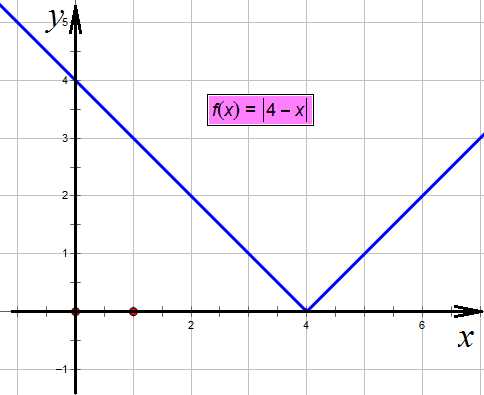
Отражаем вверх все, что ниже оси х

Теперь построим – минус перевернет наш график вверх тормашками:

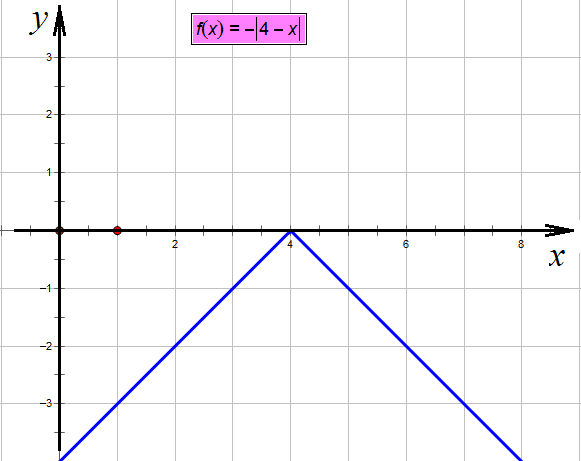
Снова отражаем

Поднимаем все вверх на три единицы:

Поднимаем вверх

«Надеваем» второй модуль, то есть снова отражаем всю отрицательную часть вверх:

Второй модуль

Снова ставим «минус»:

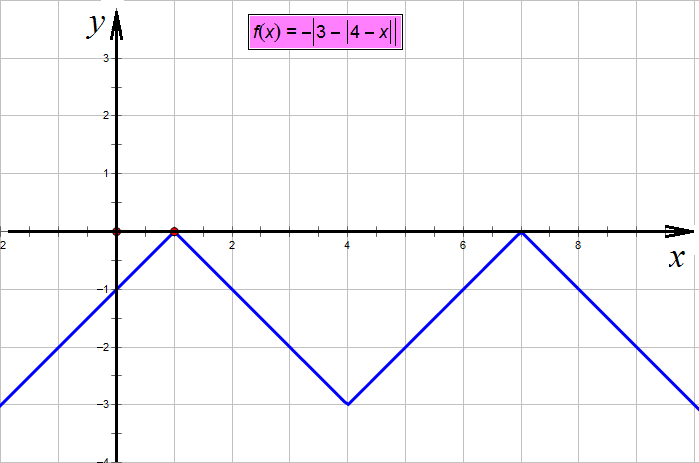
Снова отражаем

Снова поднимаем вверх на три единицы:

Поднимаем

Наконец, последний модуль: delim{

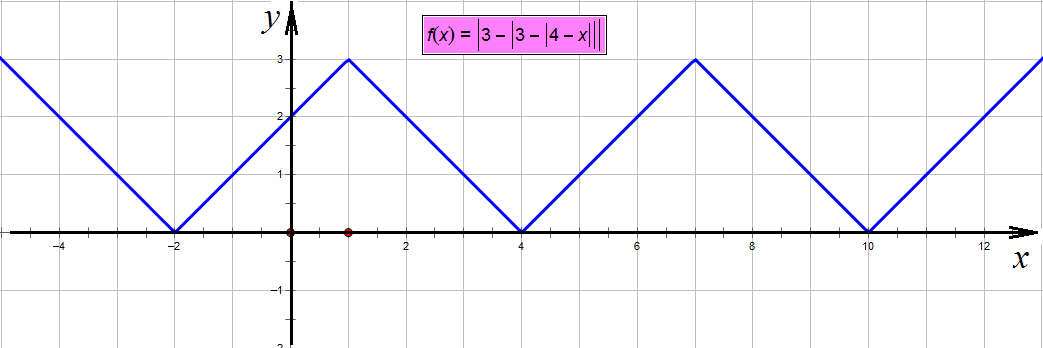
Последний модуль

И проводим прямую y= 1 , пересечения с которой и есть искомые корни:

Прямая пересекает график

Ответ:

Задание 4. Решить неравенство: delim{ delim{

Это неравенство также можно решить графически. Справа имеем прямую y= 3x-3 , слева под знаком модуля – парабола. Модуль переворачивает ту часть параболы, которая находится под осью х, вверх. Требуется найти те интервалы (отрезки), где прямая располагается выше параболы.

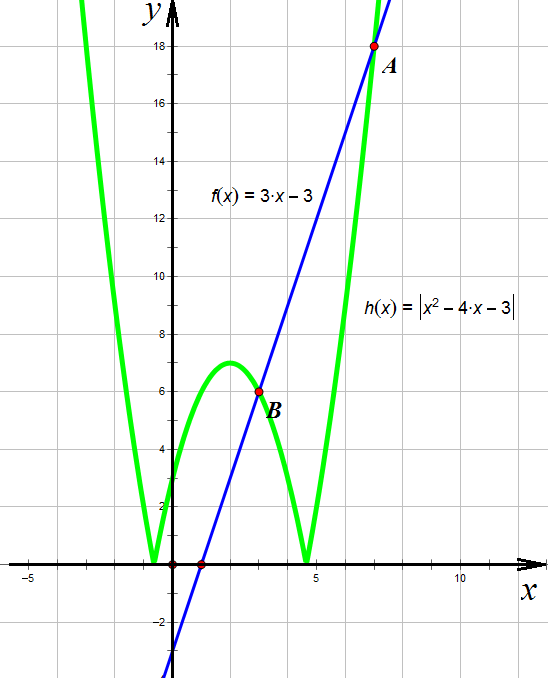
Графическое решение

Нас интересует, очевидно, интервал ВА, точки В и А не войдут в решение, так как неравенство строгое:

Можно также решить аналитически: раскрываем модуль с положительным и отрицательным знаками. $delim{lbrace}{matrix{2}{1}{{x^2-4x-3<3x-3} { -x^2+4x+3<3x-3}}}{ }$ delim{

На рисунке показаны решения первого неравенства и второго, и область пересечения этих решений закрашена.

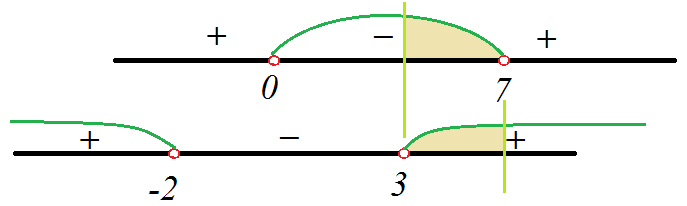
Пересечение решений

Ответ:

Задание 5. Решить уравнение: $25^{delim{$

$5^{2delim{$ delim{

Определяем точку перемены знака модуля: 2-4x=0 x={1/2}

Справа от этой точки модуль раскроем со знаком «минус», слева – со знаком «плюс»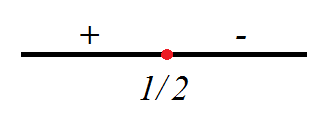

Первое решение сделано на промежутке , точка x=1 этому промежутку не принадлежит, поэтому этот корень – посторонний. Ответ: x=0,6

Задание 6. Решить уравнение: $2^{delim{$

$2^{delim{$ $2^{delim{$

Приравниваем показатели степеней: delim{

Определяем точки перемены знаков подмодульных выражений: 3x-5=0 x=5/3 x-1=0 x=1

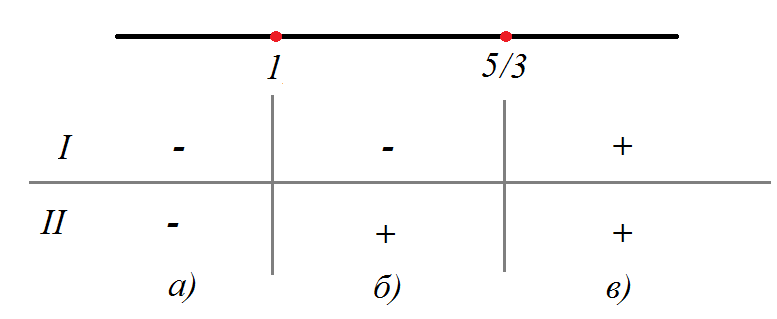
Раскрываем модуль

Раскрываем модули с соответствующими знаками на каждом из промежутков:

Интервал а) – оба модуля раскрываем со знаком «минус»:

Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»: x= 1

Интервал в) – оба модуля раскрываем со знаком «плюс»: -нет решений. Получается, что уравнению будет удовлетворять любое число из промежутка x in (]

Задание 7. Решить уравнение:

Воспользуемся формулой разности логарифмов и заменим ее частным:

По определению логарифма: {delim{

Раскрываем модуль

Интервал а) – оба модуля раскрываем со знаком «минус»: ,

Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»: , ,

Интервал в) – оба модуля раскрываем со знаком «плюс»: , – этот корень своему промежутку не принадлежит, он посторонний. Ответ:

Задание 8. Решить неравенство: $log_{delim{$ delim{

В основании логарифма – модуль, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется.

Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а) delim{

delim{

То есть область, где решение будет существовать, такая:

На этой области при решении основного неравенства мы поменяем знак:

delim{ delim{

б) Вторая область:

delim{

Знак неравенства не меняем, так как основание логарифма больше 1: $log_{delim{$ delim{

delim{ delim{ delim{

Осталось внимательно и аккуратно наложить области решения неравенства на те промежутки, где они существуют:

Наложение решений на промежутки

Ответ: x in ( ] [)

Задание 9. Решить неравенство: $log_{delim{$ delim{

В основании логарифма – модуль х, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется. Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а) delim{

Этот промежуток изображен на рисунке: Тогда знак неравенства меняем, так как основание логарифма меньше 1:

delim{

б) Знак неравенства не меняем, так как основание логарифма больше 1:

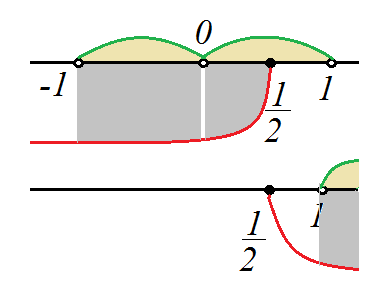
Наложим решения на области их существовавния

$log_{delim{$ delim{

$(x-1)^2<= ({delim{$ delim{ delim{

Наложим решения на области, к которым эти решения относятся:

Ответ: (]

easy-physic.ru

Метод интервалов – универсальный метод решения неравенств с модулем

Чем больше человек понимает, тем сильнее в нем желание понимать

Фома Аквинский

Метод интервалов позволяет решать любые уравнения, содержащие модуль. Суть этого метода в том, чтобы разбить числовую ось на несколько участков (интервалов), причем разбить ось нужно именно нулями выражений, стоящих в модулях. Затем на каждом из получившихся участков всякое подмодульное выражение либо положительно, либо отрицательно. Поэтому каждый из модулей может быть раскрыт или со знаком минус, или со знаком плюс. После этих действий остается лишь решить каждое из полученных простых уравнений на рассматриваемом интервале и объединить полученные ответы.

Рассмотрим данный метод на конкретном примере.

|x + 1| + |2x – 4| – |x + 3| = 2x – 6.

1) Найдем нули выражений, стоящих в модулях. Для этого нужно приравняем их к нулю, и решить полученные уравнения.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

x = 2

2) Расставим получившиеся точки в нужном порядке на координатной прямой. Они разобьют всю ось на четыре участка.

3) Определим на каждом из получившихся участков знаки выражений, стоящих в модулях. Для этого подставляем в них любые числа с интересующих нас интервалов. Если результат вычислений – число положительное, то в таблице ставим «+», а если число отрицательное, то ставим «–». Это можно изобразить так:

4) Теперь будем решать уравнение на каждом из четырех интервалов, раскрывая модули с теми знаками, которые проставлены в таблице. Итак, рассмотрим первый интервал:

I интервал (-∞; -3). На нем все модули раскрываются со знаком «–». Получим следующее уравнение:

-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:

-x – 1 – 2x + 4 + x + 3 = 2x – 6

-4x = -12

x = 3.

Полученный ответ не входит в рассматриваемый интервал, поэтому в окончательный ответ писать его не надо.

II интервал [-3; -1). На этом интервале в таблице стоят знаки «–», «–», «+». Именно так и раскрываем модули исходного уравнения:

-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Упростим, раскрыв при этом скобки:

-x – 1 – 2x + 4 – x – 3 = 2x – 6. Приведем в полученном уравнении подобные:

-5x = -6

x = 6/5. Полученное число не принадлежит рассматриваемому интервалу, поэтому оно не является корнем исходного уравнения.

III интервал [-1; 2). Раскрываем модули исходного уравнения с теми знаками, которые стоят на рисунке в третьей колонке. Получаем:

(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Избавимся от скобок, перенесем слагаемые, содержащие переменную x в левую часть уравнения, а не содержащие x в правую. Будем иметь:

x + 1 – 2x + 4 – x – 3 = 2x – 6

-4x = -8

x = 2.

В рассматриваемый интервал число 2 не входит.

IV интервал [2; +∞). Все модули раскрываем со знаком «+». Получим:

(x + 1) + (2x – 4) – (x + 3) = 2x – 6.

x + 1 + 2x – 4 – x – 3 = 2x – 6

0 = 0.

После преобразований уравнение превратилось в верное равенство. Это говорит о том, что любое число из рассматриваемого интервала будет являться решением исходного уравнения. Значит ответом, как на этом интервале, так и во всем уравнении является множество чисел, удовлетворяющих условию x ≥ 2.

Ответ: x ≥ 2.

Метод интервалов хоть и является универсальным методом решения уравнений с модулем, его применение не всегда оправдано. Порой решить уравнение выходит гораздо быстрее, используя, например, определение модуля или какие-то другие методы.

blog.tutoronline.ru

Неравенства с модулем, примеры решений

Схема решения простейших неравенств:

1) неравенство вида при равносильно системе ; при неравенство решений не имеет.

2) неравенство , при равносильно совокупности неравенств

при решением неравенства является множество ; – вся числовая ось, то есть .

При решении неравенства вида или , обе части неравенства возводят в квадрат. Если неравенство содержит несколько выражений под знаком модуля, то применяется метод интервалов.

Примеры

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Неравенство с несколькими модулями | Подготовка к ЕГЭ по математике

Неравенства с модулями. Видеоурок. Алгебра 11 Класс

Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.

Неравенства с модулем

Уравнения и неравенства с модулями

Метод интервалов – универсальный метод решения неравенств с модулем

Неравенства с модулем, примеры решений

Примеры

Добавить комментарий Отменить ответ