Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )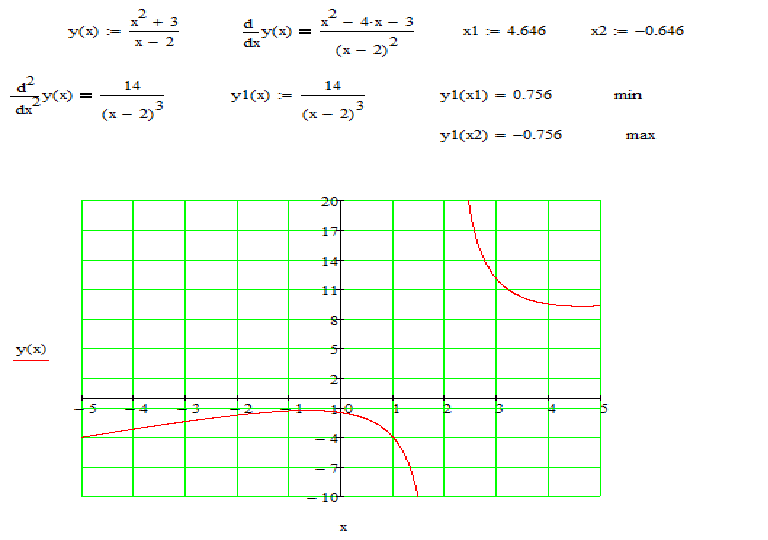
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Постройте график функции y 3x 2 6x. Постройте график функции y=

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x).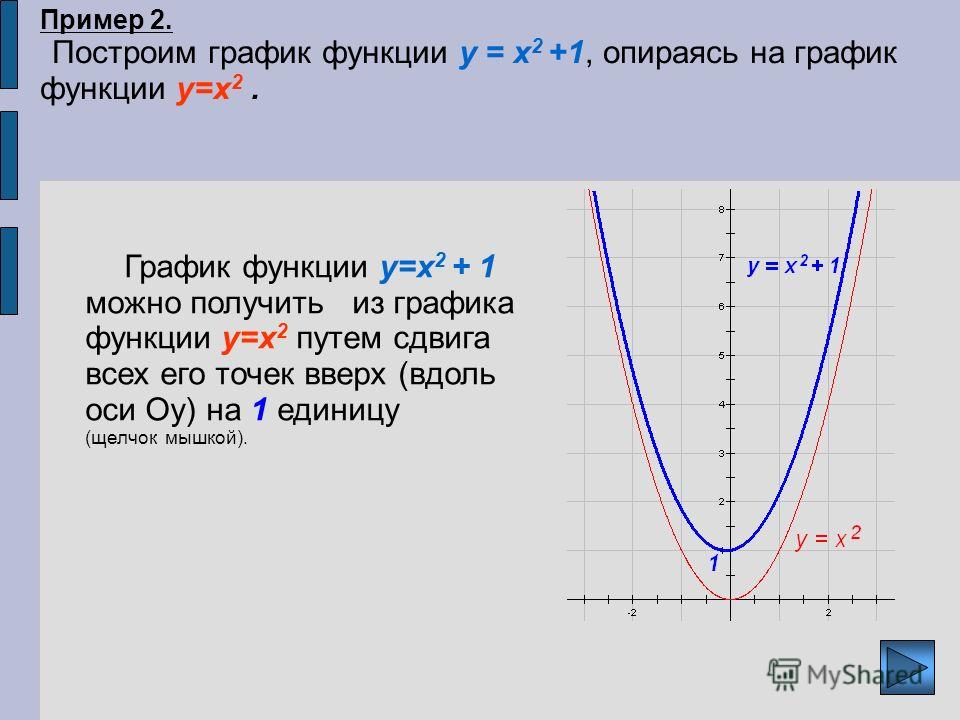 Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).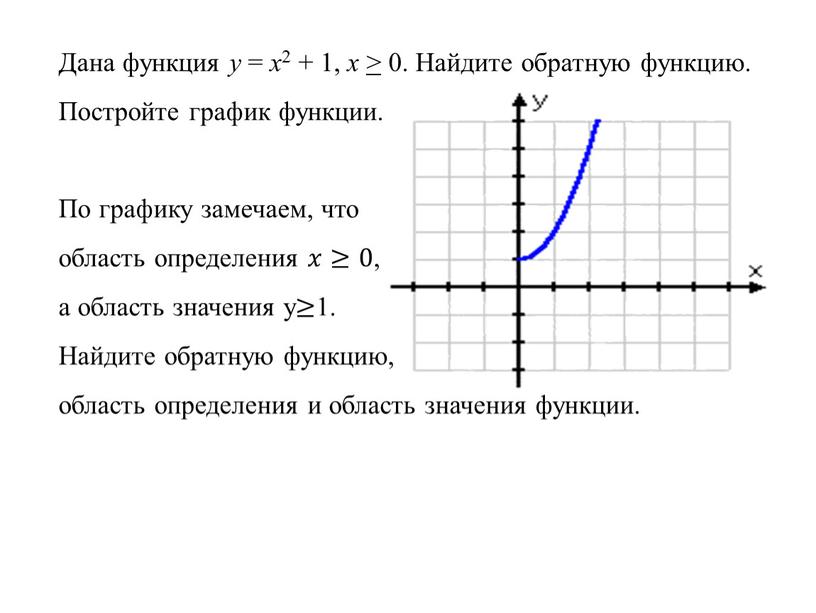

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Разберем как строить график с модулем.

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=— (x-3)-(— (x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+ (x-3)-(+ (x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }

y x 2 2x 3 график функции

Вы искали y x 2 2x 3 график функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и график функции y x 2 2x 3, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y x 2 2x 3 график функции».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как y x 2 2x 3 график функции,график функции y x 2 2x 3,график функции y x2 2x 3,построить график функции y x2 2x 3,постройте график функции y x 2 2x 3,постройте график функции y x 2 3x 2,постройте график функции y x 2x 3,постройте график функции y x2 2x 3. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и y x 2 2x 3 график функции. Просто введите задачу в окошко и нажмите «решить» здесь (например, график функции y x2 2x 3).

Где можно решить любую задачу по математике, а так же y x 2 2x 3 график функции Онлайн?

Решить задачу y x 2 2x 3 график функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Графические линейные функции | Колледж алгебры

Результаты обучения

• Построение линейной функции путем нанесения точек
• Постройте линейную функцию, используя наклон и точку пересечения оси Y
• Построение линейной функции с помощью преобразований

Ранее мы видели, что график линейной функции представляет собой прямую линию. Мы также смогли увидеть точки функции, а также начальное значение на графике.

Есть три основных метода построения графиков линейных функций.Первый заключается в нанесении точек, а затем в проведении линии через точки. Второй — с использованием точки пересечения y- и наклона. Третий — применение преобразований к тождественной функции [латекс] f \ left (x \ right) = x [/ latex].

Построение графика функции по точкам

Чтобы найти точки функции, мы можем выбрать входные значения, оценить функцию по этим входным значениям и вычислить выходные значения. Входные значения и соответствующие выходные значения образуют пары координат.Затем мы наносим пары координат на сетку. В общем, мы должны оценивать функцию как минимум на двух входах, чтобы найти как минимум две точки на графике функции. Например, учитывая функцию [латекс] f \ left (x \ right) = 2x [/ latex], мы можем использовать входные значения 1 и 2. Оценка функции для входного значения 1 дает выходное значение 2, которое представлен точкой (1, 2). Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4).Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.

Как сделать: дана линейная функция, построить график с помощью точек.

1. Выберите минимум два входных значения.
2. Оцените функцию для каждого входного значения.
3. Используйте полученные выходные значения для определения пар координат.
4. Нанесите пары координат на сетку.
5. Проведите линию через точки.

Пример: построение графика по точкам

График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] путем нанесения точек.

Показать решение

Начните с выбора входных значений. Эта функция включает дробь со знаменателем 3, поэтому давайте выберем в качестве входных значений числа, кратные 3. Мы выберем 0, 3 и 6.

Оцените функцию для каждого входного значения и используйте выходное значение для определения пар координат.

[латекс] \ begin {array} {llllll} x = 0 & & f \ left (0 \ right) = — \ frac {2} {3} \ left (0 \ right) + 5 = 5 \ Rightarrow \ left ( 0,5 \ right) \\ x = 3 & & f \ left (3 \ right) = — \ frac {2} {3} \ left (3 \ right) + 5 = 3 \ Rightarrow \ left (3,3 \ вправо) \\ x = 6 & & f \ left (6 \ right) = — \ frac {2} {3} \ left (6 \ right) + 5 = 1 \ Rightarrow \ left (6,1 \ right) \ end {array} [/ latex]

Постройте пары координат и проведите линию через точки.На приведенном ниже графике показана функция [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex].

Анализ решения

График функции представляет собой линию, как и ожидалось для линейной функции. Кроме того, график имеет наклон вниз, что указывает на отрицательный наклон. Это также ожидается от отрицательной постоянной скорости изменения уравнения для функции.

Попробуйте

График [латекс] f \ left (x \ right) = — \ frac {3} {4} x + 6 [/ latex] путем нанесения точек.

Показать решение

Построение линейной функции с использованием точки пересечения по оси Y и наклона

Другой способ построения графиков линейных функций — использование конкретных характеристик функции, а не точек.Первая характеристика — это точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти точку пересечения y- , мы можем установить [latex] x = 0 [/ latex] в уравнении.

Другой характеристикой линейной функции является ее наклон м , который является мерой ее крутизны. Напомним, что наклон — это скорость изменения функции. Наклон линейной функции равен отношению изменения выходов к изменению входов.Другой способ думать о наклоне — разделить вертикальную разницу или подъем между любыми двумя точками на горизонтальную разницу или бег. Наклон линейной функции будет одинаковым между любыми двумя точками.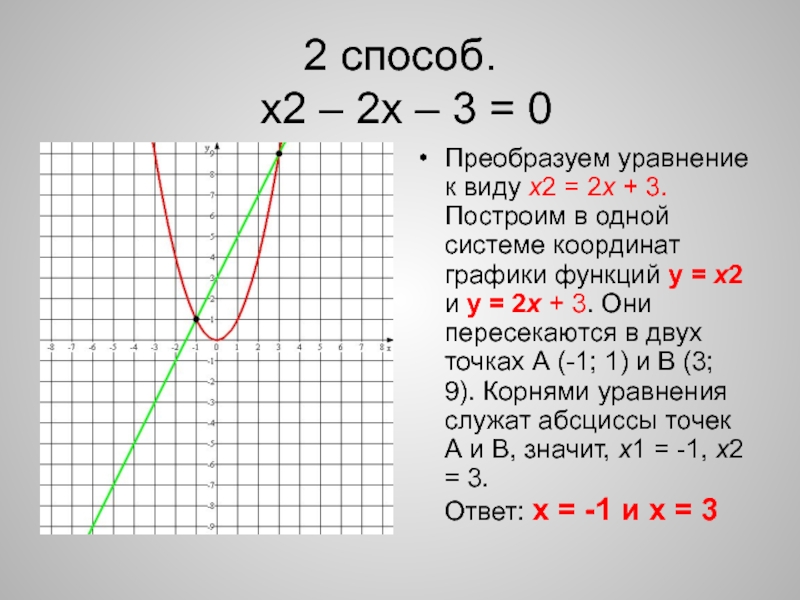 Мы столкнулись как с точкой пересечения y-, так и с наклоном в линейных функциях.

Рассмотрим следующую функцию.

[латекс] f \ left (x \ right) = \ frac {1} {2} x + 1 [/ latex]

Уклон [латекс] \ frac {1} {2} [/ latex]. Поскольку наклон положительный, мы знаем, что график будет наклоняться вверх слева направо.Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и пересечение y . Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Начиная с нашего интервала y (0, 1) , мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1.Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано ниже.

Общее примечание: графическая интерпретация линейной функции

В уравнении [латекс] f \ left (x \ right) = mx + b [/ latex]

• b — пересечение графика y и указывает точку (0, b ), в которой график пересекает ось y .
• м — это наклон линии, указывающий вертикальное смещение (подъем) и горизонтальное смещение (пробег) между каждой последовательной парой точек.Напомним формулу наклона:

[латекс] m = \ frac {\ text {изменение на выходе (подъем)}} {\ text {изменение на входе (запуск)}} = \ frac {\ Delta y} {\ Delta x} = \ frac { {y} _ {2} — {y} _ {1}} {{x} _ {2} — {x} _ {1}} [/ latex]

Вопросы и ответы

Все ли линейные функции имеют точки пересечения y ?

Да. Все линейные функции пересекают ось Y и, следовательно, имеют точки пересечения по оси Y. (Примечание: Вертикальная линия, параллельная оси y, не имеет точки пересечения оси y. Имейте в виду, что вертикальная линия — единственная линия, которая не является функцией.)

Практическое руководство. Получив уравнение для линейной функции, постройте график функции, используя точку пересечения

y и наклон.

1. Оцените функцию при нулевом входном значении, чтобы найти точку пересечения y-.
2. Определите уклон.
3. Постройте точку, представленную точкой пересечения y-.
4. Используйте [latex] \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить еще как минимум две точки на линии.
5. Проведите линию, проходящую через точки.

Пример: построение графика с использованием точки пересечения

y- и наклона

График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] с использованием точки пересечения y- и наклона.

Показать решение

Оцените функцию при x = 0, чтобы найти точку пересечения y-. Выходное значение, когда x = 0, равно 5, поэтому график пересечет ось y в точке (0, 5).

Согласно уравнению для функции, наклон линии составляет [латекс] — \ frac {2} {3} [/ latex].Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на [латекс] –2 [/ латекс] единиц, «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения y . От начального значения (0, 5) мы перемещаемся вниз на 2 единицы и вправо на 3 единицы. Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.

Анализ решения

График наклонен вниз слева направо, что означает, что он имеет отрицательный наклон, как и ожидалось.

Попробуйте

Найдите точку на графике, который мы нарисовали в примере: построение графика с использованием точки пересечения y и угла наклона, которая имеет отрицательное значение x .

Показать решение

Возможные ответы: [латекс] \ left (-3,7 \ right) [/ latex], [latex] \ left (-6,9 \ right) [/ latex] или [латекс] \ left (-9, 11 \ справа) [/ латекс].

Построение линейной функции с помощью преобразований

Другой вариант построения графиков — использовать преобразования для функции идентичности [latex] f \ left (x \ right) = x [/ latex].Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.

Вертикальное растяжение или сжатие

В уравнении [латекс] f \ left (x \ right) = mx [/ latex], m действует как вертикальное растяжение или сжатие функции идентичности. Когда м отрицательное, также имеется вертикальное отражение графика. Обратите внимание, что умножение уравнения [латекс] f \ left (x \ right) = x [/ latex] на m растягивает график f на коэффициент m единиц, если m > 1, и сжимает график f с коэффициентом м единиц, если 0 < м <1.Это означает, что чем больше абсолютное значение м , тем круче уклон.

Вертикальные растяжения, сжатия и отражения на функции [латекс] f \ left (x \ right) = x [/ latex].

Вертикальный сдвиг

В [latex] f \ left (x \ right) = mx + b [/ latex], b действует как вертикальный сдвиг , перемещая график вверх и вниз, не влияя на наклон линии. Обратите внимание, что добавление значения b к уравнению [latex] f \ left (x \ right) = x [/ latex] сдвигает график f всего на b единиц вверх, если b равно положительный и | b | единиц вниз, если значение b отрицательное.

Этот график иллюстрирует вертикальные сдвиги функции [латекс] f \ влево (x \ вправо) = x [/ латекс].

Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ определения различных типов линейных функций. Хотя это может быть не самый простой способ построить график функций такого типа, все же важно практиковать каждый метод.

Практическое руководство. Учитывая уравнение линейной функции, используйте преобразования, чтобы построить график линейной функции в виде [латекс] f \ left (x \ right) = mx + b [/ latex].

1. График [латекс] f \ left (x \ right) = x [/ latex].
2. Растянуть или сжать график по вертикали в м .
3. Сдвинуть график вверх или вниз b единиц.

Пример: построение графиков с использованием преобразований

График [латекс] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex] с использованием преобразований.

Показать решение

Уравнение для функции показывает, что [latex] m = \ frac {1} {2} [/ latex], поэтому функция идентичности сжимается по вертикали посредством [latex] \ frac {1} {2} [/ latex].Уравнение для функции также показывает, что [latex] b = -3 [/ latex], поэтому функция идентичности смещена по вертикали на 3 единицы.

Сначала изобразите функцию идентичности и покажите вертикальное сжатие.

Функция [latex] y = x [/ latex] сжата в [латекс] \ frac {1} {2} [/ latex] раз.

Затем покажите вертикальный сдвиг.

Функция [latex] y = \ frac {1} {2} x [/ latex] сдвинута на 3 единицы вниз.

Попробуйте

График [латекс] f \ left (x \ right) = 4 + 2x [/ latex], с использованием преобразований.

Показать решение

Вопросы и ответы

В примере: построение графиков с использованием преобразований, могли бы мы изобразить график, изменив порядок преобразований на противоположный?

Нет. Порядок преобразований соответствует порядку операций. Когда функция оценивается на заданном входе, соответствующий выход вычисляется в соответствии с порядком операций. Вот почему мы сначала выполнили сжатие. Например, следуя порядку операций, пусть на входе будет 2.

[латекс] \ begin {array} {l} f \ text {(2)} = \ frac {\ text {1}} {\ text {2}} \ text {(2)} — \ text {3} \ hfill \\ = \ text {1} — \ text {3} \ hfill \\ = — \ text {2} \ hfill \ end {array} [/ latex]

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Решите Свойства прямой y = 3x + 2 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

y- (3 * x +2) = 0

Шаг 1:

 
 Уравнение прямой 
 
 1.1 Решите y-3x-2 = 0 
 
 Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании). 
 
 «y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось. 
 
 В этой формуле: 
 
 y говорит нам, как далеко идет линия. 
 x говорит нам, как далеко вдоль 
 м находится наклон или градиент, т.е. насколько крутой является линия 
 b — это точка пересечения с Y i.е. где линия пересекает ось Y 
 
 Пересечения X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-3x-2 = 0 и вычислим ее свойства 
 
 График прямой линии: 
 
 
 Вычислите точку пересечения Y: 
 Обратите внимание, что когда x = 0, значение y равно 2 / 1, поэтому эта линия «обрезает» ось y в точке y = 2,00000
 y-intercept = 2/1 = 2,00000 
 Вычислите точку пересечения X: 
 Когда y = 0, значение x равно 2 / -3 Наша линия поэтому «срезает» ось x при x = -0.66667
 x-intercept = 2 / -3 = -0.66667 
 Вычислить наклон: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 2.000, а для x = 2.000 значение y равно 8.000. Таким образом, при изменении x на 2. 000 (изменение x иногда называют «RUN») мы получаем изменение на 8.000 — 2.000 = 6.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
 Наклон = 6.000 / 2.000 = 3.000 
 Геометрическая фигура: прямая 
 Наклон = 6.000 / 2.000 = 3.000
 пересечение по оси x = 2 / -3 = -0,66667
 пересечение по оси y = 2/1 = 2,00000
 Нахождение Обратная функция 
   Находка
 Обратная функция     (стр.
 3 из 7)  
  Разделы:   Определение
 / Инвертирование графика, обратная функция ?,
 Нахождение обратного, доказательство обратного 
 Обычный метод
 поиск обратного — это один из вариантов метода, который я собираюсь использовать ниже.Какой бы метод вы ни использовали, убедитесь, что вы выполняете точно такие же шаги в
 один и тот же порядок каждый раз, поэтому вы запомните эти шаги, когда получите
 к тесту.
  Найти обратное
 из  y  = 3  x  2. 
 Вот как процесс
 работ:
 Вот
 моя первоначальная функция:
 Сейчас
 Я попробую решить для « x  = «:
 Однажды
 У меня « x  знак равно
 Я заменю  x  и  y ;
 « y  = «- это
 обратный.
 Если вам нужно найти
 домен и диапазон,
 посмотрите на исходную функцию и ее график. Домен оригинала
 функция — это набор всех допустимых значений  x ;
 в этом случае функция была простым полиномом, поэтому область определения
 «все реальные числа». Диапазон исходной функции — весь  y  -значения
 вы передадите график; в этом случае прямая линия продолжается
 всегда в любом направлении, поэтому диапазон также представляет собой «все действительные числа».Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и
 диапазон от исходной функции.
 По графику,
 легко видеть, что эта функция не может иметь обратного,
 поскольку он нарушает тест горизонтальной линии:
 Обычно считается
 приемлемо для построения приведенного выше графика, проведите по нему горизонтальную линию,
 дважды пересекает график, а затем произнесите что-то вроде «Обратный
 этой функции не является функцией из-за горизонтальной линии
 Контрольная работа».Но некоторые учителя все равно хотят изучать алгебру. Быть уверенным
 чтобы уточнить у учителя, какой ответ будет приемлемым
 — и сделай это  перед  тестом! Авторские права
 Элизабет Стапель 2000-2011 Все права защищены
 Как это будет выглядеть
 когда я пытаюсь найти обратное алгебраически? Вертикаль
 Line Test говорит
 что у меня не может быть двух  и  с общим значением  x . То есть каждый  x  должен иметь УНИКАЛЬНЫЙ соответствующий  л  значение. Но посмотрите, что происходит, когда я пытаюсь найти « x  = «:
 Мой
 исходная функция:
 Решение
 для « x  = «:
 Ну я решил для « x  знак равно
 но я не получил УНИКАЛЬНЫЙ « x  знак равноВместо этого я показал, что любое заданное значение  x  фактически будет соответствовать двум различным значениям  y ,
 один от плюса к квадратному корню, а другой от
 «минус».
 Каждый раз, когда вы придумываете
 знак «», вы можете быть уверены, что обратное не
 функция.
 Единственная разница
 между этой функцией и предыдущей состоит в том, что домен
 был ограничен только отрицательной половиной  x  — ось.Это ограничение делает график таким:
 Эта функция  будет  иметь обратное, что
 тоже функция. Практически каждый раз, когда они задают вам проблему, где
 они постарались ограничить домен, вы должны позаботиться
 с алгеброй и нарисуйте красивую картинку, потому что, вероятно, обратное
 — это функция, но, вероятно, потребуются дополнительные усилия, чтобы показать это.В данном случае, поскольку размер домена  x   < 0 и
 диапазон (из графика) равен 1  <  y ,
 то обратный будет иметь область 1  <  x  и
 диапазон  y   < 0. Вот
 как выглядит алгебра:
 В
 исходная функция:
 Решить
 для « x  = «:
 Автор
 выясняя область и диапазон обратного, я знаю, что
 Я должен выбрать знак минуса для квадратного корня:
 Сейчас
 Я заменю  x  и  y ; 
 новый » г  = «- это
 обратный:
 (« x  >  1 «ограничение
 исходит из того, что  x  находится внутри квадратного корня. )
 Так  обратное —  y  =  sqrt  ( x  1),  x  >  1,
 и эта инверсия также является функцией. 
 Вот график:
 << Предыдущая
 Вверх |  1
 | 2 | 3 | 4 |
 5 | 6 | 7  | Вернуться к указателю Далее
 >>
 Цитируйте эту статью
 как:
 Стапель, Елизавета.«Нахождение обратной функции».  Пурпурная математика .
 Доступно по номеру 
  https://www.purplemath.com/modules/invrsfcn3.htm .
 Проверено [Дата] [Месяц] 2016 г. 
 Смешанный обзор с пятью вопросами 1. Что это за функция: y = 3x-2 2. Что такое пересечение оси y в приведенном выше уравнении? 3.Решите относительно x: 16 = 5x Что такое. 
 Презентация на тему: «Смешанный обзор из пяти вопросов 1. Что это за функция: y = 3x-2 2. Что такое пересечение оси y в приведенном выше уравнении? 3. Решить для x: 16 = 5x + 1 4. Что такое the. »- стенограмма презентации: 
 ins [data-ad-slot = «4502451947»] {display: none! important;}}
 @media (max-width: 1000 пикселей) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
 @media (max-width: 1000 пикселей) {# place_14 {width: 250px;}}
 @media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
 ]]>
 1 
 Смешанное рассмотрение по пяти вопросам 1. Что это за функция: y = 3x-2 2. Какова точка пересечения оси y в приведенном выше уравнении? 3. Решите относительно x: 16 = 5x + 1 4. Каков наклон этого уравнения: y = ½ x + 9 5. Запишите это уравнение в обозначении функции: y = 6p — 7
 2 
 Смешанный обзор из пяти вопросов — ключ 1. Линейный 2. -2 3,16 = 5x + 1 15 = 5x 3 = x или -1 -1 5 5 x = 3 15 = 5x 4.½ 5. f (p) = 6p — 7
 3 
 Параболы: природа или дизайнерские идеи?
 4 
 Можете ли вы найти параболические формы?
 5
 6
 7
 8
 9
 10
 11
 12
 13
 14 
 Стандартные и важные вопросы MM1A1b: Постройте график основных функций f (x) = x n Существенный вопрос: можете ли вы идентифицировать квадратичную функцию по ее компонентам?
 15 
 Сможете ли вы предсказать, как это будет выглядеть, всего за 2 очка? Наклон постоянный? Если нет, то что это? Он указывает вверх или вниз? Какая форма? Чем он отличается от линейного графика?
 16 
 Что такое парабола? КЛЮЧЕВОЕ ПРИМЕЧАНИЕ: Парабола — это U-образный график. Он может быть направлен вверх (положительный наклон) или направлен вниз (отрицательный наклон).
 17 
 Быстрый взгляд на уравнение Самая основная квадратная формула — y = x 2, она называется родительским графом. Это означает, что U-образная форма (парабола) повернута вверх, а вершина находится в точке (0,0).
 18 
 Это квадратный родительский граф. Обратите внимание, где расположена вершина (0,0). Уравнение для этого графа Is y = x 2 Помните: вершина — это то место, где квадратичный граф поворачивается и меняет направление.Это еще называют критической точкой.
 19 
 Как выглядит диаграмма ввода / вывода для этого родительского графика? xy -24 1 00 11 24 Значимые объекты Что вы замечаете? Повторяются ли значения x? Повторяются ли значения y? Как вы называете такое изображение? Вы видите вершину? Что вы заметили в наклоне?
 20 
 Что изменилось? Вершина переместилась! Он поднялся на одну единицу! Когда здесь меняется число, это показывает, как график движется вверх и вниз.
 21 год 
 Этот квадратичный график сдвинулся вниз на одну единицу. Новая вершина: (0, -1)
 22 
 Назовите эту смену!
 23 
 Назовите эту смену!
 24 
 Сдвиг вверх и вниз по оси y называется вертикальным смещением.НО вы также можете сдвигать влево и вправо по оси x? Как это называется?
 25 
 Это называется сдвигом по горизонтали (влево / вправо). Родительский граф сдвинулся влево на 1 единицу. Новое уравнение будет выглядеть так: y = (x + 1) 2 Горизонтальное перемещение всегда заключено в круглые скобки с x. Однако у этих уравнений есть одна хитрость — вы двигаетесь в противоположном направлении! Новая вершина: (-1,0)
 26 
 Назовите эту смену! Что это за? Что такое новая вершина?
 27 
 Назовите эту смену! Что это за? Что такое новая вершина?
 28 год 
 Этот график сдвигается в обе стороны! Что такое вертикальный сдвиг? Что такое сдвиг по горизонтали? Что такое вершина?
 29 
 Как насчет этого? Что такое вертикальный сдвиг? Что такое сдвиг по горизонтали? Что такое вершина? Обратите внимание, как уравнение соответствует вершине, за исключением противоположного знака внутри скобок?
 30 
 Определение наклона ЭТО ФАКТ: в родительском графе вершина находится в точке (0,0), а наклон ПЕРВЫХ точек отражения равен 1.Остальная часть наклона ПЕРЕМЕННАЯ или МЕНЯЮЩАЯСЯ Наклон = 1 Наклон = 3 Наклон = 5 Наклон = подъем / спуск =
 31 год 
 Что будет, если уклон больше 1? Slope = 4 Как он соотносится с родительским графом?
 32 
 Наклон = -4 Что случилось?
 33 
 Наклон = ½ Как это соотносится с родительским графом?
 34 
 Наклон = -½ Как это соотносится с последним графиком?
 35 год 
 Части квадратного уравнения y- пересечение вертикального сдвига = _2__ Наклон = __2_ Горизонтальный сдвиг = _2__ (противоположно значению вершины x) Вершину можно найти в точке (2, 2). Когда наклон больше 1, график становится…
 36 
 Графический организатор: части квадратного уравнения _________ _______shift _______ shift (Напротив __ значения вершины) Вершину можно найти в (__, __) ______
 37 
 Части квадратного уравнения смещение по оси y по вертикали = ___ Наклон = ___ Сдвиг по горизонтали = ___ (противоположно значению вершины x) Вершину можно найти в (__, __)
 38 
 Части квадратного уравнения y- перехват вертикального сдвига = ___ Наклон = ___ Горизонтальный сдвиг = ___ (Напротив значения вершины x) Вершину можно найти в (__, __) Когда наклон меньше 1, график становится…
 39 
 Части квадратного уравнения y- перехват вертикального сдвига = ___ Наклон = ___ Горизонтальный сдвиг = ___ (противоположно значению вершины x) Вершину можно найти в (__, __) Имеет ли значение, насколько велики числа?
 40 
 Для этого обратитесь к партнеру! Направления: Определите a) наклон b) точку пересечения y c) вершину и график 1 из них!
 41 год 
 Задача партнера — Ключевые направления: Определите a) наклон b) точку пересечения y c) вершину и график 1 из них! Бывший.у = х 2 -2
 42 
 Викторина с графическими квадратичными функциями 1-8. Выберите правило функции, соответствующее графику. Поместите письмо в бланк. 9) Какой из приведенных выше графиков является родительским для квадратичных функций? #______ 10) Сколько графиков имеют отрицательный наклон? ____
 43 год 
 Графики квадратичных функций викторины — ключевые слова 1-8. 2-6 (2) — 5 = -12-12-5 = -29 (2, -29)
 1.Нарисуйте координатную плоскость.
 2. Постройте координатные точки.
 3. Затем нарисуйте график, соединив точки плавной кривой.
 На графике мы можем наблюдать вершину ( x ,  y ) = (-1, — 2)
 Пересечения параболы  x  не существует.
  y  — точка пересечения (0, -5).
 Как построить график y 3x 2 с использованием математики класса 11 формы пересечения наклона CBSE 
  Подсказка:  В данном вопросе нам дано уравнение с двумя переменными.Мы должны построить линию на графике, который образуется из этого уравнения. Для этого мы сначала преобразуем данное уравнение в форму с пересечением наклона. Отсюда мы узнаем значение наклона и точку пересечения по оси Y. Мы наносим точку в точке пересечения оси ординат. Оттуда мы перемещаемся вверх или вниз, а затем вправо или влево в зависимости от коэффициента перед \ [x \] и \ [y \] соответственно, и соединяем точки, чтобы сформировать линию.
  Используемая формула:  
 Стандартная форма линейного уравнения в форме пересечения наклона: 
 \ [y = mx + b \]
  Полный пошаговый ответ:  
 Данное уравнение имеет вид \ [y = 3х — 2 \].
 Ясно, что это уравнение имеет тип \ [y = mx + b \], следовательно, оно уже находится в форме углового пересечения. 
 Таким образом, наклон \ [m = 3 \] 
 А, пересечение по оси Y \ [b = — 2 \] 
 Следовательно, одна точка на графике может быть принята как \ [\ left ({0, — 2} \ right ) \]. 
 Теперь, 
 \ [m = \ dfrac {{коэффициент {\ text {}} при {\ text {}} x}} {{коэффициент {\ text {}} при {\ text {}} y}} \] 
 Следовательно, мы перемещаемся вверх на \ [1 \] (коэффициент при \ [y \]) точках, а затем перемещаемся вправо на \ [3 \] (коэффициент при \ [x \]) пунктах. 
 Таким образом, вторая точка — это \ [\ left ({0 + 1, — 2 + 3} \ right) = \ left ({1,1} \ right) \].
 Теперь мы наносим две точки и соединяем их, и у нас есть линия. 
  Дополнительная информация:  
 Мы взяли одну точку в качестве точки пересечения по оси Y, потому что знаем, что точка пересечения по оси Y означает, что точка лежит на оси x. 
 Значение уклона делится на подъем, т.е. \ [\ dfrac {{коэффициент {\ text {}} при {\ text {}} x}} {{коэффициент {\ text {}} при {\ text { }} y}} \]. 
 Наклон также можно определить как $ \ dfrac {\ text {(Изменение по y)}} {\ text {(Изменение по x)}} $.
  Примечание:  
 В этом вопросе нам нужно знать только одно — как получить точки для графика, а затем как нанести точки на график.Затем мы просто вычисляем значения из уравнения, наносим их на график, соединяем точки на графике и получаем линию, которая отмечает требуемое уравнение. 
 Как отразить график через ось x, ось y или начало координат? 
 Это письмо недавно пришло от читателя Стюарта:
 Можете ли вы объяснить принципы построения графика, в котором  y  = —  f  ( x ) является отражением графика  y  =  f  ( x ) по оси  x  и график  y  =  f  (-  x ) отражение графика  y  =  f  ( x ) по оси  y- ?
 Спасибо
 Мой ответ 
 Привет Стюарт
 Давайте посмотрим, что это означает на примере.
 Пусть  f  ( x ) = 3  x  + 2
 Если вы не уверены, как это выглядит, вы можете построить график с помощью этого средства построения графиков.
 Вы увидите, что это прямая линия, наклон 3 (положительный, т. Е. Идет вверх по мере того, как мы идем слева направо) и  y  — пересечение 2.
 Теперь рассмотрим —  f  ( x ).
 Это дает нам
 —  f  ( x )  =  −3  x  — 2
 Наша новая линия имеет отрицательный наклон (он идет вниз при сканировании слева направо) и проходит через −2 на оси  y .
 Когда вы строите график двух линий на одной и той же оси, это выглядит так:
 Обратите внимание, что если вы отразите синий график ( y  = 3  x  + 2) по оси  x , вы получите зеленый график ( y  = −3  x  — 2) (как показано красными стрелками).
 Что мы сделали, так это взяли каждое значение  y  и перевернули их вверх дном (это эффект  минус  спереди).
 Теперь для 
 f  (-  x )
 Аналогично сделаем  f  (-  x ).
 Так как  f  ( x ) = 3  x  + 2, то
  f  ( −x ) = −3  x  + 2 (замените каждое « x » на « −x »).
 Теперь, построив график на тех же осях, мы имеем:
 Обратите внимание, что эффект «минуса» в  f  ( −x ) заключается в отражении синей исходной линии ( y  = 3  x  + 2) по оси  y , и мы получаем зеленая линия ( y  = −3  x  + 2).Зеленая линия также проходит через 2 на оси  y .
 Дополнительный пример 
 Вот пример использования кубического графа.
  Синий график:   f  ( x ) =  x   3  — 3  x   2  +  x  — 2
  Отражение по оси x (зеленый):  —  f  ( x ) = —  x   3  + 3  x   2  —  x  + 2
 Теперь отразим в оси ординат.
  Синий график:   f  ( x ) =  x   3  — 3  x   2  +  x  — 2
  Отражение по оси Y (зеленый):   f  ( −x ) =  −x   3  — 3  x   2  —  x  — 2
 Четные и нечетные функции 
 Мы действительно должны упомянуть  четные и нечетные функции , прежде чем покинуть эту тему.
 Для каждого из приведенных выше примеров отражения на оси  x  или  y  давали график, который был  разным .Но иногда отражение такое же, как и на исходном графике. Мы говорим, что отражение «отображается на» оригинале.
  Четные функции 
 Функция  даже  имеет свойство  f  ( −x ) =  f  ( x ). То есть, если мы отразим четную функцию по оси  y , она будет выглядеть точно так же, как оригинал.
 Пример четной функции:  f  ( x ) =  x   4 -29  x   2  + 100
 Вышеупомянутая четная функция эквивалентна:
  f  ( x ) = ( x +  5) ( x  + 2) ( x -2) ( x —  5)
 Обратите внимание: если мы отразим график по оси  y , мы получим тот же график (или мы могли бы сказать, что он «отображается на себя»).
  Нечетные функции 
 Нечетная функция   имеет свойство  f  ( −x ) =  −f  ( x ).
 На этот раз, если мы отразим нашу функцию в , как  — ось  x , так и ось  y , и если она выглядит точно так же, как оригинал, то у нас будет нечетная функция.
 Этот вид симметрии называется симметрией происхождения  . Нечетная функция либо проходит через начало координат (0, 0), либо отражается через начало координат.
 Пример нечетной функции:  f  ( x ) =  x   3  — 9  x 
 Вышеупомянутая нечетная функция эквивалентна:
  f  ( x ) =  x  ( x +  3) ( x  — 3)
 Обратите внимание: если мы отразим график по оси  x , а затем по оси  y , мы получим тот же график.
 Другие примеры четных и нечетных функций 
 На этой странице есть еще несколько примеров: Четные и нечетные функции
 Знание о четных и нечетных функциях очень полезно при изучении рядов Фурье.