Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x)<0 (знак неравенства может быть использован любой другой, например, ≤, > или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
- произведение линейных двучленов с коэффициентом 1 при переменной х;
- произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
(x+3)·(x2−x+1)·(x+2)3≥0,
(x-2)·(x+5)x+3>0 ,
(x−5)·(x+5)≤0,
(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
zaochnik.com
Неравенства методом интервалов
Рассмотрим, как решать неравенства методом интервалов, на конкретных примерах.
Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:
Полученные точки отмечаем на числовой прямой:
Для проверки знака берем 0 (желательно на числовой прямой отметить взятую точку, чтобы потом не забыть, куда ставить знак). Подставляем 0 в последнее неравенство: (2∙0-14)(5∙0+25)= -14∙25, то есть (-)∙(+)= -. Таким образом, в промежуток, из которого взяли нуль, ставим знак «-«, остальные знаки чередуем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.
Ответ:
Приравниваем к нулю левую часть:
Полученные точки отмечаем на числовой прямой:
Для проверки знака берем 0 и подставляем его в последнее неравенство. По знакам получаем:
В промежуток, которому принадлежит 0, ставим «+», остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≤0, в ответ выбираем промежутки со знаком «-«. (Не забываем, когда точки закрашенные, а когда — выколотые. Те точки, в которых знаменатель обращается в нуль, выколотые всегда).
Ответ:
Приравниваем к нулю левую часть:
По теореме, обратной теореме Виета
Полученные точки отмечаем на числовой прямой:
Для определения знака берем 0 и подставляем его в последнее неравенство. Получает (-)/(-)=(+). Остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.
Ответ:
Переносим все слагаемые в левую часть, приводим к наименьшему общему знаменателю и упрощаем:
После упрощения решаем неравенство методом интервалов.
Приравниваем к нулю левую часть:
Точек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:
Для проверки берем нуль. Подставляя его в последнее неравенство, получаем «+». На другом интервале — «-«. Нам нужен интервал с «-«.
Ответ:
Как решать более сложные неравенства методом интервалов, рассмотрим в следующий раз.
www.uznateshe.ru
Решение квадратных неравенств. Метод интервалов. Видеоурок. Алгебра 9 Класс
В течение какого времени мяч, брошенный вверх с известной начальной скоростью, будет находиться выше стенки заданной высоты (см. рис. 1)?
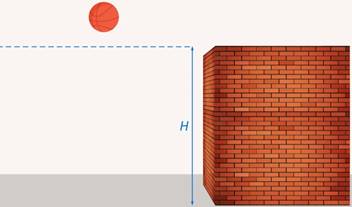
Рис. 1. Мяч находится выше стенки заданной высоты
Из физики мы знаем, что на мяч будет действовать только сила тяжести, т. е. он будет двигаться с ускорением свободного падения 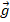 , которое будет замедлять его при движении вверх и разгонять при падении.
, которое будет замедлять его при движении вверх и разгонять при падении.
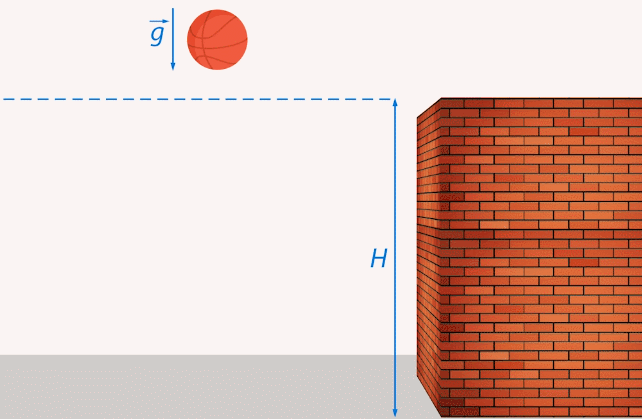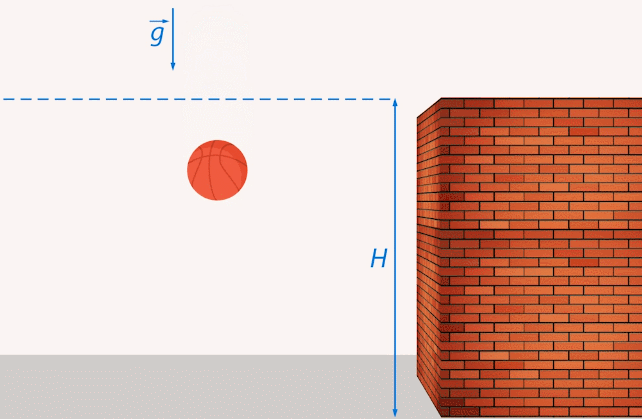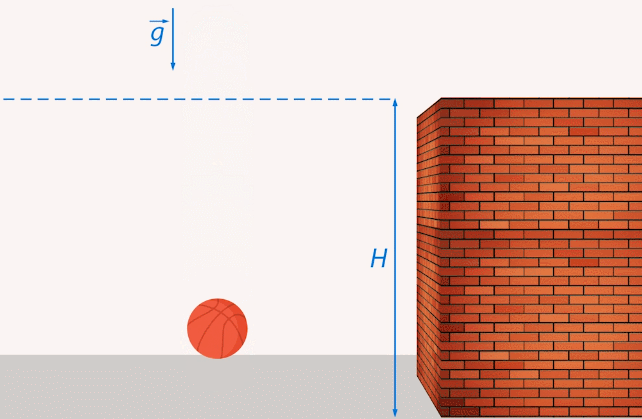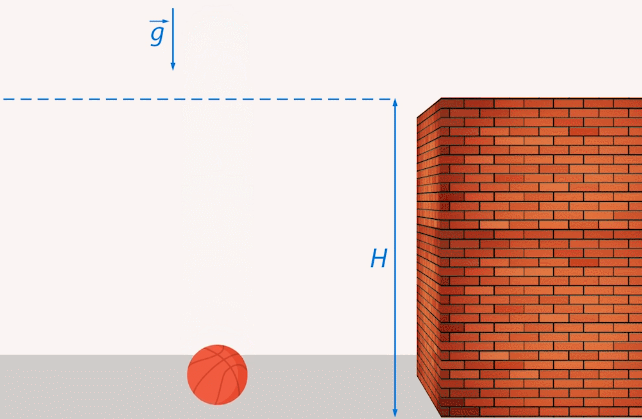
Рис. 2. Мяч двигается с ускорением свободного падения 
Можем записать формулу для перемещения при равноускоренном движении:

Знак минус появляется из-за того, что скорость и ускорение тела направлены в разные стороны (см. рис. 3).

Рис. 3. Скорость и ускорение тела направлены в разные стороны
Поскольку нас интересует, когда мяч будет находиться выше стенки высоты  , то нам нужно решить неравенство:
, то нам нужно решить неравенство:

В этом неравенстве мы знаем величины 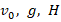 . Т. е. мы получили квадратное неравенство относительно переменной
. Т. е. мы получили квадратное неравенство относительно переменной 
Мы уже знаем, как решать задачи, математической моделью которых является линейное неравенство. Но большинство зависимостей носят более сложный, нелинейный характер. И наша задача – получить удобный инструмент, который позволит решать нелинейные неравенства.
Начнем мы именно с квадратных неравенств, т. к. они – самые простые примеры нелинейных неравенств. И вот почему.
Линейное неравенство имеет стандартный вид:

Если мы перемножим два линейных неравенства  и
и 

Параллельно мы получили идею решения квадратных неравенств – разложить многочлен в левой части на произведение линейных множителей (если это возможно).
Давайте рассмотрим на примерах, как решить квадратное неравенство, используя разложение на множители.
Пример 1. Решить неравенство:
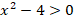
Решение.
Разложим на множители левую часть, используя формулу сокращенного умножения:
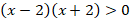
Произведение 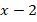
 больше нуля, т. е. положительно. Когда произведение двух множителей положительно? Либо когда они оба положительны, либо когда они оба отрицательны. Т. е.
больше нуля, т. е. положительно. Когда произведение двух множителей положительно? Либо когда они оба положительны, либо когда они оба отрицательны. Т. е.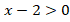 и
и  или же:
или же: 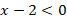 и
и 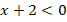 .
.Перепишем на математическом языке: союз «и» – это система условий, «или» – это совокупность. Получим:
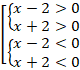
Итак, мы свели решение квадратного неравенства к решению систем и совокупностей линейных неравенств. А это мы уже умеем делать. Да, выглядит это, может, и сложно, но это лишь форма записи. Ничего сложного в решении нет – нужно просто действовать по известному нам алгоритму.
Решим первую систему:
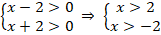
Отметим решение неравенств на оси. Заштриховав соответствующие области, видим, что решение данной системы (см. рис. 4):


Рис. 4. Иллюстрация к примеру 1
Решим вторую систему:

Заштриховав соответствующие области, получим решение системы (см. рис. 5):


Рис. 5. Иллюстрация к примеру 1
Осталась совокупность:

Отметив эти области на оси, видим, что они не пересекаются. Т. е. решением исходного квадратного неравенства будет объединение двух интервалов (см. рис. 6):
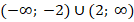

Рис. 6. Иллюстрация к примеру 1
Ответ: 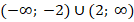 .
.
Пример 2. Решить неравенство:
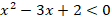
Решение.
Для разложения на множители этого квадратного трехчлена найдем его корни, решив соответствующее квадратное уравнение:  .
.
Откуда:
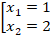
Можем разложить квадратный трехчлен на множители по формуле:

Тогда:

Неравенство примет эквивалентный вид:
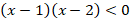
Произведение отрицательно, значит, один из множителей должен быть отрицательным, другой – положительным. Как и в предыдущем примере, получаем совокупность систем линейных неравенств, где в первом системе первый множитель – положительный, а второй – отрицательный, а во второй системе – наоборот:
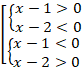
Решая системы, видим, что первая система имеет решение 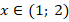 (см. рис. 7):
(см. рис. 7):
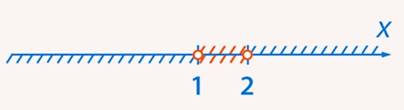
Рис. 7. Иллюстрация к примеру 2
Вторая система не имеет решений, т. к. заштрихованные области не пересекаются (см. рис. 8).

Рис. 8. Иллюстрация к примеру 2
Таким образом, решением совокупности, а значит, и исходного квадратного неравенства будет интервал (см. рис. 9):
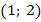
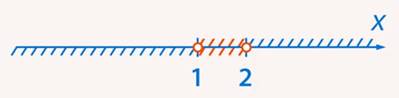
Рис. 9. Иллюстрация к примеру 2
Ответ: 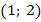 .
.
Конечно, можно решать квадратные неравенства таким способом. Но полная запись решения получается довольно громоздкой. Можно ли как-то ускорить процесс решения? Да. И сейчас мы разберем, как именно.
Обратим внимание, что решения рассмотренных неравенств – это интервалы, концы которых являются корнями соответствующего квадратного уравнения:
Неравенство 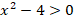 , его решение:
, его решение: 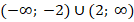 , где точки
, где точки 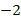 и
и 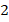 являются корнями квадратного уравнения
являются корнями квадратного уравнения 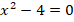 .
.
Неравенство 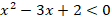 , его решение:
, его решение: 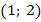 , где точки
, где точки 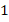 и
и 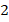 являются корнями уравнения
являются корнями уравнения  .
.
Естественно, это не совпадение. Любая функция меняет свой знак только при переходе через 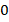 (или в точках, в которых у нее возникает разрыв из-за ОДЗ, но в квадратных неравенствах мы об этом можем не беспокоиться: ОДЗ – множество всех действительных чисел).
(или в точках, в которых у нее возникает разрыв из-за ОДЗ, но в квадратных неравенствах мы об этом можем не беспокоиться: ОДЗ – множество всех действительных чисел).
Если представить квадратный трехчлен в виде произведения линейных множителей: , то его нули – это нули каждой из скобок (произведение равно
, то его нули – это нули каждой из скобок (произведение равно 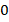 тогда и только тогда, когда хотя бы один из множителей равен
тогда и только тогда, когда хотя бы один из множителей равен 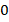 ):
):
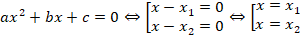
Значит, смена знака левой части будет происходить только в нулях линейных множителей. В случае квадратного трехчлена это и будут корни соответствующего квадратного уравнения (см. рис. 10).
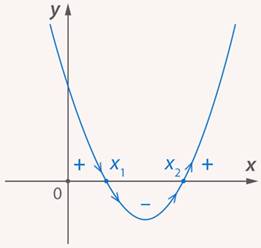
Рис. 10. Смена знака квадратного трехчлена происходит только в корнях соответствующего квадратного уравнения
Так вот, чтобы не записывать все эти системы и совокупности неравенств, для решения квадратного неравенства достаточно:
1. решить соответствующее квадратное уравнение;
2.  
interneturok.ru
Решение неравенств методом интервалов
 Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.
Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.
Метод интервалов
Пусть заданное неравенство имеет вид:  Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Во-первых, на числовую ось наносят точки  разбивающие ее на промежутки, в которых выражение
разбивающие ее на промежутки, в которых выражение 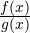 определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений
определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений 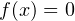 и
и  Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Во-вторых, определяют и отмечают на числовой оси знак выражения 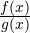 для значении
для значении 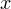 , принадлежащих каждому из полученных промежутков. Если функции
, принадлежащих каждому из полученных промежутков. Если функции 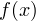 и
и 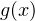 являются многочленами и не содержат множителей вида
являются многочленами и не содержат множителей вида 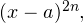 где
где 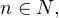 то достаточно определить знак функции
то достаточно определить знак функции 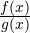 в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
Если же в числителе или знаменателе дроби 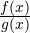 имеется множитель вида
имеется множитель вида 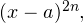 где
где 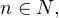 то непосредственной проверкой выясняют, удовлетворяет ли значение
то непосредственной проверкой выясняют, удовлетворяет ли значение  заданному неравенству.
заданному неравенству.
Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби  в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие
в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие  Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
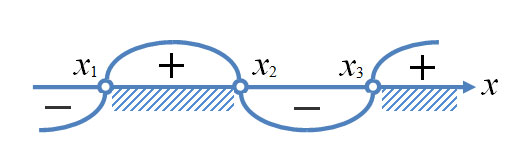
Общий вид прямой знаков в методе интервалов
Примеры решения неравенств методом интервалов
![Rendered by QuickLaTeX.com \[ \frac{1}{x^2-5x+6}\leqslant\frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-68fdc2b101fa2fb67343493c7316f5b7_l3.png)
Решение. Упрощаем неравенство путем равносильных преобразований:
При умножении или делении обеих частей неравенства на отрицательное число, меняется знак неравенства!
![Rendered by QuickLaTeX.com \[ \frac{1}{x^2-5x+6}-\frac{1}{2}\leqslant 0\Leftrightarrow \frac{2-(x^2-5x+6)}{2(x^2-5x+6)}\leqslant 0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-730734e93796110ee25c6fc4704ef9cd_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{-x^2+5x-4}{x^2-5x+6}\leqslant 0\Leftrightarrow \frac{x^2-5x+4}{x^2-5x+6}\geqslant 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d1be3fb1f05682ee0466390ab1b317ae_l3.png)
Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид:
![Rendered by QuickLaTeX.com \[ \frac{(x-4)(x-1)}{(x-2)(x-3)}\geqslant 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f24afd0353b4811ea68947bda76b9ba8_l3.png)
Далее по алгоритму решения неравенств методом интервалов находим корни уравнений 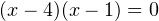 и
и 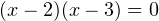 . Из первого получаем
. Из первого получаем 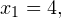
 Из второго получаем
Из второго получаем 
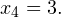 Наносим на числовую прямую получившиеся точки, причем точки
Наносим на числовую прямую получившиеся точки, причем точки 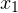 и
и 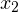 обозначаем закрашенными кружочками (для них неравенство выполняется), а точки
обозначаем закрашенными кружочками (для них неравенство выполняется), а точки 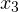 и
и 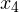 — светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
— светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
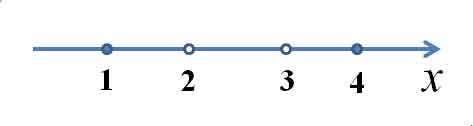
Числовая прямая с отмеченными точками
Определяем теперь знаки выражения 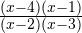 на полученных промежутках (подставляем любое значение
на полученных промежутках (подставляем любое значение 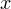 из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:

Кривая знаков для исходного неравенства
Итак, исходному неравенству удовлетворяют следующие значения: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};1]\cup(2;3)\cup[4;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d46421a915b9249fa4c19ea679359a50_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};1]\cup(2;3)\cup[4;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d46421a915b9249fa4c19ea679359a50_l3.png)
Задача для самостоятельного решения №1. Решите неравенство:
![Rendered by QuickLaTeX.com \[ \frac{x+17}{x^2-x-6}\geqslant 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-839fa1023a97b4327c3f70ebca21038a_l3.png)
Показать ответ
Ответ: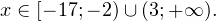 Пример 2. Решите неравенство:
Пример 2. Решите неравенство: ![Rendered by QuickLaTeX.com \[ \frac{\sqrt{x}-3}{x-2}>0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2713a0c7891d57c7c708e0f4daa14690_l3.png)
Решение. Подкоренное выражение, как известно, не может принимать отрицательных значений, также не допускается нахождение в знаменателе дроби нуля. Следовательно, область допустимых значений данного неравенства определяется неравенством 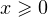 и тем условием, что
и тем условием, что  Решаем уравнения
Решаем уравнения 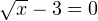 и
и 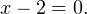 Из первого уравнения получаем, что
Из первого уравнения получаем, что 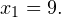 Из второго уравнения получаем, что
Из второго уравнения получаем, что 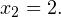 Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений
Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений 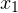 и
и 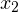 не удовлетворяет неравенству. Сразу определяем знаки выражения
не удовлетворяет неравенству. Сразу определяем знаки выражения  в каждом из полученных промежутков и рисуем кривую знаков:
в каждом из полученных промежутков и рисуем кривую знаков:
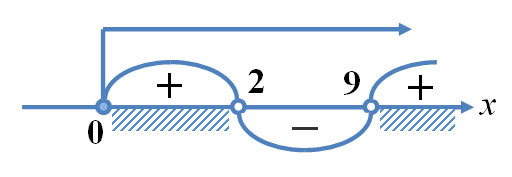
Кривая знаков для решения исходного неравенства
Верхней стрелкой на рисунке обозначена область допустимых значений неравенства. Ответом к неравенству будет являться промежуток, соответствующий на рисунке заштрихованной области.
Ответ: 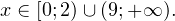
Задача для самостоятельного решения №2. Решите неравенство:
![Rendered by QuickLaTeX.com \[ \frac{\sqrt{17-15x-2x^2}}{x+3}>0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0075ad2be02241eb571efa63c22fd3f5_l3.png)
Показать ответ
Ответ: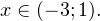 Пример 3. Решите неравенство:
Пример 3. Решите неравенство: ![Rendered by QuickLaTeX.com \[ \frac{1-\sqrt{1-8x^2}}{x}<2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ce0765d18e1c1af42f79ad43f23186ba_l3.png)
Решение. Подкоренное выражение не может принимать отрицательных значений, а в знаменателе дроби не должно быть нуля. Следовательно, область допустимых значений неравенства определяется следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-8x^2\geqslant 0, \\ x\ne 0\end{cases}\Leftrightarrow \begin{cases}-\frac{1}{2\sqrt{2}}\leqslant x\leqslant \frac{1}{2\sqrt{2}}, \\ x\ne 0.\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c5e2e667374a38c67f95ae6d66f3e3ff_l3.png)
![Rendered by QuickLaTeX.com \[ x\in\left[-\frac{1}{2\sqrt{2}};0\right)\cup\left(0;\frac{1}{2\sqrt{2}}\right]. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-45e226ad7f4db51655b74bf6d74347e9_l3.png)
Решаем уравнение  и
и  Из первого получаем, что
Из первого получаем, что  и
и 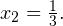 Из второго получаем, что
Из второго получаем, что 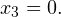 Наносим полученные точки на числовую прямую, не забывая о том, какие из них следует закрасить, а какие осветлить. Изображаем также на ней область допустимых значений и изображаем кривую знаков:
Наносим полученные точки на числовую прямую, не забывая о том, какие из них следует закрасить, а какие осветлить. Изображаем также на ней область допустимых значений и изображаем кривую знаков:
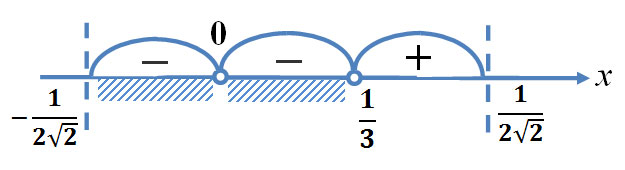
Кривая знаков для исходного неравенства
Пунктирные лини на рисунке ограничивают область допустимых значений неравенства. Заштрихованная область соответствует решению неравенства.
Ответ: 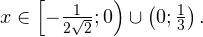
Задача для самостоятельного решения №3. Решите неравенство:
![Rendered by QuickLaTeX.com \[ \sqrt{2x+1}<\frac{2x+1}{2-x}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6824dcdfdb7d56917479eccdbc88b1c4_l3.png)
Показать ответ
Ответ:
Метод интервалов — универсальный, но не единственный метод решения неравенств. Уметь использовать этот метод, конечно, необходимо, но не достаточно для успешного решения задач по математики. Как репетитор по математике советую вам освоить и другие более частные методы решения неравенств. Успехов вам!
Сергей Валерьевич
Преподаватель математики и физики
Мы знаем столько, сколько удерживаем в памяти.
© Латинская пословица
yourtutor.info
Метод интервалов. Как решать неравенства с помощью метода интервалов
Метод интервалов применяется при решении огромного количества самых разных неравенств – квадратных, дробно-рациональных, показательных, логарифмических…
Примеры неравенств, которые удобно решать методом интервалов:
|
\((2x-5)(x+3)≤0\) |
\(\frac{-14}{x^2+2x-15}\)\(≤0\) |
|
\(x^2<361\) |
\(\frac{x^2-6x+8}{x-1}\)\(-\)\(\frac{x-4}{x^2-3x+2}\)\(≤0\) |
|
\(\frac{x-2}{3-x}\)\(≤0\) |
\(\frac{2}{5^x-1}\)\(+\)\(\frac{5^x-2}{5^x-3}\)\(≥2\) |
|
\(x^2 (-x^2-64)≤64(-x^2-64)\) |
\(\frac{5\log^2_{2}x-100}{\log^2_{2}x-25}\)\(≥4\) |
Как решать неравенства методом интервалов (алгоритм с примерами)
-
Равносильными преобразованиями приведите неравенство к виду: \(\frac{(x-x_1 )^n (x-x_2 )^k…}{(x-x_3 )^l (x-x_4 )^m…}\)\(∨0\) или \((x-x_1 )^n (x-x_2 )^k…∨0\) (\(∨\) — любой знак сравнения; \(n,k,l,m\) – любые натуральные числа большие нуля, в том числе и \(1\))
Пример:
\((2x+5)(x-2)>5\)
\(2x^2-4x+5x-10-5>0\)
\(2x^2+x-15>0\)
\(D=1-4 \cdot 2 \cdot (-15)=121=11^2\)
\(x_1=\frac{-1-11}{2 \cdot 2}=-3;\) \(x_2=\frac{-1+11}{2 \cdot 2}=\frac{5}{2}\)
\(2(x-\frac{5}{2})(x+3)>0\) \(|:2\)
\((x-\frac{5}{2})(x+3)>0\)Отметим, что здесь применено разложение на множители квадратного трехчлена.
-
Найдите корни числителя и знаменателя (т.е. такие значения икса, которые превратят их в ноль).
\(x=\frac{5}{2}; x=-3\)
-
Нанесите найденные значения на числовую ось.
Если неравенство строгое, то корни числителя обозначьте «выколотой» точкой, если нет — закрашенной. Корни знаменателя «выколоты» всегда, независимо от строгости знака сравнения.
-
Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:
— В крайнем правом интервале ставим знак плюс;
— Дальше двигаемся влево;
— Переходя через число:
— меняем знак, если скобка с этим числом была в нечетной степени (1, 3, 5…)
— не меняем знак, если скобка с этим числом была в четной степени (2, 4, 6…)
-
Выделите нужные промежутки.
Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести этот корень в ответ (такая ситуация рассмотрена в одном из примеров ниже). -
Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).
Ответ: \((-∞;-3)∪(\frac{5}{2};∞)\)
Почему алгоритм метода интервалов работает именно так?
+5 видео-примеров решения
Пример. (задание из ОГЭ) Решите неравенство методом интервалов \((x-7)^2< \sqrt{11}(x-7)\)
|
\((x-7)^2< \sqrt{11}(x-7)\) |
Чтобы в неравенстве справа был \(0\), перенесем выражение из правой части в левую. |
|
|
\((x-7)^2- \sqrt{11}(x-7)<0\) |
Вынесем за скобку \((x-7)\). |
|
|
\((x-7)(x-7-\sqrt{11})<0\) |
Находим корни. |
|
|
\(x=7;\) \(x=7+\sqrt11\) |
Расставляем на числовой оси корни, затем знаки и закрашиваем нужные интервалы |
|
|
Записываем ответ |
Ответ: \((7;7+\sqrt{11})\)
Пример. Решите неравенство методом интервалов \(\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}\)\(≥0\)
Решение:
|
\(\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}\)\(≥0\) |
Здесь на первый взгляд все кажется нормальным, а неравенство изначально приведенным к нужному виду. Но это не так – ведь в первой и третьей скобке числителя икс стоит со знаком минус.
Преобразовываем скобки, с учетом того, что четвертая степень — четная (т.е. уберет знак минус), а третья – нечетная (т.е. не уберет). |
|
|
\(\frac{-(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≥0\) |
Теперь все скобки выглядят как надо (первым идет иск без знака и только потом число). Но перед числителем появился минус. Убираем его, умножая неравенство на \(-1\), не забыв при этом перевернуть знак сравнения |
|
|
\(\frac{(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≤0\) |
Готово. Вот теперь неравенство выглядит как надо. Можно применять метод интервалов. |
|
|
\(x=4;\) \(x=-6;\) \(x=6;\) \(x=-7,5\) |
Расставим точки на оси, знаки и закрасим нужные промежутки. |
|
|
В промежутке от \(4\) до \(6\), знак не надо менять, потому что скобка \((x-6)\) в четной степени (см. пункт 4 алгоритма). Флажок будет напоминанием о том, что шестерка — тоже решение неравенства. |
Ответ: \((-∞;7,5]∪[-6;4]∪\left\{6\right\}\)
Пример. (Задание из ОГЭ) Решите неравенство методом интервалов \(x^2 (-x^2-64)≤64(-x^2-64)\)
Решение:
|
\(x^2 (-x^2-64)≤64(-x^2-64)\) |
Слева и справа есть одинаковые выражения – это явно не случайно. Первое желание – поделить на \(-x^2-64\), но это ошибка, т.к. есть шанс потерять корень. Вместо этого перенесем \(64(-x^2-64)\) в левую сторону |
|
|
\(x^2 (-x^2-64)-64(-x^2-64)≤0\) |
Вынесем за скобку общий множитель. |
|
|
\((-x^2-64)(x^2-64)≤0\) |
Вынесем минус в первой скобки и разложим на множители вторую |
|
|
\(-(x^2+64)(x-8)(x+8)≤0\) |
Обратите внимание: \(x^2\) либо равно нулю, либо больше нуля. Значит, \(x^2+64\) – однозначно положительно при любом значении икса, то есть это выражение никак не влияет на знак левой части. Поэтому можно смело делить обе части неравенства на это выражение. |
|
|
\((x-8)(x+8)≥0\) |
Теперь можно применять метод интервалов |
|
|
\(x=8;\) \(x=-8\) |
Запишем ответ |
Ответ: \((-∞;-8]∪[8;∞)\)
Смотрите также:
Квадратные неравенства
Дробно-рациональные неравенства
cos-cos.ru
Решение неравенств методом интервалов
Цели:
- Обобщить использование метода интервалов для решения неравенств,
- Показать широкие возможности этого метода для решения неравенств, содержащих переменные под знаком log, , и тригонометрические функции.
Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций.
Идея метода: Знак произведения или частного определяется знаком сомножителей.
Рис.1
Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента.
Рис.2
Квадратный трёхчлен с D>0 при переходе через каждый нуль функции меняет свой знак, причём правее большего корня знак квадратного трёхчлена совпадает со знаком его старшего коэффициента. [1]
Эти соображения приводят к следующей схеме решения неравенства:
Пример 1:[1]
- Найдём нули числителя: , , .
- Найдём нули знаменателя: .
- Наносим найденные нули на числовую ось. Т.к. неравенство строгое, то все нули изображаем выколотыми точками, которые разбивают числовую ось на интервалы:
Рис. 3
На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента:
Следовательно, дробь на этом промежутке тоже отрицательна.
- При переходе через каждый из отмеченных нулей, один и только один из сомножителей меняет знак, и поэтому каждый раз меняется знак дроби. Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
- Выбираем интервалы, на которых дробь отрицательна.
- Записываем ответ: .
В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует.
Пример 2:
- нули числителя:
-2 – нуль второй кратности
- нули знаменателя:
- наносим найденные нули на числовую ось, т.к. неравенство не строгое, то нули числителя изображаем заштрихованными точками, а нуль знаменателя мы выкалываем, т.к. это число не входит в область определения неравенства:
Рис.4
Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т.е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:
Рис.5
Это поможет понять следующая геометрическая картинка (Рис.6):
Рис.6
- Для записи ответа выбираем промежуток, где стоит знак «+» и заштрихованную точку , при которой дробь обращается в нуль.
Ответ:
Вывод: при переходе через нуль чётной кратности, знак не меняется.
Решить по вариантам, с последующим обсуждением у доски.
I вариант
Пример 3:
- нули числителя:
;
- нули знаменателя:
;
— нуль второй кратности
Рис.7
Ответ:
II вариант
Пример 4:
- нули числителя:
— нуль второй кратности - нули знаменателя:
;
— нуль третьей кратности
Рис.8
Ответ:
Применение метода интервалов не ограничивается решением рациональных неравенств.
Универсальность метода основана на достаточно наглядном свойстве непрерывных функций: «Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак».
Пример 5: [1] ,
Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*):
- нули числителя:
; — не входит в (*) - нули знаменателя:
;
Рис. 9
- на самом правом промежутке
, ,
Следовательно на этом промежутке левая часть неравенства отрицательна
- при переходе через каждый корень меняет знак один и только один из сомножителей. Учитывая это, расставляем знаки на остальных промежутках.
Ответ: .
Пример 6:
- нули числителя:
корней нет - нули знаменателя:
- решение изображаем на рис. 10:
Рис.10
Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+».
Ответ:.
Пример 7: ОДЗ:
Приведём неравенство к такому виду, чтобы в правой части был «0»:
- нули числителя:
;;;
- нули знаменателя:
- решение изображаем на рис. 11:
Рис.11
Ответ:.
Пример 8:
ОДЗ:
Рис.12
- нули числителя:
- нули знаменателя:
, но ОДЗ удовлетворяет только
- решение изображаем на рис. 13:
Рис.13
Ответ:.
Задание на дом: (Решение предоставлено в Приложении1)
- Ответ:.
- Ответ:.
- Ответ:.
- Ответ: .
- Ответ:.
Задания для факультативный занятий предоставлены в Приложении2.
Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения.
Список литературы:
[1] «Метод интервалов» //Журнал «Квант» No12, 1985 г.
urok.1sept.ru
Решение неравенств методом интервалов
9 класс
Шушпанова Ирина Владимировна
Тема урока: Решение неравенств методом интервалов.
Цели урока: 1) организовать работу по восприятию, осмыслению и первичному закреплению решение неравенств методом интервалов;
2) способствовать формированию навыка решения и оформления неравенств методом интервалов;
3) воспитывать познавательную активность, способствовать развитию логического мышления, математической и общей грамотности.
Оборудование: ноутбук, проектор, раздаточный материал с текстами самостоятельных работ, схемы -алгоритмы решения.
Тип урока: изучение нового материала.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Структура урока:
Организационный этап.
Актуализация опорных знаний.
Изучение нового материала.
Первичное закрепление.
Подведение итогов урока.
Домашнее задание.
Ход урока:
Организационный этап (2 мин.)
Приветствие. Выявление отсутствующих.
Актуализация опорных знаний (10 мин.)
Сегодня мы начнем урок с математического диктанта. Положите перед собой тетради для математических диктантов. Учащиеся отвечают на поставленные вопросы на специальных листочках.
Математический диктант.
1 вариант.
1. Зависимость переменной у от переменной х называется …
2. Все значения независимой переменной образуют…
3. Неравенство вида 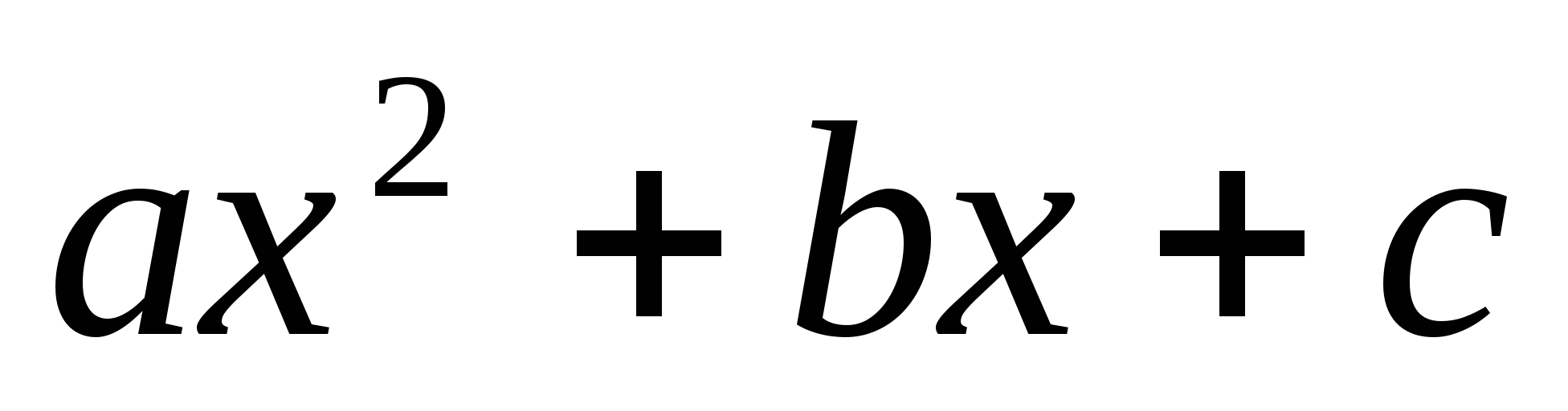 > или < 0 называется…
> или < 0 называется…
4. В каких скобках записывается ответ при решении строгого неравенства?
5. Какие значения может принимать подкоренное выражение?
2 вариант.
1. Функция вида 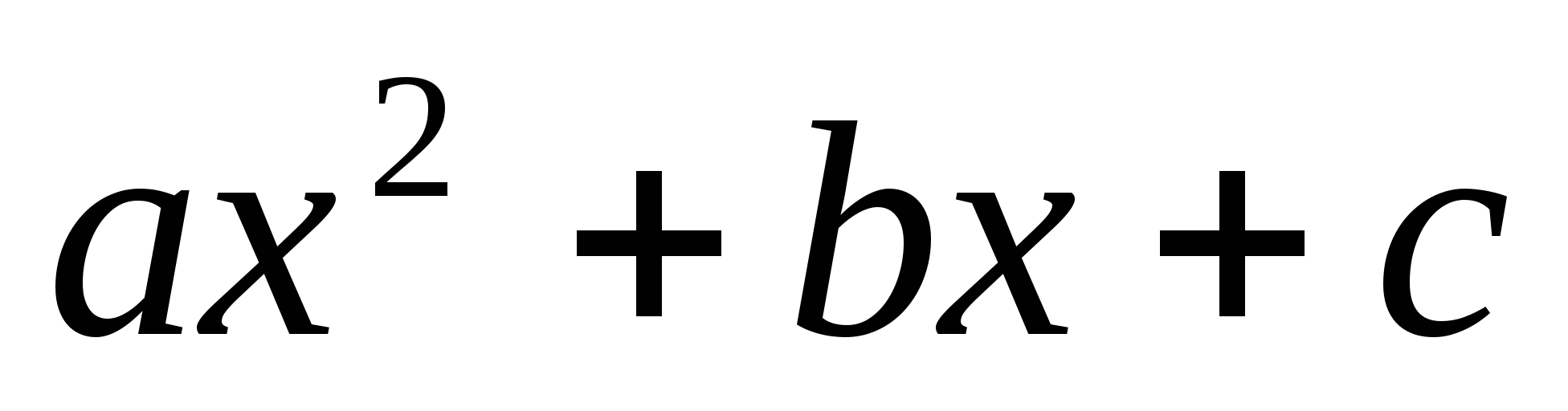 называется…
называется…
2. Все значения зависимой переменной образуют…
3. Неравенство вида 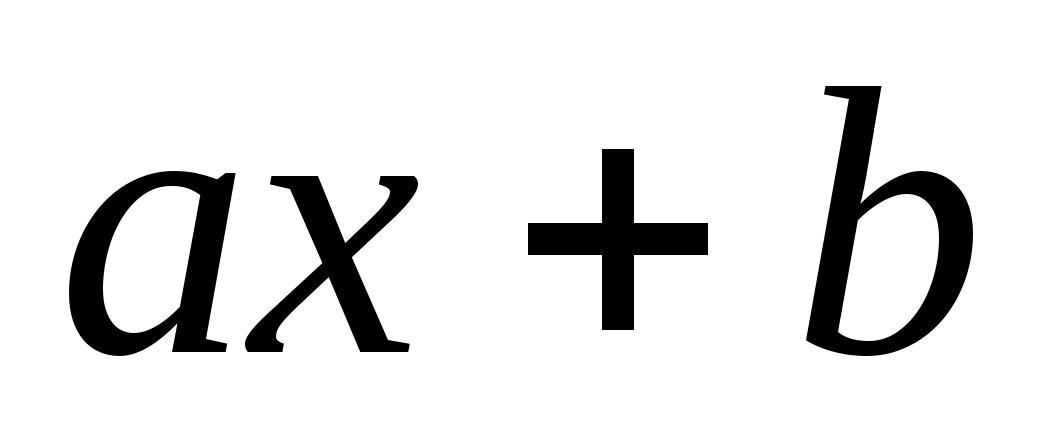 > или < 0 называется…
> или < 0 называется…
4. В каких скобках записывается ответ при решении не строгого неравенства?
5. Какие значения не должен принимать знаменатель дроби?
Диктант окончен.
После того, как диктант закончен, учащиеся обмениваются листочками и самостоятельно проверяют, сверяя свои ответ с правильными ответами, записанными на доске. После чего каждый учащийся выставляет оценку по количеству набранных правильных ответов (за каждый правильный ответ – 1 балл). Преподаватель выставляет оценки в журнал по желанию учащихся.
Изучение нового материала (15 мин.)
Вы уже знаете два вида неравенства: линейное и квадратное. Для каждого из них существует свой способ решения. В старших классах вы познакомитесь ещё с несколькими видами неравенств, такими как тригонометрические неравенства, показательные, логарифмические, рациональные, иррациональные. Каждое из этих неравенств тоже будет иметь свой способ решения. Но сегодня на уроке я познакомлю вас с универсальным способом решения неравенств, который называется метод интервалов. С его помощью вы сможете решить любое неравенство. Даже если вы забудете способ, которым решается то или иное неравенство, то всегда сможете воспользоваться методом интервалов.
Открываем рабочие тетради. Записываем число, тему урока: «Решение неравенств методом интервалов». Решение неравенства мы будем производить по алгоритму, который записан на доске. Учащиеся записывают алгоритм в свои тетради под диктовку преподавателя.
Решение неравенств методом интервалов основано на следующем свойстве функции:
Всякая функция f(x), непрерывная в своей области определения, может иметь разные знаки слева и справа от некоторой точки хо лишь только в том случае, если хо — ноль (корень) функции, либо хо— точка разрыва.
Поэтому, для нахождения интервалов постоянного знака функции достаточно найти ее область определения D(f), корни и точки разрыва нанести их на ось, определить на каждом из полученных интервалов принадлежащих D(f). Знак функции (например, подстановкой в выражении функции какого-либо значения х из соответствующего интервала) и выбрать нужные интервалы в соответствии со знаком неравенства.
Алгоритм.
Обозначить функцию, стоящую в левой части неравенства, через f(x).
Записать ОДЗ.
Найти нули функции.
Отметить ОДЗ на числовой прямой, а на ОДЗ найденные нули функции.
Определить знаки f(x) в каждом промежутке.
Записать ответ, учитывая знак неравенства.
Этот алгоритм справедлив только для непрерывных на отрезке функций, поэтому при решении неравенства методом интервалов мы должны это обязательно учитывать. Сейчас мы с вами запишем образец оформления решения неравенства.
Пример 1.
Решите неравенство: 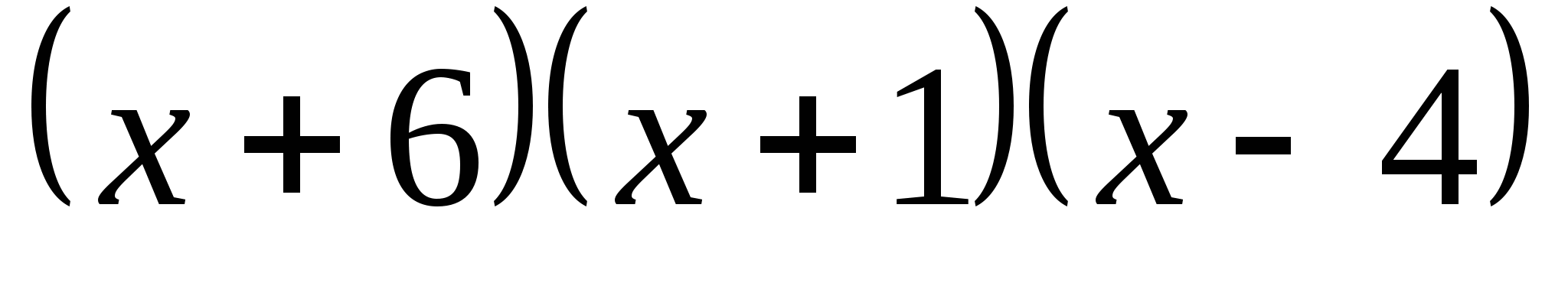 < 0
< 0
f(x) = 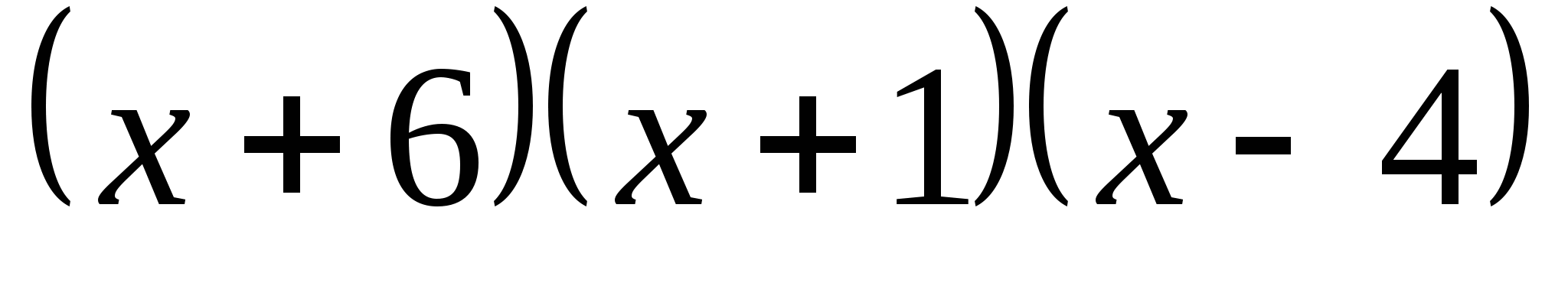
Поскольку функция f(x) = 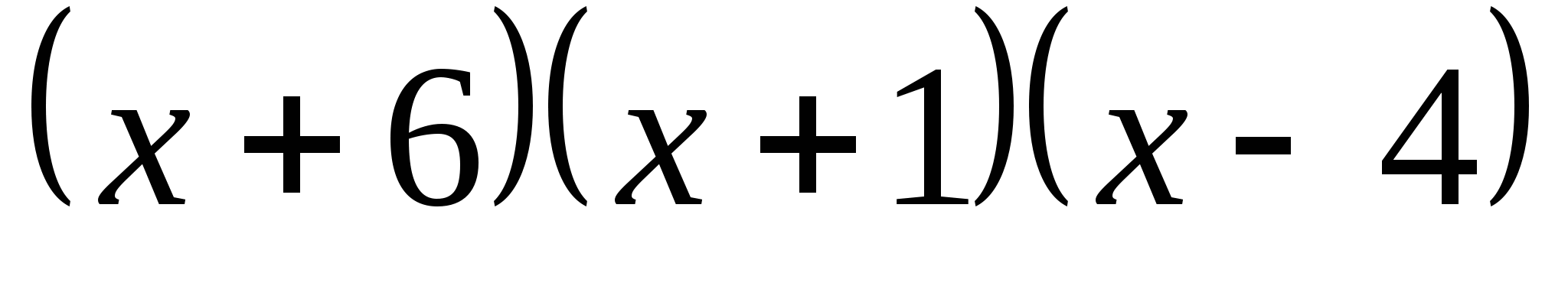 непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов.
непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов.
О ДЗ:
ДЗ: 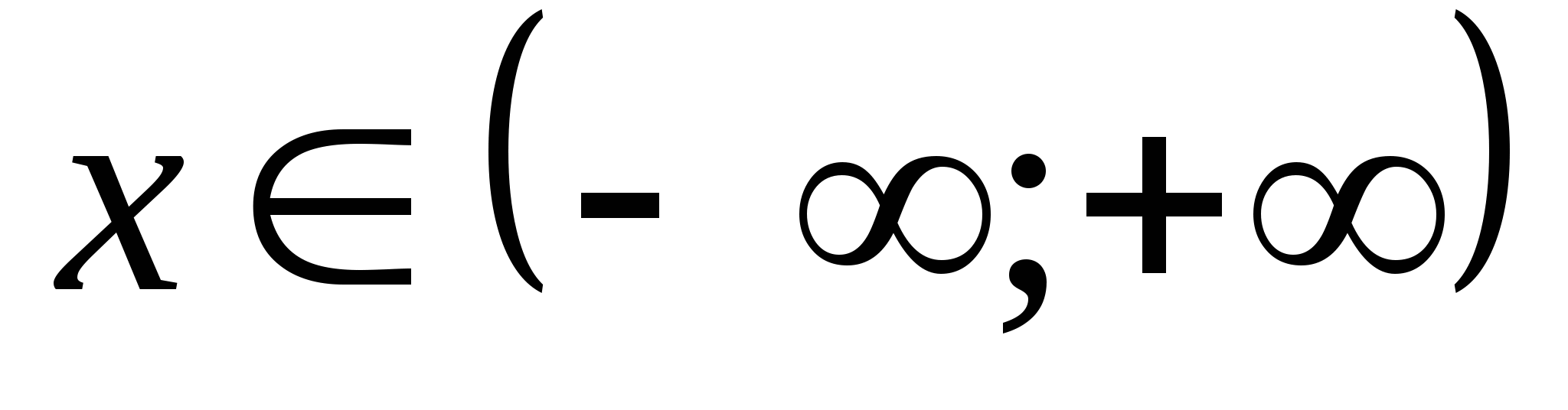
Нули функции: f(x) = 0
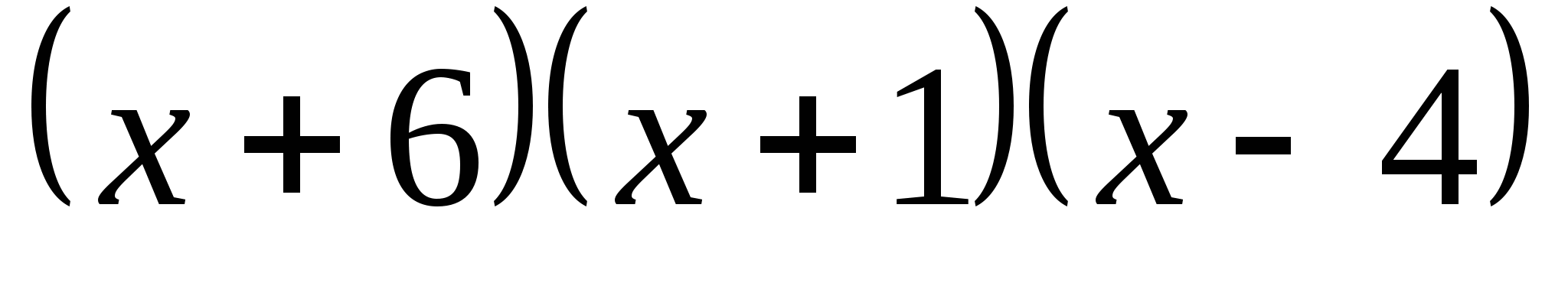
 = 0 — + — +
= 0 — + — +
х = — 6 или х = — 1 или х = 4 — 6 — 1 4 х
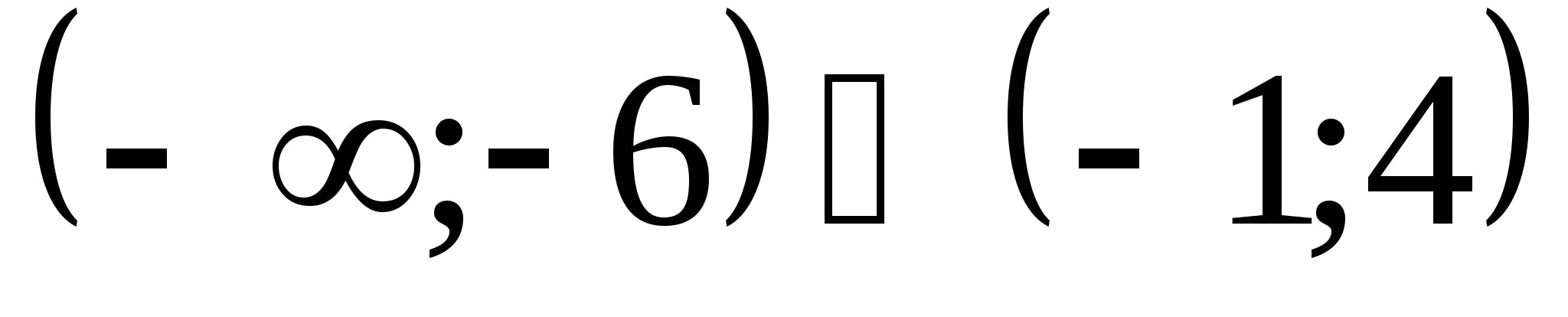
Ответ: 
Пример 2.
Решите неравенство: 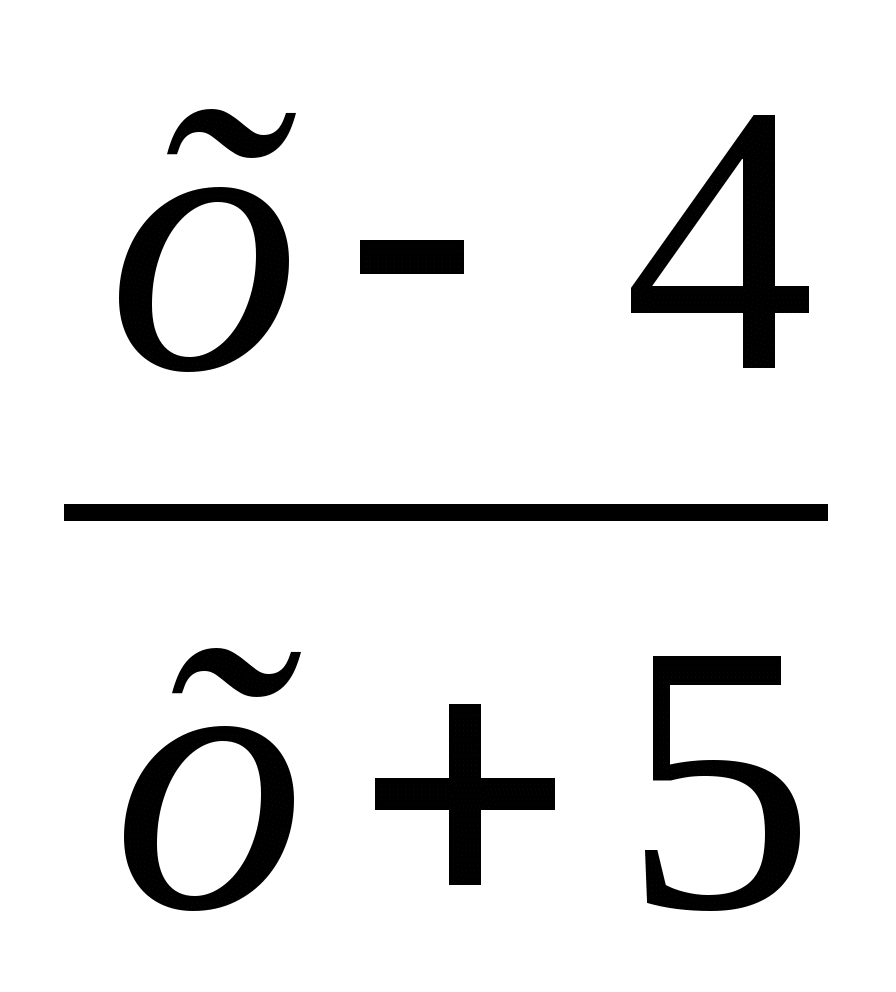 > 0
> 0
f(x) = 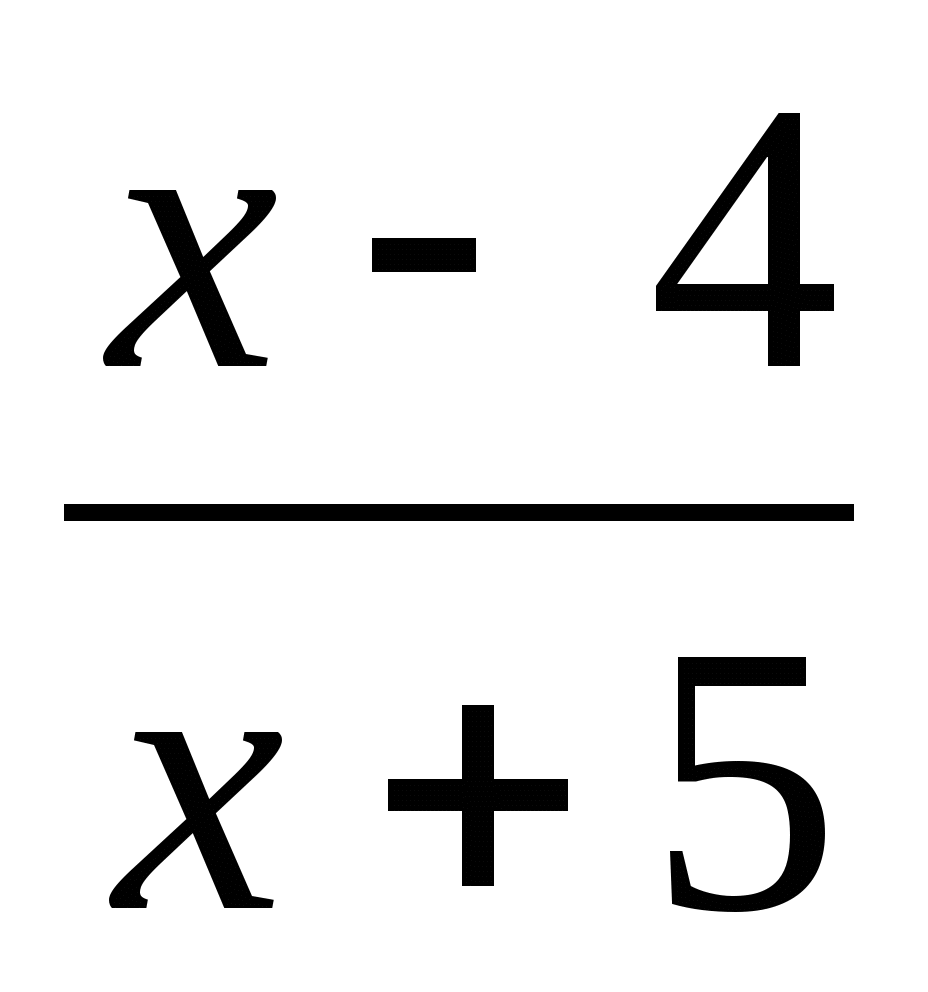
Поскольку функция f(x) = 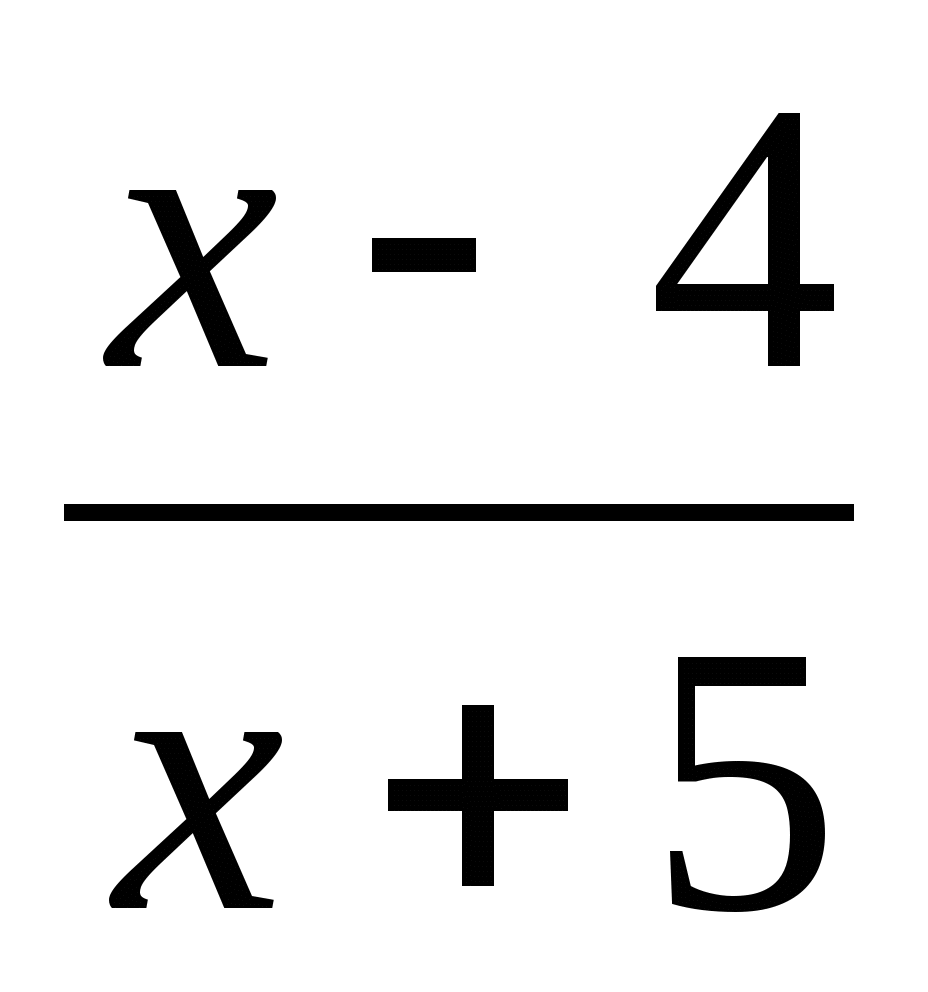 непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов.
непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов.
О ДЗ:
ДЗ:  ,
, 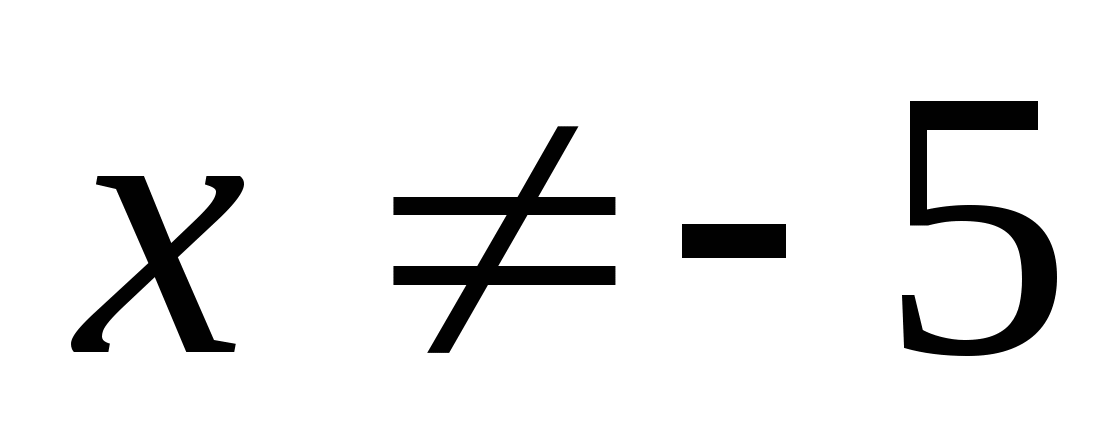
Нули функции: f(x) = 0
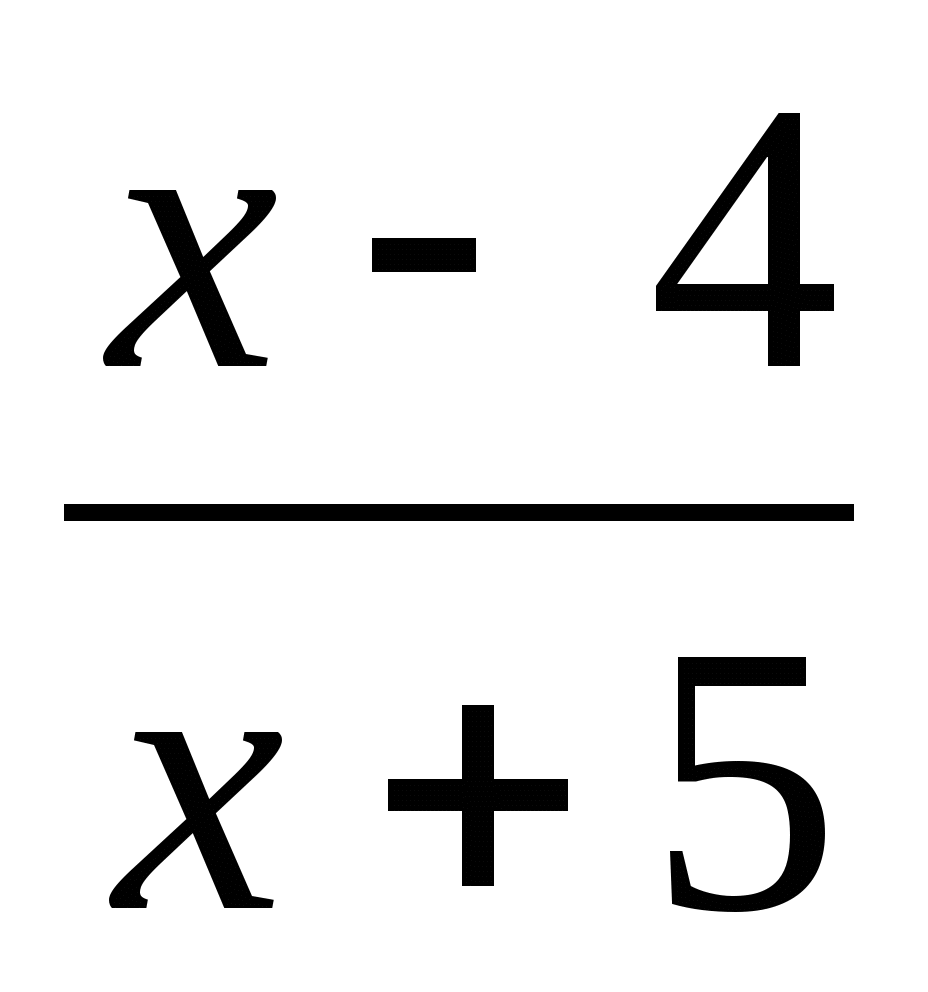
 = 0 + — +
= 0 + — +
х – 4 = 0, х = 4 — 5 4 х
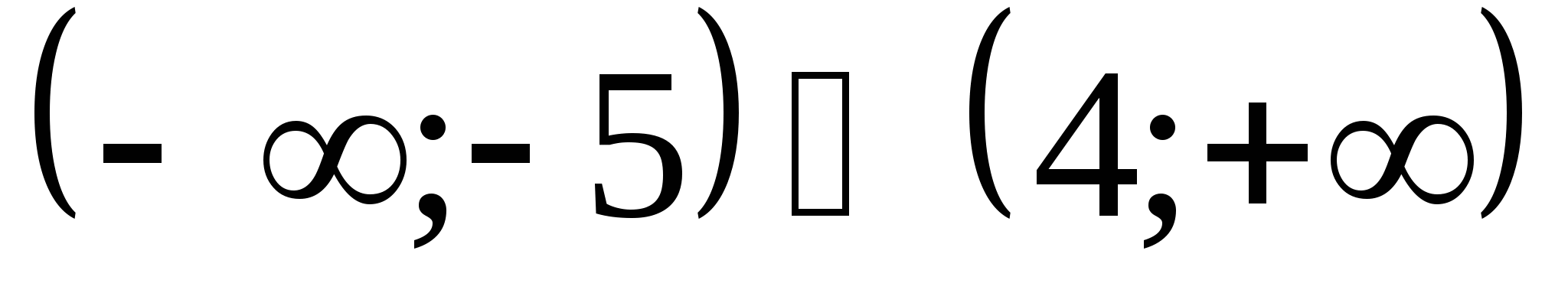
Ответ: 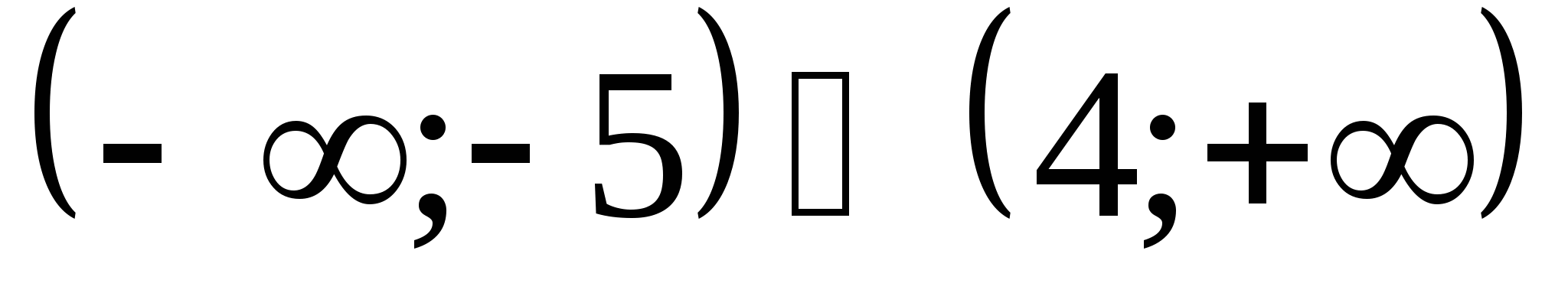 .
.
4. Первичное закрепление (10 мин.)
Как сказал великий математик Нивен «Математику нельзя изучать, наблюдая, как это делает сосед». Поэтому сейчас вы самостоятельно с помощью алгоритма и разобранных примеров решите неравенство:
а) 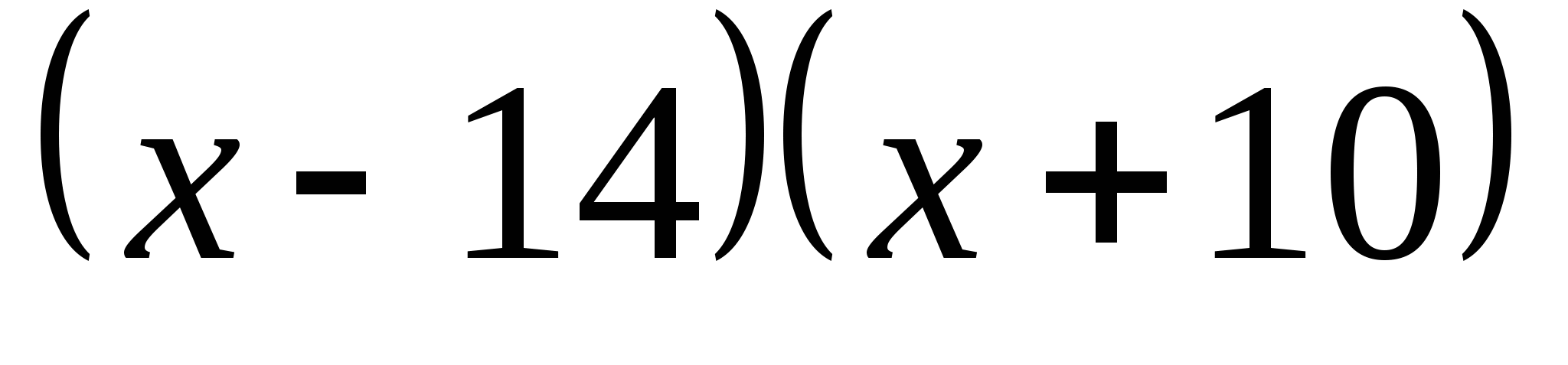 < 0
< 0
f (x) = 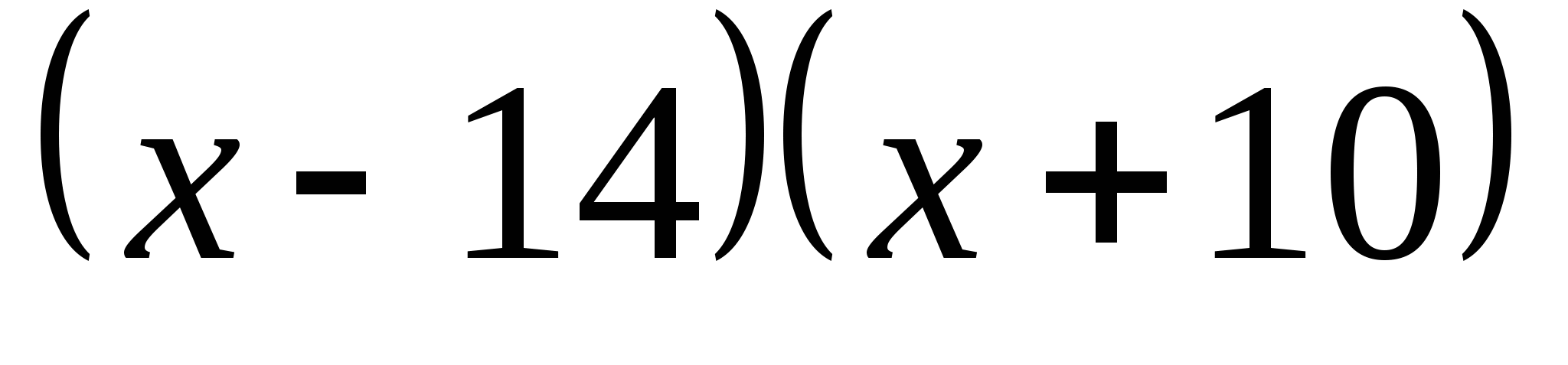
Поскольку функция f(x) = 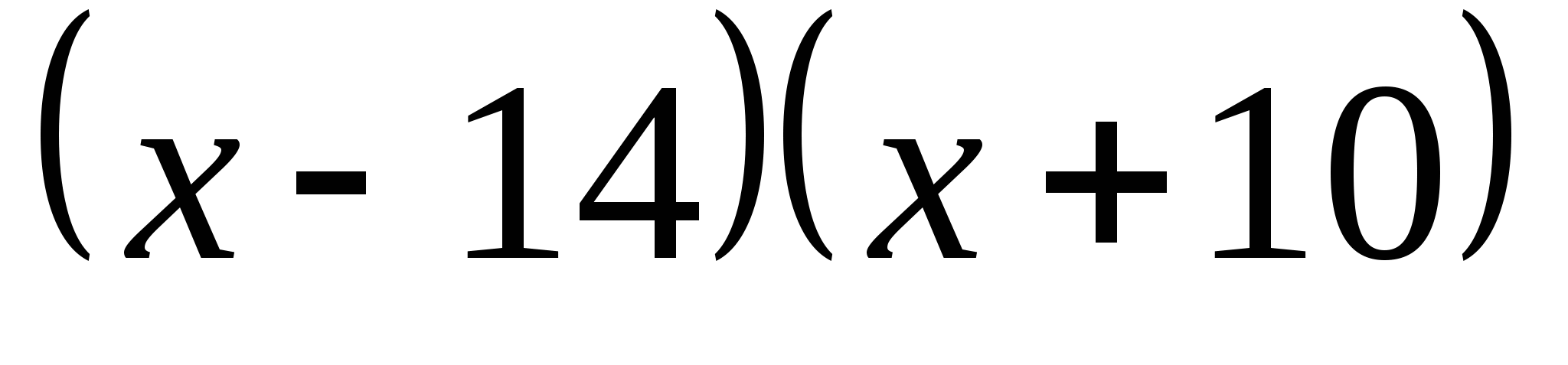 непрерывна в каждой точке своей области определения, то данное неравенство можно решить методом интервалов.
непрерывна в каждой точке своей области определения, то данное неравенство можно решить методом интервалов.
О ДЗ:
ДЗ: 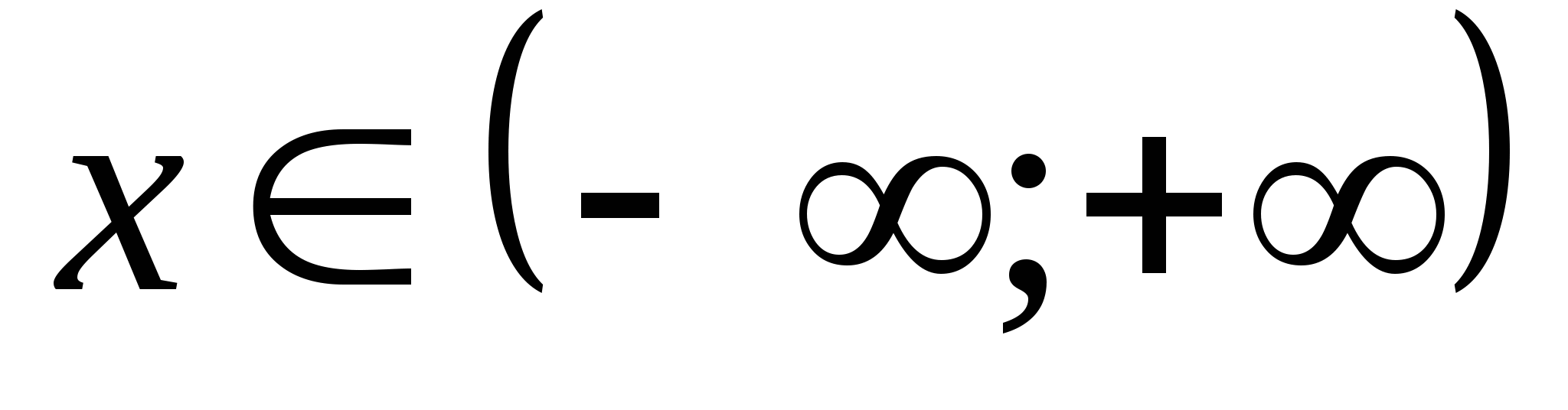
Нули функции: f(x) = 0
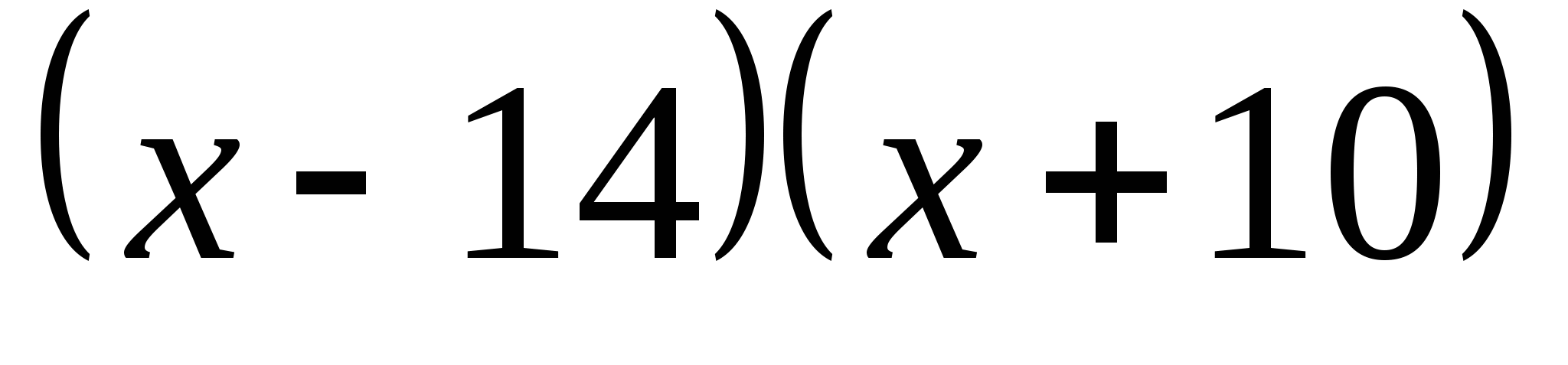
 = 0 + — +
= 0 + — +
х = 14 или х = — 10 — 10 14 х
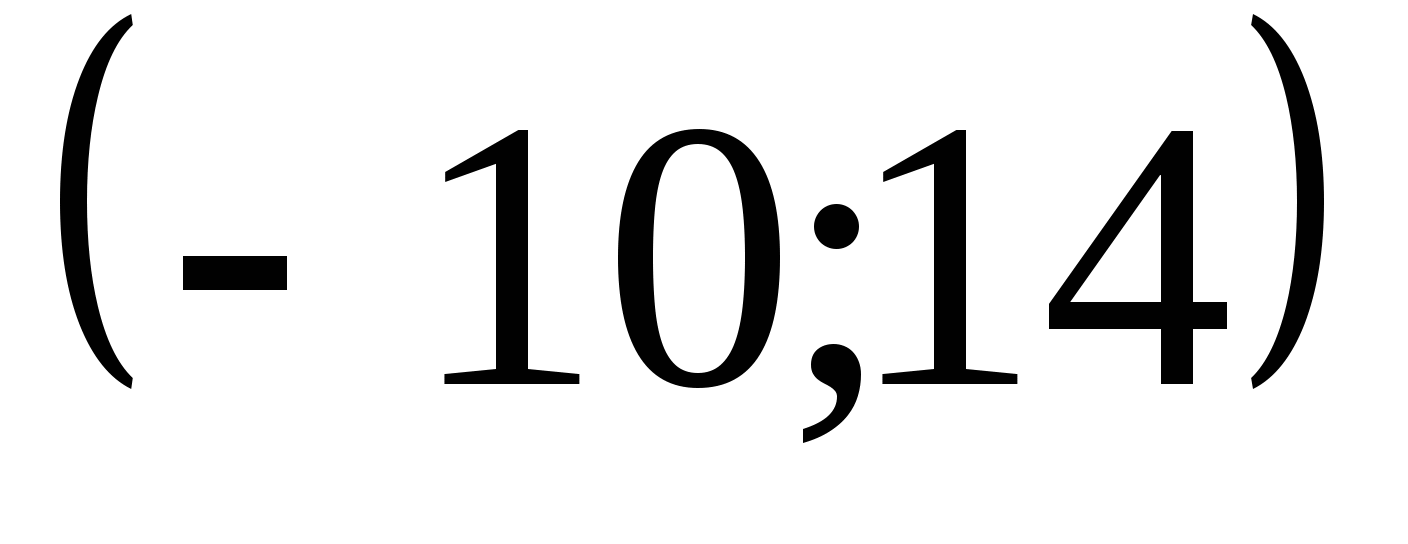
Ответ: 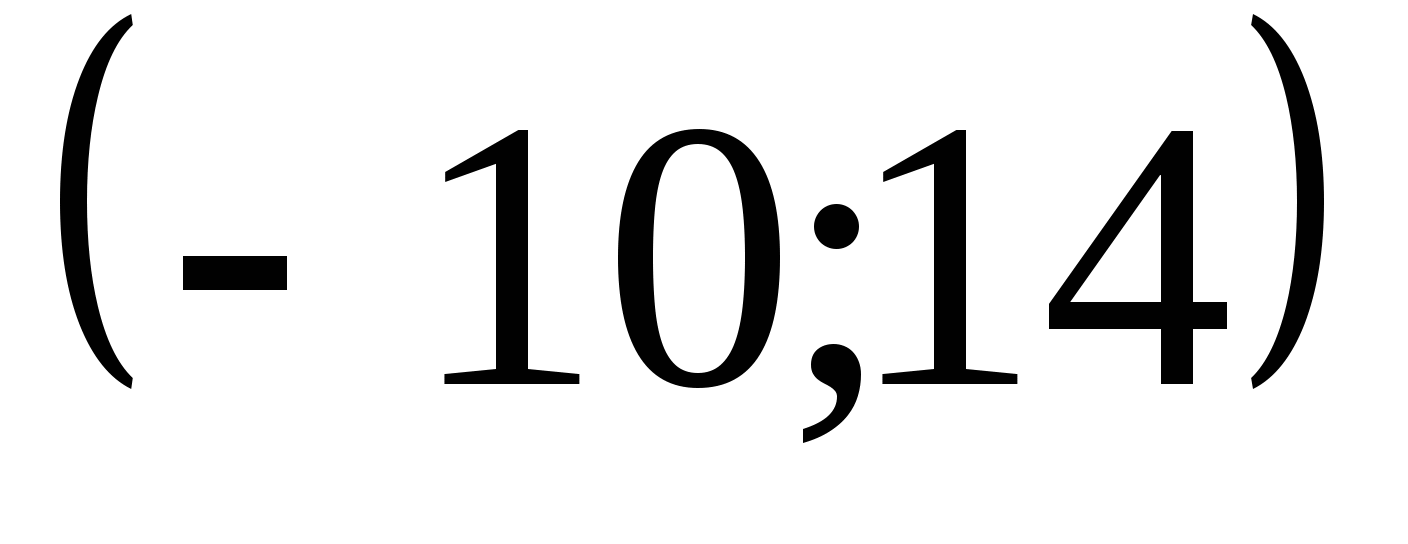 .
.
б) 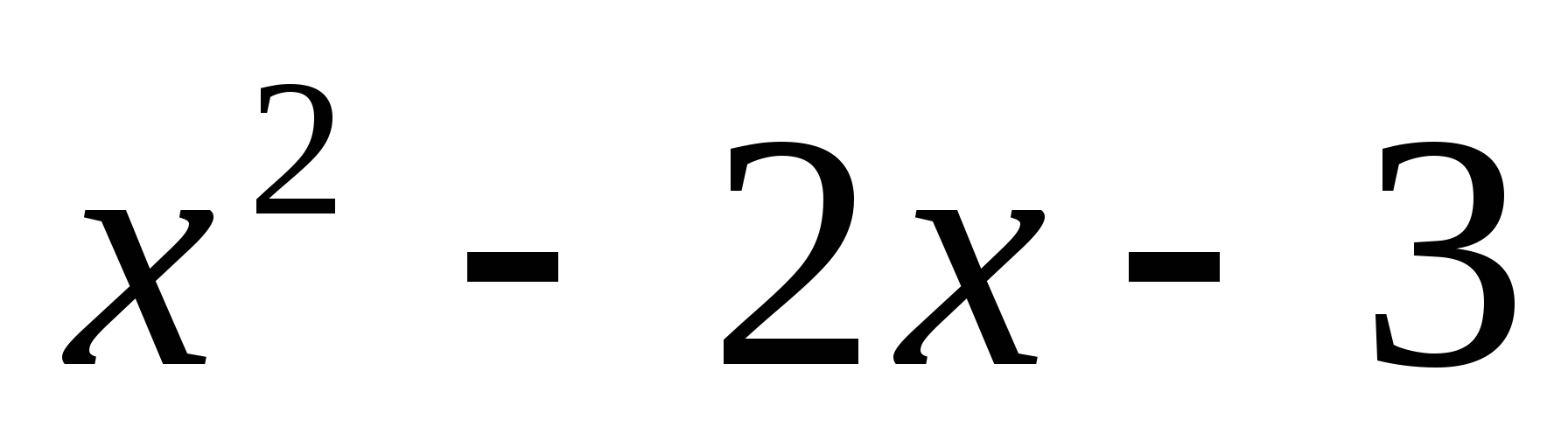 > 0
> 0
f (x) = 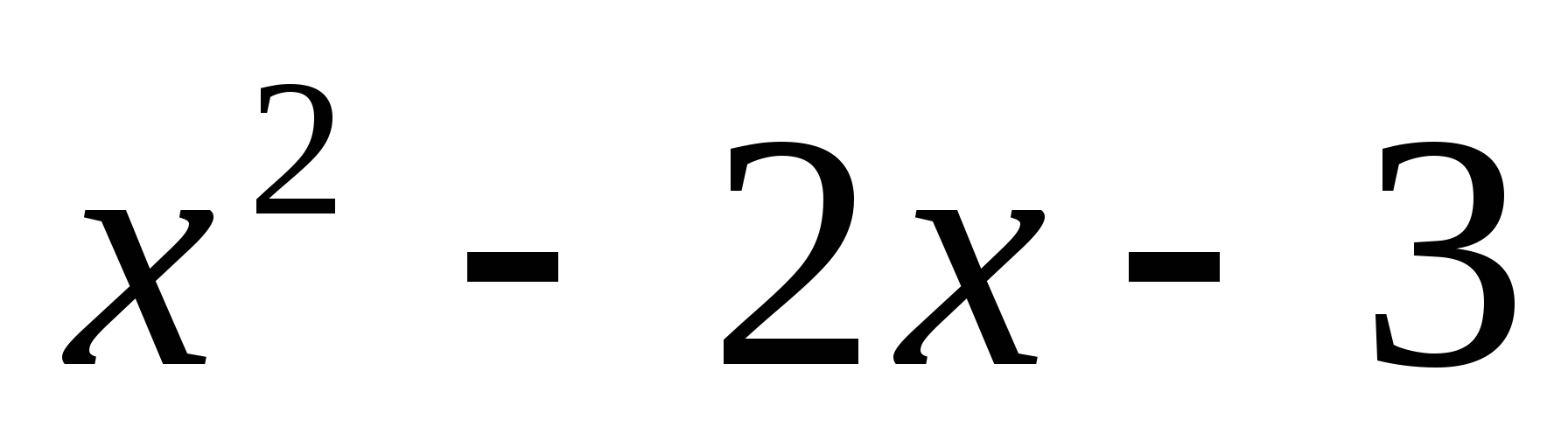
Поскольку функция f(x) = 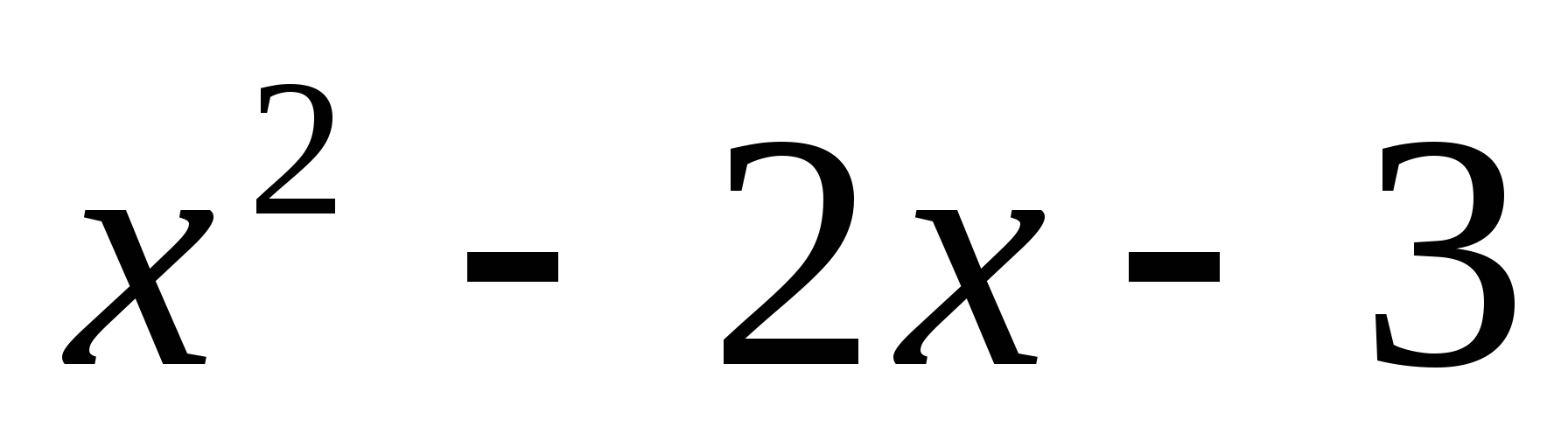 непрерывна в каждой точке своей области
непрерывна в каждой точке своей области
определения, то данное неравенство можно решить методом интервалов.
О ДЗ:
ДЗ: 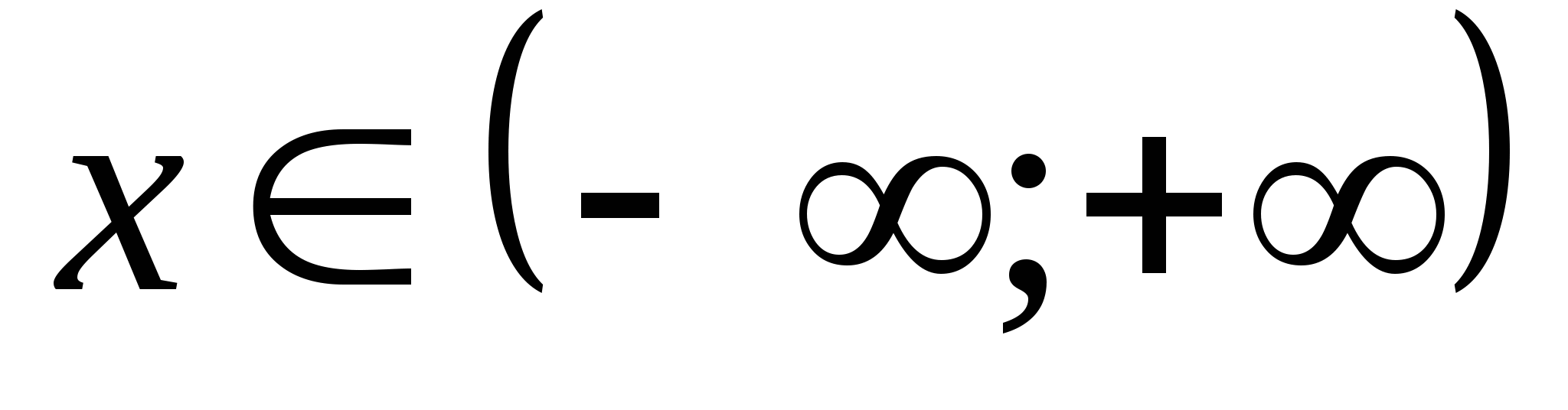
Нули функции: f(x) = 0
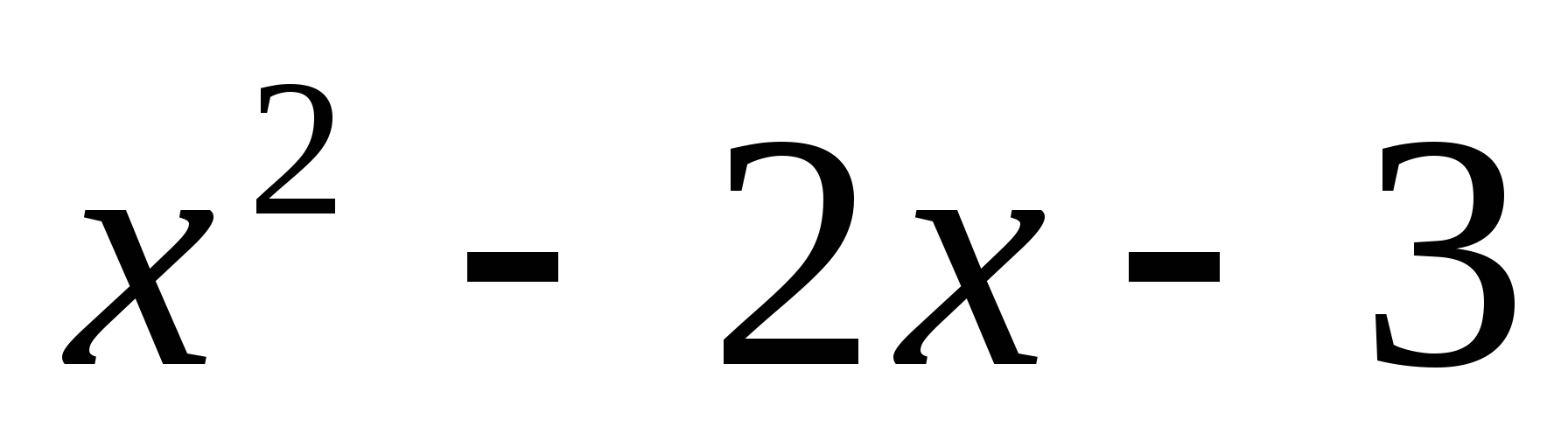
 = 0 + — +
= 0 + — +
D = 4 + 12 = 16 — 1 3 х
х1 = — 1, х2 = 3 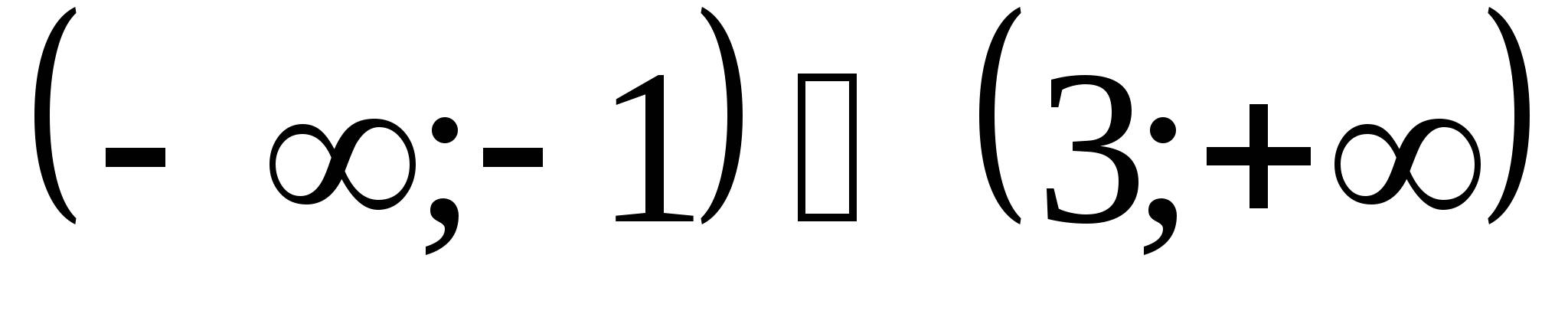
Ответ: 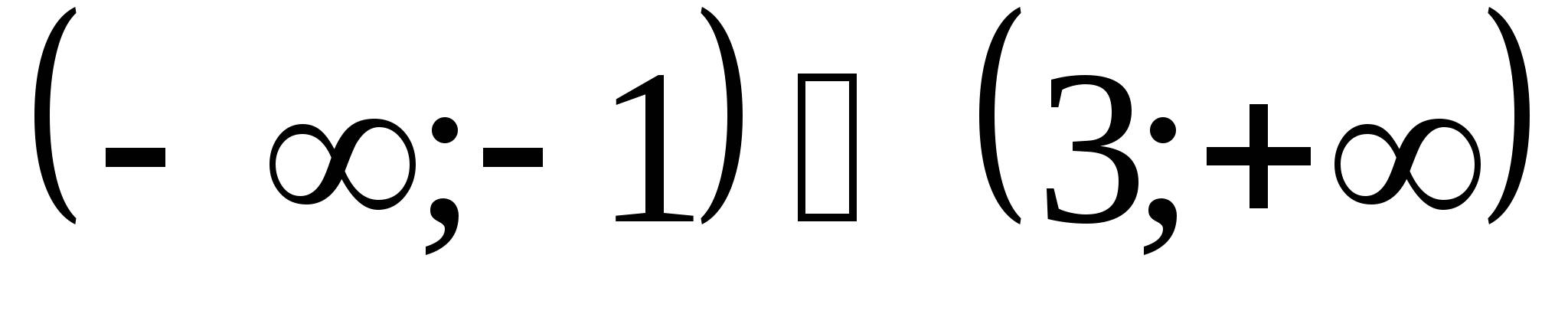 .
.
Решить № 138 (в,г).
№133 трое учащихся решают на доске, остальные- в тетрадях
№136 (в,г), 141 (в)
5. Подведение итогов урока (2 мин.)
До сегодняшнего урока вы умели решать квадратичные неравенства только одним способом, сегодня вы познакомились с методом интервалов. Какой из этих способов вам предпочтительнее для решения квадратичных неравенств?
В дальнейшем каждый из вас будет решать неравенства тем способом, который ему больше нравится.
6. Подготовка к ГИА.
Математика. 9 класс. Подготовка к ГИА-2013.
Вариант 16
№ 9
Упростите выражение (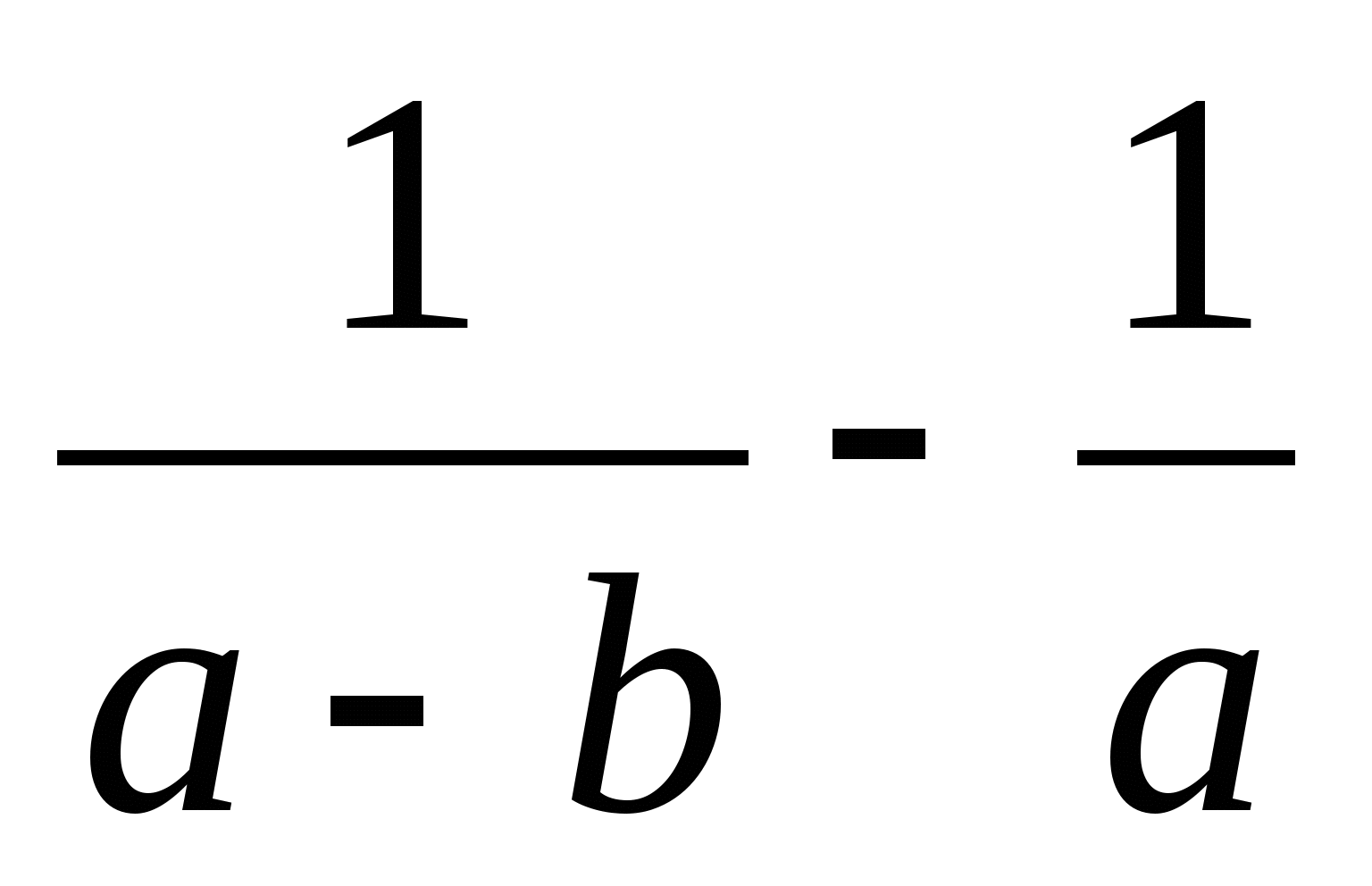 )
) 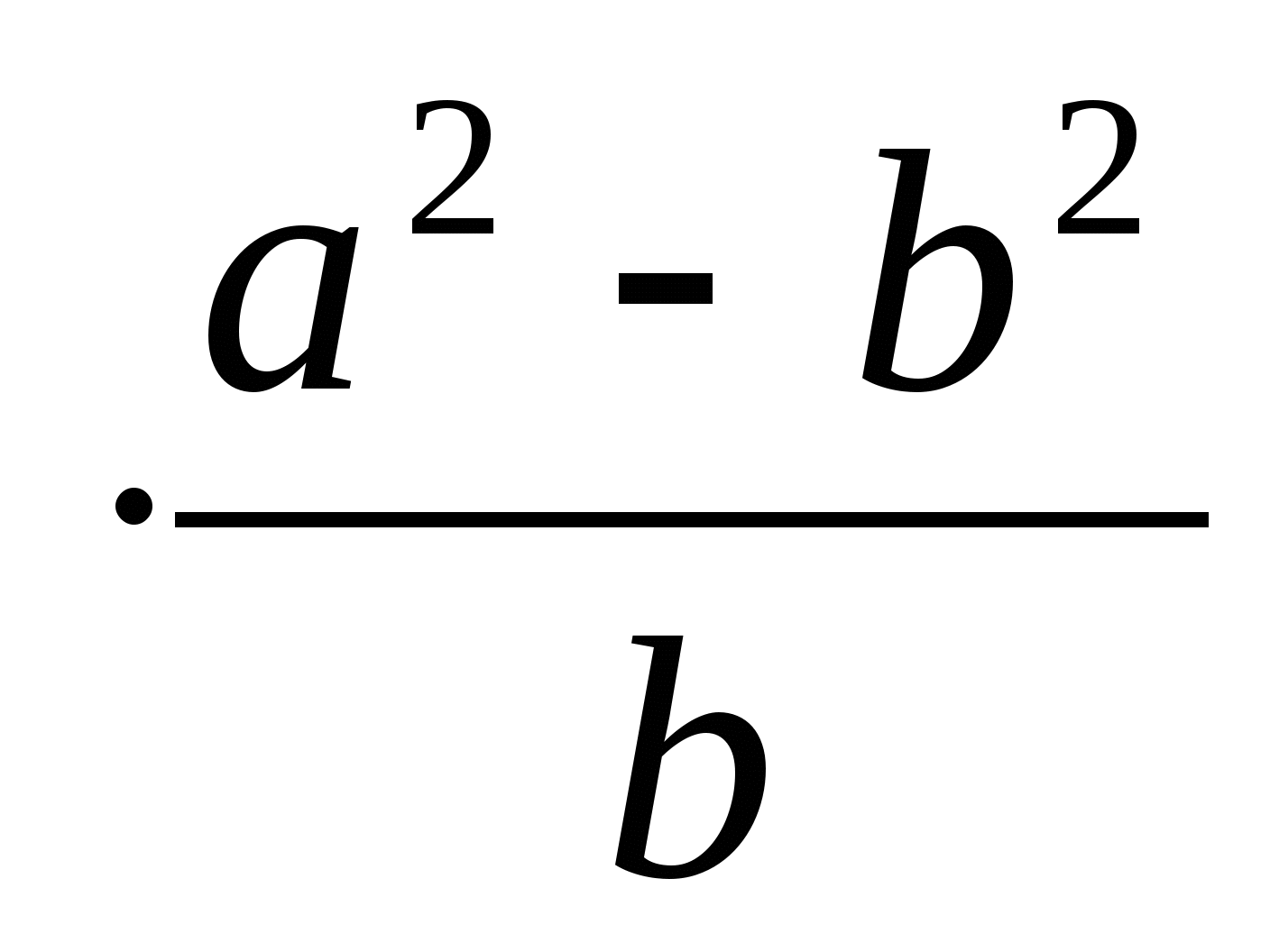 и найдите его значение при а=1, b= -0,5. В ответе запишите полученное число.
и найдите его значение при а=1, b= -0,5. В ответе запишите полученное число.
Решение:
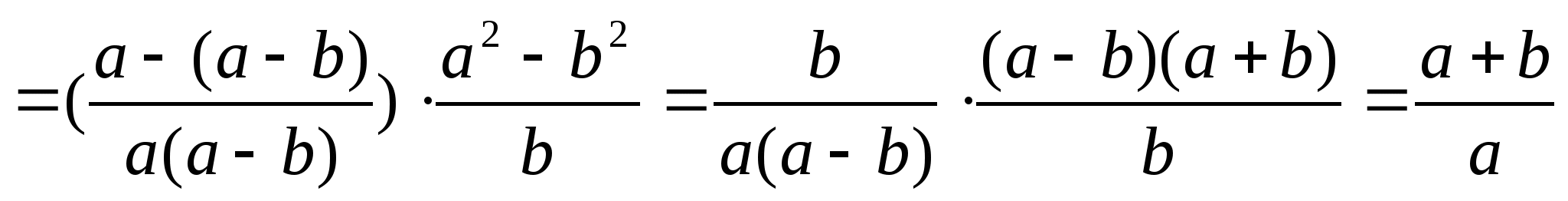
Вариант 15
№16
Найдите наибольшее значение ч, удовлетворяющее системе неравенств
 3х+12≤0,
3х+12≤0,
х+7≥1. //////////////////////////////
 х≤-4, \\\\\\\\\\\\-6\\\\\\\\\\\\\\\-4 х
х≤-4, \\\\\\\\\\\\-6\\\\\\\\\\\\\\\-4 х
х ≥ -6;
Наибольшим значением из промежутка [-6; -4] является число -4. Ответ: -4
7. Информация о домашнем задании (1 мин.)
Выучить алгоритм и обязательную фразу наизусть.
infourok.ru