Второй замечательный предел. Примеры решения.

Обычно второй замечательный предел записывают в такой форме:

\begin{equation} \lim_{x\to\infty}\left(1+\frac{1}{x}\right)^x=e\end{equation}

Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx{2{,}718281828459045}$. Если сделать замену $t=\frac{1}{x}$, то формулу (1) можно переписать в следующем виде:

\begin{equation} \lim_{t\to{0}}\biggl(1+t\biggr)^{\frac{1}{t}}=e\end{equation}

Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:

1. Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
2. Показатель степени (т.е. $x$ в формуле (1) или $\frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.

Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.

Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.

Пример №1

Вычислить предел $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}$.

Решение

Сразу отметим, что основание степени (т.е. $\frac{3x+1}{3x-5}$) стремится к единице:

$$ \lim_{x\to\infty}\frac{3x+1}{3x-5}=\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{3+\frac{1}{x}}{3-\frac{5}{x}} =\frac{3+0}{3-0} =1. $$

При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_{x\to\infty}(4x+7)=\infty$.

Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+\frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $\frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $\frac{3x+1}{3x-5}$ под вид $1+\frac{1}{x}$. Для начала прибавим и вычтем единицу:

$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} $$

Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что

$$ \frac{3x+1}{3x-5}-1 =\frac{3x+1}{3x-5}-\frac{3x-5}{3x-5} =\frac{3x+1-3x+5}{3x-5} =\frac{6}{3x-5}. $$

Так как $\frac{3x+1}{3x-5}-1=\frac{6}{3x-5}$, то:

$$ \lim_{x\to\infty}\left(1+ \frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} $$

Продолжим «подгонку». В выражении $1+\frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+\frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:

$$ 1+\frac{6}{3x-5} =1+\frac{1}{\frac{3x-5}{6}} $$

Таким образом,

$$ \lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} $$

Итак, основание степени, т.е. $1+\frac{1}{\frac{3x-5}{6}}$, подогнано под вид $1+\frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac{6}{3x-5}$. Итак, имеем:

$$ \lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} $$

Отдельно рассмотрим предел дроби $\frac{6\cdot(4x+7)}{3x-5}$, расположенной в степени:

$$ \lim_{x\to\infty}\frac{6\cdot(4x+7)}{3x-5} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{6\cdot\left(4+\frac{7}{x}\right)}{3-\frac{5}{x}} =6\cdot\frac{4}{3} =8. $$

Согласно формуле (1) имеем $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}=e$. Кроме того, $\lim_{x\to\infty}\frac{6\cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:

$$ \lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$

Полное решение без промежуточных пояснений будет иметь такой вид:

$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}=\left|1^\infty\right| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$

Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $\frac{6}{3x-5}\to{0}$ при $x\to\infty$, то применяя формулу (2), получим:

$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}=\left|1^\infty\right| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7}=\\ =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{6}{3x-5}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$

Ответ: $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$.

Пример №2

Найти предел $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}$.

Решение

Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $x\to{1}$, т.е. $\lim_{x\to{1}}(7-6x)=7-6\cdot1=1$. Для показателя степени, т.е. $\frac{x}{3x-3}$, получаем: $\lim_{x\to{1}}\frac{x}{3x-3}=\infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела.

Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $x\to{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $x\to{1}$, то ${x-1}\to{0}$, т.е. $y\to{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $y\to{0}$, получим:

$$ \lim_{x\to{1}}\biggl(7-6x\biggr )^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right|=\\ =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}} =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y} =\lim_{y\to 0}\biggl(1+(-6y)\biggr)^\frac{y+1}{3y} $$

Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $\frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $\frac{1}{-6y}$. Домножим показатель степени на выражение $\frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $\frac{-6y}{1}=-6y$:

$$ \lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y}=\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}\cdot(-6y)\cdot\frac{y+1}{3y}} =\lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} $$

Так как $\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}=e$ и $\lim_{y\to{0}}(-2(y+1))=-2$, то получим:

$$ \lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} =e^{-2} =\frac{1}{e^2}. $$

Полное решение без пояснений таково:

$$ \lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right| =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}}=\\ =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y} =\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}\cdot(-6y)\cdot\frac{y+1}{3y}} =\lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} =e^{-2} =\frac{1}{e^2}. $$

Ответ: $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$.

Пример №3

Найти предел $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}$.

Решение

Так как $\lim_{x\to{0}}(\cos{2x})=1$ и $\lim_{x\to{0}}\frac{1}{\sin^2{3x}}=\infty$ (напомню, что $\sin{u}\to{0}$ при $u\to{0}$), то мы имеем дело с неопределённостью вида $1^\infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:

$$ \lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}} =|1^\infty| =\lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} $$

Так как $\sin^2x=\frac{1-\cos{2x}}{2}$, то $\cos{2x}-1=-2\sin^2x$, поэтому:

$$ \lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} =\lim_{x\to{0}}\biggl(1+\left(-2\sin^2x\right)\biggr)^{\frac{1}{-2\sin^2x}\cdot(-2\sin^2x)\cdot\frac{1}{\sin^2 3x}}=\\ =\lim_{x\to{0}}\left(\biggl(1+\left(-2\sin^2x\right)\biggr)^{\frac{1}{-2\sin^2x}}\right)^{\frac{-2\sin^2{x}}{\sin^2{3x}}} =e^{-\frac{2}{9}}. $$

Здесь мы учли, что $\lim_{x\to{0}}\frac{\sin^2{x}}{\sin^2{3x}}=\frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.

Ответ: $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}=e^{-\frac{2}{9}}$.

Пример №4

Найти предел $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)$.

Решение

Так как при $x>0$ имеем $\ln(x+1)-\ln{x}=\ln\left(\frac{x+1}{x}\right)$, то:

$$ \lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) $$

Раскладывая дробь $\frac{x+1}{x}$ на сумму дробей $\frac{x+1}{x}=1+\frac{1}{x}$ получим:

$$ \lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(1+\frac{1}{x}\right)\right) =\lim_{x\to+\infty}\left(\ln\left(\frac{x+1}{x}\right)^x\right) =\ln{e} =1. $$

Ответ: $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)=1$.

Пример №5

Найти предел $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}$.

Решение

Так как $\lim_{x\to{2}}(3x-5)=6-5=1$ и $\lim_{x\to{2}}\frac{2x}{x^2-4}=\infty$, то мы имеем дело с неопределенностью вида $1^\infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:

$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=x-2;\;x=t+2\\&t\to{0}\end{aligned}\right| =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{2t+4}{t^2+4t}}=\\ =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{1}{3t}\cdot 3t\cdot\frac{2t+4}{t^2+4t}} =\lim_{t\to{0}}\left(\biggl(1+3t\biggr)^{\frac{1}{3t}}\right)^{\frac{6\cdot(t+2)}{t+4}} =e^3. $$

Можно решить данный пример и по-иному, используя замену: $t=\frac{1}{x-2}$. Разумеется, ответ будет тем же:

$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=\frac{1}{x-2};\;x=\frac{2t+1}{t}\\&t\to\infty\end{aligned}\right| =\lim_{t\to\infty}\left(1+\frac{3}{t}\right)^{t\cdot\frac{4t+2}{4t+1}}=\\ =\lim_{t\to\infty}\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}\cdot\frac{3}{t}\cdot\frac{t\cdot(4t+2)}{4t+1}} =\lim_{t\to\infty}\left(\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}}\right)^{\frac{6\cdot(2t+1)}{4t+1}} =e^3. $$

Ответ: $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}=e^3$.

Пример №6

Найти предел $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} $.

Решение

Выясним, к чему стремится выражение $\frac{2x^2+3}{2x^2-4}$ при условии $x\to\infty$:

$$ \lim_{x\to\infty}\frac{2x^2+3}{2x^2-4} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{2+\frac{3}{x^2}}{2-\frac{4}{x^2}} =\frac{2+0}{2-0}=1. $$

Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:

$$ \lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{2x^2+3}{2x^2-4}-1\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{7}{2x^2-4}\right)^{3x} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}\cdot\frac{7}{2x^2-4}\cdot 3x} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}}\right)^{\frac{21x}{2x^2-4}} =e^0 =1. $$

Ответ: $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x}=1$.

math1.ru

Второй замечательный предел — примеры решений

Применяемые формулы, свойства и теоремы

Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется второй замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.

Здесь мы будем иметь дело со степенно-показательной функцией, у которой основание и показатель являются функциями от некоторой переменной: . Ее удобно представить как экспоненту: . В этой связи полезна следующая лемма.

Лемма о пределе степенно-показательной функции
Пусть – функции переменной x, имеющие конечные пределы:
. Здесь .
Тогда
.
Доказательство ⇓

В случае бесконечных пределов, или когда , мы проводим исследование произведения , применяя свойства пределов бесконечно больших и малых функций.

В случае и , мы имеем неопределенность вида единица в степени бесконечность. Для ее раскрытия используется второй замечательный предел.

Раскрытие неопределенности 1 в степени бесконечность

Пусть u и v есть функции от переменной x: . И пусть при . Тогда выражение является неопределенным при . Для раскрытия этой неопределенности, мы вводим переменную t из соотношения
.
Тогда . При .
;
.

Таким образом задача сводится к вычислению предела .

Доказательство леммы о пределе степенно-показательной функции

Примеры решений

Все примеры Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓,   ⇓,   ⇓,   ⇓,   ⇓.

Пример 1

Все примеры ⇑ Найти предел:
.

Решение

При ,   . Это неопределенность вида один в степени бесконечность.

Выполняем преобразования.
;
.

Сделаем замену переменной . При . Применим второй замечательный предел:
.

Находим предел дроби, разделив числитель и знаменатель на x:
.

Применяем лемму о пределе степенно-показательной функции ⇑
.

Ответ

.

Пример 2

Все примеры ⇑ Найдите предел:
.

Решение

При ,   .   при . Это неопределенность вида один в степени бесконечность. Раскрываем ее с помощью второго замечательного предела.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.

Ответ

.

Пример 3

Все примеры ⇑ Найти предел последовательности:
.

Решение

При . Элементы последовательности равны единице. Поэтому . Рассмотрим случай .

При . Это неопределенность вида единица в степени бесконечность. Для ее раскрытия применим второй замечательный предел.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.
Эта формула справедлива и при .

Ответ

.

Пример 4

Все примеры ⇑ Найти предел:
.

Решение

Пусть . Рассмотрим функцию в проколотой окрестности точки , на которой . Для определения предела, функция должна быть определена на любой проколотой окрестности этой точки. Считаем, что . Тогда . При . Поэтому .
Теперь рассмотрим предел при .

При . У нас неопределенность вида 0/0.

Для ее раскрытия приведем степенно-показательную функцию к основанию e учитывая, что :
.
Согласно следствию второго замечательного предела:
.
В последнем множителе сделаем замену переменной:
.
При . Кроме этого, при . Тогда
.

Применяем арифметические свойства предела функции:
.
Это же значение является правильным и при .

Ответ

.

Пример 5

Все примеры ⇑ Найдите предел функции:
.

Решение с помощью второго замечательного предела и его следствий

При . Это неопределенность вида 0/0. Для ее раскрытия, применим следствия второго замечательного предела.

Преобразуем числитель дроби:

.
Преобразуем знаменатель:
.

Разделим числитель и знаменатель на x:
.
Чтобы не загромождать формулы, мы ввели обозначение .

Применяя первый замечательный предел и следствия второго, имеем:
;   ;   ;   ;   .
Применяем арифметические свойства предела функции:
.

Решение с помощью эквивалентных функций

Мы можем упростить решение, если применим теорему о замене функций эквивалентными в пределе частного. Считаем, что предел существует. Тогда мы можем заменить знаменатель эквивалентной функцией при . Из таблицы эквивалентных функций находим:
.

Получаем более простой предел:
.
Далее делаем преобразования аналогично предыдущему:
.
Поскольку при , то применяем следствие второго замечательного предела:
;
.
В дробях и заменим функции в числителе эквивалентными:
;
.

Применяем арифметические свойства предела функции:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 05-04-2019   Изменено: 05-09-2019

1cov-edu.ru

Вычисление пределов степенно-показательных функций

Пусть функции и заданы на множестве и функция на нем положительна. Функция

называется степенно — показательной.

Предположим, что – точка сгущения множества и существуют конечные пределы

, ,

где . Нужно найти

.

Воспользовавшись тождествами , запишем исходное выражение в виде

.

В силу теоремы 6.1 получим

.

При заданных значениях пределов будем иметь

.

Из проведенного рассуждения видно, что предположение о существовании конечных пределов и можно отбросить. Действительно, для нахождения предела выражения достаточно знать предел произведения (конечный или бесконечный).

1) Пусть . Тогда .

2) Если , то .

3) Если , то .

Заметим, что произведение может оказаться неопределенностью типа . Тогда и исходное выражение представляет собой неопределенность. Перечислим возникающие здесь неопределенности.

1) Если , то вычисление предела приводит к неопределенности типа .

2) Если , то вычисление предела приводит к неопределенности типа .

3) Если , то вычисление предела приводит к неопределенности типа .

Во всех указанных случаях (, , ) можно раскрыть неопределенность в показателе степени, преобразуя ее к типу и используя соответствующие эквивалентные бесконечно малые.

Замечание 8.3. Приведенные выше рассуждения справедливы и для вычисления предела степенно-показательной функции в бесконечно удаленной точке: .

Пример 8.2. Вычислить .

Решение. Здесь , , поэтому имеем неопределенность типа . Преобразуем выражение под знаком предела:

.

В показателе степени имеем неопределенность типа . Заменой при на эквивалентную бесконечно малую раскрываем ее:

.

Таким образом,

.

Замечание 8.4. Аналогично доказывается равенство .

Пределы

,

образуют две формы одного и того же равенства, которое также является замечательным пределом и часто служат определением числа .

Задачи к §8

Задача 1. Вычислить .

Решение. Здесь имеем неопределенность типа . Преобразуем числитель дроби к форме произведения:

.

Затем заменим бесконечно малую в точке функцию эквивалентной бесконечно малой .

Тогда получим

.

Ответ: .

Задача 2. Вычислить .

Решение. Здесь возникает неопределенность типа . Преобразуем знаменатель, воспользовавшись свойствами логарифмической функции, и выделим в аргументе логарифма слагаемое, равное 1:

.

Заменим бесконечно малую в точке функцию эквивалентной бесконечно малой . Числитель разложим на множители:

.

Тогда получим:

.

Ответ: .

Задача 3. Вычислить .

Решение. Здесь возникает неопределенность типа . Представим числитель в виде:

.

Затем заменим его эквивалентной бесконечно малой в точке функцией .

Функцию в точке тоже заменим на эквивалентную бесконечно малую .

Тогда

.

Ответ: .

Задача 4. Вычислить .

Решение. Здесь возникает неопределенность типа . Представим числитель в виде:

.

Затем заменим его эквивалентной бесконечно малой в точке функцией .

Преобразуем знаменатель:

и заменим его на эквивалентную бесконечно малую . Тогда получим

.

Ответ: .

Задача 5. Вычислить .

Решение. Здесь возникает неопределенность типа . Числитель можно заменить эквивалентной бесконечно малой .

Чтобы воспользоваться соотношением (8.4), преобразуем знаменатель:

и заменим его эквивалентной бесконечно малой .

Тогда

.

Ответ: .

Задача 6. Вычислить .

Решение. Здесь имеем неопределенность типа . Чтобы применить к выражению соотношение (8.3), представим его в виде:

,

и заменим бесконечно малую функцию эквивалентной бесконечно малой . Знаменатель же представим в виде:

и, используя соотношения (8.2) и (8.8), заменим его эквивалентной бесконечно малой . Учитывая проведенные выкладки и соотношение (8.4), получим:

.

Ответ: .

Задача 7. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя ряд приемов, примененных в задачах 1–7, получим

.

Ответ: .

Задача 8. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя ряд приемов, примененных в задачах 1–7 и формулы приведения для тригонометрических функций, получим

.

Ответ: .

Задача 9. Вычислить .

Решение. Здесь имеем неопределенность типа . Чтобы применить к числителю соотношение (8.2), преобразуем его следующим образом:

.

Теперь числитель согласно соотношению (8.2) можно заменить эквивалентной бесконечно малой .

Преобразуем знаменатель

.

Заменяем, используя соотношение (8.1), эквивалентной бесконечно малой .

Тогда

.

Ответ: .

Задача 10. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя приемы, описанные выше, получим

.

.

Ответ: .

Задача 11. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя теоремы 6.2 и 6.1, получим

.

Получили неопределенность типа . Преобразуем выражение с помощью формул приведения, затем переходим к эквивалентным бесконечно малым. В итоге получим

.

Ответ: .

Задача 12. Вычислить .

Решение. Здесь имеем неопределенность типа . Выделим в основании степени:

.

Заметим, что при .

Справедлива цепочка равенств

.

Заменяя логарифм эквивалентной бесконечно малой согласно соотношению (8.2) и используя замечание 6.4 для раскрытия неопределенности, получим

.

Ответ: .

Задача 13⁴. Вычислить .

Решение. Здесь имеем неопределенность типа . Введем переменную . Если , то .

.

Выделим в основании степени:

,

тогда

.

Заметим, что при . Заменим функцию эквивалентной бесконечно малой , будем иметь

.

Используя теорему 7.3, окончательно получим

.

Ответ: .

Задача 14. Вычислить .

Решение. Здесь возникает неопределенность типа . Поскольку

,

вычислим сначала . Мы имеем дело с неопределенностью типа .

Воспользовавшись последовательно соотношениями (8.2) и (8.1), будем иметь

.

Ответ: .

Задача 15. Вычислить .

Решение. Здесь возникает неопределенность типа . Воспользуемся формулой

.

Вычислим предел, стоящий в показателе степени. Для этого требуется раскрыть неопределенность типа . Преобразуем ее в неопределенность типа и воспользуемся эквивалентностью бесконечно малых:

.

Ответ: .

Задача 16. Вычислить .

Решение. Здесь возникает неопределенность типа . Преобразуем исходное предельное выражение

.

Вычислим предел, стоящий в показателе степени.

.

Ответ: .

studfile.net

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Предел числовой последовательности

      Определение 1. Число   a   называют пределом числовой последовательности

a₁ ,  a₂ , … a_n , …

если для любого положительного числа   ε   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство

| a_n – a | < ε .

      Условие того, что число   a   является пределом числовой последовательности

a₁ ,  a₂ , … a_n , … ,

записывают с помощью обозначения

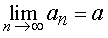
и произносят так: «Предел   a_n   при   n ,   стремящемся к бесконечности, равен   a ».

      То же самое соотношение можно записать следующим образом:

a_n → a   при .

Словами это произносится так: «a_n   стремится к   a   при   n ,   стремящемся к бесконечности».

      Замечание. Если для последовательности

a₁ ,  a₂ , … a_n , …

найдется такое число   a ,   что   a_n → a   при , то эта последовательность ограничена.

      Определение 2. Говорят, что последовательность

a₁ ,  a₂ , … a_n , …

стремится к бесконечности, если для любого положительного числа   C   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство

| a_n| > C .

      Условие того, что числовая последовательность

a₁ ,  a₂ , … a_n , … ,

стремится к бесконечности, записывают с помощью обозначения

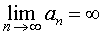
или с помощью обозначения

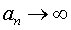 при .

      Пример 1. Для любого числа   k > 0   справедливо равенство

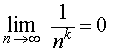
      Пример 2 . Для любого числа   k > 0   справедливо равенство

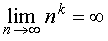
      Пример 3. Для любого числа   a   такого, что   | a | < 1,   справедливо равенство

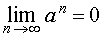
      Пример 4. Для любого числа   a   такого, что   | a | > 1,   справедливо равенство

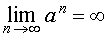
      Пример 5 . Последовательность

– 1 , 1 , – 1 , 1 , … ,

заданная с помощью формулы общего члена

a_n = (– 1)ⁿ ,

предела не имеет.

Свойства пределов числовых последовательностей

      Рассмотрим две последовательности

a₁ ,  a₂ , … a_n , … ,   и   b₁ ,  b₂ , … b_n , … .

Если при существуют такие числа   a   и   b ,  что

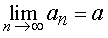  и   ,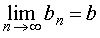

то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем

      Если, кроме того, выполнено условие

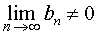
то при существует предел дроби

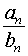
причем

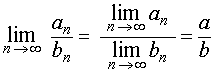      Для любой непрерывной функции   f (x)   справедливо равенство

Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии

      Рассмотрим геометрическую прогрессию

b₁ ,  b₂ , … b_n , … ,

знаменатель которой равен   q .  

      Для суммы первых   n   членов геометрической прогрессии

S_n = b₁ + b₂ + … + b_n  ,       n = 1, 2, 3, …

справедлива формула

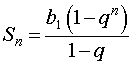
      Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение

S = b₁ + b₂ + … + b_n + … ,

то будет справедлива формула

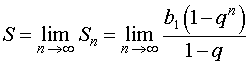
      В случае бесконечно убывающей геометрической прогрессии знаменатель   q   удовлетворяет неравенству

| q | < 1 ,

поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем

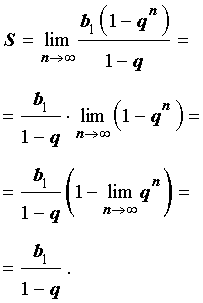
      Итак,

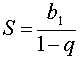
Примеры вычисления пределов последовательностей. Раскрытие неопределенностей

      Определение 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .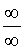

      Часто неопределенность типа 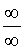удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.

      Пример 6. Найти предел последовательности

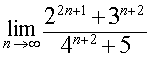
      Решение. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:

      Ответ.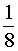

      Пример 7 . Найти предел последовательности

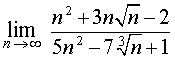
      Ответ.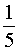

      В следующих двух примерах показано, как можно раскрыть неопределенности типа.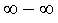

      Пример 8 . Найти предел последовательности

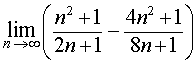
      Решение. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:

      Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:

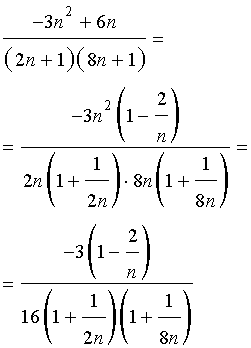
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

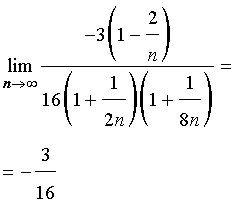
      Ответ.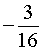

      Пример 9. Найти предел последовательности

      Решение. В рассматриваемом примере неопределенность типа 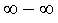возникает за счет разности двух корней, каждый из которых стремится к. Для того, чтобы раскрыть неопределенность, домножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».

      Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.

      Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби,а затем сокращая дробь на n²:

Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

      Ответ.

      Пример 10. Найти предел последовательности

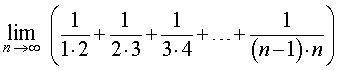
      Решение. Замечая, что для всех   k = 2, 3, 4, …   выполнено равенство

,

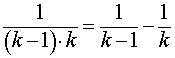получаем

      Ответ.   1 .

Число e. Второй замечательный предел

      Рассмотрим последовательность

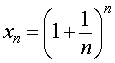(1)

      В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой   e.

      Таким образом, справедливо равенство

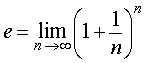(2)

причем расчеты показывают, что число

e = 2,718281828459045…

и является иррациональным и трансцендентным числом.

      Число   e   играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции

y = e ^x,

которую называют «экспонента».

      Число   e   также является пределом последовательности

(3)

что позволяет вычислять число   e   с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.

      Замечание. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

www.resolventa.ru

Второй замечательный предел, следствия, примеры

Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность . Замечательный предел имеет следующий вид

где «е»-экспонента.

Следствия второго замечательного предела

1)
2)
3)
4)
5)
6)

На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.

Примеры на замечательный предел

Рассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др.»Высшая математика в примерах и задачах. Ч.5 Тесты» (Харьков, 2007, ст. 99).

Пример 6.1. Найти предел функции
а)

Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела

В результате можем применить правило замечательного предела

 

б)

Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел

Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом

Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад — множитель единица).

————————————

в)

Решение.
Выполняем преобразование заданной функции

Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду

В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.

 

г)

Решение.
Выполним замену переменных в пределе

и определенные преобразования для нахождения предела

Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.

 

Пример 6. 2 Вычислить предел функции

а)

Решение.
Сводим функцию к правилу замечательного предела

Подставляем и вычисляем, выполняя нужные манипуляции с показателями

 

в)

yukhym.com

Замечательные пределы, примеры решений

Теория по замечательным пределам

Первый замечательный предел раскрывает неопределенность и имеет вид:

   

Следствия из первого замечательного предела:

   

Второй замечательный предел раскрывает неопределенность и имеет вид:

   

где . Он имеет следующие основные следствия:

   

Примеры

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Второй замечательный предел

Вторым замечательным пределом называется предел

,

где

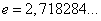— иррациональное число.

Непосредственная подстановка бесконечности в выражение приводит к бесконечности вида

.

Значит, если при непосредственном вычислении предела у вас получилась неопределённость такого вида, то решать задачу следует путём приведения ко второму замечательному пределу. Во всех этих задачах для получения второго замечательного предела требуется производить замену сложной функции более простой.

Второй замечательный предел может быть записан в другом виде, если положить тогда .

Из условия

получим

   (Alt)

Пример 1. Найти предел .

Решение. Подстановка вместо x бесконечности приводит к неопределённости:

.

Значит, нужно привести выражение ко второму замечательному пределу. Облегчим себе жизнь перед заменой сложной функции более простой, представив степень :

.

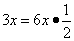Заменяем функцию 6x переменной n, которая также стремится к бесконечности:

.

Это второй замечательный предел, индивидуальна только степень числа е:

.

Пример 2. Найти предел .

Решение. Непосредственная подстановка приводит к неопределённости «бесконечность делить на бесконечность в степени бесконечность»:

.

Бесконечность в показателе степени — признак того, что выражение можно привести к отношению двух вторых замечательных пределов. В самом деле, если числитель и знаменатель поделить почленно на x, то слева и в числителе и в знаменателе будет уже по единице:

.

Почти второй замечательный предел. А чтобы это было не почти, а вторым замечательным пределом, нужно, чтобы во вторых слагаемых и в числителе, и в знаменателе были единицы. Для этого произведём замены функций:

.

.

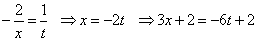Подставляем и получаем:

.

Это уже отношение вторых замечательных пределов, а степени выражений в числителе и знаменателе — индивидуальны:

.

Пример 3. Найти предел

Решение. Применяем разновидность (Alt) второго замечательного предела:

---

Второй замечательный предел служит средством решения многих задач физики, биологии, социальных наук. Показательная функция с основанием e возникает при выводе количественного закона, которому подчиняются многие естественные процессы: рост народонаселения, рост количества древесины на лесных массивах, радиоактивный распад и т.д.

Для вывода этого закона используется формула сложных процентов

,

где — сумма, наращенная через t лет, — начальная сумма, p — процентная такса, t — время роста в годах.

При этом предполагается, что проценты присоединяются к начальной сумме в конце каждого года. Если же ввести условие присоединения процентов по отдельным частям года, равным 1/n доле его, а процентная такса p по-прежнему пусть относится к целому году, то по истечении каждой такой части года наращенные суммы соответственно составят

По прошествии одного года начальная сумма обратится в , по прошествии двух лет — в , по прошествии t лет — в .

Если же предположить, что прирост процентов происходит непрерывно, т. е. число промежутков, на которые делится год, неограниченно возрастает (), а каждый из них стремится к нулю, то величина наращенной суммы выразится следующей формулой:

,

очень напоминающей второй замечательный предел.

Используя формулу альтернативного представления второго замечательного предела (Alt), приведённую в начале статьи, получим показательный закон роста:

.

Заменив p на -p, получим показательный закон убывания:

.

Например, если население страны возрастает на 2% в год, то по формуле показательного закона роста можно с неплохим приближением рассчитать численность населения страны через t лет: 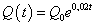, где — численность населения в начале отсчёта.

Начало темы «Предел»

Продолжение темы «Предел»

function-x.ru