Системы линейных неравенств с одной переменной
Предварительные навыкиПримеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система состоит из двух неравенств, которые уже решены.
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x < 9 соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x < 9 строгие. Ответ можно записать в виде числового промежутка:
x ∈ ( 4 ; 9 )
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
На нижней области отмечают множество решений второго неравенства x < 9
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:
Для проверки можно взять любое число из этого промежутка и подставить его в исходную систему . Возьмем, например, число 6
Возьмем, например, число 6Видим, что решение 6 удовлетворяет обоим неравенствам. Возьмём ещё какое-нибудь число из промежутка (4; 9), например, число 8
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка.
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:
В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:
x ∈ ( 17 ; +∞ )
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему . На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства (x > 6 и x > 3). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
x ∈ ( 6 ; + ∞ )
Пример 4. Решить систему неравенств
Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Решим каждое неравенство по отдельности:
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система
Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система
Ответ: решений нет.
Пример 2. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система
Ответ: решений нет.
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности:
Получили неравенства 0 < −0,2 и a > 5. Первое неравенство не является верным и не имеет решений. Решением второго неравенство
Первое неравенство не является верным и не имеет решений. Решением второго неравенство
Ответ: решений нет.
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Решение:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Решение:
Решений нет
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Системы линейных неравенств.
 {2}-5\geq11\\3+\frac{1}{x}>7\end{cases}\)
{2}-5\geq11\\3+\frac{1}{x}>7\end{cases}\)
— а это совокупность линейных неравенств, а не система
Решение систем линейных неравенств
Чтобы
решить систему неравенств мы должны найти значения иксов, которые подойдут всем неравенствам в системе.
Пример: Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:
Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс из интервала \((-\infty;7]\) или на числовой оси:
А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.
Ответ: \((4;7]\)
Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.
Если в системе находятся требующие преобразований неравенства, то при решении системы каждое неравенство независимо от других
преобразовывается к одному из видов: \(x<c\), \(x>c\), \(x\leq c\), \(x\geq c\). И только после этого ищут общее решение, пересекая решения неравенств на числовой оси.
Пример: Решить систему \(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\)
Решение:
|
\(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\) |
Перенесем \(-4\) и \(-0,3\) в правую сторону, меняя при этом их знак |
|
|
\(\begin{cases}x\geq4\\x\geq1,3\end{cases}\) |
Отметим решения на числовой оси |
|
|
|
Запишем общее решения неравенств |
Ответ: \([4;+\infty)\)
Решение:
|
\(\begin{cases}4(x-1)<3x+1\\-3x+7\geq4(1-x)\end{cases}\) |
Раскроем в каждом неравенстве скобки |
|
| \(\begin{cases}4x-4<3x+1\\-3x+7\geq4-4x\end{cases}\) |
Слагаемые с иксом в одну сторону,слагаемые без икса в другую |
|
|
\(\begin{cases}4x-3x<1+4\\-3x+4x\geq4-7\end{cases}\) |
Приведем подобные слагаемые |
|
|
\(\begin{cases}x<5\\x\geq-3\end{cases}\) |
Объединим решения на числовой оси |
|
| Запишем ответ |
Ответ: \([-3;5)\)
Заметьте, что для решения первой системы мы использовали две числовые оси, пересекая их пунктиром, а для решения второй и третьей – одну ось. Вы можете сами выбирать сколько осей вам рисовать, оба варианта допустимы. Однако в больших системах (\(3\) или более неравенства) советую для каждого неравенства чертить свою ось.
Вы можете сами выбирать сколько осей вам рисовать, оба варианта допустимы. Однако в больших системах (\(3\) или более неравенства) советую для каждого неравенства чертить свою ось.
Системы линейных неравенств и двойные неравенства
Помимо рассмотренных выше примеров, есть особый вид систем линейных неравенств: двойные неравенства. Они притворяются, что совсем не системы, но на самом деле еще какие системы!
Например:
— неравенство \(3<x-1<7\) можно записать как \(\begin{cases}x-1>3\\x-1<7\end{cases}\)
— неравенство \(2x-5<3x+7≤8x\) можно записать как \(\begin{cases}2x-5< 3x+7\\3x+7\leq8x\end{cases}\)
Первое неравенство удобнее решать в виде двойного, из-за того, что в левой и правой части нет переменных. А вот второе лучше решать как систему из-за того, что иксы есть во всех трех частях неравенства.
Системы линейных неравенств | Алгебра
Системы линейных неравенств с одной переменной с помощью тождественных преобразований сводятся к системе из простейших неравенств.
Рассмотрим на примерах, как решить систему линейных неравенств.
Чтобы решить систему, нужно решить каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их фигурной скобкой.
В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:
Решение неравенств отмечаем на числовых прямых:
В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.
Ответ: x∈[-2;1).
В первом неравенстве избавимся от дроби. Для этого обе части умножим почленно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не изменяется.
При умножении на положительное число знак неравенства не изменяется.
Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разности двух выражений.
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком и упрощаем:
Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:
Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом «меньше меньшего, больше большего«. Меньшим является 1, следовательно, система сводится к неравенству
Отмечаем его решение на числовой прямой:
Ответ: x∈(-∞;1].
Раскрываем скобки. В первом неравенстве — произведение суммы двух выражений на неполный квадрат их разности. Оно равно сумме кубов этих выражений.
Во втором — произведение суммы и разности двух выражений, что равно разности квадратов. Поскольку здесь перед скобками стоит знак «минус», лучше их раскрытие провести в два этапа: сначала воспользоваться формулой, а уже потом раскрывать скобки, меняя знак каждого слагаемого на противоположный.
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком:
Далее обе части неравенства делим на число, стоящее перед иксом. При делении на отрицательное число знак неравенства меняется на противоположный:
Оба знака «больше». Используя правило «больше большего», сводим систему неравенств к одному неравенству. Большее из двух чисел 5, следоветельно,
Решение неравенства отмечаем на числовой прямой и записываем ответ:
Ответ: x∈(5;∞).
Поскольку в алгебре системы линейных неравенств встречается не только в качестве самостоятельных заданий, но и в ходе решения разного рода уравнений, неравенств и т.д., важно вовремя усвоить эту тему.
В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений либо его решением является любое число.
Как решать систему неравенств 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Типы неравенств
Строгие — используют только больше (>) или меньше (<)
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
Другие типы
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Система неравенств
Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Если а > b , то b < а.
 Также наоборот: а < b, то b > а.
Также наоборот: а < b, то b > а.
Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
Если а > b, m — положительное число, то mа > mb и
.Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
.
Если же а > b, n — отрицательное число, то nа < nb иОбе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствием является: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то .
Если а < b , то .
Таблица числовых промежутков
Полезна тем, что с ее помощью удобно записывать множество решений.
Неравенство | Графическое решение | Форма записи ответа |
x < c | x ∈ (−∞; c) | |
x ≤ c | x ∈ (−∞; c] | |
x > c | x ∈ (c; +∞) | |
x ≥ c | x ∈ (c; +∞) |
Еще один важный шаг — запись ответа. Вот, как правильно это делать:
- Если знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.
- Если знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.
- Скобка, рядом со знаком бесконечности всегда круглая.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Решение системы неравенств
Линейное неравенство — то, в котором неизвестное представлено в первой степени. Для его решения нужно, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице. Алгоритм решения:
1. Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести подобные слагаемые. Получится одно из следующих видов:
- ax < b,
- ax ≤ b,
- ax > b,
- ax ≥ b.
2. Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть на коэффициент перед неизвестным a.
3. Если a > 0, то x ≤ ba.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.
4. Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.
Решим пример
3 * (2 − x) > 18
Как решаем
Ответ: x < −4 или в числовом промежутке x ∈ (−∞; −4). |
И еще один
Как решаем
Ответ: х < – 2. |
Последний, чтобы разобраться наверняка
Как решаем
Ответ: числовой промежуток x ∈ (– 2; 0]. |
Система неравенств — решение. Система линейных неравенств
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.
Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t1 ≤ t2, то t2 ≥ t1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t1 ≤ t2, то t1 + число ≤ t2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t1≥ t2, t3≥ t4, то t1 + t3≥ t2 + t4).

- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t1 ≤ t2, t3 ≤ t4, t1, t2, t3, t4 ≥ 0 то t1 · t3 ≤ t2 · t4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Все неравенства обладают свойством транзитивности (например, если t1 ≤ t2 и t2 ≤ t3, то t1 ≤ t3).
Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х4 — х2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х2«, далее модель переписывают в новом виде. В нашем случае получится t2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Пишут: «Пусть t = х2«, далее модель переписывают в новом виде. В нашем случае получится t2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.

- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.
Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.
Решебник
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
Некоторые из них были упомянуты выше.
Системы линейных неравенств с одной переменной
Вопросы занятия:
· вспомнить, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными;
· повторить способы решения линейных неравенств.
Материал урока
Определение.
Говорят, что задана система двух неравенств с одной переменной, если требуется найти все значения переменной, при которых оба неравенства системы обращаются в верные числовые неравенства.
Определение.
Если каждое из этих неравенств является линейным неравенством, то говорят, что задана система линейных неравенств с одной переменной.
Определение.
Решением
системы неравенств называют такое значение переменной, при
котором неравенства системы преобразуются в верные числовые неравенства.
Определение.
Решить систему неравенств – найти все её решения или доказать, что решений нет.
Алгоритм решения систем линейных неравенств довольно прост.
Но прежде чем мы приступим к решению систем, давайте вспомним, что такое пересечение и объединение числовых промежутков.
Как связаны числовые неравенства с промежутками числовой прямой, мы знаем.
Рассмотрим множество, которое состоит из нескольких интервалов на числовой оси.
Говорят, что это множество состоит из объединения числовых промежутков.
Записывают это так
Теперь давайте найдём пересечение и объединение двух числовых множеств.
Изобразим эти множества на одной числовой прямой. Для удобства, первое множество мы изобразим сверху, а второе множество изобразим снизу.
В
объединение промежутков входят все промежутки, на которых штриховка есть или
снизу или сверху или и там и там.
В пересечение множеств войдут те промежутки, на которых есть штриховка снизу и сверху одновременно.
Пересечение множеств может быть пустым множеством. Например, если мы попробуем найти пересечение этих множеств, то увидим, что нет таких значений, которые входят в каждое из этих множеств. Тогда говорят, что пересечением этих множеств является пустое множество.
Решениями систем неравенств будет пересечение множеств, которые будут решениями каждого из неравенств системы.
Пример.
Пример.
Пример.
Наравне с системами неравенств рассматривают совокупности неравенств.
Определение.
Говорят,
что задана совокупность двух неравенств с одной переменной, если
требуется найти все такие значения переменной, при каждом из которых хотя бы
одно из неравенств совокупности, обращается в верное числовое неравенство.
Определение.
Решением совокупности неравенств называют значение переменной, при котором хотя бы одно неравенство совокупности обращается в верное числовое неравенство.
Теперь давайте попробуем решить рассмотренные нами примеры, но знак системы заменим на знак совокупности.
Вернёмся к первому примеру.
Перейдём ко второму примеру.
Перейдём к последнему примеру.
К решению систем неравенств прибегают и тогда, когда надо решить двойное неравенство.
Пример.
Итоги урока
Сегодня мы вспомнили, что такое системы линейных неравенств с одной переменной, совокупности линейных неравенств с одной переменной.
Линейные неравенства с двумя переменными и их системы: решение, график и примеры
Линейное неравенство с двумя переменными и его решение
Неравенство вида ax+by $ \begin{bmatrix} \lt \\ \gt \\ \le \\ \ge \end{bmatrix} $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.
Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac{1}{2} x-8y \gt 7$
Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.
Например: для неравенства $2x+5y \lt 6$
пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина
пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь
Графическое представление линейного неравенства с двумя переменными
Графическим представлением линейного неравенства с двумя переменными вида ax+by$ \begin{bmatrix} \lt \\ \gt \\ \le \\ \ge \end{bmatrix} $ c является полуплоскость с границей ax+by = c.
Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.
Например:
$2x+3y \lt 4$
$2x+3y \le 4$
$2x+3y \gt 4$
$2x+3y \ge 4$
Графическое решение системы линейных неравенств с двумя переменными
Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.
Напомним, что:
Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.
Пересечение обозначают знаком $\cap$.
Найдём графическое решение системы линейных неравенств:
$$ {\left\{ \begin{array}{c}2x+3y \ge 4 \\ 2x-y \ge -4 \\ 2x+y \le 4 \end{array} \right.}$$
Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).
Примеры
Пример 1. Найдите графическое представление линейного неравенства:
а)$ x+y \lt 4 $
Граница x+y = 4
$y \lt -x+4$
Представление – полуплоскость под границей, сама граница не входит
б) $2x-y \ge 5$
Граница 2x-y = 5
$y \le 2x-5$
Представление – полуплоскость под границей, сама граница входит
в)$ x \ge 2$
Граница x = 2
Представление – полуплоскость справа от границы, сама граница входит
г)$ y \lt 3 $
Граница y = 3
Представление – полуплоскость под границей, сама граница не входит
Пример 2*. Найдите графическое решение системы линейных неравенств:
Найдите графическое решение системы линейных неравенств:
$$ {\left\{ \begin{array}{c} |x|+y \lt 2 \\ |x|-y \lt 4 \end{array} \right.} $$
Распишем модули:
$$ {\left\{ \begin{array}{c} y \lt -|x|+2 \\ y \gt |x|-4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} {\left\{ \begin{array}{c} y \lt -x+2, x≥0 \\ y \lt x+2, x \lt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} y \gt x-4, x \ge 0 \\ y\gt -x-4, x \lt 0 \end{array} \right.} \end{array} \right.} $$
Получаем:
Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)
Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.
Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.
Подберите состав грузовиков для выполнения заказа.
Пусть x — количество грузовиков по 3т, y – по 5т.
По условию задачи:
$$ {\left\{ \begin{array}{c} 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end{array} \right. } $$
} $$
Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.
Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна
Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит
Ответ: 2 грузовика по 3т и 5 грузовиков по 5т
Система линейных неравенств – объяснение и примеры
Прежде чем решать системы линейных неравенств , давайте посмотрим, что означает неравенство. Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.
В основном существует пять символов неравенства, используемых для представления уравнений неравенства.
Это меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и символ не равно (≠).Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Что такое система линейных неравенств?
Система линейных неравенств – это система уравнений линейных неравенств, содержащих одни и те же переменные.
Некоторые методы решения систем линейных уравнений переводятся в систему линейных неравенств. Однако решение системы линейных неравенств несколько отличается от решения линейных уравнений, поскольку знаки неравенства мешают решать методом подстановки или исключения.Возможно, лучший метод решения систем линейных неравенств — это графическое отображение неравенств.
Как решать системы линейных неравенств?
Ранее вы узнали, как решить одно линейное неравенство с помощью графика. В этой статье мы узнаем, как находить решения для системы линейных неравенств путем одновременного построения графика двух или более линейных неравенств.
Решением системы линейных неравенств называется область, в которой пересекаются графики всех линейных неравенств в системе.
Чтобы решить систему неравенств, начертите каждое линейное неравенство в системе на одной и той же оси x-y, выполнив следующие действия: :
- Изолируйте переменную y в каждом линейном неравенстве.
- Нарисуйте и заштрихуйте область над границей, используя пунктирные и сплошные линии для символов > и ≥ соответственно.
- Аналогичным образом нарисуйте и заштрихуйте область под границей, используя пунктирные и сплошные линии для символов < и ≤ соответственно.
- Закрасьте область, где все уравнения перекрываются или пересекаются.Если области пересечения нет, то делаем вывод, что система неравенств не имеет решения.
Давайте рассмотрим пару примеров, чтобы понять эти шаги.
Пример 1
График Следующая система линейных неравенств:
y ≤ x — 1 и Y <-2x + 1
Раствор
График Первое неравенство y ≤ x — 1.
- Из-за символа «меньше или равно» мы нарисуем сплошную границу и заштрихуем ниже линии.

- Также отобразите второе неравенство y < –2x + 1 на той же оси x-y.
- В этом случае наша граница будет пунктирной или пунктирной из-за символа «меньше». Заштрихуйте область ниже границы.
Таким образом, решением этой системы неравенств является более темная заштрихованная область, бесконечно простирающаяся вниз, как показано ниже.
Пример 2
Решить следующую систему неравенств:
x — 5Y ≥ 6
x — 5y ≥ 6
3x + 2y> 1
Решение
- первым, изолировать переменную Y к левому в каждом неравенстве.
Для x – 5y ≥ 6;
=> x ≥ 6 + 5y
=> 5y ≤ x – 6
=> y ≤ 0,2 x – 1,2
А для 3x + 2y > 1;
=> 2y > 1 – 3x
=> y > 0,5 – 1,5x
- Построим график y ≤ 2 x – 1,2 и y > 0,5 – 1,5x, используя сплошную и ломаную линии соответственно. .
Решением системы неравенств является более темная заштрихованная область, которая является перекрытием двух отдельных областей решения.
Пример 3
Нарисуйте следующую систему линейных неравенств.
y ≤ (1/2) x + 1,
y ≥ 2x – 2,
y ≥ -(1/2) x – 3.
Решение
Эта система имеет три уравнения, которые все соединены знаком «равно». Это говорит нам о том, что все границы будут твердыми. График трех неравенств показан ниже.
Заштрихованная область трех уравнений перекрывается прямо в средней части.Следовательно, решения системы лежат в ограниченной области, как показано на графике.
Пример 4
Нарисуйте следующую систему линейных неравенств:
Решение
Изолировать переменную y в первом полученном неравенстве;
y < – x/2 +1 Следует отметить, что неравенство y > –1 и x ≥ –3 будет иметь горизонтальные и вертикальные граничные линии соответственно.Давайте нарисуем график трех неравенств, как показано ниже.
Более темная заштрихованная область, заключенная в два отрезка пунктирной линии и один отрезок сплошной линии, дает три неравенства.
. неравенство.
–2x -y < -1 => y > –2x + 1
4x + 2y ≤ -6 => y ≤ -2x -3
Давайте построим график y > –2x + 1 и y ≤ — 2x -3:
Поскольку заштрихованные области двух неравенств не пересекаются, мы можем заключить, что система неравенств не имеет решения.
Решение систем линейных неравенств
Техника для отличается от техники для линейных уравнений, потому что знаки неравенства не позволяют нам выполнять замену, как в уравнениях. Тем не менее, мы все еще можем решить эти проблемы.
Ключевые термины
o Система линейных неравенств
o Линейная оптимизация
o Линейное программирование
Цели
o Научитесь решать задачи, связанные с системами линейных неравенств
o Понимать базовый подход к решению задач линейной оптимизации.
Системы линейных неравенств
Система линейных неравенств включает несколько выражений, решение которых может дать ряд решений. Многие из концепций, которые мы изучили при изучении систем линейных уравнений, переносятся на решение системы линейных неравенств, но этот процесс может быть несколько сложным. Возможно, самый понятный способ одновременного решения набора линейных неравенств — это использование графиков.Рассмотрим пример сразу в двух измерениях.
2 x – 5 y ≤ 3
y – 3 x ≤ 1
Из-за неравенства мы не можем использовать подстановку так же, как мы это делали с системами линейных уравнений. Давайте посмотрим на графики этих неравенств. Во-первых, мы упрощаем форму, которую легко изобразить графически.
2 x – 5 y ≤ 3 y – 3 x ≤ 1
2 x ≤ 3 + 5 y y ≤ 3 x + 1
5 у ≥ 2 x – 3
у ≥ 0. 4 x – 0,6
4 x – 0,6
Теперь построим график этих неравенств.
На графике видно, что решениям каждого неравенства соответствуют две заштрихованные области. Линии заштрихованы, поскольку неравенства нестрогие (используются ≥ и ≤). Решением системы неравенств является более темная заштрихованная область, представляющая собой перекрытие двух отдельных областей, и части линий (лучей), граничащих с областью.Символически, мы можем лучше всего выразить решение в этом случае как
0,4 x – 0,6 ≤ y ≤ 3 x + 1
Решать системы неравенств в трех и более измерениях возможно, но это гораздо сложнее — графическое изображение сплошных областей, составляющих решения, также сложнее.
Практическая задача: Найдите и начертите решение следующей системы неравенств:
x – 5 у ≥ 6
3 х + 2 у > 1
Решение : Сначала решим выражения для y .
x – 5 y ≥ 6 3 x + 2 y > 1
x ≥ 6 + 5 y 2 y > 1 – 3 x
5 y ≤ x – 6 y > 0,5 – 1,5 x
г ≤ 0,2 x – 1,2
Тогда мы можем выразить решение этой системы неравенств следующим образом:
0.5 — 1,5 x < y ≤ 0,2 x — 1,2
Построим график набора решений. Сначала мы нарисуем линии, соответствующие двум отдельным неравенствам (выбрав сплошную линию для первого и пунктирную для второго), затем соответствующим образом заштрихуем две области.
Решение представляет собой более темную заштрихованную область (которая представляет собой перекрытие двух отдельных областей решения), но давайте изобразим ее отдельно, чтобы было немного понятнее.
Линейная оптимизация
Мы можем применить то, что мы узнали выше, к линейной оптимизации (также называемой линейным программированием ), которая представляет собой процесс нахождения максимального или минимального значения для некоторой функции при определенных условиях (таких как линейные неравенства). Решение задач, связанных с линейной оптимизацией, не требует от вас изучения каких-либо новых навыков; они просто требуют, чтобы вы применяли то, что вы уже знаете.Итак, давайте перейдем непосредственно к практической задаче.
Практическая задача: Найдите максимальное значение y при условии –3 x + 2 y ≤ 4 и x + y ≤ 1 при условии, что
≥
x 5.
Решение: Нам дана система неравенств, для которой мы должны сначала найти соответствующее множество решений. Затем в этом наборе решений мы можем найти максимальное значение y .Итак, мы можем сначала применить то, что мы уже знаем: давайте преобразовать неравенства в форму, которую мы можем легко изобразить.
Затем в этом наборе решений мы можем найти максимальное значение y .Итак, мы можем сначала применить то, что мы уже знаем: давайте преобразовать неравенства в форму, которую мы можем легко изобразить.
–3 x + 2 y ≤ 4 x + y ≤ 1 x ≥ 0
2 y ≤ 3 x + 4 y ≤ 1 – x
у ≤ 1,5 x + 2
Теперь давайте изобразим каждое из этих неравенств, отметив, что в каждом случае мы должны использовать сплошные линии.
Самая темная заштрихованная область (клин в правом нижнем углу графика) удовлетворяет всем ограничениям задачи. Затем мы хотим найти максимальное значение y , которое, очевидно, равно 1. (Мы также можем найти это значение, подставив x = 0 в x + y ≤ 1 и найдя максимальное значение y , что также очевидно 1.)
4.
 2: Графики систем линейных неравенств
2: Графики систем линейных неравенствЦели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы линейных неравенств.
- Решите систему линейных неравенств с помощью графика.
- Решайте приложения систем неравенств.
Необходимые навыки
Прежде чем приступить к работе, пройдите предварительный тест.
1. Является ли \((3, 12)\) решением задачи \(y>2x+3\)?
- Нажмите здесь, чтобы проверить свой ответ
Да, потому что \(12>9\).
Если вы пропустили эту проблему, просмотрите раздел 4.1 . (Обратите внимание, что это откроется в новом окне.)
2. Постройте график всех решений \(2x-3y<12\).
- Нажмите здесь, чтобы проверить свой ответ
Если вы пропустили эту проблему, просмотрите Раздел 4.
 1 . (Обратите внимание, что это откроется в новом окне.)
1 . (Обратите внимание, что это откроется в новом окне.)
3. Где пересекаются прямые \(y=2x+1\) и \(y=-3x+6\)?
- Нажмите здесь, чтобы проверить свой ответ
\((1, 3)\)
Если вы пропустили эту проблему, просмотрите раздел 3.1 . (Обратите внимание, что это откроется в новом окне.)
Определить, является ли упорядоченная пара решением системы линейных неравенств
Определение системы линейных неравенств очень похоже на определение системы линейных уравнений.
СИСТЕМА ЛИНЕЙНЫХ НЕРАВЕНСТВ
Два или более линейных неравенства, сгруппированные вместе, образуют систему линейных неравенств.
Система линейных неравенств выглядит как система линейных уравнений, но вместо уравнений содержит неравенства.Здесь показана система двух линейных неравенств.
\[\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right. \nonumber\]
\nonumber\]
Чтобы решить систему линейных неравенств, найдем значения переменных, которые являются решениями обоих неравенств. Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика. Мы найдем область на плоскости, которая содержит все упорядоченные пары \((x,y)\), которые делают оба неравенства верными.
РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
Решениями системы линейных неравенств являются значения переменных, при которых все неравенства верны.
Решение системы линейных неравенств показано в виде заштрихованной области в системе координат x, y , которая включает все точки, упорядоченные пары которых делают неравенства верными.
Чтобы определить, является ли упорядоченная пара решением системы двух неравенств, подставим в каждое неравенство значения переменных. Если упорядоченная пара делает оба неравенства верными, это решение системы.
Пример \(\PageIndex{1}\)
Определите, является ли упорядоченная пара решением системы \(\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right. \)
\)
а. \((−2,4)\)
б. \((3,1)\)
- Ответить
а. Является ли упорядоченная пара \((−2,4)\) решением?
Упорядоченная пара \((−2,4)\) сделала оба неравенства верными. Поэтому \((−2,4)\) является решением этой системы.
б. Является ли упорядоченная пара \((3,1)\) решением?
Упорядоченная пара \((3,1)\) сделала одно неравенство истинным, а другое ложным. Поэтому \((3,1)\) не является решением этой системы.
Пример \(\PageIndex{2}\)
Определите, является ли упорядоченная пара решением системы: \(\left\{ \begin{array} {l} x−5y>10\\2x+3y>−2 \end{array} \right.\)
а. \((3,−1)\)
б. \((6,−3)\)
- Ответить
а. нет б. да
Пример \(\PageIndex{3}\)
Определить, является ли упорядоченная пара решением системы: \(\left\{ \begin{array} {l} y>4x−2\\4x−y<20 \end{array} \right. \)
\)
а. \((−2,1)\)
б. \((4,−1)\)
- Ответить
а. да б. №
Решение системы линейных неравенств с помощью графика
Решением одного линейного неравенства является область по одну сторону от граничной линии, которая содержит все точки, подтверждающие истинность неравенства. Решением системы двух линейных неравенств называется область, содержащая решения обоих неравенств.Чтобы найти эту область, мы изобразим каждое неравенство отдельно, а затем найдем область, в которой они оба верны. Решение всегда отображается в виде графика.
РЕШИТЕ СИСТЕМУ ЛИНЕЙНЫХ НЕРАВЕНСТВ С ПОМОЩЬЮ ГРАФИКА.
- Нарисуйте первое неравенство.
- Нарисуйте линию границы.
- Заштрихуйте ту сторону границы, где верно неравенство.
- На той же сетке изобразите второе неравенство.

- Нарисуйте линию границы.
- Заштрихуйте ту сторону границы, где верно неравенство.
- Решение — это область, в которой затенение перекрывается.
- Проверка путем выбора контрольной точки.
Пример \(\PageIndex{4}\): как решить систему линейных неравенств с помощью графика
Решите систему графически: \(\left\{\begin{array} {l} y\geq 2x−1 \\ y Раствор Пример \(\PageIndex{5}\) Решите систему, построив график: \(\left\{\begin{array} {l} y<3x+2\\y>−x−1\end{array}\right.\) Решение — самая темная заштрихованная область. Пример \(\PageIndex{6}\) Решите систему, построив график: \(\left\{\begin{array} {l} y<−\dfrac{1}{2}x+3 \\ y<3x−4\end{array}\right. \) Решение — самая темная заштрихованная область. Пример \(\PageIndex{7}\) Решите систему, построив график: \(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\) Точки пересечения составляют x = 3 и y = −3, а граничная линия Проверка (0, 0), которая делает неравенство ложным, поэтому закрасьте Проверка (0, 0), подтверждающая неравенство, поэтому Выберите контрольную точку в решении и убедитесь, что она является решением обоих неравенств. Точка пересечения двух линий не включена, так как обе граничные линии были пунктирными.Решением является область, заштрихованная дважды, которая выглядит как самая темная заштрихованная область. Пример \(\PageIndex{8}\) Решите систему, построив график: \(\left\{\begin{array} {l} x+y\leq 2 \\ y\geq \frac{2}{3}x−1\end{array}\right .\) Решение — самая темная заштрихованная область. Пример \(\PageIndex{9}\) Решите систему графически: \(\left\{\begin{array} {l} 3x−2y\leq 6\\y>-\frac{1}{4}x+5\end{array} \right . Решение — самая темная заштрихованная область. Пример \(\PageIndex{10}\) Решите систему графически: \(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\) Тест (0, 0), который делает неравенство верным, поэтому закрасьте Тест (0, 0), который делает неравенство Точка \((0,0)\) находится в решении, и мы уже нашли, что она является решением каждого неравенства. Точка пересечения двух линий не включена, так как обе граничные линии были заштрихованы. Решением является область, заштрихованная дважды, которая выглядит как самая темная заштрихованная область. Пример \(\PageIndex{11}\) Решите систему графически: \(\left\{\begin{array} {l} y\geq 3x−2 \\ y<−1\end{array}\right.\) Решение — самая темная заштрихованная область. Пример \(\PageIndex{12}\) Решите систему графически: \(\left\{\begin{array} {l} x>−4x−2 \\ y\geq −4 \end{array}\right.\) Решение — самая темная заштрихованная область. Системы линейных неравенств, в которых граничные линии параллельны, могут не иметь решения. Мы увидим это в следующем примере. Пример \(\PageIndex{13}\) Решите систему графически: \(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right .\) Тест (0, 0), который делает неравенство ложным, поэтому Тест (0, 0), который делает неравенство верным, поэтому В обеих заштрихованных областях нет точек, поэтому система не имеет решения. Пример \(\PageIndex{14}\) Решите систему графически: \(\left\{\begin{array} {l} 3x−2y\geq 12 \\ y\geq \frac{3}{2}x+1\end{array}\right .\) Нет решения. Пример \(\PageIndex{15}\) Решите систему, построив график: \(\left\{\begin{array} {l} x+3y>8\\y<−\frac{1}{3}x−2\end{array}\right. \) Нет решения. Некоторые системы линейных неравенств, в которых граничные линии параллельны, будут иметь решение. Пример \(\PageIndex{16}\) Решите систему, построив график: \(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\) Тест (0, 0), который делает неравенство верным, поэтому Выберите контрольную точку в решении и убедитесь, что Тест (0, 0), который делает неравенство ложным, поэтому Ни одна точка на граничных линиях не включена в решение, так как обе линии заштрихованы. Решением является дважды заштрихованная область, которая также является решением \(x−2y<−4\). Пример \(\PageIndex{17}\) Решите систему графически: \(\left\{\begin{array} {l} y\geq 3x+1 \\ −3x+y\geq −4\end{array}\right.\) Решение — самая темная заштрихованная область. Пример \(\PageIndex{18}\) Решите систему, построив график: \(\left\{\begin{array} {l} y\leq −\frac{1}{4}x+2\\x+4y\leq 4\end{array}\ правильно.\) Решение — самая темная заштрихованная область. Первое, что нам нужно сделать для решения приложений систем неравенств, — это преобразовать каждое условие в неравенство. Пример \(\PageIndex{19}\) Кристи продает свои фотографии в киоске на уличной ярмарке. В начале дня она хочет, чтобы на ее стенде было не менее 25 фотографий. Каждая маленькая фотография, которую она показывает, стоит ей 4 доллара, а каждая большая фотография — 10 долларов. Она не хочет тратить более 200 долларов на фотографии для показа. а. Напишите систему неравенств, чтобы смоделировать эту ситуацию. а. Чтобы найти систему уравнений, переведите информацию. \( \qquad \begin{array} {l} \\ \\ \text{Она хочет иметь не менее 25 фотографий.} \\ \text{Количество маленьких плюс количество больших должно быть не менее }25 .\\ \hspace{45mm} x+y\geq 25 \\ \\ \\ $4 \text{ для каждого маленького и }$10\text{ для каждого большого должно быть не более }$200 \\ \hspace{40mm} 4x +10y\leq 200 \\ \\ \\ \text{Количество маленьких фотографий должно быть больше или равно }0. \\ \hspace{50mm} x\geq 0 \\ \\ \\ \text{Количество больших фотографий должно быть больше или равно }0. \\ \hspace{50mm} y\geq 0 \end{массив} \) У нас есть система уравнений. \(\hspace{65mm} \left\{\begin{array} {l} x+y\geq 25 \\4x+10y\leq 200\\x\geq 0\\y\geq 0\end{array }\правильно.\) б. Чтобы построить график \(4x+10y\leq 200\), начертите \(4x+10y=200\) сплошной линией. Решением системы является область графика, закрашенная самым темным цветом. Участки граничной линии, которые граничат с заштрихованным участком, включены в решение, как и точки на оси x от (25, 0) до (55, 0). в. Чтобы определить, будут ли работать 10 маленьких и 20 больших фотографий, мы смотрим на график, чтобы увидеть, находится ли точка (10, 20) в области решения.Мы также можем проверить точку, чтобы увидеть, является ли она решением обоих уравнений. Это не так, Кристи не будет отображать 10 маленьких и 20 больших фотографий. д. Чтобы определить, будут ли работать 20 маленьких и 10 больших фотографий, мы смотрим на график, чтобы увидеть, находится ли точка (20, 10) в области решения. Это так, поэтому Кристи могла выбрать отображение 20 маленьких и 10 больших фотографий. Обратите внимание, что мы также можем проверить возможные решения, подставив значения в каждое неравенство. Пример \(\PageIndex{20}\) Прицеп может перевозить максимальный вес 160 фунтов и максимальный объем 15 кубических футов. Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, а принтер весит 20 фунтов и занимает 3 кубических фута. а. Напишите систему неравенств, чтобы смоделировать эту ситуацию. а.\(\left\{\begin{массив} {l} 30m+20p\leq 160\\2m+3p\leq 15\end{массив}\right. в. да Пример \(\PageIndex{21}\) Мэри нужно купить бланки для ответов и карандаши для стандартного теста, который будет сдан младшим классам ее средней школы. Необходимое количество листов для ответов как минимум на 5 больше, чем количество карандашей. Карандаши стоят 2 доллара, а листы для ответов — 1 доллар. Бюджет Мэри на эти расходные материалы предусматривает максимальную стоимость в 400 долларов. а. Напишите систему неравенств, чтобы смоделировать эту ситуацию. а. \(\left\{\begin{массив} {l} a\geq p+5 \\ a+2p\leq 400\end{массив}\right.\) в. № Когда мы используем переменные, отличные от x и y , для определения неизвестной величины, мы также должны изменить имена осей графика. Пример \(\PageIndex{22}\) Омару нужно съесть как минимум 800 калорий, прежде чем идти на тренировку своей команды. Все, что он хочет, это гамбургеры и печенье, и он не хочет тратить больше 5 долларов. В ресторане, где подают гамбургеры рядом с его колледжем, каждый гамбургер содержит 240 калорий и стоит 1 доллар 40 центов. Каждое печенье содержит 160 калорий и стоит 0,50 доллара. а. Напишите систему неравенств, чтобы смоделировать эту ситуацию. а. Чтобы найти систему уравнений, переведите информацию. Калории от гамбургеров по 240 калорий плюс калории от печенья по 160 калорий должны быть более 800. \(\qquad \begin{array} {l} \hspace{40mm} 240h+160c\geq 800 \\ \\ \\ \text{Сумма, потраченная на гамбургеры в }$1.40\text{ каждый, плюс сумма, потраченная на файлы cookie}\\\text{при }0,50$\text{ каждый не должен превышать }5,00$.\\ \hspace{40mm} 1.40h+0.50c\leq 5 \\ \\ \\ \text{Количество гамбургеров должно быть больше или равно 0.} \\ \hspace{50mm} h\geq 0 \\ \text{Количество файлов cookie должно быть больше или равно 0. }\\ \hspace{50mm} c\geq 0 \end{массив} \) \(\text{У нас есть наша система уравнений.} \qquad \left\{ \begin{array} {l} 240h+160c\geq 800 \\ 1.40h+0.50c\leq 5 \\ h\geq 0 \\ c\geq 0\end{массив} \right.\) б. Выберите (0, 0) в качестве контрольной точки. Так как это не делает неравенство верным, заштрихуйте (красным) сторону, которая не включает точку (0, 0). График \(1.40ч+0,50с\leq 5\). Граница равна \(1.40h+0.50c=5\). Мы проверяем (0, 0), и это делает неравенство верным. Заштриховываем сторону линии, включающую (0, 0). Решением системы является область графика, закрашенная самым темным цветом. Участки граничной линии, которые ограничивают затемненный участок, включены в решение, как и точки на оси x от (5, 0) до (10, 0). в. Чтобы определить, соответствуют ли 3 гамбургера и 2 печенья критериям Омара, мы смотрим, находится ли точка (3, 2) в области решения.Так и есть, поэтому Омар может съесть 3 гамбургера и 2 печенья. д. Чтобы определить, соответствуют ли 2 гамбургера и 4 печенья критериям Омара, мы смотрим, находится ли точка (2, 4) в области решения. То есть Омар может съесть 2 гамбургера и 4 печенья. Мы также можем проверить возможные решения, подставив значения в каждое неравенство. Пример \(\PageIndex{23}\) Напряжению нужно потреблять как минимум дополнительно 1000 калорий в день, чтобы подготовиться к марафону.У него есть только 25 долларов, чтобы потратить на дополнительную еду, в которой он нуждается, и он потратит их на пончики за 0,75 доллара, каждый из которых содержит 360 калорий, и энергетические напитки за 2 доллара, которые содержат 110 калорий. а. Напишите систему неравенств, моделирующую эту ситуацию. а. \(\left\{\begin{массив} {l} 0.75d+2e\leq 25\\360d+110e\geq 1000\end{массив}\right.\) в. да Пример \(\PageIndex{24}\) Врач Филипа говорит ему, что он должен добавить к своему обычному рациону еще как минимум 1000 калорий в день. Филип хочет купить протеиновые батончики по 1,80 доллара за штуку и содержащие 140 калорий, а также сок по 1,25 доллара за бутылку и содержащий 125 калорий. Он не хочет тратить больше 12 долларов. а. Напишите систему неравенств, моделирующую эту ситуацию. а. в. да Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем линейных неравенств с помощью графика. Системы линейных уравнений К концу этого раздела вы сможете: Прежде чем начать, пройдите этот тест на готовность. Определение системы линейных неравенств очень похоже на определение системы линейных уравнений. Система линейных неравенств Два или более линейных неравенства, сгруппированные вместе, образуют систему линейных неравенств. Система линейных неравенств выглядит как система линейных уравнений, но вместо уравнений содержит неравенства. Система двух линейных неравенств показана ниже. Чтобы решить систему линейных неравенств, найдем значения переменных, которые являются решениями обоих неравенств. Решения системы линейных неравенств Решениями системы линейных неравенств являются значения переменных, при которых все неравенства верны. Решение системы линейных неравенств показано в виде заштрихованной области в системе координат x-y , которая включает все точки, чьи упорядоченные пары делают неравенства верными. Чтобы определить, является ли упорядоченная пара решением системы двух неравенств, подставим в каждое неравенство значения переменных. Если упорядоченная пара делает оба неравенства верными, это решение системы. Определить, является ли заказанная пара решением системы. ⓐ (−2, 4) ⓑ (3,1) Решение Упорядоченная пара (−2, 4) сделала оба неравенства верными. Упорядоченная пара (3,1) сделала одно неравенство истинным, а другое ложным. Поэтому (3,1) не является решением этой системы. Определить, является ли заказанная пара решением системы. ⓐⓑ Определить, является ли заказанная пара решением системы. ⓐⓑ Решением одного линейного неравенства является область по одну сторону от граничной линии, которая содержит все точки, подтверждающие истинность неравенства.Решением системы двух линейных неравенств называется область, содержащая решения обоих неравенств. Чтобы найти эту область, мы изобразим каждое неравенство отдельно, а затем найдем область, в которой они оба верны. Решение всегда отображается в виде графика. Как решить систему линейных неравенств Решите систему с помощью графика. Решите систему с помощью графика. Решите систему с помощью графика. Решите систему линейных неравенств, построив график. Решите систему с помощью графика. Решите систему с помощью графика. Решите систему с помощью графика. Решите систему с помощью графика. Решите систему с помощью графика. Системы линейных неравенств, в которых граничные линии параллельны, могут не иметь решения. Решите систему с помощью графика. Решение В обеих заштрихованных областях нет точек, поэтому система не имеет решения.Эта система не имеет решения. Решите систему с помощью графика. нет решения Решите систему с помощью графика. нет решения Решите систему с помощью графика. Решение В решение не включены точки на граничных линиях, так как обе линии заштрихованы. Решением является дважды заштрихованная область, которая также является решением . Решите систему с помощью графика. Решите систему с помощью графика. Первое, что нам нужно сделать для решения приложений систем неравенств, — это преобразовать каждое условие в неравенство. Затем мы рисуем систему, как мы делали выше, чтобы увидеть область, содержащую решения. Кристи продает свои фотографии в киоске на уличной ярмарке. В начале дня она хочет, чтобы на ее стенде было не менее 25 фотографий. Каждая маленькая фотография, которую она показывает, стоит ей 4 фунта стерлингов, а каждая большая фотография стоит ей 10 фунтов стерлингов. Она не хочет тратить более 200 фунтов стерлингов на фотографии для показа. ⓐ Напишите систему неравенств для моделирования этой ситуации. ⓑ Нарисуйте график системы. ⓒ Может ли она показать 15 маленьких и 5 больших фотографий? ⓓ Может ли она показать 3 большие и 22 маленькие фотографии? Решение Обратите внимание, что мы также можем проверить возможные решения, подставив значения в каждое неравенство. Прицеп может перевозить максимальный вес 160 фунтов и максимальный объем 15 кубических футов. ⓐ Напишите систему неравенств для моделирования этой ситуации. Мэри нужно купить бланки для ответов и карандаши для стандартного теста, который будет сдан младшим классам ее средней школы. Необходимое количество листов для ответов как минимум на 5 больше, чем количество карандашей.Карандаши стоят 2 фунта стерлингов, а листы для ответов — 1 фунт стерлингов. Бюджет Мэри на эти расходные материалы предусматривает максимальную стоимость в 400 фунтов стерлингов. ⓐ Напишите систему неравенств для моделирования этой ситуации. Омару нужно съесть как минимум 800 калорий, прежде чем идти на тренировку своей команды. ⓐ Напишите систему неравенств для моделирования этой ситуации. Решение ⓐ Пусть количество гамбургеров. Сумма, потраченная на гамбургеры по 1,40 евро каждый, плюс сумма, потраченная на печенье по 0,50 евро каждый, не должна превышать 5,00 евро. У нас есть своя система неравенств. ⓑ ⓒ Чтобы определить, удовлетворяют ли 3 гамбургера и 2 печенья критериям Омара, мы смотрим, находится ли точка (3, 1) в области решения.Это. Он может съесть 3 гамбургера и 2 печенья. Мы также можем проверить возможные решения, подставив значения в каждое неравенство. Напряжению нужно потреблять как минимум дополнительно 1000 калорий в день, чтобы подготовиться к марафону. У него есть только 25 фунтов стерлингов, которые он может потратить на дополнительную еду, в которой он нуждается, и он потратит их на 0 фунтов стерлингов.75 пончиков по 360 калорий каждый и 2 энергетических напитка по 110 калорий. ⓐ Напишите систему неравенств, моделирующую эту ситуацию. Врач Филипа говорит ему, что он должен добавить к своему обычному рациону еще как минимум 1000 калорий в день. ⓐ Напишите систему неравенств, моделирующую эту ситуацию. Определить, является ли упорядоченная пара решением системы линейных неравенств В следующих упражнениях определите, является ли каждая упорядоченная пара решением системы. Решение системы линейных неравенств с помощью графика В следующих упражнениях решите каждую систему, построив график. Нет решения Нет решения Решение приложений систем неравенств В следующих упражнениях переведите систему неравенств и решите. Кейтлин продает свои рисунки на окружной ярмарке. Она хочет продать не менее 60 рисунков, у нее есть портреты и пейзажи. Она продает портреты за 15 фунтов и пейзажи за 10 фунтов. Ей нужно продать рисунков на сумму не менее 800 фунтов стерлингов, чтобы получить прибыль. ⓐ Напишите систему неравенств для моделирования этой ситуации. Джейк не хочет тратить больше 50 фунтов стерлингов на мешки с удобрениями и торфяным мхом для своего сада.Удобрение стоит 2 фунта стерлингов за мешок, а торфяной мох стоит 5 евро за мешок. Фургон Джейка может вместить не более 20 сумок. ⓐ Напишите систему неравенств для моделирования этой ситуации. Рэйко нужно отправить свои рождественские открытки и посылки, и она хочет, чтобы ее почтовые расходы не превышали 500 фунтов стерлингов. ⓐ Напишите систему неравенств для моделирования этой ситуации. Хуан готовится к выпускным экзаменам по химии и алгебре. Он знает, что у него есть только 24 часа, чтобы учиться, и ему потребуется как минимум в три раза больше времени, чтобы изучить алгебру, чем химию. ⓐ Напишите систему неравенств для моделирования этой ситуации. Джоселин беременна, и ей нужно съедать как минимум на 500 калорий в день больше, чем обычно. ⓐ Напишите систему неравенств для моделирования этой ситуации. Марк пытается нарастить мышечную массу, поэтому ему нужно дополнительно съедать не менее 80 граммов белка в день. Бутылка протеиновой воды стоит 3 фунта стерлингов.20, а протеиновый батончик стоит 1,75 фунта стерлингов. Протеиновая вода содержит 27 граммов белка, а батончик – 16 граммов. Если у него есть? 10 долларов потратить ⓐ Напишите систему неравенств для моделирования этой ситуации. Джоселин хочет увеличить потребление белка и калорий. Ей нужно как минимум 35 граммов белка в день и не более 200 дополнительных калорий в день.Унция сыра чеддер содержит 7 граммов белка и 110 калорий. Унция сыра пармезан содержит 11 граммов белка и 22 калории. ⓐ Напишите систему неравенств для моделирования этой ситуации. Марк увеличивает количество упражнений, бегая и ходя не менее 4 миль каждый день.Его цель состоит в том, чтобы сжечь минимум 1500 калорий от этого упражнения. При ходьбе сжигается 270 калорий на милю, а при беге — 650 калорий. ⓐ Напишите систему неравенств для моделирования этой ситуации. Билеты на матч Американской бейсбольной лиги для 3 взрослых и 3 детей стоят менее 75 фунтов стерлингов, а билеты для 2 взрослых и 4 детей — менее 62 фунтов стерлингов. ⓐ Напишите систему неравенств для моделирования этой задачи. Дедушка и бабушка угощают свою семью кино. Билеты на утренник стоят 4 фунта стерлингов за ребенка и 4 фунта стерлингов за взрослого. Вечерние билеты стоят 6 фунтов стерлингов за ребенка и 8 фунтов стерлингов за взрослого. ⓐ Напишите систему неравенств для моделирования этой ситуации. Нарисуйте график неравенства . Как узнать, какая сторона линии должна быть заштрихована? Граф системы .Что означает решение? ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела. ⓑ Изучив этот контрольный список, что вы сделаете, чтобы стать уверенным в выполнении всех задач? Определить, является ли упорядоченная пара решением системы уравнений . В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений. Решение системы линейных уравнений с помощью графика В следующих упражнениях решите следующие системы уравнений, построив график. совпадающие строки Определение числа решений линейной системы В следующих упражнениях без построения графика определите количество решений и затем классифицируйте систему уравнений. бесконечно много решений, непротиворечивая система, зависимые уравнения нет решений, противоречивая система, независимые уравнения Решение приложений систем уравнений с помощью графиков ЛаВель готовит кувшин кофе мокко. На каждую унцию шоколадного сиропа она использует пять унций кофе. LaVelle нужно 8 унций шоколадного сиропа и 40 унций кофе. Эли готовит смесь для вечеринок, состоящую из кренделей и печенья. На каждую чашку кренделей он использует три чашки chex. Сколько чашек кренделей и сколько чашек chex ему нужно, чтобы приготовить 12 чашек смеси для вечеринок? Решение системы уравнений путем замены В следующих упражнениях решите системы уравнений путем замены. Решение приложений систем уравнений путем замены В следующих упражнениях переведите в систему уравнений и решите. Сумма двух чисел равна 55. Одно число на 11 меньше другого. Найдите числа. Цифры 22 и 33. Периметр прямоугольника равен 128. Длина на 16 больше, чем ширина. Найдите длину и ширину. Размер одного из малых углов прямоугольного треугольника в 2 раза меньше, чем в 3 раза больше, чем размер другого малого угла. Найдите величину обоих углов. Размеры 23 градуса и 67 градусов. Габриэла работает в страховой компании, которая платит ей зарплату в размере 32 000 фунтов стерлингов плюс комиссионные в размере 100 фунтов стерлингов за каждый проданный ею полис.Она подумывает о переходе на другую работу в компанию, которая будет платить зарплату в размере 40 000 фунтов стерлингов плюс комиссионные в размере 80 фунтов стерлингов за каждый проданный полис. Сколько полисов Габриэле нужно продать, чтобы общая сумма выплат осталась прежней? Решите систему уравнений методом исключения В следующих упражнениях решите системы уравнений методом исключения. Решение приложений систем уравнений методом исключения В следующих упражнениях переведите в систему уравнений и решите. Сумма двух чисел равна . Их отличие в том. Найдите числа. Цифры и . Омар каждый день по дороге на работу останавливается в магазине пончиков. На прошлой неделе он съел 8 пончиков и 5 капучино, что дало ему в общей сложности 3000 калорий. На этой неделе он съел 6 пончиков и 3 капучино, что в сумме составило 2160 калорий. Сколько калорий в одном пончике? Сколько калорий в одном капучино? Выберите наиболее удобный метод решения системы линейных уравнений В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения. Перевод в систему уравнений В следующих упражнениях переведите систему уравнений. Сумма двух чисел равна . Одно число в два раза меньше другого. Найдите числа. Четыре раза число плюс три раза второе число . Дважды первое число плюс второе число равно трем.Найдите числа. В прошлом месяце Джим и Дебби заработали 7 200 фунтов стерлингов. Дебби зарабатывала на 1600 фунтов больше, чем Джим. Сколько каждый из них заработал? Генри инвестировал 24 000 фунтов стерлингов в акции и облигации. Сумма в акциях составляет 6000 фунтов стерлингов, что более чем в три раза превышает сумму в облигациях. Сколько стоит каждое вложение? Приложения прямого перевода Solve В следующих упражнениях переведите в систему уравнений и решите. Пэм на 3 года старше своей сестры Джен.Сумма их возрастов равна 99. Найдите их возраст. Молли хочет посадить 200 луковиц в своем саду. Она хочет все ирисы и тюльпаны. Она хочет посадить тюльпанов в три раза больше, чем ирисов. Решить геометрические задачи В следующих упражнениях переведите в систему уравнений и решите. Разница двух дополнительных углов составляет 58 градусов. Найдите меры углов. Размеры: 119 градусов и 61 градус. Два угла дополняют друг друга. Мера большего угла в пять раз больше, чем мера меньшего угла. Найдите меры обоих углов. Бекка вешает 28-футовую цветочную гирлянду с двух сторон и на вершину перголы, чтобы подготовиться к свадьбе. Высота на четыре фута меньше ширины. Найдите высоту и ширину перголы. Пергола имеет высоту 8 футов и ширину 12 футов. Периметр городского прямоугольного парка составляет 1428 футов. Длина 78 футов более чем в два раза превышает ширину. Найдите длину и ширину парка. Решение задач равномерного движения В следующих упражнениях переведите в систему уравнений и решите. Шейла и Ленор ехали к дому своей бабушки. Ленор ушла через час после Шейлы. Шейла ехала со скоростью 45 миль в час, а Ленора ехала со скоростью 60 миль в час. Сколько времени понадобится Ленор, чтобы догнать Шейлу? Это займет у Ленор 3 часа. Боб выехал из дома на велосипеде со скоростью 10 миль в час, чтобы добраться до озера. Шерил, его жена, уехала через 45 минут, ведя машину со скоростью 25 миль в час. Сколько времени потребуется Шерил, чтобы догнать Боба? Маркус может проплыть на своей лодке 36 миль вниз по реке за три часа, но ему требуется четыре часа, чтобы вернуться вверх по течению. Найдите скорость лодки в стоячей воде и скорость течения. Скорость лодки 10,5 миль в час. Скорость тока 1.5 миль в час. Пассажирский самолет может пролететь 804 мили за 2 часа при попутном ветре, но только 776 миль за 2 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. Применение смесей Solve В следующих упражнениях переведите в систему уравнений и решите. Линн заплатила в общей сложности 2780 фунтов стерлингов за 261 билет в театр. Студенческие билеты стоят 10 фунтов стерлингов, а билеты для взрослых – 15 фунтов стерлингов.Сколько студенческих билетов и сколько билетов для взрослых купила Линн? Линн купила 227 студенческих и 34 взрослых билета. В подстаканнике в машине Приама лежат десятицентовики и пенни. Общая стоимость монет составляет 4,21 фунта стерлингов. Количество десятицентовиков в три раза меньше количества пенни, чем в четыре раза. Сколько десятицентовиков и сколько пенни в стакане? Юми хочет приготовить 12 чашек смеси для вечеринок из конфет и орехов. Ее бюджет требует, чтобы смесь для вечеринок стоила ей 1 фунт стерлингов.29 за чашку. Конфеты стоят 2,49 фунта стерлингов за чашку, а орехи — 0,69 фунта стерлингов за чашку. Сколько чашек конфет и сколько чашек орехов она должна использовать? Юми должна использовать 4 чашки конфет и 8 чашек орехов. Ученому требуется 70 литров 40%-го раствора спирта. Решать процентные заявки В следующих упражнениях переведите в систему уравнений и решите. У Джека есть 12 000 фунтов стерлингов для инвестиций, и он хочет получать 7,5% годовых. Он положит часть денег на сберегательный счет, который приносит 4% в год, а остальную часть на депозитный счет, который приносит 9% в год. Сколько денег он должен положить на каждый счет? Джек должен положить 3600 фунтов стерлингов в сбережения и 8400 фунтов стерлингов в компакт-диск. Когда она закончит колледж, Линда будет должна 43 000 фунтов стерлингов в виде кредита на обучение. Процентная ставка по федеральным кредитам составляет 4,5%, а по кредитам частных банков — 2%.Общая сумма процентов, которые она должна за год, составила 1585 фунтов стерлингов. Какова сумма каждого кредита? Определить, является ли упорядоченная пара решением системы линейных неравенств В следующих упражнениях определите, является ли каждая упорядоченная пара решением системы. Решение системы линейных неравенств с помощью графика В следующих упражнениях решите каждую систему, построив график. Нет решения Решение приложений систем неравенств В следующих упражнениях переведите систему неравенств и решите. Роксана делает браслеты и ожерелья и продает их на фермерском рынке. Она продает браслеты по 12 фунтов за штуку и ожерелья по 18 фунтов за штуку. На рынке в следующие выходные у нее будет место, чтобы выставить не более 40 штук, и ей нужно продать не менее чем на 500 фунтов стерлингов, чтобы получить прибыль. У Энни есть бюджет в размере 600 фунтов стерлингов на покупку книг в мягкой обложке и книг в твердом переплете для своего класса. В следующих упражнениях решите следующие системы с помощью графика. В следующих упражнениях решите каждую систему уравнений.Используйте либо замену, либо исключение. бесконечно много решений В следующих упражнениях переведите в систему уравнений и решите. Сумма двух чисел равна −24. Цифры 40 и 64 Рамон хочет посадить огурцы и помидоры в своем саду.У него есть место для 16 растений, и он хочет посадить в три раза больше огурцов, чем помидоров. Сколько огурцов и сколько помидоров он должен посадить? Два угла дополняют друг друга. Мера большего угла в шесть раз больше, чем мера меньшего угла. Найдите меры обоих углов. Меры углов 28 градусов и 62 градуса. В понедельник Лэнс бегал 30 минут и плавал 20 минут. Его фитнес-приложение сообщило ему, что он сжег 610 калорий.В среду фитнес-приложение сообщило ему, что он сжег 695 калорий, когда бегал 25 минут и плавал 40 минут. Сколько калорий он сжег за одну минуту бега? Сколько калорий он сжег за одну минуту плавания? Кэти вышла из дома и направилась в торговый центр, быстро идя со скоростью 4 мили в час. Ее сестра Эбби вышла из дома через 15 минут и поехала на велосипеде в торговый центр со скоростью 10 миль в час. Это займет у Кэти час (или 10 минут). Самолету требуется несколько часов, чтобы пролететь 2475 миль при встречном ветре из Сан-Хосе, Калифорния, в Лихью, Гавайи. Обратный перелет из Лиуэ в Сан-Хосе при попутном ветре занимает 5 часов. Найдите скорость струи в неподвижном воздухе и скорость ветра. Лиз заплатила 160 фунтов стерлингов за 28 билетов, чтобы отвести отряд Брауни в музей науки. Детский билет стоит 5 евро, взрослый — 9 евро. Сколько детских и сколько взрослых билетов купила Лиз? Лиз купила 23 детских билета и 5 взрослых билетов. Фармацевту требуется 20 литров 2% физраствора. У него есть 1% и 5% раствор. Сколько литров однопроцентного и сколько литров пятипроцентного растворов нужно смешать, чтобы получился двухпроцентный раствор? Переведите в систему неравенств и решите. Энди хочет потратить не более 50 фунтов стерлингов на угощения на Хэллоуин. Линейные неравенства с двумя переменными имеют бесконечные множества или бесконечно много упорядоченных парных решений. Эти упорядоченные пары или наборы решений можно изобразить в соответствующей половине прямоугольной координатной плоскости. 
\(\left\{\begin{массив} {l} x−y>3\\y<−15x+4\end{массив}\right.\) График x − y > 3, путем построения графика x − y = 3
и проверки точки.
будет пунктирной.
(красным) сторону, не содержащую (0, 0). График \(y<−15x+4\) путем построения графика \(y=−15x+4\)
с использованием наклона \(m=−15\) и y -точка пересечения b = 4.
Граничная линия будет пунктирной
закрасьте (синим) сторону, содержащую (0, 0). \)
\) \(\left\{\begin{массив} {l} x−2y<5\\y>−4\end{массив}\right.\) Постройте график \(x−2y<5\), построив график \(x−2y=5\)
и проверив точку. Точки пересечения равны
Точки пересечения равны
x = 5 и y = −2,5, а граничная линия
будет пунктирной.
(красным) сторону, содержащую (0, 0). Постройте график \(y>−4\), построив график \(y=−4\) и
, признав, что это горизонтальная линия
, проходящая через \(y=−4\).Линия границы будет
пунктирной.
верным, поэтому закрасьте (синим) сторону, содержащую (0, 0).

The boundary line is dashed. Test with point with coordinates zero and zero which makes the inequality true so the side that contains this point is shaded red.»>
\(\left\{\begin{массив} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{массив}\right.\) График \(4x+3y\geq 12\) путем построения графика \(4x+3y=12\)
и проверки точки. Точки пересечения равны x = 3·
и y = 4, а линия границы будет сплошной.
закрасит (красным) сторону, не содержащую (0, 0). График \(y<−\frac{4}{3}x+1\) путем построения графика \(y=−\frac{4}{3}x+1\)
с использованием наклона \(m= −\frac{4}{3}\) и y — точка пересечения
b = 1. Линия границы будет пунктирной.
Линия границы будет пунктирной.
закрасит (синим) сторону, содержащую (0, 0).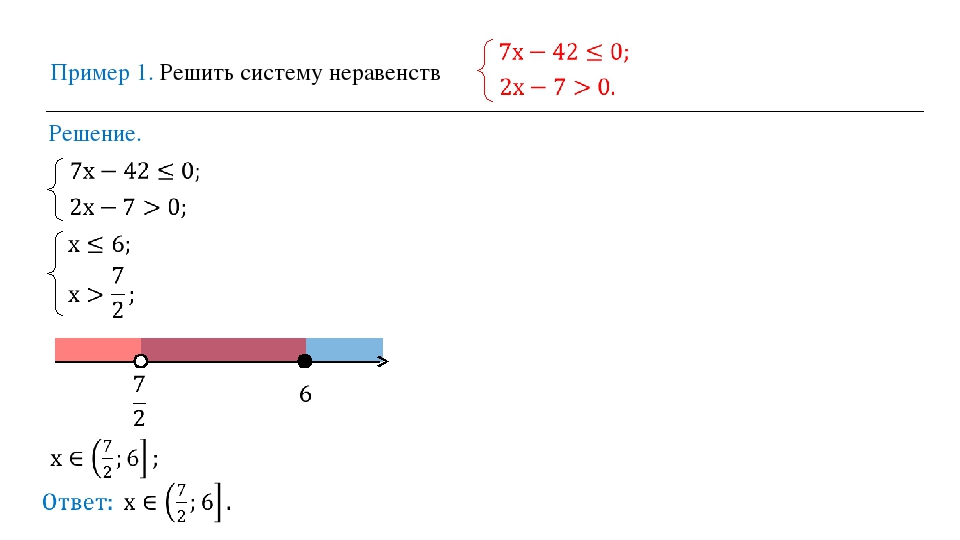 Мы увидим это в следующем примере.
Мы увидим это в следующем примере. \(\left\{\begin{массив} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{массив}\right.  \)
\) График \(y>\frac{1}{2}x−4\) путем построения графика \(y=\frac{1}{2}x−4\)
с использованием наклона \(m=\frac {1}{2}\) и точка пересечения
b = −4. Линия границы будет пунктирной.
закрасит (красным) сторону, содержащую (0, 0). Постройте график \(x−2y<−4\), построив график \(x−2y=−4\)
и проверив точку. Пересечения равны
x = −4 и y = 2, а граничная линия будет пунктирной.
является решением обоих неравенств.
закрасит (синим) сторону, не содержащую (0, 0).
Решение приложений систем неравенств
 Затем мы наносим систему на график, как мы делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичны только в том случае, если обе переменные положительны, поэтому мы добавляем в систему неравенства в качестве дополнительных требований.
Затем мы наносим систему на график, как мы делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичны только в том случае, если обе переменные положительны, поэтому мы добавляем в систему неравенства в качестве дополнительных требований.
б. Нарисуйте систему.
с. Может ли она показать 10 маленьких и 20 больших фотографий?
д.Сможет ли она показать 20 больших и 10 маленьких фотографий?
\(\begin{array} {ll} \text{Let} &{x=\text{количество маленьких фото. }} \\ {} &{y=\text{количество больших фото}}\ конец{массив}\)
}} \\ {} &{y=\text{количество больших фото}}\ конец{массив}\)
Поскольку \(x\geq 0\) и \(y\geq 0\) (оба больше или равны) все решения будут в первом квадранте. В результате на нашем графике показан только один квадрант.
Чтобы построить график \(x+y\geq 25\), нарисуйте \(x+y=25\) сплошной линией.
Выберите (0, 0) в качестве контрольной точки. Так как это не делает неравенство верным, заштрихуйте (красным) сторону, которая не включает точку (0, 0).
Выберите (0, 0) в качестве контрольной точки. Поскольку это делает неравенство верным, заштрихуйте (синим) сторону, содержащую точку (0, 0).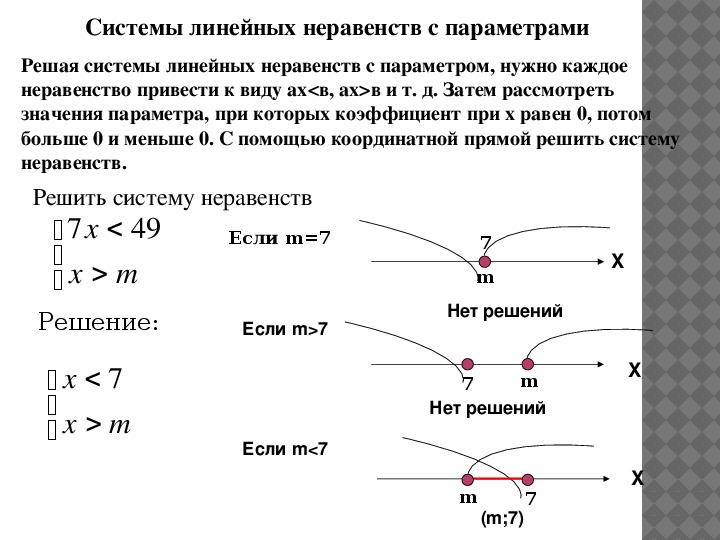 Мы также можем проверить точку, чтобы увидеть, является ли она решением обоих уравнений.
Мы также можем проверить точку, чтобы увидеть, является ли она решением обоих уравнений.
б. Нарисуйте систему.
с. Можно ли перевозить в этом прицепе 4 микроволновки и 2 принтера?
д. Можно ли перевозить в этом прицепе 7 микроволновок и 3 принтера? \)
\)
b.
д. №
б. Нарисуйте систему.
с. Может ли Мэри купить 100 карандашей и 100 листов для ответов?
д. Может ли Мэри купить 150 карандашей и 150 листов для ответов?
b.
д. №
б. Нарисуйте систему.
с. Сможет ли он съесть 3 гамбургера и 1 печенье?
д.Сможет ли он съесть 2 гамбургера и 4 печенья?
\(\begin{array} {ll} \text{Let} &{h=\text{количество гамбургеров.} \\ &{c=\text{количество файлов cookie}\end{array}\)
Так как \(h\geq 0\) и \(c\geq 0\) (оба больше или равны) все решения будут в первом квадранте. В результате на нашем графике показан только один квадрант. It is made by graphing two forty h plus one sixty c equal to eight hundred as a solid line. The point with coordinates zero and zero does not make the inequality true so the side which does not include this point is shaded red.»>
Чтобы построить график \(240h+160c\geq 800\), нарисуйте \(240h+160c=800\) сплошной линией. 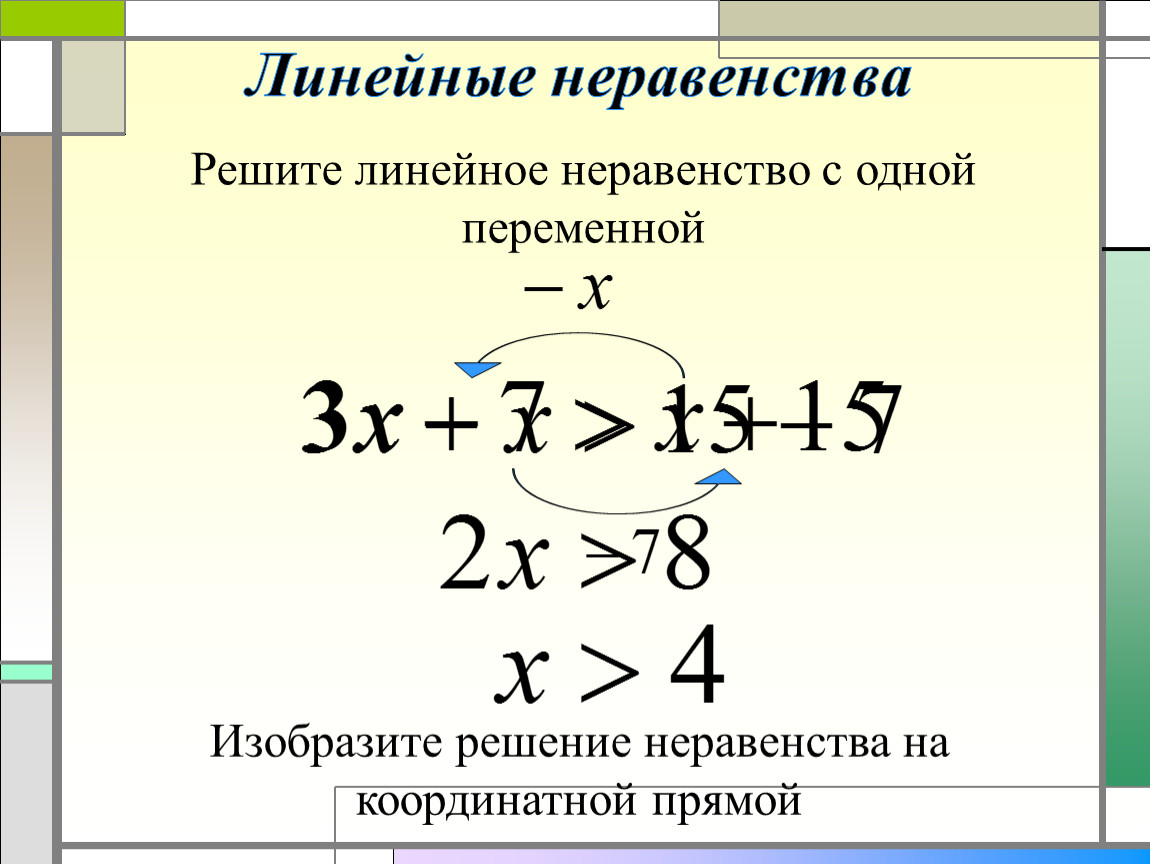

б. Нарисуйте систему.
с. Сможет ли он купить 8 пончиков и 4 энергетических напитка и удовлетворить свою потребность в калориях?
д. Сможет ли он купить 1 пончик и 3 энергетических напитка и удовлетворить свою потребность в калориях?
б.
д. №
б. Нарисуйте систему.
с. Может ли он купить 3 протеиновых батончика и 5 бутылок сока?
д. Может ли он купить 5 протеиновых батончиков и 3 бутылки сока? \(\left\{\begin{массив} {l} 140p+125j\geq 1000\\1.80p+1.25j\leq 12\end{массив}\right.\)
\(\left\{\begin{массив} {l} 140p+125j\geq 1000\\1.80p+1.25j\leq 12\end{массив}\right.\)
b.
д. № Ключевые понятия

Нарисуйте линию границы.
Заштрихуйте ту сторону границы, где верно неравенство.
Нарисуйте линию границы.
Заштрихуйте ту сторону границы, где верно неравенство.
Глоссарий
Графические системы линейных неравенств – Элементарная алгебра
Цели обучения

Если вы пропустили эту проблему, просмотрите (рисунок).
Если вы пропустили эту проблему, просмотрите (рисунок).
Если вы пропустили эту проблему, просмотрите (рисунок) Определить, является ли упорядоченная пара решением системы линейных неравенств
 Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Найдем на плоскости область, содержащую все упорядоченные пары, для которых выполняются оба неравенства.
Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Найдем на плоскости область, содержащую все упорядоченные пары, для которых выполняются оба неравенства. Поэтому (−2, 4) является решением этой системы.
Поэтому (−2, 4) является решением этой системы. Решение системы линейных неравенств с помощью графика

 Мы увидим это на (рис.).
Мы увидим это на (рис.). Решение приложений систем неравенств
 Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому их графики будут показывать только квадрант I.
Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому их графики будут показывать только квадрант I.
количество больших фотографий
Чтобы найти систему неравенств, переведите информацию.
У нас есть система неравенств.
The words say, “To graph x + y is greater than or equal 25, graph x + y = 25 as a solid line. Choose (0, 0) as a test point. Since it does not make the inequality true, shade (red) the side that does not include the point (0, 0). To graph 4x + 10y is less than or equal to 200, graph 4x + 10y = 200 as a solid line. Choose (0, 0) as a test point. Since it does make the inequality true, shade (blue) the side that include the point (0, 0). The graph show two line graphed on an x y-coordinte plane. One line has the area to the right shaded. The other line has the area to the left shaded. There is an area where the shaded areas overlap.» data-label=»»>
На график нарисуйте x + y = 25 сплошной линией.
Выберите (0, 0) в качестве контрольной точки. Так как это не делает неравенство
верным, закрасьте сторону, не содержащую точку (0, 0), красным цветом.
На график нарисуйте график 4 x + 10 y = 200 сплошной линией.
Выберите (0, 0) в качестве контрольной точки. Поскольку это не делает неравенство
верным, закрасьте сторону, содержащую точку (0, 0), синим цветом.
Решением системы является область графика, дважды заштрихованная и поэтому закрашенная темнее. Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, а принтер весит 20 фунтов и занимает 3 кубических фута.
Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, а принтер весит 20 фунтов и занимает 3 кубических фута.
ⓑ Нарисуйте график системы.
ⓒ Можно ли перевозить в этом прицепе 4 микроволновки и 2 принтера?
ⓓ Можно ли перевозить в этом прицепе 7 микроволновых печей и 3 принтера?
ⓑ Нарисуйте график системы.
ⓒ Может ли Мэри купить 100 карандашей и 100 листов для ответов?
ⓓ Может ли Мэри купить 150 карандашей и 150 листов для ответов? Все, что ему нужно, это гамбургеры и печенье, и он не хочет тратить больше пяти фунтов стерлингов. В ресторане, где подают гамбургеры рядом с его колледжем, каждый гамбургер содержит 240 калорий и стоит 1,40 фунта стерлингов. Каждое печенье содержит 160 калорий и стоит 0,50 фунта стерлингов.
Все, что ему нужно, это гамбургеры и печенье, и он не хочет тратить больше пяти фунтов стерлингов. В ресторане, где подают гамбургеры рядом с его колледжем, каждый гамбургер содержит 240 калорий и стоит 1,40 фунта стерлингов. Каждое печенье содержит 160 калорий и стоит 0,50 фунта стерлингов.
ⓑ Нарисуйте график системы.
ⓒ Сможет ли он съесть 3 гамбургера и 1 печенье?
ⓓ Мог бы он съесть 2 гамбургера и 4 печенья?
количество файлов cookie
Чтобы найти систему неравенств, переведите информацию.
Калории от гамбургеров по 240 калорий плюс калории от печенья по 160 калорий должны быть более 800.
Решением системы является область графика, заштрихованная дважды и поэтому закрашенная темнее.
ⓓ Чтобы определить, удовлетворяют ли 2 гамбургера и 4 печенья критериям Омара, мы смотрим, находится ли точка (2, 4) в области решения. Это. Он может съесть 2 гамбургера и 4 печенья.
ⓑ Нарисуйте график системы.
ⓒ Может ли он купить 8 пончиков и 4 энергетических напитка?
ⓓ Может ли он купить 1 пончик и 3 энергетических напитка? Филип хочет купить протеиновые батончики по цене 1 фунт стерлингов.80 каждый и имеют 140 калорий и сок, который стоит 1,25 фунтов стерлингов за бутылку и содержит 125 калорий. Он не хочет тратить больше 12 фунтов стерлингов.
Филип хочет купить протеиновые батончики по цене 1 фунт стерлингов.80 каждый и имеют 140 калорий и сок, который стоит 1,25 фунтов стерлингов за бутылку и содержит 125 калорий. Он не хочет тратить больше 12 фунтов стерлингов.
ⓑ Нарисуйте график системы.
ⓒ Может ли он купить 3 протеиновых батончика и 5 бутылок сока?
ⓓ Может ли он купить 5 протеиновых батончиков и 3 бутылки сока? Основные понятия
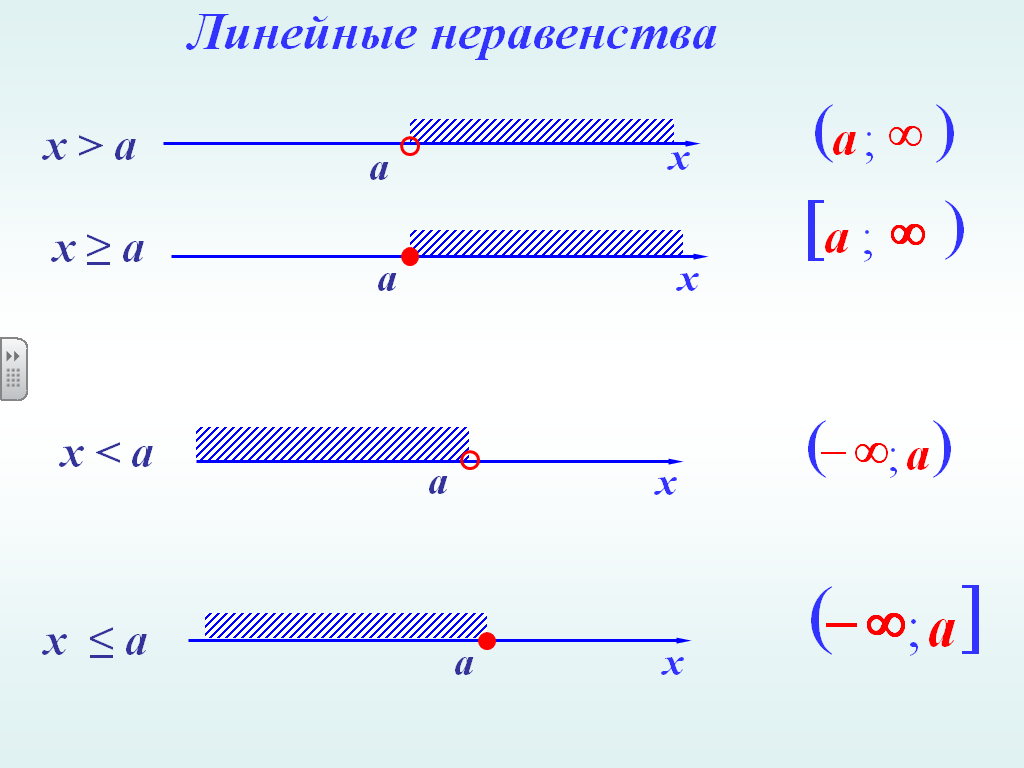
Раздел Упражнения
Практика делает совершенным

ⓑ Нарисуйте график системы.
ⓒ Получит ли она прибыль, если продаст 20 портретов и 35 пейзажей?
ⓓ Получит ли она прибыль, если продаст 50 портретов и 20 пейзажей?
ⓑ Нарисуйте график системы.
ⓒ Может ли он купить 15 мешков удобрений и 4 мешка торфа?
ⓓ Может ли он купить 10 мешков удобрений и 10 мешков торфа? Количество карт не менее чем в 4 раза превышает количество упаковок.Стоимость отправки открытки (с приложенными фотографиями) составляет 3 евро, а посылки — 7 евро.
Количество карт не менее чем в 4 раза превышает количество упаковок.Стоимость отправки открытки (с приложенными фотографиями) составляет 3 евро, а посылки — 7 евро.
ⓑ Нарисуйте график системы.
ⓒ Может ли она отправить по почте 60 открыток и 26 посылок?
ⓓ Может ли она отправить по почте 90 открыток и 40 посылок?
ⓑ Нарисуйте график системы.
ⓒ Сможет ли он потратить 4 часа на химию и 20 часов на алгебру?
ⓓ Может ли он потратить 6 часов на химию и 18 часов на алгебру? Однажды, покупая продукты с бюджетом в 15 фунтов стерлингов на дополнительную еду, она покупает бананы, каждый из которых содержит 90 калорий, и шоколадные батончики мюсли, содержащие 150 калорий каждый.Бананы стоят по 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
Однажды, покупая продукты с бюджетом в 15 фунтов стерлингов на дополнительную еду, она покупает бананы, каждый из которых содержит 90 калорий, и шоколадные батончики мюсли, содержащие 150 калорий каждый.Бананы стоят по 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
ⓑ Нарисуйте график системы.
ⓒ Может ли она купить 5 бананов и 6 батончиков мюсли?
ⓓ Может ли она купить 3 банана и 4 батончика мюсли?
ⓑ Нарисуйте график системы.
ⓒ Может ли он купить 3 бутылки протеиновой воды и 1 протеиновый батончик?
ⓓ Не мог бы он купить бутылки протеиновой воды и 5 протеиновых батончиков?
ⓑ Нарисуйте график системы.
ⓒ Может ли она съесть 1 унцию сыра чеддер и 3 унции сыра пармезан?
ⓓ Может ли она съесть 2 унции сыра чеддер и 1 унцию сыра пармезан?
ⓑ Нарисуйте график системы.
ⓒ Сможет ли он достичь своей цели, пройдя 3 мили и пробежав 1 милю?
ⓓ Сможет ли он достичь своей цели, пройдя 2 мили и пробежав 2 мили? Математика на каждый день
ⓑ Нарисуйте график системы.
ⓒ Билеты могут стоить 20 евро для взрослых и 8 евро для детей?
ⓓ Могут ли билеты стоить 15 евро для взрослых и 5 евро для детей? Они планируют потратить не более 80 фунтов стерлингов на утренние билеты и не более 100 фунтов стерлингов на билеты на вечер.
Они планируют потратить не более 80 фунтов стерлингов на утренние билеты и не более 100 фунтов стерлингов на билеты на вечер.
ⓑ Нарисуйте график системы.
ⓒ Можно ли взять на оба представления 9 детей и 4 взрослых?
ⓓ Можно ли взять на оба представления 8 детей и 5 взрослых? Письменные упражнения
Самопроверка
Упражнения на обзор главы 5
Решение систем уравнений с помощью графика

 Сколько унций шоколадного сиропа и сколько унций кофе ей нужно, чтобы приготовить 48 унций кофе мокко?
Сколько унций шоколадного сиропа и сколько унций кофе ей нужно, чтобы приготовить 48 унций кофе мокко? Решение систем уравнений путем замены

Решение систем уравнений методом исключения

Решение приложений с помощью систем уравнений
 Не решай систему.
Не решай систему. Сколько ирисов и сколько тюльпанов она должна посадить?
Сколько ирисов и сколько тюльпанов она должна посадить?
Решение задач для смесей с помощью систем уравнений

 У него есть 30% и 60% решение. Сколько литров 30-процентного и сколько литров 60-процентного раствора нужно смешать, чтобы получился 40-процентный раствор?
У него есть 30% и 60% решение. Сколько литров 30-процентного и сколько литров 60-процентного раствора нужно смешать, чтобы получился 40-процентный раствор? Графические системы линейных неравенств

ⓐ
ⓑ
ⓒ да
ⓓ нет Она хочет, чтобы количество книг в твердом переплете как минимум в 5 раз превышало количество книг в мягкой обложке.Книги в мягкой обложке стоят 4 фунта стерлингов каждая, а книги в твердом переплете — 15 фунтов каждая.
Она хочет, чтобы количество книг в твердом переплете как минимум в 5 раз превышало количество книг в мягкой обложке.Книги в мягкой обложке стоят 4 фунта стерлингов каждая, а книги в твердом переплете — 15 фунтов каждая. Практический тест
 Одно число на 104 меньше другого. Найдите числа.
Одно число на 104 меньше другого. Найдите числа. Сколько времени понадобится Эбби, чтобы догнать Кэти?
Сколько времени понадобится Эбби, чтобы догнать Кэти? Она хочет купить шоколадные батончики по 1 евро каждая и леденцы по 0,50 евро каждый, и она хочет, чтобы количество леденцов было как минимум в три раза больше, чем количество батончиков.
Она хочет купить шоколадные батончики по 1 евро каждая и леденцы по 0,50 евро каждый, и она хочет, чтобы количество леденцов было как минимум в три раза больше, чем количество батончиков.
ⓐ
ⓑ
ⓒ Нет
ⓓ Да Глоссарий
линейных неравенств с двумя переменными| Графики и уравнения | Примеры

Решенные примеры
Помогите Бобу определить, является ли (2,1/5) решением \[2x + 5y < 10\]
Раствор
Подставим эти значения (2,1/5) в данное линейное неравенство.
Это дает \begin{equation}
2(2)+5(1 / 5)<10
\end{уравнение}
\begin{уравнение} 4 + 1 < 10\end{уравнение}
\begin{equation}5 < 10\end{equation} что верно.
| \(\следовательно\) Таким образом, (2,1/5) является решением \[2x + 5y < 10\] |
Мать Брука передает ему 7 долларов на шоколад. Она говорит ему, чтобы он потратил всего 7 долларов или меньше.
Молочный шоколад стоит 2 доллара, а шоколад с орехами – 33 доллара.
Пусть x — количество молочных шоколадных конфет, а y — количество шоколадных конфет с орехами.
Составьте неравенство, соответствующее приведенной выше ситуации, и начертите неравенство.
Раствор
\[2x + 3y ≤ 7\] будет неравенством, соответствующим приведенной выше ситуации.
В этом случае мы построим сплошную линию как границу, соединяющую точки, удовлетворяющие линейному уравнению \[2x + 3y=7\]
Для \[2x + 3y=7\]
| х | 2 | 5 | -7 |
| и | 1 | -1 | 7 |
Для неравенства \[2x + 3y ≤ 7\]
- Определите некоторые конкретные решения линейного неравенства \[2x + 3y ≤ 7\] , которые могут быть следующими: \begin{equation}(0,1),(-4,0),(1,0),( -5,1),(2,-1)\конец{уравнение}
- Нанесите эти точки на график.
 Они будут лежать ниже сплошной линии.
Они будут лежать ниже сплошной линии.
Теперь положим x = 0, y = 0
Это дает 2(0) + 3(0) ≤ 7, что удовлетворяет неравенству.
Итак, заштрихуйте полуплоскость на графике линейного неравенства ниже, которая включает точку (0,0).
Постройте график набора решений для \[y > -5x + 2 \]
Решение:
\[y > -5x + 2 \] – неравенство в форме пересечения наклона; наклон=-5, точка пересечения=2.
В этом случае мы построим пунктирную линию из-за того, что меньше или равно равенству, как границу, соединяющую точки, удовлетворяющие линейному уравнению \[y = -5x + 2\]
Для \[y = -5x + 2\]
| х | 0 | 1 | 2 | -1 |
| и | 2 | -3 | -8 | 7 |
Для неравенства \[y > -5x + 2 \]
- Определите некоторые конкретные решения линейного неравенства \[y > -5x + 2 \], которые могут быть следующими: \begin{equation}(1,2), (3,-2), (4,3), (4,5), (3,6)\end{уравнение}
- Нанесите эти точки на график.
 Они будут лежать выше пунктирной линии.
Они будут лежать выше пунктирной линии.
Для \[y > -5x + 2 \] поставьте x=0, y=0
Это дает 0>-5(0)+2
, что дает 0>2
.Это неверно для данного неравенства. Итак, заштрихуйте полуплоскость на графике линейного неравенства ниже, которая не включает точку (0,0).
Интерактивные вопросы
Вот несколько упражнений для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнавать о том, что такое линейные неравенства с двумя переменными, решение линейных неравенств с двумя переменными, построение графиков неравенств с двумя переменными, бесконечные множества, упорядоченные пары, больше или равно &, меньше или равно с интерактивными вопросами. Теперь вы сможете легко находить ответы на линейные неравенства с двумя переменными и знать о решениях линейных неравенств.
Мини-урок был посвящен увлекательной концепции линейных неравенств с двумя переменными. Математическое путешествие вокруг линейных неравенств с двумя переменными начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.
О КуэматеНаша команда экспертов по математике в Cuemath стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.
Часто задаваемые вопросы o n Линейные неравенства с двумя переменными
1.
 Что такое система линейных неравенств с двумя переменными?
Что такое система линейных неравенств с двумя переменными?Система линейных неравенств с двумя переменными относится к набору не менее двух линейных неравенств с теми же переменными.
2.Как отличить линейное неравенство с двумя переменными от линейного уравнения с двумя переменными?
График линейных уравнений включает сплошную линию в любой ситуации, тогда как в случае линейных неравенств график включает либо пунктирную, либо сплошную линию. Кроме того, линейные неравенства включают заштрихованные области, а линейные уравнения — нет.
3. Что является примером линейного неравенства?
Примером линейного неравенства может быть любое линейное уравнение, но с такими символами, как <, >, ≤ или ≥ вместо =.
4. Какие символы используются в линейных неравенствах?
В линейных неравенствах используются символы <, ≤, > и ≥.
5. В чем смысл линейных неравенств?
Линейное неравенство — это неравенство, имеющее линейную функцию, состоящую из одного из символов неравенства.
6. Как определить линейное неравенство?
Когда две части уравнения имеют знак, отличный от равного.
7. Для чего используются линейные неравенства?
Система линейных неравенств часто используется для определения максимального или минимального значения ситуации с несколькими ограничениями.
8. Какие 5 символов неравенства?
Пять символов неравенства: ≠ = не равно, > = больше, < = меньше, ≥ = больше или равно & ≤ = меньше или равно.
9. Что означает R в неравенствах?
В неравенствах R соответствует действительным числам и включает все действительные числа.
Линейное неравенство: решение, построение графиков и задач — видео и расшифровка урока
Как решить
Вспомните, когда вы в последний раз решали линейное уравнение.Вы помните шаги, которые вы предприняли? Если вам дали такую задачу, как х + 2 = 6, вы, скорее всего, посмотрели на нее и поняли, что нужно переместить цифру 2 в другую часть уравнения, чтобы ваша переменная была одна. Итак, вы начали вычитать 2 из обеих частей уравнения, помня, что для того, чтобы уравнение оставалось равным, все, что вы делаете с одной частью, вы должны делать и с другой. После вычитания 2 из обеих сторон ваша переменная одна, и вы решили линейное уравнение.Ваш ответ: x = 4.
Итак, вы начали вычитать 2 из обеих частей уравнения, помня, что для того, чтобы уравнение оставалось равным, все, что вы делаете с одной частью, вы должны делать и с другой. После вычитания 2 из обеих сторон ваша переменная одна, и вы решили линейное уравнение.Ваш ответ: x = 4.
Теперь предположим, что вам дали такую задачу, как x + 2 < 6. Сначала вы заметили, что вместо знака равенства у вас есть знак неравенства. Это говорит вам, что это проблема линейного неравенства. Для решения вы используете шаги, очень похожие на шаги решения линейных уравнений. Вы заметили, что 2 находится на той же стороне, что и ваша переменная. Итак, чтобы переместить 2, вы вычитаете его с обеих сторон. Знак неравенства остается прежним. Ваш ответ х < 4.Чтобы сообщить кому-то ответ, вы должны сказать: Все решения — это числа меньше 4.
Знак неравенства дает вам диапазон чисел, которые являются вашими решениями. Чтобы проверить решение, подставьте его в неравенство, и если утверждение остается верным, решение верно. Например, если вы подставите 1 в утверждение x < 4, оно станет 1 < 4. Вы знаете, что 1 определенно меньше 4, поэтому утверждение остается верным, и 1 является допустимым решением.
Например, если вы подставите 1 в утверждение x < 4, оно станет 1 < 4. Вы знаете, что 1 определенно меньше 4, поэтому утверждение остается верным, и 1 является допустимым решением.
Практика
Давайте попробуем попрактиковаться в линейном неравенстве:
Чтобы решить, мы должны изолировать переменную, добавив 5 к обеим сторонам.Затем мы делим обе части на 2, чтобы переменная была сама по себе. В результате получается x < 3, или все числа меньше 3.
Деление на отрицательные числа
Есть один сложный аспект решения линейных неравенств, когда вы делите или умножаете на отрицательное число. В этом случае символ неравенства переворачивается. Помните об этом — это легко забываемое правило.
Например:
Сначала вы решаете неравенство, разделив каждую часть неравенства на -3.Это дает вам x больше или равно -2. Теперь переверните символ, чтобы получить решение: x меньше или равно -2. Помните, переворачивайте символ неравенства всякий раз, когда вы делите или умножаете на отрицательное число.
Теперь переверните символ, чтобы получить решение: x меньше или равно -2. Помните, переворачивайте символ неравенства всякий раз, когда вы делите или умножаете на отрицательное число.
Как построить график
Для построения графика линейных неравенств требуется несколько больше шагов, чем для построения графика линейных уравнений. Например, чтобы нарисовать линейное уравнение x = 4, вы должны поставить закрашенный кружок на число 4 на числовой прямой. Для линейного неравенства x < 4 у вас также будет кружок на числе 4, но это будет открытый кружок.Другими словами, вы рисуете круг вокруг числа 4. Если бы неравенство было меньше или равно, вы нарисовали бы сплошной круг. Чтобы показать часть неравенства, вы затем проводите линию от круга влево, показывая, что включены все числа меньше 4.
График линейного неравенства, такого как y > x + 1, аналогичен построению графика формы линейного уравнения y = x + 1. Это уравнение прямой в форме пересечения наклона, и вы графически аналогично.Однако в случае неравенств, если используется символ < или >, вместо сплошной линии вы нарисуете пунктирную линию. Если символ имеет равную часть в нем, то вы нарисуете сплошную линию.
Это уравнение прямой в форме пересечения наклона, и вы графически аналогично.Однако в случае неравенств, если используется символ < или >, вместо сплошной линии вы нарисуете пунктирную линию. Если символ имеет равную часть в нем, то вы нарисуете сплошную линию.
Заштрихованная область соответствует части неравенства. Подумайте о линейном неравенстве и о том, что оно говорит. В нем говорится, что y больше, чем x + 1. Область над линией дает вам y значений, которые больше, и поэтому это то, что заштриховано.
Итоги урока
Решение линейных неравенств очень похоже на решение линейных уравнений. Основное отличие заключается в том, что вы переворачиваете знак неравенства при делении или умножении на отрицательное число. Графики линейных неравенств имеют еще несколько отличий. При построении графика на числовой линии незакрашенный кружок соответствует символам < и >. Сплошной кружок для двух других символов. На декартовом графике пунктирная линия соответствует символам < и >. Для представления двух других символов используется сплошная линия.Заштрихованная часть включает значения, при которых верно линейное неравенство.
На декартовом графике пунктирная линия соответствует символам < и >. Для представления двух других символов используется сплошная линия.Заштрихованная часть включает значения, при которых верно линейное неравенство.
Уровень 3 — Решение систем линейных неравенств графически
В этом упражнении есть ряд условий. Начнем с их осмысления. Давайте используем b для представления количества буррито, которое покупает Марко, и t для представления количества тако. Поскольку буррито стоят 5 долларов каждый, общая сумма, потраченная только на бурриоты, составляет 5 миллиардов долларов.Точно так же, поскольку тако стоит 3 доллара, общая стоимость тако составляет 3 трлн. Таким образом, общая стоимость может быть выражена как5б+3т.
Поскольку у Марко есть 90 долларов, он не может потратить больше этой суммы. Сумма должна быть меньше или равна 90. Это означает, что5b+3t≤90.
Мы также знаем, что Марко нужно купить достаточно еды, чтобы накормить 10 человек. Предполагая, что никто не хочет делиться тако или буррито, общее количество блюд должно быть не менее 10. Это дает
Предполагая, что никто не хочет делиться тако или буррито, общее количество блюд должно быть не менее 10. Это даетб+т≥10.
Поскольку оба эти неравенства должны выполняться, мы получаем следующую систему неравенств.Решение этой системы дает все возможные комбинации буррито и тако, которые Марко может купить, покупая достаточно еды и не выходя за рамки своего бюджета. Чтобы решить систему, мы должны построить ее график. Сначала запишем неравенства, выделив b.5b+3t≤90
5b≤-3t+90
b≤-53t+590
b≤-0,6т+18
Первое неравенство можно выразить как b≤-0,6t+18. Запись второго неравенства в форме пересечения наклона может быть выполнена за один шаг. В частности, путем вычитания t с обеих сторон.Теперь система может быть выражена как Мы обозначим каждое неравенство, показав его граничную линию и заштриховав соответствующую область. Фиолетовая область представляет набор решений, удовлетворяющих обоим неравенствам. Поскольку Марко не может купить отрицательное количество буррито или тако, нас интересуют только положительные значения b и t.
Любая точка в этом регионе соответствует сочетанию буррито и тако, которое стоит менее 90 долларов и позволяет накормить не менее 10 человек. Давайте посмотрим на уголки этого региона.
Отмеченные точки представляют минимальные и максимальные возможности.
- (10,0) и (0,10) означают, что Марко покупает 10 тако или 10 буррито. Тогда он накормит ровно 10 человек, и у него останутся деньги.
- (0,18) и (30,0) показывают, сколько каждого блюда может купить Марко, если он потратил все деньги и купил только тако или буррито. Таким образом, он может купить 18 буррито или 30 тако.
Поскольку мы не знаем, насколько голодны гости и каковы их предпочтения, Марко должен купить и буррито, и тако.Выберем точку в середине области.
Одна из возможностей состоит в том, что Марко может купить 12 тако и 8 буррито. Таким образом, еды, вероятно, будет достаточно, и у него останутся деньги. Обратите внимание, что, несмотря на то, что десятичные числа являются частью набора решений, ответ следует давать целыми числами, если вы не можете купить часть тако или буррито.
 Также наоборот: а < b, то b > а.
Также наоборот: а < b, то b > а.






 1 . (Обратите внимание, что это откроется в новом окне.)
1 . (Обратите внимание, что это откроется в новом окне.)
 Они будут лежать ниже сплошной линии.
Они будут лежать ниже сплошной линии. Они будут лежать выше пунктирной линии.
Они будут лежать выше пунктирной линии.