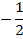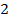Системы линейных неравенств | Алгебра

Системы линейных неравенств с одной переменной с помощью тождественных преобразований сводятся к системе из простейших неравенств.

Рассмотрим на примерах, как решить систему линейных неравенств.

   

Чтобы решить систему, нужно решить каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их  фигурной скобкой.

В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

   

После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:

   

   

Решение неравенств отмечаем на числовых прямых:

В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.

Ответ: x∈[-2;1).

   

В первом неравенстве избавимся от дроби. Для этого обе части умножим почленно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не изменяется.

Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разности двух выражений.

   

Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком и упрощаем:

   

   

Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:

   

   

Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом «меньше меньшего, больше большего«. Меньшим является 1, следовательно, система сводится к неравенству

   

Отмечаем его решение на числовой прямой:

Ответ: x∈(-∞;1].

   

Раскрываем скобки. В первом неравенстве — произведение суммы двух выражений на неполный квадрат их разности. Оно равно сумме кубов этих выражений.

Во втором — произведение суммы и разности двух выражений, что равно разности квадратов. Поскольку здесь перед скобками стоит знак «минус», лучше их раскрытие провести в два этапа: сначала воспользоваться формулой, а уже потом раскрывать скобки, меняя знак каждого слагаемого на противоположный.

   

   

   

Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком:

   

Далее обе части неравенства делим на число, стоящее перед иксом. При делении на отрицательное число знак неравенства меняется на противоположный:

   

   

Оба знака «больше». Используя правило «больше большего», сводим систему неравенств к одному неравенству. Большее из двух чисел 5, следоветельно,

   

Решение неравенства отмечаем на числовой прямой и записываем ответ:

Ответ: x∈(5;∞).

Поскольку в алгебре системы линейных неравенств встречается не только в качестве самостоятельных заданий, но и в ходе решения разного рода уравнений, неравенств и т.д., важно вовремя усвоить эту тему.

В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений либо его решением является любое число.

www.algebraclass.ru

Системы линейных неравенств. Решение систем линейных неравенств

Системой линейных неравенств – называют несколько линейных неравенств, которые должны выполняться одновременно

Например:

\begin{cases}x>4\\x\leq7\end{cases} \begin{cases}2x-5\geq11\\3+x>7\end{cases} \begin{cases}2x\leq19\\3x<14\\5x>-1\end{cases}

Примеры не систем линейных неравенств:

\(\begin{cases}3>4\\x\leq7\end{cases}\)		– первое неравенство не линейное, а числовое
\(\begin{cases}2x^{2}-5\geq11\\3+\frac{1}{x}>7\end{cases}\)		– первое неравенство квадратное, второе дробно-рациональное, т.е. оба не линейные
\(\left[ \begin{gathered} 2x\leq19 \\ 3x<14\\ 5x>-1\\ \end{gathered} \right.\)		—  а это совокупность линейных неравенств, а не система

Решение систем линейных неравенств

Чтобы решить систему неравенств мы должны найти значения иксов, которые подойдут всем неравенствам в системе.

Пример: Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:

Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс  из интервала \((-\infty;7]\) или на числовой оси:

А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.

Ответ: \((4;7]\)

Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.

Если в системе находятся требующие преобразований неравенства, то при решении системы каждое неравенство независимо от других преобразовывается к одному из видов: \(x<c\), \(x>c\), \(x\leq c\), \(x\geq c\). И только после этого ищут общее решение, пересекая решения неравенств на числовой оси.

Пример:  Решить систему \(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\)
Решение:

\(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\)		Перенесем \(-4\) и \(-0,3\) в правую сторону, меняя при этом их знак
\(\begin{cases}x\geq4\\x\geq1,3\end{cases}\)		Отметим решения на числовой оси
		Запишем общее решения неравенств

Ответ: \([4;+\infty)\)

Пример:  Решить систему \(\begin{cases}4(x-1)<3x+1\\-3x+7\geq4(1-x)\end{cases}\)
Решение:

\(\begin{cases}4(x-1)<3x+1\\-3x+7\geq4(1-x)\end{cases}\)		Раскроем в каждом неравенстве скобки
\(\begin{cases}4x-4<3x+1\\-3x+7\geq4-4x\end{cases}\)		Слагаемые с иксом в одну сторону,слагаемые без икса в другую
\(\begin{cases}4x-3x<1+4\\-3x+4x\geq4-7\end{cases}\)		Приведем подобные слагаемые
\(\begin{cases}x<5\\x\geq-3\end{cases}\)		Объединим решения на числовой оси
		Запишем ответ

Ответ: \([-3;5)\)

Заметьте, что для решения первой системы мы использовали две числовые оси, пересекая их пунктиром, а для решения второй и третьей – одну ось. Вы можете сами выбирать сколько осей вам рисовать, оба варианта допустимы. Однако в больших системах (\(3\) или более неравенства) советую для каждого неравенства чертить свою ось.

Системы линейных неравенств и двойные неравенства

Помимо рассмотренных выше примеров, есть особый вид систем линейных неравенств: двойные неравенства. Они притворяются, что совсем не системы, но на самом деле еще какие системы!

Например:  
— неравенство \(3<x-1<7\)  можно записать как  \(\begin{cases}x-1>3\\x-1<7\end{cases}\)
— неравенство \(2x-5<3x+7≤8x\) можно записать как \(\begin{cases}2x-5< 3x+7\\3x+7\leq8x\end{cases}\)

Первое неравенство удобнее решать в виде двойного, из-за того, что в левой и правой части нет

переменных. А вот второе лучше решать как систему из-за того, что иксы есть во всех трех частях неравенства.

Скачать статью

cos-cos.ru

Основные понятия, решение систем линейных неравенств. Видеоурок. Алгебра 9 Класс

На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств. Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.

Тема: Рациональные неравенства и их системы

Урок: Основные понятия, решение систем линейных неравенств

До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и

линейные неравенства, и квадратные и рациональные. Теперь перейдем к решению систем неравенств – сначала линейных систем. Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.

Найти область определения функции 

 

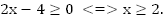
Найти область определения функции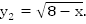 

 

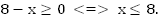
Найти область определения функции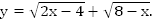

Функция существует, когда существуют оба квадратних корня, т.е.

 

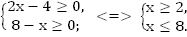
Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.

Изобразим на оси ox множество решений первого и второго неравенства.

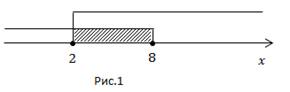
Промежуток пересечения двух лучей и есть наше решение.

Ответ: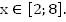

Такой метод изображения решения системы неравенств иногда называют методом крыш.

Решением системы является пересечение двух множеств.

Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.

Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.

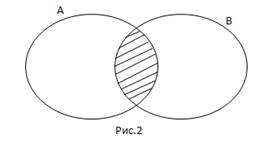
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.

Решить систему неравенств:

1.

 

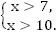
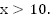
Ответ: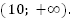

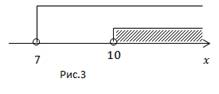
2.

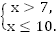
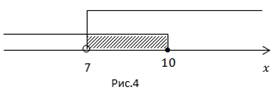
Ответ: (7; 10].

3.

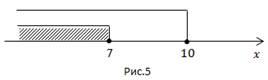
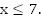
Ответ: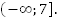

4. Решить систему

Откуда может взяться второе неравенство системы? Например, из неравенства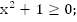

 

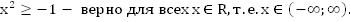
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.

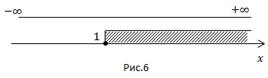
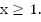
Ответ: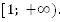

Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.

5.

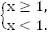
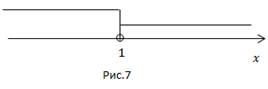
Ответ: 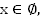система противоречива.

6.

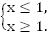
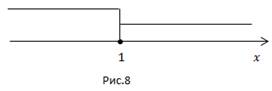
Ответ: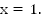

Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.

Рассмотрим следующую систему.

7.

 

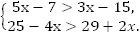
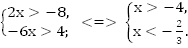
Ответ: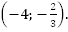

Иногда линейная система задается двойным неравенством, рассмотрим такой случай.

8.

 

 

 

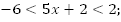
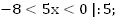
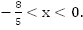
Ответ: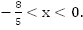

Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Рекомендованные ссылки на интернет-ресурсы

1. Портал Естественных Наук (Источник).

2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).

3. Виртуальный репетитор (Источник).

4. Центр образования «Технология обучения» (Источник).

5. Раздел College.ru по математике (Источник).

 

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.

interneturok.ru

Системы линейных неравенств с одной переменной

Предварительные навыки

Примеры решения систем линейных неравенств с одной переменной

Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.

Рассмотрим простейший пример. Система состоит из двух неравенств, которые уже решены.

Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.

Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:

Но дело в том, что неравенства x > 4 и x < 9 соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.

Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.

Значит решениями системы  являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x < 9 строгие. Ответ можно записать в виде числового промежутка:

x ∈ ( 4 ; 9 )

Также, нужно изобразить множество решений системы на координатной прямой.

Для системы линейных неравенств решение на координатной прямой изображают так:

Сначала указывают границы обоих неравенств:

На верхней области отмечают множество решений первого неравенства x > 4

На нижней области отмечают множество решений второго неравенства x < 9

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:

Для проверки можно взять любое число из этого промежутка и подставить его в исходную систему . Возьмем, например, число 6

Видим, что решение 6 удовлетворяет обоим неравенствам. Возьмём ещё какое-нибудь число из промежутка (4; 9), например, число 8

Видим, что решение 8 удовлетворяет обоим неравенствам.

Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:

Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.

Пример 2. Решить систему неравенств 

Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.

Решениями же обоих неравенств являются все числа, которые больше 17.

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка.

Для начала отметим на координатной прямой границы обоих неравенств:

На верхней области отметим множество решений первого неравенства x > 17

На нижней области отметим множество решений второго неравенства x > 12

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:

x ∈ ( 17 ; +∞ )

---

Пример 3. Решить систему неравенств 

Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок

Получили систему . На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.

Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства (x > 6 и x > 3). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы 

x ∈ ( 6 ; + ∞ )

---

Пример 4. Решить систему неравенств 

Решим каждое неравенство по отдельности:

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка:

---

Пример 5. Решить неравенство 

Решим каждое неравенство по отдельности:

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка:

---

Когда решений нет

Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.

Пример 1. Решить неравенство 

Решим каждое неравенство по отдельности:

Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.

Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:

На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система 

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система 

Ответ: решений нет.

---

Пример 2. Решить систему неравенств 

Решим каждое неравенство по отдельности:

Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:

Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система 

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система

Ответ: решений нет.

---

Пример 3.  Решить систему неравенств 

Решим каждое неравенство по отдельности:

Получили неравенства 0 < −0,2 и a > 5. Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a, то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система 

Ответ: решений нет.

---

Задания для самостоятельного решения

Задание 1. Решите неравенство:

Решение:

Задание 2. Решите неравенство:

Задание 3. Решите неравенство:

Задание 4. Решите неравенство:

Задание 5. Решите неравенство:

Задание 6. Решите неравенство:

Задание 7. Решите неравенство:

Задание 8. Решите неравенство:

Решение:

Решений нет

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

spacemath.xyz

Основные понятия, решение линейных неравенств. Видеоурок. Алгебра 9 Класс

Тема: Рациональные неравенства и их системы. Линейные и квадратные неравенства (повторение)

Урок: Основные понятия, решение линейных неравенств

Рациональные неравенства – основные понятия и решения квадратных и линейных неравенств (9 класс)

 

Линейное и квадратное неравенство, повторение, урок 1, основные понятия решения линейных неравенств

 

Неравенство с одной переменной имеет вид: f(x) > 0, вместо (> 0) может быть (≥ 0), (< 0), (≤ 0).

Для определенности будем записывать неравенство в виде f(x) > 0.

x – переменная,

f – функция, выражение, зависящее от х.

 

В зависимости от f различают разные типы неравенств. Если f – линейная функция, то это линейное неравенство. Если f – квадратичная функция, то это квадратное неравенство.

Итак, линейное неравенство имеет вид ax+b>0, предполагается, что a≠0.

Квадратное неравенство имеет вид .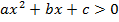

Значение x_o, при котором неравенство обращается в верное числовое неравенство, является частным решением неравенства. Решить неравенство – найти все решения неравенства. Множество всех решений неравенства называется общим решением неравенства, или просто решением неравенства.

Рассмотрим пример:

1) Решить неравенство 2x – 5 > 9.

Это линейное неравенство, найдем его решение и обсудим основные понятия.

2x – 5 > 9 <=> 2x > 14 (5 перенесли в левую часть с противоположным знаком), далее разделили все на 2 и получили x > 7. Изобразим множество решений на оси x.

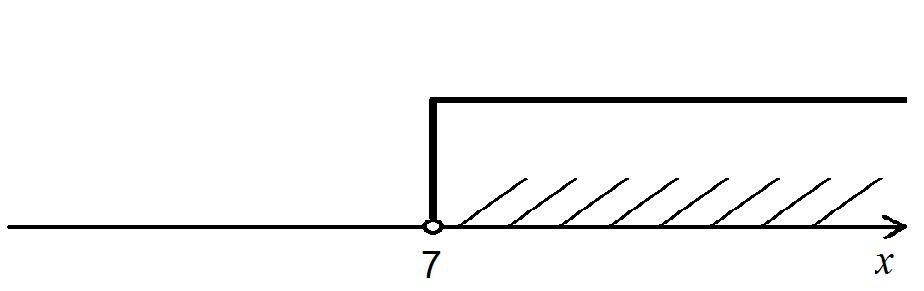
Это положительно направленный луч. Записывается множество решений либо в виде неравенства x > 7, либо в виде интервала  (7; ∞). А что является частным решением этого неравенства? Например, x = 10 – это частное решение этого неравенства, x = 12 – это тоже частное решение этого неравенства.

Частных решений много, но наша цель – найти все решения. А решений, как правило, бесчисленное множество.

Рассмотрим пример 2:

2) Решить неравенство 4a – 11 > a + 13.

Решим его: а перенесем в одну сторону, 11 перенесем в другую сторону, получим 3a > 24, и в результате после деления обеих частей на 3 получим a > 8.

4a – 11 > a + 13 <=> 3a > 24 <=> a > 8.

Тоже изобразим множество a > 8, но уже на оси а.

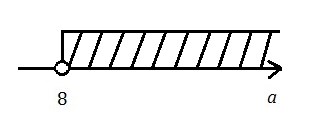
Ответ либо записывается в виде неравенства a > 8, либо а 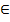 (8; +∞), 8 не включается.

При решении неравенства есть важное отличие его от уравнений, которое состоит в том, что любое решение уравнения можно проверить просто подстановкой в исходное уравнение. В неравенствах такой возможности нет, здесь бесчисленное множество решений подставить в исходное неравенство не представляется возможным. Поэтому есть важное понятие, вот эти стрелочки <=> — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными, если они не искажают множества решений. О важности эквивалентных (равносильных) преобразований можно узнать, рассмотрев следующий пример.

3) Решить неравенство  ≤ 1.

Решение будем искать среди x ≠ 0, потому что x стоит в знаменателе. Если x ≠ 0, то обе части неравенства можно умножить на x: 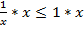, основное свойство дроби позволяет сократить в левой части 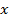, и в результате получим  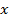≥ 1.

Однако неравенство решено неверно. Почему? Возьмем 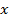 =-1, которое не входит в найденный промежуток, подставив его в исходное неравенство, получим -1 ≤ 1, т.е. это еще одно частное решение исходного неравенства: -1.

Что же мы сделали? Мы обе части неравенства  ≤ 1 умножили на 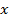, не зная знака этого выражения, ведь  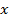может принимать как положительные значения, так и отрицательные.

Таким образом, мы подтвердили важность эквивалентных, равносильных преобразований. Вспомним, что это за равносильные, эквивалентные преобразования, и продемонстрируем их на конкретном примере.

Решить неравенство 2 – 2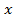 >4.

1. Любой член неравенства можно перенести в другую сторону с противоположным знаком, равносильность, эквивалентность не нарушится.

2 – 2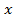 > 4 <=> -2 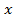> 4 – 2 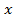<=> -2 > 2

Эквивалентность не нарушилась, о чем мы говорим вот таким знаком <=>.

2. Второе правило нам говорит, что обе части неравенства можно умножить или разделить на одно и то же отрицательное число, при этом знак неравенства изменится на противоположный.

3. И еще одно правило: обе части неравенства можно умножить или разделить на одно и то же положительное число, и знак неравенства не изменится.

Теперь исходное неравенство имеет вид: -2x > 2. Давайте обе части неравенства разделим на (-2):

-2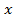 >2 <=>  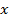<-1. Знак неравенства изменится, т.к. мы делим на (-2) и пользуемся соответствующим правилом.

Мы пользовались равносильными, эквивалентными преобразованиями и получили правильный ответ: 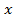 < -1.

Еще один пример, решить неравенство a(a – 2) – a² > 5 – 3a. Делаем стандартные преобразования: раскрываем скобки, получаем равносильное неравенство, которое потом упрощаем, т.е. приводим подобные члены – a² уничтожается, -3a переносим, меняя знак.

a(a – 2) – a² > 5 – 3a <=> a² – 2a — a² > 5 – 3a <=> 3a – 2a > 5 <=> a > 5.

Итак, a(a – 2) – a² > 5 – 3a – исходное неравенство, a > 5 – его решение. Мы пользовались только эквивалентными, равносильными преобразованиями и получили ответ, который не надо проверять.

Следующий пример, решить неравенство 5y² – 5y(y + 4) ≥ 100.

Любые неравенства, в том числе и простейшие, которые мы сейчас рассматриваем, решаются только эквивалентными преобразованиями. Выполняем их:   скобки, приводим подобные члены:

5y² – 5y(y + 4) ≥ 100 <=> 5y² – 5y² – 20y ≥ 100 <=> -20y ≥ 100 <=> 20y ≤ -100 <=> y ≤-5.

Исходное неравенство 5y² – 5y(y + 4) ≥ 100, его ответ y ≤-5.

Таким образом, мы рассмотрели основные понятия, связные с неравенством, вспомнили, что значит «решить неравенство», что такое «общее решение неравенства», вспомнили, что неравенства можно решать только эквивалентными преобразованиями, и выяснили, что же это за эквивалентные преобразования.

Следующий пример. Решить неравенство:

 

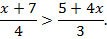
Решаем только эквивалентными преобразованиями: перенесем все в одну сторону и приведем все к общему знаменателю, далее обе части можно умножить на знаменатель и получить только числитель. Далее нам приходится разделить на отрицательное число. Это сделать можно, если знак неравенства изменить на противоположный:

 

 

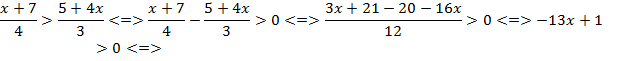
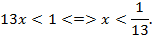
Итак, мы продемонстрировали решение некоторого количества примеров эквивалентными преобразованиями, и только ими можно решать неравенства.

Линейные неравенства – это неравенства вида ax + b > 0. Линейное неравенство тесно связано с линейной функцией. В левой части неравенства стоит линейная функция y = ax + b. Мы знаем график линейной функции, мы знаем, где она положительная, где отрицательная, и поэтому с помощью графика линейной функции мы можем решить неравенство. Например, решить неравенство: 2x + 1 > 0. Рассмотрим линейную функцию y = 2x + 1, составим таблицу:

x	0
y	1	0

Эта функция положительна при всех значениях x больше 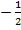. Ответ: x > .

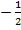Таким образом, выясняется, что линейная функция разбивает всю область определения на два больших луча. В одном луче она отрицательна, в другом луче она положительна, и, следовательно, решение неравенства очень просто.

Приведем еще один пример. Решить неравенство: -3x + 6 > 0. Снова решаем с помощью линейной функции. Рассмотрим функцию y = -3x + 6 и построим ее график с помощью таблицы:

x	0
y	6	0

 

 

Нулем этой функции является 2. Эта функция сохраняет свой знак при 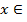(-∞; 2), и она положительна. И она также сохраняет свой знак при  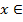(2; ∞), и при всех этих значениях функция отрицательна. Нам нужны те x, при которых функция положительна. Получим ответ x 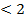, запишем его в виде промежутка (-∞; 2).

 

Итак, мы рассмотрели основные положения, которые нужны для решения неравенств, вспомнили, что такое неравенство, что такое частное решение, что такое общее решение, что такое эквивалентные преобразования, и рассмотрели решение линейных неравенств с помощью эквивалентных преобразований или с помощью графика линейной функции.

 

Список литературы

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8 класс: учебник для 8 кл. общеобраз-х учреждений; под ред. С.А. Теляковского, 15-е изд., дораб. — М.: Просвещение, 2007.

Макарычев Ю.Н. Алгебра. 8 класс. — 10-е изд., испр. — М.: Мнемозина, 2010.

Алимов Ш.А. и др. Алгебра. 8 класс. Учебник. Алимов Ш.А. и др. 17-е изд. – М.: Просвещение, 2010.

 

Домашнее задание

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8 класс: учебник для 8 кл. общеобраз-х учреждений; под ред. С.А. Теляковского, 15-е изд., дораб. — М.: Просвещение, 2007.

№№785, 789, 793, 798.

interneturok.ru

2.2.5 Системы линейных неравенств

Видеоурок: Решаем систему линейных неравенств

Лекция: Системы линейных неравенств

Системы неравенств — это несколько неравенств, объединенных системой, которые имеют одинаковые решения для некоторой переменной.

Решить систему неравенств — это значит найти такое решение или совокупность решений, которые будут удовлетворять всем неравенствам системы.

Линейные неравенства могут быть строгими — это определяется знаком неравенства: <, >. Линейные неравенство нестрогие, если в них имеется следующий знак неравенства: ≥, ≤.

Если мы рассматриваем линейное уравнение, мы знаем, что на плоскости мы имеем право начертить прямую. Решением такого уравнения будет точка пересечения прямой с осью ОХ.

Когда речь заходит о линейных неравенствах, это значит, что на плоскости мы имеем некоторое решение, которое находится в некотором диапазоне относительно построенной прямой. При рассмотрении систем линейных неравенств мы получаем две прямые на плоскости, которые ограничивают некоторый диапазон, в котором находятся все решения, удовлетворяющие неравенства.

Все мы знаем, что координатную плоскость делят на четверти. Давайте рассмотри решения некоторых простейших систем линейных неравенств:

1.

Решением первого неравенства будет первая и четвертая четверть. Решением второго — первая и вторая. Не сложно заметить, что первая четверть является решением первого и второго неравенства. Это значит, что решением данной системы будут все пары чисел, которые находятся в первой четверти.

Аналогично данному решению можно рассмотреть следующие системы:

2.

Решением первого неравенства будет вторая и третья четверть. Решением второго — первая и вторая. Не сложно заметить, что вторая четверть является решением первого и второго неравенства. Это значит, что решением данной системы будут все пары чисел, которые находятся во второй четверти.

3.

Решением первого неравенства будет вторая и третья четверть. Решением второго — третья и четвертая. Не сложно заметить, что первая четверть является решением первого и второго неравенства. Это значит, что решением данной системы будут все пары чисел, которые находятся в третьей четверти.

4.

Решением первого неравенства будет первая и четвертая четверть. Решением второго — третья и четвертая. Не сложно заметить, что четвертая четверть является решением первого и второго неравенства. Это значит, что решением данной системы будут все пары чисел, которые находятся в четвертой четверти.

Так же существуют случаи, когда системы неравенств будут несовместными, то есть неравенства не будут иметь общих решений.

cknow.ru

36. Решение систем линейных неравенств

Решение систем линейных неравенств

 

Определение 1. Совокупность точек пространства Rⁿ, координаты которых удовлетворяют уравнению а₁х₁+ а₂х₂+…+a_nx_n = b, называется (n — 1)-мерной гиперплоскостью в n-мерном пространстве.

Теорема 1. Гиперплоскость делит все пространство на два полупространства. Полупространство является выпуклым множеством.

Пересечение конечного числа полупространств является выпуклым множеством.

Теорема 2. Решением линейного неравенства с n неизвестными

а₁х₁+ а₂х₂+…+a_nx_n  b

является одно из полупространств, на которые все пространство делит гиперплоскость

а₁х₁+ а₂х₂+…+a_nx_n = b.

Рассмотрим систему из m линейных неравенств с n неизвестными.

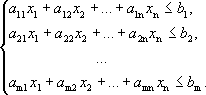
Решением каждого неравенства системы является некоторое полупространство. Решением системы будет являться пересечение всех полупространств. Это множество будет замкнутым и выпуклым.

Решение систем линейных неравенств

с двумя переменными

 

Пусть дана система из m линейных неравенств с двумя переменными.

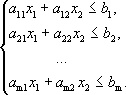
Решением каждого неравенства будет являться одна из полуплоскостей, на которые всю плоскость разбивает соответствующая прямая. Решением системы будет являться пересечение этих полуплоскостей. Данная задача может быть решена графически на плоскости Х₁0Х₂.

37. Представление выпуклого многогранника

Определение 1. Замкнутое выпуклое ограниченное множество в Rⁿ, имеющее конечное число угловых точек, называется выпуклым n-мерным многогранником.

Определение 2. Замкнутое выпуклое неограниченное множество в Rⁿ , имеющее конечное число угловых точек, называется выпуклой многогранной областью.

Определение 3. Множество А Rⁿ называется ограниченным, если найдется n-мерный шар, содержащий это множество.

 

Определение 4. Выпуклой линейной комбинацией точек 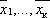называется выражение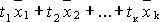, гдеt_i, .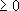

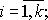
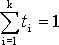Теорема (теорема о представлении выпуклого многогранника). Любую точку выпуклого многогранника можно представить в виде выпуклой линейной комбинации его угловых точек.

38. Область допустимых решений системы уравнений и неравенств.

 

Пусть дана система из m линейных уравнений и неравенств с n неизвестными.

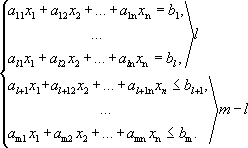
Определение 1. Точка  Rⁿ называется возможным решением системы, если ее координаты удовлетворяют уравнениям и неравенствам системы. Совокупность всех возможных решений называется областью возможных решений (ОВР) системы.

Определение 2. Возможное решение, координаты которого неотрицательны, называется допустимым решением системы. Множество всех допустимых решений называется областью допустимых решений (ОДР) системы.

Теорема 1. ОДР является замкнутым, выпуклым, ограниченным (или неограниченным) подмножеством вRⁿ.

Теорема 2. Допустимое решение системы является опорным тогда и только тогда, когда эта точка являетсяугловой точкой ОДР.

Теорема 3 (теорема о представлении ОДР). Если ОДР — ограниченное множество, то любое допустимое решение можно представить в виде выпуклой линейной комбинации угловых точек ОДР (в виде выпуклой линейной комбинации опорных решений системы).

Теорема 4 (теорема о существовании опорного решения системы). Если система имеет хотя бы одно допустимое решение (ОДР), то среди допустимых решений существует хотя бы одно опорное решение.

studfile.net