| 1. |
Определение линейного уравнения
Сложность: лёгкое |
1 |
| 2. |
Определение коэффициентов линейного уравнения
|
3 |
| 3. |
Определи значение y, зная x
Сложность: лёгкое |
1 |
| 4. |
Определи значение x, зная y
Сложность: лёгкое |
1 |
| 5. |
Принадлежность пары чисел уравнению
|
2 |
| 6. |
Определение ординаты точки прямой
Сложность: среднее |
2 |
| 7. |
Выражение одной переменной через другую
Сложность: среднее |
3 |
| 8. |
Определение пары чисел
Сложность: сложное |
3 |
| 9. |
Решение текстовой задачи с построением графиков
Сложность: сложное |
4 |
| 10. |
Расположение графика линейного уравнения в плоскости
Сложность: сложное |
3 |
| 11. |
Будут ли прямые пересекаться?
Сложность: сложное |
4 |
www.yaklass.ru
| 1. | Определение линейного уравнения | 1 вид — рецептивный | лёгкое | 1 Б. | Сравнивая данное уравнение с определением линейного уравнения, делается вывод о виде уравнения. |
| 2. | Определение коэффициентов линейного уравнения | 1 вид — рецептивный | лёгкое | 3 Б. | Для определения коэффициентов a, b и c сравниваем данное линейное уравнение с его определением. |
| 3. | Определи значение y, зная x | 1 вид — рецептивный | лёгкое | 1 Б. | Для определения значения y, соответствующего значению x, подставим в данное линейное уравнение значение x и найдём y. |
| 4. | Определи значение x, зная y | 1 вид — рецептивный | лёгкое | 1 Б. | Для определения значения x, соответствующего значению y, подставим в данное линейное уравнение значение y и найдём x. |
| 5. | Принадлежность пары чисел уравнению | 2 вид — интерпретация | среднее | 2 Б. | Определяется принадлежность пары чисел данному линейному уравнению. |
| 6. | Определение ординаты точки прямой | 2 вид — интерпретация | среднее | 2 Б. | Зная абсциссу некоторой точки прямой, заданной уравнением, определяем её ординату. |
| 7. | Выражение одной переменной через другую | 2 вид — интерпретация | среднее | 3 Б. | Используя данное в задании линейное уравнение, выражаем одну переменную через другую. |
| 8. | Определение пары чисел | 3 вид — анализ | сложное | 3 Б. | В упражнении определяется пара чисел, у которой первая координата больше, чем вторая, в несколько раз. |
| 9. | Решение текстовой задачи с построением графиков | 3 вид — анализ | сложное | 4 Б. | В решении задачи используются две переменные, и строятся затем графики полученных линейных уравнений, координаты точки пересечения являются решением. В шагах решения предложен схематичный рисунок ко всем генерациям. Точность при построении проверяет учитель. |
| 10. | Расположение графика линейного уравнения в плоскости | 3 вид — анализ | сложное | 3 Б. | Анализируется расположение графика линейного уравнения в плоскости в зависимости от значения коэффициентов a, b и c. |
| 11. | Будут ли прямые пересекаться? | 3 вид — анализ | сложное | 4 Б. | Предлагается, не выполняя построения, определить пересечение прямых в заданной точке. |
www.yaklass.ru
Урок по алгебре в 7 классе «Линейное уравнение с двумя переменными»
Тема урока: «Линейные уравнения с двумя переменными»
Тип урока: урок формирования знаний
Цель урока: формирование умения выражать одну переменную через другую, используя свойства уравнений, составлять уравнение с двумя переменными по условию задачи.
Задачи:
Задачи, которые должен решать учитель, на уроке:
учить использовать приобретённые знания для решения нестандартных задач;
учить умению математически правильно высказать свою мысль.
Задачи, которые должны решать ученики на данном уроке:
знать определение линейного уравнения с двумя переменными; что является решением линейного уравнения с двумя переменными?
уметь составлять простые линейные уравнения;
уметь выделять среди уравнений линейные уравнения с двумя переменными;
как узнать: является ли пара чисел решением уравнения?
уметь выразить одну переменную через другую;
уметь составлять уравнение с двумя переменными по условию задачи;
знать свойства уравнений.
Ход урока:
I. Организационный момент (Слайд1).
Урок я бы хотела начать со слов известного ученого Альберт Эйнштейн.
«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно»
Альберт Эйнштейн
Сообщение цели и темы урока:
Сегодня на уроке мы продолжим изучение уравнений. Записываем в тетради число и тему урока. Но прежде давайте повторим.
II. Актуализация знаний.
2x+y=-5
x+3y=-5
1) определите и прочитайте уравнения, которые являются линейными уравнениями с двумя переменными (Слайд2).
2x-y=7
5х+2у=10;
xy=0
-7х+у=5;
6х²=36;
2х-5у-9=0:
7х+3у³ =5;
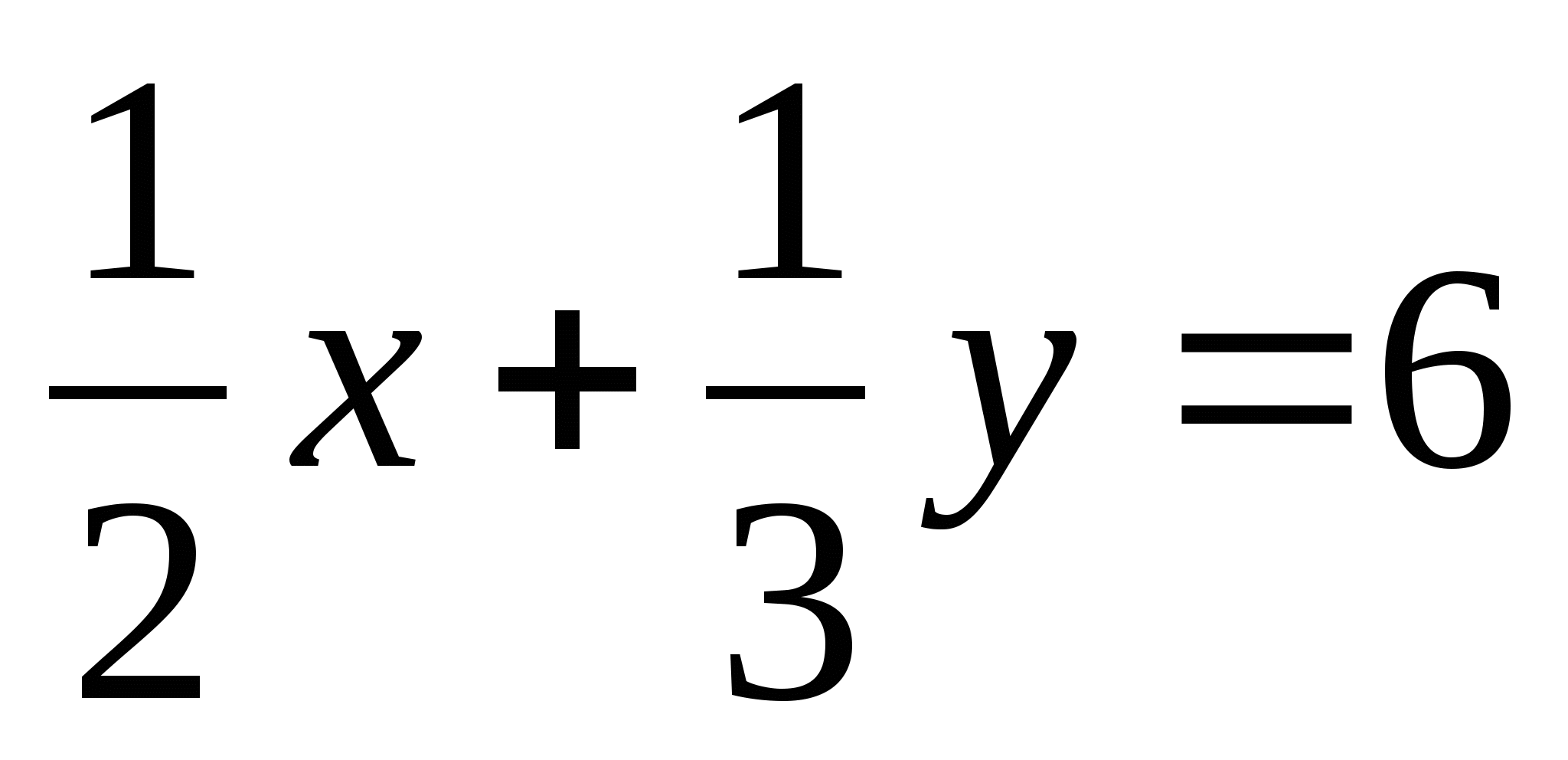
х:5- у:4=3
x2+2y=0
3x+5=7
x+y=0
2) Ответьте на вопрос: Какое уравнение называется линейным уравнением с двумя переменными?
3) (Слайд3) Определите какие из данных пар чисел являются решением уравнения x-3y=10:
(10;0) (3;11) (7;-2) (16;2) (0;10) (7;-1) (13;5)
Как определяли?
4) (Слайд 4) Сколько еще можно отыскать решений данного уравнения? Сколько решений может иметь линейного уравнения с двумя переменными?
5) Что является решением линейного уравнения с двумя переменными?
6) Как быстро отыскать ещё решения данного уравнения?
Для этого необходимо выполнить некоторые преобразования, используя свойства уравнений, выразить одну переменную через другую
x-3y=10
х = 10-3у
Мы получили формулу, которая позволит нам найти значение х, зная значение у. уравнения у=10-3х и х-3у=10-равносильные, так они имеют одинаковые решения.
II. Закрепление знаний.
1. (Слайд 5) Работа в парах: (в тетрадях)
Выразите в следующих уравнениях y через x и x через y.
x+y=7
x-2y=-8
-3x-8y=2,4
x-y=-2
x+3y=0
2x+5y=-10
y-x=0
-2x+y=5
2y-3x=0
Найдите три каких либо решения последнего уравнения.
2. Историческая справка
Иногда при решении задачи требуется найти все пары целых чисел или все пары натуральных чисел, удовлетворяющие уравнению с двумя переменными. В таком случае говорят, что надо «решить уравнение в целых числах» или «решить уравнение в натуральных числах». Уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называются диофантовыми уравнениями. (Презентация Каримовой Эльзы)
3. (Слайд 6, 7) Составим линейное уравнение с двумя переменными к задаче Диофанта и решим ее: во дворе дома ходят фазаны и кролики. Количество всех ног оказалось равным 26. Определить сколько было фазанов и кроликов.
x- количество фазанов
y-количество кроликов
2x+4y=26
Выразим y через x
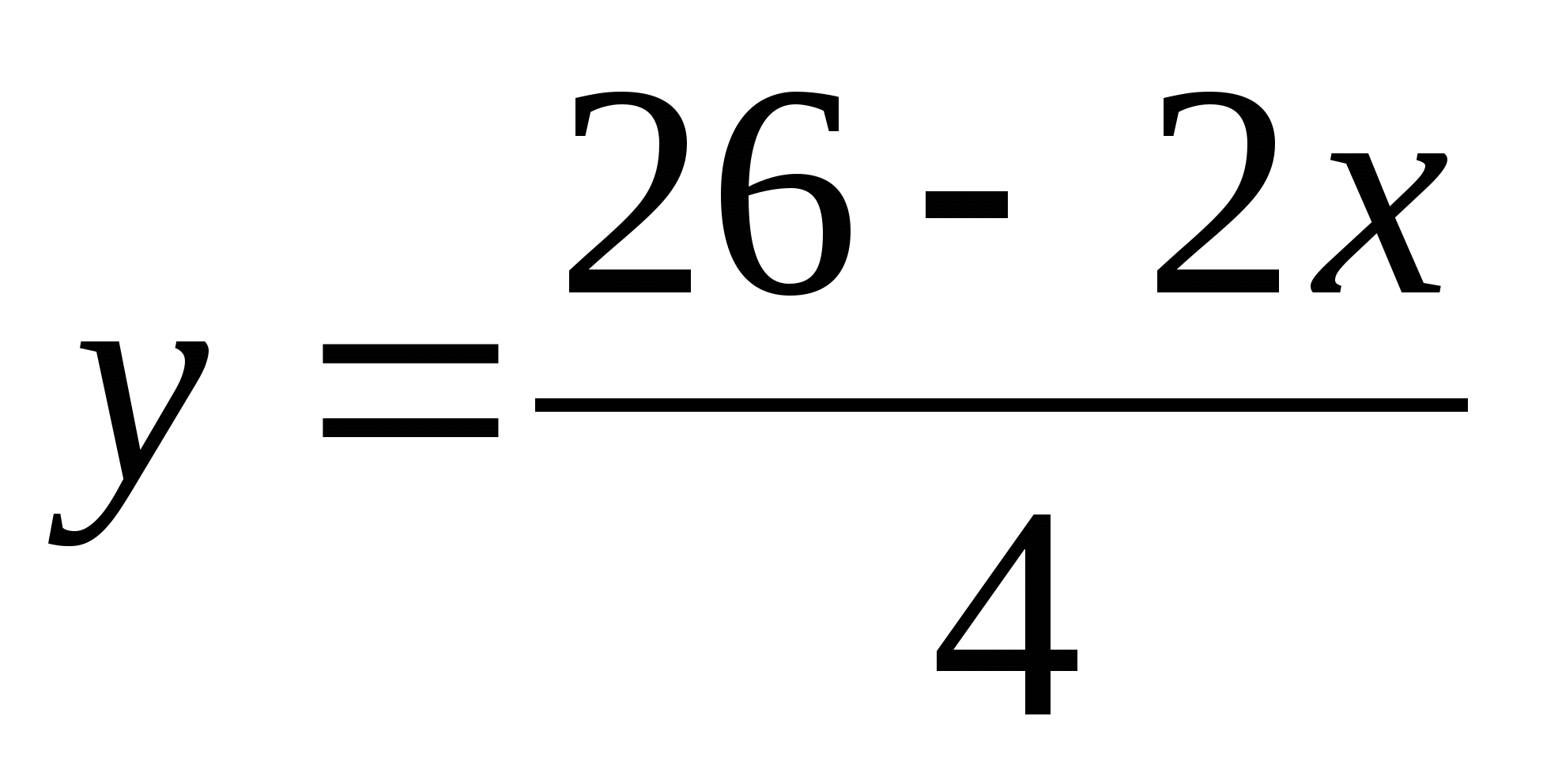
Подставим в это равенство вместо x последовательно числа 1, 2, 3 и т.д., найдем при каких натуральных значениях x соответствующие значение y являются натуральными.
x = 1, y = 6
x = 3, y = 5
x = 5, y = 4
x = 7, y = 3
x = 9, y = 2
x = 11, y = 1
Соответственно фазанов и кроликов было: 1 и 6, либо 3 и 5, 5 и 4, 7 и 3, 9 и 2, 11 и 1.
III. Разминка для глаз.
IV. Самостоятельная работа.
Для слабых:
А-I
1. Являются ли пара чисел (3; 2) решением данного линейного уравнения с двумя переменными 2х – у = 4?
2. Выразите x через y и y через x х – у = 35?
3. У Саши было несколько двухрублевых и пятирублевых монет, на общую сумму 28 р. Сколько у Саши было пятирублевых монет.
Для сильных:
У-I
1. Выразите x через y и y через x в уравнении
а) 3х – 5у = 8
б) 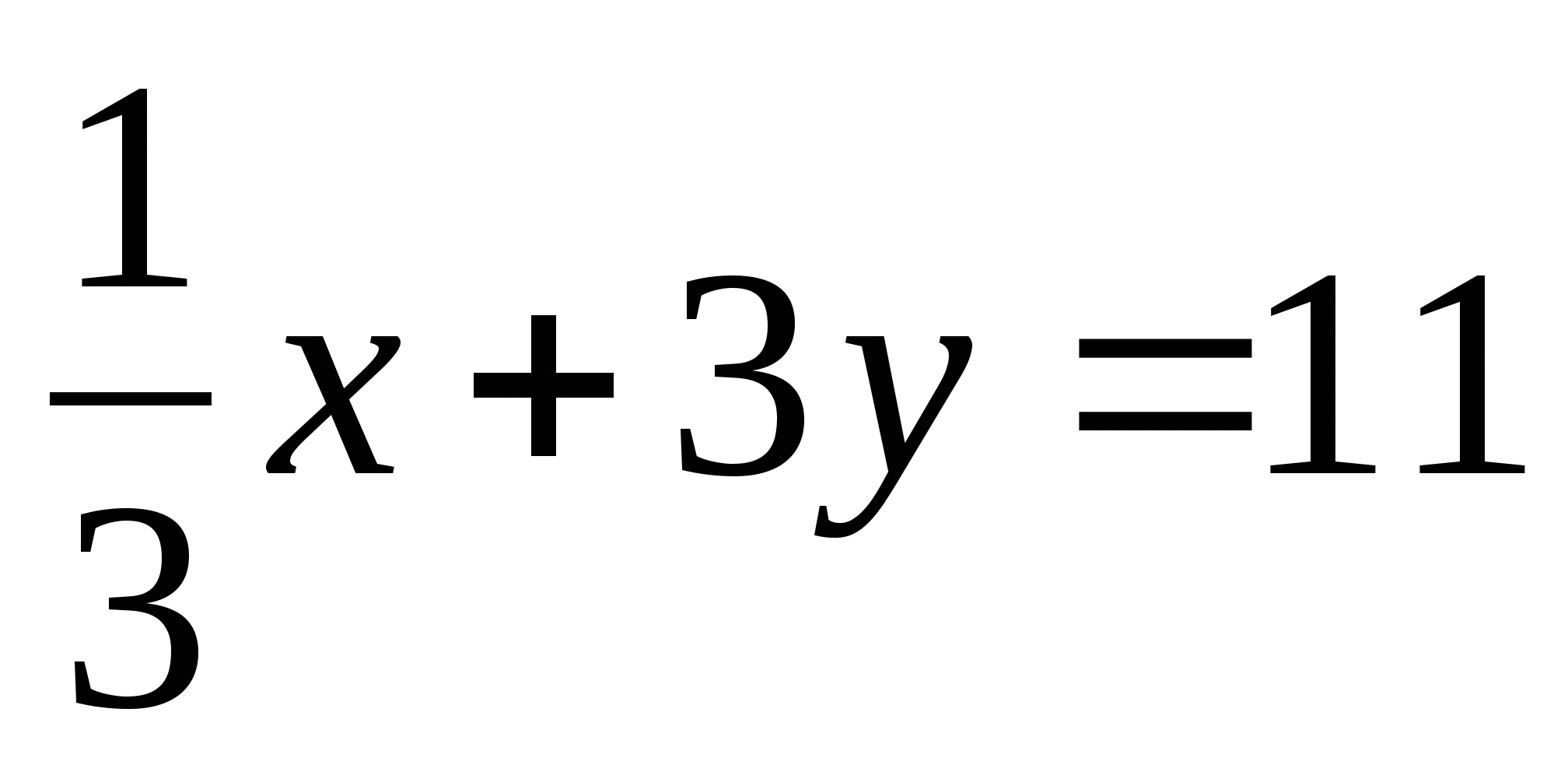
в) 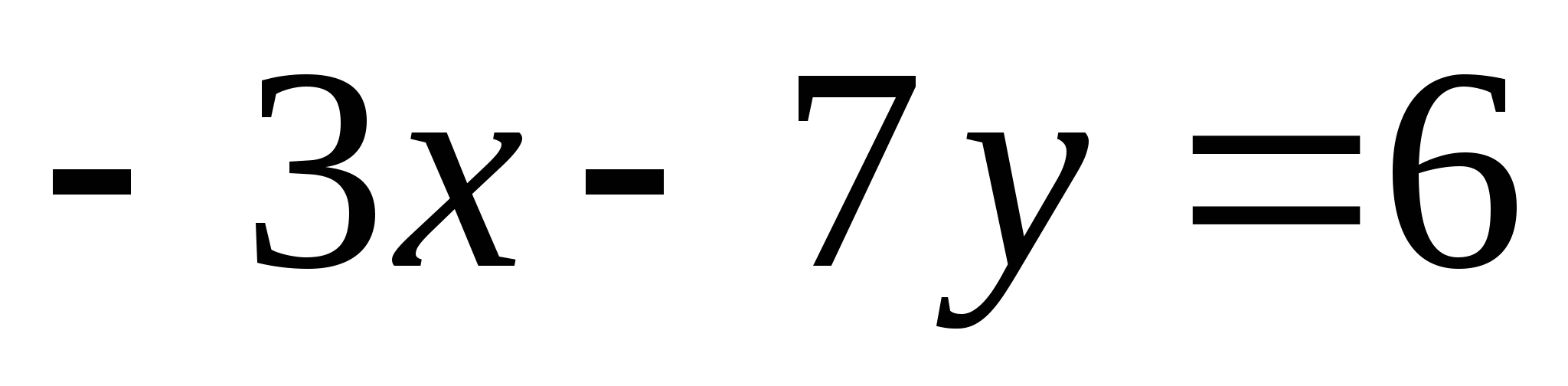
2. № 1038
3. Составьте линейное уравнение с двумя переменными по условию задачи. Периметр прямоугольника равен 32 см. Найдите какими должны быть стороны прямоугольника.
У-II
1. Выразите x через y и y через x в уравнении
а) 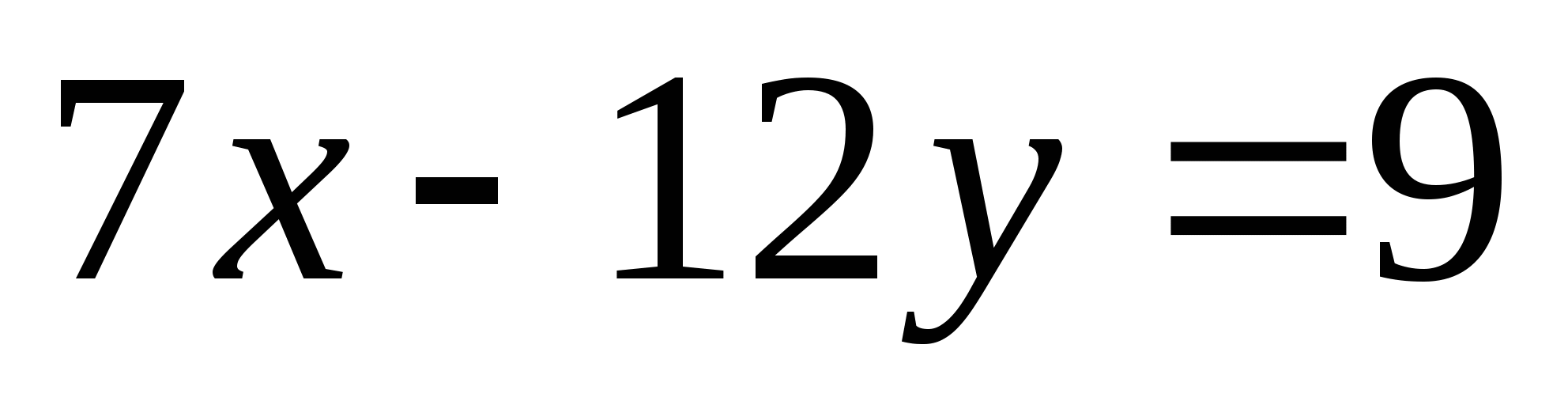
б)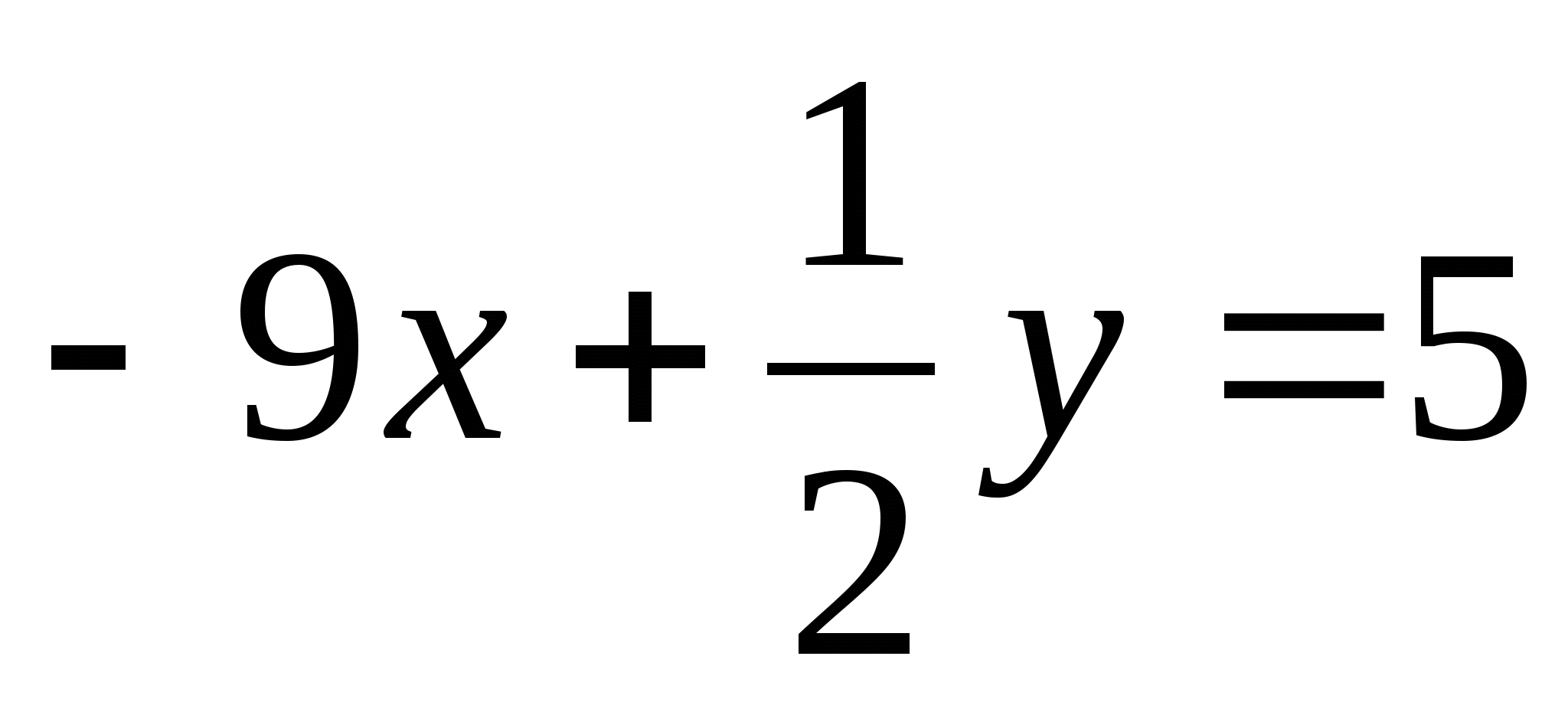
в) 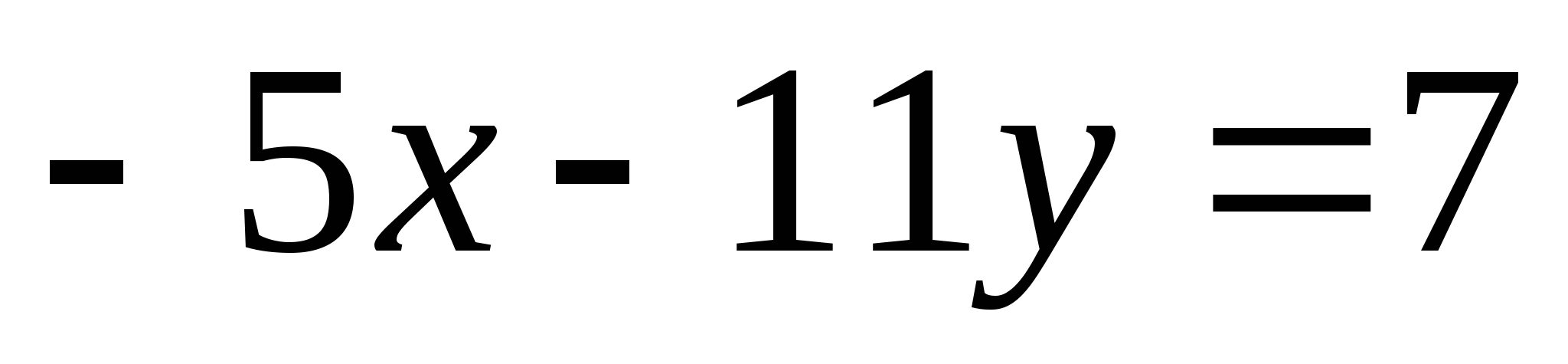
2. № 1040
3. Составьте линейное уравнение с двумя переменными по условию задачи. Периметр прямоугольника равен 32 см. Найдите какими должны быть стороны прямоугольника.
VI. Итог урока. (Слайд 8)
Как быстро отыскать решения линейного уравнения с двумя переменными?
Чем нужно воспользоваться, чтобы из уравнения выразить одну переменную через другую?
Какие уравнения называются диофантовыми?
Как составить уравнение с двумя переменными по условию задачи?
VII. Домашнее задание. (Слайд 9)
п. 40, № 1034, №1039, карточки
infourok.ru
График линейного уравнения с двумя переменными
Вопросы занятия:
· ввести понятие «график линейного уравнения с двумя переменными»;
· рассмотреть поведение графика в зависимости от значений коэффициентов перед переменными.
Материал урока
На прошлом уроке мы с вами познакомились с линейным уравнением с двумя переменным. Давайте, вспомним определение.

И сегодня на уроке мы будем вести речь о графике такого уравнения.
Сформулируем определение:
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.
Рассмотрим уравнение:

Обратите внимание, что полученная формула имеет вид линейной функции, графиком которой является прямая.
Так как прямая определяется двумя точками, то для построения графика нам достаточно указать две точки. Так:

Таким образом, получили две точки с координатами:

Теперь на координатной плоскости отметим эти точки и проведём через них линию.

Эта прямая является графиком исходного уравнения.
Все точки, принадлежащие графику, – это пары чисел, которые являются решениями нашего уравнения.
Теперь рассмотрим уравнение, в котором коэффициент при одной из переменных равен нулю.
Например,

А это постоянная функция. С предыдущих уроков нам известно, что график такой функции – это прямая, которая проходит через точку с координатами (0; 2) и параллельна оси Ox.

Все точки, принадлежащие этой прямой, – это пары чисел, которые являются решениями данного уравнения. И таких решений бесконечно много.
Сформулируем определение.
Определение.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
А теперь давайте рассмотрим случай, когда в линейном уравнении оба коэффициента при переменных равны нулю.

Давайте, рассмотрим примеры построения графиков линейных уравнений.
Пример.

Пример.

Пример.

Итоги урока.
Итак, сегодня на уроке мы выяснили, что же представляет собой график линейного уравнения с двумя переменными и научились строить такие графики.
videouroki.net