Решение уравнений четвертой степени

В общем случае решение уравнения четвёртой степени осуществляется с использованием методов решения уравнений для высших степеней, например, методом Феррари или с помощью схемы Горнера. Но некоторые уравнения 4-ой степени имеют более простое решение.

Существует несколько особых типов уравнений четвертой степени, со способами решения которых вы познакомитесь ниже:

• Биквадратное уравнения $ax^4+bx^2+c=0$;
• Возвратные уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$;
• Уравнения вида $ax^4+b=0$.

Решение биквадратных уравнений четвёртой степени

Биквадратные уравнения $ax^4+bx^2+c=0$ сводятся к квадратным путём замены переменной $x^2$ на новую, например, на $y$. После замены решается новое полученное уравнение, а затем значение найденной переменной подставляется в уравнение $x^2=y$. Результатом решения будут корни уравнения $x^2=y$.

Пример 1

Решите уравнение $x(x-1)(x-2)(x-3)=24$:

Раскроем скобки в многочлене:

$(x^2-3x)(x^2-3x+2)=24$

В таком виде становится очевидно, что в качестве новой переменной можно выбрать выражение $y=x^2-3x$, подставим её:

$y \cdot (y+2)=24$

$y^2+2y-24=0$

$y_1=4;y_2=-6$.

Теперь решим два квадратных уравнения $x^2-3x=-4$ и $x^2-3x=-6$.

Корни первого уравнения $x_1{1,2}=4;-1$, второе решений не имеет.

Решение возвратных уравнений 4 степени

Эти уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$ повторяют своими коэффициентами при младших членах коэффициенты при многочленах со старшими степенями. Для решения такого уравнения сначала делят его на $x^2$:

$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$

$ax^2+bx+c+\frac{b}{x} + \frac{a}{x^2}=0$

$a(x^2+\frac{1}{x^2})+b(x+\frac{1}{x}) + c=0$

Затем заменяют $(x+\frac{1}{x})$ на новую переменную, тогда $(x^2+\frac{1}{x^2})=y^2-2$, после подстановки получаем следующее квадратное уравнение:

$a(y^2-2)+by+c=0$

После этого ищем корни уравнений $x+\frac{1}{x}=y_1$ и $x+\frac{1}{x}=y_2$.

Аналогичным методом решаются возвратные уравнения вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.

Пример 2

Решите уравнение:

$3x^4-2x^3-9x^2-4x+12=0$

Данное уравнение – возвратное уравнение вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Поэтому разделим всё уравнение на $x^2$:

$3x^2-2x-9 \cdot \frac{2 \cdot 2}{x}+3 \cdot (\frac{2}{x})^2=0$

$3(x^2+\frac{4}{x^2})-2(x+\frac{2}{x}-9=0$

Произведём замену выражения $x+\frac{2}{x}$: $3(y^2-4)-2y-9=0$

Рассчитаем корни данного уравнения, они равны $y_1=3$ и $y_2=-\frac{7}{3}$.

Соответственно, теперь необходимо решить два уравнения $x+\frac{2}{x}=3$ и $x+\frac{2}{x}=-\frac{7}{3}$. Решение первого уравнения — $x_1=1, x_2=2$, второе уравнение не имеет корней.

Следовательно, корнями исходного уравнения являются $x_1=1, x_2=2$.

Уравнения вида $ax^4+b=0$

Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.

spravochnick.ru

Решение алгебраических уравнений 4-ой степени

Министерство образования Республики Беларусь

Белорусский национальный технический университет

Факультет транспортных коммуникаций

Кафедра “Высшая математика №3”

Доклад на СНТК

Решение алгебраических уравнений 4-ой степени

Выполнили: студенты группы 11403512

Микулёнок В.А., Ковенко В.Н.

Руководитель: Неверович Т.С.

Минск 2013

Решение алгебраических уравнений 4 степени

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

f(x)=ax⁴+bx³+cx²+dx+e=0, a<>0

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум.

График многочлена 4-ой степени с четырьмя корнями и тремя критическими точками.

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано, а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство».

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения было доказано в теореме Абеля — Руффини в 1824.

Решения:

1.Биквадратное уравнение

Биквадратное уравнение — уравнение четвёртой степени вида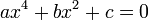

Где — заданные комплексные числа и 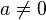. Подстановкой

сводится к квадратному уравнению относительно y.

Четыре его корня: .

2. Возвратное уравнение четвёртой степени

Возвратное уравнение четвёртой степени является также относительно легко решаемым: для такого, что , решение находится приведением к виду: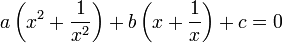

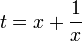и после замены ищется решение квадратного уравнения

3.Решение Декарта — Эйлера

В уравнение четвёртой степени:

алгебраический уравнение биквадратный множитель

Сделаем подстановку и получим уравнение в следующем виде (оно называется «неполным»):

где

Корни y₁, y₂, y₃, y₄ такого уравнения равны одному из следующих выражений:

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

Причём z₁, z₂, z₃ — это корни кубического уравнения

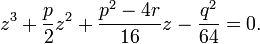
4. Решение Феррари

Схема метода Феррари

Целью данного раздела является изложение метода Феррари, с помощью которого можно решать уравнения четвёртой степени

a₀x⁴ + a₁x³ + a₂x² + a₃x + a₄ = 0, (1)

где a₀, a₁, a₂, a₃, a₄ – произвольные вещественные числа, причем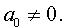

Метод Феррари состоит из двух этапов.

На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Приведение уравнений 4-ой степени.

Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

X⁴ + ax³ + bx² + cx + d = 0, (2)

где a, b, c, d – произвольные вещественные числа.

Сделаем в уравнении (2) замену

(3)

где y – новая переменная.

Тогда, поскольку

то уравнение (2) принимает вид

(4)

Если ввести обозначения

то уравнение (4) примет вид

y⁴ + py² + qy + r = 0, (5)

где p, q, r – вещественные числа.

Первый этап метода Феррари завершён.

Разложение на множители. Кубическая резольвента

Добавив и вычитая в левой части уравнения (5) выражение 2sy² + s²,

где s – некоторое число, которое мы определим чуть позже, из (5) получим

Следовательно, уравнение (5) принимает вид

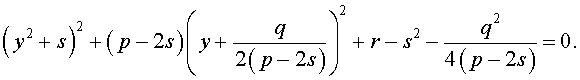(6)

Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

(7)

то уравнение (6) примет вид

(8)

или, раскрыв скобки, — в виде

(9)

Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

Действительно,

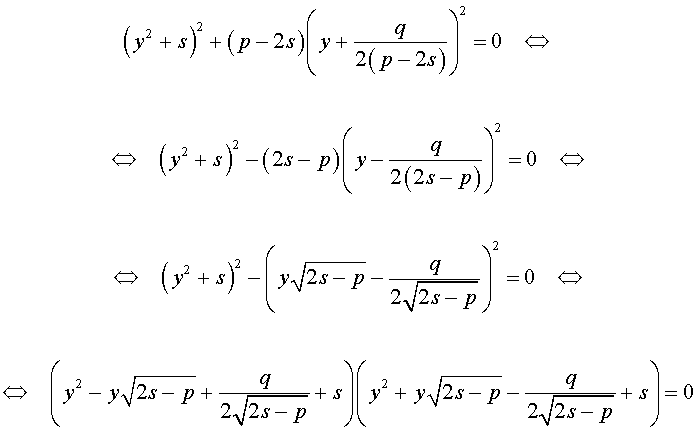
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

(10)

а также квадратное уравнение

(11)

Вывод метода Феррари завершен.

Пример. Решить уравнение

X⁴ + 4x³ – 4x² – 20x – 5 = 0. (12)

Решение. В соответствии с (3) сделаем в уравнении (12) замену

x=y – 1. (13)

Поскольку

X⁴ + 4x³ – 4x² – 20x – 5 = (y – 1)⁴ + 4(y – 1)³ – 4(y – 1)² – 20(y – 1) – 5 =

= y⁴ – 4y³ + 6y² – 4y + 1 + 4y³ – 12y² + 12y – 4 – 4y² + 8y – 4 – 20y + 20 – 5 = y⁴ – 10y² – 4y + 8,

то в результате замены (13) уравнение (12) принимает вид

y⁴ – 10y² – 4y + 8 = 0. (14)

В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

p = – 10, q = – 4, r = 8. (15)

В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение

2s³ + 10s² – 16s – 84 = 0,

которое при сокращении на 2 принимает вид:

s ³+ 5s² – 8s – 42 = 0. (16)

Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число

s = – 3. (17)

Подставляя значения (15) и (17) в формулу (10), получаем уравнение

y² – 2y – 4 = 0,

корни которого имеют вид:

(18)

Подставляя значения (15) и (17) в формулу (11), получаем уравнение

y² + 2y – 2 = 0,

корни которого имеют вид:

(19)

В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

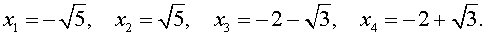
Ответ: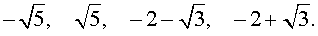

studfile.net

Схема (метод) Горнера. Примеры. Решение уравнений четвертой степени

РЕШЕНИЕ УРАВНЕНИЙ 4-ОЙ СТЕПЕНИ ПО СХЕМЕ ГОРНЕРА

2x⁴ + 5x³ — 11x² — 20x + 12 = 0

Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:

1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена

-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена

2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена

Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:

В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:

	Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки.
	2 ∙ 2 + 5 = 9
	2 ∙ 9 — 11 = 7
	2 ∙ 7 — 20 = -6
	2 ∙ (-6) + 12 = 0

Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.

Таким образом мы исходный многочлен разложили на множители:

2x⁴ + 5x³ — 11x² — 20x + 12 = (x — 2)(2x³ + 9x² + 7x — 6)

Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x³ + 9x² + 7x — 6.

Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6.

1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена

-1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена

2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена

-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена

Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:

	Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки.
	-2 ∙ 2 + 9 = 5
	-2 ∙ 5 + 7 = -3
	-2 ∙ (-3) — 6 = 0

Таким образом мы исходный многочлен разложили на множители:

2x⁴ + 5x³ — 11x² — 20x + 12 = (x — 2)(x + 2)(2x² + 5x — 3)

Многочлен 2x² + 5x — 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3

2 5 -11 -20 12 2 2 9 7 -6 0 -2 2 5 -3 0 -3 2	Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки.
2 5 -11 -20 12 2 2 9 7 -6 0 -2 2 5 -3 0 -3 2 -1	-3 ∙ 2 + 5 = -1
2 5 -11 -20 12 2 2 9 7 -6 0 -2 2 5 -3 0 -3 2 -1 0	-3 ∙ (-1) — 3 = 0

Таким образом мы исходный многочлен разложили на линейные множители:

2x⁴ + 5x³ — 11x² — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1)

А корнями уравнения являются:

x = ±2; 3; 0.5

tutata.ru

Решение уравнений четвертой степени

Решение уравнений четвертой степени — калькулятор

Чтобы найти корни уравнения 4-ой степени с помощью калькулятора, введите коэффициенты a, b, c, d и e и нажмите кнопку ‘Решить’.

Решение уравнения 4-ой степени (методом Феррари)

(1)

1. С помощью замены приходим к приведенному уравнению (2),

где

2. Если , то решаем вспомогательное кубическое уравнение

Если , то у этого уравнения всегда существует положительный корень, обозначим его .

Тогда корни исходного уравнения (1) можно получить по формулам

3. Если q = 0, то приведенное уравнение (2) становится биквадратным

И четыре корня этого уравнения можно получить по формулам

4. Оценить погрешность решения можно с помощью соответствующих невязок

чем меньше величины , тем точнее решение. Для более точной оценки имеет смысл рассмотреть относительную погрешность.

Для этого нужно решить уравнение и вычислить соответствующие невязки

Тогда относительные невязки можно найти по формулам .

ru.intemodino.com

Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени

Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.

В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, использование симметрии и даже деление многочлена на многочлен.

Вспомним основные понятия.

Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.

Например, число 3 – корень уравнения 2x = 6.

Решить уравнение – значит найти его корни или доказать, что их нет.

Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.

Например, уравнения  и  равносильны. Их корни совпадают:  или 

Замена переменной – ключ к решению многих задач.

Решим уравнение:

Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.

Сделаем замену  Тогда 

С новой переменной уравнение стало проще:

Умножим обе части на 10t. Получим квадратное уравнение:

Корни этого уравнения:  или 

Вернемся к переменной 

Если , то 

Отсюда 

Дискриминант этого уравнения отрицателен, корней нет.

Если , то  Получим квадратное уравнение для :

У этого уравнения два корня:  или  Это ответ.

Решим уравнение

Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.

Посмотрим на уравнение внимательно.

На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки 

Сделаем замену , тогда .

Тогда:

Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:

И еще одна замена: .

Обычное квадратное уравнение. Замечательно!

Подберем его корни по теореме Виета. Заметим, что

;  отсюда  ,  .

Если , то нет решений.

Если , то Тогда или

Если , то .

Если , то .

Ответ: 4; –8.

Дальше – еще интереснее.

3. Решите уравнение

Сделаем замену . То, что в правой части в скобках, заменили на новую переменную.

.

Получили квадратное уравнение:

Если , то

Если , то

Ответ:

Следующее уравнение решим с помощью группировки слагаемых.

4. Решите уравнение

Разложим левую часть уравнения на множители. Сгруппируем слагаемые:

Первые два слагаемых – сумма кубов. Применим формулу: . Получим:

.

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Записывается это так:

Ответ: -2; 1; 4.

У нас появилось новое обозначение: — знак совокупности.

Такой знак означает «или».

Запись читается как « или или ».

Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.

5. Решите уравнение

Разложить левую часть на множители с первой попытки не удается.

Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.

Выпишем целые делители числа 24:

1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24

Подставляя их по очереди в уравнение, при получаем верное равенство:

Это значит, что левую часть уравнения можно разложить на множители:

, где .

Чтобы найти , поделим выражение на . В столбик. Так же, как мы делим друг на друга числа.

Немного непривычно, да? Потренируйтесь – у вас получится!

Ответ: 2; 3; 4.

6. Решите уравнение

группируем слагаемые:

А если сделать замену ?

Тогда .

Получаем квадратное уравнение: . Удачная замена!

Если , то , нет решений.

Если , то

, .

Ответ: .

7. Решите уравнение

Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, — 5, 4, — 5, 1.

Такое уравнение называется симметрическим.

Разделим обе его части на . Мы можем это сделать, поскольку не является корнем нашего уравнения.

Теперь группируем слагаемые:

Сделаем замену .

Тогда

Получили уравнение . Легко!

Ответ:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Калькулятор уравнения четвертой степени

Уравнения четвертой степени имеет вид ах⁴; + bх³ + сх² + ах + е = 0. Общее уравнение четвертой степени (также называемый биквадратным) является четвертой степени полиномиального уравнения. Бесплатный онлайн калькулятор расчета уравнения четвертой степени, используемый для нахождения корней уравнения.

Вычисление корней:

Например, Введите a=3, b=6, c=-123, d=-126 и e=1080

1

8

Было ли это полезно?

Формула уравнения четвертой степени:

ax⁴ + bx³ + cx² + dx + e = 0

• Примечание : Допустим что p и q квадратные корни из 2 ненулевых корней.
• p = sqrt(y₁)
• q = sqrt(y₃)
• r = -g / (8pq)
• s = b / (4a)
• x₁ = p + q + r — s
• x₂ = p — q — r — s
• x₃> = -p + q — r — s
• x₄ = -p — q + r — s

Уравнением четвертой степени называется полиномиальное уравнение четвертого порядка вида, ax⁴+ bx³ + cx² + dx + e = 0:

Формула уравнения четвертой степени:

ax⁴ + bx³+ cx² + dx + e = 0

где,

• a = коэффициент для  x⁴
• b = коэффициент для x³
• c = коэффициент для x²
• d = коэффициент для x
• e = константа.

Решение уравнения четвертой степени:

• x₁ = p + q + r — s
• x₂ = p — q — r — s
• x₃ = -p + q — r — s
• x₄ = -p — q + r — s

Пример 1:

Вычислить корни (x1, x2, x3, x4) уравнения четвертой степени, 3X⁴ + 6X³ — 123X² — 126X + 1080 = 0

Шаг 1:

Из приведенного выше уравнения, значения a=3, b=6, c=-123, d=-126, e=1080.

Шаг 2:

Найдем x : Подставьте значения в приведенных ниже формул.

• f = c — ( 3b ² / 8 )
• g = d + ( b ³ / 8 ) — ( b x c / 2 )
• h = e — ( 3 x b⁴ / 256 ) + ( b ² x c / 16 ) — ( b x d / 4 )

Шаг 3:

Представим как уравнение третьей степени : y ³ + ( f / 2 ) y ² + (( f ² — 4 x h ) / 16 ) y — g ² / 64 = 0

где,

• a = коэффициент для y ³
• b = коэффициент для y²
• c = коэффициент для y
• d = константа

Шаг 4:

Из приведенного выше уравнения, значения:

• a = 1,
• b = f/2,
• c = (( f ² — 4 x h ) / 16 ),
• d = — g² / 64.

Шаг 5:

Найдем y: Подставьте значения в формулу, чтобы найти корни.

дискриминант (Δ) = q³ + r²

• q = (3c — b²) / 9
• r = -27d + b(9c — 2b²)
• s = r +√ (дискриминант)
• t = r — √(дискриминант)
• term1 = √(3.0) * ((-t + s) / 2)
• r₁₃ = 2 * √(q)
• y₁ = (- term1 + r₁₃*cos(q³/3) )
• y₂ = (- term1 + r₁₃*cos(q³+(2∏)/3) )
• y₃ = (- term1 + r₁₃*cos(q³+(4∏)/3) )

Шаг 6:

Получим корни, y₁ = 20.25 , y₂ = 0 и y₃ = 1.

Шаг 7:

После решения уравнения третьей степени решим уравнение четвертой степени.

Подставим y₁, y₂, y₃ в p, q, r, s.

Примечание : Пусть p и q квадратные корни 2 ненулевых корней.

• p = sqrt(y1) = 4.5
• q = sqrt(y3) = 1
• r = -g / (8pq) = 0
• s = b / (4a) = 0.5

Шаг 8:

Мы получили корни, x1 = 5, x2 = 3, x3 = -4 и x4 = -6.

Практический пример решения уравнения четвертой степени.

Связанные Калькуляторы

wpcalc.com

Найти корни уравнения, многочлена 4 степени онлайн

Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени.  Коэффициенты могут быть как вещественными  так и комплексными числами.

Использовалась определенная методика, которая нигде не описана и не разобрана.

Формулами Феррари не стал пользоваться — не интересно.

Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.

И по всей видимости избежать её никак не получится.  

Но дальше все идет по другому.

По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.

Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.

Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или — для одного вспомогательного  параметра. 

Теперь в виде формул

Заменой   мы получаем так называемый приведенный многочлен

Решение данного уравнения ищем в виде сумм двух функций

Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения

Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту

Например, если выразим F₂

Это кубическое уравнение которое подстановкой  превращается к классическую кубическую резольвенту.

Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?

Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его

если это условие верное  то ставится +(плюс), если условие неверное то -(минус)

Дальше все эти параметры подставляются в формулу

  и определяются корни уравнения 4 степени.

Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: «А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?»

Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.

Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.

Попробуйте решить уравнение   

Один из корней равен  

Кто считает  что действительной частью можно принебречь и отбросить как «почти ноль» глубоко ошибается. Отбросив его у нас значение функции будет , а не ноль.

И только с учетом «такой маленькой» действительной части уравнение становиться тождественным.

Поэтому точность  в вычислениях очень важны.

Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.

Несколько примеров: 

 

 

• Найти число по остатку от деления >>

abakbot.ru