2 часть ОГЭ по математике
Во вторую часть ОГЭ по математике* входят 6 заданий на проверку углубленных знаний по алгебре (с 21 по 23 задание) и геометрии (с 24 по 26 задания). Решить их реально, главное прорешать все виды заданий!
Обратите внимание на экзамене на оформление задач и конкретный ответ на поставленный вопрос в условии задачи.
За каждое верное решение задания из второй части ОГЭ, вы сможете получить 2 ценных балла. Не упускайте возможности набрать высокие баллы!
Задания 21 (C1). Алгебраические выражения, уравнения, неравенства и их системы:
21.1. Алгебраические выражения >>>;
21.2. Неравенства >>>;
21.3. Система неравенств >>>;
21.4. Уравнения >>>;
21.5. Система уравнений >>>.
Задания 22 (C2). Текстовые задачи:
22.1. Задачи на движение по воде >>>;
22.2. Задачи на проценты, растворы, смеси и сплавы >>>;
22.3. Задачи на совместную работу >>>;
22.4. Задачи на движение по прямой >>>;
22.5. Разные задачи >>>.
Задания 23 (C3). Функции и их свойства. Графики функций:
23.1. Параболы >>>;
23.2. Гиперболы >>>;
23.3. Кусочные непрерывные функции >>>;
23.4. Разные задачи >>>.
Задания 24 (C4). Геометрическая задача на вычисление:
24.1. Углы >>>;
24.2. Треугольники >>>;
24.3. Четырехугольники >>>;
24.4. Окружности >>>.
Задания 25 (C5). Геометрическая задача на доказательство:
25.1. Треугольники и их элементы >>>;
25.2. Четырехугольники и их элементы >>>;
25.3. Окружности и их элементы >>>.
Задания 26 (C6). Геометрическая задача повышенной сложности:
26.1. Треугольники >>>;
26.2. Четырехугольники >>>;
26.3. Окружности >>>;
26.4. Комбинация окружностей и многоугольников >>>.
Первая часть ОГЭ по математике >>>
*Порядок заданий представлен по состоянию на 2016-2017 учебный год
Центр развития избранных «МатРИЦА»
vekgivi.ru
Секреты эффективной и быстрой подготовки ко второй части ОГЭ по математике. — Мои статьи — Каталог статей
Уважаемые девятиклассники, настоящие или будущие!
Часто от вас приходится слышать следующие вопросы. Легко ли подготовиться к заданиям второй части ОГЭ по математике? Сколько для этого понадобится времени? Всем ли учащимся эти задачи по силам? Как эффективно распределить время и силы на подготовку?
Прежде всего замечу, что разделение заданий на задания первой и второй части носит порой условный характер. Некоторые задания из второй части могут показаться учащимся более лёгкими, чем из первой. Поэтому не стоит зацикливаться на мыслях типа «задания второй части не для меня, так как они должны быть сложными».
Однако принципиальная разница между задачами второй и первой части состоит в том, что к заданиям первой части решение давать необязательно, а к заданиям второй части — обязательно.
Из сказанного ранее также следует, что для успешного решения заданий второй части (во всяком случае некоторых) необязательно быть сильным в математике (например, получать высокие оценки по этому предмету). Но, разумеется, необходимо обладать знаниями и умениями по школьной программе в пределах того минимума, который необходим для решения определённой задачи.
Например, если для решения определённой задачи необходимо знать какие-то теоремы по геометрии, то понятно, что без знания этих теорем задачу решить не получится.
Теперь о том, как эффективно распределить время и силы на подготовку к заданиям второй части. Сразу замечу, что нет необходимости сначала долгое время заниматься решением заданий первой части и лишь только после этого переходить к задачам второй части. Это нерационально.
Давайте прежде всего определимся со сборником экзаменационных вариантов, по которому будем готовиться. Например, возьмём стандартный сборник «ОГЭ 2016. Математика. 50 типовых вариантов» (автор: Ященко):
Кстати, электронную версию этого сборника вы можете скачать здесь. Вышедший в 2017 году аналогичный сборник несущественно отличается от данного сборника.
Предположим, вы хотите освоить методы решения заданий 22 (алгебра) и 24 (геометрия). Конечно, это можно делать хаотично (как получится), то есть просто решать задания с этими номерами из разных вариантов. Но есть более рациональный способ: сначала сделать разбивку каждого из этих заданий на типы, то есть выявить, в каких вариантах задачи, имеющие один и тот же номер (22 или 24), решаются одинаковым способом, и всё это расписать.
Для заданий 22 и 24 разбивка по типам приведена на следующих фотографиях (чтобы просматривать фотографию в полном размере, кликните на неё мышкой):
Как видите, для задания каждого типа я использовал какое-то характерное для этого типа краткое описание, а для заданий по геометрии ещё и сделал чертёж. Это позволяет составить о задаче некоторое общее представление.
Когда сделана разбивка на типы, вы можете без труда определить, какие задачи решать в первую очередь, а какие оставить на потом, какие задачи для вас простые, а какие не очень.
Но вот вы начали решать задачи. Какие-то из них вы решите сами, а какие-то вам поможет решить учитель или репетитор. Не важно. После решения задания из очередного варианта, аккуратно зачёркиваем на листе номер этого варианта, а в экзаменационном сборнике делаем пометку (например, ставим «плюсик» около решённого задания и пишем ответ). Это позволит зафиксировать тот факт, что данное задание уже решено и к нему не нужно в будущем возвращаться. При необходимости решаем задачу этого же типа из другого варианта.
Необязательно решать сразу все задания одного типа из разных вариантов. Можно некоторые задания оставить на потом, для повторения материала.
Ниже я привожу фотографии с решениями некоторых типов задач с номером 22:
А вот — решения некоторых типов задач с номером 24:
Ещё хочу особо отметить, что не стоит увлекаться заучиванием алгоритмов решения задач. Старайтесь понять некоторую общую логику, из которой следует уже решение не только какой-то отдельной задачи, но и множества других задач.
И, конечно, очень важно знать школьную программу. В особенности по геометрии. Именно по этому предмету больше всего пробелов у школьников.
Как показывает практика, методы решения задач ОГЭ по математике из второй части наиболее хорошо усваиваются именно тогда, когда школьник хорошо усвоил основные сведения по школьной программе и закрепил их при решении ряда несложных задач из обычного учебника.
Вообще стоит особо отметить, что почти все задания ОГЭ по математике из первой части и примерно половина из второй на самом деле являются задачами из школьных учебников. Так что качественно проходя школьную программу с 5-го класса, вы фактически уже как бы готовитесь к сдаче экзамена по окончании 9-го класса.
Примечания к решению заданий.
Задание № 22 из варианта 44. Принцип относительности движения заключается в следующем. Предположим навстречу друг другу идут два пешехода, их скорости соответственно равны 5 км/ч и 3 км/ч, а расстояние между ними составляет 32 км. Тогда, чтобы узнать, через какое время пешеходы встретятся, можно считать, что один из них стоит на месте, а другой идёт к нему со скоростью, равной сумме скоростей, то есть со скоростью
5 км/ч + 3 км/ч = 8 км/ч
и таким образом достигает его через время, равное
32 : 8 = 4 часа.Принцип относительности движения бывает очень удобен при решении задач на движение, в которых трудно вообразить, что происходит при стандартном подходе, то есть, считая, что оба человека движутся.
Задание № 24 из варианта 40. Теорему о касательной и секущей, а также другие, связанные с касательной к окружности сведения, можно посмотреть на этой фотографии:
dmitrij.ucoz.net
Структура ОГЭ 2020 по математике
В 2020 году структура ОГЭ по математике претерпела некоторые изменения. Ниже рассмотрим эти изменения подробнее.
Демонстрационный вариант ОГЭ 2020 по математике
Шкала пересчета баллов ФИПИ 2020
Справочные материалы (выдаются на экзамене каждому)
ОГЭ 2020 по математике состоит из двух частей.
- В первой части 20 заданий (1 – 20) базового уровня сложности, каждое из которых оценивается в 1 балл.
- Во второй части 6 заданий (21 – 26) повышенного и высокого уровня сложности, каждое из которых оценивается в 2 балла.
Всего за экзамен можно набрать 32 балла.
Время, которое отводится на экзамен – 235 минут.
Структура ОГЭ 2020 по математике: первая часть
Первая часть состоит из:
Ответом к каждому заданию первой части является число, цифра или последовательность цифр. Ответы на задания первой части проверяются компьютером.
Структура ОГЭ 2020 по математике: вторая часть
Вторая часть состоит из двух модулей:
Ответом к каждому заданию второй части является письменное решение, которое проверяется двумя независимыми экспертами. Они проставляют в протокол оценки за каждое задание второй части. В случае, если оценки двух экспертов расходятся, назначается третий.
Выставление оценок за работу
- Оценка за экзаменационную работу выставляется по следующим критериям:
| Количество баллов | Оценка |
| 0 – 7 | 2 |
| 8 – 14 | 3 |
| 15 – 21 | 4 |
| 22 – 32 | 5 |
- Оценка по алгебре выставляется по следующим критериям:
| Количество баллов за модуль алгебра | Оценка |
| 0 – 4 | 2 |
| 5 – 10 | 3 |
| 11 – 15 | 4 |
| 16 – 20 | 5 |
- Оценка по геометрии выставляется по следующим критериям:
| Количество баллов за модуль геометрия | Оценка |
| 0 – 2 | 2 |
| 3 – 4 | 3 |
| 5 – 7 | 4 |
| 8 – 12 | 5 |
Результаты ОГЭ, в частности, ОГЭ по математике, влияют на дальнейшую судьбу 9-классника:
- для кого-то баллы, набранные на ОГЭ, важны для поступления в профильный класс или лицей,
- для кого-то это возможность получить аттестат и поступить в техникум,
- для кого-то это возможность улучшить годовую оценку по предмету.
В любом случае, успешная сдача экзамена – необходимый шаг, который каждому нужно совершить в своей жизни.
И это несложно!
Начать обучение.

Видео-уроки на канале Ёжику Понятно. Подпишись!
epmat.ru
Задание 2 ОГЭ-2019 по математике: разбор и решение
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 2
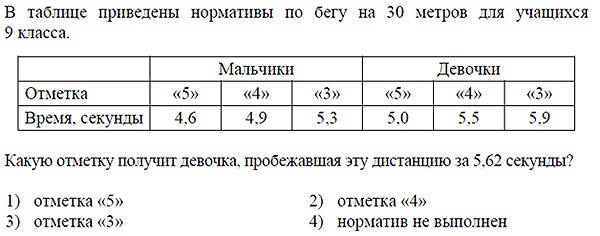
Решение
Поскольку время составляет 5,62 с., то норматив девочкой на оценку «4» не выполнен, однако, данное время не превышает 5,9 с. – норматива на оценку «3». Поэтому ее отметка «3».
Ответ: 3.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
rosuchebnik.ru
Как подготовиться к ОГЭ по математике? Часть II.
В прошлой статье мы поговорили об организационных моментах ОГЭ. Теперь давайте обсудим как подготовиться непосредственно к саму ОГЭ по математике.
Знания, умения и навыки
Основные проверяемые требования к математической подготовке учащихся:
- Уметь выполнять вычисления и преобразования.
- Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот.
- Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимостей.
- Уметь решать уравнения, неравенства и их системы.
- Решать несложные практические расчетные задачи.
- Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.
- Решать практические задачи, требующие систематического перебора вариантов с использованием аппарата вероятности и статистики.
- Уметь строить и читать графики функций.
- Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами.
- Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин.
- Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
- Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
- Уметь строить и исследовать простейшие математические модели.
Первая часть экзамена
Экзаменационная работа состоит из двух частей.
Первая часть работы – это 20 заданий, они направлена на проверку базовых компетенций и делятся на три модуля:
- “Алгебра” – 8 заданий
- “Геометрия” – 5 заданий
- “Реальная математика”- 7 заданий.
Задания этой части оцениваются по 1 баллу за каждое.
вторая часть экзамена
Вторая часть – это 6 заданий, она направлена на проверку владения материалом на повышенном уровне и делится на два модуля:
- “Алгебра”- 3 задания
- “Геометрия” – 3 задания.
Решение каждого задания этой части должно быть математически грамотным и полным.
21 задание (алгебра) – более простое:
- 2 балла начисляется за правильное выполнение преобразований и полученный верный ответ.
- 1 балл начисляется если решение доведено до конца, но допущена ошибка вычислительного характера или описка с учетом которой дальнейшие шаги выполнены верно.
22 задание (алгебра) – более высокого уровня:
- 2 балла начисляется за правильно составленное уравнение и полученный верный ответ
- 1 балла начисляется за правильно составленное уравнение при решении которого допущена вычислительная ошибка (решение доведено до ответа).
23 задание (алгебра) – высокий уровень сложности:
- 2 балла начисляется за правильно построенный график и верный ответ на поставленный вопрос.
- 1 балл начисляется за правильно построенный график, но в ответе на поставленный вопрос возможно не все верные значения.
24 задание (геометрия) – более простое:
- 2 балла начисляется за верный обоснованный ответ
- 1 балл начисляется при верных рассуждениях, но допущенной вычислительной ошибке, которая может привести к неверному ответу.
25 задание (геометрия) – более высокого уровня:
- 2 балла начисляется за верное доказательство и обоснованный ответ.
- 1 балл начисляется за верное в целом доказательство, которое может содержать неточности
26 задание (геометрия) – высокий уровень сложности:
- 2 балла начисляются за верный ход решения, правильные шаги и верный ответ
- 1 балл начисляется за верный ход решения, соответствующий задаче чертеж, но возможно пропущенные существенные объяснения или допущенной вычислительной ошибки.
Открытый банк заданий ФИПИ
Сегодня существует множество способов и средств, чтобы подготовиться к ОГЭ по математике. Один из них открытый банк заданий ФИПИ.
К сожалению, на данном сайте материал плохо систематизирован, поэтому пользоваться им сложно. Сложно, но можно!
И здесь я могу немного облегчить вашу работу. Предлагаю вам воспользоваться моими тренингом по подготовке к ОГЭ с помощью открытого банка заданий ОГЭ на сайте ФИПИ.
Тренинг расположен на отдельной платформе, а значит вы будете иметь доступ к нему из любого места, где есть стабильный интернет.
Задания разбиты по темам, перед каждым тренажером есть возможность поработать с необходимым теоретическим материалом. В тренажере задания выбираются из большого массива, поэтому каждый раз запуская тренажер вы будете работать с разными задачами по нужной теме.
Чтобы вам было легче понять на сколько данный формат обучения подходит к вам, мы сделали бесплатный доступ к первому блоку. Записывайтесь и сами все увидите.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
mathlove.ru
Разбор и решение задания №25 ОГЭ по математике
Четырехугольники
Разбор типовых вариантов заданий №25 ОГЭ по математике
Первый вариант задания
Окружности с центрами в точках I и J пересекаются в точках А и В, причём точки I и J лежат по одну сторону от прямой АВ. Докажите, что прямые АВ и IJ перпендикулярны.
Алгоритм решения:
- Делаем чертеж.
- Определяем место расположения точек I и J.
- Используем свойство серединного перпендикуляра.
- Делаем вывод.
Решение:
1. Делаем чертеж, согласно условия:
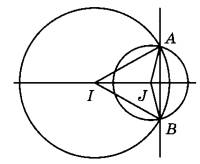
2. Определяем место расположения точек I и J:
Точка I равноудалена от точек A и B. Аналогично, точка J равноудалена от концов отрезка AB.
3. По свойству геометрического места точек, равноудаленных от концов отрезка, эти точки расположены на серединном перпендикуляре к отрезку AB.
А если две точки I и J лежат на серединном перпендикуляре, прямая IJ совпадает с ним.
Следовательно, прямые IJ и АВ перпендикулярны.
Второй вариант задания
Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.
Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники CEF и DEF и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника CED.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж по условию задачи:
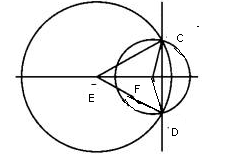
2. Рассмотрим треугольники CEF и DEF и установим их равенство:
У них CE=DE, как радиусы окружности с центром в точке Е,
Аналогично, CF = DF, как радиусы окружности с центром в точке F.
EF – общая сторона.
Значит, данные треугольники равны.
Тогда по свойству равных фигур 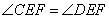 .
.
Рассмотрим треугольник CED. У него CE=DE, поскольку это соответствующие стороны равных фигур. Значит, треугольник равнобедренный.
EF – биссектриса угла E. следовательно, EF – высота по свойству равнобедренного треугольника. Отсюда следует, что 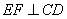 .
.
Утверждение доказано.
Третий вариант задания
Окружности с центрами в точках М и N пересекаются в точках S и Т, причём точки М и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники SMN и TMN и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника SMT.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж согласно условия задачи.
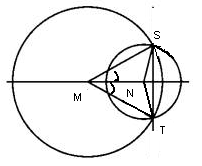
2. Рассмотрим треугольники SMN и TMN. Они равны по трем сторонам:
SM=TM как радиусы окружности с центром в точке М,
SN=TN как радиусы окружности с центром в точке N,
а MN – общая сторона (см. рисунок выше).
3. По свойству равных фигур, 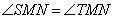 , как соответствующие углы в равных треугольниках.
, как соответствующие углы в равных треугольниках.
4. Рассмотрим треугольник SMT.
В нем по доказанному выше 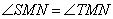 , а значит MN – биссектриса угла M. Данный треугольник равнобедренный с равными сторонами SM и TM.
, а значит MN – биссектриса угла M. Данный треугольник равнобедренный с равными сторонами SM и TM.
Следовательно, MN – высота по свойству биссектрисы равнобедренного треугольника. Следовательно, 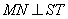 .
.
Утверждение доказано.
Четвертый вариант задания
В выпуклом четырёхугольнике ABCD углы ВСА и BDA равны. Докажите, что углы ABD и ACD также равны.
Алгоритм решения:
- Выполняем рисунок по условию задачи.
- Устанавливаем подобие треугольников BOC и AOD.
- Записываем соотношение для сторон.
- Устанавливаем подобие треугольников AOB и DOC.
- Делаем вывод.
Решение:
1. Выполняем чертеж по условию задачи:
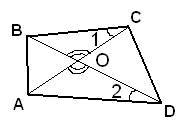
2. Рассматриваем треугольники BOC и AOD.У них:
углы ВСА и BDA равны по условию задачи,
углы BOC и AOD равны как вертикальные.
Значит, треугольники BOC и AOD подобны по двум углам.
3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон:
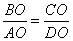
4. Рассматриваем треугольники AOB и DOC. У них:
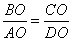
углы AOB и DOC равны как вертикальные.
Следовательно, данные треугольники подобны.
По свойству подобных фигур соответствующие углы в треугольниках равны. Значит, 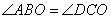 , а поскольку эти углы совпадают с углами ABD и ACD , то
, а поскольку эти углы совпадают с углами ABD и ACD , то 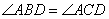 .
.
Утверждение доказано.
Демонстрационный вариант ОГЭ 2019
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC= ED. Докажите, что данный параллелограмм — прямоугольник.
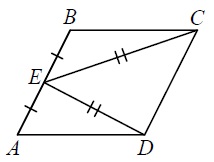
Доказательство:
Рассмотрим треугольники BEC и AED. BE = EA, так как E — середина стороны AB по условию. EC= ED по условию, а BC = AD по свойству параллелограмма (противолежащие стороны равны). Таким образом, BE = EA, EC= ED, BC = AD. Следовательно, треугольники BEC и AED равны по трём сторонам.
В равных треугольниках — равные элементы. Значит, углы CBE и DAE равны. Так как их сумма равна 180° по свойству параллелограмма , то углы равны 90° (180 / 2 = 90 ) .
Следовательно, данный параллелограмм — прямоугольник.
spadilo.ru