Закон Ньютона — Рихмана — Википедия

Материал из Википедии — свободной энциклопедии

Закон Нью́тона — Ри́хмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор.

Теплоотдача — это процесс теплообмена между теплоносителем и твёрдым телом.

Теплопередача — это процесс передачи тепла от одной среды к другой через разделяющую их стенку. Закон утверждает, что

Плотность теплового потока (выражается в Вт/м²) на границе тел пропорциональна их разности температур (так называемый температурный напор): q=αΔT.{\displaystyle q=\alpha \Delta T.}

Коэффициент пропорциональности α{\displaystyle \alpha } — коэффициент теплоотдачи (англ.) — плотность теплового потока при перепаде температур на 1 K, измеряется в Вт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.

α{\displaystyle \alpha } — количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:

• от вида теплоносителя и его температуры;
• от температуры напора, вида конвекции и режима течения;
• от состояния поверхности и направления обтекания;
• от геометрии тела.

Поэтому α{\displaystyle \alpha } — функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.

Эквивалентная запись:

ddt∂∂SQ=αΔT.{\displaystyle {\frac {d}{dt}}{\frac {\partial }{\partial S}}Q=\alpha \Delta T.}

Из вышеприведённой дифференциальной формулировки можно вывести интегральную:

Количество теплоты, отданное через площадку на границе раздела тел площадью S{\displaystyle S} за время t{\displaystyle t}, пропорционально разности температур этих тел (если считать, что она остаётся за это время постоянной): Q=αtSΔT.{\displaystyle Q=\alpha tS\Delta T.}

Закон Ньютона служит одним из видов граничных условий (синоним — «условия третьего рода»), которые ставятся в задачах теплопроводности. В этом случае он записывается так (учтён также закон Фурье):

∂T∂n=k(Tout−Tin).{\displaystyle {\frac {\partial T}{\partial n}}=k(T_{\mathrm {out} }-T_{\mathrm {in} }).}

Заметим, что данный закон описывает ситуацию только на границе тела, внутри же температура определяется температуропроводностью тела. Тепловой поток внутри тела определяется по закону Фурье, что позволяет найти распределение, решив уравнение теплопроводности.

Если внутренняя теплопроводность намного больше, чем коэффициент теплоотдачи (иначе: маленькое число Био), то внутри устанавливается почти однородная температура (если на всей поверхности также она одинакова) и тогда можно записать уравнение охлаждения тела в виде:

∂T∂t=k(Tout−T).{\displaystyle {\frac {\partial T}{\partial t}}=k(T_{\mathrm {out} }-T).}

Здесь коэффициент k=αSC{\displaystyle k={\frac {\alpha S}{C}}}, где C{\displaystyle C} — теплоёмкость тела.

Из этого уравнения несложно получить, что температура тела в такой ситуации будет приближаться по экспоненте к температуре окружающей среды Tout{\displaystyle T_{\mathrm {out} }}:

T(t)=Tout+e−kt(T0−Tout).{\displaystyle T(t)=T_{\mathrm {out} }+e^{-kt}(T_{0}-T_{\mathrm {out} }).}

10.5. Расчетные формулы конвективного теплообмена.

Приведем некоторые основные расчетные формулы конвективного теплообмена (академика М.А.Михеева), которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки.

1. Свободная конвекция в неограниченном пространстве.

а). Горизонтальная труба диаметром d при 10³<(Gr··Pr)_жd <10⁸.

Nu_жdср.= 0,5·(Gr_жd·Pr _ж)^0,25(Pr _ж/Pr_ст)^0,25. (10.13)

б). Вертикальная труба и пластина: 1). ламинарное течение — 10³<(Gr ·Pr)_ж <10⁹:

Nu_жdср.= 0,75· (Gr_жd·Pr _ж)^0,25·(Pr _ж/Pr_ст)^0,25. (10.14)

2). турбулентное течение — (Gr ·Pr)_ж > 10⁹:

Nu_жdср.= 0,15· (Gr_жd·Pr _ж)^0,33·(Pr _ж/Pr_ст)^0,25. (10.15)

Здесь значения Gr_жdи Pr _жберутся при температуре жидкости (газа), а Pr_стпри температуре поверхности стенки. Для воздуха Pr _ж/Pr_ст= 1 и формулы (10.13-10.15) упрощаются.2. Вынужденная конвекция. Режим течения определяется по величине Re.а). Течение жидкости в гладких трубах круглого сечения. 1). ламинарное течение – Re < 2100

Nu_жdср.= 0,15·Re_жd^0,33·Pr_ж^0,33·(Gr_жd·Pr_ж)^0,1·(Pr_ж/Pr_ст)^0,25·ε_l , (10.16)

где ε_l— коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d). Значения этого коэффициента представлена в таблице 10.1. Таблица 10.1. Значение ε_lпри ламинарном режиме.

l/d	1	2	5	10	15	20	30	40	50
εl	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,0

2). переходной режим – 2100 < Re < 10⁴

Nu_жdср.= К₀·Pr_ж^0,43·(Pr_ж/Pr_ст)^0,25·ε_l . (10.17)

Коэффициент К₀зависит от критерия Рейнольдса Re и представлена в таблице 10.2. Таблица 10.2. Значение К₀.

Re?104	2,1	2,2	2,3	2,4	2,5	3	4	5	6	8	10
К0	1,9	2,2	3,3	3,8	4,4	6,0	10,3	15,5	19,5	27,0	33,3

3). турбулентное течение – Re = 10⁴

Nu_жdср.= 0,021· Re_жd^0,8·Pr_ж^0,43· (Pr_ж/Pr_ст)^0,25·ε_l . (10.18)

Таблица 10.3. Значение ε_lпри турбулентном режиме.

l/d
	Re = 2·10 3	Re = 2·104	Re = 2·105
1	1,9	1,51	1,28
2	1,70	1,40	1,22
5	1,44	1,27	1,15
10	1,28	1,18	1,10
15	1,18	1,13	1,08
20	1,13	1,11	1,06
30	1,05	1,05	1,03
40	1,02	1,02	1,02
50	1,00	1,00	1,00

б).Обтекание горизонтальной поверхности. 1). ламинарное течение – Re < 4·10⁴

Nu_жdср.= 0,66·Re_жd^0,5·Pr_ж^0,33 ·(Pr_ж/Pr_ст)^0,25. (10.19)

2). турбулентное течение – Re > 4·10⁴

Nu_жdср.= 0,037·Re_жd^0,5·Pr_ж^0,33 ·(Pr_ж/Pr_ст)^0,25. (10.20)

в). Поперечное обтекание одиночной трубы (угол атаки  = 90⁰). 1). при Re_жd = 5 — 10³

Nu_жdср.= 0,57·Re

ж^0,5·Pr_ж^0,38 ·(Pr_ж/Pr_ст)^0,25. (10.21)

2). при Re_жd = 10³ — 2·10⁵

Nu_жdср.= 0,25 ·Re_ж^0,6·Pr_ж^0,38 ·(Pr_ж/Pr_ст)^0,25. (10.22)

Тема 11. Тепловое излучение.

11.1. Общие сведения о тепловом излучении.

Лучистая энергия возникает за счет энергии других видов в результате сложных молекулярных и внутриатомных процессов. Природа всех лучей одинакова. Они представляют собой распространяющиеся в пространстве электромагнитные волны. Источником теплового излучения является внутренняя энергия нагретого тела. Количество лучистой энергии в основном зависит от физических свойств и температуры излучающего тела. Электромагнитные волны различаются между собой длиной волны В зависимости от длины волнылучи обладают различными свойствами. Наименьшей длиной волны обладают космические лучи= (0,1 – 10)

оА (где^оА — ангстрем, единица длины, 1^оА = 10^-10м). Гамма-лучи, испускаемые радиоактивными веществами, имеют длину волны до 10^оА ; лучи Рентгена –= (10-200) ^оА; ультрафиолетовые лучи – л = (200^оА — 0,4мк (мк —микрон, 1мк —0,001мм), световые лучи –= (0,4-0,8)мк, инфракрасные или тепловые лучи –= (0,8 – 400)мк, радио или электромагнитные лучи -> 400мк.Из всех лучей наибольший интерес для теплопередачи представляют тепловые лучи с= (0,8 – 40)мк. Лучеиспускание свойственно всем телам, и каждое из них излучает и поглощает энергию непрерывно, если температура его не равна 0°К. При одинаковых или различных температурах между телами, расположенными как угодно в пространстве, существует непрерывный лучистый теплообмен. При температурном равновесии тел количество отдаваемой лучистой энергии будет равно количеству поглощаемой лучистой энергии. Спектр излучения большинства твердых и жидких тел непрерывен. Эти тела испускают лучи всех длин волн от малых до больших. Спектр излучения газов имеет линейчатый характер. Газы испускают лучи не всех длин волн. Такое излучение называется селективным(избирательным). Излучение газов носит объемный характер. Суммарное излучение с поверхности тела по всем направлениям полусферического пространства и по всем длинам волн спектра называетсяинтегральнымилиполнымлучистым потоком(Q). Интегральный лучистый поток, излучаемый единицей поверхности по всем направлениям,называется излучательной способностьютела и обозначается

Е = dQ / dF , [вт/м²] (11.1)

где dQ —элементарный лучистый поток, испускаемый элементом поверхности dF. Каждое тело способно не только излучать, но и отражать, поглощать и пропускать через себя падающие лучи от другого тела. Если обозначить общее количество лучистой энергии, падающей на тело, через Q, то часть энергии, равная А, поглотится телом, часть, равная R, отразится, а часть, равная D, пройдет сквозь тело. Отсюда

Q = Q_A+ Q_R+ Q_D, (11.2)

или

A + R + D = 1. (11.3)

Величину А называют коэффициентом поглощения.Он представляет собой отношение поглощенной лучистой энергии ко всей лучистой энергии, падающей на тело. Величину R называюткоэффициентом отражения. R есть отношение отраженной лучистой энергии ко всей падающей. Величину D называюткоэффициентом проницаемости. D есть отношение прошедшей сквозь тело лучистой энергии ко всей лучистой энергии, падающей на тело. Для большинства твердых тел, практически не пропускающих сквозь себя лучистую энергию, А + R = 1. Если поверхность поглощает все падающие на нее лучи, т. е. А = 1, R = 0 и D = 0, то такую поверхность называютабсолютно черной.Если поверхность отражает полностью все падающие на нее лучи, то такую поверхность называют

абсолютно белой.При этом R = 1, А = О, D = 0. Если телоабсолютно проницаемодля тепловых лучей, то D = 1, R = 0 и A = 0. В природе абсолютно черных, белых и прозрачных тел не существует, тем не менее понятие о них является очень важным для сравнения с реальными поверхностями. Кварц для тепловых лучей непрозрачен, а для световых и ультрафиолетовых лучей прозрачен. Каменная соль прозрачна для тепловых лучей и непрозрачна для ультрафиолетовых лучей. Оконное стекло прозрачно для световых лучей, а для ультрафиолетовых и тепловых почти непрозрачно. Белая поверхность (ткань, краска) хорошо отражает лишь видимые лучи, а тепловые лучи поглощает также хорошо, как и темная. Таким образом, свойство тел поглощать или отражать тепловые лучи зависят в основном от состояния поверхности, а не от ее цвета. Если поверхность отражает лучи под тем же углом, под которым они падают на нее, то такую поверхность называютзеркальной.Если падающий луч при отражении расщепляется на множество лучей, идущих по всевозможным направлениям, то такое отражение называютдиффузным(например поверхность мела). При исследовании лучистых потоков большое значение имеет распределение лучистой энергии, испускаемой абсолютно черным телом по отдельным длинам волн спектра. Каждой длине волны лучей, при определенной температуре, соответствует определенная интенсивность излучения — I_s.Интенсивность излученияилиспекnральная(монохроматическая)интенсивность,представляет собой плотность лучистого потока тела для длин волн отдо+d, отнесенная к рассматриваемому интервалу длин волн d;

I_s= dE_s/ d, (11.4)

где I_s— спектральная интенсивность излучения абсолютно черного тела.

Конвекция — Википедия

Материал из Википедии — свободной энциклопедии

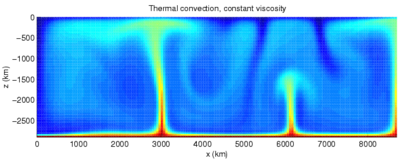Эта иллюстрация показывает расчетную картину конвективного движения в мантии Земли

Конвекция (от лат. convectiō — «перенесение») — вид теплообмена, при котором внутренняя энергия передается струями и потоками. Существует так называемая естественная конвекция, которая возникает в веществе самопроизвольно при его неравномерном нагревании в поле тяготения. При такой конвекции нижние слои вещества нагреваются, становятся легче и всплывают, а верхние слои, наоборот, остывают, становятся тяжелее и опускаются вниз, после чего процесс повторяется снова и снова. При некоторых условиях процесс перемешивания самоорганизуется в структуру отдельных вихрей и получается более или менее правильная решётка из конвекционных ячеек.

Различают ламинарную и турбулентную конвекцию.

Естественной конвекции обязаны многие атмосферные явления, в том числе, образование облаков. Благодаря тому же явлению движутся тектонические плиты. Конвекция ответственна за появление гранул на Солнце.

При вынужденной (принудительной) конвекции перемещение вещества обусловлено действием внешних сил (насос, лопасти вентилятора и т. п.). Она применяется, когда естественная конвекция является недостаточно эффективной.

Конвекцией также называют перенос теплоты, массы или электрических зарядов движущейся средой.

Виды конвекции

Термохалинная циркуляция

Естественная — нагревание/остывание жидкости, воздуха в комнате, воды в океане, устойчивые ветра (пассаты, муссоны).

Вынужденная — перемешивание жидкости или газа (мешалкой, ложкой, насосом, вентилятором).

Виды конвекции по причине появления

Математическое описание

Наиболее популярной моделью для описания конвекции в жидкостях и газах является приближение Буссинеска

См. также

Другие способы переноса теплоты

Ссылки

Литература

• Остроумов Г. А. Свободная тепловая конвекция в условиях внутренней задачи. Москва — Ленинград. Гостехиздат.— 1952.
• Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Т. 6. Гидродинамика.— М.:Наука.— 1988.—736 с.— (§ 56 Свободная конвекция).
• Гершуни Г. З., Жуховицкий Е. М. Устойчивость конвективных течений.— М.:Наука.— 1989.
• Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости.— М.:Наука.— 1972.
• Кригель А. М. О применимости приближения свободной конвекции к атмосферной турбулентности // Вестник Ленинградского гос. университета.— Сер.7.—1991.—Вып.2(14).—С.107-110.
• Кригель А. М. Вопросы термодинамики турбулентной конвекции. // Журнал Технической Физики.—2016.—86.—Вып.11.—С.136—139.

Расчетные формулы конвективного теплообмена. «ТЕПЛОТЕХНИКА. КУРС ЛЕКЦИЙ», Скрябин В.И

Приведем некоторые основные расчетные формулы конвективного теплообмена (академика М.А.Михеева), которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки. Свободная конвекция в неограниченном пространстве. а). Горизонтальная труба диаметром d при 103<(Gr·Pr)жd <108. Nuжdср. = 0,5·(Grжd ·Pr ж)0,25 (Pr ж/Prст)0,25 . (10.13) б). Вертикальная труба и пластина: 1). ламинарное течение — 103<(Gr ·Pr)ж <109: Nuжdср. = 0,75· (Grжd ·Pr ж)0,25·(Pr ж/Prст)0,25 . (10.14) 2). турбулентное течение — (Gr ·Pr)ж > 109: Nuжdср. = 0,15· (Grжd ·Pr ж)0,33 ·(Pr ж/Prст)0,25 . (10.15) Здесь значения Grжd и Pr ж берутся при температуре жидкости (газа), а Prст при температуре поверхности стенки. Для воздуха Pr ж/Prст = 1 и формулы (10.13-10.15) упрощаются. 2. Вынужденная конвекция. Режим течения определяется по величине Re. а). Течение жидкости в гладких трубах круглого сечения. 1). ламинарное течение – Re < 2100 Nuжdср. = 0,15·Reжd0,33·Prж0,33·(Grжd·Prж)0,1·(Prж/Prст)0,25·εl , (10.16) где εl - коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d). Значения этого коэффициента представлена в таблице 10.1. Таблица 10.1. Значение εl при ламинарном режиме. l/d 1 2 5 10 15 20 30 40 50 εl 1,9 1,7 1,44 1,28 1,18 1,13 1,05 1,02 1,0 2). переходной режим – 2100 < Re < 104 Nuжdср. = К0·Prж0,43·(Prж/Prст)0,25·εl . (10.17) Коэффициент К0 зависит от критерия Рейнольдса Re и представлена в таблице 10.2. Таблица 10.2. Значение К0 . Re?104 2,1 2,2 2,3 2,4 2,5 3 4 5 6 8 10 К0 1,9 2,2 3,3 3,8 4,4 6,0 10,3 15,5 19,5 27,0 33,3 3). турбулентное течение – Re = 104 Nuжdср. = 0,021· Reжd0,8·Prж0,43· (Prж/Prст)0,25·εl . (10.18) Таблица 10.3. Значение εl при турбулентном режиме. l/d     Re = 2·103 Re = 2·104 Re = 2·105 1 1,9 1,51 1,28 2 1,70 1,40 1,22 5 1,44 1,27 1,15 10 1,28 1,18 1,10 15 1,18 1,13 1,08 20 1,13 1,11 1,06 30 1,05 1,05 1,03 40 1,02 1,02 1,02 50 1,00 1,00 1,00 б).Обтекание горизонтальной поверхности. 1). ламинарное течение – Re < 4·104 Nuжdср. = 0,66·Reжd0,5·Prж0,33 ·(Prж/Prст)0,25. (10.19) 2). турбулентное течение – Re > 4·104 Nuжdср. = 0,037·Reжd0,5·Prж0,33 ·(Prж/Prст)0,25. (10.20) в). Поперечное обтекание одиночной трубы (угол атаки j = 900). 1). при Reжd = 5 — 103 Nuжdср. = 0,57·Reж0,5·Prж0,38 ·(Prж/Prст)0,25. (10.21) 2). при Reжd = 103 -2·105 Nuжdср. = 0,25 ·Reж0,6·Prж0,38 ·(Prж/Prст)0,25. (10.22) Предыдущая страница | Следующая страница СОДЕРЖАНИЕ

Приближение Буссинеска — Википедия

Материал из Википедии — свободной энциклопедии

Уравнения тепловой конвекции (уравнения Буссине́ска, приближение Буссине́ска) в приближении Буссинеска — Обербека — наиболее популярная модель для описания конвекции в жидкостях и газах.

Модель включает в себя уравнение Навье — Стокса, уравнение теплопроводности и уравнение несжимаемости. Основная идея приближения состоит в особенности учёта зависимости плотности от температуры. Именно, в системе уравнений конвекции данная зависимость учитывается только при массовых силах:

ρ0(∂v→∂t+(v→⋅∇)v→)=−∇p+ηΔv→+ρ(T)g→,{\displaystyle \rho _{0}\left({\frac {\partial {\vec {v}}}{\partial t}}+({\vec {v}}\cdot \nabla ){\vec {v}}\right)=-\nabla p+\eta \Delta {\vec {v}}+\rho (T){\vec {g}},}

∂T∂t+v→⋅∇T=χΔT,{\displaystyle {\frac {\partial T}{\partial t}}+{\vec {v}}\cdot \nabla T=\chi \Delta T,}

div⁡v→=0,{\displaystyle \operatorname {div} {\vec {v}}=0,}

где v→{\displaystyle {\vec {v}}} — скорость течения, T{\displaystyle T} — абсолютная температура, p{\displaystyle p} — давление, η{\displaystyle \eta } — динамическая вязкость, χ{\displaystyle \chi } — коэффициент температуропроводности, g→{\displaystyle {\vec {g}}} — ускорение свободного падения.

Часто для зависимости плотности от температуры применяется линейная аппроксимация:

ρ(T)=ρ0(1−βθ){\displaystyle \rho (T)=\rho _{0}(1-\beta \theta )},

где β{\displaystyle \beta } — коэффициент объёмного расширения, θ=T−T0{\displaystyle \theta =T-T_{0}} — отклонение температуры от равновесного состояния, ρ0{\displaystyle \rho _{0}} — плотность жидкости при некоторой равновесной температуре T0{\displaystyle T_{0}}. Поскольку β{\displaystyle \beta } и отклонение температуры обычно относительно невелико, то линейное приближение обладает приемлемой точностью в большинстве исследуемых задач.

Подстановка линейной зависимости плотности и перенормировка давления позволяют исключить слагаемое ρ0g→{\displaystyle \rho _{0}{\vec {g}}}. Окончательно задача конвекции несжимаемой жидкости в приближении Буссинеска принимает следующий вид:

∂v→∂t+(v→⋅∇)v→=−1ρ0∇p+νΔv→−βθg→,{\displaystyle {\frac {\partial {\vec {v}}}{\partial t}}+({\vec {v}}\cdot \nabla ){\vec {v}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \Delta {\vec {v}}-\beta \theta {\vec {g}},}

∂θ∂t+v→⋅∇θ=χΔθ,{\displaystyle {\frac {\partial \theta }{\partial t}}+{\vec {v}}\cdot \nabla \theta =\chi \Delta \theta ,}

div⁡v→=0,{\displaystyle \operatorname {div} {\vec {v}}=0,}

здесь ν{\displaystyle \nu } — кинематическая вязкость.

Приведённая задача конвекции в различных постановках неоднократно исследовалась. Наиболее широко известна задача Рэлея — Бенара о конвекции в плоском слое жидкости. При определённых условиях возможно точное решение задачи, например, для ламинарной конвекции в вертикальном слое при подогреве сбоку (иногда встречается под названием «задача Гершуни»).

• Остроумов Г. А. Свободная тепловая конвекция в условиях внутренней задачи. Москва — Ленинград. Гостехиздат.— 1952.
• Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Т. 6. Гидродинамика.— М.:Наука.— 1988.—736 с.— § 56
• Гершуни Г. З., Жуховицкий Е. М. Устойчивость конвективных течений.— М.:Наука.— 1989.
• Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости.— М.:Наука.— 1972.
• Кригель А. М. О применимости приближения свободной конвекции к атмосферной турбулентности // Вестник Ленинградского гос. университета.— Сер.7.—1991.—Вып.2(14).—С.107-110.

Коэффициент теплоотдачи, формула и примеры

Определение и формула коэффициента теплоотдачи

Конвективный теплообмен — обмен теплотой между частями жидкости (газа), имеющими разную температуру или между жидкостью (газом) и твердым телом. Конвективный теплообмен между жидкостью и твердым телом называют теплоотдачей.

Этот коэффициент часто используют в гидроаэродинамике, когда исследуют конвективный теплообмен. Часто ее обозначают буквой . Коэффициент равен:

   

где — плотность теплового потока, — температурный напор. Величина q — это количество теплоты, которое передается через единичную площадь поверхности тела в единицу времени. находят как модуль разности температур жидкости и поверхности тела. Иногда температурный напор находят, например, в случае обтекания тела потоком сжимаемой жидкостью, считают равным модулю разности температуры жидкости далеко от тела и температурой поверхности тела, которая была бы в отсутствии теплообмена.

Коэффициент теплоотдачи зависит от скорости потока носителя тепла, вида течения, какова геометрия поверхности твердого тела и т.д. Это сложная величина и ее невозможно определить общей формулой. Обычно коэффициент теплоотдачи находят экспериментально.

Так, для условий свободной конвекции воздуха: (Вт/м²К), воды: (Вт/м²К). При вынужденной конвекции величины коэффициента теплоотдачи колеблются в пределах: для воздуха: (Вт/м²К), для воды: (Вт/м²К).

Формула Ньютона-Рихмана

Коэффициент теплоотдачи входит в выражение для потока тепла в веществе жидкой или газообразной среды с интенсивным изменением температуры при увеличении расстояния от охлаждаемого или нагреваемого объекта:

   

где — количество теплоты, которая отводится от поверхности, имеющую площадь S, — температура вещества (жидкости, газа), — температура поверхности тела. Выражение (2) называется формулой Ньютона — Рихмана.

Так как интенсивность теплообмена может изменяться при передвижении вдоль площади соприкосновения жидкого носителя с поверхностью твердого тела, вводят местный коэффициент теплоотдачи, который равен:

   

На практике чаще применяют средний коэффициент теплоотдачи , вычисляя его по формуле:

   

где температуры берут средние для поверхности и для вещества.

Дифференциальное уравнение теплоотдачи

Дифференциальное уравнение теплоотдачи показывает связь между коэффициентом теплоотдачи и полем температур среды (жидкости или газа):

   

где , — градиент температуры, индекс n=0 значит то, что градиент берут на стенке.

Критерий Нуссельта

Критерий Нуссельта () является характеристикой теплообмена на границе между жидкостью и стеной:

   

где — характерный линейный размер, — коэффициент теплопроводности жидкости. Для стационарного процесса критерий Нуссельта находят, используя критериальное уравнение конвективного теплообмена:

   

где постоянные. — критерий Рейнольдса, — критерий Прандтля, — критерий Грасгофа.

Коэффициент теплоотдачи и его связь с коэффициентом теплопередачи

Коэффициентом теплопередачи через плоскую стенку связан с коэффициентами теплоотдачи выражением:

   

где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.

Единицы измерения

Основной единицей измерения коэффициента теплоотдачи в системе СИ является:

=Вт/м²К

Примеры решения задач