Задачи, решаемые с помощью уравнения. 7-й класс
Цели урока:
- Проверка практических умений и навыков решения задач на составление уравнения.
- Активизация учебной деятельности учащихся путём общения в динамических парах, когда каждый учит каждого.
- Воспитывать ответственное отношение к учебному труду, развивать логическое мышление, любознательность, умение проверять и оценивать выполненную работу.
Коллективным способом обучения (А. Г. Ривин и В.К. Дьяченко) является такая его организация, при которой обучение осуществляется путём общения в динамических парах, когда каждый учит каждого.
Ход урока
I. Работа начинается с ввода или так называемого “запуска” раздела.
Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью уравнения”.
Примеры задач:
1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх величин.
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | Х + 2 | 9 | 9(Х + 2) |
| Против течения | Х – 2 | 11 | 11(Х – 2) |
На основании условия задачи составим уравнение:
9(Х + 2) = 11(Х – 2), которое имеет единственный корень 20.
Собственная скорость теплохода 20 км/ч.
2. Увеличив среднюю скорость с 250 до300 м/мин, спортсменка стала пробегать
дистанцию на 1 мин быстрее. Какова длина дистанции?
250(Х + 1) = 300Х , которое имеет единственный корень 5.Найдём длину дистанции 300Х = 300×5 = 1500 м.
3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг. Заполним таблицу значений величин для двух бригад:
| Привезли(кг) | Расход(кг)за 1 час | Время (ч) | Осталось раствора(кг) | |
| 1-я бригада | Х | 150 | 3 | Х – 450 |
| 2-я бригада | Х + 50 | 200 | 3 | Х + 50 – 600 |
По условию задачи в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Составим уравнение:
Х – 450 = (Х + 50 – 600)×1,5 , имеющее единственный корень 750. 750 кг раствора привезли в первую бригаду, а во вторую привезли 750 + 50 = 800 кг.
4. (Задача Э.Безу) По контракту работникам причитается 48 франков за каждый
отработанный день, а за каждый неотработанный день с них вычитается по 12
франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько
дней они отработали в течение этих 30 дней?
48Х – 12 (30 – Х) = 0.
Решив это уравнение, получим Х = 6, то есть они отработали 6 дней.
5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал
на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй.
Сколько страниц прочитал ученик в первый день?
Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик
прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим
уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик
прочитал в первый день 80 страниц.
6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей.
Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
II. Самостоятельная работа учащихся.
Каждый ученик получает индивидуальную карточку с задачами. Правильность решения проверяет преподаватель, при необходимости он оказывает помощь в решении. После проверки ученику выставляется в оценочный лист плюс или оценка.
Примеры карточек для первой группы:
Карточка № 1.
1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?
2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
Ответ: № 1 – 8 дней, № 2 – 9 дней.
Карточка № 2.
1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до срока. Сколько сорочек в день должен был выпускать кооператив?
2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько кур на ферме?
Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..
Карточка № 3.
1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?
2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
Ответ: № 1 – 360 км, № 2 – 408 деталей.
Карточка № 4.
1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?
2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?
Ответ: № 1 – 9 км, № 2 – 9 дней.
Примеры карточек для второй группы:
Карточка № 5.
1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В , отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?
2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая и вторая детали вместе. Сколько деталей изготовила каждая бригада?
Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.
Карточка № 6.
1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?
2. Бригада рабочих должна была изготовить определённое количество деталей за 20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?
Ответ: № 1 – 2 ч, № 2 – 3000 деталей.
Карточка № 7.
1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1 ч вслед за ним отошёл другой теплоход со скоростью 60 км/ч. Через сколько часов после своего отправления и на каком расстоянии от А второй теплоход догонит первый?
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.
Карточка № 8.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2 ч против течения. Какова скорость катера в стоячей воде, если скорость течения 1,5 км/ч?
Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.
Примеры карточек для третьей группы:
Карточка № 9.
1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.
2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через сколько часов воды в резервуаре станет поровну?
Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.
Карточка № 10.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на один день быстрее, чем планировалось. Какова площадь луга?
Ответ: № 1 – 7 монет, № 2 – 300 га.
Карточка № 11.
1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?
2. Турист рассчитал, что если он будет идти к железнодорожной станции со скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое расстояние должен пройти турист?
Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.
Карточка № 12.
1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?
2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое число.
Ответ: № 1 – 83 ореха, № 2 – 45.
Раздел считается введённым в работу, если каждая карточка с заданиями выполнена хотя бы одним учеником.
III. Работа в группах.
Затем работа классного коллектива выглядит так: организуется 3–4 группы по 4 человека (можно до 7 человек). В группе у каждого ученика своя карточка, за которую ученик уже получил плюс или оценку в оценочный лист. Каждый в группе выбирает партнёра, и они меняются карточками. Школьники работают в парах (решают карточку своего партнера полностью), затем пары в группе меняются. Если необходима помощь, то происходит взаимообучение. Если помощь не нужна, то после выполнения задания происходит взаимопроверка и делается отметка в оценочный лист. Потом пары меняются, и процесс продолжается до тех пор, пока каждый ученик не выполнит задания других учеников группы. Затем подводится итог, и выставляется общая оценка.
Оценочный лист.
| №1 | №2 | №3 | №4 | Итоговая оценка | |
| Лаптева Алина | 5 | ||||
| Борзенков Егор | 3 | ||||
| Мартышин Сергей | 4 | ||||
| Казакова Виктория | 3 |
По диагонали оценка выставлена учителем. За выполнение карточки № 1оценка выставляется Лаптевой А., № 2 – Борзенковым Е., № 3 – Мартышиным С., № 4 – Казаковой В..
urok.1sept.ru
«Методические особенности обучения решению задач. Как решать задачи на движение по реке?»
Государственное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 115
Выборгского района Санкт-Петербурга
«Методические особенности обучения решению задач.
Как решать задачи на движение по реке?»
выполнил:
учитель математики ГБОУ школы № 115
Клюева Любовь Дмитриевна
Санкт – Петербург
2019 г.
«Методические особенности обучения решению задач.
Как решать задачи на движение по реке?»
Введение

Здесь могут встречаться задачи:
задачи на движение навстречу друг другу;
движение вдогонку;
движение в противоположном направлении.
У реки есть скорость течения, которую не стоит игнорировать. Здесь объекты будут двигаться либо по течению реки — тогда эту скорость стоит прибавить к собственной скорости объектов, либо против течения — ее необходимо вычесть из скорости движения объекта.
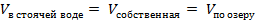 ,
,
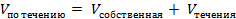 ,
,
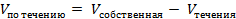 ,
,
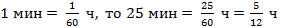 .
.
В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место. Они являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Решение задач является наиболее эффективной формой развития математической деятельности.
Наиболее удобные обозначения при решении задач на движение
S (км)– путь, расстояние;
V (км/ч) – скорость;
t (ч) – время.
Связь при равномерном движении по прямой между этими величинами такова: S=V*t
При обучении математике задачи имеют образовательное, развивающее, воспитательное значение.
Они развивают логическое и алгоритмическое мышление учащихся, вырабатывают практические навыки применения математики. При обучении теоретическим знаниям задачи способствуют мотивации введения понятий, выявлению их существенных свойств, усвоению математической символики и терминологии, раскрывают взаимосвязи одного понятия с другими.
Воспитательное воздействие оказывает общий подход к решению задач: система задач, место, методы и формы ее решения, стиль общения учителя и учащихся, учащихся между собой при решении задач. Решение задач позволяет учащимся воспитывать в себе настойчивость, трудолюбие, активность, самостоятельность, формирует познавательный интерес, помогает вырабатывать и отстаивать свою точку зрения.
Развивающие функции задач заключаются в том, что в деятельности решения задач вырабатываются умения применять теоретические знания на практике, выделять общие способы решения, переносить их на новые задачи, развиваются логическое и творческое мышление, внимание, память, воображение.
Использование исторических задач и разнообразных старинных (арифметических) способов их решения не только обогащает опыт мыслительной деятельности учащихся, но и позволяет им осваивать важный культурно-исторический пласт истории человечества, связанный с поиском решения задач. Это важный внутренний (связанный с предметом), а не внешний (связанный с отметками, поощрениями и т.п.) стимул к поиску решений задач и изучению математики.
С изменением роли и места задач в обучении обновляются и видоизменяются и сами задачи. Раньше они формулировались с помощью слов “найти”, “построить”, “вычислить”, “доказать”, в современной школе чаще используются слова “обосновать”, “выбрать из различных способов решения наиболее рациональный”, “исследовать”, “спрогнозировать различные способы решения” и т.д.
Методические подходы к решению задач по теме
Общие умения по решению задач:
• умение проводить анализ условия задачи;
• умение применять изученную теорию (определение, правило) на практике;
• умение выделять основную идею в решении отдельной задачи, находить общее в решении нескольких задач и переносить эту идею, это общее на новую задачу;
• умения по самооценке своей деятельности, самоконтролю.
Обучение краткой записи условия задачи — это и есть обучение анализу условия. Краткая запись — это модель текста задачи, материализованная форма проведения действия анализа условия. Начинать поиск решения задачи можно лишь тогда, когда ее условие полностью понято. На ранее перечисленных этапах решения задачи самоконтроль проявляет себя как естественная неотрывная составляющая поисковой деятельности, которая может и не осознаваться учеником. Последнему этапу решения задачи — проверке и исследованию полученного решения присвоен особый статус этапа, на котором осуществляется самоконтроль.
При подготовке к ЕГЭ мои ученики решают задачи на движение, работу, производительность труда, процентный прирост, процентное содержание и др. Имея богатый опыт решения текстовых задач не только с помощью составления уравнений, но и арифметическим способом они выбирают наиболее рациональный способ решения задачи. Кроме того, вовлекая их в создание разнообразных математических моделей решения, достигается одна из основных целей обучения математике: воспитание гармонично развитой личности.
«Как решать задачи на движение по реке?»
Условия задачи удобно анализировать, заполняя таблицу.
Методы решения: составление таблицы, алгебраический метод .
Основные этапы решения текстовой задачи алгебраическим методом

3. Примеры решения задач из ГИА (2-3 задачи)
Задача1. Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 час больше чем на путь по реке. Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.
Решение задачи 1.

Задача2. Теплоход проходит по течению до пункта назначения 126 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения 2 км/ч, стоянка длится 8 ч, а в пункт отправления теплоход возвращается ровно через сутки после отплытия из него.
Решение задачи 2.

infourok.ru
Решение текстовых задач на движение и работу. Видеоурок. Алгебра 11 Класс
На данном уроке мы рассмотрим задачи на движение и работу и примеры их решения.
Тема: Общее повторение курса математики. Подготовка к экзаменам
Урок: Решение текстовых задач на движение и работу
Задачи на движение и работу достаточно похожи как по смыслу, так и по структуре решения.
Рассмотрим более стандартные задачи – на движение. Основная цель, как и при решении любых текстовых задач, – составить уравнение или систему уравнений по тексту условия задачи и решить его. Здесь нам помогут два аспекта – во-первых, нужно ввести какие-нибудь переменные, исходя из данных задачи, во-вторых, стремиться к базовому уравнению движения:
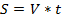 , где S – путь, V – скорость движения, t – время движения.
, где S – путь, V – скорость движения, t – время движения.
При введении переменных следует помнить о том, что все единицы измерения должны быть одинаковыми, то есть если путь введен в метрах, то скорость не может быть в километрах в час, в таком случае уравнение будет составлено неверно. Так, необходимо все единицы измерения сделать одинаковыми, то есть путь в километрах и скорость в километрах в час или путь в метрах и скорость в метрах в секунду и т. д.
Кроме того отметим, что переменные рекомендуется вводить вместо скорости или вместо искомой в задаче величины, переменную вместо времени при наличии выбора вводить не рекомендуется.
Пример 1: из пункта А в пункт В одновременно выехали два автомобиля. Причем первый проехал весь путь с постоянной скоростью. Второй же проехал первую половину пути со скоростью 24 км/час, а вторую – со скоростью 16 км/час. Найти скорость первого автомобиля (в км/час), если в пункт В оба автомобиля прибыли одновременно.
Решение:
1. Поскольку требуется найти скорость первого автомобиля, введем главную переменную 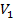 ; кроме того, для составления первого уравнения введем две второстепенных переменных:
; кроме того, для составления первого уравнения введем две второстепенных переменных: 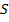 – весь путь из А в В;
– весь путь из А в В; 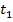 – время, за которое первый автомобиль преодолел весь путь; имеем первое уравнение:
– время, за которое первый автомобиль преодолел весь путь; имеем первое уравнение: 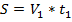 ;
;
2. Второй автомобиль преодолел первую половину пути ( ) со скоростью 24 км/час, пусть за некоторое время
) со скоростью 24 км/час, пусть за некоторое время  :
: 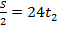 ;
;
3. Второй автомобиль преодолел вторую половину пути ( ) со скоростью 16 км/час, пусть за некоторое время
) со скоростью 16 км/час, пусть за некоторое время 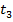 :
: 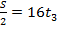 ;
;
4. Поскольку оба автомобиля прибыли в пункт В одновременно, имеем уравнение: 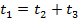 ;
;
5. Выразим
interneturok.ru
Как решать задачи за 7 класс по алгебре
В 7 классе курс алгебры усложняется. В программе возникает много увлекательных тем. В 7 классе решают задачи на различные темы, скажем: «на скорость (на движение)», «движение по реке», «на дроби», «на сопоставление величин». Мастерство с легкостью решать задачи указывает на высокий ярус математического и логичного мышления. Абсолютно,с удовольствием решаются только те, которые легко поддаются и получаются.
Инструкция
1. Разберем, как решать больше распространенные задачи.При решении задач на скорость нужно знать несколько формул и уметь верно составить уравнение.Формулы для решения :S=V*t – формула пути;V=S/t – формула скорости;t =S/V – формула времени, где S – расстояние, V – скорость, t – время.На примере разберем, как решать задания такого типа.Условие: Грузовой автомобиль на путь из города «А» в город «Б» потратил 1,5часа. 2-й грузовой автомобиль потратил 1,2 часа. Скорость второго автомобиля огромнее на 15 км/ч., чем скорость первого. Обнаружить расстояние между двумя городами.Решение: Для комфорта применяйте следующую таблицу. В ней укажите то, что вестимо по условию: 1 авто 2 автоS X XV X/1,5 X/1,2t 1,5 1,2За Х примите то, что нужно обнаружить, т.е. расстояние. При составлении уравнения будьте внимательнее, обратите внимание, дабы все величины были в идентичном измерении (время – в часах, скорость в км/ч). По условию скорость 2-го авто огромнее скорости 1-го на 15 км/ч, т.е. V1 – V2=15. Зная это, составим, и решим уравнение:X/1,2 – X/1,5=151,5Х – 1,2Х – 27=00,3Х=27Х=90(км) – расстояние между городами.Результат: Расстояние между городами 90 км.
2. При решении задач на “движение по воде” нужно знать, что существуют несколько видов скоростей: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость вопреки течения (Vпр. теч.), скорость течения (Vтеч.).Запомните следующие формулы:Vпо теч=Vс+Vтеч.Vпр. теч.=Vс-Vтеч.Vпр. теч=Vпо теч. – 2Vтеч.Vпо теч.=Vпр. теч+2Vтеч.Vс=(Vпо теч.+Vпр теч.)/2 либо Vс=Vпо теч.+Vтеч.Vтеч.=(Vпо теч. – Vпр. теч)/2На примере, разберем, как их решать.Условие: Скорость катера по течению 21,8км/ч, а супротив течения 17,2 км/ч. Обнаружить собственную скорость катера и скорость течения реки.Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, обнаружим:Vтеч = (21,8 – 17,2)/2=4,6\2=2,3 (км/ч)Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)Результат: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
3. Задачи на сопоставление величинУсловие: Масса 9 кирпичей на 20 кг огромнее, чем масса одного кирпича. Обнаружить массу одного кирпича.Решение: Обозначим за Х (кг), тогда масса 9 кирпичей 9Х (кг). Из данные следует, что:9Х – Х=208х=20Х=2,5Ответ: Масса одного кирпича 2,5 кг.
4. Задачи на дроби. Основное правило при решении таких такого типа задач: Дабы обнаружить дробь от числа, нужно это число умножить на данную дробь.Условие: Путешественник был в пути 3 дня. В 1-й день он прошел? каждого пути, во 2-й 5/9 оставшегося пути, а в 3-й день – последние 16 км. Обнаружить каждый путь путешественника.Решение: Пускай каждый путь путешественника равен Х (км). Тогда в 1-й день он прошел? х (км), во 2-й день – 5/9(х -?) = 5/9*3/4х = 5/12х. Потому что в 3-й день он прошел 16 км, то:1/4х+5/12х+16=х1/4х+5/12х-х= – 16- 1/3х=-16Х=- 16:(-1/3)Х=48Ответ: Каждый путь путешественника равен 48 км.
Решить задачу на движение относительно примитивно. Довольно знать каждого одну формулу: S=V*t.
Инструкция
1. При решении задач на движение основными параметрами считаются:пройденный путь, обозначаемый традиционно как S,скорость – V ивремя – t.Связанность между этими параметрами выражается следующими формулами:S=Vt, V=S/t и t=S/VЧтобы не запутаться в единицах измерения, перечисленные параметры обязаны быть заданы в одной системе. Скажем, если время измеряется в часах, а пройденный путь в километрах, то скорость, соответственно, должна измеряться в километр/час.При решении задач этого типа традиционно производятся следующие действия:1. Выбирается один из незнакомых параметров и обозначается буквой х (у, z и т.п.)2. Уточняется, какой из 3 основных параметров вестим.3. 3-й из оставшихся параметров с подмогой приведенных выше формул выражается через два других.4. Исходя из условий задачи , составляют уравнение, которое объединяет неведомое значение с знаменитыми параметрами.5. Решают полученное уравнение.6. Проверяют обнаруженные корни уравнения на соответствие условиям задачи .В некоторых случаях решить задачу помогает чертеж (самостоятельно от качества рисунка).
2. Пример 1.Решить задачу:Лыжник проезжает 5 км за то же время, за которое пешеход поспевает пройти 2 км.Обнаружить это время, если знаменито, что скорость лыжника огромнее скорости пешехода на 6 км/ч. Определить скорости пешехода и лыжника.Обозначим желанное время (в часах) через t.Тогда, по формуле V=S/t, скорость лыжника равна 5/t км/ч, а скорость пешехода равна 2/t км/ч.Применяя данные задачи дозволено составить уравнение:5/t – 2/t = 6Откуда определяем, что: t=0,5Следовательно: скорость пешехода равна 4 км/ч, а лыжника – 10 км/ч.Результат: 0,5 часа; 4 км/ч; 10 км/ч.
3. Пример 2.Решим вышеприведенную задачу иным методом:Обозначим скорость пешехода через V (км/ч).Тогда скорость лыжника составит (V+6) км/ч.В соответствии с формулой: t=S/V, время дозволено определить согласно дальнейшему выражению:t=5/(V+6)=2/VОткуда элементарно находится:V=4,t=0,5.
В задачах на сложение скоростей движение тел бывает, как водится, равномерным и откровенным и описывается примитивными уравнениями. Тем не менее, эти задачи дозволено отнести к сложнейшим задачам механики. При решении таких задач пользуются правилом сложения классических скоростей. Дабы осознать правило решения, отменнее разглядеть его на определенных примерах задач.
Инструкция
1. Пример на правило сложения скоростей. Пускай скорость течения реки v0, а скорость лодки, переплывающей эту реку, касательно воды равна v1 и направлена перпендикулярно храню (см рисунок 1). Лодка единовременно участвует в 2-х самостоятельных движениях: она за некоторое время t переплывает реку шириной Н со скорость ю v1 касательно воды и за это же время ее сносит вниз по течению реки на расстояние l. В итоге лодка проплывает путь S со скорость ю v касательно берега, равной по модулю: v равно корень квардратный из выражения v1 в квадрате + v0 в квадрате за это же самое время t. Следственно дозволено записать уравнения, которые решают сходственные задачи: H=v1t, l = v0t? S= корень квадратный из выражения: v1 в квадрате + v0 в квадрате, умноженный на t.
2. Иной тип таких задач задает вопросы: под каким углом к храню должне грести гребец в лодке, дабы оказаться на противоположном храню, пройдя во время переправы наименьший путь? За какое время данный путь будет пройден? С какой скорость ю лодка пройдет данный путь?Дабы ответить на эти вопросы следует сделать рисунок (см рис 2). Видимо, что наименьший путь, тот, что может пройти лодка, пересекая реку, равен ширине реки Н. Дабы проплыть данный путь, гребец должен направить лодку под таким углом а к брегу, при которм вектор безусловной скорости лодки v будет направлен перпендикулярно храню. Тогда из прямоугольного треугольника дозволено обнаружить: cos a=v0/v1. Отсель дозволено извлечь угол а. Скорость определить из этого же треугольника по теореме Пифагора: v= корень квадратный из выражения: v1 в квадрате – v0 в квадрате.И наконец время t, за которое лодка пересечет реку шириной Н, двигаясь со скорость ю v, будет t=H/v.
Видео по теме
Алгебра – это раздел математики, направленный на постижение операций над элементами произвольного множества, тот, что обобщает обыкновенные операции по сложению и умножению чисел.
Вам понадобится
- – условие задачи;
- – формулы.
Инструкция
1. Элементарная алгебраИзучает свойства операций с вещественными числами, правила реформирования математических выражений и уравнений. Именно элементарную алгебру преподают в школах. Для решения задачи требуются следующие умения:Правила записи символов элементов и операций, скажем, присутствие скобок в выражении указывает на приоритетность заключенного в них действия. Свойства операций (при перегруппировке мест слагаемых сумма не меняется). Свойства равенства (если a=b, то b=a).Другие законы (если a поменьше b, то b огромнее a).
2. Тригонометрия – часть элементарной алгебры, постигающая тригонометрические функции, скажем, синус, косинус, тангенс, котангенс и т.д. Задачи на тригонометрические функции решают с поддержкой особых формул: тригонометрических тождеств, формул сложения, формул приведения тригонометрических функций, формул двойного довода, двойного угла и т.п. Основное тождество тригонометрии: сумма квадратов синуса и косинуса угла равна 1.
3. Производные функции и их применениеВ этом разделе для решения используются основные правила дифференцирования, скажем, производная суммы равна сумме производных. Область использования производных функций – физика, скажем, производная координаты по времени равна скорости, это механический толк производной функции.
4. Первообразная и интегралОбласть использования – физика, а вернее, механика. Скажем, первообразная (интеграл) от расстояния есть скорость. для нахождения первообразной функции существуют определенные правила, скажем, если F – первообразная для f, а G – для g, то F+G – первообразная для f+g.
5. Показательная и логарифмическая функцииПоказательная функция – это функция возведения в степень. Число, возводимое в степень, именуется основанием функции, а степень – показателем функции. Подчиняется правилам, скажем, всякое основание в нулевой степени равно 1.В логарифмической функции основанием именуется степень, в которую необходимо построить основание, дабы получить итоговое значение. Некоторые примитивные правила: логарифм, у которого основание и показатель идентичны, равен 1; логарифм по основанию 1 с любым показателем будет равен 0.
Видео по теме
Полезный совет
Главно осознать область, к которой относится ваша задача, остальное – дело техники.Немыслимо запомнить все формулы, следственно имейте под рукой математический справочник.
Дабы решить задачу с дробями , необходимо обучиться делать с ними арифметические действия. Они могут быть десятичные, но почаще каждого применяются естественные дроби с числителем и знаменателем. Только позже этого дозволено переходить на решения математических задач с дробными величинами.
Вам понадобится
- – калькулятор;
- – познания свойств дробей;
- – знание изготавливать действия с дробями.
Инструкция
1. Дробью называют запись деления одного числа на другое. Нередко это сделать нацело невозможно, следственно и оставляют это действие «неоконченным . Число, которое является делимым (оно стоит над либо перед знаком дроби), именуются числителем, а второе число (под знаком дроби либо позже него) – знаменателем. Если числитель огромнее знаменателя, дробь именуется неправильной, и из нее дозволено выделить целую часть. Если числитель поменьше знаменателя, то такая дробь именуется положительной, и ее целая часть равна 0.
2. Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Примитивный вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи довольно умножить это число на дробь. Скажем, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее всеобщего числа. Сколько картошки осталось? Дабы решить эту задачу, число 8 умножьте на 3/4. Получится 8?3/4=6 т.
3. Если необходимо обнаружить число по его части, умножьте знаменитую часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Скажем, 8 человек из класса составляют 1/3 от всеобщего числа учеников. Сколько детей учится в классе? От того что 8 человек это часть, которая представляет 1/3 от каждого числа, то обнаружьте обратную дробь, которая равна 3/1 либо примитивно 3. После этого для приобретения числа учеников в классе 8?3=24 ученика.
4. Когда надобно обнаружить какую часть числа составляет одно число от иного, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть данный составит от каждого пути? Поделите часть пути 200 на полный путь 300, позже сокращения дроби получите итог. 200/300=2/3.
5. Дабы обнаружить часть незнакомую долю от числа, когда есть знаменитая, возьмите целое число за условную единицу, и отнимите от нее знаменитую долю. Скажем, если теснее прошло 4/7 части урока, сколько еще осталось? Возьмите каждый урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.
Дроби – это математическая форма записи простого разумного числа. Она представляет собой число, которое состоит из одной либо нескольких долей единицы, может быть как в десятичном, так и в обыкновенном виде. Сегодня операции по реформированию дробей имеют громадное значение не только в математике, но и в иных областях познаний.
Инструкция
1. Как водится, множество обычных дробей бывают неправильными, и в таком случае они требуют определенных действий со стороны того, кто решает примеры и задачи с данной дробью.
2. Возьмите учебник со своей задачей. Наблюдательно ознакомьтесь с условием, прочитав его несколько раз, и перейдите к решению. Посмотрите, какие дроби имеются в решаемых вами действиях. Это могут быть неправильные, положительные либо десятичные дроби. Переведите верные дроби в неправильные, но при этом помните, что для записи результата все действия придется исполнить обратно, преобразовав теснее неправильную дробь в положительную. У неправильной дроби число над дробной чертой (числитель) неизменно огромнее числа под чертой – знаменателя. Для того дабы сделать перевод из верной дроби в неправильную нужно исполнить следующие шаги.
3. Умножьте знаменатель на целое число и прибавьте к полученному итогу числитель. К примеру, если дробь вида 2 целых 7/9, нужно 9 умножить на 2 и потом к 18 прибавить 7 – финальным итогом будет 25/9.
4. Произведите все нужные действия по своей задаче (сложения, вычитания, деления, умножения), применяя преобразованные дроби.Возьмите свой результат, его нужно будет представить в обычной дроби. Для этого поделите числитель на знаменатель. К примеру, если нужно перевести число 25/9 в положительную дробь, поделите 25 на 9. Потому что 25 на 9 нацело не делится, в результате получается 2 целых и семь (числитель) девятых (знаменатель). Сейчас получена верная дробь, где числитель огромнее знаменателя и имеется целая часть.
5. Запишите результат задачи положительной дробью. Проведите проверку своим действиям, в случае если ее требует сделать условие задачи либо преподаватель.
Полезный совет
Дабы с легкостью решать задачи, нужно обучиться переводить их на “язык чисел”, применяя некоторые хитрости. Составление таблиц и схем максимально помогает осознать условие задачи, отношения величин. Так же облегчает процесс составления уравнений. Абсолютно, нужно знать нужны формулы.
jprosto.ru
Урок в 7-м классе по алгебре на тему «Задачи на движение»
Цели:
- Систематизировать, расширить и углубить знания умения учащихся при решении задач на движение;
- Способствовать развитию наблюдательности, умению анализировать, сравнивать, делать выводы.
- Побуждать учеников к самоконтролю, взаимоконтролю, вызвать у них потребность в обосновании своих высказываний;
- Способствовать дальнейшему развитию кругозора и получению ими новых естественно научных знаний;
- Продолжить формирование логического мышления, умения находить объяснения природных явлений, оценивать ситуацию;
- Содействовать формированию чувства ответственности перед одноклассниками, культуры общения, сплоченности коллектива.
Оборудование:
Портреты М.В.Ломоносова, Архимеда, Пифагора, график зависимости пути от времени, таблицы графиков линейной функции и прямой пропорциональности, цветные карандаши или фломастеры (каждому ученику), книги с биографиями М.В. Ломоносова, Пифагора, Архимеда, рисунки с примерами оптического обмана, кроссворд (для каждого ученика).
Ход урока
Учитель.
Вступительное слово.
Дорогие ребята! Сегодня урок у нас необычный. Мы отправимся с вами в царство математики, чтобы вспомнить, как решаются некоторые задачи на движение, “встретимся” с некоторыми очень известными учеными, окунемся в мир окружающий нас, чтобы понять, какова связь математики с физикой и узнаем много новых для вас, интересных фактов.
Ученик.
(читает стихотворение Савельевой Т.Н. Отличника народного просвещения, учителя математики высшей категории)
Математика-это страна
Волшебства и великих открытий.
Математика всюду нужна
Она в центре любых событий.
Без нее не растут хлеба
И дорога в космос закрыта,
Не спешат никуда поезда,
Реки вспять не текут почему-то.
Математика-это страна
Новых знаний, умений и навыков.
Математика очень нужна
В жизни всех и взрослых и маленьких.
Учитель.
Царство математики — страна очень древняя и очень интересная. Много историй на ее веку. Вот одна из них (ученик делает сообщение).
Ученик:
Мой рассказ о Михаиле Васильевиче Ломоносове.
Михаил Васильевич Ломоносов (родился 8 ноября 1711 года) – первый русский ученый естественно испытатель мирового значения, человек энциклопедических знаний, разносторонних интересов и способностей, один из основоположников физики и химии, поэт, заложивший основы современного русского литературного языка, художник, историк, поборник отечественного просвещения и развития самостоятельной русской науки.
М.В.Ломоносов родился в крестьянской семье, стремясь получить образование, в 1730 году покинул дом отца и отправился в Москву. Талантливому крестьянскому сыну удалось поступить в духовное училище в Москве-Славяно-греческую академию. В год ее окончания (1735) Ломоносов как один из лучших учеников, был послан в Петербург, а в 1736 году в Германию для изучения металлургии и горного дела.
Учитель:
Представьте себе, что Михаил Ломоносов идет в Москву. На одном из привалов он увидел, что стрекоза и муха движутся по прямой и стрекоза догоняет муху, их скорости равны 1,2 м/с и 30 см/с. Через, сколько секунд расстояние между насекомыми сократится с 6,5 м до 20 см?
Решение:
Дано: СИ 1. Относительная скорость сближения:
V1 =1, 2 м/с V=1, 2-0, 3=0, 9 м/с
V2=30 см/с=0,3м/с 2. Расстояние, которое надо сократить:
S=6,5м S=6, 5-0, 2=6,3м
S1=20см=0, 2 м 3. Время: t=s/v=6,3:0,9=7с
t-?
Учитель.
Продолжая путь, Михаил Ломоносов шел в гору 3км, по ровной местности 12 км и под гору 5км. Изобразите график движения М.Ломоносова, если известно, что по ровной местности он шел со скоростью 4 км/ч, на путь в гору он потратил 2 часа, а с горы 1,5 часа.
Решение.
а). Найти время движения по ровной местности.
12:4=3 часа.
б). Постройте график зависимости пути от времени.
в). Ответьте на вопросы:
- Что называется функцией?
- Какая зависимость показана на графике движения?
- Что является графиком прямой пропорциональности?
- Какую функцию на графике изображает прямая линия?
- Дайте определение линейной функции.
- Координаты скольких точек достаточно найти для
построения графика линейной функции? - Координаты скольких точек достаточно найти для
построения графика прямой пропорциональности?
Учитель.
Конечно, М.В.Ломоносов всем давно известен. Имя этого человека знают в нашей стране и за рубежом. Это ему принадлежат труды не только по математике и химии, но и астрономии и прочим наукам. А вот еще одна история из царства математики. Она об очень известном ученом, жившем в VI веке нашей эры, а в царстве математики он живет постоянно. Это Пифагор. В 8 классе вы познакомитесь с его удивительной великой теоремой: “Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов”.
Ученик делает сообщение.
Пифагор. Великий древнегреческий ученый, родился на острове Самос в V1 веке до н.э. Пифагор переехал в Критон-греческую колонию в Южной Италии, где основал так называемый пифагорейский союз. В сферу интересов союза входили научные исследования. Пифагорейцы называли собственные исследования “математа”, что означает “науки” и делили их на четыре части: арифметику, геометрию, астрономию и гармонию. Главной считалась арифметика – наука о числах. Она лежала в основе и геометрии, и астрономии, и гармонии.
Учитель.
Чтобы доставить послание Пифагора в другой город за 2 часа 40 мин., расстояние между городами 70,5 км , посыльный проехал сначала на ослике, скорость которого 12, 75 км/час, а затем на лошади, скорость которой 67,5 км/час. Сколько времени ехал посыльный на ослике и сколько на лошади? Какое расстояние он проехал на ослике, а какое на лошади? Постройте график зависимости пути от времени движения посыльного на ослике и на лошади. Пользуясь графиком, ответьте на вопросы:
- Какой путь был проделан посыльным на ослике?
- Сколько времени затратил посыльный Пифагора на весь путь?
- Сколько времени посыльный ехал на ослике?
- Сколько времени посыльный Пифагора ехал на лошади?
Заполните таблицу к данной задаче.
| V (км/час) | t (час) | S (км) | |
| На ослике | |||
| На лошади |
Учитель.
Придуманную Пифагором таблицу умножения вы учили во втором классе. Как она называется? Да, это таблица умножения. Зеленый огонек светофора зажигается для каждого из нас еще в детстве. Таблица умножения это одна из форм проявления закономерностей. Таблица умножения – это тропинка находок и маленьких открытий. А как она прекрасна в радужном изображении! Я предлагаю нарисовать “портрет” таблицы умножения на 2, так как эта цифра часто встречается при решении задач.
Учащиеся рисуют с помощью таблицы (приложение 1).
Учитель.
Итак, Пифагор считал, что явления всей вселенной подчинены определенным числовым отношениям, число-это закон и связь мира, сила, царящая над богами и смертными. Порядок определяется в соответствии с числами — основа его учения.
Ученик (читает стихотворение)
Далеко от нашего Союза
И до нас за много, много лет
В трудный год, родные Сиракузы
Защищал ученый Архимед…
Замыслом невиданным охвачен
Он не знал, что в городе враги.
в раздумье на земле горячей
Выводил какие-то круги…
Он чертил задумчивый и гордый,
Позабыв текущие дела…
Учитель.
Познакомимся еще с одной интересной историей из множества историй царства Математики.
Ученица (делает сообщение). Архимед (около 287-212 до н.э.). Самый гениальный ученый Древней Греции. Сын астронома Фидия он родился в греческом городе Сиракузы на Сицилии и был приближен ко двору царя Гиерон II и его сына наследника. Его труды были посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику. Ученый, механик, математик. Установил правило рычага, разрабатывая различные механизмы. Открыл наличие выталкивающей силы на погруженное в жидкость или газ тело.
Учитель.
Однажды по берегу моря вдвоем гулял Архимед с сиракузским царем Гиероном. На обратном пути во дворец Архимед первую половину времени шел со скоростью 5 км/ч, а затем пошел со скоростью 4 км/ч. Гиерон же первую половину пути шел со скоростью 4 км/ч, а затем 5 км/ч. Кто из них раньше пришел в Сиракузы?
Решение.
1. t =t1 + t2 =S: 5+S: 4=9S:20 (ч) — время, затраченное царем.
2. S=S1+S2=v1 t+v2 t=4t +5t=9t
S=9t, t=S: 9 (ч) — время, затраченное Архимедом.
9S:20>S: 9.
Ответ: первым пришел Архимед.
Учитель.
В стране математики мы можем встретить не только известных ученых, но и волшебников, фокусников, любителей отгадывать загадки и кроссворды. Да вот один из них. Великий фокусник и магистр. Он предлагает нам отправиться в город неразгаданных тайн, а для этого нам надо пройти по тропинке тестирования, преодолеть туман оптического обмана и выйти на дорогу отгадывания кроссвордов.
Учащиеся отвечают на вопросы теста.
1. Графиком, какой функции является график зависимости координаты равномерного прямолинейного движения от времени: а) линейная; б) квадратичная; в) тригонометрическая; г) обратная пропорциональность?
2. Единица измерения скорости: а) см; б) м/с; в) га; г) Н.
3. Какая из формул связана с движением: а) S=vt; б) S=ab; в) S=a2; г) S= 1/2ah?
4. Какова основная задача механики; а) измерение скорости тела; б) нахождение положения тела в любой момент времени; в) нахождение массы тела; г) измерение ускорения тела?
5. Заяц, спасаясь от собаки, делает резкий прыжок в сторону, когда собака готова схватить его зубами. Почему собаке трудно поймать зайца: а) у зайца больше скорость; б) собака движется некоторое время по инерции; в) заяц хитрый; г) собака не может резко поворачивать?
6. Выдающийся английский физик и математик, основатель классической механики: а) Пифагор; б) Евклид; в) Ньютон; г) Архимед?
7. Камень, брошенный в воду, порождает волны разбегающиеся кругами. Какой формы получаются волны от камня, брошенного в текущую воду: а) круговые; б) по прямой линии; в) по периметру прямоугольника; г) по периметру квадрата?
Учитель физики, приглашенный на урок, рассказывает учащимся об оптическом обмане и приводит примеры.
Решение кроссворда учащимися. (Приложение2).
Учитель.
Мы не сможем пройти по всем тропинкам в математике и узнать все истории этого бесконечного царства. Их очень много. Но главная тропинка та, которая ведет нас к источнику знаний за новыми неизведанными понятиями. Не уходите с этой тропы, и вы получите все награды: удовольствие от своей находчивости, радость от получения новых, неизвестных вам ранее знаний.
Творческое домашнее задание.
- Составить рассказ или сказку с использованием слов: движение, функция, график, скорость, путь, время, тайна.
- Решить задачу. Когда велосипедист проехал 2/3 пути, лопнула шина. На остальной путь пешком он затратил вдвое больше времени, чем на велосипедную езду. Во сколько раз велосипедист ехал быстрее, чем шел.
Итог урока.
Учащиеся высказывают свое мнение об уроке. Учитель выставляет учащимся оценки, комментируя их.
Литература, используемая при подготовке урока.
- Удивительный мир чисел. Б.А. Кордемский, А.А. Ахадов. Изд. “Просвещение”, 1986.
- История математики в VII-VIII классах. Г.И.Глейзер. М,: Просвещение,1982.
- Великие жизни в математике. Б.А.Кордемский. М.: Просвещение, 1995.
- Занимательная математика на уроках в 5-11 кл. (Как сделать уроки математики не скучными). Т.Д.Гаврилова. Волгоград: Учитель,2006.
- Открытые уроки. Математика 5,6,7.11 кл. Выпуск2. Волгоград: Учитель,2006.
- Открытые уроки. Алгебра 7,9,10 классы. С.Н. Зелинская. Волгоград: Учитель,2006
- Реши сам. Интересные задачи для учащихся восьмилетней школы. Часть3. А.А.Мазаник. Издательство “Народная асвета”. Минск,1972.
- Математика. Для поступающих в Вузы. И.Шарыгин. М.: Дрофа,1995.
- Энциклопедия для детей. Т.11. Математика/ Москва: Аванта + , 2005г.
- Энциклопедический словарь юного химика. Издательство “Педагогика”, Москва,1982г.
- Большая Советская энциклопедия, т.5, изд. М.1974.
Примечание. Урок можно провести как интегрированный урок по математике и физике.
urok.1sept.ru
Конспект урока алгебры в 7 классе по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной». Учебник «Алгебра-7» под редакцией Теляковского С.А.
Конспект урока алгебры в 7 классе
по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной».
Учебник «Алгебра-7» под редакцией Теляковского С.А.
Тема: Решение текстовых задач на движение с помощью составления уравнений с одной переменной.
Цели урока:
Образовательные: формирование знаний, умений и навыков учащихся решать текстовые задачи с помощью уравнений.
Развивающие: развивать умения работать в группе, формировать учебно–познавательные навыки по работе с дополнительным материалом, развивать логическое мышление, внимание;
Воспитательные: воспитывать интерес к математике, старательность, активность, мобильность, взаимопомощь, ответственность перед товарищами.
Ход урока.
1.Организационный этап.
Учитель приветствует учеников.
Проверка домашнего задания.
Сильные ученики отвечают на вопросы, которые возникли у более слабых учащихся в процессе выполнения домашнего задания.
Актуализация опорных знаний.
Написание «Теоретического текста».
Учитель раздает каждому учащемуся текст для проверки уровня усвоения обязательного теоретического материала. В тексте пропущены слова, которые ученики должны вставить. Проверка организована в форме «взаимопроверки» с демонстрацией правильных ответов на экране.
На предыдущем уроке мы изучали решение задач с помощью линейных уравнений .Много текстовых задач отображают некоторую жизненную ситуацию и используют нематематические понятия, такие задачи называют реальной математикой. Чтобы составить математическую модель задачи, надо сначала выбрать основную переменную , а потом составить соответствующее уравнение.Ответ необходимо проверить по содержанию задачи, а не уравнения. После того, как мы составили уравнение к задаче и чтобы его решить, уравнение необходимо привести к линейному.Для этого надо помнить такое правило-ориентир:
Избавляемся от знаменателей.;
Раскрываем скобки;
Переносим члены с переменными в левую часть уравнения, а другие-в правую, меняя знаки на противоположные;
Приводим подобные слагаемые;
Я считаю, что умение решать текстовые задачи необходимо для того, чтобы….
4.Мотивация учебной деятельности.
Я хочу, чтобы каждый из вас объяснил, почему считает необходимым научиться решать текстовые задачи………
Ребята! Сегодня на уроке мы должны будем с вами познакомиться с алгоритмом решения задач на движение, обращая особое внимание на табличную запись условия. Работая над новой темой, мы проследим вместе с вами, как ранее изученный материал связан с новым, как постепенно происходит расширение и углубление знаний. Одним словом, мы будем объединять отдельные факты в целостный пласт.Я буду вам помогать в процессе систематизации ваших знаний. Мы приступаем к работе.
5.Решение задач с помощью опорных схем.
Коллективное решение задачи на историческую тематику.
История сохранила нам мало фактов биографии древнего математика Диофанта. Все, что про него было известно, взято из надписи на его гробнице, составленной в виде математической задачи.
Путник! Тут прах похоронен Диофанта. И числа расскажут, о диво, как долго жизнь его длилась
х
Шестая часть ее прошла счастливым детством
х/6
Двенадцатая часть жизни еще прошла-
покрылась пушком его борода
х/12
Седьмую в бездетном браке провел Диофант
х/7
Прошло пятилетие: он был счастлив рождением прекрасного первенца-сына
5
Коему судьба только половину жизни прекрасной и светлой дала по сравнению с отцом
х/2
И в горе глубоком старик земной жизни конец принял, прожив только года 4 после того, как без сына остался.
4
Скажи, сколько лет жизни достигнув, принял смерть Диофант?
х=х/6+х/12/+ х/7+5+х/2+4
Решив уравнение, получаем, что х=84, имеем такие эпизоды биографии Диофанта: женился в 21 год, стал отцом в 38 лет, потерял сына в 80 лет.
Диофант Александрийский — древнегреческий математик.
До нас дошло стихотворение-задача, из которого видно, что Диофант прожил 84 года. Вот его содержание: «детство Диофанта продолжалось одну шестую часть его жизни, спустя ещё одну двенадцатую у него начала расти борода, он женился спустя ещё одну седьмую, через пять лет у него родился сын, сын прожил половину жизни отца, и отец умер через четыре года после смерти горько оплакиваемого им сына».
Своё основное произведение «Арифметика» Диофант посвятил Дионисию — вероятно, епископу Александрии. До нас дошло шесть первых книг «Арифметики» из тринадцати. Диофант ввёл буквенные обозначения для неизвестного, его квадрата, знака равенства и знака отрицательного числа.
Занимался неопределёнными уравнениями. Ввёл в алгебру буквенную символику.
Большую часть своей жизни Диофант Александрийский посвятил изучению алгебраических уравнений в целых числах. В дошедших до нас книгах «Арифметика» содержатся задачи и решения, в которых Диофант поясняет, как выбрать неизвестное, чтобы решить уравнение вида ax=b или ax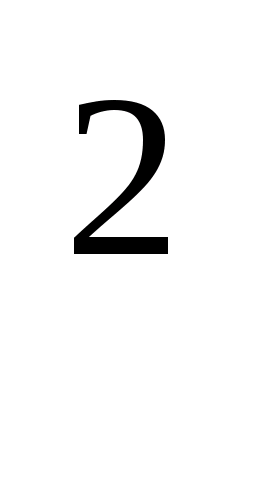 =b. Способы решения полных квадратных уравнений изложены в книгах, которые не сохранились.
=b. Способы решения полных квадратных уравнений изложены в книгах, которые не сохранились.
6.Формирование умений решать задачи на движение с помощью составления линейных уравнений с одной переменной.
Очень важно при решении любой задачи хорошо разобраться с условием и правильно его записать. Способ записи условия с помощью таблицы очень наглядный.
С задачами на движение вы встречались в начальной школе и в 5 классе. Вы знаете, что в этих задачах присутствуют три величины. Назовите мне их. Как находится расстояние? Время? Скорость?
Вы знакомы с формулами нахождения этих величин
Повторение формул: V = S : t
S = V • t
T=s:v
Интерактивная игра «Аквариум». Учитель объединяет учеников в группы по 5-6 человек и предлагает им ознакомиться с заданием. Эта группа читает задание вслух. Остальные учащиеся слушают, не вмешиваясь в процесс обсуждения. Но после дискуссии каждая группа поддерживает или выдвигает свои идеи. Наиболее удачное решение записывается на доске.
1.Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.
Образец записи.
Пусть собственная скорость катера х км/ч. Когда катер двигался по течению реки, его скорость была (х+1,5) км/ч и за 4 часа он проплыл расстояние 4(х-1,5) км. Если катер двигался против течения река, то его скорость была (х-1,5) км/ч, и за 6 часов он проплыл расстояние 6(х-1,5) км. По условию задачи катер проплыл по течению и против течения одинаковое расстояние, поэтому
4(х+1,5)=6(х-1,5)
Решим уравнение.
4(х+1,5)=6(х-1,5),
4х+6-6х-9,
4х-6х=-9-6,
-2х=-15,
Х=7,5.
Получаем, что собственная скорость катера 7,5 км/ч.
Ответ: 7,5 км/ч.
2. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2ч пройдёт столько же, сколько вторая за 3ч. С какой скоростью идут автомашины?
Х км/ч — скорость автомашины
Скорость
Время
Расстояние
первая
машина
(x + 10)
км/ч
50 + 10 = 60
2 ч
(x + 10)2 = (x – 10)3
вторая
машина
(x – 10)
км/ч
50 – 10 = 40
3 ч
60 * 2 = 40 * 3
120 = 120 (верно)
(Наименование в таблице можно не писать.)
Решение: (x + 10)2 = (x – 10)3
Раскроем скобки и приведём уравнение к виду ax = b:
2х + 20 = 3х — 30
2х — 3х = — 30 — 20
— х = — 50
х = — 50 : ( — 1 )
х = 50
Ответ: 50 км/ч.
3.Какова скорость теплохода, если по течению реки он проплывает за 2ч
то же расстояние, что за 4ч против течения? Скорость течения реки
3 км/ч.
Скорость
Время
Расстояние
по течению
реки
(x + 3)
км/ч
9 + 3 =12
2ч
(x + 3)2 = (x — 3)4
против
течения реки
(x – 3)
км/ч
9 – 3 = 6
4ч
12 * 2 = 6 * 4
24 = 24 (верно)
(Наименование в таблице можно не писать.)
Решение: (x + 3)2 = (x – 3)4
Раскроем скобки и приведём уравнение к виду ax = b:
2x + 6 = 4x — 12
2x — 4x = — 12 — 6
— 2x = — 18
x = -18 : (- 2)
x = 9
Ответ: 9 км/ч.
7. Итог урока. Рефлексия.
Учитель задает вопросы, которые касаются не только изученного материала, но и те, которые подводят их к рефлексии:
-что на уроке было главным?
— что было интересно?
— чему вы научились?
— чем пополнили свои знания?
8. Домашнее задание.
infourok.ru
Задачи на движение 7 класс
Тема: Решение задач на движение
Класс 7 класс
Цель: выработка навыка решения задач
Организационно-мотивационный блок
УЗ1-
Здравствуйте. Я хотела бы начать наш урок с демонстрации нескольких изображений. Посмотрев их вы должны ответить на вопрос: о какой части света идет речь? (Европа)
Вы все знаете, что скоро Новый год, а после праздника не менее приятное время, новогодние каникулы. И в эти каникулы есть желание исполнить мечту и съездить в турне по городам Европы. Посетить такие завораживающие слух города как: Берлин, Прага, Париж, Рим, Лондон, Мадрид. Но у нас всего 8 дней на исполнение мечты. Для передвижения по городам можно использовать два вида транспорта: автобус или экспресс. Главный вопрос, на который мы должны ответить, сколько городов я успею посетить на автобусе, а сколько на экспрессе, если первым пунктом путешествия будет Прага, в которую прибудем 01.01.2019г, а домой должны вернуться 08.01.2019г из последнего пункта турне?
Как вы думаете, что необходимо учесть при планировании маршрута? (Скорость, время, расстояние)
Сформулируйте тему урока «Решение задачи на движение с помощью уравнений»
Сформулируйте цель урока (Научиться решать задачи на движение с помощью уравнений)
Демонстрация слайда с достопримечательностями Европы (Берлин, Прага, Париж, Рим, Лондон, Мадрид)
Слайд (тема урока, цель)
Информационно-аналитический
УЗ2- научиться решать задачи на движения с помощью уравнения, вспомнить зависимость между величинами и алгоритм решения задач с помощью уравнений,
Что нам необходимо, для того, чтобы спланировать маршрут? (Карта)
У вас на столах лежит карта Европы, при помощи которой мы будем планировать маршрут.
Итак, первый пункт турне — это Прага. В какую страну приехали? (Чехия)
Как мне нужно двигаться, чтобы попасть в наибольшее количество городов? (По кратчайшему пути)
Какой из перечисленных городов ближе всего находится к Праге? (Берлин)
Рассмотрим расписание движения автобуса и экспресса из Праги в Берлин
Прага — Берлин | 4.01 | 14:00 | 18:00 |
Прага — Берлин | 5.01 | 1:00 | 5:00 |
Прага — Берлин | 4.01 | 8:00 | 9:00 |
Прага — Берлин | 5.01 | 8:00 | 9:00 |
Скорость экспресса на 210 км/ч больше скорости автобуса. Найдите расстояние от Праги до Берлина.
Что нужно сделать, чтобы решить задачу?
Ввести переменную
Установить взаимосвязи между компонентам задачи
Составить уравнение и решить его
Проверить результат
У вас на столах лежат таблицы для составления краткой записи
Пусть скорость автобуса будет х км/ч
1) 4х=х+2104х-х=210
3х=210
х=70 км/ч
2) 70+210=280 (км)
Мы выполнили только 3 пункта по алгоритму. 4 пункт алгоритма предполагает проверку результата. Я предлагаю проверить правильность решения с помощью карты. Карта выполнена в масштабе 1:20 000 000. Что это значит? (1см на карте соответствует 20 000 000 см на местности)
Переведите 20 000 000 см в км (200 км). Т.е. 1см на карте равен 200 км на местности. Измерьте расстояние от Праги до Берлина. Чему оно равно? (1.4см).
Как найти расстояние на местности? (Умножить 1.4 на 200)
Верно мы посчитали?
Теперь посмотрим, в какой город мы поедем дальше? (Париж)
Посмотрим расписание
Берлин-Париж | 6.01 | 9:00 | 13:00 |
Берлин-Париж | 7.01 | 9:00 | 13:00 |
Берлин-Париж | 6.01 | 19:00 | 7:00 |
Берлин-Париж | 7.01 | 9:00 | 21:00 |
Скорость экспресса на 129 км/ч больше скорости автобуса. Найдите расстояние от Берлина до Парижа, которое проедет экспресс, если расстояние пройденное автобусом на 172 км больше.
Пусть скорость автобуса будет х км/ч
12х-4(х+129)=17212х-4х-516=172
8х=688
х=86 км/ч
4(86+129)=860 км
Выполним проверку с помощью карты и масштаба
Давайте посмотрим на карту, куда мы можем поехать дальше? (Лондон)
Париж-Лондон | 8.01 | 19:00 | 23:00 |
Париж-Лондон | 9.01 | 9:00 | 13:00 |
Париж-Лондон | 8.01 | 19:00 | 00:00 |
Париж-Лондон | 9.01 | 9:00 | 14:00 |
Скорость экспресса на 126 км/ч больше скорости автобуса. Найдите расстояние от Парижа до Лондона, которое проедет автобус, если расстояние пройденное экспрессом в 2 раза больше.
Пусть скорость автобуса будет х км/ч
10х=4(х+126)10х=4х+504
10х-4х=504
6х=504
х=84км/ч; 84*5=420 км
Выполним проверку с помощью карты и масштаба
Успеем ли мы, в поставленных условиях, пройти весь путь нашей мечты? (нет).
Сумели ли мы найти ответ на вопрос, который мы поставили для себя в начале урока? (да)
Слайд с картой
Слайд с достопримечательностями Праги
Слайд с расписанием + задача
Карточки
Слайд с краткой записью
Слайд карта Европы
Слайд с Парижем
Слайд с расписание + задача
Слайд расписание + задача
Слайд Лондон
Слайд расписание + задача
Слайд
Оценочно-рефлексивный
УЗ3- Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.
Наше увлекательное путешествие подходит к завершению.
Сегодня мы с вами попробовали вместе спланировать турне по городам Европы. Что мы для этого сделали?
Благодарю вас за проделанную работу.
Надеюсь, что совместные усилия, не пройдут напрасно. Теперь вы сможете заметить язык МАТЕМАТИКИ в окружающем нас мире.
А еще надеюсь, что каждый из вас захотел побывать в одном из увиденных городов. В память о нашем уроке дарю вам брелки, которые будут напоминать вам о создании нашего турне.
infourok.ru