Понятие дифференциального уравнения. Общее и частное решения
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»


Кафедра высшей математики
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Дифференциальные уравнения первого порядка
При изучении различных явлений часто не удаётся найти закон, который непосредственно связывает независимую переменную и искомую функцию, но можно установить связь между искомой функцией и её производными.
Соотношение, связывающее независимую переменную, искомую функцию и её производные, называется дифференциальным уравнением:
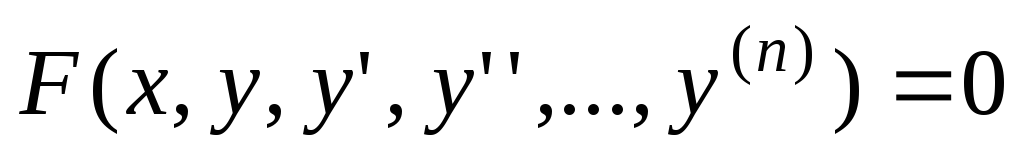 .
(1)
.
(1)
Здесь x – независимая переменная, y – искомая функция,  —
производные искомой функции. При этом
в соотношении (1) обязательно наличие
хотя бы одной производной.
—
производные искомой функции. При этом
в соотношении (1) обязательно наличие
хотя бы одной производной.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Рассмотрим дифференциальное уравнение
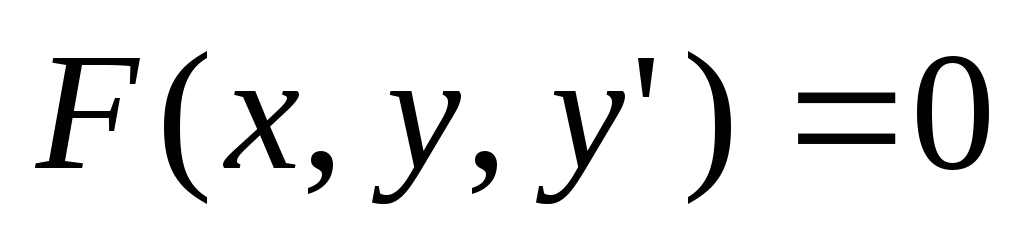
Так в это уравнение входит производная только первого порядка, то оно называется дифференциальным уравнением первого порядка.
Если уравнение (2) можно разрешить относительно производной и записать в виде
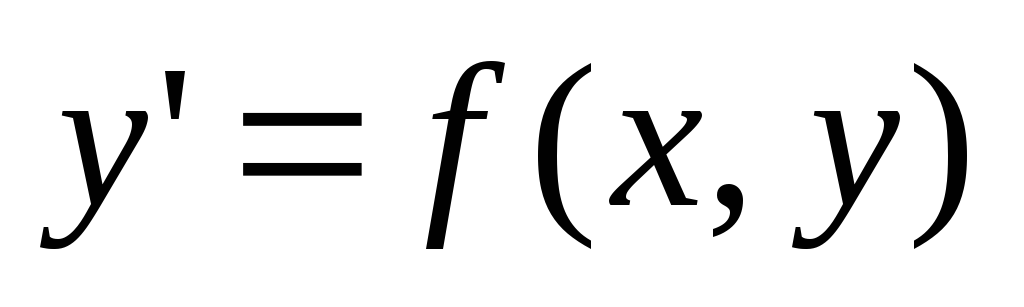 ,
(3)
,
(3)
то такое уравнение называется дифференциальным уравнением первого порядка в нормальной форме.
Во многих случаях целесообразно рассматривать уравнение вида
 ,
(4)
,
(4)
которое называется дифференциальным уравнением первого порядка, записанным в дифференциальной форме.
Так
как 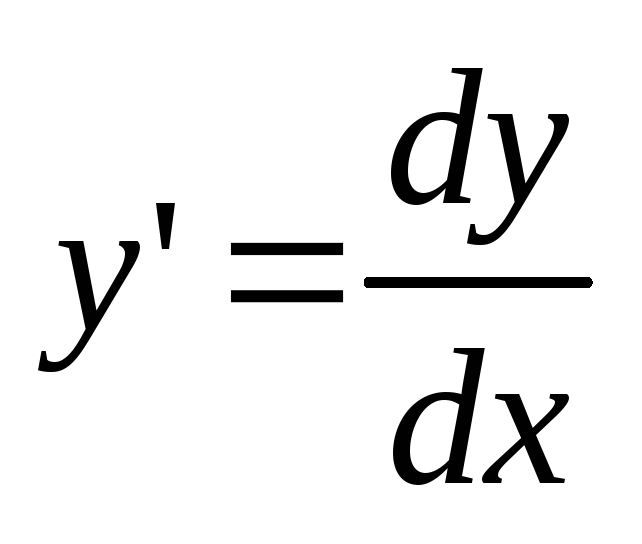 ,
то уравнение (3) можно записать в виде
,
то уравнение (3) можно записать в виде 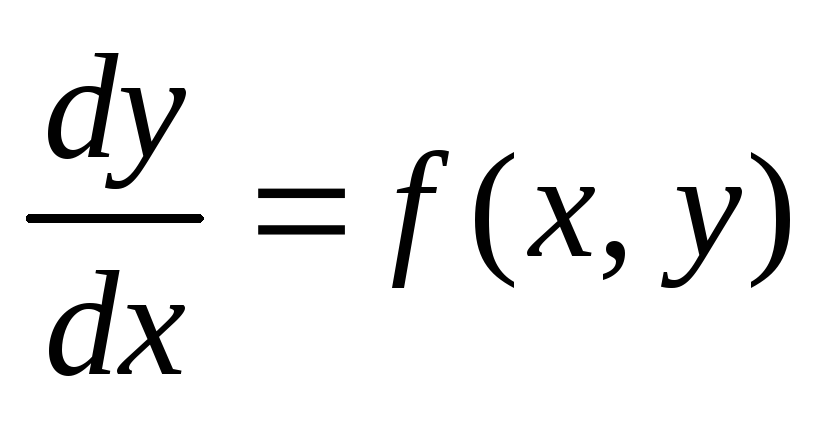 или
или 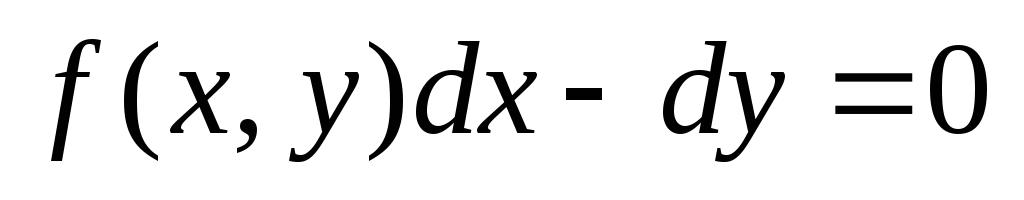 ,
где можно считать
,
где можно считать 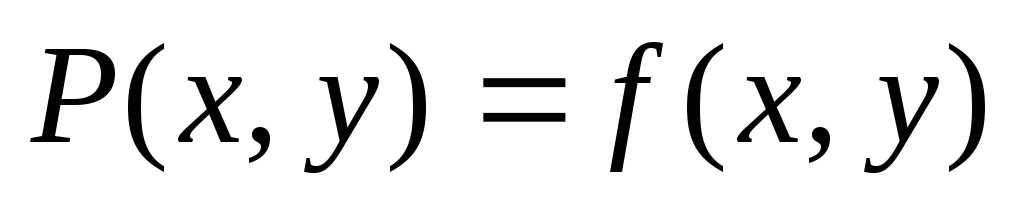 и
и  .
Это означает, что уравнение (3) преобразовано
в уравнение (4).
.
Это означает, что уравнение (3) преобразовано
в уравнение (4).
Запишем
уравнение (4) в виде 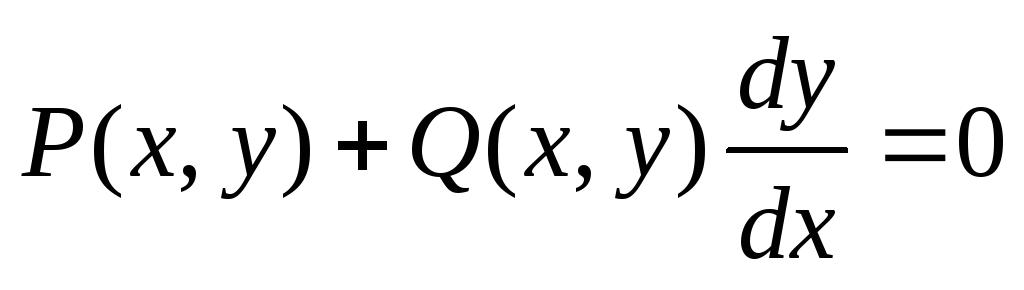 .
Тогда
.
Тогда 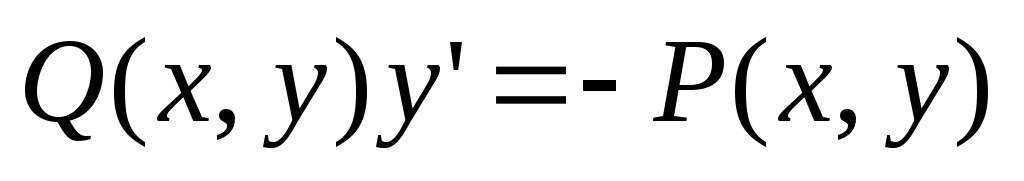 ,
, 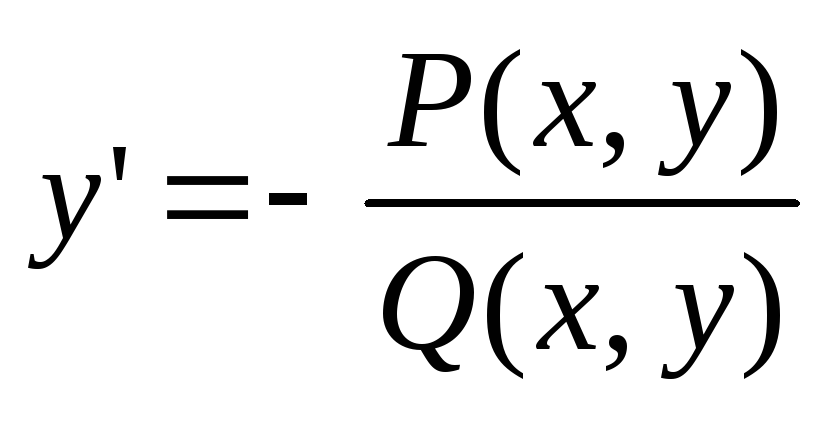
 ,
где можно считать
,
где можно считать 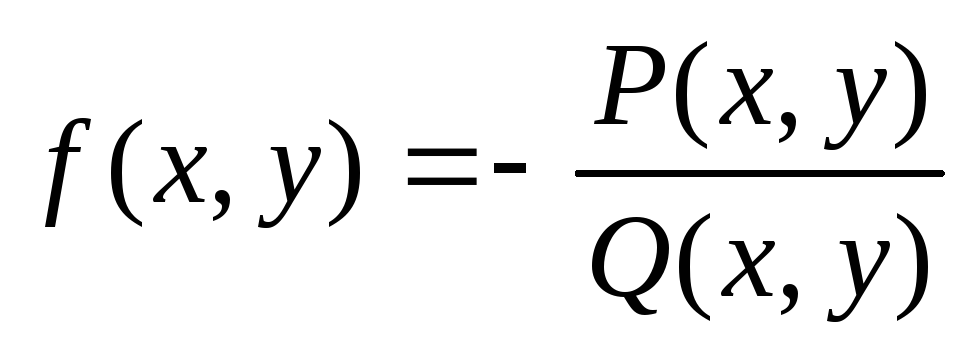 , т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны.
, т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны. Решением
дифференциального уравнения (2) или (3) называется любая функция 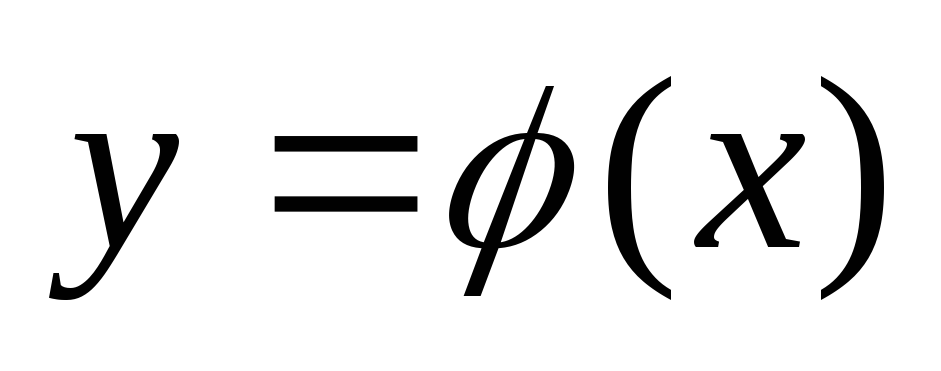 ,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
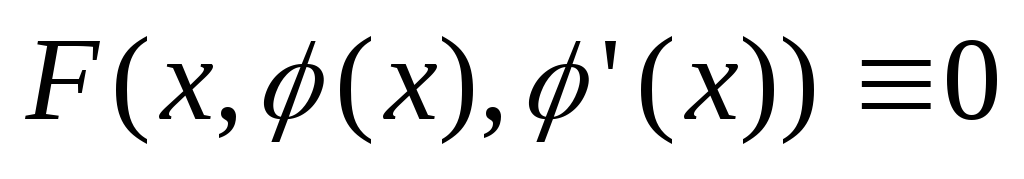 или
или 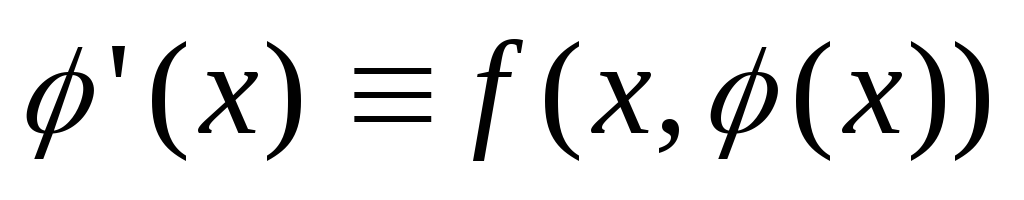 .
.
Процесс
нахождения всех решений дифференциального
уравнения называется его интегрированием,
а график решения 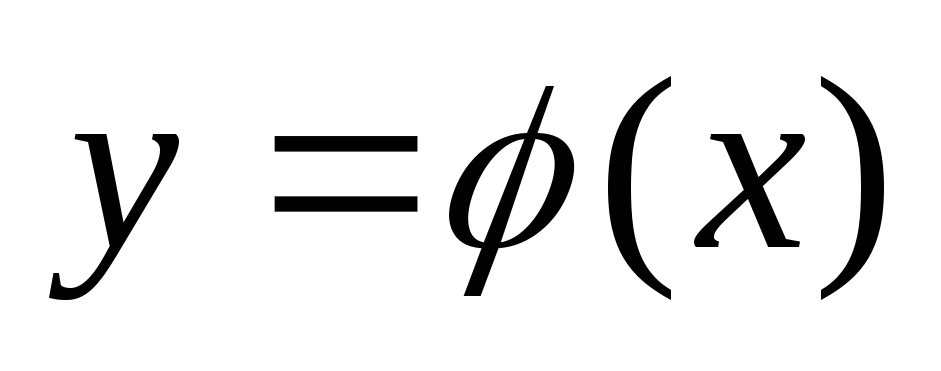
Если
решение дифференциального уравнения
получено в неявном виде 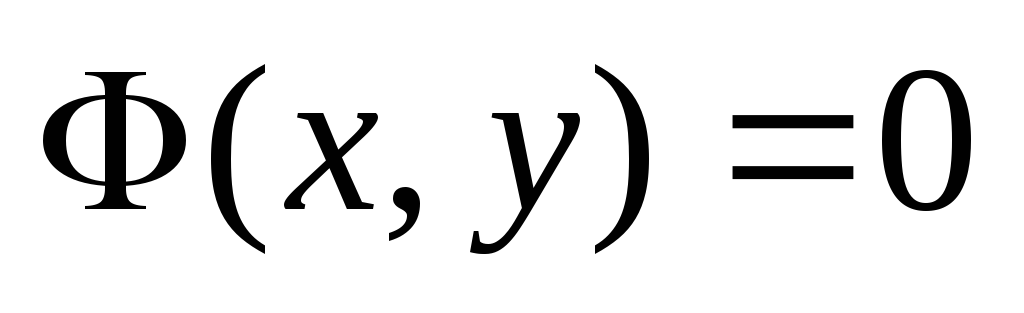 ,
то оно называется интегралом данного дифференциального уравнения.
,
то оно называется интегралом данного дифференциального уравнения.
Общим
решением дифференциального уравнения первого
порядка называется семейство функций
вида  ,
зависящее от произвольной постоянной С,
каждая из которых является решением
данного дифференциального уравнения
при любом допустимом значении произвольной
постоянной С.
Таким образом, дифференциальное уравнение
имеет бесчисленное множество решений.
,
зависящее от произвольной постоянной С,
каждая из которых является решением
данного дифференциального уравнения
при любом допустимом значении произвольной
постоянной С.
Таким образом, дифференциальное уравнение
имеет бесчисленное множество решений.
Частным
решением дифференциального уравнения называется
решение, получаемое из формулы общего
решения при конкретном значении
произвольной постоянной С,
включая 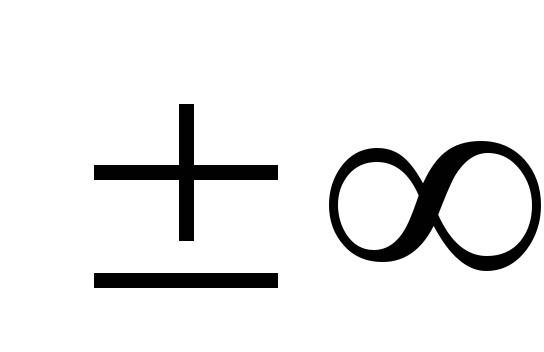 .
.
Задача Коши и её геометрическая интерпретация
Уравнение (2) имеет бесчисленное множество решений. Чтобы из этого множества выделить одно решение, которое называется частным, нужно задать некоторые дополнительные условия.
Задача отыскания частного решения уравнения (2) при заданных условиях называется задачей Коши. Эта задача является одной из важнейших в теории дифференциальных уравнений.
Формулируется
задача Коши следующим образом: среди
всех решений уравнения (2) найти такое
решение  ,
в котором функция
,
в котором функция 
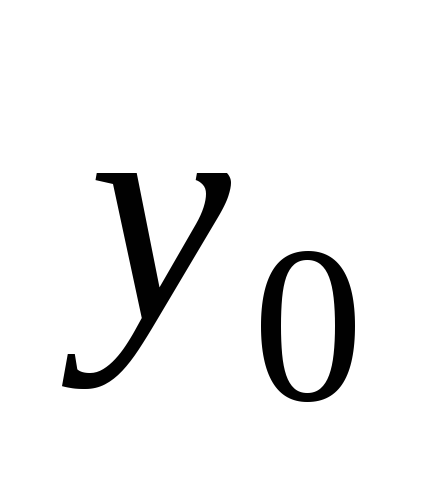 ,
если независимая переменная x принимает заданное числовое значение
,
если независимая переменная x принимает заданное числовое значение 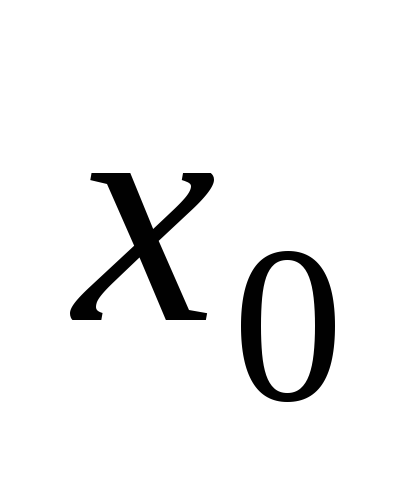 ,
т.е.
,
т.е.  ,
, 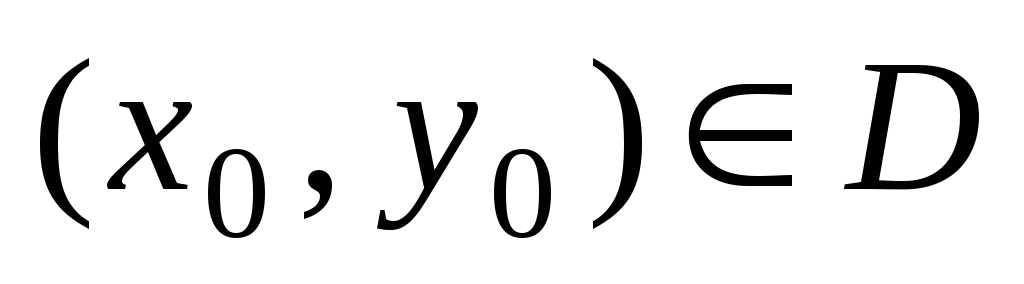 ,
(5)
,
(5)
где D – область определения функции 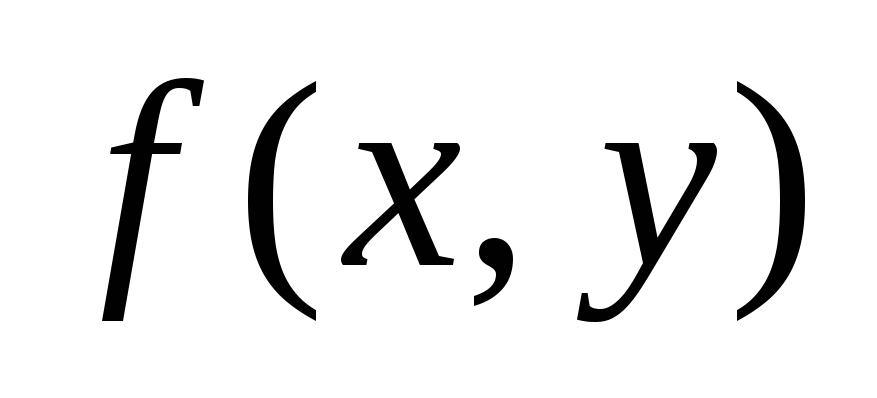 .
.
Значение 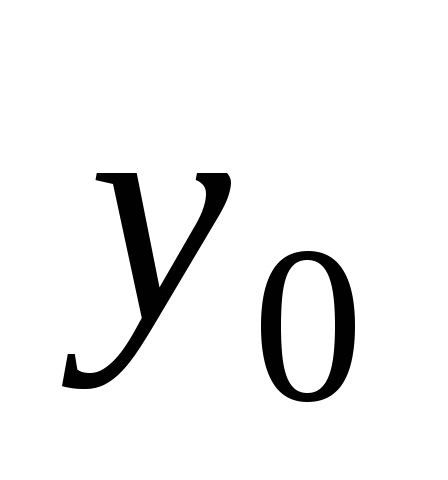 называется начальным
значением функции,
а
называется начальным
значением функции,
а 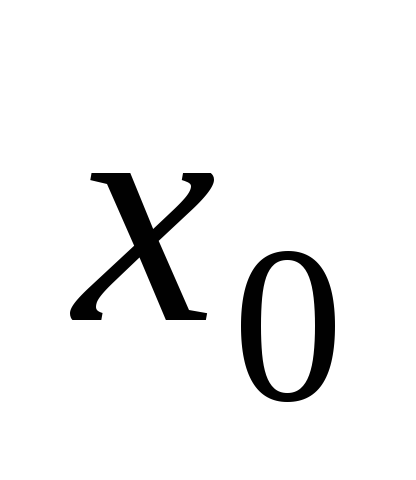 – начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
– начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
С
геометрической точки зрения задачу
Коши для дифференциального уравнения
(2) можно сформулировать следующим
образом: из
множества интегральных кривых уравнения
(2) выделить ту, которая проходит через
заданную точку 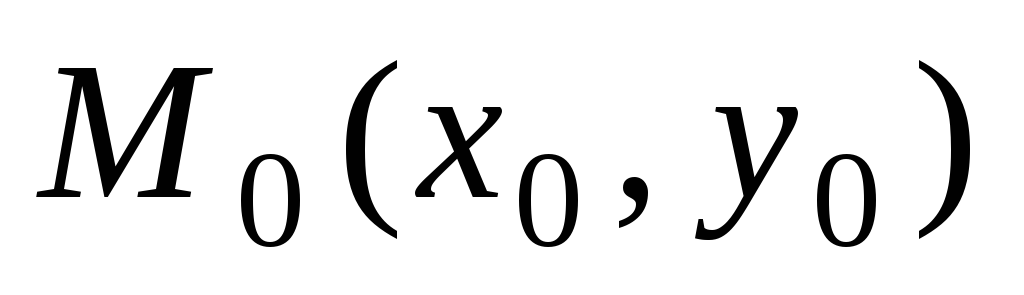 .
.
studfile.net
Дифференциальные уравнения в полных дифференциалах
Введение
- Дифференциальное уравнение первого порядка в полных дифференциалах
- – это уравнение вида:
(1) ,
где левая часть уравнения является полным дифференциалом некоторой функции U(x, y) от переменных x, y:
.
При этом .
Если найдена такая функция U(x, y), то уравнение принимает вид:
dU(x, y) = 0.
Его общий интеграл:
U(x, y) = C,
где C – постоянная.
Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx. Тогда . В результате получаем уравнение, выраженное через дифференциалы:
(1) .
Свойство дифференциального уравнения в полных дифференциалах
Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .
Доказательство
Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y. Точка x0, y0 также принадлежит этой области.
Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U(x, y):
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что . Необходимость условия (2) доказана.
Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2) .
Покажем, что можно найти такую функцию U(x, y), что ее дифференциал:
.
Это означает, что существует такая функция U(x, y), которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x0 до x, считая что y – это постоянная:
;
;
(5) .
Дифференцируем по y считая, что x – это постоянная и применим (2):
.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y0 до y:
;
;
.
Подставляем в (5):
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.
В формуле (6), U(x0, y0) является постоянной – значением функции U(x, y) в точке x0, y0. Ей можно присвоить любое значение.
Как распознать дифференциальное уравнение в полных дифференциалах
Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.
Пример
Проверить, является ли уравнение в полных дифференциалах:
.
Решение
Здесь
, .
Дифференцируем по y, считая x постоянной:
.
Дифференцируем по x, считая y постоянной:
.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.
Методы решения дифференциальных уравнений в полных дифференциалах
Метод последовательного выделения дифференциала
Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d(u ± v);
v du + u dv = d(uv);
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.
Пример 1
Решить уравнение:
.
Решение
Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;
.
Подставляем в (П1):
;
.
Ответ
.
Метод последовательного интегрирования
В этом методе мы ищем функцию U(x, y), удовлетворяющую уравнениям:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x, считая y постоянной:
.
Здесь φ(y) – произвольная функция от y, которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ(y) и, тем самым, U(x, y).
Пример 2
Решить уравнение в полных дифференциалах:
.
Решение
Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
, .
Ищем Функцию U(x, y), дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x, считая y постоянной:
(П2)
.
Дифференцируем по y:
.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):
.
Общий интеграл уравнения:
U(x, y) = const.
Объединяем две постоянные в одну.
Ответ
.
Метод интегрирования вдоль кривой
Функцию U, определяемую соотношением:
dU = p(x, y) dx + q(x, y) dy,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x0, y0) и (x, y):
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной (x0, y0) и конечной (x, y) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x0 и y0 – постоянные. Поэтому U(x0, y0) – также постоянная.
Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y, от точки (x0 , y0) до точки (x0 , y) . Затем интегрирование производится по отрезку, параллельному оси x, от точки (x0 , y) до точки (x, y) .
В более общем случае, нужно представить уравнение кривой, соединяющей точки (x0 , y0) и (x, y) в параметрическом виде:
x1 = s(t1); y1 = r(t1);
x0 = s(t0); y0 = r(t0);
x = s(t); y = r(t);
и интегрировать по t1 от t0 до t.
Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x0 , y0) и (x, y). В этом случае:
x1 = x0 + (x – x0) t1; y1 = y0 + (y – y0) t1;
t0 = 0; t = 1;
dx1 = (x – x0) dt1; dy1 = (y – y0) dt1.
После подстановки, получается интеграл по t от 0 до 1.
Данный способ, однако, приводит к довольно громоздким вычислениям.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.
Общий вид линейного дифференциального уравнения первого порядка таков:
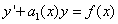 ,
,
где 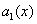 и
и
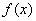 — непрерывные функции от x.
— непрерывные функции от x.
Как решить линейное дифференциальное уравнение первого порядка?
Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций
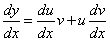
и линейное дифференциальное уравнения первого порядка примет вид
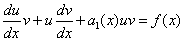
или
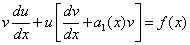 . (*)
. (*)
Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:
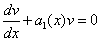 ,
,
то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися
переменными, отличное от нуля. Разделяя в уравнении 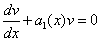 переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v —
решение уравнения, то её подстановка в уравнение
переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v —
решение уравнения, то её подстановка в уравнение 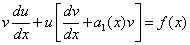 даёт
даёт
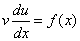 .
.
Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.
Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.
Пример 1. Решить линейное дифференциальное уравнение первого порядка
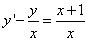 .
.
Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для
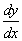 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
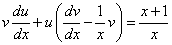 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
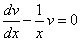 или
или 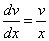 .
.
После разделения переменных это уравнение принимает вид
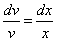 .
.
Почленное интегрирование даёт
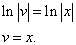
Подставив найденное значение функции v в равенство (* *), получим
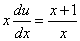 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:
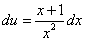
и, интегрируя находим u:
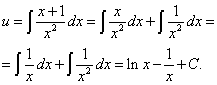
Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
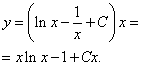
Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!
Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 2. Решить линейное дифференциальное уравнение первого порядка
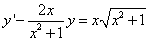 .
.
Решение. Подставляя выражения для
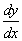 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
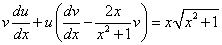 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
 .
.
После разделения переменных это уравнение принимает вид
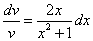 .
.
Почленное интегрирование даёт
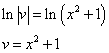
Подставив найденное значение функции v в равенство (* *), получим
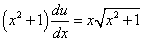 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:
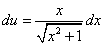
и, интегрируя находим u:
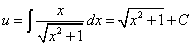
Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:
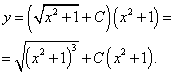
В следующем примере — обещанная экспонента.
Пример 3. Решить линейное дифференциальное уравнение первого порядка
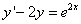 .
.
Решение. Подставляя выражения для
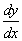 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
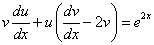 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
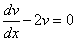 или
или 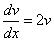 .
.
После разделения переменных это уравнение принимает вид
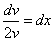 .
.
Почленное интегрирование даёт
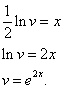
Подставив найденное значение функции v в равенство (* *), получим
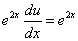 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находимu:
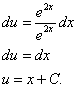
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
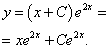
Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.
Пример 4. Решить линейное дифференциальное уравнение первого порядка
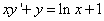 .
.
Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим
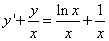 .
.
Подставляя выражения для
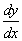 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
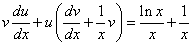 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
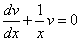 или
или 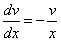 .
.
После разделения переменных это уравнение принимает вид
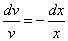 .
.
Почленное интегрирование даёт
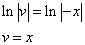
Подставив найденное значение функции v в равенство (* *), получим
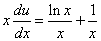 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.
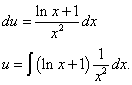
В интеграле 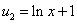 ,
,
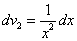 .
.
Тогда 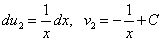 .
.
Интегрируем и находим u:
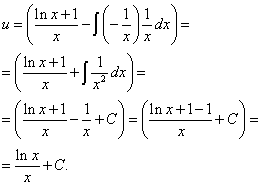
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
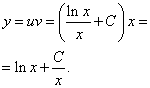
И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.
Пример 5. Решить линейное дифференциальное уравнение первого порядка
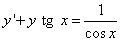 .
.
Решение. Подставляя выражения для
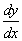 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
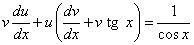 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
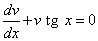 или
или 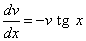 .
.
После разделения переменных это уравнение принимает вид
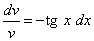 .
.
Почленное интегрирование даёт
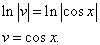
Подставив найденное значение функции v в равенство (* *), получим
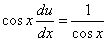 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
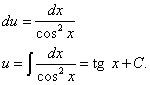
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
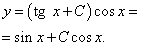
В последних двух примерах требуется найти частное решение уравнения.
Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка
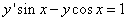 при условии
при условии  .
.
Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на
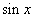 и получим
и получим
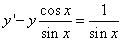
или
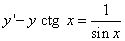 .
.
Подставляя выражения для
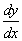 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
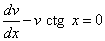 или
или 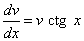 .
.
После разделения переменных это уравнение принимает вид
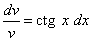 .
.
Почленное интегрирование даёт
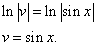
Подставив найденное значение функции v в равенство (* *), получим
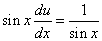 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
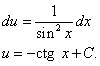
Записываем общее решение данного линейного дифференциального уравнения первого порядка:
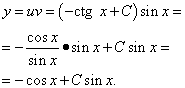
Найдём частное решение уравнения. Для этого в общее решение подставим 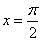 и
и
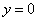 и найдём значение C:
и найдём значение C:
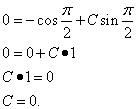
Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
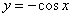 .
.
Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка
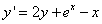 при условии
при условии 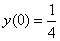 .
.
Перенесём функцию «игрека» в левую часть и получим
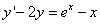 .
.
Подставляя выражения для
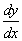 и y в уравнение вида (*), получим
и y в уравнение вида (*), получим
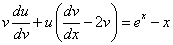 (* *).
(* *).
Выберем функцию v(x) так, чтобы выполнялось равенство
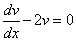 или
или 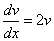 .
.
После разделения переменных это уравнение принимает вид
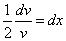 .
.
Почленное интегрирование даёт
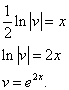
Подставив найденное значение функции v в равенство (* *), получим
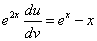 .
.
Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:
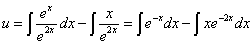 .
.
Первый интеграл равен 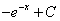 ,
второй находим интегрированием по частям.
,
второй находим интегрированием по частям.
В нём 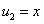 ,
,
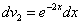 .
.
Тогда 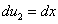 ,
, 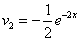 .
.
Находим второй интеграл:
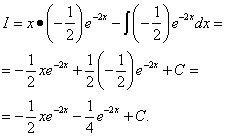 .
.
В результате получаем функцию u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:
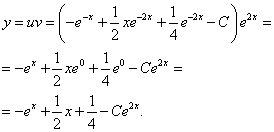
Найдём частное решение уравнения. Для этого в общее решение подставим 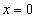 и
и
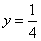 и найдём значение C:
и найдём значение C:
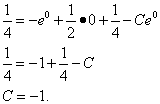
Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:
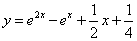 .
.
Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
function-x.ru