Как решать показательные уравнения
Мы уже неоднократно писали о том, как научиться решать показательные уравнения. Вопрос всегда сводится к знанию и умению применять алгоритм. Давайте еще раз повторим основные теоретические положения этой важной темы.
Если в уравнении неизвестное содержится в показателе степени, то такое уравнение называется показательным. Простейшее показательное уравнение имеет вид: ах = аb, где а>0, а≠1, х — неизвестное.
Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.
- a0 = 1, a1= а.
- a-n = 1/ an
- an × am = an+m
- an/am = an-m
- (an)m = anm
- (ab)n = an×bn
- (a/b)n = an/bn.

Для представления числа в виде степени используют
- Решение уравнений вида аf(x)=aq(x) сводится к решению уравнения f(x)=q(x). Иногда в таких уравнениях требуется привести обе части к одинаковому основанию степени, как правило, это разные степени одного основания.
- Решение уравнений вида аf(x)=b. Для решения используем логарифмирование по основанию а, т.е. решаем уравнение f(x)=logab.
- Уравнения, решаемые с помощью вынесения за скобки общего множителя.
- Уравнения, решаемые с помощью замены переменной.
- Уравнения, содержащие степени с двумя различными (не сводящимися друг к другу) основаниями, af(x)=bf (x). Решением является решения уравнения f(x)=0.

- Уравнения, однородные относительно ax и bx.
Успехов!
Автор — Дмитрий Айстраханов
Как решать показательные уравнения?
Преподаватель математики Андрей Алексеевич продолжает рассматривать задачи профильного уровня для подготовки к ЕГЭ. Разбираемся с заданием из темы «Показательные уравнения».
Задание №13
Условие:
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Преобразуем уравнение, используя свойства степени.
В первом слагаемом «+1», это «4». Запишем первое слагаемое как «4», умноженное на оставшееся выражение. Это выражение получится точно такое же, как и второе слагаемое.
Затем вынесем за скобку общий множитель этих двух слагаемых, это будет целиком второе слагаемое.
 В скобках останется выражение «(4 + 1)», что соответственно будет равно «5».
В скобках останется выражение «(4 + 1)», что соответственно будет равно «5».Разделим обе части уравнения на «5». В правой части получим «20 : 5 = 4». «4» мы можем представить как «4 в первой степени». Поскольку в обеих частях уравнения мы пришли к выражениям, где в основании степени стоит одно и то же число «4», то мы имеем право перейти к рассмотрению отдельного уравнения, в котором приравниваем показатели степени. После преобразований получаем классическое квадратное уравнение. Кратко запишем ход решения:
Найдем корни этого уравнения через дискриминант. Дискриминант получается «больше нуля», значит у нас будет два корня. Вычисляем корни, получаем
Первую часть задания мы выполнили. Переходим ко второй части.
б) Оценим сначала целыми числами: В это неравенство во все три части внесем «1» двумя способами. Сначала прибавим «1» ко всем трем частям, а во втором случае отнимем «1».

Тогда получим:
и
Мы видим, что в средней части неравенства стоят выражения, соответствующие полученным корням уравнения. И мы их можем оценить относительно заданного отрезка.
Отрезку принадлежит только один корень:
Записываем ответ.
Ответ а) б)
Автор: Андрей Найдёнов.
Решение показательных уравнений через преобразования
Направления проведения преобразований. Примеры.
Выше мы рассмотрели самые основные и характерные преобразования показательных уравнений по отдельности, а также разобрали примеры их проведения. Но на практике при решении показательных уравнений обычно приходится проводить не одно какое-то преобразование, а серию последовательных преобразований. Естественно, при этом необходимо четко понимать, для чего проводится то или иное преобразование. Сейчас мы обозначим основные направления проведения преобразований, которых следует придерживаться при решении показательных уравнений.

Можно выделить три основных направления проведения преобразований показательных уравненийM:
- К одинаковым степеням.
- К одинаковым основаниям степеней.
- К одинаковым показателям степеней.
Придерживаясь указанных направлений, следует от исходного показательного уравнения продвигаться к уравнениям, для которых известен метод решения, то есть, к уравнениям a
f(x)=b, af(x)=ac, af(x)=ag(x), f(g(x))=0, f1(g(x))=f2(g(x)), f1(x)·f2(x)·…·fn(x)=0 и др. Давайте разбираться с этим на конкретных примерах.К одинаковым степеням
Стремление к одинаковым степеням, то есть, к степеням с одинаковыми основаниями и одинаковыми показателями, при решении показательных уравнений легко объяснимо – после получения одинаковых степеней появляется возможность привести уравнение к удобному для дальнейшего решения виду, ввести новую переменную или каким-либо другим способом продвинуться в решении.
 Приведем примеры.
Приведем примеры.
Возьмем показательное уравнение 3x+2+3x+1+3x=39. Очевидна возможность получить одинаковые степени 3
Рассмотрим еще один пример. В показательном уравнении 49·72·x−50·7x+1=0 тоже несложно получить одинаковые степени 7x. Достичь этого позволяет опора на свойство степени в степени. По свойству степени в степени мы можем заменить 72·x выражением (7x)2, то есть, перейти к уравнению 49·(7x)2−50·7x+1=0.
Это открывает путь к решению показательного уравнения через введение новой переменной 7x=t.
К одинаковым основаниям
Когда нет возможности получить одинаковые степени или такая возможность не очевидна, то можно довольствоваться получением одинаковых оснований. Это тоже бывает полезно при решении показательных уравнений. Проиллюстрируем сказанное примерами.
Несложно заметить, что выражения, отвечающие частям показательного уравнения , можно преобразовать в степени с основаниями 3. Это позволяют сделать свойства степеней и связь между корнями и степенями с дробными показателями. Действительно, так как и , то исходное показательное уравнение можно преобразовать в уравнение , которое легко решается, например, методом уравнивания показателей.
Переход к одинаковым основаниям позволяет уменьшать количество степеней с разными основаниями, что часто неплохо продвигает в решении показательных уравнений.

Аналогично, в показательном уравнении представление степени 504x−2 в виде 504x−2=23·x−6·32·x−4
·7x−2 уменьшает количество степеней с разными основаниями, и открывает дорогу к дальнейшему решению через деление обеих частей уравнения на 23·x−6·32·x−4·7x−2.
К одинаковым показателям
Если нет возможности вести преобразования в сторону получения одинаковых степеней или хотя бы одинаковых оснований степеней, то стоит рассмотреть возможность продвижения к одинаковым показателям степеней. Это тоже может быть полезно в плане решения показательных уравнений. Приведем примеры.
Легко заметить, что показатели степеней в записи показательного уравнения 5−3−x·133+x=1 различаются только знаками. В подобных случаях можно переходить к одинаковым показателям. В нашем случае степень 5−3−x можно рассматривать как , ведь в силу свойства степени в степени . Это позволяет от исходного уравнения перейти к показательному уравнению , в записи которого степени имеют одинаковые показатели, что в свою очередь позволяет с опорой на свойство степени произведения перейти к простейшему показательному уравнению , и получить искомое решение.

Давайте разберем еще один пример. Возьмем показательное уравнение 2·32·x=9·2x. Здесь можно осуществить переход к степеням с одинаковыми показателями, заменив 32·x на 9x. Это преобразование дает уравнение 2·9x=9·2x, которое через деление обеих частей на 2x приводится к простейшему показательному уравнению . Его решением является x=1.
Как решать показательные неравенства графически. Показательные уравнения и неравенства. Выделение устойчивого выражения и замена переменной
Урок и презентация на тему: «Показательные уравнения и показательные неравенства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»Определение показательных уравнений
Ребята, мы изучили показательные функций, узнали их свойства и построили графики, разобрали примеры уравнений, в которых встречались показательные функции. 2+2x-15≥0$.
2+2x-15≥0$.
$(x-3)(x+5)≥0$.
Воспользуемся интервальным методом решения:
Ответ: $(-∞;-5]U» title=»Rendered by QuickLaTeX.com»>Группируем степени с одинаковыми основаниями. Удобнее для этого развести их по разные стороны неравенства:
Title=»Rendered by QuickLaTeX.com»>
Из каждой пары степеней выносим за скобки общий множитель — степень с меньшим показателем. Вынести за скобки общий множитель- значит, каждое слагаемое разделить на этот множитель. При делении степеней с одинаковыми основаниями основание оставляем прежним, а показатели вычитаем:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Делить можно сразу на 20 (20=4∙5), но практика показывает, что деление в два этапа позволяет избежать возможных ошибок:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.
 com»>
com»>Title=»Rendered by QuickLaTeX.com»>
Так как основание 2/5
убывает, поэтому знак неравенства между показателями степеней изменяется на противоположный:
Квадратичное неравенство решим методом интервалов . Нули функции, стоящей в левой части неравенства — x1=-1; x2=2. Отмечаем их на числовой прямой.
Для проверки знака возьмем нуль: 0²-0-2=-2, в промежуток, которому принадлежит нуль, ставим «-«. Остальные знаки расставляем в шахматном порядке. Так как решаем неравенство, в котором левая часть меньше нуля, выбираем промежуток со знаком «-«.
Ответ: x ∈ (-1; 2).
Вариант неравенств такого вида — все степени имеют одинаковые основания, но отличаются коэффициентами при x в показателях.
В левой части выносим за скобки степень с наименьшим показателем
Title=»Rendered by QuickLaTeX.com»>
Пришли к показательному неравенству . Так как основание 7>1, функция
возрастает, знак неравенства между показателями не изменяется:
Чтобы решить это неравенство методом интервалов перенесем все слагаемые в левую часть и приведём дроби к
Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
Теорема. Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 .
Обоснуем рассмотренное утверждение.
Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . В обоих случаях мы получили противоречие условию а х 1 = а х 2 .
Рассмотрим несколько задач.
Решить уравнение 4 ∙ 2 х = 1.
Решение.
Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2.
Ответ. х = -2.
Решить уравнение 2 3х ∙ 3 х = 576.
Решение.
Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 .
Отсюда получаем х = 2.

Ответ. х = 2.
Решить уравнение 3 х+1 – 2∙3 х — 2 = 25.
Решение.
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25,
откуда 3 х — 2 = 1, т.е. х – 2 = 0, х = 2.
Ответ. х = 2.
Решить уравнение 3 х = 7 х.
Решение.
Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0.
Ответ. х = 0.
Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0.
Решение.
Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0.
Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ. х = 2.
Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х
Рассмотрим некоторые задачи.

Решить неравенство 3 х
Решение.
Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей.
Следовательно, при х
Таким образом, при х 3 х
Ответ. х
Решить неравенство 16 х +4 х – 2 > 0.
Решение.
Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.
Это неравенство выполняется при t 1.
Так как t = 4 х, то получим два неравенства 4 х 1.
Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R.
Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0.
Ответ. х > 0.
Графически решить уравнение (1/3) х = х – 2/3.
Решение.
1) Построим графики функций у = (1/3) х и у = х – 2/3.
2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что
х = 1 – корень данного уравнения:
(1/3) 1 = 1/3 и 1 – 2/3 = 1/3.

Иными словами, мы нашли один из корней уравнения.
3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х
Ответ. х = 1.
Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению . В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств.
 Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.Прежде чем приступить к разбору конкретных показательных уравнений и неравенств , как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией .
Основные свойства показательной функции y = a x :
График показательной функции
Графиком показательной функции является экспонента :
Графики показательных функций (экспоненты)
Решение показательных уравнений
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.

Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение a f (x ) = a g (x ) (где a > 0, a ≠ 1) равносильно уравнению f (x ) = g (x ).
Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Title=»Rendered by QuickLaTeX.com»>
Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
Title=»Rendered by QuickLaTeX.com»>
Это означает, что данное уравнение имеет два корня. Находим их:
Переходя к обратной подстановке, получаем:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3.
 Это и будет являться ответом к заданию.
Это и будет являться ответом к заданию.Ответ: x = 3.
Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю).
Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1.
Ответ: x = 6.
Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0.
Пример 4.
 Решите уравнение:
Решите уравнение:Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x .
Ответ: x = 0.
Пример 5. Решите уравнение:
Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x -2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.
Ответ: x = -1.
Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
Ответ: x = 2.

Решение показательных неравенств
Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.
Для решения показательных неравенств требуется знание следующей теоремы:
Теорема 2. Если a > 1, то неравенство a f (x ) > a g (x ) равносильно неравенству того же смысла: f (x ) > g (x ). Если 0 a a f (x ) > a g (x ) равносильно неравенству противоположного смысла: f (x ) g (x ).
Пример 7. Решите неравенство:
Решение: представим исходное неравенство в виде:
Разделим обе части этого неравенства на 3 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится:
Воспользуемся подстановкой:
Тогда неравенство примет вид:
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически.
 Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t :
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9.
 Решите неравенство:
Решите неравенство:Решение:
Делим обе части неравенства на выражение:
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
t , находящиеся в промежутке:
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
Пример 10. Решите неравенство:
Решение:
Ветви параболы y = 2x +2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
Ветви параболы y = x 2 -2x +2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x +2 , стоящая в правой части уравнения.
 Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.Ответ: x = 1.
Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене.
Сергей ВалерьевичP. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений.
 К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.Здравствуйте! Дорогие мои ученики, в этой статье мы научимся с вами решать показательные неравенства.
Каким бы сложным не показалось вам показательное неравенство, после некоторых преобразований (о них мы поговорим чуть позже) все неравенства сводятся к решению простейших показательных неравенств :
а х > b , a x и a x ≥ b , a x ≤ b .
Давайте попробуем разобраться как же решаются такие неравенства.
Мы рассмотрим решение строгих неравенств . Отличие при решении нестрогих неравенств заключается только в том, что полученные соответствующие корни включаются в ответ.
Пусть надо решить неравенство вида а f (x) > b , где a>1 и b>0 .
Посмотрите на схему решения таких неравенств (рисунок 1):
Сейчас рассмотрим конкретный пример.
 Решить неравенство: 5 х – 1 > 125 .
Решить неравенство: 5 х – 1 > 125 .Так как 5 > 1 и 125 > 0, то
х – 1 > log 5 125, то есть
х – 1 > 3,
х > 4.Ответ: (4; +∞) .
А каким же будет решение этого же неравенства а f (x) >b , если 0 и b>0 ?
Итак, схема на рисунке 2
Пример: Решить неравенство (1/2) 2x — 2 ≥ 4
Применяя правило (рисунок 2), получаем
2х – 2 ≤ log 1/2 4,
2х – 2 ≤ –2,
2х ≤ 0,
х ≤ 0.Ответ: (–∞; 0] .
Снова рассмотрим это же неравенство а f (x) > b , если a>0 и b.
Итак, схема на рисунке 3:
Пример решения неравенства (1/3) х + 2 > –9 . Как мы замечаем, какое бы число мы не подставили вместо х, (1/3) х + 2 всегда больше нуля.
Ответ: (–∞; +∞) .
А как же решаются неравенства вида а f (x) , где a>1 и b>0 ?
Схема на рисунке 4:
И следующий пример: 3 3 – х ≥ 8 .

Поскольку 3 > 1 и 8 > 0, то
3 – х > log 3 8, то есть
–х > log 3 8 – 3,
хОтвет: (0; 3–log 3 8) .
Как же измениться решение неравенства а f (x) , при 0 и b>0 ?
Схема на рисунке 5:
И следующий пример: Решить неравенство 0,6 2х – 3 .
Cледуя схеме на рисунке 5, получаем
2х – 3 > log 0,6 0,36 ,
2х – 3 > 2,
2х > 5,
х > 2,5Ответ: (2,5; +∞) .
Рассмотрим последнюю схему решения неравенства вида а f (x) , при a>0 и b, представленную на рисунке 6:
Например, решим неравенство:
Замечаем, что какое бы число мы не подставили вместо х, левая часть неравенства всегда больше нуля, а у нас это выражение меньше -8, т.е. и нуля, значит решений нет.
Ответ: решений нет .
Зная как решаются простейшие показательные неравенства, можно приступить и к решению показательных неравенств .

Пример 1.
Найти наибольшее целое значение х, удовлетворяющее неравеству
Так как 6 х больше нуля (ни при каком х знаменатель в ноль не обращается), умножим обе части неравенства на 6 х, получим:
440 – 2· 6 2х > 8, тогда
– 2· 6 2х > 8 – 440,
– 2· 6 2х > – 332,
6 2х 2хx
Ответ: 1 .
Пример 2 .
Решить неравенство 2 2 x – 3·2 x + 2 ≤ 0
Обозначим 2 х через у, получим неравенство у 2 – 3у + 2 ≤ 0, решим это квадратное неравенство.
у 2 – 3у +2 = 0,
у 1 = 1 и у 2 = 2.Ветви параболы направлены вверх, изобразим график:
Тогда решением неравенства будет неравенство 1
Ответ: (0; 1) .
Пример 3 . Решите неравенство 5 x +1 – 3 x +2
Соберем выражения с одинаковыми основаниями в одной части неравенства5 x +1 – 2·5 x
Вынесем в левой части неравенства за скобки 5 x , а в правой части неравенства 3 х и получим неравенство
5 х (5 – 2) 3·5 х
Разделим обе части неравенства на выражение 3·3 х, знак неравенства не изменится, так как 3·3 х положительное число, получим неравенство:
х 1).

Ответ: (–∞; 2) .
Если у вас возникнут вопросы по решению показательных неравенств или вы захотите попрактиковаться в решении подобных примеров, записывайтесь ко мне на уроки. Репетитор Валентина Галиневская .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение показательных уравнений. Видеоуроки
В этой статье вы познакомитесь со всеми типами показательных уравнений и алгоритмами их решения, научитесь распознавать, к какому типу принадлежит показательное уравнение, которое вам надо решить, и применять для его решения соответствующий метод. Подробное решение примеров показательных уравнений каждого типа вы сможете посмотреть в соответствующих ВИДЕОУРОКАХ.
Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.
Прежде чем начать решать показательное уравнение, полезно сделать несколько предварительных действий, которые могут значительно облегчить ход его решения.
 Вот эти действия:
Вот эти действия:1. Разложите все основания степеней на простые множители.
2. Корни представьте в виде степени.
3. Десятичные дроби представьте в виде обыкновенных.
4. Смешанные числа запишите в виде неправильных дробей.
Пользу этих действий вы осознаете в процессе решения уравнений.
Рассмотрим основные типы показательных уравнений и алгоритмы их решения.
1. Уравнение вида
Это уравнение равносильно уравнению
Посмотрите в этом ВИДЕОУРОКЕ решение уравнения этого типа.
2. Уравнение вида
В уравнениях этого типа:
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени равны.
Чтобы решить это уравнение, нужно вынести за скобку множитель в наименьшей степени.

Пример решения уравнения этого типа:
посмотрите в ВИДЕОУРОКЕ.
3. Уравнение вида
Уравнения этого типа отличаются тем, что
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени разные.
Уравнения такого типа решаются с помощью замены переменных. Прежде чем вводить замену, желательно освободиться от свободных членов в показателе степени. (, , и т.д)
Посмотрите в ВИДЕОУРОКЕ решение уравнения этого типа:
4. Однородные уравнения вида
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.

Однородные уравнения решаются по сходному алгоритму.
Чтобы решить уравнение такого типа, разделим обе части уравнения на (можно разделить на или на )
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
В нашем случае, поскольку выражение не равно нулю ни при каких значениях неизвестного, мы можем делить на него без опаски. Разделим левую часть уравнения на это выражение почленно. Получим:
Сократим числитель и знаменатель второй и третьей дроби:
Введем замену:
, причем при всех допустимых значениях неизвестного.
Получим квадратное уравнение:
Решим квадратное уравнение, найдем значения , которые удовлетворяют условию , а затем вернемся к исходному неизвестному.
Смотрите в ВИДЕОУРОКЕ подробное решение однородного уравнения:
5. Уравнение видаПри решении этого уравнения будем исходить из того, что
Исходное равенство выполняется в двух случаях:
1. Если , поскольку 1 в любой степени равна 1,
или
2. При выполнении двух условий:
Посмотрите в ВИДЕОУРОКЕ подробное решение уравнения
И.В. Фельдман, репетитор по математике.
«Решение показательных уравнений с помощью замены переменных». 11-й класс
Цель урока: изучить способ решения показательных уравнений с помощью замены переменных.
Задачи:
1) образовательная:
– повторить известные способы решения показательных уравнений;
– показать алгоритм решения с помощью замены переменных;
2) воспитательная:
– создавать условия для формирования навыков организации своей деятельности – самостоятельного поиска решения, самоконтроля;
– приучать к аккуратности выполнения записей в тетради и на доске;
– воспитывать умение работать в парах, взаимопомощь;
– воспитывать умение анализировать результаты своей деятельности;
3) развивающая:
– формировать умение сравнивать, выявлять закономерности, обобщать;
– формировать грамотную математическую речь;
– формировать умение применять знания в конкретной ситуации.

Преподавание ведется по учебнику А.Н.Колмогорова.
Ход урока
1. Оргмомент.
Приветствие.
Сегодня мы продолжим знакомство с методами решения показательных уравнений.
Запишите тему урока: “Решение показательных уравнений”, но оставьте строчку, тему мы чуть позже уточним.
2. Актуализация знаний.
Устная работа с классом.
Решите уравнения.
3. Постановка проблемы.
Уравнения 1 – 7 решали, приводя их к виду или . Последнее уравнение решить таким способом не удается.
Обратите внимание: . Предложите способ решения. Нужно ввести новую переменную у = и решить полученное квадратное уравнение.
Какова будет наша цель сегодня? Научиться решать показательные уравнения с помощью замены переменных.
Уточним тему урока: “Решение показательных уравнений с помощью замены переменных”.

4. Изучение нового материала.
Пусть у = , причем у > 0.
Уравнение примет вид .
Решим это уравнение: = –1; = 5.
не удовлетворяет условию у > 0.
= 5; х = 1.
Ответ: 1.
Решим уравнение .
Перепишем его в виде .
Далее решает ученик у доски с комментированием.
Пусть , причем у > 0.
3у – 8 = ; 3– 8у = 3; 3– 8у – 3 = 0;
Решим это уравнение: = –; = 3.
не удовлетворяет условию у > 0.
= 3; х = 1.
Ответ: 1.
Решим уравнение .
Почему не удается решить? Нельзя привести степени к одному основанию.
Перепишем уравнение в виде
Разделим обе части уравнения на : .
Далее решает у доски ученик с комментированием.
Пусть у =, причем у > 0.
Уравнение примет вид .
.

Решим это уравнение: = 1; =.
= 1; х = 0. = ; х = 1.
Ответ: 0; 1.
Можно было делить на ? Что изменилось бы в решении? Ввели бы обозначение у =.
5. Первичное закрепление изученного материала.
Ученики работают в парах, более сильные ребята помогают соседям.
Два ученика работают за крыльями доски.
6. Самостоятельная работа.
Чтобы проверить, как усвоен новый материал, выполните самостоятельную работу.
1) ;
2) ;
3) .
По окончании работы ученики самостоятельно проверяют решение по образцу (раздаточный материал), фиксируя места, где допущены ошибки.
7. Итог урока.
- Обсуждение результатов самостоятельной работы.
- Кто выполнил правильно все задания?
- Кто допустил ошибки в первом (втором, третьем) задании? Какие?
- Повторим, какие приемы использовали при решении
показательных уравнений.

- Оцените свою работу на уроке.
- Вам предстоит еще раз применить полученные знания при выполнении домашнего задания: № 464(в,г), 470(в,г), 166(г) (стр. 299).
Решение неравенств с неизвестной степенью. Показательные уравнения и неравенства
Исходя из этого и применяя теорему о корне, получим, что уравнение a x = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = a c .
Тогда очевидно, что с будет являться решением уравнения a x = a c .Рассмотрим следующий пример: решить уравнение 5 (x 2 — 2*x — 1) = 25.
Представим 25 как 5 2 , получим:
5 (x 2 — 2*x — 1) = 5 2 .
Или что равносильно:
x 2 — 2*x — 1 = 2.
Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.
Ответ: 3;-1.
Решим уравнение 4 x — 5*2 x + 4 = 0. Сделаем замену: t=2 x и получим следующее квадратное уравнение:
t 2 — 5*t + 4 = 0.

Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4Теперь решаем уравнения 2 x = 1 и 2 x = 4.
Ответ: 0;2.
Решение показательных неравенств
Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0, то данная функция будет убывающей на всем множестве вещественных чисел.
Рассмотрим пример: решить неравенство (0.5) (7 — 3*x)
Заметим, что 4 = (0.5) 2 . Тогда неравенство примет вид (0.5)(7 — 3*x)
Получим: 7 — 3*x>-2.
Отсюда: х
Ответ: х
Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.
Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое.
 {2}}-16}{2x} \lt 0. \\\end{align}\]
{2}}-16}{2x} \lt 0. \\\end{align}\]Теперь используем стандартный метод интервалов. Нули числителя: $x=\pm 4$. Знаменатель обращается в ноль только при $x=0$. Итого три точки, которые надо отметить на числовой прямой (все точки выколоты, т.к. знак неравенства строгий). Получим:
БолееРешение экспоненциальных уравнений из определения
Пурпурная математика
Чтобы решить экспоненциальные уравнения без логарифмов, вам нужно иметь уравнения со сравнимыми экспоненциальными выражениями по обе стороны от знака «равно», чтобы вы могли сравнить степени и решить. Другими словами, у вас должно быть «(некоторая база) в (некоторая степень) равна (той же основе) в (какая-то другая степень)», где вы устанавливаете две степени равными друг другу и решаете полученное уравнение.Например:
Поскольку основания (в каждом случае «5») одинаковы, то единственный способ, которым два выражения могут быть равны, — это чтобы степени также были одинаковыми.
 То есть:
То есть:MathHelp.com
Это решение демонстрирует логическую основу того, как решается весь этот класс уравнений: если основания одинаковы, то и степени должны быть равны; это единственный способ, чтобы две части уравнения были равны друг другу.Поскольку степени должны быть одинаковыми, мы можем положить две степени равными друг другу и решить полученное уравнение.
Так как основания одинаковые, то я могу приравнять силы и решить:
1 – х = 4
1 – 4 = х
–3 = х
Тогда мое решение:
Не все экспоненциальные уравнения даны в терминах одного и того же основания по обе стороны от знака «равно».
 Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какое-то другое основание, прежде чем мы сможем установить степени равными друг другу. Например:
Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какое-то другое основание, прежде чем мы сможем установить степени равными друг другу. Например:Поскольку 9 = 3 2 , мне действительно нужно решить:
Преобразовав 9 в 3 2 , я преобразовал правую часть уравнения так, чтобы она имела то же основание, что и левая часть. Поскольку базы теперь одинаковы, я могу установить две степени равными друг другу:
В этом случае у меня есть экспонента с одной стороны от «равно», а число с другой.Я могу решить уравнение, если я могу выразить «27» как степень числа 3. Поскольку 27 = 3 3 , я могу преобразовать и перейти к решению:
3 2 х –1 = 27
3 2 х –1 = 3 3
2 х – 1 = 3
2 х = 4
х = 2
Если я не уверен в своем ответе или хочу проверить его перед сдачей (например, на тесте), я могу проверить его, вставив его обратно в исходное упражнение.
. Степень в левой части исходного уравнения упростилась бы как:
Степень в левой части исходного уравнения упростилась бы как:А 3 3 = 27, что является правой частью исходного уравнения. Тогда мое (подтвержденное) решение:
Как вы, вероятно, уже заметили, вам нужно хорошенько освоить свои числовые степени, такие как степени от 2 до 2 6 = 64, степени от 3 p до 3 5 = 243, степени 4 до 4 4 = 256, степени 5 до 5 4 = 625, степени 6 до 6 3 = 216, и все квадраты.
Не планируйте во всем полагаться на свой калькулятор, потому что необходимость находить для каждого значения в вашем калькуляторе может привести к пустой трате времени. Вы захотите иметь определенную степень легкости (то есть определенную степень знакомства и скорости) к тому времени, когда вы достигнете теста, поэтому ознакомьтесь с меньшими способностями сейчас.

Примечание по форматированию: HTML обычно не любит вложенные надстрочные индексы, поэтому в приведенном выше примере для обозначения степени используется нотация «карат».2–3 x = 3 4
х 2 – 3 х = 4
х 2 – 3 х – 4 = 0
( х – 4)( х + 1) = 0
х = –1, 4
Итак, мой ответ:
Это уравнение похоже на два предыдущих, но не совсем то же самое, потому что 8 не является степенью числа 4.2+4 х = 2 3
4 х 2 + 4 х = 3
4 х 2 + 4 х – 3 = 0
(2 х – 1)(2 х + 3) = 0
х = 1 / 2 , –3 / 2
Отрицательные показатели степени могут использоваться для обозначения того, что основание принадлежит другой стороне дробной линии.
 Поскольку 64 = 4 3 , то я могу использовать отрицательные показатели степени, чтобы преобразовать дробь в экспоненциальное выражение:
Поскольку 64 = 4 3 , то я могу использовать отрицательные показатели степени, чтобы преобразовать дробь в экспоненциальное выражение:Используя это, я могу решить уравнение:
4 x +1 = 1 / 64
4 x +1 = 4 –3
х + 1 = –3
х = –4
Чтобы решить это, мне сначала нужно вспомнить, что квадратные корни — это то же самое, что и половинные степени, и преобразовать радикал в экспоненциальную форму.Тогда я могу решить уравнение:
8 x –2 = кв [8]
8 x –2 = 8 1/2
х – 2 = 1/2
x = 2 + 1 / 2 = 5 / 2
Тогда мой ответ:
Ниже приведен пример обычного вопроса с подвохом:
Подумайте об этом: какая степень положительного числа «2» может , возможно, дать отрицательное число? Число никогда не может перейти от положительного к отрицательному, взяв степени; Я никогда не смогу превратить положительную двойку в отрицательную что-либо , четверку или что-то еще, умножая два на себя, независимо от того, сколько раз я выполняю умножение.
 Возведение в степень просто так не работает. Итак, ответ здесь:
Возведение в степень просто так не работает. Итак, ответ здесь:URL: https://www.purplemath.com/modules/solvexpo.htm
Экспоненциальные уравнения — определение, решение и примеры
Экспоненциальные уравнения, как следует из их названия, включают показатели степени.Мы знаем, что показатель степени числа (основания) показывает, сколько раз число (основание) умножается. Но что произойдет, если степень числа является переменной? Когда мощность является переменной и если она является частью уравнения, то это называется показательным уравнением. Нам может понадобиться использовать связь между показателями степени и логарифмами для решения экспоненциальных уравнений.
Давайте изучим определение показательных уравнений вместе с процессом их решения, когда основания одинаковы и когда основания не совпадают, а также несколько решенных примеров и практических вопросов.

Какие Показательные уравнения?
Экспоненциальное уравнение представляет собой уравнение с показателями, где показатель степени (или) частью экспоненты является переменным. Например, 3 х = 81, 5 х — 3 = 625, 6 2y — 7 = 121, и т.д., некоторые примеры показательных уравнений. Мы можем прийти через использование показательных уравнений, когда мы решаем проблемы алгебры, сложные проценты, экспоненциального роста, экспоненциального распада и т.д.
Типы показательных уравнений
Есть три типа показательных уравнений. Они следующие:
- Уравнения с теми же основаниями с обеих сторон. (Пример: 4 х = 4 2 )
- Уравнения с различными основаниями могут быть сделаны одинаковыми. (Пример: 4 х = 16, которая может быть записана в виде 4 х = 4 2 )
- Уравнения с различными основаниями, которые не могут быть выполнены так же.
 (Пример: 4 x = 15)
(Пример: 4 x = 15)
Формулы экспоненциальных уравнений
При решении экспоненциального уравнения основания в обеих частях могут совпадать или не совпадать. Вот формулы, которые используются в каждом из этих случаев, которые мы подробно изучим в следующих разделах.
Свойство равенства для экспоненциальных уравнений
Это свойство полезно для решения показательного уравнения с теми же основаниями.В нем говорится, что если основания в обеих частях экспоненциального уравнения равны, то показатели степени также должны быть равны. то есть a x = a y ⇔ x = y .
Экспоненциальные уравнения в логарифмической форме
Мы знаем, что логарифмы не что иное, как показатели степени, и наоборот. Следовательно, показательное уравнение может быть преобразовано в логарифмическое уравнение. Это помогает в процессе решения показательного уравнения с разными основаниями.
 Вот формула для преобразования показательных уравнений в логарифмические уравнения.
Вот формула для преобразования показательных уравнений в логарифмические уравнения.б х = а ⇔ log б а = х
Решение экспоненциальных уравнений с одинаковыми основаниями
Иногда показательное уравнение может иметь одинаковые основания в обеих частях уравнения. Например, 5 x = 5 3 имеет одинаковое основание 5 с обеих сторон. Иногда, хотя показатели с обеих сторон неодинаковы, их можно сделать одинаковыми. Например, 5 x = 125. Хотя у него разные основания в обеих частях уравнения, их можно сделать одинаковыми, записав как 5 x = 5 3 (поскольку 125 = 5 3 ).Чтобы решить показательные уравнения в каждом из этих случаев, мы просто применяем свойство равенства показательных уравнений, используя которое, мы устанавливаем показатели равными и решаем для переменной.
Вот еще пример, где базы не одинаковые, но можно сделать одинаковыми.

Пример: Решить показательное уравнение 7 y + 1 = 343 y .
Решение:
Мы знаем, что 343 = 7 3 .Используя это, данное уравнение можно записать как
7 у + 1 = (7 3 ) у
7 г + 1 = 7 3 года
Теперь базы с обеих сторон одинаковые. Таким образом, мы можем установить показатели степени одинаковыми.
года + 1 = 3 года
Вычитание у с обеих сторон,
2 года = 1
Деление обеих частей на 2,
г = 1/2
Решение экспоненциальных уравнений с разными основаниями
Иногда основания в обеих частях экспоненциального уравнения могут не совпадать (или) не могут быть сделаны одинаковыми.Мы решаем показательные уравнения с помощью логарифмов, когда основания не совпадают в обеих частях уравнения. Например, 5 x = 3 не имеет одинаковых оснований с обеих сторон, и основания не могут быть одинаковыми.
 В таких случаях мы можем сделать одну из следующих вещей.
В таких случаях мы можем сделать одну из следующих вещей.- Преобразуйте экспоненциальное уравнение в логарифмическую форму, используя формулу b x = a ⇔ log b a = x, и найдите переменную.
- Примените логарифм (log) к обеим частям уравнения и найдите переменную.В этом случае нам придется использовать свойство логарифма, log a m = m log a.
Решим уравнение 5 x = 3 каждым из этих способов.
Метод 1:
Преобразуем 5 х = 3 в логарифмическую форму. Тогда мы получаем,
журнал 5 3 = х
Использование изменения базового свойства,
х = (лог. 3) / (лог. 5)
Метод 2:
Приложим лог с обеих сторон 5 х = 3.Тогда мы получаем log 5 x = log 3. Используя свойство log a m = m log a в левой части уравнения, мы получаем x log 5 = log 3. Разделив обе части на log 5,
х = (лог.
 3) / (лог. 5)
3) / (лог. 5)Важные примечания:
Вот несколько важных замечаний относительно экспоненциальных уравнений.
- Чтобы решить экспоненциальные уравнения с одинаковыми основаниями, просто приравняйте показатели степени.
- Чтобы решить показательные уравнения по разным основаниям, примените логарифмирование к обеим частям.
- Показательные уравнения с теми же основаниями также могут быть решены с использованием логарифмов.
- Если экспоненциальное уравнение имеет 1 с любой стороны, то мы можем записать его как 1 = a 0 для любого ‘a’. Например, чтобы решить 5 x = 1, мы можем записать это как 5 x = 5 0 , тогда мы получим x = 0, .
- Чтобы решить экспоненциальное уравнение с помощью логарифмов, мы можем либо применить «log», либо применить «ln» к обеим сторонам.
Связанные темы:
Вот связанные темы экспоненциальных уравнений.

Часто задаваемые вопросы по экспоненциальным уравнениям
Что такое экспоненциальные уравнения?
Показательное уравнение — это уравнение, которое имеет переменную в показателе(ях). Например, 5 2x — 3 = 125, 3 7 — 2x = 91 и т. д. являются показательными уравнениями.
Какие бывают типы экспоненциальных уравнений?
Существует три типа экспоненциальных уравнений. Они,
- Показательные уравнения с одинаковыми основаниями с обеих сторон.
- Показательные уравнения с разными основаниями с обеих сторон, которые можно сделать одинаковыми.
- Показательные уравнения с разными основаниями с обеих сторон, которые нельзя сделать одинаковыми.
Как решать экспоненциальные уравнения?
Чтобы решить показательные уравнения с одинаковыми основаниями, мы приравняем показатели степени, тогда как для решения показательных уравнений с разными основаниями мы применим логарифмирование с обеих сторон.

Как записать экспоненциальное уравнение в логарифмической форме?
Запись показательного уравнения в логарифмической форме помогает нам решить его.Это можно сделать по формуле b x = a ⇔ log b a = x.
Что такое свойство равенства экспоненциальных уравнений?
Свойство равенства экспоненциальных уравнений говорит об установлении показателей степени равными всякий раз, когда основания в обеих частях уравнения равны. т. е. а х = а у ⇔ х = у.
Как решать экспоненциальные уравнения с одинаковыми основаниями?
Если экспоненциальное уравнение имеет одинаковые основания с обеих сторон, просто приравняйте показатели степени и найдите переменную.Вот пример: 4 2x — 1 = 4 1 — x . Здесь основания с обеих сторон равны. Таким образом, мы можем установить показатели равными.
2х — 1 = 1 — х
3x = 2
х = 2/3.Как решать показательные уравнения с разными основаниями?
Если экспоненциальное уравнение имеет разные основания с обеих сторон, примените log к обеим сторонам и найдите переменную.
 Вот пример, 4 х — 5 = 8. Берем бревно с двух сторон,
Вот пример, 4 х — 5 = 8. Берем бревно с двух сторон,
журнал 4 х — 5 = журнал 8
(x — 5) журнал 4 = журнал 8
х — 5 = (логарифм 8) / (логарифм 4)
х = [(журнал 8) / (лог 4)] + 5.Как решить экспоненциальные уравнения с помощью логарифмов?
Мы решаем экспоненциальные уравнения, используя логарифмы двумя способами.
- Преобразуйте экспоненциальное уравнение в логарифмическое уравнение с использованием B x = A ⇔ LOG B A = X.
- Примените «Журнал» или «LN» с обеих сторон и решить.
Урок объяснения: решение экспоненциальных уравнений с использованием логарифмов
в этом объяснении мы узнаем, как использовать логарифмы для решения экспоненциальных уравнения.
Начнем с рассмотрения показательного уравнения 2=8. Мы видим, что 2 возводится в степень 𝑥 с левой стороны. Другими словами, переменная находится в экспонента.
 Это общая черта всех экспоненциальных уравнений.
Это общая черта всех экспоненциальных уравнений.Определение: показательное уравнение
Показательное уравнение – это уравнение, в котором переменная используется в одном экспонента или больше.
Прежде чем посмотреть, как решить 2=8 с помощью логарифмов, давайте рассмотрим два альтернативных метода, которые мы могли бы использовать для ее решения.Мы должны получить то же решение, используя эти методы, что и те, которые мы получаем, когда используя логарифмы.
Первый альтернативный метод заключается в том, чтобы начать с определения функций 𝑓(𝑥)=2 и 𝑔(𝑥)=8. Затем мы могли бы построить график 𝑦=𝑓(𝑥) и 𝑦=𝑔(𝑥) на той же плоскости координат и определить точку пересечения графиков, как показано на рисунке.
𝑥-координата точки пересечения равна 3, поэтому с помощью этого метода мы получаем решение 𝑥=3.
Второй альтернативный метод заключается в том, чтобы начать с использования того факта, что 8 — это степени 2, чтобы переписать уравнение.
 Мы знаем это
2=2×2×2=8, поэтому мы могли бы заменить
2 для 8, чтобы получить 2=2. Тогда мы могли бы
приравняйте показатели, чтобы снова получить решение 𝑥=3.
Мы знаем это
2=2×2×2=8, поэтому мы могли бы заменить
2 для 8, чтобы получить 2=2. Тогда мы могли бы
приравняйте показатели, чтобы снова получить решение 𝑥=3.Теперь давайте рассмотрим, как решить 2=8 с помощью Связь экспоненциальной и логарифмической функций.
Определение: логарифмическая функция
Логарифмическая функция является обратной экспоненциальной функцией. Если 𝑦=𝑎, то 𝑥=𝑦log.
Так как 2=8 или 8=2 находится в вид 𝑦=𝑎, мы знаем, что значение 𝑦 равно 8, а значение 𝑎 равно 2.Таким образом, мы можем написать уравнение 𝑥=8log. Чтобы упростить справа, мы можем спросить себя: «В какой степени основание из 2 возведено в равно 8?» Ответ 3, поэтому мы получаем 𝑥=3, то же самое ответ, к которому мы пришли с помощью предыдущих двух методов.
Однако некоторые экспоненциальные уравнения более сложны, поэтому при их решении используя логарифмы, нам часто нужно использовать одно или несколько правил логарифмирования ниже.

Свойства: Правила логарифмов
Правило продукта: logloglog𝑚𝑛𝑚𝑛 = 𝑚 + 𝑛
Кожающее правило: logloglog𝑚𝑛𝑚𝑛 = 𝑚-𝑛
Правило питания: loglog 𝑚=𝑘𝑚
Обратите внимание, что в каждом из правил основания логарифмов одинаковы. с обеих сторон уравнения.
- Правило продукта гласит, что журнал продукта двух чисел есть сумма логарифма первого множителя и журнал второго фактора. Мы бы использовали правило продукта , чтобы найти, что logloglog(9⋅27)=9+27=2+3=5.
- Частное правило утверждает, что журнал частного двух чисел есть разность логарифма делимого и журнал делителя. Мы бы использовали частное правило , чтобы найти, что logloglog6416=64−16=6−4=2.
- Правило силы гласит, что бревно поднятой базы
к степени является произведением мощности и логарифма основания. Мы воспользуемся степенным правилом , чтобы найти loglog4=84=8(1)=8.

При решении показательных уравнений с помощью логарифмов мы часто используем основание 10 или основание 𝑒 для журнала из-за кнопки на наших калькуляторах. Однако база не имеет значения. Напомним, что когда основание равно 10, по соглашению его указывать не нужно, а когда основание равно 𝑒, мы берем натуральное бревно.Важно отметить, что если мы используем основание 10 или основание 𝑒 при снятии логарифма числа часто результатом будет не целое число. Это хорошо, потому что одно из преимуществ решения экспоненциальное уравнение с использованием логарифмов заключается в том, что уравнение не должно иметь целочисленное решение. Мы можем использовать научный калькулятор для аппроксимации решения. Давайте посмотрим, как это сделать, на следующих примерах.
Пример 1. Решение экспоненциальных уравнений с помощью логарифмов
Решите 3=11 относительно 𝑥, получив ответ до трех знаков после запятой.

Ответ
Начнем с того, что вспомним, что логарифмическая функция является обратной показательная функция. Если 𝑦=𝑎, то 𝑥=𝑦log. Поскольку 3=11, или 11=3, имеет вид 𝑦=𝑎, мы знаем, что значение 𝑦 равно 11 и что значение 𝑎 равно 3. Таким образом, мы можем написать уравнение 𝑥=11.log
Поскольку 11 не является степенью числа 3, нам нужно использовать научный калькулятор, чтобы упростить правую часть. Мы должны убедиться, что используем соответствующий нажатия клавиш, имея в виду, что база равна 3, а не 10.При этом мы получаем 𝑥=2.182658…, Задача требует указать значение 𝑥 до трех знаков после запятой, поэтому нам нужно считать цифру в десятитысячном разряде, что равно 6. Поскольку эта цифра больше, чем или равно 5, мы должны округлить цифру 2 в разряде тысяч, чтобы получить ответ 𝑥≈2,183.
Другой способ решить уравнение 3=11 состоит в том, чтобы взять лог обеих сторон.
 Использование базы 10 дает нам
логлог(3)=11.
Использование базы 10 дает нам
логлог(3)=11.Обратите внимание, что основание в уравнении не указано. То правило степени логарифмов позволяет нам переписать log(3) как 𝑥⋅3log так что уравнение становится 𝑥⋅3=11.loglog
Затем мы можем разделить обе части на log3, чтобы получить 𝑥=113loglog а затем используйте кнопку журнала на научном калькуляторе, чтобы получить 𝑥=113≈1,041390,47712≈2,182658…loglog.
Точно так же, как и раньше, округляем цифру 2 в тысячных до получить ответ 𝑥≈2.183.
Примечание
При использовании инженерного калькулятора для приближения значения выражение loglog113, важно, чтобы мы запишите как log11, так и log3 в достаточный количество знаков после запятой, если мы вычисляем их отдельно. Если, например, если бы мы записывали их только до трех знаков после запятой, мы бы получили 𝑥=113≈1.
 0410.477≈2.182389….loglog
0410.477≈2.182389….loglogВ этом случае мы бы сохранили 2 в разряде тысячных вместо округляя его, мы получили бы неправильный ответ 𝑥≈2.182. По этой причине лучше всего войти loglog113 в наш калькулятор как единый выражение, а не вычислять каждый отдельный журнал.
Далее мы будем работать над решением задачи, связанной с показательным уравнением с биномиальным показателем.
Пример 2. Решение экспоненциальных уравнений с биномиальными показателями с использованием Логарифмы
Найдите с точностью до сотых значение 𝑥 для что 2=9.
Ответ
Чтобы решить уравнение для 𝑥, мы можем начать с взяв бревно с обеих сторон.Если мы используем базу 10, нам не нужно будет его указывать и мы получим уравнение loglog2=9.
Используя правило степени логарифмов, мы можем переписать log2 как (𝑥+8)(2)log, так что уравнение принимает вид (𝑥+8)(2)=9.
 loglog
loglogРазделив обе части уравнения на log2, мы получим 𝑥+8=92,логлог и после вычитания 8 с обеих сторон получаем 𝑥=92−8.loglog
Теперь мы можем использовать кнопку журнала на научном калькуляторе. чтобы приблизить значение 𝑥.При этом лучше всего ввести loglog92−8 в калькулятор как одно выражение, а не найти log9 и log2 отдельно перед упрощением. Таким образом, есть отсутствие опасности ошибок округления. Это дает нам 𝑥=92−8=−4,830074999…, loglog что дает нам ответ 𝑥≈−4,83 с точностью до ближайшего сотый.
Теперь посмотрим, как решить уравнение с двумя биномиальными показателями вместо одного.
Пример 3. Решение экспоненциальных уравнений с биномиальными показателями с использованием Логарифмы
Используйте калькулятор, чтобы найти значение 𝑥, для которого 3=8. Дайте правильный ответ на два десятичные разряды.

Ответ
Для начала возьмем бревно с обеих сторон уравнение. Используя основание 10, мы получаем loglog3=8.
Затем правило степени логарифмов позволяет нам переписать журнал3 как (–4𝑥–3)(3)log и log8 как (𝑥+4.7)(8)log, что дает нам уравнение (–4𝑥–3)(3)=(𝑥+4,7)(8).loglog
После распределения log3 на левой стороне уравнение и log8 справа, уравнение становится −4𝑥⋅3−33=𝑥⋅8+4.78.loglogloglog
Теперь, чтобы изолировать переменную, переместим члены, содержащие 𝑥 в одну часть уравнения, а члены не содержащий 𝑥 на другую сторону. Во-первых, мы будем добавьте 4𝑥⋅3log с обеих сторон, чтобы получить −33=𝑥⋅8+4.78+4𝑥⋅3.loglogloglog
Далее мы вычтем 4,78log с обеих сторон, так что уравнение становится −33−4,78=𝑥⋅8+4𝑥⋅3.loglogloglog
Теперь мы можем вынести 𝑥 из правая часть уравнения, что дает нам −33−4,78=𝑥(8+43),loglogloglog и после того, как мы разделим обе части уравнения на выражение loglog8+43, получаем −33−4,788+43=𝑥.
 loglogloglog
loglogloglogНаконец, мы можем использовать кнопку журнала на научном калькуляторе, чтобы ввести выражение для 𝑥.Калькулятор дает нам 𝑥=−2,018756992…, что дает нам ответ 𝑥≈−2,02 на два десятичные разряды.
В следующем примере мы также должны переместить переменные термины в одна сторона уравнения.
Пример 4. Решение экспоненциальных уравнений с использованием логарифмов
Решите 2⋅3=5⋅4 для 𝑥, давая ответ с точностью до трех знаков после запятой.
Ответ
Первый шаг решения 2⋅3=5⋅4 для 𝑥 перемещает члены с показателем степени 𝑥 в одну часть уравнения и члены без показатель 𝑥 в другую сторону.Если разделить оба стороны уравнения на 2⋅4, получаем 2⋅32⋅4=5⋅42⋅4.
Мы видим, что теперь и в числителе, и в знаменатель дроби в левой части уравнения и 4 как в числителе, так и в знаменателе дробь в правой части.
 Эти условия отменяются, давая нам
34=52.
Эти условия отменяются, давая нам
34=52.Напомним, что если две константы 𝑎 и 𝑏 оба возведены в степень 𝑥, то 𝑎𝑏=𝑎𝑏; так что мы можем заменить 34 с 34, получая 34=52.
Поскольку логарифмическая функция является обратной экспоненциальной функции, мы знаем, что если 𝑦=𝑎, тогда 𝑥=𝑦log. Уравнение 34=52, или 52=34, т.е. в виде 𝑦=𝑎, что говорит нам о том, что значение 𝑦 составляет 52 и что значение 𝑎 равно 34. Таким образом, мы можем написать уравнение 𝑥=52.log
Теперь мы можем использовать научный калькулятор, чтобы упростить правую часть, учитывая, что основание равно 34 и не 10.При этом получаем 𝑥=−3,185081…, что дает нам ответ 𝑥≈−3,185 на три десятичных знака.

Мы также можем взять логарифм обеих частей уравнения 34=52 решить Это. Если мы используем основание 10, мы получаем loglog34=52.
Используя правило степени логарифмов, мы можем переписать log34 как 𝑥⋅34log, что дает нам уравнение 𝑥⋅34=52.loglog
Теперь мы можем разделить обе части на log34 чтобы получить 𝑥=,логлог а затем используйте кнопку журнала на научном калькуляторе чтобы ввести выражение для 𝑥, давая нам 𝑥=−3,185081….
Опять же, мы бы оставили цифру 5 в тысячном разряде, чтобы получить ответ 𝑥≈−3,185.
Наконец, давайте рассмотрим пример, в котором мы должны использовать два разных правила логарифмов.
Пример 5. Решение экспоненциальных уравнений с биномиальными показателями с использованием Логарифмы
Используйте калькулятор, чтобы найти значение 𝑥 для что 2×7=16×7.
 Дай свой ответ
с точностью до двух знаков после запятой.
Дай свой ответ
с точностью до двух знаков после запятой.Ответ
Начнем с логарифма обеих частей уравнения. Использование базы 10 дает нам loglog(2×7)=16×7.
Правило произведения логарифмов позволяет нам переписать log(2×7) как loglog(2)+7 и log16×7 как loglog16+7, что приводит к уравнение loglogloglog(2)+7=16+7.
Теперь мы можем использовать правило степени логарифмов , чтобы переписать log(2) как 𝑥⋅2log. Мы также можем использовать его для перезаписи log7 как (𝑥+9)7log, что дает нам уравнение 𝑥⋅2+7=16+(𝑥+9)7.loglogloglog
После того, как мы распределим 𝑥+9 с правой стороны, мы получили 𝑥⋅2+7=16+𝑥⋅2+97.logloglogloglog
Далее мы должны переместить члены, содержащие 𝑥, в одну сторону уравнения и члены, не содержащие 𝑥 к Другая сторона.
 Вычитание 𝑥⋅7log с обеих сторон
дает нам
𝑥⋅2+7−𝑥⋅7=16+97,логлоглоглоглог
а затем вычитание log7 с обеих сторон дает нам
𝑥⋅2−𝑥⋅7=16+97−7.logloglogloglog
Вычитание 𝑥⋅7log с обеих сторон
дает нам
𝑥⋅2+7−𝑥⋅7=16+97,логлоглоглоглог
а затем вычитание log7 с обеих сторон дает нам
𝑥⋅2−𝑥⋅7=16+97−7.logloglogloglogПоследние два члена в правой части теперь можно объединить, чтобы получить уравнение 𝑥⋅2−𝑥⋅7=16+87.loglogloglog
Теперь мы можем вынести 𝑥 из левая часть уравнения, что дает нам 𝑥(2−7)=16+87,логлоглоглог и после того, как мы разделим обе части уравнения на выражение loglog2–7, получаем 𝑥=16+872–7.loglogloglog
Наконец, мы можем использовать кнопку журнала на научном калькулятор, чтобы ввести выражение для 𝑥. Калькулятор дает нам 𝑥=−14,63953707…, что дает нам ответ 𝑥≈−14,64 на два десятичные разряды.
Теперь давайте закончим, повторив некоторые ключевые моменты.
Ключевые моменты
- Показательное уравнение — это уравнение, в котором переменная используется в
один показатель или более.

- Логарифмическая функция является обратной экспоненциальной функцией.Если 𝑦=𝑎, то 𝑥=𝑦log.
- При решении экспоненциальных уравнений с помощью логарифмов часто приходится использовать один или несколько правил логарифмирования. Три логарифмических правила, которые используются при решении экспоненциальных уравнений правило произведения , частное правило и степенное правило .
- Правило продукта , или logloglog𝑚𝑛=𝑚+𝑛, утверждает, что журнал произведение двух чисел есть сумма логарифма первый фактор и логарифм второго фактора.
- Частное правило , или logloglog𝑚𝑛=𝑚−𝑛, утверждает, что журнал от частного двух чисел есть разность логарифма делимого и журнал делителя.
- Правило мощности , или loglog𝑚=𝑘𝑚,
утверждает, что логарифм основания, возведенного в степень, равен
произведение мощности и логарифма основания.
 {p }=p * \log _{b} M
{p }=p * \log _{b} M
\]
Причина этого исходит из правила для показателей степени.{2 x+3}=\ln 17 \\
(2 x+3) \ln 5=\ln 17
\end{array}
\]
Есть несколько возможностей закончить задачу с этого момента. Остановимся на двух из них, наиболее полезных для решения более сложных задач. Сначала мы распределим \(\ln 5\) в круглых скобках, а затем получим \(x\) сам по себе.\[
\begin{align}
(2 x+3) \ln 5 &=\ln 17 \\
x * 2 \ln 5+3 \ln 5 &=\ln 17 \\
-3 \ln 5 &=-3 \ln 5 \\
x * 2 \ln 5 &=\ln 17-3 \ln 5 \\
x &=\frac{\ln 17-3 \ln 5}{2 \ln 5 } \приблизительно-0.{1,760} \приблизительно 16,9897 \приблизительно 17
\]Мы также можем аппроксимировать логарифмы в задаче и решить для приблизительного ответа:
\[
\begin{aligned}
(2 x+3) \ln 5 &=\ln 17 \\
x * 2 \ln 5 +3 \ln 5 &=\ln 17 \\
3,2189 х+4,8283 &\приб 2,8332 \\
-4,8283 &\приб-4,8283\
3,2189 х &\приб-1,9951 \\
х &\приб-0,620
\end{aligned}
\]
Если вы используете метод аппроксимации, важно сделать хорошую аппроксимацию. {2 x-1} \\
{2 x-1} \\
3 x * \log 4 &=(2 x-1) \log 9 \\
x * 3 \log 4 &=x * 2 \log 9-\log 9
\end {выровнено}
\]Если мы соберем подобные термы, то получим:
\[
\begin{aligned}
x * 3 \log 4 &=x * 2 \log 9-\log 9 \\
\log 9 &= x * 2 \log 9-x * 3 \log 4
\end{aligned}
\]
На этом этапе, если мы хотим получить \(x\) сам по себе, нам нужно вынести \(x \) справа:
\[
\begin{array}{l}
\log 9=x * 2 \log 9-x * 3 \log 4 \\
\log 9=x(2 \ лог 9-3 \ лог 4)
\end{массив}
\]Затем разделить в обе стороны на коэффициент в скобках:
\[
\frac{\log 9}{2 \log 9-3 \log 4}=\frac{x\cancel{(2 \log 9-3 \ log 4)}}{\cancel{2 \log 9-3 \log 4}} \\
\frac{\log 9}{2 \log 9-3 \log 4}=x \\
9.{2 x-1} \\
3 x * \log 4 &=(2 x-1) \log 9 \\
3 x(0,60206) & \приблизительно(2 x-1) 0,95424 \\
1,80618 x & \ приблизительно 1,9085 x-0,95424 \\
0,95424 & \ приблизительно 0,10232 x \\
9,326 & \ приблизительно x
\end{aligned}
\]
Этот ответ менее точен, чем другое приближение \((9,326036 \text { vs . {х-2}\)
{х-2}\)Решение экспоненциальных уравнений | Блестящая математика и естественные науки вики
Учитывая 1728 = 2a.n,(6) 1m=1n,
, где a≠0a\neq0a=0 и b≠0.b\neq0.b=0. Всегда будьте осторожны с (5)(5)(5) и (6)(6)(6); никогда не забывайте проверять, работает ли подстановка нуля в экспоненте, или есть ли основания, равные 1.
Свойства степеней и корней
Содержание этой страницы:
Введение
Экспоненциальное уравнение является одним имеет экспоненциальные выражения, иными словами, полномочия, имеющиеся в их экспоненциальные выражения с неизвестный фактор x .6 $$
Очевидно, что значение, которое должно принимать x , чтобы равенство было истинным, равно 3.
Чтобы получить выражения такого типа, мы должны разложить на множители , выразить все числа в виде степеней , применить свойства степеней и записать корни как степени.

Иногда нам нужно будет изменить переменную для преобразования уравнение в квадратное.
Мы также можем решить с помощью логарифмов, но мы оставим этот тип процедуры для более сложных уравнений с разными основаниями в экспоненциальные выражения, что делает невозможным использование предыдущего метод уравнивания.х $$
, имеющее действительное решение с использованием логарифмов
$$ x = \frac{3 ln(3)}{ln\left(\frac{5}{3}\right)} $$
Прежде чем мы начнем… давайте вспомним свойства сил
Продукт Мощность Частное Отрицательный показатель степени Обратный Инверсия инверсии Уравнение 1
Показать решение
Учитывая, что
$$ 27=3^2 $$
Мы можем переписать уравнение как
Следовательно,
Уравнение 2
Показать решение
Учитывая, что
Мы можем переписать уравнение как
Следовательно,
Уравнение 3
Показать решение
Учитывая, что
Оперируем выражением, используя свойства степеней
Таким образом, мы имеем линейное уравнение
Уравнение 4
Показать решение
Учитывая, что
Мы можем переписать уравнение как
Таким образом, мы можем извлечь общий делитель 2 x :
Следовательно,
Уравнение 5
Показать решение
Учитывая, что
Мы можем переписать уравнение как
У нас есть общее основание 3 x , но так как одно из них возведено в квадрат, мы пишем
Подставляя, уравнение заканчивается как
Другими словами, квадратное уравнение:
Умножаем полное уравнение на 9:
Решаем:
Следовательно,
Итак, получаем
Второй вариант невозможен, так как он отрицательный.
 Следовательно,
Следовательно,Откуда получаем
Уравнение 6
Показать решение
Учитывая, что
Перепишем уравнение как
Мы называем т = 3 х :
Подставляя, уравнение заканчивается как
Решаем квадратное уравнение:
Итак,
Итак,
Второе решение невозможно, потому что оно отрицательное, а первое возможно.
Уравнение 7
Показать решение
Учитывая, что
Перепишем уравнение как
Звоним
Подставляя, уравнение заканчивается как
Решаем предыдущее уравнение:
Поэтому
Второй вариант невозможен.
 Итак,
Итак,Следовательно,
Уравнение 8
Показать решение
Учитывая, что
Перепишем уравнение как
Звоним
Подставляя, уравнение заканчивается как
Решаем квадратное уравнение:
Поэтому
Обратите внимание, что
Итак, оба являются степенью числа 3.
Тогда два решения равны
Уравнение 9
Показать решение
Учитывая, что
Мы можем переписать уравнение как
Звоним
Подставляя, уравнение заканчивается как
Решаем уравнение:
Итак, у нас есть
Но решения
невозможны, потому что одно равно нулю, а другое отрицательно.

Итак, единственное решение
Уравнение 10
Показать решение
Учитывая, что
Мы можем переписать уравнение как
Следовательно,
Уравнение 11
Показать решение
Учитывая, что
Мы можем переписать уравнение как
Звоним
Подставляя, получаем квадратное уравнение
Решаем:
Так
Первое решение невозможно, так как оно равно нулю.
 Тогда
ТогдаУравнение 12
Показать решение
Учитывая, что
перепишем уравнение как
Звоним
Подставляя, получаем квадратное уравнение:
Решаем:
Следовательно,
Первое решение невозможно, так как оно равно нулю.
Следовательно, решение x = 1 .
Уравнение 13
Показать решение
Обратите внимание, что
Итак, уравнение можно записать как
Поскольку у нас есть экспоненциальное деление, мы умножаем на него полное уравнение, и таким образом оно исчезает:
Теперь звоним
Подставляя, уравнение заканчивается как
Решаем:
Следовательно,
Второе решение невозможно, так как оно отрицательное.

Итак, решение
Уравнение 14
Показать решение
Обратите внимание, что
Итак, мы запишем уравнение как
Звоним
Итак,
Подставляя, получаем уравнение четвертой степени (уравнение четвертой степени):
Решаем:
Первое решение невозможно, так как оно равно нулю.
Итак,
Уравнение 15
Показать решение
Обратите внимание, что
Таким образом, мы можем записать уравнение как
Поскольку у нас есть экспоненциальное деление, мы умножаем на него полное уравнение, и таким образом оно исчезает:
Звоним
Подставляя, получаем кубическое уравнение (третьей степени)
Переписываем
Применяем правило Руффини:
Одно из решений: t = 4 .

Вычисляем два других:
Но это не возможные решения, потому что они отрицательные.
Следовательно,
Уравнение 16
Показать решение
Перепишем уравнение:
Следовательно, решение
Уравнение 17
Показать решение
Перепишем уравнение:
Умножаем полное уравнение на экспоненту, и таким образом оно исчезает:
Следовательно,
Уравнение 18
Показать решение
Обратите внимание, что
Перепишем уравнение:
Мы работаем:
Следовательно,
Уравнение 19
Показать решение
Обратите внимание, что
Итак, мы перепишем уравнение как
Звоним
Тогда получаем выражение
Теперь определим
Обратите внимание, что
Предположим, что
Поэтому
Так
А это невозможно.

Итак, допустим
Следовательно,
Одним из решений было бы t = 0 , но, как и раньше, это невозможно.
Другое решение
Но мы предположили, что k = -1 и надо проверить, что это правда:
Поскольку это правда, решение уравнения равно x = 2 .
Уравнение 20
Показать решение
Перепишем уравнение как
Мы используем 25 = 5 2 и свойства степеней (корень пишем в виде степени):
, у нас есть
Наконец, мы решаем уравнение:
Уравнение 21
Показать решение
Запишем корни в виде степеней
Мы хотим, чтобы это было правдой:
Следовательно, у нас есть два решения:
$$ х = 0,\ х = -2 $$
Уравнение 22
Показать решение
У нас есть три вложенных корня (один внутри другого).

Запишем корни в виде степеней.
Уравнения заканчиваются как
Решаем уравнение и получаем решение
Уравнение 23
Показать решение
Запишем корни в виде степеней:
Мы хотим, чтобы это было правдой:
Наконец, мы решаем линейное уравнение:
Уравнение 24
Показать решение
Записываем корень в виде степеней:
Мы хотим, чтобы это было правдой:
Учитывая, что x не может быть 0.

Применяем правило Руффини:
Одно решение: x = 2 . Рассчитываем остальные:
Реальных решений нет.
Следовательно, единственным решением экспоненциального уравнения является
$$ х = 2 $$
Уравнение 25
Показать решение
Запишем корни в виде степеней.
Уравнение заканчивается так:
Обратите внимание, что -8 = (-2) 3
Мы хотим, чтобы это было правдой:
Matesfacil.com J. Llopis имеет лицензию творческий Commons Attribution-NonCommercial 4.


 В скобках останется выражение «(4 + 1)», что соответственно будет равно «5».
В скобках останется выражение «(4 + 1)», что соответственно будет равно «5».

 Приведем примеры.
Приведем примеры.




 2+2x-15≥0$.
2+2x-15≥0$. com»>
com»>



 Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
 Это и будет являться ответом к заданию.
Это и будет являться ответом к заданию. Решите уравнение:
Решите уравнение:
 Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: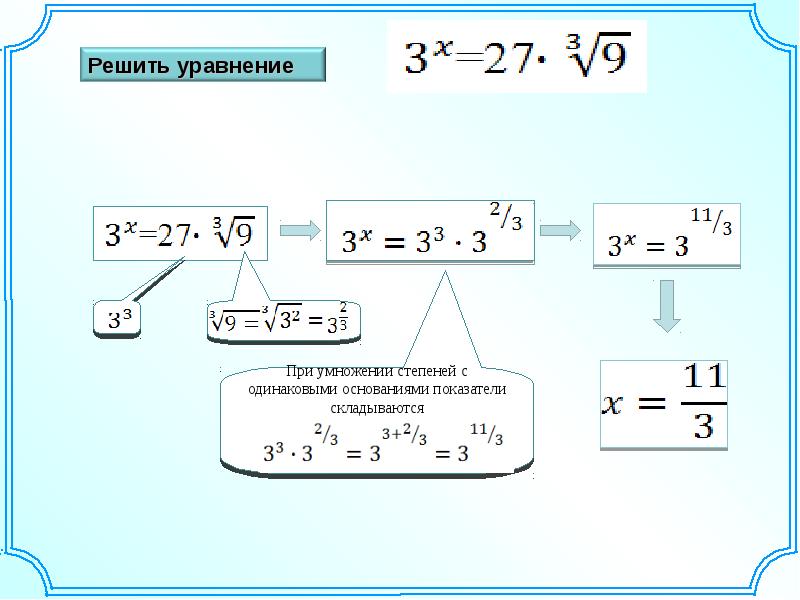 Решите неравенство:
Решите неравенство: Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Решить неравенство: 5 х – 1 > 125 .
Решить неравенство: 5 х – 1 > 125 .


 Вот эти действия:
Вот эти действия:






 {2}}-16}{2x} \lt 0. \\\end{align}\]
{2}}-16}{2x} \lt 0. \\\end{align}\] То есть:
То есть: Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какое-то другое основание, прежде чем мы сможем установить степени равными друг другу. Например:
Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какое-то другое основание, прежде чем мы сможем установить степени равными друг другу. Например: Степень в левой части исходного уравнения упростилась бы как:
Степень в левой части исходного уравнения упростилась бы как:
 Поскольку 64 = 4 3 , то я могу использовать отрицательные показатели степени, чтобы преобразовать дробь в экспоненциальное выражение:
Поскольку 64 = 4 3 , то я могу использовать отрицательные показатели степени, чтобы преобразовать дробь в экспоненциальное выражение: Возведение в степень просто так не работает. Итак, ответ здесь:
Возведение в степень просто так не работает. Итак, ответ здесь:
 (Пример: 4 x = 15)
(Пример: 4 x = 15) Вот формула для преобразования показательных уравнений в логарифмические уравнения.
Вот формула для преобразования показательных уравнений в логарифмические уравнения.
 В таких случаях мы можем сделать одну из следующих вещей.
В таких случаях мы можем сделать одну из следующих вещей. 3) / (лог. 5)
3) / (лог. 5)
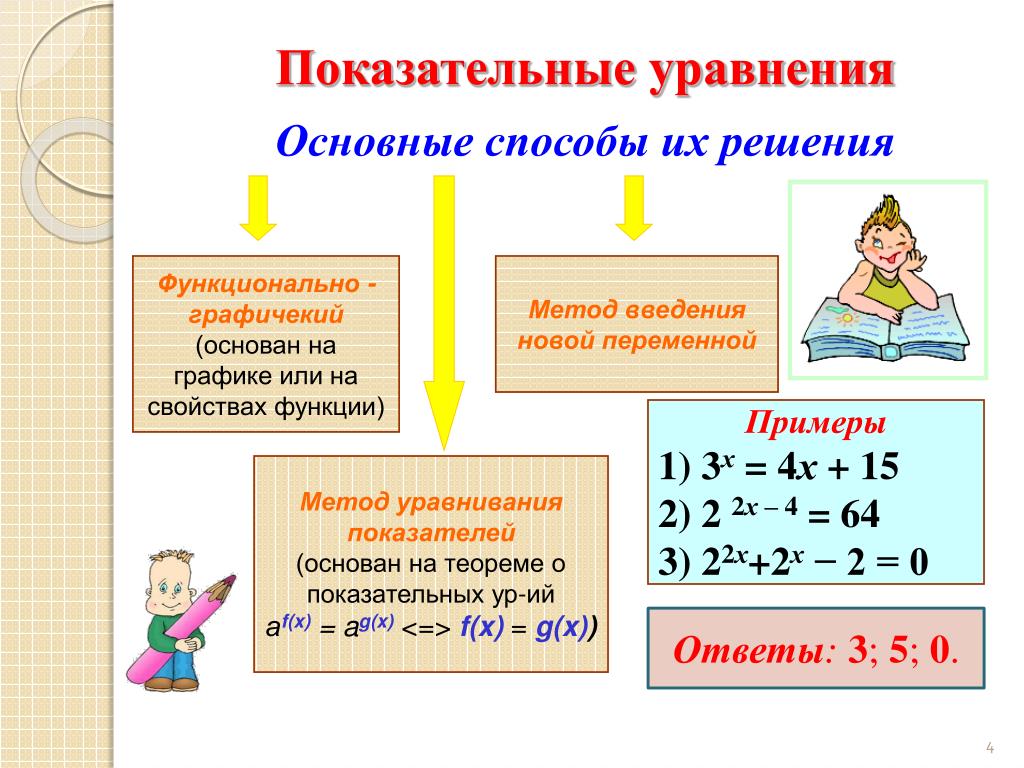
 Вот пример, 4 х — 5 = 8. Берем бревно с двух сторон,
Вот пример, 4 х — 5 = 8. Берем бревно с двух сторон,  Это общая черта всех экспоненциальных уравнений.
Это общая черта всех экспоненциальных уравнений. Мы знаем это
2=2×2×2=8, поэтому мы могли бы заменить
2 для 8, чтобы получить 2=2. Тогда мы могли бы
приравняйте показатели, чтобы снова получить решение 𝑥=3.
Мы знаем это
2=2×2×2=8, поэтому мы могли бы заменить
2 для 8, чтобы получить 2=2. Тогда мы могли бы
приравняйте показатели, чтобы снова получить решение 𝑥=3.


 Использование базы 10 дает нам
логлог(3)=11.
Использование базы 10 дает нам
логлог(3)=11. 0410.477≈2.182389….loglog
0410.477≈2.182389….loglog loglog
loglog
 loglogloglog
loglogloglog Эти условия отменяются, давая нам
34=52.
Эти условия отменяются, давая нам
34=52.
 Дай свой ответ
с точностью до двух знаков после запятой.
Дай свой ответ
с точностью до двух знаков после запятой. Вычитание 𝑥⋅7log с обеих сторон
дает нам
𝑥⋅2+7−𝑥⋅7=16+97,логлоглоглоглог
а затем вычитание log7 с обеих сторон дает нам
𝑥⋅2−𝑥⋅7=16+97−7.logloglogloglog
Вычитание 𝑥⋅7log с обеих сторон
дает нам
𝑥⋅2+7−𝑥⋅7=16+97,логлоглоглоглог
а затем вычитание log7 с обеих сторон дает нам
𝑥⋅2−𝑥⋅7=16+97−7.logloglogloglog
 {p }=p * \log _{b} M
{p }=p * \log _{b} M  {2 x-1} \\
{2 x-1} \\  {х-2}\)
{х-2}\)
 Следовательно,
Следовательно, Итак,
Итак,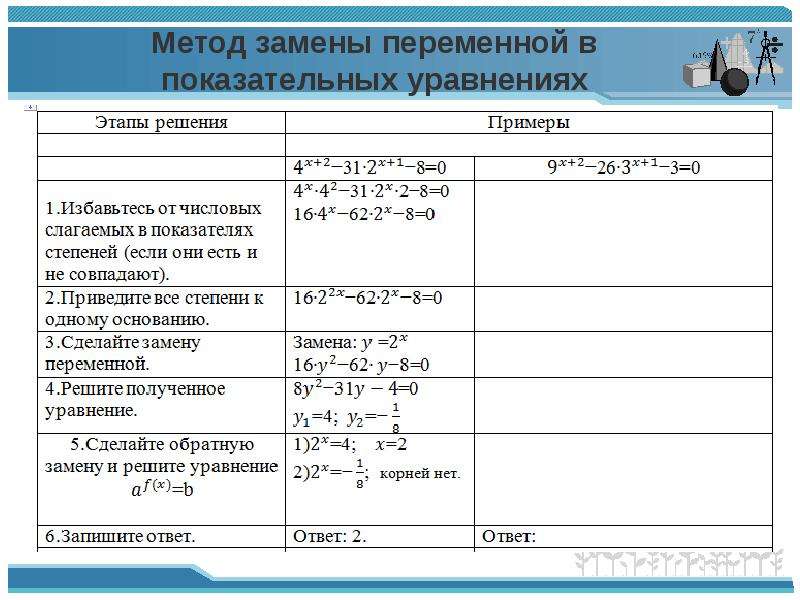
 Тогда
Тогда




