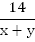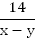Как решать задачи на движение – 3 простых шага

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

1. Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
2. Как решать задачи на движение: 3 простых шага
3. Задачи на движение вдогонку: примеры с решением
4. Задачи на движение навстречу: примеры с решением
5. Задачи на движение по течению и против течения: примеры с решением

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается  – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем  – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

3 простых шага решения задачи на движение

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

Решение:

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х² + 160х – 50х – 2000) / х (х+40) = 0

(4х² + 160х – 2000) / (х² + 40х) = 0

Умножим обе части уравнение на х² + 40х:

4х² + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х² + 40х – 500 = 0

Находим дискриминант:

D = 40² – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₁ = 10

х₂ = — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

Решение:

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Составим таблицу.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило).  Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 =  (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х² + 4х = 0

— 2х² — 4х + 160 = 0

Делим обе части уравнения на -2:

х² + 2х – 80 = 0

Находим дискриминант:

D = 2² – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

х₁ = 8

х₂ = — 10

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Ответ: 8 км/ч.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

Решение:

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

350/х = 120/60 + 3

350/х = 5

Решаем полученное уравнение:

5х = 350

х = 70

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Ответ: 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

Решение:

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через  4 часа после начала движения  и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) +  (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) +  (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х² + 6х) / (х (х — 6))  = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х² + 14х — 24 = 0

Умножим обе части уравнение на -1:

х² — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14² – 4 * 1 * 24 = 100

Находим корни уравнения:

х₁ = 12

х₂ = 2

х₂ < 6, следовательно, корнем уравнения не является.

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.

Ответ: 12 часов.

Задачи на движение по течению и против течения: примеры с решением

В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.

При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.

Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.

Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.

Давайте рассмотрим примеры решения задач на движение по реке.

Задача 1

Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.

Решение:

1. Обозначим собственную скорость катера – х.

Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.

По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:

160 / (х + 5) + 8 = 160 / (х — 5)

Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:

(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0

(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5)  = 0

Умножаем обе части уравнения на (х – 5) (х + 5):

-1600 + 8х² + 40х – 40х – 200 = 0

8х² – 1800 = 0

8х² = 1800

х² = 225

х_1,2 = ±15

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Ответ: 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

Решение:

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х² = 0

8х² = 32

х² = 4

х_1,2 = ±2

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Ответ: 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2019 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также в нашей группе Вконтакте.

 

yourrepetitor.ru

Системы уравнений в задачах на движение. Видеоурок. Алгебра 9 Класс

В этом уроке мы рассмотрим задачи на движение, переведем реальные ситуации на математический язык, составим математические модели – нелинейные системы уравнений – и решим их, тем самым решив исходную задачу.

Задача 1.

Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения – за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.

Решение:

Вспомним уравнение прямолинейного равномерного движения: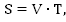

S – расстояние,

V – скорость,

T – время.

Переведем 2 часа 48 минут в часы, это составит

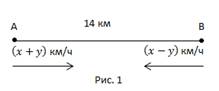
Пусть x км/ч – скорость лодки в стоячей воде, y км/ч – скорость течения реки. Составим математическую модель.

Если лодка движется по течению, то она имеет скорость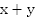

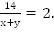км/ч  и пройдет 14 км за время  Если лодка движется против течения, она идет со скоростью  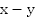км/ч и пройдет 14 км за время .

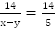Мы получили математическую модель. То же самое можно получить с помощью таблицы.

	S	V	T
По течению	14
Против течения	14

Решим полученную систему.

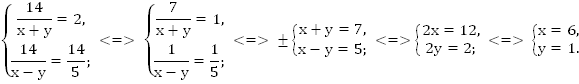
Ответ: 6 км/ч; 1 км/ч.

Перед тем как приступить к более сложным задачам, решим две опорные задачи на движение.

1. Первая опорная задача (сближение).

Из пунктов А и В одновременно выехали навстречу друг другу два поезда.

Дано: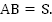

x, y – скорости поездов, км/ч.

Найти: Время t до их встречи, и расстояния 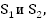 пройденные до момента их встречи каждым из поездов.

Решение:

Найдем скорость сближения: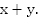

Найдем время t до встречи:

Найдем искомые расстояния: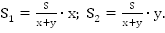

Ответ: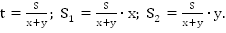

2. Вторая опорная задача.

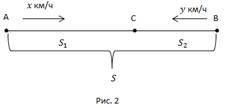
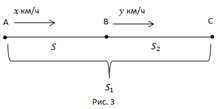
Первый турист вышел из пункта А. Одновременно второй турист вышел из пункта В. Оба двигаются в направлении луча АВ. Первый догнал второго в пункте С.

Дано: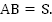

x, y – скорости первого и второго туристов, км/ч.

Найти: Время t до встречи туристов, расстояния

 пройденные первым и вторым туристами до встречи.

Решение:

Найдем скорость сближения: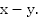

Найдем время t до встречи: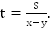

Найдем искомые расстояния:

Ответ: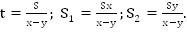

Задача 2.

Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда, и встречаются через 5 часов. Если второй поезд отправится на 7 часов раньше первого, то они встретятся через два часа после отправления первого поезда. Найти скорость каждого поезда.

Решение:

Пусть x км/ч, y км/ч – скорости первого и второго поездов.

S – расстояние между городами.

Рассмотрим вначале первый случай. Легко увидеть, что это задача на сближение, т.е. мы сможем пользоваться данными, полученными в первой опорной задаче.

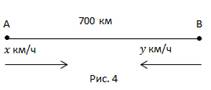
700 км оба поезда пройдут за 5 часов со скоростью сближения

 

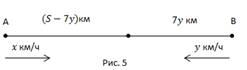
Второй случай: те же условия, но первый поезд начал движение через 7 часов после второго. За 7 часов второй поезд прошел 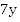км, осталось  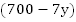км, и только тогда начинает движение первый поезд. Начинается сближение. Поездам нужно пройти  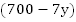км с  общей скоростью  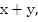и они встретятся через 2 часа, т.е.

Мы получили математическую модель.

Упростим полученные уравнения.

 

 

 

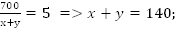
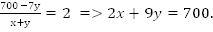
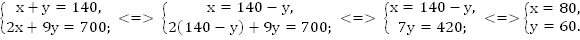
Ответ: 80 км/ч, 60 км/ч.

Задача 3.

Пристани В и С находятся ниже пристани А по течению реки соответственно на 30 км и 45 км. Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 часа 40 минут. В другой раз эта же лодка отошла от пристани, дошла до А, сразу повернула назад и пришла в В, затратив на весь путь 7 часов. Чему равна собственная скорость лодки и скорость течения реки?

Решение:

Пусть x км/ч – собственная скорость лодки, y км/ч – скорость течения реки.

Время движения переведем в часы, 4 часа 40 минут =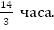

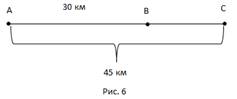
Опишем первый рейс: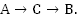

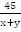Из А в С лодка шла 45 км по течению со скоростью  км/ч, время в пути составило  ч.

Из С в В лодка шла 15 км против течения, т.е.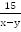

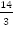 ч. Суммарное время в пути составило  ч, т.е.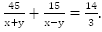  

Опишем второй рейс: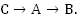

Из С в А лодка шла 45 км против течения, т.е. была в пути 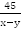 ч. Из А в В шла 30 км по течению, т.е. была в пути  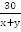ч. Общее время в пути составило 7 ч, т.е.

 

Решаем полученную систему:

 

Произведем замену переменных: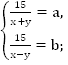

 

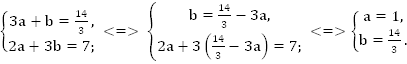
Переходим к старым переменным:

 

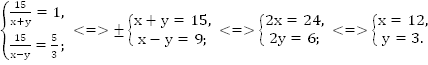
Ответ: 12 км/ч, 3 км/ч.

Мы рассмотрели текстовые задачи на движение, составили для них математические модели и решили полученные системы. На следующем уроке будут рассматриваться задачи на работу.

 

Список литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 159, 160, 178 – 180.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

interneturok.ru

Задачи на движение по реке | Мел

Задачи на движение по реке трудны для пятиклассников, а взрослые недоумевают: чего же там трудного? Бревно или плот плывут со скоростью течения реки Vт., которая считается постоянной.

Скорость катера в стоячей воде Vс. называют собственной скоростью катера. Скорость катера по течению реки Vпо теч. больше собственной скорости катера на скорость течения реки: Vпо теч. = Vс. + Vт.

Скорость катера против течения реки Vпр теч. меньше собственной скорости катера на скорость течения реки: Vпо теч. = Vс. + Vт.

Эти соотношения полезно проиллюстрировать рисунком.

Скорость катера по течению больше его скорости против течения на две скорости течения.

Задача 1. Скорость катера в стоячей воде равна 15 км/ч, а скорость течения реки — 3 км/ч. Какова скорость катера по течению и против течения реки?

Решение.

1) 15 + 3 = 18 (км/ч) — скорость катера по течению реки,

2) 15 — 3 = 12 (км/ч) — скорость катера против течения реки.

Ответ. 18 км/ч и 12 км/ч.

Обратим внимание: скорость катера по течению реки — это сумма его собственной скорости и скорости течения реки, а скорость катера против течения реки— это разность его собственной скорости и скорости течения реки, поэтому скорость по течению реки больше скорости против течения на удвоенную скорость течения.

Задача 2. Скорость моторной лодки по течению реки равна 48 км/ч, а против течения — 42 км/ч. Какова скорость течения реки и собственная скорость моторной лодки?

Решение.

1) 48 — 42 = 6 (км/ч) — удвоенная скорость течения реки,

2) 6: 2 = 3 (км/ч) — скорость течения реки,

3) 48 — 3 = 45 (км/ч) — собственная скорость.

Ответ. 3 км/ч и 45 км/ч.

Задачи для закрепления берём в учебнике «Математика» для 5 класса (Просвещение, С. М. Никольский и др.) или в книге для учителя «Обучение решению текстовых задач в 5-6 классах» (раздел Книги на сайте www.shevkin.ru). Приведём три задачи из учебника.

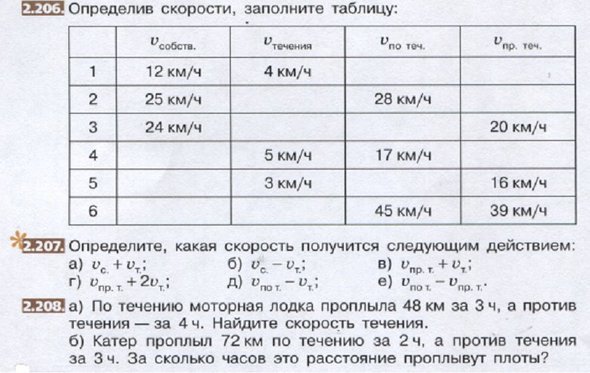
В качестве примера применения формируемого умения приведём задачу из сборника для подготовки к ГИА-9.

Задача 3. Теплоход проходит по течению реки до пункта назначения 160 км и после стоянки возвращается в пункт отправления. Найдите скорость течения реки, если скорость теплохода в неподвижной воде равна 18 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается ровно через 20 часов после отплытия из него.

Составлять и решать уравнение с неизвестным в знаменателе научат в 8 классе, если новый стандарт не отменит изучение таких уравнений, а находить скорость теплохода по течению и против течения реки надо научиться в 5 классе.

mel.fm

Движение вдогонку (формула). Решение задач на движение вдогонку

Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.

Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.

Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, — все это примеры движения.

Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.

Движение вдогонку и его особенности

Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.

Согласно определению, особенностями движения вдогонку являются следующие:

• Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей «некого» будет догонять.
• Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
• Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.

Формулы движения вдогонку

В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:

• Скорость — величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
• Путь — это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
• Время — период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.

Описав основные величины, приведем формулы движения вдогонку:

• s = v*t;
• v = s/t;
• t = s/v.

Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.

Пример решения задачи №1

Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: «Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?».

Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.

Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s₁ = v₁*t и s₂ = v₂*t, здесь s₁, v₁ = 60 км/ч и s₂, v₂ = 80 км/ч — пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s₂ — s₁ = 40. Подставляя в последнее выражение формулы для путей s₁ и s₂, получим: v₂*t — v₁*t = 40 или 80*t — 60*t = 40, откуда t = 40/20 = 2 ч.

Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.

Пример решения задачи №2

Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): «Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?».

Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s₁ = v₁*(t+3) и s₂ = v₂*t, здесь s₁, v₁ и s₂, v₂ — пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.

Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s₂ = s₁ или v₁*(t+3) = v₂*t. Скорости v₁ и v₂ нам не известны, однако в условии задачи сказано, что v₂ = 4*v₁. Подставляя это выражение в формулу для равенства путей, получим: v₁*(t+3) = 4*v₁*t или t+3 = 4*t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.

Некоторые советы

Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.

fb.ru

Задачи на движение по реке: примеры и решение

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?

Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:

30 — 2 = 28 (км/ч) – скорость движения катера против течения.

Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:

112 : 28 = 4 (ч)

Решение задачи по действиям можно записать так:

1) 30 — 2 = 28 (км/ч) – скорость движения катера против течения

2) 112 : 28 = 4 (ч)

Ответ: За 4 часа катер преодолеет расстояние 112 км.

Задача 2. Расстояние от пункта A до пункта B по реке равно 120км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?

Рассмотрите два варианта: 1) лодка движется по течению реки; 2) лодка движется против течения реки.

Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:

27 + 3 = 30 (км/ч)

Значит расстояние между пунктами лодка преодолеет за:

120 : 30 = 4 (ч)

Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:

27 — 3 = 24 (км/ч)

Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:

120 : 24 = 5 (ч)

Решение задачи по действиям для движения по течению реки можно записать так:

1) 27 + 3 = 30 (км/ч) – скорость лодки

2) 120 : 30 = 4 (ч)

Для движения против течения реки решение задачи по действиям можно записать так:

1) 27 — 3 = 24 (км/ч) – скорость лодки

2) 120 : 24 = 5 (ч)

Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.

naobumium.info

Как решать задачи на движение?

Задачи на движение не любят многие, так как зачастую недопонимают, как их решать. Но, как известно, нет ничего невозможного, и поэтому можно научиться тому, как решать задачи на движение, было бы желание.

Как решать задачи на движение: теория

Все задачи, связанные с движением решаются по одной формуле, которую вы должны знать наизусть. Вот она: S=Vt. S – это расстояние, V- скорость движения, и t – это время.

Эта формула — ключ к решению всех этих задач, а все остальное написано в тексте задачи, главное, задачу внимательно прочесть и понять.

Второй важный момент, это приведение всех данных в задаче величин к единым единицам измерения. То есть, если время дается в часах, то расстояние должно измеряться в километрах, если в секундах, то расстояние в метрах соответственно.

Решение задач

Итак, рассмотрим три основных примера на решение задач на движение.

Два объекта выехали друг за другом.

Предположим, что вам дана такая задача: из города выехал первый автомобиль со скоростью 60 км/ч, через полчаса выехал второй автомобиль со скоростью 90 км/ч. Через сколько километров, второй автомобиль догонит первый?Для решения такой задачи у нас имеется формула: t = S /(v1 — v2).Так как время нам известно, а расстояние нет, то мы ее трансформируем S= t(v1 — v2).Подставляем цифры: S=0,5(90-60), S=15 км.То есть оба автомобиля встретятся через 15 км.

Два объекта выехали в противоположенном направлении

Если вам дана задача, в которой два объекта выехали навстречу друг другу, и нужно узнать, когда они встретятся, то нужно применять следующую формулу:t = S /(v1 + v2).Например, из пункта А и Б, между которыми 43 км, ехал автомобиль со скоростью 80 км/ч, а из пункта Б в А ехал автобус со скоростью 60 км/ч. Через сколько времени они встретятся?Решение: 43/(80+60)=0,30 часа.

Два объекта выехали одновременно в одном направлении

Дана задача: из пункта А в пункт Б вышел пешеход, двигающийся со скоростью 5 км/ч , а также выехал велосипедист со скоростью 15 км/ч. Во сколько раз велосипедист быстрее доберется из пункта А в пункт Б, если известно, что расстояние между этими пунктами 10 км.Сначала нужно найти время, за которое пешеход пройдет это расстояние. Переделываем формулу S=Vt, получаем t =S/V. Подставляем числа 10/5=2. то есть пешеход потратит на дорогу 2 часа.

Теперь высчитываем время для велосипедиста. t =S/V или 10/15=0,7 часа.Третье действие совсем уж простое, мы должны найти разность времени пешехода и человека на велосипеде. 2/0,7=2,8. Ответ таков: велосипедист доберется до пункта Б быстрее пешехода в 2,8 раза.

Таким образом, применяя эти нехитрые формулы, вы всегда будет знать, как решаются задачи на движение. Нужно только очень внимательно прочитать задачу, принять во внимание все данные, привести их в одну систему измерения, а потом уж подобрать для решения нужную формулу.

Но будьте бдительны, не обязательно, что у вашей задачи будет одно только действие, иногда, прежде чем применить наши формулы, вам придется выполнить еще ряд промежуточных действий, чтобы найти необходимые данные. Не забывайте о них, и тогда у вас непременно все получится.

elhow.ru

Учимся на отлично! — Виды задач на движение

ВИДЫ ЗАДАЧ НА ДВИЖЕНИЕ

В задачах на движение  рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное за единицу времени.

• Расстояние – это произведение скорости на время движения;

S = V • t

• Скорость – это расстояние, которое тело проходит за единицу времени;
• Скорость  — это частное от деления расстояния на время движения;

V = S : t

• Время – это частное от деления расстояния на скорость движения

t = S : V

 

Какие могут быть ситуации?

 

Встречное  движение     

Два объекта движение начинают одновременно навстречу друг другу.

 

 Движение в противоположных направлениях из одного пункта 

Два объекта движение начинают одновременно в противоположных направлениях.

 

Движение в одном направлении

Два объекта движение начинают одновременно в одном направлении.

При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».

 

ЗАДАЧА 1

В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого  -68 км /ч., и они выезжают навстречу друг другу одновременно?

Первый способ решения
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2) 140 • 2 = 280 (км) – на такое расстояние таксисты    приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.

Второй способ решения

1) 72 • 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.

2)  68 • 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.

3) 144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.

4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.

Ответ: 145 км.

ЗАДАЧА 2

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему  из В в А  вышел

пассажирский поезд  со  скоростью 60 км /ч. Через  сколько  часов после   выхода  пассажирского  поезда  эти  поезда встретятся?

Решение

1) 80 • 2=160(км) -прошёл скорый поезд за 2 часа.

2) 720-160=560(км) -осталось пройти поездам.

3) 80+60=140(км/ч) -скорость сближения 2 поездов.

4) 560:140=4(ч) -был в пути пассажирский поезд.

Ответ: 4часа.

ЗАДАЧА 3

Из двух пунктов навстречу друг другу одновременно выехали два автобуса.  Скорость  одного  автобуса  45 км /ч,  а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.

Решение

Первый способ решения
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2) 72 • 3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.

Второй способ решения

1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.

2) 45 +72 = 117 (км/ ч.). – скорость сближения автобусов .

3) 117 • 3 = 351 (км) – расстояние между пунктами.

Ответ: 351 км.

Что такое скорость сближения?

ЗАДАЧА 4

Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч.  Какое расстояние будет между машинами через 5 часов?

Решение

Первый способ решения

1) 50 • 5 = 250 (км) – проедет машина до встречи.

2) 70 • 5 = 350 (км) – проедет автобус до встречи.

3) 250 + 350 = 600 (км) — на такое расстояние они приблизятся друг к другу.

4) 740 — 600 = 140 (км)  — такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

Второй способ решения

1) 50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.

2) 120 • 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.

3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

ЗАДАЧА 5

Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч.  Через какое время они встретятся?

Решение

1) 100+120=220(км/ч)- скорость сближения машин .

2) 660:220=3(ч) -через такое время встретятся гоночные машины.

Ответ: через 3 часа.

ЗАДАЧА 6

Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч.,  а  другого  – 54 км ч. Какое расстояние будет между тиграми через 3 часа?

Решение

Первый способ решения

1) 48 • 2 = 96 (км) – пробежит один тигр за 2 часа.

2) 54 • 2 = 108 (км) – пробежит другой тигр за 2 часа.

3) 96 + 108 = 204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

Второй способ решения

1) 48 + 54 =102 (км /ч.) – скорость удаления тигров.

2) 102 • 2 =204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

ЗАДАЧА 7

Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут  Рома догонит Максима и Сашу?

Решение

1) 80 — 50 = 30 (км /ч.) –скорость сближения мальчиков.

2) 50 • 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.

3) 300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.

Ответ: через 10 мин.

 

ИТОГИ

1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».

2) При решении задач на встречное движение  и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.

3) При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.

По материалам сайта http://iumka.ru

teplyakova.ucoz.com