Логарифмические уравнения на примерах

Логарифмическими называются уравнения содержащие неизвестную величину под знаком логарифма или в основании логарифма (или в обоих местах одновременно). Их легко свести к квадратным или степенным уравнениям относительно переменной если знать свойства логарифма. Например, логарифмическими будут следующие уравнения

Необходимо отметить что во время решения логарифмических уравнений необходимо учитывать область допустимых значений ( ОДЗ ) : под знаком логарифма могут находиться только положительные величины, в основе логарифмов — положительные, отличные от единицы. Однако нахождения ОДЗ порой может быть очень громоздким и на практике имеем возможность или искать ОДЗ, или сделать проверку подстановкой корней уравнения.

Простейшим логарифмическим уравнением называют уравнение вида

Его решение вычисляется потенцированием (нахождение числа или выражения по его логарифму)

В некоторых случаях, решая логарифмические уравнения, целесообразно производить замену переменной. Например в уравнении

удобно сделать замену и мы приходим к квадратному уравнению. Причем оба корни этого квадратного уравнения можно подставить в замену чтобы найти подходящее х.

Стоит запомнить что десятичный логарифм от единицы со следующими нулями равно количеству нулей в записи этого числа.

Для десятичного логарифма от единицы с предыдущими нулями правило подобное. Он равен количеству всех нулей в записи этого числа, включая и ноль целых, взятых со знаком минус. Для примера

На этом необходимый теоретический материал рассмотрен и можно переходить к рассмотрению практических примеров. Внимательно рассмотрите их решения это позволит усвоить некоторые правила логарифмов и увеличит практическую базу, которая пригодится при прохождении ВНО , контрольных, тестах и т.д.

Пример 1. Решить уравнение.

Решение. Используя свойство логарифмов переписываем уравнение в виде

Делаем замену

и переписываем

Умножаем на переменную и записываем в виде квадратного уравнения

Вычисляем дискриминант

Корни уравнения приобретут значения

Возвращаемся к замене и находим


Уравнение имеет два решения

 

Пример 2. Решить уравнение.

Решение. Раскрываем скобки и записываем в виде суммы логарифмов

Учитывая что уравнение примет вид

Переносим слагаемое за знаком равенства в правую сторону


Оба множители приравниваем к нулю и находим

 

Пример 3. Решить уравнение.

Решение. Перепишем правую сторону в виде квадрата и прологарифмируем по основанию 10 обе части уравнения

делаем замену

и сводим уравнение к квадратному

Дискриминант такого уравнения принимает нулевое значение — уравнение имеет два одинаковых решения

Возвращаемся к замене которую делали выше

 

Пример 4. Решить уравнение.

Решение. Выполним некоторые преобразования с слагаемыми уравнения



Логарифмическое уравнение упростится до следующего

Поскольку логарифмы имеют одинаковые основания то значение под знаком логарифма тоже равны. На основе этого имеем

Расписываем и решаем с помощью дискриминанта



Второй корень не может быть решением, поскольку никакое положительное число при возведены в степени не даст в результате -1. Итак x=2 – единственное решение уравнения.

 

Пример 5. Найти решение уравнения .

Решение. Выполняем упрощения уравнения




По свойству переходим ко второй основы во втором логарифме



По правилу логарифмирования имеем

Сводим уравнение к квадратному и решаем его


Дискриминант равен нулю, следовательно имеем один корень кратности два

 

Пример 6. Найти решение уравнения.

Решение. Заданное уравнение и подобные ему решаются путем сведения к общей основе. Для этого преобразуем правую сторону уравнения к виду

и подставим в уравнение

Поскольку основы логарифмов ровны переходим до показательного уравнения

Выполняем замену и сводим к квадратному уравнению



Возвращаемся к замене и вычисляем

 

Пример 7. Найти решение уравнения.

Решение. Не пугайтесь подобных задач, если делать все по правилам то решение получается без труда. Забегая вперед скажу что корни в скобках к примеру отношения не имеют. Они для того чтобы напугать простых математиков.
Упростим сначала второй логарифм

Дальше выполняем подстановку и сведения слагаемых под один логарифм

Приравниваем к правой части уравнения и упрощаем




Как видите — решение оказалось проще чем выглядело до решения, а результат x=100 только подтверждает это.

При решении логарифмических уравнений важно хорошо знать свойства логарифмов. Все остальные действия сводятся, как правило, к решению квадратных уравнений или степенных зависимостей относительно неизвестных. Поэтому практикуйте самостоятельно и не имейте проблем с логарифмическими уравнениями.

Решение логарифмических уравнений

Логарифмические уравнения

Решение простейших логарифмических уравнений

Как известно, решение простейшего логарифмического уравнения log_ax=b — это x=a^b. Другими словами, простейшее логарифмическое уравнение log_ax=b имеет единственный корень, которым является степень a^b.

Приведем пример.

Первый пример. Проще некуда.

Решите уравнение log₅x=2

Решение

Все понятно без слов:
log₅x=2
x=5²
x=25

Ответ:

При решении простейших логарифмических уравнений переход от log_a

x=b к x=a^b, обычно, не представляет сложности. Часто, куда сложнее вычислить значение степени a^b или упростить ее вид. Следующие примеры иллюстрируют сказанное.

Второй пример. А вычислить значение?

Решите логарифмическое уравнение

Решение

Это простейшее логарифмическое уравнение. Оно имеет единственный корень . Очевидно, полученная степень нуждается в доработке.

Сначала заменим квадратный корень из семи степенью: .

Теперь используем свойства степеней:

Остается вспомнить, как определяется степень с отрицательным показателем, и закончить вычисления:

На этом решение простейшего логарифмического уравнения завершено.

Ответ:

Третий пример. Извольте упростить.

Решите уравнение

Решение

Начинаем со стандартного при решении простейших логарифмических уравнений перехода:

Надо бы упростить полученную степень.

Возвести дробь в минус первую степень – это кувыркнуть ее вверх ногами:

Теперь глаза мозолит иррациональность в знаменателе, исправим эту ситуацию:

Таким образом, — искомое решение простейшего логарифмического уравнения.

Ответ:

К началу страницы

Решение логарифмических уравнений разными методами

Сейчас пройдемся по всем основным методам решения логарифмических уравнений, и рассмотрим решения наиболее характерных и интересных, по нашему мнению, логарифмических уравнений.

Приступаем.

по определению логарифма

По определению логарифма в первую очередь проводится решение логарифмических уравнений log_af(x)=b, где a и b — числа, причем a>0, a≠1, а f(x) – выражение с переменной x, таких как log₂(x²+4·x+3)=3, и др. Решение состоит в переходе от уравнения log_af(x)=b к уравнению f(x)=a^b. Например, решение логарифмического уравнения log₂(x²+4·x+3)=3 с опорой на определение логарифма заменяется решением уравнения x²+4·x+3=2³.

На определение логарифма можно опираться и при решении логарифмических уравнений log_h(x)f(x)=g(x), таких как log_x(x²−3·x+6)=2, log₂(9−2^x)=3−x, log_x(3·x^lgx+4)=2·lgx и др. Решение уравнения log

h(x)f(x)=g(x) заключается в решении уравнения f(x)=(h(x))^g(x) на области допустимых значений (ОДЗ) для исходного уравнения. Например, чтобы решать логарифмическое уравнение log_x(x²−3·x+6)=2 по определению логарифма, надо решить уравнение x²−3·x+6=x², и взять все корни, принадлежащие ОДЗ для исходного уравнения.

Итак,

• Чтобы решить логарифмическое уравнение log_af(x)=b по определению логарифма, надо перейти к уравнению f(x)=a^b и найти его решение.
• А чтобы решить по определению логарифма уравнение log_h(x)f(x)=g(x), надо перейти к уравнению f(x)=(h(x))^g(x), решить его, и взять корни, принадлежащие ОДЗ для исходного логарифмического уравнения.

Обоснования приведены в статье «Метод решения уравнений по определению логарифма».

Рассмотрим примеры решения логарифмических уравнений.

Пример

Решите уравнение

Решение

Обычно решение оформляется кратко:

А теперь поясним, какие рассуждения за всем этим скрываются.

Заданное логарифмическое уравнение имеет вид log_af(x)=b, где f(x)=2·x−4, a=1/2, b=−2. Такое логарифмическое уравнение можно решать по определению логарифма, то есть, заменять решение уравнения log_af(x)=b решением уравнения f(x)=a^b.

Итак, переходим от исходного уравнения к уравнению . Это рациональное уравнение, решаем его:

Так получено решение исходного логарифмического уравнения.

Ответ:

Пример. Не забыть про проверку.

Решите логарифмическое уравнение log_x(−x²+5·x+3)=2

Решение

Заданное уравнение можно рассматривать как уравнение log_h(x)f(x)=g(x), где f(x)=−x²+5·x+3, h(x)=x, g(x)=2, и мы знаем, что такие уравнения можно решать по определению логарифма. Решение этим методом на первом этапе предполагает переход от уравнения log_h(x)f(x)=g(x) к уравнению f(x)=(h(x))^g(x). Имеем −x²+5·x+3=x².

Теперь нам надо решить полученное уравнение −x²+5·x+3=x². Оно сводится к квадратному уравнению 2·x²−5·x−3=0. Решаем его:

Остается пройти последний шаг решения логарифмического уравнения по определению логарифма – выяснить, какие из корней принадлежат ОДЗ для исходного уравнения. ОДЗ для исходного логарифмического уравнения log

x(−x²+5·x+3)=2 определяется системой .

Очевидно, не удовлетворяет второму условию, значит, это посторонний корень для исходного уравнения. А корень x₂=3 удовлетворяет всем условиям: . Значит, x₂=3 – это корень уравнения log_x(−x²+5·x+3)=2.

На этом решение завершено. Уравнение имеет единственный корень 3.

Естественно, так подробно решение не описывают. Обычно его оформляют кратко, но без ущерба для логики действий, например, так:

Ответ:

К началу страницы

методом потенцирования

Метод потенцирования применяется для решения логарифмических уравнений, части которых являются логарифмами с одинаковыми основаниями, например, log

5(x−1)=log₅7, и др. Решение логарифмических уравнений методом потенцирования состоит в переходе от уравнения log_h(x)f(x)=log_h(x)g(x) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения. Так решение уравнения можно заменить решением уравнения x+1=x²−1 на ОДЗ для исходного уравнения.

Название метода становится понятным, если вспомнить, что потенцирование – это восстановление выражения по его логарифму.

Обосновать метод можно, сославшись на свойства логарифмов. Из них мы знаем, что логарифмы двух положительных чисел с одинаковыми положительными и отличными от единицы основаниями равны тогда и только тогда, когда равны сами числа, то есть, , a>0, a≠1, b₁>0, b₂>0. Так вот переход от логарифмического уравнения log_h(x)f(x)=log_h(x)g(x) к уравнению f(x)=g(x) — это аналог замены log

ab₁=log_ab₂ на b₁=b₂, а нахождение в рамках ОДЗ для исходного уравнения – это аналог выполнения условий a>0, a≠1, b₁>0, b₂>0.

Итак, чтобы решить логарифмическое уравнение log_h(x)f(x)=log_h(x)g(x) методом потенцирования, надо

• Перейти к уравнению f(x)=g(x).
• Решить полученное уравнение.
• И взять корни, принадлежащие ОДЗ для исходного уравнения, остальные отбросить как посторонние. Другими словами, провести отсеивание посторонних корней.

Остается рассмотреть пример с решением.

Пример. Потенцируем.

Решите уравнение .

Решение

Мы видим, что части уравнения являются логарифмами с одинаковыми основаниями. Подобные логарифмические уравнения удобно решать методом потенцирования.

Согласно выбранному методу, переходим от исходного уравнения к уравнению x+1=x²−1.

Теперь нам надо решить полученное уравнение x+1=x²−1. Перенос слагаемых из одной части уравнения в другую с противоположным знаком и приведение подобных слагаемых дает квадратное уравнение x²−x−2=0, которое можно решить, например, через дискриминант:

Остается проверить принадлежность найденных корней области допустимых значений переменной x для исходного уравнения. Для нашего логарифмического уравнения ОДЗ определяют два условия x+1>0 и x²−1>0. Очевидно, x₁=−1 не удовлетворяет первому условию (−1+1>0 — неверное), значит, это посторонний корень для решаемого уравнения. А корень x

2=2 удовлетворяет обоим условиям (2+1>0 – верное, 2²−1>0 — верное). Значит, он является корнем уравнения .

На этом решение логарифмического уравнения методом потенцирования завершено. Уравнение имеет единственный корень, им является число 2.

Ответ:

К началу страницы

методом разложения на множители

Пример. Все как всегда.

Решите уравнение

Решение

Решение логарифмического уравнения можно провести методом разложения на множители, так как в левой части уравнения находится произведение двух выражений с переменной, а в правой – нуль.

Первый шаг – переход к совокупности уравнений:

Второй шаг – решение полученных логарифмических уравнений.

Первое уравнение можно решить по определению логарифма, а второе — методом потенцирования, после предварительного переноса второго логарифма в правую часть со знаком «плюс»:

На последнем шаге остается выяснить, принадлежат ли найденные корни 2 и 5 ОДЗ для решаемого логарифмического уравнения :

На этом решение логарифмического уравнения методом разложения на множители завершено.

Ответ:

К началу страницы

путем введения новой переменной (замены переменной)

Решение логарифмических уравнений методом введения новой переменной, как правило, проводится в следующих типичных ситуациях:

• Когда переменная находится в составе некоторой сложной функции, как, например, в уравнении
• Когда переменная фигурирует в нескольких одинаковых выражениях и нигде более. Вот примеры логарифмических уравнений, соответствующие сказанному:
  

  
  (часто, одинаковые выражение с переменной прячут за свойствами степеней, и приведенное выше в пример логарифмическое уравнение, скорее, будет выглядеть так или так )

• Когда в логарифмическом уравнении переменная находится только под знаками логарифмов, которые получаются один из другого перестановкой местами выражения под его знаком и в основании. Вот такое логарифмическое уравнение

Пример №1. Вводить или не вводить?

Решите логарифмическое уравнение

Решение

Введение новой переменной 2−log₂x=t позволяет перейти от логарифмического уравнения к сравнительно простому уравнению t⁴=16 с понятной структурой и очевидным решением:

Возврат к старой переменной дает два логарифмических уравнения 2−log₂x=2 и 2−log₂x=−2, решив которые находим интересующее нас решение исходного уравнения:

Итак, логарифмическое уравнение имеет два корня 1 и 16.

В заключение заметим: введение новой переменной в подобных и, прямо скажем, простых ситуациях настолько прозрачно, что его проводят «в уме», и не отражают в решении:

Ответ:

Пример №2. Оказывается, оно квадратное.

Решить уравнение

Решение

Выражения 2^{2·(log₅x)2} и 2^(log₅x)2, в которых содержится переменная в заданном логарифмическом уравнении, почти одинаковые. Различие вносит лишь число 2 в показателе первой степени. Здесь несложно догадаться, что по свойству степени в степени, выражение 2^{2·(log₅x)2} можно переписать как (2^(log₅x)2)², что открывает дорогу к замене переменной 2^(log₅x)2=t и переходу к квадратному уравнению t²−15·t−16=0 с новой переменной t.

Итак, проведем решение логарифмического уравнения через замену переменной:

Ответ:

Пример. Взаимно обратные логарифмы.

Решите логарифмическое уравнение

Решение

Здесь полезно вспомнить следствие из формулы перехода к новому основанию логарифма, которому отвечает формула log_ab=1/log_ba, a>0, a≠1, b>0, b≠1. Так возникает идея обозначить один из логарифмов в заданном логарифмическом уравнении за t, тогда другой логарифм будет выражаться через новую переменную t как 1/t.

Остается вернуться к старой переменной x, и закончить решение. Мы принимали log_x+3(3·x+13)=t и нашли t=2, поэтому

Итак, логарифмическое уравнение имеет единственное решение 1.

Ответ:

К началу страницы

дробь равна нулю

Пример

Решите логарифмическое уравнение

Решение

Решение логарифмических уравнений, в левых частях которых находится дроби, а в правых – нули, проводится в соответствии с методом решения уравнений «дробь равна нулю». При этом надо приравнять числитель дроби к нулю, и решить это уравнение на ОДЗ для исходного уравнения.

Итак, решение начинаем с приравнивания к нулю числителя дроби из левой части заданного уравнения. Это дает уравнение log₃(x−3)²−4=0, которое равносильно уравнению log₃(x−3)²=4. Решение полученного логарифмического уравнения можно провести по определению логарифма:

Остается проверить, принадлежат ли найденные корни области допустимых значений переменной x для исходного логарифмического уравнения. В нашем случае условий, которые определяют ОДЗ, довольно много, поэтому, кажется, рациональнее действовать через непосредственную подстановку. Подставим найденные корни в исходное уравнение и посмотрим, что при этом получается.

Подстановка x₁=12 дает верное числовое равенство

Поэтому, 12 является корнем.

При подстановке x₂=−6 получается не имеющее смысла выражение , так как под знаками логарифмов в знаменателе – отрицательные числа. Значит, −6 – посторонний корень.

Ответ:

К началу страницы

методом логарифмирования

Решение логарифмических уравнений в определенных случаях приходится проводить через логарифмирование обеих частей уравнения. Обычно, к логарифмированию прибегают тогда, когда в одной части уравнения находится показательно степенное выражение, а в другой – положительное число, как в следующих уравнениях , и т.п.

Давайте решим одно из них, чтобы стало понятно, что дает логарифмирование уравнения.

Пример. Дожили, лог уравнения логарифмируем

Решите уравнение

Решение

Данное уравнение – это типичный представитель уравнений, для решения которых используется метод логарифмирования. В левой части уравнения – степень, на ОДЗ для уравнения эта степень принимает только положительные значения. Это открывает возможность прологарифмировать обе части заданного уравнения. В нашем случае логарифмирование целесообразно проводить по основанию 2, так как в исходном уравнении присутствует логарифм с таким основанием. Так и поступим:

Для нашего уравнения ОДЗ определяется условием x>0. Поэтому, мы спокойно можем вынести степень из-под знака логарифма, оперевшись на соответствующее свойство логарифмов (подробнее про решение логарифмических уравнений через преобразования поговорим в одном из следующих пунктов):

И это, собственно, то, ради чего логарифмирование затевалось – привести логарифмическое уравнение к более простому и привычному виду. Дальнейшие преобразования не требуют комментирования:

Полученное логарифмическое уравнение, очевидно, можно решить методом замены переменной:

Ответ:

К началу страницы

графическим методом

К решению логарифмических уравнений графическим методом обычно прибегают тогда, когда, во-первых, функции, отвечающие частям заданного логарифмического уравнения, довольно простые в плане построения их графиков, и, во-вторых, не видно других более простых вариантов получить решение.

Пример. Графически так графически.

Сколько корней имеет уравнение

Решение

Сама формулировка задания подсказывает, что, скорее всего, решить уравнение, что называется, в лоб, и указать не только количеств корней, но и сами эти корни, не выйдет. Иначе бы вопрос стоял «решить уравнение». Действительно, путей решения этого уравнения не видно.

Однако, количество корней удобно определять по графикам функций, соответствующих частям уравнения. Более того, в данном случае построить графики этих функций довольно просто. Нам хорошо известны функции и y=log₂x и их графики. Графики интересующих нас функций и y=log₂(x−2) будут иметь схожую геометрию с точностью до преобразований растяжения и симметрии. Поэтому, нам достаточно взять несколько опорных точек, чтобы изобразить нужные кривые. Давайте получим их, учитывая, что область определения функции — это x≤15/4, а область определения функции y=log₂(x−2) — это x>2.

Имеем

и

Отмечаем эти точки на плоскости в прямоугольной системе координат, соединяем их плавными линиями, и чертеж готов:

Видно, что графики имеют одну точку пересечения на отрезке от трех до пятнадцати четвертых. Больше их быть не может, так как функция убывает на указанном отрезке от до нуля, а функция y=log₂(x−2) возрастает на этом отрезке от нуля до log₂(7/4).

Это позволяет нам утверждать, что уравнение имеет один корень.

Ответ:

К началу страницы

через подбор корня и возрастание-убывание функций

Решение логарифмических уравнений иногда приходится проводить, основываясь на возрастании и убывании функций, соответствующих частям уравнения. Это касается ситуаций, когда простые и привычные пути решения не просматриваются, но зато очевиден или легко подбирается корень логарифмического уравнения, а также легко обосновывается возрастание и убывание соответствующих функций. Приведем пример.

Пример. Подбор и единственность.

Решите уравнение

Решение

Для заданного уравнения не видно других подходов к решению, кроме как обращаться к функциям и их свойствам. Можно строить графики, но делать это для функции, отвечающей правой части уравнения, не очень приятно из-за довольно «большого» числа 11 и довольно «высокой» степени 5. Попробуем обойтись без чертежа.

Вместо этого обопремся на возрастание логарифмической функции, отвечающей левой части уравнения, и убывание функции, отвечающей правой части уравнения (она убывает, как возрастающая от убывающей). Это позволяет утверждать, что если уравнение имеет корень, то он единственный. А найти корень позволяет подбор по рекомендациям, данным в статье, посвященной методу решения уравнений через возрастание-убывание, – им является число 10.

На этом решение логарифмического уравнения завершено.

Ответ:

К началу страницы

методом оценки

Пример. Оценить и дорешать.

Решить уравнение

Решение

Своего рода оценочная классика: логарифм, синус, косинус, корень – все в одном уравнении. Итак, пробуем провести решение уравнения методом оценки. Но сначала, все же, квадратный корень из квадрата заменим модулем:

Теперь к оценкам.

Косинус принимает значения из отрезка −1 до 1, а его модуль – [0, 1]. Следовательно, . С другой стороны, как четная степень, откуда . Таким образом, значения выражения из левой части уравнения не превосходят 1, а значения выражения из правой части уравнения не меньше 1. Это позволяет нам заменить решение исходного уравнения решением следующей системы

Что делать с первым уравнением системы — сразу не понятно, зато вполне реально получить решение второго логарифмического уравнения:

Теперь путем подстановки выясним, удовлетворяют ли найденные корни логарифмического уравнения 2 и 3 первому уравнению системы, а значит, системе в целом, и исходному уравнению.

Давайте начнем с числа 3, с ним все просто:

Это верное равенство, следовательно, 3 – решение системы и корень исходного уравнения.

А вот с числом 2 придется повозиться.

Это равенство неверное (обоснуем чуть ниже), следовательно, 2 – не является решением системы, и не является корнем исходного уравнения.

Таким образом, уравнение имеет один единственный корень 3.

А вот обещанное обоснование.

Модуль косинуса равен единице, если аргумент косинуса равен . А не равно sin10 ни при каком целом k. Действительно, при k=0, очевидно, sin10≠0. При любом другом целом k равенство неверное, так как значения синуса находятся в отрезке от −1 до 1.

Ответ:

К началу страницы

через ОДЗ

Решение логарифмических уравнений часто требует нахождения ОДЗ: когда для проведения преобразований, когда для проверки. А порою ОДЗ позволяет даже получить решение.

Пример. ОДЗ от безысходности.

Решите уравнение

Решение

Беглый анализ уравнения, можно сказать, ставит в тупик относительно способа его решения. И почти единственным и, так или иначе, адекватным мероприятием выглядит нахождение ОДЗ. Что называется, в любом случае пригодится.

Находим ОДЗ:

Вот как все обернулось: ОДЗ есть пустое множество. Следовательно, уравнение не имеет корней.

Ответ:

К началу страницы

методом освобождения от внешней функции

Признаемся, почти никогда для решения логарифмических уравнений не приходилось прибегать к методу освобождения от внешней функции. Однако для полноты картины не помешает привести решение соответствующего примера.

Пример. Попробуй разгляди.

Найдите решение уравнения

Решение

Как тут действовать? Непонятно, что здесь можно предложить в альтернативу методу освобождения от внешней функции.

А так заданное логарифмическое уравнение можно рассматривать как уравнение , где функция f такая, что . Очевидно, f – возрастающая функция как сумма двух возрастающих. Это позволяет освободиться от внешней функции f в уравнении , то есть, на ОДЗ перейти к уравнению .

Здесь заметим, что область допустимых значений переменной для полученного уравнения совпадает с ОДЗ для исходного уравнения (она такова ). Значит, решение полученного уравнения является решением исходного уравнения.

Остается решить логарифмическое уравнение , что можно сделать через потенцирование:

Ответ:

К началу страницы

Решение логарифмических уравнений через преобразование

Редкий раз решение логарифмических уравнений обходится без проведения преобразований. Характерными для логарифмических уравнений являются преобразования, проводящиеся на базе свойств корней и степеней. Все они по отдельности разобраны в статье «Преобразование логарифмических уравнений». Здесь мы рассмотрим примеры решения логарифмических уравнений со сравнительно сложными последовательностями преобразований.

Для начала напомним о необходимости использования модулей при вынесении четных показателей степеней из-под знаков логарифмов, а также при переходе от логарифмов произведений (частных) к суммам (разностям) логарифмов.

Пример. Про модуль не забыть.

Решите логарифмическое уравнение

Решение

Просматривается возможность прийти к одинаковым логарифмам в левой части уравнения. Для начала вынесем показатель 2 из-под знака логарифма, и так как он есть четное число, то не забудем про модуль:

Для раскрытия модуля нам потребуется ОДЗ для исходного уравнения:

С учетом этого, имеем

Дальше все просто:

Ответ:

Теперь еще раз обратим внимание на преобразование квадратов, кубов и других степеней логарифмов. Уж очень часто приходится видеть неверные преобразования, типа , вместо , или , вместо и т.п.

Пример. Квадраты логарифмов.

Решите уравнение

Решение

Просматривается возможность упростить вид заданного логарифмического уравнения. Для начала перепишем его как , чтобы не наделать ошибок при преобразовании квадратов логарифмов. Дальше все довольно прозрачно:

Теперь пора ввести новую переменную:

Остается вернуться к старой переменной:

Ответ:

Наконец, рассмотрим пример решения довольно сложного логарифмического уравнения, где сильно переплетены степени и логарифмы.

Пример

Решите уравнение

Решение

Просматриваются черты основного логарифмического тождества. Сейчас поработаем в этом направлении. Но сначала давайте найдем область допустимых значений переменной x – она бывает нужна при проведении преобразований и при проведении проверки. Тем более, в нашем случае ОДЗ находится легко:

Теперь приступаем к преобразованию:

А дальше все легко:

При найденных значениях переменной знаменатели дробей в уравнении в нуль не обращаются, а также 0 и 2 принадлежат ОДЗ для исходного уравнения, следовательно, являются его корнями.

Ответ:

К началу страницы

Решение однородных логарифмических уравнений

В задачниках встречаются логарифмические уравнения, которые являются однородными уравнениями относительно некоторых логарифмов. Например, lg²(x+1)−lg(x+1)·lg(x−1)−2·lg²(x−1)=0 – это логарифмическое уравнение, однородное относительно логарифмов lg(x+1) и lg(x−1).

Решение однородных логарифмических уравнений завязано на преобразовании, заключающемся в делении обеих частей уравнения на «старшую» степень одного из логарифмов, что в дальнейшем позволяет ввести новую переменную. При этом необходимо отдельно проверять, не являются ли корнями уравнения те значения переменной, при которых обращается в нуль логарифм, на который планируется проводить деление. Давайте обратимся к конкретному примеру.

Возьмем наше уравнение lg²(x+1)−lg(x+1)·lg(x−1)−2·lg²(x−1)=0. Оно, как мы отметили, является однородным относительно логарифмов lg(x+1) и lg(x−1). Давайте разделим обе части этого уравнения на старшую степень второго из этих логарифмов, то есть, на lg²(x−1). Но, как известно, делить обе части уравнения мы имеем право только на выражение, не обращающееся в нуль, в противном случае можно потерять корни. Поэтому, стоит отдельно проверить, не являются ли корнями уравнения значения переменной, при которых lg²(x−1)=0, а уже после этого спокойно проводить задуманное деление, не опасаясь потерять корни. В нашем случае lg²(x−1)=0 только при x=2. Но x=2 не является решением исходного уравнения, так как его подстановка в исходное уравнение дает неверное числовое равенство. Теперь можно переходить к делению, считая lg²(x−1)≠0. Имеем:

Дальше напрашиваются следующие преобразования

Остается закончить решение, воспользовавшись методом введения новой переменной. Приняв , имеем

Откуда

Ответ: , 3.

К началу страницы

Методика решения логарифмических уравнений

Введение

Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем как поддержать у студентов интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль студентов, стимулировали бы их к самостоятельному приобретению знаний.

Возникновение интереса к математике у значительного числа студентов зависит в большей степени от методики ее преподавания, от того, на сколько умело будет построена учебная работа. Вовремя обращая внимание студентов на то, что математика изучает общие свойства объектов и явлений окружающего мира, имеет дело не с предметами, а с отвлеченными абстрактными понятиями, можно добиться понимания того, что математика не нарушает связи с действительностью, а, напротив, дает возможность изучить ее глубже, сделать обобщенные теоретические выводы, которые широко применяются в практике.

Участвуя в фестивале педагогических идей «Открытый урок» 2004-2005 учебного года, я представила урок-лекцию по теме «Логарифмическая функция» (диплом № 204044). Считаю этот метод наиболее удачным в данном конкретном случае. В результате изучения у студентов имеется подробный конспект и краткая схема по теме, что облегчит им подготовку к следующим урокам. В частности, по теме «Решение логарифмических уравнений», которая полностью опирается на изучение логарифмической функции и ее свойств.

При формировании основополагающих математических понятий важно создать у студентов представление о целесообразности введения каждого из них и возможности их применения. Для этого необходимо, чтобы при формулировке определения некоторого понятия, работе над его логической структурой, рассматривались вопросы об истории возникновения данного понятия. Такой подход поможет студентам осознать, что новое понятие служит обобщением фактов реальной действительности.

История возникновения логарифмов подробно представлена в работе прошлого года.

Учитывая важность преемственности при обучении математике в среднем специальном учебном заведении и в вузе и необходимость соблюдения единых требований к студентам считаю целесообразным следующую методику ознакомления студентов с решением логарифмических уравнений.

Уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма), называются логарифмическими. Рассмотрим логарифмические уравнения вида:

(1)

Решение этих уравнений основано на следующей теореме.

Теорема 1. Уравнение равносильно системе

(2)

Для решения уравнения (1) достаточно решить уравнение

(3)

и его решения подставить в систему неравенств

(4),

задающую область определения уравнения (1).

Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1).

При решения логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения, обязательна.

Пример 1: Решить уравнение

Решение:

Оба значения х удовлетворяют условиям системы.

Ответ:

Рассмотрим уравнения вида:

(5)

Их решение основано на следующей теореме

Теорема 2: Уравнение (5) равносильно системе

(6)

Корнями уравнения (5) будут только те корни уравнения , которые

принадлежат области определения, задаваемой условиями .

Логарифмическое уравнение вида (5) можно решить различными способами. Рассмотрим основные из них.

1. ПОТЕНЦИНИРОВАНИЕ (применение свойств логарифма).

Пример 2: Решить уравнение

Решение: В силу теоремы 2 данное уравнение равносильно системе:

Решим уравнение:

Всем условиям системы удовлетворяет лишь один корень. Ответ:

2. ИСПОЛЬЗОВАНИЕ ОПРЕДЕЛЕНИЯ ЛОГАРИФМА .

Пример 3: Найти х, если

Решение:

Значение х = 3 принадлежит области определения уравнения. Ответ х = 3

3. ПРИВЕДЕНИЕ К КВАДРАТНОМУ УРАВНЕНИЮ.

Пример 4: Решить уравнение

Оба значения х являются корнями уравнения.

Ответ:

4. ЛОГАРИФМИРОВАНИЕ.

Пример 5: Решить уравнение

Решение: Прологарифмируем обе части уравнения по основанию 10 и применим свойство «логарифм степени».

Оба корня принадлежат области допустимых значений логарифмической функции.

Ответ: х = 0,1; х = 100

5. ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ.

Пример 6: Решить уравнение

Воспользуемся формулой и перейдем во всех слагаемых к логарифму по основанию 2:

Тогда данное уравнение примет вид:

Так как , то это корень уравнения.

Ответ: х = 16

6. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ.

Решим способом введения вспомогательной переменной уравнение, заданное в примере 6.

Пусть ; тогда

Учитывая, что

Получим уравнение:

После проверки, проведенной устно, легко убеждаемся в правильности найденного ответа.

7. ГРАФИЧЕСКИЙ СПОСОБ.

Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически.

Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении.

Пример 7: Решить уравнение

Решение: Построим графики функций и y = x

Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).

Ответ: корней нет

8. МЕТОД ПОДБОРА.

Пример 8: Найти х, если

Решение: С помощью рассмотренных выше способов корни уравнения найти не удается. Найдем какой-нибудь корень методом подбора.

Пусть, например, х = 10. Проверкой убедимся в том, что 10 — корень уравнения. Действительно,

истинно

Докажем, что других корней данное уравнение не имеет.

Эти корни следует искать во множестве значений х.

Допустимые значения х находятся в промежутке

На этом промежутке функция убывает, а функция возрастает. И, значит, если уравнение имеет решение, то оно единственное.

Итак, получаем

Ответ: х = 10

Упражнения для закрепления:

Решение логарифмических уравнений. Как решать, на примерах.

Логарифмическим уравнением называется уравнение, в котором неизвестное (х) и выражения с ним находятся под знаком логарифмической функции. Решение логарифмических уравнений подразумевает, что вы уже знакомы с понятием и видами логарифмов и основными формулами.
Как решать логарифмические уравнения?

Самое простое уравнение имеет вид log_ax = b, где a и b -некоторые числа,x — неизвестное.
Решением логарифмическое уравнения является x = a ^b при условии: a > 0, a 1.

Следует отметить, что если х будет находиться где-нибудь вне логарифма, например log₂х = х-2, то такое уравнение уже называется смешанным и для его решения нужен особый подход.

Идеальным случаем является ситуация, когда Вам попадется уравнение, в котором под знаком логарифма находятся только числа, например х+2 = log₂2. Здесь достаточно знать свойства логарифмов для его решения. Но такая удача случается не часто, поэтому приготовьтесь к более сложным вещам.

Но сначала, все-таки, начнём с простых уравнений. Для их решения желательно иметь самое общее представление о логарифме.

Решение простейших логарифмических уравнений

К таковым относятся уравнения типа log₂х = log₂16. Невооруженным глазом видно, что опустив знак логарифма получим х = 16.

Для того, чтобы решить более сложное логарифмическое уравнение, его обычно приводят к решению обычного алгебраического уравнения или к решению простейшего логарифмического уравнения log_ax = b. В простейших уравнениях это происходит в одно движение, поэтому они и носят название простейших.

Вышеиспользованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. В математике эта операция носит название потенцирования. Существуют определенные правила или ограничения для подобного рода операций:

• одинаковые числовые основания у логарифмов
• логарифмы в обоих частях уравнения находятся свободно, т.е. без каких бы то ни было коэффициентов и других разного рода выражений.

Скажем в уравнении log₂х = 2log₂ (1- х) потенцирование неприменимо — коэффициент 2 справа не позволяет. В следующем примере log₂х+log₂ (1 — х) = log₂ (1+х) также не выполняется одно из ограничений — слева логарифма два. Вот был бы один – совсем другое дело!

Вообщем, убирать логарифмы можно только при условии, что уравнение имеет вид:

log_a (…) = log_a (…)

В скобках могут находится совершенно любые выражения, на операцию потенцирования это абсолютно никак не влияет. И уже после ликвидации логарифмов останется более простое уравнение – линейное, квадратное, показательное и т.п., которое Вы уже, надеюсь, умеете решать.

Возьмем другой пример:

log₃ (2х-5) = log₃х

Применяем потенцирование, получаем:

2х-5 = х

х=5

Пойдем дальше. Решим следующий пример:

log₃ (2х-1) = 2

Исходя из определения логарифма, а именно, что логарифм — это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (4х-1), получаем:

3 ² = 2х-1

Дальше уже дело техники:

2х-1 = 9

х =5

Опять получили красивый ответ. Здесь мы обошлись без ликвидации логарифмов, но потенцирование применимо и здесь, потому как логарифм можно сделать из любого числа, причем именно такой, который нам надо. Этот способ очень помогает при решении логарифмических уравнений и особенно неравенств.

Решим наше логарифмическое уравнение log₃ (2х-1) = 2 с помощью потенцирования:

Представим число 2 в виде логарифма, например, такого log₃9, ведь 3 ²=9.

Тогда log₃ (2х-1) = log₃9 и опять получаем все то же уравнение 2х-1 = 9. Надеюсь, все понятно.

Вот мы и рассмотрели как решать простейшие логарифмические уравнения, которые на самом деле очень важны, ведь решение логарифмических уравнений, даже самых страшных и закрученных, в итоге всегда сводится к решению простейших уравнений.

Во всем, что мы делали выше, мы упускали из виду один очень важный момент, который в последующем будет иметь решающую роль. Дело в том, что решение любого логарифмического уравнения, даже самого элементарного, состоит из двух равноценных частей. Первая – это само решение уравнения, вторая — работа с областью допустимых значений (ОДЗ). Вот как раз первую часть мы и освоили. В вышеприведенных примерах ОДЗ на ответ никак не влияет, поэтому мы ее и не рассматривали.

А вот возьмем другой пример:

log₃ (х ²-3) = log₃ (2х)

Внешне это уравнение ничем не отличается от элементарного, которое весьма успешно решается. Но это не совсем так. Нет, мы конечно же его решим, но скорее всего неправильно, потому что в нем кроется небольшая засада, в которую сходу попадаются и троечники, и отличники. Давайте рассмотрим его поближе.

Допустим необходимо найти корень уравнения или сумму корней, если их несколько:

log₃ (х ²-3) = log₃ (2х)

Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.

х ²-3 = 2х

х ²-2х-3 = 0

Находим корни уравнения:

х₁= 3

х₂= -1

Получилось два корня.

Ответ: 3 и -1

С первого взгляда все правильно. Но давайте проверим результат и подставим его в исходное уравнение.

Начнем с х₁= 3:

log₃6 = log₃6

Проверка прошла успешно, теперь очередь х₂= -1:

log₃ (-2) = log₃ (-2)

Так, стоп! Внешне всё идеально. Один момент — логарифмов от отрицательных чисел не бывает! А это значит, что корень х = -1 не подходит для решения нашего уравнения. И поэтому правильный ответ будет 3, а не 2, как мы написали.

Вот тут-то и сыграла свою роковую роль ОДЗ, о которой мы позабыли.

Напомню, что под областью допустимых значений принимаются такие значения х, которые разрешены или имеют смысл для исходного примера.

Без ОДЗ любое решение, даже абсолютно правильное, любого уравнения превращается в лотерею — 50/50.

Как же мы смогли попасться при решении, казалось бы, элементарного примера? А вот именно в момент потенцирования. Логарифмы пропали, а с ними и все ограничения.

Что же в таком случае делать? Отказываться от ликвидации логарифмов? И напрочь отказаться от решения этого уравнения?

Нет, мы просто, как настоящие герои из одной известной песни, пойдем в обход!

Перед тем, как приступать к решению любого логарифмического уравнения, будем записывать ОДЗ. А вот уж после этого можно делать с нашим уравнением все, что душа пожелает. Получив ответ, мы просто выбрасываем те корни, которые не входят в нашу ОДЗ, и записываем окончательный вариант.

Теперь определимся, как же записывать ОДЗ. Для этого внимательно осматриваем исходное уравнение и ищем в нем подозрительные места, вроде деления на х, корня четной степени и т.п. Пока мы не решили уравнение, мы не знаем – чему равно х, но твердо знаем, что такие х, которые при подстановке дадут деление на 0 или извлечение квадратного корня из отрицательного числа, заведомо в ответ не годятся. Поэтому такие х неприемлемы, остальные же и будут составлять ОДЗ.

Воспользуемся опять тем же уравнением:

log₃ (х ²-3) = log₃ (2х)

log₃ (х ²-3) = log₃ (2х)

Как видим, деления на 0 нет, квадратных корней также нет, но есть выражения с х в теле логарифма. Тут же вспоминаем, что выражение, находящееся внутри логарифма, всегда должно быть >0. Это условие и записываем в виде ОДЗ:

Т.е. мы еще ничего не решали, но уже записали обязательное условие на всё подлогарифменное выражение. Фигурная скобка означает, что эти условия должны выполняться одновременно.

ОДЗ записано, но необходимо еще и решить полученную систему неравенств, чем и займемся. Получаем ответ х > v3. Теперь точно известно – какие х нам не подойдут. А дальше уже приступаем к решению самого логарифмического уравнения, что мы и сделали выше.

Получив ответы х₁= 3 и х₂= -1, легко увидеть, что нам подходит лишь х1= 3, его и записываем, как окончательный ответ.

На будущее очень важно запомнить следующее: решение любого логарифмического уравнения делаем в 2 этапа. Первый — решаем само уравнение, второй – решаем условие ОДЗ. Оба этапа выполняются независимо друг от друга и только лишь при написании ответа сопоставляются, т.е. отбрасываем все лишнее и записываем правильный ответ.

Для закрепления материала настоятельно рекомендуем посмотреть видео:

На видео другие примеры решения лог. уравнений и отработка метода интервалов на практике.

На это по вопросу, как решать логарифмические уравнения, пока всё. Если что то по решению лог. уравнений осталось не ясным или непонятным, пишите свои вопросы в комментариях.

Заметка: Академия социального образования (КСЮИ) — готова принять новых учащихся.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Решение логарифмических уравнений.

Часть 1.

Решение логарифмических уравнений. Часть 1.

Логарифмическим уравнением называется уравнение, в котором неизвестное содержится под знаком логарифма ( в частности, в основании логарифма).

Простейшее логарифмическое уравнение имеет вид:

Решение любого логарифмического уравнения предполагает переход от логарифмов к выражениям, стоящим под знаком логарифмов. Однако это действие расширяет область допустимых значений уравнения и может привести к появлению посторонних корней. Чтобы избежать появления посторонних корней, можно поступить одним из трех способов:

1. Сделать равносильный переход от исходного уравнения к системе, включающей область допустимых значений уравнения:

   

или

   

,

в зависимости от того, какое неравенство  или проще.

Если уравнение содержит неизвестное в основании логарифма:

,

то мы переходим к системе:

   

 

2. Отдельно найти область допустимых значений уравнения, затем решить уравнение и проверить, удовлетворяют ли найденные решения ОДЗ уравнения.

3. Решить уравнение, и потом сделать проверку: подставить найденные решения в исходное уравнение, и проверить, получим ли мы верное равенство.

Логарифмическое уравнение любого уровня сложности в конечном итоге всегда сводится к простейшему логарифмическому уравнению.

Все логарифмические уравнения можно  условно разделить на четыре типа:

1. Уравнения, которые содержат логарифмы только в первой степени. Они с помощью  преобразований и использования свойств логарифмов  приводятся к виду

или

Пример. Решим уравнение:

Решение.

Выпишем ОДЗ уравнения:

   

 

Внимание! Мы всегда ищем ОДЗ исходного уравнения, а не того, которое получится в процессе преобразований. То есть ОДЗ записываем перед тем, как переходим к решению уравнения. 

Для упрощения вычислений давайте перенесем логарифмы с отрицательными коэффициентами в противоположную часть уравнения — из соображений, что умножать проще, чем делить:

Представим число 2 в виде логарифма по основанию 4:

Получим уравнение:  

Воспользуемся свойствами логарифмов:

Приравняем выражения, стоящие под знаком логарифма:

Проверим, удовлетворяет ли наш корень ОДЗ уравнения:

   

Да, удовлетворяет.

Ответ: х=5

2. Уравнения, которые содержат логарифмы в степени, отличной от 1 (в частности, в знаменателе дроби). Такие уравнения решаются с помощью введения замены переменной.

Пример. Решим уравнение:

Решение.

Найдем ОДЗ уравнения:

Уравнение содержит логарифмы в квадрате, поэтому решается с помощью замены переменной.

Важно! Прежде чем вводить замену, нужно «растащить» логарифмы, входящие в состав уравнения на «кирпичики», используя свойства логарифмов.

При «растаскивании» логарифмов важно очень аккуратно применять свойства логарифмов:

Кроме того, здесь есть еще одно тонкое место, и, чтобы избежать распространенной ошибки, воспользуемся промежуточным равенством: запишем степень логарифма в таком виде:

Аналогично,

.

Подставим полученные выражения в исходное уравнение. Получим:

Теперь мы видим, что неизвестное  содержится в уравнении в составе . Введем замену: . Так как может принимать любое действительное значение, на переменную мы никаких ограничений не накладываем.

Получили уравнение:

Раскроем скобки, приведем подобные члены и решим квадратное уравнение:

,

Вернемся к исходной переменной:

,  

Отсюда:

,  

Ответ: ,  

Решение  логарифмических уравнений остальных типов мы рассмотрим здесь и здесь.

 

И.В. Фельдман, репетитор по математике.

Логарифмические уравнения и методы их решения. Решение логарифмических уравнений

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Логарифмические уравнения. От простого — к сложному.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже. ..»)

Что такое логарифмическое уравнение?

Это уравнение с логарифмами. Вот удивил, да?) Тогда уточню. Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся внутри логарифмов. И только там! Это важно.

Вот вам примеры логарифмических уравнений :

log 3 х = log 3 9

log 3 (х 2 -3) = log 3 (2х)

log х+1 (х 2 +3х-7) = 2

lg 2 (x+1)+10 = 11lg(x+1)

Ну, вы поняли… )

Обратите внимание! Самые разнообразные выражения с иксами располагаются исключительно внутри логарифмов. Если, вдруг, в уравнении обнаружится икс где-нибудь снаружи , например:

log 2 х = 3+х,

это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Кстати, попадаются уравнения, где внутри логарифмов только числа . Например:

Что тут сказать? Повезло вам, если попалось такое! Логарифм с числами — это какое-то число. И всё. Достаточно знать свойства логарифмов, чтобы решить такое уравнение. Знания специальных правил, приёмов, приспособленных именно для решения логарифмических уравнений, здесь не требуется.

Итак, что такое логарифмическое уравнение — разобрались.

Как решать логарифмические уравнения?

Решение логарифмических уравнений — штука, вообще-то, не очень простая. Так и раздел у нас — на четвёрку… Требуется приличный запас знаний по всяким смежным темам. Кроме того, существует в этих уравнениях особая фишка. И фишка это настолько важная, что её смело можно назвать главной проблемой в решении логарифмических уравнений. Мы с этой проблемой в следующем уроке детально разберёмся.

А сейчас — не волнуйтесь. Мы пойдём правильным путём, от простого к сложному. На конкретных примерах. Главное, вникайте в простые вещи и не ленитесь ходить по ссылкам, я их не просто так поставил… И всё у вас получится. Обязательно.

Начнём с самых элементарных, простейших уравнений. Для их решения желательно иметь представление о логарифме, но не более того. Просто без понятия логарифма, браться за решение логарифмических уравнений — как-то и неловко даже… Очень смело, я бы сказал).

Простейшие логарифмические уравнения.

Это уравнения вида:

1. log 3 х = log 3 9

2. log 7 (2х-3) = log 7 х

3. log 7 (50х-1) = 2

Процесс решения любого логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них. В простейших уравнениях этот переход осуществляется в один шаг. Потому и простейшие.)

И решаются такие логарифмические уравнения на удивление просто. Смотрите сами.

Решаем первый пример:

log 3 х = log 3 9

Для решения этого примера почти ничего знать и не надо, да… Чисто интуиция!) Что нам особо не нравится в этом примере? Что-что… Логарифмы не нравятся! Правильно. Вот и избавимся от них. Пристально смотрим на пример, и у нас возникает естественное желание. .. Прямо-таки непреодолимое! Взять и выкинуть логарифмы вообще. И, что радует, это можно сделать! Математика позволяет. Логарифмы исчезают, получается ответ:

Здорово, правда? Так можно (и нужно) делать всегда. Ликвидация логарифмов подобным образом — один из основных способов решения логарифмических уравнений и неравенств. В математике эта операция называется потенцирование. Есть, конечно, свои правила на такую ликвидацию, но их мало. Запоминаем:

Ликвидировать логарифмы безо всяких опасений можно, если у них:

а) одинаковые числовые основания

в) логарифмы слева-справа чистые (безо всяких коэффициентов) и находятся в гордом одиночестве.

Поясню последний пункт. В уравнении, скажем,

log 3 х = 2log 3 (3х-1)

убирать логарифмы нельзя. Двойка справа не позволяет. Коэффициент, понимаешь… В примере

log 3 х+log 3 (х+1) = log 3 (3+х)

тоже нельзя потенцировать уравнение. В левой части нет одинокого логарифма. Их там два.

Короче, убирать логарифмы можно, если уравнение выглядит так и только так:

log а (…..) = log а (…..)

В скобках, где многоточие, могут быть какие угодно выражения. Простые, суперсложные, всякие. Какие угодно. Важно то, что после ликвидации логарифмов у нас остаётся более простое уравнение. Предполагается, конечно, что решать линейные, квадратные, дробные, показательные и прочие уравнения без логарифмов вы уже умеете.)

Теперь легко можно решить второй пример:

log 7 (2х-3) = log 7 х

Собственно, в уме решается. Потенцируем, получаем:

Ну что, очень сложно?) Как видите, логарифмическая часть решения уравнения заключается только в ликвидации логарифмов… А дальше идёт решение оставшегося уравнения уже без них. Пустяшное дело.

Решаем третий пример:

log 7 (50х-1) = 2

Видим, что слева стоит логарифм:

Вспоминаем, что этот логарифм — какое-то число, в которое надо возвести основание (т. е. семь), чтобы получить подлогарифменное выражение, т.е. (50х-1).

Но это число равно двум! По уравнению. Стало быть:

Вот, в сущности, и всё. Логарифм исчез, осталось безобидное уравнение:

Мы решили это логарифмическое уравнение исходя только из смысла логарифма. Что, ликвидировать логарифмы всё-таки проще?) Согласен. Между прочим, если из двойки логарифм сделать, можно этот пример и через ликвидацию решить. Из любого числа можно логарифм сделать. Причём, такой, какой нам надо. Очень полезный приём в решении логарифмических уравнений и (особо!) неравенств.

Не умеете из числа логарифм делать!? Ничего страшного. В разделе 555 этот приём подробно описан. Можете освоить и применять его на полную катушку! Он здорово уменьшает количество ошибок.

Совершенно аналогично (по определению) решается и четвёртое уравнение:

Вот и все дела.

Подведём итоги этого урока. Мы рассмотрели на примерах решение простейших логарифмических уравнений. Это очень важно. И не только потому, что такие уравнения бывают на контрольных-экзаменах. Дело в том, что даже самые злые и замороченные уравнения обязательно сводятся к простейшим!

Собственно, простейшие уравнения — это финишная часть решения любых уравнений. И эту финишную часть надо понимать железно! И ещё. Обязательно дочитайте эту страничку до конца. Есть там сюрприз…)

Решаем теперь самостоятельно. Набиваем руку, так сказать…)

Найти корень (или сумму корней, если их несколько) уравнений:

ln(7х+2) = ln(5х+20)

log 2 (х 2 +32) = log 2 (12x)

log 16 (0,5х-1,5) = 0,25

log 0,2 (3х-1) = -3

ln(е 2 +2х-3) = 2

log 2 (14х) = log 2 7 + 2

Ответы (в беспорядке, разумеется): 42; 12; 9; 25; 7; 1,5; 2; 16.

Что, не всё получается? Бывает. Не горюйте! В разделе 555 решение всех этих примеров расписано понятно и подробно. Там уж точно разберётесь. Да ещё и полезные практические приёмы освоите.

Всё получилось!? Все примеры «одной левой»?) Поздравляю!

Пришло время открыть вам горькую правду. Успешное решение этих примеров вовсе не гарантирует успех в решении всех остальных логарифмических уравнений. Даже простейших, подобных этим. Увы.

Дело в том, что решение любого логарифмического уравнения (даже самого элементарного!) состоит из двух равноценных частей. Решение уравнения, и работа с ОДЗ. Одну часть — решение самого уравнения — мы освоили. Не так уж и трудно, верно?

Для этого урока я специально подобрал такие примеры, в которых ОДЗ никак на ответе не сказывается. Но не все такие добрые, как я, правда?…)

Посему надо обязательно освоить и другую часть. ОДЗ. Это и есть главная проблема в решении логарифмических уравнений. И не потому, что трудная — эта часть ещё проще первой. А потому, что про ОДЗ просто забывают. Или не знают. Или и то, и другое). И падают на ровном месте…

В следующем уроке мы расправимся с этой проблемой. Вот тогда можно будет уверенно решать любые несложные логарифмические уравнения и подбираться к вполне солидным заданиям.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Решение логарифмических уравнений. Часть 1.

Логарифмическим уравнением называется уравнение, в котором неизвестное содержится под знаком логарифма (в частности, в основании логарифма).

Простейшее логарифмическое уравнение имеет вид:

Решение любого логарифмического уравнения предполагает переход от логарифмов к выражениям, стоящим под знаком логарифмов. Однако это действие расширяет область допустимых значений уравнения и может привести к появлению посторонних корней. Чтобы избежать появления посторонних корней , можно поступить одним из трех способов:

1. Сделать равносильный переход от исходного уравнения к системе, включающей

в зависимости от того, какое неравенство или проще.

Если уравнение содержит неизвестное в основании логарифма:

то мы переходим к системе:

2. Отдельно найти область допустимых значений уравнения , затем решить уравнение и проверить, удовлетворяют ли найденные решения уравнения.

3. Решить уравнение, и потом сделать проверку: подставить найденные решения в исходное уравнение, и проверить, получим ли мы верное равенство.

Логарифмическое уравнение любого уровня сложности в конечном итоге всегда сводится к простейшему логарифмическому уравнению.

Все логарифмические уравнения можно условно разделить на четыре типа:

1 . Уравнения, которые содержат логарифмы только в первой степени. Они с помощью преобразований и использования приводятся к виду

Пример . Решим уравнение:

Приравняем выражения, стоящие под знаком логарифма:

Проверим, удовлетворяет ли наш корень уравнения:

Да, удовлетворяет.

Ответ: х=5

2 . Уравнения, которые содержат логарифмы в степени, отличной от 1 (в частности, в знаменателе дроби). Такие уравнения решаются с помощью введения замены переменной .

Пример. Решим уравнение:

Найдем ОДЗ уравнения:

Уравнение содержит логарифмы в квадрате, поэтому решается с помощью замены переменной.

Важно! Прежде чем вводить замену, нужно «растащить» логарифмы, входящие в состав уравнения на «кирпичики», используя свойства логарифмов.

При «растаскивании» логарифмов важно очень аккуратно применять свойства логарифмов:

Кроме того, здесь есть еще одно тонкое место, и, чтобы избежать распространенной ошибки, воспользуемся промежуточным равенством: запишем степень логарифма в таком виде:

Аналогично,

Подставим полученные выражения в исходное уравнение. Получим:

Теперь мы видим, что неизвестное содержится в уравнении в составе . Введем замену : . Так как может принимать любое действительное значение, на переменную мы никаких ограничений не накладываем.

Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях « » , « » . В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.

Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство.

Определение :

Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.

Например:

Log 3 9 = 2, так как 3 2 = 9

Свойства логарифмов:

Частные случаи логарифмов:

Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.

Найдите корень уравнения: log 3 (4–x) = 4

Так как log b a = x b x = a, то

3 4 = 4 – x

x = 4 – 81

x = – 77

Проверка:

log 3 (4–(–77)) = 4

log 3 81 = 4

3 4 = 81 Верно.

Ответ: – 77

Решите самостоятельно:

Найдите корень уравнения: log 2 (4 – x) = 7

Найдите корень уравнения log 5 (4 + x) = 2

Используем основное логарифмическое тождество.

Так как log a b = x b x = a, то

5 2 = 4 + x

x =5 2 – 4

x = 21

Проверка:

log 5 (4 + 21) = 2

log 5 25 = 2

5 2 = 25 Верно.

Ответ: 21

Найдите корень уравнения log 3 (14 – x) = log 3 5.

Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.

14 – x = 5

x = 9

Сделайте проверку.

Ответ: 9

Решите самостоятельно:

Найдите корень уравнения log 5 (5 – x) = log 5 3.

Найдите корень уравнения: log 4 (x + 3) = log 4 (4x – 15).

Если log c a = log c b, то a = b

x + 3 = 4x – 15

3x = 18

x = 6

Сделайте проверку.

Ответ: 6

Найдите корень уравнения log 1/8 (13 – x) = – 2.

(1/8) –2 = 13 – x

8 2 = 13 – x

x = 13 – 64

x = – 51

Сделайте проверку.

Небольшое дополнение – здесь используется свойство

степени ().

Ответ: – 51

Решите самостоятельно:

Найдите корень уравнения: log 1/7 (7 – x) = – 2

Найдите корень уравнения log 2 (4 – x) = 2 log 2 5.

Преобразуем правую часть. воспользуемся свойством:

log a b m = m∙log a b

log 2 (4 – x) = log 2 5 2

Если log c a = log c b, то a = b

4 – x = 5 2

4 – x = 25

x = – 21

Сделайте проверку.

Ответ: – 21

Решите самостоятельно:

Найдите корень уравнения: log 5 (5 – x) = 2 log 5 3

Решите уравнение log 5 (x 2 + 4x) = log 5 (x 2 + 11)

Если log c a = log c b, то a = b

x 2 + 4x = x 2 + 11

4x = 11

x = 2,75

Сделайте проверку.

Ответ: 2,75

Решите самостоятельно:

Найдите корень уравнения log 5 (x 2 + x) = log 5 (x 2 + 10).

Решите уравнение log 2 (2 – x) = log 2 (2 – 3x) +1.

Необходимо с правой стороны уравнения получить выражение вида:

log 2 (……)

Представляем 1 как логарифм с основанием 2:

1 = log 2 2

log с (ab) = log с a + log с b

log 2 (2 – x) = log 2 (2 – 3x) + log 2 2

Получаем:

log 2 (2 – x) = log 2 2 (2 – 3x)

Если log c a = log c b, то a = b, значит

2 – x = 4 – 6x

5x = 2

x = 0,4

Сделайте проверку.

Ответ: 0,4

Решите самостоятельно: Далее необходимо решить квадратное уравнение. Кстати,

корни равны 6 и – 4.

Корень «– 4″ не является решением, так как основание логарифма должно быть больше нуля, а при » – 4″ оно равно « – 5». Решением является корень 6. Сделайте проверку.

Ответ: 6.

Решите самостоятельно:

Решите уравнение log x –5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Заключительные видео из длинной серии уроков про решение логарифмических уравнений. В этот раз мы будем работать в первую очередь с ОДЗ логарифма — именно из-за неправильного учета (или вообще игнорирования) области определения возникает большинство ошибок при решении подобных задач.

В этом коротком видеоуроке мы разберем применение формул сложения и вычитания логарифмов, а также разберемся с дробно-рациональными уравнениями, с которыми у многих учеников также возникают проблемы.

О чем пойдет речь? Главная формула, с которой я хотел бы разобраться, выглядит так:

log a (f g ) = log a f + log a g

Это стандартный переход от произведения к сумме логарифмов и обратно. Вы наверняка знаете эту формулу с самого начала изучения логарифмов. Однако тут есть одна заминка.

До тех пор, пока в виде переменных a , f и g выступают обычные числа, никаких проблем не возникает. Данная формула работает прекрасно.

Однако, как только вместоf и g появляются функции, возникает проблема расширения или сужения области определения в зависимости от того, в какую сторону преобразовывать. Судите сами: в логарифме, записанном слева, область определения следующая:

fg > 0

А вот в сумме, записанной справа, область определения уже несколько иная:

f > 0

g > 0

Данный набор требований является более жестким, чем исходный. В первом случае нас устроит вариант f 0 выполняется).

Итак, при переходе от левой конструкции к правой возникает сужение области определения. Если же сначала у нас была сумма, а мы переписываем ее в виде произведения, то происходит расширение области определения.

Другими словами, в первом случае мы могли потерять корни, а во втором — получить лишние. Это необходимо учитывать при решении реальных логарифмических уравнений.

Итак, первая задача:

[Подпись к рисунку]

Слева мы видим сумму логарифмов по одному и тому же основанию. Следовательно, эти логарифмы можно сложить:

[Подпись к рисунку]

Как видите, справа мы заменил ноль по формуле:

a = log b b a

Давайте еще немного преобразуем наше уравнение:

log 4 (x − 5) 2 = log 4 1

Перед нами каноническая форма логарифмического уравнения, мы можем зачеркнуть знак log и приравнять аргументы:

(x − 5) 2 = 1

|x − 5| = 1

Обратите внимание: откуда взялся модуль? Напомню, что корень из точного квадрата равен именно модулю:

[Подпись к рисунку]

Затем решаем классическое уравнение с модулем:

|f | = g (g > 0) ⇒f = ±g

x − 5 = ±1 ⇒x 1 = 5 − 1 = 4; x 2 = 5 + 1 = 6

Вот два кандидат на ответ. Являются ли они решением исходного логарифмического уравнения? Нет, ни в коем случае!

Оставить все просто так и записать ответ мы не имеем права. Взгляните на тот шаг, когда мы заменяем сумму логарифмов одним логарифмом от произведения аргументов. Проблема в том, что в исходных выражениях у нас стоят функции. Следовательно, следует потребовать:

х(х − 5) > 0; (х − 5)/х > 0.

Когда же мы преобразовали произведение, получив точный квадрат, требования изменились:

(x − 5) 2 > 0

Когда это требование выполняется? Да практически всегда! За исключением того случая, когда х − 5 = 0. Т.е. неравенство сведется к одной выколотой точке:

х − 5 ≠ 0 ⇒ х ≠ 5

Как видим, произошло расширение области определения, о чем мы и говорили в самом начале урока. Следовательно, могут возникнуть и лишние корни.

Как же не допустить возникновения этих лишних корней? Очень просто: смотрим на наши полученные корни и сравниваем их с областью определения исходного уравнения. Давайте посчитаем:

х (х − 5) > 0

Решать будем с помощью метода интервалов:

х (х − 5) = 0 ⇒ х = 0; х = 5

Отмечаем полученные числа на прямой. Все точки выколотые, потому что неравенство строгое. Берем любое число, больше 5 и подставляем:

[Подпись к рисунку]

На интересуют промежутки (−∞; 0) ∪ (5; ∞). Если мы отметим наши корни на отрезке, то увидим, что х = 4 нас не устраивает, потому что этот корень лежит за пределами области определения исходного логарифмического уравнения.

Возвращаемся к совокупности, вычеркиваем корень х = 4 и записываем ответ: х = 6. Это уже окончательный ответ к исходному логарифмическому уравнению. Все, задача решена.

Переходим ко второму логарифмическому уравнению:

[Подпись к рисунку]

Решаем его. Заметим, что первое слагаемое представляет собой дробь, а второе — ту же самую дробь, но перевернутую. Не пугайтесь выражения lgx — это просто десятичный логарифм, мы можем записать:

lgx = log 10 x

Поскольку перед нами две перевернутые дроби, предлагаю ввести новую переменную:

[Подпись к рисунку]

Следовательно, наше уравнение может быть переписано следующим образом:

t + 1/t = 2;

t + 1/t − 2 = 0;

(t 2 − 2t + 1)/t = 0;

(t − 1) 2 /t = 0.

Как видим, в числителе дроби стоит точный квадрат. Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:

(t − 1) 2 = 0; t ≠ 0

Решаем первое уравнение:

t − 1 = 0;

t = 1.

Это значение удовлетворяет второму требованию. Следовательно, можно утверждать, что мы полностью решили наше уравнение, но только относительно переменной t . А теперь вспоминаем, что такое t :

[Подпись к рисунку]

Получили пропорцию:

lgx = 2 lgx + 1

2 lgx − lgx = −1

lgx = −1

Приводим это уравнение к канонической форме:

lgx = lg 10 −1

x = 10 −1 = 0,1

В итоге мы получили единственный корень, который, по идее, является решением исходного уравнения. Однако давайте все-таки подстрахуемся и выпишем область определения исходного уравнения:

[Подпись к рисунку]

Следовательно, наш корень удовлетворяет всем требованиям. Мы нашли решение исходного логарифмического уравнения. Ответ: x = 0,1. Задача решена.

Ключевой момент в сегодняшнем уроке один: при использовании формулы перехода от произведения к сумме и обратно обязательно учитывайте, что область определения может сужаться либо расширяться в зависимости от того, в какую сторону выполняется переход.

Как понять, что происходит: сужение или расширение? Очень просто. Если раньше функции были вместе, а теперь стали по отдельности, то произошло сужение области определения (потому что требований стало больше). Если же сначала функции стояли отдельно, а теперь — вместе, то происходит расширение области определения (на произведение накладывается меньше требований, чем на отдельные множители).

С учетом данного замечания хотел бы отметить, что второе логарифмическое уравнение вообще не требует данных преобразований, т. е. мы нигде не складываем и не перемножаем аргументы. Однако здесь я хотел бы обратить ваше внимание на другой замечательный прием, который позволяет существенно упростить решение. Речь идет о замене переменной.

Однако помните, что никакие замены не освобождает нас от области определения. Именно поэтому после того были найдены все корни, мы не поленились и вернулись к исходному уравнению, чтобы найти его ОДЗ.

Часто при замене переменной возникает обидная ошибка, когда ученики находят значение t и думают, что на этом решение закончено. Нет, ни в коем случае!

Когда вы нашли значение t , необходимо вернуться к исходному уравнению и посмотреть, что именно мы обозначали этой буквой. В результате нам предстоит решить еще одно уравнение, которое, впрочем, будет значительно проще исходного.

Именно в этом состоит смысл введения новой переменной. Мы разбиваем исходное уравнение на два промежуточных, каждое из которых решается существенно проще.

Как решать «вложенные» логарифмические уравнения

Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.

Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого. Оба уравнения мы будем решать с помощью канонической формы. Напомню, если у нас есть простейшее логарифмическое уравнение вида log a f (x ) = b , то для решения такого уравнения мы выполняем следующие шаги. В первую очередь, нам нужно заменить число b :

b = log a a b

Заметьте: a b — это аргумент. Точно так же в исходном уравнении аргументом является функция f (x ). Затем мы переписываем уравнение и получаем вот такую конструкцию:

log a f (x ) = log a a b

Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:

f (x ) = a b

В результате мы получим новое уравнение. При этом никаких ограничений на функцию f (x ) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.

Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:

log 2 (1 + 3 log 2 x ) = 2

Как видим, перед нами простейшее логарифмическое уравнение. В роли f (x ) выступает конструкция 1 + 3 log 2 x , а в роли числа b выступает число 2 (в роли a также выступает двойка). Давайте перепишем эту двойку следующим образом:

Важно понимать, что первые две двойки пришли к нам из основания логарифма, т. е. если бы в исходном уравнении стояла 5, то мы бы получили, что 2 = log 5 5 2 . В общем, основание зависит исключительно от логарифма, который изначально дан в задаче. И в нашем случае это число 2.

Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:

log 2 (1 + 3 log 2 x ) = log 2 4

Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:

1 + 3 log 2 x = 4

Отсюда легко находится 3 log 2 x :

3 log 2 x = 3

log 2 x = 1

Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:

1 = log 2 2 1 = log 2 2

Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:

log 2 x = log 2 2

Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:

Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.

Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.

Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.

Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.

Давайте перейдем ко второму уравнению, оно чуть интересней:

log 2 (log 1/2 (2x − 1) + log 2 4) = 1

Если обозначить выражение внутри большого логарифма функцией f (x ), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log 2 2 1 = log 2 2.

Переписываем наше большое уравнение:

log 2 (log 1/2 (2x − 1) + log 2 4) = log 2 2

Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log 2 4 = 2:

log 1/2 (2x − 1) + 2 = 2

log 1/2 (2x − 1) = 0

Перед нами снова простейшее логарифмическое уравнение вида log a f (x ) = b . Переходим к канонической форме, т. е. представляем ноль в виде log 1/2 (1/2)0 = log 1/2 1.

Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:

log 1/2 (2x − 1) = log 1/2 1

2x − 1 = 1

Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.

Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.

А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.

Откуда возникают такие лишние корни? Этот момент нужно очень четко понимать. Взгляните на исходные уравнения: везде функция х стоит под знаком логарифма. Следовательно, поскольку мы записали log 2 x , то автоматически выставляем требование х > 0. Иначе данная запись просто не имеет смысла.

Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.

Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.

Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.

Случаи разного основания

Этот урок посвящен уже более сложным конструкциям. Логарифмы в сегодняшних уравнениях уже не будут решаться «напролом» — сначала потребуется выполнить некоторые преобразования.

Начинаем решение логарифмических уравнений с совершенно разными основаниями, которые не являются точными степенями друг друга. Пусть вас не пугают подобные задачи — решаются они ничуть не сложнее, чем самые простые конструкции, которые мы разбирали выше.

Но прежде, чем переходить непосредственно к задачам, напомню о формуле решения простейших логарифмических уравнений с помощью канонической формы. Рассмотрим задачу вот такого вида:

log a f (x ) = b

Важно, что функция f (x ) является именно функцией, а в роли чисел а и b должны выступать именно числа (без всяких переменных x ). Разумеется, буквально через минуту мы рассмотрим и такие случаи, когда вместо переменных а и b стоят функции, но сейчас не об этом.

Как мы помним, число b нужно заменить логарифмом по тому же самому основанию а, которое стоит слева. Это делается очень просто:

b = log a a b

Разумеется, под словом «любое число b » и «любое число а» подразумеваются такие значения, которые удовлетворяют области определения. В частности, в данном уравнении речь идет лишь основание a > 0 и a ≠ 1.

Однако данное требование выполняется автоматически, потому что в исходной задаче уже присутствует логарифм по основанию а — оно заведомо будет больше 0 и не равно 1. Поэтому продолжаем решение логарифмического уравнения:

log a f (x ) = log a a b

Подобная запись называется канонической формой. Ее удобство состоит в том, что мы сразу можем избавиться от знака log, приравняв аргументы:

f (x ) = a b

Именно этот прием мы сейчас будем использовать для решения логарифмических уравнений с переменным основанием. Итак, поехали!

log 2 (x 2 + 4x + 11) = log 0,5 0,125

Что дальше? Кто-то сейчас скажет, что нужно вычислить правый логарифм, либо свести их к одному основанию, либо что-то еще. И действительно, сейчас нужно привести оба основания к одному виду — либо 2, либо 0,5. Но давайте раз и навсегда усвоим следующее правило:

Если в логарифмическом уравнении присутствуют десятичные дроби, обязательно переведите эти дроби из десятичной записи в обычную. Такое преобразование может существенно упростить решение.

Подобный переход нужно выполнять сразу, еще до выполнения каких-либо действий и преобразований. Давайте посмотрим:

log 2 (x 2 + 4x + 11) = log 1 /2 1/8

Что нам дает такая запись? Мы можем 1/2 и 1/8 представить как степень с отрицательным показателем:

[Подпись к рисунку]

Перед нами каноническая форма. Приравниваем аргументы и получаем классическое квадратное уравнение:

x 2 + 4x + 11 = 8

x 2 + 4x + 3 = 0

Перед нами приведенное квадратное уравнение, которое легко решается с помощью формул Виета. Подобные выкладки в старших классах вы должны видеть буквально устно:

(х + 3)(х + 1) = 0

x 1 = −3

x 2 = −1

Вот и все! Исходное логарифмическое уравнение решено. Мы получили два корня.

Напомню, что определять область определения в данном случае не требуется, поскольку функция с переменной х присутствует лишь в одном аргументе. Поэтому область определения выполняется автоматически.

Итак, первое уравнение решено. Переходим ко второму:

log 0,5 (5x 2 + 9x + 2) = log 3 1/9

log 1/2 (5x 2 + 9x + 2) = log 3 9 −1

А теперь заметим, что аргумент первого логарифма тоже можно записать в виде степени с отрицательным показателем: 1/2 = 2 −1 . Затем можно вынести степени с обеих сторон уравнения и разделить все на −1:

[Подпись к рисунку]

И вот сейчас мы выполнили очень важный шаг в решении логарифмического уравнения. Возможно, кто-то что-то не заметил, поэтому давайте я поясню.

Взгляните на наше уравнение: и слева, и справа стоит знак log, но слева стоит логарифм по основанию 2, а справа стоит логарифм по основанию 3. Тройка не является целой степенью двойки и, наоборот: нельзя записать, что 2 — это 3 в целой степени.

Следовательно, это логарифмы с разными основаниями, которые не сводятся друг к другу простым вынесением степеней. Единственный путь решения таких задач — избавиться от одного из этих логарифмов. В данном случае, поскольку мы пока рассматриваем довольно простые задачи, логарифм справа просто сосчитался, и мы получили простейшее уравнение — именно такое, о котором мы говорили в самом начале сегодняшнего урока.

Давайте представим число 2, которое стоит справа в виде log 2 2 2 = log 2 4. А затем избавимся от знака логарифма, после чего у нас остается просто квадратное уравнение:

log 2 (5x 2 + 9x + 2) = log 2 4

5x 2 + 9x + 2 = 4

5x 2 + 9x − 2 = 0

Перед нами обычное квадратное уравнение, однако оно не является приведенным, потому что коэффициент при x 2 отличен от единицы. Следовательно, решать мы его будем с помощью дискриминанта:

D = 81 − 4 5 (−2) = 81 + 40 = 121

x 1 = (−9 + 11)/10 = 2/10 = 1/5

x 2 = (−9 − 11)/10 = −2

Вот и все! Мы нашли оба корня, а значит, получили решение исходного логарифмического уравнения. Ведь в исходной задачи функция с переменной х присутствует лишь в одном аргументе. Следовательно, никаких дополнительных проверок на область определения не требуется — оба корня, которые мы нашли, заведомо отвечают всем возможным ограничениям.

На этом можно было бы закончить сегодняшний видеоурок, но в заключении я хотел бы сказать еще раз: обязательно переводите все десятичные дроби в обычные при решении логарифмических уравнений. В большинстве случаев это существенно упрощает их решение.

Редко, очень редко попадаются задачи, в которых избавление от десятичных дробей лишь усложняет выкладки. Однако в таких уравнениях, как правило, изначально видно, что избавляться от десятичных дробей не надо.

В большинстве остальных случаев (особенно если вы только начинаете тренироваться в решении логарифмических уравнений) смело избавляйтесь от десятичных дробей и переводите их в обычные. Потому что практика показывает, что таким образом вы значительно упростите последующее решение и выкладки.

Тонкости и хитрости решения

Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.

И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.

Сложные задачи

Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:

1. Возникновение лишних корней из-за расширения области определения логарифмов. Чтобы не допускать такие обидные ошибки, просто внимательно следите за каждым преобразованием;
2. Потери корней из-за того, что ученик забыл рассмотреть некоторые «тонкие» случаи — именно на таких ситуациях мы сегодня и сосредоточимся.

Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.

Первое уравнение выглядит вполне стандартно:

log x + 1 (x − 0,5) = log x − 0,5 (x + 1)

Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:

log a b = 1/log b a

Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:

b > 0

1 ≠ a > 0

Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма (следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но log b 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.

Итак, ограничения на переменную a сохраняется. Но что происходит с переменной b ? С одной стороны, из основания следует b > 0, с другой — переменная b ≠ 1, потому что основание логарифма должно быть отлично от 1. Итого из правой части формулы следует, что 1 ≠ b > 0.

Но вот беда: второе требование (b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить , что аргумент b отличен от единицы!

Вот давайте и проверим. Применим нашу формулу:

[Подпись к рисунку]

1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0

Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:

Предлагаю ввести новую переменную:

log x + 1 (x − 0,5) = t

В этом случае наша конструкция перепишется следующим образом:

(t 2 − 1)/t = 0

Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:

(t − 1)(t + 1)/t = 0

Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:

t 1 = 1;

t 2 = −1;

t ≠ 0.

Как видим, оба значения переменной t нас устраивают. Однако на этом решение не заканчивается, ведь нам требуется найти не t , а значение x . Возвращаемся к логарифму и получаем:

log x + 1 (x − 0,5) = 1;

log x + 1 (x − 0,5) = −1.

Давайте приведем каждое из этих уравнений к канонической форме:

log x + 1 (x − 0,5) = log x + 1 (x + 1) 1

log x + 1 (x − 0,5) = log x + 1 (x + 1) −1

Избавляемся от знака логарифма в первом случае и приравниваем аргументы:

х − 0,5 = х + 1;

х − х = 1 + 0,5;

Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:

(х − 0,5)/1 = 1/(х + 1)

Решаем пропорцию — получим:

(х − 0,5)(х + 1) = 1

Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:

(х − 1/2)(х + 1) = 1;

x 2 + x − 1/2x − 1/2 − 1 = 0;

x 2 + 1/2x − 3/2 = 0.

Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:

(х + 3/2) (х − 1) = 0;

x 1 = −1,5;

x 2 = 1.

Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:

1,5 ≠ х > 0,5; 0 ≠ х > −1.

Эти требования равносильны двойному неравенству:

1 ≠ х > 0,5

Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.

Переходим ко второй задаче:

log x 25 + log 125 x 5 = log 25 x 625

На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:

25 = 5 2 ; 625 = 5 4

А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:

log a b n = n ∙ log a b

На данное преобразование также накладываются ограничения в том случае, когда на месте b стоит функция. Но у нас b — это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:

2 ∙ log x 5 + log 125 x 5 = 4 ∙ log 25 x 5

Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.

Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:

[Подпись к рисунку]

Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:

log 5 x = t

В этом случае наше уравнение будет переписано следующим образом:

Выпишем числитель и раскроем скобки:

2 (t + 3) (t + 2) + t (t + 2) − 4t (t + 3) = 2 (t 2 + 5t + 6) + t 2 + 2t − 4t 2 − 12t = 2t 2 + 10t + 12 + t 2 + 2t − 4t 2 − 12t = −t 2 + 12

Возвращаемся к нашей дроби. Числитель должен быть равен нулю:

[Подпись к рисунку]

А знаменатель — отличен от нуля:

t ≠ 0; t ≠ −3; t ≠ −2

Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.

Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t :

[Подпись к рисунку]

Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:

[Подпись к рисунку]

У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:

1 ≠ х > 0;

С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.

Итого мы получили четыре ограничения:

1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25

А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.

С другой стороны, 1 = 5 0 , 1/25 = 5 −2 , 1/125 = 5 −3 , а это значит, что данные ограничения для наших корней (у которых, напомню, в показателе стоит иррациональное число) также выполнены, и оба ответа являются решениями задачи.

Итак, мы получили окончательный ответ.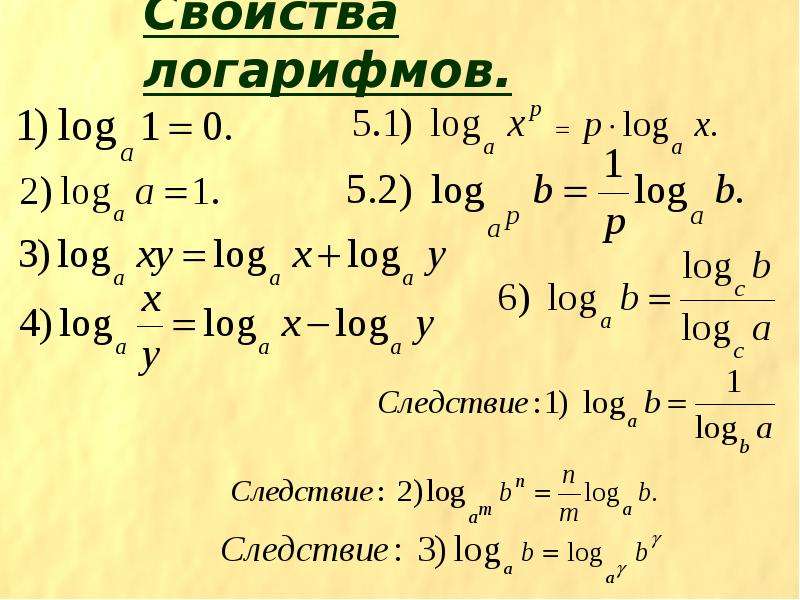 Ключевых моментов в данной задаче два:

1. Будьте внимательны при перевороте логарифма, когда аргумент и основание меняются местами. Подобные преобразования накладывают лишние ограничения на область определения.
2. Не бойтесь преобразовывать логарифмы: их можно не только переворачивать, но и раскрывать по формуле суммы и вообще менять по любым формулам, которые вы изучали при решении логарифмических выражений. Однако при этом всегда помните: некоторые преобразования расширяют область определения, а некоторые — сужают.

Как решить логарифмическое уравнение с параметром, в котором логарифмы имеют разные основания? | Соловьева Светлана Александровна

Математика онлайн. Доступно о сложном

Логарифмическое уравнение с параметром

Логарифмическое уравнение с параметром

Здравствуйте, уважаемые любители математики!

Разберем, как решать логарифмическое уравнение с параметром, левая часть которого – сумма k логарифмов с разными основаниями.

Начнем с того, что приведем все логарифмы к одному основанию.

Переход к новому основанию

Переход к новому основанию

Теперь упростим знаменатели.

Сначала представим корни в виде степеней и, используя одно из свойств логарифмов, вынесем показатель степени вперед.

Упрощаем знаменатели

Упрощаем знаменатели

Затем вычислим логарифм в знаменателях, «перевернем» дроби и вынесем общий множитель за скобки.

Продолжаем упрощение

Продолжаем упрощение

Наше уравнение с параметром и логарифмами существенно упростилось.

Теперь можно заметить, что выражение в скобках – это сумма n первых членов арифметической прогрессии.

В левой части — сумма n первых членов арифметической прогрессии

В левой части — сумма n первых членов арифметической прогрессии

Возвращаемся к уравнению и вместо левой части подставляем только что полученное выражение.

Получили простейшее логарифмическое уравнение

Получили простейшее логарифмическое уравнение

Записываем правую часть через логарифм, приравниваем подлогарифмические выражения и получаем простейшее показательное уравнение с параметром.

Осталось извлечь корень.

Решение показательного уравнения

Решение показательного уравнения

Ответ готов.

Если было интересно, не забудьте подписаться на канал.

Все статьи серии «Нестандартные задачи»

Рубрикатор канала

Алгебра — Решение уравнений логарифмов

Решите каждое из следующих уравнений.

a \({\log _5}\left({2x + 4} \right) = 2\) Показать решение

Чтобы решить их, нам нужно привести уравнение к тому виду, в котором оно находится. Нам нужен один логарифм в уравнении с коэффициентом, равным единице, и константой по другую сторону от знака равенства. Как только мы получим уравнение в этой форме, мы просто преобразуем его в экспоненциальную форму.

Итак, давайте сделаем это с этим уравнением.2} = 25\]

Обратите внимание, что это уравнение мы можем легко решить.

\[2x = 21\hspace{0,25 дюйма} \Rightarrow \hspace{0,25in}x = \frac{{21}}{2}\]

Теперь, как и в первом наборе примеров, нам нужно подключить это обратно к исходному уравнению и посмотреть, будет ли оно давать отрицательные числа или нули в логарифмах. Если да, то это не может быть решением, а если нет, то это решение.

\[\ begin{align*}{\log _5}\left( {2\left( {\ frac {{21}}{2}} \right) + 4} \right) & = 2\\ {\log _5}\left( {25} \right) & = 2\end{align*}\]

Только положительные числа в логарифме, поэтому \(x = \frac{{21}}{2}\) на самом деле является решением.

b \(\log x = 1 — \log \left( {x — 3} \right)\) Показать решение

В этом случае у нас есть два логарифма в задаче, поэтому нам нужно объединить их в один логарифм, как мы сделали в первом наборе примеров. Выполнение этого для этого уравнения дает

\[\begin{align*}\log x + \log \left( {x — 3} \right) & = 1\\ \log \left( {x\left( {x — 3} \right)} \ справа) & = 1\end{align*}\]

Теперь, когда уравнение приведено в правильную форму, мы преобразуем его в экспоненциальную форму.2} — 3x — 10 & = 0\\ \left( {x — 5} \right)\left( {x + 2} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in} х = — 2,\,\,х = 5\конец{выравнивание*}\]

Итак, у нас есть два возможных решения. Давайте проверим их обоих.

\(*х = — 2:\)

\[\log \left( { — 2} \right) = 1 — \log \left( { — 2 — 3} \right)\]

У нас есть отрицательные числа в логарифмах, поэтому это не может быть решением.

\(х = 5:\)

\[\begin{align*}\log 5 & = 1 — \log \left( {5 — 3} \right)\\ \log 5 & = 1 — \log 2\end{align*}\]

Нет отрицательных чисел или нулей в логарифмах, так что это решение. 2} — 6\left( 2 \right)} \right) & = 3 + {\log _2}\left( {1 — 2} \right)\\ {\log _2}\left( {4 — 12} \right) & = 3 + {\log _2}\left( { — 1} \right)\end{align*}\]

В этом случае, несмотря на то, что потенциальное решение положительное, мы получаем отрицательные числа в логарифмах и, следовательно, это не может быть решением.

Следовательно, мы получаем единственное решение этого уравнения \(x = — 4\).

Решить логарифмические уравнения — Precalculus

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105

Или заполните форму ниже:

 

Как решать системы логарифмических уравнений

Решение систем логарифмических уравнений подстановкой

В других случаях невозможно исключить переменную путем сложения двух уравнений. Метод подстановки позволяет исключить одну переменную, найдя ее в ОДНОМ из уравнений системы, а затем подставив в другое уравнение.

Применим этот метод к решению следующей системы уравнений:

Сложение этих двух уравнений НЕ удалит одну из переменных, поэтому лучший способ решить эту систему уравнений — использовать метод подстановки. Сначала возьмем одно из уравнений и решим одну из переменных через другую.В этой задаче возьмем первое уравнение и решим x через y .

Затем подставьте это значение вместо x во второе уравнение и найдите y .

Еще раз, после того как вы знаете одну из переменных (в данном случае y ), вы можете использовать ее в любом из двух уравнений исходной системы, чтобы найти x .

Решение систем логарифмических уравнений в графическом виде

Помимо использования алгебры для решения системы логарифмических уравнений с использованием методов замены или исключения, вы также можете решить систему уравнений с помощью графика.

Нарисуйте график каждого уравнения, и точка пересечения двух графиков будет решением системы уравнений.

Давайте еще раз посмотрим на эту систему уравнений.

Существует несколько графических онлайн-калькуляторов, которые можно использовать для построения графиков этих уравнений. Хорошим является Desmos (Desmos.com), потому что вам не нужно решать уравнения для y , чтобы построить их в виде графика, как это делается в большинстве графических калькуляторов.

Если построить график каждого из этих уравнений с помощью Desmos, он будет выглядеть так:

Видите, что графики пересекаются в точке (2, 5)? Это означает, что решение этой системы уравнений равно x = 2 и y = 5.

Итоги урока

Система уравнений содержит несколько уравнений и несколько неизвестных переменных. Чтобы решить любую систему уравнений, включая ту, которая содержит логарифмические уравнения, вы можете объединить уравнения, чтобы получить одно уравнение только с ОДНОЙ неизвестной переменной.

В методе исключения вы складываете два уравнения вместе, чтобы избавиться от одной из переменных. Чтобы использовать метод подстановки , исключите одну переменную, найдя ее в ОДНОМ из уравнений системы, а затем подставив в другое уравнение.

Наконец, вы также можете решить систему логарифмических уравнений, построив график каждого уравнения и найдя точку пересечения двух графиков. Координаты этой точки x и y будут решением системы уравнений!

Объяснение урока: Логарифмические уравнения с разными основаниями

В этом объяснении мы научимся решать логарифмические уравнения, включающие логарифмы с разными основаниями.

Давайте сначала вспомним связь между логарифмической и экспоненциальной формами.

Определение: связь между логарифмическим и экспоненциальным Формы

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎, что позволяет конвертировать из одной формы в другую, как только мы идентифицируем 𝑎, 𝑥 и 𝑦.

Показательная функция 𝑦=𝑎 – это , обратное логарифмической функции 𝑦=𝑥log. Это означает, что если вы возведете 𝑎 в логарифмическую степень 𝑥 с основанием 𝑎 или если вы сделаете рейз 𝑎 в степени 𝑥 сначала возьми бревно с основанием 𝑎 результата вы получите 𝑥: 𝑎=(𝑎)=𝑥.loglog

Связь между логарифмической и экспоненциальной формами позволяет нам вывести свойства, которым удовлетворяют логарифмические формы, известные как законы логарифмы, которые следуют из законов показателей. Давайте вспомним законы логарифмов.

Определение: законы логарифмов

Предположим, 𝑥, 𝑦, 𝑎 и 𝑏 — положительные числа с 𝑎,𝑏≠1. Законы логарифмов

• Продукт : logloglog (𝑥𝑦) = 𝑥 + 𝑦,
• division : logloglog𝑥𝑦𝑥𝑦 = 𝑥-𝑦,
• powers : loglog (𝑥)=𝑛𝑥,
• изменение основания : logloglog𝑥=𝑥𝑎.

Они будут полезны для решения логарифмических уравнений с разными основаниями, особенно последний, который позволяет нам преобразовать логарифм по одному основанию в Другая. Чтобы понять, откуда это взялось, сначала обратите внимание, что 𝑥=𝑎,𝑎=𝑏,логлог которые непосредственно следуют из того факта, что показатели степени и логарифмы обратны. Если подставить второе выражение в первое, то получим 𝑥=𝑏.loglog

Используя закон экспонент (𝑝)=𝑝, мы можем переписать это как 𝑥=𝑏.loglog⋅

Логарифмируя обе части по основанию 𝑏, находим loglogloglogloglog𝑥=𝑎⋅𝑥𝑥=𝑥𝑎, как требуется. Эта формула вместе с законами логарифмов и эквивалентом экспоненциальная форма позволяет нам решать логарифмические уравнения, включающие логарифмы разные базы. Еще один факт, который будет важен для решения логарифмической уравнения loglog𝑥=𝑦⟺𝑥=𝑦, что непосредственно следует из соотношения между логарифмической и экспоненциальной формы, в частности, из того, что логарифмическая и экспоненциальная функции строго монотонные функции.Мы можем показать это непосредственно, используя законы логарифмы: logloglogloglog𝑥=𝑦𝑥−𝑦=0𝑥𝑦=0.

Преобразуя последнее выражение в экспоненциальную форму, находим 𝑥𝑦=𝑎=1, и, таким образом, 𝑥=𝑦, как и требовалось.

В качестве примера предположим, что мы хотим найти решения логарифмического уравнения loglog(2𝑥−1)=𝑥.

Сначала мы преобразуем логарифм в левой части в логарифм по основанию 2. используя формулу изменения основания: loglogloglogloglog(2𝑥−1)=(2𝑥−1)4=(2𝑥−1)2=12(2𝑥−1), где мы использовали тот факт, что log𝑎=𝑛 для получить последнюю строку.Таким образом, используя это и законы логарифмов, логарифмическое уравнение становится 12(2𝑥−1)=𝑥(2𝑥−1)=2𝑥(2𝑥−1)=𝑥. loglogloglogloglog

Используя установленный факт, если loglog𝑥=𝑦, то 𝑥=𝑦, или приведя к экспоненциальному виду, получим 2𝑥−1=𝑥𝑥−2𝑥+1=0(𝑥−1)=0.

Таким образом, единственное решение логарифмического уравнения loglog(2𝑥−1)=𝑥 равно 𝑥=1.

Теперь давайте рассмотрим несколько примеров, чтобы попрактиковаться и углубить наши знания. понимание решения логарифмических уравнений.В первом примере имеем два логарифма по разным основаниям и появляется неизвестное 𝑥 внутри логарифма.

Пример 1. Поиск набора решений логарифмического уравнения по множеству действительных Числа

Найдите набор решений loglog𝑥=4 в ℝ.

Ответ

В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри логарифм.

Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥). loglog

Применяя формулу замены основания, мы можем написать правую часть данного логарифмического уравнения, log4, как логарифм по основанию 3, используя 9=3 и журнал𝑎=𝑛: loglogloglogloglog4=49=43=124.

Используя это, данное уравнение становится loglogloglogloglog𝑥=124𝑥=4𝑥=2.

Так как loglog𝑥=𝑥⟺𝑥=𝑥, то 𝑥=2. Таким образом, решение набор дается {2}.

Теперь рассмотрим пример, в котором логарифмическое уравнение содержит два логарифма по разным основаниям, в каждом из которых стоит неизвестное.

Пример 2. Поиск набора решений логарифмического уравнения по множеству действительных Числа

Определить множество решений уравнения loglog𝑥+𝑥+3=0 в ℝ.

Ответ

В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри два логарифма по разным основаниям.

Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog

Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, log𝑥, как логарифм по основанию 3 с использованием 243=3 и log𝑎=𝑛: logloglogloglogloglog𝑥=𝑥243=𝑥3=15𝑥=𝑥.

Подставляя это в данное логарифмическое уравнение, получаем loglogloglogloglog𝑥+𝑥+3=0𝑥+𝑥+3=02𝑥=−3𝑥=−32.

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.

Наконец, преобразование log𝑥=−32 в экспоненциальную форму мы имеем 𝑥=3=13=13×3=13√3.

Таким образом, множество решений 13√3.

В следующем примере мы найдем решение логарифмического уравнения которое содержит сумму трех логарифмов по разным основаниям и неизвестное внутри каждого из логарифмов.

Пример 3. Поиск набора решений логарифмического уравнения по множеству действительных Числа

Найдите набор решений logloglog𝑥+𝑥+𝑥=21 в ℝ.

Ответ

В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри логарифм.

Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog

Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, log𝑥, как логарифм по основанию 2 с использованием 4=2 и log𝑎=𝑛, loglogloglogloglog𝑥=𝑥4=𝑥2=12𝑥, и аналогично для третьего члена log𝑥, используя 16=2 как loglogloglogloglog𝑥=𝑥16=𝑥2=14𝑥.

Подставляя эти выражения в логарифмическое уравнение, получаем loglogloglogloglogloglog𝑥+𝑥+𝑥=21𝑥+12𝑥+14𝑥=2174𝑥=21𝑥=12.

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.

Таким образом, переводя log𝑥=12 в показательную форму, получаем 𝑥=2=4096.

Следовательно, множество решений {4096}.

Теперь давайте рассмотрим пример, в котором нам нужно найти решение задачи. логарифмическое уравнение, содержащее сумму обратной трех логарифмы по разным основаниям и неизвестное, появляющееся внутри каждого из логарифмы.

Пример 4. Поиск набора решений логарифмического уравнения по множеству действительных Числа

Найдите набор решений 1𝑥+1𝑥+1𝑥=3logloglog в ℝ.

Ответ

В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри три логарифма по разным основаниям.

Чтобы решить уравнение, воспользуемся заменой основания формула, loglogloglogloglog𝑥=𝑥𝑎1𝑥=𝑎𝑥, и степенной закон, 𝑛𝑥=(𝑥). loglog

Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, 1𝑥log в виде логарифма по основанию 2 с использованием 4=2 и log𝑎=𝑛, 1𝑥=4𝑥=2𝑥=2𝑥,логлоглоглоглоглоглог и аналогично для третьего члена 1𝑥log, используя 8=2 как 1𝑥=8𝑥=2𝑥=3𝑥.loglogloglogloglog

Подставляя эти выражения в логарифмическое уравнение, получаем 1𝑥+1𝑥+1𝑥=31𝑥+2𝑥+3𝑥=36𝑥=3𝑥=2.loglogloglogloglogloglog

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.

Таким образом, переводя log𝑥=2 в экспоненциальную форму, находим 𝑥=2=4.

Таким образом, множество решений {4}.

В следующем примере мы решим логарифмическое уравнение, содержащее логарифмы по разным основаниям, включая дробное основание, и неизвестное появляется внутри журналов как линейный и квадратичный член.

Пример 5. Решение логарифмических уравнений, использующих законы логарифмов

Найдите набор решений loglog𝑥−𝑥=6 в ℝ.

Ответ

В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри два логарифма по разным основаниям.

Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog

Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, log𝑥 в виде логарифма по основанию 3 с использованием 13=3 и журнал𝑎=𝑛: logloglogloglogloglog𝑥=𝑥=𝑥3=−𝑥=−2𝑥.

Наконец, подставляя это выражение в данное логарифмическое уравнение, имеем loglogloglogloglog𝑥−𝑥=6𝑥+2𝑥=63𝑥=6𝑥=2. 

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.

Наконец, переводя log𝑥=2 в экспоненциальную форму, мы имеем 𝑥=3=9.

Таким образом, множество решений {9}.

Как мы видели в предыдущих примерах, изменение базового правила для логарифмы также позволяют нам вычислять выражения вида log𝑥, переписав этот логарифм по основанию 𝑎 как логарифм по основанию 𝑎 (т.е. 𝑏=𝑎) вместе со степенным законом loglog(𝑥)=𝑛𝑥 и факт этот журнал𝑎=𝑘: loglogloglog𝑥=𝑥𝑎=1𝑘𝑥.

Теперь давайте рассмотрим пример, где у нас есть логарифмическое уравнение который содержит логарифм логарифма с двумя различными основаниями и неизвестное, появляющееся внутри логарифма как квадратное.

Пример 6. Решение логарифмических уравнений с использованием законов логарифмов и Квадратные уравнения

Решить loglog𝑥−8𝑥=1, где 𝑥∈ℝ.

Ответ

В этом примере мы хотим определить решение конкретного логарифмическое уравнение с разными основаниями и неизвестной фигурой внутри логарифм логарифма в виде квадратного уравнения.

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, показательная форма 𝑦=𝑎 эквивалентна логарифмической форме 𝑥=𝑦log, что позволяет нам конвертировать из одного форму к другой, как только мы идентифицируем 𝑎, 𝑥, и 𝑦.

Преобразуя loglog𝑥−8𝑥=1 в экспоненциальную форму, получаем log𝑥−8𝑥=2=2.

Повторяя процесс, получаем 𝑥−8𝑥=3𝑥−8𝑥−9=0(𝑥−9)(𝑥+1)=0,

Следовательно, получаем 𝑥=−1 или 𝑥=9.Набор решений {−1,9}.

До сих пор в примерах, которые мы рассматривали, была неизвестная переменная 𝑥, которую мы должны решить, появляющуюся внутри сам логарифм. Мы также можем найти решения логарифмических уравнений, где неизвестное может появиться в основании логарифма.

В следующем примере рассмотрим логарифмическое уравнение с тройной логарифм по разным основаниям и неизвестное в качестве основания.

Пример 7. Решение логарифмических уравнений над набором действительных чисел

Решить logloglog36=0, где 𝑥∈ℝ.

Ответ

В этом примере мы хотим определить решение конкретного логарифмическое уравнение с тремя разными основаниями и неизвестной фигурой как основание логарифма.

Напомним, что для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентна экспоненциальному форма 𝑥=𝑎. Десятичный логарифм без основания указанный имеет основание 10: loglog=.

Переводя logloglog36=0 в экспоненциальную форму, получаем loglog36=10=1.

Повторяя этот процесс для полученного выражения, мы получаем лог36=2=2.

И повторив это еще раз напоследок, получим 𝑥=36. 

Таким образом, решения 𝑥=6 или 𝑥=−6, но мы игнорируем второе решение, так как логарифм отрицательного основания (т. е. log36), не определено.

Следовательно, решение логарифмического уравнения равно 𝑥=6.

Теперь давайте рассмотрим пример, где у нас есть логарифмическое уравнение содержащие логарифмы по разным основаниям и неизвестное, находящееся как внутри логарифм и основание того же логарифма.

Пример 8. Поиск решения системы экспоненциальных уравнений с логарифмами над набором действительных чисел

Найдите набор решений 𝑥=10logвойти ℝ.

Ответ

В этом примере мы хотим определить решение конкретного логарифмическое уравнение с двумя разными основаниями и неизвестной фигурой внутри и выступает как основание логарифма.

Для решения данного уравнения воспользуемся степенным законом: 𝑛𝑥=(𝑥).loglog

Применяя это и используя log𝑎=1, мы получаем loglog𝑥=6𝑥=6 и loglog10=6410=64. 

Подставляя их в данное уравнение, получаем 𝑥=64.

Решения: 𝑥=2 и 𝑥=−2; однако мы будем игнорировать второй как логарифм отрицательного числа или с отрицательным основанием не определено. Таким образом, множество решений {2}.

Используя формулу замены основания, мы можем поменять местами аргумент логарифм и основание.Изменение логарифма log𝑥 в базу 𝑏=𝑥 и используя log𝑥=1, имеем loglogloglog𝑥=𝑥𝑎=1𝑎.

Предположим, мы хотим найти решение loglog5=3; мы хотим определить значения 𝑥, которые удовлетворяют этому логарифмическому уравнению. С log𝑎=1, это упрощается до лог5=1.

Таким образом, преобразуя это в экспоненциальную форму с основанием 𝑥, получаем 𝑥=𝑥=5.

Наконец, давайте рассмотрим пример, когда неизвестное 𝑥, который мы должны решить, появляется как внутри логарифм и как основание другого логарифма.

Пример 9.

Поиск решения набора логарифмических уравнений по множеству вещественных Числа

Определить множество решений уравнения loglog𝑥+254=10 в ℝ.

Ответ

В этом примере мы хотим определить решение конкретного логарифмическое уравнение с двумя разными основаниями и неизвестной фигурой внутри и выступает как основание логарифма.

Чтобы решить логарифмическое уравнение, воспользуемся изменение базовой формулы: logloglog𝑥=𝑥𝑎.

Если мы используем основание 𝑏=𝑥, эта формула позволяет нам поменять местами аргумент логарифма и основание: loglogloglog𝑥=𝑥𝑎=1𝑎, где мы использовали тот факт, что log𝑥=1. Используя это, данное уравнение становится loglog𝑥+25𝑥=10.

Итак, если мы допустим 𝑦=𝑥log, то мы должны решить 𝑦+251𝑦=10.

Умножение обеих частей этого уравнения на 𝑦 и переставляя, получаем 𝑦−10𝑦+25=0(𝑦−5)=0. 

Таким образом, 𝑦=𝑥=5.log

Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентна экспоненциальной форме 𝑥=𝑎.

Таким образом, при преобразовании к экспоненциальному виду имеем 𝑥=4=1024.

Таким образом, множество решений {1024}.

Подведем итог тому, что мы узнали из этого объяснения.

Ключевые моменты

• Для решения логарифмических уравнений мы использовали законы logarithms:
  • Продукт : logloglog (𝑥𝑦) = 𝑥 + 𝑦,

  6 division : logloglog𝑥𝑦𝑥𝑦 = 𝑥-𝑦,

  • powers : loglog (𝑥 )=𝑛𝑥,
  • изменение основания : logloglog𝑥=𝑥𝑎.
• Если у нас есть логарифм основания 𝑎, мы также можем преобразовать его в логарифм основания 𝑎 с использованием loglog𝑥=1𝑘𝑥.
• Мы также можем поменять местами основание и аргумент логарифма, используя loglog𝑥=1𝑎. 2=b a2=b.

  ---

  Перепишите это как

  log⁡(10)log⁡(a)+log⁡(100)log⁡(b)=log⁡(1000000)log⁡(ab),\frac{\log(10)}{\log(a)} + \frac{\log(100)}{\log(b)} = \frac{\log(1000000)}{\log(ab)},log(a)log(10)​+log(b)log (100)​=log(ab)log(1000000)​,

  , где все журналы с основанием 10 10 10. Это упрощается до

  1log⁡(a)+2log⁡(b)=6log⁡(ab).\frac1{\log(a)}+\frac2{\log(b)} = \frac6{\log(ab)}.log (a)1​+log(b)2​=log(ab)6​.

  Пусть m=log⁡(a) m = \log(a) m=log(a) и n=log⁡(b) n = \log(b) n=log(b).2=б а2=б. □_\квадрат □​

  Отправьте свой ответ

  Сумма всех (положительных) решений уравнения

  log⁡16x+log⁡x16=log⁡512x+log⁡x512\log_{16}x +\log _x 16=\log_{512} x + \log_x {512}log16​x+logx​16=log512​ х+logx​512

  можно записать как ab \frac{a}{b} ba​, где aaa и bbb — взаимно простые положительные целые числа. {2}}992.

  Примечание : Вы можете использовать тот факт, что log⁡103=0,4771\log_{10} 3 = 0,4771log10​3=0,4771 исправить до 4 знаков после запятой.

  Экспоненциальные и логарифмические уравнения

  Экспоненциальные и логарифмические уравнения

  ---

  Содержание: Эта страница соответствует § 4.4 (стр. 348) текста.

  Предлагаемые проблемы из текста:

  р.355 #13,17,21,25,27,29,31,51,53,57,59,81,89

  Экспоненциальные уравнения

  Логарифмические уравнения

  ---

  Экспоненциальные уравнения

  Некоторые показательные уравнения можно решить, используя тот факт, что показательные функции взаимно однозначны. В других Другими словами, экспоненциальная функция не может принимать два разных значения одного и того же числа.

  Пример 1.

  3 ^х = 9

  3 ^х = 3 ²

  Функция f(x) = 3 ^x является взаимно однозначной, поэтому она не принимает два разных значения равных 9, поэтому x должен быть равен 2.

  х = 2

  Уравнение в примере 1 было легко решить, потому что мы могли выразить 9 как степень числа 3. Однако часто необходимо использовать логарифм при решении показательного уравнения.

  
  Пример 2.

  е ^х = 20

  Мы собираемся использовать тот факт, что натуральный логарифм является обратной экспоненциальной функцией, поэтому ln e ^x = x, по логарифмическому тождеству 1.Мы должны взять натуральный логарифм обеих частей уравнения.

  ln e ^x = ln 20

  Теперь левая часть упрощается до x, а правая часть представляет собой число. Это примерно 2,9957.

  х = 2,9957

  Упражнение 1 :

  Используйте калькулятор, чтобы проверить ответ, который мы нашли для уравнения в примере 2.

  Пример 3.

  5 ^x = 16 Мы решим это уравнение двумя разными способами.

  Первый подход: мы используем тот факт, что log ₅ 5 ^x = x (логарифмический тождество 1 снова).

  5 ^х = 16

  логарифм ₅ 5 ^x = логарифм ₅ 16

  х = журнал ₅ 16

  x = ln 16 / ln 5 по формуле замены основания.

  х = 1,7227 (приблизительно)

  Второй подход: мы будем использовать натуральный логарифм и свойство 3.

  5 ^x = 16 Возьмем натуральный логарифм обеих частей.

  ряд 5 ^x = ряд 16

  х пер. 5 = пер. 16

  х = пер. 16 / пер. 5

  х = 1,7227 (приблизительно)

  Во втором подходе мы могли использовать любой логарифм.Второй подход — тот, который вы видите чаще всего. довольно часто.

  Упражнение 2 :

  Используйте калькулятор, чтобы проверить ответ, который мы нашли для уравнения в примере 3.

  Уравнения, подобные приведенному в следующем примере, часто встречаются в приложениях.

  Пример 4.

  200 е ^0,07т = 500

  Сначала мы изолируем экспоненциальную часть, разделив обе части уравнения на 200.

  е ^0,07т = 2,5

  Теперь возьмем натуральный логарифм обеих частей.

  ln e ^{0,07 т} = ln 2,5

  Левая часть упрощается до 0,07t по логарифмическому тождеству 1.

  0,07t = ln 2,5

  т = ln (2,5) / 0,07

  т = 13,1 (приблизительно)

  Упражнение 3 :

  Решите следующие уравнения и проверьте ответы.

  (а) 3 ^х = 10

  (б) 150 е ^{0,05 т} = 350

  Ответить

  Вернуться к содержанию

  Логарифмические уравнения

  При решении экспоненциальных уравнений мы часто использовали логарифмическое тождество 1, потому что оно предполагает применение логарифмическая функция, чтобы «отменить» эффект экспоненциальной функции. При работе с логарифмическими уравнениями мы будем использовать логарифмическое тождество 2, где экспоненциальная функция применяется для «отмены» эффекта логарифмическая функция.

  Пример 5.

  2 log х = 12

  Мы хотим изолировать журнал x, поэтому делим обе части на 2.

  лог х = 6

  Поскольку log — это логарифм по основанию 10, мы применяем экспоненциальную функцию по основанию 10 к обеим частям уравнения.

  10 ^{журнал x} = 10 ⁶

  По логарифмическому тождеству 2 левая часть упрощается до x.

  х = 10 ⁶ = 1000000

  Пример 6.

  7 + 3 ln x = 15 Первый изолят ln x.

  3 ln х = 8

  ln х = 8/3

  Теперь применим экспоненциальную функцию к обеим сторонам.

  e ^{ln x} = e ^8/3

  х = е ^8/3

  Это точный ответ.Если вы воспользуетесь калькулятором для вычисления этого выражения, вы получите аппроксимацию . к ответу.

  х примерно равно 14,39.

  Упражнение 4 :

  Проверьте ответы в примерах 5 и 6.

  Пример 7.

  пер (х + 4) + пер (х — 2) = пер 7

  Сначала мы используем свойство 1 логарифмов, чтобы скомбинировать члены слева.

  пер (х + 4)(х — 2) = пер 7

  Теперь применим экспоненциальную функцию к обеим сторонам.

  e ^{ln (x + 4)(x — 2)} = e ^{ln 7}

  Логарифмическое тождество 2 позволяет упростить обе части.

  (х + 4)(х — 2) = 7

  х ² + 2х — 8 = 7

  х ² + 2х — 15 = 0

  (х — 3)(х + 5) = 0

  х = 3 или х = -5

  x = 3 проверки, для ln 7 + ln 1 = ln 7.

  x = -5 не проверяет , потому что, когда мы пытаемся заменить x на -5 в исходном уравнении, мы получаем натуральный логарифм отрицательных чисел, который не определен.

  Итак, x = 3 — единственное решение.

  Вернуться к содержанию

  ---

  Алгебра 2: Решение логарифмических уравнений: Алгебра II: TI Math Nspired

  Управляйте настройками файлов cookie

  Вы можете контролировать свои предпочтения относительно того, как мы используем файлы cookie для сбора и использования информации, когда вы находитесь на веб-сайтах TI, настраивая статус этих категорий.

  Категория	Описание	Разрешить
  Аналитические и эксплуатационные файлы cookie	Эти файлы cookie, в том числе файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, упрощая поиск информации на сайте).
  Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления, чтобы они лучше соответствовали вашим интересам, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
  Функциональные файлы cookie	Эти файлы cookie помогают определить, кто вы, и хранить информацию о вашей деятельности и учетной записи, чтобы обеспечить расширенные функциональные возможности, включая более персонализированный и актуальный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и службы сайта могут работать неправильно. Если вы не разрешите эти файлы cookie, некоторые или все функции и службы сайта могут работать неправильно.
  Файлы cookie социальных сетей	Эти файлы cookie позволяют идентифицировать пользователей и контент, связанный с онлайн-социальными сетями, такими как Facebook, Twitter и другие платформы социальных сетей, и помогают TI улучшить охват социальных сетей.
  Строго необходимо	Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы положили в свою корзину на TI. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт