Решение логарифмических уравнений (продолжение). Видеоурок. Алгебра 11 Класс
На данном уроке мы продолжим решать разнообразные типовые логарифмические уравнения, рассмотрим уравнения повышенной сложности.
Ключом к решению логарифмических уравнений являются свойства логарифмической функции, т. е. функции вида 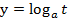 (
(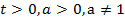 ). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.
). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.
Вспомним основные свойства логарифмической функции.
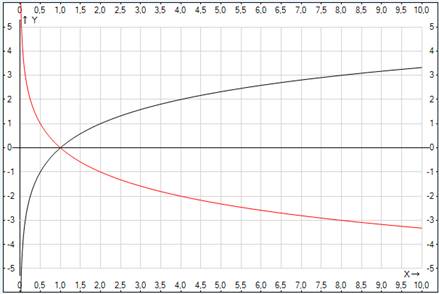
Рис. 1. График логарифмической функции при различных основаниях
Функция монотонна на всей своей области определения. При 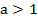
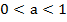 монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности). Именно монотонность функции позволяет решать простейшие логарифмические уравнения (т. к. из равенства логарифмов по одному основанию вытекает равенство подлогарифмических выражений
монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности). Именно монотонность функции позволяет решать простейшие логарифмические уравнения (т. к. из равенства логарифмов по одному основанию вытекает равенство подлогарифмических выражений 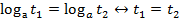 ), все остальные логарифмические уравнение сводятся к простейшим:
), все остальные логарифмические уравнение сводятся к простейшим: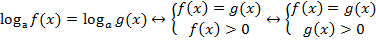
ОДЗ заданного уравнения определяется системой. Под логарифмом может стоять только положительное число, имеем:
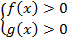
Мы выяснили, что функции f и g равны, поэтому достаточно выбрать одно любое неравенство, чтобы соблюсти ОДЗ.
Имеем смешанную систему. Неравенство, как правило, решать необязательно, достаточно решить уравнение и найденные корни подставить в неравенство, таким образом выполнить проверку.
Напомним методику решения простейших логарифмических уравнений:
Уравнять основания логарифмов;
Приравнять подлогарифмические функции;
Выполнить проверку.
Перейдем к решению примеров.
Пример 1 – решить уравнение:
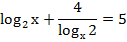
Отметим ОДЗ: 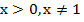
Нам известно следующее свойство логарифма:
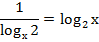
Получаем:

Приведем подобные:
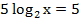
Сократим численный множитель
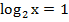
Преобразуем согласно определению логарифма:
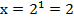
Пример 2 – решить показательное уравнение:
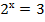
Способ 1 (по определению логарифма):
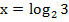
Способ 2 (прологарифмировать обе части):
Рекомендация – если неизвестное находится в показателе, то часто применяется такой способ решения. Но нужно обратить внимание на вопрос – можно ли в данном случае логарифмировать? В заданном примере и левая, и правая части строго положительны, поэтому имеем право записать:

Вынесем показатель степени как сомножитель согласно свойству логарифма:
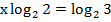
Упростим:
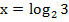
Способ 3 (уравнять основания в показательном уравнении):
Воспользуемся основным логарифмическим тождеством:
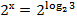
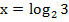
Пример 3 – решить показательно-степенное уравнение:
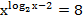
Укажем ОДЗ: 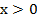
Теперь имеем право прологарифмировать обе части. Выбираем основание логарифма 2, т. к. такое основание уже представлено в уравнении:
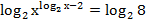
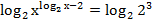
Вынесем показатели степени как сомножители:
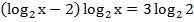
Упростим правую часть:
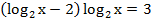
Введем замену переменых:
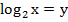
Получаем:
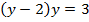
Раскроем скобки и перенесем все члены в одну сторону:
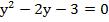
Получили квадратное уравнение, согласно теореме Виета, имеем корни:
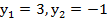
Вернемся к исходным переменным:
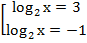
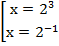
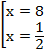
Ответ: 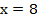
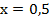
Пример 4 – решить уравнение:
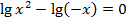
ОДЗ: 
Вынесем показатель степени как сомножитель, при этом используем модуль, чтобы не исказить область определения:
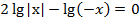
Раскроем модуль, учитывая ОДЗ:
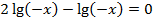
Приведем подобные:
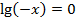

Ответ: 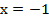
Итак, мы рассмотрели решение более сложных типовых логарифмических уравнений. Далее перейдем к изучению логарифмических неравенств.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Reshit.ru (Источник).
- Egesdam.ru (Источник).
- Math.md (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 518–520;
2. Решить уравнение:
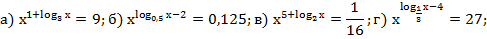
3. Решить уравнение:

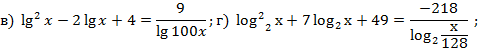
interneturok.ru
Логарифмические уравнения — подготовка к ЕГЭ по Математике
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
.
При этом .
Обратим внимание на область допустимых значений логарифма:
.
Основное логарифмическое тождество:
,
.
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
.
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
1.Решите уравнение:
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Получаем:
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
Ответ: -124
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
;
;
;
4. Решите уравнение:
Область допустимых значений: Значит,
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .
.
Ответ: 21.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
6.Решите уравнение: .
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
Ответ: 19.
7.Решите уравнение: .
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие .
Ответ:
8. Решите уравнение .
ОДЗ уравнения:
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
9.Решите уравнение:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
«Отбрасываем» логарифмы.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Ответ: .
Логарифмические уравнения могут встретиться вам и в задании №5 Профильного ЕГЭ по математике, и в задании №13. И если в задании №5 нужно решить простейшее уравнение, то в задаче 13 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Логарифмические уравнения в задаче C1
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
log2x = 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
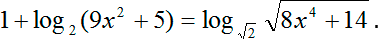
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не cодержали, обязательно нужно привести к уравнению вида:
logaf (x) = logag(x)
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
logaf (x) + logag(x) = logaf (x) · g(x)
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
a = logbba
Здесь нужно понимать: когда мы говорим «Любое основание b», то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0 < b ≠ 1
Давайте посмотрим, что происходит в нашем случае:
1 = log2 21 = log2 2
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
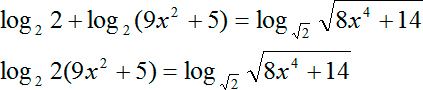
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
logabn = n · logab
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
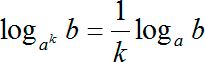
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k.
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
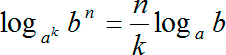
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n), окажется в числителе. А то, что было степенью у основания, ak, отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Вынесение степени из основания логарифма
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
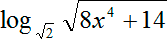
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
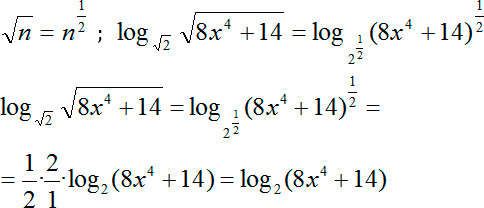
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log2 2(9x2 + 5) = log2 (8x4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
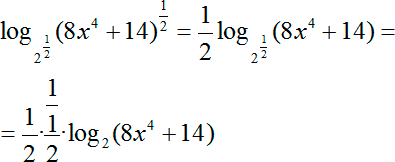
Давайте разберемся, что такое дробь. Запишем:
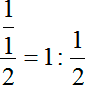
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
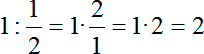
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x2 + 5) = 8x4 + 14
Давайте раскроем скобки слева. Получим:
18x2 + 10 = 8x4 + 14
Перенесем все из левой части в правую:
8x4 + 14 − 18x2 − 10 = 0
Приведем подобные и получим:
8x4 − 18x2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x4 − 9x2 + 2 = 0
Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x, а x2, потому что у нас биквадратное уравнение. Итак, наши варианты:
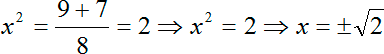
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
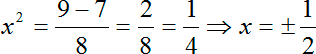
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x2 + 5 (эта функция всегда положительна), либо 8x4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
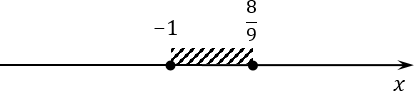
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9 < 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:
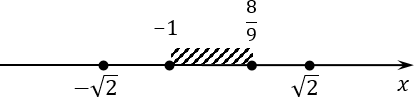
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:

Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
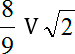
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
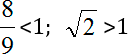
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
- Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
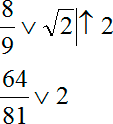
Теперь это все легко сравнивается. Дело в том, что 64/81 < 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b, именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Смотрите также:
- Задача C1: логарифмы и тригонометрия в одном уравнении

- Задача C1: еще одно показательное уравнение

- Пробный ЕГЭ-2011 по математике, вариант №8

- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)

- Метод коэффициентов, часть 1

- Изюм и виноград (смеси и сплавы)

www.berdov.com
Уравнения, квадратные относительно логарифма
На уравнениях такого вида многие ученики «зависают». При этом сами задачи отнюдь не являются сложными — достаточно просто выполнить грамотную замену переменной, для чего следует научиться выделять устойчивые выражения.
В дополнение к этому уроку вас ждет довольно объемная самостоятельная работа, состоящая из двух вариантов по 6 задач в каждом.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе… впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.
Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2x · log2 (x − 3) + 1 = log2 (x2 − 3x)
В первую очередь отметим, что x2 − 3x можно разложить на множители:
log2x(x− 3)
Затем вспоминаем замечательную формулу:
logafg = logaf + logag
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g— обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f < 0; g < 0
В этом случае произведение fg будет положительным, следовательно, loga (fg) будет существовать, а вот logaf и logag отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
В нашем случае все просто. Поскольку в исходном уравнении есть функция log2x, то x > 0 (ведь переменная x стоит в аргументе). Также имеется log2 (x − 3), поэтому x − 3 > 0.
Следовательно, в функции log2x(x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2x log2 (x − 3) + 1 = log2x + log2 (x − 3)
log2x log2 (x − 3) + 1 − log2x− log2 (x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
log2x = а
log2 (x − 3) = b
Получим:
a· b + 1 − a − b = 0
А теперь сгруппируем третье слагаемое с первым:
(a · b − a) + (1 − b) = 0
a(1 · b − 1) + (1 − b) = 0
Заметим, что и в первой, и во второй скобке стоит b− 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − (b − 1) = 0
(b − 1)(а · 1 − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
b − 1 = 0 ⇒ b = 1;
a − 1 = 0 ⇒ a = 1.
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
log2x = 1 ⇒ log2x = log2 2 ⇒ x1 =2;
log2 (x − 3) = 1 ⇒ log2 (x − 3) = log2 2 ⇒ x2 = 5
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
x > 0
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
x − 3 > 0 ⇒ x > 3
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 (x2 − 6x + 2) = log0,7 (7 − 2x)
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x2 − 6x + 2 = 7 − 2x
x2 − 6x + 2 − 7 + 2x = 0
x2 − 4x − 5 = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
(x − 5) (x + 1) = 0;
x − 5 = 0 ⇒ x = 5;
x + 1 = 0 ⇒ x = −1.
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
x2 − 6x + 2 > 0
С другой — второй аргумент тоже должен быть больше нуля:
7 − 2x > 0
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x2 − 6x + 2 > 0 и 7 − 2x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
−2x > −7
x < 3,5
Поскольку мы делили обе части на отрицательное число, знак неравенства поменялся.
Итак, мы нашли ОДЗ без всяких квадратных неравенств, дискриминантов и пересечений. Теперь осталось просто выбрать корни, которые лежат на данном интервале. Очевидно, что нас устроит лишь x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
- Не бойтесь раскладывать логарифмы на множители, а потом множители раскладывать на сумму логарифмов. Однако помните, что разбивая произведение на сумму двух логарифмов, вы тем самым сужаете область определения. Поэтому прежде чем выполнять такое преобразование, обязательно проверьте, каковы требования области определения. Чаще всего никаких проблем не возникает, однако лишний раз перестраховаться не помешает.
- Избавляясь от канонической формы, старайтесь оптимизировать вычисления. В частности, если от нас требуется, чтобы f > 0 и g > 0, но в самом уравнении f = g, то смело вычеркиваем одно из неравенств, оставляя себе лишь самое простое. Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Вот, собственно, и все, что я хотел рассказать о группировке.:)
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Дробно-рациональные уравнения с логарифмами
Сразу следует отметить, что это довольно коварный тип уравнений, в которых отнюдь не всегда сразу присутствует дробь с логарифмом где-то в знаменателе. Однако в процессе преобразований такая дробь обязательно возникнет.
При этом будьте внимательны: в процессе преобразований изначальная область определения логарифмов может существенно измениться!
Переходим к еще более жестким логарифмическим уравнениям, содержащим дроби и переменные основания. Чтобы за один короткий урок успеть больше, я не буду рассказывать элементарную теорию. Сразу перейдем к задачам:
4 log25 (x − 1) − log3 27 + 2 logx− 1 5 = 1
Посмотрев на это уравнение, кто-то спросит: «При чем здесь дробно-рациональное уравнение? Где в этом уравнении дробь?» Давайте не будем спешить и внимательно посмотрим на каждое слагаемое.
Первое слагаемое: 4 log25 (x − 1). Основанием логарифма является число, но в аргументе стоит функция от переменной x. С этим мы пока ничего сделать не можем. Идем дальше.
Следующее слагаемое: log 3 27. Вспоминаем, что 27 = 33. Следовательно, весь логарифм мы можем переписать следующим образом:
log 3 27 = 33 = 3
Итак, второе слагаемое — это просто тройка. Третье слагаемое: 2 logx− 1 5. Тут тоже не все просто: в основании стоит функция, в аргументе — обычное число. Предлагаю перевернуть весь логарифм по следующей формуле:
logab = 1/logba
Такое преобразование можно выполнить только если b ≠ 1. Иначе логарифм, который получится в знаменателе второй дроби, просто не будет существовать. В нашем случае b= 5, поэтому все в порядке:
2 logx− 1 5 = 2/log5 (x− 1)
Перепишем исходное уравнение с учетом полученных преобразований:
4 log25 (x − 1) − 3 + 2/ log5 (x− 1) = 1
В знаменателе дроби у нас стоит log5 (x− 1), а в первом слагаемом мы имеем log25 (x − 1). Но 25 = 52, поэтому выносим квадрат из основания логарифма по правилу:

Другими словами, степень в основании логарифма становится дробью спереди. А выражение перепишется так:
4 1/2 log5 (x− 1) − 3 + 2/ log5 (x− 1) − 1 = 0
У нас получилось длинное уравнение с кучей одинаковых логарифмов. Введем новую переменную:
log5 (x − 1) = t;
2t− 4 + 2/t = 0;
А вот это уже дробно-рациональное уравнение, которое решается средствами алгебры 8—9 класса. Для начала разделим все на двойку:
t− 2 + 1/t = 0;
(t2 − 2t + 1)/t = 0
В скобках стоит точный квадрат. Свернем его:
(t− 1)2/t = 0
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Никогда не забывайте про этот факт:
(t− 1)2= 0
t = 1
t ≠ 0
Вспоминаем, что такое t:
log5 (x − 1) = 1
log5 (x − 1) = log5 5
Избавляемся от знаков log, приравниваем их аргументы, и получаем:
x− 1 = 5 ⇒ x = 6
Все. Задача решена. Но давайте вернемся к исходному уравнению и вспомним, что там присутствовали сразу два логарифма с переменной x. Поэтому нужно выписать область определения. Поскольку x− 1 стоит в аргументе логарифма, это выражение должно быть больше нуля:
x− 1 > 0
С другой стороны, тот же x− 1 присутствует и в основании, поэтому должен отличаться от единицы:
x− 1 ≠ 1
Отсюда заключаем:
x > 1; x ≠ 2
Эти требования должны выполняться одновременно. Значение x = 6 удовлетворяет обоим требованиям, поэтому является x = 6 окончательным решением логарифмического уравнения.
Переходим ко второй задаче:

Вновь не будем спешить и посмотрим на каждое слагаемое:
log4 (x + 1) — в основании стоит четверка. Обычное число, и его можно не трогать. Но в прошлый раз мы наткнулись на точный квадрат в основании, который пришлось выносить из-под знака логарифма. Давайте сейчас сделаем то же самое:
log4 (x + 1) = 1/2 log2 (x + 1)
Фишка в том, что у нас уже есть логарифм с переменной x, хоть и в основании — он является обратным к логарифму, который мы только что нашли:
8 logx + 1 2 = 8 · (1/log2 (x + 1)) = 8/log2 (x + 1)
Следующее слагаемое — log2 8. Это константа, поскольку и аргументе, и в основании стоят обычные числа. Найдем значение:
log2 8 = log2 23 = 3
То же самое мы можем сделать и с последним логарифмом:

Теперь перепишем исходное уравнение:
1/2 · log2 (x + 1) + 8/log2 (x + 1) − 3 − 1 = 0;
log2 (x + 1)/2 + 8/log2 (x + 1) − 4 = 0
Приведем все к общему знаменателю:

Перед нами опять дробно-рациональное уравнение. Введем новую переменную:
t = log2 (x + 1)
Перепишем уравнение с учетом новой переменной:

Будьте внимательны: на этом шаге я поменял слагаемые местами. В числителе дроби стоит квадрат разности:

Как и в прошлый раз, дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:
(t− 4)2 = 0 ⇒ t = 4;
t ≠ 0
Получили один корень, который удовлетворяет всем требованиям, поэтому возвращаемся к переменной x:
log2 (x + 1) = 4;
log2 (x + 1) = log2 24;
x + 1 = 16;
x = 15
Все, мы решили уравнение. Но поскольку в исходном уравнении присутствовало несколько логарифмов, необходимо выписать область определения.
Так, выражение x + 1 стоит в аргументе логарифма. Поэтому x + 1 > 0. С другой стороны, x + 1 присутствует и в основании, т.е. x + 1 ≠ 1. Итого:
0 ≠ x > −1
Удовлетворяет ли найденный корень данным требованиям? Безусловно. Следовательно, x = 15 является решением исходного логарифмического уравнения.
Напоследок хотел бы сказать следующее: если вы смотрите на уравнение и понимаете, что вам предстоит решать что-то сложное и нестандартное, по старайтесь выделить устойчивые конструкции, которые впоследствии будут обозначены другой переменной. Если же какие-то слагаемые вообще не содержат переменную x, их зачастую можно просто вычислить.
Вот и все, о чем я хотел сегодня рассказать. Надеюсь, этот урок поможет вам в решении сложных логарифмических уравнений. Смотрите другие видеоуроки, скачивайте и решайте самостоятельные работы, и до встречи в следующем видео!
Смотрите также:
- Заключительный комплект уроков по решению логарифмических уравнений

- Логарифмические уравнения: несколько видеоуроков по теме

- Пробный ЕГЭ 2012. Вариант 8 (без производных)

- Пробный ЕГЭ-2011 по математике, вариант №4

- Задачи B6 с монетами

- Задачи на проценты считаем проценты с помощью формулы

www.berdov.com
Методика решения логарифмических уравнений
Введение
Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем как поддержать у студентов интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль студентов, стимулировали бы их к самостоятельному приобретению знаний.
Возникновение интереса к математике у значительного числа студентов зависит в большей степени от методики ее преподавания, от того, на сколько умело будет построена учебная работа. Вовремя обращая внимание студентов на то, что математика изучает общие свойства объектов и явлений окружающего мира, имеет дело не с предметами, а с отвлеченными абстрактными понятиями, можно добиться понимания того, что математика не нарушает связи с действительностью, а, напротив, дает возможность изучить ее глубже, сделать обобщенные теоретические выводы, которые широко применяются в практике.
Участвуя в фестивале педагогических идей «Открытый урок» 2004-2005 учебного года, я представила урок-лекцию по теме «Логарифмическая функция» (диплом № 204044). Считаю этот метод наиболее удачным в данном конкретном случае. В результате изучения у студентов имеется подробный конспект и краткая схема по теме, что облегчит им подготовку к следующим урокам. В частности, по теме «Решение логарифмических уравнений», которая полностью опирается на изучение логарифмической функции и ее свойств.
При формировании основополагающих математических понятий важно создать у студентов представление о целесообразности введения каждого из них и возможности их применения. Для этого необходимо, чтобы при формулировке определения некоторого понятия, работе над его логической структурой, рассматривались вопросы об истории возникновения данного понятия. Такой подход поможет студентам осознать, что новое понятие служит обобщением фактов реальной действительности.
История возникновения логарифмов подробно представлена в работе прошлого года.
Учитывая важность преемственности при обучении математике в среднем специальном учебном заведении и в вузе и необходимость соблюдения единых требований к студентам считаю целесообразным следующую методику ознакомления студентов с решением логарифмических уравнений.
Уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма), называются логарифмическими. Рассмотрим логарифмические уравнения вида:
(1)
Решение этих уравнений основано на следующей теореме.
Теорема 1. Уравнение равносильно системе
(2)
Для решения уравнения (1) достаточно решить уравнение
(3)
и его решения подставить в систему неравенств
(4),
задающую область определения уравнения (1).
Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1).
При решения логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения, обязательна.
Пример 1: Решить уравнение
Решение:
Оба значения х удовлетворяют условиям системы.
Ответ:
Рассмотрим уравнения вида:
(5)
Их решение основано на следующей теореме
Теорема 2: Уравнение (5) равносильно системе
(6)
Корнями уравнения (5) будут только те корни уравнения , которые
принадлежат области определения, задаваемой условиями .
Логарифмическое уравнение вида (5) можно решить различными способами. Рассмотрим основные из них.
1. ПОТЕНЦИНИРОВАНИЕ (применение свойств логарифма).
Пример 2: Решить уравнение
Решение: В силу теоремы 2 данное уравнение равносильно системе:
Решим уравнение:
Всем условиям системы удовлетворяет лишь один корень. Ответ:
2. ИСПОЛЬЗОВАНИЕ ОПРЕДЕЛЕНИЯ ЛОГАРИФМА .
Пример 3: Найти х, если
Решение:
Значение х = 3 принадлежит области определения уравнения. Ответ х = 3
3. ПРИВЕДЕНИЕ К КВАДРАТНОМУ УРАВНЕНИЮ.
Пример 4: Решить уравнение
Оба значения х являются корнями уравнения.
Ответ:
4. ЛОГАРИФМИРОВАНИЕ.
Пример 5: Решить уравнение
Решение: Прологарифмируем обе части уравнения по основанию 10 и применим свойство «логарифм степени».
Оба корня принадлежат области допустимых значений логарифмической функции.
Ответ: х = 0,1; х = 100
5. ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ.
Пример 6: Решить уравнение
Воспользуемся формулой и перейдем во всех слагаемых к логарифму по основанию 2:
Тогда данное уравнение примет вид:
Так как , то это корень уравнения.
Ответ: х = 16
6. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ.
Решим способом введения вспомогательной переменной уравнение, заданное в примере 6.
Пусть ; тогда
Учитывая, что
Получим уравнение:
После проверки, проведенной устно, легко убеждаемся в правильности найденного ответа.
7. ГРАФИЧЕСКИЙ СПОСОБ.
Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически.
Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении.
Пример 7: Решить уравнение
Решение: Построим графики функций и y = x
Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).
Ответ: корней нет
8. МЕТОД ПОДБОРА.
Пример 8: Найти х, если
Решение: С помощью рассмотренных выше способов корни уравнения найти не удается. Найдем какой-нибудь корень методом подбора.
Пусть, например, х = 10. Проверкой убедимся в том, что 10 — корень уравнения. Действительно,
истинно
Докажем, что других корней данное уравнение не имеет.
Эти корни следует искать во множестве значений х.
Допустимые значения х находятся в промежутке
На этом промежутке функция убывает, а функция возрастает. И, значит, если уравнение имеет решение, то оно единственное.
Итак, получаем
Ответ: х = 10
Упражнения для закрепления:
urok.1sept.ru
Решение логарифмических уравнений. Как решать, на примерах.
Логарифмическим уравнением называется уравнение, в котором неизвестное (х) и выражения с ним находятся под знаком логарифмической функции. Решение логарифмических уравнений подразумевает, что вы уже знакомы с понятием и видами логарифмов и основными формулами.
Как решать логарифмические уравнения?
Самое простое уравнение имеет вид logax = b, где a и b -некоторые числа,x — неизвестное.
Решением логарифмическое уравнения является x = a b при условии: a > 0, a 1.
Следует отметить, что если х будет находиться где-нибудь вне логарифма, например log2х = х-2, то такое уравнение уже называется смешанным и для его решения нужен особый подход.
Идеальным случаем является ситуация, когда Вам попадется уравнение, в котором под знаком логарифма находятся только числа, например х+2 = log22. Здесь достаточно знать свойства логарифмов для его решения. Но такая удача случается не часто, поэтому приготовьтесь к более сложным вещам.
Но сначала, все-таки, начнём с простых уравнений. Для их решения желательно иметь самое общее представление о логарифме.
Решение простейших логарифмических уравнений
К таковым относятся уравнения типа log2х = log216. Невооруженным глазом видно, что опустив знак логарифма получим х = 16.
Для того, чтобы решить более сложное логарифмическое уравнение, его обычно приводят к решению обычного алгебраического уравнения или к решению простейшего логарифмического уравнения logax = b. В простейших уравнениях это происходит в одно движение, поэтому они и носят название простейших.
Вышеиспользованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. В математике эта операция носит название потенцирования. Существуют определенные правила или ограничения для подобного рода операций:
- одинаковые числовые основания у логарифмов
- логарифмы в обоих частях уравнения находятся свободно, т.е. без каких бы то ни было коэффициентов и других разного рода выражений.
Скажем в уравнении log2х = 2log2 (1- х) потенцирование неприменимо — коэффициент 2 справа не позволяет. В следующем примере log2х+log2 (1 — х) = log2 (1+х) также не выполняется одно из ограничений — слева логарифма два. Вот был бы один – совсем другое дело!
Вообщем, убирать логарифмы можно только при условии, что уравнение имеет вид:
loga (…) = loga (…)
В скобках могут находится совершенно любые выражения, на операцию потенцирования это абсолютно никак не влияет. И уже после ликвидации логарифмов останется более простое уравнение – линейное, квадратное, показательное и т.п., которое Вы уже, надеюсь, умеете решать.
Возьмем другой пример:
log3 (2х-5) = log3х
Применяем потенцирование, получаем:
2х-5 = х
х=5
Пойдем дальше. Решим следующий пример:
log3 (2х-1) = 2
Исходя из определения логарифма, а именно, что логарифм — это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (4х-1), получаем:
3 2 = 2х-1
Дальше уже дело техники:
2х-1 = 9
х =5
Опять получили красивый ответ. Здесь мы обошлись без ликвидации логарифмов, но потенцирование применимо и здесь, потому как логарифм можно сделать из любого числа, причем именно такой, который нам надо. Этот способ очень помогает при решении логарифмических уравнений и особенно неравенств.
Решим наше логарифмическое уравнение log3 (2х-1) = 2 с помощью потенцирования:
Представим число 2 в виде логарифма, например, такого log39, ведь 3 2=9.
Тогда log3 (2х-1) = log39 и опять получаем все то же уравнение 2х-1 = 9. Надеюсь, все понятно.
Вот мы и рассмотрели как решать простейшие логарифмические уравнения, которые на самом деле очень важны, ведь решение логарифмических уравнений, даже самых страшных и закрученных, в итоге всегда сводится к решению простейших уравнений.
Во всем, что мы делали выше, мы упускали из виду один очень важный момент, который в последующем будет иметь решающую роль. Дело в том, что решение любого логарифмического уравнения, даже самого элементарного, состоит из двух равноценных частей. Первая – это само решение уравнения, вторая — работа с областью допустимых значений (ОДЗ). Вот как раз первую часть мы и освоили. В вышеприведенных примерах ОДЗ на ответ никак не влияет, поэтому мы ее и не рассматривали.
А вот возьмем другой пример:
log3 (х 2-3) = log3 (2х)
Внешне это уравнение ничем не отличается от элементарного, которое весьма успешно решается. Но это не совсем так. Нет, мы конечно же его решим, но скорее всего неправильно, потому что в нем кроется небольшая засада, в которую сходу попадаются и троечники, и отличники. Давайте рассмотрим его поближе.
Допустим необходимо найти корень уравнения или сумму корней, если их несколько:
log3 (х 2-3) = log3 (2х)
Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.
х 2-3 = 2х
х 2-2х-3 = 0
Находим корни уравнения:
х1= 3
х2= -1
Получилось два корня.
Ответ: 3 и -1
С первого взгляда все правильно. Но давайте проверим результат и подставим его в исходное уравнение.
Начнем с х1= 3:
log36 = log36
Проверка прошла успешно, теперь очередь х2= -1:
log3 (-2) = log3 (-2)
Так, стоп! Внешне всё идеально. Один момент — логарифмов от отрицательных чисел не бывает! А это значит, что корень х = -1 не подходит для решения нашего уравнения. И поэтому правильный ответ будет 3, а не 2, как мы написали.
Вот тут-то и сыграла свою роковую роль ОДЗ, о которой мы позабыли.
Напомню, что под областью допустимых значений принимаются такие значения х, которые разрешены или имеют смысл для исходного примера.
Без ОДЗ любое решение, даже абсолютно правильное, любого уравнения превращается в лотерею — 50/50.
Как же мы смогли попасться при решении, казалось бы, элементарного примера? А вот именно в момент потенцирования. Логарифмы пропали, а с ними и все ограничения.
Что же в таком случае делать? Отказываться от ликвидации логарифмов? И напрочь отказаться от решения этого уравнения?
Нет, мы просто, как настоящие герои из одной известной песни, пойдем в обход!
Перед тем, как приступать к решению любого логарифмического уравнения, будем записывать ОДЗ. А вот уж после этого можно делать с нашим уравнением все, что душа пожелает. Получив ответ, мы просто выбрасываем те корни, которые не входят в нашу ОДЗ, и записываем окончательный вариант.
Теперь определимся, как же записывать ОДЗ. Для этого внимательно осматриваем исходное уравнение и ищем в нем подозрительные места, вроде деления на х, корня четной степени и т.п. Пока мы не решили уравнение, мы не знаем – чему равно х, но твердо знаем, что такие х, которые при подстановке дадут деление на 0 или извлечение квадратного корня из отрицательного числа, заведомо в ответ не годятся. Поэтому такие х неприемлемы, остальные же и будут составлять ОДЗ.
Воспользуемся опять тем же уравнением:
log3 (х 2-3) = log3 (2х)
log3 (х 2-3) = log3 (2х)
Как видим, деления на 0 нет, квадратных корней также нет, но есть выражения с х в теле логарифма. Тут же вспоминаем, что выражение, находящееся внутри логарифма, всегда должно быть >0. Это условие и записываем в виде ОДЗ:
Т.е. мы еще ничего не решали, но уже записали обязательное условие на всё подлогарифменное выражение. Фигурная скобка означает, что эти условия должны выполняться одновременно.
ОДЗ записано, но необходимо еще и решить полученную систему неравенств, чем и займемся. Получаем ответ х > v3. Теперь точно известно – какие х нам не подойдут. А дальше уже приступаем к решению самого логарифмического уравнения, что мы и сделали выше.
Получив ответы х1= 3 и х2= -1, легко увидеть, что нам подходит лишь х1= 3, его и записываем, как окончательный ответ.
На будущее очень важно запомнить следующее: решение любого логарифмического уравнения делаем в 2 этапа. Первый — решаем само уравнение, второй – решаем условие ОДЗ. Оба этапа выполняются независимо друг от друга и только лишь при написании ответа сопоставляются, т.е. отбрасываем все лишнее и записываем правильный ответ.
Для закрепления материала настоятельно рекомендуем посмотреть видео:
На видео другие примеры решения лог. уравнений и отработка метода интервалов на практике.
На это по вопросу, как решать логарифмические уравнения, пока всё. Если что то по решению лог. уравнений осталось не ясным или непонятным, пишите свои вопросы в комментариях.
Заметка: Академия социального образования (КСЮИ) — готова принять новых учащихся.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Логарифмы и логарифмические уравнения
Логарифмические уравнения и решение логарифмических уравнений входят в обязательный комплекс знаний и умений школьника, если он стремится сдать ЕГЭ по математике на высокий балл и поступить в ВУЗ, стать студентом. Рассмотрим, что же это такое — логарифм, логарифмические уравнения и как их решать.
Логарифм — что это
Логарифмом числа 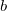 по основанию
по основанию  (
(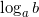 =c)называется такой показатель степени
=c)называется такой показатель степени  , в которую нужно возвести
, в которую нужно возвести  , чтобы получить
, чтобы получить 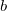 (то есть
(то есть 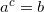 ). При этом задаются ограничения:
). При этом задаются ограничения: 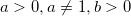 . Значение
. Значение  логарифма может быть любым.
логарифма может быть любым.
Вычислите:
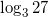 ,
, 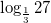 .
.
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
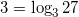 .
.
2. При возведении 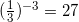 , значит
, значит 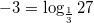 .
.
Ответ: 3; -3.
Изобретенные в 17 веке для ускорения вычислений, логарифмы значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в числовой работе более 300 лет, пока совершенство механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделали их устаревшими для крупномасштабных вычислений. Однако натуральный логарифм (с основанием e ≅ 2.71828 и записываемый как ln n) продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Логарифмическая функция и ее график
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть 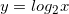 . Подставим вместо
. Подставим вместо  разные числа и определим соответствующие значения переменной.
разные числа и определим соответствующие значения переменной.
Отметим координаты точек на плоскости и соединим их плавной линией.
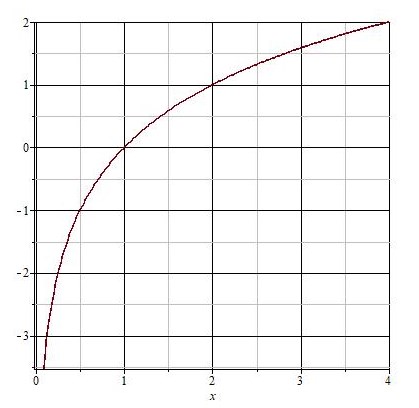
Логарифмическая функция все время возрастает.
Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь 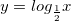 . Составим таблицу значений для этого случая.
. Составим таблицу значений для этого случая.
Получим следующий график функции:
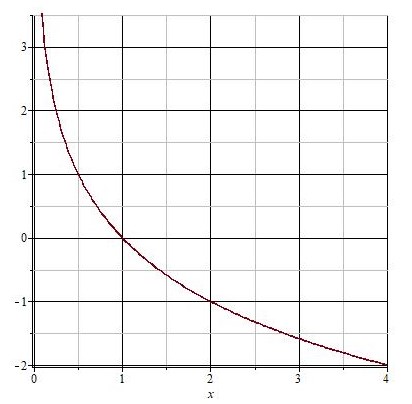
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять 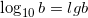 и логарифмы с натуральным основанием
и логарифмы с натуральным основанием 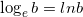 .
.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.
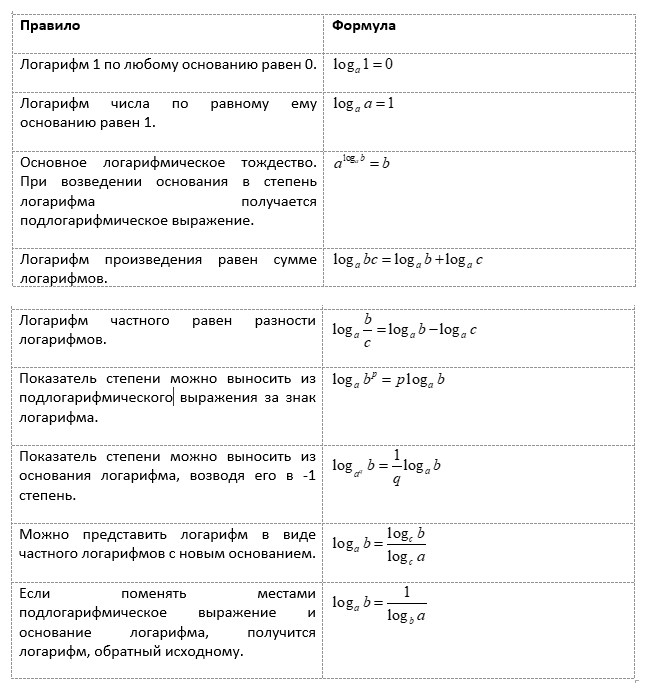
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие, утомительные вычисления.
В частности, ученые могли найти произведение двух чисел m и n, посмотрев логарифм каждого числа в специальной таблице, сложив логарифмы, а затем снова сверившись с таблицей, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в терминах обычных логарифмов, эта связь определяется как log m n = log m + log n.
Например, 100 × 1000 можно рассчитать, просмотрев логарифмы 100 по основанию 10 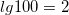 и 1000
и 1000 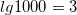 . Сложив логарифмы
. Сложив логарифмы 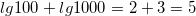 , а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.
, а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.
Аналогично, задачи деления преобразуются в задачи вычитания с логарифмами: log m/n = log m — log n.
Это еще не все. Расчет степеней и корней может быть упрощен с использованием логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1).
В логарифмические таблицы обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа вне этого диапазона, число было сначала записано в удобном виде как произведение его значащих цифр и его степени по основанию 10 —
например, 358 будет записано как 3,58 × 10 2,
а 0,0046 будет записано как 4,6 × 10-3.
Тогда логарифм значащих цифр — десятичная дробь между 0 и 1, известная как мантисса — будет найдена в таблице. Например, чтобы найти логарифм 358, можно посмотреть таблицу значений логарифмов 3,58 ≅ 0,55388. Следовательно, lg 358 = lg 3,58 + lg 100 = 0,55388 + 2 = 2,55388.
В примере числа с отрицательным показателем степени, такого как 0,0046, можно посмотреть lg 4,6 ≅ 0,66276. Следовательно, lg 0,0046 = lg 4,6 + lg 0,001 = 0,66276 — 3 = -2,33724.
История логарифмов
Изобретению логарифмов предшествовало сравнение арифметических и геометрических последовательностей.
В геометрической последовательности каждый член образует постоянное соотношение (знаменатель прогрессии) с предыдущим и последующим членами прогрессии: например,… 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как разность прогрессии, например,… −3, −2, −1, 0, 1, 2, 3… имеет разность 1.
Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения, для приведенной выше примерной геометрической последовательности:… 10−3, 10 −2, 10 −1, 10 0, 10 1, 10 2, 10 3….
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равно суммированию соответствующих показателей степеней с основанием 10: -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение преобразуется в сложение.
Однако первоначальное сравнение между двумя возможностями вычислений произведения не было основано на каком-либо явном использовании экспоненциальной записи: это было последующее развитие.
В 1620 году в Праге швейцарским математиком Йостом Бурги была опубликована первая таблица, основанная на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Непер опубликовал свое открытие логарифмов в 1614 году. Его целью было помочь в умножении величин, которые были связаны с вычислением синуса в прямоугольном треугольнике.
Вычисления Непера и Бригса
В сотрудничестве с английским математиком Генри Бригсом Непер приспособил свой логарифм к его современной форме. Для неперова логарифма сравнение будет происходить между точками, движущимися по градуированной прямой линии, точка L (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, точка Х (для синуса) движется от нуля до бесконечности со скоростью пропорционально его расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорость в этой точке равна.
Суть открытия Непера состоит в том, что он связал между собой арифметические и геометрические прогрессии — то есть умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничивать движение L и X требованием, чтобы L = 1 при X = 10, в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бригиану, или общему логарифму.
Непер умер в 1617 году, а Бригс продолжил расчеты в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанную до 14 знаков после запятой для чисел от 1 до 20 000 и от 90 000 до 100 000. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги появилось только в 1857 году в Берлине.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — логарифмические линейки были незаменимы в инженерных расчетах.

Современное определение логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Где используются логарифмы
Некоторые области науки, где применяются логарифмы:
- Децибелы, используемые для измерения звукового давления, определяются с помощью логарифмов.
- Шкала Рихтера, которая используется для измерения интенсивности землетрясений, определяется с помощью логарифмов
- Значения pH в химии, которое используется для определения уровня кислотности вещества, также определяется с использованием понятия логарифма.
- Когда две измеренные величины оказываются связанными степенной функцией, параметры функции могут быть оценены с использованием логарифмов.
- Логарифмы могут быть использованы для решения уравнений, таких как 2х = 3.
Решение логарифмических уравнений
Рассмотрим простейшие логарифмические уравнения и примеры их решения.
Задание 1
Решите уравнение log5(x2+x)=log5(x2+9)
Ответ:9
Решение: Так как основания логарифмов одинаковы, то числа, стоящие под знаком логарифмов — одинаковы:
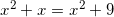 ,
,
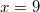
Задание 2
Решите уравнение logx-5 49 = 2.
Если уравнение с логарифмами имеет более одного корня, в ответе укажите наибольший из них.
Ответ: 12
Решение:
(x – 5)2 = 49;
x2 – 10 x + 25 = 49;
x2 – 10 x – 24 = 0;
a = 1 , b = -10, c = -24;
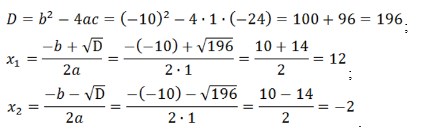
При х = –2 основание логарифма отрицательно (известно, что основание должно быть положительным). Решением является корень 12. Сделайте проверку.
Задание 3
Найдите корень уравнения log2(4 – x) = 7.
Ответ:-124
Решение:
27 = 4 – x;
128=4-х;
х = 4 – 128;
х = −124.
Задание 4
Найдите корень уравнения 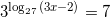 .
.
Ответ: 115
Решение: 27=33, тогда 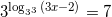
или 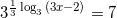 или
или 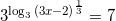 уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть:
уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть: 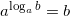 . Тогда получим:
. Тогда получим: 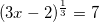 .
.
Решая данное уравнение, получим: 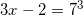 ,
,
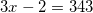
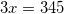 .
.
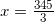
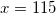
Задание 5
Решите уравнение logx+725 = 2. Если уравнение имеет более одного корня, в ответе укажите наименьший из них.
Ответ: -2
Решение: 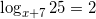 .
.
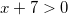 ,
, 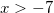 .
.
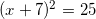
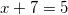 и
и 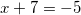
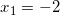 и
и 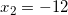
Так как x должен быть больше -7, то корень 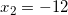 не подходит. И остается один единственный корень:
не подходит. И остается один единственный корень: 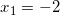 .
.
Таким образом, уже не важно — наибольший это корень или наименьший, он один подходит. Поэтому в ответе указываем его.
Задание 6
Решите уравнение log2(2 – x) = log2(2 – 3x) + 1
Ответ: x=0,4.
Решение: мы знаем, что 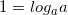 , тогда пусть в нашем случае
, тогда пусть в нашем случае 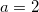 :
: 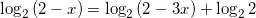 ,
,
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
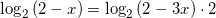
или
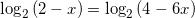
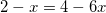
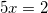
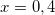 .
.
Задание 7
Решите уравнение log5(7 – x) = log5(3 – x) + 1
Ответ: 2
Решение: мы знаем, что 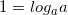 , тогда пусть в нашем случае
, тогда пусть в нашем случае 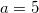 :
: 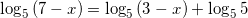 .
.
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
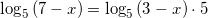
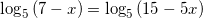
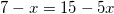
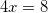
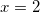 .
.
Задание 8
Найдите корень уравнения 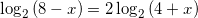
Ответ: x=-1
Решение:
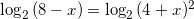
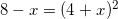
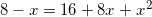
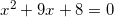
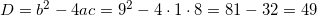
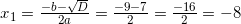
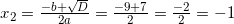 .
.
так как у нас должно выполняться условие:
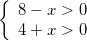 , откуда
, откуда 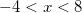 , таким образом нам подходит только один корень
, таким образом нам подходит только один корень 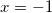 .
.
Итак, мы рассмотрели решение логарифмических уравнений с подробным решением каждого из них. Вы узнали, что такое логарифм, историю возникновения логарифма и имена ученых, которые схватили идею расчета произведения через сложение и изобрели логарифм, который на многие годы облегчил расчеты инженеров, строителей, ученых.
novstudent.ru