Неравенства с модулем — подготовка к ЕГЭ по Математике
Если вы научились решать уравнения с модулями – значит, сможете справиться и с неравенствами.
1. 2|x − 4| + |3x + 5| ≥ 16.
1) x ≥ 4. Имеем:
Полученное неравенство выполняется при всех рассматриваемых x ≥ 4. Иными словами, все числа из промежутка [4; +∞) являются решениями нашего неравенства.
2) Имеем в данном случае:
Учитывая, в каком промежутке мы сейчас находимся, получаем в качестве решений исходного неравенства множество [3; 4].
3) . Имеем:
Так как − , то все значения x из полученного промежутка служат решениями исходного неравенства.
Остаётся объединить множества решений, полученные в трёх рассмотренных случаях.
Ответ:
2. |x2 − 2x − 3| < 3x − 3.
Это задача №6 теоретической части урока 8 книги В. В. Ткачука «Математика — абитуриенту». Автор решает её методом интервалов. Обязательно разберите авторское решение!
Заметим, что метод интервалов здесь проходит весьма безболезненно по той причине, что корни квадратного трёхчлена под модулем — целые числа. А если дискриминант не будет точным квадратом? Замените, например, под модулем −3 на −5. Объём вычислительной работы тогда существенно возрастёт.
Мы покажем вам другой способ решения этой задачи, не зависящий от капризов дискриминанта.
Наше неравенство имеет вид |A| < B. Очевидны следующие утверждения.
• Если B ≤ 0, то неравенство не имеет решений.
• Если B > 0, то неравенство равносильно двойному неравенству −B < A < B или, что то же самое, системе
Иными словами, мы берём пересечение множества решений данной системы с множеством решений неравенства B > 0, то есть решаем систему
В нашей задаче получаем:
Изобразим множества решений этих неравенств на рисунке. Чёрным цветом показаны решения первого (двойного) неравенства; зелёный цвет — решения совокупности; синий цвет — решения последнего неравенства системы.

Решением системы служит пересечение этих множеств, т. е. множество, над которым присутствуют линии всех трёх цветов. Оно заштриховано.
Ответ: (2; 5).
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Решение системы неравенств с модулем
Решим систему неравенств с модулем из варианта №50 А. Ларина.

Решим каждое неравенство системы по отдельности, а потом совместим решения обоих неравенств на одной координатной прямой.
1. Решим первое неравенство системы.


Чтобы решить неравенство, содержащее модули, нужно раскрыть модули.
Приравняем каждое подмодульное выражение к нулю и найдем точки, в которых подмодульные выражения меняют знак.


Нанесем эти значения  на числовую прямую:
на числовую прямую:

Мы получили три промежутка. Найдем знаки каждого подмодульного выражения на каждом промежутке:

Раскроем модули на каждом промежутке (мы можем граничные точки 
 включать в оба промежутка):
включать в оба промежутка):а) 
На этом промежутке оба подмодульных выражения отрицательны, поэтому мы раскрываем модули с противоположным знаком:

 (1)
(1)
Так как исходное неравенство «превращается» в неравенство (1) только при 

 .
.
Решим первое неравенство, и получим систему:


Решением системы неравенств является промежуток:

б) 
На этом промежутке первое подмодульное выражение положительно, а второе отрицательно, поэтому первый модуль мы раскрываем с тем же знаком, а второй с противоположным.
Получаем неравенство:


Так как исходное неравенство «превращается» в неравенство (2) только при  , получим систему неравенств:
, получим систему неравенств:


или


Решением системы неравенств является промежуток:

в) 

На этом промежутке оба подмодульных выражения положительны, поэтому оба модуля мы раскрываем с тем же знаком.
Получаем неравенство:

 (3)
(3)
Так как исходное неравенство «превращается» в неравенство (3) только при  , получим систему неравенств:
, получим систему неравенств:


или


Решением системы является промежуток:

Объединим три промежутка и получим решение первого неравенства исходной системы:

![delim{[}{-2;2,4}{]} delim{[}{-2;2,4}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_986.5_ca4e9a80fd839d21baf908158fdf33fb.png)
2. Решим второе неравенство системы.


Приведем левую часть неравенства к общему основанию. Сначала разложим на множители знаменатель первой дроби:






Решим это неравенство методом интервалов.
Найдем корни числителя и знаменателя и нанесем их на числовую ось.


На самом правом промежутке 
 , поэтому знаки расставим так:
, поэтому знаки расставим так:

Нас интересуют промежутки со знаком «-«:

следовательно, решение этого неравенства: 
Совместим решения первого и второго неравенств исходной системы на одной координатной прямой и найдем их пересечение:

Ответ: [-2;1) (2;2,4]
(2;2,4]

И.В. Фельдман, репетитор по математике.


ege-ok.ru
5.4. Неравенства с модулем
Рассмотрим некоторые виды неравенств, содержащих знак модуля, и методы их решения.
1. 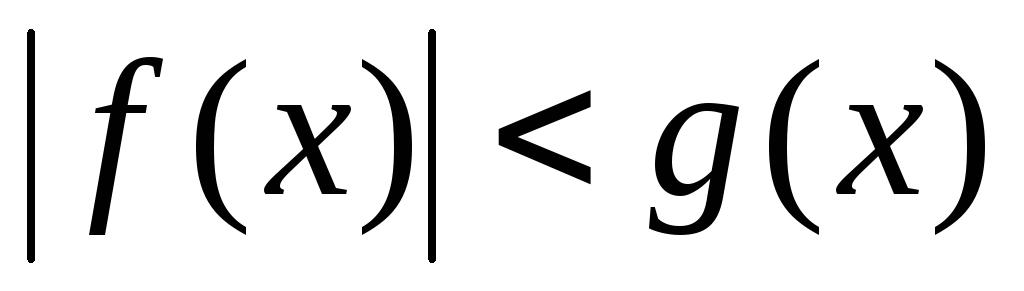
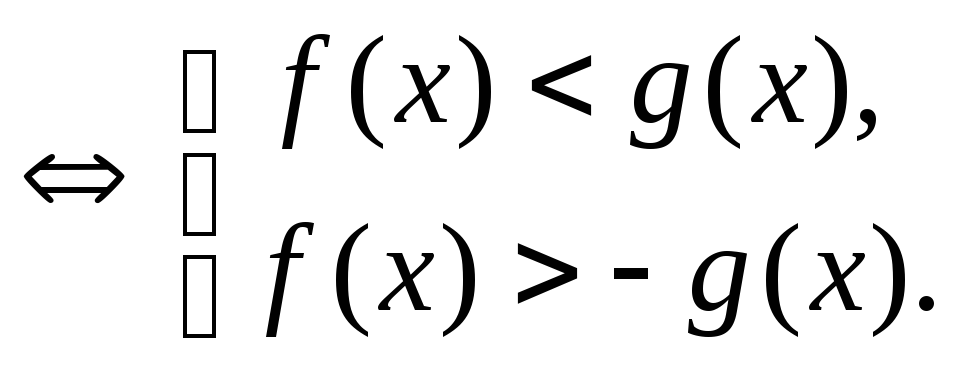
В частности, 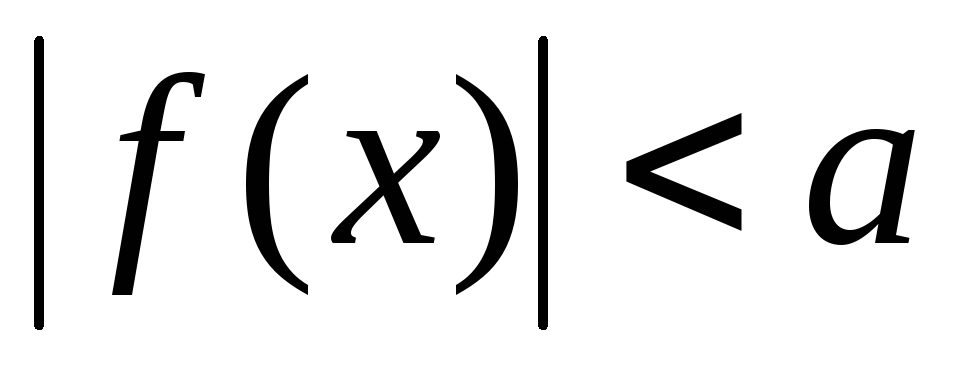
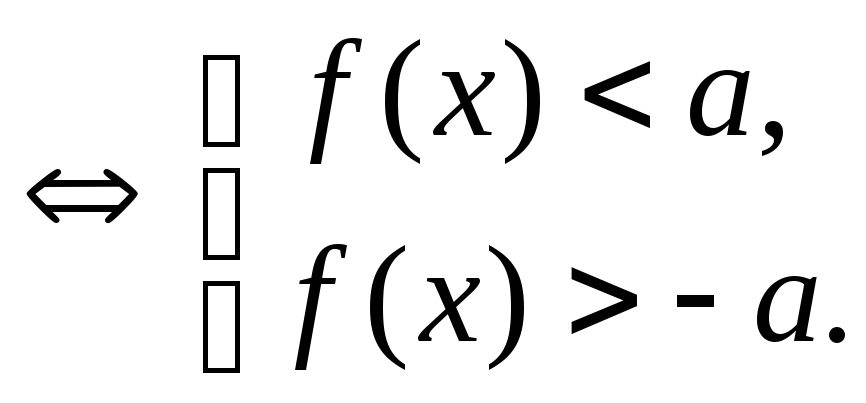
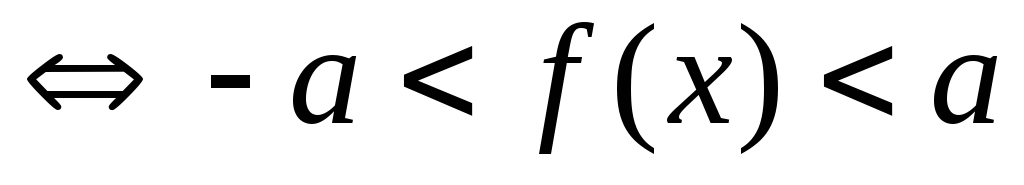 ,
где
,
где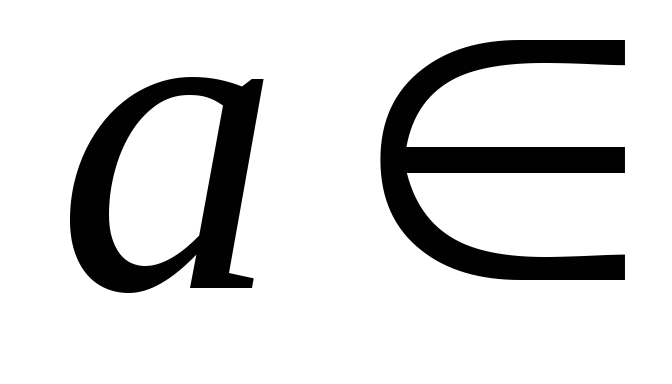
 ,
,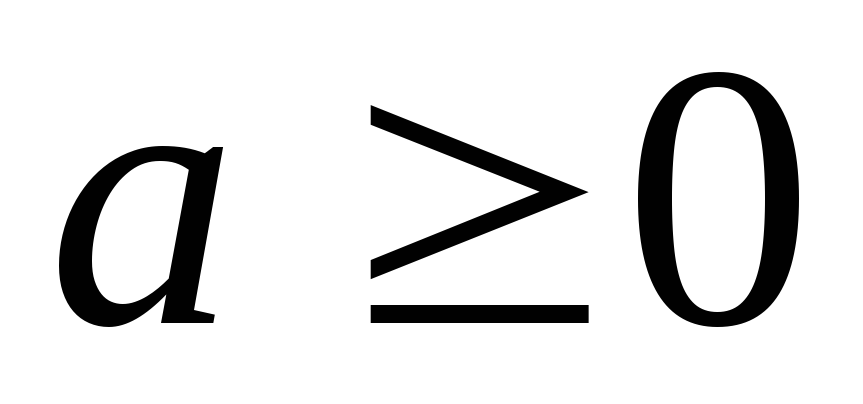 .
При
.
При неравенство решений не имеет.
неравенство решений не имеет.
2. 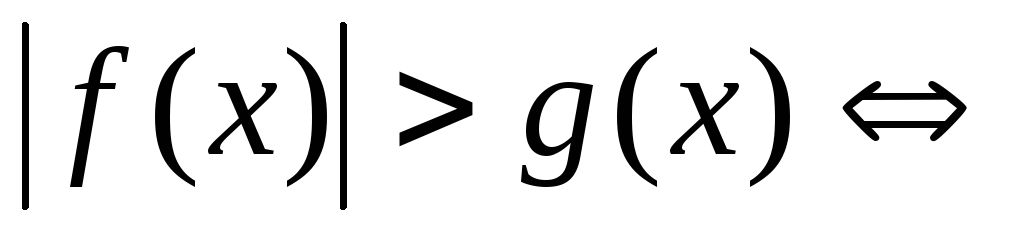
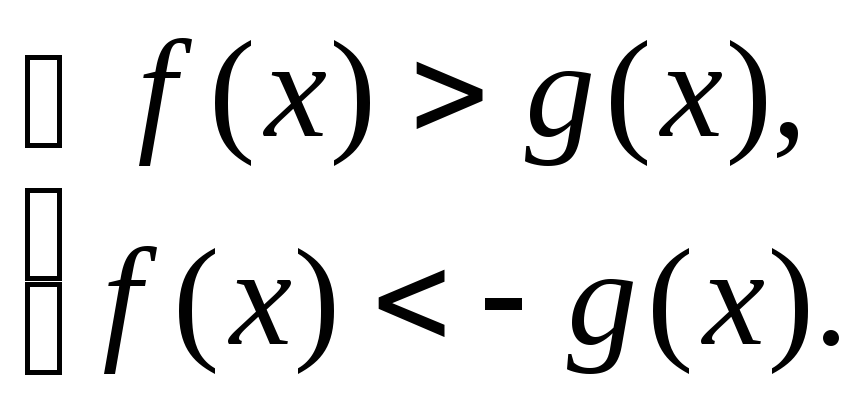
В частности, 
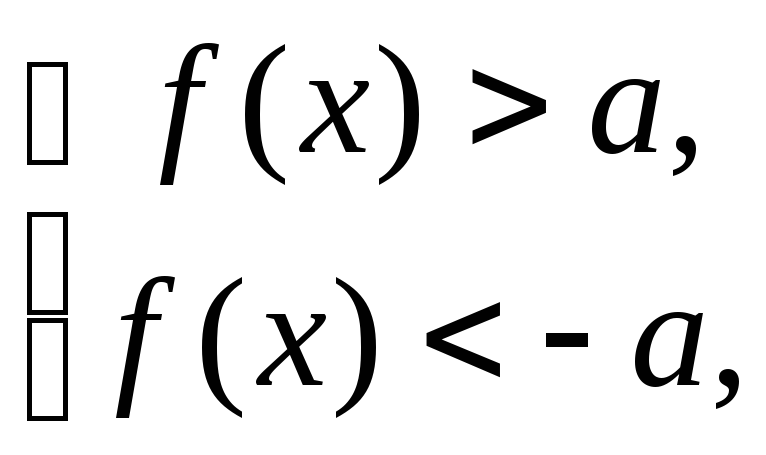
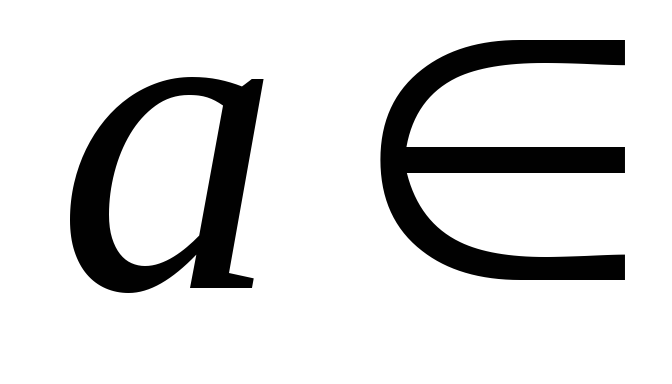
 ,
,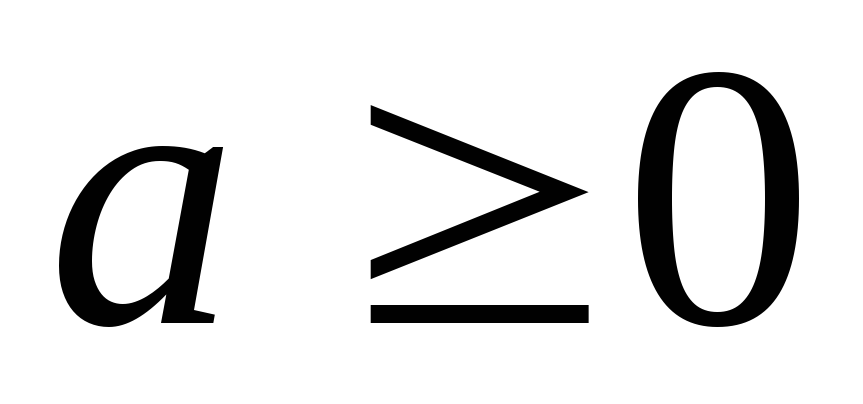 .
При
.
При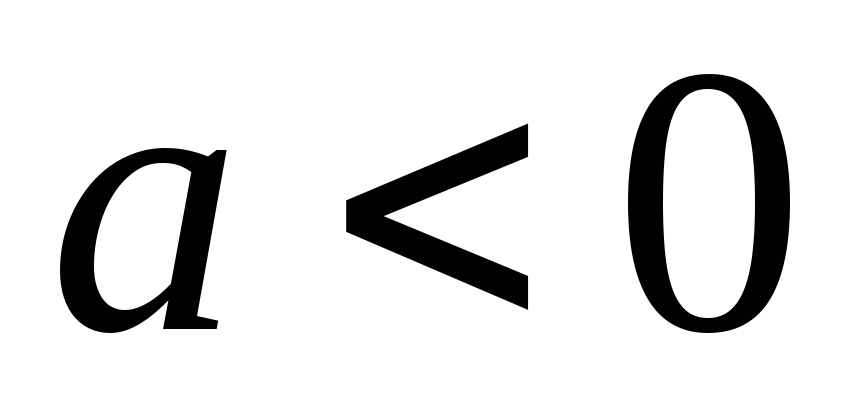 неравенство выполняется для всех
неравенство выполняется для всех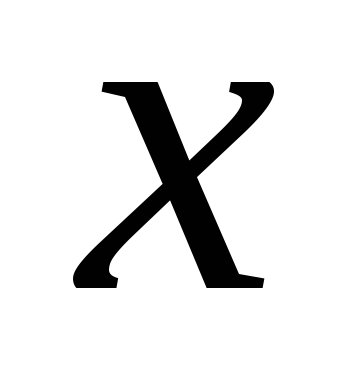 при которых функция
при которых функция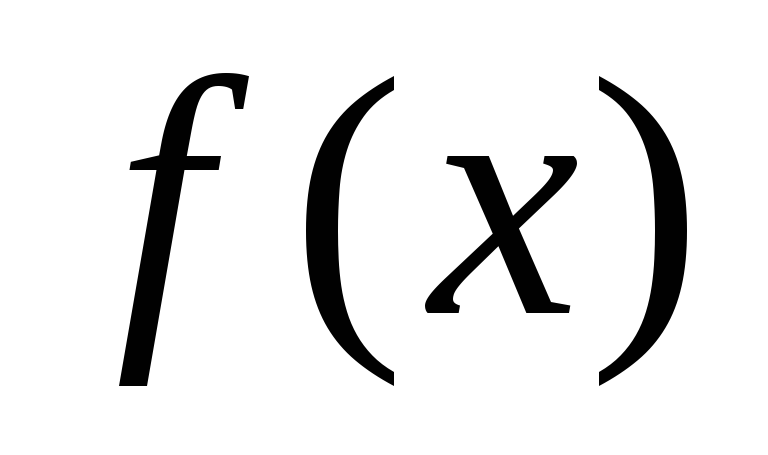 определена.
определена.
3. 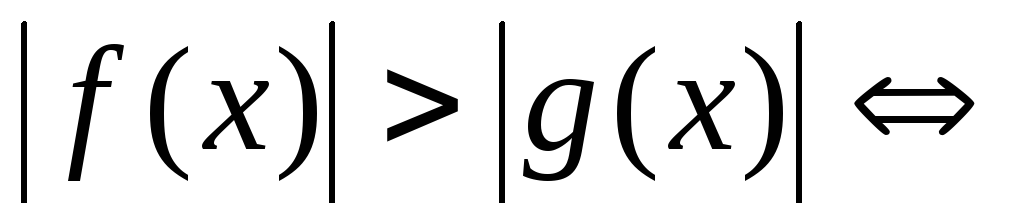
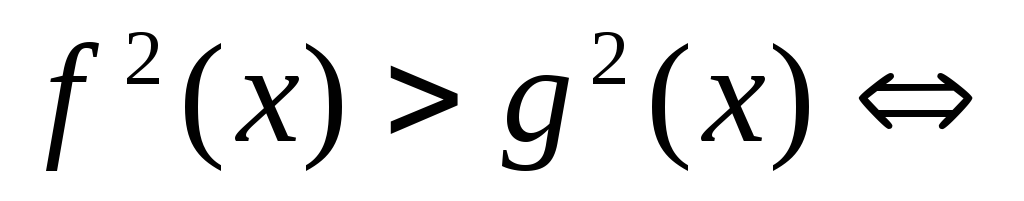
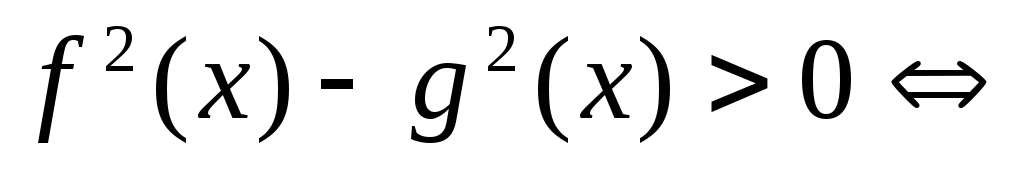
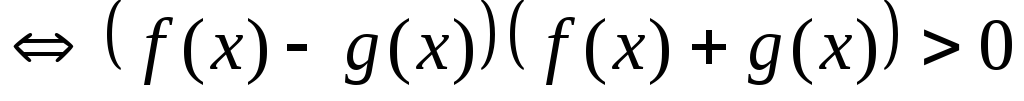 .
.
Последнее неравенство решается методом интервалов.
4. Неравенство вида 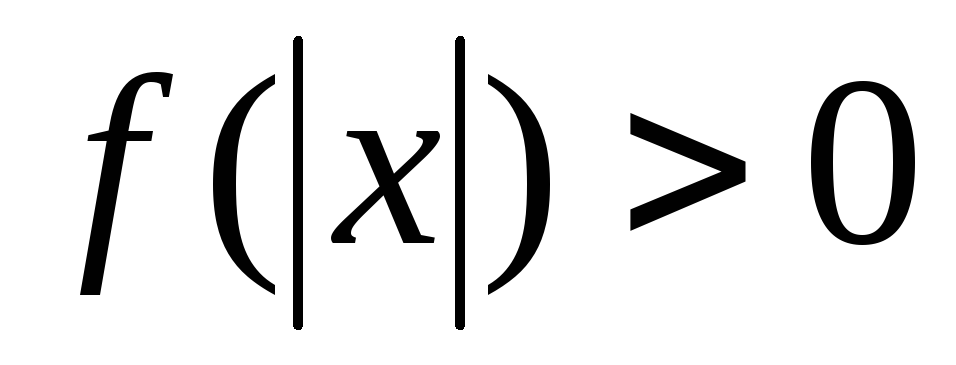 решают с помощью замены
решают с помощью замены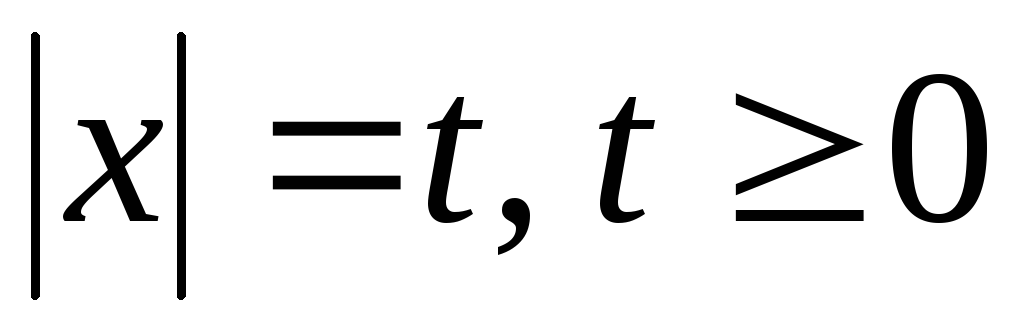 .
.
Пример 5.6. Решить
неравенство 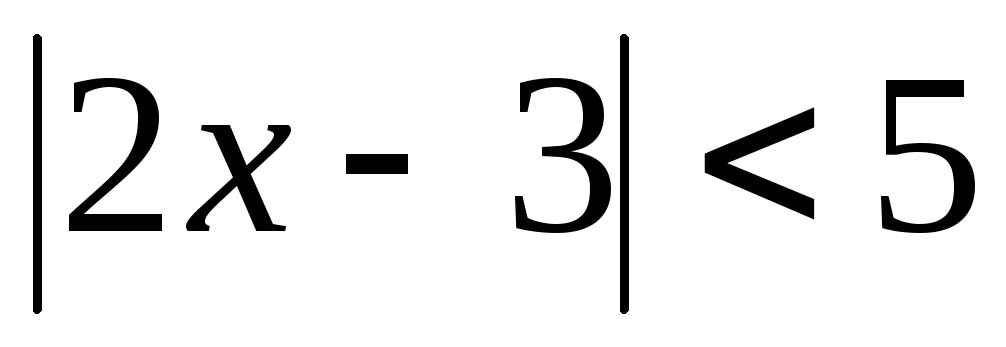 .
.
Решение. 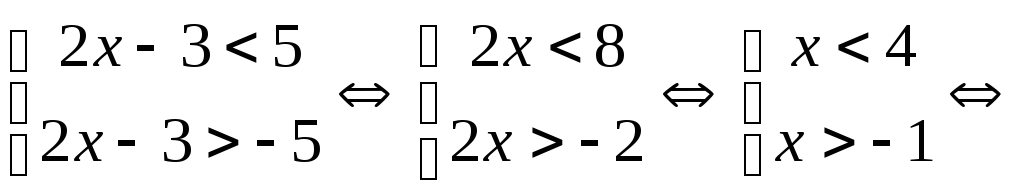
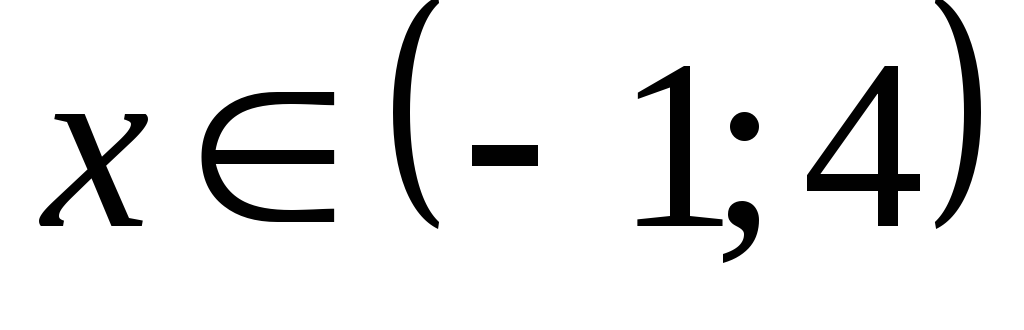 .
.
Ответ: 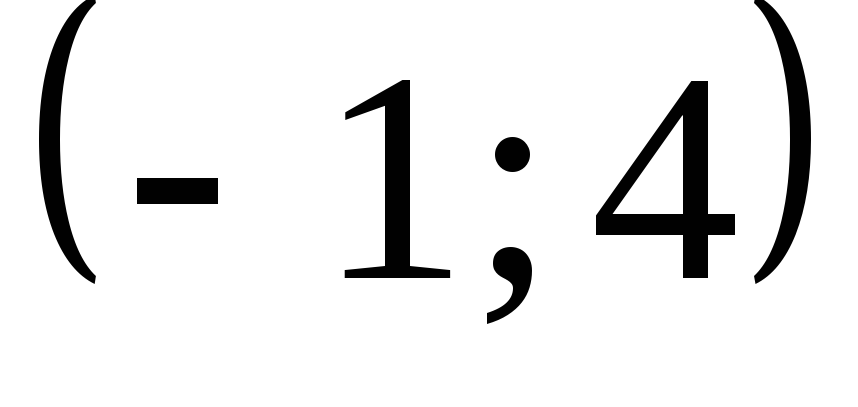 .
.
Пример 5.7. Решить
неравенство 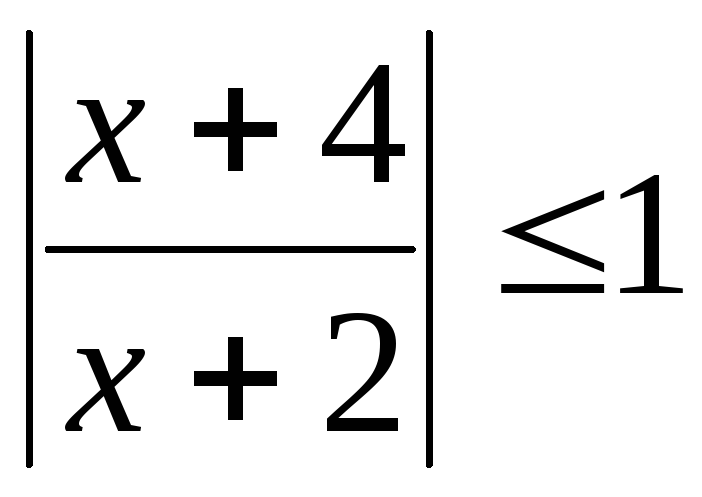 .
.
Решение. 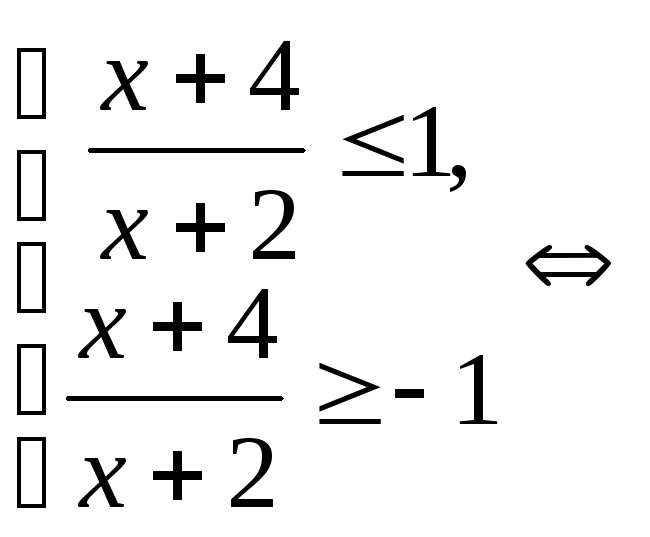
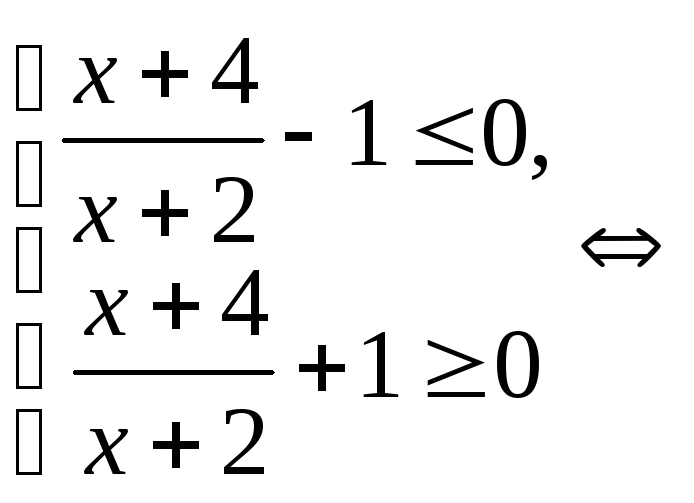
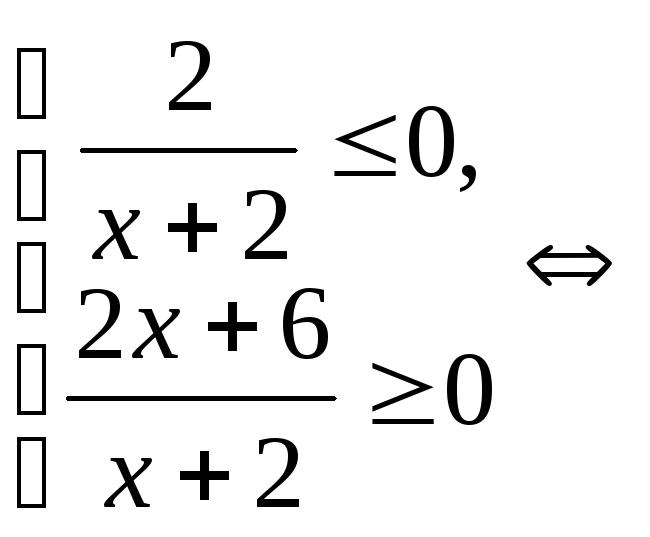
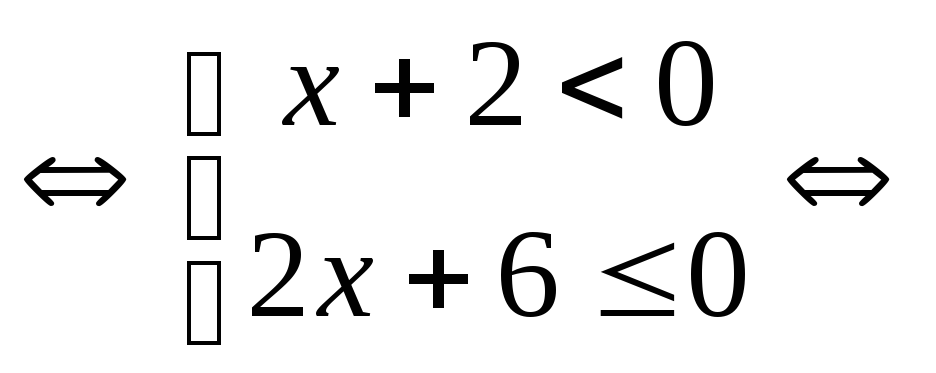
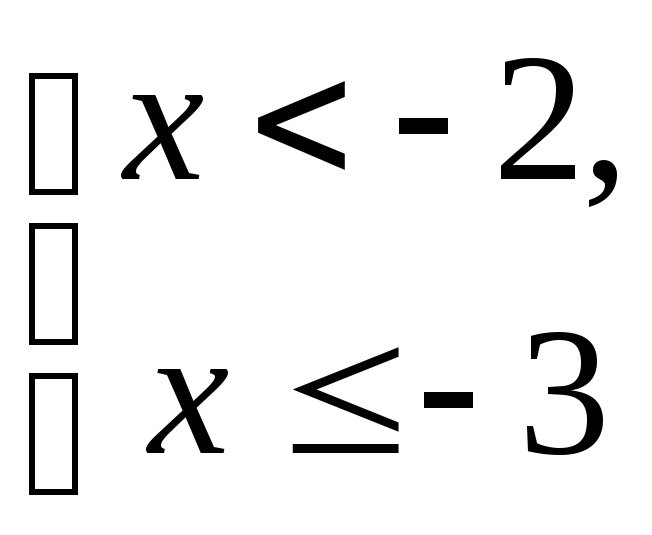
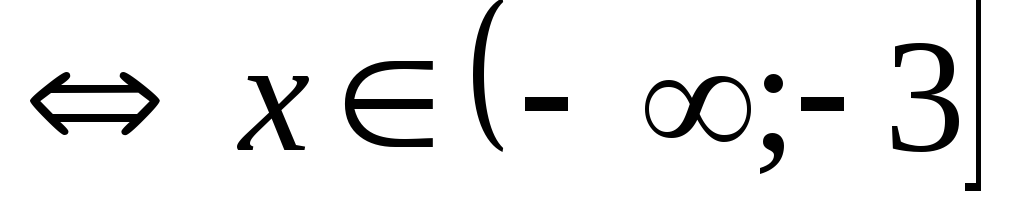 .
.
Ответ: 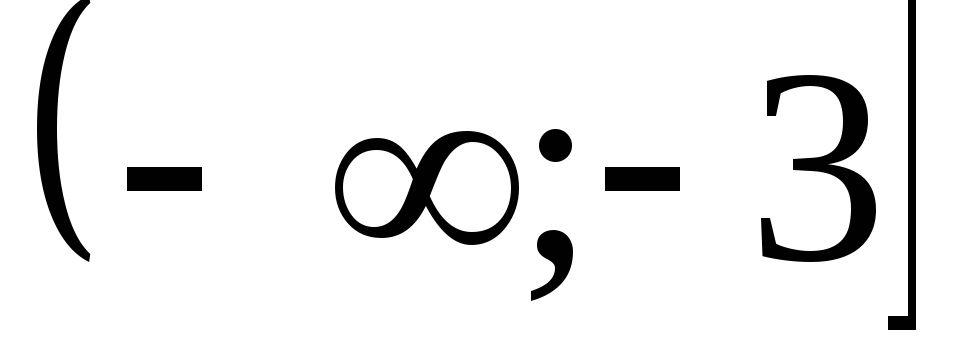 .
.
Пример 5.8. Решить
неравенство 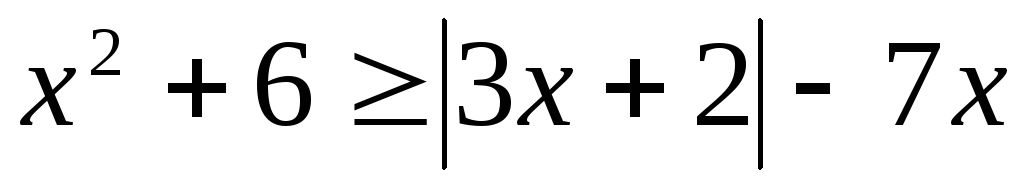 .
.
Решение.
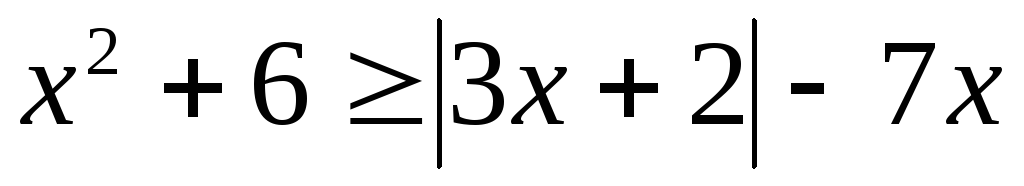
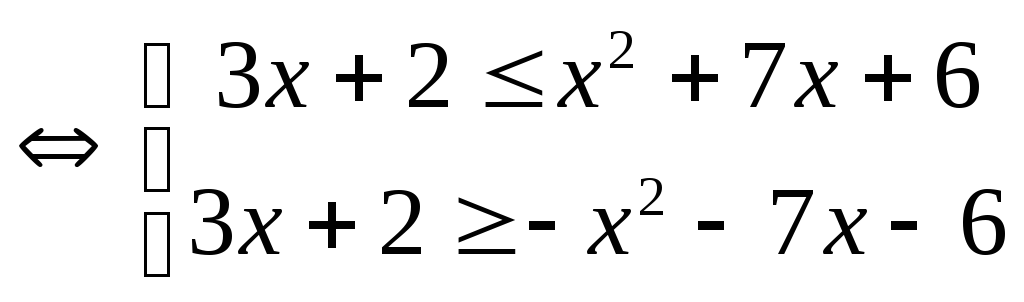
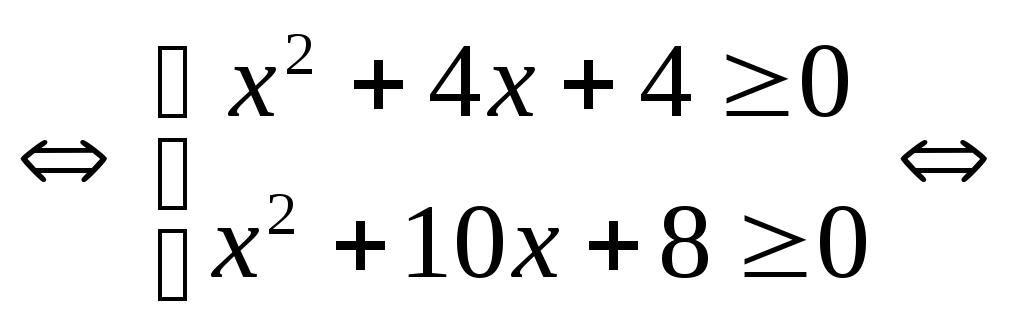
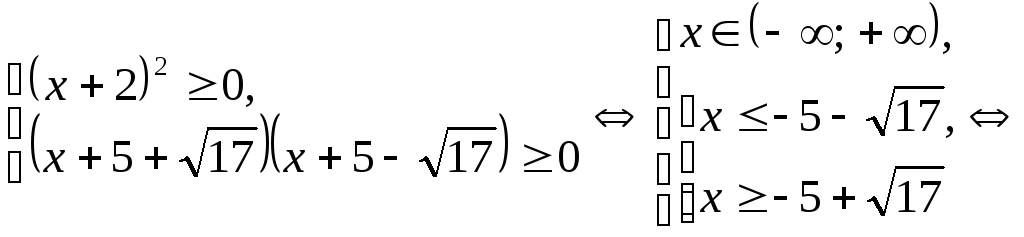
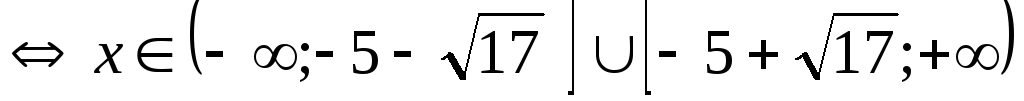 .
.
Ответ: 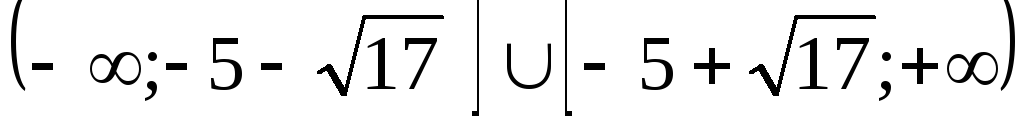 .
.
Пример 5.9. Решить
неравенство 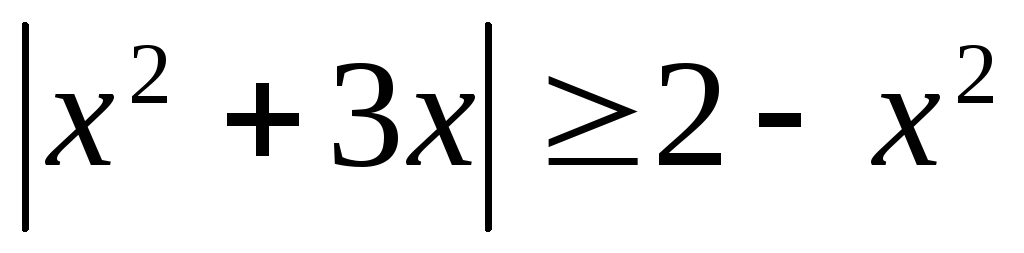 .
.
Решение. 

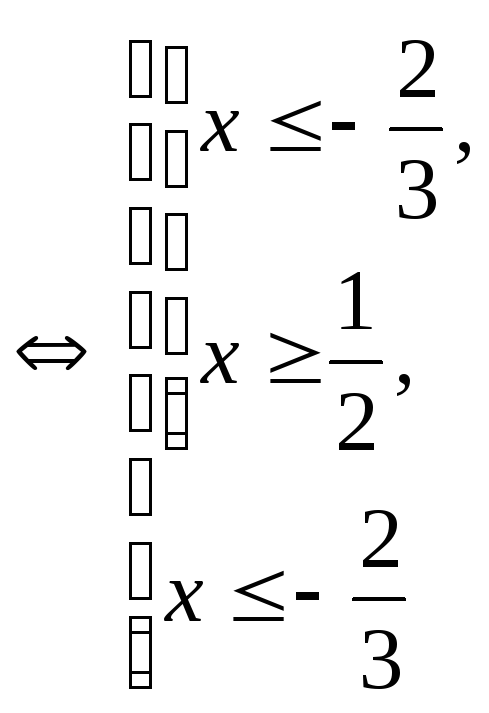
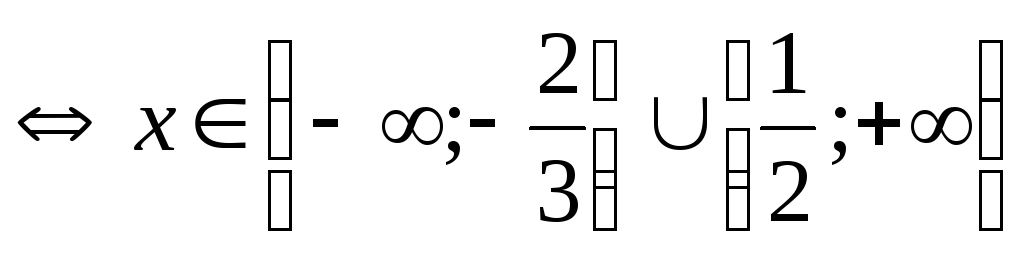 .
.
Ответ:  .
.
Пример 5.10. Решить
неравенство 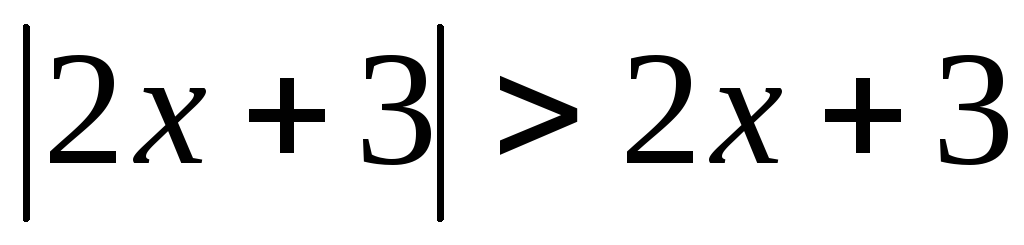 .
.
Решение. Из
свойств модуля следует, что  .
Поэтому
.
Поэтому
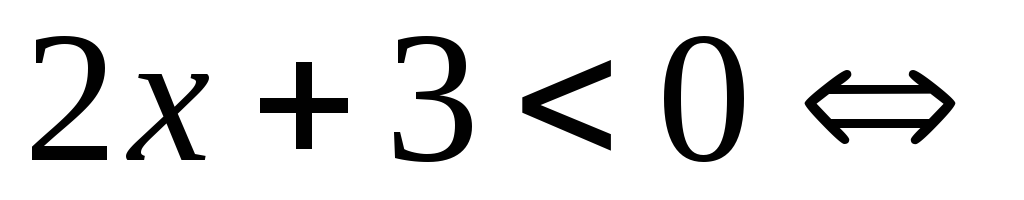
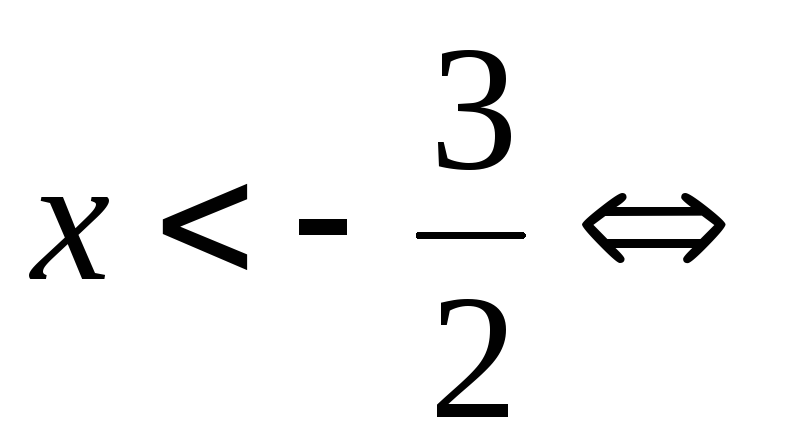
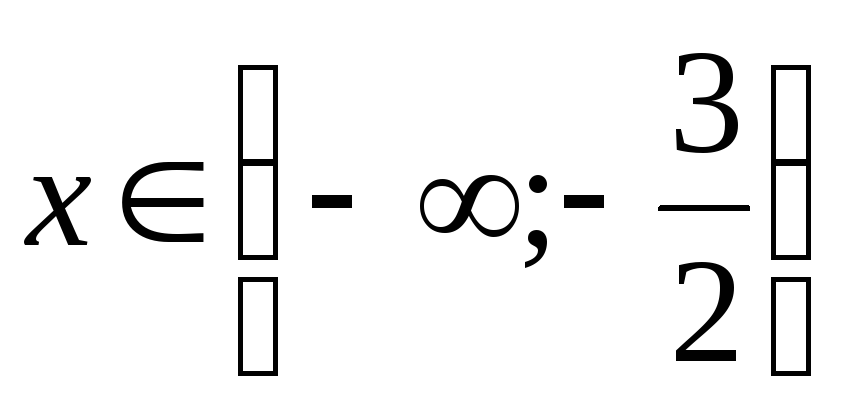 .
.
Ответ: 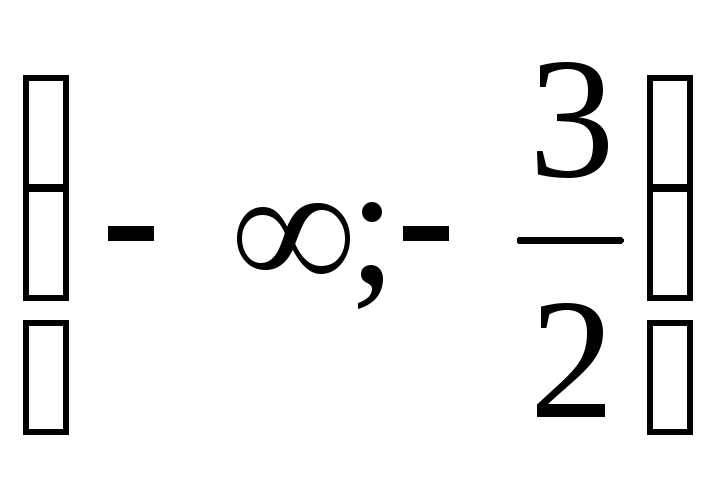 .
.
Пример 5.11. Решить
неравенство 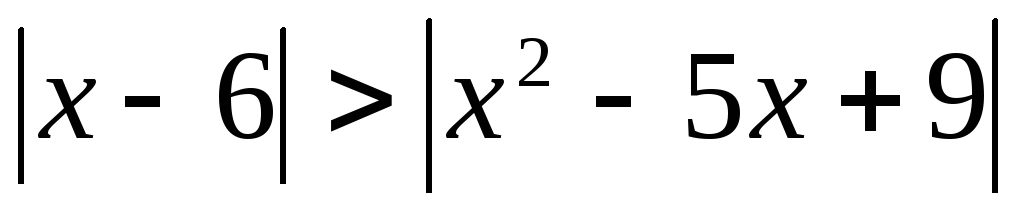 .
.
Решение. 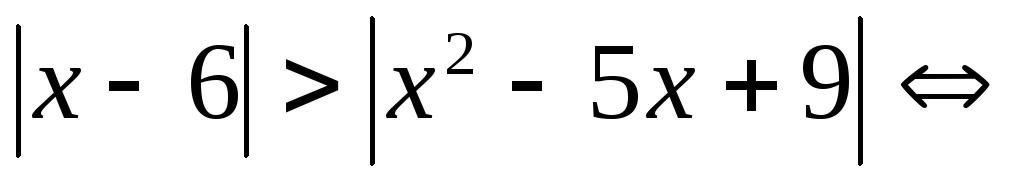
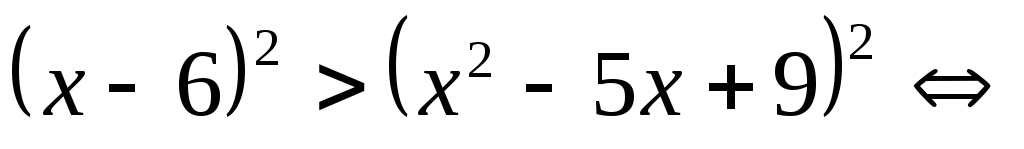
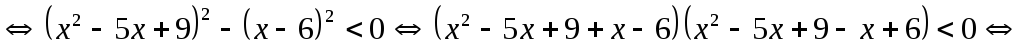
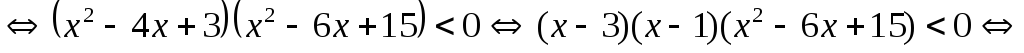
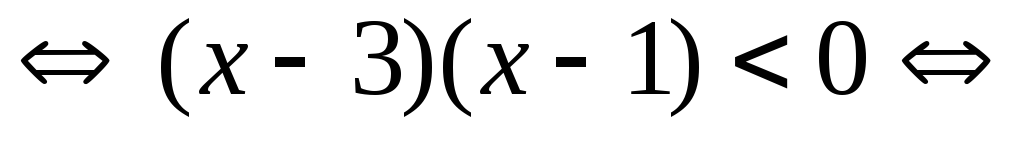
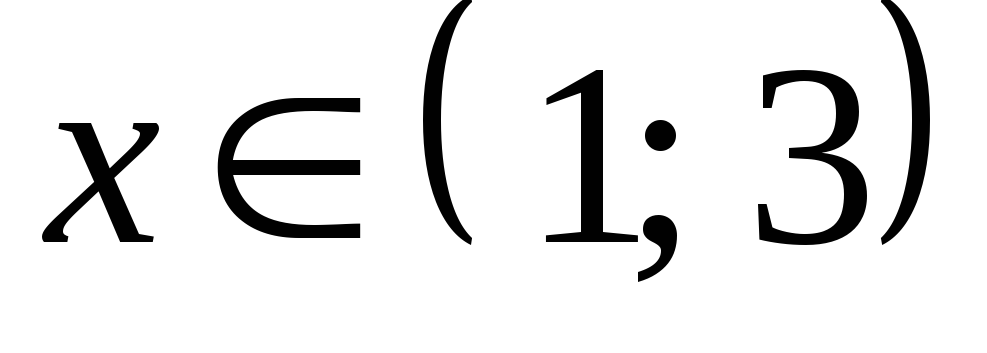
Ответ: 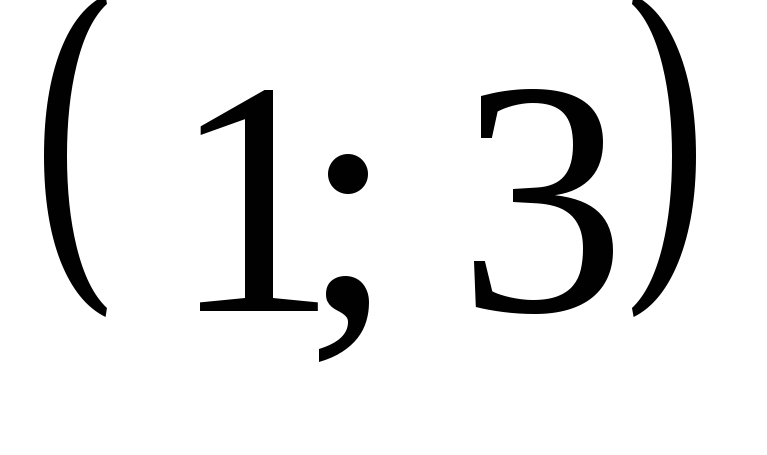 .
.
Пример 5.12. Решить
неравенство 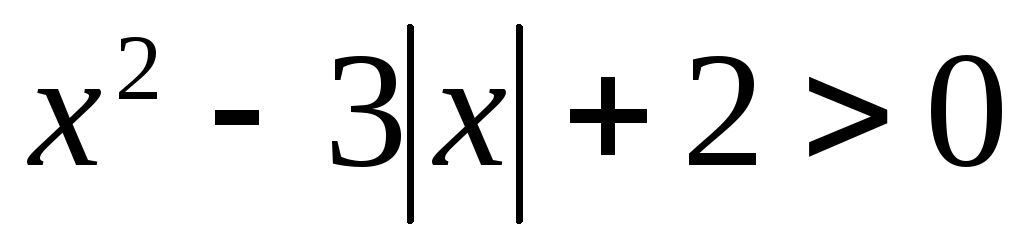 .
.
Решение. Введем
замену 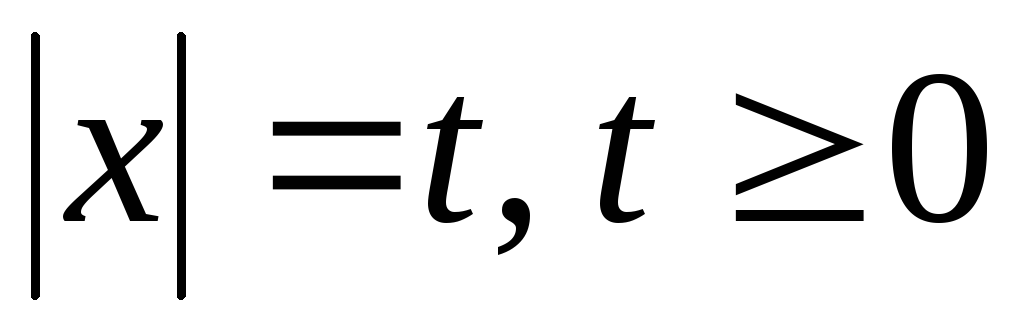 ,
тогда исходное неравенство имеет вид:
,
тогда исходное неравенство имеет вид:
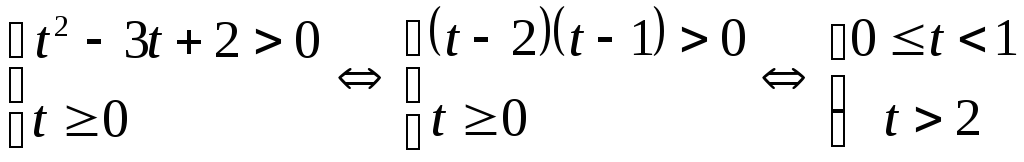 .
.
Переходя обратно
к переменной 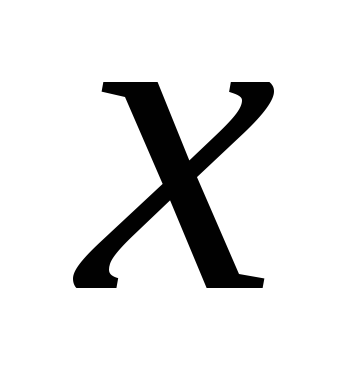 ,
получим:
,
получим:
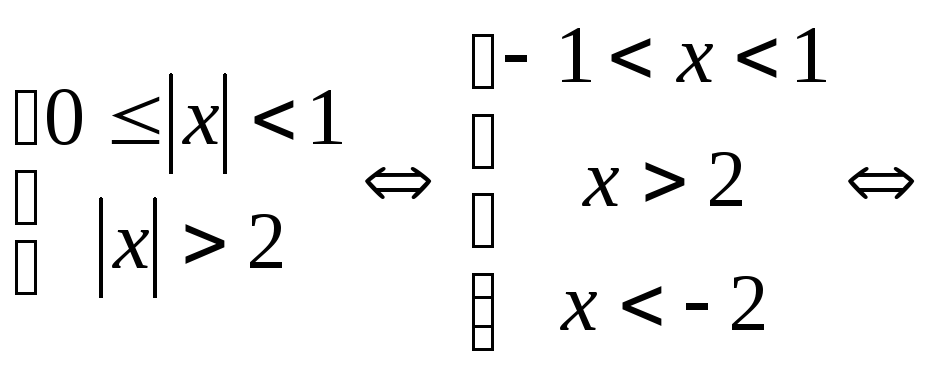
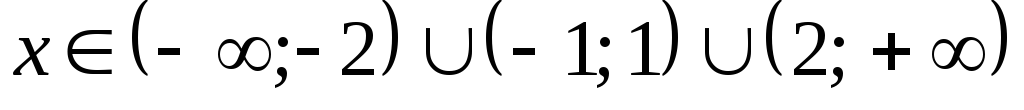 .
.
Ответ: 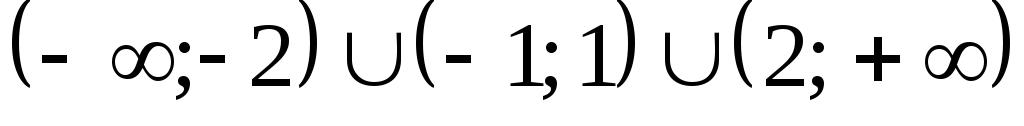 .
.
Пример 5.13. Решить
неравенство 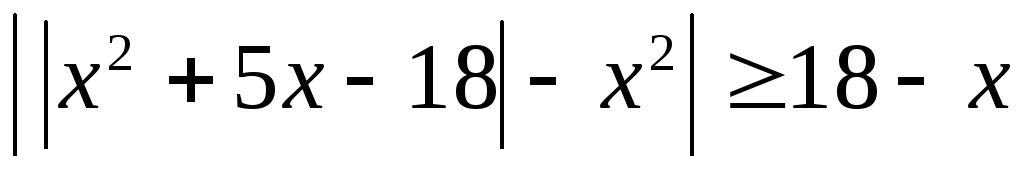 .
.
Решение. 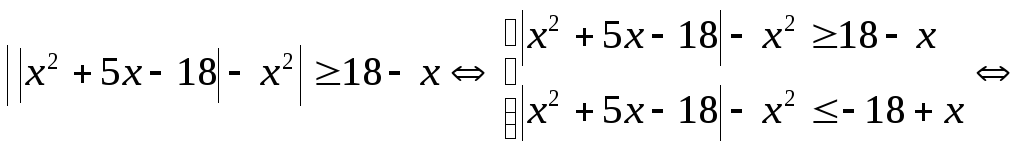
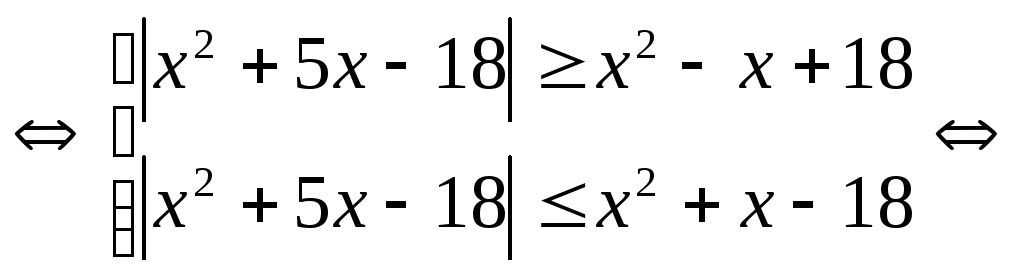
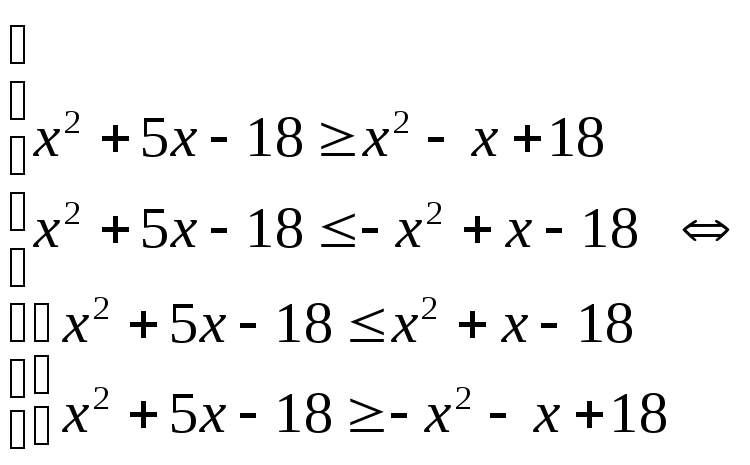
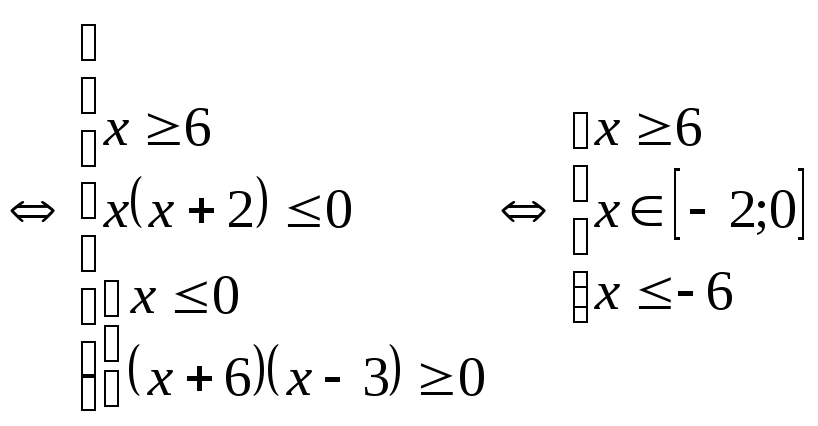
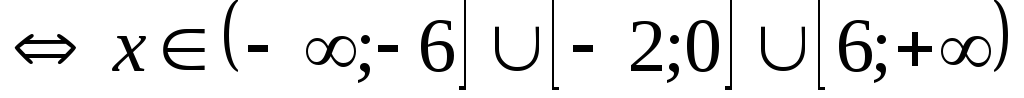 .
.
Ответ: 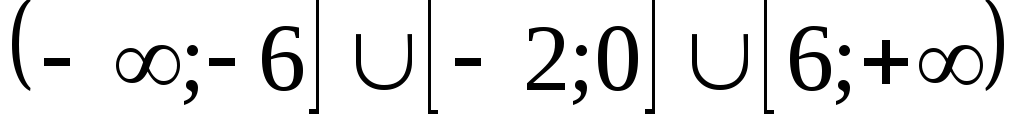 .
.
Пример 5.14. Решить
неравенство 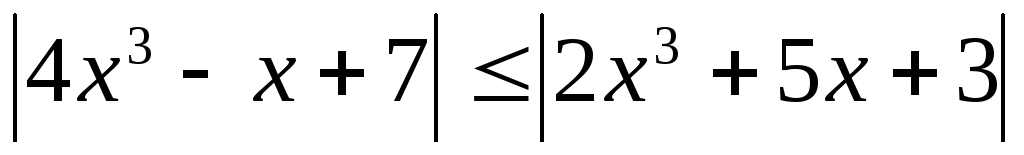 .
.
Решение.
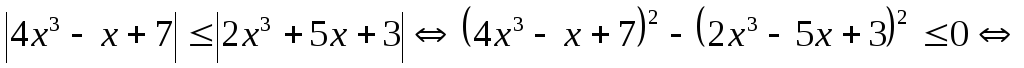
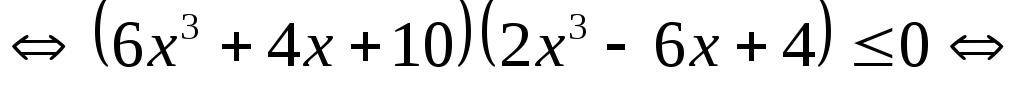
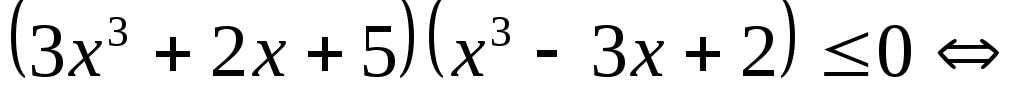
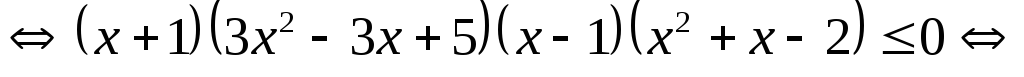
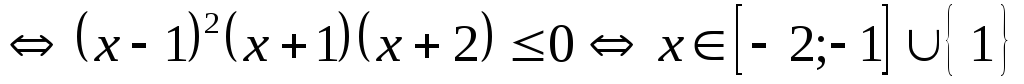 .
.
Ответ: 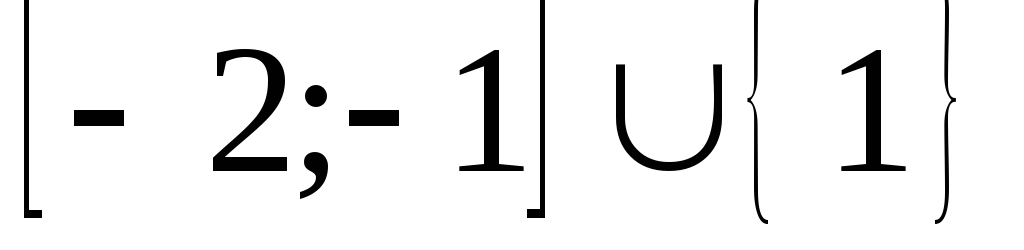 .
.
5.5. Иррациональные неравенства
К основным методам решения иррациональных неравенств относятся:
1. сведение исходного неравенства к равносильной системе рациональных неравенств или к совокупности неравенств:
a) 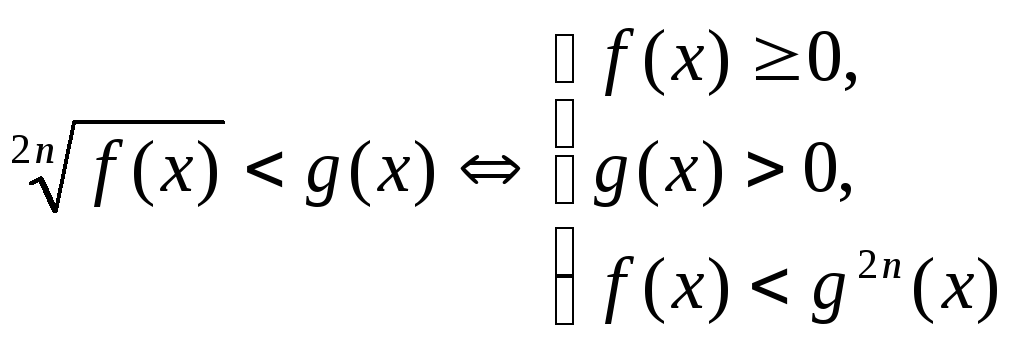 ,
,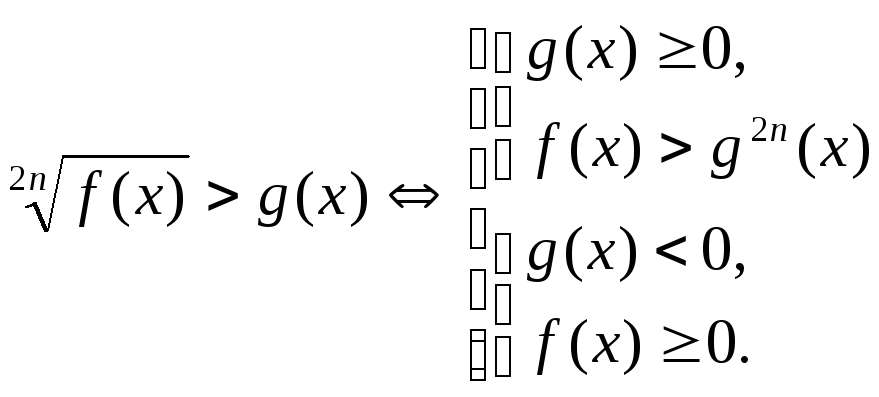
в частности, для 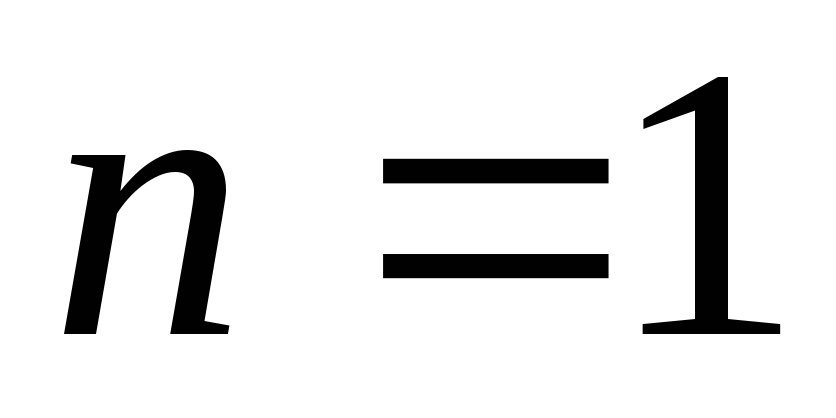
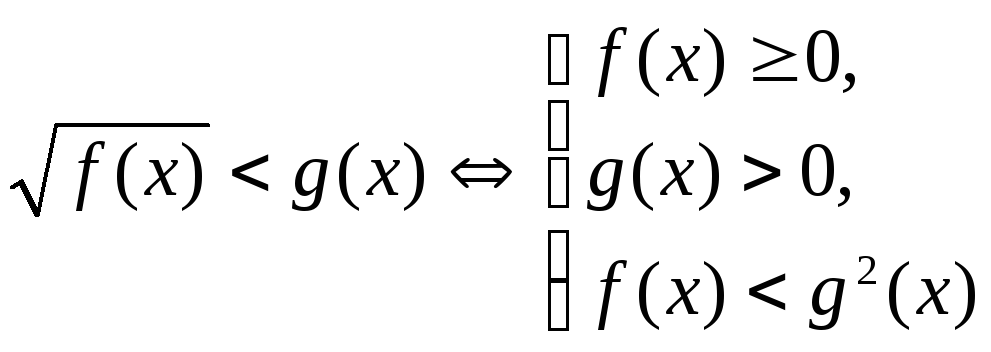 ,
, 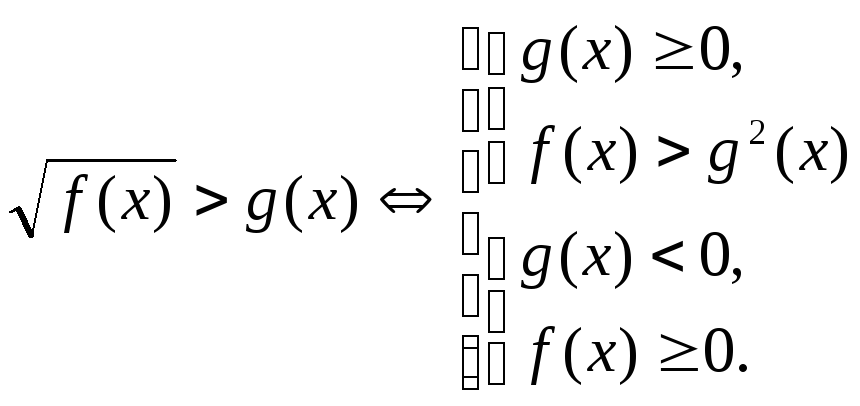
б)  ,
, ,
,
в частности, для 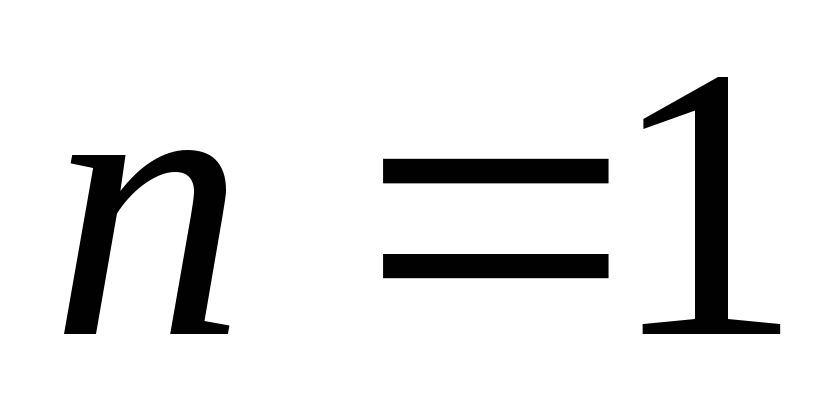
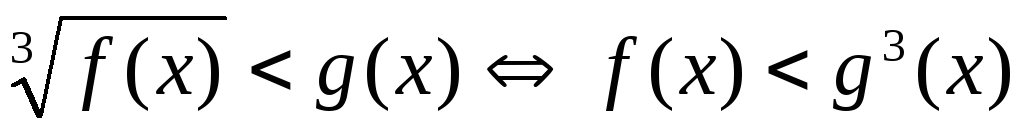 ,
, 
б) 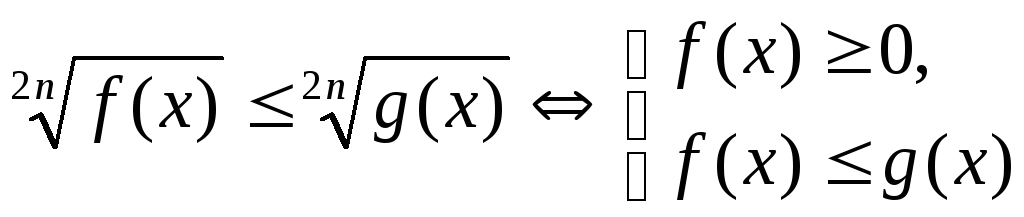 ,
,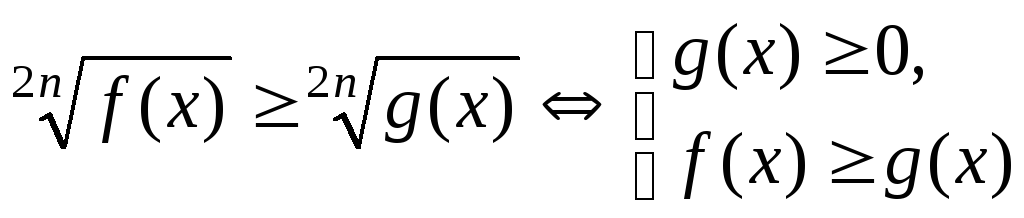
в частности, для 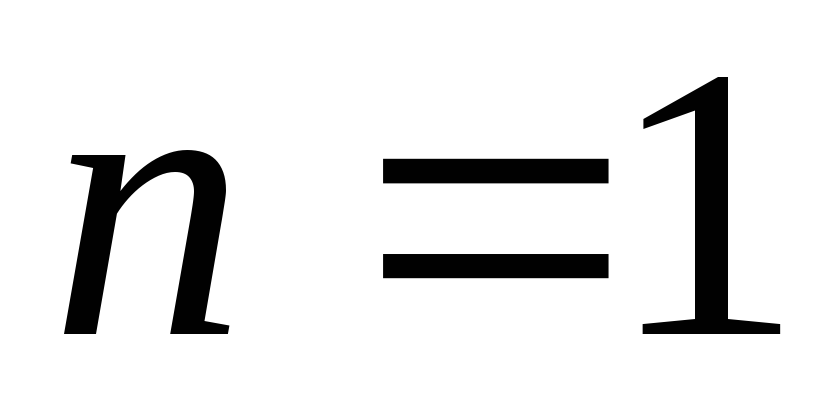
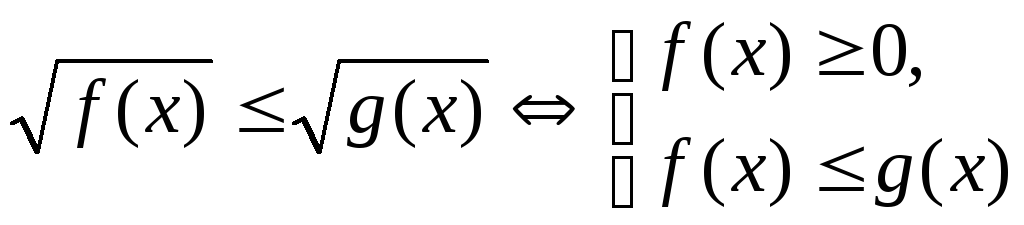 ,
, 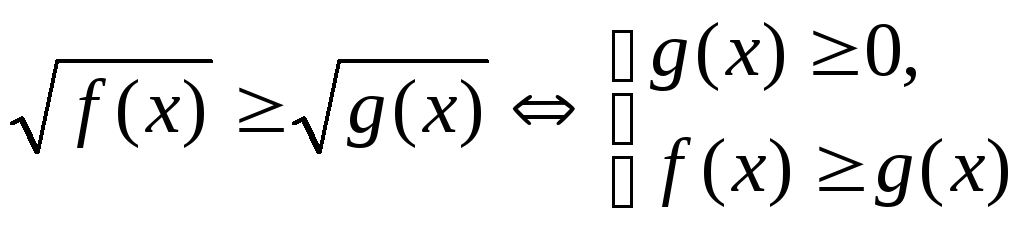 ;
;
2. введение новой переменной;
3. 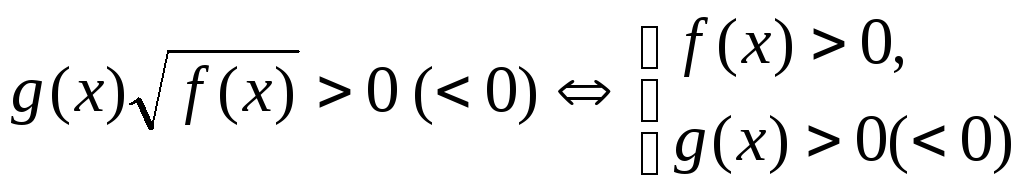 ,
,
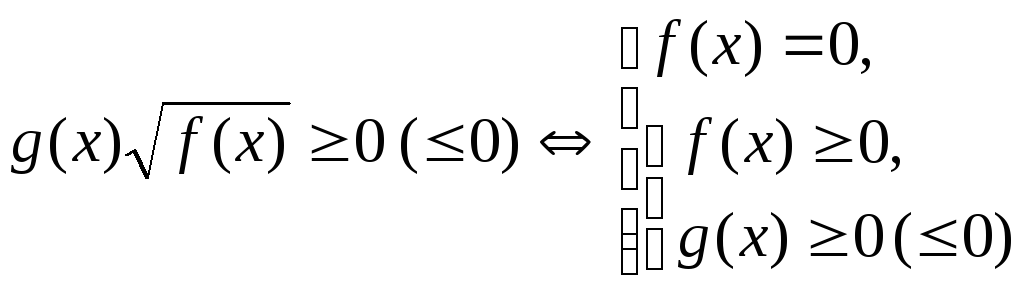
4. 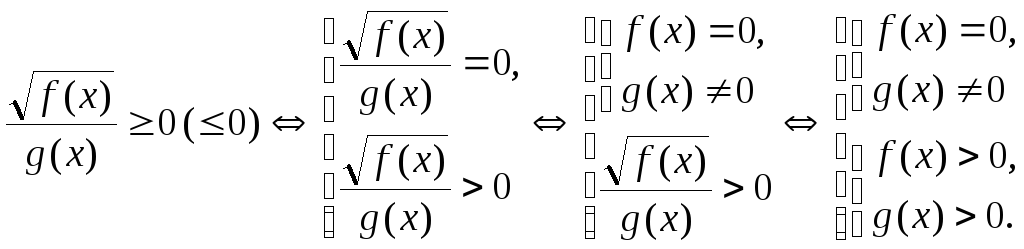
Пример 5.15. Решить
неравенство 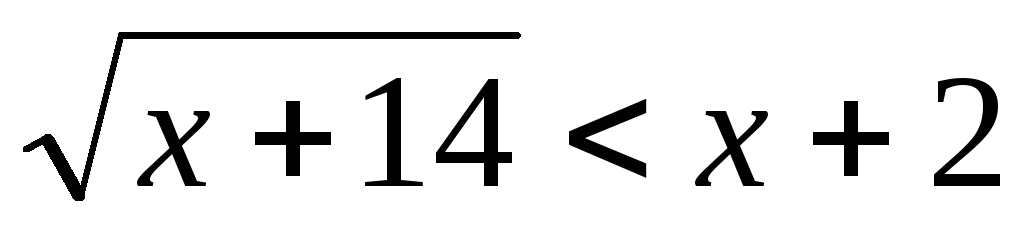 .
.
Решение. 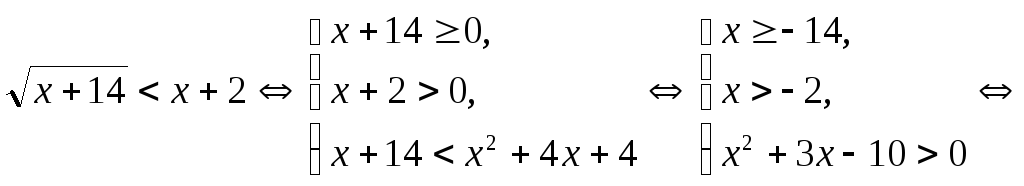
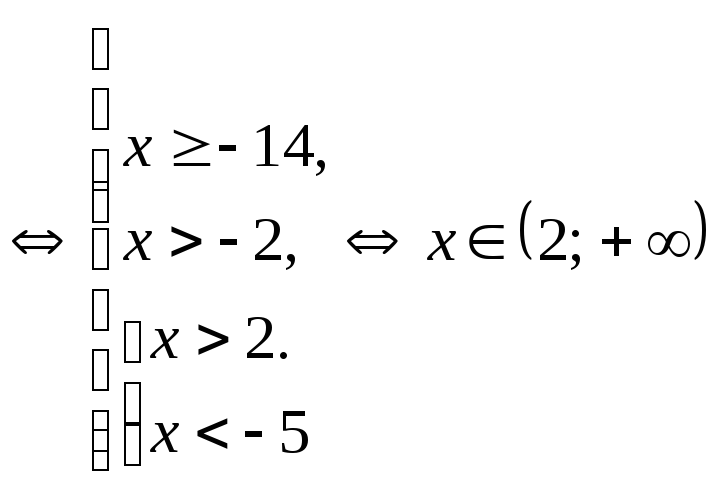 .
.
Ответ: 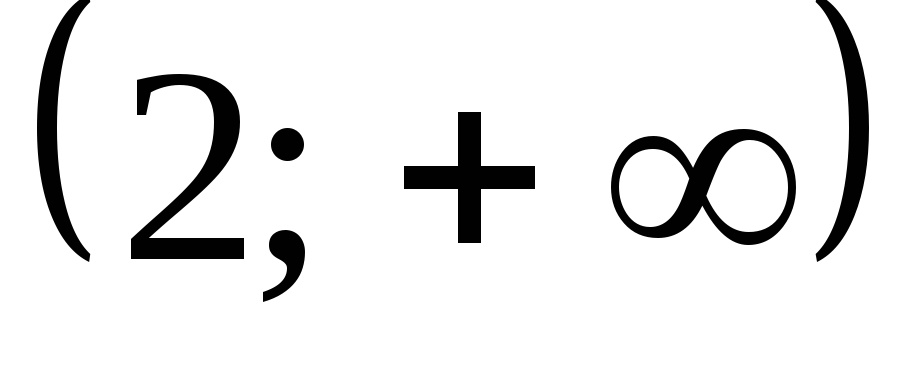 .
.
Пример 5.16. Решить
неравенство 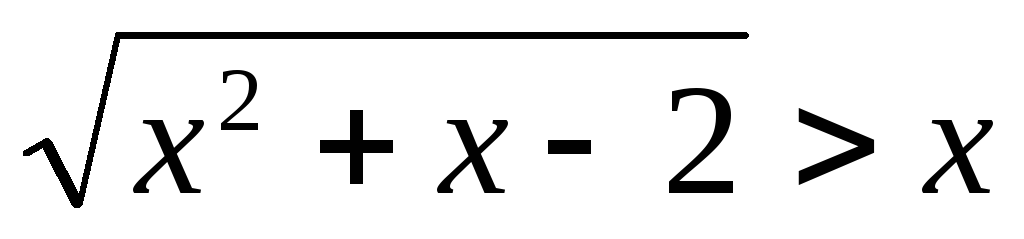 .
.
Решение. 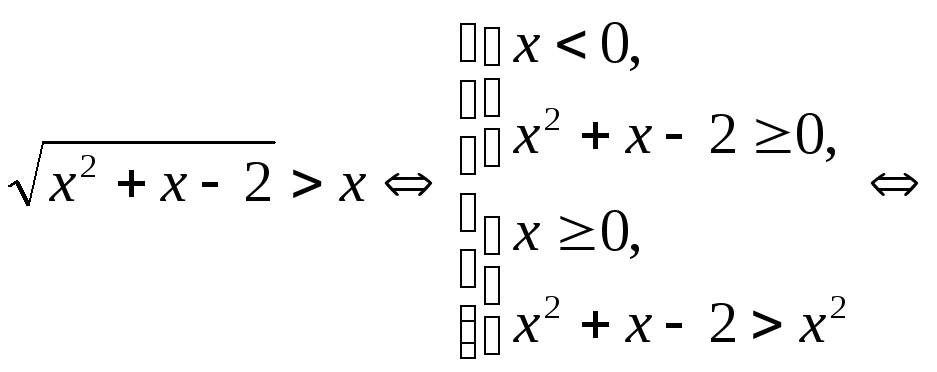
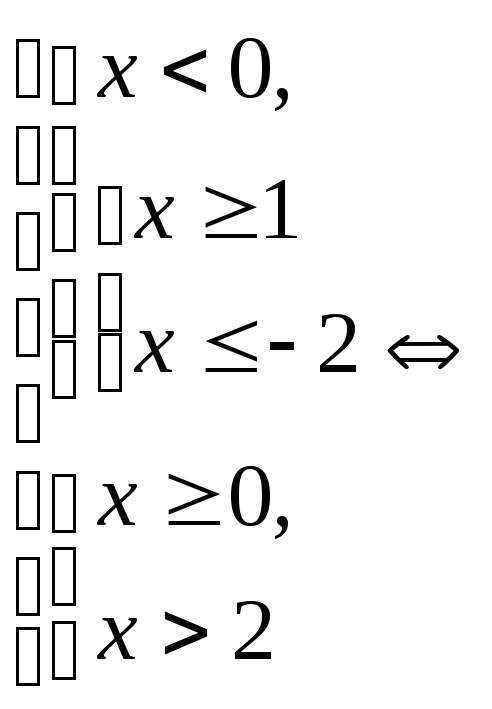
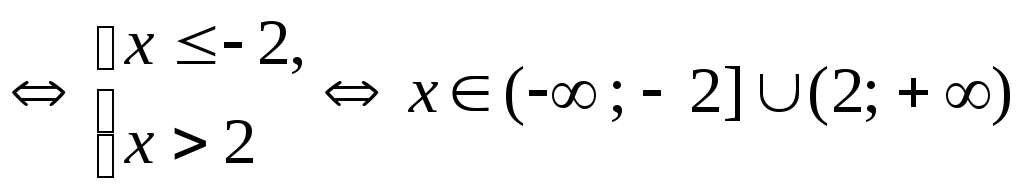 .
.
Ответ: 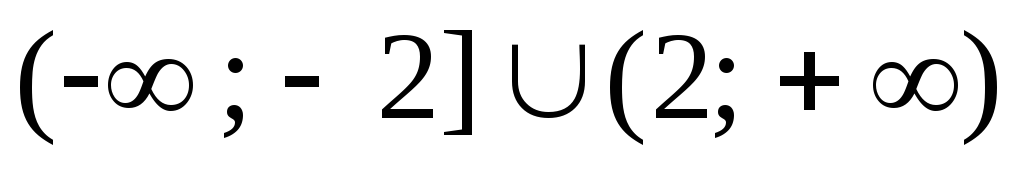 .
.
Пример 5.17. Решить неравенство
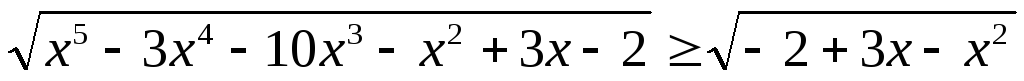 .
.
Решение. 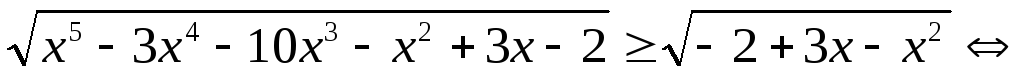
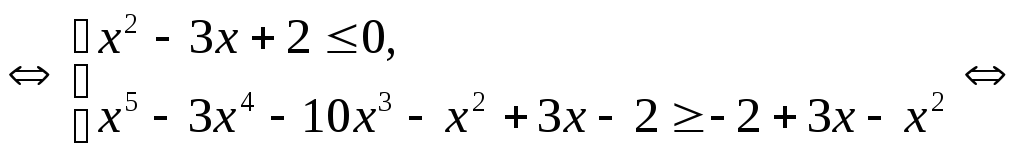
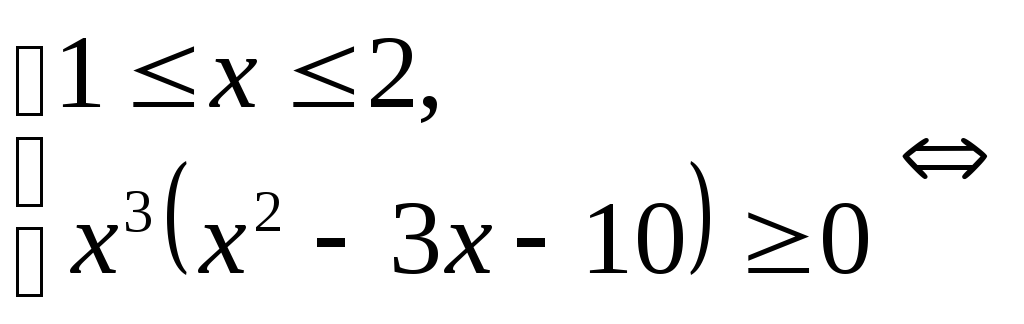
 ,
,
последняя система, а, следовательно, и исходное неравенство, решений не имеет.
Ответ: решений нет.
Пример 5.18. Решить
неравенство 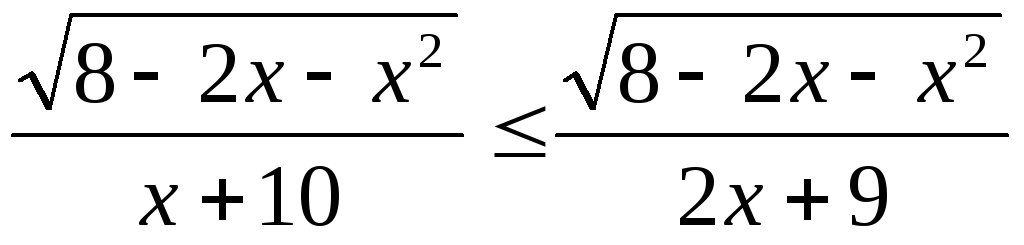 .
.
Решение. 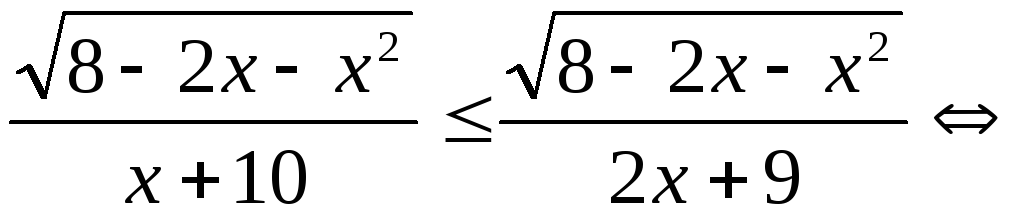
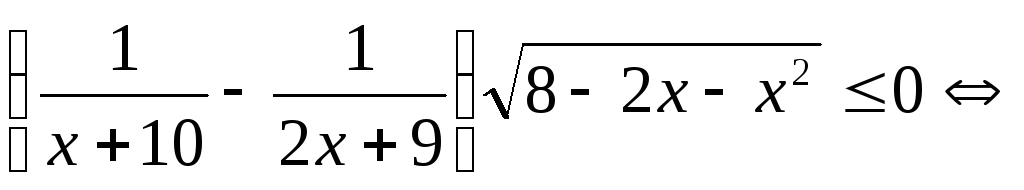
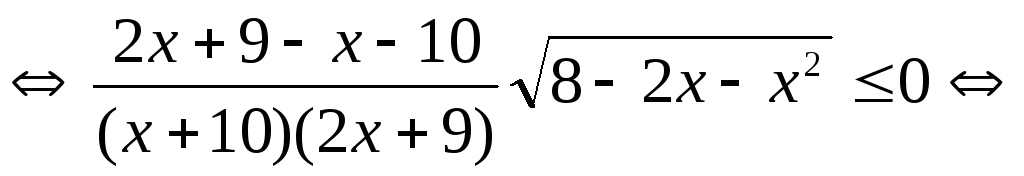
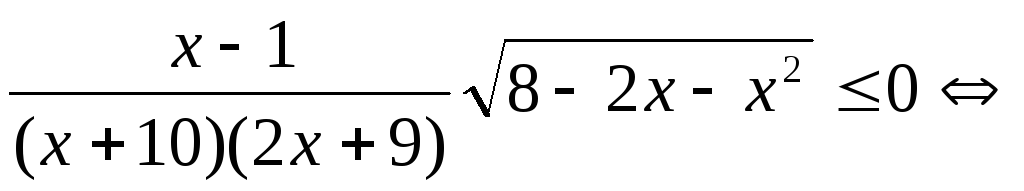
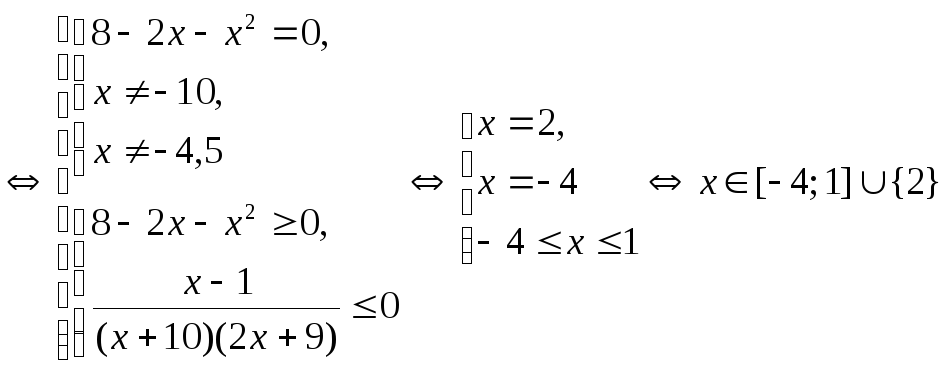 .
.
Ответ: 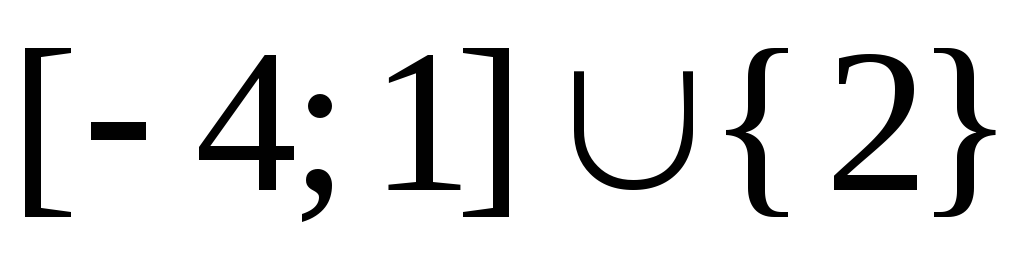 .
.
Задачи для самостоятельного решения Группа а
1. Укажите длину промежутка, который является решением неравенства:
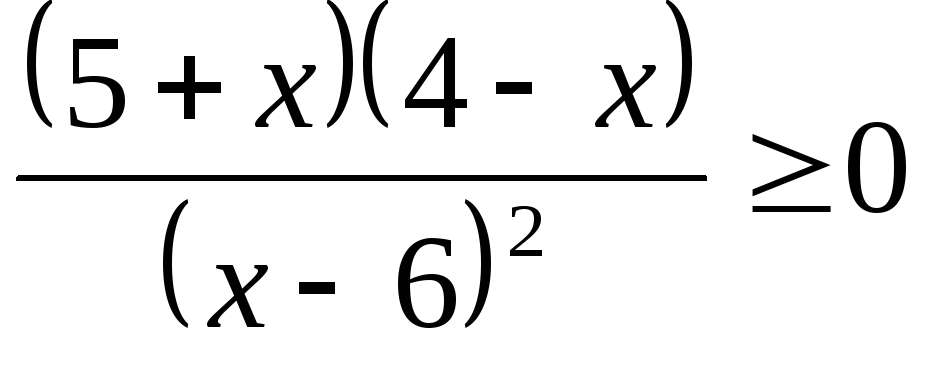 (Ответ:
(Ответ:  .)
.)
2. Найти произведение всех целых решений неравенства:
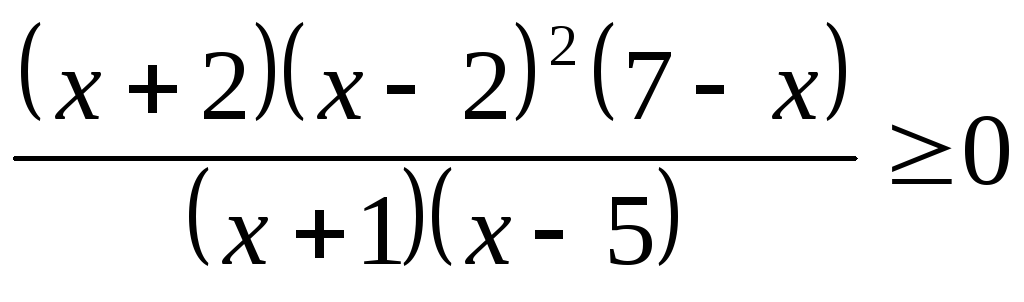 .
(Ответ:
.
(Ответ: 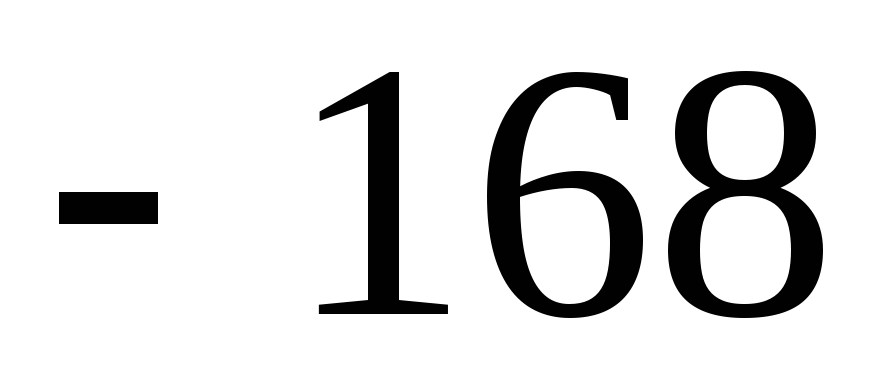 .)
.)
Решить неравенство (3-15)
3. 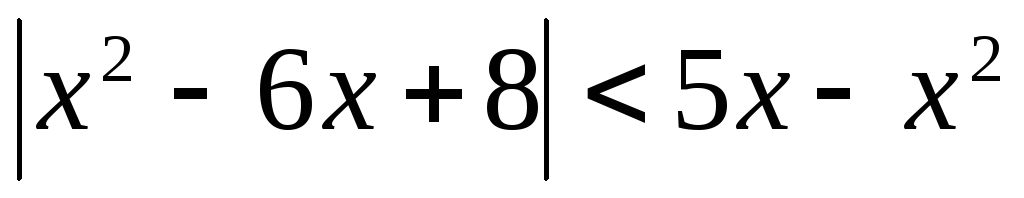 .
(Ответ:
.
(Ответ: 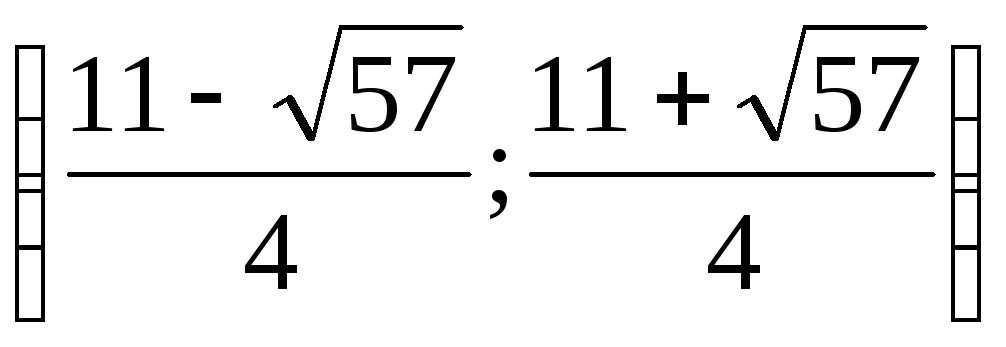 .)
.)
4. 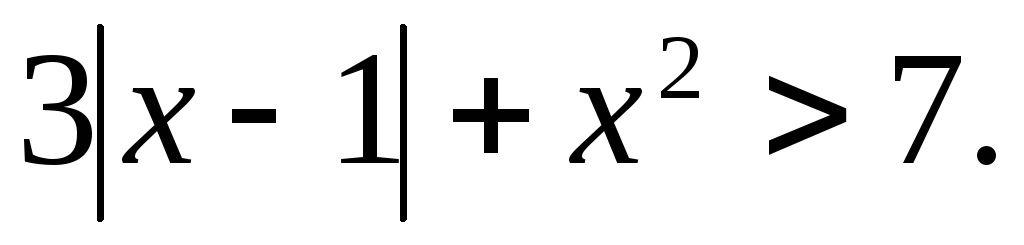 (Ответ:
(Ответ: 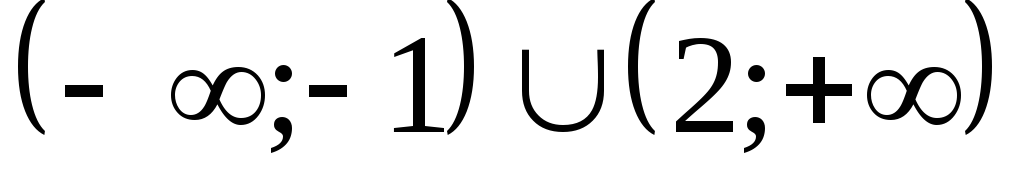 .)
.)
5. 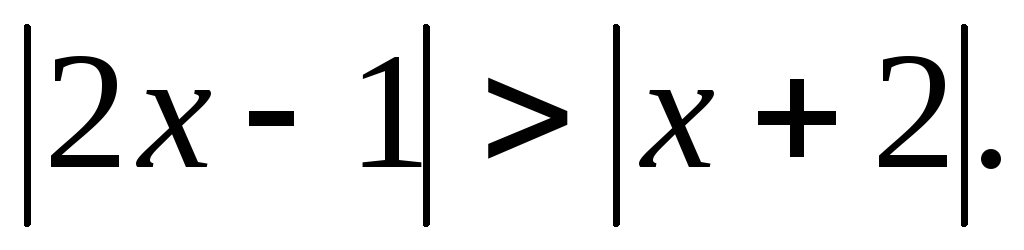 (Ответ:
(Ответ:  .)
.)
6. 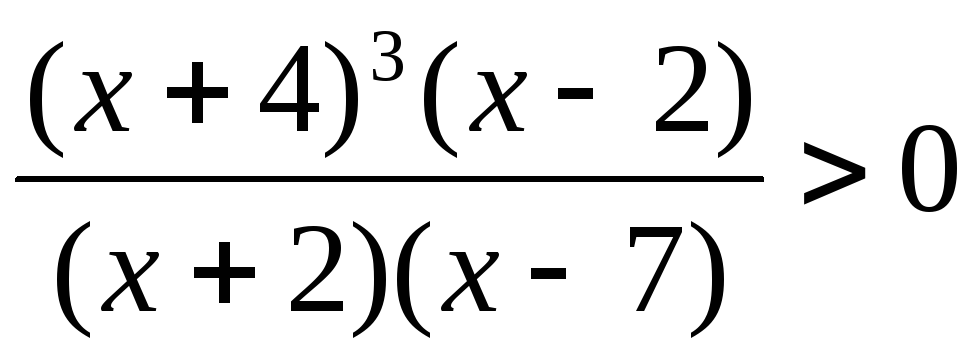 .
(Ответ:
.
(Ответ: 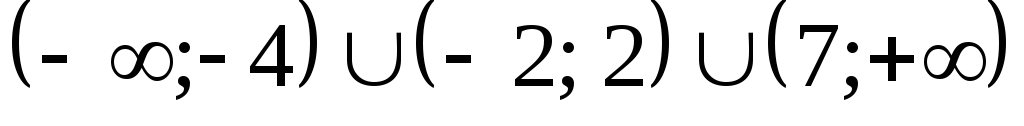 .)
.)
7. 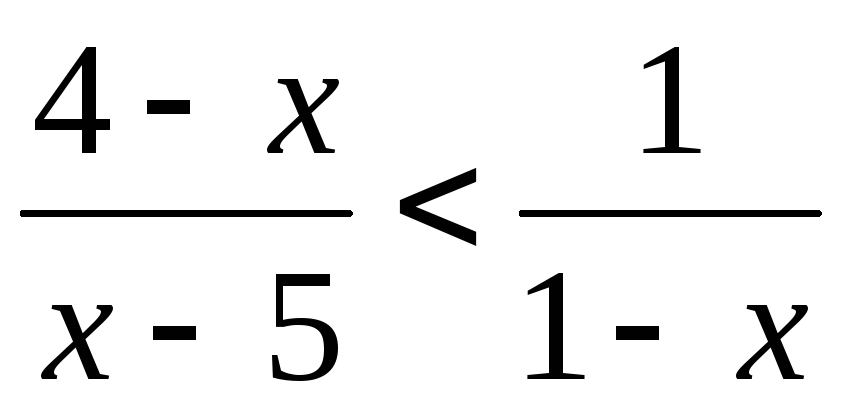 .
(Ответ:
.
(Ответ: 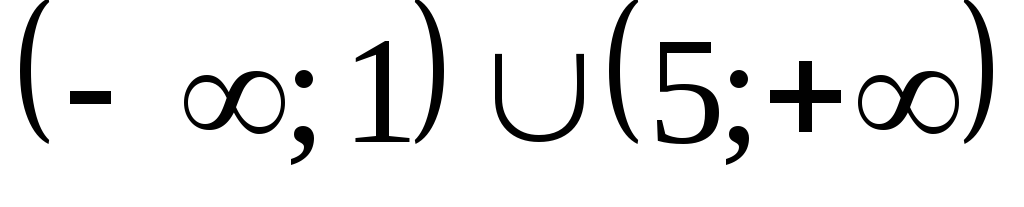 .)
.)
8. 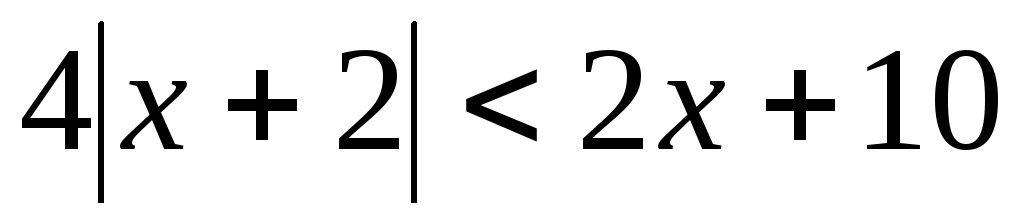 .
(Ответ:
.
(Ответ: 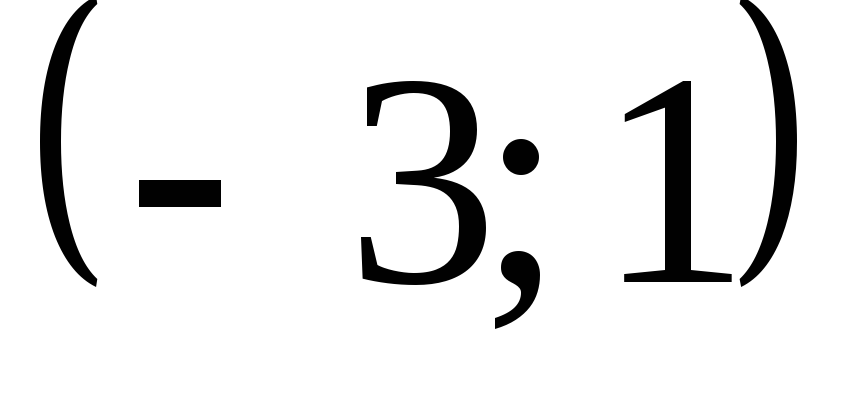 .)
.)
9. 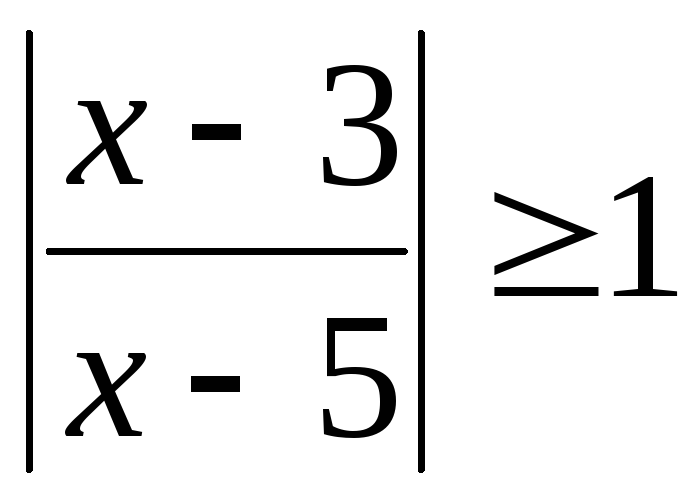 .
(Ответ:
.
(Ответ: 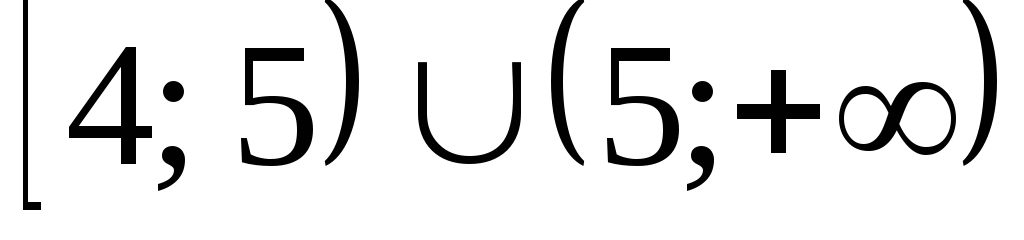 .)
.)
10. 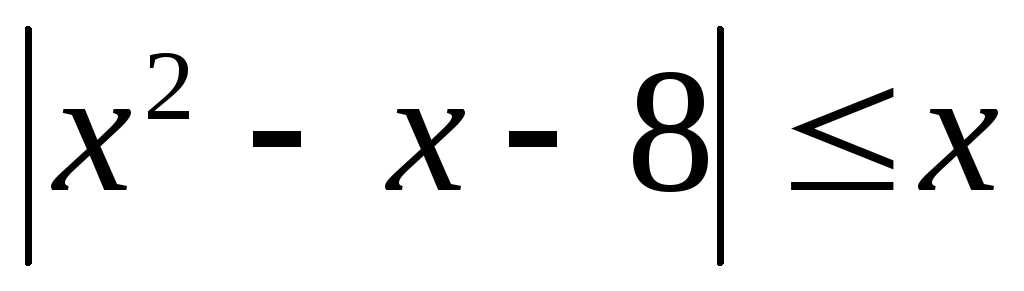 .
(Ответ:
.
(Ответ: 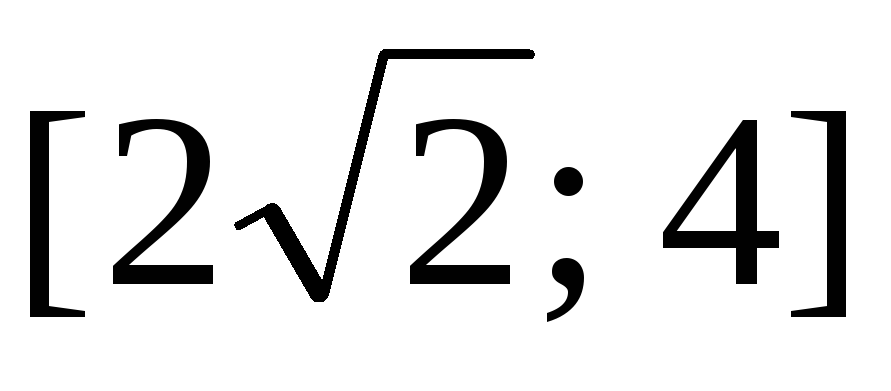 .)
.)
11. 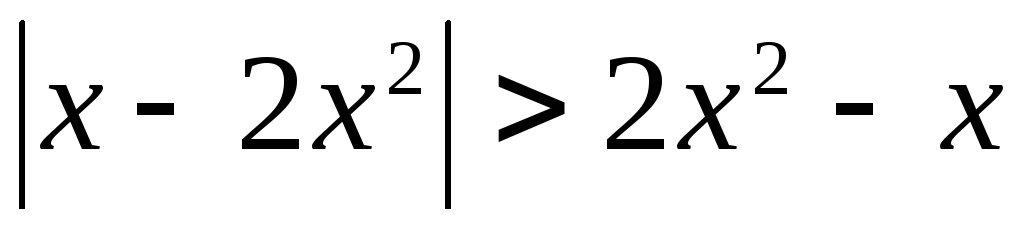 .
(Ответ:
.
(Ответ: 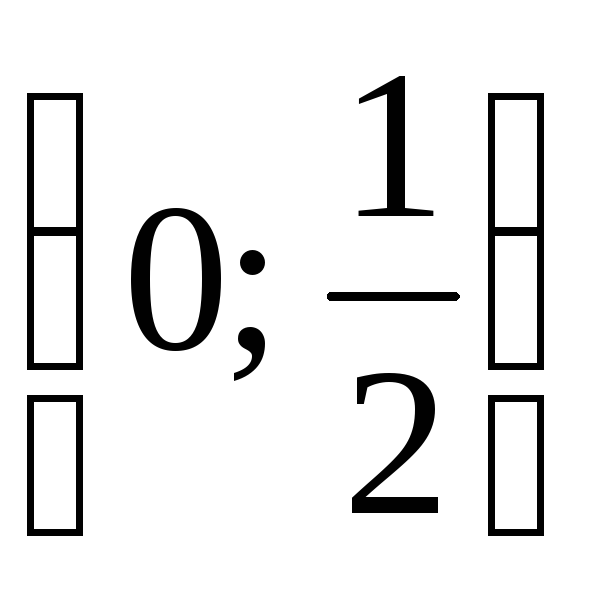 .)
.)
12. 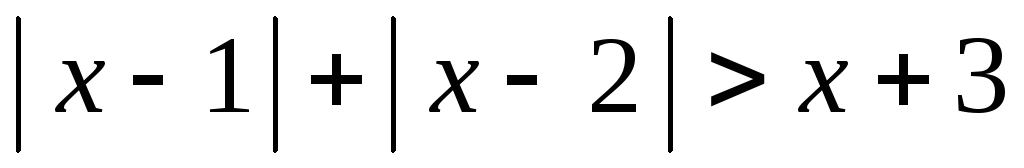 .
(Ответ:
.
(Ответ:  .)
.)
13.  .
(Ответ:
.
(Ответ: 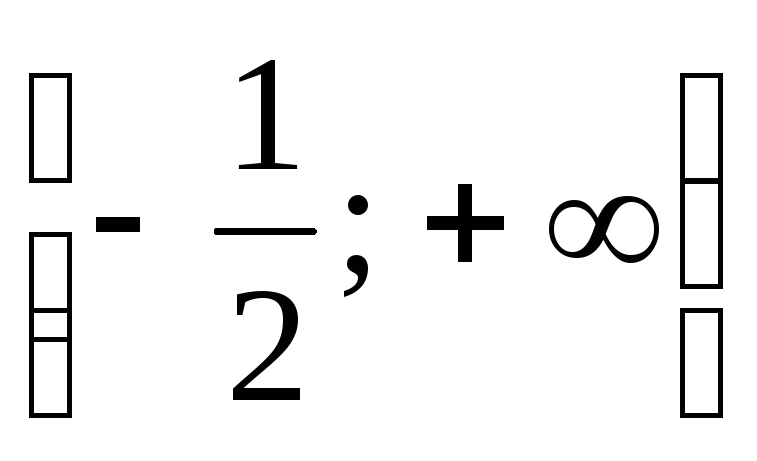 .)
.)
12. 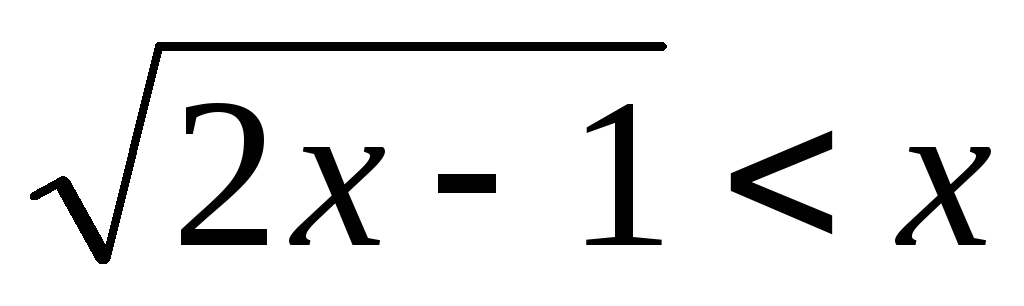 .
(Ответ:
.
(Ответ: 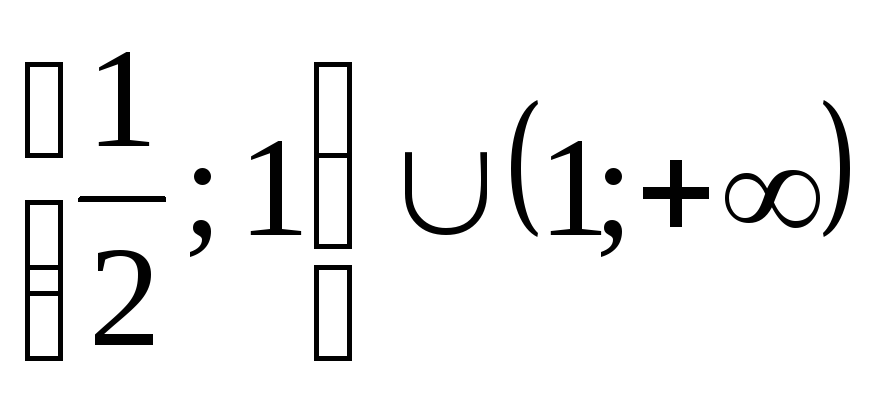 .)
.)
13. 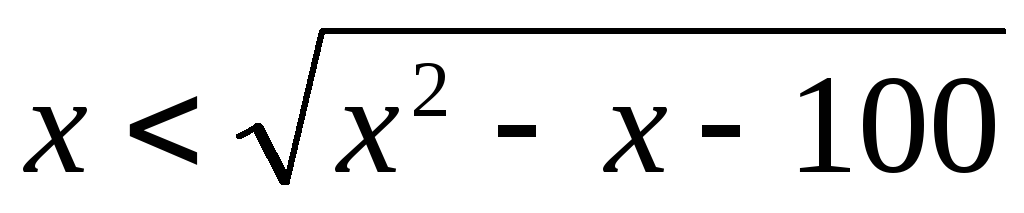 .
(Ответ:
.
(Ответ:  .)
.)
14. 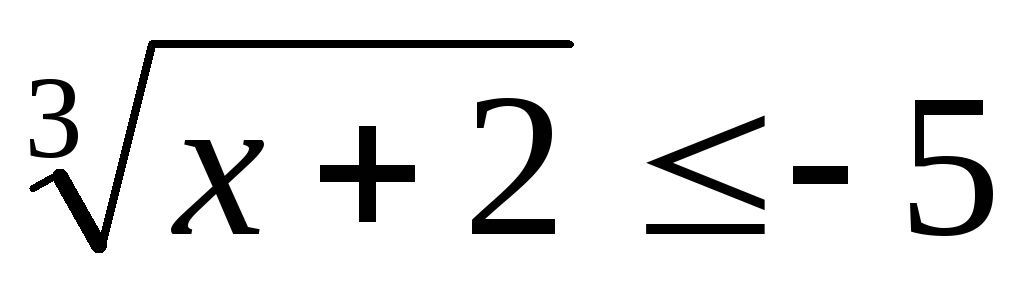 .
(Ответ:
.
(Ответ: 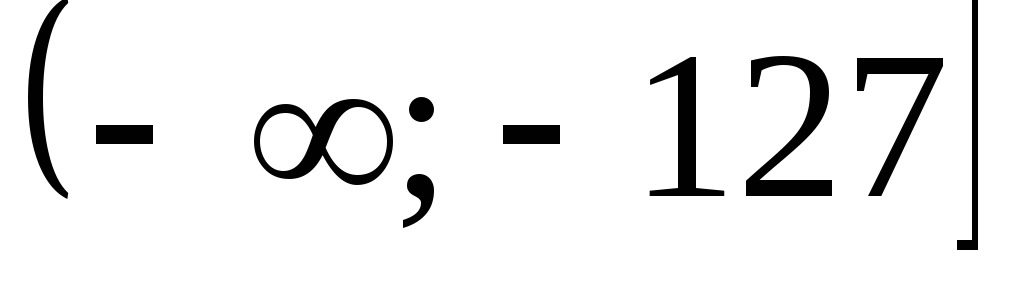 .)
.)
15. 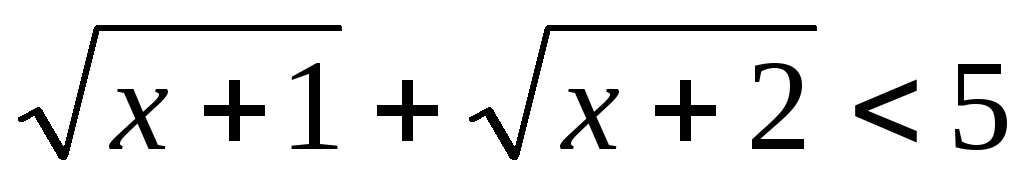 .
(Ответ:
.
(Ответ: 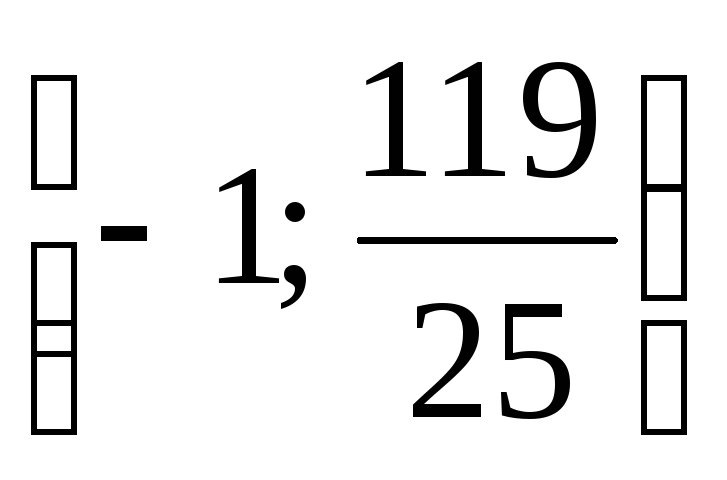 .)
.)
studfile.net
25. Неравенства с модулем | Решение задач по математике и другим предме
I тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:
где (3.27)
Решение зависит от знака числа А.
1. Если то неравенство (3.27) не имеет решений.
2. Если то неравенство (3.27) равносильно системе неравенств
где (3.28)
1. Если то неравенство (3.28) не имеет решений.
2. Если то неравенство (3.28) равносильно уравнению
3. Если , то неравенство (3.28) равносильно системе неравенств
где (3.29)
1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что
3. Если то неравенство (3.29) равносильно совокупности
где (3.30)
1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
2. Если то неравенство (3.30) равносильно совокупности
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
(3.31)
Где – некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения
1. Если
(3.32)
То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).
2. Если
То решением является множество всех значений Х, которые удовлетворяют системе
3. Если решение определяется системой
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
где (3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
Решение неравенства (3.33) сводится к решению неравенства
Аналогично решают неравенства IV типа (3.33), если они заданы со знаками
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) 2)
3) 4)
5) 6)
Решение. 1) Решаем как неравенство I типа:
Получаем ответ:
2) Решаем как неравенство I типа:
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
Его решение: это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:
Получаем ответ:
4) Заданное неравенство может быть записано в виде
Заменим переменную Решаем неравенство
Его решение
Возвращаемся к переменной Х и решаем совокупность
Получаем
Т. е. приходим к ответу
5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ:
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
(3.34)
Решаем неравенство
Получаем
Система (3.34) сводится к системе
На данном промежутке решений нет.
Б)
Если , то С учетом рассматриваемого промежутка имеем:
Получаем
В)
Решением является промежуток:
Объединим полученные решения и приходим к ответу:
6)
ОДЗ:
Введем новую переменную:
тогда и приходим к неравенству вида
Решаем его
Используем метод интервалов (рис. 3.11).
Рис. 3.11
Запишем полученное решение в виде совокупности:
Вернемся к переменной Х:
(3.35)
– выполняется при любых
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
Получаем ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Урок «Решение неравенств с модулем, содержащих параметр»
Тема: Решение неравенств с модулем, содержащих параметр.
Цели урока:
Обучающая — познакомить с методом решения неравенств с модулем, содержащих параметр.
Развивающая — развитие познавательной активности, логического мышления.
Воспитательная — воспитание организованности, внимания, математической наблюдательности.
ТСО: Проектор, компьютер. Дискета со приложениями №1,№2. Переносная доска.
Наглядность: таблица с формулами
Ход урока:
I. Актуализация знаний и проверка домашнего задания.
Вступительное слово учителя.
Задачи с параметром встречаются на ЕГЭ в группе «С» под номерами 3 и 5.
Так как среди вас есть те, кто претендует на высокий балл, то тема важна для изучения. Начнем с повторения ключевых задач по теме «Решение неравенств с модулем».
Назовите идею решения неравенств, записанных на доске и решите их:
| Ответы. | Ученик. |
Фёдоров С. Свиршевская М. Васильева А. Михеев А. |
На переносной доске работает Клинов А.
Решить неравенство:
Приходилось ли вам встречать и другие способы решения неравенств?
Ответ: графический. Приложение 1.
Рассмотрим, в чем заключается графический способ решения.
Решить неравенство :
Соловцов: – строим графики функций
Отмечаем точку пересечения графиков А.
Знак > понимаем так, что 1 график выше графика 2 и пишем ответ:
X < 2
Приложение 1.
Повторим алгоритм решения линейных неравенств с параметром:
Клинов А. объясняет решение на переносной доске.
x(a+1)<a
если
если
если
II. Изучение новой темы:
Учитель: рассмотрим методы решения типовых примеров.
В числовых неравенствах заменив число на букву, получим неравенство с параметром.
Рассмотрим методы решения этих неравенств. Они аналогичны рассмотренным способам решения неравенств с модулем.
Т.к. знак модуля определён, т.е.
Решение зависит от выражения а+1
Учитель: решим следующее неравенство:
Ответ:
Если ;
Учитель: Решим 3 пример.
Какими способами можно решить неравенство, если бы вместо буквы а стояло число?
Ответ: возведение обеих частей неравенства в квадрат, методом «промежутков».
Те же способы применяются и для неравенства с параметром.
Методом «промежутков» пойдет решать Семенова Д.
Методом возведения в квадрат- Федоров С.
,
,
Проверили решения данного примера.
Каким еще способом можно решить данное неравенство?
Ответ: графический.
Показывается приложение 2.
1.Строим графики функций
Найдем те значения переменной Х, когда первый график лежит выше второго.
Приложение 2.
Возможны варианты, когда а < 5 и а > 5
Рассмотрев различные способы решения, сделаем вывод- какой метод наиболее рациональный? Какими методами можно решить неравенства с параметром?
Вывод:
Методы решения неравенств с модулем, содержащие параметр, аналогичны тем, что применяются при решении числовых неравенств с модулем: по определению модуля, возведение обеих частей в квадрат, метод интервалов, графический. Необходимо выбирать наиболее рациональный.
Домашнее задание:
Подобрать и решить 3 уравнения с модулем, 3 неравенства с модулем и 3 неравенства с модулем, содержащие параметр. Можно придумать самим.
urok.1sept.ru
Примеры решения неравенств с модулем
Решим это неравенство методом интервалов. Найдем нули подмодульных выражений:
Эти значения разбивают числовую ось на три интервала: . Решим заданное неравенство на каждом из этих промежутков.
1) , при этом неравенство примет вид
Пересекая найденное решение с рассматриваемым интервалом , получаем решение .
2) , на этом интервале неравенство имеет вид:
Таким образом, может принимать любые значения на этом интервале то есть решением и будет сам интервал .
3) , тогда модули раскроются следующим образом:
Пересекая это решение с рассматриваемым промежутком, получим, что .
Для получения окончательного ответа объединим полученные решения:
confetti-matematika.ru
Решение неравенств с модулем | Математика, которая мне нравится
Для решения неравенств с модулем следует раскрыть модуль так же, как это делалось при решении уравнений, а затем решить полученные неравенства на соответствующих множествах (иными словами, решить полученные системы неравенств).
Пример 1. Решить неравенство
Решение. Рассмотрим два случая: 1) и 2) .
1) В этом случае неравенство равносильно системе
Преобразуя первое неравенство к виду , получим (см. рис. 13):
Рис. 13
Решение неравенства (-\infty;0]\cup[5;+\infty).
Преобразуя второе неравенство , получим (см. рис. 14):
Рис. 14
Решение неравенства . Решением системы является пересечение решений неравенств, то есть .
2) В этом случае неравенство равносильно системе:
Решение первого неравенства (см. рисунок к случаю 1)). Неравенство преобразуется к , его решение (см. рис. 15):
Рис. 15
Решение системы — пересечение множеств решений двух неравенств, то есть .
Общее решение исходного неравенства — объединение решений обоих случаев.
Ответ. .
Замечание. В данном случае проще было из определения модуля получить двойное неравенство , а затем его решить.
Пример 2. Решить неравенство
Решение. Точки и (корни выражений, стоящих под модулем) разбивают всю числовую ось на три интервала, на каждом из которых следует раскрыть модули.
1) При выполняется , и неравенство имеет вид , то есть . В этом случае ответ .
2) При выполняется , неравенство имеет вид , то есть . Это неравенство верно при любых значениях переменной , и, с учетом того, что мы решаем его на множестве , получаем ответ во втором случае .
3) При выполняется , неравенство преобразуется к , и решение в этом случае . Общее решение неравенства — объединение трех полученных ответов.
Ответ. .
Задачи. Решите неравенства:
1. .
2. .
3. .
4. .
hijos.ru