Решение систем линейных уравнений способом сложения калькулятор. Решение систем уравнений способом сложения
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы — это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 — y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным.
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны, то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х, на втором у.
Ответ: (4; 3)
Пример 2 . Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3(-2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Метод алгебраического сложения
Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменной.
В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится — это способ алгебраического сложения.
А откуда вообще взялась идея — что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.
Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.е. по отдельности складывают подобные слагаемые в левой части, затем в правой. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим сказанное на конкретных примерах.
Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число -у. Значит, это уравнение можно решить методом сложения.
Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.
А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с -у, 8 сложим с 7.
Получим систему уравнений
Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.
Ответ: (3; — 1).
Образец оформления:
Решить методом алгебраического сложения систему уравнений
В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь видим, что при переменной х есть противоположные коэффициенты. Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Теперь у нас система уравнений:
Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.
Образец оформления:
Давайте подведём итоги:
Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.
 Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007. - Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.
Способ сложения состоит из трёх простых шагов:
- Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
- Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
- Решить новое уравнение, получившееся после второго шага.

Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.
Однако на практике всё не так просто. Причин тому несколько:
- Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
- Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?
Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:
Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.
Каждое из них будет являться линейным.
Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.
Вообще, существует два метода решения подобных систем:
- Метод сложения;
- Метод выражения одной переменной через другую.
Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.
Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.
Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.
Решение легких задач с применением способа сложения
Итак, учимся применять метод сложения на примере двух простейших выражений.
Задача № 1
\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right.\]
Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:
Решаем простейшую конструкцию:
Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:
\[-4y=12\left| :\left(-4 \right) \right.\]
Ответ: $\left(2;-3 \right)$.
Задача № 2
\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]
Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:
Сложим их:
Мы получили простейшее линейное уравнение, давайте решим его:
Теперь давайте найдем $x$:
Ответ: $\left(-3;3 \right)$.
Важные моменты
Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:
- Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении. В этом случае одна из них уничтожится.
- Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
- Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left(…;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
- Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.
В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.
Решение легких задач с применением метода вычитания
Задача № 1
\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right.\]
Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:
Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:
Ответ: $\left(2;5 \right)$.
Задача № 2
\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right.\]
Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:
Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:
Ответ: $\left(-3;-2 \right)$.
Нюансы решения
Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.
Мы проводим алгебраическое вычитание.
Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.
Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.
Решение задач методом домножения на коэффициент
Пример № 1
\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right. \]
\]
Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:
\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]
Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:
Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:
\[-9y=18\left| :\left(-9 \right) \right.\]
Ответ: $\left(4;-2 \right)$.
Пример № 2
\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right. \]
\]
Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:
\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]
\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]
Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:
Теперь найдем $y$, подставив $x$ в первое уравнение:
Ответ: $\left(-2;1 \right)$.
Нюансы решения
Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:
- Смотрим на систему и анализируем каждое уравнение.
- Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях.
 Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении. - Находим одну переменную.
- Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.
- Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.
Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.
Решение задач с дробными числами
Пример № 1
\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]
Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:
Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:
\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]
Вычитаем уравнения друг из друга:
$n$ мы нашли, теперь посчитаем $m$:
Ответ: $n=-4;m=5$
Пример № 2
\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right.\]
Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:
\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]
Применяем метод вычитания:
Давайте найдем $p$, подставив $k$ во вторую конструкцию:
Ответ: $p=-4;k=-2$.
Нюансы решения
Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.
В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.
Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.
В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:
Решение сложных систем уравнений
В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.
Система № 1
\[\left\{ \begin{align}& 3\left(2x-y \right)+5=-2\left(x+3y \right)+4 \\& 6\left(y+1 \right)-1=5\left(2x-1 \right)+8 \\\end{align} \right. \]
\]
Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.
Итого мы получим окончательную систему, которая равносильна исходной:
\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right.\]
Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:
\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right.\]
Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$
Теперь найдем $y$:
Ответ: $\left(0;-\frac{1}{3} \right)$
Система № 2
\[\left\{ \begin{align}& 4\left(a-3b \right)-2a=3\left(b+4 \right)-11 \\& -3\left(b-2a \right)-12=2\left(a-5 \right)+b \\\end{align} \right.\]
Преобразуем первое выражение:
Разбираемся со вторым:
\[-3\left(b-2a \right)-12=2\left(a-5 \right)+b\]
\[-3b+6a-12=2a-10+b\]
\[-3b+6a-2a-b=-10+12\]
Итого, наша первоначальная система примет такой вид:
\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right. 3
3
 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Решение уравнений методом сложения. Калькулятор онлайн
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y — (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы — это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 — y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
|K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
ГДЗ по Алгебре 7 класс: Макарычев
Готовые домашние задания для 7 класса по алгебре Макарычева
Если в прошлом к решебникам относились скептически, то сегодня они стали важным дополнением учебного процесса. Пособиями с готовыми ответами активно пользуются не только ученики, но и их родители, которые хотят проконтролировать своих детей.
ГДЗ от Ответкина это не просто краткие материалы для списывания. Наш сайт не имеет аналогов, потому что здесь вы можете найти подробный алгоритм решения задач, несколько вариантов ответов, комментарии, благодаря которым можно понять трудную тему.
Что такое Ответкин?
- Это актуальная база данных. В других решебниках школьники вынуждены сверять номера, тратить дополнительное время на поиск нужного ответа. Но на нашем портале мы разместили только свежие ГДЗ к актуальным учебникам, по которым учатся в школах Российской Федерации.
- Подробные решения. Практически к каждому заданию на Ответкине есть короткий ответ и подробный, с алгоритмом выполнения примера, комментариями к нему. Когда нет времени и нужно быстро ответить на уроке, ученик может воспользоваться кратким решением, но если нужно разобраться с непонятной темой – помогут пояснения.
- Бесплатный помощник. Наш сайт бесплатно помогает учащимся и их родителям контролировать правильность выполнения домашней работы. Это позволяет сэкономить деньги на репетиторах.
- Несколько вариантов ответа. Видя альтернативные способы решения – школьник понимает механизм выполнения задачи, ему становятся понятны важные нюансы, которые он пропустил или не усвоил на уроке.

- Удобный поиск по сайту. Учебное пособие с пояснениями можно просматривать как с компьютера, так с мобильного телефона. Чтобы быстро найти определенный номер нужно лишь ввести его в строку поиска. Кроме того, в личном кабинете сохраняется история просмотров, с помощью которой удобно возвращаться к предыдущим заданиям.
ГДЗ от Ответкина становятся незаменимы в конце четверти или учебного года, когда нужно быстро повторить пройденный материал, подтянуть успеваемость.
Уникальные подробные решения с пояснениями Ответкина
С 7 класса школьники начинают изучать новый для них раздел математики – алгебру. Это важный, но не простой предмет, который тесно связан с экономикой, информатикой, физикой и другими точными науками.
Нередко семиклассники теряются при выполнении разнообразных алгебраических задач. Теперь им нужно решать уравнения не только с одной, но и двумя переменными, строить графики функций, осуществлять разложение многочленов на множители. Далеко не каждый учитель может объяснить эти сложные темы простым и понятным для детей способом. Поэтому родители ломают голову, где бы найти хорошего репетитора, как проверить домашнее задание ребенку, когда сам уже забыл пройденную школьную программу.
Далеко не каждый учитель может объяснить эти сложные темы простым и понятным для детей способом. Поэтому родители ломают голову, где бы найти хорошего репетитора, как проверить домашнее задание ребенку, когда сам уже забыл пройденную школьную программу.
С решением этих проблем помогает Ответкин. Он дает возможность узнать правильный ответ и его разные варианты, понять алгоритм выполнения примера.
Почему наш сайт достойная альтернатива занятиям с репетитором?
- Это быстро и бесплатно. Использование учебного пособия с пояснениями позволяет родителям сэкономить деньги. Ученикам не нужно тратить дополнительное время на дорогу к репетитору и обратно домой. В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
- Это удобно. Репетитор занимается с ребенком в назначенное время, поэтому все вопросы школьник вынужден откладывать до следующего дополнительного занятия.
 А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома.
А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома. - Ответкин приучает к самостоятельности. Готовые домашние задания на нашем сайте — это не просто материалы для списывания, а подробное объяснение важных нюансов школьной программы. Практически каждый номер содержит не только несколько вариантов ответа, на и комментарии, с помощью которых можно восполнить пробелы в знаниях алгебры.
Если говорить о видеоуроках, то они не могут сравниться с нашим порталом по эффективности, удобству и актуальности данных. Нередко спикеры объясняют материал 7 класса, не имея опыта преподавания в школе. Они могут говорить много, но без конкретики, не дают подсказок к выполнению домашней работы. Видеоролики нужно проматывать несколько раз, тратить 30-40 минут на усвоение одной только темы. В то время как школьник, возможно, хочет уточнить несколько важных нюансов, а не прослушивать материал всего урока.
Как пользоваться сайтом и открывать нужную задачу с комментариями?
Наша команда сделала Ответкин максимально удобным для пользователей. Мы учли, что семиклассники часто просматривают готовые домашние задания в мобильном телефоне. В отличие от других сайтов у нас все материалы размещены на узком полотне, выполнены красивым понятным шрифтом, который комфортно читать со смартфона.
Мы учли, что семиклассники часто просматривают готовые домашние задания в мобильном телефоне. В отличие от других сайтов у нас все материалы размещены на узком полотне, выполнены красивым понятным шрифтом, который комфортно читать со смартфона.
Подсказки как пользоваться сайтом:
- Чтобы найти нужное задание введите его в строку быстрого поиска. Ознакомьтесь с кратким вариантом ответа, который откроется на новой странице. Если вы хотите увидеть подробный алгоритм решения задачи с разными вариантами – зарегистрируйтесь на нашем сайте.
- Вы можете выбрать один из двух, наиболее удобный для вас вариант авторизации. Первый – через социальные сети. Рядом с кнопкой «Войти» нажмите на социальную сеть, например, гугл аккаунт. Подтвердите вход, дайте свое согласие, что ознакомлены с правилами пользования сайтом. Второй вариант – регистрация с нуля с использованием почтового ящика. Напишите адрес вашей почты и ждите письма со ссылкой для активизации аккаунта. Перейдите по ссылке и пользуйтесь сайтом.

- После авторизации вам откроется доступ в личный кабинет. По умолчанию вам будет предоставлена бесплатная подписка, где будет видно количество оставшихся ответов. Каждые сутки пользователь может открывать не более трех заданий. Открытые решения будут храниться в личном кабинете в течение 24 часов, которые можно просматривать неограниченное количество раз.
- Если пользователь желает получить большее число открываний в сутки – ему стоит приобрести подписку на платной основе сроком на месяц. В этом случае в личном кабинете исчезнет реклама. В профиле будет видно сколько дней еще действует платная подписка.
Для удобства, чтобы пользователь быстро сориентировался в задании – на белом фоне изображен краткий ответ для записи в тетрадь, на цветном фоне отображена теория и подробные пояснения к номеру. Но даже краткие решения на нашем сайте более подробные, чем в других ГДЗ.
Решебник алгебры седьмого класса к учебнику Ю.Н. Макарычева, Н.Г. Миндюка, К.И. Нешкова, С.
 Б. Суворова
Б. СувороваРешения с пояснениями по алгебре за 7 класс составлены на основе учебника Макарычева 2013 года, который соответствует Федеральным государственным образовательным стандартам. Номера в пособии с готовыми домашними заданиями соответствуют нумерации учебника.
Алгебра седьмого класса содержит 5 глав, состоящих из 16 параграфов, которые в свою очередь в общей сложности разбиты на 46 подпунктов. К каждой теме помимо теории есть практические упражнения. Для коллективного решения предусмотрены «задачи-исследования» и задания для работы в парах. В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе.
Готовые домашние задания по алгебре от Ответкина направлены на усвоение следующих тем и понятий:
- Числовые выражения, сравнение их значений и преобразование.
- Уравнение, решение задач с его помощью, линейные уравнения с одной и двумя переменными, графики и системы линейных уравнений.
 Линейные неравенства с двумя переменными. Способ подстановки и способ сложения.
Линейные неравенства с двумя переменными. Способ подстановки и способ сложения. - Функция, линейная функция и ее график, вычисление функции по формуле.
- Статистические характеристики: медиана, среднее арифметическое, мода, размах.
- Степень, умножение и деление степеней.
- Стандартный вид одночлена и многочлена. Умножение одночленов, одночлена на многочлен, многочлена на многочлен. Возведение одночлена в степень. Сложение и вычитание многочленов. Преобразование целого выражения в многочлен. Разложение многочлена на множители.
- Квадрат суммы и квадрат разности. Возведение в квадрат разности и суммы двух выражений. Разложение на множители разности квадратов, суммы и разности кубов.
Подробные ответы с комментариями по алгебре за 7 класс помогут школьникам вспомнить пройденный материал: различные действия с дробями и целыми числами, решение текстовых задач, поиск корня уравнения. Но главное, решебник станет надежным советчиком в изучении новых тем, которые впервые вводятся с 7 класса. Это операции с многочленами, решение системных уравнений с двумя переменными, построение графиков функций.
Это операции с многочленами, решение системных уравнений с двумя переменными, построение графиков функций.
Мы уверены, что учебное пособие от Ответкина поможет полюбить новый предмет – алгебру. С его помощью школьники разберутся в пропущенных темах, подтянут успеваемость, будут уверены в правильности выполнения упражнений.
Решение систем линейных уравнений с использованием исключения
Системы линейных уравнений:
А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.
В двух переменных ( Икс и у ) , график системы двух уравнений представляет собой пару прямых на плоскости.
Есть три возможности:
- Линии пересекаются в нулевых точках.(Прямые параллельны.)
- Линии пересекаются ровно в одной точке. (Большинство случаев.
 )
) - Прямые пересекаются в бесконечном числе точек. (Два уравнения представляют одну и ту же прямую.)
Как решить систему линейных уравнений методом исключения (он же метод сложения, он же метод линейной комбинации)
- Шаг 1 : Прибавьте (или вычтите) число, кратное одному уравнению, к другому уравнению (или из него) таким образом, чтобы Икс -термины или у -термины отменяются.
- Шаг 2 : Затем решите для Икс (или у , в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.
Откуда мы знаем, что линейное уравнение, полученное сложением первого уравнения со скалярным умножением второго, эквивалентно первому?
Возьмем пример. Рассмотрим систему
3
Икс
+
2
у
знак равно
3
Икс
−
у
знак равно
−
4
.
Рассмотрим уравнение, полученное умножением второго уравнения на константу м а затем добавить полученное уравнение к первому.
Это, ( 3 Икс + 2 у ) + м ( Икс − у ) знак равно ( 3 ) + м ( − 4 ) .
Нам нужно доказать, что это уравнение эквивалентно уравнению 3 Икс + 2 у знак равно 3 .
У нас есть Икс − у знак равно − 4 ⇒ м ( Икс − у ) знак равно − 4 м .
С
м
(
Икс
−
у
)
знак равно
−
4
м
, вычесть
м
(
Икс
−
у
)
с левой стороны и
−
4
м
из правой части уравнения
(
3
Икс
+
2
у
)
+
м
(
Икс
−
у
)
знак равно
(
3
)
−
4
м
который сохранит равновесие.
( 3 Икс + 2 у ) + м ( Икс − у ) − м ( Икс − у ) знак равно ( 3 ) − 4 м − ( − 4 м )
Отменив общие условия, мы получим, 3 Икс + 2 у знак равно 3 что эквивалентно первому уравнению.
Поэтому системы уравнений
3
Икс
+
2
у
знак равно
3
Икс
−
у
знак равно
−
4
и
(
3
Икс
+
2
у
)
+
м
(
Икс
−
у
)
знак равно
3
+
м
(
−
4
)
Икс
−
у
знак равно
−
4
эквивалентны.
В общем случае для любой системы уравнений К знак равно л и п знак равно Вопрос , можно показать, что К + м п знак равно л + м Вопрос эквивалентно К знак равно л .
Пример:
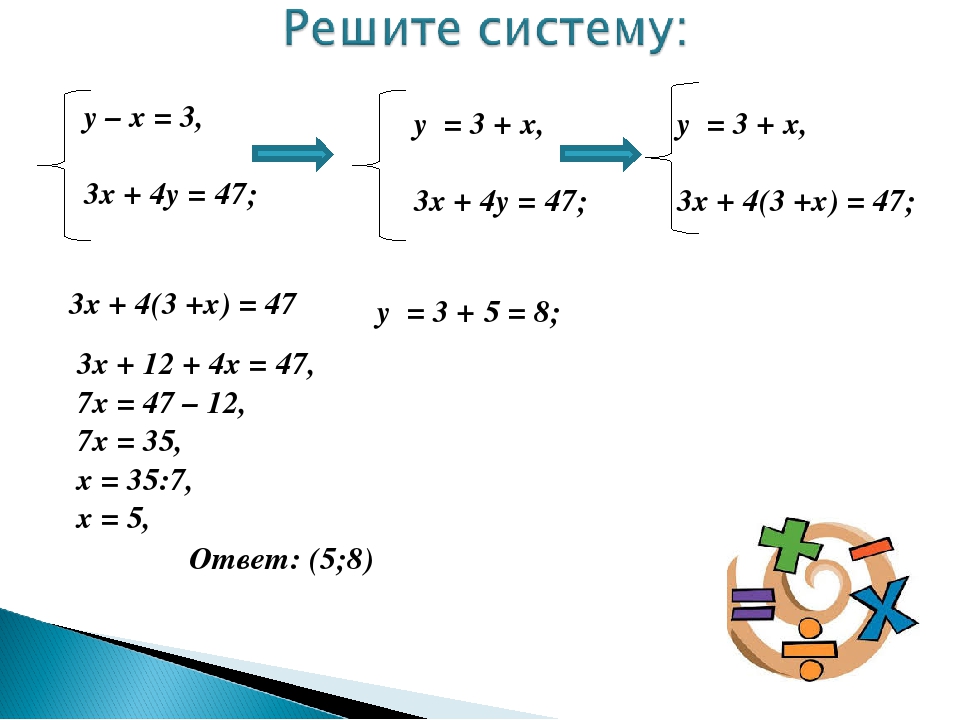
Решите систему { 4 Икс + 3 у знак равно − 2 8 Икс − 2 у знак равно 12
Умножьте первое уравнение на − 2 и добавьте результат ко второму уравнению.
− 8 Икс − 6 у знак равно 4 8 Икс − 2 у знак равно 12 _ − 8 у знак равно 16
Решить для
у
.
у знак равно − 2
Замена для у в любом из исходных уравнений и решить для Икс .
4 Икс + 3 ( − 2 ) знак равно − 2 4 Икс − 6 знак равно − 2 4 Икс знак равно 4 Икс знак равно 1
Решение
(
1
,
−
2
)
.
Решение систем линейных уравнений методом исключения
Как решить систему уравнений:
Прежде чем мы приступим к решению систем линейных уравнений методом исключения, давайте сначала рассмотрим и поймем, что значит «решить» систему уравнений. Когда мы говорим «решить» по отношению к линейному, квадратичному, экспоненциальному или любому другому типу уравнения, на самом деле мы имеем в виду, что пытаемся найти значения «x» — зависимой переменной — которые удовлетворяют «y» — независимая переменная.
Возьмем, к примеру, следующее простое уравнение: y = 2x = 2
В этом примерном уравнении мы знаем, что y равно 2x, а также равно 2. Зная это, поскольку y равно и 2x, и 2, мы можем сказать, что 2x = 2. Затем следующий естественный шаг: решить это уравнение с помощью алгебры, что дает нам «решение», в котором x = 1,
В случае с системами уравнений процесс ничем не отличается. При решении систем уравнений мы пытаемся найти значения x и y, которые делают два различных уравнения равными друг другу, эффективно «решая» оба уравнения. Дополнительную информацию о системе уравнений можно найти в другом уроке. В системе уравнений есть несколько результатов, которые могут произойти в зависимости от количества решений. У нас есть специальные уроки, как определить количество решений линейных уравнений и системы линейно-квадратичных уравнений. У нас также есть графические системы уравнений и неравенств!
Дополнительную информацию о системе уравнений можно найти в другом уроке. В системе уравнений есть несколько результатов, которые могут произойти в зависимости от количества решений. У нас есть специальные уроки, как определить количество решений линейных уравнений и системы линейно-квадратичных уравнений. У нас также есть графические системы уравнений и неравенств!
Для этого существует два основных метода: решение систем заменой и решение систем методом исключения.В этой статье мы сосредоточимся на подстановке, которая, возможно, немного проще, чем другой метод — исключение. Для устранения, пожалуйста, ознакомьтесь с видео и статьями, посвященными именно этому методу. Чтобы убедиться, что вы готовы к исключению, важно освоить сложение и вычитание полиномов, а также сложение и вычитание рациональных выражений.
Теперь, когда мы рассмотрели основы, давайте решать системы методом исключения!
Решение систем уравнений методом исключения:
Прежде чем мы перейдем к использованию метода исключения, убедитесь, что вы хорошо разбираетесь в алгебре, просмотрев урок по решению линейных уравнений с переменными в обеих частях.
Процедура решения методом исключения не слишком сложна. Учитывая системы линейных уравнений, мы пытаемся «модифицировать» одно или оба уравнения, чтобы мы могли складывать/вычитать их, чтобы «исключить» переменную. Трудно описать процедуру исключения без конкретного примера, поэтому давайте рассмотрим шаги метода исключения на примере.
Пример 1:
Возьмите следующие одновременные уравнения и решите методом исключения.
3х + 4у = 11 х — 4у = -7Шаг 1. Определите модификации и операции, необходимые для устранения переменной
В этом примере нам повезло иметь одинаковый коэффициент при y для обоих уравнений. В первом уравнении 4y, а во втором уравнении -4y. В этом случае очень легко сложить эти уравнения вместе, чтобы «исключить» y. Это потому, что когда мы сложим эти два уравнения вместе, 4y + (-4y) будет равно 0, оставив x как единственную оставшуюся переменную, которую мы можем легко найти.
Таким образом, чтобы исключить из обоих уравнений общую переменную 4y, складываем уравнения вместе:
3х + 4у = 11 (+) х — 4у = -7 (=) 4x + 0 = 4 х = 1Шаг 2: Найдите x
Теперь, когда у нас есть уравнение 4x = 4 из нашего шага исключения, мы можем легко найти x.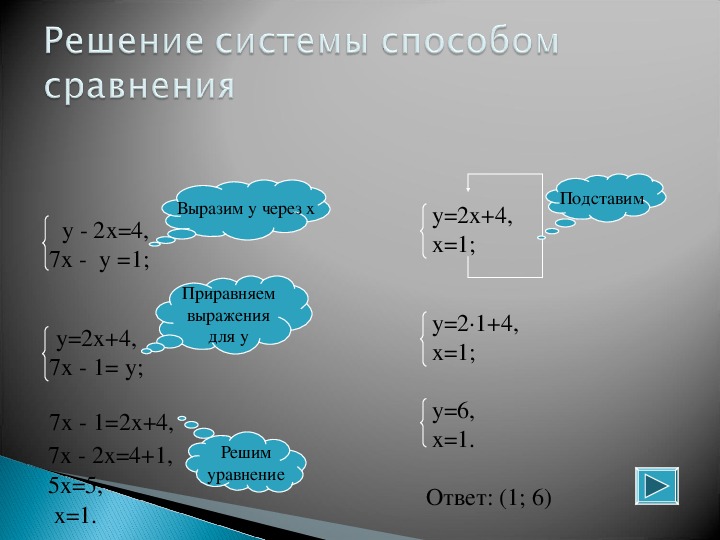
Шаг 3: Найдите у
Теперь, когда у нас есть x = 1, все, что нам нужно сделать, это подставить x = 1 в любое из уравнений, чтобы найти y.
3(1) + 4у = 11 3 + 4г = 11 4г = 8 у = 2Шаг 4: Запишите окончательный ответ как координату
Следовательно, наш окончательный ответ: (1, 2)
Изображение ниже суммирует все, что мы только что сделали:
Исключение, решение линейного уравненияТеперь, когда мы знаем, как использовать метод исключения для решения систем линейных уравнений, давайте рассмотрим другой, более сложный пример.
Пример 2:
Решите следующую систему уравнений методом исключения.
6х — 1 = 2у 9х + 4 = 5уШаг 1. Определите модификации и операции, необходимые для устранения переменной
В этом примере нам не повезло иметь одинаковый коэффициент при y для обоих уравнений. Итак, чтобы исключить y, нам нужно умножить оба уравнения на обыкновенное отношение следующим образом:
(6х — 1 = 2у) х 5 (9х + 4 = 5у) х 2Что дает нам:
30х — 5 = 10у 18х + 8 = 10уТеперь, когда у нас есть общая переменная 10y в обоих уравнениях, мы можем вычесть уравнения, чтобы исключить y:
30х — 5 = 10у (-) 18х + 8 = 10у (=) 12x — 13 = 0 х = 1312\фракция{13}{12}1213Шаг 2: Найдите x
Теперь, когда у нас есть уравнение 12x = 13 из нашего шага исключения, мы можем легко найти x.
Шаг 3: Найдите у
Теперь, когда у нас есть 1312\frac{13}{12}1213, все, что нам нужно сделать, это подставить 1312\frac{13}{12}1213 в любое из уравнений, чтобы найти y.
6(1312\frac{13}{12}1213) — 1 = 2г 112\frac{11}{2}211 = 2 года 114\frac{11}{4}411 = уШаг 4: Запишите окончательный ответ как координату
Таким образом, наш окончательный ответ: (1312,114\frac{13}{12}, \frac{11}{4}1213,411)
Изображение ниже суммирует все, что мы только что сделали:
Решение линейного уравнения методом исключенияВот и все! Теперь убедитесь, что вы выполняете много практических задач, чтобы освоить этот метод.Кроме того, проверьте эту замечательную ссылку, которая позволит вам легко проверить свою работу.
Решение системы двух линейных уравнений Пошаговое решение математических задач
Решение системы линейных уравнений подстановкой
Пример 1
Метод подстановки заключается в подстановке выражения одной переменной через другую в другое уравнение системы. Например, чтобы решить систему
Например, чтобы решить систему
подстановкой, замените на в первом уравнении
, заметив, что круглые скобки обязательны.Затем решите это уравнение относительно х.
Замените x на 1 в y = x + 3, чтобы найти, что y = 1 + 3 = 4. Набор решений для этой системы равен {(1, 4)}.
Пример 2:
Решить систему
Начните с решения одного уравнения для одной из переменных через другую. Например, решение первого уравнения для x дает:
Теперь подставьте этот результат для x в уравнение (2).
Чтобы исключить дробь слева, умножьте обе части уравнения на 2 и найдите лет.
Подставьте y = 5 обратно в уравнение (3), чтобы найти x
Набор решений для системы равен ((-2, 5)}. Проверьте, подставив -2 вместо x и 5 вместо y в каждом из уравнений системы.
Решение системы линейных уравнений сложением
Другим методом решения систем двух уравнений является метод сложения. В этом методе мы сначала умножаем уравнения с обеих сторон на подходящие числа, чтобы при их сложении исключалась одна переменная.В результате получается уравнение с одной переменной, которое можно решить методами, используемыми для линейных уравнений. Затем решение подставляется в одно из исходных уравнений, что позволяет найти другую переменную. В этом процессе данная система заменяется новыми системами, имеющими тот же набор решений, что и исходная система. Системы с одинаковым набором решений называются эквивалентными системами. Метод добавления иллюстрируется следующими примерами.
Решить систему
исключить x, умножить обе части уравнения (4) на -2 и обе части уравнения (S) на 3, чтобы получить уравнения (6) и (7).
Хотя эта новая система отличается от данной системы, у нее будет тот же набор решений.
Теперь сложите два уравнения, чтобы исключить x, и решите результат относительно y.
Подставьте 2 вместо уравнения инь (4) или (5). Выбор уравнения (4) дает
Множеством решений данной системы является { (3, 2)}, что можно проверить, подставив 3 вместо x и 2 вместо y в уравнении (5).
Поскольку метод решения сложения приводит к исключению из системы одной переменной, его также называют методом исключения.
4 полезных совета по решению систем уравнений методом исключения
Вот как решать системы уравнений методом исключения Решение систем уравнений методом исключения — это метод решения системы двух линейных уравнений. Решение систем уравнений методом исключения следует определенному процессу, чтобы упростить решения. Первое, что вы должны сделать, когда Решение систем уравнений методом исключения , это умножить любое уравнение так, чтобы при сложении их по вертикали одна из переменных сокращалась. Затем вы должны сложить уравнения вместе по вертикали, чтобы исключить одну переменную. Затем вы решаете для переменной, которая не была отменена. Используйте решение переменной для подстановки обратно в любое из исходных уравнений. Последним шагом при решении систем уравнений методом исключения является решение последней переменной в следующем порядке операций.
Затем вы должны сложить уравнения вместе по вертикали, чтобы исключить одну переменную. Затем вы решаете для переменной, которая не была отменена. Используйте решение переменной для подстановки обратно в любое из исходных уравнений. Последним шагом при решении систем уравнений методом исключения является решение последней переменной в следующем порядке операций.
Общий базовый стандарт: 8.EE.C
Связанные темы: Идентификация одного, ни одного, бесконечного числа решений, решение систем с помощью графического изображения, решение систем с помощью подстановки
Вернуться в: Дом, 8-й класс
Краткое руководство по выполнению любого примера метода исключения
Решение систем уравнений методом исключения — это метод объяснения расположения двух математических утверждений.Первое, что вы должны сделать при решении систем уравнений методом исключения, — это изменить любое математическое утверждение с мыслью, что они будут отменены, когда вы сложите их вместе. Затем вы должны сложить уравнения вместе по вертикали, чтобы исключить одну переменную. В этот момент вы упрощаете переменную, которая не была устранена. Используйте ответ для переменной, чтобы подставить ее обратно в любое математическое выражение. Последняя часть при решении систем уравнений методом исключения заключается в упрощении последней переменной с использованием порядка операций.
Затем вы должны сложить уравнения вместе по вертикали, чтобы исключить одну переменную. В этот момент вы упрощаете переменную, которая не была устранена. Используйте ответ для переменной, чтобы подставить ее обратно в любое математическое выражение. Последняя часть при решении систем уравнений методом исключения заключается в упрощении последней переменной с использованием порядка операций.
6 быстрых шагов для решения систем уравнений методом исключения
- Несколько уравнений или обоих, чтобы при сложении их вместе одна переменная отменялась.
- После умножения сложите уравнения.
- Найдите переменную, оставшуюся после отмены другой.
- Подставьте свое решение вместо первой переменной обратно в любое уравнение.
- Найдите вторую переменную.
- Ваш ответ должен быть в координатах x и y.
Посмотрите видео, в котором мы заполняем рабочий лист метода исключения
Посмотрите наше бесплатное видео о том, как решать систем уравнений методом исключения . В этом видео показано, как решать проблемы, описанные в нашей бесплатной рабочей таблице Метод устранения , которую вы можете получить, отправив свое электронное письмо выше.
В этом видео показано, как решать проблемы, описанные в нашей бесплатной рабочей таблице Метод устранения , которую вы можете получить, отправив свое электронное письмо выше.
Посмотрите бесплатное видео «Решение систем уравнений методом исключения» на YouTube здесь: «Решение систем уравнений методом исключения»
Стенограмма видео:
Это видео о решении систем уравнений методом исключения.Вы можете получить рабочий лист, использованный в этом видео, бесплатно, нажав на ссылку в описании ниже.
Вот номер один в нашем листе решения систем уравнений методом исключения. Эта задача дает нам два отдельных уравнения в нашей системе. Первое уравнение 3x минус y равно 7, а второе уравнение отрицательное 2x плюс y равно 2. Когда вы используете метод исключения для решения систем уравнений, вы собираетесь складывать каждую часть вашего уравнения по вертикали, чтобы одна или несколько из условия будут отменены. В случае решения систем с использованием метода исключения вы должны визуализировать, как вы не можете добавить их по вертикали, чтобы увидеть, какие члены или переменные будут сокращаться. Теперь не имеет значения, аннулируете ли вы X или Y, но по крайней мере один из них должен аннулироваться.
В случае решения систем с использованием метода исключения вы должны визуализировать, как вы не можете добавить их по вертикали, чтобы увидеть, какие члены или переменные будут сокращаться. Теперь не имеет значения, аннулируете ли вы X или Y, но по крайней мере один из них должен аннулироваться.
Мы можем посмотреть на наши уравнения, и мы можем увидеть, что если бы мы сложили их прямо вниз, то Y отменились бы, так что вы бы сделали 3x плюс отрицательное 2x было бы 1x или 3x минус 2x было бы 1x, а затем отрицательное y плюс 1г.Это отрицательное значение: 1 y плюс 1 Y будет 0 Y, а затем 7 плюс 2 будет 9. Другими словами, мы взяли Y, потому что сейчас у нас есть 0y, и мы его аннулировали. Теперь его нет, и у нас остается 1x или просто x равно 9. Теперь мы знаем, что x равно 9, мы можем взять x равно 9 и подставить x равно 9 обратно в одно из наших уравнений.
В этом случае мы возьмем эту 9 и подставим ее обратно в наше первое уравнение. Это 9, потому что X равно 9, может быть заменено на X. Теперь у нас есть 3 умножить на 9, что мы подставили в 4 минус y равно 7. Итак, теперь мы знаем, что X равно девяти, но мы должны найти y, потому что мы должны знать X и координату y для этого решения этой системы мы взяли наш X, который был девятью, и мы заменили его на X, тогда мы собираемся упростить это. 3 умножить на 9 равно 27 минус у равно 7. Тогда нам нужно найти у. Мы собираемся пойти дальше и вычесть 27 с этой стороны, вычесть 27 с этой стороны, это отменяет, у вас есть минус y, равный 7 минус 27, это минус 20, и тогда мы должны избавиться от этого минуса.Мы делим обе стороны на минус 1, они сокращаются, и у вас есть положительное значение y, равное положительному 20. Мы знаем нашу координату x, и мы знаем, что наша координата Y теперь равна 20. Мы знаем, что наше решение — это координата 9, 20, и это будет наша отвечать.
Теперь у нас есть 3 умножить на 9, что мы подставили в 4 минус y равно 7. Итак, теперь мы знаем, что X равно девяти, но мы должны найти y, потому что мы должны знать X и координату y для этого решения этой системы мы взяли наш X, который был девятью, и мы заменили его на X, тогда мы собираемся упростить это. 3 умножить на 9 равно 27 минус у равно 7. Тогда нам нужно найти у. Мы собираемся пойти дальше и вычесть 27 с этой стороны, вычесть 27 с этой стороны, это отменяет, у вас есть минус y, равный 7 минус 27, это минус 20, и тогда мы должны избавиться от этого минуса.Мы делим обе стороны на минус 1, они сокращаются, и у вас есть положительное значение y, равное положительному 20. Мы знаем нашу координату x, и мы знаем, что наша координата Y теперь равна 20. Мы знаем, что наше решение — это координата 9, 20, и это будет наша отвечать.
Следующая задача на нашем листе решения систем уравнений методом исключения — номер два. У нас есть X плюс y равно 4, а затем 2x минус 3y равно 18. Когда мы перейдем к их исключению, вы заметите, что если бы мы складывали их прямо вверх или вниз, ничто не отменялось бы.Если бы мы добавили их прямо сейчас, например, X плюс 2 X было бы 3 X, а затем Y минус 3 y было бы отрицательным 2y, а затем 4 плюс 18 было бы 22. Ничего не отменяется, так что это означает, что мы не можем этого сделать, мы должны умножьте одно или оба уравнения, чтобы получить ситуацию, когда при сложении по вертикали что-то отменяется.
Когда мы перейдем к их исключению, вы заметите, что если бы мы складывали их прямо вверх или вниз, ничто не отменялось бы.Если бы мы добавили их прямо сейчас, например, X плюс 2 X было бы 3 X, а затем Y минус 3 y было бы отрицательным 2y, а затем 4 плюс 18 было бы 22. Ничего не отменяется, так что это означает, что мы не можем этого сделать, мы должны умножьте одно или оба уравнения, чтобы получить ситуацию, когда при сложении по вертикали что-то отменяется.
Наше первое уравнение можно умножить на то, что когда мы добавим их, они сократятся. Теперь проще всего умножить верхнее уравнение на 3, потому что, если мы умножим все на 3, мы получим 3y, а затем Y сократятся.Положительные 3y и отрицательные 3y будут сокращаться, когда мы складываем, мы также можем умножать на отрицательные два, потому что, если мы умножаем на отрицательные два, мы можем сложить x, а эти отрицательные два и положительные 2x сокращаются. Вы можете выбрать, хотите ли вы сделать X или хотите отменить Y, но в этом случае я собираюсь отменить Y.
Что мы собираемся сделать, так это пойти дальше и умножить верхнее уравнение на три, чтобы получить положительное значение 3y, а затем умножить на три и умножить все на три.Мы должны распределить эту тройку как на X, так и на Y на этой стороне. Мы собираемся сказать, что 3 умножить на X равно 3x, а затем трижды умножить на 3y, а затем будет равно 4 умножить на 3, что равно 12. Тогда наше второе уравнение нам не нужно менять, потому что мы знаем, что это положительное 3y и это отрицательные 3 года собираются отменить. Мы просто собираемся переписать второе уравнение здесь, как 2x минус 3y равно 18. Затем мы собираемся сделать сложение по вертикали. Мы сложим оба уравнения вместе, потому что знаем, что Y сократятся.3x плюс 2x равно 5x, а затем 3y плюс отрицательные три Y будут равны 0y, иначе Y просто отменятся. И тогда 12 плюс 18 будет 30, теперь 0y ушел. Мы просто отменим это так. Теперь у нас есть 5x равно 30. Затем, чтобы найти X, мы разделим обе части на 5. Они сокращаются, а затем 30, деленное на 5, равно 6.
Теперь, когда мы знаем, что x равно 6, мы возьмем x равным 6 и подставим его обратно в любое уравнение. В случае этой системы проще всего заменить 6 в первом уравнении, потому что наше первое уравнение — это просто X плюс у равно 4, и оно не имеет коэффициента.Перепишем наше уравнение. У нас есть X, который равен 6, поэтому мы заменили X на шесть, плюс y равно четырем. Тогда мы должны решить для y. Мы вычтем шесть из обеих сторон, они сократятся, и мы получим y равно минус два. Наше решение: x равно шести, y равно отрицательным двум, и это ответ.
Решение систем линейных уравнений [Видео и практика]
Привет! Добро пожаловать в это видео об использовании замены и исключения для решения линейных систем!
«Решить» систему уравнений означает определить точную координату \((x,y)\), которая удовлетворяет обоим уравнениям в системе.Процесс решения системы зависит от структуры уравнений. Некоторые системы могут быть легко решены путем построения обоих уравнений и определения точной точки пересечения , в то время как другие системы более подходят для решения .
Это видео будет посвящено двум алгебраическим подходам, а именно замене и исключению .
Чтобы решить систему двух уравнений с двумя переменными , мы пытаемся найти точную точку, которая удовлетворяет обоим уравнениям.Что я имею в виду под словом «удовлетворить»?
Это означает, что если вы подставите эту точку в ОБА уравнений, вы получите «верное» утверждение.
Мы уже упоминали, что «структура» системы будет определять, какой из методов решения использовать.
Метод подстановки
Метод подстановки обычно используется, когда одно из уравнений в системе уже решено для одной из переменных. В этом случае вы можете подставить выражение, которому равна переменная, в другое уравнение:
Например:
\(y=x+2\)
и
\(x+2y= -5 \)
Поскольку мы знаем, что переменная \(y=x+2\), мы можем заменить \((x+2)\) на переменную \(y\) во втором уравнении:
\ (x+2(x+2)=-5\)
Обратите внимание, что после замены в уравнении больше нет переменной \(y\).
На этом этапе мы находим \(x\), распределяя коэффициент при 2 в скобках.
\(x+2x+4= -5\)
Объедините одинаковые члены \(x+2x\) и соберите константы, вычитая 4 из обеих частей уравнения:
\(x +2x+4= -5\)
\(3x+4-4= -5-4\)
\(3x= -9\)
Затем мы разделим обе части на 3 и получим результат в \(х=-3\).
На данный момент мы на полпути к нашему решению. Чтобы определить \(y\)-переменную, просто подставьте \(x= -3\) в любое из исходных уравнений.Подстановка в первое уравнение дает самое быстрое решение:
\(y=(-3)+2= -1\)
Решением этой системы является упорядоченная пара \((-3,-1 )\).
Давайте попрактикуемся в методе подстановки, рассмотрев вместе еще одну задачу:
\(y=-2x+4\)
\(3x+2y=1\)
Поскольку \(y\) решается в выражения \(x\) в первом уравнении, подставьте выражение \((-2x+4)\) вместо \(y\) во втором уравнении.
\(3x+2(-2x+4)=1\)
Распределите 2 в скобках.Объедините одинаковые термины и найдите \(x\):
\(3x-4x+8=1\)
\(-x+8=1\)
\(-x+8-8=1-8 \)
\(-x=-7\)
\(x=7\)
Найдите \(y\), подставив \(x= 7\) в первое уравнение системы:
\(y=-2(7)+4\)
\(y= -14+4\)
\(y= -10\)
Упорядоченная пара, \((7,-10)\) , является решением этой системы.
Чтобы проверить свою работу, просто подставьте эту упорядоченную пару в оба уравнения, чтобы убедиться, что вы получили верное утверждение.
Помните, эти типы систем хорошо подходили для метода подстановки, потому что одна из переменных уже была решена.
Метод исключения
Для систем уравнений, которые имеют два уравнения в «стандартной форме», может быть предпочтительным метод исключения. Напомним, что уравнения стандартной формы имеют как переменные члены с одной стороны уравнения, так и постоянные члены с другой.
Общая концепция этого метода заключается в «исключении» одной из переменных из системы путем сложения одинаковых членов каждого уравнения вместе.Показан простой пример метода исключения:
\(2x+y=1\)
\(x -y=8\)
Оба эти уравнения имеют стандартную форму. Если уравнения складываются путем объединения одинаковых членов, \(y\)-переменная исключается, потому что старшие коэффициенты \(y\)-переменных имеют разные знаки:
\(3x+0y=9\)
\(3x=9\)
Найдите \(x\), разделив обе части на 3, что даст \(x=3\). Теперь, как и раньше, используйте это значение, чтобы определить значение \(y\), подставив \(x=3\) в любое из исходных уравнений.Давайте воспользуемся вторым уравнением системы, потому что оно довольно простое:
\(3-y=8\)
Чтобы найти \(y\), вычтите 3 из обеих частей и разделите на -1 для решение \(y=-5\). Таким образом, окончательным решением этой системы является упорядоченная пара \((3,-5)\).
Как уже упоминалось, этот пример был довольно простым, потому что коэффициенты переменных \(y\) сокращались при сложении. Когда коэффициенты не сокращаются, вы можете использовать Свойство умножения равенства , чтобы умножить уравнение на любое значение, которое вам нужно исключить.
Обзор
В завершение посмотрим, помните ли вы, какой метод решения наиболее подходит для следующих систем: = −5x − 17\)
Показать ответ Правильный ответ — подстановка.
Для этого вы должны использовать подстановку, так как \(y\) решается во втором уравнении.
2.
\(−4x + y = 6\)
\(−5x − y = 21\)
Показать ответ Правильный ответ — исключение.
Для второго мы бы использовали исключение, так как оба уравнения имеют стандартную форму и \(y\)-член исключается путем сложения.
Спасибо за просмотр и удачной учебы!
Как решить систему уравнений с помощью исключения
vimeo.com/video/62917176?title=0&byline=0&portrait=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Научитесь решать систему уравнений методом исключения. После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре 1 и практические задачи.
Чтобы решить систему уравнений с помощью исключения, вы начинаете со сложения их вместе, чтобы сформировать одно уравнение.Это делается путем объединения подобных терминов.
Однако вы должны установить уравнения так, чтобы переменная уравновешивалась, когда вы складываете 2 уравнения вместе.
Это можно сделать, умножив каждое уравнение на общий множитель, чтобы можно было сократить переменную в обоих уравнениях.
Вы должны оставить только одну переменную и действительные числа.
После этого вы упростите поиск того, чему равна эта переменная.
Затем вы подставляете свой ответ в одно из исходных уравнений, чтобы найти другую переменную и найти координаты.
Чтобы проверить свой ответ, подставьте оба значения x и y в исходное уравнение, чтобы проверить, верно ли оно.
Пример:
Таким образом, координаты точки пересечения будут (7,-10).
Чек:
Примеры системы уравнений с исключением
Пример 1
Мы можем исключить -переменную, добавив два уравнения.
Разделите обе стороны
Теперь значение можно подставить в любое из исходных уравнений, чтобы найти значение .
Итак, координаты
Пример 2
Начните с умножения первого уравнения на так, чтобы коэффициенты были противоположны
Теперь мы можем исключить -переменную, добавив два уравнения.
Разделить обе стороны
Подставьте любое из исходных уравнений, чтобы получить значение
.
Итак, координаты
Стенограмма видеоурока
В этом уроке мы рассмотрим метод исключения, используемый для решения систем уравнений.
Здесь у нас есть система уравнений
Выполним исключение, сложив уравнения таким образом, чтобы одна из переменных сокращалась.
Сложим эти два и получим
Здесь у нас есть уравнение только с одной переменной.
Мы можем легко решить для .
Но давайте посмотрим, как это работало.
Во-первых, уравнения должны быть записаны в одинаковом формате.
-term плюс -term равно числу
Убедитесь, что они выстроены правильно, когда мы их добавляем.
Еще один важный аспект заключается в том, что когда мы добавляем их, одно из условий должно сокращаться.
Теперь давайте продолжим решение для
.Теперь воспользуемся значением для решения .
Возьмем первое уравнение и подставим
Вычесть с обеих сторон
Наше решение
Давайте проверим наш ответ.
Так как мы использовали первое уравнение для определения значения , теперь давайте используем второе уравнение для проверки.
Это проверено.
В этой системе уравнений уравнения записаны в другом формате.
Итак, мы перепишем нижнее уравнение, чтобы оно соответствовало формату верхнего уравнения.
Перенесем -термин влево, вычитая с обеих сторон.
Теперь наши два уравнения равны
.В этот момент мы можем их объединить, используя исключение. Ответ
Тогда давайте найдем
Теперь давайте используем это для решения для .
Подставим в первое уравнение
Итак, наше решение
.Можно получить дробь в качестве одной из переменных.
Если два уравнения записаны в разном формате, просто манипулируйте функцией или уравнением, переставляя члены в нужном вам порядке.
И тогда мы можем использовать исключение.
Давайте посмотрим на эту систему уравнений и попробуем решить методом исключения.
Он имеет правильный формат и правильно выстроен.
Но ни одна из переменных не может быть отменена, если мы их суммируем.
Теперь мы должны изменить одно из уравнений, чтобы использовать исключение.
Чтобы изменить его, нам просто нужно умножить уравнение на константу.
Мы можем умножить уравнение дна на, чтобы наш -термин был таким же.
Таким образом, процесс, если в системе уравнений нет переменной, которую можно сократить, заключается в выборе уравнения, в котором можно умножить постоянное число. Убедитесь, что ответ приведет к уравнению, которое сокращается другим уравнением.
Итак, у нас будет
Теперь продолжим решение. Сложим наши два уравнения
Ответ
Затем найдите
.Теперь мы можем использовать это значение для определения .
Давайте подставим это в первое уравнение.
Вычесть с обеих сторон
Затем разделите обе части на
.Итак, наше решение
.
Подводя итог, мы должны умножить одно уравнение на число, чтобы одна из переменных сокращалась.
Давайте посмотрим на второй способ сделать это.
Возьмем тот же пример
В первом методе мы отменили -term.
Но что, если вы хотите избавиться от ?
Здесь умножить не просто, так что аннулируется.
Нам нужно умножить два уравнения на два разных числа, чтобы получить одинаковые -члены.
Нам нужно подумать, чему равно общее кратное чисел и .
Ну это .
Мы умножим верхнее уравнение на и умножим нижнее уравнение на, чтобы получить оба уравнения.
Но это не так!
Мы будем складывать уравнения, поэтому, если мы сложим оба положительных числа, у нас тоже будет положительное.
Итак, сделаем один из множителей отрицательным.
Просто сделайте один из них положительным, а другой отрицательным, чтобы мы могли отменить.
Теперь все готово для решения
Складываем их и получаем
Наш ответ такой же, как и при использовании первого метода.
Давайте использовать, чтобы решить с помощью верхнего уравнения.
Снова наше решение
Иногда можно умножить одно уравнение на число, чтобы исключить одну из переменных.
Или вы также можете умножить оба уравнения на два разных числа так, чтобы одна переменная сокращалась.
Просто убедитесь, что вы делаете это с той переменной, которую хотите отменить.
В этом случае мы хотим сократить -члены, коэффициенты были и получить общее кратное .
Убедитесь, что один положительный, а другой отрицательный, чтобы они компенсировались при добавлении.
Метод исключения (системы линейных уравнений)
Основная концепция метода исключения заключается в создании терминов с противоположными коэффициентами, поскольку они аннулируют друг друга при добавлении.В конце концов, мы должны решить простое линейное уравнение, подобное одношаговому уравнению относительно x или y.
Два идеальных случая метода исключения
Я могу обобщить «большие» идеи о методе исключения при решении систем линейных уравнений, используя иллюстрации ниже. Здесь я представляю два идеальных случая, которых я хочу достичь в процессе решения. Взгляните на них, и, надеюсь, это имеет смысл. В противном случае перейдите непосредственно к шести (6) проработанным примерам, чтобы увидеть, как решаются реальные проблемы.
Здесь я представляю два идеальных случая, которых я хочу достичь в процессе решения. Взгляните на них, и, надеюсь, это имеет смысл. В противном случае перейдите непосредственно к шести (6) проработанным примерам, чтобы увидеть, как решаются реальные проблемы.
Случай 1 : При сложении двух уравнений переменная «x» исключается
Коэффициенты переменной х противоположны.
Случай 2 : При сложении двух уравнений переменная «y» исключается
Коэффициенты переменной y противоположны.
Примеры решения систем линейных уравнений методом исключения
Пример 1: Решите систему линейных уравнений методом исключения.
Я заметил, что добавление столбца x не удалит переменную x. Однако, если я добавлю столбец y, переменная y исчезнет. Это происходит потому, что коэффициенты при y противоположны друг другу по знаку. Теперь я продолжу второй вариант.
После этого я прихожу к простому уравнению.
Я делю обе части на коэффициент x, что дает ответ x = 4.
Следующий шаг — найти соответствующее значение y.Это легко найти, так как я уже знаю, что такое x. Я выберу любое из двух исходных уравнений, в данном случае я выбрал верхнее уравнение. Затем я подставлю значение x = 4, чтобы получить y. Процесс или процедура решения для y должны быть аналогичны ниже.
Здесь я получаю y = — \,4. Окончательный ответ в точечной нотации показан ниже.
Графически решение выглядит так.
Пример 2: Решить систему линейных уравнений методом исключения.
Это довольно интересно, потому что никакие переменные не отменяются при добавлении. Я хочу ввести множитель в одно из уравнений или в оба, а затем посмотреть, получу ли я некоторые коэффициенты, которые отличаются только знаками.
Есть несколько способов сделать это. Однако, глядя на столбец x, я могу легко превратить -3 в -12, умножив первое уравнение на +4. Теперь я могу продолжить добавление столбца x.
Теперь я могу продолжить добавление столбца x.
Умножение всего уравнения на любое ненулевое число не меняет его исходного значения.Что изменится, так это только его форма. Я называю этот процесс, уравнение «пересмотром» или «модификацией».
Это одношаговое уравнение, поэтому я решаю y, разделив обе части на коэффициент.
Отлично! Я получил значение y = 2. Далее я решу x с помощью обратной подстановки, используя любое из исходных уравнений. Для этого я буду использовать первое уравнение, потому что оно менее сложное.
Я получил значение x = — 1. Теперь я могу записать окончательный ответ в виде упорядоченной пары, написанной ниже.
Приведенный ниже график подтверждает правильность нашего решения.
Пример 3: Используйте метод исключения или линейной комбинации для решения .
В этой задаче есть некоторая хитрость, потому что коэффициенты переменных x абсолютно одинаковы, и — 2. Единственное, что мне нужно здесь исправить, это сделать один из них положительным. Теперь я решил умножить верхнее уравнение на — 1. Оно также должно работать нормально, если я умножу нижнее уравнение на — 1.
Единственное, что мне нужно здесь исправить, это сделать один из них положительным. Теперь я решил умножить верхнее уравнение на — 1. Оно также должно работать нормально, если я умножу нижнее уравнение на — 1.
Вы должны увидеть, что план работает, так как добавление результатов столбца x к отмене x.
Я решил значение y, разделив обе части на −17, в результате чего y = 3. На этот раз я решу значение x с помощью нижнего уравнения, потому что я знаю, что такое y.
После нескольких шагов решения приведенного выше уравнения я прихожу к x = 2. Окончательный ответ в виде упорядоченной пары показан ниже.
Действительно, две линии пересекаются в точке, которую мы нашли в наших расчетах.
Пример 4: Для решения используйте метод исключения или линейной комбинации.
Этот пример повторяет пример 3, где у нас точно такие же коэффициенты. Я вижу, что обе переменные y имеют коэффициенты, равные 8. Поэтому мне нужно будет немного изменить их, чтобы сделать их знаки противоположными. Теперь у меня есть два варианта дальнейших действий. Я могу умножить верхнее уравнение на -1 или нижнее уравнение на -1. Для этого упражнения я выбираю последнее.
Поэтому мне нужно будет немного изменить их, чтобы сделать их знаки противоположными. Теперь у меня есть два варианта дальнейших действий. Я могу умножить верхнее уравнение на -1 или нижнее уравнение на -1. Для этого упражнения я выбираю последнее.
Применение множителя − 1 к нижнему уравнению и сложение их вместе приводит к исчезновению y.
Решите полученное из него простое уравнение.
Я получил x = 4, разделив обе части на −9. Следующий очевидный шаг — найти другую переменную y с помощью обратной подстановки. Выберите любое из исходных уравнений, подставьте x = 4, и вы мгновенно получите y.
Ответ: y = — \,1. Окончательный ответ в виде упорядоченной пары показан ниже.
Графическое решение выглядит следующим образом.
Пример 5: Для решения используйте метод исключения или линейной комбинации.
В задаче такого типа нужно одновременно умножить и верхнее, и нижнее уравнения на некоторое число, чтобы получить коэффициенты с противоположными знаками.
Если я решу исключить x, я могу умножить верхнее уравнение на — 2, а нижнее на 9. Таким образом, я должен получить x слагаемых, 18x и -18x соответственно, которые сокращаются при сложении.
В этом упражнении я хочу исключить y. Поэтому я умножу верх на 5, а низ на 3.
Как и предполагалось, я смог избавиться от y, что оставило нам простое уравнение.
Вы должны прийти к x = 1. Продолжайте решать другую переменную, которая является y. Подставьте х = 1 и найдите у.
Я получил у = — \,2. Собрав все вместе, наш окончательный ответ — упорядоченная пара ниже .
Графическое представление двух линий, пересекающихся в решенной точке, равно…
Пример 6: Для решения используйте метод исключения или линейной комбинации.
Последний пример очень похож на предыдущий. В настоящее время никакие переменные не будут удалены после добавления столбцов x и y.
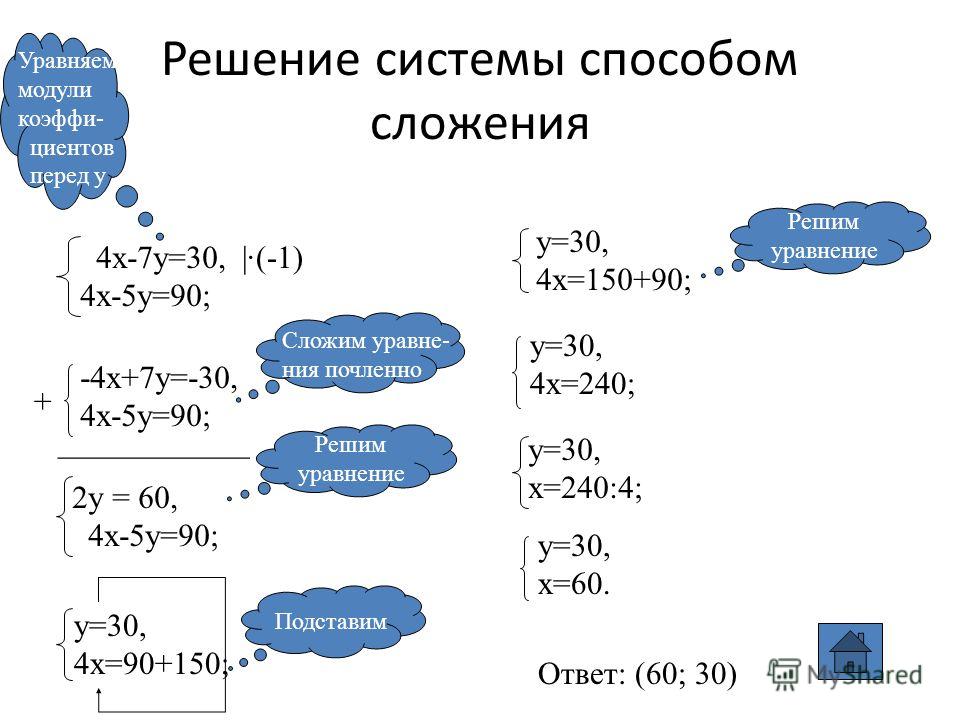 Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
 Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении. д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
 А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома.
А решебником можно воспользоваться в любой момент, как находясь на уроке в школе, так и дома.
 Линейные неравенства с двумя переменными. Способ подстановки и способ сложения.
Линейные неравенства с двумя переменными. Способ подстановки и способ сложения. )
)