Гипербола график. Гипербола график функции.
График гиперболы имеет вид \(y =\frac{k}{x}\) , где k-вещественное число и x ≠ 0. Также данную функцию называют обратной пропорциональностью, где \(k-\)коэффициент обратной пропорциональности. Как выглядит сам график в зависимости стоит ли функция с минусом или без перед \(x \):
Каковы особенности гиперболы?
График \(y =\frac{k}{x}\) приближается к оси \(x \) по мере увеличения значения \(x \), но никогда не встречается с осью \(X\). Это называют горизонтальной асимптотой графика.
Каждая часть графика также становится ближе к оси \(y\), поскольку \(x \) приближается к \(0\), но никогда не встречается с осью \(y\), потому что нет значения для \(y\), когда \(x = 0\). Это называется вертикальной асимптотой графика.
Пример 1.
Построим график \(y =\frac{5}{x}\) на промежутке от \(4\) до \(4\), за исключением точки когда \(x = 0\). Выберем призвольное значение \(x \) и посчитаем соответствующее значение \(y\):
По высчитанным точка из таблицы построим график:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».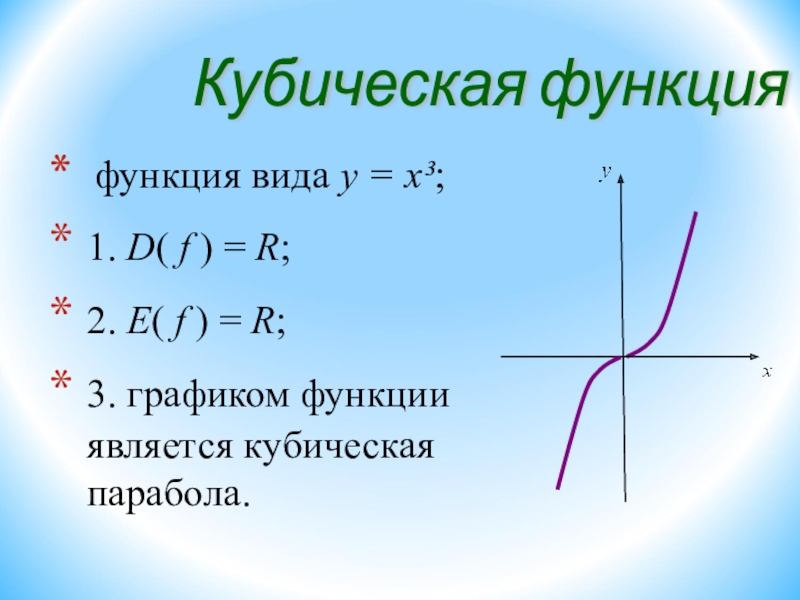 Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку Репетитор по математикеАвтономная некоммерческая организация высшего профессионального образования
Проведенных занятий:
Дистанционно (Скайп)
Репетитор по математике 5-9 классов. Научу не заучивать трудные темы, а работать будем вместе с вами на их понимание и разрешение сложных проблем.
Жду вас на своих занятиях!
Научу не заучивать трудные темы, а работать будем вместе с вами на их понимание и разрешение сложных проблем.
Жду вас на своих занятиях!
Репетитор по математике
Тульский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 6-11 классов и по физике 7-9 классов. Также готовлю к ОГЭ и ЕГЭ по математике и к ОГЭ по физике. Люблю свой предмет за интересные задачи, решая которые можно хорошенько «прокачать» свои мозги, научиться видеть причинно-следственные связи, развить своё логическое мышление, научиться последовательно и аргументированно выражать свои мысли.
Всегда стараюсь поддерживать открытую и позитивную атмосферу во время проведения урока. Объясняю материал на понятном и доступном для ученика языке. Вовлекаю ученика в диалог и обсуждение решения заданий. Особый упор делаю на приобретение учеником практических знаний и навыков, необходимых для решения задач.
Уделяю внимание повышению интереса ученика к предмету.
Также готовлю к ОГЭ и ЕГЭ по математике и к ОГЭ по физике. Люблю свой предмет за интересные задачи, решая которые можно хорошенько «прокачать» свои мозги, научиться видеть причинно-следственные связи, развить своё логическое мышление, научиться последовательно и аргументированно выражать свои мысли.
Всегда стараюсь поддерживать открытую и позитивную атмосферу во время проведения урока. Объясняю материал на понятном и доступном для ученика языке. Вовлекаю ученика в диалог и обсуждение решения заданий. Особый упор делаю на приобретение учеником практических знаний и навыков, необходимых для решения задач.
Уделяю внимание повышению интереса ученика к предмету.
Репетитор по математике
Запорожский национальный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-10 классов. Помогаю школьникам в закреплении и углублении школьной программы, в подготовке к экзаменам. Подбираю подход к каждому ученику, учитывая его интересы, жизненные взгляды. Стремлюсь к тому, чтобы каждый ученик, независимо от возраста и уровня знаний, понял и полюбил математику.
Помогаю школьникам в закреплении и углублении школьной программы, в подготовке к экзаменам. Подбираю подход к каждому ученику, учитывая его интересы, жизненные взгляды. Стремлюсь к тому, чтобы каждый ученик, независимо от возраста и уровня знаний, понял и полюбил математику.
Математика по Skype
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
ЕСЛИ (функция ЕСЛИ)
Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.
Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.
Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.
Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).
Синтаксис
Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.
ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])
Например:
|
Имя аргумента |
Описание |
|---|---|
|
лог_выражение (обязательно) |
Условие, которое нужно проверить. |
|
значение_если_истина (обязательно) |
Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА. |
|
значение_если_ложь (необязательно) |
Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ. |
Простые примеры функции ЕСЛИ
В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)
В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.
Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.
В примере выше функция ЕСЛИ в ячейке D2 означает: ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)
На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).
В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)
Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»). Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.
Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.
Распространенные неполадки
|
Проблема |
Возможная причина |
|---|---|
|
0 (ноль) в ячейке |
Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ. |
|
#ИМЯ? в ячейке |
Как правило, это указывает на ошибку в формуле. |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Операторы вычислений и их приоритеты в Excel
Использование вложенных функций в формуле
Использование функции ЕСЛИ для проверки ячейки на наличие символов
Видео: расширенное применение функции ЕСЛИ
Функция ЕСЛИМН (Microsoft 365, Excel 2016 и более поздних)
Усложненные функции ЕСЛИ: как работать с вложенными формулами и избежать ошибок
Обучающие видео: усложненные функции ЕСЛИ
Подсчет значений на основе одного условия с помощью функции СЧЁТЕСЛИ
Подсчет значений на основе нескольких условий с помощью функции СЧЁТЕСЛИМН
Суммирование значений на основе одного условия с помощью функции СУММЕСЛИ
Суммирование значений на основе нескольких условий с помощью функции СУММЕСЛИМН
Функция И
Функция ИЛИ
Функция ВПР
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Логические функции
Функции Excel (по алфавиту)
Функции Excel (по категориям)
1.  Понятие функции. Понятие функции.2.Свойства функций. 3.Основные элементарные функции.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Понятие функции Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией.
|
||||
2. Cвойства функций 1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т. 2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1< (>) x2, f(x1) < (>) f(x2). 3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической. 4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.
|
||||
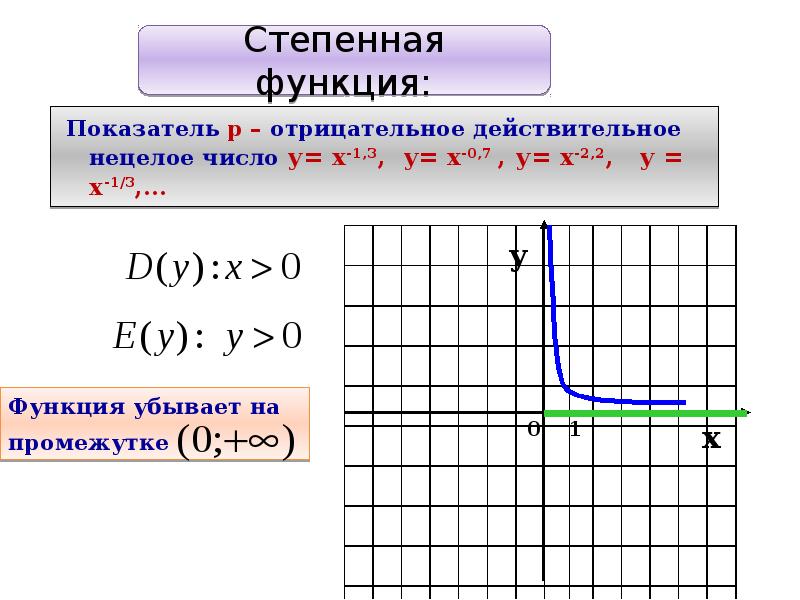
3. Основные элементарные функции Основные элементарные функцииСтепенная функция у = х |
|
|||
| у = х² область определения (-∞,∞) |
|
|||
| у = х³ область определения (-∞,∞) |
|
|||
| у = 1/х область определения (-∞,0)U(0,∞) |
|
|||
| у = 1/х² область определения (-∞,0)U(0,∞) |
|
|||
|
область определения [0,∞) |
|
|||
|
область определения (-∞,∞) |
|
|||
Показательная функция у = а ͯ (a>0 a≠1) область определения (-∞,∞) |
|
|||
Логарифмическая функция у = log ₐ x (a>0 a≠1) область определения (0,∞) |
|
|||
Тригонометрические функции y = sin x область определения (-∞; ∞) |
|
|||
y = cos x область определения (-∞; ∞) |
|
|||
y = tg x область определения |
|
|||
y = ctg x область определения |
|
|||
y = arcsin x область определения [-1; 1] |
|
|||
y = arccos x область определения [-1; 1] |
|
|||
y = arctg x область определения (-∞; ∞) |
|
|||
y = arcctg x область определения (-∞; ∞) |
||||
Пример 1.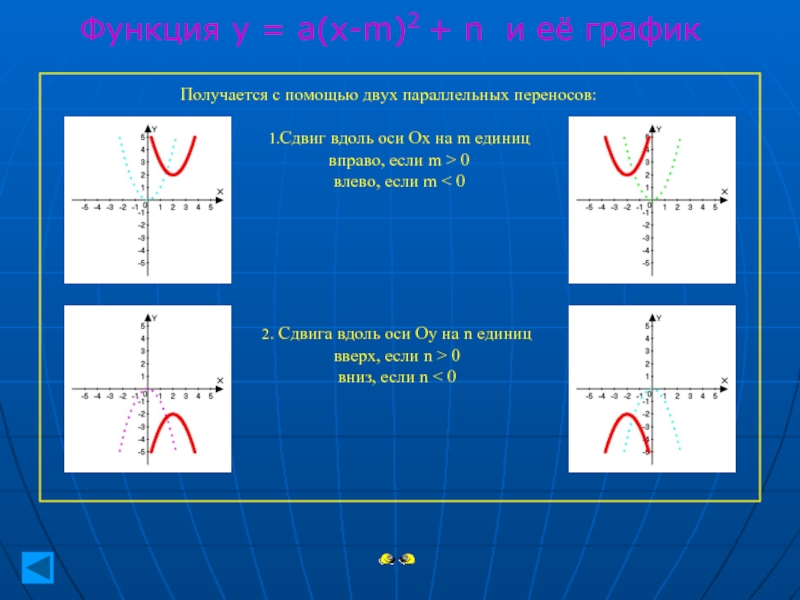
Найти область определения функции. |
||||
Пример 2Выяснить четность или нечетность функции. |
График функции y=x³+2sin x |
|||
Пример 3 |
||||
| 1 2 3 4 5 6 7 8 9 | ||||
Функции и их типы – объяснение, типы и важные часто задаваемые вопросы
Истинное значение функций состоит в том, что они представляют собой отношения, в месте которых каждый вход имеет определенный выход.
Глава «Функции и их типы» объясняет основные понятия, а также различные типы функций в математике. Все они описаны ниже с использованием нескольких примеров для лучшего понимания.
Само определение функции таково: это ассоциация между набором входных данных и набором допустимых выходных данных, при этом каждый входной сигнал может быть связан ровно с одним выходным сигналом.
Здесь вы можете узнать о различных типах функций, а также о типах графиков функций, в математике, вкратце.
Типы функций в математике
Типы функций в математике:
Различные типы функций
Различные типы функций объясняют различные математические отношения и их графическое представление.
Функция тождества
Рассмотрим R как множество действительных чисел.Говорят, что функция является функцией тождества, если f: R→R объясняется как f(x) = y = x, для x ∈ R, домен и диапазон равны R. Типы функций в множествах можно понять. с помощью этих функций.
Типы функций в множествах можно понять. с помощью этих функций.
График функции идентичности представляет собой прямую линию, которая всегда проходит через начало координат.
[Изображение будет загружено в ближайшее время]
Постоянная функция
Здесь условие относительно функции f: R→R различно, поскольку f(x) = y = c, для x ∈ R и c равно константа в R, на данный момент такая функция определяется как функция константы.R — область определения функции (f), а ее диапазон — константа (c).
Построив график, мы обнаружим прямую линию, параллельную оси x.
[Изображение будет загружено в ближайшее время]
Полиномиальная функция
Полиномиальная функция объясняется выражением y = a0 + a1x + a2x2 + … + anxn, здесь n — целое неотрицательное число, а a0, a1, a2,…, n ∈ R. Старшая степень в уравнении — это степень полиномиальной функции.
Старшая степень в уравнении — это степень полиномиальной функции.
Кроме того, эти полиномиальные функции классифицируются по их степеням:
y = x + 1 или y = x или y = 2x – 5 и т. д.
Если мы рассмотрим уравнение, y = x – 6. R – это домен, а также диапазон. График представляет собой прямую линию.
[Изображение будет загружено в ближайшее время]
Квадратичная функция
Функция называется квадратичной, если степень полиномиальной функции равна двум. Это можно представить как f(x) = ax2 + bx + c, где a ≠ 0, a, b, c — константа, а x — переменная. R — домен и диапазон. График квадратичной функции для функции: f(x) = x2 – 4 равно
[Изображение будет загружено в ближайшее время]
Рациональная функция
Рациональная функция может быть охарактеризована следующим образом: f (x) / g(x), где и f(x), и g(x) являются полиномиальными функциями от x при условии g(x) ≠ 0.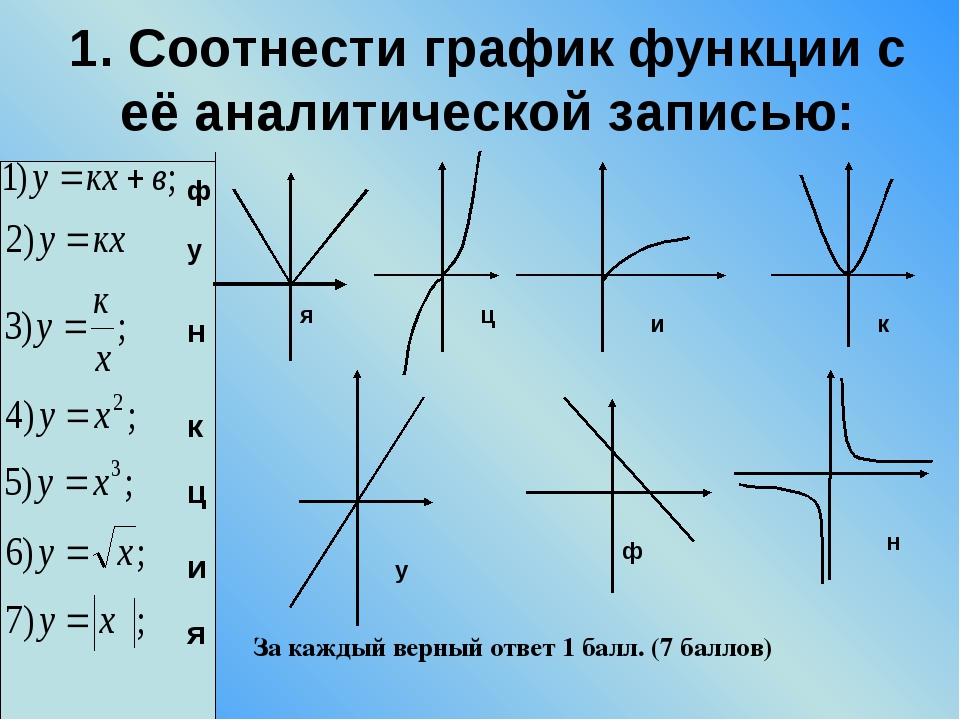
Если f: R → R и сказано, что f(x) = 1 / (x + 2,5).
Графическое представление показывает асимптоты, кривые, которые как бы касаются осей-линий.
[Изображение будет загружено в ближайшее время]
Функция модуля
Прямое значение любого числа c характеризуется в виде |c|. Можно сказать, что f: R→ R корректно определяется формулой f(x) = |x|.
f(x) = x: для каждого неотрицательного значения x и
f(x) = — x: для каждого отрицательного значения x если x < 0
= {– x, если x ≥ 0.
[Изображение будет загружено в ближайшее время]
Signum Function
f: R→ R можно объяснить как
f(x) = {0, если x = 0
, когда > 0
= {-1, если x < 0
[Изображение будет загружено в ближайшее время]
Функция наибольшего целого числа
Условие для функции f: R→ R обозначается f(x) = [х]; такой, что x ∈ X. Он дополняет действительное число до целого числа, меньшего числа.Типы функций в наборах легче понять с помощью соответствующих графиков.
Он дополняет действительное число до целого числа, меньшего числа.Типы функций в наборах легче понять с помощью соответствующих графиков.
Предположим, что интервал имеет форму (k, k+1), максимальное целочисленное значение функции равно k, что является целым числом.
Для иллюстрации:
[-21] = 21, [5.12] = 5. Графическая демонстрация:
[Изображение будет загружено в ближайшее время]
Типы графиков функций функции и их графики легко, обратившись к иллюстрациям.
Некоторые распространенные типы графиков функций показаны ниже.
[Изображение будет загружено в ближайшее время]
Типы функций в наборах
Существуют различные типы функций, которые распространяются в наборах. Эти типы функций в наборах обсуждаются ниже.
я. Функция «один к одному»
Условие для функции f: A → B быть один к одному, когда каждый элемент A является отдельным элементом B.
[Изображение будет загружено в ближайшее время]
ii.Функция «многие к одному»
Этот тип функции связывает два или более элементов A с элементом идентичности множества B.
[Изображение будет загружено в ближайшее время]
iii. Onto Function
Функция вызывается в функции, которая представляет, что каждый элемент множества B является (являются) прообразами множества A.
[Изображение будет загружено в ближайшее время]
iv. Функция One-One and Onto
Эта функция возможна, когда каждый элемент A является отличительным элементом B.
[Изображение будет загружено в ближайшее время]
Функция как особое отношение одного множества к другому
Математическая функция — это мощный инструмент, используемый в бизнес-целях, приложениях, науке и технике, поскольку они действуют в реальном мире. Чтобы четко понять концепцию функций и отношений, нужно немного погрузиться в упорядоченные пары, отношения и множества.
Функция изображается как особый вид отношения одного вида к множеству другого.
Учитывая реальный мир, задачи систематизированы и решаются с использованием функций.
Понимание отношений необходимо для понимания данных функций. И необходимо понять концепцию декартовых произведений, чтобы понять отношения. Декартово произведение, принадлежащее двум наборам A и B, относится к набору всех упорядоченных пар (a,b), таких как a∈A и b∈B
Отношение относится к подмножеству декартова произведения.Таким образом, отношение относится к правилу, которое связывает элемент из 1 множества с элементом из другого или другого множества. Действительно, функция относится к особому виду отношения.
Теперь давайте посмотрим на отношение F прямо из множества A в множество B.
Определение 1: Связь
F считается функцией, если каждый из ее элементов в множестве A связан ровно с 1 элементом в множестве B.
Чтобы лучше понять разницу между функциями и отношениями, теперь возьмем любой, например.Набор A содержит названия стран, выигравших чемпионат мира по крикету, а набор B включает те годы, когда был сыгран этот конкретный чемпионат мира.
Диаграмма на рисунке 1 изображает отношение R, но, конечно же, не функцию. Это связано с тем, что элементы в наборе A коррелируют с более чем 1 элементом набора B.
Но если вы определяете отношение F множества A к множеству B таким образом, что оно коррелирует со странами, сопровождающими тот год, в котором они впервые выиграли чемпионат мира по крикету, и для каждого из элементов в наборе A у нас будет ровно 1 корреляция в наборе B.Это отношение F, представленное на рис. 2, удостоверяет, что оно является функцией.
Как определить домен функции?
- Чтобы определить домен, необходимо увидеть значения независимых переменных, которые признаются для использования, как описано ниже, которые не имеют нулевого значения в нижней части дробей и не имеют отрицательного знака в квадратных скобках.

Диапазон
- Набор всех выходов функции называется диапазоном функции i.е. x или После замены домена весь набор всех значений, которые возможны как вывод зависимой переменной, которой является y.
Допустим, диапазон функции «F» составляет {годы — 1983, 1992, 1987, 1996}. Иными словами, все множество B называется со-областью функции. Это относится к набору, который охватывает все выходные данные функции.
Таким образом, набор действительных чисел относится к кодовой области для каждой из функций, которые являются вещественными. Кодовый домен функции F установлен в B.
Как определить диапазон функции?
- Расширение всех значений y, прямо от минимального значения до максимального значения — это диапазон функции.
- Как указано в выражении y, при подстановке всех значений x для проверки, является ли оно +ve, -ve или равным другим значениям.
- Вычислить максимальное и минимальное значения y
- Соответственно, нарисуйте график для того же.

Так по заключению,
- Диапазон вычисляется после подстановки возможных значений x для определения значений y.
- Идентификатор домена объясняется как весь набор значений, который возможен для независимых переменных.
| Биномиальное распределение Кумулятивная функция распределения. |
| Функция выживания биномиального распределения. |
| Функция, обратная к |
| Функция, обратная к |
| Функция, обратная к |
| Суммарная функция распределения бета-распределения. |
| p -й квантиль бета-распределения. |
| Инверсия |
| Инверсия |
| F кумулятивная функция распределения. |
| Функция выживания F. |
| p -й квантиль F-распределения. |
| Инверсия к |
| Гамма-распределение Кумулятивная функция распределения. |
| Функция выживания гамма-распределения. |
| Инверсия |
| Инверсия |
| Инверсия |
| Отрицательная биномиальная кумулятивная функция распределения. |
| Отрицательная биномиальная функция выживания. |
| Инверсия |
| Инверсия |
| Инверсия |
| Кумулятивная функция распределения нецентрального F-распределения. |
| Вычислите степени свободы (знаменатель) для нецентрального F-распределения. |
| Вычислить степени свободы (числитель) для нецентрального F-распределения. |
| Инверсия по отношению к f CDF нецентрального F-распределения. |
| Рассчитать параметр нецентральности для нецентрального F-распределения. |
| Кумулятивная функция распределения нецентрального t распределения. |
| Расчет степеней свободы для нецентрального распределения t. |
| Обратная кумулятивная функция распределения нецентрального t-распределения. |
| Рассчитать параметр нецентральности для нецентрального распределения t. |
| Вычислить среднее значение нормального распределения с учетом других параметров. |
| Вычислить стандартное отклонение нормального распределения с учетом других параметров. |
| Кумулятивная функция распределения Пуассона. |
| Функция выживания Пуассона |
| Инверсия к |
| Инверсия к |
| Распределение Стьюдента Кумулятивная функция распределения |
| Инверсия |
| Инверсия |
| Кумулятивная функция распределения хи-квадрат. |
| Хи-квадрат функции выживания. |
| Инверсия к |
| Обратно к |
| Суммарная функция распределения Гаусса. |
| Логарифм интегральной функции распределения Гаусса. |
| Инверсия |
| Инверсия |
| Нецентральная кумулятивная функция распределения хи-квадрат |
| Инверсия к |
| Обратный к |
| Инверсия к |
| Дополнительная кумулятивная функция распределения Колмогорова-Смирнова |
| Обратный к |
| Дополнительная кумулятивная функция распределения (функция выживания) распределения Колмогорова. |
| Обратная функция выживания распределения Колмогорова |
| Кумулятивная функция распределения Тьюки-Лямбда |
| Logit ufunc для ndarrays. |
| Выезд (а.к.а. |
| Вычисление преобразования Бокса-Кокса. |
| Вычислите преобразование Бокса-Кокса для 1 + x . |
| Вычисление обратного преобразования Бокса-Кокса. |
| Вычисление обратного преобразования Бокса-Кокса. Об аппроксимации модифицированной функции Бесселя второго родадои: 10. 1186/с13660-017-1317-з.
Epub 2017 13 февраля. 1186/с13660-017-1317-з.
Epub 2017 13 февраля.Принадлежности Расширять Принадлежности
Элемент в буфере обмена Чжэнь-Ханг Ян и соавт. Показать варианты Формат АннотацияPubMedPMID doi: 10.1186/s13660-017-1317-z. Epub 2017 13 февраля.Принадлежности
Элемент в буфере обмена Полнотекстовые ссылки Параметры отображения цитированияПоказать варианты Формат АннотацияPubMedPMID Абстрактный В статье доказывается, что двойные неравенства [Формула: см. текст] выполняются для всех [Формула: см. текст] тогда и только тогда, когда [Формула: см. текст] и [Формула: см. текст], если [Формула: см. текст], где [Формула: см. текст] — модифицированная функция Бесселя второго рода.В качестве приложений мы предоставляем границы для [Формула: см. текст] с помощью [Формула: см. текст] и представляем необходимое и достаточное условие, чтобы функция [Формула: см. текст] строго возрастала (убывала) на [Формула: см. Ключевые слова: гамма-функция; модифицированная функция Бесселя; монотонность. Похожие статьи
Цитируется3 статьи
использованная литература
Показать все 11 ссылок LinkOut — больше ресурсов
 |

 Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.
Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.
е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.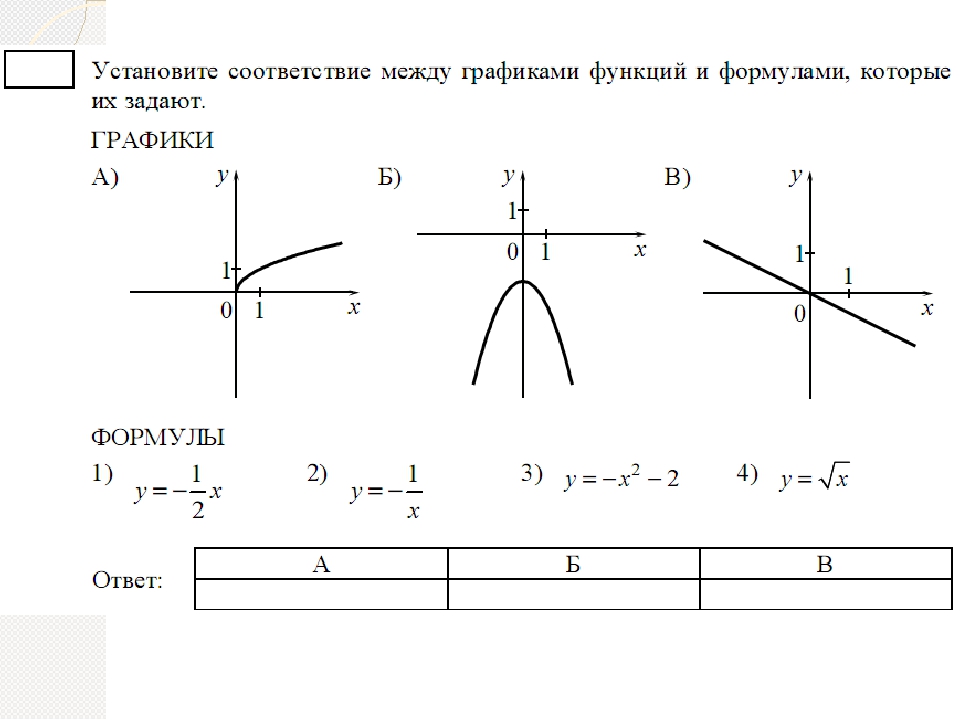







 «AcZUXHj,Htc1%*QV0hSS9″Sh*$&7&1a`l7ZAB6gH(Is?4#08?E9hlP7#RR4*:rHs*(I6q(-s5%5+?»h+K9:u»A2P3a»;’457+ i947O(dHYg@,;)3,2 ч
5m2oS$A$=\1:_58%gds17hFXd69-2
конечный поток
эндообъект
17 0 объект
6981
эндообъект
14 0 объект
>
/ProcSet 2 0 R
>>
/Содержание 16 0 Р
>>
эндообъект
7 0 объект
>
эндообъект
8 0 объект
>
эндообъект
9 0 объект
>
эндообъект
10 0 объект
>
эндообъект
11 0 объект
>
эндообъект
15 0 объект
>
эндообъект
2 0 объект
[/PDF/текст]
эндообъект
5 0 объект
>
эндообъект
1 0 объект
>
эндообъект
3 0 объект
>
эндообъект
внешняя ссылка
0 18
0000000000 65535 ф
0000013209 00000 н
0000013087 00000 н
0000013353 00000 н
0000003753 00000 н
0000013118 00000 н
0000003918 00000 н
0000012360 00000 н
0000012489 00000 н
0000012613 00000 н
0000012739 00000 н
0000012867 00000 н
0000000010 00000 н
0000003732 00000 н
0000012206 00000 н
0000012973 00000 н
0000005110 00000 н
0000012185 00000 н
трейлер
>
startxref
13402
%%EOF
«AcZUXHj,Htc1%*QV0hSS9″Sh*$&7&1a`l7ZAB6gH(Is?4#08?E9hlP7#RR4*:rHs*(I6q(-s5%5+?»h+K9:u»A2P3a»;’457+ i947O(dHYg@,;)3,2 ч
5m2oS$A$=\1:_58%gds17hFXd69-2
конечный поток
эндообъект
17 0 объект
6981
эндообъект
14 0 объект
>
/ProcSet 2 0 R
>>
/Содержание 16 0 Р
>>
эндообъект
7 0 объект
>
эндообъект
8 0 объект
>
эндообъект
9 0 объект
>
эндообъект
10 0 объект
>
эндообъект
11 0 объект
>
эндообъект
15 0 объект
>
эндообъект
2 0 объект
[/PDF/текст]
эндообъект
5 0 объект
>
эндообъект
1 0 объект
>
эндообъект
3 0 объект
>
эндообъект
внешняя ссылка
0 18
0000000000 65535 ф
0000013209 00000 н
0000013087 00000 н
0000013353 00000 н
0000003753 00000 н
0000013118 00000 н
0000003918 00000 н
0000012360 00000 н
0000012489 00000 н
0000012613 00000 н
0000012739 00000 н
0000012867 00000 н
0000000010 00000 н
0000003732 00000 н
0000012206 00000 н
0000012973 00000 н
0000005110 00000 н
0000012185 00000 н
трейлер
>
startxref
13402
%%EOF  J Неравное применение
2017.
J Неравное применение
2017.
 текст] .
текст] . doi: 10.1186/s13660-018-1648-4. Epub 2018 9 марта.
J Неравное применение 2018.
PMID: 29568211
Бесплатная статья ЧВК.
doi: 10.1186/s13660-018-1648-4. Epub 2018 9 марта.
J Неравное применение 2018.
PMID: 29568211
Бесплатная статья ЧВК.


 Дж. Матем. Анальный. заявл. 2011;374(2):516–528. doi: 10.1016/j.jmaa.2010.09.030.
—
DOI
Дж. Матем. Анальный. заявл. 2011;374(2):516–528. doi: 10.1016/j.jmaa.2010.09.030.
—
DOI