Как решить уравнение матричным способом: Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы. — Детская игровая комната «Волшебный лес»

Posted on 22.10.197322.01.2022 by alexxlab

{3+3}\left|\begin{array}{rr} 2 & 1 \\ 1 & -1 \end{array}\right|=-3$$

Таким образом,

$$\tilde{A}=\left(\begin{array}{rrr} -2 & -2 & 2 \\ -3 & 1 & 5 \\ 1 & 1 & -3 \end{array}\right)$$

Определитель матрицы $A$

$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$

А тогда

$$\tilde{A}=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)$$

Отсюда искомая матрица

$$X=\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)\left(\begin{array}{r} 2 \\ -2 \\ 2 \end{array}\right)=$$ $$=\left(\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\right) \Rightarrow\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.

$$ $$\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$$

Содержание

Матричный способ решения систем линейных алгебраических уравнений

Запрос solve, который был использован ранее, чтобы получить решение системы линейных алгебраических уравнений (СЛАР) в Wolfram|Alpha, на самом деле является универсальным запросом для решения уравнений и их систем в Wolfram|Alpha. Собственно для решения системы линейных алгебраических уравнений он применяется лишь тогда, когда эта система задана в естественном виде: после запроса solve все уравнения системы перечисляются через запятую. Этот способ хорош тем, что позволяет решать не только определенные, но также и неопределенные системы — в общем виде.

Для решения определенных систем линейных алгебраических уравнений применяется также

матричный способ.

В Wolfram|Alpha для решения систем линейных алгебраических уравнений матричным способом служит специальный запрос LinearSolve, после которого указываем матрицу коэффициентов системы и вектор (матрицу-столбец) свободных членов.

Чтобы понять особенности синтаксиса запроса LinearSolve, изучите следующие примеры.

Для начала рассмотрим решение однородных систем линейных алгебраических уравнений. После запроса LinearSolve вводим матрицу коэффициентов системы и нулевой вектор свободных членов. Получаем:

LinearSolve[{{a, b}, {c, d}}, {0, 0}]

Здесь Wolfram|Alpha дает тривиальное решение {0, 0}.

Точно также легко Wolfram|Alpha выводит тривиальное решение и для однородных систем линейных алгебраических уравнений более высокой размерности.

LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {0, 0, 0, 0}]

Теперь взглянем на решение неоднородных систем линейных алгебраических уравнений.

После запроса LinearSolve вводим матрицу коэффициентов системы и ненулевой вектор свободных членов. В ответ получаем вектор неизвестных. Вот два примера.

LinearSolve[{{a, b}, {c, d}}, {1, 2}]

LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {1, 1, 1, 2}]

Решить систему уравнений матричным методом по математике.

Метод алгебраического сложения

ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»

Центр дистанционного образования

Урок алгебры в 7 классе

Тема урока: Метод алгебраического сложения.

Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.

Задачи урока:

Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.

Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.

Форма работы: индивидуальная

Этапы урока:

1) Организационный этап.

организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.

2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.

Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.

3. Изучение нового материала.

1). формировать умение решать системы линейных уравнений способом сложения;

2). развивать и совершенствовать имеющиеся знания в новых ситуациях;

3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.

http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html

Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.

5. Закрепление изученного материала

Цель: проверить знания, умения и навыки, полученные на уроке

6. Итог урока, информация о домашнем задании, рефлексия.

Ход урока (работа в электронном документе Google):

1. Сегодня урок я хотела начать с философской загадки Вальтера.

Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?

Время

Вспомним основные понятия по теме:

Перед нами система двух уравнений.

Вспомним, как мы решали системы уравнений на прошлом уроке.

Методом подстановки

Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?

Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.

Только получив уравнение с одной переменной нам удалось решить систему уравнений.

3. Мы приступаем к решению следующей системы:

Выберем уравнение, в котором удобно одну переменную выразить через другую.

Такого уравнения нет.

Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?

Найти новый метод.

Попытаемся сформулировать цель урока.

Научиться решать системы новым методом.

Что нам необходимо сделать, чтобы научиться решать системы новым методом?

знать правила (алгоритм) решения системы уравнения, выполнить практические задания

Приступим к выведению нового метода.

Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.

Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.

Сложить уравнения.

Что значит сложить уравнения?

По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.

Попробуем. Работаем вместе со мной.

13x+14x+17y-17y=43+11

Получили линейное уравнение с одной переменной.

Решили систему уравнений?

Решение системы — пара чисел.

Как найти у?

Найденное значение х подставить в уравнение системы.

Имеет значение, в какое уравнение подставим значение х?

Значит найденное значение х можно подставить в…

любое уравнение системы.

Мы познакомились с новым методом — методом алгебраического сложения.

Решая систему, мы проговорили алгоритм решения системы данным методом.

Алгоритм мы рассмотрели. Теперь применим его к решению задач.

Умение решать системы уравнений может пригодится в практике.

Рассмотрим задачу:

В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?

Зная, что всего кур и овец 19, составим первое уравнение: х + у =19

4х — число ног у овец

2у — число ног у кур

Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46

Составим систему уравнений:

Решим систему уравнений, применяя алгоритм решения методом сложения.

Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?

Рассмотрим ещё один пример!

Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.

4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html

5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.

Дополнительные задания:

Рефлексия.

Я за свою работу на уроке ставлю оценку — …

6. Использованные ресурсы-интернет:

сервисы Google для образования

Учитель математики Соколова Н. Н.

Метод алгебраического сложения

Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменной.

В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится — это способ алгебраического сложения.

А откуда вообще взялась идея — что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.

Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.е. по отдельности складывают подобные слагаемые в левой части, затем в правой. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим сказанное на конкретных примерах.

Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число -у. Значит, это уравнение можно решить методом сложения.

Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.

А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с -у, 8 сложим с 7.

Получим систему уравнений

Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.

Ответ: (3; — 1).

Образец оформления:

Решить методом алгебраического сложения систему уравнений

В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.

Тогда первое уравнение примет вид:

Теперь видим, что при переменной х есть противоположные коэффициенты. Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.

Теперь у нас система уравнений:

Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.

Образец оформления:

Давайте подведём итоги:

Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.

Список использованной литературы:

Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А. Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.

Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:

{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2

Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Пример решения способом сложения

Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

{3*x + 2*y = 10;
{5*x + 3*y = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2

Получим следующую систему уравнений:

{9*x+6*y = 30;
{10*x+6*y=24;

Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

10*x+6*y — (9*x+6*y) = 24-30; x=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

{3*(-6) + 2*y =10;
{2*y=28; y =14;

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

{3*x + 2*y = 10;
{5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Как видите, получились два верных равенства, следовательно, мы нашли верное решение.

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.

Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
Почленно сложить полученное выражение и найти одно из неизвестных.
Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.

Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.

Решение для полученных в итоге системы находят методом сложения.

Наглядный метод решения систем

Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.

Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.

Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.

В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.

Матрица и ее разновидности

Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.

Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.

Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Решение примеров систем линейных уравнений матричным методом

Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.

Способ сложения состоит из трёх простых шагов:

Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
Решить новое уравнение, получившееся после второго шага.

Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.

Однако на практике всё не так просто. Причин тому несколько:

Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?

Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:

Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.

Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.

Вообще, существует два метода решения подобных систем:

Метод сложения;
Метод выражения одной переменной через другую.

Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т. е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.

Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.

Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.

Решение легких задач с применением способа сложения

Итак, учимся применять метод сложения на примере двух простейших выражений.

Задача № 1

\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right.\]

Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:

Решаем простейшую конструкцию:

Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:

\[-4y=12\left| :\left(-4 \right) \right.\]

Ответ: $\left(2;-3 \right)$.

Задача № 2

\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]

Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:

Мы получили простейшее линейное уравнение, давайте решим его:

Теперь давайте найдем $x$:

Ответ: $\left(-3;3 \right)$.

Важные моменты

Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:

Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении. В этом случае одна из них уничтожится.
Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left(…;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.

В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.

Решение легких задач с применением метода вычитания

Задача № 1

\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right.\]

Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:

Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:

Ответ: $\left(2;5 \right)$.

Задача № 2

\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right. \]

Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:

Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:

Ответ: $\left(-3;-2 \right)$.

Нюансы решения

Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.

Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.

Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.

Решение задач методом домножения на коэффициент

Пример № 1

\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right.\]

Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:

\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]

Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:

Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:

\[-9y=18\left| :\left(-9 \right) \right.\]

Ответ: $\left(4;-2 \right)$.

Пример № 2

\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right.\]

Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:

\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]

\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]

Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:

Теперь найдем $y$, подставив $x$ в первое уравнение:

Ответ: $\left(-2;1 \right)$.

Нюансы решения

Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:

Смотрим на систему и анализируем каждое уравнение.
Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях. Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
Находим одну переменную.
Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.
Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.

Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.

Решение задач с дробными числами

Пример № 1

\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]

Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:

\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]

Вычитаем уравнения друг из друга:

$n$ мы нашли, теперь посчитаем $m$:

Ответ: $n=-4;m=5$

Пример № 2

\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right.\]

Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:

\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]

Применяем метод вычитания:

Давайте найдем $p$, подставив $k$ во вторую конструкцию:

Ответ: $p=-4;k=-2$.

Нюансы решения

Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.

Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.

В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:

Решение сложных систем уравнений

В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.

Система № 1

\[\left\{ \begin{align}& 3\left(2x-y \right)+5=-2\left(x+3y \right)+4 \\& 6\left(y+1 \right)-1=5\left(2x-1 \right)+8 \\\end{align} \right.\]

Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.

Итого мы получим окончательную систему, которая равносильна исходной:

\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right. \]

Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:

\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right.\]

Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$

Теперь найдем $y$:

Ответ: $\left(0;-\frac{1}{3} \right)$

Система № 2

\[\left\{ \begin{align}& 4\left(a-3b \right)-2a=3\left(b+4 \right)-11 \\& -3\left(b-2a \right)-12=2\left(a-5 \right)+b \\\end{align} \right.\]

Преобразуем первое выражение:

Разбираемся со вторым:

\[-3\left(b-2a \right)-12=2\left(a-5 \right)+b\]

\[-3b+6a-12=2a-10+b\]

\[-3b+6a-2a-b=-10+12\]

Итого, наша первоначальная система примет такой вид:

\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right.\]

Посмотрев на коэффициенты при $a$, мы видим, что первое уравнение нужно домножить на $2$:

\[\left\{ \begin{align}& 4a-30b=2 \\& 4a-4b=2 \\\end{align} \right. \]

Вычитаем из первой конструкции вторую:

Теперь найдем $a$:

Ответ: $\left(a=\frac{1}{2};b=0 \right)$.

Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!

Решение СЛАУ матричным методом — презентация онлайн

1. Решение СЛАУ матричным методом

2. Матричный метод решения СЛАУ

Матричный метод – это метод решения
через обратную матрицу квадратных
(с числом уравнений, равным числу
неизвестных) систем линейных
алгебраических уравнений с
ненулевым определителем.

3. Пусть дана система линейных уравнений с n неизвестными

Пусть дана система линейных уравнений с n неизвестными
Запишем ее в матричной форме:
A — основная матрица системы, состоящая из
коэффициентов при неизвестных.

B — вектор — столбец свободных членов (слагаемых)
X — вектор – столбец решений системы

4. Запишем СЛАУ в виде матричного уравнения и решим его

AX = B
Умножим это матричное уравнение слева на A − 1 — матрицу,
обратную матрице A:
Так как A − 1A = E по определению обратной матрицы, получаем
E X = A − 1B
X = A − 1B
где A – 1=1/∆ (A*)Т ,
∆≠0
(A*)Т — транспонированная матрица алгебраических дополнений
соответствующих элементов матрицы A.

5. Пример Решить СЛАУ матричным методом:

Сначала убедимся в том, что определитель матрицы из
коэффициентов при неизвестных СЛАУ не равен нулю.

6. Вычислим алгебраические дополнения для элементов основной матрицы

Вычислим алгебраические дополнения для
элементов основной матрицы

7. Найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы

Найдём союзную матрицу, транспонируем её и подставим
в формулу для нахождения обратной матрицы

8.

Найдем неизвестные, перемножив обратную матрицу и столбец свободных членов Найдем неизвестные, перемножив обратную
матрицу и столбец свободных членов
Ответ: x=2; y=1; z=4.

9. Отдохнем на песочке…

11. Самостоятельная работа

1 вариант
2 вариант
Решить СЛАУ:
Решить СЛАУ:
2 x1 3 x2 x3 7
3 x1 2 x2 x3 5
4 x 7 x 3 x 4
2
3
1
x1 2x 2 — x 3 4
3×1 2 x 3 8
4x — 2x 5x 0
1
2
3

12. Домашнее задание

Решить СЛАУ:

решаем системы линейных алгебраических уравнений (слау)

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1. 8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A — 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1. 15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………. .
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = — 3 + 2t

x 2 = — 1 — 3t

x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Решение систем линейных уравнений с использованием матриц

Привет! Эта страница будет иметь смысл только в том случае, если вы немного разбираетесь в системах линейных уравнений и матрицах, поэтому, пожалуйста, идите и узнайте о них, если вы еще этого не знаете!

Пример

Одним из последних примеров по системам линейных уравнений был этот:

Пример: решить

х + у + г = 6
2г + 5г = -4
2x + 5y — z = 27

Затем мы перешли к решению с помощью «исключения». .. но мы можем решить это с помощью матриц!

Использование матриц облегчает жизнь, потому что мы можем использовать компьютерную программу (такую как Калькулятор матриц), чтобы выполнить всю «обработку чисел».

Но сначала нам нужно написать вопрос в матричной форме.

В форме матрицы?

ОК. Матрица — это массив чисел, верно?

Матрица

Ну, вдумайтесь в уравнения:

х	+	и	+	из	=	6
		2 года	+	5з	=	−4
2x	+	5 лет	−	из	=	27

Их можно превратить в таблицу чисел, например:

1	1	1	=	6
0	2	5	=	−4
2	5	−1	=	27

Мы могли бы даже разделить числа до и после «=» на:

1	1	1		6
0	2	5	и	−4
2	5	−1		27

Теперь похоже, что у нас есть 2 матрицы.

На самом деле у нас есть третий, который равен [x y z]:

Почему [x y z] идет туда? Потому что, когда мы умножаем матрицы, левая сторона становится:

Это исходная левая часть наших уравнений выше (вы можете это проверить).

Матричное решение

Мы можем написать так:

вот так:

АХ = В

где

A — матрица 3×3 из x, y и z коэффициентов
X равно x, y и z и
B это 6, −4 и 27

Тогда (как показано на странице, обращенной к матрице) решение таково:

Х = А ^-1 В

Что это значит?

Это означает, что мы можем найти значения x, y и z (матрица X) путем умножения обратной матрицы A на матрицу B .

Итак, давайте сделаем это.

Во-первых, нам нужно найти обратную матрицу A (при условии, что она существует!)

С помощью Калькулятора матриц получаем:

(я оставил 1/определитель вне матрицы, чтобы упростить числа)

Затем умножьте A ^-1 на B (мы можем снова использовать матричный калькулятор):

Готово! Решение:

х = 5,
у = 3,
г = -2

Как на странице «Системы линейных уравнений».

Довольно аккуратно и элегантно, и человек думает, а компьютер делает расчеты.

Просто для удовольствия … Сделай это снова!

Для развлечения (и чтобы помочь вам научиться) давайте проделаем все это снова, но сначала поставьте матрицу «X».

Я хочу показать вам этот способ, потому что многие люди думают, что приведенное выше решение настолько изящно, что должно быть единственным способом.

Итак, мы решим это так:

ХА = В

И из-за того, как перемножаются матрицы, нам нужно настроить матрицы по-другому.Ряды и столбцы должны быть переключены («транспонированы»):

И XA = B выглядит так:

Матричное решение

Затем (также показано на странице, обращенной к матрице) решение таково:

Х = БА ^-1

Вот что мы получаем за A ^-1 :

На самом деле это то же самое, что инверсия, которую мы получили раньше, но с транспонированием (строки и столбцы меняются местами).

Затем мы умножаем B на A ^-1 :

И решение то же:

х = 5, у = 3 и г = -2

Это решение выглядело не так аккуратно, как предыдущее, но оно показывает нам, что существует более одного способа составления и решения матричных уравнений.Только будьте осторожны со строками и столбцами!

Решение систем уравнений матричным методом

Матричный метод решения систем уравнений также известен как метод строк-эшелонов.
Матричный метод аналогичен методу исключения, но намного чище
, чем метод исключения.

Решение систем уравнений матричным методом включает в себя выражение системы
уравнений в виде матрицы, а затем преобразование этой матрицы в то, что известно как форма эшелона строк
.

Ниже приведены два примера матриц в форме Row Echelon Form

Первая представляет собой матрицу 2 x 2 в форме Row Echelon, а вторая представляет собой матрицу 3 x 3
в форме Row Echelon.

Выражение систем уравнений в виде матриц

Учитывая следующую систему уравнений:

Приведенная выше система уравнений с двумя переменными может быть выражена в виде матричной системы, поскольку
следует за

Если мы решим приведенное выше, используя правила умножения матриц, мы должны получить
с системой уравнений, с которой мы начали.Мы можем дополнительно изменить приведенные выше матрицы
и скрыть матрицу, содержащую переменные. Мы не удаляем его, а просто прячем
, чтобы сделать наши вычисления чище.

Вышеупомянутое далее преобразуется в единую матрицу, как показано ниже

Часто вертикальная линия рисуется, чтобы указать, что самый правый столбец представляет
записей справа от знака равенства в системе уравнений.

То же самое можно сделать для системы уравнений с тремя переменными.

Вышеупомянутое может быть выражено как произведение матриц в виде:

Скрывая матрицу, содержащую переменные, мы можем выразить это как:

Затем помещаем все это в одну матрицу:

или как

Вышеупомянутая форма называется расширенной матрицей .В расширенной матрице
выше мы знаем, что элементы слева представляют коэффициенты к переменным
в системе уравнений.

Метод приведения к форме

рядного эшелона

Прежде чем читать этот раздел, вы должны взглянуть на раздел «Сокращение до формы эшелона
» в разделе «Матрицы».

Теперь, когда вы знаете, как преобразовать матрицу в форму эшелона строк, давайте посмотрим, как применить
алгоритм к расширенным матрицам, сформированным из систем уравнений.

Пример 1:

Найдите решение следующей системы уравнений

Решение:

Первый шаг состоит в том, чтобы выразить приведенную выше систему уравнений в виде расширенной матрицы.

Далее мы маркируем строки:

Теперь мы начнем фактически приводить матрицу к форме эшелона строк.Сначала мы меняем старший коэффициент
первой строки на 1.

Мы достигаем этого, умножая R ₁ на ^-1 ⁄ ₃ :

Затем мы меняем коэффициент во второй строке, который находится ниже старшего коэффициента
в первой строке. Это достигается путем умножения R ₂ на ^-1 ⁄ ₅
и последующего прибавления результата к R ₁ .

Добавление результата к R’ ₁ :

Итак, теперь наша новая матрица выглядит так:

На этом этапе мы повторно вводим переменные в строку 2, так как теперь у нас будет одно уравнение с
переменными:

Мы можем найти y из приведенного выше уравнения:

Теперь, когда у нас есть y , мы можем использовать обратную подстановку для решения x с помощью
, заменив y в уравнении с двумя переменными, составленном из R’ ₁ :

Следовательно, решение системы уравнений {x,y} = {2,-2}

Пример 2:

Найдите x, y и z в системе уравнений ниже

Решение:

Первый шаг — превратить систему уравнений с тремя переменными в расширенную матрицу 3×4
.

Далее мы помечаем строки матрицы:

Поскольку в приведенной выше расширенной матрице мы не можем найти ни одной строки с единицей в качестве ведущего коэффициента
, нам не нужно выполнять операцию переключения строк. Однако нам нужно изменить
строку 1 так, чтобы ее старший коэффициент был равен 1.

Мы можем добиться этого, умножив строку 1 на ¹ ⁄ ₃ :

Далее нам нужно изменить все записи ниже старшего коэффициента первой строки
на нули.

Для второй строки мы можем добиться этого, сначала умножив на ^-1 ⁄ ₃
, а затем добавив результат к строке 1.

Добавление результата в строку 1:

Затем мы переходим к строке 3; здесь мы умножаем строку на ^-1 ⁄ ₅
, а затем добавляем результат к строке 1, чтобы обнулить первый элемент.

Добавление результата в строку 1:

Нам нужно, чтобы ведущий элемент во второй строке тоже был единицей.Мы получаем этот результат
, умножая вторую строку на ^-3 ⁄ ₂ :

Затем мы обнуляем элемент в третьей строке под старшим коэффициентом во второй строке
. Для этого умножаем третью строку на ⁵ ⁄ ₄

Добавление результата к строке 2:

Наконец, мы умножаем строку 3 на -12, чтобы ведущий элемент третьей строки
был равен единице:

Из приведенной выше матрицы мы находим переменные, начинающиеся с z в последней строке

Затем мы находим y, заменяя z в уравнении, образованном второй строкой:

Наконец, мы находим x, подставляя значения y и z в уравнение, сформированное
первой строкой:

Следовательно, решение системы уравнений {x,y,z} = {1,-2,1}

Решение матричных уравнений

А матричное уравнение уравнение, в котором переменная обозначает матрица .

Вы можете решить более простые матричные уравнения, используя сложение матриц и скалярное умножение .

Примеры 1:

Решите для матрицы Икс : Икс + [ 3 2 1 0 ] знак равно [ 6 3 7 − 1 ]

Икс + [ 3 2 1 0 ] − [ 3 2 1 0 ] знак равно [ 6 3 7 − 1 ] − [ 3 2 1 0 ] Икс + [ 0 0 0 0 ] знак равно [ 6 − 3 3 − 2 7 − 1 − 1 − 0 ] Икс знак равно [ 3 1 6 − 1 ]

Примеры 2:

Решите для матрицы Икс : Икс − [ − 9 − 3 6 0 ] знак равно [ 4 0 12 − 10 ]

Икс − [ − 9 − 3 6 0 ] знак равно [ 4 0 12 − 10 ] Икс − [ − 9 − 3 6 0 ] + [ − 9 − 3 6 0 ] знак равно [ 4 0 12 − 10 ] + [ − 9 − 3 6 0 ] Икс − [ 0 0 0 0 ] знак равно [ 4 + ( − 9 ) 0 + ( − 3 ) 12 + 6 − 10 + 0 ] Икс знак равно [ − 5 − 3 18 − 10 ]

Решение систем линейных уравнений с использованием матриц:

Матричные уравнения можно использовать для решать системы линейных уравнений используя левую и правую части уравнений.

Примеры 3:

Решите систему уравнений с помощью матриц: { 7 Икс + 5 у знак равно 3 3 Икс − 2 у знак равно 22

7 Икс + 5 у знак равно 3 3 Икс − 2 у знак равно 22 → [ 7 Икс + 5 у 3 Икс − 2 у ] знак равно [ 3 22 ]

Запишите матрицу слева как произведение коэффициентов и переменных.

[ 7 5 3 − 2 ] [ Икс у ] знак равно [ 3 22 ]

↑ ↑ ↑

коэффициент Переменная постоянный матрица матрица матрица

Сначала найдите обратную матрицу коэффициентов. Обратное [ 7 5 3 − 2 ] является

1 7 ( − 2 ) − ( 3 ) ( 5 ) [ − 2 − 5 − 3 7 ] знак равно − 1 29 [ − 2 − 5 − 3 7 ] знак равно [ 2 29 5 29 3 29 − 7 29 ]

Затем умножьте каждую часть матричного уравнения на обратная матрица .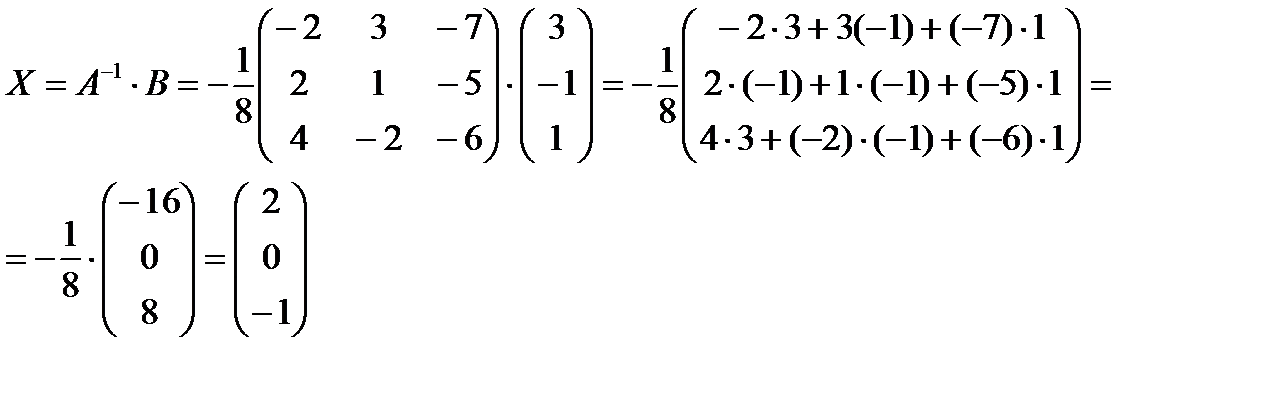 Так как умножение матриц нет коммутативной, обратная матрица должна быть слева на каждый часть матричного уравнения.

[ 2 29 5 29 3 29 − 7 29 ] [ 7 5 3 − 2 ] [ Икс у ] знак равно [ 2 29 5 29 3 29 − 7 29 ] [ 3 22 ]

[ 1 0 0 1 ] [ Икс у ] знак равно [ 4 − 5 ]

То единичная матрица слева подтверждает, что обратная матрица была вычислена правильно.

[ Икс у ] знак равно [ 4 − 5 ]

Решение ( 4 , − 5 ) .

Решение уравнений матричным методом

Решение уравнений матричным методом

Одновременные уравнения в двух переменные могут быть решены разными методами: методом подстановки, перекрестным метод умножения и др.Здесь мы имеем дело с методом решения линейных уравнения двух переменных с использованием матриц .

*************************************

10 математических задач официально объявляет о выпуске Quick Math Solver , приложение Android в Google Play Store для учащихся со всего мира.

****************************

Рассмотрим следующую линейную уравнения,

а ₁ х + б ₁ у = с ₁ ………………. (и)

а ₂ х + б ₂ у = с ₂ ………………. (ii)

Запись уравнений (i) и (ii) на матричный вид, получаем

Приравнивание соответствующих элементов равных матрицы X и A ^-1 B, получаем решение.

Примечание: Если определитель |A| = 0 система уравнений не имеет единственного решение, поэтому, когда |A| ≠ 0, уравнения имеют единственное решение.

Разработанные примеры

Пример 3: Если стоимость 17 кг сахара и 4 кг чая составляет рупий.1110 и Стоимость 8 кг сахара и 2 кг чая 500 рублей. 540. Найдите стоимость сахара за кг и чая на кг по матричному методу.

Решение: Пусть,

Стоимость сахара за кг = рупий. х

Стоимость чая за кг = рупий. у

Далее по вопросам

1 ^st футляр , 17x + 4y = 1110 …………… (i)

2 ^и ящик , 8x + 2y = 540 ……………… (ii)

Записав данные уравнения в матричной форме, получим

Сравнивая соответствующие элементы, получаем

х = 30, у = 150

Следовательно, стоимость сахара за кг = рупий. 30

Стоимость чая за кг = рупий. 150

У вас есть вопросы по матричному методу решения уравнений?

Вы можете задать свои вопросы или проблемы здесь, в раздел комментариев ниже.

Использование матриц при решении системы уравнений (Алгебра 2, Матрицы) — Mathplanet

Матрицы можно использовать для решения систем уравнений, но сначала нужно научиться находить обратную матрицу C ^-1 .{-1}=\frac{1}{ad-bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}$$

Сейчас мы на примере покажем, как решать системы уравнений с использованием матриц и обратных матриц.

Пример

Рассмотрим следующие одновременные уравнения (этот пример также показан в нашем видеоуроке)

$$\left\{\begin{matrix} 3x+y=5\\ 2x-y=0\\ \end{matrix}\right.$$

При условии, что мы знаем, как перемножать матрицы, мы понимаем, что наши уравнения могут быть записаны как

$$\begin{bmatrix} 3 & 1\\ 2 & -1 \end{bmatrix}\cdot \begin{bmatrix} x\\ y\\ \end{bmatrix}=\begin{bmatrix} 5\\ 0 \end{bmatrix}$$

Сначала находим обратную матрицу коэффициентов:

$$C^{-1}=\frac{1}{3\cdot -1-1\cdot 2}\begin{bmatrix} -1 & -1\\ -2& 3 \end{bmatrix}=$$

$$=-\frac{1}{5}\begin{bmatrix} -1 & -1\\ -2& 3 \end{bmatrix}$$

Следующим шагом будет умножение обеих частей нашего матричного уравнения на обратную матрицу:

$$-\frac{1}{5}\begin{bmatrix} -1 & -1\\ -2& 3 \end{bmatrix} \begin{bmatrix} 3 & 1\\ 2 & -1 \end{bmatrix }\cdot \begin{bmatrix} x\\ y\\ \end{bmatrix}= -\frac{1}{5}\begin{bmatrix} -1 & -1\\ -2& 3 \end{bmatrix} \ begin{bmatrix} 5\\ 0 \end{bmatrix}$$

$$-\frac{1}{5}\begin{bmatrix} -5 & 0\\ 0 & -5 \end{bmatrix}\cdot \begin{bmatrix} x\\ y \end{bmatrix}=- \frac{1}{5}\begin{bmatrix} -5\\ -10 \end{bmatrix}$$

$$\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} 1\\ 2 \end{ bmatrix}$$

Наше решение (1,2), самый простой способ проверить, правы ли мы, — это подставить наши значения в исходные уравнения.

Видеоурок

Пример выше в видеоформате.

4.6: Решение систем уравнений с использованием матриц

Как только система уравнений будет представлена в форме расширенной матрицы, мы будем выполнять операции над строками, которые приведут нас к решению.

Чтобы решить методом исключения, не имеет значения, в каком порядке мы расположим уравнения в системе. Точно так же в матрице мы можем поменять местами строки.

Когда мы решаем методом исключения, мы часто умножаем одно из уравнений на константу. Поскольку каждая строка представляет собой уравнение, и мы можем умножать каждую часть уравнения на константу, аналогичным образом мы можем умножать каждую запись в строке на любое действительное число, кроме 0,

При исключении мы часто добавляем кратное число одной строки к другой строке. В матрице мы можем заменить строку на ее сумму, кратную другой строке.

Эти действия называются операциями со строками и помогут нам использовать матрицу для решения системы уравнений.

РЯДНЫЕ ОПЕРАЦИИ

В матрице следующие операции могут быть выполнены с любой строкой, и результирующая матрица будет эквивалентна исходной матрице.

Поменяйте местами любые два ряда.
Умножить строку на любое действительное число, кроме 0.
Добавить ненулевое кратное одной строки к другой строке.

Выполнить эти операции несложно, но все арифметические действия могут привести к ошибке. Если мы используем систему для записи операций со строками на каждом этапе, гораздо проще вернуться и проверить нашу работу.

Мы используем заглавные буквы с нижними индексами для представления каждой строки. Затем мы показываем операцию слева от новой матрицы. Чтобы показать перестановку строк:

Чтобы умножить строку 2 на $−3$:

Чтобы умножить строку 2 на $−3$ и прибавить к строке 1:

Пример $\PageIndex{7}$

Выполнить указанные операции над расширенной матрицей:

ⓐ Поменять местами ряды 2 и 3.

ⓑ Умножить строку 2 на 5.

$ \left[ \begin{массив} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{массив} \right] $

Ответить

ⓐ Меняем местами 2 и 3 ряды.

ⓑ Умножаем 2-й ряд на 5.

Пример $\PageIndex{8}$

Выполнить указанные операции над расширенной матрицей:

ⓐ Поменяйте местами ряды 1 и 3.

ⓑ Умножить строку 3 на 3.

$ \left[ \begin{массив} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{массив} \справа]$

Ответить

ⓐ \( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] \ )

ⓑ \( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] \ )

Пример $\PageIndex{9}$

Выполнить указанные операции над расширенной матрицей:

ⓐ Поменять местами ряды 1 и 2,

ⓑ Умножить строку 1 на 2,

$ \left[ \begin{массив} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{массив} \right] $

Ответить: ⓐ $ \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓑ $ \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓒ $ \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $

Теперь, когда мы попрактиковались в операциях со строками, мы рассмотрим расширенную матрицу и выясним, какую операцию мы будем использовать для достижения цели.Это именно то, что мы сделали, когда мы сделали исключение. Мы решили, на какое число умножить строку, чтобы при сложении строк исключалась переменная.

Учитывая эту систему, что бы вы сделали, чтобы исключить x ?

Следующий пример делает то же самое, но с матрицей.

Пример $\PageIndex{10}$

Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: $ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{массив} \right] $

Ответить

Чтобы число 4 стало равным 0, мы могли бы умножить строку 1 на $−4$, а затем прибавить ее к строке 2.

Пример $\PageIndex{11}$

Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: $ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{массив} \right] $

Ответить: $ \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] $

Пример $\PageIndex{12}$

Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: $ \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{массив} \right] $

Ответить: $ \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] $

Метод наименьших квадратов

Начнем с уточнения того, что именно мы будем подразумевать под «наилучшим приближенным решением» противоречивого матричного уравнения Ax=b.

Определение

Пусть A — матрица размера m × n, а b — вектор в Rm. Решением по методу наименьших квадратов матричного уравнения Ax=b является вектор Kx в Rn такой, что

расстояние(b,AKx)≤расстояние(b,Ax)

для всех остальных векторов x в Rn.

Напомним, что dist(v,w)=Av−wA — это расстояние между векторами v и w. Термин «наименьшие квадраты» происходит от того факта, что dist(b,Ax)=Ab−AKxA — это квадратный корень из суммы квадратов элементов вектора b−AKx.Таким образом, решение методом наименьших квадратов минимизирует сумму квадратов разностей между элементами AKx и b. Другими словами, решение по методу наименьших квадратов максимально точно решает уравнение Ax=b в том смысле, что сумма квадратов разности b-Ax минимизируется.

Метод наименьших квадратов: изображение

Предположим, что уравнение Ax=b несовместно. Напомним из этого примечания в разделе 2.3, что пространство столбцов A — это множество всех других векторов c, таких что Ax=c непротиворечиво. Другими словами, Col(A) — это множество всех векторов вида Ax. Следовательно, ближайший к b вектор формы Ax является ортогональной проекцией b на Col(A). Это обозначено как bCol(A), следуя этим обозначениям в Разделе 6.3.

ColAAxAxAxAKx=bCol(A)bb−AKx=bCol(A)⊥0

Решением уравнения Ax=b методом наименьших квадратов является решение Kx согласованного уравнения Ax=bCol(A)

Где находится Kx на этом рисунке? Если v1,v2,…,vn — столбцы A, то

AKx=AEIIGKx1Kx2…KxnFJJH=Kx1v1+Kx2v2+···+Kxnvn.

Следовательно, элементы Kx являются «координатами» bCol(A) относительно остовного множества {v1,v2,…,vm} Col(A). (Они являются честными B-координатами, если столбцы A линейно независимы.)

ColAv1v2Kx1v1Kx2v2AKx=bCol(A)bb−AKx=bCol(A)⊥0 Рис. 4. Фиолетовая плоскость — Col(A). Ближайший вектор, который Ax может подобрать к b, — это ближайший к b вектор на Col(A), который является ортогональной проекцией bCol(A) (синий). Векторы v1,v2 — это столбцы A, а коэффициенты Kx — это длины зеленых линий.

Нажмите и перетащите b, чтобы переместить его.

Мы научились решать такую задачу ортогональной проекции в разделе 6.3.

Теорема

Пусть A — матрица размера m × n, а b — вектор в Rm. Решения наименьших квадратов Ax=b являются решениями матричного уравнения

ATAx=ATb

Доказательство

По этой теореме из раздела 6.3, если Kx является решением матричного уравнения ATAx=ATb, то AKx равно bCol(A). Выше мы утверждали, что решение Ax=b методом наименьших квадратов является решением Ax=bCol(A).

В частности, поиск решения методом наименьших квадратов означает решение непротиворечивой системы линейных уравнений. Мы можем перевести приведенную выше теорему в рецепт:

Рецепт 1. Вычисление решения методом наименьших квадратов

Пусть A — матрица размера m×n, а b — вектор в Rn. Вот метод вычисления решения по методу наименьших квадратов Ax=b:

Вычислить матрицу ATA и вектор ATb.
Сформируйте расширенную матрицу для матричного уравнения ATAx=ATb и сократите строку.
Это уравнение всегда согласовано, и любое решение Kx является решением методом наименьших квадратов.

Повторяю: как только вы нашли решение методом наименьших квадратов Kx для Ax=b, тогда bCol(A) равно AKx.

Читатель, возможно, заметил, что мы постарались сказать «решение методом наименьших квадратов» во множественном числе, а «решение методом наименьших квадратов» — с неопределенным артиклем. Это связано с тем, что решение методом наименьших квадратов не обязательно должно быть уникальным: действительно, если столбцы A линейно зависимы, то Ax=bCol(A) имеет бесконечно много решений.Следующая теорема, дающая эквивалентные критерии единственности, является аналогом этого следствия из раздела 6.3.

Теорема

Пусть A — матрица размера m × n, а b — вектор в Rm. Следующие эквивалентны:

Ax=b имеет единственное решение методом наименьших квадратов.
Столбцы A линейно независимы.
АТА является обратимым.

В этом случае решение методом наименьших квадратов равно

Kx=(ATA)−1ATb.

Доказательство

Множество решений уравнения Ax=b методом наименьших квадратов является множеством решений согласованного уравнения ATAx=ATb, которое является преобразованием множества решений однородного уравнения ATAx=0.Поскольку ATA — квадратная матрица, эквивалентность 1 и 3 следует из теоремы об обратимой матрице в разделе 5.1. Множество решений методом наименьших квадратов также является множеством решений согласованного уравнения Ax=bCol(A), которое имеет единственное решение тогда и только тогда, когда столбцы A линейно независимы в соответствии с этим важным примечанием в разделе 2.5.

Как обычно, вычисления с проекциями становятся проще при наличии ортогонального множества. Действительно, если A — матрица размера m×n с ортогональными столбцами u1,u2,…, гм, тогда мы можем использовать формулу проецирования в разделе 6.4, чтобы записать

bCol(A)=b·u1u1·u1u1+b·u2u2·u2u2+···+b·umum·umum=AEIIG(b·u1)/(u1·u1)(b·u2)/(u2·u2).

..(b·um)/(um·um)FJJH.

Обратите внимание, что решение методом наименьших квадратов в этом случае единственно, поскольку ортогональное множество линейно независимо.

Рецепт 2. Вычисление решения методом наименьших квадратов

Пусть A — матрица размера m×n с ортогональными столбцами u1,u2,…,um, и пусть b — вектор в Rn. Тогда решением Ax=b методом наименьших квадратов является вектор

Kx=Lb·u1u1·u1,b·u2u2·u2,…,б·умум·умМ.

Эта формула особенно полезна в естественных науках, так как в природе часто возникают матрицы с ортогональными столбцами.

В этом подразделе мы даем применение метода наименьших квадратов к моделированию данных. Начнем с базового примера.

Пример (наиболее подходящая линия)

Предположим, что мы измерили три точки данных

(0,6),(1,0),(2,0),

и что наша модель для этих данных утверждает, что точки должны лежать на прямой. Конечно, эти три точки на самом деле не лежат на одной линии, но это может быть связано с ошибками в наших измерениях.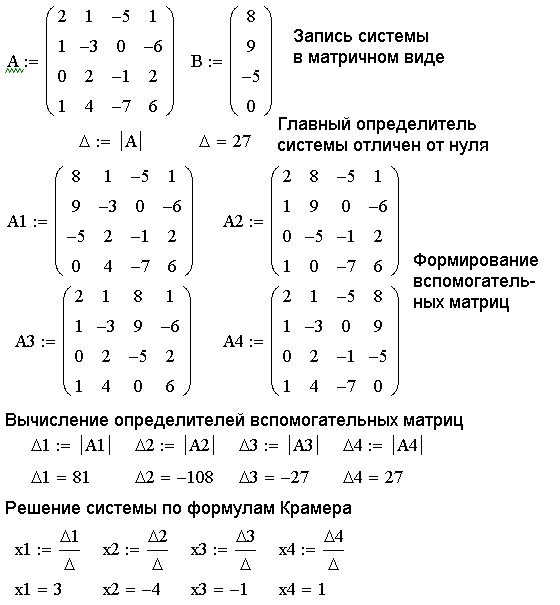 Как мы можем предсказать, на какой линии они должны лежать?

Общее уравнение для (невертикальной) линии:

у=Мх+В.

Если бы наши три точки данных лежали на этой прямой, то удовлетворялись бы следующие уравнения:

6=М·0+В0=М·1+В0=М·2+В.(6.5.1)

Чтобы найти наилучшую прямую, мы пытаемся решить приведенные выше уравнения с неизвестными M и B. Поскольку три точки на самом деле не лежат на прямой, фактического решения нет, поэтому вместо этого мы вычисляем наименьшую- решение квадратов.

Приведя наши линейные уравнения в матричный вид, мы пытаемся решить Ax=b для

А=C011121Dx=LMBMb=C600D.

В этом примере мы решили эту задачу наименьших квадратов: единственное решение методом наименьших квадратов для Ax=b — это Kx=AMBB=A−35B, поэтому наиболее подходящая линия — это

у=-3х+5.

Что именно минимизирует линия y=f(x)=−3x+5? Решение Kx методом наименьших квадратов минимизирует сумму квадратов элементов вектора b−AKx. Вектор b является левой частью (6.5.1) и

AL-35M=C-3(0)+5-3(1)+5-3(2)+5D=Cf(0)f(1)f(2)D.

Другими словами, AKx — это вектор, элементами которого являются координаты y графика линии при значениях x, которые мы указали в наших точках данных, а b — вектор, элементами которого являются координаты y этих точек данных . Разница b−AKx представляет собой вертикальное расстояние графика от точек данных:

(0,6)(1,0)(2,0)−12−1y=−3x+5b−AKx=C600D−AL−35M=C−12−1D

Линия наилучшего соответствия минимизирует сумму квадратов этих вертикальных расстояний.

Все приведенные выше примеры имеют следующий вид: задано некоторое количество точек данных (x,y), и мы хотим найти функцию

y=B1g1(x)+B2g2(x)+···+Bmgm(x)

, наилучшим образом аппроксимирующий эти точки, где g1,g2,…,gm — фиксированные функции от x. Действительно, в примере с наилучшей линией у нас было g1(x)=x и g2(x)=1; в примере с наилучшей параболой мы имеем g1(x)=x2, g2(x)=x и g3(x)=1; и в примере наилучшей линейной функции у нас было g1(x1,x2)=x1, g2(x1,x2)=x2 и g3(x1,x2)=1 (в этом примере мы берем x как вектор с две записи). Мы оцениваем приведенное выше уравнение для заданных точек данных, чтобы получить систему линейных уравнений с неизвестными B1, B2,…, Bm — как только мы оцениваем gi, они просто становятся числами, поэтому не имеет значения, какие они — и находим решение методом наименьших квадратов. Полученная функция наилучшего соответствия минимизирует сумму квадратов вертикальных расстояний от графика y = f (x) до наших исходных точек данных.

Чтобы подчеркнуть, что природа функций gi на самом деле не имеет значения, рассмотрим следующий пример.

Следующий пример несколько отличается от предыдущих.