Урок 72. сложение смешанных дробей — Математика — 5 класс

Математика

5 класс

Урок № 72

Сложение смешанных дробей

Перечень рассматриваемых вопросов:

– сложение смешанной дроби с целым числом;

– сложение смешанной дроби с правильной дробью;

– сложение смешанных дробей с общим знаменателем;

– сложение смешанных дробей с разными знаменателями;

– преобразование неправильных дробей в смешанное число.

Тезаурус

Смешанная дробь – сумма натурального числа и правильной дроби, записанная без знака плюс.

Целая часть смешанной дроби – натуральное число в смешанной дроби.

Дробная часть смешанной дроби – правильная дробь в смешанной дроби.

Переместительное свойство сложения – от перестановки слагаемых местами сумма не меняется.

Сочетательное свойство сложения – чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.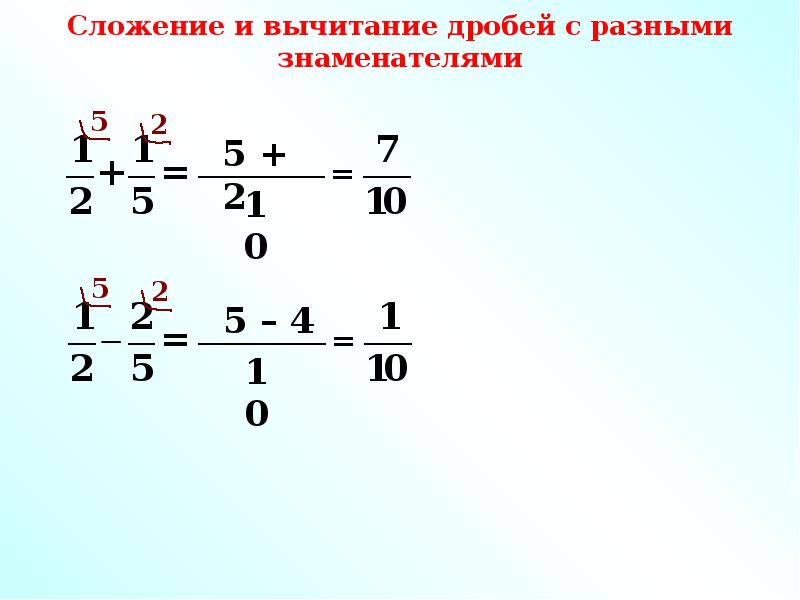

Порядок убывания – расположение элементов от большего к меньшему.

Порядок возрастания – расположение элементов от меньшего к большему.

Обязательная литература

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Ранее мы говорили, что смешанная дробь – это сумма натурального числа и правильной дроби. При сложении смешанных дробей используют законы сложения. Рассмотрим это на примере:

Каждую смешанную дробь представим, как сумму целой и дробной части.

Вспомним переместительное свойство сложения – от перестановки слагаемых местами сумма не меняется. Перегруппируем слагаемые. Запишем сначала сумму целых частей, а затем сумму дробных частей. Сложим отдельно целые и дробные части обеих дробей. Полученную сумму запишем смешанной дробью, то есть уберём знак плюс между натуральным числом и правильной дробью.

Для удобства будем считать, что у каждого натурального числа есть дробная часть, равная нулю, а у каждой правильной дроби есть целая часть, равная нулю. С учётом этого складывать натуральные числа и правильные дроби со смешанными дробями можно по тому же правилу.

Например:

Проведём те же преобразования, что и в предыдущем примере: отдельно сложим целые и дробные части обоих чисел. Запишем сумму целой и дробной части в виде смешанной дроби, т. е. без знака плюс.

Рассмотрим пример, в котором к смешанной дроби прибавляют простую дробь.

Отдельно складываем целые части и дробные части. Сумму натурального числа и дроби записываем смешанным числом, т. е. без знака плюс.

При сложении двух смешанных дробей сумма дробных частей может оказаться неправильной дробью. Посмотрим на примере, как действовать в таком случае.

Сумма дробных частей получилась равной семи пятым. Преобразуем неправильную дробь в смешанную. Семь пятых – это одна целая и две пятых. С учётом этого сумма данных смешанных чисел равна четырём целым и двум пятым.

Если необходимо сложить смешанные дроби, дробные части которых имеют разные знаменатели, то сначала нужно привести дробные части к общему знаменателю, а потом выполнить сложение.

Общий знаменатель дробных частей равен пятнадцати. Сумма будет равна семи целым тринадцати пятнадцатым. Обратите внимание на запись решения данного примера. Здесь уже нет промежуточных вычислений сумм целых и дробных частей. Записывать эти вычисления не нужно, достаточно понимать последовательность своих действий.

Рассмотрим ещё одно выражение:

В этом выражении у обоих слагаемых есть и целая, и дробная части. Дробные части имеют различные знаменатели. Приводим дробные части к общему знаменателю. Отдельно складываем целые и дробные части, не записывая это подробно. Сумма дробных частей оказалась равной сорока трём тридцатым, это неправильная дробь. Преобразуем её в смешанную дробь. Сорок три тридцатых – это одна целая тринадцать тридцатых. Выполним сложение семи и одной целой тринадцати тридцатых. Получим восемь целых тринадцать тридцатых.

Вычислим:

При решении этого выражения можно выполнить действия по порядку: сначала найти суммы в скобках, затем сложить полученные суммы.

В этом случае нам придётся приводить дроби к общему знаменателю. Выполним это решение:

Можно решить это выражение другим способом, вспомнив сочетательный и переместительные свойства сложения:

Во втором случае решение получилось короче, нам не пришлось приводить дроби к общему знаменателю.

Сегодня мы рассмотрели сложение смешанных дробей с натуральными числами, правильными дробями и смешанными дробями. Во всех этих случаях мы действовали по одному правилу: отдельно складывали целые и дробные части слагаемых, а затем складывали полученные результаты.

Тренировочные задания

№ 1. Выберите выражения, в решении которых допущены ошибки или решение не доведено до верного ответа:

В первом выражении приведено полное, верное решение: отдельно сложены целые и дробные части смешанных дробей. Дробные части приведены к общему знаменателю. Сумма дробных частей оказалась неправильной дробью, эта дробь правильно преобразована в смешанную дробь. Сложение натурального числа и смешанной дроби выполнено верно.

Во втором выражении при сложении дробных частей, правильно приведённых к общему знаменателю, также получилась неправильная дробь, верно произведено сокращение этой неправильной дроби, но она не преобразована в смешанную дробь. В ответе получилось число, дробная часть которого является неправильной дробью. Это неверная запись ответа, хотя вычисления произведены правильно.

В третьем выражении неправильно выполнено сложение дробных частей. Дроби не приводятся к общему знаменателю, складывается числитель с числителем, знаменатель со знаменателем, что не является верным нахождением суммы двух дробей. В ответе получилась сократимая дробь, которая сокращена верно.

Ответ: ошибки допущены во 2 и 3 выражениях.

№ 2. Вычислите периметр прямоугольного участка земли, если его ширина м, а длина на м больше.

Периметр прямоугольника – это сумма длин всех его сторон. Так как у прямоугольника противоположные стороны попарно равны, достаточно знать длину и ширину прямоугольника. Ширина известна, она равна м, а о длине сказано, что она на м больше. Найдём длину прямоугольника, для этого к ширине прибавим м.

(м) – длина прямоугольника.

При сложении мы привели дробные части к общему знаменателю, сложили их, преобразовали получившуюся неправильную дробь в смешанную дробь и сложили её с суммой целых частей.

Теперь найдём периметр прямоугольника. Сложим длины четырёх его сторон:

(м) – периметр прямоугольника

Заметим, что промежуточные вычисления – отдельное сложение целых и дробных частей – записывать не обязательно.

Смешанные числа. Сложение и вычитание смешанных чисел 5 класс онлайн-подготовка на Ростелеком Лицей

Смешанные числа. Сложение и вычитание смешанных чисел.

Разделить поровну 5 одинаковых апельсинов между тремя детьми можно двумя способами.

Во-первых, можно разделить между ними поровну каждый апельсин. Тогда один ребенок получит по 5 частей, а каждая из этих частей равна 13 целого апельсина. Поэтому каждый ребенок получит 53 апельсина.

Во-вторых, можно сначала дать каждому ребенку по целому апельсину, а оставшиеся 2 апельсина разделить между ними поровну. Тогда каждый ребенок получит 1+23 апельсина.

Сумму 1+23 принято записывать короче: 123. Запись 123 читают так: «одна целая две третьих».

Число 1 называют целой частью числа 123, а число 23 – его дробной частью.

Так как в обоих случаях каждый ребенок получает одно и то же количество апельсинов, то числа равны: 53=123.

Как перейти от записи числа 53 к записи 123?

Для этого нужно разделить 5 на 3. Получаем неполное частное 1 и остаток 2. Число 1 дает целую часть, а остаток 2 – числитель дробной части.

Сформулируем правило:

Чтобы из неправильной дроби выделить целую часть, надо:

1. Разделить с остатком числитель на знаменатель.

2. Неполное частное будет целой частью.

3. Остаток (если он есть) дает числитель, а делитель – знаменатель дробной части.

Пример 1. Выделим целую часть из неправильной дроби 479.

Разделим число 47 на 9. Неполное частное 5, а остаток – 2. Значит 479=529.

Запись числа, содержащую целую и дробную части, называют смешанной дробью или смешанным числом.

Чтобы представить смешанное число в виде неправильной дроби, нужно:

1.

Умножить его целую часть на знаменатель дробной части.

2. К полученному произведению прибавить числитель дробной части.

3. Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Пример 2. Представим смешанное число 423 в виде неправильной дроби.

Решение: 423=4+23=4∙33+23=12+23=143.

При сложении (и вычитании) смешанных чисел целые части складывают (вычитают) отдельно, а дробные – отдельно.

Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части.

Пример 3. 379+249=3+2+79+49=5+119=5+129=629 .

Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, то поступают так:

Пример 4. 637-257=6+37-257=5+1+37-257=5+107-257=5107-257=357

.

Обычно пишут короче: 637-257=5107-257=357.

Таким же образом поступают и при вычитании дроби из натурального числа, и при вычитании смешанного числа из натурального числа.

Пример 5. 4-58=388-58=338.

Пример 6. 8-356=766-356=416.

Как сложить обыкновенные дроби: с одинаковыми/разными знаменателями

В данной публикации мы рассмотрим, каким образом можно сложить обыкновенные (простые) дроби с одинаковыми/разными знаменателями и смешанные дроби. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Сложение дробей

С одинаковыми знаменателями

В данном случае все предельно просто. При сложении дробей с одинаковыми знаменателями суммируются числители, а знаменатель остается неизменным.

 
Примечание: полученную путем сложения новую дробь в некоторых случаях можно сократить.

С разными знаменателями

Для того, чтобы сложить дроби с разными знаменателями, выполняем следующие действия:

1. Приводим заданные дроби к наименьшему общему знаменателю.
2. Складываем полученные результаты как дроби с одинаковыми знаменателями.

Сумма смешанных дробей

Чтобы сложить смешанные дроби, необходимо отдельно просуммировать целые части, и отдельно дробные.

X

a/b

+ Y

c/d

= (X + Y) + (

a/b

+

c/d

)

 
Примечание: Если дробные части имеют разные знаменатели, значит их сперва нужно привести к наименьшему общему знаменателю, и только после этого складывать.

Примеры задач

Задание 1

Найдите сумму дробей 

4/11

 и 

7/11

.

 
Решение

Т.к. у нас дроби с одинаковыми знаменателями, то:

4/11

+

7/11

=

4+7/11

=

11/11

=1

 
Задание 2

Найдите сумму дробей 

5/12

 и 

4/7

.

 
Решение

В данном случае нам сначала нужно привести дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 84, следовательно, дополнительный множитель для первой дроби – число 7, для второй – 12.

5/12

=

5⋅7/12⋅7

=

35/84

4/7

=

4⋅12/7⋅12

=

48/84

 
Таким образом, мы получили дроби с одинаковыми знаменателями, и теперь их можно сложить:

35/84

+

48/84

=

35+48/84

=

83/84

 
Задание 3

Найдите сумму дробей 2

6/13

 и 5

3/13

.

 
Решение

Дробные части имеют один и тот же знаменатель, значит мы сразу же можем выполнить сложение:

2

6/13

 + 5

3/13

 = 2 + 5 + (

6/13

 + 

3/13

) = 7 + 

6+3/13

 = 7

9/13

правила, примеры, решения, как умножить натуральное число на смешанную дробь

Данная статья дана для разбора смешанных чисел. Научимся выполнять умножения смешанных чисел и натурального числа.

Умножение смешанных чисел

Умножение смешанных чисел сводится к умножению обыкновенных дробей. Для этого нужно сделать перевод смешанных чисел в неправильные дроби.

Используем правила умножения смешанных чисел:

Определение 1

• Умножаемые смешанные числа нужно заменить неправильными дробями;
• Использование правила умножения дроби на дробь.

Рассмотрим решения на примерах.

Пример 1

Сделать умножение 357 и 1211.

Решение

Для начала умножаем смешанные числа в виде неправильных дробей: 357=3·7+57=267 и 1211=1·11+211=1311.

Умножение смешенных дробей заменяем умножением обыкновенных: 357·1211=267·1311.

После чего получим 267·1311=26·137·11=33877.

Дробь несократимая, поэтому выделяем целую часть:33877=43077.

В итоге получим 357·1211=267·1311=26·137·11=33877=43077.

Ответ: 357·1211=43077.

Чтобы закрепить знания умножения смешанных чисел, рассмотрим пример решения.

Пример 2

Произвести умножение 715·119.

Решение

Смешанные числа 715 и 119 можно представить в виде неправильных дробей: 135 и 109.

Получим, что 715·119=365·109=36·105·9.

Этот этап характеризуется применением правила сокращения дроби, тогда получим 36·105·9.

Мы раскладываем на простые множители и выполняем сокращение одинаковых множителей:

36·105·9=2·2·3·3·2·55·3·3=2·2·21=8

Ответ: 715·119=8.

Умножение смешенного и натурального числа

После того, как произведется замена неправильной дробью, умножение смешенного и натурального числа сводится к умножению обыкновенной дроби  и натурального числа.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 3

Произвести умножение 2518 и 45.

Решение

Представляем смешанное число 2518 в виде неправильной дроби 4118, получим 2518·45=4118·45=41·4518. Необходимо заменить на простые множители и выделить целую часть:

41·4518=41·3·3·52·3·3=41·52=2052=10212

Ответ: 2518·45=10212.

Умножение смешенного и натурального числа рассматривается, как решение с распределительным свойством умножения относительно сложения. Получаем, что произведение смешанного  и натурального числа равно сумме произведений целой части на натурально число и дробной части на данное натуральное число, тогда получаем, что abc·n=a+bc·n=a·n+bc·n.

Пример 4

Вычислить 1038·8.

Решение

Необходимо заменить смешанное число суммой целой или дробной его части. Далее используем свойство распределительного умножения:

1038·8=10+38·8=10·8+38·8=80+3=83

Ответ: 1038·8=83.

Умножение смешанного числа и обыкновенной дроби

Умножение смешанного числа и обыкновенной дроби лучше представить в виде произведения обыкновенных дробей, умноженное на смешенное число неправильной дробью.

Пример 5

Умножить 323 на 415.

Решение

Заменим данное смешанное число 323 при помощи дроби 113, тогда получим, что 323·415=113·415=4·113·15=4445.

Ответ: 323·415=4445.

Сложение и вычитание смешанных чисел (Вольфсон Г.И.). Вычитание смешанных дробей

Решение сложных примеров правильно – непосильная задача для тех, кто не понимает в математике элементарных правил и законов. Сложение и вычитание смешанных чисел по праву можно отнести к сложным примерам. Однако, при правильном разборе самих чисел можно легко проводить любые действия.

Что это такое?

Смешанное число – это комбинация целой части и дробной. К примеру, имеется 2 и 3, из них 2 – это простое число, а вот 3 – это уже смешанное, где 3 – целая часть, а – дробная. Представленные разновидности складываются и вычитаются по-разному, но не влекут сложностей в самостоятельном решении примеров.

Полноценный разбор примера

Для полноценного представления сущности смешанного значения следует привести в пример задачу, которая поможет отобразить смысл повествования задуманного. Итак, Вася проехал круг вокруг школы на велосипеде за 1 минуту и 30 секунд, а потом еще круг прошел пешком за 3 минуты и 30 секунд. Сколько времени затратил Вася на всю прогулку вокруг школы?

Этот пример направлен на сложение смешанных чисел, которые предварительно в данном случае даже не придется переводить в секунды. Получается, что сложение осуществляется путем отдельного прибавления минут и секунд. В результате получим следующий результат:

1. Сложение минут – 1+3=4.
2. Сложение секунд = 30+30=60 секунд = 1 минута.
3. Общее значение 4 минуты+1 минута = 5 минут.

Если исходить из математического отображения, то представленные действия можно выделить в одном выражении:

Из представленного выше становится понятным, что складывать смешанные числа следует в отдельности по частям – сначала целые части, а затем дробные. Если дробное число дает еще целое значение, его также складывают с целым полученным ранее значением. К полученному целому значению прибавляют дробную часть – получается смешанное число.

Правила сложения

Для закрепления изученного следует привести правило сложения смешанных чисел. Здесь следует воспользоваться следующей последовательностью:

1. Для начала отделить от значения части – на целую и дробную.
2. Теперь сложить целые части.
3. Далее сложить дробные.
4. Если из дробного числа можно извлечь еще целую часть – перевести в смешанное значение – значит, проводят подобную разбивку.
5. Полученную целую часть из дробного значения складывают с целым ранее полученным значением.
6. К целой части прибавляют дробную.

Для пояснения следует привести несколько примеров:

Сложение смешанных чисел происходит по тому же алгоритму, что и вычитание, поэтому далее будет подробно рассмотрено следующее действие.

Правила вычитания

Как и в первом случае, для вычитания смешанных значений существует правило, но оно в корне отличается от предыдущей последовательности. Итак, здесь следует придерживаться последовательности:

1. Пример на вычитание представляется в виде: уменьшаемое – вычитаемое = разность.
2. В связи с приведенным уравнением следует предварительно сравнить дробные части представленных чисел.
3. Если у уменьшаемого дробная часть больше, значит, вычитание проводится по тому же признаку, что и при сложении – сначала вычитаются целые, а затем дробные значения. Оба результата складывают.
4. Если у уменьшаемого дробное значение меньше, значит, их предварительно переводят в неправильную дробь и осуществляют стандартное вычитание.
5. Из полученной разницы определяют целую часть и дробную.

Для пояснения следует привести следующие примеры:

Из представленной статьи стало понятным, как проводить сложение и вычитание смешанных чисел. В описанном выше примере видно, что не всегда приходится видоизменять числа – переводить их из простых дробей в сложные. Зачастую достаточно просто сложить или вычесть целые и дробные значения по отдельности, что для человека с большим опытом можно легко провести в уме.

В статье подробно рассмотрены примеры, решение которых представлено в полном соответствии с математическими правилами и основами. Разобраны отдельные ситуации, для каждого приведен пример видоизменений, с которыми можно столкнуться в решении задач и сложных примеров.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Учитель математики Кузнецова Марина Николаевна Сложение и вычитание смешанных чисел

Домашнее задание

Астрид Линдгрен

Устный счет 1 0

На какие группы мы можем разделить данные дроби?

На какие группы мы можем разделить данные дроби? Правильные дроби Неправильные дроби

Найдите лишний пример:

Сложение и вычитание смешанных чисел. Цель урока: Научится выполнять сложение и вычитание смешанных чисел.

Справка 1. К целой части прибавить целую часть. К полученной целой части прибавить дробную часть. Сформулировать правило сложения смешанного числа с натуральным. 2. К целой части прибавить целую часть. К дробной части прибавить дробную часть К полученной целой части прибавить полученную дробную часть. Сформулировать правило сложения смешанных чисел. 3. Из целой части вычесть целую часть. Из дробной части вычесть дробную часть К оставшейся целой части прибавить оставшуюся дробную часть. Сформулировать правило вычитания смешанных чисел. 4. Если дробная часть уменьшаемого меньше дробной части вычитаемого. Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби. Полученную дробь складываем с дробной частью уменьшаемого. Вычитаем отдельно целые части и дробные части. К оставшейся целой части прибавляем оставшуюся дробную часть. Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.

Чтобы сложить два смешанных числа, нужно сложить отдельно их целые и дробные части, сложить полученные результаты. Чтобы вычесть из смешанного числа смешанное число, нужно отдельно вычесть их целые и дробные части, сложить полученные результаты.

= (3 + 2) + () = 5 + = 5 – = (5 – 3) + ()= 2 + = 2

Физкультминутка Потрудились — отдохнём, Встанем, глубоко вздохнём. Руки в стороны, вперёд, Влево, вправо поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили.

4 – В 7 – О 3 – У 4 – Е 5 – Х 4 – П 5 – С У С П Е В Х О

Решение задач Стр. 175, № 1115 Стр. 175, № 1116

Что такое смешанное число? Чему вы сегодня научились? Как сложить смешанные числа? Как вычесть смешанные числа?

Домашнее задание: П. 29 (учить правила) Стр. 178, № 1136, 1137

Спасибо за урок!

Предварительный просмотр:

Учитель математики Кузнецова М.Н.

Урок в 5 классе по теме:

Сложение и вычитание смешанных чисел.

Цели:

Учебные:

1. Познакомить учащихся с алгоритмами сложения и вычитания смешанных чисел путем включения учащихся в практическую деятельность.
2. Продолжить работу по развитию вычислительных навыков.

Развивающие:

1. Развитие умения решать задачи изученных видов.
2. Создание условий для формирования мыслительных операций.

Воспитательная:

1. Воспитывать чувство товарищества и взаимовыручки.

Ход урока

I. Организационный момент.

Посмотрите, все ль в порядке:

Книжка, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

II. Проверка домашнего задания.

Дата, классная работа.

Дома вы выполнили задание. Вы разгадали ребус. (Слайд 1)И какой же ответ? (Астрид Линдгрен) (Слайд 2)

Д/з. 1. Выделить целую часть и расположить в порядке возрастания. 18 -И 7 -А 14 -Р 11 -Т 9 -С 21 -Д 5 5 5 5 5 5 1 2/5 1 4/5 2 1/5 2 4/5 3 3/5 4 1/5 А С Т Р И Д 2. Запиши в виде неправильной дроби и расшифруй. 41/2-Д 2 3/7-Н 4 9/10-Р 32/5-И 14/6-Г 2 2/8-Е 3 ¾ -Л 5 1/6-Н 15 4 17 5 17 7 9 2 10 6 49 10 20 8 31 6

А кто такая Астрид Линдгрен? Какую сказку написала эта шведская писательница? («Малыш и Карлсон») (Слайд 3)

Но к сожалению Карлсон улетел, но оставил письмо.

Письмо: Ребята, я полетел искать старательных, внимательных, трудолюбивых, дружных, умеющих придти на помощь ребят. Найду – вернусь.)

Ребята, давайте быстрее встретимся с другом, для этого выполним математические задания. Если мы их выполним правильно, то у нас к возвращению Карлсона — сладкоежки получится большой общий торт. И у каждого – свой маленький.

Первое задание.

III. Устный счет

1. Решение цепочек (стр. 175, № 1111).

2/5 + 1/5 + 2/5 – 3/7 – 1/7 = 3/7

5/17 + 7/17 – 12/17 + 7/9 – 4/9 = 3/9

2. На какие группы мы можем разделить данные дроби: (правильные и неправильные дроби) (Слайд 6)

9 5 8 10 24 15 7 12

8 12 11 6 13 16 7 25

Какие дроби называются правильными?

Какие дроби называются неправильными?

Как по-другому представить неправильные дроби?

Из чего состоит смешанное число?

(Кусок торта.)

IV. Актуализация знаний.

Найдите лишний пример:

2/8 + 3/8 14/12 – 7/12 7/9 + 1/9 3 1/7 + 2 3/7 18/27 -5/27

Попробуйте сформулировать тему урока (Сложение смешанных чисел) (Слайд8)

Сегодня на уроке мы научимся выполнять сложение и вычитание смешанных чисел, для достижения этой цели сформулируем правила.

V. Исследование

Учащиеся работают в группах, выполняя задания различной сложности. Все учащиеся делятся на 4 группы. На парту каждой группы раздается задание и справочный материал. Для решения задания нужно выбрать соответственное правило.

Задание 1 . Выполнение сложения 2 ½ + 3

Задание 2. Выполнение сложения 2 1/4 + 1 2/4

Задание 3 . Выполнение вычитания 3 5/6 – 3/6

Задание 4. Выполнение вычитания 5 1/4 — 3 2/4

Справка

1. К полученной целой части прибавить дробную часть.
2. Сформулировать правило сложения смешанного числа с натуральным.

1. К целой части прибавить целую часть.
2. К дробной части прибавить дробную часть
3. К полученной целой части прибавить полученную дробную часть.
4. Сформулировать правило сложения смешанных чисел.

1. Из целой части вычесть целую часть.
2. Из дробной части вычесть дробную часть
3. К оставшейся целой части прибавить оставшуюся дробную часть.
4. Сформулировать правило вычитания смешанных чисел.

1. Если дробная часть уменьшаемого меньше дробной части вычитаемого.
2. Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби.
3. Полученную дробь складываем с дробной частью уменьшаемого.
4. Вычитаем отдельно целые части и дробные части.
5. К оставшейся целой части прибавляем оставшуюся дробную часть.
6. Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.

VI. Обмен информацией .

Вы рассмотрели правила сложения и вычитания смешанных чисел. Что общего у них? (Действия выполняются сначала с целыми числами, затем с дробными частями.)

Сформулируйте правило сложения смешанных чисел. (Слайд 9)

Сформулируйте правило вычитания смешанных чисел. (Слайд 10)

Стр. 174 учебника, правило

(Кусок торта.)

VII. Применение

— Вернемся к примеру:

3 1/7 + 2 3/7= (3+2)+(1/7+3/7)=5+4/7=54/7

Как убедиться, что сложение выполнено правильно? (Вычитанием). Сделать проверку.

54/7-31/7=(5-3)+(4/7-1/7)= 2+3/7= 23/7

(Кусок торта.)

VIII. Физкультминутка (Слайд)

Потрудились — отдохнём,

Встанем, глубоко вздохнём.

Руки в стороны, вперёд,

Влево, вправо поворот.

Три наклона, прямо встать.

Руки вниз и вверх поднять.

Руки плавно опустили,

Всем улыбки подарили.

IX. Закрепление изученного материала

1. Карлсон прислал телеграмму, но все слова перепутались. Давайте решим примеры и соотнесем их с ответами. (Слайд 11)

3 7/13 – 4/13= 4 – В

5 2/5+1/5= 7 4/6 – О

10 2/3-6= 3 3/13 – У

2 2/7+2 4/7= 4 6/7 – Е

8 5/9-3= 5 5/9 – Х

3/6+7 1/6 = 4 2/3 – П

7 4/5-3 4/5= 5 3/5 – С

(Кусок торта.)

«Охота за пятерками»

2. Работа над задачами.

а) Стр. 175, №1115.

1. Прочитайте задачу.
2. Сколько конфет в одной коробке?
3. Сколько конфет в другой коробке?
4. Как ответить на вопрос задачи?
5. Решите задачу. Прочитайте ответ. (В двух коробках 4 4/8 кг конфет.)

б) Стр. 175, № 1116.

1. Чему равна длина красной ленты?
2. Что сказано про длину белой?
3. Что значит на 2 1/5 м короче?
4. Как будете решать эту задачу?

Решите. Прочитайте ответ. (Длина белой ленты 1 2/5 метра.)

(Кусок торта.)

Вы – замечательные ученики: старательные, внимательные, дружные, помогаете друг другу.

(прилетел Карлсон) Карлсон увидел, что вы такие ребята, каких он искал, и вернулся. Мы дарим ему торт.

X. Итог урока (вопросы Карлосона).

1. Что такое смешанное число?
2. Чему вы сегодня научились? (Складывать и вычитать смешанные числа.)
3. Как сложить смешанные числа?
4. Как вычесть смешанные числа?

Это вам поможет справиться с домашним заданием.

XI. Домашнее задание: Стр. 178, № 1136,1137

XII. Рефлексия.

Соберите заработанные кусочки в тортик. (3-5 частей – «5»)

Учитель оценивает работу учащихся. (Мордашка). (Слайд 13)

Смешанные дроби также, как и простые дроби можно вычитать. Чтобы отнять смешанные числа дробей нужно знать несколько правил вычитания. Изучим эти правила на примерах.

Вычитание смешанных дробей с одинаковыми знаменателями.

Рассмотрим пример с условием, что уменьшаемое целое и дробная часть больше соответственно вычитаемого целой и дробной части. При таких условиях вычитание происходит отдельно. Целую часть вычитаем из целой части, а дробную часть из дробной .

Рассмотрим пример:

Выполните вычитание смешанных дробей \(5\frac{3}{7}\) и \(1\frac{1}{7}\).

\(5\frac{3}{7}-1\frac{1}{7} = (5-1) + (\frac{3}{7}-\frac{1}{7}) = 4\frac{2}{7}\)

Правильность вычитания проверяется сложением. Сделаем проверку вычитания:

\(4\frac{2}{7}+1\frac{1}{7} = (4 + 1) + (\frac{2}{7} + \frac{1}{7}) = 5\frac{3}{7}\)

Рассмотрим пример с условием, когда дробная часть уменьшаемого меньше соответственно дробной части вычитаемого. В таком случае мы занимаем единицу у целого в уменьшаемом.

Рассмотрим пример:

Выполните вычитание смешанных дробей \(6\frac{1}{4}\) и \(3\frac{3}{4}\).

У уменьшаемого \(6\frac{1}{4}\) дробная часть меньше чем у дробной части вычитаемого \(3\frac{3}{4}\). То есть \(\frac{1}{4}

\(\begin{align}&6\frac{1}{4}-3\frac{3}{4} = (6 + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {1} + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {\frac{4}{4}} + \frac{1}{4})-3\frac{3}{4} = (5 + \frac{5}{4})-3\frac{3}{4} = \\\\ &= 5\frac{5}{4}-3\frac{3}{4} = 2\frac{2}{4} = 2\frac{1}{4}\\\\ \end{align}\)

Следующий пример:

\(7\frac{8}{19}-3 = 4\frac{8}{19}\)

Вычитание смешанного дроби из целого числа.

Пример: \(3-1\frac{2}{5}\)

Уменьшаемое 3 не имеет дробной части, поэтому сразу отнять мы не сможем. Займем у целой части у 3 единицу, а потом выполним вычитание. Единицу мы запишем как \(3 = 2 + 1 = 2 + \frac{5}{5} = 2\frac{5}{5}\)

\(3-1\frac{2}{5}= (2 + \color{red} {1})-1\frac{2}{5} = (2 + \color{red} {\frac{5}{5}})-1\frac{2}{5} = 2\frac{5}{5}-1\frac{2}{5} = 1\frac{3}{5}\)

Вычитание смешанных дробей с разными знаменателями.

Рассмотрим пример с условием, если дробные части уменьшаемого и вычитаемого с разными знаменателями. Нужно привести к общему знаменателю, а потом выполнить вычитание .

Выполните вычитание двух смешанных дробей с разными знаменателями \(2\frac{2}{3}\) и \(1\frac{1}{4}\).

Общим знаменателем будет число 12.

\(2\frac{2}{3}-1\frac{1}{4} = 2\frac{2 \times \color{red} {4}}{3 \times \color{red} {4}}-1\frac{1 \times \color{red} {3}}{4 \times \color{red} {3}} = 2\frac{8}{12}-1\frac{3}{12} = 1\frac{5}{12}\)

Вопросы по теме:
Как вычитать смешанные дроби? Как решать смешанные дроби?
Ответ: нужно определиться к какому типу относиться выражение и по типу выражения применять алгоритм решения. Из целой части вычитаем целое, у дробной части вычитаем дробную часть.

Как из целого числа вычесть дробь? Как от целого числа отнять дробь?
Ответ: у целого числа нужно занять единицу и записать эту единицу в виде дроби

\(4 = 3 + 1 = 3 + \frac{7}{7} = 3\frac{7}{7}\),

а потом целое отнять от целого, дробную часть отнять от дробной части. Пример:

\(4-2\frac{3}{7} = (3 + \color{red} {1})-2\frac{3}{7} = (3 + \color{red} {\frac{7}{7}})-2\frac{3}{7} = 3\frac{7}{7}-2\frac{3}{7} = 1\frac{4}{7}\)

Пример №1:
Выполните вычитание правильной дроби из единицы: а) \(1-\frac{8}{33}\) б) \(1-\frac{6}{7}\)

Решение:
а) Представим единицу как дробь со знаменателем 33. Получим \(1 = \frac{33}{33}\)

\(1-\frac{8}{33} = \frac{33}{33}-\frac{8}{33} = \frac{25}{33}\)

б) Представим единицу как дробь со знаменателем 7. Получим \(1 = \frac{7}{7}\)

\(1-\frac{6}{7} = \frac{7}{7}-\frac{6}{7} = \frac{7-6}{7} = \frac{1}{7}\)

Пример №2:
Выполните вычитание смешанной дроби из целого числа: а) \(21-10\frac{4}{5}\) б) \(2-1\frac{1}{3}\)

Решение:
а) Займем у целого числа 21 единицу и распишем так \(21 = 20 + 1 = 20 + \frac{5}{5} = 20\frac{5}{5}\)

\(21-10\frac{4}{5} = (20 + 1)-10\frac{4}{5} = (20 + \frac{5}{5})-10\frac{4}{5} = 20\frac{5}{5}-10\frac{4}{5} = 10\frac{1}{5}\\\\\)

б) Займем у целого числа 2 единицу и распишем так \(2 = 1 + 1 = 1 + \frac{3}{3} = 1\frac{3}{3}\)

\(2-1\frac{1}{3} = (1 + 1)-1\frac{1}{3} = (1 + \frac{3}{3})-1\frac{1}{3} = 1\frac{3}{3}-1\frac{1}{3} = \frac{2}{3}\\\\\)

Пример №3:
Выполните вычитание целого числа из смешанной дроби: а) \(15\frac{6}{17}-4\) б) \(23\frac{1}{2}-12\)

а) \(15\frac{6}{17}-4 = 11\frac{6}{17}\)

б) \(23\frac{1}{2}-12 = 11\frac{1}{2}\)

Пример № 4:
Выполните вычитание правильной дроби из смешанной дроби: а) \(1\frac{4}{5}-\frac{4}{5}\)

\(1\frac{4}{5}-\frac{4}{5} = 1\\\\\)

Пример №5:
Вычислите \(5\frac{5}{16}-3\frac{3}{8}\)

\(\begin{align}&5\frac{5}{16}-3\frac{3}{8} = 5\frac{5}{16}-3\frac{3 \times \color{red} {2}}{8 \times \color{red} {2}} = 5\frac{5}{16}-3\frac{6}{16} = (5 + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {1} + \frac{5}{16})-3\frac{6}{16} = \\\\ &= (4 + \color{red} {\frac{16}{16}} + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {\frac{21}{16}})-3\frac{3}{8} = 4\frac{21}{16}-3\frac{6}{16} = 1\frac{15}{16}\\\\ \end{align}\)

теория и практика на примерах

Решение сложных примеров правильно – непосильная задача для тех, кто не понимает в математике элементарных правил и законов. Сложение и вычитание смешанных чисел по праву можно отнести к сложным примерам. Однако, при правильном разборе самих чисел можно легко проводить любые действия.

Что это такое?

Смешанное число – это комбинация целой части и дробной. К примеру, имеется 2 и 3, из них 2 – это простое число, а вот 3 – это уже смешанное, где 3 – целая часть, а  – дробная. Представленные разновидности складываются и вычитаются по-разному, но не влекут сложностей в самостоятельном решении примеров.

Полноценный разбор примера

Для полноценного представления сущности смешанного значения следует привести в пример задачу, которая поможет отобразить смысл повествования задуманного. Итак, Вася проехал круг вокруг школы на велосипеде за 1 минуту и 30 секунд, а потом еще круг прошел пешком за 3 минуты и 30 секунд. Сколько времени затратил Вася на всю прогулку вокруг школы?

Этот пример направлен на сложение смешанных чисел, которые предварительно в данном случае даже не придется переводить в секунды. Получается, что сложение осуществляется путем отдельного прибавления минут и секунд. В результате получим следующий результат:

1. Сложение минут – 1+3=4.
2. Сложение секунд = 30+30=60 секунд = 1 минута.
3. Общее значение 4 минуты+1 минута = 5 минут.

Если исходить из математического отображения, то представленные действия можно выделить в одном выражении:

Из представленного выше становится понятным, что складывать смешанные числа следует в отдельности по частям – сначала целые части, а затем дробные. Если дробное число дает еще целое значение, его также складывают с целым полученным ранее значением. К полученному целому значению прибавляют дробную часть – получается смешанное число.

Правила сложения

Для закрепления изученного следует привести правило сложения смешанных чисел. Здесь следует воспользоваться следующей последовательностью:

1. Для начала отделить от значения части – на целую и дробную.
2. Теперь сложить целые части.
3. Далее сложить дробные.
4. Если из дробного числа можно извлечь еще целую часть – перевести в смешанное значение – значит, проводят подобную разбивку.
5. Полученную целую часть из дробного значения складывают с целым ранее полученным значением.
6. К целой части прибавляют дробную.

Для пояснения следует привести несколько примеров:

Сложение смешанных чисел происходит по тому же алгоритму, что и вычитание, поэтому далее будет подробно рассмотрено следующее действие.

Правила вычитания

Как и в первом случае, для вычитания смешанных значений существует правило, но оно в корне отличается от предыдущей последовательности. Итак, здесь следует придерживаться последовательности:

1. Пример на вычитание представляется в виде: уменьшаемое – вычитаемое = разность.
2. В связи с приведенным уравнением следует предварительно сравнить дробные части представленных чисел.
3. Если у уменьшаемого дробная часть больше, значит, вычитание проводится по тому же признаку, что и при сложении – сначала вычитаются целые, а затем дробные значения. Оба результата складывают.
4. Если у уменьшаемого дробное значение меньше, значит, их предварительно переводят в неправильную дробь и осуществляют стандартное вычитание.
5. Из полученной разницы определяют целую часть и дробную.

Для пояснения следует привести следующие примеры:

Из представленной статьи стало понятным, как проводить сложение и вычитание смешанных чисел. В описанном выше примере видно, что не всегда приходится видоизменять числа – переводить их из простых дробей в сложные. Зачастую достаточно просто сложить или вычесть целые и дробные значения по отдельности, что для человека с большим опытом можно легко провести в уме.

В статье подробно рассмотрены примеры, решение которых представлено в полном соответствии с математическими правилами и основами. Разобраны отдельные ситуации, для каждого приведен пример видоизменений, с которыми можно столкнуться в решении задач и сложных примеров.

Сложение смешанных чисел. Вычитание смешанных чисел

Приветствие со школьниками, определение отсутствующих. Сообщение темы и цели урока, ожидаемых результатов.

Краткий опрос учащихся с целью повторения пройденного материала по стратегии «мозговой штурм»:

Дайте определения следующих понятий:

• обыкновенная дробь;

• числитель;

• знаменатель;

• наименьший общий делитель;

• правильная дробь;

• неправильная дробь.

Как производится сложение обыкновенных дробей?

Как производится вычитание обыкновенных дробей?

Определение. Если обыкновенная дробь записана в виде , тагда такую дробь называют смешанной дробью, при этом: a – целая часть дроби, b – числитель дроби, c – знаменатель дроби.

Для того чтобы перевести неправильную дробь в правильную, надо:

1. разделить с остатком числитель на знаменатель;

2. в качестве целой части взять неполное частное

3. остаток будет числителем, а делитель – знаменателем дробной части;

4. результат записываем в виде .

Групповая работа.

Ученики делятся на 4 группы. Учитель предлаает расчитаться на 1, 2, 3, 4.

По стретегии «Тур по галлерее» каждая группа по материалам учителя готовят свои постеры.

І группа.

Сложение смешанных дробей с одинаковым знаменателем.

Пример №1.

Чтобы найти сумму смешанных дробей с одинаковыми знаменателеми, надо:

1) найти сумму их целых частей, сумму их дробных частей;

2) записать результат в виде смешанного числа.

Вычитание смешанных дробей с одинаковым знаменателем.

Пример №2.

Чтобы найти разность смешанных дробей с одинаковыми знаменателеми, надо:

1) найти разность целых частей, разность их дробных частей;

2) записать результат в виде смешанного числа.

Внимание! Если числитель дробной части уменьшаемого менье числителя дробной части вычитаемого, тогда:

1. Вычесть 1 из целой части уменьшаемой дроби, ее представить в виде дроби.

Например:Если уменьшаемое равно , тогдазаписываем его в виде .

1. Сложить 1 в дробном виде с дробной частью смешанного числа и представить результат в виде неправильной дроби:

1. Представить результат в виде смешанной дроби где дробная часть является неправильной дробью:

. То есть, .

Пример №3.

ІІ группа.

Сложение смешанных дробей с разными знаменателями

Пример №1.

Либо:

Чтобы найти сумму смешанных дробей с разными знаменателеми, надо:

1) привести к наименьшему общему знаменателю дробные части смешанных чисел;

2) сложить смешанные дроби с общим знаменателем.

Вычитание смешанных дробей с разными знаменателями

Чтобы найти разност смешанных дробей с разными знаменателеми, надо:

1) привести к наименьшему общему знаменателю дробные части смешанных чисел;

2) вычесть смешанные дроби с общим знаменателем.

Пример №2.

Либо:

Пример №3.

.

ІІІ группа.

Сложение наутрального числа и смешанной дроби.

Пример №1.

Чтобы сложить смешанное число и натуральное число, надо к целой части смешанного числа прибавить данное натуральное число, а дробную часть оставить без изменения.

Вычитание смешанного числа из натурального числа.

Чтобы из натурального числа вычесть смешанное число, надо натуральное число представить в виде смешанной дроби.

Пример №2.

Либо:

ІV группа.

Сложение смешанного числа и обыкновенной дроби.

Чтобы сложить смешанное число и обыкновенную дробь, надо:

1. Привести их к общему знаменателю;

2. Сложить дробные части и присоединить к целой части.

Пример №1.

Вычитание натурального числа из смешанноой дроби.

Чтобы вычесть натуральное число из смешанной дроби, надо из целой части смешанной дроби вычесть натуральное число и присоединить дробную часть.

Пример №2.

Либо:

.

Разминка: «Лучи солнца». Раздаются белые листы формата А4, затем по поручению учителя рисуются круг, по краям 10 треугольников, внутри 2 круга поменьше, 1 полуокружность, 1 отрезок. В итоге получается изображение улыбающегося солнца. Дети с хорошим настроением продолжают урок.

Далее от каждой группы выбирается ученик-эксурсовод. Постеры вывешиваются по классу и группам предлагается пройти по галлерее, используя маршрутные листы. Экскурсоводы рассказывают о своей работе другим ученикам, отвечают на вопросы других групп.

Проводится оценивание работы групп. Оценивание групповой работы проходит с помощью стратегии «Две звезды, одно пожелание». Две группы отмечают то, что понравилось более всего, одна выссказывает пожелания по улучшению презентации.

Парная работа.

Ученикам предлагаются задания по уровням сложности А, В, С. Каждая пара определяет уровень сложности индивидуально.

Проверка осуществляется путем показа правильных ответов на презентации.

А. Вычислите

Б. Решите задачу.

Из 12 м рулона материи первый раз отрезали а затем еще м материи. Сколько метров материи осталось в рулоне?

С. Решите уравнение: .

По окончании проверки учитель опрашивает учащихся:

1. Что получилось при решении?

2. Какие возникли сложности?

Формативная оценочная работа

Учащимся предлагается выполнить работу, результаты которой будут озвучены на следующем уроке. Для тех кто выполнит полностью все три задания, предлагается дополнительное 4 задание

ФИО ученика:

Класс: 5 « » Дата:

Цели обучения: 5.1.1.11 зание определения смешанных чисел; 5.1.2.13 перевод неправильной дроби в смешанную и смешанной в неправильную; 5.1.2.20 сложение и вычитание смешанных чисел

№1. Определите смешанные дроби: №2. Представьте смешанные числа из №1 в виде неправилной дроби. №3.Выполните действия: . №4*. Выполните вычитание: 5- . Критерии оценивания: 1) определяет все смешанные числа; 2) переводит все смешанные числа в неправильные дроби; 3) выполняет вычитание смешанного числа из натурального; 4) выполняет вычитание смешанных чисел с разными знаменателями; 5) складывает смешанные числа с разными знаменателями.

Учащиеся производят рефлексию по пройенной теме по стратегии «Незаконченные фразы»

До этого я умел: ……………………………………………………………………………………

Сегодня я научился: ……………………………………………………………………………………

По сегодняшней теме мне осталось неясным: ………………………………………………………………………….. ………….

дробей — сложение и вычитание смешанных чисел

Как Как вы помните, смешанное число состоит из целого числа и дробной части. Любое смешанное число также можно записать как неправильную дробь, в которой числитель больше знаменателя, как показано в следующем примере:

Пример 1

Добавить смешанный чисел, складываем сначала целые числа, а затем дроби.

Если сумма дробь — неправильная дробь, тогда мы меняем ее на смешанное число. Вот пример. Сумма целых чисел 3 и 1 равна 4. Дроби 2/5 и 3/5, сложите до 5/5, или 1. Добавьте 1 к 4, чтобы получить ответ, который равен 5.

Пример 2

Если знаменатели дробей различны, то сначала найдите эквивалентные дроби с общий знаменатель перед сложением.Например, добавим 4 1/3 к 3 2/5. Используя изученные нами методы, вы можете найти наименьший общий знаменатель из 15. Ответ 7/15.

Вычитание смешанные числа очень похожи на их добавление. Но что происходит, когда дробное часть вычитаемого числа больше дробной части числа, из которого вы вычитаете?

Вот пример: вычтем 3 3/5 из 4 1/3.Сначала вы найдете ЖК-дисплей; вот 15.

4 1/3 — 3 3/5 4 15/5 — 3 15/9	Написать обе дроби как эквивалентные дроби со знаминателем 15.
3 + 1 5/15 — 3 9/15 3 + 20/15 — 3 9/15	С вы пытаетесь вычесть большую дробь из меньшей, вам нужно «позаимствовать» единицу из целого числа 4, изменить его на 15/15 и добавить его к дроби.
3 20/15 — 3 9/15 15/11	Сейчас задача становится 3 20/15 минус 3 9/15, и ответ — 11/15.

назад наверх

Сложение и вычитание смешанных дробей

	Быстрое определение: смешанная дробь — это целое число и дробная часть вместе, , например 1 3 4
1 3 / 4
(одна и три четверти)

Чтобы упростить их сложение и вычитание, просто сначала преобразуйте в неправильные дроби:

	Быстрое определение: неправильная дробь имеет верхнее число , большее или равное нижнему числу , , например 7 4 или же 4 3 (это « верхняя »)
7 / 4
(семь четвертей или семь четвертей)

Вы видите, что 1 3 4 совпадает с 7 4 ?

Другими словами, «одна и три четверти» — это то же самое, что «семь четвертей».

Добавление смешанных фракций

Я считаю, что это лучший способ добавить смешанные фракции:

(Вы можете прочитать, как преобразовать из или в смешанные дроби)

Пример: что такое 2

3 4 + 3 1 2 ?

Преобразовать в неправильные дроби:

2 3 4 знак равно 11 4

3 1 2 знак равно 7 2

Общий знаменатель 4:

11 4 остается как 11 4

7 2 становится 14 4
(путем умножения верха и низа на 2)

Теперь добавьте:

11 4 + 14 4 знак равно 25 4

Преобразовать обратно в смешанные дроби:

25 4 = 6 1 4

Когда вы набираетесь опыта, вы можете делать это быстрее, как в этом примере:

Пример: Что такое 3

5 8 +1 3 4

Преобразуйте их в неправильные дроби:

3 5 8 знак равно 29 8
1 3 4 знак равно 7 4

Сделайте тот же знаменатель: 7 4 становится 14 8 (путем умножения верха и низа на 2)

И добавить:

29 8 + 14 8 знак равно 43 8 = 5 3 8

Вычитание смешанных дробей

Просто следуйте тому же методу, но вместо сложения вычтите:

Пример: что такое 15

3 4 — 8 5 6 ?

Преобразовать в неправильные дроби:

15 3 4 знак равно 63 4

8 5 6 знак равно 53 6

Общий знаменатель 12:

63 4 становится 189 12

53 6 становится 106 12

Теперь вычесть:

189 12 — 106 12 знак равно 83 12

Преобразовать обратно в смешанные дроби:

83 12 = 6 11 12

Калькулятор смешанных чисел

Использование калькулятора

Выполняет математические вычисления со смешанными числами (смешанными дробями), выполняя операции с дробями, целыми числами, целыми числами, смешанными числами, смешанными дробями и неправильными дробями.Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.

Калькулятор смешанных чисел (также называемый смешанными дробями):

Этот онлайн-калькулятор выполняет простые операции с целыми числами, целыми числами, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения. Ответ дается в сокращенной дроби и в смешанном числе, если таковой существует.

Введите смешанные числа, целые числа или дроби в следующих форматах:

• Смешанные числа: введите 1 1/2, что составляет полтора или 25 3/32, что составляет двадцать пять и три тридцать секунд.Сохраняйте ровно один пробел между целым числом и дробью и используйте косую черту для ввода дробей. Вы можете ввести до 3 цифр для каждого целого числа, числителя или знаменателя (123 456/789).
• Целые числа: до 3 цифр.
• Дроби: введите 3/4, что составляет три четверти, или 3/100, что составляет три сотых. Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).

Сложение смешанных чисел по формуле сложения дробей

1. Преобразование смешанных чисел в неправильные дроби
2. Используйте алгебраическую формулу для сложения дробей:
   a / b + c / d = (ad + bc) / bd
3. Уменьшить дроби и, если возможно, упростить

Формула сложения дробей

ab + cd = (a × d) + (b × c) b × d

Пример

Сложить 1 2/6 и 2 1/4

126 + 214 = 86 + 94 = (8 × 4) + (9 × 6) 6 × 4 = 32 + 5424 = 8624 = 4312 = 3712

1 2/6 + 2 1/4 = 8/6 + 9/4 = (8 * 4 + 9 * 6) / 6 * 4 = 86/24

Итак, мы получаем 86/24 и упрощаем до 3 7/12

Вычитание смешанных чисел по формуле вычитания дробей

1. Преобразование смешанных чисел в неправильные дроби
2. Используйте алгебраическую формулу для вычитания дробей: a / b — c / d = (ad — bc) / bd
3. Уменьшить дроби и, если возможно, упростить

Формула вычитания дробей

ab − cd = (a × d) — (b × c) b × d

Пример

Вычтем 2 1/4 из 1 2/6

1 2/6 — 2 1/4 = 8/6 — 9/4 = (8 * 4 — 9 * 6) / 6 * 4 = -22/24

Уменьшите дробь, чтобы получить -11/12

Умножение смешанных чисел по формуле умножения дробей

1. Преобразование смешанных чисел в неправильные дроби
2. Используйте алгебраическую формулу для умножения дробей: a / b * c / d = ac / bd
3. Уменьшить дроби и, если возможно, упростить

Формула умножения дробей

ab × cd = a × cb × d

Пример

умножить 1 2/6 на 2 1/4

1 2/6 * 2 1/4 = 8/6 * 9/4 = 8 * 9/6 * 4 = 72/24

Уменьшите дробь, чтобы получить 3/1, и упростите до 3

Разделение смешанных чисел по формуле деления на дроби

1. Преобразование смешанных чисел в неправильные дроби
2. Используйте алгебраическую формулу для деления дробей: a / b ÷ c / d = ad / bc
3. Уменьшить дроби и, если возможно, упростить

Формула деления дробей

ab ÷ cd = a × db × c

Пример

разделить 1 2/6 на 2 1/4

1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8 * 4/9 * 6 = 32/54

Уменьшите дробь, чтобы получить 16/27

Связанные калькуляторы

Для выполнения математических операций с простыми правильными или неправильными дробями используйте нашу Калькулятор дробей.Этот калькулятор превращает неправильные дробные ответы в смешанные числа.

Если вы хотите упростить отдельную дробь до наименьших значений, используйте наш Упростите калькулятор дробей.

Для объяснения того, как множить числа, чтобы найти наибольший общий множитель (GCF), см. Калькулятор наибольшего общего коэффициента.

Если вы вручную упрощаете большие дроби, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целые числа и остатки.

Примечание:

Этот калькулятор выполняет расчет сокращения быстрее, чем другие, которые вы можете найти. Основная причина в том, что код использует теорему Евклида для сокращения дробей, которую можно найти на Математический форум: LCD, LCM.

Сложение смешанных чисел с общими знаменателями

Результаты обучения

• Используйте модель для сложения двух смешанных чисел с одинаковыми знаменателями
• Используйте два разных метода для сложения смешанных чисел с одинаковыми знаменателями

Модель сложения двух смешанных чисел с одинаковыми знаменателями

До сих пор мы складывали и вычитали правильные и неправильные дроби, но не смешанные числа.Давайте начнем с размышления о сложении смешанных чисел с использованием денег.
Если у Рона [latex] 1 [/ latex] доллар и [latex] 1 [/ latex] четверть, у него есть [latex] 1 \ frac {1} {4} [/ latex] доллар.
Если у Дона [latex] 2 [/ latex] доллара и [latex] 1 [/ latex] четверть, у него есть [latex] 2 \ frac {1} {4} [/ latex] доллара.
Что, если Рон и Дон сложат свои деньги? У них будет [латекс] 3 [/ латекс] доллара и [латекс] 2 [/ латекс] четверти. Они складывают доллары и складывают четвертинки. Это дает [latex] 3 \ frac {2} {4} [/ latex] доллара.Поскольку две четверти — это полдоллара, у них будет [латекс] 3 [/ latex] с половиной доллара или [латекс] 3 \ frac {1} {2} [/ latex] доллара.

[латекс] 1 \ frac {1} {4} [/ латекс]
+ [латекс] 2 \ frac {1} {4} [/ латекс]
[латекс] \ text {________} [/ латекс]
[ латекс] 3 \ frac {2} {4} = 3 \ frac {1} {2} [/ латекс]

Когда вы складывали доллары, а затем четверти, вы складывали целые числа, а затем складывали дроби.

[латекс] 1 \ frac {1} {4} +2 \ frac {1} {4} [/ latex]
Мы можем использовать дробные круги для моделирования того же примера:

		[латекс] 1 \ frac {1} {4} +2 \ frac {1} {4} [/ латекс]
Начните с [latex] 1 \ frac {1} {4} [/ latex].	одно целое и одно [латекс] \ frac {1} {4} [/ latex] куски		[латекс] 1 \ frac {1} {4} [/ латекс]
Добавьте еще [latex] 2 \ frac {1} {4} [/ latex].	две целые и одна [латекс] \ frac {1} {4} [/ латекс] штука		[латекс] + 2 \ frac {1} {4} [/ латекс]
Сумма:	три целых и два [латекс] \ frac {1} {4} [/ latex]		[латекс] 3 \ frac {2} {4} = 3 \ frac {1} {2} [/ латекс]

Выполнение упражнения по манипуляции математикой «Сложение / вычитание смешанных чисел» поможет вам лучше понять, как складывать и вычитать смешанные числа.

Пример

Модель [латекс] 2 \ frac {1} {3} +1 \ frac {2} {3} [/ latex] и укажите сумму.

Решение:
Мы будем использовать дробные круги, целые круги для целых чисел и кусочки [latex] \ frac {1} {3} [/ latex] для дробей.

два целых и один [латекс] \ frac {1} {3} [/ latex]		[латекс] 2 \ frac {1} {3} [/ латекс]
плюс одно целое и два [латекс] \ frac {1} {3} [/ latex] s		[латекс] + 1 \ frac {2} {3} [/ латекс]
сумма — три целых и три [латекс] \ frac {1} {3} [/ latex] s		[латекс] 3 \ frac {3} {3} = 4 [/ латекс]

Это то же самое, что и [латекс] 4 [/ латекс] целые.Итак, [латекс] 2 \ frac {1} {3} +1 \ frac {2} {3} = 4 [/ latex].

Пример

Модель [латекс] 1 \ frac {3} {5} +2 \ frac {3} {5} [/ latex] и выведите сумму как смешанное число.

Показать решение

Решение:
Мы будем использовать дробные круги, целые круги для целых чисел и кусочки [latex] \ frac {1} {5} [/ latex] для дробей.

одно целое и три [латекс] \ frac {1} {5} \ text {s} [/ latex]		[латекс] 1 \ frac {3} {5} [/ латекс]
плюс два целых и три [латекс] \ frac {1} {5} \ text {s} [/ latex].		[латекс] + 2 \ frac {3} {5} [/ латекс]
сумма — три целых и шесть [латекс] \ frac {1} {5} \ text {s} [/ latex]		[латекс] 3 \ frac {6} {5} = 4 \ frac {1} {5} [/ латекс]

Сложив целые круги и пятые части, мы получили сумму [latex] 3 \ frac {6} {5} [/ latex]. Мы видим, что [latex] \ frac {6} {5} [/ latex] эквивалентно [latex] 1 \ frac {1} {5} [/ latex], поэтому мы добавляем это к [latex] 3 [ / latex], чтобы получить [latex] 4 \ frac {1} {5} [/ latex].

Попробуй

Модель

и дайте сумму как смешанное число. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.

[латекс] 2 \ frac {5} {6} +1 \ frac {5} {6} [/ латекс]

Показать решение

[латекс] 4 \ frac {2} {3} [/ латекс]

Модель

и дайте сумму как смешанное число. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
[латекс] 1 \ frac {5} {8} +1 \ frac {7} {8} [/ латекс]

Показать решение

[латекс] 3 \ frac {1} {2} [/ латекс]

Сложить смешанные числа с одинаковыми знаменателями

Моделирование с помощью дробных кругов помогает проиллюстрировать процесс сложения смешанных чисел: мы складываем целые числа и складываем дроби, а затем, если возможно, упрощаем результат.

Сложите смешанные числа с общим знаменателем

Шаг 1. Сложите целые числа.
Шаг 2. Сложить фракции.
Шаг 3. По возможности упростите.

Пример

Добавьте: [латекс] 3 \ frac {4} {9} +2 \ frac {2} {9} [/ latex].

Решение:

	[латекс] 3 \ frac {4} {9} +2 \ frac {2} {9} [/ латекс]
Сложите целые числа.	[латекс] \ color {красный} {3} \ frac {4} {9} [/ латекс] [латекс] \ frac {+ \ color {red} {2} \ frac {2} {9}} {\ color {red} {5}} [/ latex]
Сложите дроби.	[латекс] 3 \ color {красный} {\ frac {4} {9}} [/ латекс] [латекс] \ frac {+2 \ color {red} {\ frac {2} {9}}} {5 \ color {red} {\ frac {6} {9}}} [/ latex]
Упростим дробь.	[латекс] 3 \ frac {4} {9} [/ латекс] [латекс] \ frac {+2 \ frac {2} {9}} {\ color {красный} {5 \ frac {6} {9}} = 5 \ frac {2} {3}} [/ латекс]

В приведенном выше примере сумма дробей была правильной. Теперь мы рассмотрим пример, в котором сумма является неправильной дробью.

Пример

Найдите сумму: [латекс] 9 \ frac {5} {9} +5 \ frac {7} {9} [/ latex].

Показать решение

Решение:

	[латекс] 9 \ frac {5} {9} +5 \ frac {7} {9} [/ латекс]
Сложите целые числа, а затем дроби.	[латекс] \ begin {array} {} \\ \ hfill 9 \ frac {5} {9} \\ \ hfill \ underset {\ text {_____}} {+ 5 \ frac {7} {9}} \ \ \ hfill 14 \ frac {12} {9} \ end {array} [/ latex]
Запишите [латекс] \ frac {12} {9} [/ latex] как неправильную дробь.	[латекс] 14 + 1 \ frac {3} {9} [/ латекс]
Доп.	[латекс] 15 \ frac {3} {9} [/ латекс]
Упростить.	[латекс] 15 \ frac {1} {3} [/ латекс]

В следующем видео мы показываем еще один пример сложения двух смешанных чисел.

Альтернативный метод сложения смешанных чисел — преобразовать смешанные числа в неправильные дроби, а затем сложить неправильные дроби. Этот метод обычно пишется горизонтально.

Пример

Сложите путем преобразования смешанных чисел в неправильные дроби: [латекс] 3 \ frac {7} {8} +4 \ frac {3} {8} [/ latex].

Показать решение

Решение:

	[латекс] 3 \ frac {7} {8} +4 \ frac {3} {8} [/ латекс]
Преобразовать в неправильные дроби.	[латекс] \ frac {31} {8} + \ frac {35} {8} [/ латекс]
Сложите дроби.	[латекс] \ frac {31 + 35} {8} [/ латекс]
Упростим числитель.	[латекс] \ frac {66} {8} [/ латекс]
Записываем смешанное число.	[латекс] 8 \ frac {2} {8} [/ латекс]
Упростим дробь.	[латекс] 8 \ frac {1} {4} [/ латекс]

Поскольку задача была задана в смешанной числовой форме, мы запишем сумму как смешанное число.

В таблице ниже сравниваются два метода сложения на примере выражения [latex] 3 \ frac {2} {5} +6 \ frac {4} {5} [/ latex].Какой способ ты предпочитаешь?

Смешанные числа	Неправильные дроби
[латекс] \ begin {array} {} \\ \\ \ hfill 3 \ frac {2} {5} \ hfill \\ \ hfill \ frac {+6 \ frac {4} {5}} {9 \ frac {6} {5}} \ hfill \\ \ hfill 9+ \ frac {6} {5} \ hfill \\ \ hfill 9 + 1 \ frac {1} {5} \ hfill \\ \ hfill 10 \ frac {1} {5} \ hfill \ end {array} [/ latex]	[латекс] \ begin {array} {} \\ \ hfill 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill \ frac {17} {5} + \ frac {34} {5} \ hfill \\ \ hfill \ frac {51} {5} \ hfill \\ \ hfill 10 \ frac {1} {5} \ hfill \ end {array} [/ latex]

2.6: Умножение и деление смешанных дробей

Мы начнем с определений правильных и неправильных дробей.

Правильные и неправильные дроби

Правильная дробь — это дробь, числитель которой меньше ее знаменателя. Неправильная дробь — это дробь, числитель которой больше знаменателя.

Например,

\ [\ frac {2} {3}, ~ — \ frac {23} {39}, \ text {и} \ frac {119} {127} \ nonumber \]

— это все примеры правильных дробей.С другой стороны,

\ [\ frac {4} {3}, ~ — \ frac {317} {123}, \ text {и} — \ frac {233} {101} \ nonumber \]

— это все примеры неправильных дробей.

Смешанная дробь ¹ — это часть целого числа, часть дроби.

Смешанные фракции

Число

\ [5 \ frac {3} {4} \ nonumber \]

называется смешанной фракцией . Это означает

\ [5 \ frac {3} {4} = 5 + \ frac {3} {4}. \ Nonumber \]

В смешанной дроби \ (5 \ frac {3} {4} \) 5 — это целая часть , а 3/4 — дробная часть .

Замена смешанных фракций на неправильные

У нас есть все инструменты, необходимые для преобразования смешанной фракции в неправильную. Начнем с примера.

Пример 1

Превратите смешанную дробь \ (4 \ frac {7} {8} \) в неправильную дробь.

Решение

Мы используем определение смешанной дроби, составляем эквивалентную дробь для целой части числа, затем складываем.

\ [\ begin {align} 4 \ frac {7} {8} = 4 + \ frac {7} {8} ~ & \ textcolor {red} {\ text {По определению.}} \\ = \ frac {4 \ cdot \ textcolor {red} {8}} {\ textcolor {red} {8}} + \ frac {7} {8} ~ & \ textcolor {red} {\ text { Эквивалентная дробь с LCD = 8.}} \\ = \ frac {4 \ cdot 8 + 7} {8} ~ & \ textcolor {red} {\ text {Добавьте числители над общим знаменателем.}} \\ = \ frac { 39} {8} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ End {align} \ nonumber \]

Таким образом, \ (4 \ frac {7} {8} \) равно 39/8.

Упражнение

Заменить \ (5 \ frac {3} {4} \) на неправильную дробь.

Ответ

23/4

Существует быстрый способ превратить смешанную дробь в неправильную.

Быстрый способ заменить смешанную фракцию на неправильную

Чтобы преобразовать смешанную дробь в неправильную, умножьте целую числовую часть на знаменатель, добавьте числитель, затем поместите результат над знаменателем.

Таким образом, чтобы быстро заменить \ (4 \ frac {7} {8} \) на неправильную дробь, умножьте целое число 4 на знаменатель 8, добавьте числитель 7, затем поместите результат над знаменателем. В символах это будет выглядеть так:

\ [4 \ frac {7} {8} = \ frac {4 \ cdot 8 + 7} {8}.\ nonumber \]

Именно так выглядит третий шаг в примере 1; мы просто избавляемся от большого количества работы.

Пример 2

Заменить \ (4 \ frac {2} {3} \) на неправильную дробь.

Решение

Возьмите \ (4 \ frac {2} {3} \), умножьте целую часть числа на знаменатель, добавьте числитель, затем поместите результат над знаменателем.

\ [4 \ frac {2} {3} = \ frac {4 \ cdot 3 + 2} {3} \ nonumber \]

Таким образом, результат

\ [4 \ frac {2} {3} = \ frac {14} {3}.\ nonumber \]

Упражнение

Заменить \ (7 \ frac {3 {8} \) на неправильную дробь.

Ответ

59/8

Промежуточный шаг в примере 2 очень легко проделать мысленно, позволяя пропустить промежуточный шаг и перейти непосредственно от смешанной дроби к неправильной дроби, не записывая ни единой части работы.

Пример 3

Не записывая никакой работы, используйте мысленную арифметику, чтобы заменить \ (- 2 \ frac {3} {5} \) на неправильную дробь.

Решение

Чтобы заменить \ (- 2 \ frac {3} {5} \) на неправильную дробь, игнорируйте знак минус, действуйте как прежде, затем ставьте знак минус перед полученной неправильной дробью. Итак, умножьте 5 на 2 и прибавьте 3. Положите результат 13 над знаменателем 5, а затем поставьте перед полученной неправильной дробью знак минус. То есть

\ [- 2 \ frac {3} {5} = — \ frac {13} {5}. \ Nonumber \]

Упражнение

Заменить \ (- 3 \ frac {5} {12} \) на неправильную дробь.

Ответ

−41/12

Замена неправильных фракций на смешанные

Первым шагом в изменении неправильной дроби 27/5 на смешанную дробь является запись неправильной дроби в виде суммы.

\ [\ frac {27} {5} = \ frac {25} {5} + \ frac {2} {5} \ nonumber \]

Упрощая уравнение 4.1, получаем

\ [\ begin {align} \ frac {27} {5} = 5 + \ frac {2} {5} \\ = 5 \ frac {2} {5} \ end {align} \ nonumber \]

Комментарий. Нельзя просто выбрать любую сумму. Сумма, используемая в уравнении 4.1, построена так, что первая дробь будет равна целому числу, а вторая дробь — правильной. Любая другая сумма не даст правильной смешанной дроби. Например, сумма

\ [\ frac {27} {5} = \ frac {23} {5} + \ frac {4} {5} \ nonumber \]

бесполезен, потому что 23/5 — это не целое число. Аналогично, сумма

\ [\ frac {27} {5} = \ frac {20} {5} + \ frac {7} {5} \ nonumber \]

никуда не годится.Несмотря на то, что 20/5 = 4 — целое число, вторая дробь 7/5 по-прежнему неверна.

Пример 4

Измените 25/9 на смешанную дробь.

Решение

Разбейте 25/9 на соответствующую сумму.

\ [\ begin {align} \ frac {25} {9} = \ frac {18} {9} + \ frac {7} {9} \\ = 2 + \ frac {7} {9} \\ = 2 \ frac {7} {9} \ end {align} \ nonumber \]

Упражнение

Измените 25/7 на смешанную дробь.

Ответ

\ (3 \ frac {4} {7} \).

Комментарий. Возникает закономерность. • В случае 27/5 обратите внимание, что 27, разделенное на 5, равно 5 с остатком 2. Сравните это с результатом смешанной дроби: 27/5 = 5 2 5. • В случае примера 4 обратите внимание, что 25, разделенное на 9, равно 2 с остатком 7. Сравните это с результатом смешанной дроби: 25/9 = 2 7 9. Эти наблюдения мотивируют следующую методику.

Быстрый способ заменить неправильную фракцию на смешанную

Чтобы преобразовать неправильную дробь в смешанную, разделите числитель на знаменатель.Частное будет целой частью смешанной дроби. Если вы поместите остаток над знаменателем, это будет дробная часть смешанной дроби.

Пример 5

Заменить 37/8 на смешанную дробь.

Решение

37 разделить на 8 дает 4, а остаток 5. То есть:

Частное превращается в целую часть числа, а остаток кладется на делитель. Таким образом,

\ [\ frac {37} {8} = 4 \ frac {5} {8}.\ nonumber \]

Примечание. Вы можете проверить свой результат с помощью «Быстрого способа заменить смешанную дробь на неправильную дробь». 8 умножить на 4 плюс 5 будет 37. Поместите это над 8, чтобы получить 37/8.

Упражнение

Заменить 38/9 на смешанную дробь.

Ответ

\ (4 \ frac {2} {9} \)

Пример 6

Измените −43/5 на смешанную дробь.

Решение

Игнорируйте знак минус и действуйте так же, как в примере 5.43 делить на 5 дает 8, а остаток 3.

Частное — это целая часть числа, затем мы кладем остаток на делитель. Наконец, поставьте перед знаком минус.

\ [- \ frac {43} {5} = -8 \ frac {3} {5} \ nonumber \]

Умножение и деление смешанных дробей

У вас есть все инструменты, необходимые для умножения и деления смешанных дробей. Сначала измените смешанные дроби на неправильные дроби, затем умножьте или разделите, как вы делали в предыдущих разделах.

¹ Смешанную дробь иногда называют смешанной числом .

Пример 7

Упростить: \ (- 2 \ frac {1} {12} \ cdot 2 \ frac {4} {5} \).

Решение

Изменить на неправильные дроби, разложить на множители, отменить и упростить.

\ [\ begin {align} -2 \ frac {1} {12} \ cdot 2 \ frac {4} {5} = — \ frac {25} {12} \ cdot \ frac {14} {5} ~ & \ textcolor {red} {\ text {Изменить на неправильные дроби.}} \\ = — \ frac {25 \ cdot 14} {12 \ cdot 5} ~ & \ textcolor {red} {\ begin {align} \ text {Умножение числителей; умножьте знаменатели.} \\ \ text {В отличие от знаков; продукт отрицательный.} \ end {align}} \\ = — \ frac {(5 \ cdot 5) \ cdot (2 \ cdot 7)} {2 \ cdot 2 \ cdot 3) \ cdot (5)} ~ & \ textcolor {red} {\ text {Prime factor.}} \\ = — \ frac {\ cancel {5} \ cdot 5 \ cdot \ cancel {2} \ cdot 7} {\ cancel {2} \ cdot 2 \ cdot 3 \ cdot \ cancel {5}} ~ & \ textcolor {red} {\ text {Отменить общие множители.}} \\ = — \ frac {35} {6} ~ & \ textcolor {red} {\ text { Умножьте числители и знаменатели.}} \ End {align} \ nonumber \]

Это совершенно хороший ответ, но если вы хотите получить ответ со смешанной дробью, 35, разделенное на 6, будет 5, а остаток — 5.Следовательно,

\ [-2 \ frac {1} {12} \ cdot 2 \ frac {4} {5} = -5 \ frac {5} {6}. \ Nonumber \]

Упражнение \ (\ PageIndex {1} \)

Упростить:

\ [- 3 \ frac {3} {4} \ cdot 2 \ frac {2} {5} \ nonumber \]

Ответ

−9

Пример 8

Упростить:

\ [- 4 \ frac {4} {5} \ div 5 \ frac {3} {5}. \ Nonumber \]

Решение

Изменять дроби на неправильные, инвертировать и умножать, множить, отменять и упрощать.

\ [\ begin {align} -4 \ frac {4} {5} \ div 5 \ frac {3} {5} = — \ frac {24} {5} \ div \ frac {28} {5} ~ & \ textcolor {red} {\ text {Изменить на неправильные дроби.}} \\ = — \ frac {24} {5} \ cdot \ frac {5} {28} ~ & \ textcolor {red} {\ text { Инвертировать и умножить.}} \\ = — \ frac {2 \ cdot 2 \ cdot 2 \ cdot 3} {5} \ cdot \ frac {5} {2 \ cdot 2 \ cdot 7} ~ & \ textcolor {red} {\ text {Prime factor.}} \\ = — \ frac {\ cancel {2} \ cdot \ cancel {2} \ cdot 2 \ cdot 3} {\ cancel {3}} \ cdot \ frac {\ cancel { 5}} {\ cancel {2} \ cdot \ cancel {2} \ cdot 7} ~ & \ textcolor {red} {\ text {Отменить общие множители.}} \\ = — \ frac {6} {7} ~ & \ textcolor {red} {\ text {Умножение числителей и знаменателей.}} \ cdot \ end {align} \ nonumber \]

Упражнение

Упростить:

\ [- 2 \ frac {4} {9} \ cdot 3 \ frac {2} {3} \ nonumber \]

Ответ

−2/3

Упражнения

В упражнениях 1–12 преобразуйте смешанную дробь в неправильную дробь.

1. \ (2 \ frac {1} {3} \)

2.\ (1 \ frac {8} {11} \)

3. \ (1 \ frac {1} {19} \)

4. \ (- 1 \ frac {1} {5} \)

5. \ (- 1 \ frac {3} {7} \)

6. \ (1 \ frac {3} {17} \)

7. \ (1 \ frac {1} {9} \)

8. \ (1 \ frac {5} {11} \)

9. \ (- 1 \ frac {1} {2} \)

10. \ (- 1 \ frac {5} {8} \)

11. \ (1 \ frac {1} {3} \)

12. \ (- 1 \ frac {5} {7} \)

---

В упражнениях 13-24 преобразуйте неправильную дробь в смешанную.

13.\ (\ frac {13} {7} \)

14. \ (\ frac {−17} {9} \)

15. \ (\ frac {−13} {5} \)

16. \ (\ frac {−10} {3} \)

17. \ (\ frac {−16} {5} \)

18. \ (\ frac {16} {13} \)

19. \ (\ frac {9} {8} \)

20. \ (\ frac {16} {5} \)

21. \ (\ frac {−6} {5} \)

22. \ (\ frac {−17} {10} \)

23. \ (\ frac {−3} {2} \)

24. \ (\ frac {−7} {4} \)

---

В упражнениях 25–48 умножьте числа и представьте свой ответ в виде смешанной дроби.

25. \ (1 \ frac {1} {7} \ cdot 2 \ frac {1} {2} \)

26. \ (1 \ frac {1} {8} \ cdot 1 \ frac {1} {6} \)

27. \ (4 \ cdot 1 \ frac {1} {6} \)

28. \ (1 \ frac {7} {10} \ cdot 4 \)

29. \ (\ left (−1 \ frac {1} {12} \ right) \ left (3 \ frac {3} {4} \ right) \)

30. \ (\ left (−3 \ frac {1} {2} \ right) \ left (3 \ frac {1} {3} \ right) \)

31. \ (7 \ frac {1} {2} \ cdot 1 \ frac {1} {13} \)

32. \ (2 \ frac {1} {4} \ cdot 1 \ frac {5} {11} \)

33.\ (\ left (1 \ frac {2} {13} \ right) \ left (−4 \ frac {2} {3} \ right) \)

34. \ (\ left (1 \ frac {1} {14} \ right) \ left (−2 \ frac {2} {5} \ right) \)

35. \ (\ left (1 \ frac {3} {7} \ right) \ left (−3 \ frac {3} {4} \ right) \)

36. \ (\ left (1 \ frac {4} {5} \ right) \ left (−3 \ frac {3} {4} \ right) \)

37. \ (9 \ cdot \ left (−1 \ frac {2} {15} \ right) \)

38. \ (4 \ cdot \ left (−2 \ frac {5} {6} \ right) \)

39. \ (\ left (−2 \ frac {1} {8} \ right) (−6) \)

40.\ ((- 9) \ left (−3 \ frac {1} {6} \ right) \)

41. \ (\ left (−4 \ frac {1} {2} \ right) \ left (−2 \ frac {2} {5} \ right) \)

42. \ (\ left (−1 \ frac {3} {7} \ right) \ left (−3 \ frac {3} {4} \ right) \)

43. \ (\ left (−2 \ frac {1} {6} \ right) \ cdot 4 \)

44. \ ((- 6) \ cdot \ left (1 \ frac {1} {9} \ right) \)

45. \ (\ left (−1 \ frac {4} {15} \ right) \ left (2 \ frac {1} {2} \ right) \)

46. \ (\ left (−1 \ frac {1} {5} \ right) \ left (1 \ frac {5} {9} \ right) \)

47.\ (\ left (−2 \ frac {1} {2} \ right) \ left (−1 \ frac {7} {11} \ right) \)

48. \ (\ left (−1 \ frac {7} {11} \ right) \ left (−1 \ frac {7} {12} \ right) \)

---

В упражнениях 49–72 разделите смешанные дроби и выразите свой ответ в виде смешанных дробей.

49. \ (8 \ div 2 \ frac {2} {9} \)

50. \ (4 \ frac {2} {3} \ div 4 \)

51. \ (\ left (−3 \ frac {1} {2} \ right) \ div \ left (1 \ frac {1} {16} \ right) \)

52. \ (\ left (−1 \ frac {2} {5} \ right) \ div \ left (1 \ frac {1} {15} \ right) \)

53.\ (6 \ frac {1} {2} \ div 1 \ frac {7} {12} \)

54. \ (5 \ frac {1} {2} \ div 1 \ frac {9} {10} \)

55. \ ((- 4) \ div \ left (1 \ frac {5} {9} \ right) \)

56. \ (\ left (−4 \ frac {2} {3} \ right) \ div 4 \)

57. \ (\ left (−5 \ frac {2} {3} \ right) \ div \ left (−2 \ frac {1} {6} \ right) \)

58. \ (\ left (−2 \ frac {1} {2} \ right) \ div \ left (−2 \ frac {2} {9} \ right) \)

59. \ (\ left (−6 \ frac {1} {2} \ right) \ div \ left (4 \ frac {1} {4} \ right) \)

60.\ (\ left (−1 \ frac {1} {6} \ right) \ div \ left (1 \ frac {1} {8} \ right) \)

61. \ ((- 6) \ div \ left (−1 \ frac {3} {11} \ right) \)

62. \ (\ left (−6 \ frac {2} {3} \ right) \ div (−6) \)

63. \ (\ left (4 \ frac {2} {3} \ right) \ div (−4) \)

64. \ (\ left (6 \ frac {2} {3} \ right) \ div (−6) \)

65. \ (\ left (1 \ frac {3} {4} \ right) \ div \ left (−1 \ frac {1} {12} \ right) \)

66. \ (\ left (2 \ frac {4} {7} \ right) \ div \ left (−1 \ frac {1} {5} \ right) \)

67.\ (\ left (5 \ frac {2} {3} \ right) \ div 1 \ frac {1} {9} \)

68. \ (1 \ frac {2} {3} \ div 1 \ frac {2} {9} \)

69. \ (\ left (−7 \ frac {1} {2} \ right) \ div \ left (−2 \ frac {2} {5} \ right) \)

70. \ (\ left (−5 \ frac {1} {3} \ right) \ div \ left (−2 \ frac {5} {6} \ right) \)

71. \ (\ left (3 \ frac {2} {3} \ right) \ div \ left (−1 \ frac {1} {9} \ right) \)

72. \ (\ left (8 \ frac {1} {2} \ right) \ div \ left (−1 \ frac {3} {4} \ right) \)

---

73. Малые участки .Сколько участков в четверть акра можно сделать из \ (6 \ frac {1} {2} \) акров земли?

74. Большое поле. Поле было сформировано из участков размером \ (17 \ frac {1} {2} \) по полакра. Сколько гектаров получилось в результате поля?

75. Ювелирные изделия. Чтобы сделать украшения, слиток серебра длиной \ (4 \ frac {1} {2} \) дюймов был разрезан на куски длиной в \ (\ frac {1} {12} \) дюйм. Сколько штук было изготовлено?

76. Маффины. По этому рецепту приготовят 6 кексов: 1 стакан молока, \ (1 \ frac {2} {3} \) стакан муки, 2 яйца, 1/2 чайной ложки соли, \ (1 \ frac {1} {2} \) чайные ложки разрыхлителя.Напишите рецепт шести десятков маффинов.

---

ответы

1. \ (\ frac {7} {3} \)

3. \ (\ frac {20} {19} \)

5. \ (- \ frac {10} {7} \)

7. \ (\ frac {10} {9} \)

9. \ (- \ frac {3} {2} \)

11. \ (\ frac {4} {3} \)

13. \ (1 \ frac {6} {7} \)

15. \ (- 2 \ frac {3} {5} \)

17. \ (- 3 \ frac {1} {5} \)

19. \ (1 \ frac {1} {8} \)

21. \ (- 1 \ frac {1} {5} \)

23. \ (- 1 \ frac {1} {2} \)

25.\ (2 \ frac {6} {7} \)

27. \ (4 \ frac {2} {3} \)

29. \ (- 4 \ frac {1} {16} \)

31. \ (8 \ frac {1} {13} \)

33. \ (- 5 \ frac {5} {13} \)

35. \ (- 5 \ frac {5} {14} \)

37. \ (- 10 \ frac {1} {5} \)

39. \ (12 \ frac {3} {4} \)

41. \ (10 ​​\ frac {4} {5} \)

43. \ (- 8 \ frac {2} {3} \)

45. \ (- 3 \ frac {1} {6} \)

47. \ (4 \ frac {1} {11} \)

49. \ (3 \ frac {3} {5} \)

51. \ (- 3 \ frac {5} {17} \)

53.\ (4 \ frac {2} {19} \)

55. \ (- 2 \ frac {4} {7} \)

57. \ (2 \ frac {8} {13} \)

59. \ (- 1 \ frac {9} {17} \)

61. \ (4 \ frac {5} {7} \)

63. \ (- 1 \ frac {1} {6} \)

65. \ (- 1 \ frac {8} {13} \)

67. \ (5 \ frac {1} {10} \)

69. \ (3 \ frac {1} {8} \)

71. \ (- 3 \ frac {3} {10} \)

73. Участки по 26 соток

75,54 штуки

Что такое смешанные числа? — Определение, факты и пример

Что такое смешанные числа?

Смешанное число — это целое число и правильная дробь, представленные вместе.Обычно представляет собой число между любыми двумя целыми числами.

Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число.

Некоторые другие примеры смешанных чисел:

Части смешанного числа

Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя.Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.

Свойства смешанных номеров

Преобразование неправильных дробей в смешанные.

Шаг 1 : Разделите числитель на знаменатель.

Шаг 2 : Запишите частное как целое число.

Шаг 3 : Запишите остаток в числителе и делитель в знаменателе.

Например, мы следуем указанным шагам, чтобы преобразовать 7/3 в смешанную числовую форму.

Шаг 1 : разделить 7 на 3

Шаг 2 : Запишите частное, делитель и остаток в форме, как на шагах 2 и 3 выше.

Сложение смешанных чисел

Можно складывать смешанные числа, переставляя целые числа, складывая их по отдельности, складывая оставшиеся дроби по отдельности и, в конце концов, расчесывая их все.

1 ¹ ⁄ ₂ + 3 ³ ⁄ ₄

Сложение целых чисел отдельно и дробей отдельно.

Для целых чисел:

1 + 3 = 4

Для дробей: найдите НОК и прибавьте

.

В конце складываем обе части вместе.

4 + 1 ¹ ⁄ ₄ = 5 ¹ ⁄ ₄

Примеры из жизни

Мы можем проверить наше понимание смешанных дробей, выразив части целого как смешанные дроби, подавая пиццу или пирог дома.Образцы смешанных фракций образуют остатки пиццы, наполовину заполненные стаканы молока.

Интересные факты

Обзор дробей: смешанные числа и неправильные дроби

Purplemath

Если у вас большая вечеринка с пиццей и после этого у вас осталась одна пицца с ананасом и половина пиццы с анчоусами, вы бы сказали, что у вас есть «полторы» пиццы.«Полтора» — это стандартный разговорный английский способ выражения этого числа, он записывается как «1 ¹ / ₂ ». Этот символ, «1 ¹ / ₂ », называется «смешанным числом», потому что он объединяет «обычное» число «1» с дробью « ¹ / ₂ ».

Хотя смешанные числа являются естественным выбором для разговорного английского языка (и поэтому хорошо подходят для ответов на словесные задачи), они, как правило, не самые простые дроби для вычисления.В алгебре вы почти всегда предпочитаете, чтобы дроби , а не были смешанными числами.

MathHelp.com

Вместо этого вы будете использовать так называемые «неправильные» дроби (также иногда называемые «вульгарными» дробями), когда верхнее число больше нижнего числа.

Стандартный способ преобразовать смешанное число в неправильную дробь — это умножить нижнее число на «обычное» число, добавить верхнее число, а затем поместить его поверх исходного нижнего числа как новую дробь.

Например, чтобы преобразовать 1 ¹ / ₂ в неправильную дробь, выполните следующие действия:

Я умножил нижние 2 на «обычную» 1, а затем добавил 1 сверху, получив 3.Затем я положил эти 3 поверх 2 снизу.

• Преобразовать в неправильную дробь.

Для преобразования я умножу знаменатель (16) на целое число (2), чтобы получить 32. Затем я добавлю числитель (3) к 32, чтобы получить новый числитель (35). Знаменатель останется прежним; а именно, 16.

---

• Преобразовать в неправильную дробь.

Для преобразования я умножу знаменатель (5) на целое число (6), чтобы получить 30. Затем я добавлю числитель (2) к 30, чтобы получить новый числитель (32). Знаменатель останется прежним; а именно 5.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании процентов в десятичные числа. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

---

Чтобы перейти от неправильной дроби к смешанному числу, вы помните, что «дроби — это деление», и применяете длинное деление, чтобы найти частное целого числа плюс остаток.Другими словами, вы делите верхнее число на нижнее число. Все, что вы видите поверх символа деления, является частным и является частью вашего «обычного числа» смешанного числа. Каким бы ни был ваш остаток, положите это число поверх числа, на которое вы делили; это дробная часть вашего смешанного числа.

Примечание. Когда вы конвертируете неправильную дробь в смешанные числа, не продолжайте длинное деление на десятичные разряды , а не .Просто найдите частное и остаток. Тогда остановись.

• Преобразование в смешанное число.

Сначала я делаю полные числа, чтобы найти целую часть (являющуюся частным) и остаток:

Частное сверху — 11, так что это будет целая часть смешанного числа.Поскольку остаток равен 1, а я делю на 4, дробная часть будет равна ¹ / ₄ .

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании неправильной дроби в смешанное число. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

---

Эта процедура отлично работает с рациональными выражениями (полиномиальные дроби). Вы можете увидеть это в примере ниже (или можете сразу перейти к умножению обычных дробей):

• Преобразование в смешанное число.

Сначала проделайте длинное деление, чтобы найти правильную часть многочлена и остаток:

Полином сверху равен « x + 1», а остаток равен –1. Поскольку вы делите на « x + 2», дробная часть будет «(–1) / ( x + 2)»:

---

URL: https: // www.