Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькуляторВ механике существуют два типа величин:
Рассмотрим сначала алгебраический подход к сложению векторов. Покоординатное сложение векторов. Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.): Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле: Теперь перейдем к геометрическому смыслу сложения двух векторов: . При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Процедура сложения векторов по правилу параллелограмма заключается в следующем:
|
Сложение и вычитание векторов. Видеоурок. Геометрия 8 Класс
Тема: Векторы
Урок: Сложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора 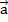 и
и 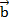 . Найдем сумму этих двух векторов
. Найдем сумму этих двух векторов 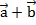 . Для этого отложим из некоторой точки А вектор
. Для этого отложим из некоторой точки А вектор 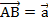 . Из точки В отложим вектор
. Из точки В отложим вектор 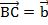
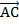 называют суммой заданных векторов:
называют суммой заданных векторов:  (см. Рис. 1).
(см. Рис. 1).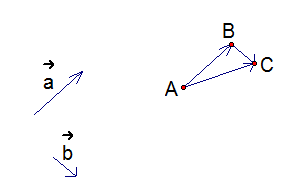
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила 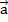 – он переместился из точки А в точку В, после этого подействовала сила
– он переместился из точки А в точку В, после этого подействовала сила 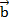
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов 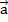
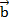 и
и 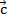 справедливы следующие равенства:
справедливы следующие равенства: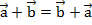 – переместительный закон.
– переместительный закон.
Доказательство: отложим из точки сначала вектор 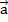 , получаем точку В, из нее откладываем вектор
, получаем точку В, из нее откладываем вектор 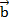 , получаем точку С и вектор
, получаем точку С и вектор 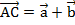
Теперь отложим из точки А сначала вектор 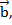 получим точку В, из нее отложим вектор
получим точку В, из нее отложим вектор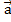 , получим точку С и вектор
, получим точку С и вектор 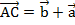 .
.
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
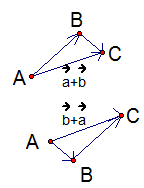
Рис. 2
Откладываем из точки А вектор 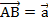
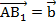 . Из точки В откладываем вектор
. Из точки В откладываем вектор 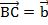 , вектора
, вектора  и
и 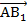 равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. 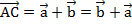 , таким образом, мы доказали переместительный
, таким образом, мы доказали переместительный 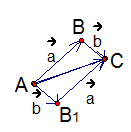
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
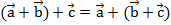 – сочетательный закон;
– сочетательный закон;
Из произвольной точки А отложим вектор 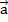 , прибавим к нему вектор
, прибавим к нему вектор 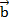
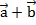 . К этой сумме прибавим вектор
. К этой сумме прибавим вектор 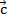 , получим результат
, получим результат  (см. Рис. 4).
(см. Рис. 4).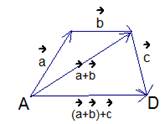
Рис. 4
В правой части выражения мы сначала получили сумму векторов  , после прибавили ее к вектору
, после прибавили ее к вектору 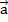 и получили результат:
и получили результат: 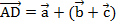
Таким образом, мы доказали сочетательный закон сложения векторов.

Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).
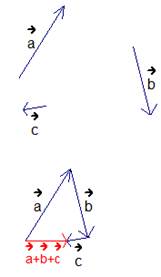
Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.
Пусть задано два вектора – векторы 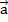 и
и 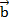 . Найдем разность этих двух векторов
. Найдем разность этих двух векторов 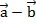 .
.
Определение
Разностью двух векторов 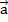 и
и 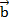 называют такой третий вектор, сумма которого с вектором
называют такой третий вектор, сумма которого с вектором 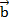 равна вектору
равна вектору 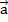 .
.
Если задан вектор 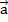 , то можно построить противоположный ему вектор
, то можно построить противоположный ему вектор 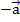 , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор:
, который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор: 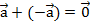 . Таким образом,
. Таким образом,  .
.
Отложим из произвольной точки вектор 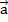 , из его конца отложим вектор
, из его конца отложим вектор 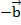 , получим в результате вектор
, получим в результате вектор 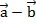 (см. Рис. 7).
(см. Рис. 7).
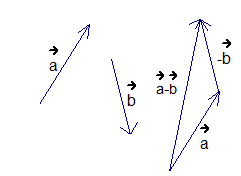
Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы 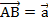 и
и  . Из точек В и D отложим векторв
. Из точек В и D отложим векторв 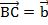 и
и 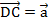 соответственно. Диагональ АС – это сумма векторов
соответственно. Диагональ АС – это сумма векторов 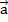 и
и 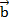 :
: 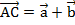 . Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору
. Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору 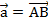 вектор
вектор 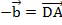 , получим вектор
, получим вектор 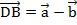 (см. Рис. 8).
(см. Рис. 8).
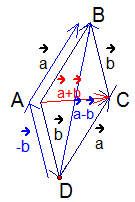
Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Emomi.com (Источник).
- Prosto-o-slognom.ru (Источник).
- Изучение математики онлайн (Источник).
Домашнее задание
- Задание 1: дан треугольник
 , найдите сумму векторов:
, найдите сумму векторов:  и
и  ;
;  и
и  ;
;  и
и  ;
;  и
и  .
. - Задание 2: турист прошел 20 км на восток из города А в город В, а потом 30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы
 и
и  Равны ли векторы
Равны ли векторы  и
и  ?
? - Задание 3: начертите попарно неколлинеарные векторы
 ,
,  и
и  и постройте векторы
и постройте векторы  ,
,  ,
,  .
.
длина суммы векторов и теорема косинусов
Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».
Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:
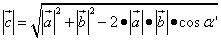 .
.
Перейдём к примерам.
Проверить решение можно на Калькуляторе онлайн.
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 3. Даны длины векторов 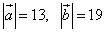 и длина их суммы
и длина их суммы  .
Найти длину их разности
.
Найти длину их разности 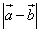 .
.
Решение.
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:

Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
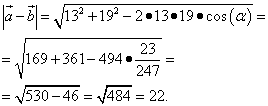
Проверить решение можно на Калькуляторе онлайн.
Пример 4. Даны длины векторов  и длина их разности
и длина их разности 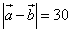 .
Найти длину их суммы
.
Найти длину их суммы 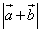 .
.
Решение.
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:
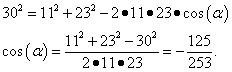
Шаг 2. Меняем знак косинуса и получаем косинус смежного
угла между 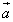 и
и
 :
:
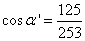
Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
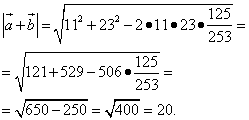
Проверить решение можно на Калькуляторе онлайн.
Пример 6. Какому условию должны удовлетворять векторы
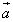 и
и 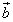 , чтобы имели место
слелующие соотношения:
, чтобы имели место
слелующие соотношения:
1) длина суммы векторов равна длине разности векторов, т. е. 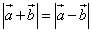 ,
,
2) длина суммы векторов больше длины разности векторов, т. е. 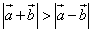 ,
,
3) длина суммы векторов меньше длины разности векторов, т. е. 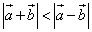 ?
?
Решение.
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
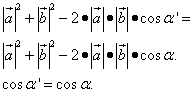
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
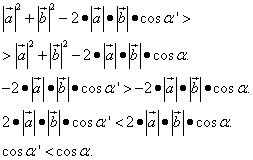
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.
Проверить решение можно на Калькуляторе онлайн.

Поделиться с друзьями
Начало темы «Векторы»
Продолжение темы «Векторы»
как сложить и отнять два вектора?
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника. Правило треугольника. Для сложения двух векторов \vec{u} и \vec{v} по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Правило параллелограмма. Для сложения двух векторов \vec{u} и \vec{v} по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
8 класс форевер если тебе даны 2 вектора, то можно воспользоваться свойством сложением векторов. Свойство треугольника или параллелограмма. Самая простая, это треугольника. Допустим у нас есть вектор a и вектор b. Снач строим вектор а, потом из конца вектора а проводим вектор b, а начало вектора a соединяем с кконцом вектора b. СДЕЛАЙ ОТВЕТ ЛУЧШИМ! <img src=»//content.foto.my.mail.ru/mail/server.cs-1.6/_answers/i-1.jpg» >
Сложение векторов — PhysBook
Скаляры можно складывать, умножать и делить так же, как обычные числа.
Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора \(\vec c = \vec a + \vec b\) не будет равна 7 м (рис. 1).
Рис. 1.Для того, чтобы построить вектор \(\vec c = \vec a + \vec b\) (рис. 2), применяются специальные правила сложения векторов.
Рис. 2.А длину вектора суммы \(\vec c = \vec a + \vec b\) определяют по теореме косинусов \(c = \sqrt{a^2+b^2-2a\cdot b\cdot \cos \alpha}\), где \(\alpha\,\) – угол между векторами \(\vec a\) и \(\vec b\).
Правило треугольника
В зарубежной литературе этот метод называют «хвост к голове».
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 3, а) нужно переместить вектор \(\vec b\) параллельно самому себе так, чтобы его начало совпадало с концом вектора \(\vec a\) (рис. 3, б). Тогда их суммой будет вектор \(\vec c\), начало которого совпадает с началом вектора \(\vec a\), а конец — с концом вектора \(\vec b\) (рис. 3, в).
а б в Рис. 3.Результат не поменяется, если перемещать вместо вектора \(\vec b\) вектор \(\vec a\) (рис. 4), т.е. \(\vec b + \vec a = \vec a + \vec b\) (свойство коммутативности векторов).
а б в Рис. 4. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-1.swf</swf> «Правило треугольников» Пример 1 Увеличить Flash <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-2.swf</swf> «Правило треугольников» Пример 2 Увеличить Flash Рис. 5.При помощи правила треугольника можно сложить два параллельных вектора \(\vec a\) и \(\vec b\) (рис. 6, а) и \(\vec a\) и \(\vec d\) (рис. 7, а). Суммы этих векторов \(\vec c = \vec a + \vec b\) и \(\vec f = \vec a + \vec d\) изображены на рис. 6, б и 7, б. Причем, модули векторов \(c = a + b\) и \(f=\left|a-d\right|\).
а б Рис. 6. а б Рис. 7.Правило треугольника можно применять при сложении трех и более векторов. Например, \(\vec c = \vec a_1 + \vec a_2 +\vec a_3 +\vec a_4\) (рис. 8).
Рис. 8.Правило параллелограмма
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 9, а) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\vec a\) и \(\vec b\) находились в одной точке (рис. 9, б). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 9, в). Тогда суммой \(\vec a+ \vec b\) будет вектор \(\vec c\), начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма (рис. 9, г).
а б в г Рис. 9. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-paral-1.swf</swf> «Правило параллепипеда» Увеличить Flash Рис. 10.Вычитание векторов
Для того чтобы найти разность двух векторов \(\vec a\) и \(\vec b\) (рис. 11) нужно найти вектор \(\vec c = \vec a + \left(-\vec b \right)\) (см. Умножение вектора на скаляр) по правилу треугольника (рис. 12) или по правилу параллелограмма (рис. 13).
Рис. 11 а б в Рис. 12. а б б в Рис. 13.Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Поделиться:
| |||
 , найдите сумму векторов:
, найдите сумму векторов: 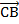 ;
; 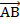 и
и 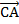 и
и 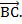 Равны ли векторы
Равны ли векторы 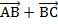 и
и 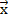 ,
,  и
и 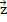 и постройте векторы
и постройте векторы  ,
,  ,
, 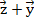 .
.