Показательные неравенства — Youclever.org
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Ты слышал старый анекдот? «Вопрос: Что будет, если скрестить ежа и ужа?
Ответ: 2 метра колючей проволоки». Мне его рассказал мой коллега-математик. Это один из основных приемов, который они используют, чтобы из простого и простого делать что-то сложное и понятное только «посвященным». Их любимая формула гласит:
Простое+простое=жуть!!!!
Я же попробую сегодня рассеять этот миф. Хотя бы отчасти. Или же ты просто станешь одним из посвященных и сможешь умничать направо и налево. Хотя без ужей и ежей нам сейчас тоже не обойтись. Итак, вместо ежей я буду использовать показательные уравнения, а вместо ужей – простейшие неравенства. Что же получится, если их скрестить? Правильно – простейшие показательные неравенства. Ну или не совсем простейшие, разберемся. Ну что, пора приступать, готов? Поехали!
А вот и первая кочка на нашем пути: чтобы без труда справиться (или почти без труда) с решением показательных неравенств, тебе надо:
- Вспомнить простейшие свойства степеней.
- Вспомнить, как решаются линейные неравенства и квадратичные неравенства.
- Вспомнить, как решаются показательные уравнения.
Ну что, вспомнил?
Тогда приступим.
Как тебе теперь стало известно, если , то . Легко, правда?
Вот вам еще одна задачка: . Вот и угадай, каким же должен быть ? Я думаю, что ты без труда понял, что .
Знаешь, тут бы стоило привести какой-нибудь пример из жизни (с бутылками, яблоками и т.п.), которые бы демонстрировали, для чего вообще показательные неравенства нужны, но, к сожалению, простейшие показательные неравенства, которые употребимы в жизни, описывают такие сложные процессы, как скорость размножения бактерий, скорость роста клеток и т.п. Так что начнем с самых азов.
В уже ранее рассмотренном примере, где , заменим знак « » на знак « », что же мы получим? Как ты, конечно, догадался, . И так как , то вы вполне резонно можете предположить, что .
А вот пример позабористее: . Опять таки, легко сосчитать, что (если не лень, можешь перепроверить, сосчитав в столбик). Так что же у нас получится? А получится . И какой можно из этого сделать вывод? Может быть, как и в предыдущем примере, ? На первый взгляд, это кажется вполне очевидным. Но ты будешь неприятно удивлен, когда из-за такой глупой ошибки завалишь контрольную работу. Потому что, как ни парадоксально, из следует, что !!
Неожиданно, правда? Однако, это суровая правда.
Я бы мог долго распространяться, почему это так, умничая направо и налево, и бросаясь такими словами, как «монотонное возрастание» и «показательная функция», но я пожалею твое время и объясню простое правило.
Условимся называть то число, которое стоит ниже или «под» , основанием. А число над основанием – показателем. То есть в выражении , – основание, а – показатель. Итак, о чем это я..? Ах да, правило. Оно гласит нам о следующем:
|
Если основание в неравенстве больше , то знак неравенства выполняется и для его показателей. Если же основание больше и меньше , то знак неравенства между его показателями меняется на противоположный. Кратко это правило можно записать так: (при ) (при ) |
Такие же правила ты можешь получить для трех оставшихся знаков неравенств: , , . Я сказал «можешь»? Нет, я ошибся: должен составить! Так тебе легче будет запомнить это нехитрое (самое нехитрое) правило.
Да, кстати, если ты внимательно читал мое изложение, то у тебя вполне мог назреть вопрос: а что если:
- Основание ?
- Основание ?
- Правая часть неравенства меньше нуля, например:
Кажется, пришло время ответить на все эти вопросы по-порядку: во-первых, не принято и не умеют решать показательные неравенства в которых . Почему, спросишь ты? Да все потому, что сколько единицу не умножай саму на себя (а именно это и делает степень), ничего кроме самой единицы ты все равно не получишь. Итак, показательные неравенства с мы не решаем. То же самое касается и неравенств, в которых основание меньше нуля. Просто забудем о таких, хорошо?
Отдельного разговора (и абзаца) заслуживает последний случай: Давай вместо основания возьмем число и будем возводить его во всевозможные степени:
Ты понял, как я заполнил эту таблицу? Нет!? Стыд и позор, я же просил повторить свойства степени. Вернись и перечитай, а потом возвращайся к нам. Итак, все стало понятно? Ну что же, продолжим. Что мы видим в этой таблице? Чем больше степень, тем больше значение выражения , и наоборот: чем меньше степень, тем это значение меньше. Но, тем не менее, видно (правда?) что, всегда больше нуля. ВСЕГДА. Это же свойство справедливо ДЛЯ ЛЮБОГО ОСНОВАНИЯ С ЛЮБЫМ ПОКАЗАТЕЛЕМ!!
| (для любых и ). |
Таким образом, уравнения вида имеют решения для любых (это, как ты помнишь, записывается, ), а вот неравенствам повезло куда меньше: они не имеют решений.
Ну вот, все приличия соблюдены, теперь можно переходить уже к некоторым примерам:
Решил? Честно? Ну хорошо, давай проверять вместе:
1. , так как , то . Ответ, как ты помнишь, мы записываем следующим образом: . Так как знак неравенства «строгий», то скобки будут «круглыми».
2. Здесь уже чуточку посложнее, но я уверен, ты тоже справился без проблем. Сверяемся:
так как , то
, откуда ,
поэтому ответ:
.
3. Продолжаем нагромождать: в третьем примере нас ждет беда: так получилось, что это не целая степень числа , (в чем несложно убедиться, возводя число в различные целые степени , , …). И что же теперь делать? Бросать решение примера? Нет! Этого не одобрю ни я, ни твой школьный учитель по математике. Давай немного напряжемся и заметим, что и и это степени одного и того же числа. Какого? Конечно, это степени тройки ( ). Тогда все становится сразу понятным:
(напомню, что при такой «замене» степени умножаются!), так как , то знак неравенства не меняется и мы получаем:
, раскроем скобки:
.
Отсюда, ответ:
.
4. Теперь мы решим еще более «навороченный» пример:
На самом деле, у нас есть аж два способа решить данное неравенство: во-первых, представить как (если для тебя это «превращение» показалось магическим, перечитай свойства степени с отрицательным показателем), либо представить как . Мне хочется сейчас пойти именно вторым путем, ну а ты сам можешь применить первый. Как ты понимаешь, ответы должны совпасть.
Теперь слева и справа в неравенстве мы имеем одинаковые основания, значит мы можем перейти к неравенству относительно их показателей. Однако, можно (и нужно!) заметить, что , поэтому знак неравенства меняется на противоположный. Итого, мы получим:
откуда простым делением на обеих частей неравенства очевидно следует, что .
Записываем ответ: .
5. Ну что же, здесь все нам тоже более-менее знакомо, единственно, что нужно вспомнить, так это то, что , теперь окончательно получим:
.
Опять-таки , а значит знак неравенства меняется на противоположный:
.
Данное линейное неравенство решается делением левой и правой стороны на число, стоящее перед иксом: то есть делением на . Но мы ведь с тобой уже грамотные люди? Конечно! А потому мы помним, что при делении (или умножении) обеих частей неравенства на отрицательное число, знак неравенства МЕНЯЕТСЯ НА ПРОТИВОПОЛОЖНЫЙ. А это значит, что
Нам осталось лишь записать полученный правильный ответ:
.
Теперь я предлагаю тебе задачки для совсем самостоятельного решения:
- ;
- ;
- ;
- ;
- .
А вот и ответы, заданные в измененном порядке, сверяйся!
Нашел свои ответы в приведенном списке? Ничего лишнего и ничего не потерялось? Прекрасно, это значит, ты сумел победить простейшие показательные неравенства. Это значит, что теперь ты умеешь решать почти все показательные неравенства из части B в ЕГЭ. Но мы ведь с тобой хотим стать еще лучше и уметь решать еще более сложные неравенства?
Как ты без труда (или почти без труда) заметил, каждый раз, когда мы решали показательное неравенство, оно сводилось к некоторому линейному неравенству для показателей. Более того, каждая из частей (правая и левая) неравенства состояла ровно из одного выражения. Что же запрещает природе вмешаться и сделать, например, с каждой стороны неравенства, скажем, не по одному выражению, а по три или даже четыре? Или же что ей запрещает составить такое неравенство, которое сводится уже не к линейному, а к квадратичному? Правильно, ничего не запрещает. Поэтому мы должны быть готовы к решению и таких неравенств тоже. Но рано пугаться, и говорить: «Вот это уж точно не по мне!». Давай вначале посмотрим на некоторые примеры:
Применим к нему уже знакомую не понаслышке технику. Что же мы получим в итоге? Верно:
.
Кто знает, как называется такое неравенство? Конечно квадратное! А теперь быстренько вспоминаем, как они решаются! Да почти что как квадратные уравнения. А вот уж их ты точно умеешь решать, я не сомневаюсь.
,
,
.
Вычисляем дискриминант:
Так как дискриминант больше нуля, то уравнение имеет два корня:
, .
Если бы мы решали уравнение, то на этом можно было бы и остановиться. Но у нас с тобой более «высокая цель» — решение неравенства. Отметим эти точки на координатной прямой и разделим эту прямую на три интервала, затем выберем какое-нибудь число в любом из интервалов и вычислим, чему равно наше исходное выражение в этой точке. Мне нравится брать такое число, чтобы нужно было как можно меньше считать. Догадался, какое же это число? Верно, это ноль. Ноль принадлежит самому левому интервалу. Наше выражение, если подставить в него ноль вместо икса, будет равно , . Поэтому в левом интервале я ставлю знак . Далее чередую.

Поскольку мы решаем неравенство , то нас интересуют те промежутки, где это выражение положительно (то есть стоит ), таким образом, наш ответ будет:
.
Теперь мне кажется, что ты без особого труда решишь следующие примеры:
Давай сверяться вместе:
1. ;
;
так как , то , откуда , заменяю знак в последнем неравенстве на , решаю уравнение , нахожу его корни: , .
Отмечаю эти точки на координатной прямой и выясняю знак выражения на каждом из полученных интервалов. Меня интересует знак » «. Тогда получу ответ:
2. Второе неравенство тоже решается элементарно, давай проверим:
,
откуда , что эквивалентно следующему квадратному неравенству:
, корни соответствующего уравнения равны
Тогда решением исходного неравенства будет объединение двух промежутков:
.
Как видишь (ты ведь внимательно за всем следил, правда?) решение подобных примеров чуть сложнее, чем тех, которые мы решали в самом начале. Но тем не менее здесь нам уже требуется использовать такой мощный метод, как МЕТОД ИНТЕРВАЛОВ. Вообще говоря, большинство неравенств именно с его помощью и решается. Так что можно сказать, что в начале нам просто «везло» и мы обходились без него.
Теперь мне осталось остановиться на еще одном методе решения неравенств: методе группировки. Я тебе напомню: впервые ты столкнулся с этим термином в 7 классе, когда раскладывал сложные выражения на простые множители, например:
Как ни парадоксально, но что-то подобное может применяться и при решении таких монстров как показательные неравенства. Да и что сказать, их используют, чтобы справиться с такими чудовищами, по сравнению с которыми наши неравенства покажутся белыми и пушистыми. Но перейдем от слов к делу:
Допустим, нам требуется решить следующее неравенство:
Согласись, до этих пор мы ни с чем подобным не сталкивались. Однако не время унывать. Давай подумаем, что общего есть у слагаемых слева? Верно, все они – это тройка в некоторой степени. Со свойствами степени мы уже давно на «ты», я ведь прав? Отлично! Тогда давай вынесем, например из каждого выражения. Что мы получим?
Эврика! У нас есть общий множитель! Так чего же мы ждем? Срочно выносим его за скобки!
Теперь вычисляем значение выражения внутри скобок:
;
Ну теперь осталась самая малость: подставим полученное выражение в наше неравенство:
.
Мы видим, что обе части имеют общий множитель . Разделим на него. Поскольку , то знак неравенства не измен
Решение показательных и логарифмических уравнений и неравенств
Цели урока:
- Обобщение и систематизация знаний по теме;
- Вооружить учащихся глубокими и прочными знаниями, но обучать их самостоятельной деятельности по владению знаниями;
- Выстроить индивидуальные траектории повторения и эффективно подготовиться к сдаче ЕГЭ;
- Ознакомить учащихся с видами заданий повышенной сложности по данной теме в заданиях части C ЕГЭ;
- Научить рационально распределять время при выполнении заданий ЕГЭ.
Основные теоремы о логарифмах.
Проверка домашнего задания.
№1 Решите уравнение
Решение:
Разделим обе части уравнения на
Пусть , , тогда
,
.
Ответ: -1.
№2 Решить уравнение
Решение:
Пусть
тогда
,
Исходное уравнение с помощью группировки приведем к виду:
, то есть
- Если
- ;
. - ;
.
- ;
- Если , то
;
;
Ответ: 1;
№3 Решите неравенство
Решение:
Пусть
Ответ:
№4 Сравнить числа
Решение:
,
Итак, .
Ответ:
Работа по теме урока.
Ребята, сегодня на уроке продолжим решать показательные и логарифмические уравнение и неравенства повышенной сложности.
№1 Решить уравнение
Решение:
;
;
;
;
;
;
.
Ответ: 2.
№2 Задача.
Иван и Маша решали задачу: некоторое заданное трехзначное число прологарифмировать по основанию 2, из полученного числа вычесть некоторое заданное натуральное число, а затем разность разделить на то же самое натуральное число.
Иван перепутал и в первом действии прологарифмировал по основанию 3,а Маша посчитала правильно. Когда они сравнили свои результаты, оказалось, что полученные ими числа взаимно обратны. Найти исходное трехзначное число.
Решение:
— натуральное число, вычитаемое во втором действии, тогда:
;
;
Ответ: 216.
№3 Найдите наибольшее целое решение неравенства
Решение:
;
Наибольшее целое решение исходного неравенства равно 0.
Ответ: 0.
№4 Решите неравенство при всех значениях параметра a.
Решение:
Преобразуем неравенство
Рассмотрим 2 случая: 0<a<1 и a>1
1 случай: полученное неравенство равносильно системе:
2 случай: полученное неравенство равносильно системе:
Ответ:
Самостоятельная работа.
Тест на 15 минут. Работа за компьютерами.(каждый ученик вводит свои данные, получает текст теста; работает над ним; вводит ответы. По истечению 15 мин. Компьютер блокирует работу; на экране появляется оценка, за выполненный тест).
Примерный тест.
- Решите неравенство:
- Решите неравенство:
- Решите неравенство:
- Решите уравнение:
- Решите уравнение:
- Решите уравнение:
- Решите уравнение:
- Решите уравнение:
- Решите уравнение:
- Решите уравнение:
Подведение итогов урока.
Домашнее задание.
№1 Решить неравенство
Решение:
Разделим обе части неравенства на :
Пусть =m, m>0, тогда
;
;
;
Ответ: .
№2 Найти все значения x, при каждом из которых выражения
принимают равные значения.
Решение:
Из условия задания следует
Решим данное уравнение:
Ответ: -0,5; 0.
№3 Решить неравенство
Решение:
Так как то последнее соотношение равносильно
Ответ: (3; 4).
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Решение показательных уравнений и неравенств: алгоритм решения и примеры
аx = b — простейшее показательное уравнение. В нем a больше нуля и а не равняется единице.
Решение показательных уравнений
Из свойств показательной функции знаем, что ее область значений ограничена положительными вещественными числами. Тогда если b = 0, уравнение не имеет решений. Такая же ситуация имеет место быть, в уравнении где b
Теперь положим, что b>0. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a
Исходя из этого и применяя теорему о корне, получим, что уравнение ax = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = ac.
Тогда очевидно, что с будет являться решением уравнения ax = ac.
Рассмотрим следующий пример: решить уравнение 5(x2 — 2*x — 1) = 25.
Представим 25 как 52, получим:
5(x2 — 2*x — 1) = 52.
Или что равносильно :
x2 — 2*x — 1 = 2.
Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.
Ответ: 3;-1.
Решим уравнение 4x – 5*2x + 4 = 0. Сделаем замену: t=2x и получим следующее квадратное уравнение:
t2 — 5*t + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4
Теперь решаем уравнения 2x = 1 и 2x = 4.
Ответ: 0;2.
Решение показательных неравенств
Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a<1, то данная функция будет убывающей на всем множестве вещественных чисел.
Рассмотрим пример: решить неравенство (0.5)(7 — 3*x) < 4.
Заметим, что 4 = (0.5)2. Тогда неравенство примет вид (0.5)(7 — 3*x) < (0.5)(-2). Основание показательной функции 0.5 меньше единицы, следовательно, она убывает. В этом случае надо поменять знак неравенства и не записывать только показатели.
Получим: 7 — 3*x>-2.
Отсюда: х<3.
Ответ: х<3.
Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.
Нужна помощь в учебе?
Предыдущая тема: Показательная функция: график и основные свойства функции
Следующая тема:   Логарифмы и их свойства: определение и алгоритм решения
Все неприличные комментарии будут удаляться.
«Показательная функция, ее свойства. Простейшие показательные уравнения и неравенства»
МОУ ИРМО «Вечерняя (сменная) общеобразовательная школа»
Открытый урок по алгебре и началам анализа в 12Д классе
Тема: «Показательная функция, ее свойства и график.
Решение простейших показательных уравнений и неравенств»
Учитель первой квалификационной категории, Земляничкина Тамара Михайловна
Тема урока:
«Показательная функция, ее свойства.
Простейшие показательные уравнения и неравенства»
Класс-12Д Учитель-Земляничкина Тамара Михайловна
Дата проведения:06.10.2015г
Тип урока: Урок изучения нового материала.
Оборудование урока: таблицы по алгебре, компьютер , проектор, карточки.
Цели урока:
*Образовательные:
знать график показательной функции и ее свойства и умение применять свойства при решении простейших уравнений и неравенств.
*Развивающие:
развивать умения решать простейшие показательные уравнения и неравенства . Развивать умение рассуждать по аналогии. Прививать интерес к предмету.
*Воспитательные:
формировать культуру общения, уважение друг к другу, культуру математической речи.
План урока:
1.Актуализация знаний.
5.Рефлексия.
6.Домашнее задание.
1.Актуализация знаний
Представьте в виде степени ( проверить ответы)
1/4= 0.25= 1.21= корень 2-й степени из числа 6
1/25= 0.04= 2.25= корень третьей степени из числа 36
1/64= 0.027= 0.125= корень пятой степени из числа 81
. Вычислить:
Повторить свойства степени по таблице и решить примеры на доске. 1. 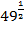 ; б)
; б) 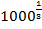 ; в)
; в) 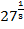 ; г)
; г) 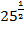 ; д)
; д) 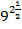 ; е)
; е) 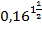 ; ж)
; ж) 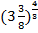 ; з)
; з) 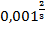
Дополнительные задания для сильных учащихся
2. . 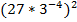 ; б)
; б) 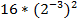 ; в)
; в) 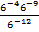 ; г)
; г) 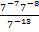
3. 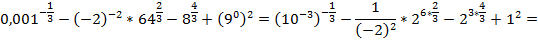
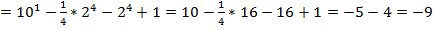 .
.
.2.Изучение н/м (при обЪяснении использую видеоурок)
На данном уроке мы рассмотрим показательную функцию, ее график и основные свойства. Также научимся решать простейшие показательные уравнения и неравенства.
1. Опреедление показательной функции, свойства, графики
Рассмотрим основное определение.
Функцию вида 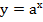 , где
, где 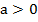 и
и 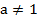 называют показательной функцией.
называют показательной функцией.
Например: 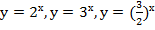 и т. д.
и т. д.
Рассмотрим первый случай, когда основание степени больше единицы: 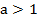 :. График показательной функции, основание степени больше единицы
:. График показательной функции, основание степени больше единицы
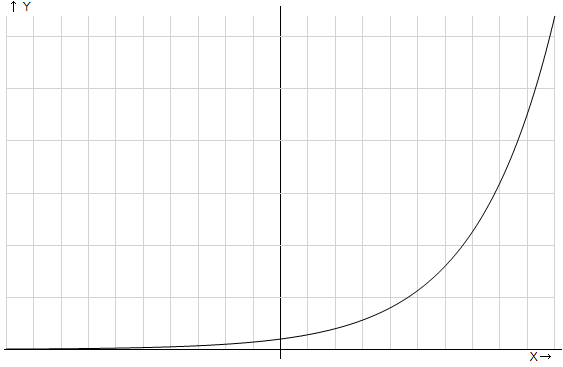
. Основные свойства данного семейства функций:
Область определения: 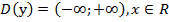 ;
;
Область значений: 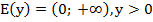 ;
;
Функция возрастает, т. е. большему значению аргумента соответствует большее значение функции;
Рассмотрим второй случай, когда основание степени меньше единицы 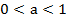 :
:
Например: 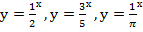 и т. д.
и т. д.
График показательной функции, основание степени меньше единицы
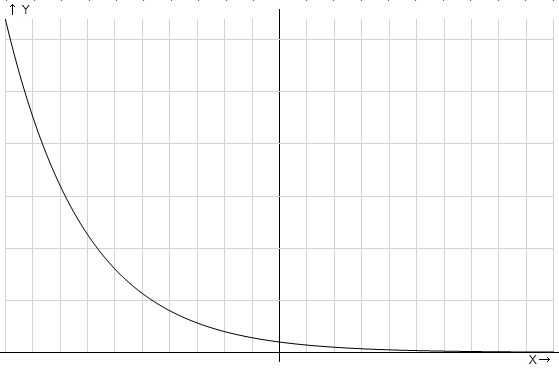
График показательной функции, основание степени меньше единицы
Свойства данного семейства функций:
Область определения: 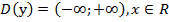 ;
;
Область значений: 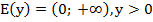 ;
;
Функция убывает, т. е. большему значению аргумента соответствует меньшее значение функции;
2. Решение элементарных показательных уравнений и неравенств
Решение показательных уравнений и неравенств основывается на свойствах показательной функции.
Пример 1 – решить уравнение:
а) 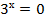
Ответ: 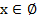 , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
б) 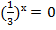
Ответ: 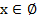 , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
Пример 2 – решить неравенство:
а) 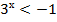
Ответ: 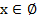 , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
б) 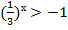
Ответ: 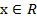 , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
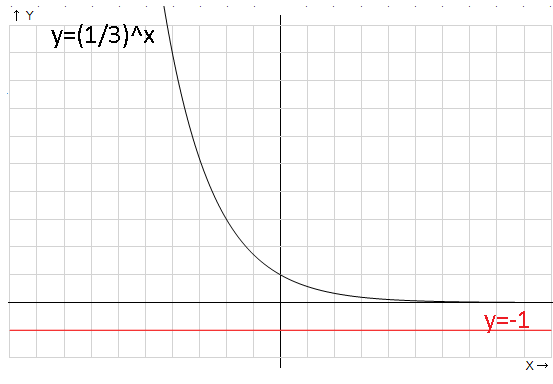
3. Простейшие показательные уравнения и неравенствав общем виде, конкретные примеры
Рассмотрим простейшие уравнения и неравенства на графике:
а) 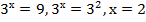
б) 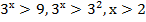 ,
,
в) аналогично решить неравенство с основанием 1/3
функция монотонно возрастает на всей области определения
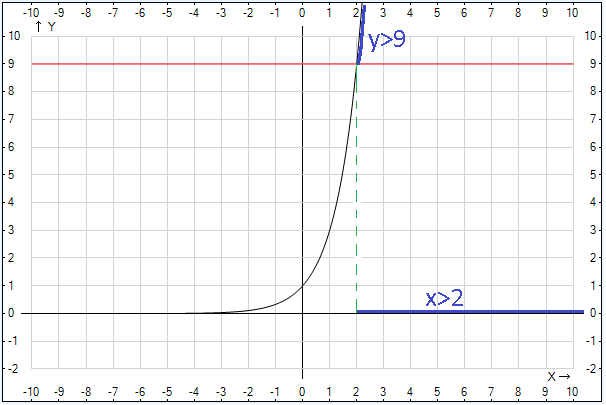
Сделаем вывод:
Рассмотрим простейшие показательные уравнения в общем виде.
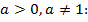
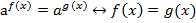
Равенство показателей степени при равных основаниях обусловлено свойством показательной функции, а именно ее монотонностью. Это означает, что каждое свое значение функция приобретает при единственном значении аргумента.
Таким образом, получаем методику решения показательных уравнений:
Уравнять основания степеней;
Приравнять показатели степеней;
Рассмотрим простейшие показательные неравенства в общем виде:
* Монотонное возрастание функций данного семейства является ключом к решению показательных неравенств, при условии, что основание степени 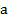 больше единицы.
больше единицы.
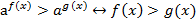
*Монотонное убывание функций данного семейства является ключом к решению показательных неравенств, при условии, что основание степени 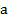 меньше единицы, но больше нуля.
меньше единицы, но больше нуля.
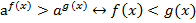
*Методика решения подобных неравенств:
1. Уравнять основания степеней.
2. Сравнить показатели, изменив знак неравенства.
Примеры решения показательных уравнений:
1. 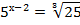
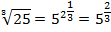
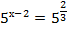
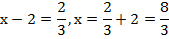
2.
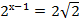
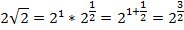
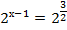
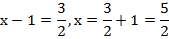
3.
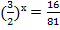
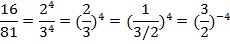
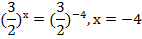
Примеры решения показательных неравенств по учебнику № 466
3.Закрепление . Самостоятельная работа
а) решить уравнения по учебнику № 460 б) решить неравенства по учебнику № 466
4. Итоги урока : Все учащиеся справились с работой.
Итак, мы рассмотрели показательную функцию, ее график и свойства, научились решать простейшие показательные уравнения и неравенства, рассмотрели простейшие показательные уравнения и неравенства в общем виде. На следующем уроке мы рассмотрим приемы решений показательных уравнений и неравенств.
С самостоятельной работой все справились.
5.Рефлексия : Молодцы, все работали хорошо. Какие вопросы вы хотели бы задать?
Урок закончен ,всем спасибо за урок.
6.Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 2012г п 35 п36, № 446, 461;467
Решить уравнение:
а) 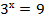 ; б)
; б) 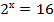 ; в)
; в) 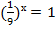 ; г)
; г) 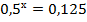
Список литературы
Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Mathematics-repetition.com (Источник).
Terver.ru (Источник).
Egesdam.ru (Источник).
Урок 44. показательные и логарифмические уравнения и неравенства с двумя переменными — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс Урок №44. Показательные и логарифмические уравнения и неравенства.
Перечень вопросов, рассматриваемых в теме
1) показательные уравнения и неравенства;
2) логарифмические уравнения и неравенства;
3) системы уравнений.
Глоссарий по теме
Показательными называются уравнения и неравенства, у которых переменная содержится в показатели степени.
Логарифмические уравнения и неравенства — это уравнения и неравенства, в которых переменная величина находится под знаком логарифма.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Вы уже умеете решать все виды уравнений и неравенств. Наша задача обобщить изученное, привести знания в систему. Начнем с показательных уравнений.
Показательные уравнения
aх=b. где a>0, a≠1
Если b>0, уравнение имеет один корень: x=loga b. График функции y=ax пересекает прямую y=b в одной точке.
Если b≤0 корней нет. График функции y=ax не пересекает прямую y=b.

При решении неравенств, обращаем внимание на основание. Если а>0, знак неравенства сохраняется. Если а<0, знак неравенства меняется.
Логарифмические уравнения
logax=b , где a>0, a≠1.
Логарифмическое уравнение logax=b имеет один положительный корень x=ab при любом значении b.
График функции пересекает прямую y=b в одной точке.

Уравнение имеет один положительный корень x=ab при любом b. График функции у= logax пересекает прямую y=b в одной точке.
При решении логарифмических неравенств обращаем внимание на область допустимых значений. Затем с учетом ОДЗ и значения решаем неравенство.
Теперь рассмотрим методы решения. Основных приема два: приведение к одинаковому знаменателю и замена переменной.
1 прием. Как в показательном, так и в логарифмическом уравняем основания. Затем сравним показатели или числа, стоящие под знаком логарифма.
2 прием. Замена переменных.
Находим корни и делаем обратную замену. При решении неравенств применяем те же самые приемы.
При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Решить уравнение:
lg(x+1)+lg(x-1)=lg3
lg(x+1)(x-1)=lg 3
x2-1=3
x2=4
х1=2 х2= -2
При х= -2 выражение lg(x-1) не имеет смысла, т.е. х=-2 посторонний корень. Ответ: х=2.
Пример 2. Найти значение выражения (х+у). x
lg x+lg y =2 x
Найдем область определения: х>0, у>0.
- lg(xy)=lg100 ↔ xy=100 ↔ 2xy=200
- сложим два уравнения: х2+2ху+у2=425+200=625 ↔ (х+у)2=625
значит х+у =25 с у четом ОДЗ. Ответ: 25
Внеклассный урок — Показательные уравнения и неравенства
Показательные уравнения и неравенства
Показательное уравнение.
Показательное уравнение – это уравнение вида af(x) = ad(x), где а – положительное число, отличное от 1.
Уравнения, сводящиеся к этому виду, тоже считаются показательными.
|
Пример:
Решим уравнение 22х – 4 = 64.
Решение.
Представим 64 в виде 26. Тогда:
22х – 4 = 26.
Мы получили одинаковое значение основания в левой и правой частях уравнения (число 2). Значит, можем убрать основания, получив равносильное уравнение, и решить его:
2х – 4 = 6
2х = 6 + 4 = 10
х = 10 : 2
х = 5.
Показательное неравенство.
Показательное неравенство – это неравенство вида af(x) > ad(x), где а – положительное число, отличное от 1.
Неравенства, сводящиеся к этому виду, тоже считаются показательными.
Если a > 1, то показательное неравенство равносильно неравенству того же смысла: Если 0 < a < 1, то показательное неравенство равносильно неравенству противоположного смысла: |
Пример 1:
Решим неравенство 3х + 2 > 81
Решение:
Представим 81 в виде 34. Тогда:
3х + 2 < 34.
Теперь в обеих частях неравенства одинаковое основание 3. Оно больше 1. Значит, заменяем неравенство равносильным неравенством того же смысла и решаем его:
х + 2 < 4
х < 4:2
х < 2.
Пример 2:
Решим неравенство 0,5х – 3 < 0,25.
Решение:
Представим 0,25 в виде 0,52. Тогда:
0,5х – 3 < 0,52.
Теперь у нас одинаковое основание в обеих частях неравенства: 0,5. Это число меньше 1. Значит, заменяем неравенство на равносильное неравенство с противоположным смыслом и решаем его:
х – 3 > 2
х > 2 + 3
x > 5.
11 класс. Алгебра. Показательная и логарифмическая функции. Показательные уравнения и неравенства. — Показательные неравенства.
Комментарии преподавателя
Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция – это функция вида  , где основание степени
, где основание степени  и
и  Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.
Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.

Рис. 1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции:
Область определения:  ;
;
Область значений:  ;
;
Функция монотонна, при  возрастает, при
возрастает, при  убывает.
убывает.
Монотонная функция принимает каждое свое значение при единственном значении аргумента.
При  , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (
, когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию ( ). При
). При  наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию (
наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию ( ).
).
На основании вышесказанного приведем методику решения простейших показательных неравенств:


Методика решения неравенств:
Уравнять основания степеней;
Сравнить показатели, сохранив или изменив на противоположный знак неравенства.
Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.
Пример 1:

Преобразуем правую часть согласно свойствам степени:


Основание степени больше единицы, значит, знак неравенства сохраняется:



Пример 2:

Преобразуем правую часть согласно свойствам степени:


Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:


Для решения квадратного неравенства решим соответствующее квадратное уравнение:

По теореме Виета находим корни:

Ветви параболы направлены вверх.
Таким образом, имеем решение неравенства:

Пример 3:

Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:

Основание степени больше единицы, знак неравенства не меняется, получаем:

Напомним методику решения таких неравенств.
Рассматриваем дробно-рациональную функцию:

Находим область определения:

Находим корни функции:
Функция имеет единственный корень, 
Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:

Рис. 2. Интервалы знакопостоянства
Таким образом, получили ответ.
Ответ: 
Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.
Пример 4:

Одно из свойств показательной функции – она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:



Основание степени больше единицы, знак неравенства сохраняется.
Ответ: 
Проиллюстрируем решение:
На рисунке 6.3 изображены графики функций  и
и  . Очевидно, что когда аргумент больше нуля, график функции
. Очевидно, что когда аргумент больше нуля, график функции  расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция
расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция  проходит ниже, она меньше. При значении аргумента
проходит ниже, она меньше. При значении аргумента  функции равны, значит, данная точка также является решением заданного неравенства.
функции равны, значит, данная точка также является решением заданного неравенства.

Рис. 3. Иллюстрация к примеру 4
Пример 5:

Преобразуем заданное неравенство согласно свойствам степени:

Приведем подобные члены:

Разделим обе части на  :
:

Теперь продолжаем решать аналогично примеру 4, разделим обе части на  :
:


Основание степени больше единицы, знак неравенства сохраняется:
Ответ: 
Пример 6 – решить неравенство графически:

Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.

Функция  – экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.
– экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Функция  – линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.
– линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ( )
)
Несложно заметить, что корнем данной системы является  :
:

Таким образом, графики функций пересекаются в точке с аргументом, равным единице.
Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ:  (рисунок 6.4)
(рисунок 6.4)

Рис. 4. Иллюстрация к примеру 6
Итак, мы рассмотрели решение различных типовых показательных неравенств.
Решение более сложных показательных неравенств заключается, как правило, в их сведении к более простым, или, как говорят, простейшим показательным неравенствам. Простейшие показательные неравенства решаются, в свою очередь, на основе свойств показательной функции.
Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция – это функция вида  , где основание степени
, где основание степени  и
и 

Рис. 1. График показа&
% PDF-1.6 % 95 0 объект > endobj Xref 95 80 0000000016 00000 н. 0000002574 00000 н. 0000002637 00000 н. 0000002888 00000 н. 0000003022 00000 н. 0000003156 00000 п. 0000003288 00000 н. 0000003429 00000 н. 0000003570 00000 н. 0000003711 00000 н. 0000003846 00000 н. 0000004076 00000 н. 0000004852 00000 н. 0000005521 00000 н. 0000006303 00000 п. 0000007037 00000 н. 0000007911 00000 п. 0000008546 00000 н. 0000009262 00000 н. 0000009905 00000 н. 0000010036 00000 п. 0000010170 00000 п. 0000010300 00000 п. 0000010431 00000 п. 0000010563 00000 п. 0000010695 00000 п. 0000010827 00000 п. 0000010958 00000 п. 0000011089 00000 п. 0000011222 00000 п. 0000011355 00000 п. 0000011488 00000 п. 0000011619 00000 п. 0000011751 00000 п. 0000011882 00000 п. 0000044499 00000 п. 0000045105 00000 п. 0000045795 00000 п. 0000065093 00000 п. 0000065476 00000 п. 0000065994 00000 п. 0000085689 00000 п. 0000086122 00000 п. 0000086873 00000 п. 0000103376 00000 н. 0000103761 00000 п. 0000104441 00000 н. 0000123630 00000 н. 0000124019 00000 н. 0000124732 00000 н. 0000137242 00000 н. 0000137522 00000 н. 0000138189 00000 н. 0000150609 00000 н. 0000151196 00000 н. 0000151846 00000 н. 0000161922 00000 н. 0000162320 00000 н. 0000163023 00000 н. 0000170764 00000 н. 0000171022 00000 н. 0000171670 00000 н. 0000194299 00000 н. 0000194755 00000 н. 0000195398 00000 н. 0000228344 00000 п. 0000228765 00000 н. 0000229424 00000 н. 0000253662 00000 н. 0000254232 00000 н. 0000254897 00000 н. 0000272979 00000 н. 0000273340 00000 н. 0000274055 00000 н. 0000283959 00000 н. 0000284346 00000 п. 0000285041 00000 н. 0000302356 00000 п. 0000302673 00000 н. 0000001896 00000 н. прицеп ] >> startxref 0 %% EOF 174 0 объект > поток xb«a«_ Ab @ YI2ooLeO} 9C & ˁ? wj ɠKI 㒪 LPmYV099mӋ ٚ \ & d ԗW \ 86ww # D \ xy \ Ythf% * szy \ T {WyS ] N & J ~ фм: c7oΞg # рН’S & \ F] Lv ޚ с ~ _’/ 7rly 㱱} YeZE2 & и4:% bkai) г = Н5 + 0X8ww @ А * ‘Rebp 5o: 9iɑ ݒ Hq8u30ԀS / + r03u2133fL @ A | 60 Խ шд ݧ ш # W # AV3Ljwd143q? Cdbi0fTcg $ G͐Ya *: `y @ ۧ 001 D0i3020_fPĤjeaL
.Решение экспоненциального уравнения с помощью sympy?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
- Авторизоваться зарегистрироваться
текущее сообщество
Устранение неравенств
Иногда нам нужно решить такие неравенства:
Символ | слов | Пример |
|---|---|---|
| > | больше | х + 3 > 2 |
| < | менее | 7x < 28 |
| ≥ | больше или равно | 5 ≥ x — 1 |
| ≤ | меньше или равно | 2 года + 1 ≤ 7 |
Решение
Наша цель — иметь x (или другую переменную) отдельно слева от знака неравенства:
| Что-то вроде: | х <5 | |
| или: | г ≥ 11 |
Мы называем это «решенным».
Пример: x + 2> 12
Вычтем 2 с обеих сторон:
х + 2 — 2> 12 — 2
Упростить:
х> 10
Решено!
Как решить
Решение неравенств очень похоже на решение уравнений … мы делаем почти то же самое …
… но мы также должны обратить внимание на направление неравенства .
Направление: куда «указывает» стрелка
Некоторые вещи могут изменить направление !
<становится>
> становится <
≤ становится ≥
≥ становится ≤
Безопасные дела
Эти вещи не влияют на направление неравенства:
- Сложить (или вычесть) число с обеих сторон
- Умножьте (или разделите) обе стороны на положительное число
- Упростить сторону
Пример: 3x <7 + 3
Мы можем упростить 7 + 3, не затрагивая неравенство:
3x <10
Но эти вещи действительно меняют направление неравенства (например, «<" становится ">«):
Пример: 2y + 7 <12
Когда мы меняем местами левую и правую части, мы также должны изменить направление неравенства :
12 > 2лет + 7
Вот подробности:
Сложение или вычитание значения
Мы часто можем решить неравенства, добавляя (или вычитая) число с обеих сторон (точно так же, как во Введении в алгебру), например:
Пример: x + 3 <7
Если вычесть 3 с обеих сторон, получим:
х + 3 — 3 <7 — 3
х <4
И вот наше решение: x <4
Другими словами, x может быть любым значением меньше 4.
Что мы сделали?
Мы пошли от этого: Кому: | х + 3 <7 х <4 | |||
И это хорошо работает для , добавляя и , вычитая , потому что, если мы прибавляем (или вычитаем) одинаковую сумму с обеих сторон, это не влияет на неравенство
Пример: У Алекса больше монет, чем у Билли.Если и Алекс, и Билли получат по три монеты больше, у Алекс все равно будет больше монет, чем у Билли.
Что, если я решу, но «x» справа?
Неважно, просто поменяйте местами стороны, но переверните знак , чтобы он по-прежнему «указывал» на правильное значение!
Пример: 12
Если отнять 5 с обеих сторон, получим:
12 — 5
7 <х
Вот и решение!
Но это нормально, если поставить «х» слева…
… так давайте обратим внимание (и знак неравенства!):
x> 7
Вы видите, как знак неравенства все еще «указывает» на меньшее значение (7)?
И вот наше решение: x> 7
Примечание: «x» может быть справа, но людям обычно нравится видеть его слева.
Умножение или деление на значение
Также мы умножаем или делим обе стороны на значение (как в алгебре — умножение).
Но мы должны быть немного осторожнее (как вы увидите).
Положительные значения
Все хорошо, если мы хотим умножить или разделить на положительное число :
Пример: 3y <15
Если разделить обе части на 3, получим:
3 года /3 <15 /3
г <5
И вот наше решение: y <5
Отрицательные значения
| Когда мы умножаем или делим на отрицательное число , мы должны обратить неравенство. |
Почему?
Ну, посмотрите на числовую строку!
Например, от 3 до 7 это , увеличение ,
, но от -3 до -7 — , уменьшение.
| −7 <−3 | 7> 3 |
Видите, как меняет знак неравенства (с <на>)?
Давайте попробуем пример:
Пример: −2y <−8
Разделим обе части на −2… и отменяют неравенство !
−2y <−8
−2y / −2 > −8 / −2
г> 4
И это правильное решение: y> 4
(Обратите внимание, что я перевернул неравенство в той же строке , разделенное на отрицательное число.)
Итак, запомните:
При умножении или делении на отрицательное число отменяет неравенство
Умножение или деление на переменные
Вот еще один (хитрый!) Пример:
Пример: bx <3b
Кажется легко просто разделить обе стороны на b , что дает нам:
х <3
… но подождите … если b равно отрицательное , нам нужно изменить неравенство следующим образом:
x> 3
Но мы не знаем, положительное или отрицательное значение b, поэтому мы не можем ответить на этот вопрос !
Чтобы помочь вам понять, представьте, что замените b на 1 или −1 в примере bx <3b :
- , если b равно 1 , то ответ будет x <3
- , но если b равно −1 , тогда мы решаем −x <−3 , и ответим x> 3
Ответом может быть x <3 или x> 3 , и мы не можем выбрать, потому что не знаем b .
Так:Не пытайтесь делить на переменную для решения неравенства (если вы не знаете, что переменная всегда положительна или всегда отрицательна).
Пример побольше
Пример: x − 3 2 <−5
Во-первых, давайте уберем «/ 2», умножив обе части на 2.
Поскольку мы умножаем на положительное число, неравенства не изменятся.
x − 3 2 × 2 <−5 × 2
х-3 <-10
Теперь прибавьте 3 к обеим сторонам:
х − 3 + 3 <−10 + 3
х <−7
И это наше решение: x <−7
Два неравенства сразу!
Как решить задачу сразу с двумя неравенствами?
Пример: −2 < 6−2x 3 <4
Во-первых, давайте очистим «/ 3», умножив каждую часть на 3.
Поскольку мы умножаем на положительное число, неравенства не меняются:
−6 <6−2x <12
Теперь вычтите 6 из каждой части:−12 <−2x <6
Теперь разделите каждую часть на 2 (положительное число, чтобы неравенства снова не изменились):
−6 <−x <3
Теперь умножьте каждую часть на -1. Поскольку мы умножаем на отрицательное число , неравенства изменяют направление .
6> х> −3
И это решение!
Но для наглядности лучше иметь меньшее число слева, большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства указывают правильно):
−3 <х <6
Сводка
- Многие простые неравенства могут быть решены путем сложения, вычитания, умножения или деления обеих частей, пока не останется переменная сама по себе.
- Но эти вещи изменят направление неравенства:
- Умножение или деление обеих сторон на отрицательное число
- Замена левой и правой сторон
- Не умножайте и не делите на переменную (если вы не знаете, что она всегда положительна или всегда отрицательна)
Решение экспоненциальных уравнений — Скачать PDF бесплатно
Решение проблем со сложными процентами
 Решение проблем со сложными процентами Что такое сложные проценты? Если вы зайдете в банк и откроете сберегательный счет, вы будете получать проценты с денег, которые вы кладете в банк.Если начислены проценты
Решение проблем со сложными процентами Что такое сложные проценты? Если вы зайдете в банк и откроете сберегательный счет, вы будете получать проценты с денег, которые вы кладете в банк.Если начислены проценты
РЕШЕНИЕ УРАВНЕНИЙ В EXCEL
 РЕШЕНИЕ УРАВНЕНИЙ В EXCEL В программах Excel и Lotus есть функции, которые позволяют пользователю определять корень уравнения. Под корнем мы подразумеваем такие значения x, что данное уравнение отменяет
РЕШЕНИЕ УРАВНЕНИЙ В EXCEL В программах Excel и Lotus есть функции, которые позволяют пользователю определять корень уравнения. Под корнем мы подразумеваем такие значения x, что данное уравнение отменяет
8.7 Экспоненциальный рост и упадок
 Раздел 8.7 Экспоненциальный рост и спад 847 8.7 Экспоненциальный рост и спад Модели экспоненциального роста Вспоминая исследования в разделе 8.3, мы начали с разработки формулы для дискретного соединения
Раздел 8.7 Экспоненциальный рост и спад 847 8.7 Экспоненциальный рост и спад Модели экспоненциального роста Вспоминая исследования в разделе 8.3, мы начали с разработки формулы для дискретного соединения
Функции — Экспоненциальные функции
 0.4 Функции — Экспоненциальные функции Цель: решить экспоненциальные уравнения, найдя общую основу.По мере того, как наше изучение алгебры становится все более продвинутым, мы начинаем изучать более сложные функции. Одна пара
0.4 Функции — Экспоненциальные функции Цель: решить экспоненциальные уравнения, найдя общую основу.По мере того, как наше изучение алгебры становится все более продвинутым, мы начинаем изучать более сложные функции. Одна пара
Раздел 1. Логарифмы
 Рабочий лист 2.7. Логарифмы и экспоненты Раздел 1 Логарифмы. Математика логарифмов и экспонент естественным образом встречается во многих областях науки. Это очень важно при решении проблем, связанных с
Рабочий лист 2.7. Логарифмы и экспоненты Раздел 1 Логарифмы. Математика логарифмов и экспонент естественным образом встречается во многих областях науки. Это очень важно при решении проблем, связанных с
Отрицательные целые показатели
 7.7 отрицательных целых показателей 7.7 ЗАДАЧИ. Определите нулевую экспоненту 2. Используйте определение отрицательной экспоненты, чтобы упростить выражение 3. Используйте свойства экспоненты, чтобы упростить выражения
7.7 отрицательных целых показателей 7.7 ЗАДАЧИ. Определите нулевую экспоненту 2. Используйте определение отрицательной экспоненты, чтобы упростить выражение 3. Используйте свойства экспоненты, чтобы упростить выражения
Экспоненциальные и логарифмические уравнения
 Экспоненциальные и логарифмические уравнения Эта глава посвящена использованию обратных экспонент или логарифмов для решения уравнений, включающих экспоненты или логарифмы.Решение экспоненциальных уравнений Экспоненциальная
Экспоненциальные и логарифмические уравнения Эта глава посвящена использованию обратных экспонент или логарифмов для решения уравнений, включающих экспоненты или логарифмы.Решение экспоненциальных уравнений Экспоненциальная
Программа MBA Jump Start
 Программа MBA Jump Start Модуль 2: Математика Модуль Томаса Гилберта Математика Онлайн-приложение: Основные математические концепции 2 1 Спектр чисел Обычно мы изображаем числа, возрастающие слева направо
Программа MBA Jump Start Модуль 2: Математика Модуль Томаса Гилберта Математика Онлайн-приложение: Основные математические концепции 2 1 Спектр чисел Обычно мы изображаем числа, возрастающие слева направо
Фактор Алмазной Практики Проблемы
 Фактор Алмазной Практики Проблемы 1.x 2 + 5x + 6 2. x 2 + 7x + 12 3. x 2 + 9x + 8 4. x 2 + 9x +14 5. 2x 2 7x 4 6. 3x 2 x 4 7. 5x 2 + x -18 8. 2y 2 x 1 9. 6-13x + 6x 2 10. 15 + x -2x 2 Factor Diamond Practice
Фактор Алмазной Практики Проблемы 1.x 2 + 5x + 6 2. x 2 + 7x + 12 3. x 2 + 9x + 8 4. x 2 + 9x +14 5. 2x 2 7x 4 6. 3x 2 x 4 7. 5x 2 + x -18 8. 2y 2 x 1 9. 6-13x + 6x 2 10. 15 + x -2x 2 Factor Diamond Practice
Размещение в высшем образовании по математике
 Типы задач для оценки зачисления в высшие учебные заведения по математике 1. Целые числа, дроби и десятичные дроби 1.1 Операции с сложением целых чисел с переносом Вычитание с заимствованием Умножение
Типы задач для оценки зачисления в высшие учебные заведения по математике 1. Целые числа, дроби и десятичные дроби 1.1 Операции с сложением целых чисел с переносом Вычитание с заимствованием Умножение
3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
 3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ РАЦИОНАЛЬНЫЕ ЧИСЛА На предыдущих курсах вы научились работать (выполнять сложение, вычитание, умножение и деление) над рациональными числами (дробями). Рациональные числа
3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ РАЦИОНАЛЬНЫЕ ЧИСЛА На предыдущих курсах вы научились работать (выполнять сложение, вычитание, умножение и деление) над рациональными числами (дробями). Рациональные числа
Precalculus Ориентация и часто задаваемые вопросы
 Precalculus Orientation и FAQ MATH 1011 (Precalculus) — это четырехчасовой курс по 3 кредита, который готовит студента к математическому анализу.Охватываемые темы включают линейные, квадратичные, полиномиальные, рациональные, экспоненциальные,
Precalculus Orientation и FAQ MATH 1011 (Precalculus) — это четырехчасовой курс по 3 кредита, который готовит студента к математическому анализу.Охватываемые темы включают линейные, квадратичные, полиномиальные, рациональные, экспоненциальные,
Математический тест общего керна
 Алгебра средней школы Основной учебный план Математический тест Математический тест с образцом общего ядра Наш сэмплер по алгебре средней школы охватывает двадцать наиболее распространенных вопросов, которые, по нашему мнению, предназначены для этого уровня. Для полных тестов
Алгебра средней школы Основной учебный план Математический тест Математический тест с образцом общего ядра Наш сэмплер по алгебре средней школы охватывает двадцать наиболее распространенных вопросов, которые, по нашему мнению, предназначены для этого уровня. Для полных тестов
Рентабельность инвестиций (ROI)
 ROI 1 Рентабельность инвестиций (ROI) Подготовлено Сарой Мейджор Что такое ROI? Рентабельность инвестиций (ROI) — это мера, которая исследует сумму дополнительной прибыли, полученной за счет определенных инвестиций.Предприятия
ROI 1 Рентабельность инвестиций (ROI) Подготовлено Сарой Мейджор Что такое ROI? Рентабельность инвестиций (ROI) — это мера, которая исследует сумму дополнительной прибыли, полученной за счет определенных инвестиций.Предприятия
MATH-0910 Обзор концепций (Haugen)
 Раздел 1 Целые числа и дроби MATH-0910 Обзор концепций (Haugen) Экзамен 1 Разделы 1.5, 1.6, 1.7, 1.8, 2.1, 2.2, 2.3, 2.4 и 2.5 Деление целых чисел Эквивалентные способы выражения деления: a b,
Раздел 1 Целые числа и дроби MATH-0910 Обзор концепций (Haugen) Экзамен 1 Разделы 1.5, 1.6, 1.7, 1.8, 2.1, 2.2, 2.3, 2.4 и 2.5 Деление целых чисел Эквивалентные способы выражения деления: a b,
9.2 Обозначение суммирования
 9.Обозначение суммирования 66 9. Обозначение суммирования В предыдущем разделе мы ввели последовательности, а теперь мы представим обозначения и теоремы, касающиеся суммы членов последовательности. Начнем с
9.Обозначение суммирования 66 9. Обозначение суммирования В предыдущем разделе мы ввели последовательности, а теперь мы представим обозначения и теоремы, касающиеся суммы членов последовательности. Начнем с
Д-р Брайан Бодри стр. 1
 Умножение десятичных знаков Имя: Умножение десятичной дроби на целое число может быть представлено моделью повторного сложения. Например, 3 0,14 означает добавить 0.14 трижды, перегруппируйтесь и упростите,
Умножение десятичных знаков Имя: Умножение десятичной дроби на целое число может быть представлено моделью повторного сложения. Например, 3 0,14 означает добавить 0.14 трижды, перегруппируйтесь и упростите,
Руководство по арифметике Accuplacer
 Руководство для изучения арифметики Accuplacer Раздел первый: Числитель терминов: число в верхней части дроби, которое показывает, сколько частей у вас есть. Знаменатель: число внизу дроби, указывающее, как
Руководство для изучения арифметики Accuplacer Раздел первый: Числитель терминов: число в верхней части дроби, которое показывает, сколько частей у вас есть. Знаменатель: число внизу дроби, указывающее, как
Практическая математическая алгебра
 Практическая математическая алгебра Пэм Мидер и Джуди Сторер, иллюстрированная Джули Мазур. Содержание Учителю… v Тема: Соотношение и пропорции 1. Продвижение конфет … 1 2. Оценка популяций диких животных … 6 3.
Практическая математическая алгебра Пэм Мидер и Джуди Сторер, иллюстрированная Джули Мазур. Содержание Учителю… v Тема: Соотношение и пропорции 1. Продвижение конфет … 1 2. Оценка популяций диких животных … 6 3.
ФРАКЦИИ ОПЕРАЦИИ
 ОПЕРАЦИИ С ДРУГАМИ Резюме 1. Элементы дроби … 1. Эквивалентные дроби … 1. Упрощение дроби … 4. Правила сложения и вычитания дробей … 5. Правило умножения для двух дробей …
ОПЕРАЦИИ С ДРУГАМИ Резюме 1. Элементы дроби … 1. Эквивалентные дроби … 1. Упрощение дроби … 4. Правила сложения и вычитания дробей … 5. Правило умножения для двух дробей …
Дроби и линейные уравнения
 Дроби и линейные уравнения Операции с дробями Хотя вы можете выполнять операции с дробями с помощью калькулятора, для этого рабочего листа вы должны выполнять операции вручную.Вы должны показать все шаги
Дроби и линейные уравнения Операции с дробями Хотя вы можете выполнять операции с дробями с помощью калькулятора, для этого рабочего листа вы должны выполнять операции вручную.Вы должны показать все шаги
Примеры проблем. Проблемы с практикой
 Конспект лекций Задачи о квадратичных словах стр. 1 Примеры задач 1. Сумма двух чисел равна 31, их разность равна 41. Найдите эти числа .. Произведение двух чисел равно 640. Их разность равна 1. Найдите эти
Конспект лекций Задачи о квадратичных словах стр. 1 Примеры задач 1. Сумма двух чисел равна 31, их разность равна 41. Найдите эти числа .. Произведение двух чисел равно 640. Их разность равна 1. Найдите эти
Решения упражнений, раздел 4.5
 Руководство по решениям для инструктора, раздел 4.5. Упражнение 1. Решения для упражнений, раздел 4.5. 1. Какой суммой станет первоначальная сумма в 2000 долларов, постоянно накапливаемая под 6% годовых, через 25 лет?
Руководство по решениям для инструктора, раздел 4.5. Упражнение 1. Решения для упражнений, раздел 4.5. 1. Какой суммой станет первоначальная сумма в 2000 долларов, постоянно накапливаемая под 6% годовых, через 25 лет?
Раздел 4.1 Правила экспонентов
 Раздел 4.1. Правила экспоненты ЗНАЧЕНИЕ ЭКСПОНЕНТЫ Экспонента — это аббревиатура для повторного умножения.Повторяющееся число называется фактором. x n означает n факторов x. Показатель показывает
Раздел 4.1. Правила экспоненты ЗНАЧЕНИЕ ЭКСПОНЕНТЫ Экспонента — это аббревиатура для повторного умножения.Повторяющееся число называется фактором. x n означает n факторов x. Показатель показывает
Дроби в десятичные дроби
 Рабочий лист 4 Раздел «Дроби и десятичные дроби». Дроби в десятичные числа. Наиболее распространенный метод преобразования дробей в десятичные — использование калькулятора. Дробь представляет собой деление, поэтому это еще один способ
Рабочий лист 4 Раздел «Дроби и десятичные дроби». Дроби в десятичные числа. Наиболее распространенный метод преобразования дробей в десятичные — использование калькулятора. Дробь представляет собой деление, поэтому это еще один способ
Решение систем путем исключения
 1 декабря 2008 г. Решение систем методом исключения стр. 1 Решение систем методом исключения Вот еще один метод решения системы двух уравнений.Иногда этот метод проще, чем построение графика
1 декабря 2008 г. Решение систем методом исключения стр. 1 Решение систем методом исключения Вот еще один метод решения системы двух уравнений.Иногда этот метод проще, чем построение графика
23. РАЦИОНАЛЬНЫЕ ПОКАЗАТЕЛИ
 23. РАЦИОНАЛЬНЫЕ ОБРАЗЦЫ переименование радикалов в рациональные числа, запись радикалов с рациональными показателями Когда необходимо проделать серьезную работу с радикалами, их обычно меняют на имя, в котором используются показатели степени,
23. РАЦИОНАЛЬНЫЕ ОБРАЗЦЫ переименование радикалов в рациональные числа, запись радикалов с рациональными показателями Когда необходимо проделать серьезную работу с радикалами, их обычно меняют на имя, в котором используются показатели степени,
Математика больших идей.Бревенчатая гонка
 Эпоненциальные и логарифмические функции Большие идеи Математический журнал Гонка u Материалы: шестигранный кубик Фишки для игрового поля Игровые карты Бумажный карандаш u Указания: Студенты собираются в группы игроков. Игроки по очереди катят
Эпоненциальные и логарифмические функции Большие идеи Математический журнал Гонка u Материалы: шестигранный кубик Фишки для игрового поля Игровые карты Бумажный карандаш u Указания: Студенты собираются в группы игроков. Игроки по очереди катят