Квадратичная функция. Как построить параболу?
Квадратичная функция – это функция вида \(y=ax^2+bx+c\). График квадратичной функции – парабола.
Примеры:|
\(y= x^2+6x+5\) |
\(y=x^2-4x+5\) |
||
|
\(y=-2x^2-4x+4\) |
\(y=-3x^2+21x-34\) |
«Анатомия» квадратичной функции:
\(x_в\) и \(y_в\) – координаты вершины параболы. \(x_в\) можно найти с помощью формулы: \(x_в=\frac{-b}{2a}\). \(y_в\) можно найти подставив в формулу квадратичной функции вместо \(x\) значение \(x_в: y_в=ax_в^2+bx_в+с\)
Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.
3 параметра позволяющих сопоставить формулу квадратичной функции и график:
|
1. |
\(a>0\) — ветви параболы направлены вверх |
|
|
\(a<0\) — ветви параболы направлены вниз |
|
|
|
2. |
\(c\) равна ординате точки пересечения |
|
|
3. |
координата вершины параболы \(x_в=-\frac{b}{2a}\) |
|
Пример (задание из ОГЭ). На рисунке изображён график квадратичной функции \(y=ax^2+bx+c\)
Какие знаки параметров \(a\) и \(c\)?
Решение:
Ветви параболы направлены вниз, значит \(a<0\)
График функции пересекает ось \(y\) в точке лежащий ниже оси \(x\), значит \(c<0\)
Ответ: \(a<0\),\(c<0\)
Пример (задание из ОГЭ). Установите соответствие между квадратичными функциями и их графиками:
Решение:
Во втором графике ветви параболы направлены вниз, значит \(a<0\). Под этот график подходит только функция под буквой В.
Во втором и третьем графике \(a>0,c=1\) – по этим параметрам нам определить их функции. Тогда найдем \(x_в\) функций под буквой А и Б:
А. \(y=x^2-5x+1\) \(x_в=\frac{5}{2}=2,5\) так же как на графике 1
Б. \(y=x^2+5x+1\) \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3
Ответ:
Как построить график квадратичной функции (параболу)?
Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.
- Найдите координаты вершины параболы. Поставьте точку вершины на координатной плоскости и проведите через неё ось симметрии параболы.
- Найдите точку пересечения графика с осью \(y\): \(x=0;y=c\). Постройте точку симметричную точке \((0;c)\) относительно оси параболы.
- Найдите координату целой точки, лежащей вблизи оси параболы. Отметьте симметричную ей точку на плоскости.
- Соедините точки плавной линией.
|
\(a=2\), \(b=8\), \(c=2\) 1. \(x_в=\frac{-b}{2a}=\frac{-8}{2 \cdot 2}=-2\) |
|
|
2. \(x=0, y=2\) |
|
|
3. При \(x=-3\), |
|
|
Готово! |
Связь квадратичной функции и квадратных уравнений:
Давайте сравним общий вид квадратичной функции и общий вид квадратного уравнения:
|
\(y=ax^2+bx+c\) |
\(ax^2+bx+c=0\) |
Пример:
|
\(y=x^2+6x+5\) |
\(y=x^2-4x+5\) |
|
|
|
|
Судя по графику, корнями уравне- |
У уравнения \(x^2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\)) |
Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства
cos-cos.ru
Построение графика квадратичной функций: алгоритм и примеры
Квадратичной функцией называется функция вида:
y=a*(x^2)+b*x+c,
где а – коэффициент при старшей степени неизвестной х,
b – коэффициент при неизвестной х,
а с — свободный член.
Графиком квадратичной функции является кривая, называемая параболой. Общий вид параболы представлен на рисунке ниже.
Рис.1 Общий вид параболы.
Есть несколько различных способов построения графика квадратичной функции. Мы рассмотрим основной и самый общий из них.
Алгоритм построения графика квадратичной функции y=a*(x^2)+b*x+c
1. Построить систему координат, отметить единичный отрезок и подписать координатные оси.
2. Определить направление ветвей параболы (вверх или вниз).
Для этого надо посмотреть на знак коэффициента a. Если плюс — то ветви направлены вверх, если минус — то ветви направлены вниз.
3. Определить координату х вершины параболы.
Для этого нужно использовать формулу Хвершины = -b/2*a.
4. Определить координату у вершины параболы.
Для этого подставить в уравнение Увершины = a*(x^2)+b*x+c вместо х, найденное в предыдущем шаге значение Хвершины.
5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.
6. Найти точки пересечения графика с осью Ох.
Для этого требуется решить квадратное уравнение a*(x^2)+b*x+c = 0 одним из известных способов. Если в уравнение не имеет вещественных корней, то график функции не пересекает ось Ох.
7. Найти координаты точки пересечения графика с осью Оу.
Для этого подставляем в уравнение значение х=0 и вычисляем значение у. Отмечаем эту и симметричную ей точку на графике.
8. Находим координаты произвольной точки А(х,у)
Для этого выбираем произвольное значение координаты х, и подставляем его в наше уравнение. Получаем значение у в этой точке. Нанести точку на график. А также отметить на графике точку, симметричную точке А(х,у).
9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.
Пример построения графика
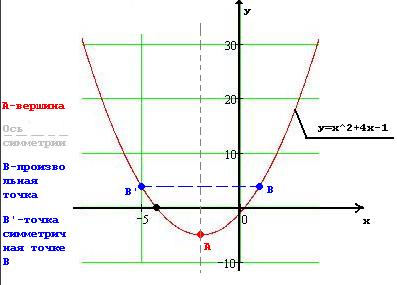
В качестве примера, построим график квадратичной функции заданной уравнением y=x^2+4*x-1
1. Рисуем координатные оси, подписываем их и отмечаем единичный отрезок.
2. Значения коэффициентов а=1, b=4, c= -1. Так как а=1, что больше нуля ветви параболы направлены вверх.
3. Определяем координату Х вершины параболы Хвершины = -b/2*a = -4/2*1 = -2.
4. Определяем координату У вершины параболы
Увершины = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) – 1 = -5.
5. Отмечаем вершину и проводим ось симметрии.
6. Находим точки пересечения графика квадратичной функции с осью Ох. Решаем квадратное уравнение x^2+4*x-1=0.
х1=-2-√3 х2 = -2+√3. Отмечаем полученные значения на графике.
7. Находим точки пересечения графика с осью Оу.
х=0; у=-1
8. Выбираем произвольную точку B. Пусть она имеет координату х=1.
Тогда у=(1)^2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.
В результате получится такой график.
Нужна помощь в учебе?
Предыдущая тема: Графики функции: от чего зависит вид графика функции
Следующая тема:   Решение неравенств второй степени с одной переменной: приводим примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Построение графика квадратичной функции
Графиком
любой квадратичной функции является парабола.
У каждой параболы есть вершина, при изображении графика важно знать её
координаты. Вершина параболы  имеет
координаты (m,n).
имеет
координаты (m,n).
Определите координаты вершин для парабол:


Определим
координаты вершины параболы, которая является графиком квадратичной функции
записанной в виде  .
.
Преобразуем квадратный трёхчлен, выделим из него квадрат двучлена:

Второе слагаемое представим в виде удвоенного произведения:

Выделим квадрат суммы:

После сокращения получаем:


Отсюда запишем, что:

Вывод.
Графиком функции
 является
парабола, которую можно получить из
параболы с помощью двух параллельных переносов: сдвига относительно оси
является
парабола, которую можно получить из
параболы с помощью двух параллельных переносов: сдвига относительно оси
 ,
,
 .
Осью симметрии является прямая x=m.
.
Осью симметрии является прямая x=m.Пример.
Найти
координаты вершины параболы  .
.
Вершина будет иметь координаты (m,n), каждую из которых можно получить по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти значения:

Вершина параболы имеет координаты (-2,-5).
Воспользуемся наиболее простым способом: сначала найдём m вершины по формуле. И учитывая, что вершина принадлежит графику функции, подставим m вместо аргумента в функцию:

Получили вершину, которая имеет координаты (-2,-5).
Алгоритм построения графика квадратичной функции:
1. Определить направление ветвей парабола. Если a>0, то ветви направлены вверх, если a<0, то — вниз.
2.
Найти
координаты вершины параболы и отметить её на координатной плоскости. Применив
формулу 
3. Определить ось симметрии x=m.
4. Построить ещё несколько точек принадлежащих параболе, составив таблицу значений функции с учётом оси симметрии.
5. Соединить отмеченные точки плавной линией.
Пример.
Изобразить
график функции  .
.
1. Определим направление ветвей параболы:

2. Найдём координаты вершины:

Получили вершину с координатами (-2, -3).
3. Определим ось симметрии:

4. Составим таблицу значений:

Выбранные значения симметричны относительно оси симметрии.
5. Отметим и соединим полученные точки на координатной плоскости:

Получили параболу, которая является графиком функции.
Пример.
Изобразить
график функции 
Изобразим график функции:

1. Определим направление ветвей параболы:

2. Найдём координаты вершины параболы:

Вершина имеет координаты (-2,-4).
3. Определим ось симметрии:

4. Составим таблицу значения функции:

5. Соединив эти точки, получаем:

Определим свойства функции.
Областью определения и областью значений являются:

Определим нули функции:

Перечислим промежутки знакопостоянства функции:

Опишем промежутки монотонности:

videouroki.net
Алгоритм построения графика квадратичной функции
Алгоритм построения графика квадратичной функции y=a*(x^2)+b*x+c
1. Построить систему координат, отметить единичный отрезок и подписать координатные оси.
2. Определить направление ветвей параболы (вверх или вниз).
Для этого надо посмотреть на знак коэффициента a. Если плюс — то ветви направлены вверх, если минус — то ветви направлены вниз.
3. Определить координату х вершины параболы.
Для этого нужно использовать формулу вершины х0= -b/2*a.
4. Определить координату у вершины параболы.
Для этого подставить в уравнение функции у0 = a*(x^2)+b*x+c вместо х, найденное в предыдущем шаге значение х0.
5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.
6. Найти точки пересечения графика с осью Ох.
Для этого требуется решить квадратное уравнение a*(x^2)+b*x+c = 0 одним из известных способов. Если в уравнение не имеет вещественных корней, то график функции не пересекает ось Ох.
7. Найти координаты точки пересечения графика с осью Оу.
Для этого подставляем в уравнение значение х=0 и вычисляем значение у. Отмечаем эту и симметричную ей точку на графике.
8. Находим координаты произвольной точки А(х,у)
Для этого выбираем произвольное значение координаты х, и подставляем его в наше уравнение. Получаем значение у в этой точке. Нанести точку на график. А также отметить на графике точку, симметричную точке А(х,у).
9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.
Пример построения графика
В качестве примера, построим график квадратичной функции заданной уравнением y=x^2+4*x-1
1. Рисуем координатные оси, подписываем их и отмечаем единичный отрезок.
2. Значения коэффициентов а=1, b=4, c= -1. Так как а=1, что больше нуля ветви параболы направлены вверх.
3. Определяем координату х0 вершины параболы вершины = -b/2*a = -4/2*1 = -2.4. Определяем координату у0 вершины параболы вершины = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) – 1 = -5.
5. Отмечаем вершину и проводим ось симметрии.
6. Находим точки пересечения графика квадратичной функции с осью Ох. Решаем квадратное уравнение x^2+4*x-1=0.
х1=-2-√3 х2 = -2+√3. Отмечаем полученные значения на графике.
7. Находим точки пересечения графика с осью Оу. х=0; у=-1
8. Выбираем произвольную точку B. Пусть она имеет координату х=1. Тогда у=(1)^2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.
В результате получится такой график.
infourok.ru
Квадратичная функция — урок. Алгебра, 8 класс.
Функция y=kx2 и её график
В \(7\)-м классе мы изучали функции \(у = m\), \(у = kx\), \(у = kx + m\), y=x2 и пришли в итоге к выводу, что уравнение с двумя переменными вида \(у = f(x)\) (функция) есть математическая модель, удобная для того, чтобы, задав конкретное значение независимой переменной \(x\) (аргумента), вычислить соответствующее значение зависимой переменной \(y\).
На самом деле функция y=kx2 в одном случае нам немного знакома. Смотри: если \(k = 1\), то получаем y=x2; эту функцию мы изучили в \(7\)-м классе, и ты, наверное, помнишь, что её графиком является парабола.

Обсудим, что происходит при других значениях коэффициента \(k\).
Рассмотрим две функции: y=2×2 и y=0.5×2. Составим таблицу значений для первой функции y=2×2:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(1.5\) | \(-1.5\) |
| \(y\) | \(0\) | \(2\) | \(2\) | \(8\) | \(8\) | \(4.5\) | \(4.5\) |
Построим точки \((0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5)\) на координатной плоскости; они намечают некоторую линию. Проведём её.

Составим таблицу значений для второй функции y=0.5×2:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(0.5\) | \(0.5\) | \(2\) | \(2\) | \(4.5\) | \(4.5\) |
Построим точки \((0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), (3; 4,5), (-3; 4,5)\) на координатной плоскости; они намечают некоторую линию. Проведём её.

Сравни полученные рисунки. Не правда ли, проведённые линии похожи? Каждую из них называют параболой.
Точку \((0; 0)\) называют вершиной параболы, а ось \(y\) — осью симметрии параболы.
Обрати внимание!
От величины коэффициента \(k\) зависит «скорость устремления» ветвей параболы вверх или, как ещё говорят, «степень крутизны» параболы.
Точно так же обстоит дело с любой другой функцией вида y=kx2, где \(k > 0\).
Графиком её является парабола с вершиной в начале координат, ветви параболы направлены вверх, причём тем круче, чем больше коэффициент \(k\).
Ось \(y\) является осью симметрии параболы.
Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции y=kx2» говорят «парабола y=kx2», а вместо термина «ось симметрии параболы» используют термин «ось параболы».
Ты замечаешь, что имеется аналогия с функцией \(у = kx\)?
Если \(k > 0\), то графиком функции \(у = kx\) является прямая, проходящая через начало координат (помнишь, мы говорили коротко: прямая \(у = kx\)), причём и здесь от величины коэффициента \(k\) зависит «степень крутизны» прямой. Это хорошо видно на рисунке, где в одной системе координат изображены графики линейных функций \(у = kx\) при трёх значениях коэффициента \(k\).

Вернёмся к функции y=kx2. Выясним, как обстоит дело в случае отрицательного коэффициента \(k\). Построим, например, график функции y=−x2 (здесь \(k = — 1\)). Составим таблицу значений:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(-1\) | \(-1\) | \(-4\) | \(-4\) | \(-9\) | \(-9\) |
Отметим точки \((0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; — 9)\) на координатной плоскости; они намечают некоторую линию. Проведём её.

Это парабола с вершиной в точке \((0; 0)\), ось \(y\) — ось симметрии, но в отличие от случая, когда \(k > 0\), на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента \(k\).
Обрати внимание!
Итак, графиком функции y=kx2 (k≠0) является парабола с вершиной в начале координат; ось \(y\) является осью параболы; ветви параболы направлены вверх при \(k>0\) и вниз — при \(k<0\).
Отметим ещё, что парабола y=kx2 касается оси \(x\) в точке \((0; 0)\), т. е. одна ветвь параболы плавно переходит в другую, как бы прижимаясь к оси \(x\).
Если построить в одной системе координат графики функций y=x2 и y=−x2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси \(x\), что хорошо видно на рисунке.

Точно так же симметричны друг другу относительно оси \(x\) параболы y=2×2 и y=−2×2.

Обрати внимание!
Вообще график функции \(у = — f(x)\) симметричен графику функции \(у = f(x)\) относительно оси абсцисс.
www.yaklass.ru
Как построить график квадратичной функции
Автор Сергей Валерьевич
Четверг, 10 декабря, 2015
Построение графика квадратичной функции всегда было проблемой для многих школьников. Проблема в том, что на уроках в школе этому важнейшему материалу зачастую уделяют не достаточно внимания. В результате, когда появляется необходимость, ученику очень трудно отыскать в школьном учебнике или интернете чёткий алгоритм построения графика квадратичной функции (параболы), а вместо этого приходится по крупицам выискивать необходимую информацию из множества различных источников. Решим эту проблему раз и навсегда! В данной статье репетитором по математике и физике представлен алгоритм построения параболы.
Алгоритм построения графика функции y=ax²+bx+c
Данный алгоритм продемонстрируем на примере построения графика квадратичной функции  . В этом случае:
. В этом случае: 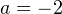 ,
, 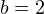 и
и 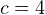 .
.
1. Определим, куда направлены ветви соответствующей параболы. Если 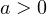 , то ветви параболы направлены вверх, если
, то ветви параболы направлены вверх, если 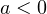 , то ветви параболы направлены вниз.
, то ветви параболы направлены вниз.
В нашем примере 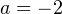 . Следовательно, ветви параболы направлены вниз.
. Следовательно, ветви параболы направлены вниз.
2. Найдем координаты вершины параболы. Абсцисса вершины параболы определяется по формуле:
![Rendered by QuickLaTeX.com \[ x_0 = -\frac{b}{2a}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e9188690f1b0ea560a1aba4cf8b0dc0b_l3.png)
Ордината вершины параболы 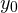 определяется путем подстановки
определяется путем подстановки 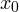 в уравнение квадратичной функции и вычисления соответствующего значения.
в уравнение квадратичной функции и вычисления соответствующего значения.
В нашем случае абсцисса 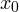 вершины параболы равна:
вершины параболы равна:
![Rendered by QuickLaTeX.com \[ x_0 = -\frac{2}{2\cdot (-2)} = \frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a12339444a7add771ae2672583f4bbb1_l3.png)
Тогда ордината 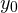 вершины параболы равна:
вершины параболы равна:
![Rendered by QuickLaTeX.com \[ y_0 = -2\cdot \left(\frac{1}{2}\right)^2+2\cdot \frac{1}{2} + 4 = \frac{9}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6d250574287aa0ce5cef93877b14e270_l3.png)
3. Определим еще несколько точек вблизи вершины, принадлежащих параболе. Удобнее всего оформить эти точки в виде таблицы.
В нашем случае получаем следующую таблицу значений:
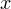 | -2 | -1 | 0 | 1 | 2 | 3 |
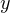 | -8 | 0 | 4 | 4 | 0 | -8 |
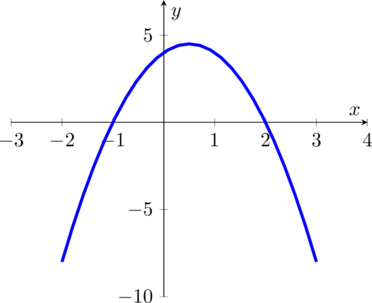
4. Отметить полученные точки и вершину параболы на координатной плоскости и соединить их плавной линией. В результате получится требуемый график квадратичной функции.
В нашем случае получается следующая парабола:
Репетитор по математике и физике
Сергей Валерьевич
| Квадрат — зародыш всех возможностей. (Казимир Малевич) |
yourtutor.info
Построение графика квадратичной функции
Построение графика квадратичной функции, заданной формулой
Предмет: алгебра
Класс: 8 «Б»
Тема: Построение графика квадратичной функции, заданной формулой
Тип: комбинированный урок.
Форма организации учебной деятельности: индивидуально-групповая.
Цели
Обучающие
· проверить знания, умения и навыки построения графика квадратичной функции, заданной формулой
· внедрить алгоритм построения графика квадратичной функции, заданной формулой
· отработать алгоритм при построении графиков квадратичной функции.
Развивающая
· продолжить работу по развитию умения работать с книгой, сравнивать; развивать коммуникативные связи, информационную грамотность, логику.
Воспитательная
· стимулировать учащихся к самооценке образовательной деятельности, вызывая чувство самопознания, самоопределения и самореализации.
Оборудование
· Доска, компьютеры, экран с проектором, карточки с алгоритмами.
Ход урока
1) Организационный момент (2 мин)
· Учитель формулирует тему и цели урока, сообщает план работы, который проецируется на экран и по мере выполнения стираются пункты плана. Учащиеся записывают число и тему урока в тетради.
Работа по плану
1) Работая устно, вспоминаем решение уравнений.
2) Учащиеся проверяют свои знания по построению графика квадратичной функции способом перемещения.
3) Знакомство с алгоритмом.
4) Отработка алгоритма при построении графиков функции, заданной формулой
2) Актуализация знаний учащихся (13 мин).
1) Фронтальная устная работа.
1. Что является графиком функции у = аx2. (парабола)
2. Как зависит график функции у = аx2 от коэффициента а.
а) Сформулируйте правило переноса графика функции вдоль оси абсцисс.
б) Сформулируйте правило переноса графика функции вдоль оси ординат.
(если а>0, то происходит растяжение графика функции от оси Ох вдоль оси Оу, ели 0<a<1, то происходит сжатие графика функции к оси Ох вдоль оси Оу)
3. Вспомни алгоритм построения графиков функций , если известен график функции у = аx2.
(График функции является парабола, получаема сдвигом параболы у = аx2:
вдоль оси абсцисс вправо на х0, если х0>0, влево на , если х0<0;
вдоль оси ординат вверх на у0, если у0>0, вниз на , если у0<0).
4. Как определить координаты вершины параболы?
5. Как определить точку, через которую проходит ось симметрии параболы?
6. Как определить направление «ветвей» параболы?
· Заполни пропуски (работа с интерактивной доской): все записывают в тетради. Взаимопроверка.
1. Функция у = aх2 + bx + c, где а, b, c – заданные действительные числа, а ¹ 0,
х – действительная переменная, называется … функцией. (квадратичной)
2. График функции у = ах2 при любом а ¹ 0 называют … .(параболой)
3. Функция у = х2 является … (возрастающей, убывающей) на промежутке
х £ 0. (убывающей)
4. Значения х, при которых квадратичная функция равна нулю, называют … функции (нулями функции)
5. Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы)
6. При а >0 ветви параболы у = ах2 направлены … . (вверх)
7. Если а< о и х ¹ 0, то функция у = ах2 принимает … (отрицательные)
(положительные, отрицательные) значения.
Работа у доски (индивидуальны карточки у доски)
1. Найдите координаты вершины параболы у=х2-4х+4 Ответ: (2;0)
2.Найдите нули квадратичной функции у=х2+х-2 Ответ: -2; 1
3. Выдели полный квадрат x2 — 4х + 5. И постройте график полученной функции.
Ответ: х2 — 4х + 5 = (х2 — 4х + 4) + 1 = (х — 2)2 + 1
Фронтальная работа с классом. (Презентация)
3.Учитель поясняет задание. Для каждой из функций, графики которых изображены, выберите соответствующее условие и отметьте знаком «+». Ученики выполняют работу на распечатанных листочках, осуществляя самопроверку. Листочки заранее раздать ученикам.
После того, как учащиеся закончили решение теста, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, один ученик выполняет задание на интерактивной доске, на экране с помощью анимации появляются правильные ответы. ( Презентация)
После проверки учащиеся оценивают работу соседа по следующему критерию:
- «5» — нет ошибок;
- «4» — 1 ошибка;
- «3» — 2 ошибки;
- «2» — 3 и более ошибки.
Проверка работ учащихся у доски
4.
Ответ:
(Находим нули функции: =0 х1=0; х2=-5, ветви параболы направлены вверх а>0).
Ответ: (3,0) ;
2) Индивидуальное задание
· Индивидуальная работа на компьютерах. Первая группа, проверяет свои знания по построению графиков функции – в течение 4 минут выполняет теств Excel. (11 человек). Ученикам раздаются по окончанию работы образцы для проверки.
Образец для проверки
· Фронтальная устная работа (проверка работы, анализ и комментирование). Учащиеся второй группы выполняют тест с помощью системы голосования Verdict. На экране появляется изображение соответствующего графика с указанной функцией. (15 человек).
Тест
«Квадратичная функция»
В системе Verdict
10. Функция задана формулой . Найдите .
1) 24 2) 0 3) 8 4) -8
1. График какой функции изображен на рисунке?
1) 2)
3) 4)
4. Найдите нули функции .
1) 2 и 3 2) -6 и -1 3) 1 и 6 4) -3 и -2
2. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
3. График какой функции изображен на рисунке?
1) 2)
3) 4)
0
1
1
у
х
8. На каком промежутке функция, изображенная на рисунке убывает?1) 2) 3) 4)
5. График какой функции изображен на рисунке?
1) 2)
3) 4)
6. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
7. График какой функции изображен на рисунке?
1) 2)
3) 4)
0
1
infourok.ru