Построение графиков функций. КОМПАС-3D V10 на 100 %
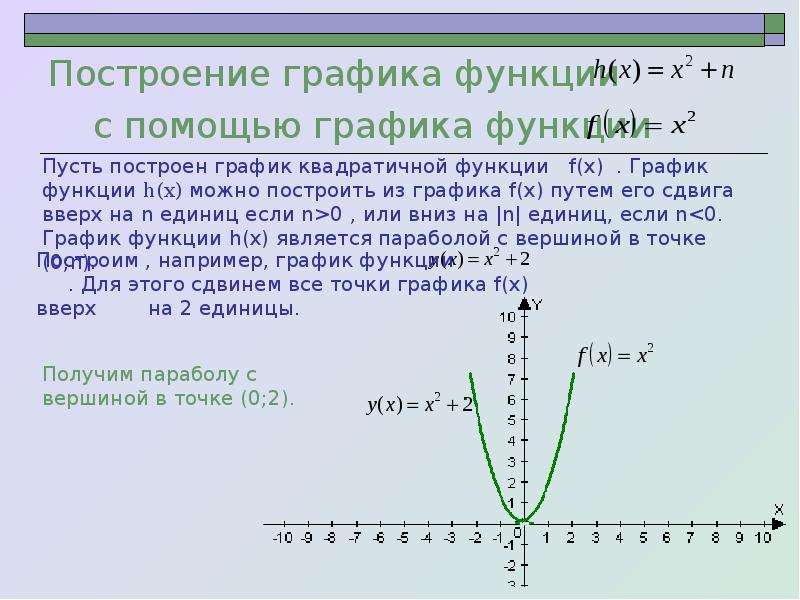
Построение графиков функций
В завершение практического раздела данной главы я решил добавить еще один параграф, описывающий способы построения графиков всевозможных функций в системе КОМПАС-График. Этот вопрос неоднократно поднимался пользователями во время работы с программой, причем многие из них даже не подозревали о заложенной в КОМПАС-График возможности построения функций по их уравнениям.
Специально для этой цели в системе есть отдельное приложение – библиотека FTDraw, которую вы можете найти в разделе Прочие менеджера библиотек. Библиотека позволяет выполнять следующие действия (рис. 2.144):
• строить графики функциональных зависимостей в декартовых координатах;
• строить графики функций в полярных координатах;
• строить графики по загруженным табличным данным (взятым, например, из табличного редактора Excel).
Рис. 2.144. Библиотека FTDraw
После запуска библиотеки в менеджере откроется ее меню, состоящее из двух команд: Библиотека построения графиков FTDraw и Простейший математический калькулятор.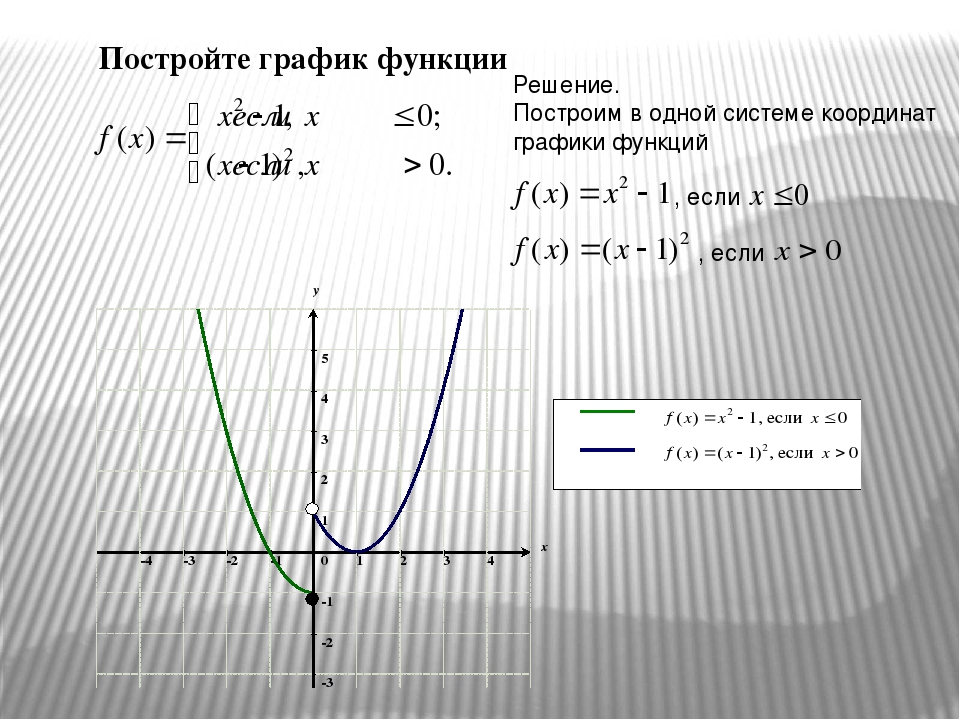
Внимание!
Перед тем как запускать библиотеку, обязательно создайте (или сделайте активным) чертеж или фрагмент.
Давайте рассмотрим пример построения графика какой-либо сложной функции в декартовых координатах. Предположим, что рассматривается функция вида y(x) = 4?x + 3cos(x) + 2ln(x) в диапазоне от 0,1 до 100. Щелкните на первой из больших квадратных кнопок главного окна библиотеки, чтобы перейти в режим построения графиков в декартовых координатах. В результате перед вами откроется новое окно (рис. 2.145), в котором необходимо задать уравнение, по которому будет строиться график, а также параметры построения.
Рис. 2.145. Построение графиков функций в декартовых координатах
По умолчанию в поле для введения функции стоит Sqrt(x), что означает, что система настроена на построение графика y(x) = ?x.
Данная утилита имеет весьма несложный синтаксис, к тому же вы всегда можете воспользоваться подсказкой при выборе нужной функции, щелкнув правой кнопкой мыши в поле, где нужно вводить формулу (рис. 2.146).
Рис. 2.146. Подсказка для выбора и вставки функций
Пользуясь приведенными подсказками и клавиатурой, введите в поле для функций следующую строку: 4*Sqrt(x)+3*Cos(x)+2*Ln(x). После этого в полях Пределы изменения Х задайте нужный диапазон, а в поле Количество точек установите значение 50. Нажмите кнопку Указать положение базовой точки графика
после чего щелкните в точке, где планируете поместить начало координат создаваемого графика. После задания точки система вернется к окну задания функциональных зависимостей, в котором теперь должна активироваться кнопка Построить график
Щелкните на этой кнопке, затем нажмите OK, чтобы завершить построение. Если вы все сделали правильно, в результате должен получиться график, показанный на рис. 2.147.
Рис.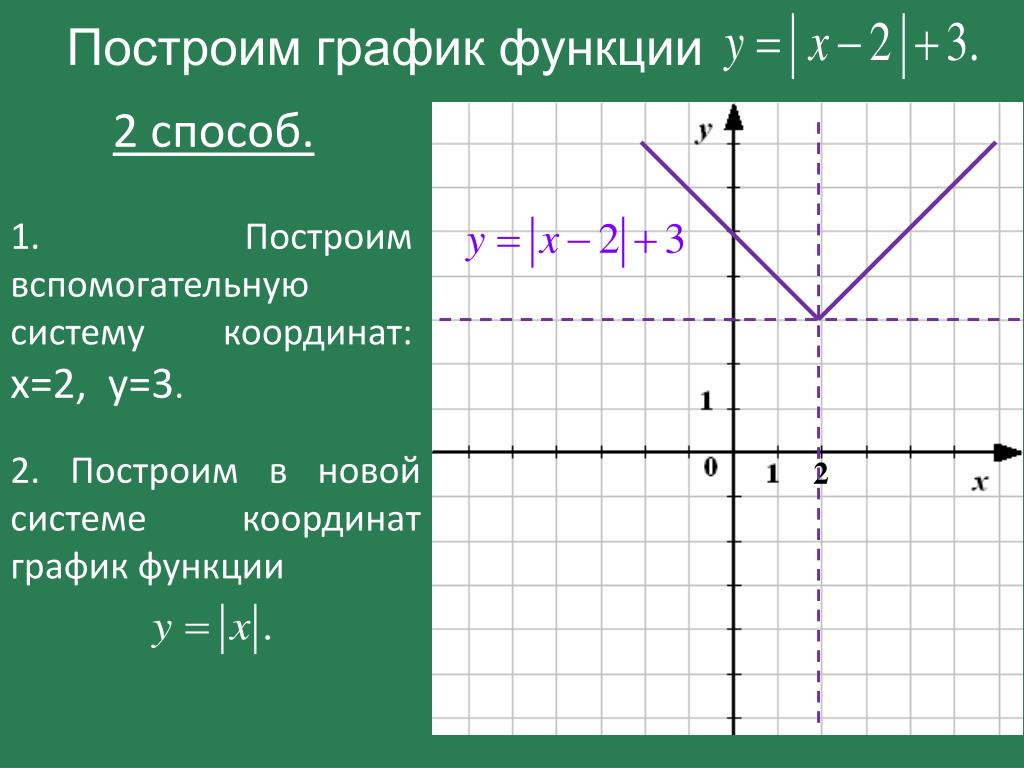
2.147. График функции в декартовых координатах
В качестве еще одного примера приведу порядок построения графика в полярных координатах. Для рассмотрения возьмем несложную и достаточно известную спираль Архимеда, уравнение которой в полярных координатах имеет вид r = kj, где k – произвольный коэффициент, отличный от 0.
Запустите вновь библиотеку FTDraw и нажмите вторую справа большую кнопку, запустив режим построения графиков в полярных координатах. В строке для формул введите значение 2*Х, диапазон задайте от 0 до 20*Pi, а количество точек установите равным 200 (рис. 2.148).
Рис. 2.148. Построение графика функции в полярных координатах
После того как вы укажете начальную точку для построения, нажмите по очереди кнопки Построить график и ОK. В результате вы получите архимедову спираль, построенную на фрагменте в системе КОМПАС-3D (рис. 2.149).
Рис. 2.149. Архимедова спираль
Данный текст является ознакомительным фрагментом.
n
Возвращает 1, если x>0
Возвращает 0, если x=0
Возвращает -1, если x<0
Построение графиков функций в Excel
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
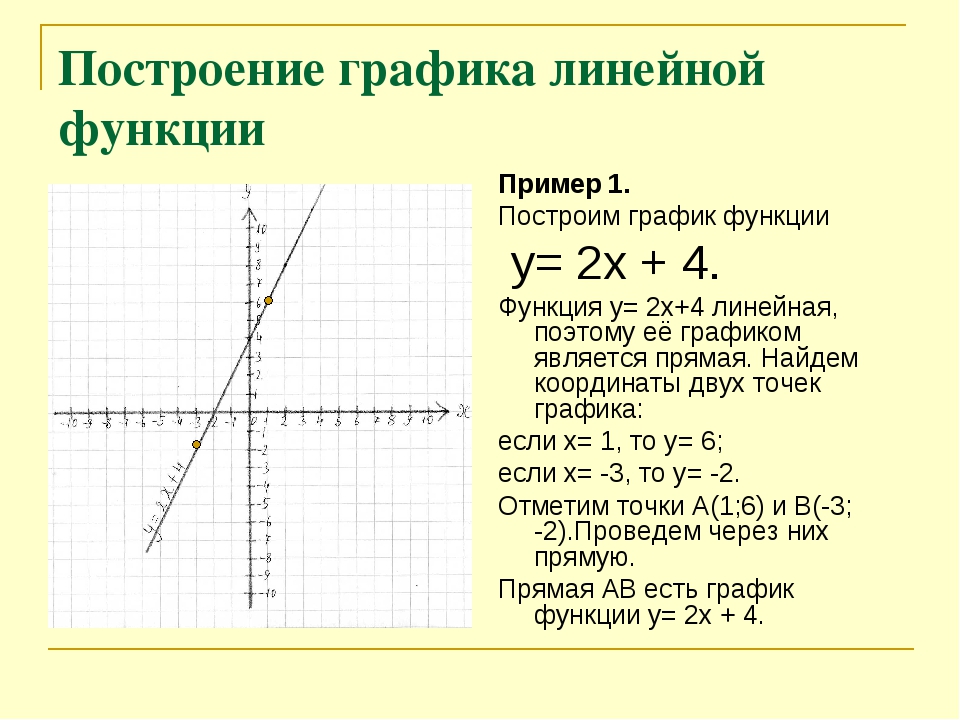
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2.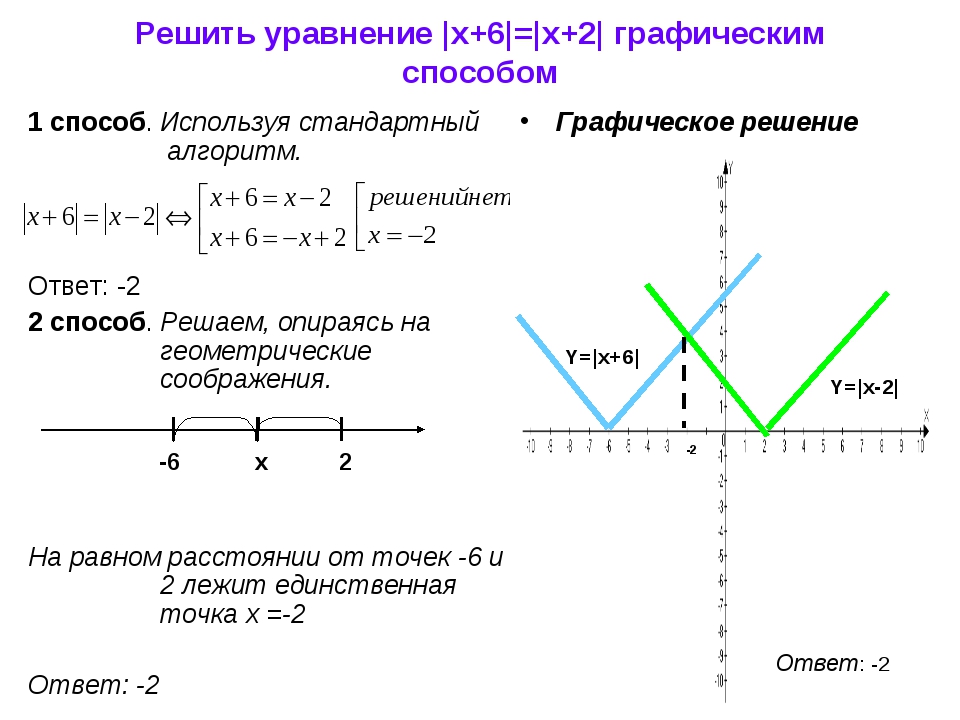
В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола.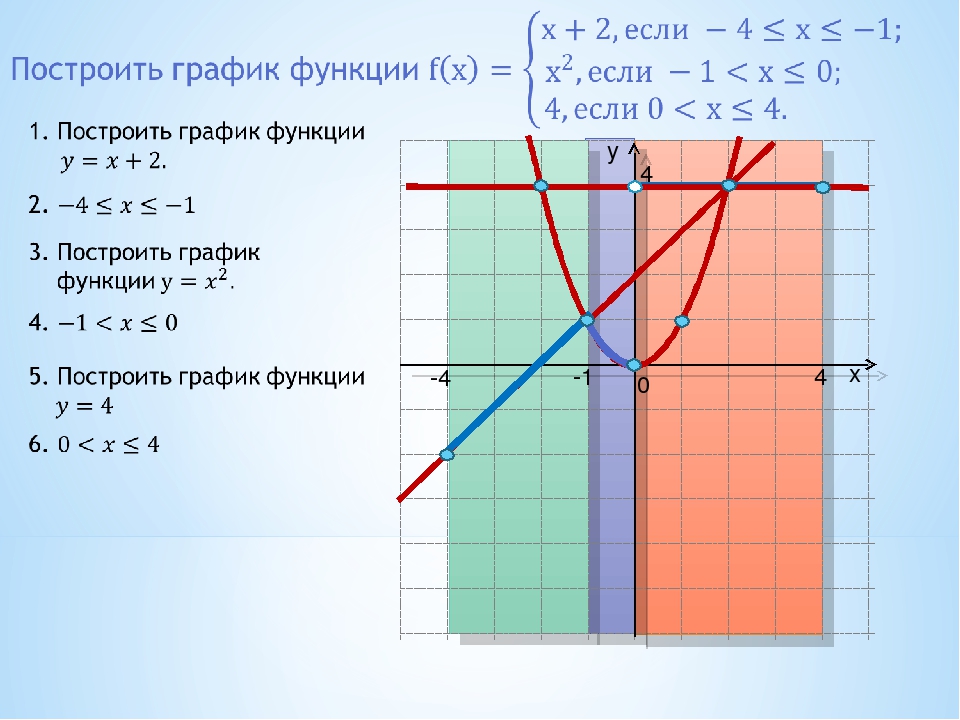
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
на Ваш сайт.
Алгебра — Рациональные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечанияПохоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-8: Рациональные функции
В этом заключительном разделе нам нужно обсудить построение графиков рациональных функций.
Вероятно, лучше всего начать с довольно простого, который мы можем сделать, не зная, как это работает.
Давайте нарисуем график \(f\left( x \right) = \frac{1}{x}\). Во-первых, поскольку это рациональная функция, мы должны быть осторожны с проблемами деления на ноль. Итак, из этого уравнения видно, что нам придется избегать \(x = 0\), так как это даст деление на ноль.
Теперь подставим несколько значений \(x\) и посмотрим, что получится.
| \(х\) | \(f(x)\) |
|---|---|
| -4 | -0.25 |
| -2 | -0,5 |
| -1 | -1 |
| -0,1 | -10 |
| -0,01 | -100 |
| 0,01 | 100 |
| 0,1 | 10 |
| 1 | 1 |
| 2 | 0. 5 |
| 4 | 0,25 |
Итак, когда \(x\) становится больше (положительно и отрицательно), функция сохраняет знак \(x\) и становится все меньше и меньше. Точно так же, когда мы приближаемся к \(x = 0\), функция снова сохраняет тот же знак, что и \(x\), но начинает становиться довольно большой. Вот набросок этого графика.
Во-первых, обратите внимание, что график состоит из двух частей. Почти все рациональные функции будут иметь такие графики, состоящие из нескольких частей.
Далее обратите внимание, что на этом графике нет никаких пересечений. Это достаточно легко проверить на себе.
Напомним, что граф будет иметь \(y\)-пересечение в точке \(\left( {0,f\left( 0 \right)} \right)\). Однако в этом случае мы должны избегать \(x = 0\), и поэтому этот график никогда не пересечет ось \(y\). Он подходит очень близко к оси \(y\), но никогда не пересекает ее и не касается ее, а значит, не пересекается с \(y\).
Далее напомним, что мы можем определить, где на графике будут \(x\)-пересечения, решив \(f\left( x \right) = 0\).Для рациональных функций это может показаться беспорядком. Однако есть хороший факт о рациональных функциях, который мы можем здесь использовать. Рациональная функция будет равна нулю при определенном значении \(x\) только в том случае, если числитель равен нулю при этом \(x\), а знаменатель не равен нулю при этом \(x\). Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно убедитесь, что ни одно из них не делает знаменатель равным нулю.
В нашем случае числитель равен единице и никогда не будет равен нулю, поэтому у этой функции не будет \(x\)-перехватов. Опять же, график подойдет очень близко к оси \(x\), но никогда не коснется ее и не пересечет ее.
Наконец, нам нужно учесть тот факт, что график подходит очень близко к осям \(x\) и \(y\), но никогда не пересекает их.
Поскольку в самих осях нет ничего особенного, мы будем использовать тот факт, что ось \(x\) на самом деле является линией, заданной \(y = 0\), а ось \(y\) действительно линия, заданная \(x = 0\).
На нашем графике, когда значение \(x\) приближается к \(x = 0\), график становится очень большим по обе стороны от линии, заданной \(x = 0\). Эта линия называется вертикальной асимптотой .
Кроме того, поскольку \(x\) становятся очень большими, как положительными, так и отрицательными, график приближается к линии, заданной \(y = 0\). Эта линия называется горизонтальной асимптотой .
Вот общие определения двух асимптот.
- Линия \(x = a\) является вертикальной асимптотой , если график неограниченно увеличивается или уменьшается с одной или обеих сторон линии по мере того, как \(x\) приближается все ближе и ближе к \(x = a \).
- Линия \(y = b\) является горизонтальной асимптотой , если график приближается к \(y = b\) при неограниченном увеличении или уменьшении \(x\).
m} + \cdots }}\], где \(n\) — наибольший показатель в числителе, а \(m\) — наибольший показатель в знаменателе.
Тогда мы имеем следующие факты об асимптотах.
- График будет иметь вертикальную асимптоту в точке \(x = a\), если знаменатель равен нулю в точке \(x = a\), а числитель отличен от нуля в точке \(x = a\).
- Если \(n < m\), то ось \(x\) является горизонтальной асимптотой.
- Если \(n = m\), то линия \(\displaystyle y = \frac{a}{b}\) является горизонтальной асимптотой.
- Если \(n > m\), то горизонтальных асимптот не будет.
Процесс построения графика рациональной функции довольно прост. Вот.
Процесс построения графика рациональной функции
- Найдите перехваты, если они есть. Помните, что \(y\)-перехват задается как \(\left( {0,f\left( 0 \right)} \right)\), и мы находим \(x\)-перехваты, устанавливая числитель равные нулю и решающие.
- Найдите вертикальные асимптоты, приравняв знаменатель к нулю и решив.
- Найдите горизонтальную асимптоту, если она существует, используя приведенный выше факт.
- Вертикальные асимптоты разделят числовую прямую на области. В каждом регионе графика не менее одной точки в каждом регионе. Эта точка скажет нам, будет ли график выше или ниже горизонтальной асимптоты, и если нам нужно, мы должны получить несколько точек, чтобы определить общую форму графика.
- Нарисуйте график.
Обратите внимание, что набросок, который мы получим в процессе, будет довольно грубым, но это нормально.Это все, что нам действительно нужно, — это основная идея того, на что будет смотреть график.
Давайте рассмотрим пару примеров.
Пример 1 Нарисуйте график следующей функции. \[f\left( x \right) = \frac{{3x + 6}}{{x — 1}}\] Показать решениеИтак, начнем с перехватов.
\[f\left( 0 \right) = \frac{6}{{ — 1}} = — 6\hspace{0,25 дюйма} \Rightarrow \hspace{0.25 дюймов}\влево( {0, — 6} \вправо)\] \(y\)-перехват равен\(x\)-перехваты будут,
\[\begin{align*}3x + 6 & = 0\\ x & = — 2\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( { — 2,0} \right)\end{ выровнять*}\]Теперь нам нужно определить асимптоты. Сначала найдем вертикальные асимптоты.
\[x — 1 = 0\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}x = 1\]Итак, у нас есть одна вертикальная асимптота.Это означает, что теперь есть две области \(x\). Это \(x < 1\) и \(x > 1\).
Теперь наибольший показатель степени в числителе и знаменателе равен 1, поэтому на линии будет горизонтальная асимптота.
\[y = \frac{3}{1} = 3\]Теперь нам просто нужны точки в каждой области \(x\). Поскольку \(y\)-перехват и \(x\)-перехват уже находятся в левой области, нам не нужно будет получать там какие-либо точки.
\[f\left( 2 \right) = \frac{{3\left( 2 \right) + 6}}{{2 — 1}} = \frac{{12}}{1} = 12\hspace{ 0,25 дюйма} \стрелка вправо \hspace{0,25 дюйма}\влево ({2,12} \вправо)\] Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.Итак, сложив все это вместе, мы получим следующий график.
Обратите внимание, что асимптоты показаны пунктирными линиями.2} — 9}}\] Показать решение
Хорошо, начнем с перехватов. \(y\)-перехват равен
\[f\left( 0 \right) = \frac{9}{{ — 9}} = — 1\hspace{0.25in} \Стрелка вправо \hspace{0.25in}\left( {0, — 1} \right )\]Числитель является константой, поэтому никаких пересечений \(x\) не будет, поскольку функция никогда не может быть равна нулю.
2} — 9 = 0\hspace{0.25 дюймов} \Стрелка вправо \hspace{0,25 дюйма}x = \pm 3\]Итак, в этом случае у нас будет три области на нашем графике: \(x < - 3\), \( - 3 < x < 3\), \(x > 3\).
Кроме того, наибольший показатель степени в знаменателе равен 2, и, поскольку в числителе нет \(x\), наибольший показатель степени равен 0, поэтому ось \(x\) будет горизонтальной асимптотой.
Наконец, нам нужны очки. Здесь мы будем использовать следующие моменты.
\[\begin{align*}f\left( { — 4} \right) & = \frac{9}{7} & \hspace{0.25in} & \left( { — 4,\frac{9}{ 7}} \right)\\ f\left( { — 2} \right) & = — \frac{9}{5} & \hspace{0.25in} & \left( { — 2, — \frac{9 {5}} \right)\\ f\left( 2 \right) & = — \frac{9}{5} & \hspace{0.25in} & \left( {2, — \frac{9}{ 5}} \right)\\ f\left( 4 \right) & = \frac{9}{7} & \hspace{0.25in} & \left( {4,\frac{9}{7}} \ вправо)\конец{выравнивание*}\]Обратите внимание, что вместе с точкой пересечения \(y\) у нас фактически есть три точки в средней области.
2} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]Итак, у нас снова два и три региона, которые у нас есть, это \(x < 0\), \(0 < x < 4\) и \(x > 4\).
Далее, наибольший показатель степени как в числителе, так и в знаменателе равен 2, так что на линии будет горизонтальная асимптота,
\[y = \frac{1}{1} = 1\]Теперь один из \(x\)-перехватов находится в крайней левой области, поэтому нам там не нужны точки.Другой \(x\)-перехват находится в средней области. Итак, нам понадобится точка в крайней правой области, и, как отмечалось в предыдущем примере, мы хотим получить еще пару точек в средней области, чтобы полностью определить ее поведение.
\[\begin{align*}f\left( 1 \right) & = 1 & \hspace{0.25in} & \left( {1,1} \right)\\ f\left( 3 \right) & = — \frac{5}{3} & \hspace{0.25in} & \left( {3, — \frac{5}{3}} \right)\\ f\left( 5 \right) & = \frac {{21}}{5} и \hspace{0. 25 дюймов} & \left( {5,\frac{{21}}{5}} \right)\end{align*}\]Вот скетч для этой функции.
Обратите внимание, что на этот раз средняя область не имеет такого же поведения на асимптотах, как мы видели в предыдущем примере. Это может и будет происходить довольно часто. Иногда поведение на двух асимптотах будет таким же, как в предыдущем примере, а иногда оно будет иметь противоположное поведение на каждой асимптоте, как мы видим в этом примере.Из-за этого нам всегда нужно будет получить пару точек в этих типах регионов, чтобы определить, каким будет поведение.
Как построить график функции в Excel | Малый бизнес
Математическая функция — это формула, которая принимает входные данные x, применяет к ним набор вычислений и выдает результат с именем y. Вычисляя функцию на большом количестве заданных интервалов, можно построить график рассеяния функции.В бизнесе это имеет много применений.
Например, вы можете построить график прибыли за вычетом затрат при различных объемах продаж или оценить общие затраты, нанеся постоянные затраты на различные приращения переменных затрат.Создайте заголовки для таблицы данных. Введите входную переменную в ячейку A1 и выходную переменную в ячейку B1. Если хотите, вы можете использовать математические стандарты «x» и «y» или что-то более описательное, например, «продажи» и «прибыль».
Введите первый и второй интервал вашей входной переменной (например, «x» или «продажи»), которые вы будете использовать для построения графика функции.Например, если ваши интервалы представляют собой целые числа, вы можете начать с ввода «1» в ячейку A2 и «2» в ячейку A3. Выберите обе эти ячейки, а затем щелкните и перетащите маленький черный квадрат в правом нижнем углу области выбора вниз, пока не получите столько значений, сколько хотите отобразить.
Введите знак равенства «=» в ячейку B2, а затем введите формулу сразу после него, не оставляя пробелов.
Например, чтобы определить количество продаж, которое вам необходимо совершить для определенного продукта, чтобы покрыть затраты, вы можете использовать:=(A2*50)-3500
Замените «50» на цену продажи, а «3500» на ваши расходы.
Выберите ячейку B2, а затем перетащите, чтобы скопировать формулу вниз по столбцу тем же методом, который вы использовали на шаге 2. Убедитесь, что каждое из ваших значений x имеет соответствующую функцию справа от него. При этом столбец будет автоматически заполняться решениями для каждой функции в зависимости от значения x в столбце A.
Выберите все ячейки, в которые вы ввели данные, включая заголовок.
Перейдите на вкладку «Вставка», нажмите «Разброс» в области «Диаграммы», а затем выберите нужный тип графика.После этого график появится на вашем рабочем листе.
8 Функции обучения и обучения | Как учатся студенты: история, математика и естествознание в классе
ПРИМЕЧАНИЯ
ССЫЛКИ1.
Изучение функций, как мы определяем его здесь, существенно пересекается с темой «алгебры», традиционно преподаваемой в Соединенных Штатах в девятом классе, хотя национальные стандарты и стандарты многих штатов теперь рекомендуют, чтобы аспекты алгебры рассматривались в более ранних классах (как делается в большинстве других стран).Хотя функции являются важной частью алгебры, другие аспекты алгебры, такие как решение уравнений, в этой главе не рассматриваются.
2.
Томас, 1972, с. 17.
3.
Гольденберг, 1995 г.; Лейнхардт и др., 1990; Ромберг и др., 1993.
4.
Натан и Кёдингер, 2000.
5.
Кёдингер и Натан, 2004 г.
6.
Кёдингер и Натан, 2004 г.
7.
Кёдингер и др., 1997.
8.
Кальчман, 2001.
9.
Шенфельд и др., 1993.
10.
Шонфельд и др., 1987.
11.
Шенфельд и др., 1998, с. 81.
12.
Чи и др., 1981.
13.
Чи и др., 1981; Шонфельд и др., 1993.
14.
Кальчман, 2001.
Chi, M.T.H., Feltovich, PJ, and Glaser, R. (1981). Категоризация и представление задач по физике экспертами и новичками. Когнитивные науки , 5 , 121-152.
Гольденберг, Е.П. (1995). Множественные представления: средство для понимания. В Д. Перкинс, Дж. Шварц, М. Уэст и М.
Виске (ред.), Программное обеспечение идет в школу: обучение для понимания с помощью новых технологий (стр. 155-171). Нью-Йорк: Издательство Оксфордского университета.Кальчман, М. (2001). Использование неопиажеской структуры для изучения и обучения математическим функциям .Докторская диссертация, Торонто, Онтарио, Университет Торонто.
Кёдингер, К. Р., и Натан, М. Дж. (2004). Настоящая история, стоящая за задачами истории: влияние представлений на количественные рассуждения. Journal of the Learning Sciences , 13 (2).
Koedinger, K.R., Anderson, J.R., Hadley, W.H., and Mark, MA (1997). Интеллигентное репетиторство ходит в школу в большом городе. Международный журнал искусственного интеллекта в образовании , 8 , 30-43.
Лейнхардт Г., Заславский О. и Штейн М. (1990). Функции, графики и графики: задачи, обучение и преподавание. Review of Educational Research , 60 (1), 1-64.
Натан, М.Дж., и Кёдингер, К.Р. (2000). Представления учителей и исследователей о раннем развитии алгебры. Journal for Research in Mathematics Education , 31 (2), 168-190.
Ромберг Т., Феннема Э.и Карпентер Т.П. (1993). Интеграция исследований по графическому представлению функций . Махва, Нью-Джерси: Lawrence Erlbaum Associates.
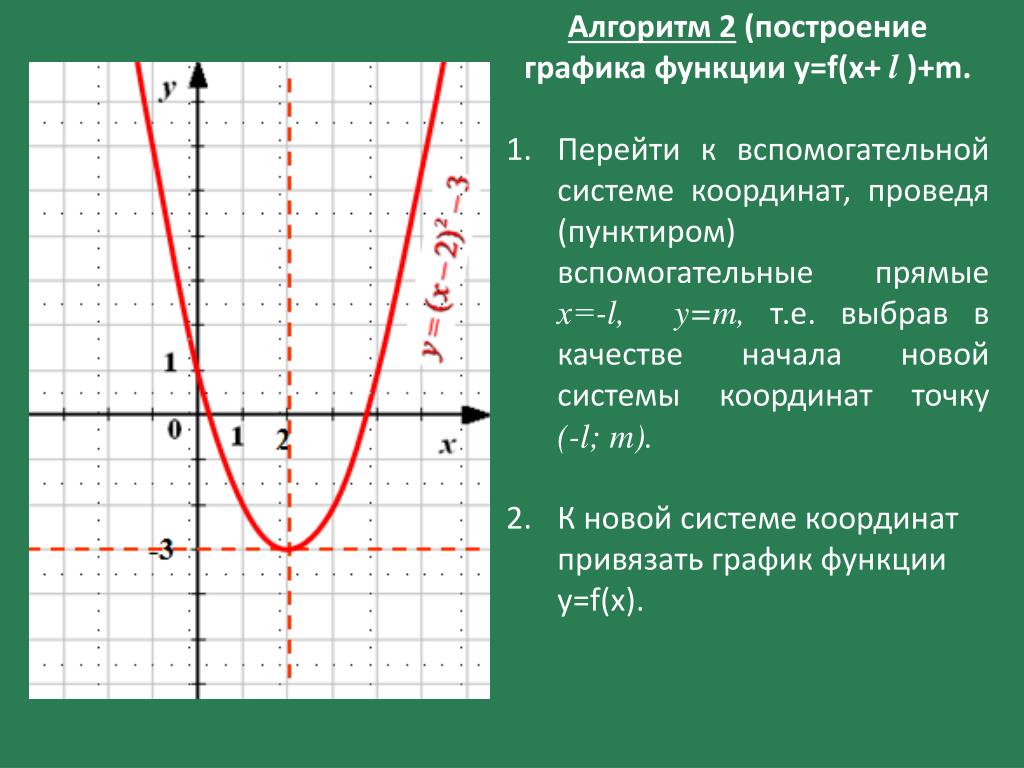
Графики основных функций и их… Пошаговое решение математических задач
4.4 — Графики основных функций и их вариантов ВАРИАНТЫ
Многие графики, рассмотренные в главе 3, являются графиками функций. Согласно тесту вертикальной линии любая прямая линия, которая не является вертикальной, является графиком функции, как и график любой вертикальной параболы.2+5=(г{омикрон}ч)(х)
В оставшейся части этого раздела мы обсудим графики нескольких основных функций, которые не являются ни линейными, ни квадратичными.
Графики этих функций состоят из участков различных прямых или прямых и кривых.ФУНКЦИИ АБСОЛЮТНЫХ ЗНАЧЕНИЙ Одной из общих функций, которая не является линейной и не квадратичной, является функция абсолютного значения, определяемая формулой f(x) = |x| ори = |х|. Поскольку |х| можно найти для любого действительного числа x, область определения (-inf,inf.Кроме того, |x|>=0 для любого действительного числа x , поэтому диапазон равен (0,inf). x. С другой стороны, если x<0, то y= |x|=-x, а y=-xi отображается на графике для отрицательных значений x. График представляет собой объединение двух лучей. Окончательный график показан на рисунке 4.6. Согласно критерию вертикальной линии, график представляет собой график функции. Обратите внимание, что график функции f(x) = |x| симметричен относительно оси y.
Пример 2
ГРАФИК ФУНКЦИИ АБСОЛЮТНОГО ЗНАЧЕНИЯ
График f(x) = |x-2|.
Обратите внимание, что это составная функция g{omicron}h, где g(x) = |x| и h(x) = x — 2. Область определения f равна (-inf,inf, а диапазон равен (0,inf). Этот граф имеет ту же форму, что и граф y = |x|, но «вершина» .point смещается на 2 единицы вправо, от (0,0) до (2,0). См. Рисунок 4.7. Ось симметрии – вертикальная линия x=2, проходящая через (2,0)
ГРАФИК ФУНКЦИИ АБСОЛЮТНОГО ЗНАЧЕНИЯ
График f(x) = |3x +4|+1.
Значение f(x) = y всегда больше или равно 1, так как |3x+4|>=0.Таким образом, y-значение «вершины» равно 1, а диапазон – [1,inf]. Домен (-inf,inf. Значение x «вершины» можно найти, подставив 1 вместо y в уравнении.
y= |3x +4|+1
1= |3x +4|+1 Пусть y=1.
0= |3x +4| Вычесть 1.x=-4/3Решите 3x + 4 = 0
Построение нескольких других упорядоченных пар приводит к графику на рис. 4.8. На графике показана «вершина», переведенная в (-4/3,1).Ось симметрии x=-4/3. Коэффициент x, равный 3, определяет наклоны двух лучей, образующих график.
Один имеет наклон 3, а другой — наклон -3. Поскольку абсолютное значение наклона больше 1, лучи круче, чем лучи, формирующие график y = |x|.ФУНКЦИИ, ЗАДАННЫЕ ЧАСТЬЮ Графики функций абсолютного значения в примерах 2 и 3 состоят из частей двух разных прямых линий. Такие функции, называемые функциями, определенными кусочно , часто задаются разными уравнениями для разных частей области.
Пример 4
График функции
Мы должны изобразить каждую часть домена отдельно. Если x<=2 , эта часть графика имеет конечную точку x=2. Найдите значение y, подставив 2 вместо xin y=x+1 , чтобы получить y=3. Для построения этой части графика требуется еще одна точка. Выберите значение x меньше 2. Если выбрать x=-1 , получится y=-1+1=0. Нарисуйте график через (2,3) и (-1,0) как луч с конечной точкой в (2,3).Аналогично нарисуйте луч для x>2. Этот луч будет иметь открытую конечную точку, когда x = 2 и y = -2 (2) + 7 = 3. Выбор x = 4 дает sy = -2 (4) + 7 = -1 . Луч, проходящий через (2,3) и (4,-1), завершает граф. В этом примере два луча
встречаются в точке (2,3), хотя это не всегда так. График показан на рис. 4.9Пример 5 ПОКАЗ ФУНКЦИИ, ОПРЕДЕЛЕННОЙ ПО ЧАСАМ
График
Начертите график луча y=x+2, выбрав x так, чтобы x<=0, со сплошной конечной точкой в (0,2).Луч имеет наклон 1 и точку пересечения y 2. Тогда график y=1/2 для x>0. Этот график будет половиной параболы с открытым концом в точке (0,0). См. Рисунок 4.10. Обратите внимание, что в этом примере две части не встречаются.ФУНКЦИИ НАИБОЛЬШИХ ЦЕЛЫХ Другим типом функций с графиком, состоящим из отрезков, является функция наибольшего целого числа, записываемая y=[x] и определяемая следующим образом:
[x] — наибольшее целое число, меньшее или равное x.
Например, [8] = 8 ,[-5]=-5 , [{Pi}] = 3, [12, 1/9]=12, [-2. 001] = -3 и так далее.Пример 6 ГРАФИК ФУНКЦИИ НАИБОЛЬШЕГО ЦЕЛОГО
График у=[х]
Для любого значения x в интервале 0,1 [x]=0. Кроме того, для x в 1,2 [x]=1. Этот процесс продолжается; x в 2,3 значение [x] равно 2. Значения y постоянны между целыми числами, но они скачут при целых значениях x. Таким образом, график, показанный на рис. 4.11, представляет собой серию отрезков. В каждом случае включается левая конечная точка сегмента, а правая конечная точка исключается.Домен функции равен ,(-inf,inf, а диапазон – набор целых чисел {…,-2,-1,0,1,2,…}.
Каждый из графиков в примерах 6, 7 и 8 состоит из серии горизонтальных отрезков. (См. рис. 4.11, 4.12 и 4.13.) Функции, формирующие эти графики, называются ступенчатыми.ПРОСТО
Специальные функции, называемые ступенчатыми, используются, когда ожидается, что значение диапазона останется постоянным для заданного интервала значений домена.
Например, плата за парковку часто рассчитывается путем взимания определенной фиксированной платы за первый час и другой платы за каждый дополнительный час (или часть часа).Предположим, что ежедневная парковка в центре города взимает базовую плату в размере 5 долларов США за первый час и 1 доллар США за каждый дополнительный час или его часть. Максимальная плата в день составляет 15 долларов. Парковка на 7 часов будет стоить 5 долларов + 1 (6) долларов = 11 долларов.
РЕШИТЬ КАЖДУЮ ПРОБЛЕМУ
A. Сколько будет стоить парковка на ежедневной парковке в центре города на 3 человек.5 часов?
B. Мелисса и ее дети планируют провести весь день, путешествуя по городу. Сколько ей будет стоить припарковаться на 12-часовой парковке в центре города?
ОТВЕТА А. Это будет стоить 8 долларов. B. это будет стоить 15 долларов, максимальная плата в день.
Пример 7 ГРАФИК СТУПЕНЧАТОЙ ФУНКЦИИГрафик y=[1/2x+1
Попробуйте некоторые значения x в уравнении, чтобы увидеть, как ведут себя значения y. Здесь приведены некоторые образцы упорядоченных пар.
Эти упорядоченные пары предполагают, что если x находится в интервале 0,2, то y=1.Для x в 2,4, y=2
2 и т. д. График показан на рисунке 4.12. Опять же, домен (-inf,inf. Диапазон {…-1,0,1,2,…}.
Функция наибольшего целого числа может использоваться для описания многих распространенных практик ценообразования, встречающихся в повседневной жизни, как показано в следующем примере.
Пример 8 ПРИМЕНЕНИЕ ФУНКЦИИ НАИБОЛЬШЕГО ЦЕЛОГО
Компания экспресс-почты берет 10 долларов за посылку весом 1 фунт или менее. Каждый дополнительный фунт или часть фунта стоит на 3 доллара больше.Найдите стоимость отправки посылки весом 2 фунта; 2,5 фунта; 5,8 фунтов. График заказанных пар (фунты, стоимость). Это график функции?
Стоимость посылки весом 2 фунта составляет 10 долларов США за первый фунт и 3 доллара США за второй фунт, всего 13 долларов США.
Для пакета весом 2,5 фунта стоимость будет такой же, как и для пакета весом 3 фунта: 10 + 2(3) = 16, или 16 долларов. Пакет весом 5,8 фунта будет стоить столько же, сколько пакет весом 6 фунтов: 10 + 5 (3) = 25, или 25 долларов. График этой ступенчатой функции показан на рисунке 4.13. Обратите внимание, что в данном случае включены правые конечные точки, а не левые.ОБРАТНЫЕ ФУНКЦИИ
Сложение и вычитание являются обратными операциями: начиная с числа x, прибавляя 5 и вычитая 5, в результате возвращается x. Точно так же некоторые функции являются обратными друг другу. Например, функции
f(x)=8x и g(x)=1/8x
обратны друг другу. Это означает, что если выбрано значение x, такое как x=12, так что
f(x)=8*12=96
вычисление g(96) дает
g(96)=1/8*96=12
Таким образом, g[ f(12)] = 12 .
Кроме того, f[ g(12)] = 12. Для этих функций f и g можно показать, что f[ g(x)] = x и g[ f(x)] = x для любого значения x.В этом разделе показано, как начать с такой функции, как f(x)=8x, и получить обратную функцию g(x) = (1/8)x . Не все функции имеют обратные функции. Единственные функции, у которых есть обратные функции, — это функции «один к одному».
ВЗАИМОДЕЙСТВУЮЩИЕ ФУНКЦИИ Для функции y=5x-8 любые два разных значения x дают два разных значения y.2 = 16. Такая функция, как y = 5x -8, где разные элементы домена всегда ведут к разным элементам диапазона, называется однозначной функцией.
ВЗАИМНО-ОДНА ФУНКЦИЯ Функция f является взаимно однозначной, если для элементов a и b из домена функции f из
a!=b следует f(a)!=f(b)
Пример 1 РЕШЕНИЕ, ЯВЛЯЕТСЯ ЛИ ФУНКЦИЯ ОДИН-К-ОДНООБРАЗНОЙОпределите, является ли каждая из следующих функций взаимно однозначной.
(a)f(x) = -4x + 12
Предположим, что a!=b.2)=root(25-9)=4Здесь, хотя 3!=-3, f(3)!=f(-3). По определению, это не однозначная функция.
Как показано в примере 1(b), способ показать, что функция не является однозначной, состоит в том, чтобы создать пару неравных чисел, которые приводят к одному и тому же значению функции.
Существует также полезный графический тест, который показывает, является ли функция взаимно однозначной. Этот тест горизонтальной линии для функций «один к одному» можно резюмировать следующим образом.ТЕСТ ГОРИЗОНТАЛЬНОЙ ЛИНИИ Если каждая горизонтальная линия пересекает график функции не более чем в одной точке, то функция является однозначной.
ПРИМЕЧАНИЕ В примере 1(b) график функции представляет собой полукруг. Горизонтальных линий, пересекающих график полукруга в двух точках, бесконечно
, поэтому проверка горизонтальной линии показывает, что функция не является взаимно однозначной.Пример 2 ИСПОЛЬЗОВАНИЕ ТЕСТА ГОРИЗОНТАЛЬНОЙ ЛИНИИ
Используйте тест горизонтальной линии, чтобы определить, являются ли графики на рисунках 4.14 и 4.15 графиками взаимно однозначных функций.
(а)
Каждая точка, в которой горизонтальная линия пересекает график, имеет одно и то же значение y, но другое значение x. Поскольку более одного (здесь три) различных значения x приводят к одному и тому же значению y, функция не является взаимно однозначной.
(б)
Каждая горизонтальная линия будет пересекать график на рис. 4.15 ровно в одной точке. Эта функция один к одному.ОБРАТНЫЕ ФУНКЦИИ Как упоминалось ранее, некоторые пары однозначных функций «отменяют» друг друга. Например, если
f(x)=8x+5 и g(x)=(x-5)/8
f(10)=8*10+5=85 и g(85)=(85-5)/8=10
Начиная с 10, мы «применили» функцию f, а затем «применили» функцию g к результату, который вернул число 10.См. Рисунок 4.16. Аналогично для этих же функций проверьте, что
f(3)=29 и g(29)=3,f(-5)=-35 и g(-35)=-5
g(2)=-3/8 и f(-3/8)=2
В частности, для этих функций
f[g(x)]=2 и 8[f(2)]=2На самом деле для любого значения x
f [g (x)]=x и g[f(x)]=x
или (f{omicron}g)(x)=x и (g{omicron}f )(х)=хИз-за этого свойства g называется обратным к f.
-1 являются набором действительных чисел.-1 являются зеркальными отражениями по отношению к этой строке.ПРОСТО
Обратные функции используются государственными учреждениями и другими предприятиями для отправки и получения закодированной информации. Функции, которые они используют, обычно очень сложны. Простой пример включает функцию f(x) = 2x + 5. Если каждой букве алфавита присвоить числовое значение в соответствии с ее положением (a=1,…,z=26, слово АЛГЕБРА будет закодировано как7 29 191594177.-1(х)=корень(3,х+1)
OpenAlgebra.com: отношения, графики и функции
В этом разделе мы изучим функции более глубоко и начнем с определения отношения как любого набора упорядоченных пар.
Пример отношения может выглядеть как {(2,3), (2,5), (0,1)}. Здесь мы имеем отношение, состоящее из трех упорядоченных пар или точек в декартовой системе координат. Мы знакомы с упорядоченными парами и обычно видим, что они обозначаются как ( x , y ). Обычно значение x (первый компонент) будет независимой переменной или входом, а значение y (второй компонент) будет зависимой переменной или выходом.
Пример { (2,3), (2,5), (0,1) } является НЕ функцией, потому что x -значение 2 присвоено более одного y -значения, а именно 3 и 5 . Для каждого значения x может быть только одно значение y . Затем мы определяем домен как набор значений x и диапазон как набор значений y , для которых определено отношение.
Пример:
Совет : При просмотре списка упорядоченных пар, если есть повторяющиеся значения x , то отношение не является функцией.Обычно это указывает на наличие входа с несколькими выходами. (Это не относится к значениям и )Определите, являются ли отношения функциями. Если да, укажите домен и диапазон.
Отношения могут состоять из бесконечного числа упорядоченных пар, и в этом случае составить большой список будет невозможно. Граф может представлять отношение, рассматривая его как большой список упорядоченных пар. Каждая точка на графике представляет упорядоченную пару ( x , y ).
Обратите внимание, что если мы сможем провести вертикальную линию, дважды пересекающую график, мы сможем идентифицировать одно значение x с двумя соответствующими значениями y . Следовательно, это не может быть функцией.
В качестве альтернативы, если какая-либо вертикальная линия пересекает график только один раз, то она представляет собой функцию.
Используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
Будьте готовы указать домен и диапазон данных на графике.Не забывайте думать о графе как о бесконечном наборе упорядоченных пар ( x , y ). По графику определите значения x и y . Сначала заштрихуйте домен и диапазон, затем преобразуйте в нотацию интервала.
На данный момент должно быть ясно, что показанный круг не является функцией. Тем не менее, мы все еще можем определить домен и диапазон отношения, которое оно представляет.Видео на YouTube:
—Использование графика для решения системы линейных уравнений x+y=5 и y−2x=−4
«Используйте график для решения» означает, что вы должны их нарисовать!
Метод 1: решить для x = 0 и y = 0 (т.е. ось y и ось x соответственно):
x + y = 5
установите x = 0, затем 0 + y = 5 => y = 5, чтобы линии проходили через (0, 5)
установите y = 0, тогда x + 0 = 5 => x = 5, поэтому прямая проходит через (5,0)
постройте обе точки, проведите через них прямую линию
y — 2x = -4
, если x = 0, то y = -4, поэтому прямая проходит через (0, -4)
, если y = 0, то x = 2, поэтому прямая проходит через (2,0)
, постройте обе точки, начертите прямая, проходящая через них
Способ 2: с использованием формы пересечения наклона.
Первым шагом является преобразование каждого уравнения в форму пересечения наклона y = mx + b.
m = градиент = изменение y / изменение x, и b = y точка пересечения через (0, b) или (0,5)
теперь вы можете нанести точку (0,5) и отметить вторую точку, например (1, 4)
провести прямую линию, проходящую через них
y — 2x = -4 становится y = 2x — 4
градиент = 2 (4 вверх, 2 поперек) и проходит через (0, b) или (0, -4)
нанесите точку (0, -4) и отметьте вторую точку на основе градиента e.г. (2, 0)
Нарисуйте прямую, проходящую через них
Решите
После того, как вы нарисовали обе линии, найдите «решение». Это точка пересечения двух линий.
Математически это место, где две функции равны, поэтому (сделайте это, если вопрос требует «решить», «найти» и т. д.):
, если y = -x + 5 и y = 2x — 4 мы можем сказать, что поэтому -x + 5 = 2x — 4
=> 3x = 9 => x = 3
теперь у нас есть x, подставьте любое из уравнений, чтобы получить y = 2(3) — 4 = 2
, следовательно, точка пересечения или решения (3,2)
Математическая сцена — Функции 2 — Урок 3
Математическая сцена — Функции 2 — Урок 3 — Рациональные функции и асимптоты2009 Расмус Эф ог Джанн Сак Функции 2
Урок 3 Рациональный функции и асимптоты
Функция формы где t(x) и n(x) — многочлены, называется рациональной функцией.
Графики рациональных функций можно узнаваемы по тому факту, что они часто распадаются на две или более частей. Эти части выходят за пределы системы координат по воображаемой прямой линии, называемой асимптота.
Давайте посмотрим на функцию
Этот график следует горизонтальной линии (красная на диаграмме) по мере его перемещения из системы влево или вправо. Это горизонтальная асимптота с уравнением y = 1.Когда x приближается к значениям 1 и 1 график построен по вертикальным линиям (синие). Эти вертикальные асимптоты происходят, когда знаменатель функции n(x) равен нулю (не числитель).
Чтобы найти уравнения вертикальных асимптот, мы должны решить уравнение:x 2 1 = 0
х 2 = 1
х = 1 или х = 1
Рядом с значения х = 1 и x = 1 график идет почти вертикально вверх или вниз, а функция стремится либо к +∞, либо к ∞.
Получаем горизонтальная асимптота, потому что числитель и знаменатель, t(x) = x 2 и n(x) = x 2 1 почти равны, поскольку x становится все больше и больше.
Если, например, x = 100, то x 2 = 10000 и x 2 1 = 9999, так что, разделив одно на другое, мы получим почти 1. Чем больше значение x, тем ближе мы к 1.Вертикальные асимптоты можно найти, решив уравнение n(x) = 0, где n(x) — знаменатель функции (примечание: это применимо только в том случае, если числитель t (x) не равен нулю для одного и того же x ценность).
Горизонтальные асимптоты можно найти, найдя предел
Пример 1
Найдите асимптоты для функция .
Чтобы найти вертикаль асимптотой решаем уравнение
х 1 = 0
х = 1
График имеет вертикальную асимптота с уравнением х = 1.
Чтобы найти горизонталь асимптота, которую мы вычисляем .
Числитель всегда занимает значение 1, поэтому чем больше x становится, тем меньше становится дробь.
Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.Это говорит нам о том, что у = 0 (которая является осью x) является горизонтальной асимптотой.
Наконец нарисуйте график в ваш калькулятор, чтобы подтвердить то, что вы нашли.
Пример выше предлагает следующее простое правило:
Рациональная функция, у которой степень знаменателя выше чем степень числителя имеет ось x как горизонтальную асимптота.Пример 2
Найдите асимптоты для .
Сразу видно, что вертикальных асимптот нет, так как знаменатель никогда не может быть равен нулю.
x 2 + 1 = 0
x 2 = 1 не имеет вещественных раствор
Теперь посмотрим, что происходит, когда x становится бесконечно большим:
Метод, который мы использовали ранее для решения этого типа Проблема состоит в том, чтобы разделить на наибольшую степень x.
Разделить все на x 2 и затем отменитьдроби, где х стоит в знаменателе а не числитель стремится к 0 . График имеет горизонтальную асимптота г = 2 .
Теперь нарисуем график с помощью калькулятора
Сначала выберите ГРАФИК в меню.
Затем введите формулу будьте осторожны, чтобы включить скобки, как показано на рисунке
Вот что такое калькулятор показывает нам. График фактически пересекает свою асимптоту в одной точке. (Это никогда не может происходит с вертикальной асимптотой).
Пример 3
Теперь пример, где числитель на одну ступень выше знаменателя.
. Числитель является полиномом второй степени, а знаменатель – полиномом второй степени.
первая степень.Сначала вертикаль асимптоты:
х 1 = 0
x = 1
Одна вертикальная асимптота с уравнением x = 1 .
Мы используем длинное деление и разделить числитель на знаменатель
Теперь мы можем переписать ф(х):
Мы знаем, что это означает, что f(x) ≈ x + 1 по мере увеличения x.
говорит нам, что прямая линия у = х + 1 есть наклонная асимптота
График показан ниже.
Если мы хотим спекулировать на дальнейшие возможности, мы можем видеть, что если степень числителя равна 2 степени больше, чем у знаменателя, то график выходит за пределы система координат по параболической кривой и так далее.
Пример 4
Найдите асимптоты функция .
В этом примере деление уже сделано, так что мы можем видеть, что есть наклонная асимптота с уравнение y = х .
Чтобы найти вертикаль асимптоты решаем уравнение п(х) = 0,
x 2 1 = 0
x 2 = 1
х = 1 или х = 1
Вертикальные асимптоты х = 1 и х = 1.
Вот график
Резюме1) Вертикальные асимптоты может произойти, когда знаменатель n(x)
.
равен нулю.
Для их финансирования необходимо решить уравнение n(x) = 0,2) Если степень знаменатель n(x) больше, чем у
числитель t(x), то ось x представляет собой асимптота.3) Если степень знаменатель n(x) такой же, как у
числитель t(x), то находим асимптота по
расчет .4) Если степень знаменатель n(x) на единицу меньше, чем у
числитель t(x), то мы можем найти уравнение
наклонная асимптота деления.
m} + \cdots }}\]
\(y\)-перехват равен
Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.
2} — 9 = 0\hspace{0.25 дюймов} \Стрелка вправо \hspace{0,25 дюйма}x = \pm 3\]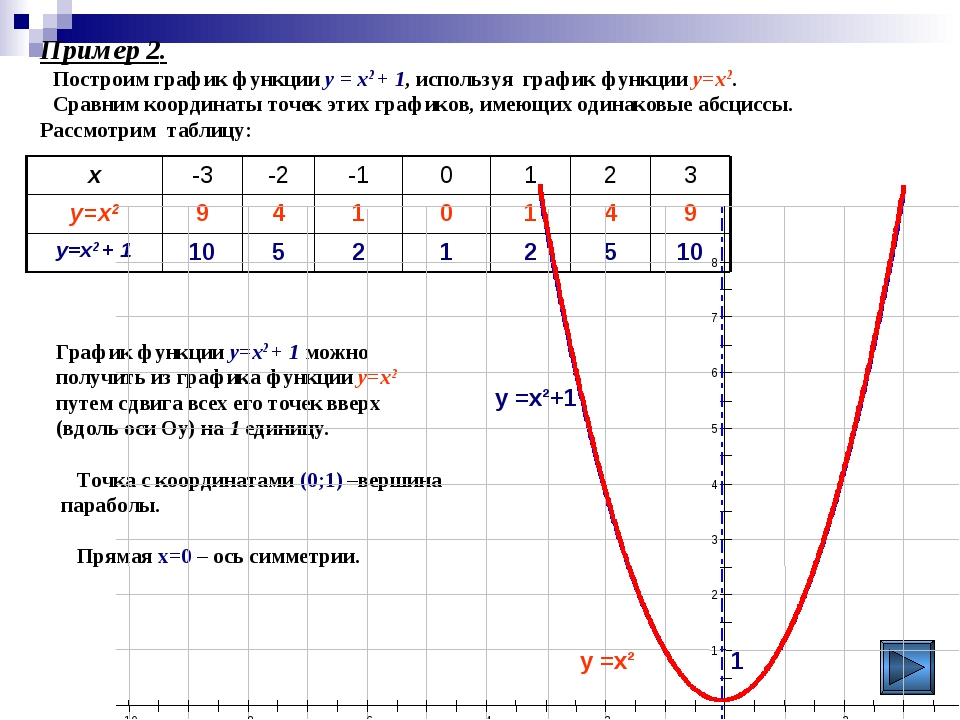
2} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]
25 дюймов} & \left( {5,\frac{{21}}{5}} \right)\end{align*}\]
Например, вы можете построить график прибыли за вычетом затрат при различных объемах продаж или оценить общие затраты, нанеся постоянные затраты на различные приращения переменных затрат.
Например, чтобы определить количество продаж, которое вам необходимо совершить для определенного продукта, чтобы покрыть затраты, вы можете использовать:
Виске (ред.), Программное обеспечение идет в школу: обучение для понимания с помощью новых технологий (стр. 155-171). Нью-Йорк: Издательство Оксфордского университета.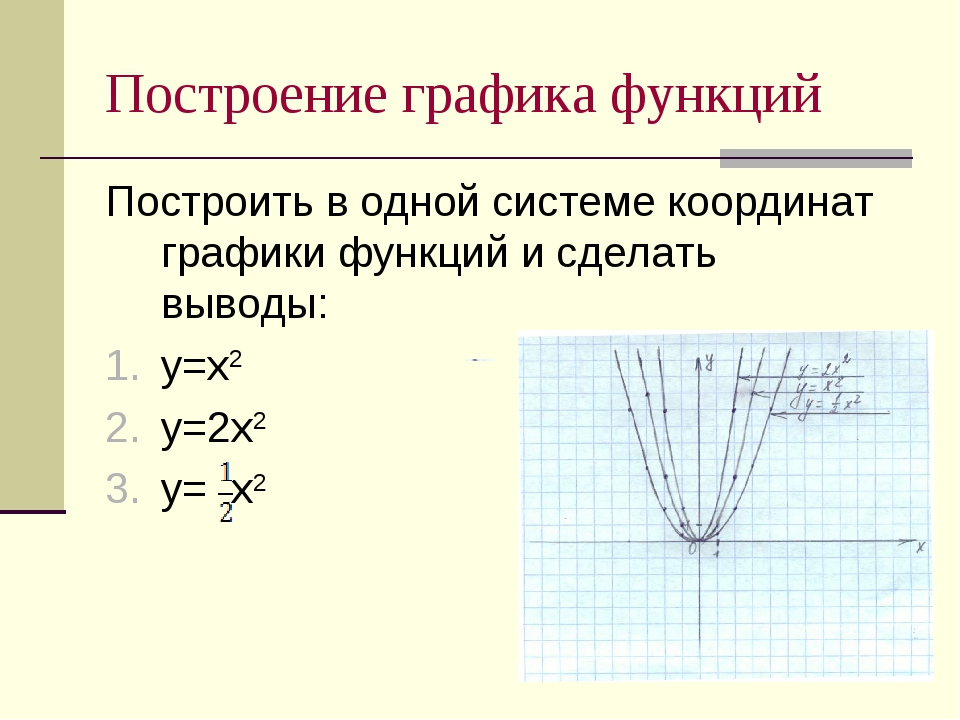
Графики этих функций состоят из участков различных прямых или прямых и кривых.
Область определения f равна (-inf,inf, а диапазон равен (0,inf). Этот граф имеет ту же форму, что и граф y = |x|, но «вершина» .point смещается на 2 единицы вправо, от (0,0) до (2,0). См. Рисунок 4.7. Ось симметрии – вертикальная линия x=2, проходящая через (2,0) 
Один имеет наклон 3, а другой — наклон -3. Поскольку абсолютное значение наклона больше 1, лучи круче, чем лучи, формирующие график y = |x|.
Выбор x = 4 дает sy = -2 (4) + 7 = -1 . Луч, проходящий через (2,3) и (4,-1), завершает граф. В этом примере два луча 
001] = -3 и так далее.
Например, плата за парковку часто рассчитывается путем взимания определенной фиксированной платы за первый час и другой платы за каждый дополнительный час (или часть часа).
Здесь приведены некоторые образцы упорядоченных пар. 
Для пакета весом 2,5 фунта стоимость будет такой же, как и для пакета весом 3 фунта: 10 + 2(3) = 16, или 16 долларов. Пакет весом 5,8 фунта будет стоить столько же, сколько пакет весом 6 фунтов: 10 + 5 (3) = 25, или 25 долларов. График этой ступенчатой функции показан на рисунке 4.13. Обратите внимание, что в данном случае включены правые конечные точки, а не левые.
Существует также полезный графический тест, который показывает, является ли функция взаимно однозначной. Этот тест горизонтальной линии для функций «один к одному» можно резюмировать следующим образом.
Поскольку более одного (здесь три) различных значения x приводят к одному и тому же значению y, функция не является взаимно однозначной. 
-1 являются набором действительных чисел.-1 являются зеркальными отражениями по отношению к этой строке.
Обычно значение x (первый компонент) будет независимой переменной или входом, а значение y (второй компонент) будет зависимой переменной или выходом.
Граф может представлять отношение, рассматривая его как большой список упорядоченных пар. Каждая точка на графике представляет упорядоченную пару ( x , y ).
По графику определите значения x и y . Сначала заштрихуйте домен и диапазон, затем преобразуйте в нотацию интервала. 
Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.
первая степень.
