Внеклассный урок — Построение графика квадратичной функции
Построение графика квадратичной функции
Возьмем формулу квадратичной функции y = ax2 + bx + c. Проведя вычисления, можно прийти к другому виду этой формулы (можете вычислить сами):
b b2 – 4ac
y = a(x + — )2 – ————.
2a 4a
Заменим полученные дроби буквами m и n. Тогда мы получим формулу, которая уже известна нам из предыдущего раздела:
y = a(x – m)2 + n, где
b
m = – ——,
2a
b2 – 4ac
n = – ————
4a
Вывод:
Графиком функции y = ax2 + bx + c является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов — сдвига вдоль оси x вправо или влево, а вдоль оси y – вверх или вниз.
b b2 – 4ac
Вершиной этой параболы является (m; n), где m = – ——, n = – ————.
2a 4a
Три особенности этой параболы:
1) x = m (пояснение: ось симметрии параболы параллельна оси y)
2) y = n (пояснение: y = ax2 + bx + c = a(x – m)2 + n = n)
3) при a > 0 ветви параболы направлены вверх, при a<0 – вниз.
Чтобы построить график квадратичной функции, надо в первую очередь найти координаты вершины параболы.
Пример.
Надо построить график функции y = –2x2 + 12x – 19.
Начинаем решать. Для этого отметим, что a = –2, b = 12, c = –19.
Мы видим, что a < 0. Значит, графиком данной функции является парабола, ветви которой направлены вниз.
Найдем координаты ее вершины – то есть значения m и n:
b 12
m = – —— = – ———— = 3
2a 2 · (–2)
Значение n можно вычислить двумя способами. Один из них – формула, приведенная выше. Но поскольку x = m, а y = n (см.выше), то можно найти n более простым способом – непосредственно с помощью нашего выражения –2x2 + 12x – 19, вставляя вместо x значение m, равное 3:
n = –2 · 32 + 12 · 3 – 19 = –1
Итак, вершина параболы имеет координаты (3; –1).
Далее с помощью приведенных формул просто находим координаты еще нескольких точек, отмечаем их на оси координат, соединяем точки – и получаем нашу параболу.
raal100.narod.ru
Три способа построения графика квадратичной функции
Три способа построения графика квадратичной функции
I способ
Построение графика с помощью таблицы значений x и y.
Пример. Построить график функции 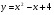
1. Составим таблицу значений x и y.
х
-4
-3
-2
-1
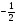
0
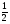
1
2
у
-8
-2
2
4
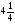
4
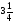
2
-2
-8
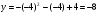
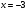
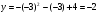
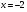
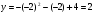
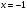
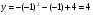
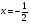
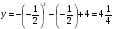
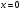

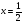
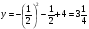
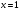

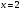



2. Построим соответствующие точки по заданным координатам на координатной плоскости
3. Соединим последовательно полученные точки линией.
4. Полученный график – порабола.
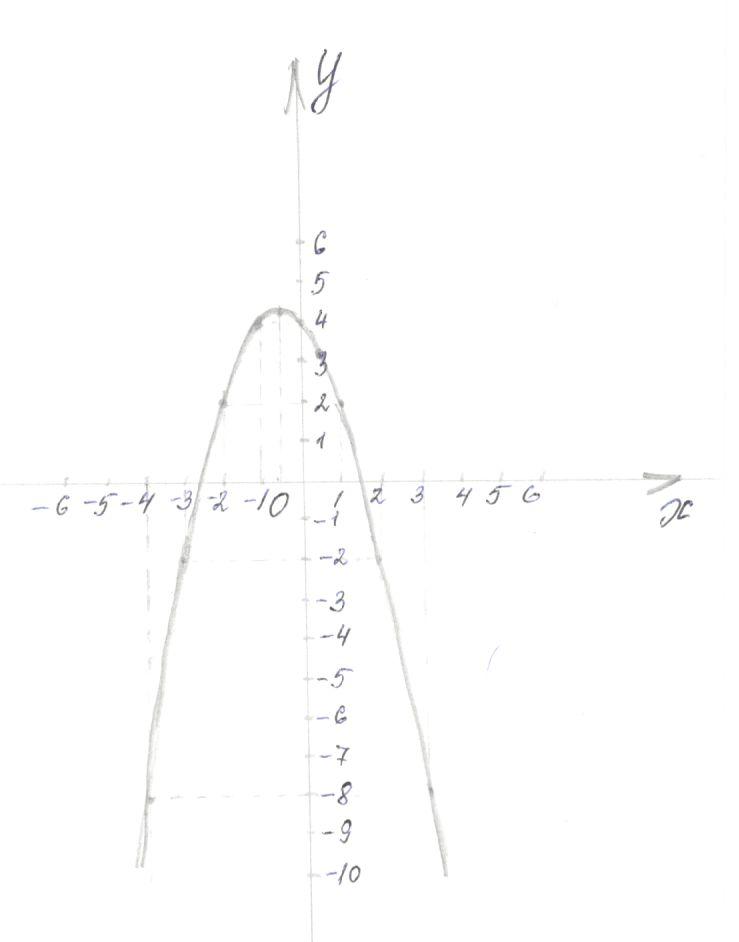
II способ
Построим график функции 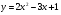
1. Найдем координаты вершины пораболы
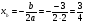

Вершиной пораболы является т.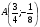
2. Определим ось симметрии пораболы
прямая 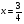
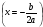
3. Найдем точки пересечения пораболы с осью ох. На оси ох значения у равны 0
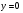

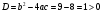 два корня
два корня
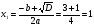
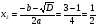
График пересекает ось ох в двух точках (1;0) и (0,5;0)
4. Найдем точки пересечения пораболы с осью оу. На оси оу значения х равны 0
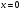
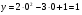
График пересекает ось в одной точке (0:1)
5. Определим направление ветвей пораболы
Построим график по найденным точкам
Дополнительные точки
а) Найти точку, симметричную т.(0;1) относительно оси симметрии пораболы
б) 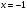
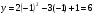 (-1;6) и симметричную ей относительно оси симметрии пораболы.
(-1;6) и симметричную ей относительно оси симметрии пораболы.
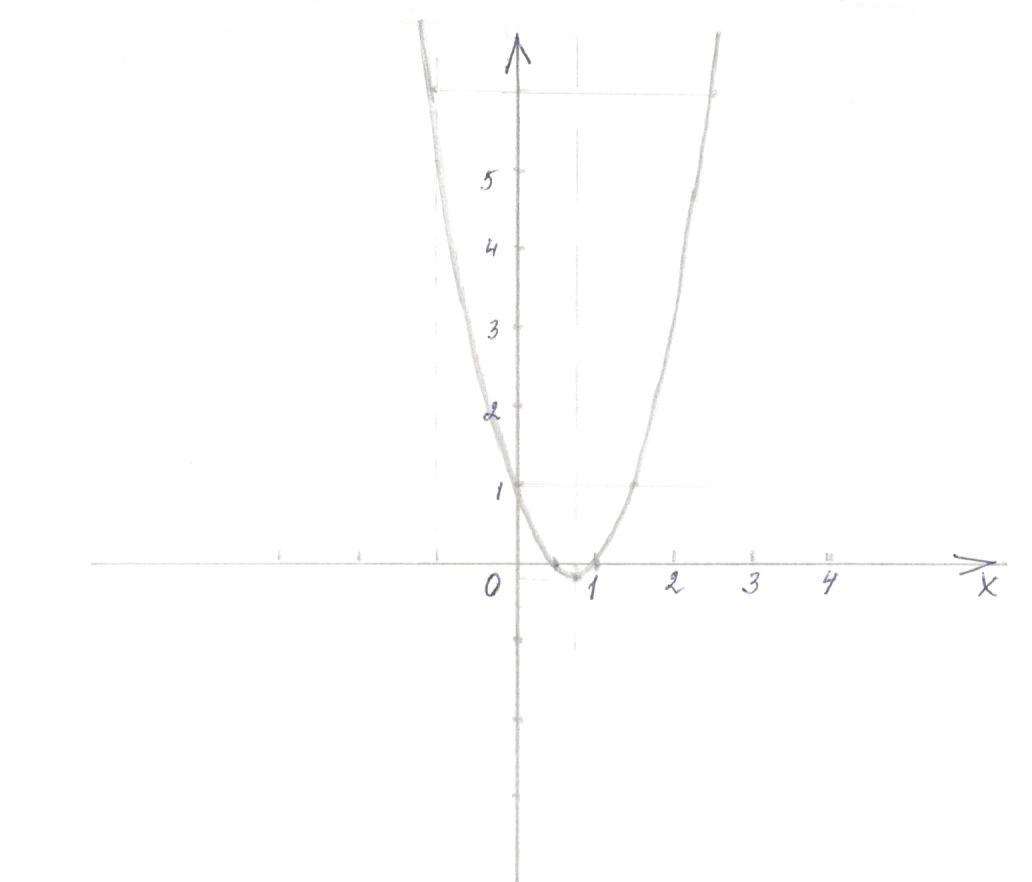
III способ
Построить график функции 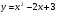
Воспользуемся теорией. Выделив квадрат двучлена из трехчлена, можно представить функцию вида 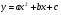
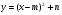 , где m и n – координаты вершины пораболы.
, где m и n – координаты вершины пораболы.1. Выделим квадрат двучлена в функции 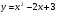 и заменим
и заменим 
Координаты вершины пораболы (1; 2)
2. Через полученную точку проведем прямую, параллельную оси ординат – ось симметрии пораболы.
3. Найдем координаты точек пересечения пораболы с осями
а) с осью ох , у=0, 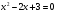
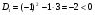 график ось х не пересекает
график ось х не пересекаетб) с осью оу, х=0, у=3, (0; 3)
4. а=1, 1>0 ветви направлены вверх
Дополнительные точки: точка симметричная точке (0; 3) относительно оси симметрии пароболы (2; 3)
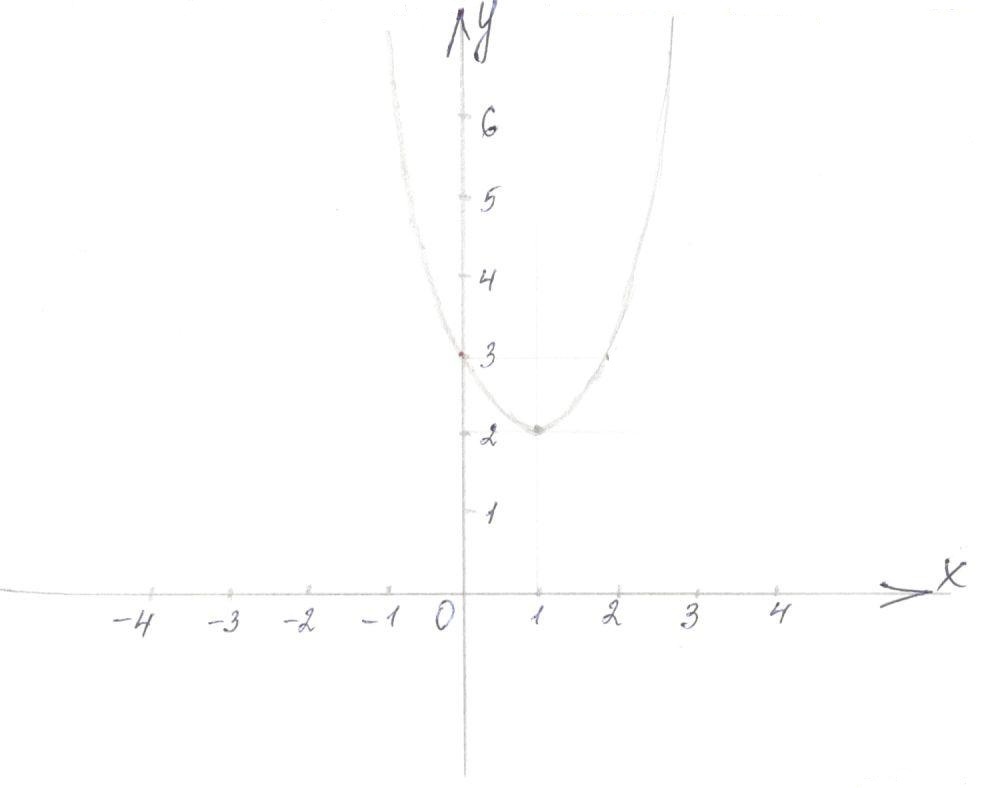
График функции 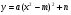 можно получить из графика функции
можно получить из графика функции 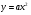 параллельным пересечением на
параллельным пересечением на 
 единиц вдоль оси оу
единиц вдоль оси оуinfourok.ru
Как построить параболу | Алгебра
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
y=x²+2x-3
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
y= -x²+2x+8
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Примеры.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
y=x²+5x+4
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
y= -x²-3x
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
www.algebraclass.ru
«Построение графика квадратичной функции»
Урок алгебры
9 класс
учитель математики
с. Могилевское
2019 год
Цель урока: выработать умение строить и исследовать графики квадратичной функции
у = ах2 + вх + с, выполнять преобразования графика квадратичной функции.
Образовательные задачи урока:
способствовать развитию у учащихся навыков чтения и построения графиков функций;
формировать навык простейших преобразований графиков функций;
формировать умения и навыки исследовать графики функций;
формировать умения анализировать, выделять главное, сравнивать, обобщать.
Развивающие задачи урока:
развивать творческую сторону мыслительной деятельности учащихся,
развивать умение обобщать, классифицировать, проводить анализ и делать выводы;
развивать коммуникативную компетенцию учащихся;
создать условия для проявления познавательной активности учащихся;
показать взаимосвязь математики с окружающей действительностью
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать графическую и функциональную культуру учащихся.
Тип урока: Комбинированный.
Формы роботы: фронтальная, работа в парах, самостоятельная работа, устный счет
с использование взаимоконтроля, самоконтроль, использование
опережающих заданий.
Учебник: «Алгебра» Учебник для 9 кл. общеобразоват. Учреждений / Ю.Н.Макарычев, Н.Г.Миндюк и др.; Под ред. С.А.Теляковского. — М: «Просвещение», 2008
План урока:
1.Орг.момент.
2. Актуализация знаний.
3. Усвоение новых знаний. (презентация)
4. Работа с алгоритмом.
Построение графика(образец).
5.Физминутка
6.Закрепление: функции и графики в заданиях ОГЭ.
7.Итог урока. Запись дом.зад-я.
8.Рефлексия..
Итак, еще раз здравствуйте, ребята! Сегодняшний урок математики у вас проведу я, зовут меня Арзамулова Рима Исаевна. С вами я познакомлюсь по ходу урока, надеюсь на плодотворную совместную работу. Улыбнитесь друг другу, соседу напротив, справа, слева.
Эпиграф к уроку:
«Предмет математика настолько
серьезен, что полезно не
упустить случая сделать его
немного занимательнее».
Блез Паскаль
Эпиграф к нашему сегодняшнему уроку поощряет нас не останавливаться на достигнутом, а двигаться дальше. Расширяя горизонты своих знаний. Мы начнем наш урок с небольшого видеоряда. Сколько теплых воспоминаний навеивают эти фотографии! Каскады падающей воды, фонтаны украшают многие города, развлекательные центры, дома.
Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи. При высоте статуи Евы 3м и угле наклона 60º, получим неравенств
Как вы думаете, что объединяет все эти рисунки? Правильно, на каждом из них мы видим форму, напоминающую нам параболу. Сегодня мы продолжим разговор об этой удивительной линии, обобщим уже имеющиеся знания по теме урока, откроем для себя много нового и интересного.












Девиз урока: “Математику нельзя изучать,
наблюдая, как это делает сосед!”
Нивен А.
Ход урока.
I. Организационный этап.
Учащимся сообщается тема урока, цели урока, формы работы на уроке.
Сегодня вам самим предстоит подвести итог изучению и получению новых знаний. Прежде, чем мы это сделаем, давайте проверим себя, готовы ли мы совершить его, всё ли было усвоено на уроках, имеются ли слабые места. Для этого проверим, как мы справились с домашним творческим заданием..
II Актуализация знаний:
Повторение теоретического материала (фронтальная работа с классом).
Все вопросы и задания высвечиваются на слайдах.
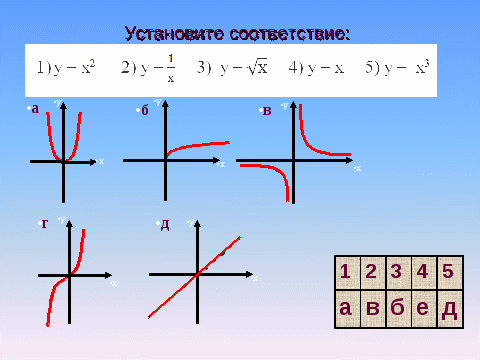
1.Какая функция называется квадратичной?
2.Проверь себя: соотнеси графики и функции.

3. Из приведенных примеров укажите те функции, которые являются квадратичными. (слайд 1)
Примеры:
у=5х+1;
у=3х2-1;
у=-2х2+х+3;
у=x3+7x-1;
у=4х2;
у=-3х2+2х.
4. Что является графиком квадратичной функции? ( парабола) (слайд 2)
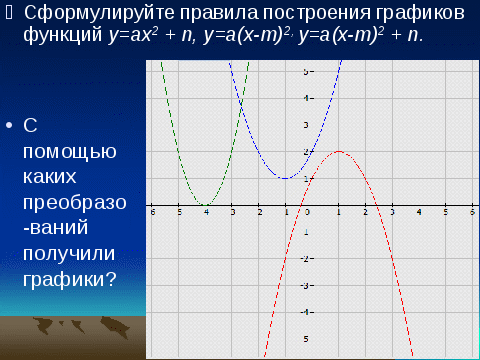
5. Сформулируйте правила построения графиков функций у=ах2 + n, у=а(х-m)2, у=а(х-m)2 + n.
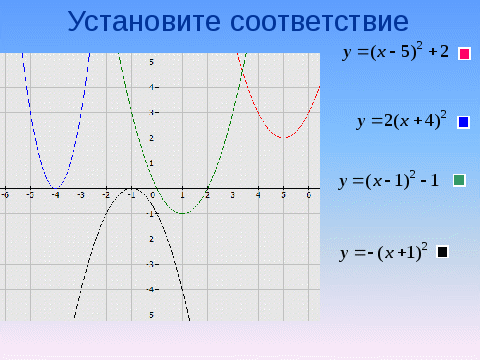
6.Установите соответствие
3. Усвоение новых знаний. (презентация)

4.Работа с алгоритмом.
Учащиеся получают алгоритм построения графика квадратичной функции
y = ax2+bx+c
Определить направление ветвей параболы
Определить координаты вершины параболы (m; n) и отметить ее в координатной плоскости: m = —b/2a; n = y(m)
Построить несколько точек, принадлежащих параболе
Соединить отмеченные точки
Мы с вами знаем как определить направление ветвей:
Вопрос? Как же определить вершины параболы?

 или мы находим значение функции подставив значение аргумента, то есть значение х.
или мы находим значение функции подставив значение аргумента, то есть значение х.
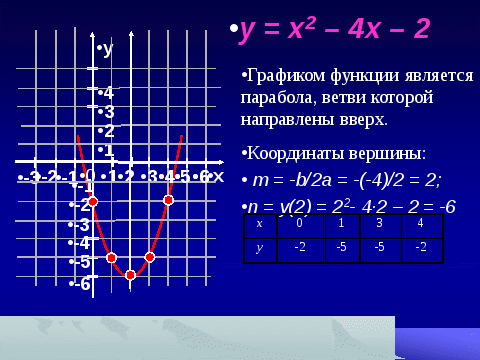
y = x2 – 4x – 2
IV.Физкультминутка.
Ребята, сейчас проверим как вы, зная преобразования графика функции, можете показать их с помощью физических упражнений.
Напомним: параллельный перенос вдоль оси ОХ –наклон вправо или влево;
параллельный перенос вдоль оси ОУ – поднимаем руки вверх или приседание;
коэффициент а >0 – движение рук вдоль туловища – прижимание,
а <0 – движение рук вдоль туловища – растяжение.
И так, начинаем изобразите схематически график функции у = х2 ; у = 3х2 ; у = 1/5 х2 ;
у = (х+2)2; у = (х-1)2; у = (х+2)2— 3; у = (х-2)2 + 1; у = 2(х+3)2 .
Спасибо, молодцы. Заряд бодрости получили и присели на свои места.
Продолжаем наш урок. А сейчас проверим, как вы сами справитесь с квадратичной функцией, кто из вас сильнее и умнее. Если с заданиями справляетесь, значит, вы умнее и сильнее, если нет – то нужно еще потренироваться. Желаю вас успехов в математическом соревновании.
Работа по учебнику:
Задание №121(а). Квадратичная функция задана формулой:
а) у = х² — 4х +7
Найдите координаты вершин параболы.
Наметив на координатной плоскости вершину параболы и
ее ось симметрии , изобразите схематичекси график
№125(в)
Постройте график функции
у = -х² + 6х -9
VI Подведение итогов урока. Функции и графики в заданиях ОГЭ:(устно)

VII Домашнее задание
П. 7
Т.З. № 122 (в), №126(а-в)
 VIII Рефлексия Мы стали друзьями, мы стали умнее,
VIII Рефлексия Мы стали друзьями, мы стали умнее,
Богаче на целый волшебный урок!
Нас знания делают выше, сильнее,
А дружба крепче и добрей.
Ты согласен, дружок?
На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Моё настроение стало лучше / стало хуже
Материал урока мне был понятен / не понятен
полезен / бесполезен
интересен / скучен
«лесенка удовлетворённости»
По окончании урока дети прикрепляют на лесенке
урок прошёл полезно, плодотворно;
урок прошёл довольно неплохо;
не совсем удовлетворён уроком;
урок не понравился, скучно.
По окончанию урока учитель предлагает ученикам взять стик в форме листика и, если учащийся уходит с урока в хорошем настроении, приклеить его на заранее подготовленную лесенку..
Источники информации:
1.https://kittymcteague.files.wordpress.com/2013/05/7730_1.jpg
2. http://player.myshared.ru/547694/data/images/img25.jpg
3. http://textarchive.ru/images/836/1670841/ac145154.gif
4.http://turizm.lib.ru/img/b/bersenewa_n_b/ergakimart2010/skalaparabola.jpg
5.http://mathforum.org/mathimages/imgUpload/thumb/Fountain.jpg/400px-Fountain.jpg
6.http://www.fresher.ru/manager_content/images2/kak-otmetili-alye-parusa-2014-v-sankt-peterburge/15.jpg
7.http://images.aif.ru/006/633/def5f1e6b6cdc7208dc252436988f991.jpg
8.http://player.myshared.ru/589208/data/images/img76.jpg
9https://upload.wikimedia.org/wikipedia/commons/5/5a/Troms%C3%B8_library_-_2005-09-13.jpg
10.ttps://upload.wikimedia.org/wikipedia/commons/5/5a/Troms%C3%B8_library_-_2005-09-13.jpg
11.https://yandex.ua/images/#!/images/search?text=%
12 http://prezentacii.com/matematike/6989-kvadratichnaya-funkciya-i-ee-grafik.html слайд 7
13 http://www.uztest.ru/plugins/lessons/pazl/moe/tests/fun1/eigensch.html).
14. Алгебра 9 класс. Поурочные планы по учебнику “Алгебра 9 класс” / Ю.Н. Макарычев/ Под редакцией С.А. Теляковского . М.: Просвещение, 2002. /Сост. Д.Ф. Айвазян.– Волгоград – АСТ, 2008
15. ГИА-9. Математика. Учебно-тренировочные тесты под ред.Ф. Ф. Лысенко.
16. Шалкина С.В. «Здоровьесберегающие технологии на уроках математики»/ festival.1september.ru / Фестиваль педагогических идей«Открытый урок» 2006-2007 учебный год +
17. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Под ред. С.А. Теляковского. – М.: Просвещение, 2002.
18. Цукарь А.Я. Рисуем графиками функций // Математика. – 1999. – № 7, № 22, № 23, № 24, № 25.
19. Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – № 4. – С. 80-81.
20.. http://festival.1september.ru/articles/101475/img27.gifкартинка тюльпана,колокольчика
21. http://1.bp.blogspot.com/-rOOH6x_2qsg/Ta3ca_DrzEI/AAAAAAAAQRY/GVaCD0LZKls/s1600/vihmavari.jpg зонтик
22. http://4.bp.blogspot.com/-RvwIRt2MrWw/Ta3cdtIOTeI/AAAAAAAAQRc/1X7bWfaYIJ8/s1600/prillid.jpg очки
23. http://festival.1september.ru/articles/101475/img2.jpg жаба
24. http://festival.1september.ru/articles/589062/ таблица
infourok.ru
Построение графика квадратичной функции

«Построение графика квадратичной функции» (9 класс)
Урок 2

Цели урока:
- Образовательные: научиться построению графика квадратичной функции и использованию графика для получения её свойств.
- Развивающие: развивать логическое мышление, алгоритмическую культуру, внимание, навыки самостоятельной работы с источником информации и самоконтроля, поддерживать интерес к математике.
- Воспитательные: воспитывать последовательность, ответственность, самостоятельность, настойчивость, дисциплинированность.

Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c , где х — независимая переменная, a, b и с -некоторые числа (причём а≠0).
Например: у = 5х²+6х+3,
у = -7х²+8х-2,
у = 0,8х²+5,
у = ¾х²-8х,
у = -12х²
— квадратичные функции
 0) или вниз (если ау= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ). Например: у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а у 0 х у 0 х «
0) или вниз (если ау= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ). Например: у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а у 0 х у 0 х «
Графиком квадратичной функции является парабола , ветви которой направлены вверх (если а0) или вниз (если а
- у= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ).
Например:
- у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а
у
0
х
у
0
х
 0) «
0) «
Чтобы построить график функции надо:
1. Описать функцию:
название функции,
что является графиком функции,
куда направлены ветви параболы.
Пример: у = х ²-2х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т.к. а=1, а0)

Чтобы построить график функции надо:
Пример: у = х ²-2х-3 (а = 1; b = -2; с = -3) Найдём координаты вершины параболы
n = 1²-2·1-3 = -4
А(1;-4) – вершина параболы.
х=1 – ось симметрии параболы.
2. Найти координаты вершины параболы А( m;n) по формулам:
;
или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
Прямая x=m является ось ю симметрии параболы.

Чтобы построить график функции надо:
3. Заполнить таблицу значений функции:
Прямая x=m является осью симметрии параболы, т.е. точки графика симметричны относительно этой прямой.
В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. Например, следующим образом:
*- посчитать значение функции в выбранных значениях х.
Пример: у = х ²-2х-3
А(1;- 4) – вершина параболы
х=1 – ось симметрии параболы.
Составим таблицу значений функции:
Х
у
— 1
0
0
— 3
1
— 4
2
— 3
3
0
Х
у
m-2
*
m-1
*
m
m+1
n
*
m+2
*

Чтобы построить график функции надо:
4. Построить график функции: — отметить в координатной плоскости точки, координаты которых указаны в таблице; — соединить их плавной линией.
х
у
-1
0
0
-3
1
-4
2
-3
3
0
У
4
-4
3
-3
2
-2
1
-1
у = х ²-2х-3
0
-2
1
-1
-3
2
3
-4
4
-5
5
6
х

Попробуйте ответить на контрольные вопросы:
- Сформулируйте определение квадратичной функции.
- Что представляет собой график квадратичной функции?
- Куда могут быть направлены ветви параболы и от чего это зависит?
- В какой последовательности нужно строить график квадратичной функции?

Стоит немного отдохнуть от компьютера.
Попробуйте построить в тетради график функции
у = -2х²+8х-3

Постройте график функции у = -2х ²+8х-3 План построения графика квадратичной функции:
1. Описать функцию:
- название функции; что является графиком функции; куда направлены ветви параболы
- название функции;
- что является графиком функции;
- куда направлены ветви параболы
2. Найти координаты вершины параболы А( m;n)
по формулам:
или n = у(m)
3. Заполнить таблицу значений функции.
4. Построить график функции:
- отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.
- отметить в координатной плоскости точки, координаты которых указаны в таблице;
- соединить их плавной линией.

Проверьте себя. Ваше задание должно быть выполнено следующим образом:
у = -2х ²+8х-3 — квадратичная функция, графиком является парабола, ветви которой направлены вниз (т.к. а=-2, а
Найдём координаты вершины параболы
n = -2·2²+8·2-3 =5
А ( 2; 5 ) – вершина параболы.
х=5 ось симметрии параболы.
Составим таблицу значений функции.
у = -2х ²+8х-3
у
7
6
5
4
-3
3
-2
2
-1
1
0
-1
1
-2
-3
2
3
-4
4
5
6
х
Х
у
0
-3
1
3
2
3
5
3
4
-3

Если у вас получилось тоже самое – вы молодец и мы вас поздравляем!!! Вы можете перейти к следующей странице .
Если вы допустили ошибку – не огорчайтесь. У вас всё ещё впереди! Вы можете заглянуть в свой учебник (п.7)
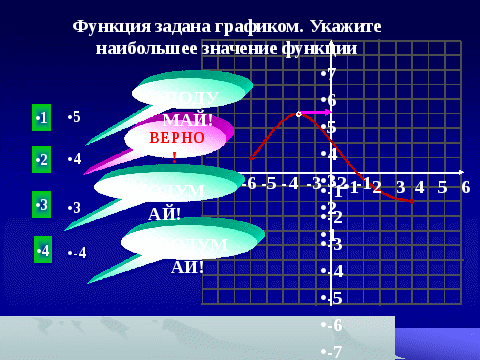
 0 на промежутке (0,5;3,5) y Функция возрастает на промежутке (-∞;2] функция убывает на промежутке [2;+∞) Наибольшее значение функции равно 5 у 7 6 5 4 3 у = -2х ²+8х-3 2 -1 1 0 -2 1 -1 2 -3 3 -4 4 х «
0 на промежутке (0,5;3,5) y Функция возрастает на промежутке (-∞;2] функция убывает на промежутке [2;+∞) Наибольшее значение функции равно 5 у 7 6 5 4 3 у = -2х ²+8х-3 2 -1 1 0 -2 1 -1 2 -3 3 -4 4 х «
Рассмотрим свойства этой квадратичной функции. (листаем свойства по щелчку мыши)
- Область определения функции (-∞;+∞)
Область значений функции (-∞;5]
- Нули функции х =0,5 и х =3,5
- у 0 на промежутке (0,5;3,5)
y
- Функция возрастает на промежутке (-∞;2]
функция убывает на промежутке [2;+∞)
- Наибольшее значение функции равно 5
у
7
6
5
4
3
у = -2х ²+8х-3
2
-1
1
0
-2
1
-1
2
-3
3
-4
4
х

Перед продолжением работы запишите домашнее задание,
№ 122, 124(а),
244(б,в)
Далее выполните тест.
- прочитайте задание;
- выполните его устно или, сделав записи в тетради;
- и выберите правильный ответ

Выполните тест
1 вопрос: Выберите квадратичную функцию а)
б)
в)
г)

Выполните тест
2 вопрос: Куда направлены ветви параболы ?

Выполните
3 вопрос: Укажите координаты вершины параболы
а) А(3;6)
б) А(-1;-17)
в) А(1;-5)
г) А(1;-1)

Выполните тест
у
У
У
0 6
х
-6 0
х
-6 0
х
4 вопрос:
На рисунке показаны графики квадратичных функций. Выберите график функции
у= — 4х²-16х+1, подведите к нему стрелку и нажмите левую кнопку мыши .
у
у
17
5
у
1
0 2,5
х
-2 х
2,5
6
0
х

Выполните тест
5 вопрос: Укажите формулу квадратичной функции, график которой изображён на рисунке.
- у = -x 2 +6x
- у = — 3х²+8х-11
- у = — 4х²-16х+1
- у = х²-6х
- у = х²+6х
- у = 1,2х²-6х+5
У
-6 0
х
Выполните следующую работу в тетрадях по вариантам. Постройте графики функций:
у = -х ²+6х-8
Укажите свойства функции.
у = х ²-6х-7
Укажите свойства функции.
multiurok.ru