Внеклассный урок — Построение графика квадратичной функции
Построение графика квадратичной функцииВозьмем формулу квадратичной функции y = ax2 + bx + c. Проведя вычисления, можно прийти к другому виду этой формулы (можете вычислить сами):
b b2 – 4ac
y = a(x + — )2 – ————.
2a 4a
Заменим полученные дроби буквами m и n. Тогда мы получим формулу, которая уже известна нам из предыдущего раздела:
y = a(x – m)2 + n, где
b
m = – ——,
2a
b2 – 4ac
n = – ————
4a
Вывод:
Графиком функции y = ax2 + bx + c является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов — сдвига вдоль оси x вправо или влево, а вдоль оси y – вверх или вниз.
b b2 – 4ac
Вершиной этой параболы является (m; n), где m = – ——, n = – ————.
2a 4a
Три особенности этой параболы:
1) x = m (пояснение: ось симметрии параболы параллельна оси y)
2) y = n (пояснение: y = ax2 + bx + c = a(x – m)2 + n = n)
3) при a > 0 ветви параболы направлены вверх, при a<0 – вниз.
Чтобы построить график квадратичной функции, надо в первую очередь найти координаты вершины параболы.
Пример.
Надо построить график функции y = –2x2 + 12x – 19.
Начинаем решать. Для этого отметим, что a = –2, b = 12, c = –19.
Мы видим, что a < 0. Значит, графиком данной функции является парабола, ветви которой направлены вниз.
Найдем координаты ее вершины – то есть значения m и n:
b 12
m = – —— = – ———— = 3
2a 2 · (–2)
Значение n можно вычислить двумя способами. Один из них – формула, приведенная выше. Но поскольку x = m, а y = n (см.выше), то можно найти n более простым способом – непосредственно с помощью нашего выражения –2x2 + 12x – 19, вставляя вместо x значение m, равное 3:
n = –2 · 32 + 12 · 3 – 19 = –1
Итак, вершина параболы имеет координаты (3; –1).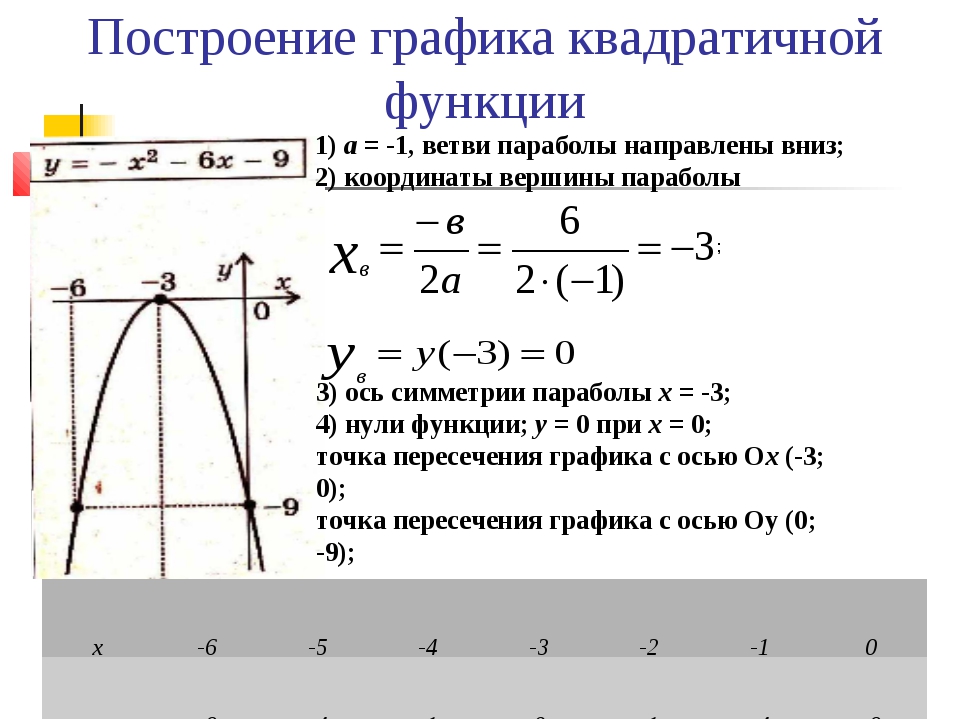
Далее с помощью приведенных формул просто находим координаты еще нескольких точек, отмечаем их на оси координат, соединяем точки – и получаем нашу параболу.
Разработка открытого интегрированного урока на тему «Построение графика квадратичной функции»
Цели урока:
- Образовательные: повторить с учащимися алгоритм построения графика квадратичной функции; закрепление умений и навыков учащихся по теме с использованием программы «Advanced Graphed».
- Развивающие: продолжать формировать обще учебные умения и навыки, развивать вычислительные навыки, навыки самостоятельной работы, логическое мышление, способность применять знания на компьютере, познавательный интерес к предметам.
- Воспитательные: воспитывать внимательность, аккуратность.
Тип урока интегрированный.
Раздаточный материал Карточки для тестовой работы.
Оборудование: Проекционный аппарат.
Учебник: «Алгебра» Учебник для 9 кл. общеобразоват. Учреждений / Ю.Н.Макарычев, Н.Г.Миндюк и др. Под ред. С.А.Теляковского. — М: «Просвещение», 2009.
Ход урока
Первая часть урока (алгебра)
1. Организационный этапПриветствие, проверка присутствующих на уроке и проверка готовности учащихся к уроку. Ознакомление с видом и темой урока. (Слайд 1)
Важно задать высокий темп урока, чётко формулируя требования учащимся.
2. Проверка домашнего заданияПрежде чем приступим к проверки домашнего задания давайте вспомним, какой вид графика имеет функция квадратичного уравнения.
Презентация
Задание 1: Назовите, под какими цифрами обозначены графики квадратичной функции? (ответ 1,3,5). (слайд 2)
Задание 2: Ваше домашнее задание заключалось в решении графическим способом уравнение квадратичной функции y = –3x2 + 7x + 2. Вам необходимо назвать какой из изображенных вариантов ответов верный. (Слайд 3)
Вам необходимо назвать какой из изображенных вариантов ответов верный. (Слайд 3)
(Слайд 4)
- Повторить определение квадратичной функции п.5, алгоритм построения ее графика п.7
- Повторить свойства функции, формулы корней квадратного уравнения.
- Решить и построить в программе функции у = – 7х² + 8х – 2.
Задание 1: На экране слайд, на котором дано 4 вида квадратных уравнений. Учащимся необходимо для каждого уравнения найти соответствующий график.
Ответы (1 — красный, 2 — голубой, 3 – зеленый, 4 — оранжевый). (Слайд 5)
3адание 2: На экране отображено задание: «Построить график функции y = х² – 4. Учащимся необходимо словесно пояснить в каком направлении будет перемещаться парабола по оси У или Х. После ответа на экране будет отображено движение графика по оси У вниз на 4 единицы.
Задание 3: На экране отображено задание: «Построить график функции y = (х + 2)². Учащимся необходимо словесно пояснить в каком направлении будет перемещаться парабола по оси У или Х. После ответа на экране будет отображено движение графика по оси Х влево на 2 единицы. (Слайд 7)
Задание 4: На экране отображено задание: «Построить график функции y = (х – 3)² – 1. Учащимся необходимо словесно пояснить в каком направлении будет перемещаться парабола по оси У или Х. После ответа на экране будет отображено движение графика по оси Х на 3 единицы вправо и по оси У на 1 единицу вниз. (Слайд 8)
Задание 5: Данное задание заключается в опросе учащихся по основным этапам (правилам) построения графика функции. Учащиеся называют первый шаг к построению графика, а на экране появляется верный ответ и иллюстрацией. Это для того, чтобы зрительно проанализировать правильность ответа учащихся.
Проверочный тест по теме «Квадратичная функция» (Приложение 1)
Ответы для самопроверки (Слайд 14)
Вторая часть урока (информатика)
6. ФизкультминуткаУчащимся предлагается отдохнуть: учитель зачитывает правила техники безопасности в компьютерном классе, а учащиеся должны кивать головой «Да», «Нет» медленно. (Слайд 15)
7
. Компьютерный практикум«Построение графиков квадратичной функции в MS Excel» (Приложение 2, Приложение 3)
Задание 1.
- y1 = х²
- y2 = х² + 5
- y3 = х² – 2
На одной координатной плоскости построить графики трех функций на отрезке [–4;4] с шагом 1. (Слайд 16)
Образец пошагового выполнения заполнения таблицы данными.
Слайды 18–23
Задание 2. Построить график функции на одной координатной плоскости. (Слайд 24, 25)
Изучив построенные графики, вам необходимо ответить на вопрос:
— Как, имея график функции y= х², построить график функции y = х² + 5 (y = х² – 2)? (Слайд 26)
ВЫВОД: У предложенных функций изменялось значение функции, поэтому график сдвигался вверх по оси ОУ, если m> 0 и вниз, если m<0
Дополнительное задание:
Теперь учащимся предлагается рассмотреть, как ведут себя графики функций y = (х + l)² по отношению графику функции y = х². (Слайд 27)
Строят графики функций: y1 = х²; y2 = (х + l)²; y 3 = (х – 2)² на отрезке [– 4;4].
Вопрос: Какие формулы нужно изменить, чтобы построить графики данных функций в уже созданной системе координат? (Слайд 28)
Учащиеся должны подойти к выводу, что необходимо изменить формулы для вычисления функций y2 и y3 следующим образом.
Изучив построенные графики, вам необходимо ответить на вопрос: — Как, имея график функции y1 = х², построить график функции y1 = х², y = (х + l)²? (Слайд 29)
Вывод: У предложенных функций изменялось значение аргумента, поэтому график сдвигался влево по оси Ох, если > 0 и вправо, если <0 . (Слайд 30)
8. Комплекс упражнений для глаз9. РефлексияРезультаты моей работы на уроке:
- Я узнал…
- Я могу…
- На уроке было легко…
- На уроке было трудно…
- Мне надо еще поработать над…
Спасибо за урок
Что означает c в параболе. Построение графика квадратичной функции. Визуальный гид (2019)
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы.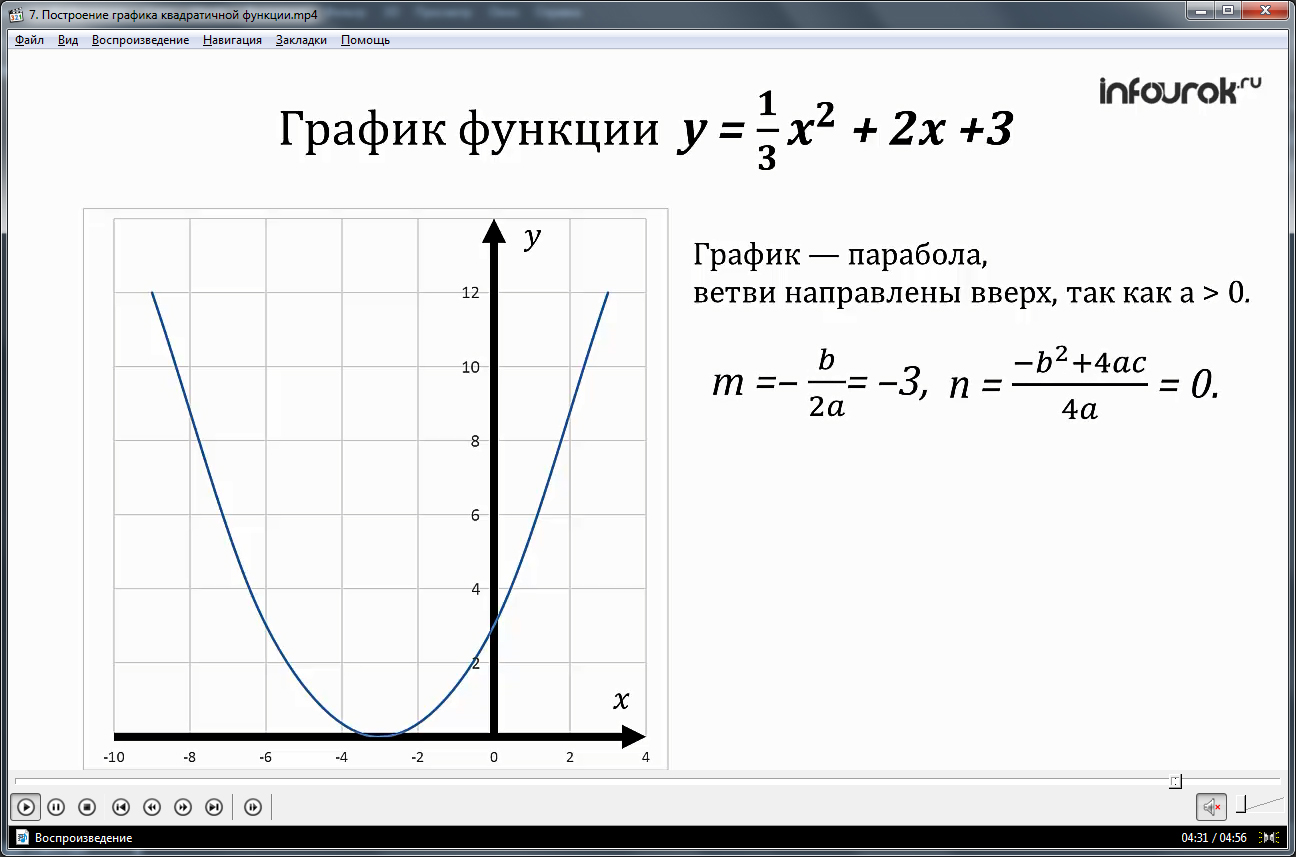 Рассмотрим два способа.
Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция.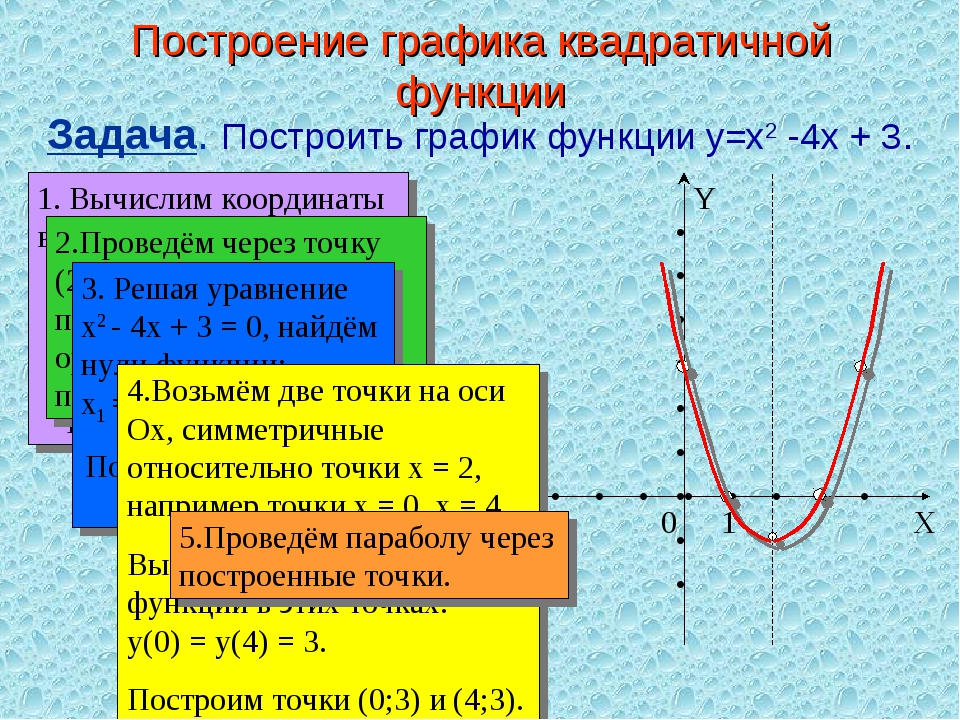 График — парабола ветвями вниз. Координаты вершины параболы
График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция.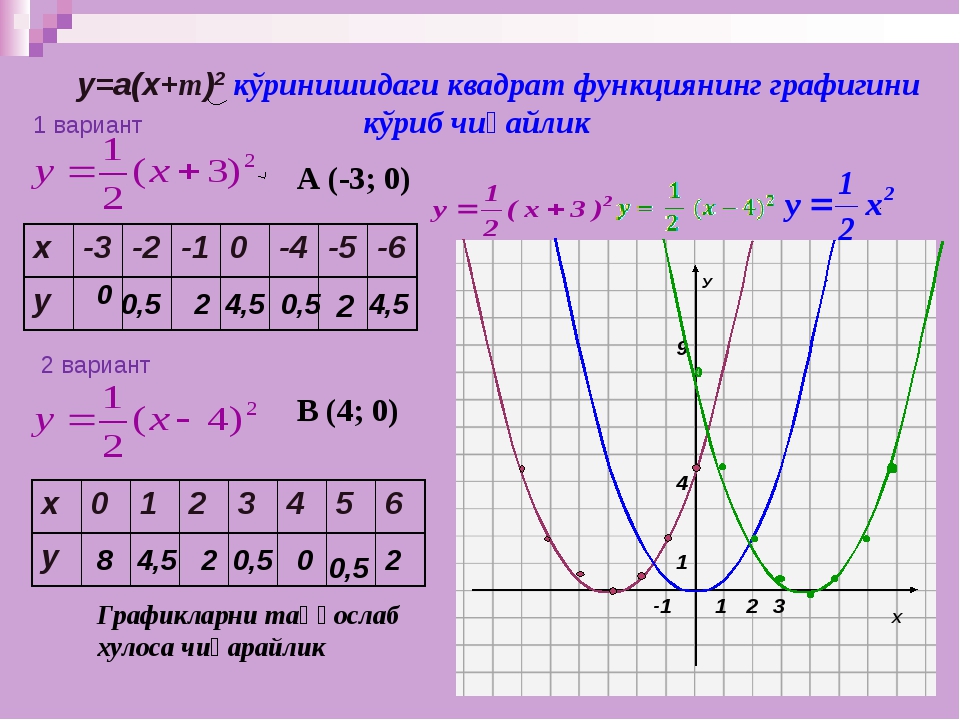 График — парабола ветвями вверх. Координаты вершины параболы
График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Определение квадратичной функции построение графика. Квадратичная функция
Рассмотрим выражение вида ах 2 +вх+с, где а, в, с — действительные числа, а отлично от нуля. Это математическое выражение известно как квадратный трехчлен.
Напомним, что ах 2 — это старший член этого квадратного трехчлена, а — его старший коэффициент.
Но не всегда у квадратного трехчлена присутствуют все три слагаемые. Возьмем для примера выражение 3х 2 + 2х, где а=3, в=2, с=0.
Перейдем к квадратичной функции у=ах 2 +вх+с, где а, в, с — любые произвольные числа. Эта функция является квадратичной, так как содержит член второй степени, то есть х в квадрате.
Довольно легко построить график квадратичной функции, например, можно воспользоваться методом выделения полного квадрата.
Рассмотрим пример построения графика функции у равно -3х 2 — 6х + 1.
Для этого первое, что вспомним, схему выделения полного квадрата в трехчлене -3х 2 — 6х + 1.
Вынесем -3 у первых двух слагаемых за скобки. Имеем -3 умножить на сумму х квадрат плюс 2х и прибавить 1. Добавив и отняв единицу в скобках, получаем формулу квадрата суммы, которую можно свернуть. Получим -3 умножить на сумму (х+1) в квадрате минус 1 прибавить 1. Раскрывая скобки и приводя подобные слагаемые, выходит выражение: -3 умноженное на квадрат суммы (х+1) прибавить 4.
Построим график полученной функции, перейдя к вспомогательной системе координат с началом в точке с координатами (-1; 4).
На рисунке из видео эта система обозначена пунктирными линиями. Привяжем функцию у равно -3х 2 к построенной системе координат. Для удобства возьмем контрольные точки. Например, (0;0), (1;-3), (-1;-3), (2;-12), (-2;-12). При этом отложим их в построенной системе координат. Полученная при построении парабола является необходимым нам графиком. На рисунке это красная парабола.
Применяя метод выделения полного квадрата, мы имеем квадратичную функцию вида: у = а*(х+1) 2 + m.
График параболы у = ах 2 + bx + c легко получить из параболы у=ах 2 параллельным переносом. Это подтверждено теоремой, которую можно доказать, выделив полный квадрат двучлена. Выражение ах 2 + bx + c после последовательных преобразований превращается в выражение вида: а*(х+l) 2 + m. Начертим график. Выполним параллельное перемещение параболы у = ах 2 , совмещая вершину с точкой с координатами (-l;m).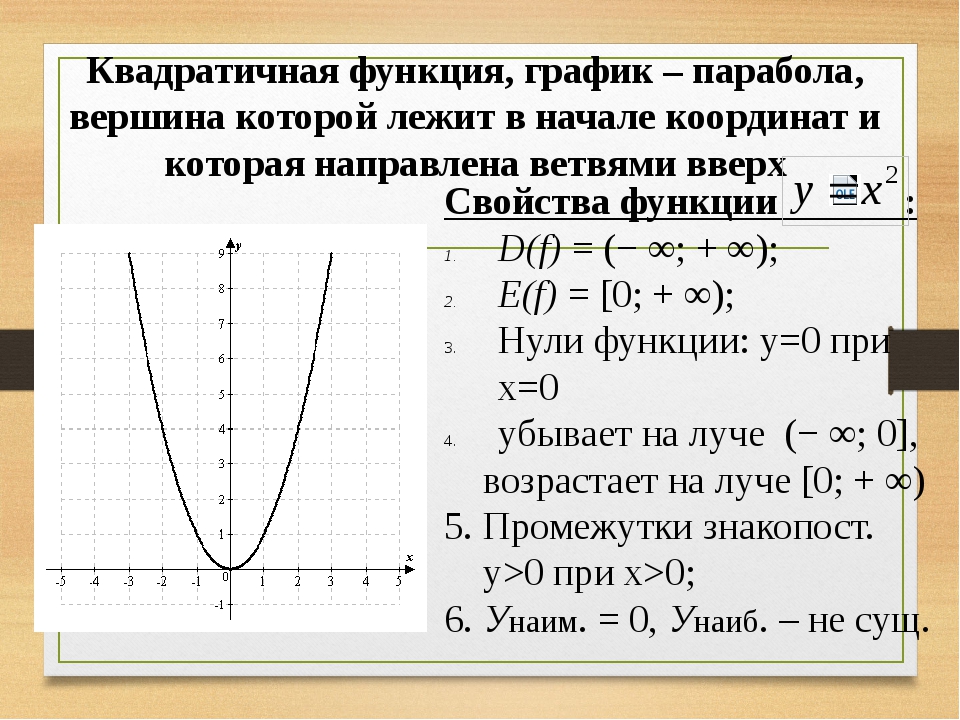 Важно то, что х= -l, а значит -b/2а. Значит эта прямая является осью параболы ах 2 + bx + c, ее вершина находится в точке с абсциссой х нулевое равно минус в, деленное на 2а, а ордината вычисляется по громоздкой формуле 4ас — b 2 /. Но эту формулу запоминать не обязательно. Так как, подставив значение абсциссы в функцию, получим ординату.
Важно то, что х= -l, а значит -b/2а. Значит эта прямая является осью параболы ах 2 + bx + c, ее вершина находится в точке с абсциссой х нулевое равно минус в, деленное на 2а, а ордината вычисляется по громоздкой формуле 4ас — b 2 /. Но эту формулу запоминать не обязательно. Так как, подставив значение абсциссы в функцию, получим ординату.
Для определения уравнения оси, направления ее ветвей и координат вершины параболы, рассмотрим следующий пример.
Возьмем функцию у = -3х 2 — 6х + 1. Составив уравнение оси параболы, имеем, что х=-1. А это значение является координатой х вершины параболы. Осталось найти только ординату. Подставив значение -1 в функцию, получим 4. Вершина параболы находится в точке (-1; 4).
График функции у = -3х 2 — 6х + 1 получен при параллельном переносе графика функции у = -3х 2 , значит, и ведет себя аналогично. Старший коэффициент отрицателен, поэтому ветви направлены вниз.
Мы видим, что для любой функции вида y = ах 2 + bx + c, самым легким является последний вопрос, то есть направление веток параболы.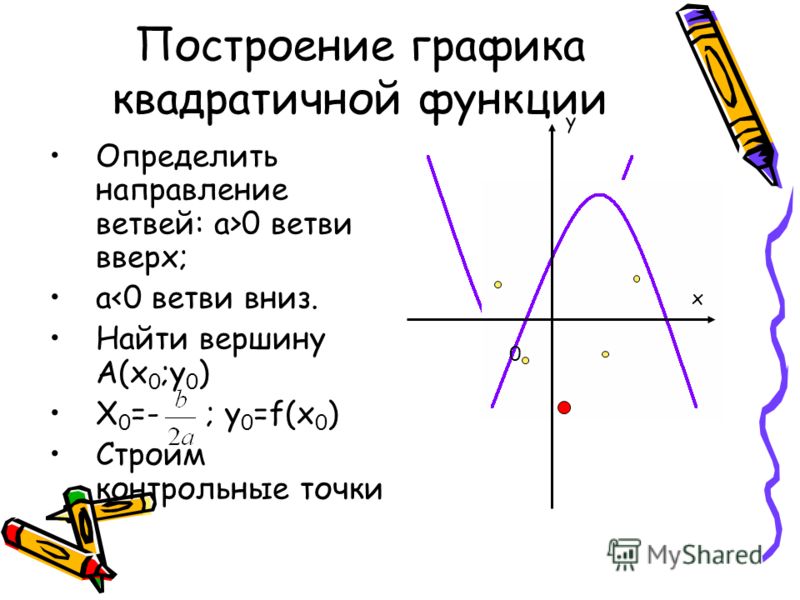 Если коэффициент а положительный, то ветви — вверх, а если отрицательный, то — вниз.
Если коэффициент а положительный, то ветви — вверх, а если отрицательный, то — вниз.
Следующим по сложности идет первый вопрос, потому что требует дополнительных вычислений.
И самый сложный второй, так как, кроме вычислений, еще необходимы знания формул, по которым находятся х нулевое и у нулевое.
Построим график функции у = 2х 2 — х + 1.
Определяем сразу — графиком является парабола, ветви направлены вверх, так как старший коэффициент равен 2, а это положительное число. По формуле находим абсциссу х нулевое, она равна 1,5. Для нахождения ординаты вспомним, что у нулевое равно функции от 1,5, при вычислении получим -3,5.
Вершина — (1,5;-3,5). Ось — х=1,5. Возьмем точки х=0 и х=3. у=1. Отметим данные точки. По трем известным точкам строим искомый график.
Для построения графика функции ах 2 + bx + c необходимо:
Найти координаты вершины параболы и отметить их на рисунке, потом провести ось параболы;
На оси ох взять две симметричные, относительно оси, параболы точки, найти значение функции в этих точках и отметить их на координатной плоскости;
Через три точки построить параболу, при необходимости можно взять еще несколько точек и строить график по ним.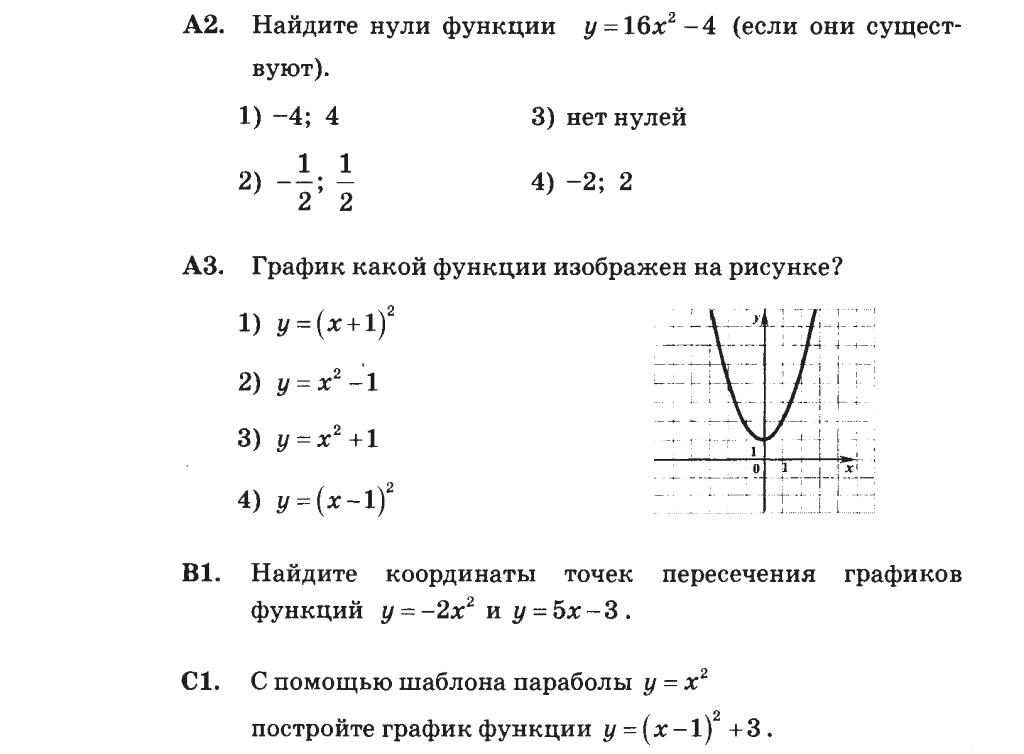
В следующем примере мы научимся находить наибольшее и наименьшее значения функции -2х 2 + 8х — 5 на отрезке .
По алгоритму: а=-2, в=8, значит х нулевое равно 2, а у нулевое — 3, (2;3) — вершина параболы, а х=2 является осью.
Возьмем значения х=0 и х=4 и найдем ординаты этих точек. Это -5. Строим параболу и определяем, что наименьшее значение функции -5 при х=0, а наибольшее 3, при х=2.
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика.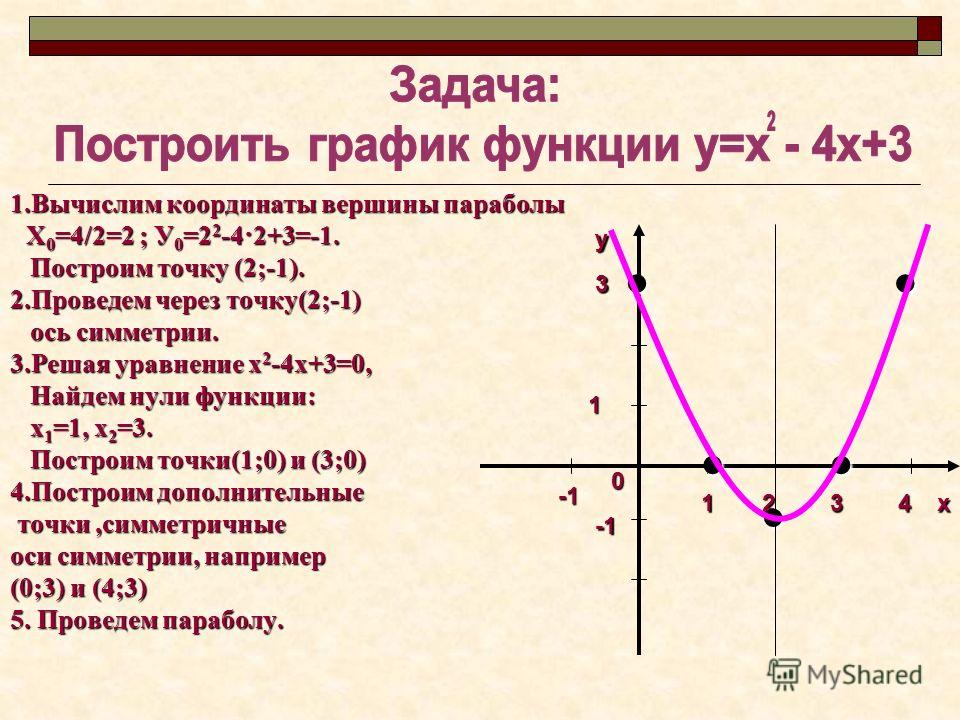 На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax 2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая простая зависимость для коэффициента а . Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а а > 0.
y = 0,5x 2 — 3x + 1
В данном случае а = 0,5
А теперь для а
y = — 0,5×2 — 3x + 1
В данном случае а = — 0,5
Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
y = a 0 2 + b 0 + c = c . Получается, что у = с . То есть с — это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с
с > 0:
y = x 2 + 4x + 3
с
y = x 2 + 4x — 3
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:
y = x 2 + 4x
Сложнее с параметром b . Точка, по которой мы будем его находить, зависит не только от b но и от а . Это вершина параболы. Ее абсцисса (координата по оси х ) находится по формуле х в = — b/(2а) . Таким образом, b = — 2ах в . То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х в > 0) или левее (х в
Однако это не все.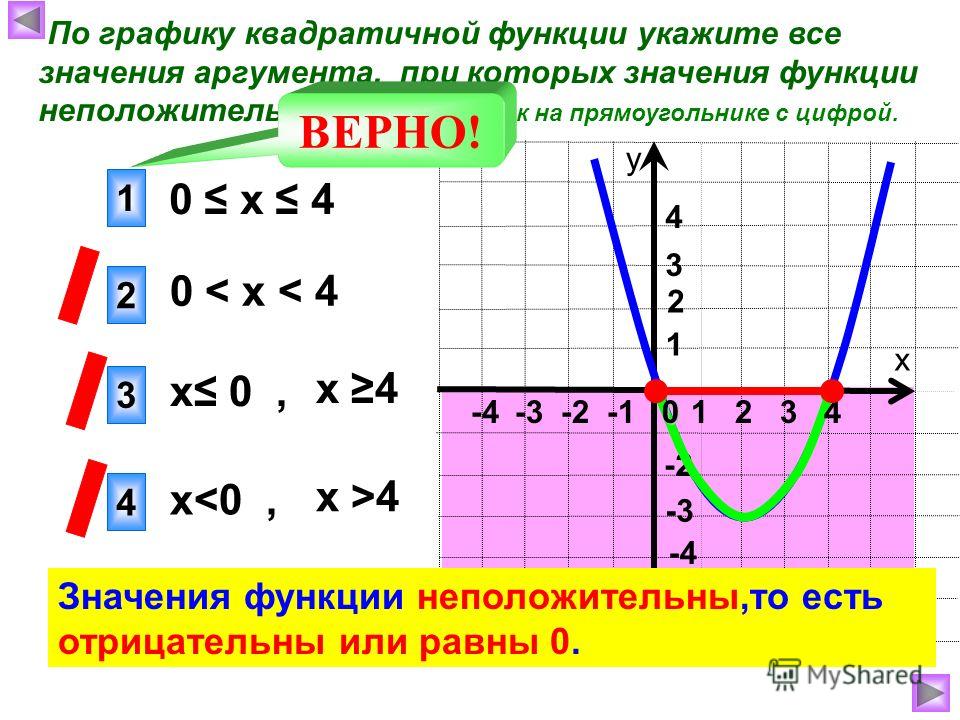 Надо еще обратить внимание на знак коэффициента а . То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = — 2ах в определить знак b .
Надо еще обратить внимание на знак коэффициента а . То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = — 2ах в определить знак b .
Рассмотрим пример:
Ветви направлены вверх, значит а > 0, парабола пересекает ось у ниже нуля, значит с х в > 0. Значит b = — 2ах в = -++ = -. b а > 0, b с
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.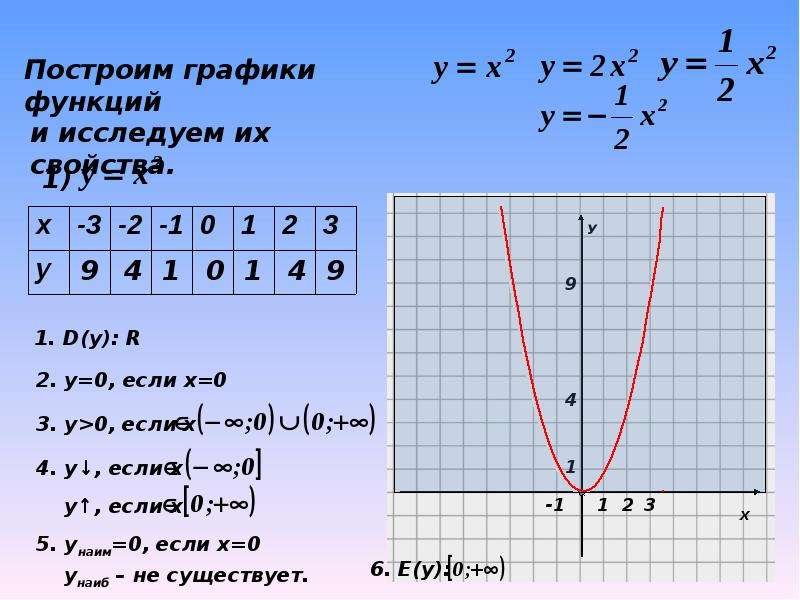 2 + 4*(1)-1= 4.
2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.
Построение графика квадратичной функции
[музыка] на прошлых уроках мы подробно рассмотрели частные случаи квадратичные функции y равен x в квадрате y равен x в квадрате плюс n и y равен a умножить на квадрат x минус m при этом последние два получаются параллельным переносом из первого случая y равен x в квадрате плюс n сдвигом вдоль оси y на n единиц вверх если n больше нуля или на n единиц вниз если n меньше 0 функция y равна а умножить на квадрат x минус m получается с помощью сдвига вдоль оси x на м единиц вправо если n больше нуля или на м единиц влево если m меньше 0 также мы получили график функции y равен a умножить на квадрат x минус m + n с помощью двух параллельных переносов которые можно производить в любом порядке известно что графиком любой квадратичной функции является парабола при изображении графика важно знать координаты вершины параболы мы говорили что парабола y равен a умножить на квадрат x минус m + n имеет вершину с координатами м. н. как же определить координаты вершины параболы которые является графиком квадратичной функции записанные формулой общего вида а как мы умеем находить вершину параболы y равен a умножить на квадрат x минус m + n попробуем привести квадратичную функцию к данному виду запишем правую часть и выделим из нее квадрат двучлена вынесем за скобки второе слагаемое в скобках представим виде удвоенного произведения тогда второе выражение равно b деленное на 2а добавим и отнимем квадрат второго выражения выделим квадрат суммы после упрощения получаем выражение мы получили формулу вида а умножить на квадрат x минус m + n значит можем записать следующее равенство m равно минус b деленное на 2а n равно минус дробь в числителе которой b в квадрате минус 4ac и знаменателе 4 а значит график квадратичной функции есть парабола которую можно получить из графика функции y равен x в квадрате с помощью двух параллельных переносов сдвига вдоль оси x и сдвига вдоль оси y вершина параболы имеет координаты м.н. при этом m равно минус b деленное на 2а n равно минус дробь в числителе которой b в квадрате минус 4ac и знаменателе 4 а оси симметрии параболы служит прямая x равен m параллельна оси y найдём координаты вершины параболы y равен минус 2x в квадрате плюс 5x минус 3 для удобства выпишем коэффициенты квадратного трехчлена вычислим значение m подставляя соответствующие значения формулу минус b деленное на 2а получим m равно одной целой 1 4 вычислим н по формуле подставим значение коэффициентов и получим n равно 1 8 таким образом получили координаты вершины параболы одна целая 1 4 1 8 так как прямая x равен m является осью симметрии параболы то ордината вершины параболы можно вычислить без формулы для n подставим значение m функцию получим значение y равно 1 8 она совпадает со значением n значит для того чтобы найти координаты вершины параболы надо вычислить м по формуле минус b деленное на 2а и подставить полученное значение функцию получим значение ординаты вершины запишем алгоритм построения графика квадратичной функции первый шаг определить направление ветви параболы ветви направлены вверх если коэффициент а положительный ветви параболы направлены вниз если коэффициент а отрицательный 2 шаг найти координаты вершины параболы и отметить ее на координатной плоскости третьим шагом определить ось симметрии x равен m четвертый шаг построить еще несколько точек принадлежащих параболе то есть составить таблицу значений функции с учетом оси симметрии последний пятый шаг соединить полученные точки плавные линии построим график квадратичной функции y равен x в квадрате плюс 6x плюс один придерживаясь полученного алгоритма сначала определим направление ветви параболы а равно единице это больше нуля значит ветви параболы направлены вверх найдем координаты вершины м.
н. как же определить координаты вершины параболы которые является графиком квадратичной функции записанные формулой общего вида а как мы умеем находить вершину параболы y равен a умножить на квадрат x минус m + n попробуем привести квадратичную функцию к данному виду запишем правую часть и выделим из нее квадрат двучлена вынесем за скобки второе слагаемое в скобках представим виде удвоенного произведения тогда второе выражение равно b деленное на 2а добавим и отнимем квадрат второго выражения выделим квадрат суммы после упрощения получаем выражение мы получили формулу вида а умножить на квадрат x минус m + n значит можем записать следующее равенство m равно минус b деленное на 2а n равно минус дробь в числителе которой b в квадрате минус 4ac и знаменателе 4 а значит график квадратичной функции есть парабола которую можно получить из графика функции y равен x в квадрате с помощью двух параллельных переносов сдвига вдоль оси x и сдвига вдоль оси y вершина параболы имеет координаты м.н. при этом m равно минус b деленное на 2а n равно минус дробь в числителе которой b в квадрате минус 4ac и знаменателе 4 а оси симметрии параболы служит прямая x равен m параллельна оси y найдём координаты вершины параболы y равен минус 2x в квадрате плюс 5x минус 3 для удобства выпишем коэффициенты квадратного трехчлена вычислим значение m подставляя соответствующие значения формулу минус b деленное на 2а получим m равно одной целой 1 4 вычислим н по формуле подставим значение коэффициентов и получим n равно 1 8 таким образом получили координаты вершины параболы одна целая 1 4 1 8 так как прямая x равен m является осью симметрии параболы то ордината вершины параболы можно вычислить без формулы для n подставим значение m функцию получим значение y равно 1 8 она совпадает со значением n значит для того чтобы найти координаты вершины параболы надо вычислить м по формуле минус b деленное на 2а и подставить полученное значение функцию получим значение ординаты вершины запишем алгоритм построения графика квадратичной функции первый шаг определить направление ветви параболы ветви направлены вверх если коэффициент а положительный ветви параболы направлены вниз если коэффициент а отрицательный 2 шаг найти координаты вершины параболы и отметить ее на координатной плоскости третьим шагом определить ось симметрии x равен m четвертый шаг построить еще несколько точек принадлежащих параболе то есть составить таблицу значений функции с учетом оси симметрии последний пятый шаг соединить полученные точки плавные линии построим график квадратичной функции y равен x в квадрате плюс 6x плюс один придерживаясь полученного алгоритма сначала определим направление ветви параболы а равно единице это больше нуля значит ветви параболы направлены вверх найдем координаты вершины м.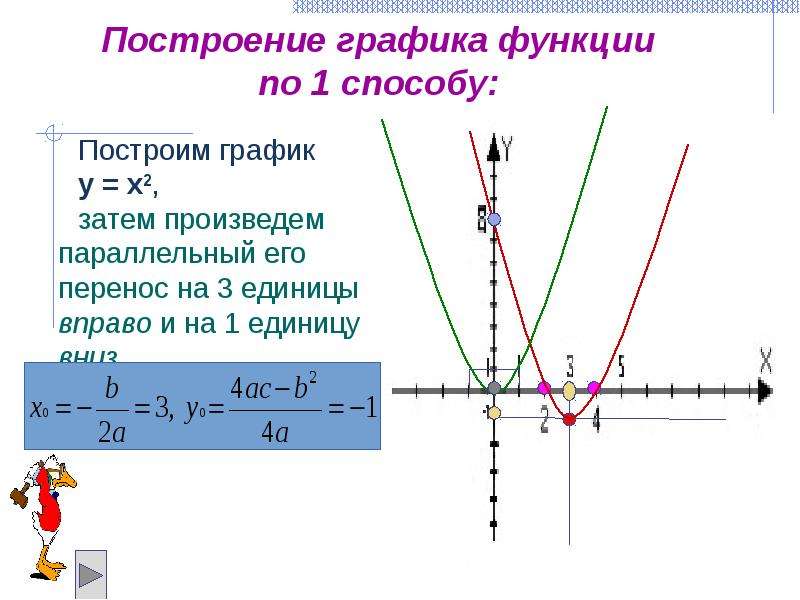 н. вычислим м по формуле минус b деленное на 2а подставим коэффициенты квадратичной функции m равно минус трём вычислим н подставив вместо x формулу полученное значение m n равно -8 отметим на координатной плоскости вершину с координатами минус 3 минус 8 определим оси симметрии это прямая x равен минус трём теперь составим таблицу значений чтобы получить еще несколько точек параболы возьмем значение x минус 6 минус 5 минус 4 минус 2-минус 10 выбранные значения симметричной относительно оси симметрии подставим их в формулу получим значение y 1 минус 4 минус семь минус 7 минус 4 и 1 отметим полученные точки на координатной плоскости соединим их плавной линией получили параболу которая является графиком функции y равен x в квадрате плюс 6x плюс 1
н. вычислим м по формуле минус b деленное на 2а подставим коэффициенты квадратичной функции m равно минус трём вычислим н подставив вместо x формулу полученное значение m n равно -8 отметим на координатной плоскости вершину с координатами минус 3 минус 8 определим оси симметрии это прямая x равен минус трём теперь составим таблицу значений чтобы получить еще несколько точек параболы возьмем значение x минус 6 минус 5 минус 4 минус 2-минус 10 выбранные значения симметричной относительно оси симметрии подставим их в формулу получим значение y 1 минус 4 минус семь минус 7 минус 4 и 1 отметим полученные точки на координатной плоскости соединим их плавной линией получили параболу которая является графиком функции y равен x в квадрате плюс 6x плюс 1
Квадратичная функция — Графики функций
•Квадратичной функцией называется функция вида y=ax2+bx+c, где a,b,c — числа, причем a≠0.
•Графиком квадратичной функции является парабола.
Чтобы построить график функции y=x2 составим таблицу значений
и построим график, используя полученные точки:
Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x2 при любых значениях остальных коэффициентов.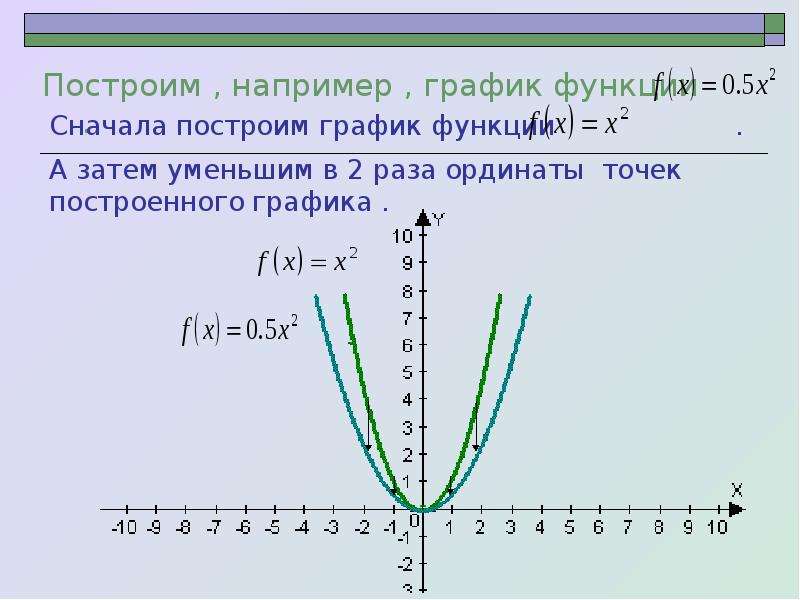
График функции y=-x2 имеет вид:
Итак:
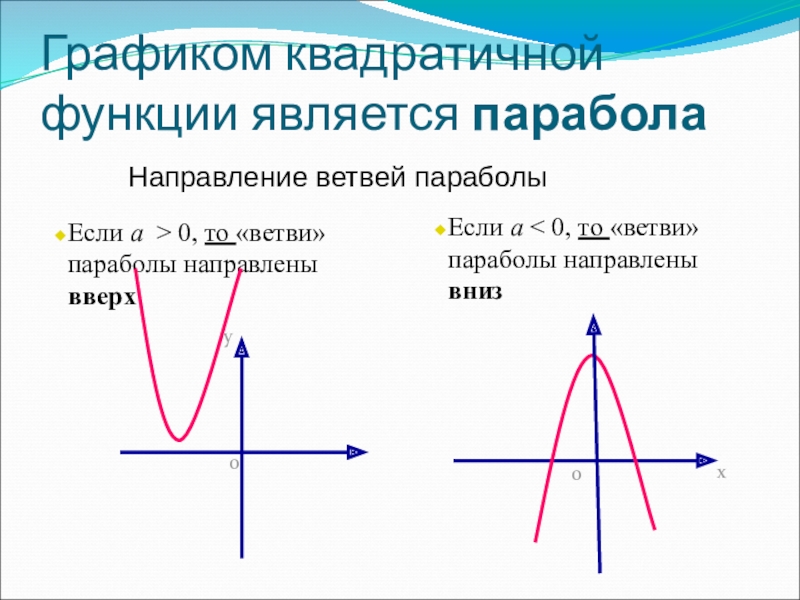
•Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
•Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй этап построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.
В случае квадратичной функции y=ax2+bx+c нужно решить квадратное уравнение ax2+bx+c=0.
В процессе решения квадратного уравнения мы находим дискриминант: D=b2-4ac, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если D<0 ,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax2+bx+c не имеет точек пересечения с осью ОХ.
Если D<0 ,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax2+bx+c не имеет точек пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:
2. Если D=0 ,то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, парабола y=ax2+bx+c имеет одну точку пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:
3.Если D>0, то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, парабола y=ax2+bx+c имеет две точки пересечения с осью ОХ: ,
Если a>0, то график функции выглядит примерно так:
Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный этап построения графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один этап построения графика функции – точка пересечения параболы y=ax2+bx+c с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax2+bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные моменты построения графика квадратичной функции показаны на рисунке:
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Повторим
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
• Повторим? Назовите координаты вершин парабол, ось симметрии.
Сформулируйте правила построения графиков функций у=ах2 + n, у=а(х-m)2 + n. • С помощью каких преобразований получили графики?
Установите соответствие
ПАДЕНИЕ БАСКЕТБОЛЬНОГО МЯЧА
ПАРАБОЛИЧЕСКИЙ ФОНТАН
БИБЛИОТЕКА С КРЫШЕЙ В ФОРМЕ ПАРАБОЛЫ В НОРВЕГИИ
ЛУЧИ ПРОЖЕКТОРА
ВРАЩАЮЩИЙСЯ СОСУД С ЖИДКОСТЬЮ
ТЕМА УРОКА: Построение графика квадратичной функции ЦЕЛИ УРОКА: Сформулировать алгоритм построения графика квадратичной функции, т. е. функции вида y = ax 2+bx+c. Научиться строить график квадратичной функции по алгоритму.
е. функции вида y = ax 2+bx+c. Научиться строить график квадратичной функции по алгоритму.
АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ y = ax 2+bx+c Определить направление ветвей параболы Определить координаты вершины параболы (хо; у о) и отметить ее в координатной плоскости: хо = -b/2 a; у о= y(хо) Построить несколько точек, принадлежащих параболе Соединить отмеченные точки
y= y 3 2 1 0 -1 1 2 – 4 x – 2 Графиком функции является парабола, ветви которой направлены вверх. 4 -3 -2 -1 2 x 3 4 5 6 x -2 -3 -4 -5 -6 Запишите свойства: Координаты вершины: Хо = -b/2 a = -(-4)/2 = 2; Уо = y(2) = 22 — 4∙ 2 – 2 = -6 х 0 1 3 4 у -2 -5 -5 -2
График функции у = |х| а) Если х≥ 0, то |х| = х функция у = х, т. е. график совпадает с биссектрисой первого координатного угла. б) Если х
ГРАФИКИ КАКИХ ФУНКЦИЙ ИЗОБРАЖЕНЫ? y y x 0 y = |x| x 0 y = — |x|
y y 2 2 x 0 y = — |x| + 2 x y 0 y = |x| + 2
y y x 0 x y 2 -2 0 y = |x — 2| y = |x+2|
ЗАДАНИЕ: ПРОЧИТАЙТЕ ГРАФИКИ ФУНКЦИЙ y y 4 -2 x 0 y = |x| + 4 x 0 -2 y = |x+2| — 2
ЗАДАНИЕ: ПРОЧИТАЙТЕ ГРАФИКИ ФУНКЦИЙ y 1 x 0 y = |x -1| x 0 -3 y = -|x| -3
КВАДРАТИЧНАЯ ФУНКЦИЯ y y 1. где f (x) > 0? 2. где f (x)
где f (x) > 0? 2. где f (x)
y x 0 y=
y 5 x 0 y= +5
y 4 x 0 -4 y =| — 4|
САМОСТОЯТЕЛЬНАЯ РАБОТА: 1 вариант Построить графики функций, записать свойства: 2 -2 у=х 1) 2) у=Iх-1 I+3 2 вариант Построить графики функций, записать свойства: 2+2 у=-х 1) 2) у=Iх+2 I-3
ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ СКАЖИ МНЕ — И Я ЗАБУДУ, ПОКАЖИ МНЕ — И Я ЗАПОМНЮ, ВОВЛЕКИ МЕНЯ – И Я ПОЙМУ
Графики квадратичных функций — вершинная форма, стандартная форма, примеры
Графики квадратичных функций — это процесс построения квадратичных функций в координатной плоскости. График квадратичной функции представляет собой параболу и говорит о характере квадратичной функции. Графики квадратичных функций дают параболы U-образной формы, широкие или узкие, в зависимости от коэффициентов функции.
В этой статье мы рассмотрим графики квадратичных функций. Мы изучим квадратичный граф, вершинную форму квадратичной функции, графическое изображение квадратичной функции в вершинной форме, стандартную форму квадратичной функции, графическое изображение квадратичной функции в стандартной форме, граф квадратной функции и другие интересные факты по теме.
Мы изучим квадратичный граф, вершинную форму квадратичной функции, графическое изображение квадратичной функции в вершинной форме, стандартную форму квадратичной функции, графическое изображение квадратичной функции в стандартной форме, граф квадратной функции и другие интересные факты по теме.
Что такое график квадратичных функций?
Графики квадратичных функций — это метод графического изучения природы квадратичных функций. Форма параболы (графика квадратичной функции) определяется коэффициентом «а» квадратичной функции f(x) = ax 2 + bx + c, где a, b, c — действительные числа, a ≠ 0.Теперь, с точки зрения построения графика квадратичных функций, мы поймем пошаговую процедуру построения графика любой квадратичной функции.
Форма вершины квадратичной функции такова: f(x) = a(x — h) 2 + k, где (h, k) — вершина параболы. Коэффициент а определяет, будет ли график квадратичной функции размыкаться вверх или вниз.
Графики квадратичных функций в форме вершин
Мы рассмотрим пошаговую процедуру построения графика любой квадратичной функции. Рассмотрим общую квадратичную функцию f(x) = ax 2 + bx + c. Сначала преобразуем его (методом дополнения квадратов) к следующему виду: f(x) = a(x + b/2a) 2 — D/4a. Член D является дискриминантом, определяемым формулой D = b 2 — 4ac. Здесь вершина параболы (h, k) = (-b/2a, -D/4a). Теперь, чтобы построить график f(x), мы начнем с того, что возьмем график x 2 и применим к нему ряд преобразований:
Рассмотрим общую квадратичную функцию f(x) = ax 2 + bx + c. Сначала преобразуем его (методом дополнения квадратов) к следующему виду: f(x) = a(x + b/2a) 2 — D/4a. Член D является дискриминантом, определяемым формулой D = b 2 — 4ac. Здесь вершина параболы (h, k) = (-b/2a, -D/4a). Теперь, чтобы построить график f(x), мы начнем с того, что возьмем график x 2 и применим к нему ряд преобразований:
- Шаг 1: от x 2 до ax 2 : Это подразумевает вертикальное масштабирование исходной параболы.Если а отрицательно, парабола также перевернет свое устье с положительной на отрицательную сторону. Величина масштабирования зависит от величины a.
- Шаг 2: x 2 в a(x + b/2a) 2 : Это сдвиг по горизонтали на величину |b/2a| единицы. Направление сдвига будет определяться знаком b/2a. Новая вершина параболы будет в точке (-b/2a,0).
 На следующем рисунке показан пример смены:
На следующем рисунке показан пример смены:
- Шаг 3: a(x + b/2a) 2 в a(x + b/2a) 2 — D/4a: Это преобразование представляет собой сдвиг по вертикали на величину |D/4a| единицы.Направление сдвига будет определяться знаком D/4a. Конечная вершина параболы будет в точке (-b/2a, -D/4a). На следующем рисунке показан пример смены:
График квадратичных функций также можно получить с помощью графического калькулятора квадратичных функций.
Графики квадратичных функций в стандартной форме
Общее уравнение квадратичной функции: f(x) = ax 2 + bx + c.Теперь для построения графика квадратичных функций с использованием стандартной формы функции мы можем либо преобразовать общую форму в вершинную форму, а затем построить график квадратичной функции, либо определить ось симметрии и точку пересечения y графика и построить Это.
Например, имеем квадратичную функцию f(x) = 2x 2 + 4x + 4. Коэффициент a = 2 > 0 означает, что график квадратичной функции будет открываться вверх. Коэффициент а также управляет скоростью возрастания (или убывания) графика квадратичной функции от вершины.Большее и положительное значение «а» заставляет функцию возрастать быстрее, а график выглядит тоньше.
Коэффициент a = 2 > 0 означает, что график квадратичной функции будет открываться вверх. Коэффициент а также управляет скоростью возрастания (или убывания) графика квадратичной функции от вершины.Большее и положительное значение «а» заставляет функцию возрастать быстрее, а график выглядит тоньше.
Далее, для построения графика квадратичной функции f(x) = 2x 2 + 4x + 4, мы определяем ось симметрии параболы, которая определяется выражением x = -b/2a = -4/(2.2) = — 1. Следовательно, x = -1 является осью симметрии для графика f(x) = 2x 2 + 4x + 4, и вершина графа также имеет координату x, равную -1.
Теперь мы определим точку пересечения у параболы, которая определяется как (0, с) = (0, 4).Используя всю эту информацию, мы можем построить график квадратичной функции f(x) = 2x 2 + 4x + 4,
Важные замечания по построению графика квадратичных функций
- График квадратичной функции имеет форму параболы.

- Коэффициент a в f(x) = a(x — h) 2 + k определяет, будет ли график квадратичной функции открываться вверх или вниз.
- Графики квадратичных функций можно выполнять как в общей форме, так и в форме вершин.
Темы, связанные с построением графиков квадратичных функций
Часто задаваемые вопросы о построении графиков квадратичных функций
Что такое график квадратичных функций?
Графики квадратичных функций — это процесс построения квадратичных функций в координатной плоскости. Графики квадратичных функций — это метод графического изучения природы квадратичных функций.
Как построить график квадратичных функций?
- Шаг 1: от x 2 до ax 2 : Это подразумевает вертикальное масштабирование исходной параболы.Если а отрицательно, парабола также перевернет свое устье с положительной на отрицательную сторону. Величина масштабирования зависит от величины a.

- Шаг 2: ax 2 в a(x + b/2a) 2 : Это сдвиг по горизонтали на величину |b/2a| единицы. Направление сдвига будет определяться знаком b/2a. Новая вершина параболы будет в точке (-b/2a,0).
- Шаг 3: a(x + b/2a) 2 в a(x + b/2a) 2 — D/4a: Это преобразование представляет собой сдвиг по вертикали на величину |D/4a| единицы.Направление сдвига будет определяться знаком D/4a. Конечная вершина параболы будет в точке (-b/2a, -D/4a).
Как найти вершину при построении графика квадратичных функций?
Для определения вершины параболы при построении квадратных уравнений определяем x-координату вершины по формуле x = -b/2a. Затем подставьте это значение x в квадратичную функцию f(x) = ax 2 + bx + c, чтобы определить координату y вершины.
Как построить график квадратичных функций в стандартной форме?
Для построения графика квадратичных функций, используя стандартную форму функции, мы можем либо преобразовать общую форму в вершинную форму, а затем построить график квадратичной функции, либо определить ось симметрии и точку пересечения y графика и построить его. {2}+k\), заполнив квадрат.{2}+3\)
{2}+k\), заполнив квадрат.{2}+3\)
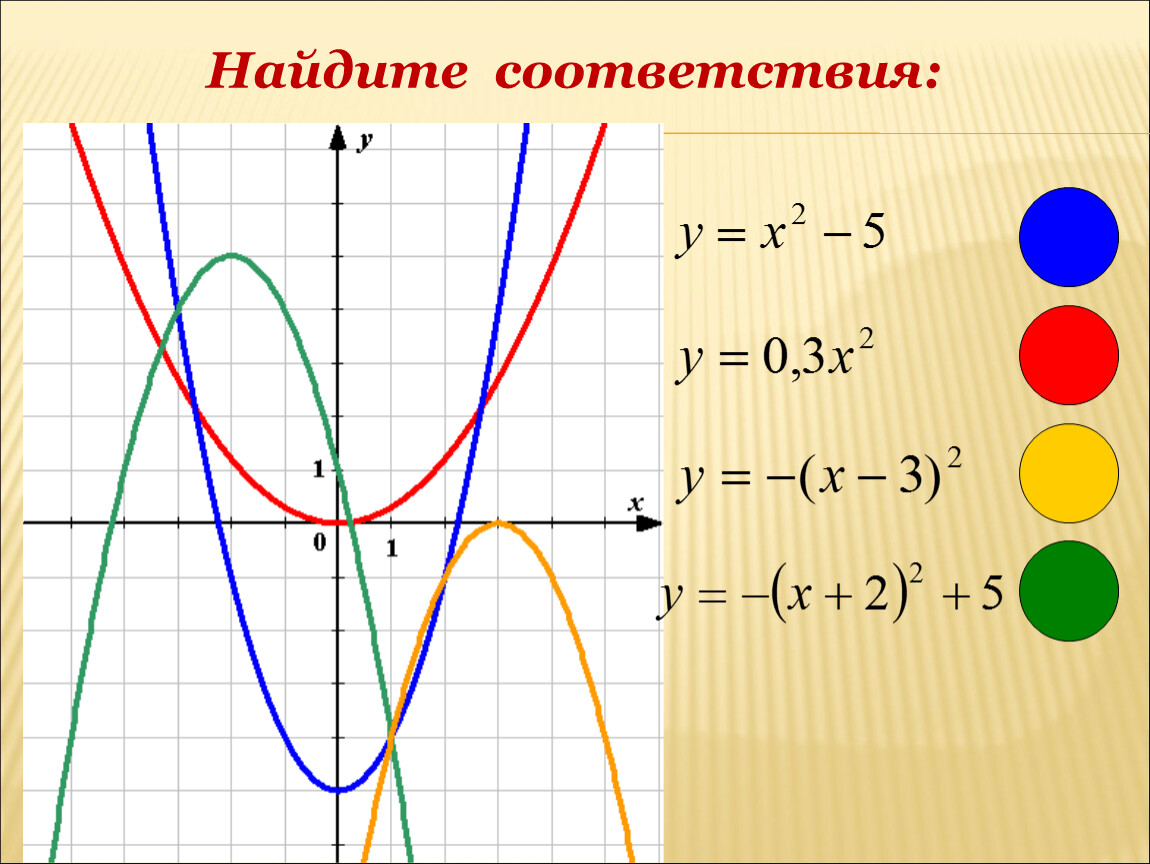 {2}+k\).{2}-1\)
{2}+k\).{2}-1\)Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики построения графиков квадратичных функций с использованием преобразований.
Пошаговое руководство по построению графика квадратичной функции
от Каталин Дэвид
Чтобы нарисовать график функции в декартовой системе координат системы нам нужны две перпендикулярные линии xOy (где O – точка пересечения x и y), называемая «координатными осями». и единица измерения.
Точка в этой системе имеет две координаты.
M(x, y): M — название точки, x — абсцисса, отсчитываемая от Ox, y — ордината, отсчитываемая от Oy.
Две координаты представляют расстояния от точки до двух осей.
Если рассмотреть функцию f: A -> B (A — область определения определение, B — домен), то точка, найденная на графике функция имеет вид P(x, f(x)).
Пример
f:A -> B, f(x) = 3x — 1
Если x = 2 => f(2) = 3×2 — 1 = 5 => P(2, 5) ∈ Gf(где Gf — график функции).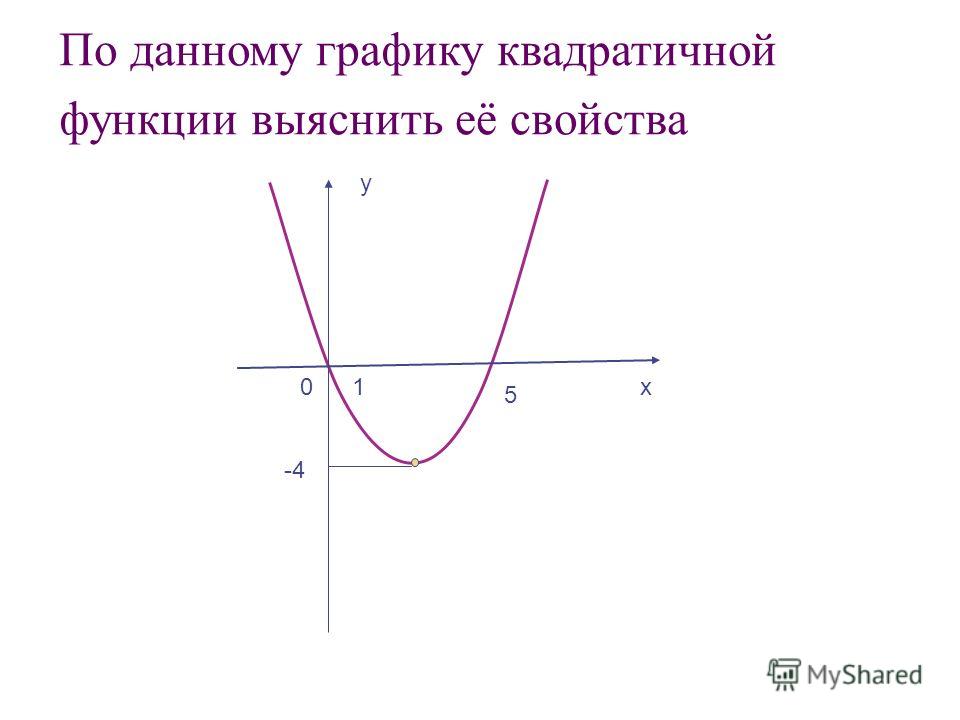 2-\frac{\Delta}{4a}$
2-\frac{\Delta}{4a}$
, где Δ = b 2 — 4ac
Если a > 0, минимальное значение f(x) будет $-\frac{\Delta}{4a}$, которое получается, если $x=-\frac{b}{2a}$. Граф будет выпуклой параболой , вершина которой (точка поворота параболы) равна $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, максимальное значение f(x) будет $-\frac{\Delta}{4a}$ который получается, если $x=-\frac{b}{2a}$.Граф будет вогнутой параболой с вершиной $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, пересекающей $x=-\frac{b}{2a}$,
которая называется «осью симметрии» .
Вот почему, когда мы присваиваем значения x , мы
выбирать значения, симметричные относительно $-\frac{b}{2a}$.
При построении графика очень важны точки пересечения с осями координат.
|.Точка, найденная на оси Ox , имеет форму P(x, 0) , потому что расстояние от нее до Ox равно 0. Если точка найдена и на Ox , и на графике функции, оно также имеет вид P(x, f(x)) ⇒ f(x) = 0 .
Если точка найдена и на Ox , и на графике функции, оно также имеет вид P(x, f(x)) ⇒ f(x) = 0 .
Таким образом, чтобы найти координаты точек пересечения Ox с осью , мы должны решить уравнение f(x)=0 . Получаем уравнение a 2 + bx + c = 0 .
Решения уравнения зависят от знака Δ = b 2 — 4ac .
Имеем следующие ситуации:
1) Δ < 0
уравнение не имеет решений в R (множество действительных чисел) график не пересекает Ox . Форма графика будет:
или
2) Δ = 0
уравнение имеет два равных решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы.Форма графика:
или
3) Δ > 0
уравнение будет иметь два разных решения.
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ох в точках М(х 1 и Ох . Вид графика будет:
Вид графика будет:
или
||. Точка, найденная на оси Oy , имеет вид R(0, y) , потому что расстояние от нее до Oy равно 0 .Если точка находится и на Oy , и на графике функции, то она также имеет вид R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)) .
В случае квадратичной функции
f(0) = a×0 2 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax 2 + bx + c
1. Рисуем таблицу переменных, в которую записываем некоторые важные значения для x .
2. Находим координаты вершины $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также запишем 0 в таблице и симметрию 0 относительно $-\frac{b}{2a}$.
или
4. Определяем точку пересечения с осью Ох , решая уравнение f(x)=0 и записываем в таблицу х 1 и х 2 .
Δ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет.В этом случае мы выберем два удобных значения, симметричных относительно $-\frac{b}{2a}$
Δ = 0 ⇒ граф касается Ox прямо в своей вершине. Мы снова выберем два удобных значения, симметричных относительно $-\frac{b}{2a}$. Чтобы лучше определить форму графика, мы также можем выбрать другие пары значений для x , но они также должны быть симметричны относительно $-\frac{b}{2a}$.
5. Записываем все эти значения в системе координат и строим график, соединяя точки.
Пример 1
f: R → R
f(x) = x 2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b 2 — 4×a×c = (-2) 2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметрия 0 относительно 1 равна 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2 -4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет таким:
Пример 2
f: R → R
f(x) = -x 2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b 2 — 4×a×c = (-2) 2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}=-1$
⇒ V(-1; 9)
1. $-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
$-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
f(-2) = 8 (симметричность 0 относительно -1 равна -2)
3. f(x) = 0 ⇒ -x 2 — 2x + 8 = 0
Δ = 36
x 1 = 2 и x 2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x 2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b 2 — 4×a×c = ( -4) 2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1.$-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричность 0 относительно 2 равна 4)
3. f(x) = 0 ⇒ x 2 — 4x + 4 = 0
Δ = 0
x 1 = x 2 = $-\frac{b}{2a}$ = 2
A(-2; 9)
B(0; 4)
V(2; 0)
C(4; 4)
D(5; 9)
Пример 4
f: R → R
f(x) = -x 2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b 2 — 4×a×c = 4 2 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1. $-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
$-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
2. f(0) = -5
f(4) = -5 (симметричность 0 относительно 2 равна 4)
3. f(x) = 0 ⇒ -x 2 + 4x — 5 = 0,
Δ < 0
Уравнение не имеет решения.
Мы должны выбрать значения, симметричные относительно 2
A(-1;-10)
B(0;5)
V(2;-1)
C(4;-5)
D(5;-10)
Если областью определения является не R (множество действительных чисел), а интервал, мы стираем часть графика, соответствующую значениям x , которых нет в интервале.В таблицу необходимо записать конечные точки.
Пример 5
f: [0; +∞) → R
f(x) = x 2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b 2 — 4×a×c = (-2 ) 2 — 4×1×(-3) = 16
$-\frac{b}{2a}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-4$
2. f(0) = -3
f(2) = -3 (симметричность 0 относительно 1 равна 2)
3. f(x) = 0 ⇒ x 2 — 2x — 3 = 0,
Δ = 16
x 1 = -1 ∉ [0; ∞)
х 2 = 3
А(0;-3)
В(1;-4)
Б(2;-3)
С(3;0)
Как построить параболу — анимация
Сравнение графиков квадратичных и линейных функций — видео и расшифровка урока
Родительские графики
Родительские функции — самая простая форма функции с коэффициентами 1 или 0. Все остальные графы являются просто преобразованиями этих родительских графов. Родительский график для линейной функции просто y = x . В этой родительской функции m равно 1, а b равно 0. Это показано красным на изображении.
Все остальные графы являются просто преобразованиями этих родительских графов. Родительский график для линейной функции просто y = x . В этой родительской функции m равно 1, а b равно 0. Это показано красным на изображении.
Родительский график для квадратичной функции: y = x 2. Здесь a равно 1, а b и c равны 0. На изображении это показано синим цветом.Разница в форме между этими двумя родительскими функциями довольно велика. Опять же, линейная функция прямая, а квадратичная кривая.
Примеры
Независимо от того, какие числа подставлены для коэффициентов, графики всегда будут иметь одну и ту же основную форму. На картинке ниже вы можете видеть графики для y = -4 x — 1 красным цветом и y = -4 x 2 + 6 x + 4 синим цветом. Линейный график перевернут из-за отрицательного значения m , а квадратичный график перевернут из-за отрицательного значения a . Но в целом эти два графа являются просто вариациями родительского графа, просто каким-то образом преобразованными.
Линейный график перевернут из-за отрицательного значения m , а квадратичный график перевернут из-за отрицательного значения a . Но в целом эти два графа являются просто вариациями родительского графа, просто каким-то образом преобразованными.
Как построить график линейной функции
Теперь, когда мы увидели различия между формами графика, давайте поговорим о том, как мы можем их изобразить.При построении графика линейной функции рекомендуется начинать с y -точки пересечения , которая является точкой пересечения графика с вертикальной осью y . Когда у вас есть линейная функция в форме y = m x + b , используйте значение b , чтобы узнать, где график пересекает вертикальную ось. В примере y = -4 x — 1 значение b равно -1. Это означает, что график пересекает ось y в точке -1.Эта точка будет равна (0,-1). Так что здесь можно поставить точку.
Это означает, что график пересекает ось y в точке -1.Эта точка будет равна (0,-1). Так что здесь можно поставить точку.
Затем мы можем использовать уклон или значение м , чтобы найти другую точку. Значение м находится прямо перед x . В нашем примере наклон равен -4. Это означает, что наша следующая точка будет на 4 клетки вниз и на 1 клетку вправо от точки пересечения и . Это будет отображаться как (1,-5). Когда у нас есть две точки, мы можем просто провести линию через них и далее.
Как построить график квадратичной функции
С квадратичными функциями лучше всего начать с точки максимума или минимума в вершине графика , которая является местом, где график изгибается, как самая высокая точка моста.Используйте следующую формулу, чтобы найти значение x этой точки: x = — b / 2 a . Как только вы найдете значение x , подключите его к функции, чтобы найти значение y .
Как только вы найдете значение x , подключите его к функции, чтобы найти значение y .
В нашем примере y = -4 x 2 + 6 x + 4, a равно -4 и b равно 6. Таким образом, x равно -(6) / 2(-4), что упрощается до -6/-8 и 3/4. Таким образом, значение x нашей вершины равно 3/4 или 0.75. Мы можем подключить это к функции, чтобы найти значение y . Когда мы это сделаем, мы получим y = -4(0,75)2 + 6(0,75) + 4. Это упрощается до 6,25. Таким образом, координаты нашей вершины равны (0,75, 6,25), что является точкой максимума, поскольку график направлен вниз.
Здесь вы можете либо ввести несколько разных значений x и составить таблицу, либо найти свои x -перехваты. Поскольку x -перехваты здесь довольно просты, давайте найдем их.Мы можем легко разложить это на множители, сначала вытащив -2, чтобы получить y = (-2) 2 x 2 — 3 x — 2. Как только мы это сделаем, мы можем разложить на множители остальные, чтобы получить (-2 ) (2 x + 1) ( x — 2). Чтобы получить точки пересечения, установите коэффициенты равными 0 и найдите x . Когда это сделано, x равняется -1/2 и 2. Это наши точки пересечения, которые можно записать в виде координат (-0,5, 0) и (2, 0). Они нанесены на картинке фиолетовым и оранжевым цветом.
Чтобы получить точки пересечения, установите коэффициенты равными 0 и найдите x . Когда это сделано, x равняется -1/2 и 2. Это наши точки пересечения, которые можно записать в виде координат (-0,5, 0) и (2, 0). Они нанесены на картинке фиолетовым и оранжевым цветом.
Затем мы можем нанести все три эти точки и провести между ними красивую изогнутую линию, чтобы закончить наш график.Наша изогнутая линия нарисована синим цветом и простирается за точки пересечения x .
Краткий обзор урока
Линейные функции обычно имеют форму y = m x + b и изображаются прямыми линиями. Чтобы нарисовать линейный график, начните со значения точки пересечения y или b , затем используйте наклон, чтобы найти вторую точку. Квадратичные функции обычно имеют форму y = x 2 + bx + c и изображаются в виде изогнутых парабол. 2+ 5x + 3`
2+ 5x + 3`
Рисование парабол
Чтобы нарисовать график квадратного уравнения, мы делаем следующие шаги:
(a) Проверьте, является ли `a > 0` или `a < 0`, чтобы решить, является ли он U-образным или n-образным.
(б) Вершина: x -координата минимальной точки (или максимальной точки) определяется как
`х=-b/(2а)`
(что можно показать с помощью метода заполнения квадрата, с которым мы познакомились ранее).
Подставляем это значение x в нашу квадратичную функцию (выражение y ). Тогда у нас будут ( x , y ) координаты минимальной (или максимальной) точки. Это называется вершиной параболы.
(c) Координаты точки пересечения и (подставьте `x = 0`). Это всегда легко найти!
(d) Координаты точки пересечения x (подставьте `y = 0` и решите квадратное уравнение), если их легко найти.2− 8x + 6`
Ответить
Сначала мы определяем, что `a = 2`, `b =
-8` и `с = 6`. 2 — 8(2) + 6 = -2`
2 — 8(2) + 6 = -2`
Таким образом, минимальная точка равна `(2, -2)`
Этап (с)
Отрезок y находится путем подстановки `x = 0` в выражение y .2 -4x -3`, показывающая точку максимума и пересечения с осями
Графики квадратичных функций — Подготовка к оценке TSI
Квадратичную функцию можно легко нарисовать, найдя всего несколько точек. Наиболее важной частью квадратичной функции является ее вершина. Напомним, что x -значение вершины квадратичной функции, f ( x ) = ax ² + bx + c , может быть найдено по формуле x = –b/ (2 и ).
Квадратичные функции можно нарисовать, найдя вершину и найдя не менее двух точек по обе стороны от вершины. Найдя эти пять точек, вы всегда получите красивую кривую в форме «∪».
Пример 1 :
Постройте график функции, найдя вершину и две точки на каждой стороне вершины.
f ( x ) = x ² – 2 x – 3
Решение :
Формула дает ось симметрии и значение x вершины.В этом случае a = 1, b = –2 и c = –3.
= 1
Вершина находится путем подстановки x = 1 в функцию, f ( x ) = x ² – 2 x – 3.
f (1) = 1² – 2(1) – 3 = 1 – 2 – 3 = –4
Вершина находится в точке (1, –4). Это самая нижняя точка на графике.
Теперь перейдите к таблице значений и определите две точки слева от вершины и две точки справа от вершины.
|
Пример 2 :
Постройте график функции, найдя вершину и две точки на каждой стороне вершины.
f ( x ) = 4 x ² – 2 x
Решение :
Формула дает ось симметрии и значение x вершины. В этом случае a = 4, b = –2 и c = 0 .
Вершина находится путем подстановки x = 1/4 в функцию, f ( x ) = 4 x ² – 2 x
ф (1/4) =
Вершина находится в точке .Это самая нижняя точка на графике.
Теперь перейдите к таблице значений и определите две точки слева от вершины и две точки справа от вершины.
|
Определите функцию, показанную на графике выше.
а. f(x) = — (x + 1) 2 + 4
б. f(x) = -(x — 1) 2 + 4
в. f(x) = (x + 1) 2 + 4
д. f(x) = (x — 1) 2 — 4
Форма вершины квадратичной функции такова: f(x) = a(x — h) 2 + k, где вершина находится в точке (h, k).
Из графика видно, что вершина находится в точке (-1, 4),
Функция f(x) = a(x — (-1)) 2 + 4 для некоторого значения a.
Когда парабола направлена вверх, значение a положительно.
Когда парабола открывается вниз, значение a отрицательно.
В этом случае «а» должно быть отрицательным, так как парабола направлена вниз.
Правильный вариант ответа должен быть
f(x) = -(x + 1) 2 + 4
Правильный ответ: а
Мяч был подброшен в воздух с балкона на высоте 20 футов над землей, и высота мяча над землей в футах через t секунд после удара по мячу была равна h(t) = 20 — 16t 2 + 32t.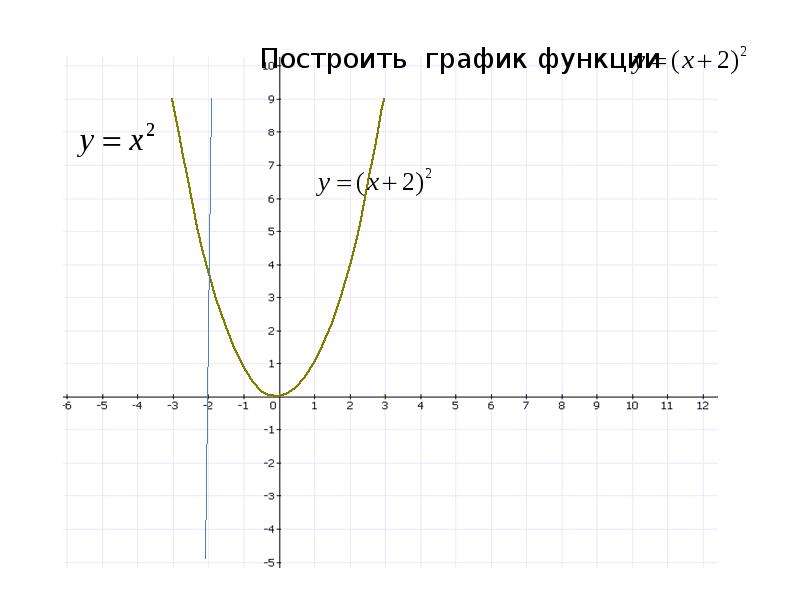

 На следующем рисунке показан пример смены:
На следующем рисунке показан пример смены: