Что важнее признаки равенства треугольника или подобие треугольников
Представление
Учащиеся 7 и 8 класса приняли участие в создание проект «Что важнее признаки равенства треугольника или подобие треугольников»
Краткое описание работы.
Проект «Что важнее признаки равенства треугольника или подобие треугольников» представлен в номинации учебных проектов «Сделаем мир лучше» в создании проекта приняли участие учащиеся 7-8 класса. У каждого было свое задание защитить свои утверждения.
Цель работы:
Определить понятие необходимости изучения признаков равенства и подобие треугольников в жизни человека, и связь их с другими предметами.
Задачи исследовательской работы:
Формирование умение проектно-исследовательской деятельности.
Оценить важность исследуемого объекта.

Объяснение возникновения признаков равенства и дальнейшего появления подобия треугольников.
Развитие умения использовать дополнительные источники (интернет ресурсы. Справочники. Энциклопедии.)
Подготовить презентацию с картинками и дискуссию по теме: что важнее признаки равенства треугольника и подобие треугольников.
Показ презентация для 8-9 классов под девизом «Зачем нам признаки равенства треугольников и подобие, и какую роль они играю в жизни человека»
Муниципальное бюджетное общеобразовательное учреждение
«Орловская средняя общеобразовательная школа
Городищенского района Волгоградской области»
Районный конкурс
социальных и
учебных проектов
«Сделаем мир лучше!»
«Что важнее признаки равенства треугольника или
подобие треугольников»
Выполнили обучающиеся
7 класса
Кривогузова Мария
Карагичева Ирина
8класса
Киселева Юлия
Руководитель проекта:
Захарова
Луиза Александровна
2015
Паспорт исследователя-проектировщика
№
п/п
Этапы работы над проектом (исследованием)
Деятельность ученика
Деятельность учителя
Выявление проблемы.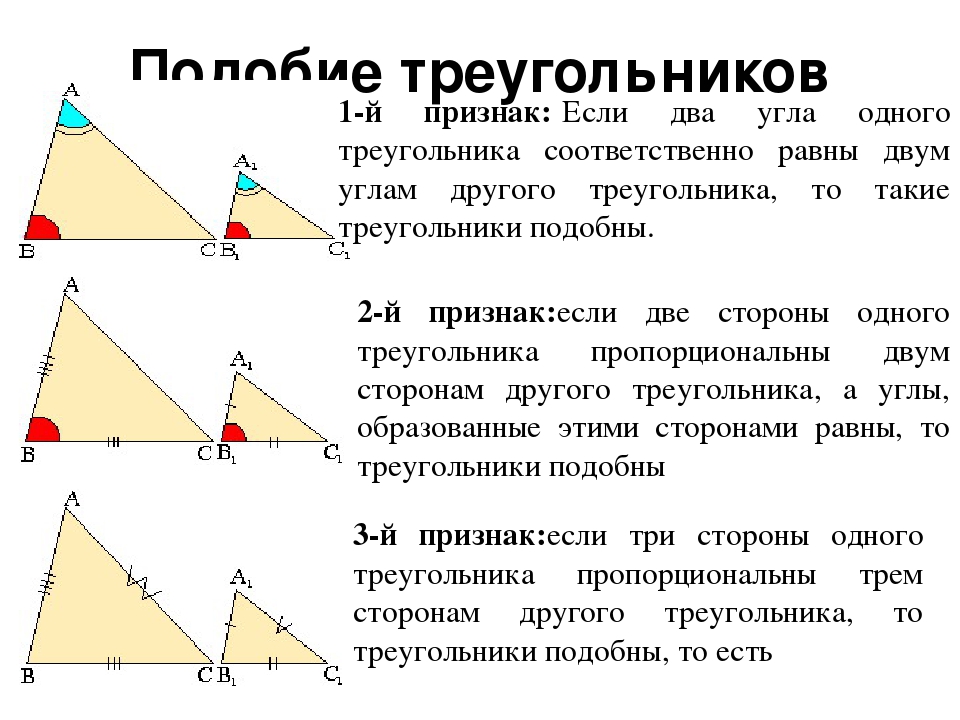
Почему заинтересовала эта проблема.
Обсуждение с учителем темы проекта, что важнее признаки равенства треугольника или подобие треугольников.
Обсуждение с учащимися темы проблемы проекта.
Определение цели и задач проекта.
Цель работы: выявить закономерность и зависимость рассматриваемых вопросов.
Определить понятие необходимости изучения признаков равенства треугольников и их подобие в жизни человека, и связь его с другими предметами.
Задачи:
Формирование и умение проектно-исследовательской деятельности.
Оценить важность исследуемого объекта.
Объяснение возникновения признаков равенства и подобия треугольников.
Проанализировать как человеком они могут применятся в жизни.

Развитие умения использовать дополнительные источники: Интернет ресурсы. Справочники. Энциклопедии
Приготовить картинки по разделам проекта.
Провести презентации в 8-9 классах «Что важнее признаки равенства треугольника или подобие треугольников»
Помощь в постановке цели и определение задач.
Планирование самостоятельной деятельности.
Выработка плана действий.
Как можно это сделать?
Определение основных методов исследования.
Работа с учебниками, энциклопедией и интернет ресурсами.
Отобрать нужный материал по разделам: строительство, искусство, военное дело.
Сделать вывод: зачем нужно признаки равенства и подобие треугольников.
Создать презентацию «Что важнее признаки равенства треугольника или подобие треугольников» и ее защиту.

Познакомить обучающегося с разными средствами и приёмами познавательной, исследовательской деятельности.
Использование исследовательских методов. Сбор информации.
Проведение исследования:
Поиск и обработка необходимой информации.
Работа с различными источниками.
Подбор рисунков.
Создание презентации.
Наблюдения, совет, помощь в работе с компьютерными программами.
Оформление конечных результатов.
Оформление защиты:
План защиты по рубрикам.
Составление презентации.
Оформление страницы «Зачем нам признаки равенства и подобия треугольников?»
Знакомство с готовой работой.
Учитель помогает оформить проект «Путешествие в прошлое.»
Презентация своего исследования.
Участие в мероприятиях:
На уроках геометрии 8-9 классах во II полугодии.
Оценивание.
Вывод.
Участники сами анализируют свое творение. Дают своей работе самооценку.
Учащиеся класса высказывают свое мнение «Зачем нам признаки равенства и подобия треугольников?»
Самое главное заинтересовать обучающихся в изучение «Признаков равенства и подобия треугольников».
Участие в оценке путём коллективного обсуждения и самооценок.
Содержание.
Вступление. Актуальность проекта.
Историческая справка:
Подобия.

Признаки равенства треугольников.
Признаки равенства и подобия треугольников.
Равенства треугольников по стороне и двум углам.
Подобие треугольников по двум углам.
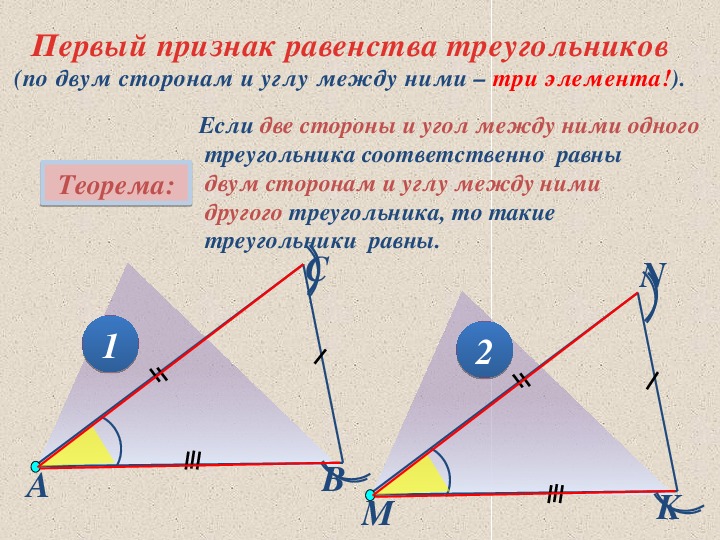
- Равенство треугольников по двум сторонам и углу между ними.
Подобие треугольников по пропорциональности двух сторон одного треугольника к другому и равенству угла между ними.
Жесткий треугольник.
Подобие пропорциональности трех сторон одного треугольника к другому.
Признак равенства треугольников по трем углам.
Заключение:
Вывод.
Применение на практике.
Применение при возведение зданий.
Защита проекта.

Вступление
Меня зовут Кривогузова Мария, я ученица 7 класса будут вам представлять признаки равенства треугольников и их историю.
Меня зовут Киселева Юлия, я ученица 8 класса буду вам представлять признаки подобия треугольников их историю возникновения и необходимость их изучать.
Основной целью нашего исследования является определить важность изучения данных утверждений.
Для начала мы решили провести опрос в более старших классов. Вопросы с вариантами ответа были таковыми:
Что важнее равенство треугольников или подобие треугольников?
Равенство треугольников;
Подобие треугольников;
Важны оба утверждения.
Пригодились ли вам признаки равенства треугольников и подобие треугольников при дальнейшем изучении геометрии?
Да;
Нет.

Как вы думаете, где больше пригодится вам этот изученный материал?
Я думаю, что мне это пригодится при учебе в высшем учебном заведении;
Я изучал(а) для того чтобы в будущем не выглядеть тупым перед своими детьми.
Мне это совсем не как не нужно.
Поэтому мы сами решили выяснить, что важнее равенство или подобие треугольников, и как они применимы в жизни человека.
Актуальность.
Треугольник является центральной фигурой всей геометрии. При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике. Например, в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различны деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации: для проложения правильного и максимально точного маршрута; в астрологии и астрономии, одним словом просто необходимо знать треугольник и все его свойства.
Историческая справка подобия треугольников
Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.
Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию.
Историческая справка о признаках равенства треугольников:
Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Равенство треугольников по стороне и двум прилежащим углам.
Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC AB; в противоположном направлении восстанавливают CE AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).
Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).
Признак подобия треугольников по двум углам.
Но так не удобно решать задачу для этого можно воспользоваться первым признаком подобия треугольников. И как не странно его создатель также Фалес Милетский
Давайте представим картину такую
Мы с вами в Египте сейчас оказались.
Стоим и смотрим на пирамиду большую
Её высотою большой восхищаясь.
И тут сам фараон задачу нам ставит
Измерить нам надо высоту пирамиды.
Как же рулетку к ней приставить
Ведь конца её даже не видно.
Но всё-таки задачу можно решить
Вспомнив подобие треугольников.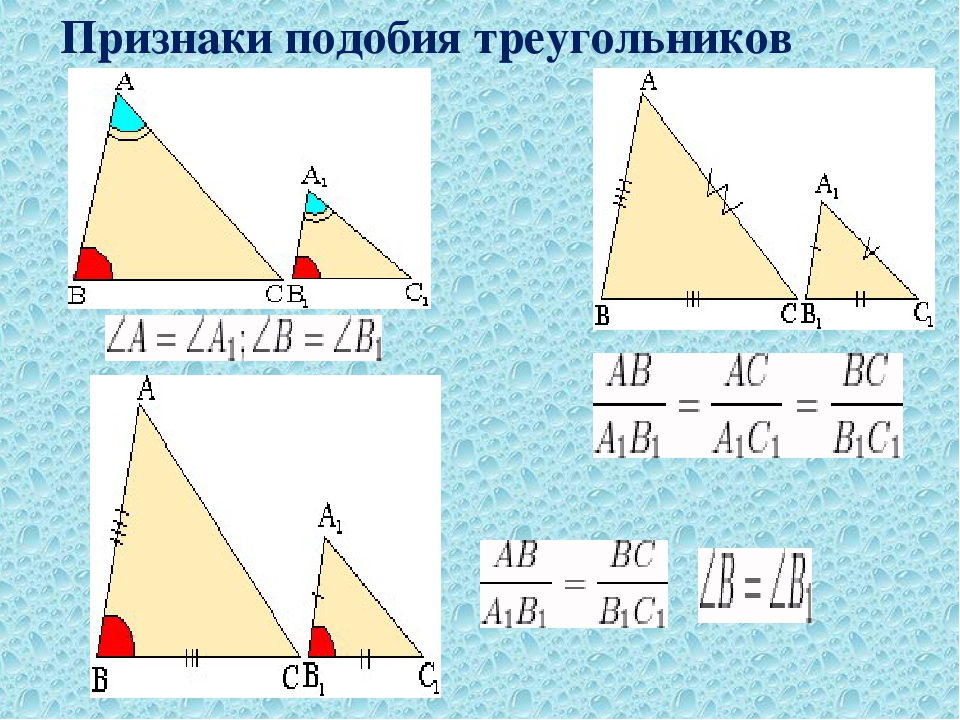
Фалес Милетский нам предложил
Пример преподавший для школьников.
Он подождал пока тень его
Точно совпадет с его ростом.
Как оказалось немного терпения
Задача решилась легко и просто.
В этот миг теорему применив
Высота пирамиды равна её тени.
Знай про подобие треугольников
И применяй её в жизни без лени.
Используя этот признак подобия мы можем измерить высоту любой башни и не только высоту, а спроектировать на чертежах любую постройку.
Равенства треугольников по двум сторонам и углу между ними.
Для исследования этого признака я решила взять практическую задачу на вычисление длины озера.
При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500м.
Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500м.
Сколько же нужно много свободного пространства чтобы сделать эти измерения, а не легче ли применить второй признак подобия треугольников.
Подобия треугольника по пропорциональности двух сторон одного треугольника к другому и равенству угла между ними.
При измерении длины озера: так же можно отметить на местности точки А, В и С, а затем еще две точки D и К, так, чтобы отношения DC:CB и KC:AC оказалась равными.
Равенства треугольников по трем сторонам. Жесткий треугольник
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, (рис 1) у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой однако сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек.(рис 2) Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Такая конструкция не является жёсткой однако сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек.(рис 2) Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Если все три стороны
треугольников равны,
То давно понятно всем
Что равны они совсем.
Подобие треугольников пропорциональности трех сторон одного треугольника к другому.
Если жесткий треугольник мы решим увеличить или уменьшить в несколько раз, то увечится или уменьшится в это число раз каждая его сторона, и тем самым получим третий признак подобия треугольника «Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны».
Если три стороны треугольника одного
Пропорциональны трём сторонам другого,
То эти треугольники будут абсолютно подобны
Даже если один маленький, а другой огромный.
Равенства треугольников по трем углам.
Был такой великий русский философ математик Николай Лобачевский, который доказал четвертый признак равенства треугольников. «Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны»
Такого признака равенства треугольников нет. Это часть определение подобия треугольника. «Если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны».
Вывод.
Наш спор был долгим и упорным что важнее: признаки равенства треугольников или подобия. Мы сделали следующий вывод – если бы не было признаков равенства треугольников, то не было бы и подобия. Такой вывод помог сделать нам древнегреческий филосов и математик Фалес Милетский, который доказал не толькоодин из признаки равенства треугольников, но а также один из основных признаков подобие.
Мы сделали следующий вывод – если бы не было признаков равенства треугольников, то не было бы и подобия. Такой вывод помог сделать нам древнегреческий филосов и математик Фалес Милетский, который доказал не толькоодин из признаки равенства треугольников, но а также один из основных признаков подобие.
«Природа формулирует свои законы языком математики» Г.Галилей.
В наше время чтобы измерить высоту здание, найти расстояние мы не обходимся без гениальных идей Фалеса Милетского.
Прежде чем построить здание делают его уменьшенный макет, а уж потом его возводят в реальные размеры.
Защита проекта:
Уроки геометрии 8, 9, 10, 11 класс.
«Природа формулирует свои законы языком математики» Г. Галилей
Галилей
Защита проекта на конкурсе «Сделаем мир лучше»
Используемые источники в написание проекта.
Энциклопедия «Аванта» по математике. 2004 г
«Википедия» свободная энциклопедия. http://ru.wikipedia.org/wiki/Заглавная_страница
http://to-name.ru/biography/biografii.htm
Глейзер Г.И. «История математики в школе 7-8 классах», Просвещение 1982 г.
http://nytva.taba.ru/page1291435753/fest/542212_OF_IV-6_Priznaki_ravenstva_treugolnikov_Geometriya_7_klass.html
ГусеваТ.М. Признаки подобия треугольников.- М.// Первое сентября, приложение«Математика», 1999, №28
Автор всех стихо Сусь Р.С.
Третий признак подобия треугольников
Прежде, чем познакомиться с третьим признаком
подобия треугольников, вспомним известные нам первый и второй.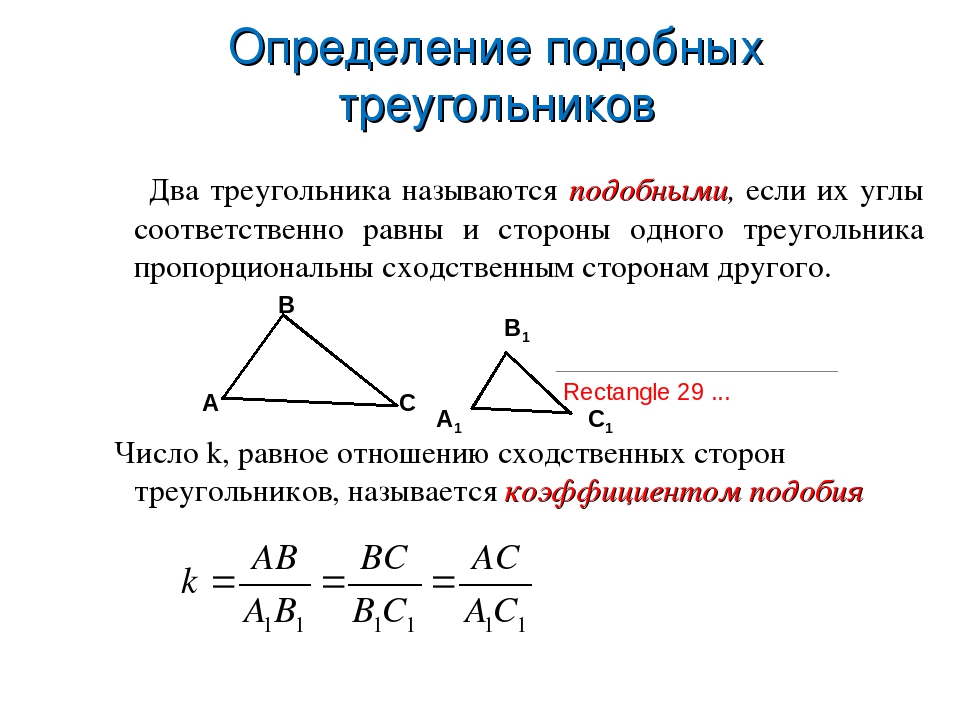
Итак, первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
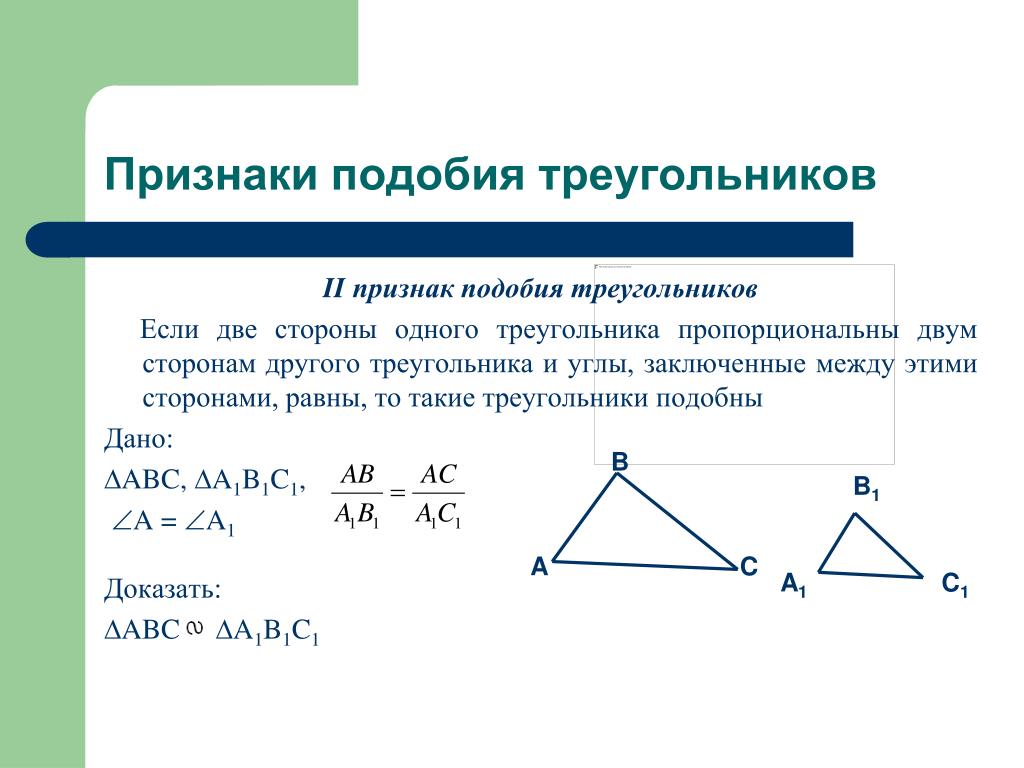
Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
Ну а теперь сформулируем третий признак подобия треугольников.
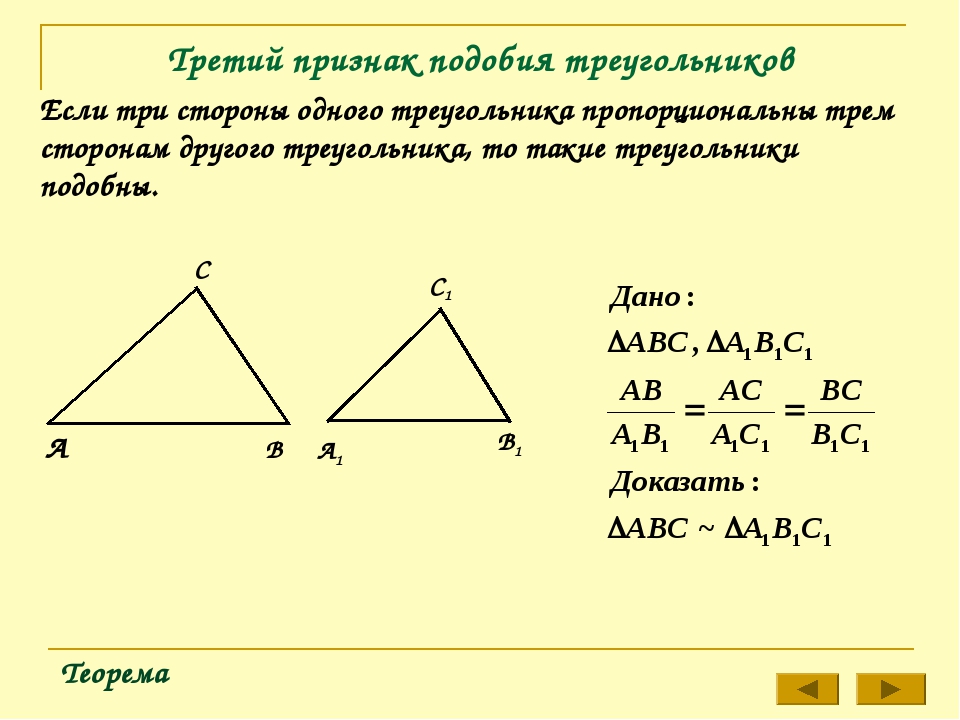
Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство.
.
, , тогда по 1-му признаку.
.
Получаем, что , .
Тогда по 3-му признаку.
Следовательно, .
Так как , то .
Следовательно, .
Что и требовалось доказать.
Давайте найдём среди следующих треугольников
подобные.
У каждого из треугольников известны длин трёх его сторон, а тогда воспользуемся только что доказанным третьим признаком подобия треугольников.
Посмотрим внимательно на значения их длин и заметим, что стороны треугольника а пропорциональны сторонам треугольника в, а значит, эти треугольники подобны. При этом коэффициент подобия равен 2.
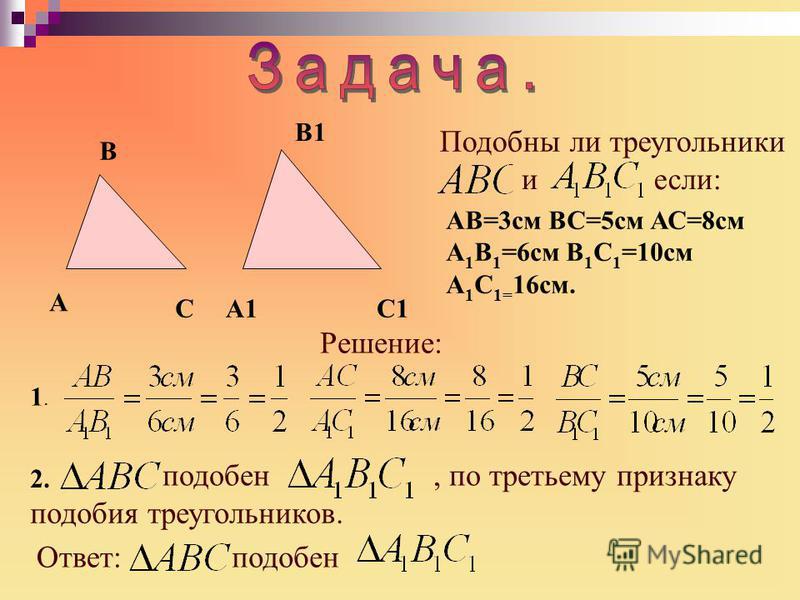
Задача. Подобны ли треугольники и , если см, см, см, см, см, см?
Решение.
,
,
.
Значит, .
Следовательно, .
Ответ: .
Задача. Докажите, что прямоугольные треугольники и подобны, если стороны и треугольника соответственно равны см и см, а стороны и треугольника соответственно равны см и см.
Решение.
,,
(см).
, ,
(см).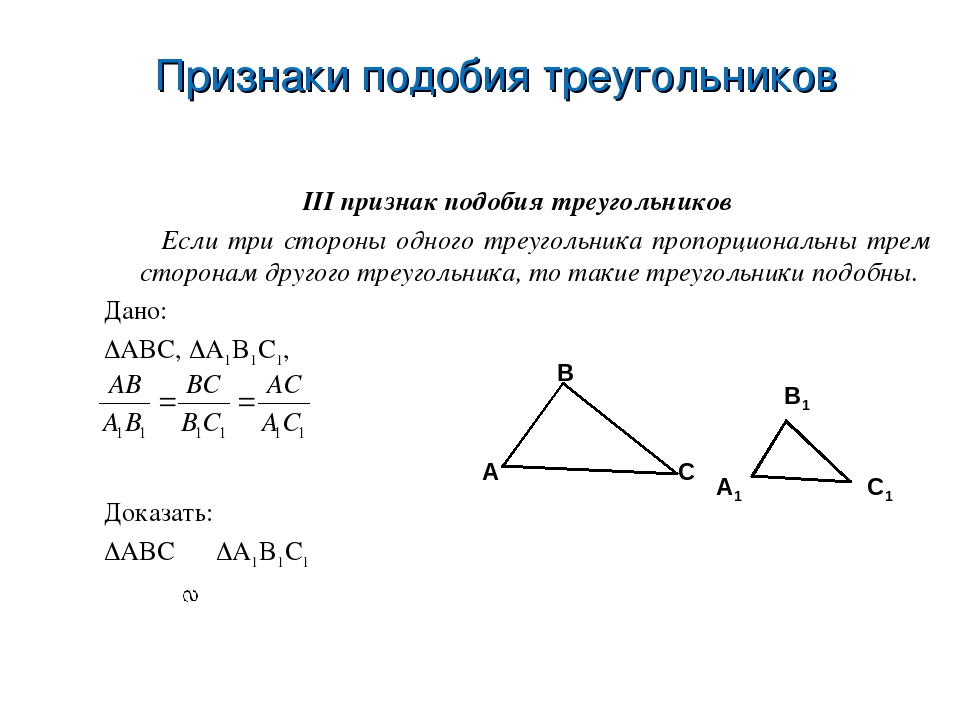
; ; .
Значит, .
Следовательно, по 3-му признаку.
Что и требовалось доказать.
Итак, сегодня на уроке мы познакомились с ещё одним признаком подобия треугольников: если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Также мы закрепили материал на практике.
Признаки подобных треугольников | Треугольники
Признаки подобия треугольников позволяют доказать, что треугольники являются подобными, на основании 2-3 равенств (вместо 6 по определению).
В школьном курсе геометрии, как правило, изучают три признака подобия произвольных треугольников.
1-й признак подобия треугольников
( подобие треугольников по двум углам)
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2-й признак подобия треугольников
( подобие треугольников по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.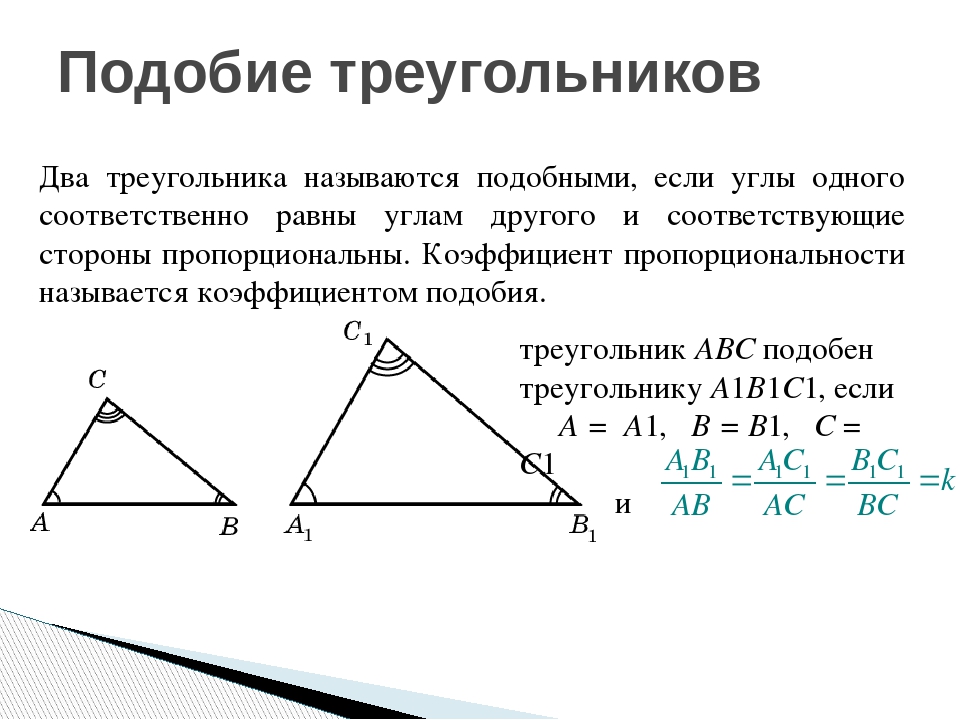
3-й признак подобия треугольников
( подобие треугольников по трём сторонам)
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Есть еще 4-й признак подобия треугольников —
( подобие треугольников по двум сторонам и наибольшему углу)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а наибольший угол одного равен наибольшему углу другого, то такие треугольники подобны.
Доказав, что треугольники подобны, можно использовать свойства подобных треугольников.
Для доказательства подобия прямоугольных треугольников используют другие признаки. Их мы запишем в следующий раз.
Подобие правильных и подобие равнобедренных треугольников рассмотрим позже.
Признаки подобия треугольников широко используются при решении задач как в курсе планиметрии, так и в курсе стереометрии. Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.
Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.
Разработка модуля по геометрии «Признаки подобия треугольников» — К уроку — Математика, алгебра, геометрия
РАЗРАБОТКА МОДУЛЯ ПО ГЕОМЕТРИИ В 9 КЛАССЕ ПО ТЕМЕ:
«ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ»
РАЗРАБОТАЛА:
учитель математики 1 категории
МОКУ «ЛАРБИНСКАЯ СОШ»
ХИЖАК АЛЛА АЛЕКСЕЕВНА
2013 г.
МОДУЛЬ «ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ»
ЦЕЛЬ: 1) знать формулировку признаков подобия треугольников;
2) уметь доказывать один из признаков подобия треугольников;
3) научиться применять признаки подобия треугольников;
4) отработать навык по решению задач по данной теме;
5) уметь анализировать, сравнивать, обобщать.
ХОД УРОКА
ПРОВЕРКА
ДОМАШНЕГО ЗАДАНИЯ:
сформулировать понятия подобия, свойства
преобразований подобия, гомотетии и
гомотетичных фигур.
Обратить внимание на то, чем может быть задана гомотетия:
указанием центра гомотетии и коэффициента гомотетии;
двумя парами соответствующих точек.
ПОДГОТОВИТЕЛЬНЫЙ ЭТАП.
Ввиду общности идеи доказательства признаков подобия треугольников целесообразно рассмотреть все три теоремы одновременно, используя единую схему – рисунок и общий план доказательства каждой из теорем.
Прежде чем приступить к непосредственному изучению признаков подобия треугольников, полезно предварительно провести подготовительную работу с классом:
а) повторить признаки равенства треугольников;
б) сформулировать определение подобных треугольников, исходя из общего определения подобных фигур.
Важно обратить внимание на порядок записи вершин подобных треугольников и пропорциональности сторон, предложив учащимся упражнения:
Дано: ∆ MNR ∞ ∆ АВС. Укажите, какие углы равны и какие
стороны
пропорциональны.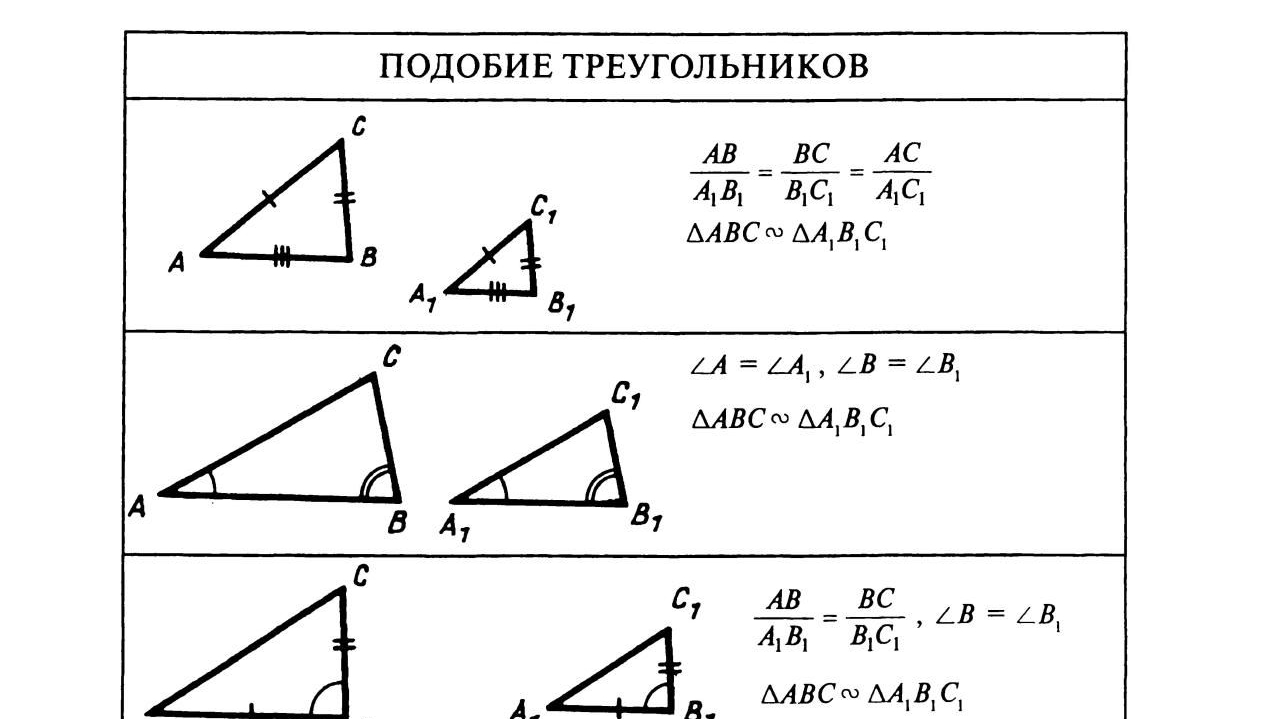
Два треугольника подобны. Два угла одного треугольника 100 и 60 . Чему равен меньший угол второго треугольника?
3.Сравните определения равных и подобных треугольников.
Что можно сказать о соответствующих углах в том и другом случаях? О соответствующих сторонах?
Лабораторная работа.
Цель работы: Исходя из названий признаков равенства треугольников и определения подобных треугольников, дать по аналогии названия признакам подобия треугольников и сформулировать их.
Учитель заранее вычерчивает на доске таблицу, которую учащиеся воспроизводят в рабочих тетрадях и заполняют ее Таблица сравнения признаков равенства и подобия треугольников
Признаки равенства треугольников | Признаки подобия треугольников | |||
Условие теоремы | Название признака | Условие теоремы | Название признака | Формулировка признака |
Дано: АВ = А1 В1 АС = А1 С1 , угол
А равен углу А1. Доказать: ∆АВС = ∆А1В1С1. Дано: АВ = А1В!, АС = А1С1, ВС = В1С1. Доказать: ∆АВС = ∆А1В1С1. Дано: Угол А равен углу А1, угол В равен углу В1, АВ = А1В1. Доказать: ∆АВС = ∆А1В1С1. | Дано: АВ = к А1В1, АС = к А1С1, Угол А равен углу А1. Доказать: ∆АВС ∞∆А1В1С1. Дано: АВ = к А1В1, АС = к А1С1, ВС = к В1С1. Доказать: ∆АВС ∞∆А1В1С1. Дано: Угол А равен углу А1, Угол В равен углу В1, АВ
= к А1В1. Доказать: ∆АВС ∞∆А1В1С1. | |||
Дополнительные вопросы:
Сколько соответствующих пар равных элементов указывается в условиях признаков равенства элементов? Почему?
Есть ли отличия в условиях признаков подобия треугольников? Чем они объяснимы? Существенны ли они?
111.ДОКАЗАТЕЛЬСТВО ПРИЗНАКОВ ПОДОБИЯ ТРЕУГОЛЬНИКОВ.
К ласс получает задание: прочитать в учебнике доказательство одного из признаков и составить план основных этапов доказательства.
АААА
В это время учитель на доске (экране, таблице) представляет рисунок теоремы (рис.1)А2 С2
А С
В2 2
1
А1 С1 3
В
В1
В результате обсуждения работы над составлением плана доказательства делается вывод, что во всех трех теоремах можно выделить три этапа доказательства (учащиеся записывают их в тетради):
∆ А В С → ∆ А2 В2 С2 , где к =
∆ А2 В2С 2 = ∆АВС – по одному из признаков
равенства треугольников (см.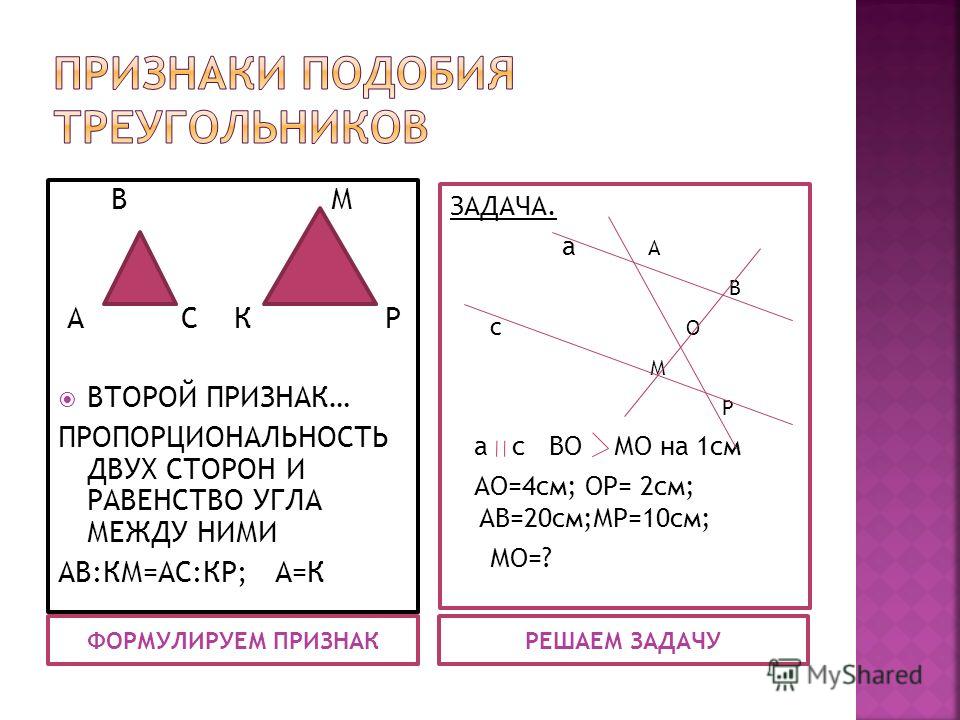 таблицу).
таблицу).
∆ АВС ∞ ∆ А1 В1 С 1 — по определению подобия.
Далее учащиеся совместно с учителем приступают к подробному обоснованию каждого из этапов доказательства всех теорем и записывают его в тетрадях, заполняя такую таблицу:
Доказательство признаков подобия треугольников | |||
по двум углам | по двум сторонам и углу между ними | по трем сторонам | |
1 11 111 | |||
Проверка усвоения признаков подобия треугольников.
Подобны ли прямоугольные треугольники, если в одном из них имеется угол 42 , а в другом – угол 48 ?
Н
а
рисунке параллельные прямые показаны
одинаково направленными стрелками. Найти на этих рисунках подобные
треугольники и объяснить, почему они
подобны?
Найти на этих рисунках подобные
треугольники и объяснить, почему они
подобны?
В В С
В1
В2
А С
А1 А2 А Д
1У. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА.
Д ля первичного закрепления изученной теории учащимся предлагаются упражнения: 1.Дано: АВ МN (рис.2) Доказать: ∆ ОАВ ∞ ∆ ОNM. Как найти коэффициент подобия треугольников?
М
А
О
В N
рис.2 2.Подобны ли треугольники АВС и А1 В1 С1 если:
а) АВ=10 см; АС=6см; А1 В1=5см; А 1С1 =3см; угол А равен углу А1;
б) АВ=2м; АС=3 м; ВС= 4м; А1 В1 =6 м; А1 С1 =9 м; В1 С 1=8 м?
3. Подобны ли любые два равносторонних треугольника?
4. Известно, что у треугольников АВС и А1 В1 С1 угол А равен углу А1;
угол В равен углу В1;
АВ=5 м; ВС=7 м; А1 В1 =10 м; А1 С1 =8 м. Найдите
Известно, что у треугольников АВС и А1 В1 С1 угол А равен углу А1;
угол В равен углу В1;
АВ=5 м; ВС=7 м; А1 В1 =10 м; А1 С1 =8 м. Найдите
АС и В1С1.
5.Имеет ли место следующий признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и один из углов одного треугольника равен какому-то углу другого, то такие треугольники подобны?
Ответ. Нет. Для обоснования ответа достаточно привести пример, противоречащий данному утверждению.
6.Продолжите фразу: «Два равнобедренных треугольника подобны, если…». Сколько вы нашли вариантов ответа?
ПРИМЕЧАНИЕ. Упражнения 1 – 4 относятся к обязательному уровню усвоения.
У. ПРАКТИЧЕСКАЯ ЧАСТЬ.
Решение задач (см. рабочую тетрадь)
Тип 1.Задачи
в чертежах на нахождение подобных треугольников,
где нужно назвать по какому признаку
подобны эти треугольники.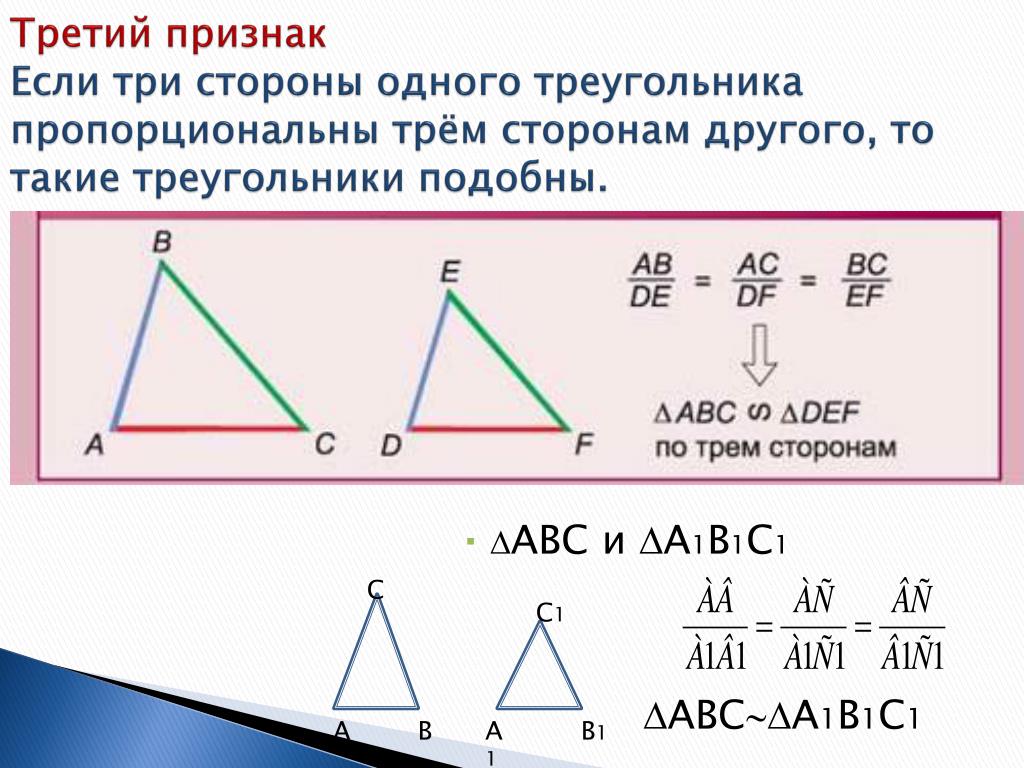
№№ 13, 28, 37.
Тип 2. Вычислительные задачи
Инструкция №1 к применению:
Чтобы найти неизвестные стороны подобных треугольников, нужно:
записать пропорциональность сходственных сторон,
подставить значения известных сторон,
вычислить неизвестную сторону, решив пропорцию.
Например:
Дано: ∆ АВС ∞ ∆ МРК, АВ=12, ВС=15, РК=40, МК=24.
Найти: МР и АС.
Р е ш е н и е:
Так как ∆ АВС ∞ ∆ МРК, то .
Тогда .
Из пропорции имеем
15 МР = 12∙40, МР = , МР = 32.
Из пропорции = имеем
40 АС = 15 24, АС = , АС =9.
Ответ: АС = 9, МР =32.
Инструкция №2 к применению:
Чтобы записать пропорциональность сходственных сторон подобных треугольников, нужно:
выяснить, при каких вершинах углы равны,
определить, какие стороны являются сходственными (лежат против равных углов),
записать
пропорцию, где в числителях – стороны
одного треугольника, а в знаменателях
– сходственные им стороны другого.
№№14, 16, 17, 29, 30, 38, 39.
Тип 3. Задачи на доказательство
№№ 15, 31.
Инструкция №3 к применению:
При доказательстве подобия треугольников часто используют свойства углов при параллельных прямых ( см. рис.3, 4).
О
А В
М Р Р
С М
К Е
рис.3 рис.4
1 .Если МР КЕ, то угол ОМР равен углу ОКЕ (как соответственные при параллельных прямых МР и КЕ и секущей МК).
Тогда у треугольников ОМР и ОКЕ: угол О – общий и угол ОМР равен углу ОКЕ т.е. треугольник ОМР подобен треугольнику ОКЕ по двум углам (рис.3)
2 .Если АВ СМ, то угол РСМ равен углу РВА (как внутренние накрест лежащие при параллельных прямых АВ и СМ и секущей ВС).
Тогда у треугольников
РАВ и РМС: угол РСМ равен углу РВА и
угол СРМ равен углу ВРА (как вертикальные
углы), т.е. треугольник РАВ подобен
треугольнику РМС по двум углам (рис.4).
Работа с учебником.
Решение задач №№ 12,18, 20, 24, 35, 44.
У1. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ
В треугольнике МЕК проведена прямая ЕР так, что угол ЕРК равен углу МЕК. Докажите, что треугольник ЕРК подобен треугольнику МЕК.
В треугольнике РЕК ОD РК. Докажите, что треугольник ОЕD подобен треугольнику РЕК.
Д ан треугольник КМN. Через точку О на стороне К N и точку Р на стороне КМ проведена прямая, причем ОР МN:
Докажите, что треугольник КМ N подобен треугольнику КРО.
Найдите длину отрезка ОР, если: а) М N =20 см; РК=12 см; КМ = 16 см; б) ОК = 12 см; К N =16 см; М N = 24 см.
В трапеции ВCDЕ с основаниями ВЕ и СD диагонали пересекаются в точке Н:
Доказать, что
треугольник ВНЕ подобен треугольнику
DНС.
Найти СD , если: а) ВЕ = 32 см; ВН = 28 см; НД = 21 см;
б) ВЕ = 36 см; ЕН = 32 см; СН = 24 см.
5. Диагонали трапеции АС и ВD пересекаются в точке О. ВС=5 см,
АD = 15 см, ВD = 12 см. Найдите ВО и ОD .
6.Через точку Е стороны КD треугольника F К D проведена прямая, параллельная стороне FК и пересекающая сторону FD в точке О.Найдите ОЕ, если F К = 15 дм, F О = 4 дм, ОD = 8 дм.
ЛИТЕРАТУРА:
А.В. Погорелов, Геометрия, 7-9 класс, изд-во «Просвещение», Москва, 2012.
Ю.П. Дудницын, Геометрия, рабочая тетрадь, изд-во «Просвещение», Москва, 2008.
Т.И. Купорова, Геометрия, 9 класс, поурочные планы, изд-во «Учитель», Волгоград, 2001.
Н. Б.Мельникова, Г.Б. Лудина, Н.М. Лепихова, Геометрия, Дидактические материалы для 7-9 классов, «Мнемозина», Москва, 1999.
В.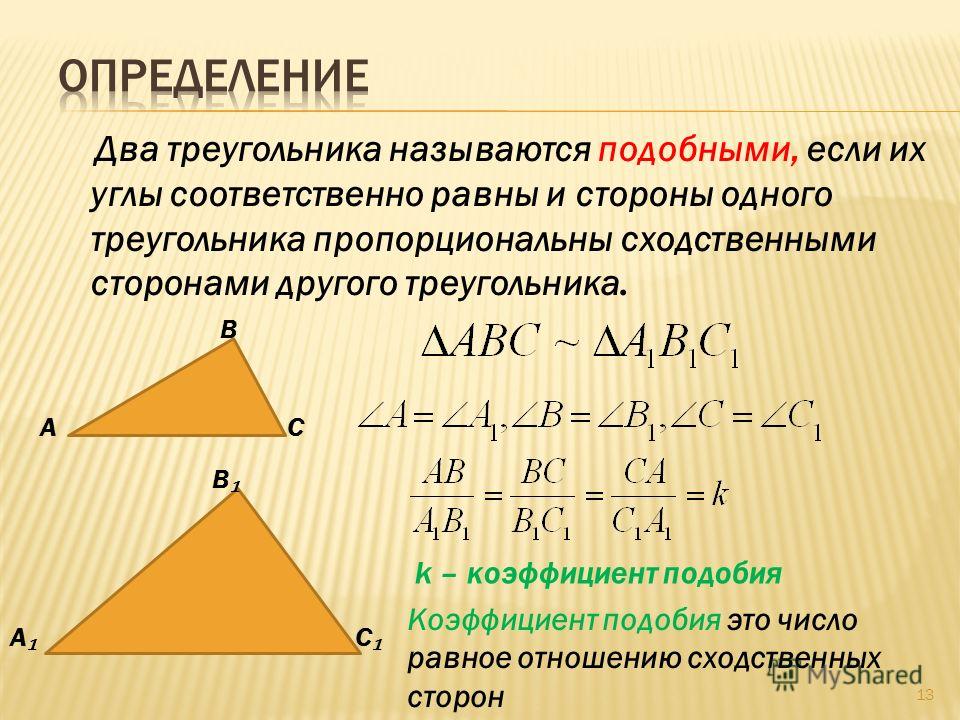 И.Жохов,
Л.Б.Крайнева, Геометрия, Карточки для
проведения контрольных работ и зачетов,
«Вербум-М», Москва, 2001.
И.Жохов,
Л.Б.Крайнева, Геометрия, Карточки для
проведения контрольных работ и зачетов,
«Вербум-М», Москва, 2001.
Треугольник. Подобие треугольников. Первый признак подобия треугольников.
Что такое треугольник? Из школьного определения треугольник:
Также можно сказать, что треугольник – это многоугольник с тремя углами. У треугольника всегда три стороны и три угла, тем больше сторона, чем больше угол и наоборот.
В этой статье мы научимся определять, являются ли подобными треугольники. Различие между подобием и равенством треугольников заключается в том, что в подобных треугольниках длины сторон треугольника умноженные или разделенные на одно и то же число, то есть их стороны имеют одинаковый коэффициент пропорциональности. Равные треугольники имеют равные углы и стороны. Как определить, подобны ли треугольники? Существуют признаки подобия треугольников. В школе изучают три основных признака подобия треугольников. Давайте узнаем их. Первый признак подобия треугольников:
Давайте узнаем их. Первый признак подобия треугольников:Второй признак подобия треугольников (по двум сторонам и углу между ними):
Третий признак (по трем сторонам):
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Белорусский государственный экономический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов.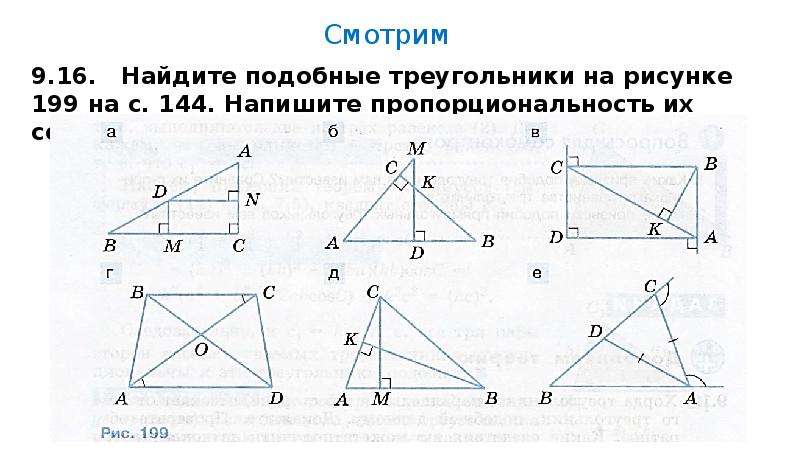 Правильно задаю вопросы, умею слушать и слышать учеников. Смотрю на все сквозь призму юмора и стремлюсь влюбить всех в свой предмет. Требовательная, но понимающая. Я люблю математику за то, что она развивает мышление и приводит в порядок ум.
Правильно задаю вопросы, умею слушать и слышать учеников. Смотрю на все сквозь призму юмора и стремлюсь влюбить всех в свой предмет. Требовательная, но понимающая. Я люблю математику за то, что она развивает мышление и приводит в порядок ум.
Репетитор по математике
Чувашский государственный педагогический институт им.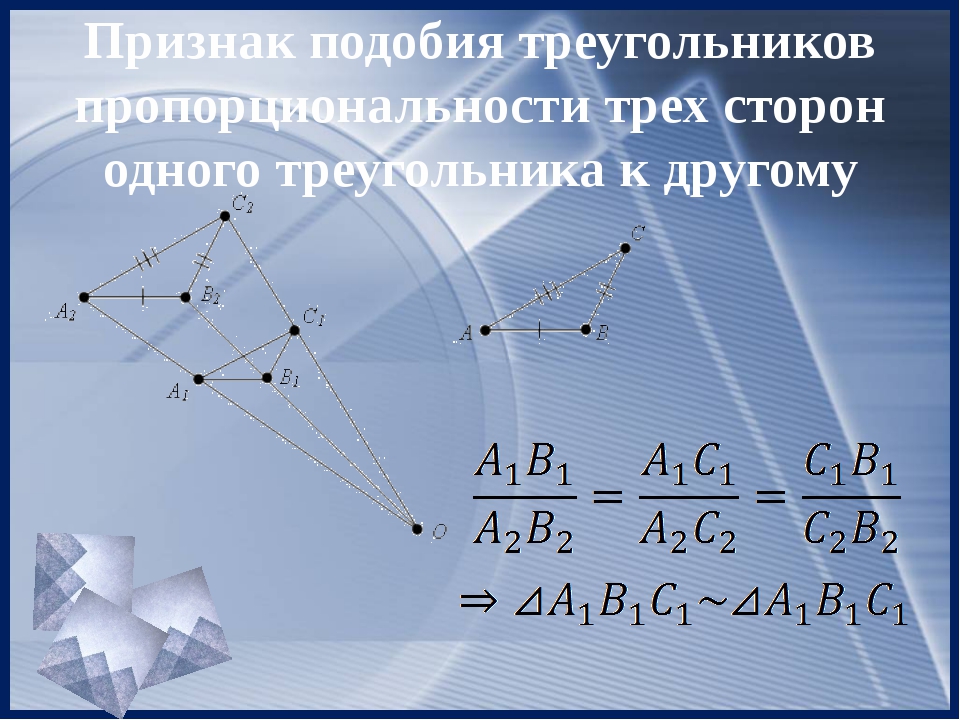 И.Я.Яковлева
И.Я.Яковлева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов по русскому языку. Люблю свой предмет и своих учеников. Мне всегда интересно показать своим ученикам что-то новое и интересное в своём предмете, помогать сделать трудное легким, непонятное понятным и научить искать информацию в огромном «море знаний». Всегда радуют успехи учеников, которые получают высокие баллы на ОГЭ и ЕГЭ.
Люблю свой предмет и своих учеников. Мне всегда интересно показать своим ученикам что-то новое и интересное в своём предмете, помогать сделать трудное легким, непонятное понятным и научить искать информацию в огромном «море знаний». Всегда радуют успехи учеников, которые получают высокие баллы на ОГЭ и ЕГЭ.
Репетитор по математике
Алтайский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-4 классов по математике и русскому языку. К каждому ученику нахожу индивидуальный подход, учитывая сильные и слабые стороны. Объясняю сложные темы простым языком, помогаю ученику найти несколько решений для одной задачи. Со мной Ваш ребёнок поймёт и полюбит математику и русский язык.
К каждому ученику нахожу индивидуальный подход, учитывая сильные и слабые стороны. Объясняю сложные темы простым языком, помогаю ученику найти несколько решений для одной задачи. Со мной Ваш ребёнок поймёт и полюбит математику и русский язык.
Математика по Skype
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Курсы ОГЭ
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Записаться на бесплатный урок
Подобные треугольники — презентация онлайн
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ2.
 ПЛАН Пропорциональные отрезки.
ПЛАН Пропорциональные отрезки.Свойство биссектрисы треугольника.
Определение подобных
треугольников.
Отношение периметров подобных
фигур.
Отношение площадей подобных
фигур.
Признаки подобия треугольников.
3. Пропорциональные отрезки
• Отношением отрезковназывается отношение
их длин.
• Отрезки AB и CD
пропорциональны
отрезкам A1B1 и C1D1,,
если
AB A B
CD
B
A
D
C
AB
CD
A
A1
B
С
D
B1 С1
1 1
C1D1
ПРИМЕР
D1
4. ПРИМЕР
• Даны два прямоугольных треугольникаСтороны ΒC и CA пропорциональны MN и MK,
так как
B
5
BC
3
MN 15
3
C
A
4
N
т.е.
?
15
M
K
20
и
AC
4
MK 20
BC AC 1
MN MK 5
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО
ТРЕУГОЛЬНИКА.
5. Пропорциональность отрезков
• Понятие пропорциональности вводится длялюбого числа отрезков.
B
например
5
3
C
A
BC AC AB
MN MK NK
4
N
25
15
M
K
20
6. Подобные фигуры
Предметы одинаковойформы, но разных
размеров
Фотографии, отпечатанные с
одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.
7. Подобные фигуры
• В геометрии фигуры одинаковой формыназывают подобными фигурами
Подобными являются
любые два квадрата
два куба
Подобными являются
любые два круга
два шара
8. Подобные треугольники
• Даны два треугольника AΒC и A1Β1C1,у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1, лежащие
против равных углов, называют сходственными
Β1
Β
A
C
A1
C1
9. Определение
• Два треугольника называются подобными, если ихуглы соответственно равны и стороны одного
треугольника пропорциональны сходственным
сторонам другого.
Β
A
ΔAΒC ~ ΔA1Β1C1
C
A1
Β1
A = A1, Β = Β1, C = C1.
AB
BC
AC
A1B1 B1C1 A1C1
C1
10. Коэффициент подобия
ΒΔAΒC ∞ ΔA1Β1C1
Β1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
C
A1
k – коэффициент подобия.
• Число k , равное отношению сходственных сторон,
называется коэффициентом подобия.
C1
11. Дополнительные свойства
Отношение высот подобных треугольников,проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение биссектрис подобных треугольников,
проведенных к сходственным сторонам, равно
коэффициенту подобия.
12. Отношение периметров
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
PABC
k
PA1B1C1
A
C
A1
ДОКАЗАТЕЛЬСТВО
• Отношение периметров подобных
треугольников равно
• коэффициенту подобия.

C1
13. Отношение периметров
ΔAΒC ~ ΔA1Β1C1Β
Β1
A
AB
BC
AC
k
A1B1 B1C1 A1C1
C
A1
AB kA1B1
C1
BC kB1C1
AC kA1C1
PABC
AB BC AC
kA1B1 kB1C1 kA1C1
PA1B1C1 A1B1 B1C1 A1C1
A1B1 B1C1 A1C1
Выносим общий множитель за скобку и
сокращаем дробь.
PABC
k
PA1B1C1
14. Отношение площадей
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
• Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
A
C
A1
SABC
2
k
SA1B1C1
ДОКАЗАТЕЛЬСТВО
C1
15. Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,коэффициент подобия k
AB
BC
AC
k
A1B1 B1C1 A1C1
Β
Β1
A
A = A1, по теореме об отношении
площадей треугольников, имеющих по
равному углу, имеем
C
A1
SABC
AB AC
AB AC
k k k2
SA1B1C1 A1B1 A1C1 A1B1 A1C1
C1
16.
 Свойство биссектрисы треугольника Биссектриса треугольника
Свойство биссектрисы треугольника Биссектриса треугольникаделит противоположную
сторону на отрезки,
пропорциональные
прилежащим сторонам
треугольника.
BD DC
AB AC
или
A
ПРИМЕР
B
BD AB
DC AC
ДОКАЗАТЕЛЬСТВО
D
C
17. Свойство биссектрисы треугольника
A2
1
H
ΔABD и ΔACD имеют
общую высоту AH
S ABD DB
S ACD DC
B
ИМЕЕМ
D
BD AB
DC AC
C
ΔABD и ΔACD имеют
равные углы 1 = 2
SABD AB AD AB
SACD AD AC AC
18. Свойство биссектрисы треугольника
Дано: ΔABCAD – биссектриса
AB = 14 см
BC = 20 см
AC = 21 см
Найти: BD,CD.
Решение:
A
1
B
D
20см
2
C
19. Свойство биссектрисы треугольника
A1
B
D
20см
2
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы
треугольника BD DC
AB AC
имеем
x
20 x
C
14
21
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.
20. Признаки подобия треугольников
Первый признак подобия треугольников.(по двум углам)
Второй признак подобия треугольников.
(по углу и двум пропорциональным сторонам)
Третий признак подобия треугольников.
(по трем пропорциональным сторонам)
21. Первый признак подобия треугольников.
Если два угла одного треугольникасоответственно равны двум углам другого
треугольника, то такие треугольники
подобны.
C1
C
A
B
A1
B1
22. Первый признак подобия треугольников.
CA
B
C1
A1
B1
Дано:
ΔABC и ΔA1B1C1,
A = A1,
B = B.
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
23. Первый признак подобия треугольников.
CA
A1
C1 B
Доказательство:
A = A1, B = B1.
C = 180º – A – B,
C1 = 180º – A1 – B1.
C = C1
Таким образом углы
треугольников
B1 соответственно равны.
24. Первый признак подобия треугольников.
 Доказательство:
Доказательство:A = A1,
B = B1.
Имеем
SABC
AB AC
SA1B1C1 A1B1 A1C1
SABC
AB BC
SA1B1C1 A1B1 B1C1
BC
AC
B1C1 A1C1
Аналогично, рассматривая равенство углов
C= C1, A= A1, получим
BC
AB
B1C1 A1B1
Итак, сходственные стороны пропорциональны.
25. Второй признак подобия треугольников.
Если две стороны одного треугольникапропорциональны двум сторонам другого
треугольника и углы, заключенные между
этими сторонами, равны, то такие
треугольники подобны.
Β
A
Β1
AB
AC
A1B1 A1C1
C
A1
C1
26. Второй признак подобия треугольников.
Дано:ΔABC и ΔA1B1C1,
A = A1,
Β
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Β1
A
AB
AC
A1B1 A1C1
C
A1
C1
27. Второй признак подобия треугольников.
СДоказательство:
Достаточно доказать, что B = B1.
A
1
2 B
C1
С2
A1
ΔABC2, 1= A1, 2= B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
AB
AC2
(из подобия).
A1B1 A1C1 AB
AC
По условию
A1B1 A1C1
AC=AC2.
B1 ΔABC=ΔABC , т.е. B = B .
2
1
28. Третий признак подобия треугольников.
Если три стороны одного треугольникапропорциональны трем сторонам другого
треугольника, то такие треугольникиΒ
1
подобны.
Β
A1
A
C
AB
BC
AC
A1B1 B1C1 A1C1
C1
29. Третий признак подобия треугольников.
Дано:ΔABC и ΔA1B1C1,
Β1
A1
C1
Β
A
AB
BC
AC
A1B1 B1C1 A1C1
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
C
30. Третий признак подобия треугольников.
СДоказательство:
Достаточно доказать, что A= A1
ΔABC2, 1= A1, 2= B1,
2 B ΔABC2 ~ ΔA1B1C1 по двум углам.
1
Отсюда
AB BC2 AC2
Β1 По условиюA1B1 B1C1 A1C1
С2
A
AB
BC
AC
A1B1 B1C1 A1C1
A1
ΔABC=ΔABC2 по трем сторонам,
C1 A = A1
т.
 е.
е.31. ТЕСТ
1. По данным рисунка хравен
7
х
А) 7
Б) 14
В) 3,5
Г) 14/3
32. ТЕСТ
2) По данным рисункапериметр ΔABC
равен
В
3
2
А
4
С
А) 9
Б) 27
В) 36
Г) 18
33. ТЕСТ
3) По данным рисункаотрезок BC равен
В
3
3
2,5
А
4
0,5
С
А) 3,75
Б) 7,5
В) 5
Г) 4,5
34. ТЕСТ
BТЕСТ
E
12
9
3
A
18
C
D
4
6
4) По данным рисунка площади данных
треугольников относятся
А)
Б)
В)
Г)
3:1
9:1
6:1
9:4
F
35. ТЕСТ
BE
12
9
3
A
18
C
D
4
6
5) По данным рисунка прямые AB и DE
А) нельзя ответить
Б) пересекаются
В) параллельны
F
Подобие Признаки подобия треугольников 1 I в Какие
Подобие. Признаки подобия треугольников. 1. I в. Какие фигуры являются подобными? 1 2 1 3 5 Ответ: 1 и 4; 2 и 3 4 6 II в. 2 3 4 5 6 Ответ: 1 и 5; 2 и 3; 4 и 6 Подобные фигуры — фигуры, одинаковые по форме, но разные по размерам.
Признаки подобия треугольников. 1. I в. Какие фигуры являются подобными? 1 2 1 3 5 Ответ: 1 и 4; 2 и 3 4 6 II в. 2 3 4 5 6 Ответ: 1 и 5; 2 и 3; 4 и 6 Подобные фигуры — фигуры, одинаковые по форме, но разные по размерам.
Треугольники подобны, найдите Сходственные стороны – стороны, лежащие против равных углов. сходственные стороны I в. II в. S B K P A 2. A C N D Ответ: KB и CD; KN и AD; BN и AC X F M Ответ: MF и AP; SF и AX; SM и PX
3. I в. Найти коэффициент подобия, если сходственные стороны треугольников равны: Ответ: а). 5 и 25 II в. Ответ: а). 3 и 6 2 в). 30 и 10 с). 20 и 21 с). 5 и 7 в). 10 и Коэффициент подобия – равен отношению сходственных сторон подобных треугольников.
4. Периметры подобных треугольников относятся Найти коэффициент подобия, как коэффициент подобия k. если периметры подобных треугольников равны: I в. а). 20 и 40 в). 9 и 10 5. а). 2 и 4 в). 19 и 10 Найти коэффициент подобия, Площади подобных треугольников относятся как если площади подобных коэффициент подобия в квадрате k 2.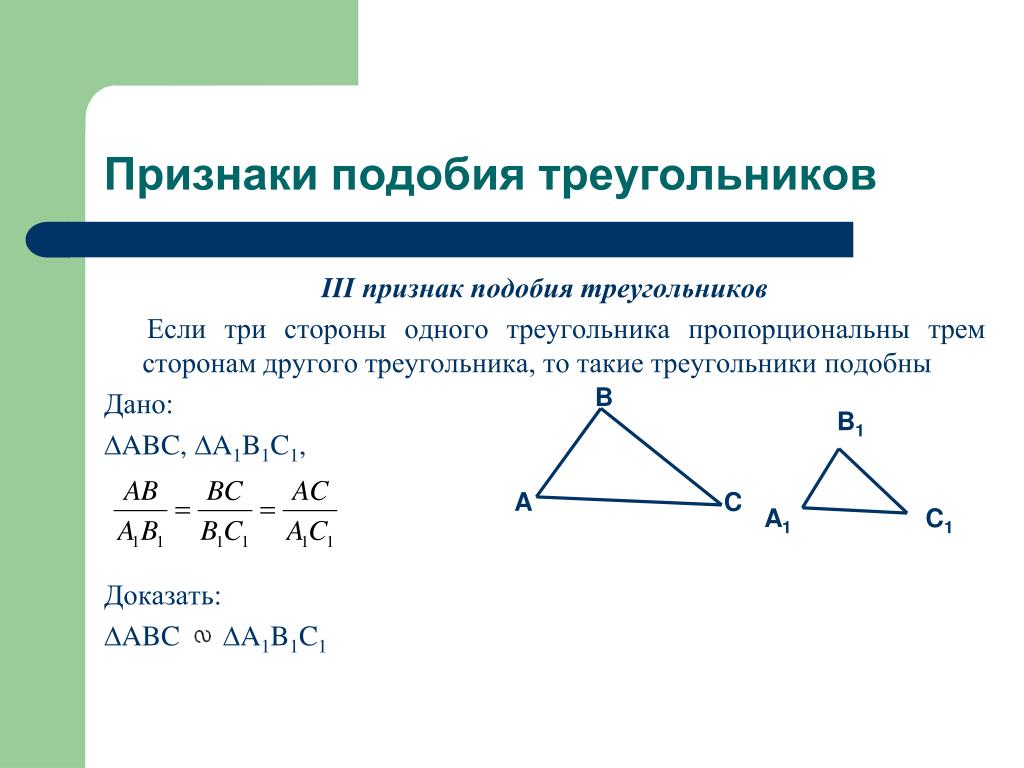 треугольников равны: а). 1 и 4 а). 32 и 2 в). 8 и 2 в). 18 и 3 II в.
треугольников равны: а). 1 и 4 а). 32 и 2 в). 8 и 2 в). 18 и 3 II в.
6. Подобные треугольники – это треугольники, у которых 1). углы Могут ли быть подобны соответственно равны 2). сходственные стороны пропорциональны треугольники, у которых углы равны: I I в. ΔABC~ΔDEF
Подобные треугольникибыть подобны у которых Могут ли – это треугольники, 1). углы соответственно равны треугольники, у которых 7. 2). сходственные стороны пропорциональны стороны равны: I в. II в. ΔABC~ΔDEF АB = 12 DF = 7 АB = 8 DF = 7 АС = 21 FE = 10 АС = 14 FE = 10 ВС = 30 ED = 4 ВС = 20 и почему? Ответ: Да, так как и ED = 4 почему? Ответ: Да, так как
Площади подобных треугольников Заданы площадитреугольников относятся как 8. коэффициент подобия второго треугольника. в квадрате k 2. и одна сторон Найти сторону, сходственную ей. I в. II в. S 1 = 270 S 1 = 144 S 2 = 30 S 2 = 36 Сторона 2 Δ = 4 см Сторона 2 Δ = 10 Найти сходственную сторону 1 Δ -? Ответ: 12 см Найти сходственную сторону 1 Δ -? Ответ: 20 Сход. сторона 1Δ: 4 ∙ k = 4∙ 3 = 12 Сход. сторона 1Δ: 10∙k = 10 ∙ 2=20
сторона 1Δ: 4 ∙ k = 4∙ 3 = 12 Сход. сторона 1Δ: 10∙k = 10 ∙ 2=20
I признак подобия Δ: III признак подобия Δ: (по равенству двух углов) Теория (по пропорциональности трех 9. Если два угла одного сторон ) I в. II в. треугольника соответственно Если три стороны одного равны двум углам другого треугольника пропорциональны 1. Первый признак треугольника, то такие трем сторонам другого 1. Третий то такие подобия треугольников треугольника, признак подобия треугольники подобны. треугольников треугольники подобны. II признак подобия Δ: (по пропорциональности двух сторон и равенству угла между 2. Второй признак ними) Еслиподобия треугольников двe стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны. Коэффициент подобия – это 2. Коэффициент подобия – число, показывающее во сколько это… раз один треугольник больше (или меньше) другого, подобного ему. Равен отношению сходственных сторон подобных Δ.
(видео и примеры) // Tutors.com
Содержание
- Пропорциональные детали в треугольниках и параллельных линиях
- Что такое теорема о пропорциональности треугольника?
- Подобные пропорциональные треугольники
- Примеры теоремы о пропорциональности треугольника
- Практика теоремы пропорциональности треугольника
Пропорциональные части в треугольниках и параллельных линиях
Параллельные линии могут показаться скучными, но у них есть свое применение.Одно из их применений появляется в Теореме о пропорциональности треугольника , в которой используется линия, построенная параллельно одной стороне треугольника, для установления пропорций для двух других сторон.
Сначала кратко рассмотрим параллельные линии. Две прямые параллельны, если они не пересекаются. Части этих линий, такие как лучи и отрезки, также параллельны. На рисунке ниже отрезок WO параллелен отрезку LF:
На рисунке ниже отрезок WO параллелен отрезку LF:
WO ∥ LF
Что такое теорема о пропорциональности треугольника?
Теорема о пропорциональности треугольника утверждает, что если провести линию, построенную параллельно одной стороне треугольника, она пересечет две другие стороны треугольника и пропорционально разделит оставшиеся две стороны.
Давайте разберем это. Нарисуйте треугольник (разносторонний, прямоугольный, тупоугольный — неважно) с одной стороной, горизонтальной вам. Назовите его △SLI со стороной LI внизу, горизонтально к вам. Боковая SL должна быть слева от вас, а SI справа от вас.
Постройте линию, параллельную LI, в любом месте так, чтобы она пересекала внутреннюю часть треугольника. Там, где параллельная линия пересекает стороны SL и SI, обозначьте эти точки C и E.
В любом случае слайс это, △SCE и △SLI пропорциональны друг другу.Более того, сторона SL была разделена на два сегмента, SC и CL, которые пропорциональны двум сегментам, на которые делится сторона SI, SE и EI. Теорема о пропорциональности треугольника гарантирует, что эти выводы верны.
Теорема о пропорциональности треугольника гарантирует, что эти выводы верны.
Вы можете написать отношения, чтобы показать эти пропорции:
CLSC = EISE
SCCL = SEEI
SCSL = SESI
CLSL = EISE
Подобные пропорциональные треугольники
Вот △BOX. Постройте прямую, параллельную отрезку (и стороне) ОХ.Там, где параллельная линия пересекает стороны BO и BX, отметьте точки E и D. Запишите две известные вам пропорции.
Вы получили два из них?
BEEO = BDDX
EOBE = DXBD
EOBO = DXBX
БЕБО = BDBX
Примеры теоремы о пропорциональности треугольника
Вы можете использовать эту теорему, чтобы найти неизвестные длины частей сторон треугольников, если вы знаете три другие части. Предположим, вы намечаете маршрут доставки и замечаете, что ваши пять остановок R, O, U, T, E образуют большой треугольник:
. Дорожное управление сообщает, что дорога от О до У закрыта из-за ремонта моста. Вы знаете, что дорога, идущая от T к E, параллельна дороге OU.
Вы знаете, что дорога, идущая от T к E, параллельна дороге OU.
Вы знаете, что расстояние от начальной точки O до T равно 6 км, а TR равно 15 км. Вы также знаете, что расстояние от остановки R до E равно 10 км, но не представляете, сколько вы проедете от E до U.
Благодаря теореме о пропорциональности треугольника его легко вычислить. Вы все это знаете:
OTTR = EUER
615 = x10
Все, что вам нужно сделать, это решить пропорции. Вы можете использовать перекрестное умножение и деление, или вы можете умножить обе стороны на 10, чтобы изолировать x.
Перекрестное умножение и деление:
6 × 1015 = х
—ИЛИ—
Умножьте обе стороны на 10, чтобы изолировать x:
6015 = х
Упрощенный, дает 4 км. Расстояние от E до U составляет 4 км.
х = 4
Практика теоремы пропорциональности треугольника
Вот немного ненормальная причина для применения теоремы о пропорциональности треугольника, если только вы не смотритель зоопарка.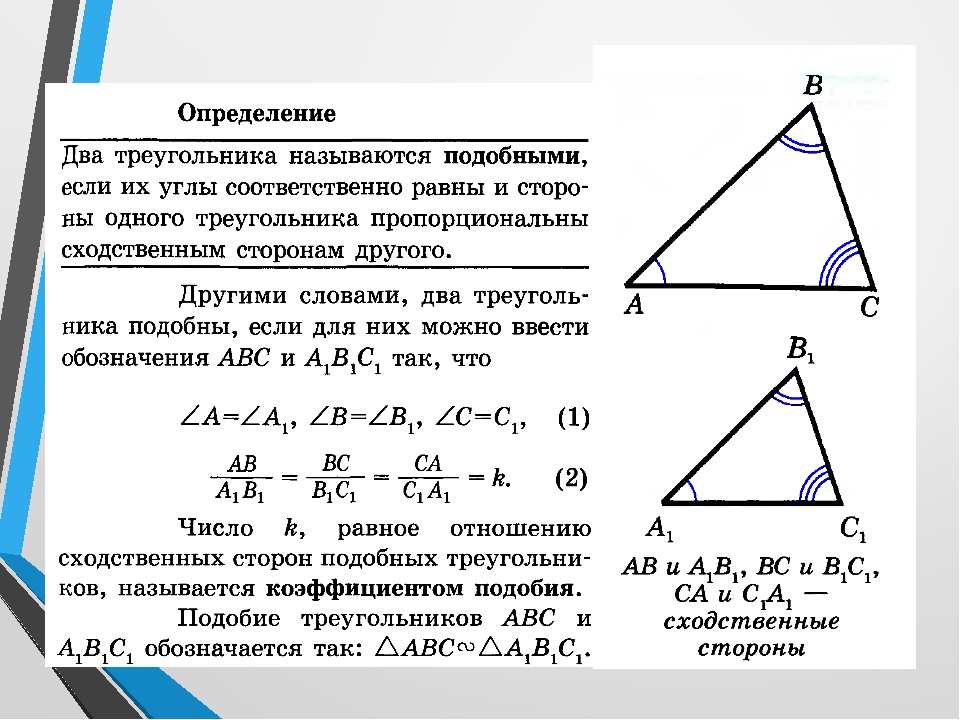 Тогда это может быть полезно.
Тогда это может быть полезно.
Ваш вольер для крокодилов состоит из двух высоких параллельных стен, причем ближняя стена высотой 10 м, но все же короче дальней.Вы знаете, что расстояние от одной стены до другой 12 метров (у ваших крокодилов много места).
Погода становится холодной, поэтому вы планируете предоставить своим крокодилам успокаивающие верхние тепловые лампы. Вам нужно проложить алюминиевые трубы (для поддержки ламп) от ближней короткой стены к более высокой дальней стене. Какой длины должны быть трубы, чтобы пройти через них? Если вы обрежете их слишком коротко, они упадут в корпус.
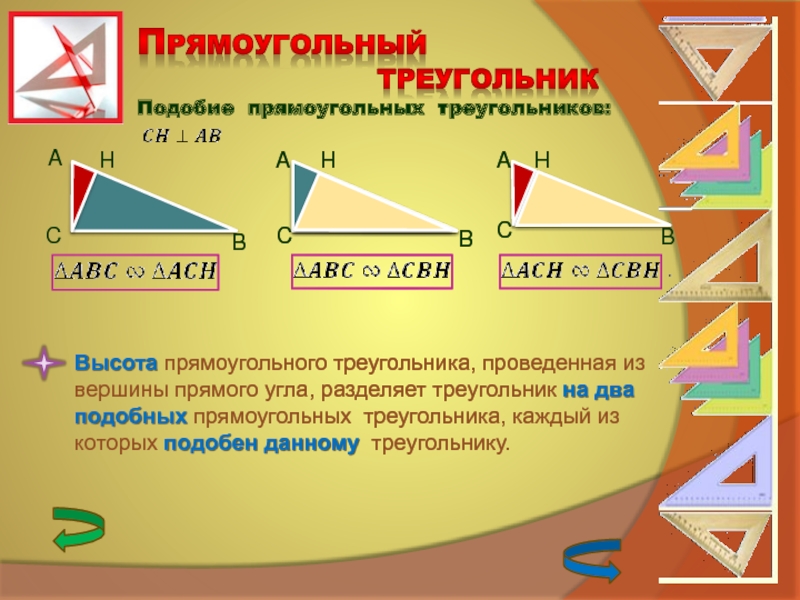
Пропорции прямоугольного треугольника
Постройте воображаемый треугольник от ближней стены вольера с крокодилами.Выйдите на 24 м и измерьте расстояние от земли до вершины ближней стены, а еще лучше, используйте теорему Пифагора, чтобы вычислить гипотенузу прямоугольного треугольника, не выходя из кабинета смотрителя зоопарка!
Соотношения теперь ясны:
1224 = x26
Какой длины должны быть ваши алюминиевые осветительные трубки, чтобы безопасно охватывать крокодил? Вы получили правильный ответ? Они должны быть 13 метров в длину.
Итоги урока
Если вы внимательно прочитали этот урок, изучили рисунки и посмотрели видео, то теперь вы можете описать и применить Теорему о пропорциональности треугольника, которая утверждает, что прямая, параллельная одной стороне треугольника, пересекает две другие стороны треугольника и делит остальные две стороны пропорционально.Вы также можете использовать теорему о пропорциональности треугольника, чтобы найти решения для распространенных ситуаций, возникающих в повседневной жизни.
Следующий урок:
Что такое прямоугольный треугольник?
8.4 Треугольники | Евклидова геометрия
Докажите, что \(BD\) делит пополам \(\hat{D}\).
\[\begin{массив}{rll}
A\шляпа{D}B &= A\шляпа{B}D & (AD = AB) \\
A\hat{B}D &= B\hat{D}C & (AB \параллельный DC,
\текст{ альт. } \угол \текст{с}) \\
\поэтому A\шляпа{D}B &= B\шляпа{D}C & \\
\поэтому BD & \text{ делит пополам } \шляпа{D} &
\конец{массив}\]
} \угол \текст{с}) \\
\поэтому A\шляпа{D}B &= B\шляпа{D}C & \\
\поэтому BD & \text{ делит пополам } \шляпа{D} &
\конец{массив}\]
Докажите, что две диагонали равны в длина.
\[\begin{массив}{rll} AD &= BC & (\text{данный}) \\ A\шляпа{D}C &= B\шляпа{C}D & (\text{данный}) \\ DC &= DC & \\ \поэтому \треугольник ADC &\equiv \треугольник BCD & (\текст{САС}) \\ \поэтому AC &= BD & \конец{массив}\]
Если \(DC:AB = 5:4\), показать эту область \(ABCD =
\text{2,25} \times \text{ площадь } \треугольник ABC\).
\[\begin{массив}{rll} \frac{DC}{AB} &= \frac{5}{4} & (\text{данный}) \\ & & \\ \поэтому \dfrac{\text{Площадь} \треугольник BDC}{\text{Площадь } \triangle BDA} &= \frac{5}{4} & (\text{то же высота, } DC \параллельно AB ) \\ & & \\ \поэтому \dfrac{\text{Площадь} ABCD}{\text{Площадь} \треугольник BDA} &= \frac{9}{4} & \\ & & \\ \text{И } \треугольник BDA &= \треугольник ABC & (\text{такая же высота, та же база}AB) \\ & & \\ \поэтому \dfrac{\text{Площадь} ABCD}{\text{Площадь} \треугольник ABC} &= \text{2,25} & \\ & & \\ \text{Область} ABCD &= \text{2,25} \left( \text{Область} \треугольник ABC \справа) & \конец{массив}\]
Пропорциональность в подобных треугольниках: межкультурное сравнение — Древнегреческий вклад
Сходство уходит своими корнями в древность, и идеи пропорции, вероятно, были известны пифагорейцам в V веке [4, с. 82-83], а Евдокс Книдский (ок. 408-355) установил понятие того, что сегодня назвали бы равенством отношений [3, с. 28], решающим в случае несоизмеримых величин. Евклид (третий век) посвящает книгу V «Элементы » изучению пропорций, включающую многие идеи, разработанные ранее в Древней Греции, особенно те, которые практиковались Пифагором и Евдоксом. Предложение четвертое в Книге VI Элементы [1] гласит:
82-83], а Евдокс Книдский (ок. 408-355) установил понятие того, что сегодня назвали бы равенством отношений [3, с. 28], решающим в случае несоизмеримых величин. Евклид (третий век) посвящает книгу V «Элементы » изучению пропорций, включающую многие идеи, разработанные ранее в Древней Греции, особенно те, которые практиковались Пифагором и Евдоксом. Предложение четвертое в Книге VI Элементы [1] гласит:
VI.4. В равноугольных треугольниках стороны при равных углах пропорциональны, и это соответствующие стороны, опирающиеся на равные углы.
В модели дедуктивного рассуждения Евклид доказывает это утверждение, которое опирается на предложения VI.2, VI.1, Книгу V и, в конечном счете, на Книгу I для построений в евклидовой геометрии. Чтобы дать читателю представление о развитии VI.4 и заглянуть в идеи, лежащие в основе результата, вот предложения VI.2 и VI.1, в обратном порядке, как представлено в The Elements [1].
VI. 2. Если провести прямую линию параллельно одной из сторон треугольника, она пропорционально рассечет стороны треугольника; и [наоборот].
2. Если провести прямую линию параллельно одной из сторон треугольника, она пропорционально рассечет стороны треугольника; и [наоборот].
VI.1. Треугольники и параллелограммы, находящиеся на одной высоте, относятся друг к другу как их основания.
Высота здесь относится к перпендикулярной высоте, а под отношением двух треугольников «один к другому» понимается отношение их площадей.Говоря современным языком, VI.1 утверждает, что отношение площадей двух треугольников с одинаковой высотой равно отношению их оснований, и этот результат справедлив и для параллелограммов. Для треугольников с соизмеримыми основаниями доказательство Евклида VI.1 начинается с построения целых чисел, кратных двум основаниям, чтобы получить два треугольника с равными основаниями. Тогда результат следует из I.38, обсуждавшегося во введении. Вопросы несоизмеримости решаются с помощью теории пропорции Евдокса.
Рисунок 1: Предложение VI.2.
Чтобы доказать VI. 2, Евклид начинает с треугольника ABC (не обязательно равнобедренного) и строит DE , параллельный BC (рис. 1). Заметим, что треугольники DEB и DEC имеют одинаковую площадь, так как лежат на одном основании DE и находятся на одних и тех же параллелях (между DE и BC ). Отсюда следует, что треугольник ABE и треугольник ACD имеют одинаковую площадь. Современная интерпретация Евклида будет читать
2, Евклид начинает с треугольника ABC (не обязательно равнобедренного) и строит DE , параллельный BC (рис. 1). Заметим, что треугольники DEB и DEC имеют одинаковую площадь, так как лежат на одном основании DE и находятся на одних и тех же параллелях (между DE и BC ). Отсюда следует, что треугольник ABE и треугольник ACD имеют одинаковую площадь. Современная интерпретация Евклида будет читать
| Площадь (треугольник ABE ) Площадь (треугольник DEB ) | = | Площадь (треугольник ACD ) Площадь (треугольник DEC ) | . |
Так как треугольники ABE и DEB имеют одинаковую высоту, они расположены друг к другу в качестве своих оснований, и аналогично для треугольника ACD и треугольника DEC . Таким образом,
Таким образом,
|
Отсюда следует, что AB / DB = AC/ EC .
Рисунок 2: Предложение VI.4.
Чтобы быстро доказать VI.4, начните с подобных треугольников ABC и DEF и постройте треугольник DEF внутри треугольника ABC вдоль конгруэнтной пары углов (рис.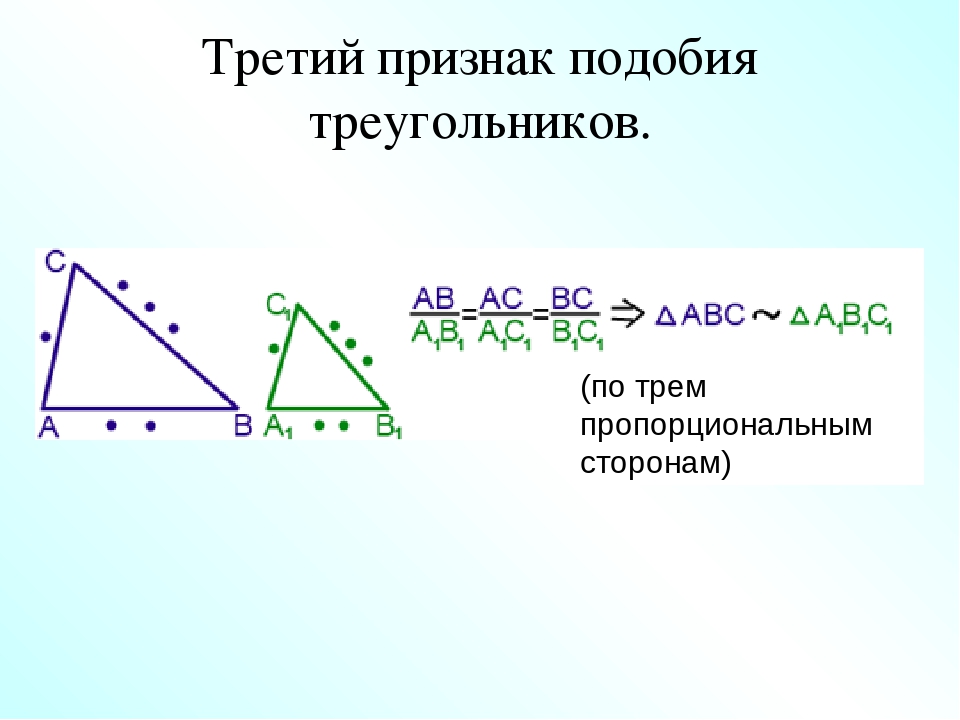 2). Затем результат следует из предложения VI.2 и аргумента общего положения, утверждающего, что треугольник DEF может быть построен внутри треугольника ABC вдоль любой пары конгруэнтных углов.Однако Евклид избегает общего аргумента в пользу более буквального доказательства. (См. [1]).
2). Затем результат следует из предложения VI.2 и аргумента общего положения, утверждающего, что треугольник DEF может быть построен внутри треугольника ABC вдоль любой пары конгруэнтных углов.Однако Евклид избегает общего аргумента в пользу более буквального доказательства. (См. [1]).
Соотношение и пропорция. Подобные треугольники. Темы по тригонометрии:
Темы | Дом
1
Натуральные числа: кардинальное и порядковое
Части натуральных чисел
Части во множественном числе
Отношение натуральных чисел
Названия дробей
Пропорции
Теорема альтернативной пропорции
Теорема одного и того же кратного
Похожие фигурки
ТРИГОНОМЕТРИЯ исторически является изучением треугольников.Название буквально означает измерение треугольников. Он начинается с изучения прямоугольных треугольников, то есть треугольников, имеющих прямой угол, и с отношений — соотношений — их сторон.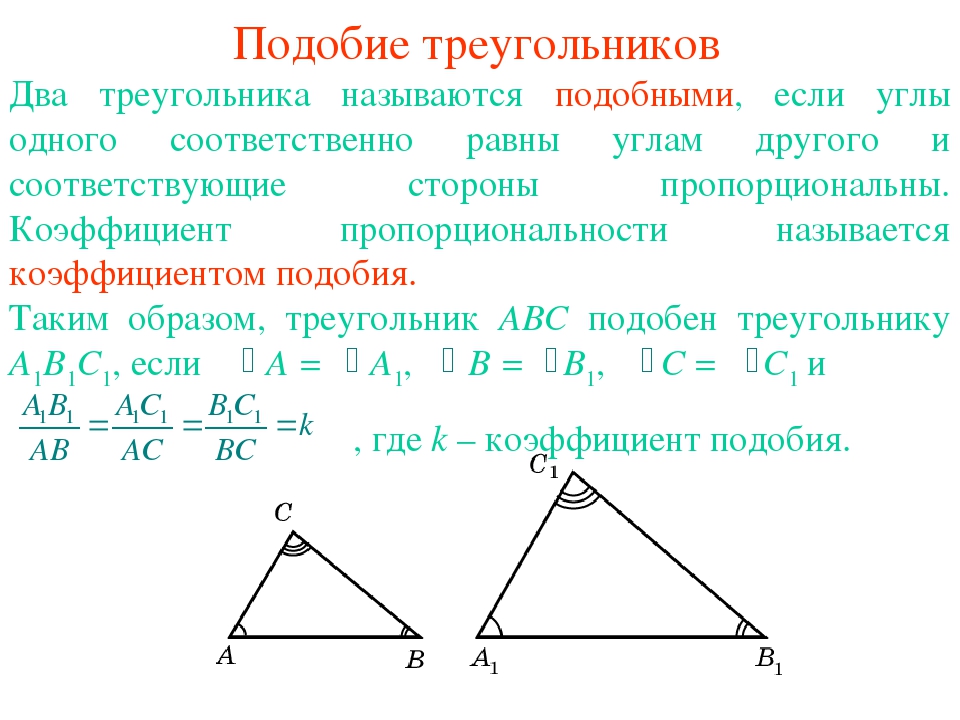 Значение отношения зависит от того, что мы подразумеваем под частями числа. А части называем порядковыми номерами: третья часть, четвертая часть, пятая и так далее. Вот с них и начнем.
Значение отношения зависит от того, что мы подразумеваем под частями числа. А части называем порядковыми номерами: третья часть, четвертая часть, пятая и так далее. Вот с них и начнем.
Натуральные числа: количественные и порядковые
Натуральные числа — это счетные числа.Они имеют две формы: кардинальную и порядковую. Кардинальные формы
Раз, два, три, четыре и так далее.
Отвечают на вопрос Сколько? или Сколько?. Порядковые формы
Первый, второй, третий, четвертый, и так далее.
Они отвечают на вопрос Какой?.
Части натуральных чисел
Мы говорим, что меньшее число является частью большего числа, если большее число является его кратным.
Вот несколько первых кратных 5:
5, 10, 15, 20, 25, 30, 35.
5 — это первое число 90 364, кратное 5. 10 – второе число, кратное 90 364 числу 90 365; 15, третий ; и так далее.
5 является частью каждого из них, кроме самого себя.
Теперь, поскольку 15, например, является третьим кратным 5, мы говорим, что 5 является третьей частью 15. Мы используем то же самое порядковое число, чтобы назвать часть.
5 – это четвертая часть от 20. Это пятая часть от 25; шестая часть 30. И так далее.
5 какая часть 10? Мы не говорим о второй части. Мы говорим половина . 5 составляет половину от 10.
Итак, за исключением половины , мы называем части порядковыми номерами. Каждое порядковое число именует , часть которого .
Опять же, 5 не является частью самого себя. Нет такой вещи, как первая часть.(См. Навыки арифметики, урок 15.)
Важно понимать, что здесь речь не идет о правильных дробях: — это числа , которые меньше 1 и которые нам нужны для измерения. Мы объясняем, как порядковые числительные — третья, четвертая, пятая и так далее — называют части количественных числительных. Вскоре мы подойдем к этим дробным символам.
Задача 1. 7 является частью числа 28? Четвертый.
7 является частью числа 28? Четвертый.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова прикрыть ответ, нажмите «Обновить» («Reload»).
Задача 2. Какая часть числа 45 равна 9? Пятый.
Задача 3. 6 является частью числа 12? Половина.
Задача 4. Какое число составляет восьмую часть числа 24? 3
Задача 5. 3 является десятой частью какого числа? 30
Части, множественные
Из рисунка видно, что мы поделили 15 на трети, то есть на три равные части, и что каждое 5 есть третья часть 15.
5, 10, 15.
Следовательно, 10 — а это две пятерки — это две третьи части числа 15. Одна третья. Две трети . 5, 10.
Итак, 10 не является частью числа 15, потому что 15 не кратно 10. Мы говорим, что это части 15 во множественном числе: Две третьи части или просто две трети. Эти слова следует понимать буквально.
Эти слова следует понимать буквально.
Точно так же, если мы разделим 15 на пятые, то есть на пять равных частей —
— тогда
3 — пятая часть из 15.
6 две пятая часть 15.
9 равно трем пятым частям 15. (Считайте их!)
12 — это четыре пятых части 15 или просто четыре пятых.
А 15 это все пять его пятых частей.
Теперь мы можем сказать, что мы подразумеваем под
.Отношение натуральных чисел
ОПРЕДЕЛЕНИЕ. Отношение двух натуральных чисел — это их отношение по отношению к относительной величине, которую мы всегда можем назвать.В частности, мы можем сказать, что одно число является 90 364 кратным 90 365 другого (во столько раз), 90 364 частью его 90 365 или 90 364 частями его 90 365.
(Навык арифметики, Урок 17.)
Пример 1. Несколько В каком соотношении 15 к 5?
Ответить . 15 это трижды 5.
15 это трижды 5.
Это отношение — отношение — 15 к 5.
Мы не отвечаем «3 к 1», потому что хотим явно назвать отношение 15 к 5.Это правда, что 15 имеет 90 364 такое же отношение 90 365 к 5, как 3 к 1. 3 — это три раза по 1, так же как 15 — это три раза по 5.
Два числа в отношении называются терминами; первый термин и второй.
Обратите внимание, что мы отвечаем полным предложением, начинающимся с первого члена и заканчивающимся вторым: «15 — это три раза по 5». Ибо отношение есть отношение.
Пример 2. Часть В каком соотношении 5 к 15?
Ответить .5 третья часть из 15.
Это обратное отношение 15 к 5. Условия меняются местами.
Пример 3. Части Какое отношение имеет 10 к 15?
Ответить . 10 это два трети от 15.
Это три вида соотношения: Одно число кратно другому — во столько раз — часть его или части его.
Задача 6. Какое соотношение имеет следующее? Ответьте полным предложением, начинающимся с первого термина.
Какое соотношение имеет следующее? Ответьте полным предложением, начинающимся с первого термина.
а) от 2 до 10? 2 — пятая часть числа 10.
б) 10 к 2? 10 пять раз 2.
Большее число будет столько-то умножить на меньшее.
в) 7 к 1? 7 семь раз 1.
г) от 1 до 7? 1 является седьмой частью 7.
д) от 25 до 100? 25 — четвертая часть числа 100.
е) от 75 до 100? 75 это три четверти от 100.
г) от 12 до 6? 12 вдвое больше 6, или вдвое больше 6, или вдвое больше 6.
ч) от 6 до 12? 6 составляет половину от 12.
Названия дробей
В английском языке правильные дроби называются так же, как отношение числителя к знаменателю. Число, которое мы записываем как 1 на 3 — — называется «одной третью» из-за отношения 1 к 3. 1 составляет одну треть от 3.
И дробь имеет то же отношение к 1, что и .
По этой причине дроби называются рациональными числами. Дроби относятся к 1 так же, как и два натуральных числа.
Дроби относятся к 1 так же, как и два натуральных числа.
Таким образом, дробные символы можно рассматривать как символы отношения, поскольку они обозначают отношение числителя к знаменателю.
| 1 2 | = | 2 4 | = | 5 10 | = | 9 18 | и др. |
1 соответствует 2, 2 соответствует 4, 5 соответствует 10 и т. д.
Каждый числитель равен половине своего знаменателя.
Пример 4. В каком отношении 3 к 4?
Ответ. Мы можем выразить отношение любого меньшего числа к большему, просто позволив каждому числу произнести свое имя. Число 3 составляет три четверти числа 4. Число 3 говорит о своем кардинальном имени «три». 4 говорит о своем порядковом имени «четвертые».
С практической точки зрения, поскольку учащийся, скорее всего, сначала выучил названия дробей, отношение 3 к 4 выражается числом
.
| наименование фракции | 3 4 | . |
Пропорции
Пропорция — это утверждение о том, что два соотношения одинаковы.
5 равно 15, как 8 соответствует 24.
5 — третья часть числа 15, так же как 8 — третья часть числа 24.
Теперь мы введем этот символ 5 : 15 , чтобы обозначить соотношение от 5 до 15. Тогда пропорция будет выглядеть следующим образом:
5 : 15 = 8 : 24.
«5 равно 15, как 8 соответствует 24.»
Или мы можем представить пропорцию дробными символами —
— и читайте так же:
«5 равно 15, как 8 соответствует 24.»
Четыре числа в пропорции называются членами. 1-й, 2-й, 3-й, 4-й.
Пример 5. 12 : 2 = 42 : 7. («12 равно 2, как 42 равно 7»)
Почему это пропорция?
Ответить .Потому что 12 — это шесть раз по 2, а 42 — это шесть раз по 7.
Если студент скажет соотношение 1-го семестра ко 2-му, то ответ будет ясен.
Задача 7. Почему каждая из них является пропорцией?
а) 10 : 2 = 5 : 1. 10 — это пять раз по 2, так же как 5 — это пять раз по 1.
б) 3 : 9 = 4 : 12. 3 – третья часть числа 9. 4 – третья часть числа 12.
в) 10 : 15 = 2 : 3.10 составляет две трети от 15. 2 составляет две трети от 3.
Задача 8. Заполните каждую пропорцию.
| а) 2 : 8 = 9 : 36 | б) 14 : 2 = 35 : 5 | в) 3 : 4 = 75 : 100 | ||
| г) 5 : 15 = 8 : 24 | д) 72 : 9 = 16 : 2 | е) 2 : 3 = 40 : 60 | ||
Теорема альтернативной пропорции
Вот пропорция:
1-й : 2-й = 3-й : 4-й
Мы говорим, что 1-й и 3-й являются соответствующими терминами, как и 2-й и 4-й.
Ниже приводится теорема об альтернативной пропорции:
| Если четыре числа пропорциональны, то пропорциональны и соответствующие члены . То есть, как первое слагаемое к третьему, так и второе будет к четвертому. |
| Если |
| а : б = м : п, |
| затем попеременно |
| а : м = б : н. |
С
1 : 3 = 5 : 15,
затем попеременно
1 : 5 = 3 : 15.
(Навык арифметики: Урок 17, Вопрос 2.)
Пример 6. Заполните эту пропорцию:
4 : 5 = 12 : ?
4 составляет четыре пятых («») от 5, но не очевидно, что число 12 составляет четыре пятых от.
Однако, с другой стороны, 4 — это треть от 12, или мы могли бы сказать, что 4 — это , умноженное на 3, . Поэтому 5 тоже надо умножить на 3,
Поэтому 5 тоже надо умножить на 3,
4 : 5 = 12 : 15
То есть
4 : 5 = 3 × 4 : 3 × 5
Поскольку одна четверка соответствует одной пятерке, любое количество четверок соответствует равному количеству пятерок. Три четверки — это четыре пятых от трех пятерок.
Это теорема о том же кратном.
| Если мы умножим два числа на одно и то же число, 90 153, то произведение будет иметь то же отношение 90 153, что и числа, которые мы умножили. |
Пример 7. Заполните эту пропорцию, 5 : 8 = 35 : ?
Ответить . Посмотрите на это поочередно. 35 это семь раз по 5. Следовательно, пропущенный член будет семь раз по 8, что равно 56.
Пример 8. Решите эту пропорцию — 8 : 12 = 2 : ?
Ответить . Чтобы получить 2, нужно 8 разделить на 4. Следовательно, 12 также нужно разделить на 4.
8 : 12 = 2 : 3
Теорема об одном и том же кратном может быть обращена так, что мы можем разделить оба термина на одно и то же число.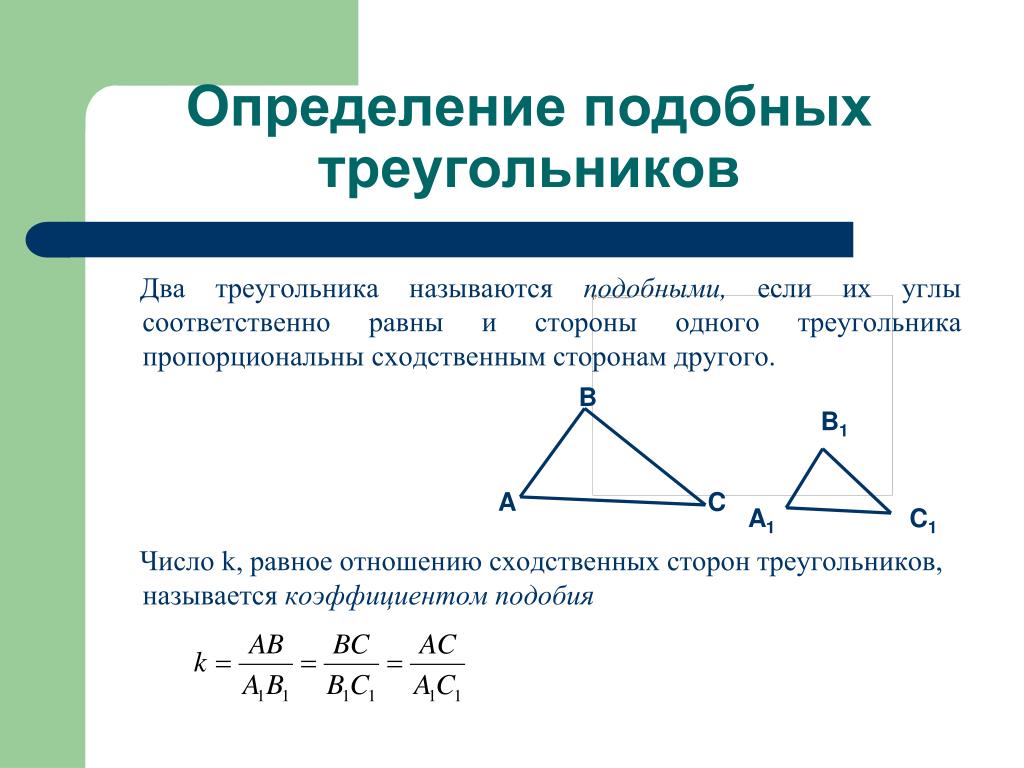
Слишком распространенный метод в наши дни — сделать это алгебраической задачей.
Учащегося учат перекрестно умножать и решать x . Это метод для людей, которые не понимают отношений и пропорций. Его учат для того, чтобы не учить соотношениям и пропорциям на словах.Это проистекает из сопротивления 19 века языку в математике.
Мы будем часто использовать это основное свойство радикала квадратного корня:
Радикал, умноженный сам на себя
производит подкоренное число.
(См. Урок 26 Алгебры, Радикалы.)
Задача 9. Заполните каждую пропорцию.
| а) 3 : 5 = 18 : 30 | б) 7 : 9 = 21 : 27 | в) 11 : 2 = 55 : 10 | ||
| г) 14 : 35 = 2 : 5 | д) 18 : 21 = 6 : 7 | е) 2 : 7 = 10 : 35 | ||
| ж) √3 : 2 = 3 : 2√3 | ч) 2 : √2 = 2√5 : √10 | i) √2 : 1 = 1 : ½√2 | ||
Аналогичные фигурки
Тригонометрия зависит от значения подобных фигур.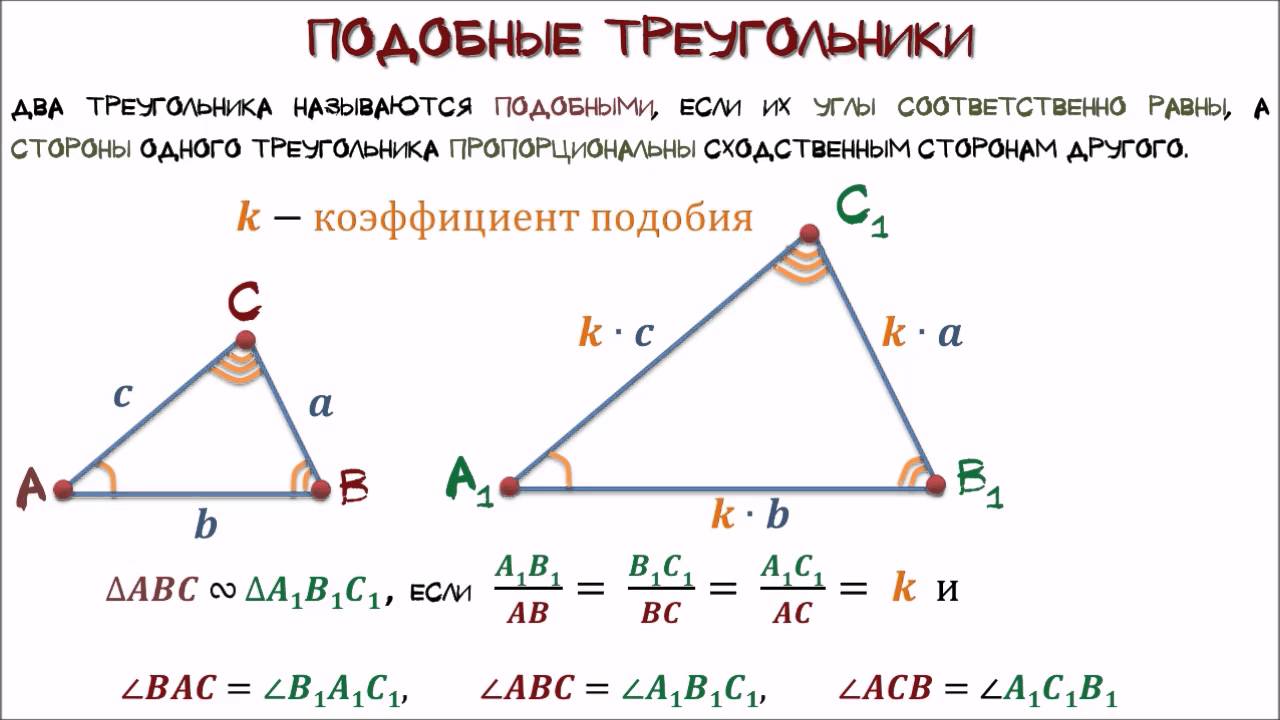
Подобные фигуры равноугольны, а стороны, образующие равные углы, пропорциональны.
Сказать, что фигуры ABCDE, PQRST подобны, значит сказать, что угол при A равен углу при P, угол при B равен углу при Q и т. д.; и, пропорционально, как AB относится к BC, так PQ относится к QR.
И так далее для каждой пары равных углов и сторон, которые их составляют.
Однако, чтобы треугольники были подобны, достаточно, чтобы они были равноугольными.(Теорема 15 из «Некоторых теорем плоской геометрии».) Отсюда следует:
Прямоугольные треугольники будут подобны, если острый угол одного
равен острому углу другого.
В прямоугольных треугольниках ABC, DEF, если острый угол при B равен острому углу при E, то эти треугольники будут подобны. Следовательно, стороны, образующие равные углы, пропорциональны. Например,
до н.э.: CA = EF: FD.
Если бы BC был в два раза длиннее CA, то EF также был бы в два раза длиннее FD.
И наоборот, соответствующие стороны пропорциональны:
до н.э. : EF = CA : FD.
Если бы BC был половиной EF, то CA также был бы половиной FD.
Таким образом, прямоугольные треугольники будут подобны, если острый угол одного равен острому углу другого. Мы увидим, что это основа тригонометрии треугольника.
Проблема 10.Прямоугольные треугольники HJK, LMN подобны, HJ = 3 см,
JK = 4 см и KH = 5 см. Если LM = 12 см, то какой длины MN и NL?
Альтернативно,
LM : HJ = MN : JK.
Так как LM в четыре раза больше HJ, то MN будет в четыре раза больше JK — это будет 16 см.
Аналогично, NL будет в четыре раза больше KH, это будет 20 см.
Проще говоря: сторона, соответствующая HJ, умножается на 4.Следовательно, поскольку треугольники подобны, каждая сторона будет умножена на 4.
Задача 11. Треугольники ABC, DEF подобны.
AB = 6 см, BC = 11 см, CA = 7 см и DE = 18 см. Какова длина EF и DF?
Какова длина EF и DF?
Сторона, соответствующая AB, была умножена на 3. Следовательно, каждая сторона будет умножена на 3. EF = 33 см, а DF = 21 см.
*
Мы определили пропорцию как отношение натуральных чисел.Стороны треугольника, однако не являются натуральными числами. Это длины, которые являются величинами — вещи, которые имеют размер — это не числа. И величины не обязательно имеют то же отношение, что и натуральные числа. Они могут быть «несоизмеримыми». Следовательно, требуется новая теория отношения и пропорции, которая будет применима к величинам. Заинтересованный студент обращается к Тема 11 «Эволюции действительных чисел», в частности раздел «Новая теория пропорций.»
Следующая тема: Определения тригонометрических функций
острого угла
Темы | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: teacher@themathpage. com
com
Пропорциональные сегменты между параллельными линиями — концепция
Когда линия проводится параллельно одной стороне треугольника, образуются два подобных треугольника, потому что соответствующие углы дают сокращение подобия AA.Поскольку треугольники подобны, сегменты, образованные параллельной линией, составляют пропорциональных сегментов . Находя одно из оснований треугольников, будьте внимательны при настройке пропорции, так как отношение равно стороне маленького треугольника к стороне большого треугольника.
Если у нас есть треугольник, и если я нарисую линию, параллельную одному из оснований, вопрос, на котором я собираюсь сделать паузу, состоит в том, создает ли это 2 подобных треугольника?
Что ж, для этого нам нужно будет сказать, что один из наших сокращений угол угол, сторона угол сторона или сторона сторона сторона должны применяться, чтобы мы могли сказать, что этот меньший треугольник dve подобен большему треугольнику абв. Обратите внимание, что я обозначил наши углы 1, 2, 3 и 4. Причина, по которой я сделал это, заключается в том, что я собираюсь сказать, что углы 1 и 2 являются соответствующими углами, а это означает, что они должны быть конгруэнтны друг другу. разное. Так как у нас есть секущая ab и две параллельные прямые, то 1 и 2 — соответствующие углы. В аналогичном аргументе bc является секущей, где у нас есть 2 параллельные прямые, что означает, что углы 3 и 4 должны быть конгруэнтны друг другу. И сейчас у нас есть 2 угла в каждом из этих треугольников, что достаточно, чтобы сказать, что они должны быть подобны.Так треугольник abc подобен треугольнику dbe? Да, и нашим ярлыком был угол угол.
Обратите внимание, что я обозначил наши углы 1, 2, 3 и 4. Причина, по которой я сделал это, заключается в том, что я собираюсь сказать, что углы 1 и 2 являются соответствующими углами, а это означает, что они должны быть конгруэнтны друг другу. разное. Так как у нас есть секущая ab и две параллельные прямые, то 1 и 2 — соответствующие углы. В аналогичном аргументе bc является секущей, где у нас есть 2 параллельные прямые, что означает, что углы 3 и 4 должны быть конгруэнтны друг другу. И сейчас у нас есть 2 угла в каждом из этих треугольников, что достаточно, чтобы сказать, что они должны быть подобны.Так треугольник abc подобен треугольнику dbe? Да, и нашим ярлыком был угол угол.
Итак, здесь произошла пара интересных вещей: мы можем использовать обратное и сказать, что если у вас есть 2 линии и вопрос в том, параллельна ли эта линия, то вы можете сказать, что эти 2 треугольника должны быть подобны. И еще один способ сказать, что если эти 2 угла конгруэнтны и если эти 2 угла конгруэнтны, то у вас должны быть параллельные прямые и у вас должно быть 2 подобных треугольника.
Давайте рассмотрим 2 коротких примера.Прямо здесь у меня есть треугольник, и меня спрашивают, у нас есть 2 подобных треугольника? Ну, если я смотрю на это, у нас есть 70 градусов, 70 градусов, так что они конгруэнтны, и у нас есть 2 других конгруэнтных угла, что означает, что мы можем использовать сокращение угла, чтобы сказать, что эти два угла должны быть конгруэнтны.
Теперь давайте рассмотрим еще один пример. Здесь у нас есть треугольник, и снова у нас нет ничего, что было бы отмечено параллельно. Итак, что я собираюсь сделать, так это перерисовать здесь свой меньший треугольник. Итак, это треугольник со стороной 4 и стороной 6.Теперь я собираюсь установить пропорцию между соответствующими сторонами здесь. Итак, у нас есть 4 — это сторона слева от меньшего треугольника, а большая сторона не 8, а 12, потому что вся длина равна 12. А здесь у нас 6, а вся сторона равна 18, 6 плюс 12. Итак. если я уменьшу эти 4 двенадцати, я могу разделить их оба на 4 и получить одну треть, а здесь я могу разделить оба этих числа на 6 и получить одну треть. Итак, подобны ли эти треугольники, и ответ — да. И нашим сокращением здесь будет сокращение бокового угла, потому что они оба имеют один и тот же угол прямо здесь, поэтому он должен быть конгруэнтным самому себе.
Итак, подобны ли эти треугольники, и ответ — да. И нашим сокращением здесь будет сокращение бокового угла, потому что они оба имеют один и тот же угол прямо здесь, поэтому он должен быть конгруэнтным самому себе.
Теперь еще одна интересная вещь, которую вы должны заметить, не только пропорциональны 4 и 12 и пропорциональны 6 и 18, но если бы я только что посмотрел на 4 и 8. 4:8, если я напишу, что отношение здесь равно отношению 6 :12. Итак, если у вас есть параллельные линии или если у вас есть одна линия, параллельная основанию, вы создадите сегменты, пропорциональные друг другу. Так что вам даже не нужно думать о соотношении 4 ко всей стороне. Вы могли бы просто сказать, если бы мы не знали эту длину прямо сейчас, что если это 6:12, то это должно быть 4 в каком-то числе.Таким образом, вместо использования 8 у нас будет х, и мы увидим, что наше отношение удваивается. Таким образом, чтобы получить от 4 до x, нам нужно умножить на 2, и тогда мы сможем найти 8.
Итак, с параллельной линией и треугольником произошли две ключевые вещи. Во-первых, это создаст два подобных треугольника, и соотношение этих сторон, созданных этой параллельной линией, будет одинаковым.
Во-первых, это создаст два подобных треугольника, и соотношение этих сторон, созданных этой параллельной линией, будет одинаковым.
Отношение, пропорция и среднее геометрическое
Отношение, пропорция и среднее геометрическое
Прежде чем приступить к анализу подобных треугольников, вам нужно подобрать еще несколько алгебраических принадлежностей.В этом разделе вы будете много иметь дело с дробями и отношениями, так что вы могли бы сначала освежить эти навыки алгебры.
Отношение представляет собой частное a / b , где b 0. Отношение обеспечивает сравнение между числами a и b. Например, если a в два раза больше b, то отношение a / b равно 2 / 1 . Отношение a / b читается как a к b и иногда записывается в виде a:b.
Бывают случаи, когда вам может понадобиться сравнить три или более элементов.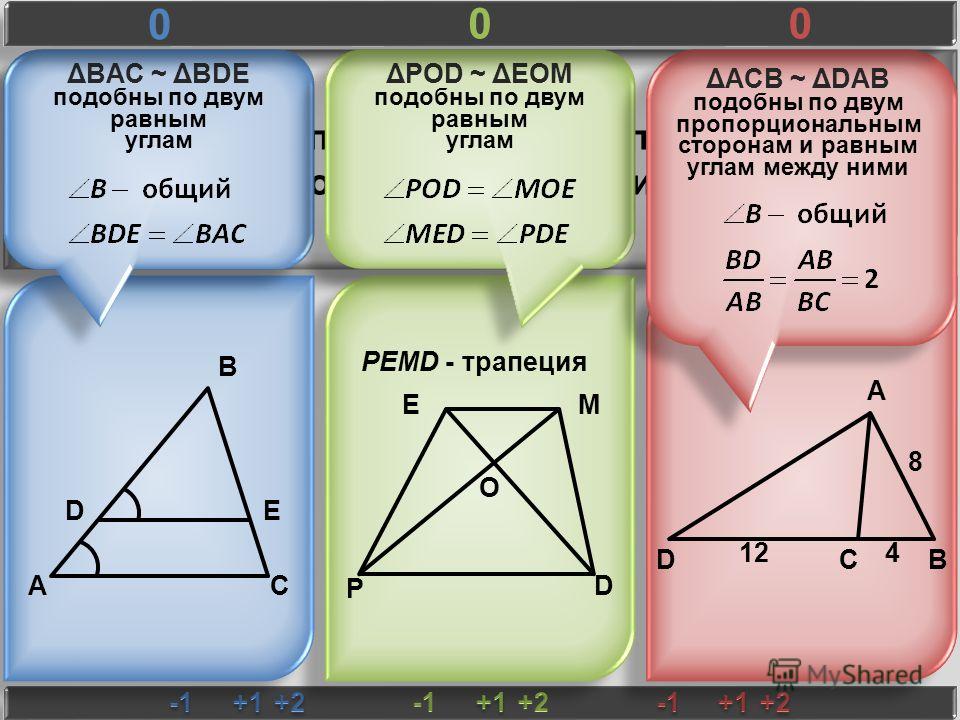 Когда это произойдет, простая дробь просто не поможет. Вам нужно будет использовать так называемый расширенный коэффициент. Расширенное отношение записывается в виде a:b:c (если вы сравниваете три величины) или a:b:c:d (если вы сравниваете четыре величины). Если вы сравниваете много величин, просто добавляйте их, разделяя каждое количество двоеточием.
Когда это произойдет, простая дробь просто не поможет. Вам нужно будет использовать так называемый расширенный коэффициент. Расширенное отношение записывается в виде a:b:c (если вы сравниваете три величины) или a:b:c:d (если вы сравниваете четыре величины). Если вы сравниваете много величин, просто добавляйте их, разделяя каждое количество двоеточием.
Эврика!
Расширенное отношение сравнивает более двух величин и не может быть выражено в виде одной дроби.
Пропорция — это утверждение, что два отношения равны.Пропорция a / b читается как a к b, как c к d. Первый и последний члены (a и d) называются крайними , а средние члены (b и c) называются средними . Есть несколько полезных свойств, связанных с пропорциями, и эти свойства можно установить с помощью алгебры.
- Свойство 1 : Свойство средних и крайних значений. В пропорции произведение средних равно произведению крайностей.
 То есть, если a / b = c / d (где b 0 и d 0), то a d = b c.
То есть, если a / b = c / d (где b 0 и d 0), то a d = b c.
Это просто старомодный шаг перекрестного умножения, используемый в алгебре, чтобы избавиться от нежелательных знаменателей при работе с дробями. Вы можете использовать свойство Means-Extremes для решения алгебраических уравнений.
- Пример 1 : Используйте свойство «Средние-экстремальные» для вычисления x: x + 1 / 9 = x — 3 / 3 .
Решение : Если мы применим к нашему уравнению свойство средних и крайних значений, мы получим
3(x + 1) = 9(x 3)
3x + 3 = 9x 27 5
Пример 2 : Используйте свойство «Средние-экстремальные» для нахождения x: 4 / x = x / 9 .
Решение . Если вы примените к уравнению свойство «среднее-экстремальное», то получите
36 = x 2
x = 36 = 6.

Теперь объедините эти идеи с задачей, связанной с геометрией.
- Пример 3 : Предположим, что два дополнительных угла относятся как 2 к 3. Найдите величину каждого угла.
- Решение: Пусть один из ваших углов имеет меру x, а другой угол имеет меру y.Поскольку ваши два угла дополняют друг друга, x + y = 90, поэтому y = 90 x. Поскольку отношение угловых измерений равно 2 к 3, получается следующая пропорция:
- x / y = x / 90 x = 2 / 3
5 Свойство средних-крайностей:
- 3x = 2(90 x)
- 3x = 180 2x
- 5x = 180
- x = 36
Теперь, когда вы знаете величину одного из ваших углов, вы можете найти мера второго угла, потому что два угла дополняют друг друга:
Существуют и другие свойства пропорций.Вы можете переворачивать пропорции и смешивать и сопоставлять числители и знаменатели. Свойство 2 пропорций предоставляет список изменений, которые вы можете сделать.
Свойство 2 пропорций предоставляет список изменений, которые вы можете сделать.
- Свойство 2 : В пропорции средние или крайние значения (или как средние, так и крайние значения) могут быть заменены местами. То есть, если a / b = c / d и все a, b, c и d отличны от нуля, то a / c = b /1 2d , d / b = c / a и d / c = b / a .
Опять же, в смешении числителей и знаменателей нет ничего удивительного, потому что вы делали это в алгебре годами! Но есть еще одно свойство пропорций, которое может немного удивить. Вы должны быть осторожны, применяя это свойство, потому что оно включает в себя добавление или вычитание вещей.
- Property 3 : если A / B = C = C / D , где B 0 и D 0, затем A + B / B = C + D / д .

Чтобы получить это свойство, начните с a / b = c / d , добавьте 1 к обеим частям и добавьте дроби.
Теперь, когда у вас есть за плечами пропорции, вы можете поговорить о среднем геометрическом двух чисел. Если вы начнете с пропорции, в которой два средних одинаковы (и два крайних значения могут быть разными), например, a / b = b / d , то b является средним геометрическим a и d .Вы нашли среднее геометрическое чисел 4 и 9 в примере 2. Хотя пара чисел на самом деле имеет два средних геометрических (одно положительное, а другое отрицательное), геометров интересует только положительное. После еще одного примера вы будете готовы применить эти алгебраические свойства к геометрии.
- Пример 4 : На рисунке 13.1 предположим, что AD является средним геометрическим между BD и DC. Если BC = 13 и BD = 9, найдите AD.
Рисунок 13. 1 AD — среднее геометрическое BD и DC, BC = 13 и BD = 9.
1 AD — среднее геометрическое BD и DC, BC = 13 и BD = 9.
- Решение: Поскольку AD представляет собой среднее геометрическое BD и DC, вы знаете, что BD / AD = AD / DC . Вам дано, что BD = 9, но нужно еще найти DC. Используя постулат сложения сегментов, BC = BD + DC. Замена BC и BD дает 13 = 9 + DC или DC = 4. Теперь вы можете подставить значения в пропорцию и найти AD:
- BD / AD = AD / DC
- 9 / 9 / ad = ad = ad = 4
- (AD) 2 = 36
- AD = 6
Выдержка с Полный идиотский Руководство по геометрии 2004 от Denise Szecsei, PH .D.. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.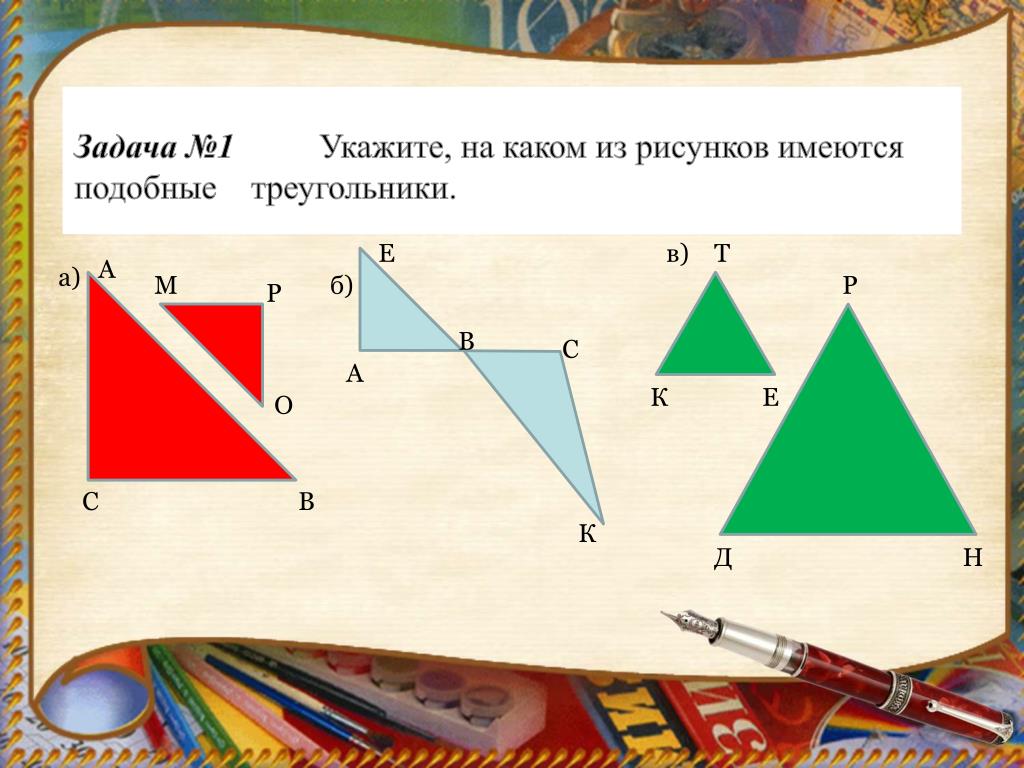
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
РЕШЕНО:угол пропорционален? Значит ли это, что треугольники подобны?» а. Используйте \( \underline{2} \) -70a Student eTool (CPM) (или соломинки и транспортиры) для проверки треугольников с двумя парами соответствующих сторон, которые пропорциональны, с конгруэнтными углами.{\circ} \) что не похоже? б. Проверьте свои идеи из части (а) на треугольнике ниже. Можно ли построить второй треугольник, у которого две стороны пропорциональны данным длинам сторон и с тем же прилежащим к нему углом, но он не подобен? Попрактикуйтесь с инструментом \( \underline{2-70 b \text { Студент }} \) \( (\mathrm{CPM}) \).
Пенсильванский университет Кларион
Два треугольника подобны, если они имеют одинаковую форму (но не обязательно одинаковый размер). Подобные треугольники имеют пропорциональные стороны. На рисунке показаны два подобных треугольника. Обратите внимание, что все отношения соответствующих сторон равны $\frac{3}{2}$ :
$$
\frac{3}{2}=\frac{3}{2}, \quad \frac{4.5}{3}=\frac{3}{2}, \quad \frac{6}{4}=\ трещина{3}{2}
$$
Если мы знаем, что два треугольника подобны, мы можем составить пропорцию для нахождения длины неизвестной стороны.
С помощью пропорции найдите длины $x$ и $y$ каждой пары подобных треугольников.
(Изображение не может быть скопировано)
Подобные треугольники имеют пропорциональные стороны. На рисунке показаны два подобных треугольника. Обратите внимание, что все отношения соответствующих сторон равны $\frac{3}{2}$ :
$$
\frac{3}{2}=\frac{3}{2}, \quad \frac{4.5}{3}=\frac{3}{2}, \quad \frac{6}{4}=\ трещина{3}{2}
$$
Если мы знаем, что два треугольника подобны, мы можем составить пропорцию для нахождения длины неизвестной стороны.
С помощью пропорции найдите длины $x$ и $y$ каждой пары подобных треугольников.
(Изображение не может быть скопировано)


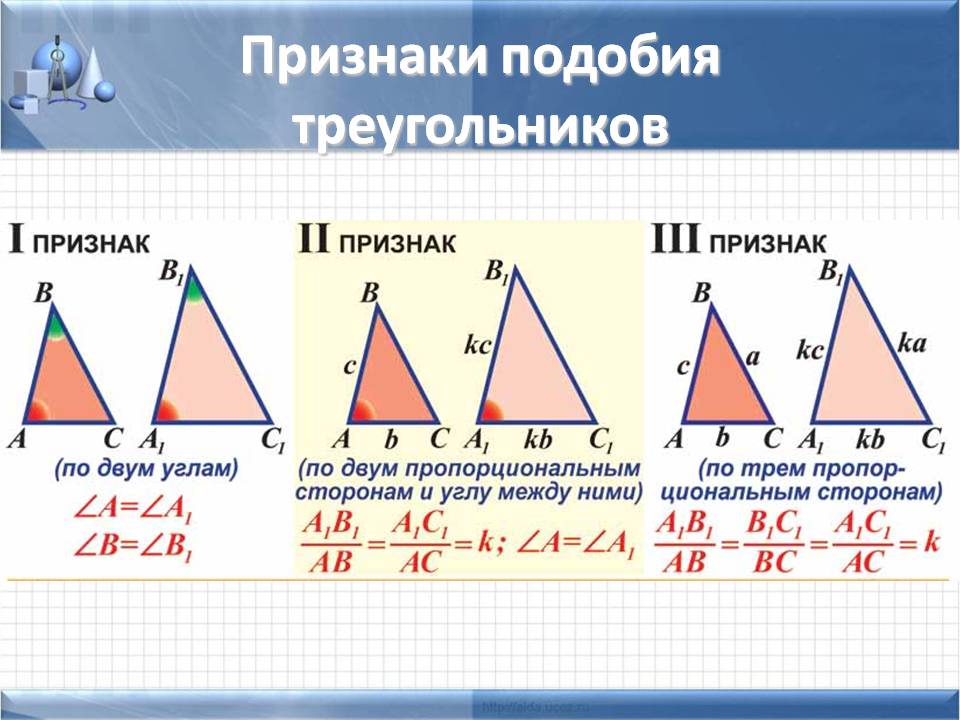

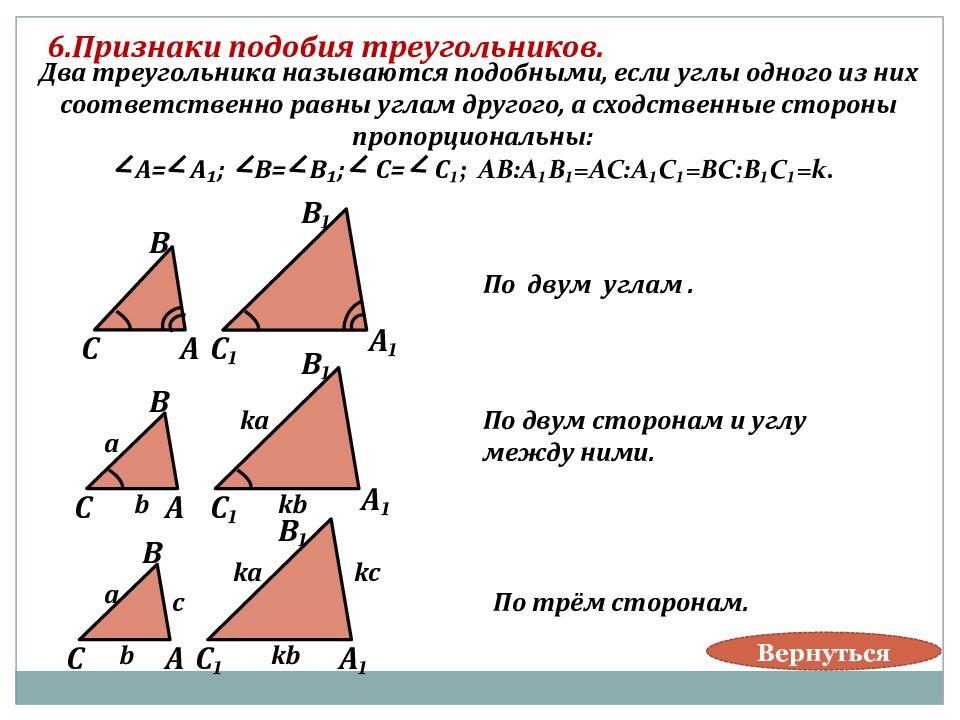
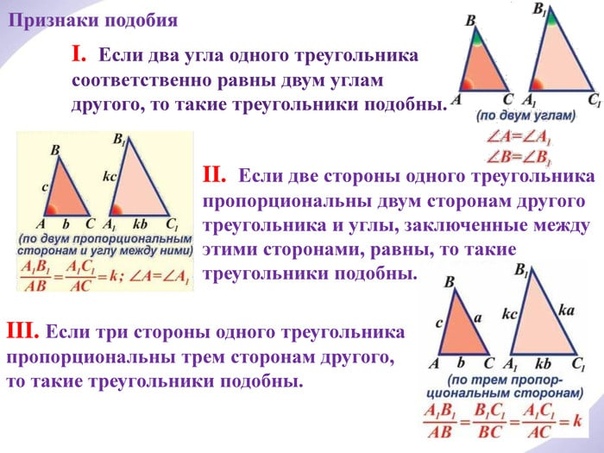
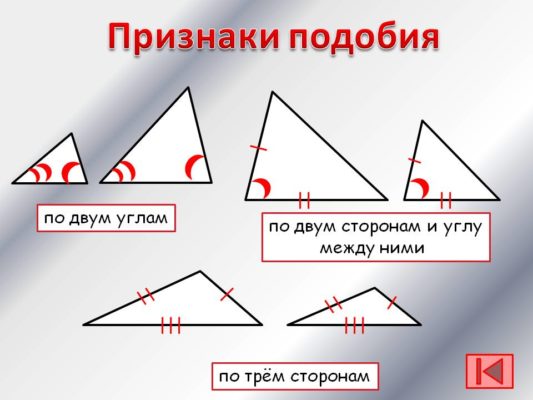


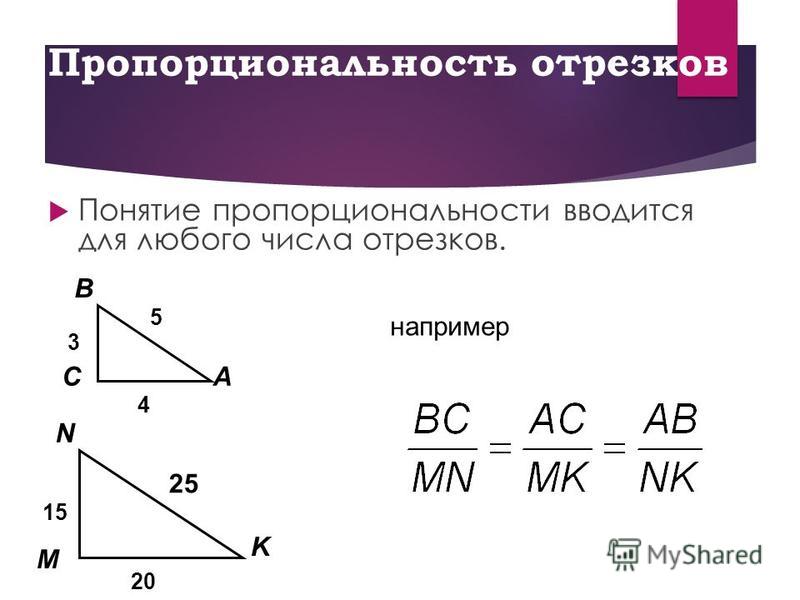 То есть, если a / b = c / d (где b 0 и d 0), то a d = b c.
То есть, если a / b = c / d (где b 0 и d 0), то a d = b c.
