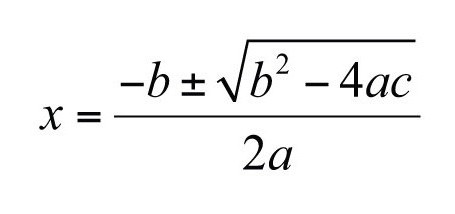как определить линейное уравнение или нет

Вы искали как определить линейное уравнение или нет? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и что значит уравнение линейное, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как определить линейное уравнение или нет».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как определить линейное уравнение или нет,что значит уравнение линейное. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как определить линейное уравнение или нет. Просто введите задачу в окошко и нажмите «решить» здесь (например, как определить линейное уравнение или нет).

Где можно решить любую задачу по математике, а так же как определить линейное уравнение или нет Онлайн?

Решить задачу как определить линейное уравнение или нет вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru

Как определить линейное уравнение или нет. Линейные уравнения: формулы и примеры

Линейное уравнение — это алгебраическое уравнение, полная степень многочленов которого равна единице. Решение линейных уравнений — часть школьной программы, причем не самая сложная. Однако некоторые все же испытывают затруднения при прохождении данной темы. Надеемся, прочитав данный материал, все трудности для вас останутся в прошлом. Итак, давайте разбираться. как решать линейные уравнения.

Общий вид

Линейное уравнение представляется в виде:

• ax + b = 0, где a и b — любые числа.

Несмотря на то, что a и b могут быть любыми числами, их значения влияют на количество решений уравнение. Выделяют несколько частных случаев решения:

• Если a=b=0, уравнение имеет бесконечное множество решений;
• Если a=0, b≠0, уравнение не имеет решения;
• Если a≠0, b=0, уравнение имеет решение: x = 0.

В том случае, если оба числа имеют не нулевые значения, уравнение предстоит решить, чтобы вывести конечное выражения для переменной.

Как решать?

Решить линейное уравнение — значит, найти, чему равна переменная. Как же это сделать? Да очень просто — используя простые алгебраические операции и следуя правилам переноса. Если уравнение предстало перед вами в общем виде, вам повезло, все, что необходимо сделать:

1. Перенести b в правую сторону уравнения, не забыв изменить знак (правило переноса!), таким образом, из выражения вида ax + b = 0 должно получиться выражение вида: ax = -b.
2. Применить правило: чтобы найти один из множителей (x — в нашем случае), нужно произведение (-b в нашем случае) поделить на другой множитель (a — в нашем случае). Таким образом, должно получиться выражение вида: x = -b/а.

Вот и все — решение найдено!

Теперь давайте разберем на конкретном примере:

1. 2x + 4 = 0 — переносим b, равное в данном случае 4, в правую сторону
2. 2x = -4 — делим b на a (не забываем о знаке минус)
3. x = -4/2 = -2

Вот и все! Наше решение: x = -2.

Как видите, решение линейного уравнения с одной переменной найти довольно просто, однако так просто все, если нам повезло встретить уравнение в общем виде. В большинстве случаев, прежде чем решать уравнение в описанные выше две ступени, нужно еще привести имеющееся выражение к общему виду. Впрочем, это тоже не архисложная задача. Давайте разберем некоторые частные случаи на примерах.

Решение частных случаев

Во-первых, давайте разберем случаи, которые мы описали в начале статьи, и объясним, что же значит бесконечное множество решений и отсутствие решения.

• Если a=b=0, уравнение будет иметь вид: 0x + 0 = 0. Выполняя первый шаг, получаем: 0x = 0. Что значит эта бессмыслица, воскликните вы! Ведь какое число на ноль ни умножай, всегда получится ноль! Верно! Поэтому и говорят, что уравнение имеет бесконечное множество решений — какое число ни возьми, равенство будет верным, 0x = 0 или 0=0.
• Если a=0, b≠0, уравнение будет иметь вид: 0x + 3 = 0. Выполняем первый шаг, получаем 0x = -3. Снова бессмыслица! Очевидно же, что данное равенство никогда не будет верным! Потому и говорят — уравнение не имеет решений.
• Если a≠0, b=0, уравнение будет иметь вид: 3x + 0 = 0. Выполняя первый шаг, получаем: 3x = 0. Какое решение? Это легко, x = 0.

Трудности перевода

Описанные частные случаи — это не все, чем нас могут удивить линейный уравнения. Иногда уравнение вообще с первого взгляда трудно идентифицировать. Разберем пример:

Разве это линейное уравнение? А как же ноль в правой части? Торопиться с выводами не будем, будем действовать — перенесем все составляющие нашего уравнения в левую сторону. Получим:

Теперь вычтем подобное из подобного, получим:

Узнали? Самое что ни на есть линейное уравнение! Решение которого: x = 20/10 = 2.

А что если перед нами такой пример:

• 12((x + 2)/3) + x) = 12 (1 — 3x/4)

Да, это тоже линейное уравнение, только преобразований нужно провести побольше. Сначала раскроем скобки:

1. (12(x+2)/3) + 12x = 12 — 36x/4
2. 4(x+2) + 12x = 12 — 36x/4
3. 4x + 8 + 12x = 12 — 9x — теперь выполняем перенос:
4. 25x — 4 = 0 — осталось найти решение по уже известной схеме:
5. 25x = 4,
6. x = 4/25 = 0.16

Как видите, все решаемо, главное — не переживать, а действовать. Запомните, если в вашем уравнении только переменные первой степени и числа, перед вами линейное уравнение, которое, как бы оно ни выглядело изначально, можно привести к общему виду и решить. Надеемся, у вас все получится! Удачи!

При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.

Чтобы найти корень уравнения нужно равносильными преобразования привести данное нам уравнение к виду

\(x=[число]\)

Это число и будет корнем.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

Например : прибавим \(5\) к обеим частям уравнения \(6x-5=1\)

\(6x-5=1\) \(|+5\)
\(6x-5+5=1+5\)
\(6x=6\)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».

2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.

Например : разделим уравнение \(-2x=8\) на минус два

\(-2x=8\) \(|:(-2)\)
\(x=-4\)

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.

3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.

Ответ : \(7\)

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.

Проверка:
\(6(4-7)+7=3-2\cdot7\)
\(6\cdot(-3)+7=3-14\)

\(-18+7=-11\)
\(-11=-11\)

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ответ прост:

Ваша цель – привести уравнение к виду \(x=[число]\), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных. Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.

Чтобы лучше это понять, разберем по шагам решение линейного уравнения \(x+3=13-4x\).

Давайте подумаем: чем данное уравнение отличается от \(x=[число]\)? Что нам мешает? Что не так?

Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать — вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.

\(x+3=13-4x\) \(|-3\)
\(x+3-3=13-4x-3\)
\(x=10-4x\)

Хорошо. Теперь что мешает? \(4x\) справа, ведь там должны быть только числа. \(4x\) вычитается — убираем прибавлением .

\(x=10-4x\) \(|+4x\)
\(x+4x=10-4x+4x\)

Теперь приводим подобные слагаемые слева и справа.

Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением .

\(5x=10\) \(|:5\)
\(\frac{5x}{5}\) \(=\)\(\frac{10}{5}\)
\(x=2\)

Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.

Заметим, что чаще всего корень в линейных уравнениях только один . Однако могут встретиться два особых случая.

Особый случай 1 – в линейном уравнении нет корней.

Пример . Решить уравнение \(3x-1=2(x+3)+x\)

Решение :

Ответ

: нет корней.

На самом деле, то, что мы придем к такому результату было видно раньше, еще когда мы получ

		Прибавляем \(2x\) слева и справа
		Вычитаем \(24\) из обеих частей уравнения
		Опять приводим подобные слагаемые
		Теперь делим уравнение на \(-3\), тем самым убирая перед иксом в левой части.

slovarslov.ru

Теория о линейных уравнениях

ТЕОРИЯ ОБ УРАВНЕНИЯХ

Линейное уравнение с одной переменной

Линейное уравнение с двумя

переменными

Опр.

Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная

Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные

Решение

Это значение переменной х , при котором линейное уравнение превращается в верное равенство

Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество

Например

3х = — 99

Если х = — 33 , значит

3 * ( — 33 )= — 99- верное равенство

3х + 2у = 7

Если х =1, у = 2 или ( 1 ; 2) , значит

3*1 + 2 * 2= 7 — верное тождество

Решить

уравнения

Значит найти все его корни или доказать , что их нет

0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)

Опр.

Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.

Св.ва

Свойства линейных уравнений с одной или двумя переменными

1. Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.

График

Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки

ТЕОРИЯ ОБ УРАВНЕНИЯХ

Линейное уравнение с одной переменной

Линейное уравнение с двумя

переменными

Опр.

Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная

Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные

Решение

Это значение переменной х , при котором линейное уравнение превращается в верное равенство

Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество

Например

3х = — 99

Если х = — 33 , значит

3 * ( — 33 )= — 99- верное равенство

3х + 2у = 7

Если х =1, у = 2 или ( 1 ; 2) , значит

3*1 + 2 * 2= 7 — верное тождество

Решить

уравнения

Значит найти все его корни или доказать , что их нет

0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)

Опр.

Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.

Св.ва

Свойства линейных уравнений с одной или двумя переменными

1. Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.

График

Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки

ТЕОРИЯ ОБ УРАВНЕНИЯХ

Линейное уравнение с одной переменной

Линейное уравнение с двумя

переменными

Опр.

Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная

Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные

Решение

Это значение переменной х , при котором линейное уравнение превращается в верное равенство

Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество

Например

3х = — 99

Если х = — 33 , значит

3 * ( — 33 )= — 99- верное равенство

3х + 2у = 7

Если х =1, у = 2 или ( 1 ; 2) , значит

3*1 + 2 * 2= 7 — верное тождество

Решить

уравнения

Значит найти все его корни или доказать , что их нет

0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)

Опр.

Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.

Св.ва

Свойства линейных уравнений с одной или двумя переменными

1. Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.

График

Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки

infourok.ru

линейного, квадратного, кубического? :: SYL.ru

Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.

Что это такое?

Уравнение – это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество – одна.

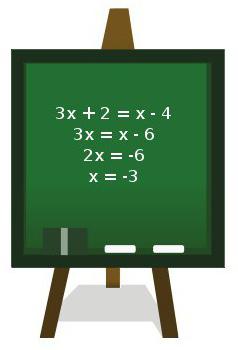
Решить его – это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.

Какие виды уравнений существуют?

Линейное. Оно содержит переменную, степень которой равна единице.

• Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени.
• Уравнение высшей степени.
• Дробно-рациональное. Когда переменная величина оказывается в знаменателе дроби.
• С модулем.
• Иррациональное. То есть такое, которое содержит алгебраический корень.

Как решается линейное уравнение?

Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.

• Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые.
• Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой.
• Привести подобные члены в каждой части решаемого уравнения.
• В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой – число.
• Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.

Как найти корни квадратного уравнения?

Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.

• Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение.
• Оцените значение дискриминанта. Он отрицательный – решение закончено, так как у него корней нет. Равен нулю – ответом будет одно число. Положительный – два значения у переменной.

• 

  Найдите два корня уравнения по формуле, в которой квадратный корень из дискриминанта нужно вычесть или сложить с отрицательным коэффициентом при переменной в первой степени. Потом разделить на удвоенный коэффициент, стоящий перед квадратом неизвестной. (В случае равенства дискриминанта нулю прибавлять или вычитать нужно будет ноль, поэтому два корня совпадут.)

Как решить кубическое уравнение?

Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х³ — 3х² — 4х + 12 = 0.

Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 – это первый корень кубического уравнения.

Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х² — х — 6 = 0.

Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.

Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.

Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.

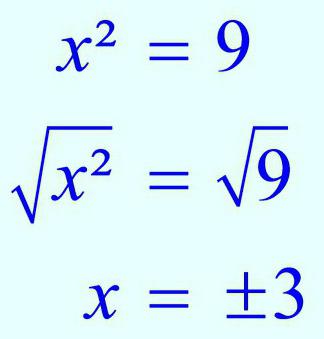
Если в них переменные обозначены буквами х₁ и х₂, то можно из первого равенства вывести, к примеру, х₂. Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.

Теперь возвратитесь к первому уравнению и найдите корень уравнения x₂, используя получившееся равенство. Эти два числа являются ответом.

Простой совет

Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку. Ее не обязательно записывать.

Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось – решение верное.

При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.

www.syl.ru