Все формулы основания прямоугольной трапеции
1. Формула длины оснований прямоугольной трапеции через среднюю линию
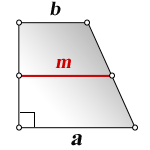
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
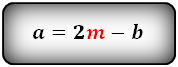

2. Формулы длины оснований через боковые стороны и угол при нижнем основании
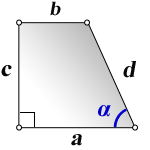
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
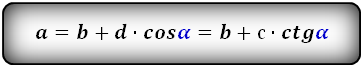
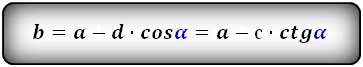
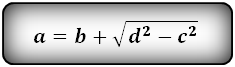

3. Формулы длины оснований трапеции через диагонали и угол между ними
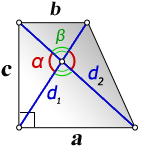
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
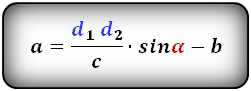
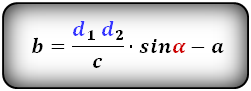
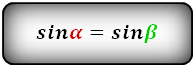
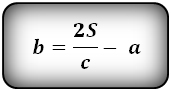
4. Формулы длины оснований трапеции через площадь
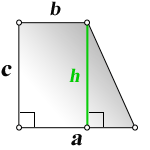
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
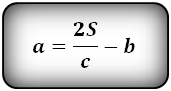
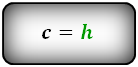
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
zdesformula.ru
Как найти основание трапеции
Добрый вечер.
Трапеция — это нередкий вопрос. Надеюсь, мы сможем помочь Вам разобраться в этом.
Для начала, давайте подумаем, что же такое трапеция. Трапеция — это такой четырёхугольник, у которого две стороны параллельны (они называются основаниями), а остальные две — непараллельны (это боковые стороны).
Хорошо, а теперь давайте разбираться, как найти основание трапеции.
В первую очередь рассмотрим вариант через периметр. Как мы знаем, периметр — это сумма всех сторон. То есть, логично, что если мы знаем две боковые стороны, а также у нас есть хоть какие-то сведения об одной из основания трапеции. То это очень легко будет сделать.
Второй наш случай — это через площадь трапеции. У нас есть вариант, который может подойти:
- площадь мы можем найти через сумму оснований ( a + b) и их половину, плюс это всё умноженное на высоту:
Как вы видите, мы можем найти основание трапеции через периметр или площадь, но этого условия недостаточно.
Теперь давайте найдём большее основание (AD/a):
Ответ: см
ru.solverbook.com
Найти большее основание трапеции

Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:

Рассмотрим задачи:

27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Площадь трапеции (формула):

Нам известны основания и площадь, можем записать:

Ответ: 8

27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Формула площади при данных обозначениях вершин:

Нам известны основание, площадь и высота, можем записать:

Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.

27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Формула площади при данных обозначениях вершин:

Нам известны средняя линя и площадь, можем записать:

Ответ: 8

27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:

Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:

Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):

По теореме Пифагора:

Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30

27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:

Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:

Таким образом площадь будет равна:

Ответ: 160

27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:

Теперь выполним дополнительные построения (опустим высоты):

Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:

Ответ: 5

27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.

Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:

Высоту нашли, вычисляем площадь:

Ответ: 42

27593. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.

Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.

Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.

Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
matematikalegko.ru
Как найти основание трапеции?
Прежде чем начать разговор о том, как найти основание трапеции, важно понимать, что же представляет собой трапеция. Трапеция – это геометрическая фигура, которая является четырёхугольником с двумя параллельными сторонами, которые противолежат друг другу. Эти стороны в математике называют основаниями трапеции. Две другие стороны именуются боковыми сторонами. Если соединить между собой центральные точки боковых сторон, мы получим среднюю линию трапеции.Данные свойства этой геометрической фигуры являются основой всех вычислений её характеристик.
Для вычисления основания трапеции, как большого, так и малого, используется ряд способов. Выбор способа зависит от количества знаний, которое мы имеем об объекте. Большинство задач располагают условиями, которые содержат в себе данные, заметно упрощающие поиск решения задачи. Зачастую, решение заключается в том, чтобы опустить высоту на основание, применяя теорему Пифагора, в этом случае решить задачу легко.
Как найти основание равнобедренной трапеции
Похожим образом вычисляется основание равнобедренной трапеции. Равнобедренная трапеция – трапеция, которая имеет равные боковые стороны. Фигура имеет симметричный вид относительно центра, это делает пары её углов равными. Таким образом, сведения об одном угле упрощают задачу вычисления всех остальных углов.
Боковые части трапеции равны друг другу. Например, мы должны найти основание через фрагмент этого основания. Длина второго фрагмента в данном случае будет совпадать с длиной первого фрагмента с абсолютной точностью. Мы можем также получить искомую часть основания через изображение высоты, которая образует треугольник. Параметры углов и одной стороны треугольника помогут нам сделать точные вычисления. В задачах требуется решить вопрос о том, как найти большее основание равнобедренной трапеции или меньшее основание. Рассмотрим пример вычисления величины меньшего основания трапеции.
Как найти меньшее основание равнобедренной трапеции
В случае, когда нам известна величина большего основания, вопрос о том, как найти меньшее основание равнобедренной трапеции перестанет быть острым. Это можно следующим образом:
- На большее основание нужно опустить высоту.
- Записать две теоремы Пифагора, одна из которых отразит параметры треугольника, а другая будет нужна для треугольника, состоящего из гипотенузы. В случае с первой теоремой, в треугольнике роль гипотенузы исполнит диагональ, роль одного катета достанется высоте, а другого – большее основание, не имеющее отрезка. Отрезок будет отсечён высотой. Вторая теорема используется для треугольника, составляющими которого станут гипотенуза – боковая сторона и катет – отрезок большого основания, ограниченный высотой.
- Составить систему уравнений, которые получили, решить их.
- Найти отрезок, отсечённый высотой от наибольшего расстояния.
- Отнять удвоенные параметры полученного отрезка от параметров наибольшего основания.
- Получить результат – длину наименьшего основания.
Как найти основание прямоугольной трапеции
Прямоугольной трапецией – это вид геометрической трапеции , один из углов которой равен девяноста градусам. Вычислить основание прямоугольной трапеции наиболее легко. Условие задачи, по обыкновению, уже содержит данные о втором основании. От вас потребуется только лишь определить фрагмент основания, образующий угол фигуры вместе с боковой стороной.
По теореме Пифагора, вычисляем эту часть, затем нужно прибавить или отнять эту часть от второго основания. В результате вычислений мы получим искомый параметр. Теперь вы знаете, как найти основание прямоугольной трапеции.
elhow.ru
Как найти высоту трапеции, если известны основания
Найти высоту трапеции, если известны только основания, невозможно. Высоту трапеции можно найти, если известна площадь трапеции и ее основания, то высота трапеции равна h = 2S/(a+b), где S — площадь, a и b — основания. Можно найти высоту трапеции по теореме Пифагора, если известны все стороны трапеции, а сама трапеция равнобедренная. В этом случае находим сначала основание треугольника, которое будет равно половине разности оснований, а затем применить теорему Пифагора. Если известны площадь трапеции и средняя линия, то для определения высоты трапеции достаточно разделить площадь трапеции на длину средней линии.
Никак, не хватает данных
Нужно ещё знать площадь трапеции, и через неё выразить высоту
touch.otvet.mail.ru
Как найти меньшее основание трапеции
Как найти меньшее основание трапеции
Для начала вспомним, что меньшее основание трапеции называют ту из двух параллельных ее сторон, длина которой меньше от другой параллельной стороны.
Разберемся как находить длину этого основания в разных ситуациях (при разных исходных данных).
Длину меньшего основания можно легко найти, если известна длина большого основания, средняя линия трапеции, высота трапеции или ее площадь.
Известно большое основание трапеции и ее средняя линия
Самый простой случай. Поскольку согласно свойству средней линии трапеции она равна половине суммы обоих оснований, то, используя всего одну формулу, можно найти неизвестное меньшее основание:
- Известны площадь, высота трапеции и длина большого основания
Воспользуемся формулой площади трапеции:
Выразим малое основание из этой формулы:
- Известны большое основание, высота, углы при большом основании
Если трапеция остроугольная, то, при известных углах при большом основании, длину малого основания можно найти с помощью следующей формулы:
Если же трапеция тупоугольная, тогда нужно использовать другую формулу:
Здесь — тупой.
ru.solverbook.com