Калькулятор онлайн
Этот удобный калькулятор производит элементарные арифметичиеские операции (сложение, вычитание, умножение, деление) с положительными и отрицательными целыми числами и дробями. Доступны действия с процентами, возведение в степень, вычисление корня из числа, а также логарифм.
Для всех возможных действий приведены примеры. Если вам нужны дополнительные функции, то откройте инженерный калькулятор.
Арифметические операции
Сложение
Сложение объединяет два числа (слагаемые) в одно (сумму чисел).
2 + 3 =
Вычитание
Вычитание является обратной операцией к сложению. Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).
3 − 2 =
Умножение
Умножение объединяет два числа в одно число – произведение чисел. Два исходных числа называются множимым и множителем.
2 × 3 =
Деление
Деление является обратной операцией к умножению. Деление находит частное от двух чисел (делимого, поделенного на делитель). Деление любого числа на 0 не определено.
4 ÷ 2 =
Действия с дробями
Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.
1 ÷ 2 + 1 ÷ 4 =
Десятичные дроби
Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.
. 2 + . 0 3 =
Нахождение обратного числа
Обратное число к x, обозначаемое 1/x или x-1, представляет собой число, которое при умножении на x дает единицу.
2 1/x =
Действия с процентами
Процент — сотая часть (обозначается знаком %), используется для обозначения доли чего-либо по отношению к целому.
Нахождение процента от числа
40 × 5 % =
Увеличение (уменьшение) числа на процент
40 + 5 % =
Возведение в степень
Возведение в степень — математическая операция, записанная как xy, включающая два числа: основание x и показатель степени (или степень) y. Когда y — положительное целое число, возведение в степень соответствует многократному умножению основания на себя: то есть, xy — произведение умножения y оснований.
2 xy 4 =
Возведение числа в квадрат
Выражение x2 называется «квадратом x» или «x в квадрате», потому что площадь квадрата с длиной стороны x равна x×x или x2.
2 x2 =
Возведение числа в куб
Выражение x3 называется «кубом x» или «x в кубе», потому что объем куба с длиной стороны x равен x×x×x или x3.
2 x3 =
Возведение в степень числа 10
Возведение в степень с основанием
4 10x =
Мнимая единица
Мнимая единица i определяется только тем свойством, что её квадрат равен −1.
i x2 =
Корень из числа
В математике y-ый корень числа x, где y обычно является положительным целым числом, представляет собой число z, которое при возведении в степень y дает x, где y — степень корня.
16 y√x 4 =
Квадратный корень
Квадратный корень числа x — это число z, которое в квадрате становится x.
9 √x =
Кубический корень
Кубический корень числа x — это число z, куб которого является x.
8 3√x =
Вычисление логарифма
Логарифм заданного числа x является показателем степени, в которую должно быть возведено другое фиксированное число (основание) y, чтобы получить это число x.log 8 , 2 =
Десятичный логарифм
Десятичным логарифмом является логарифм с основанием 10.
log 100 =
Натуральный логарифм
Натуральный логарифм числа — это его логарифм по основанию число е.
log 3 , e =
okcalc.com
Как на калькуляторе посчитать корень в n-ой степени
Либо в дробной степени, 1/n, либо поставить птицу inv в инженерном виде калькулятора винды, перед фyнкцией возведения в степень. X^n, где n степень корня
Корень энной степени из числа или корень (квадратный) в энной степени?
через логарифм
если корень допустим пятой степени нажать на знак корня 5 раз
Х^ (1/n) — можно так если калькулятор поддерживает запись формул (для примера: выражение квадратный корень из числа Y будет выглядеть — Y^(1/2)
нужно чтобы на калькуляторе было n кнопок с корнем
нажимаем сначала число, которое нужно возвести в 3 степень, затем жмем 2ndF (зеленая такая), затем значек корня. все.
touch.otvet.mail.ru
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * — необязателен: выражение 2sin(3 x ) эквивалентно 2*sin(3*x ).Cкобки используются для группирования выражений. |
0.5 |
Десятичные дроби записываются через точку:
|
Элементарные функции |
|
| Возведение в степень: xn , напримерx ^2 значитx 2 |
|
| Квадратный корень: √ x . Эквивалентно root(x ,2) илиx ^(1/2) |
|
| Кубический корень: 3√ x . Эквивалентно root(x ,3) илиx ^(1/3) |
|
| Корень n -той степени изx . Эквивалентноx ^(1/n ) |
|
| Логарифм от x по основаниюa |
|
| Натуральный логарифм (логарифм c основанием e ) |
|
| Десятичный логарифм (логарифм по основанию 10) | |
| Экспоненциальная функция, эквивалентно e ^x |
|
Тригонометрические функции |
|
| Синус от x |
|
| Косинус от x |
|
| Тангенс от x . Можно вводить tg(x ) или tan(x ) |
|
| Котангенс от x . Можно вводить ctg(x ) или cot(x ) |
|
| Секанс от x , определяется как 1/cos(x ) |
|
| Косеканс от x , определяется как 1/sin(x ) |
|
| Арксинус от x . Можно вводить arcsin(x ) или asin(x ) |
|
| Арккосинус от x . Можно вводить arccos(x ) или acos(x ) |
|
| Арктангенс от x . Можно вводить arctg(x ) или atan(x ) |
|
| Арккотангенс от x . Можно вводить arcctg(x ) или acot(x ) |
|
| Арксеканс от x |
|
| Арккосеканс от x |
|
Некоторые константы |
|
| Число Эйлера e = 2.718281828459045… |
|
| Число π = 3.141592653589793… |
|
ru.onlinemschool.com
Возведение в степень и извлечение корня из числа онлайн.
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби .Обратная операция также верна , любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
calcs.su
Вычисление квадратного корня из любого числа без калькулятора

Во время сдачи ЕГЭ по математике использование калькулятора, как известно, запрещено. Поэтому любой репетитор по математике всегда заставляет своих учеников считать все устно или на бумаге. Но время от времени встречаются задачи, при решении которых требуется извлекать квадратные корни из достаточно больших чисел, и на ЕГЭ по математике такие задачи тоже есть. С проблемой нахождения алгоритма вычисления квадратного корня из вещественного числа читатель может столкнуться (помимо ЕГЭ по математике) на различного рода математических конкурсах и олимпиадах. Итак, как найти квадратный корень без использования калькулятора?
Как репетитор по физике и математике, занимающийся подготовкой к ЕГЭ и ГИА, предлагаю вашему вниманию один действенный алгоритм, не претендующий на максимальную эффективность, но работающий безотказно с любыми вещественными числами. Приведенный метод может со временем стать столь же известным, как, к примеру, метод умножения двух чисел «столбиком», ведь он во многом на него похож.
Вот наглядная схема алгоритма вычисления квадратного корня из любого числа без использования калькулятора (кликабельно):
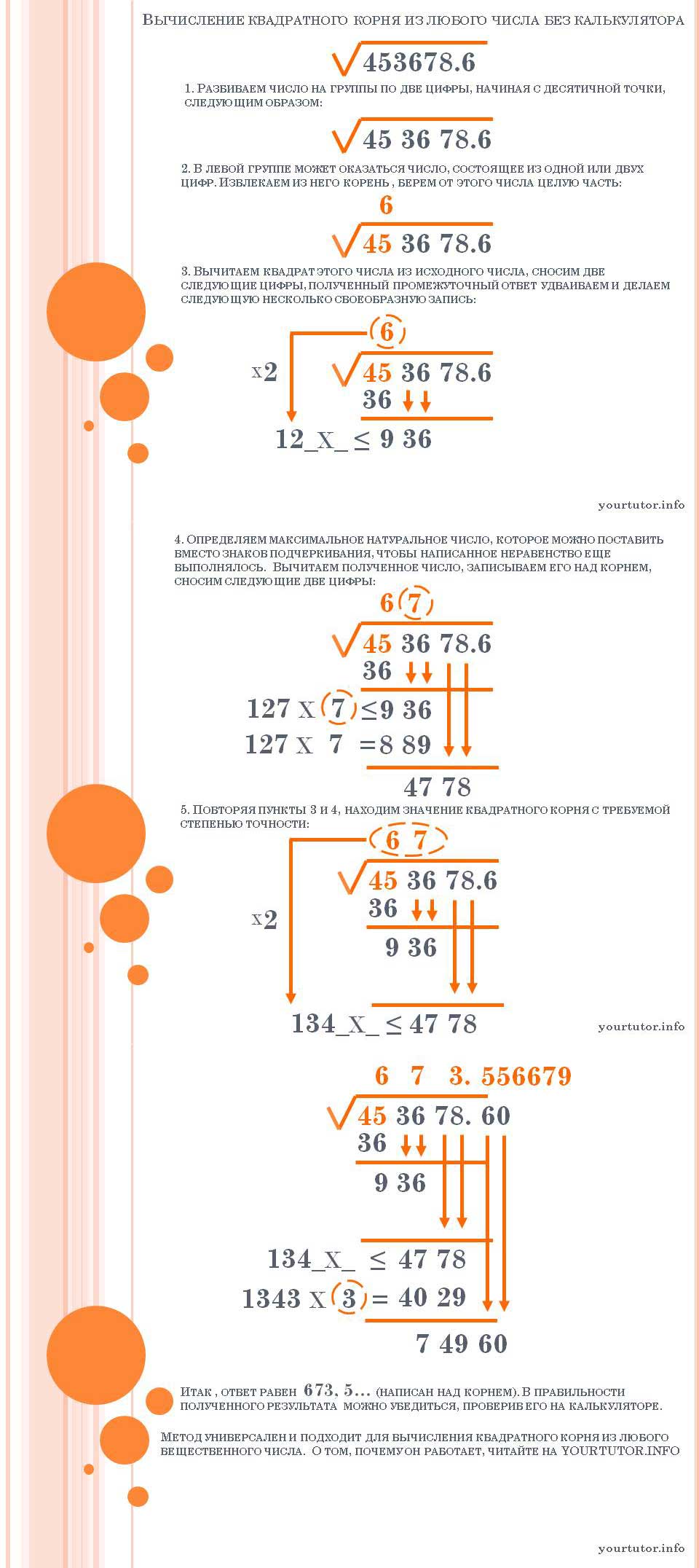
Алгоритм вычисления квадратного корня из любого вещественного числа без использования калькулятора
Однако, вопрос о том, почему данный алгоритм работает, остается пока открытым. Для того, чтобы разобраться в этом, возьмем, для примера, число, цифрами которого являются 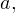
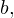
 и
и 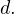 То есть само число имеет вид
То есть само число имеет вид 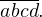 Пусть корнем будет число
Пусть корнем будет число 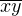 , состоящее из цифр
, состоящее из цифр 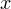 и
и 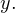 То есть
То есть 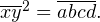 Выполним «столбиком» умножение
Выполним «столбиком» умножение 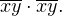
Последовательно:
![Rendered by QuickLaTeX.com \[ 10x\cdot 10x = 100x^2,\, 2\cdot x\cdot 10y=20xy,\, y\cdot y = y^2.\]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-06e4c59360c0873f2ddf3abb30e96c67_l3.png)
То есть:
![Rendered by QuickLaTeX.com \[ \overline{abcd} = 100x^2+20 xy+y^2.\]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3dc210e5f487a90964d9b256fcba8dc4_l3.png)
Проанализировав это разложение, понимаем, что разделяя число 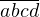 на пары
на пары 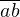 и
и 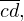 числу в первой паре мы ставим в соответствие число, содержащееся в
числу в первой паре мы ставим в соответствие число, содержащееся в  Иначе говоря, квадратный корень из числа
Иначе говоря, квадратный корень из числа 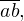 округленный до нижнего целого числа, есть
округленный до нижнего целого числа, есть 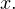
Теперь, зная значение 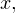 для нахождения
для нахождения 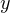 необходимо вычислить значение выражения
необходимо вычислить значение выражения 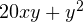 или, что то же самое, значение выражения
или, что то же самое, значение выражения 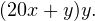 Поразмыслив над этим, понимаем, что в этом, собственно, и состоит суть действия, совершаемого при подборе числа, которое необходимо подставить на четвертом шаге алгоритма вместо знаков подчеркивания. Таким образом мы находим
Поразмыслив над этим, понимаем, что в этом, собственно, и состоит суть действия, совершаемого при подборе числа, которое необходимо подставить на четвертом шаге алгоритма вместо знаков подчеркивания. Таким образом мы находим 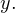 Зная
Зная 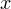 и
и 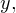 знаем
знаем 
Такой подход может быть обобщен на случай любого количества разрядов в исходном числе. Если корень не является рациональным, вычисления могут продолжаться сколь угодно долго (с любой необходимой степенью точности). Вот такой простой алгоритм. Запомните его, возможно, он пригодится вам при сдаче ЕГЭ по математике.
Репетитор по математике
Сергей Валерьевич
Я съел две курицы, мой сосед — ни одной, но в среднем мы съели по одной курице. Такая вот математика.
© Марк Твен
yourtutor.info
Онлайн калькулятор: Математический калькулятор
Калькулятор был создан в ответ на многочисленные запросы наших пользователей, которые желают воспользоваться нашим сервисом чтобы посчитать результат какого-либо математического выражения, например, что-нибудь сложить, вычесть, поделить возвести в степень, извлечь корень и т. п. Вводите последовательность математических выражений в поле математическое выражение и получайте результат.
Все тригонометрические функции принимают аргументы в радианах, а не в градусах. Обратные тригонометрические функции, также возвращают угол в радианах. Для преобразования градусов в радианы — умножайте градусы на pi/180, например, sin 30 градусов надо записывать как sin(30*pi/180).

Математический калькулятор
Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точность вычисленияЗнаков после запятой: 10
Исходное выражение
Результат вычисления
save Сохранить share Поделиться extension Виджет
В математическом выражении допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
planetcalc.ru
как на калькуляторе извлечь кубический корень
Нужен инженерный калькулятор
нужно произнести заклинание
<a rel=»nofollow» href=»http://lib.rus.ec/i/69/160369/i_188.png» target=»_blank»>http://lib.rus.ec/i/69/160369/i_188.png</a>
логарифм+экспонента x^a=exp(ln(x^a)) = exp(a*ln(x))
Найти кнопку с кубическим корнем.. . Обычно это дополнительная надпись, рядом с кнопкой.
Если инженерный калькулятор не виндусовский, а карманный, то там должна быть кнопка [ x ^ y ] и скобки, набрать число [ x ^ y ] (1/3)= или число [ x ^ y ] 0.3333333333333= то же можно сделать и в виндоусовском калькуляторе, но там проще так как советует Александр Потетнин. Вообще галочка в поле [ V ] Inv, означает, что действие клавиши инвертируется, то есть наоборот вместо x ^ 2, будет корень квадратный вместо ln (x), будет e ^ x вместо синуса, арксинус и так далее
лучше в церковь сходи
Пишешь число. Например «8», нажимаешь «2ndF», затем на кубический корень. И получается, что 8=2^3
touch.otvet.mail.ru