Abitur
Линейная функция и ее график Область определения и область значений функции.
Определение 1: Область определения функции — это множество всех значений Х, для которых функция имеет смысл.
Определение 2: Область значений функции — это множество всех значений Y, которые принимает функция.
Определение линейной функции.
Определение 3: Функция вида y=kx+b, где k, b — любые числа, называется линейной функцией.
Графиком линейной функции является прямая.
Исследование линейной функции.
Приведем схему исследование линейной функции:
1) Возрастающая функция или убывающая.
2) Точки пересечения линейной функции с осями координат.
3) Промежутки на которых функция 0.
Решение примеров.
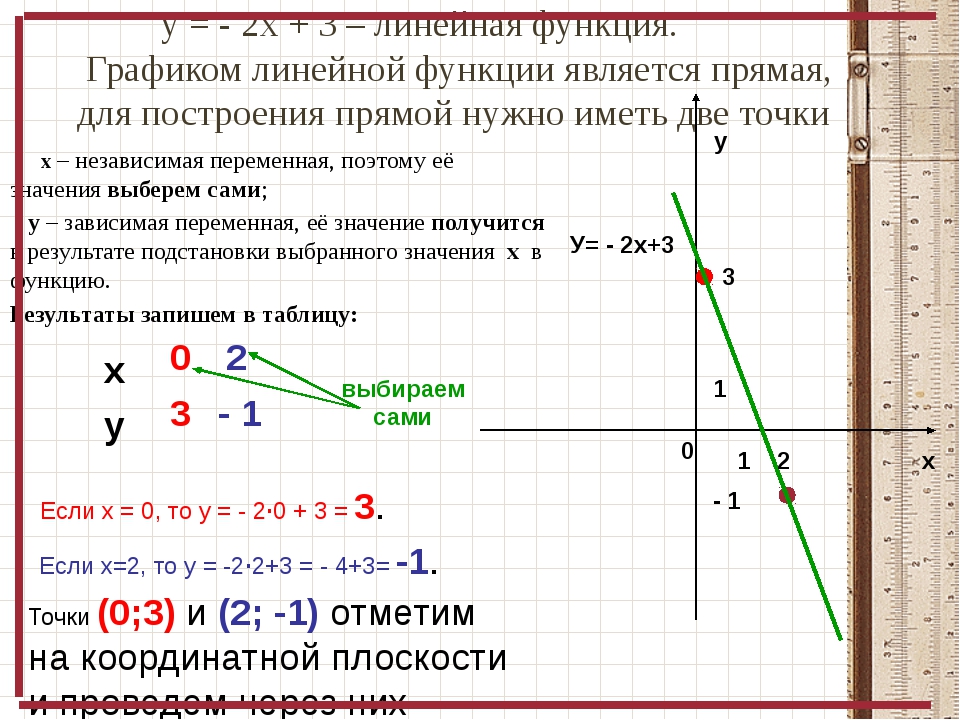
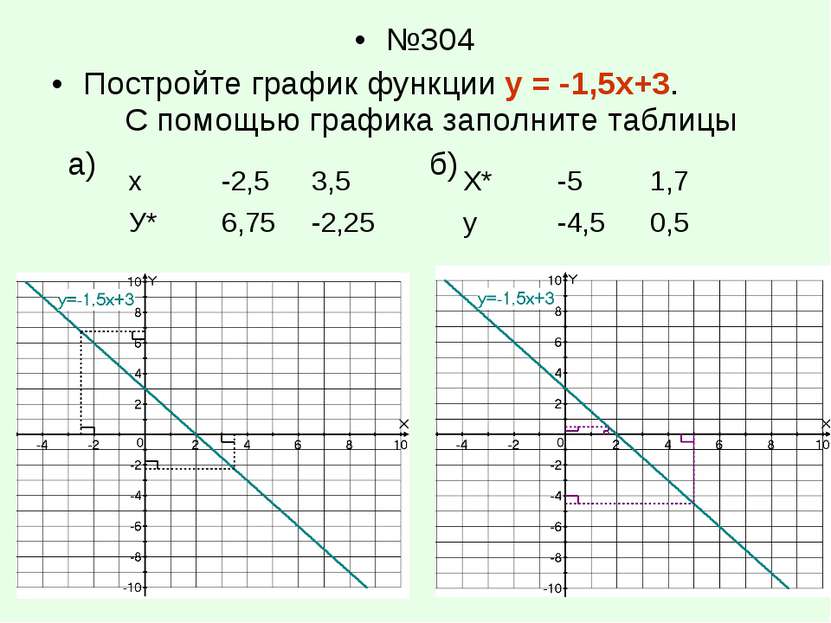
1. Исследуйте функцию и постройте ее график:
| a). |
| 1). | Функция убывающая, так как коэффициент при x меньше нуля |
| 2). | Найдем точку пересечения с осью Х: |
| Т. е. функция пересекает ось Х в точке с координатами |
| 3). | Найдем точку пересечения с осью Y: |
| Т. е. функция пересекает ось Х в точке с координатами (0;2) |
| 4). | Построим через 2 найденные точки | и (0:2) график функции: |
Задания.
1. Исследуйте функцию и постройте ее график:
| d). | e). |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейная функция
Линейной функцией называют функцию, заданную формулой
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия.
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом.
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 1, 2 и 3.
| k > 0 | ||||||
|
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
| k = 0 | ||||||
|
При k < 0 линейная функция (1) убывает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 7, 8 и 9.
| k < 0 | ||||||
|
Прямые линии
y = kx + b1 и y = kx + b2 ,
имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны.
Прямые линии
y = k1x + b1 и y = k2x + b2 ,
имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.
Прямые линии
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
|
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .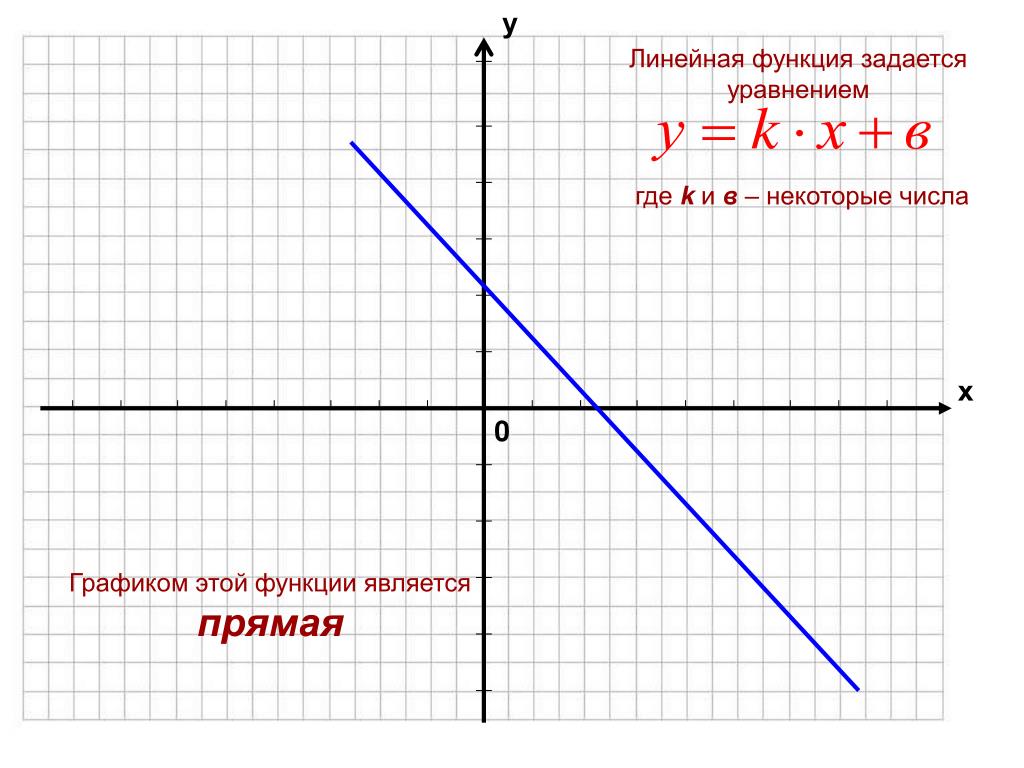
При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
Прямые, параллельные оси ординат
Прямые, параллельные оси Oy, задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
|
Замечание 1. Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
Рассмотрим уравнение
где p, q, r – произвольные числа.
В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию.
Действительно,
что и требовалось.
В случае, когда получаем:
откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:
В случае, когда уравнение (5) решений вообще не имеет.
Замечание 2. При любом значении r1, не совпадающем с r прямая линия, заданная уравнением
При любом значении r1, не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4).
Замечание 3. При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4).
Пример. Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
- перпендикулярной к прямой (8).
Решение.
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
4x + 5y = 7,
задаётся уравнением
4x + 5y = – 7 .
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, прямая, перпендикулярная к прямой
4x + 5y = 7 ,
задаётся уравнением
– 5x + 4y = – 22 .
Линейная функция и ее график | Математика для чайников
Функция – правило, с помощью которого для каждого значения независимой переменной можно найти единственное значение зависимой переменной.
Для разных значений независимой переменной значения зависимой могут совпадать, но для одного и того же значения аргумента будет только одно значение функции!
Функции могут быть заданы таблично, графически и с помощью формулы.
График функции – это графическое выражение функциональной зависимости на координатной плоскости. По оси абсцисс – Ох – откладываются значения аргумента функции, а по оси ординат – Оу – значения функции.
Важный момент – это область определения и область значений функции. Область определений – это те значения, которые может принимать Х. Для многих функций – это все множество действительных чисел, но есть функции, например, обратная пропорциональность, логарифм, квадратный корень, когда область определения ограничена. Область значений – это то множество значений, которые принимать Y.
Самая простая функция – это линейная. Ее форма y(x)=kx+b, k – коэффициент, b – свободный член. График этой функции – прямая. Частный случай линейной функции – прямая пропорциональность – y(x)=kx, при этом b=0. Если же k=0, тогда имеем прямую, параллельную оси Ox, y(x)=b, хотя вне зависимости от х, значение функции не изменится.
Для линейной функции можно даже не строя график, определить как он будет выглядеть. Если k>0, функция возрастает, ее график будет иметь наклон вверх /. Если k<0, функция убывает, график имеет наклон вниз \.
Если мы имеем дело с прямой пропорциональностью, то ее график пройдет через начало координат. Если же свободный член не равен нулю, то наша прямая сместится вверх, если b>0, или вниз, если b<0.
Различный вид графика линейной функции в зависимости от значений коэффициентовБывают ситуации, когда функция задана разными формулами для разных интервалов. Тогда ее график будет состоят из отдельных кусочков.
Для построения графика линейной функции достаточно найти координаты двух точек. Если b не равен нулю, то координаты первой точки (0; b), если b=0, то координаты первой точки (0; 0) — график пройдет через начало координат. Вторую точку находим, подставив вместо х конкретное значение, наиболее удобное для расчета.
Построить график линейной функции y 3. Линейная функция и её график. Свойства линейной функции
Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.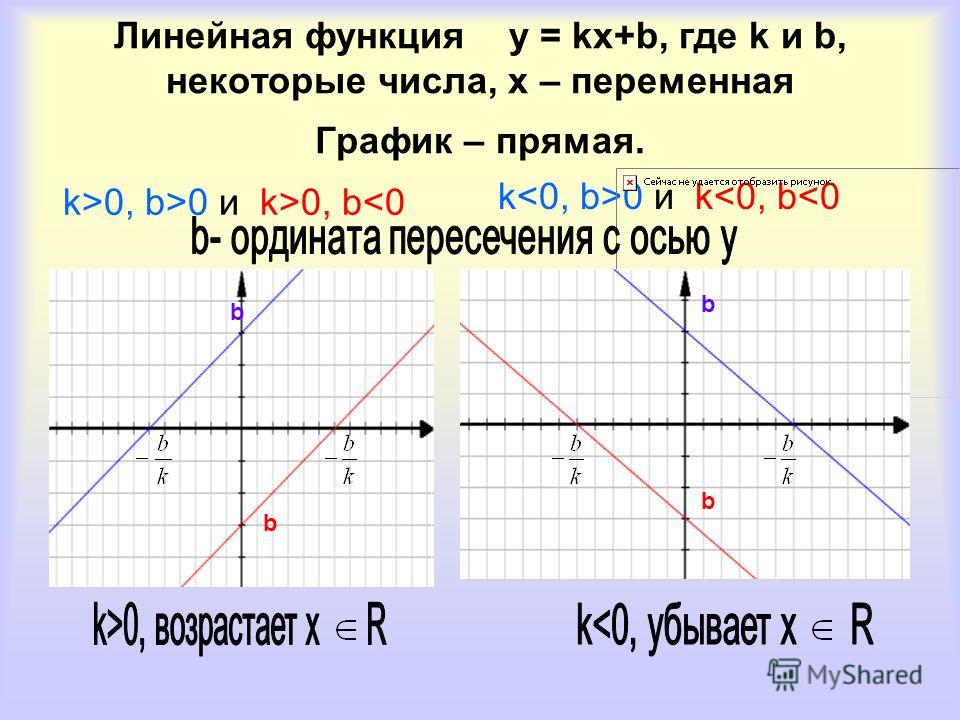
Графиком линейной функции является прямая.
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓
x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½
x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают.
Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0
Если k>0 и b>0 , то график функции y=kx+b имеет вид:
Если k>0 и b , то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2
5. Условие перепендикулярности двух прямых:
График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2
6. Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
Определение линейной функции
Введем определение линейной функции
Определение
Функция вида $y=kx+b$, где $k$ отлично от нуля называется линейной функцией.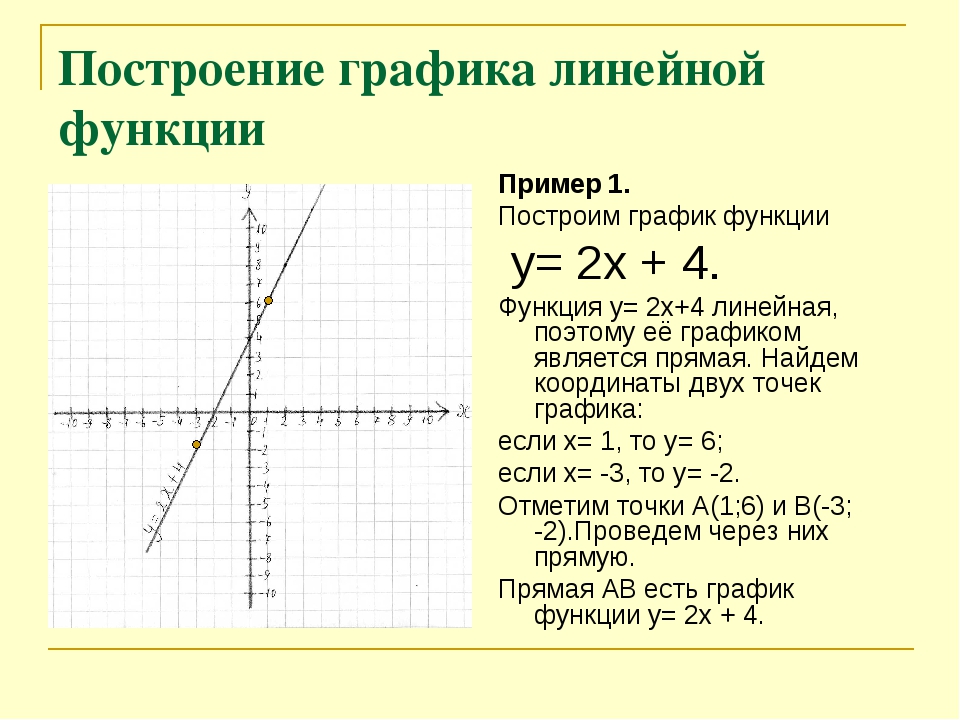 {«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
{«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0 , получим постоянную функцию y = b , график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b) .
Если b = 0 , то получим функцию y = kx , которая является прямой пропорциональностью.
b – длина отрезка , который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;2) Если k ≠ 0 , то область значений линейной функции есть вся вещественная ось. Если k = 0 , то область значений линейной функции состоит из числа b ;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b .
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k , следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b , следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0 , то функция y = 0 обращается в ноль при любом значении переменной х . Если b ≠ 0 и k = 0 , то функция y = b не обращается в ноль ни при каких значениях переменной х .
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞) ,
y = kx + b – отрицательна при x из (-∞; -b/k) .
b) k
y = kx + b – положительна при x из (-∞; -b/k) ,
y = kx + b – отрицательна при x из (-b/k; +∞) .
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k .
k > 0 , следовательно y = kx + b возрастает на всей области определения,
k , следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
| ||||
На рисунке изображены графики y kx b. Линейная функция
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax 2 + bx + c называется квадратичной, графиком ее является парабола.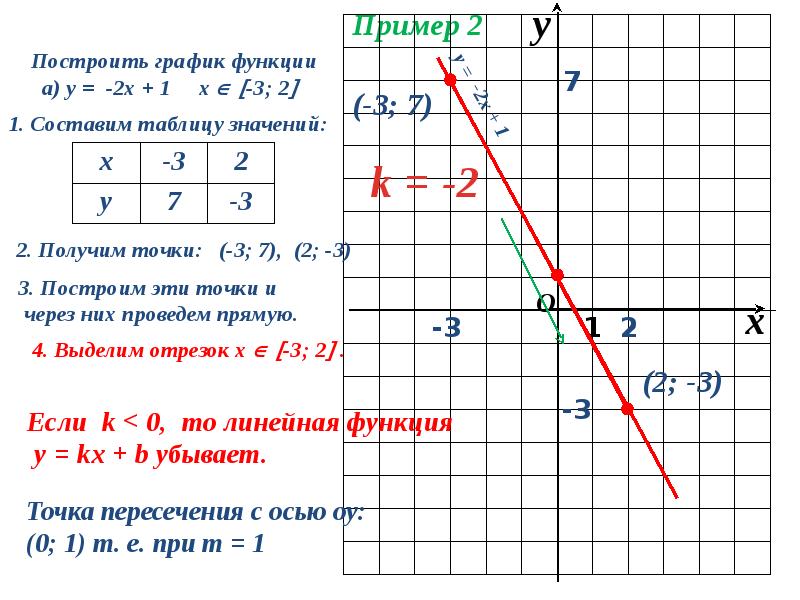 Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.
Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая простая зависимость для коэффициента а . Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а а > 0.
y = 0,5x 2 — 3x + 1
В данном случае а = 0,5
А теперь для а
y = — 0,5×2 — 3x + 1
В данном случае а = — 0,5
Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
y = a 0 2 + b 0 + c = c . Получается, что у = с . То есть с — это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с
с > 0:
y = x 2 + 4x + 3
с
y = x 2 + 4x — 3
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:
y = x 2 + 4x
Сложнее с параметром b . Точка, по которой мы будем его находить, зависит не только от b но и от а . Это вершина параболы. Ее абсцисса (координата по оси х ) находится по формуле х в = — b/(2а) . Таким образом, b = — 2ах в . То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х в > 0) или левее (х в
Однако это не все. Надо еще обратить внимание на знак коэффициента а . То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = — 2ах в определить знак b .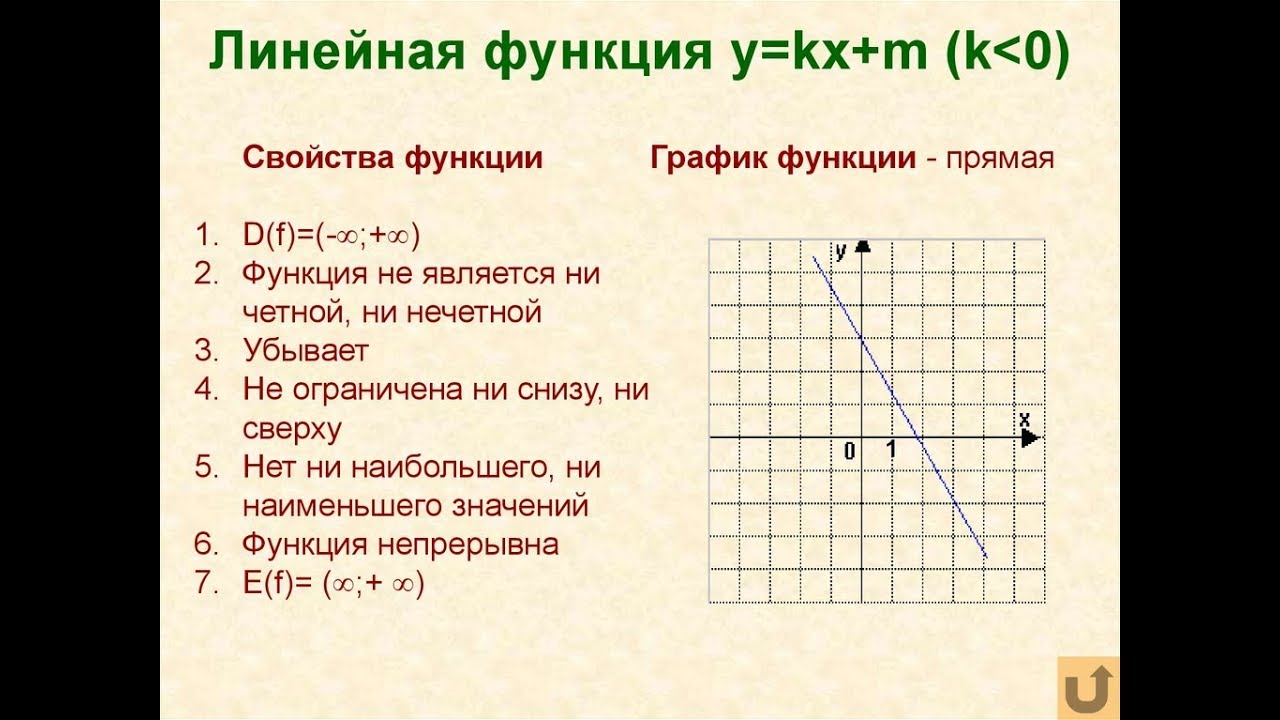
Рассмотрим пример:
Ветви направлены вверх, значит а > 0, парабола пересекает ось у ниже нуля, значит с х в > 0. Значит b = — 2ах в = -++ = -. b а > 0, b с
Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0 , получим постоянную функцию y = b , график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b) .
Если b = 0 , то получим функцию y = kx , которая является прямой пропорциональностью.
b – длина отрезка , который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0 , то область значений линейной функции есть вся вещественная ось. Если k = 0 , то область значений линейной функции состоит из числа b ;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b .
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k , следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b , следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0 , то функция y = 0 обращается в ноль при любом значении переменной х . Если b ≠ 0 и k = 0 , то функция y = b не обращается в ноль ни при каких значениях переменной х .
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞) ,
y = kx + b – отрицательна при x из (-∞; -b/k) .
b) k
y = kx + b – положительна при x из (-∞; -b/k) ,
y = kx + b – отрицательна при x из (-b/k; +∞) .
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k .
k > 0 , следовательно y = kx + b возрастает на всей области определения,
k , следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.
Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓
x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½
x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0
Если k>0 и b>0 , то график функции y=kx+b имеет вид:
Если k>0 и b , то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2
5. Условие перепендикулярности двух прямых:
График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2
6. Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
5. Одночленом называется произведение числовых и буквенных множителей. Коэффициентом называется числовой множитель одночлена.
6. Чтобы одночлен записать в стандартном виде, надо: 1) Перемножить числовые множители и их произведение поставить на первое место; 2) Перемножить степени с одинаковыми основаниями и полученное произведение поставить после числового множителя.
7. Многочленом называется алгебраическая сумма нескольких одночленов.
8. Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена и полученные произведения сложить.
9. Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
10. Через любые две точки можно провести прямую, и притом только одну.
11. Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
12. Две геометрические фигуры называются равными, если их можно совместить наложением.
13. Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.
14. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
15. Развернутый угол равен 180°.
16. Угол называется прямым, если он равен 90°.
17. Угол называется острым, если он меньше 90°, т. е. меньше прямого угла.
18. Угол называется тупым, если он больше 90°, но меньше 180°, т. е. больше прямого, но меньше развернутого угла.
19. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
20. Сумма смежных углов равна 180°.
21. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
22. Вертикальные углы равны.
23. Две пересекающиеся прямые называются перпендикулярными (или взаимно
перпендикулярными), если они образуют четыре прямых угла.
24. Две прямые, перпендикулярные к третьей, не пересекаются.
25.Разложить многочлен на множители – значит представить его в виде произведения нескольких одночленов и многочленов.
26.Способы разложения многочлена на множители:
а) вынесение за скобки общего множителя,
б) использование формул сокращённого умножения,
в) способ группировки.
27.Чтобы разложить многочлен на множители способом вынесения общего множителя за скобки, надо :
а) найти этот общий множитель,
б) вынести его за скобки,
в) каждое слагаемое многочлена разделить на этот множитель и полученные результаты сложить.
Признаки равенства треугольников
1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Образовательный минимум
1. Разложение на множители по формулам сокращенного умножения :
a 2 – b 2 = (а – b) (а + b)
а 3 – b 3 = (а – b) (а 2 + ab + b 2)
а 3 + b 3 = (а + b) (а 2 – аb + b 2)
2. Формулы сокращенного умножения :
(а + b) 2 =а 2 + 2аb + b 2
(а – b) 2 = а 2 – 2аb + b 2
(а + b) 3 =а 3 + 3а 2 b + 3аb 2 + b 3
(а – b) 3 = а 3 – 3а 2 b + 3аb 2 – b 3
3. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называетсямедианой треугольника.
4. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называетсявысотой треугольника.
5. В равнобедренном треугольнике углы при основании равны.
6. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
7. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
8. Отрезок, соединяющий центр с какой-либо точкой окружности называетсярадиусом окружности.
9. Отрезок, соединяющий две точки окружности, называетсяеехордой.
Хорда, проходящая через центр окружности, называетсядиаметром
10.Прямой пропорциональностью у = кх , где х – независимая переменная, к – не равное нулю число (к – коэффициент пропорциональности).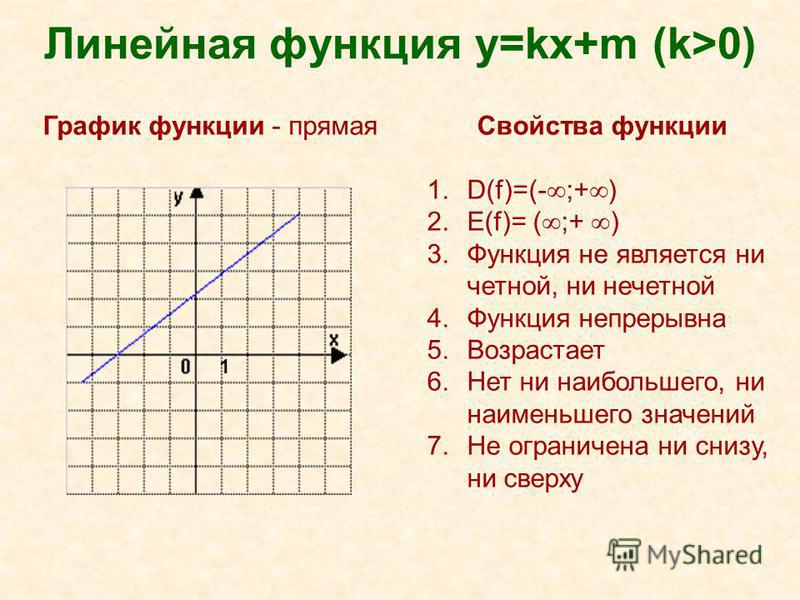
11. График прямой пропорциональности – это прямая, проходящая через начало координат.
12. Линейной функцией называется функция, которую можно задать формулой у = кх + b , где х – независимая переменная, к и b – некоторые числа.
13. График линейной функции – это прямая.
14 х – аргумент функции (независимая переменная)
у – значение функции (зависимая переменная)
15. При b=0 функция принимает вид y=kx , ее график проходит через начало координат.
При k=0 функция принимает вид y=b , ее график — горизонтальная прямая, проходящая через точку (0;b ).
Соответствие между графиками линейной функции и знаками коэффициентов k и b
1.Две прямые на плоскости называются параллельными, если они не пересекаются.
Линейная функция. Теория
Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓
x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½
x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими.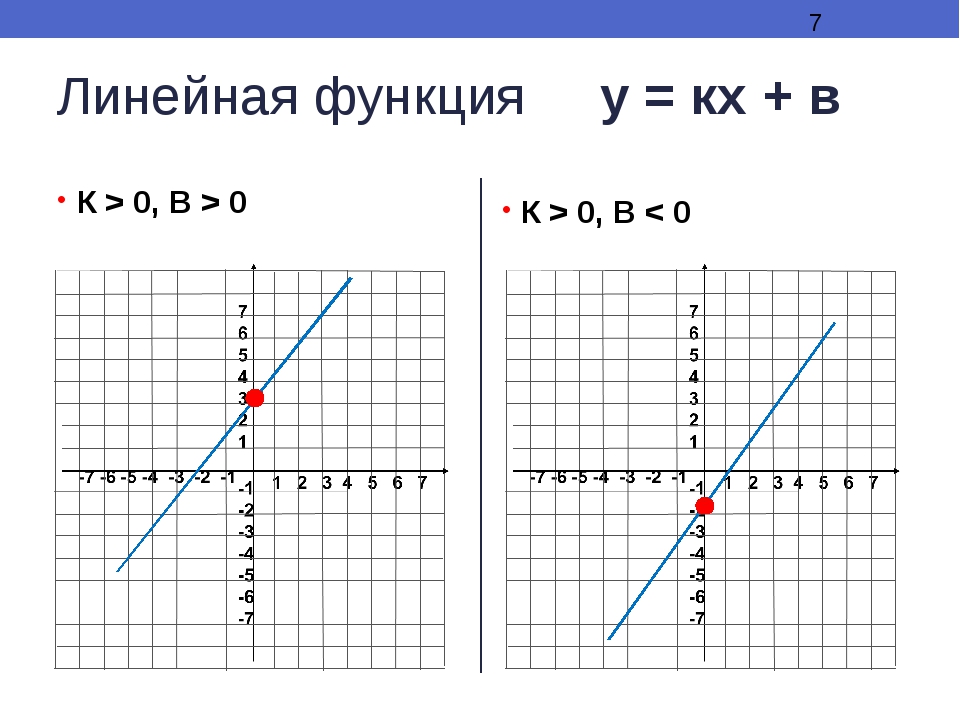 Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0
Если k>0 и b>0 , то график функции y=kx+b имеет вид:
Если k>0 и b , то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2
5. Условие перепендикулярности двух прямых:
Условие перепендикулярности двух прямых:
График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2
6. Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0 , получим постоянную функцию y = b , график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b) .
Если b = 0 , то получим функцию y = kx , которая является прямой пропорциональностью.
b – длина отрезка , который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0 , то область значений линейной функции есть вся вещественная ось. Если k = 0 , то область значений линейной функции состоит из числа b ;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b .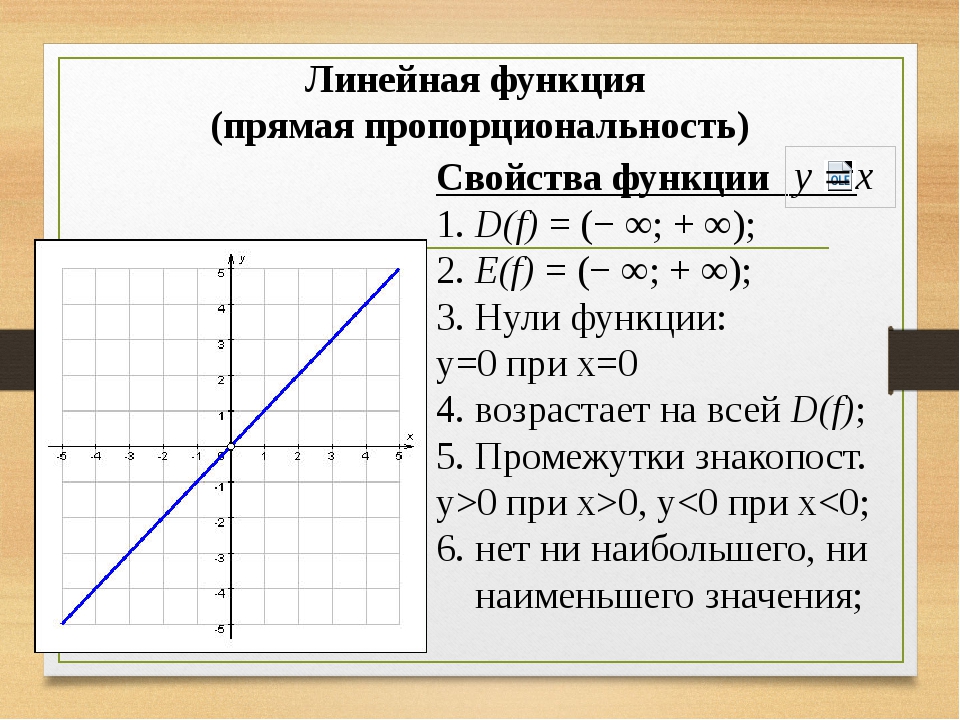
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k , следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b , следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0 , то функция y = 0 обращается в ноль при любом значении переменной х . Если b ≠ 0 и k = 0 , то функция y = b не обращается в ноль ни при каких значениях переменной х .
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞) ,
y = kx + b – отрицательна при x из (-∞; -b/k) .
b) k
y = kx + b – положительна при x из (-∞; -b/k) ,
y = kx + b – отрицательна при x из (-b/k; +∞) .
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k .
k > 0 , следовательно y = kx + b возрастает на всей области определения,
k , следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой
достаточно знать две точки. Положение прямой на координатной плоскости
зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.
Ниже приведена таблица, которая наглядно это иллюстрирует.
Линейной функцией называется
функция, заданная формулой y = kx + b , где k и b — любые действительные числа.
Графиком линейной функции является прямая.
Если k = 0, то функция y = b называется постоянной. Её графиком, является прямая, параллельная оси Ox .
Если b = 0, то формула y = kx задает прямо пропорциональную зависимость. Графиком такой функции является прямая, проходящая через начало координат.
Верно и обратное — любая прямая, не параллельная оси Oy , является графиком некоторой линейной функции.
Число k называется угловым коэффициентом прямой , оно равно тангенсу угла между прямой и положительным направлением оси Ox .
На рисунке — угол α.
Построить график
линейной функции очень легко.
Положение любой прямой однозначно определяется заданием двух её точек. Поэтому линейная функция вполне определяется заданием её значений для двух значений аргумента.
Например,
Если Вы являетесь моим учеником или , то можете поработать с интерактивными версиями этих графиков.
Свойства линейной функции
при k ≠ 0, b ≠ 0.
1) Область определения функции — множество всех действительных чисел: R или (−∞; ∞).
2) Функция y = kx + b ни четна, ни нечетна.
3) При k > 0 функция монотонно возрастает, а при k
Упражнение:
На рисунке представлены 4 прямые линии. Могут ли они являться графиками функций? Если да, то определите каких.
Посмотреть ответ.
Прямые, наклоненные к оси абсцисс под острым или тупым углом — графики линейной функции общего вида: y = kx + b. Параметр b легко определить по точке пересечения линии с осью ординат (Oy ). Параметр k определяется построеним по клеточкам треугольника, содержащего угол α для острых углов или смежный с ним — для тупых. 2 $, дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки $ (1,1) $, $ (2,4) $ и (3,9) $, которые не находятся на прямой линии .
2 $, дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки $ (1,1) $, $ (2,4) $ и (3,9) $, которые не находятся на прямой линии .
Запятая указывает на то, что предложение «чей график представляет собой прямую линию» не является существенным для определения словосочетания «линейная функция». Это превращает предложение в дополнительную информацию: «Кстати, знаете ли вы, что график линейной функции представляет собой прямую линию?» Этот факт часто представляется очевидным; в конце концов, если вы начертите график или построите его с помощью графической утилиты, он определенно будет выглядеть как прямая линия.
Когда я спросил будущих учителей, почему это так, я получил примерно такие ответы:
Мы знаем, что линейная функция имеет постоянную скорость изменения $ m $.Если вы перейдете на 1 на графике, вы всегда подниметесь на $ m $, например:
Итак, график похож на лестницу. Он всегда идет вверх ступенями одинакового размера, так что это прямая линия.
Это нормально. Он определяет определяющее свойство линейной функции — то, что она имеет постоянную скорость изменения — и связывает это свойство с геометрической особенностью графика. Но это «Вот, смотри!» доказательство. В конце концов, показывает, что что-то истинно, а не показывает , почему истинно.То есть это не доказательство.
Тем не менее, переход к геометрическому свойству линейных функций — это шаг в правильном направлении, потому что он фокусирует наши умы на основной концепции. Все мы знаем, что любые две точки лежат на одной линии, а три точки могут не лежать. Что такого особенного в трех точках на графике линейной функции, из которого следует, что они должны лежать на прямой линии?
Линия от $ A $ до $ B $ до $ C $ пунктирна, потому что мы еще не знаем, что это линия
Поскольку линейная функция имеет постоянную скорость изменения, наклон между любыми двумя из трех точек $ A $, $ B $ и $ C $ одинаков.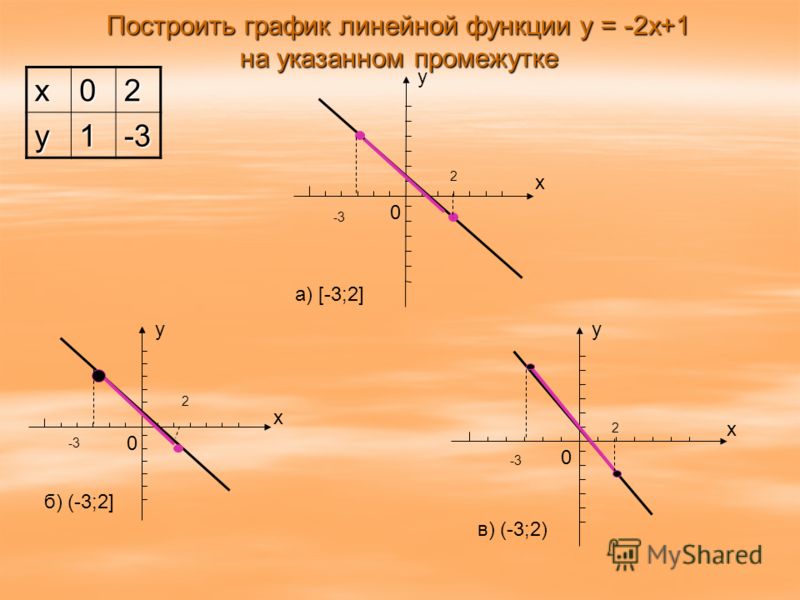 Итак, $ | BP | / | AP | = | CQ | / | AQ | $, что означает наличие масштабного фактора $ k = | AQ | / | AP | = | CQ | / | BP | $, так что расширение с центром $ A $ и масштабным фактором $ k $ переводит $ P $ в $ Q $, а вертикальный отрезок $ BP $ переводит в вертикальный отрезок на основе $ Q $ той же длины, что и $ CQ $. Это означает, что это должно занять от $ B $ до $ C $.
Итак, $ | BP | / | AP | = | CQ | / | AQ | $, что означает наличие масштабного фактора $ k = | AQ | / | AP | = | CQ | / | BP | $, так что расширение с центром $ A $ и масштабным фактором $ k $ переводит $ P $ в $ Q $, а вертикальный отрезок $ BP $ переводит в вертикальный отрезок на основе $ Q $ той же длины, что и $ CQ $. Это означает, что это должно занять от $ B $ до $ C $.
Но (барабанная дробь) это означает, что есть расширение с центром $ A $, которое переводит $ B $ в $ C $. Расширения всегда принимают точки на луче от центра к другим точкам того же луча.Итак, $ A $, $ B $ и $ C $ лежат на одной линии.
Я действительно не ожидаю, что студенты получат все это, по крайней мере, не сразу. Я был бы счастлив, если бы они поняли, что здесь играет роль геометрический факт; что видеть не всегда означает верить.
Уильям МакКаллум
Билл МакКаллум, основатель «Иллюстративной математики», является заслуженным профессором математики Университета Аризоны.Он работал как в области математических исследований, в области теории чисел и арифметической алгебраической геометрии, так и в области математического образования, писал учебники и консультировал исследователей и политиков. Он является одним из основателей Гарвардского консорциума по исчислению и ведущим автором его учебников по алгебре и многомерному исчислению. В 2009–2010 годах он был одним из ведущих авторов Общих государственных стандартов по математике. Он имеет докторскую степень по математике Гарвардского университета и степень бакалавра наук. из Университета Нового Южного Уэльса.
Linear Equations — Бесплатная справка по математике
Простое определение линейного уравнения:
Уравнение, образующее прямую линию на графике.
Точнее, линейное уравнение — это уравнение, которое зависит только от констант и переменной в первой степени. Например, \ (y = 6x + 2 \) является линейным, потому что у него нет квадратов, кубов, квадратных корней, синусов и т. Д. Линейными уравнениями всегда можно манипулировать, чтобы они приняли такую форму:
$$ ax + b = 0 $$Вы не всегда увидите линейные уравнения, написанные именно так, но имейте в виду, что мы можем манипулировать уравнениями, чтобы при необходимости придать им определенную форму.
Линейные уравнения часто записываются с более чем одной переменной, обычно с x и y. В таких уравнениях будет много возможных комбинаций x и y, которые работают. Когда эти точки (известные как пары координат) нанесены на ось x-y, они образуют прямую линию. Давайте посмотрим на это графически ниже. Два нарисованных уравнения линейны. Обратите внимание, что одно уравнение имеет форму \ (y = 3 \) (оно зависит только от константы 3), а другое уравнение — \ (y = 0,75x — 0,5 \) (линейный член и постоянный ).
Как узнать, линейно ли уравнение?
Включает ли уравнение (или функция) какие-либо члены в квадрате? Как насчет других членов с показателем, отличным от 1 (или, технически, нуля)? Если функция не имеет членов с порядком выше 1 (причудливый способ обозначить показатель степени), то она линейна!
Что делать, если у него есть функция журнала или триггера и т. Д.?
Это нелинейные члены. Просто они не являются константами (обычными числами) или переменными с показателем степени 1, поэтому функция не является линейной.Если бы мы могли записать sin (x) или log (x) как нечто линейное, например \ (2x + 3 \), то мы бы сделали это вместо использования сложных нелинейных функций, таких как синус и логарифм! Конечно, если вы еще не рассмотрели эти концепции в своем классе, даже не беспокойтесь об этом.
Итак, как мне решить линейное уравнение?
Некоторые линейные уравнения действительно очень легко решить.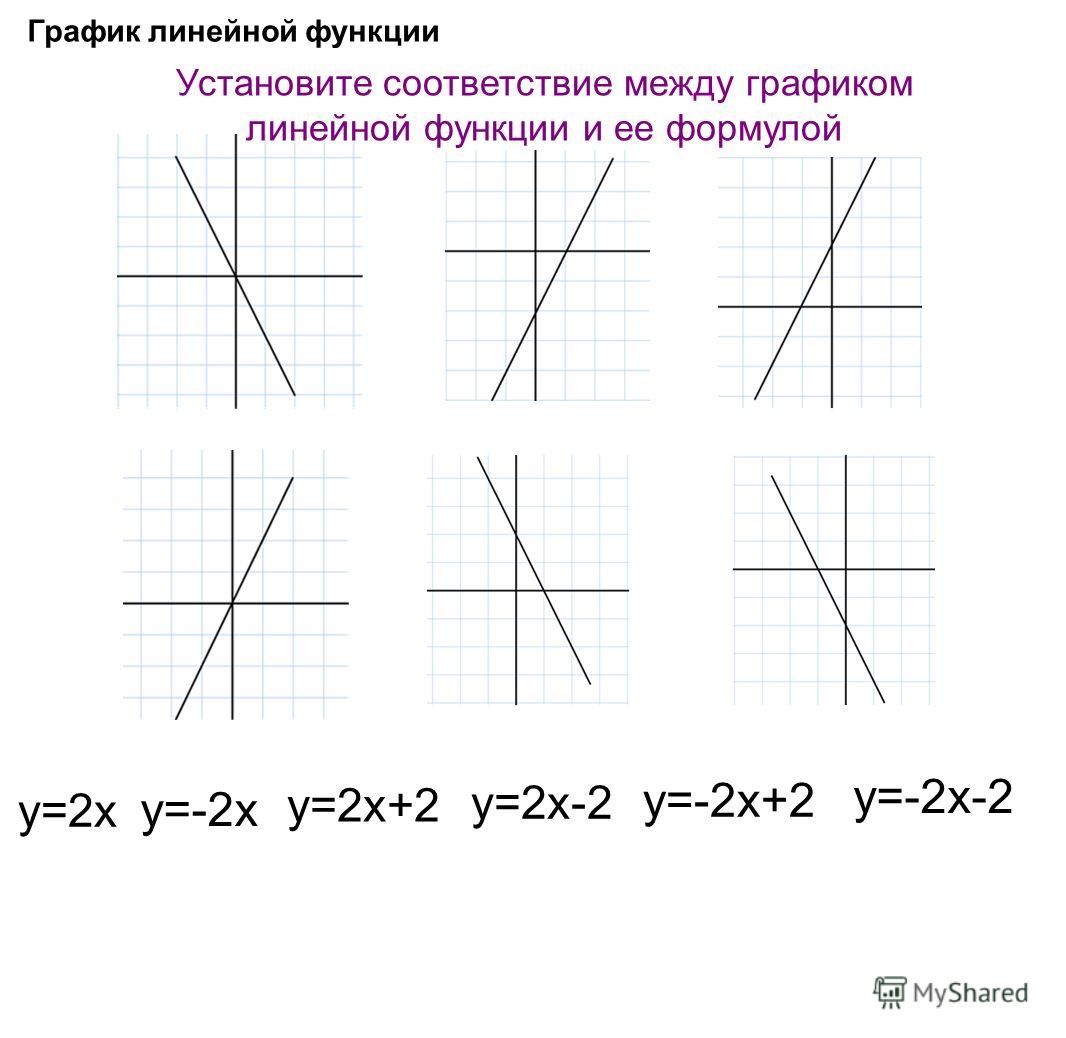 А что насчет этого:
А что насчет этого:
Это линейное уравнение, и оно уже решено относительно y! Это просто … здесь нечего делать.Но этот довольно тривиальный пример действительно показывает нам, что линейные уравнения могут быть довольно простыми, а также показывает нам нашу цель: переписать уравнение так, чтобы переменная, которую мы решаем, находилась с одной стороны, а все остальное — с другой.
Сделаем крошечный шаг вперед:
$$ y + 2 = 4 $$В этом уравнении мы просто должны вычесть 2 из обеих частей, чтобы преобразовать наше уравнение в решенную форму с y = 2. Решение любого линейного уравнения — это просто вопрос выполнения операций по обе стороны от знака равенства до тех пор, пока уравнение не приобретет желаемую форму (обычно решается для одной переменной, например X или Y).Шаги подробно показаны ниже:
$$ y + 2 = 4 $$ $$ y + 2-2 = 4-2 $$ $$ y + 0 = 2 $$ $$ y = 2 $$А как насчет более сложных уравнений?
К счастью, с линейными уравнениями шаги всегда относительно просты. Нет единого способа сделать это, и со временем вы сможете продумывать линейное уравнение, не записывая каждый шаг. Попробуйте следующий подход для решения уравнений и посмотрите, работает ли он для вас:
- Собирать одинаковые термины — это означает собрать все x вместе, все y вместе и все обычные числа (известные как константы) и сложить их по отдельности.Например, выражение \ (4x + 2y + 3x-5 + 10 \) превращается в \ (7x + 2y + 5 \). Помните, что вы можете складывать, вычитать, умножать или делить, если вы делаете это с обеими сторонами уравнения.
- Выделите переменную, которую вы хотите решить — Если проблема требует от вас решения для y, вам нужно получить y с одной стороны от знака равенства, а все остальные вещи с другой стороны. Здесь вы можете перейти от \ (2y — 6 = 4 \) к \ (2y = 10 \).
- Удалите все коэффициенты, оставшиеся в этой переменной — если ваш ответ после шага 2 выглядит как \ (5y = 7x — 10 \), просто разделите обе стороны на 5, чтобы получить \ (y = \ frac {7x} {5} — \ гидроразрыв {10} {2} \).

- Проверьте свой ответ. Кажется, ваш ответ имеет смысл? Сможете ли вы подставить свой ответ в исходное уравнение, и оно все еще будет работать?
Давайте рассмотрим несколько примеров решения линейных уравнений.
Следует иметь в виду, что вы не можете всегда решать уравнение к чему-то определенному, например, y = 5. Совершенно нормально иметь y = x + 5, и это просто означает, что y зависит от x. Фактически, для каждого значения x существует ровно одно значение y, и все они образуют точки, лежащие на прямой линии (как я показал в начале).
Пример 1:
Решить относительно y: \ (2y + 5 = 9 \)
Если вы снова замените y на 2 в исходной задаче, вы получите 9 = 9, так что это правильно!
Пример 2:
Решить относительно y: \ (2y-x = 4 + x + 3x \)
Пример 3:
Решить относительно y: \ (2x + 7 = \ frac {y + 6} {2} \)
Подводя итог
Помните, что линейные уравнения по своей сути просты — не пытайтесь слишком много обдумывать! Они состоят только из линейных членов (например, 3x, 2y, y / 2 и т. Д.) И констант.Если вы застряли, пытаясь упростить или решить проблему, просто не забывайте делать это шаг за шагом. Соберите похожие термины, объединив все свои переменные по отдельности, затем выделите переменную, которую вы хотите найти, и, наконец, выполните любые дополнительные математические вычисления, чтобы у вас осталось только «y =» или «x =» на одной стороне уравнения.
Линейные функции и прямые
6.2 — Линейные функции и прямые линии6.2 — Линейные функции и прямые
Линейные функции
Щелкните здесь, чтобы просмотреть функции.Линейные функции — самые простые из всех типов функций. Линейная функция принимает на вход число x и возвращает число m x + b как выход: m и b — постоянные. Проще говоря, x умножается на м (это называется масштабированием на коэффициент м ). а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:
а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:f ( x ) = м x + b .Если мы положим y = f ( x ), то это будет выглядеть так:
y = м x + b .Это называется уравнением прямой линии , потому что если мы построим точки, которые удовлетворяют этому уравнению на графике y против x , тогда, как мы увидим ниже, все точки лежат на прямой линии.
Типичное использование линейной функции — преобразование одного набора единиц в другой. Простой пример: если i — это расстояние, измеренное в дюймах, а c — то же самое. расстояние в сантиметрах; тогда c = 2,54 i . Это просто масштабирование. Более сложный пример: если c — температура измеряется в градусах Цельсия и f то же самое температура измеряется в градусах Фаренгейта; тогда f = 1.8 с + 32. Это масштабирование и сдвиг.
Уравнение прямой
В разделе 6.1 мы ввели декартову плоскость с осью x , нарисованной горизонтально, и осью y , нарисованной вертикально. Предположим, что m и b — постоянные. Мы хотим построить график линейной функции:y = м x + b ,на этой плоскости и покажите, что график представляет собой прямую линию.Для этого составляем следующую таблицу значений из y (то есть выражения м x + b ) по сравнению с x :
Обратите внимание на следующее:
- Каждая строка таблицы показывает точку на графике.
- В одной из строк указано, что когда x = 0, тогда y = b . Таким образом, точка (0, b )
это точка на графике. Поскольку эта точка лежит на оси y ,
число b называется точкой пересечения y .

- При переходе от одной строки таблицы к следующей, значение x увеличивается на 1, а значение y увеличивается на m . Потому что увеличение устойчиво, точки должны лежать на прямой , а не на какой-либо другой кривой.
- Более крупный м , тем быстрее увеличивается y . Если m отрицательное, то значение y фактически уменьшается .Номер м известен как склон .
- x не обязательно должно быть целым числом — это может быть любое действительное число. Так как вещественные числа плотные, точки на графике бесконечно близко друг к другу и образуют сплошную линию (т.е. без зазоров).
| Вывод: Уравнение y = м x + b ,где m и b — константы, это уравнение прямой . м называется уклоном и b называется перехват y . Эта форма уравнения называется пересечением угла наклона . форма . Возможны и другие формы; Нажмите здесь, чтобы увидеть их. |
Нахождение уравнения прямой
Учитывая график прямой, есть несколько способов найти ее уравнение.
Метод 1: Этот метод работает, только если видна точка пересечения y .
- Найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Получите b из просмотра пересечения y графика.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 2: Этот метод работает, даже если точка пересечения y не видна.
- Как и в методе 1, найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Замените полученное число м на
уравнение y = m x + b .Также возьмите одну из точек, скажем ( x 1 , y 1 ),
и подставим его координаты в уравнение. Это дает:
y 1 = m x 1 + b
- Это может не выглядеть так, но это уравнение имеет только одну переменную, b , и вы легко можете решить эту проблему.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 3: Этот метод имеет то преимущество, что он использует только алгебру, а не геометрию, и может применяться к любому типу функции, а не только к прямой:
- Найдите две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), которые находятся на линии.
Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой, y = м x + b .Это дает:
y 1 = m x 1 + b
Аналогичным образом возьмем вторую точку ( x 2 , y 2 ) и подставляем его в уравнение прямой, y = м x + b . Это дает:y 2 = м x 2 + b
- Вместе эти два уравнения составляют систему двух уравнений с двумя неизвестными: m и b .
 Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:
Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:y 2 — y 1 = м x 2 — м x 1 ,
которое при решении для м дает то же уравнение, что и в двух других методах, а именно: - Найти b обратной подстановкой.Чтобы быть конкретным, замените номер, который вы полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b . Это может не выглядеть так, но это уравнение имеет только одну переменную, b , и вы легко можете решить эту проблему.
Пример: Воспользуйтесь методом 1, чтобы найти уравнение прямой на графике справа.
Решение: Две точки на этой линии: ( x 1 , y 1 ) = (0, 15) и ( x 2 , y 2 ) = (3, 0). Подставляя эти координаты в формулу наклона, получаем
= -5.При осмотре перехватчик y
б = 15.Подставляя эти два значения для m и b в уравнение прямой линии, y = м x + b , дает
y = −5 x + 15.
Пример: Воспользуйтесь методом 3, чтобы найти уравнение прямой на графике справа.
Решение: Две точки на этой линии — это (7, 15) и (1, 3).
Подставляем координаты точки (7, 15)
в уравнение прямой, y = m x + b ,
а затем проделайте то же самое с точкой (1, 3).
Это дает систему двух уравнений с двумя неизвестными: m и b .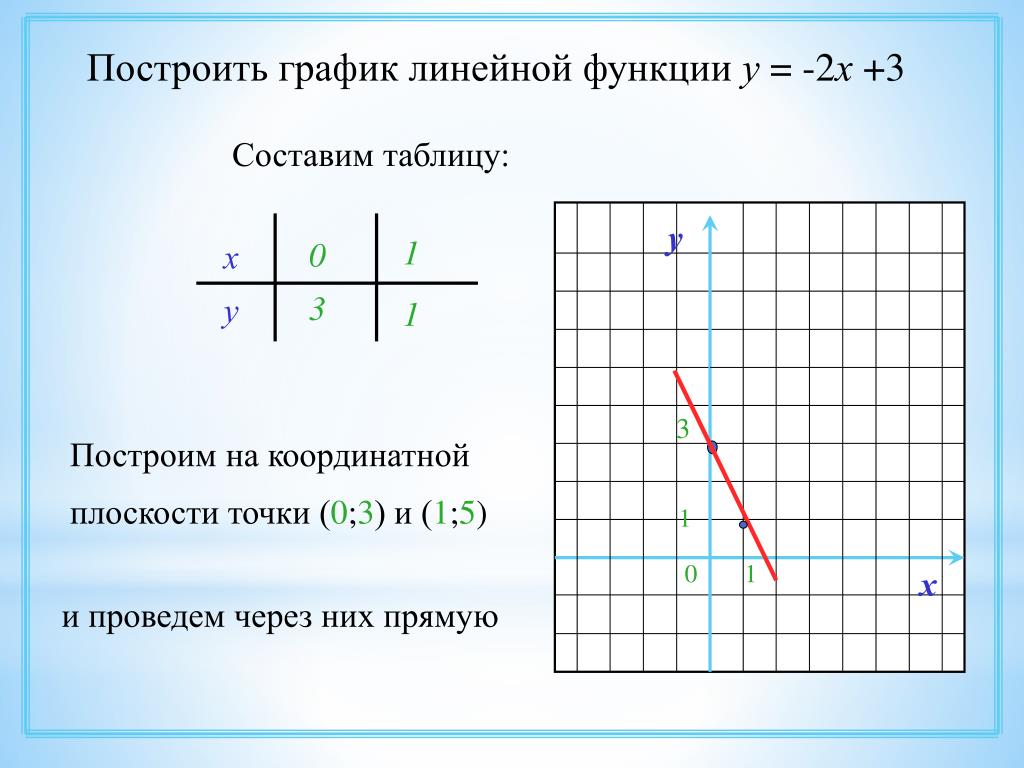 Неизвестный b может быть исключен путем вычитания уравнений:
Неизвестный b может быть исключен путем вычитания уравнений:
y = 2 x + 1.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Функция, обратная линейной функции — ChiliMath
Обратную линейную функцию найти намного проще по сравнению с другими видами функций, такими как квадратичные и рациональные. Причина в том, что область определения и диапазон линейной функции естественным образом охватывают все действительные числа, если область определения не ограничена.
Прежде чем я приведу пять (5) примеров, чтобы проиллюстрировать процедуру, я хочу показать вам, как связаны домен и диапазон данной функции и ее обратной функции.
Домен и Диапазон просто поменялись местами!
Примечания к диаграмме :
- Область определения исходной функции становится диапазоном обратной функции.
- Диапазон исходной функции становится областью определения обратной функции.
- Обычно используется буква \ large {\ color {blue} x} для домена и \ large {\ color {red} y} для диапазона.{- 1}} \ left (x \ right), чтобы получить обратную функцию.
- Иногда полезно использовать домен и диапазон исходной функции, чтобы определить правильную обратную функцию из двух возможных. Это случается, когда в конце вы получаете «плюс-минус».
- Линейное уравнение имеет только одну или две переменные.
- Никакая переменная в линейном уравнении не возводится в степень больше 1 или не используется в качестве знаменателя дроби.
- Когда вы находите пары значений, которые делают линейное уравнение истинным, и наносите эти пары на координатную сетку, все точки лежат на одной линии. График линейного уравнения представляет собой прямую линию.
- Линейная связь (или линейная связь) — это статистический термин, используемый для описания прямолинейной связи между двумя переменными.
- Линейные отношения могут быть выражены либо в графическом формате, либо в виде математического уравнения вида y = mx + b.
- Линейные отношения довольно часто встречаются в повседневной жизни.

Примеры того, как найти обратную линейную функцию
Пример 1: Найти обратную линейную функцию
Эта функция работает хорошо, поскольку домен и диапазон являются действительными числами. Это гарантирует, что его обратная функция тоже должна быть функцией. Возможно, вы знакомы с тестом горизонтальной линии, который гарантирует, что он будет иметь инверсию всякий раз, когда ни одна горизонтальная линия не пересекает или пересекает график более одного раза.
Это гарантирует, что его обратная функция тоже должна быть функцией. Возможно, вы знакомы с тестом горизонтальной линии, который гарантирует, что он будет иметь инверсию всякий раз, когда ни одна горизонтальная линия не пересекает или пересекает график более одного раза.
Используйте приведенные выше ключевые шаги в качестве руководства для решения обратной функции:
Это было легко!
Пример 2: Найти обратную линейную функцию
В конце решения я хочу сделать знаменатель положительным, чтобы оно выглядело «хорошо».Я сделал это, умножив числитель и знаменатель на -1.
Пример 3: Найти обратную линейную функцию
Некоторые студенты могут рассматривать это как рациональную функцию, потому что уравнение содержит некоторые рациональные выражения. Пусть вас не смущают дроби. Да, в нем есть дроби, но в знаменателе нет переменных. Это делает его просто обычной линейной функцией.
Чтобы решить эту проблему, я должен избавиться от знаменателя.Я добьюсь этого, умножив обе части уравнения на их наименьший общий знаменатель (LCD).
Как показано выше, вы можете написать окончательные ответы двумя способами. Один с одним знаменателем, а другой разложен на частичные дроби.
Пример 4: Найдите обратную линейную функцию, указанную ниже, и укажите ее область определения и диапазон.
Это «нормальная» линейная функция, однако с ограниченной областью. Допустимые значения x начинаются с x = 2 и увеличиваются до положительной бесконечности.Диапазон можно определить с помощью его графика. Помните, что диапазон — это набор всех значений y, когда допустимые значения x (домен) подставляются в функцию.
Обратите особое внимание на то, как домен и диапазон определяются с помощью его графика.
Найти инверсию этой функции очень просто. Но имейте в виду, как правильно описать область и диапазон обратной функции. Мы рассмотрели эту концепцию в начале этого раздела о замене домена и диапазона.
Всегда проверяйте домен и диапазон обратной функции, используя домен и диапазон оригинала. Они просто меняются местами.
Пример 5: Найдите обратную линейную функцию, указанную ниже, и укажите ее область определения и диапазон.
Первый шаг — построить график функции по оси xy. Четко обозначьте домен и диапазон.
Открытый кружок (незатененная точка) означает, что число в этой точке исключено. Если вам нужно освежить эту тему, посмотрите мой отдельный урок о решении линейных неравенств.
Во-вторых, найдите обратную алгебру, используя предложенные шаги. Убедитесь, что вы указали правильный домен и диапазон обратной функции.
Переменная x в исходном уравнении имеет коэффициент -1. Следите за этим, решая обратное.
Я надеюсь, что вы получите некоторые основные идеи о том, как найти обратную линейную функцию . Я рекомендую вам просмотреть соответствующие уроки о том, как находить инверсии других типов функций.
Практика с рабочими листами
Возможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Обратная экспоненциальная функция
Обратная логарифмическая функция
Обратная квадратичная функция
Обратная рациональная функция
Функция, обратная квадратному корню
Обучение линейным уравнениям в математике
Для многих учеников 8-х классов и выше числа и формы, которые они узнали, действительно начинают сходиться, когда они составляют и решают линейные уравнения.Эта тема объединяет идеи об алгебре, геометрии и функциях, и многим детям — и взрослым может быть сложно осмыслить. В этой статье объясняется, что такое линейное уравнение, и рассматриваются различные примеры. Затем он предлагает учащимся идеи уроков по введению и развитию концепции линейных уравнений с одной переменной.
Что такое линейное уравнение?
Как и любое другое уравнение, линейное уравнение состоит из двух равных друг другу выражений.Есть некоторые ключевые особенности, общие для всех линейных уравнений:
Линейное уравнение с двумя переменными можно описать как линейное соотношение между x и y , то есть двумя переменными, в которых значение одной из них (обычно y ) зависит от значение другого (обычно x ).В этом случае x является независимой переменной, а y зависит от нее, поэтому y называется зависимой переменной.
Независимая переменная, помеченная как x , обычно отображается по горизонтальной оси. Большинство линейных уравнений — это функции. Другими словами, для каждого значения x существует только одно соответствующее значение y . Когда вы присваиваете значение независимой переменной x , вы можете вычислить значение зависимой переменной y .Затем вы можете нанести точки, названные каждой парой ( x , y ), на координатной сетке.
Описание линейных отношений
Студенты уже должны знать, что любые две точки определяют линию. Таким образом, для построения графика линейного уравнения на самом деле требуется всего лишь найти две пары значений и провести линию через точки, которые они описывают. Все остальные точки на линии предоставят значения x и y , которые удовлетворяют уравнению.
Графики линейных уравнений всегда представляют собой линии. Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — это время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).
Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — это время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).
Как выглядит линейное уравнение?
Пример 1: расстояние = скорость × времяВ этом уравнении для любой заданной постоянной скорости соотношение между расстоянием и временем будет линейным.Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этой взаимосвязи будут отображаться только точки в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо. Линии, идущие в этом направлении, имеют положительный наклон . Положительный наклон указывает, что значения на обеих осях увеличиваются слева направо.
Определение линейной связи
Что такое линейная связь?
Линейная связь (или линейная связь) — это статистический термин, используемый для описания прямолинейной связи между двумя переменными.Линейные отношения могут быть выражены либо в графическом формате, где переменная и константа связаны прямой линией, либо в математическом формате, где независимая переменная умножается на коэффициент наклона, добавляемый на константу, которая определяет зависимую переменную.
Линейная зависимость может быть противопоставлена полиномиальной или нелинейной (криволинейной) зависимости.
Ключевые выводы
Линейное уравнение:
Математически линейная зависимость — это такая зависимость, которая удовлетворяет уравнению:
Взаимодействие с другими людьми y знак равно м Икс + б где: м знак равно склон б знак равно y-перехват \ begin {align} & y = mx + b \\ & \ textbf {где:} \\ & m = \ text {slope} \\ & b = \ text {y-intercept} \\ \ end {align} Y = mx + b, где: m = наклон b = точка пересечения с y
В этом уравнении «x» и «y» — две переменные, которые связаны параметрами «m» и «b».Графически y = mx + b отображается в плоскости x-y как линия с наклоном «m» и точкой пересечения оси y «b». Y-точка пересечения «b» — это просто значение «y», когда x = 0. Наклон «m» рассчитывается из любых двух отдельных точек (x 1 , y 1 ) и (x 2 , y 2 ) как:
Взаимодействие с другими людьми м знак равно ( y 2 — y 1 ) ( Икс 2 — Икс 1 ) m = \ frac {(y_2 — y_1)} {(x_2 — x_1)} т = (х2 — х1) (у2 — у1)
О чем вам говорят линейные отношения?
Существует три набора необходимых критериев, которым должно соответствовать уравнение, чтобы считаться линейным: уравнение, выражающее линейную зависимость, не может состоять более чем из двух переменных, все переменные в уравнении должны быть в первой степени. , и уравнение должно быть построено в виде прямой линии.
Обычно используемая линейная зависимость — это корреляция, которая описывает, насколько близко к линейному изменению одна переменная изменяется по сравнению с изменениями другой переменной.
В эконометрике линейная регрессия — часто используемый метод построения линейных отношений для объяснения различных явлений. Он обычно используется для экстраполяции событий из прошлого, чтобы делать прогнозы на будущее. Однако не все отношения линейны. Некоторые данные описывают изогнутые отношения (например, полиномиальные отношения), в то время как другие данные нельзя параметризовать.
Линейные функции
Математически аналогично линейной зависимости концепция линейной функции. В одной переменной линейную функцию можно записать следующим образом:
Взаимодействие с другими людьми ж ( Икс ) знак равно м Икс + б где: м знак равно склон б знак равно y-перехват \ begin {align} & f (x) = mx + b \\ & \ textbf {где:} \\ & m = \ text {slope} \\ & b = \ text {y-intercept} \\ \ end {align} F (x) = mx + b, где: m = наклон b = точка пересечения с y
Это идентично данной формуле для линейной зависимости, за исключением того, что символ f (x) используется вместо y. Эта замена сделана, чтобы подчеркнуть значение того, что x отображается в f (x), тогда как использование y просто указывает, что x и y — две величины, связанные между собой A и B.
При изучении линейной алгебры свойства линейных функций тщательно изучаются и становятся строгими. Учитывая скаляр C и два вектора A и B из R N , наиболее общее определение линейной функции гласит, что: c × ж ( А + B ) знак равно c × ж ( А ) + c × ж ( B ) с \ умножить на f (A + B) = c \ умножить на f (A) + c \ умножить на f (B) c × f (A + B) = c × f (A) + c × f (B)
Примеры линейных отношений
Пример 1
Линейные отношения довольно распространены в повседневной жизни.Возьмем, к примеру, понятие скорости. Формула, которую мы используем для расчета скорости, выглядит следующим образом: показатель скорости — это расстояние, пройденное с течением времени. Если кто-то в белом минивэне Chrysler Town and Country 2007 года выпуска путешествует между Сакраменто и Мэрисвиллем в Калифорнии, протяженностью 41,3 мили по шоссе 99, и полное путешествие занимает 40 минут, то он ехал со скоростью чуть ниже 60 миль в час. Взаимодействие с другими людьми
Хотя в этом уравнении более двух переменных, это все еще линейное уравнение, потому что одна из переменных всегда будет постоянной (расстояние).
Пример 2
Линейную зависимость также можно найти в уравнении: расстояние = скорость x время. Поскольку расстояние является положительным числом (в большинстве случаев), эта линейная зависимость будет выражена в верхнем правом квадранте графика с осями X и Y.
Если велосипед, рассчитанный на двоих, ехал со скоростью 30 миль в час в течение 20 часов, в конечном итоге велосипедист проехал 600 миль. Графически представленная расстоянием по оси Y и временем по оси X, линия, отслеживающая расстояние за эти 20 часов, будет проходить прямо от точки схождения осей X и Y.
Пример 3
Чтобы преобразовать Цельсий в Фаренгейт или Фаренгейт в Цельсий, вы должны использовать приведенные ниже уравнения. Эти уравнения выражают линейную зависимость на графике:
Взаимодействие с другими людьми ° C знак равно 5 9 ( ° F — 3 2 ) \ степень C = \ frac {5} {9} (\ степень F — 32) ° С = 95 (° F − 32)
Взаимодействие с другими людьми ° F знак равно 9 5 ° C + 3 2 \ степень F = \ frac {9} {5} \ степень C + 32 ° F = 59 ° C + 32
Пример 4
Предположим, что независимая переменная — это размер дома (измеренный в квадратных футах), который определяет рыночную цену дома (зависимая переменная), умноженная на коэффициент наклона 207.65, а затем добавляется к постоянному члену 10 500 долларов. Если площадь дома составляет 1250 квадратных метров, то рыночная стоимость дома составляет (1250 x 207,65) + 10 500 долларов США = 270 062,50 долларов США. Графически и математически это выглядит следующим образом:
Изображение Джули Банг © Investopedia 2019В этом примере, когда размер дома увеличивается, рыночная стоимость дома увеличивается линейно.
Некоторые линейные отношения между двумя объектами можно назвать «пропорциональными отношениями». Эти отношения выглядят как
Взаимодействие с другими людьми Y знак равно k × Икс где: k знак равно постоянный Y , Икс знак равно пропорциональные количества \ begin {выровнены} & Y = k \ times X \\ & \ textbf {где:} \\ & k = \ text {constant} \\ & Y, X = \ text {пропорциональные величины} \\ \ end {выровнены} Y = k × X, где: k = постоянная Y, X = пропорциональные величины
При анализе поведенческих данных редко бывает идеальная линейная связь между переменными. Однако в данных можно найти линии тренда, которые образуют грубую версию линейной зависимости. Например, вы можете посмотреть на ежедневные продажи мороженого и дневную высокую температуру как на две действующие переменные на графике и найти грубую линейную зависимость между ними.
Однако в данных можно найти линии тренда, которые образуют грубую версию линейной зависимости. Например, вы можете посмотреть на ежедневные продажи мороженого и дневную высокую температуру как на две действующие переменные на графике и найти грубую линейную зависимость между ними.
Линейные и нелинейные уравнения
Пояснение:
Данное уравнение имеет вид y = 2x + 3.Поскольку уравнение имеет две переменные x и y, возьмем две случайные значения x и вычислить соответствующие значения y, подставив x в уравнение.
Возьмем x = 1 и x = –1.
х у
+1 2 (+1) + 3 = 5
–1 2 (–1) + 3 = 1
Теперь нанесем две точки (1,5) и (–1,1) на график, как показано на рисунке. ниже.
Теперь вы можете просто соединить эти две точки прямой линией, и это даст вам требуемый график данного уравнения.
Вы также можете изменить полученный график в виде прямой линии, взяв более двух точек.
и объединение их в качестве уравнения является линейным уравнением первой степени.Полный сюжет
график с использованием 5 точек (1,5) , (0,3) , (–1,1) , (–2, –1) , (–3, –3) показано ниже, которое представляет собой прямую линию, как и ожидалось.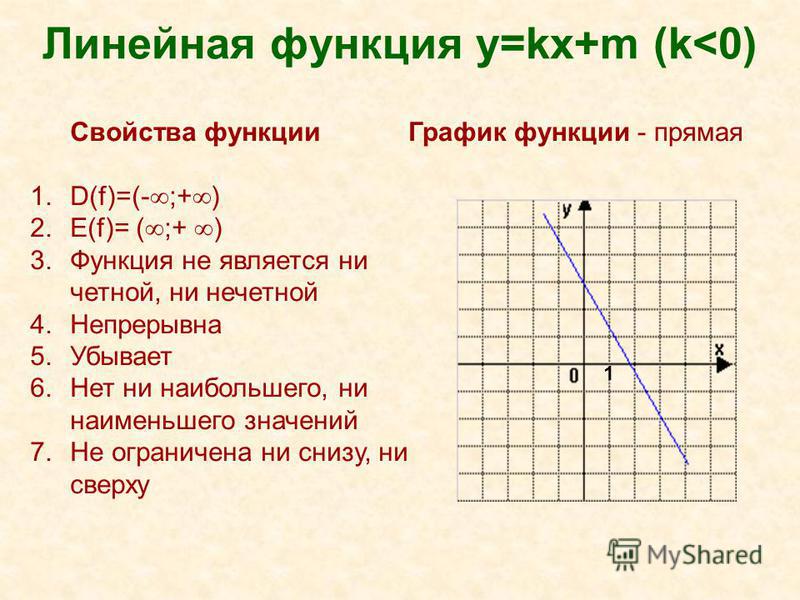
 6
6
 Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a. [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.
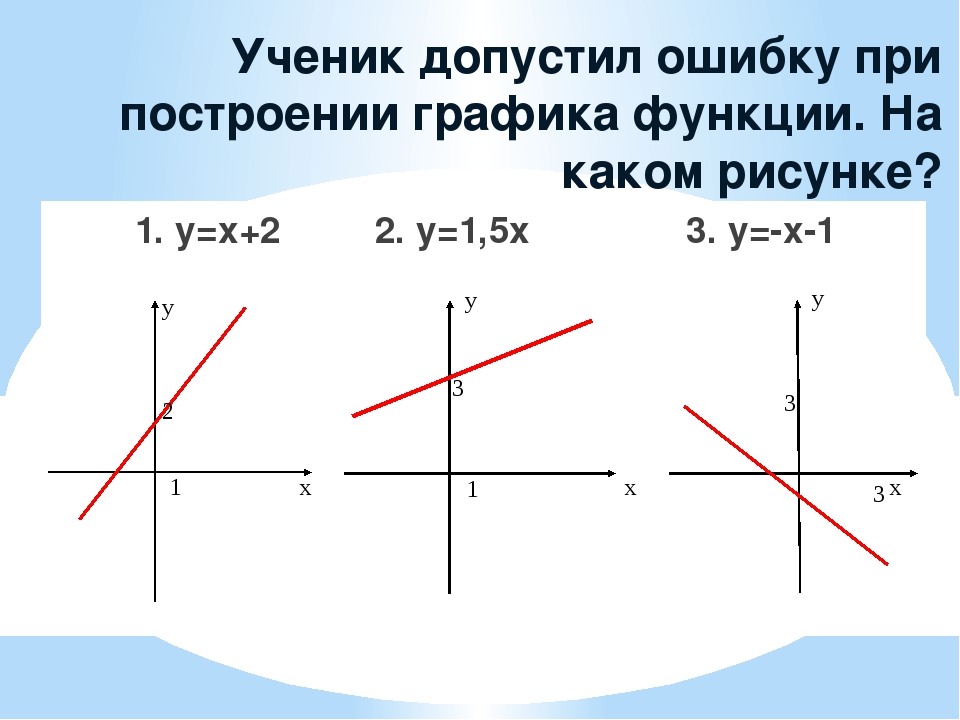
[+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.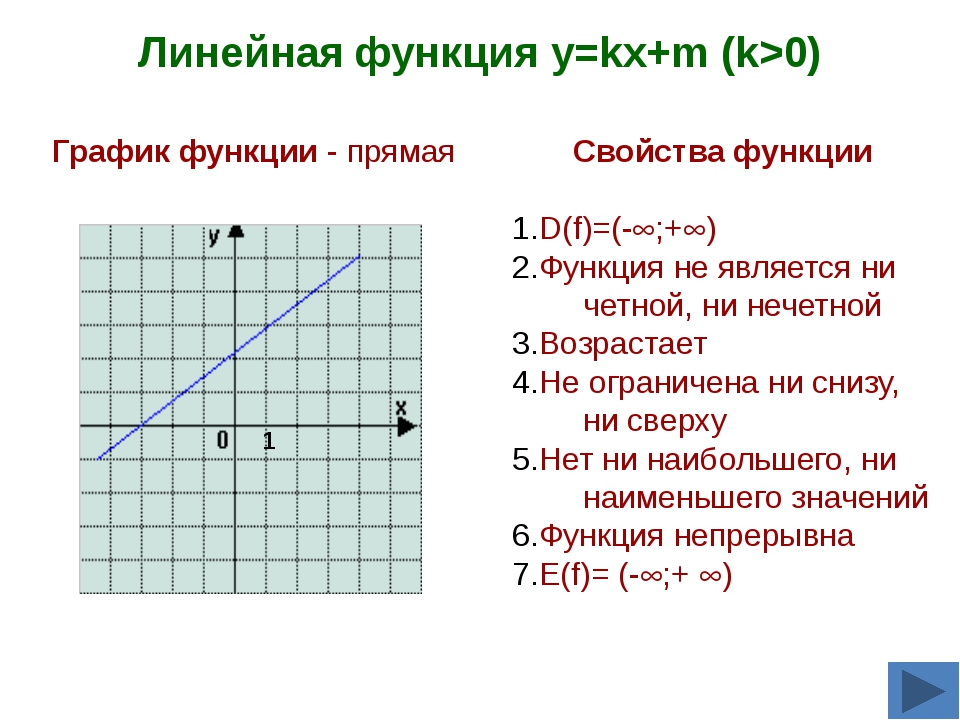
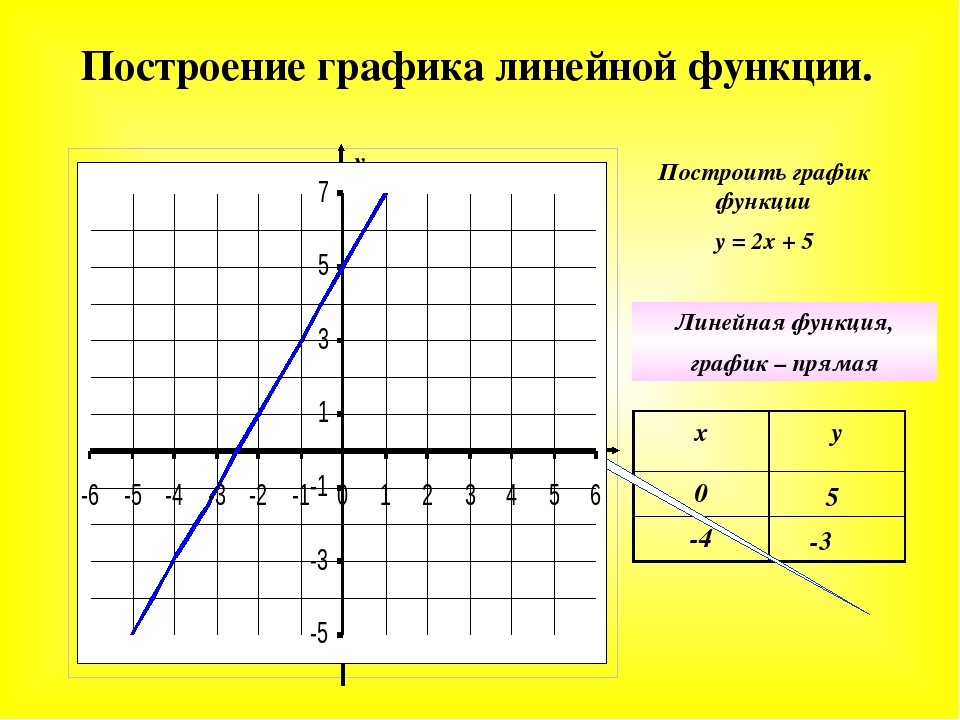
 Значит мы может полагать, что коэффициент bу обоих графиков равен 4.
Значит мы может полагать, что коэффициент bу обоих графиков равен 4.

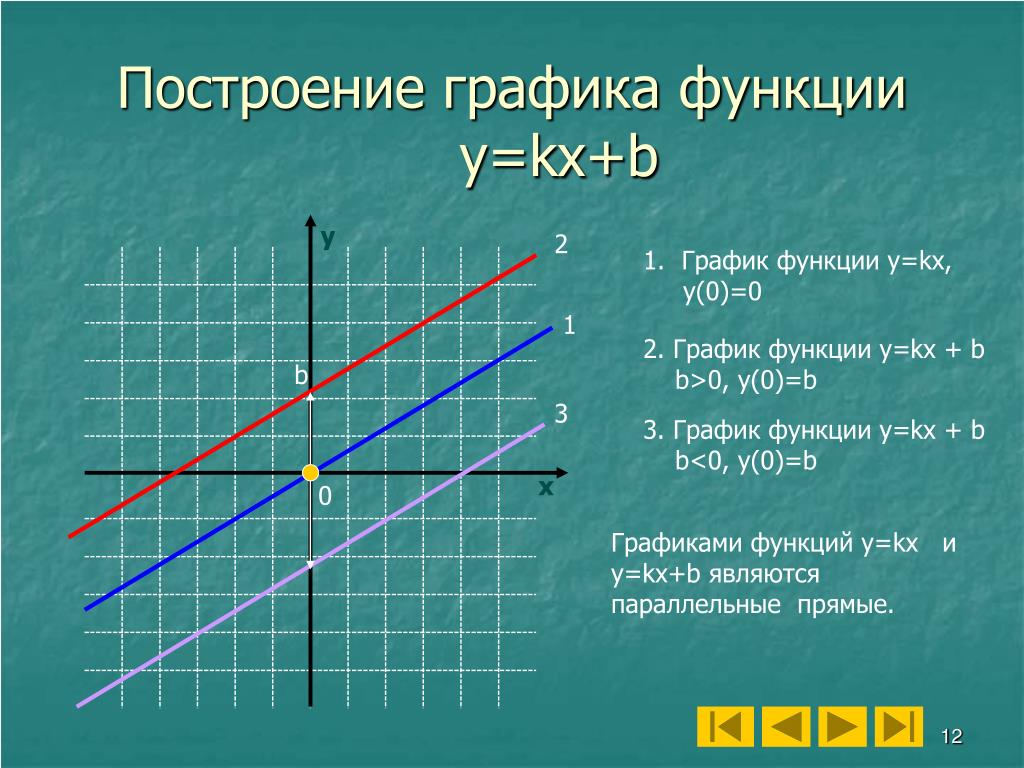
 Здесь k = 1.
Здесь k = 1. Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций».

 Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:
Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение: