Определение числовой функции, способы ее задания. Видеоурок. Алгебра 10 Класс
Пусть 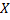 и
и 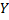 – это два множества.
– это два множества.
Функция 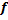 – это соответствие, которое каждому элементу из множества
– это соответствие, которое каждому элементу из множества  сопоставляет единственный элемент из множества
сопоставляет единственный элемент из множества 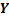 .
.
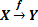
Рассмотрим такой пример.
Предположим, есть 4 самолета и 6 городов. Согласно расписанию первый и второй самолет летят в первый город; третий самолет летит в третий город; четвертый самолет летит в пятый город (см. Рис. 1).

Рис. 1. Множество 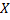 и
и 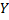
В этом примере множество самолетов – это множество 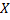 , множество городов – это множество
, множество городов – это множество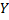
Если элемент 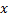 из множества
из множества 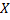 переходит в элемент
переходит в элемент 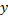 из множества
из множества 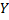 , то этот элемент
, то этот элемент 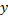 обозначается
обозначается 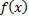
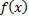 – это образ элемента
– это образ элемента 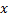 . Множество всех
. Множество всех 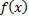 называется множеством значений функции (областью значений функции). В приведенном примере множество значений функции – это первый, третий и пятый город.
называется множеством значений функции (областью значений функции). В приведенном примере множество значений функции – это первый, третий и пятый город.
Множество 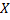 – это область определения функции.
– это область определения функции.
Рассмотрим еще несколько примеров.
1. Площади
Каждой замкнутой фигуре на плоскости сопоставляется неотрицательное число (ее площадь 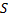

Рис. 2. Каждой фигуре сопоставляется неотрицательное число (площадь)
Множество 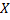 – это множество всех замкнутых фигур на плоскости. Множество
– это множество всех замкнутых фигур на плоскости. Множество 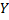 – все неотрицательные числа, то есть луч
– все неотрицательные числа, то есть луч 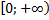
В данном случае множество значений функции совпадает с 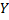 , то есть множество значений – это луч
, то есть множество значений – это луч 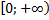 .
.
2. Движение
Движение – это такое преобразование плоскости, при котором сохраняются расстояния между всеми ее точками.
Множество 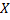 – это плоскость (множество всех точек плоскости),
– это плоскость (множество всех точек плоскости), 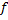
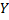 – та же самая плоскость (см. Рис. 3).
– та же самая плоскость (см. Рис. 3).
Рис. 3. Движение плоскости
Если даны числовое множество 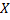 и правило
и правило 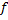 , позволяющее поставить в соответствие каждому элементу
, позволяющее поставить в соответствие каждому элементу 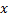
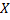 определенное число
определенное число 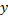 , то говорят, что задана функция
, то говорят, что задана функция 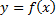 с областью определения
с областью определения 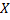 .
.Областью определения функции 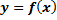 называют множество всех значений
называют множество всех значений 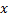
Множество всех значений функции 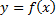 ,
, 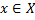 называют областью значения функции.
называют областью значения функции.
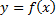 ,
, 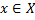
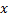 – независимая переменная (аргумент)
– независимая переменная (аргумент)
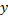 – зависимая переменная
– зависимая переменная – область определения функции
– область определения функции
 – область значений функции
– область значений функции
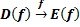
Графиком функции называется множество всех точек (на координатной плоскости) вида  , где
, где 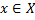
Пример
Задана функция 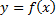 ,
, 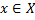 , которая показывает изменение температуры воздуха в зависимости от времени года (с весны до весны). Построим график этой функции.
, которая показывает изменение температуры воздуха в зависимости от времени года (с весны до весны). Построим график этой функции.
Независимая переменная 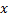 – это время; зависимая переменная
– это время; зависимая переменная 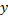 – это температура (см. Рис. 4).
– это температура (см. Рис. 4).
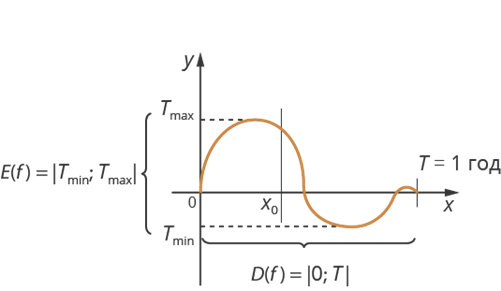
Рис. 4. График функции 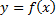 ,
, 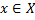
Любая вертикальная прямая 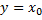 (если
(если 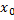 принадлежит области определения) пересекает график в единственной точке, так как согласно определению функции закон
принадлежит области определения) пересекает график в единственной точке, так как согласно определению функции закон 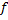 такой, что каждому значению аргумента соответствует только одно значение функции.
такой, что каждому значению аргумента соответствует только одно значение функции.
Область определения – это проекция графика функции на ось 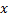 .
.
Область значения – это проекция графика функции на ось 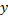 .
.
Функция, заданная аналитически, – это функция, которая задана формулами. Чем хорош аналитический способ задания функции? Тем, что, если у вас есть формула – вы знаете про функцию всё. Вы можете составить табличку. Построить график. Исследовать эту функцию полностью. Точно предсказать, где и как будет вести себя эта функция. Весь математический анализ стоит именно на таком способе задания функций.
Примеры:
1. 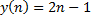 ,
, 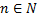 (все натуральные числа) – такая функция называется последовательностью.
(все натуральные числа) – такая функция называется последовательностью.
Построим график 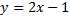 функции (см. Рис. 5). Это прямая, на которой лежат точки с координатами
функции (см. Рис. 5). Это прямая, на которой лежат точки с координатами 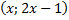 .
.
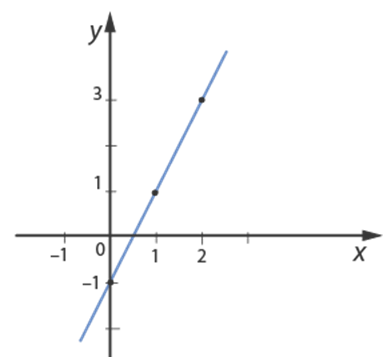
Рис. 5. График функции 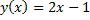
Все точки графика функции 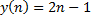 ,
, 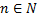 лежат на построенной прямой (некоторые из них отмечены на рис. 5). Например:
лежат на построенной прямой (некоторые из них отмечены на рис. 5). Например:
если 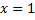 , то
, то
interneturok.ru
Способы задания функции
1. Аналитический
способ: функция
задается в виде формулы 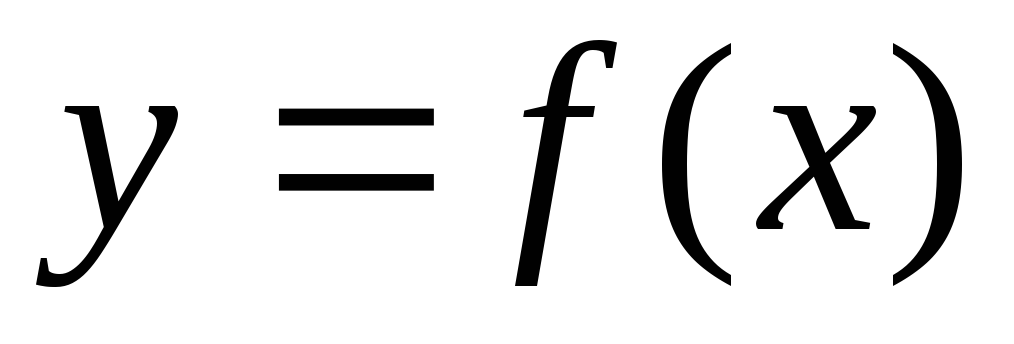 ,
где переменная
,
где переменная – элемент множества значений аргумента,
а переменная
– элемент множества значений аргумента,
а переменная – соответствующее значение функции.
– соответствующее значение функции.
2. Табличный
способ: зависимость задается таблицей значений
аргумента  и соответствующих им значений функции
и соответствующих им значений функции .
Такие функции называютдискретными (заданными в отдельных точках).
.
Такие функции называютдискретными (заданными в отдельных точках).
3. Графический способ: функция задается c помощь своего графика.
любая прямая,
параллельная оси 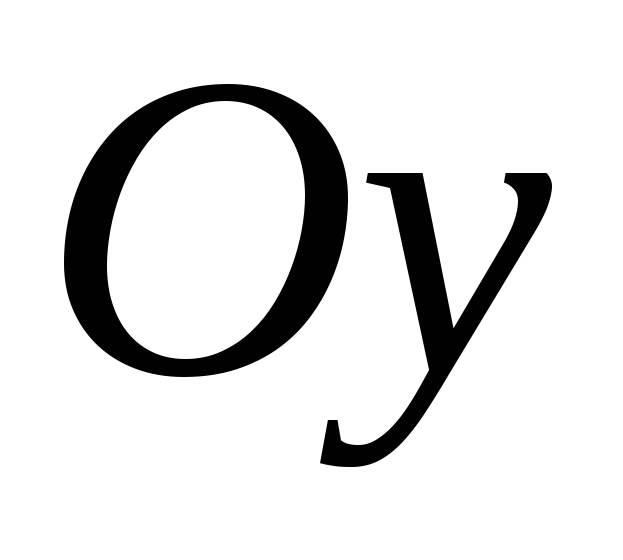 ,
пересекается с указанным графиком не
более чем в одной точке.
,
пересекается с указанным графиком не
более чем в одной точке.
4. Алгоритмический способ: значение функции вычисляется с помощью некоторого алгоритма, на вход которого подается значение аргумента, а на выходе получается значение функции.
5. Словесный
(описательный) способ: при описательном способе зависимость
между 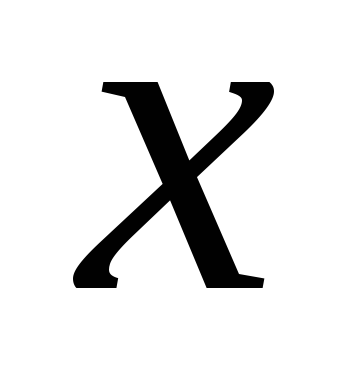 и
и выражается словесным описанием. Например,
выражается словесным описанием. Например, есть наибольшее целое число, не
превосходящее
есть наибольшее целое число, не
превосходящее .
Эта функция называется антье и обозначается
.
Эта функция называется антье и обозначается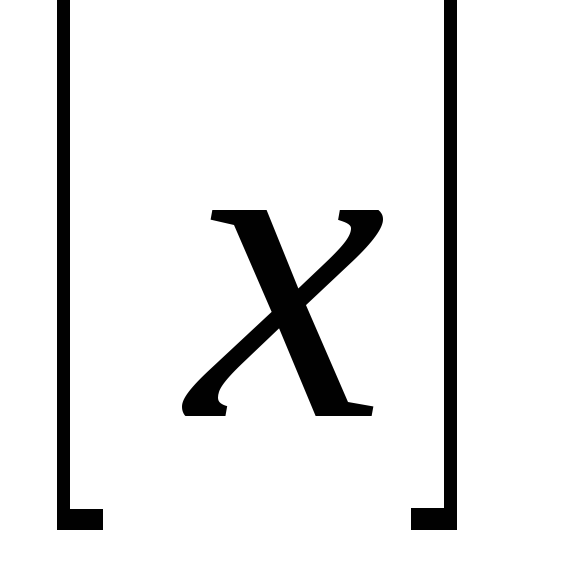 .
Пусть
.
Пусть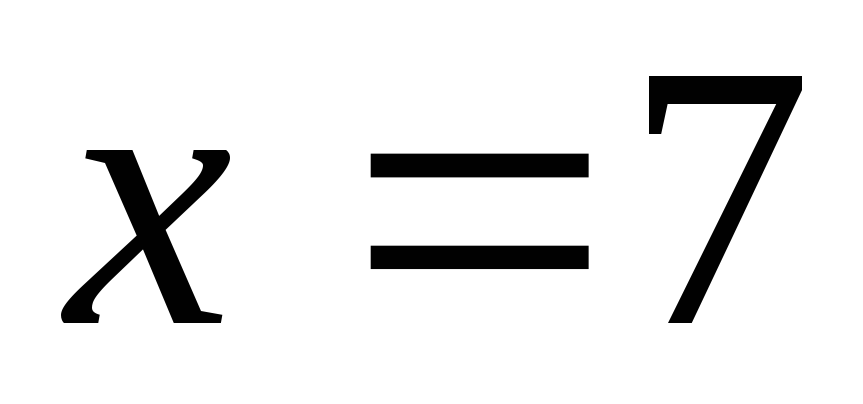 ,
тогда
,
тогда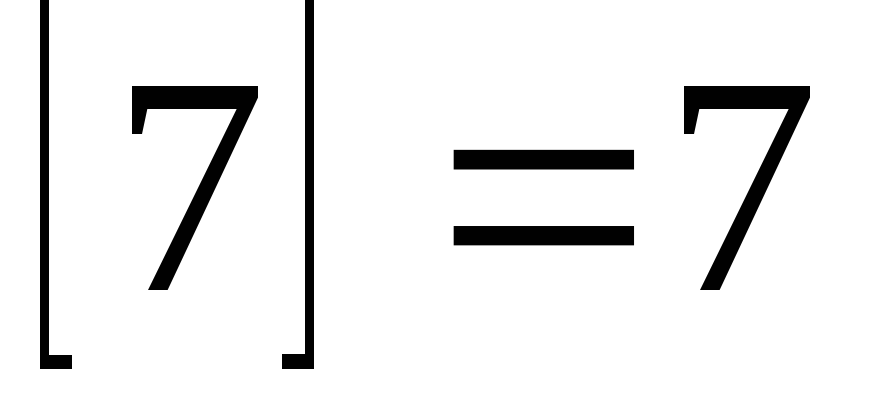 .
Если
.
Если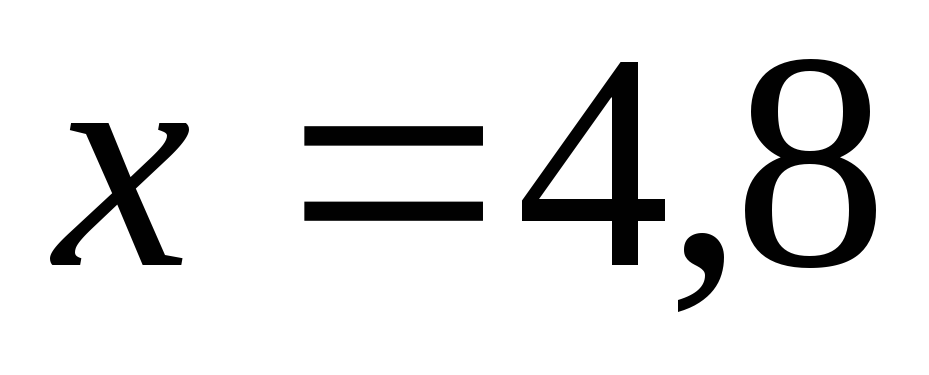 ,
то
,
то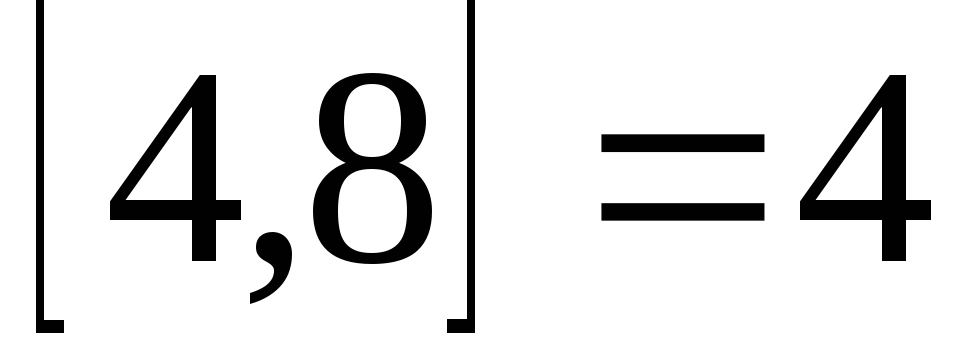 .
А при
.
А при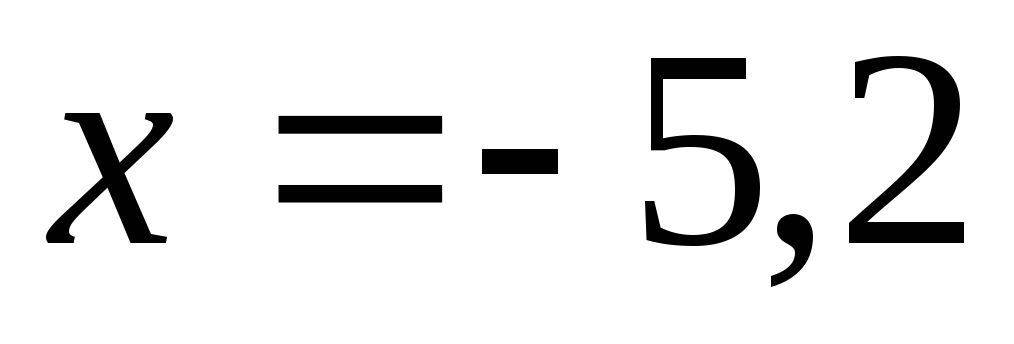 получаем
получаем .
.
2.2. Свойства функции Монотонность функции
Определение
2.4. Функция 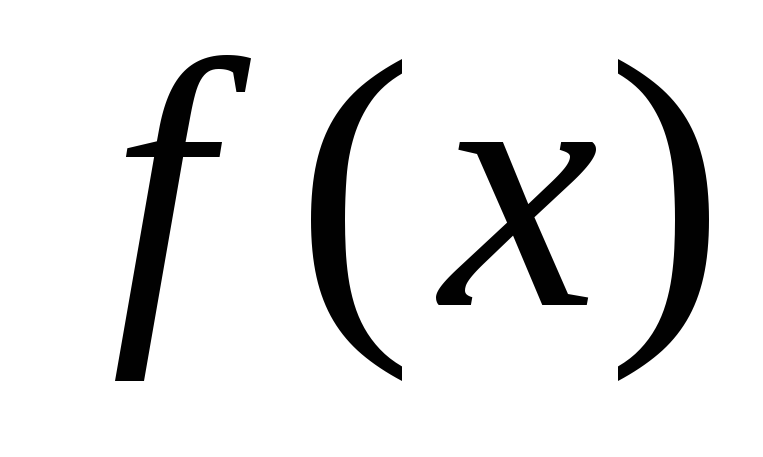 называетсявозрастающей на данном числовом промежутке
называетсявозрастающей на данном числовом промежутке 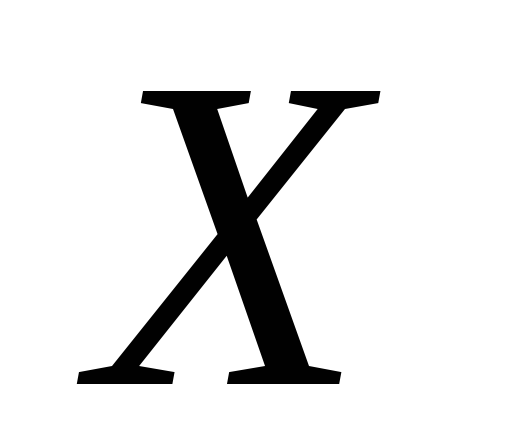 ,
если большему значению аргумента
,
если большему значению аргумента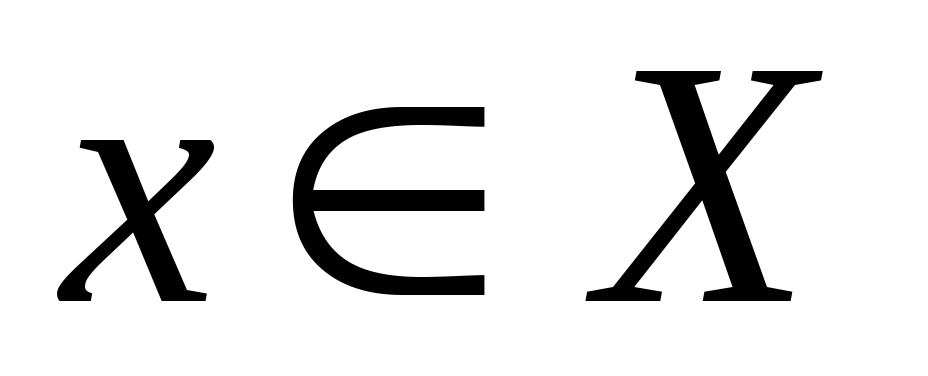 соответствует большее значение функции
соответствует большее значение функции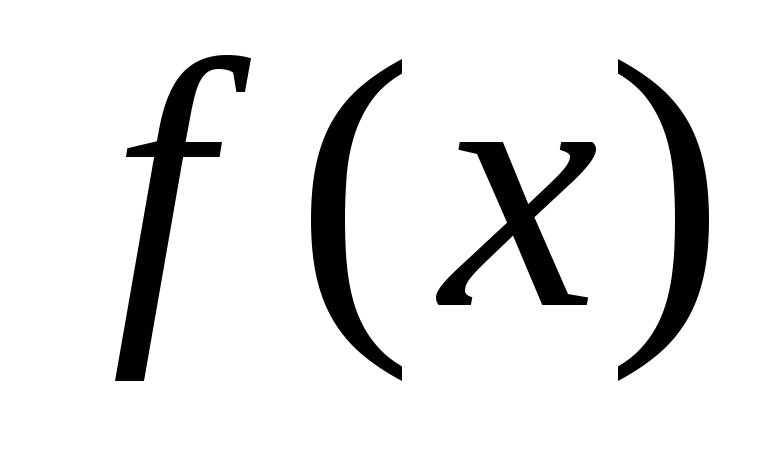 ,
то есть для любых
,
то есть для любых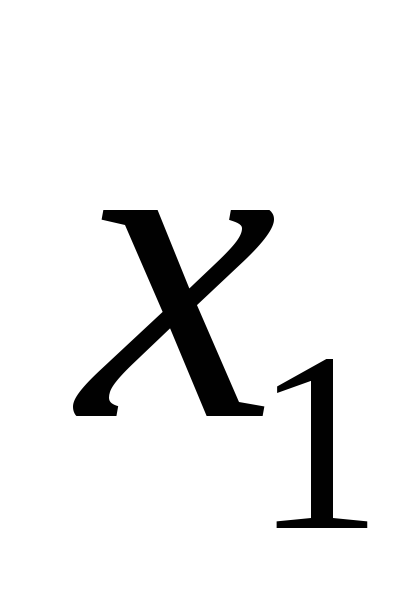 и
и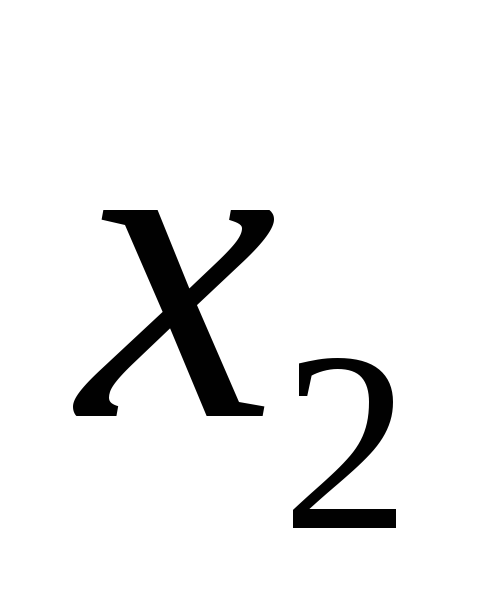 из промежутка
из промежутка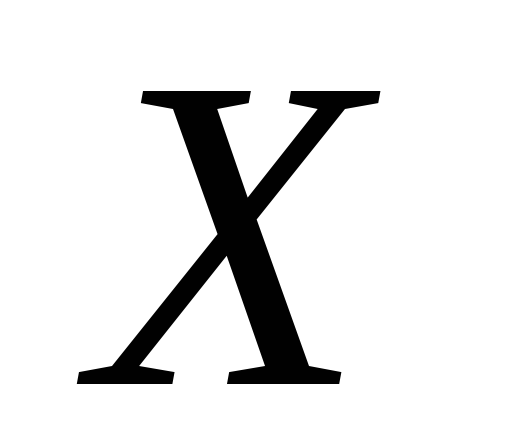 ,
таких, что
,
таких, что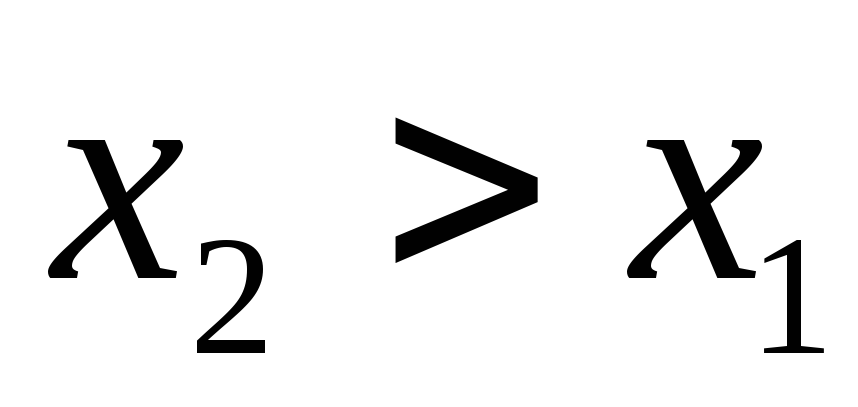 ,
выполнено неравенство
,
выполнено неравенство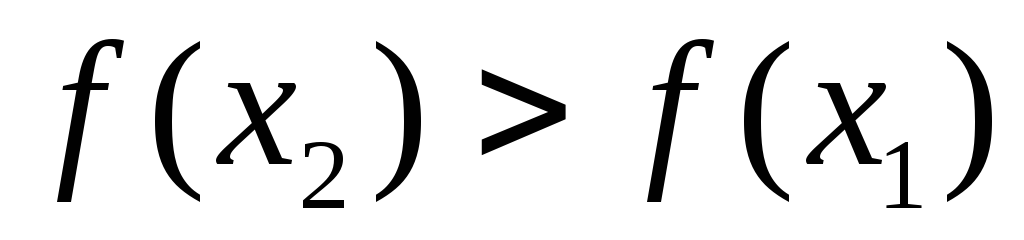 .
.
Определение
2.5. Функция  называетсяубывающей на данном числовом промежутке
называетсяубывающей на данном числовом промежутке 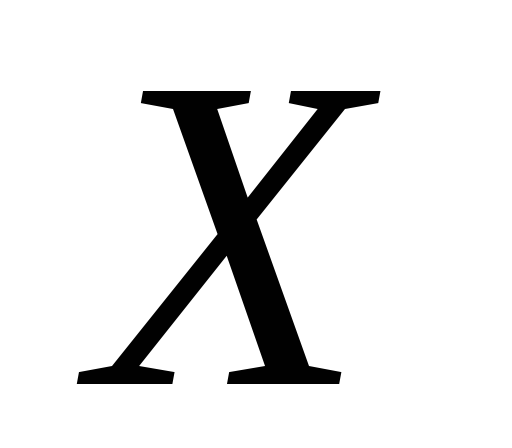 ,
если большему значению аргумента
,
если большему значению аргумента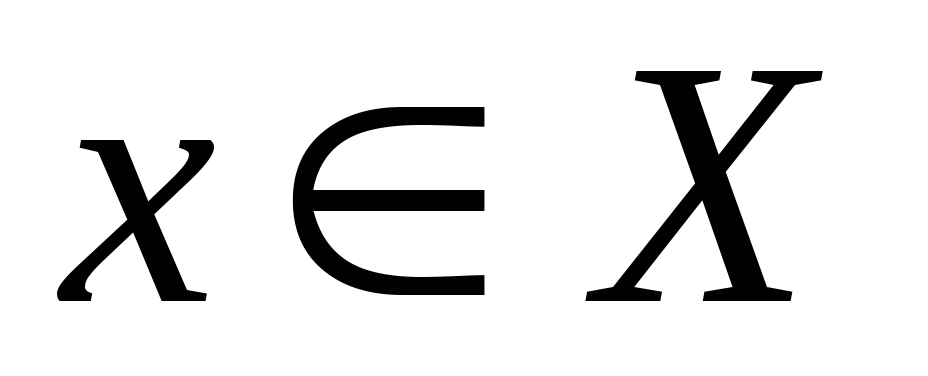 соответствует меньшее значение функции
соответствует меньшее значение функции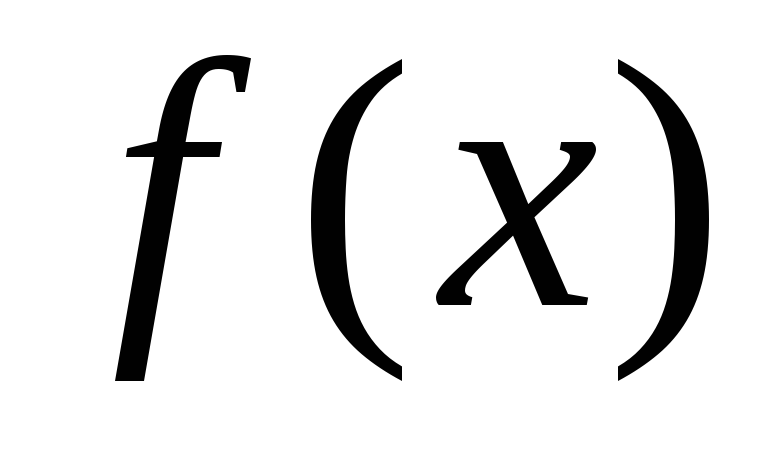 ,
то есть для любых
,
то есть для любых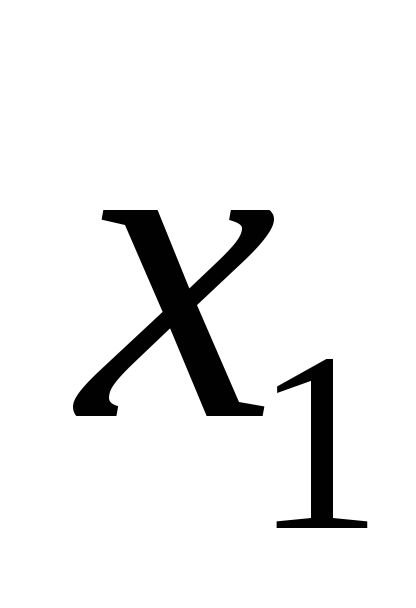 и
и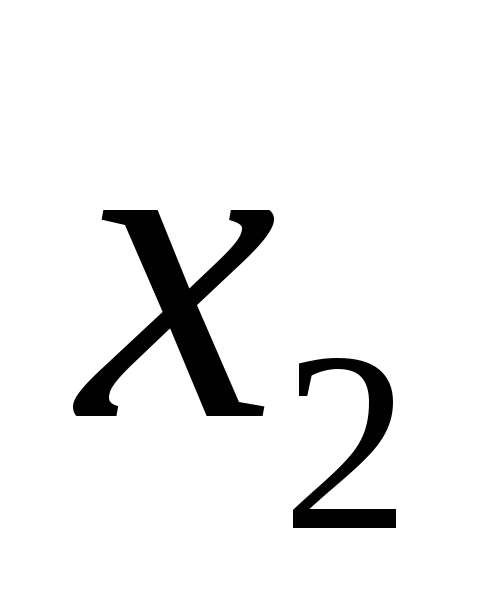 из промежутка
из промежутка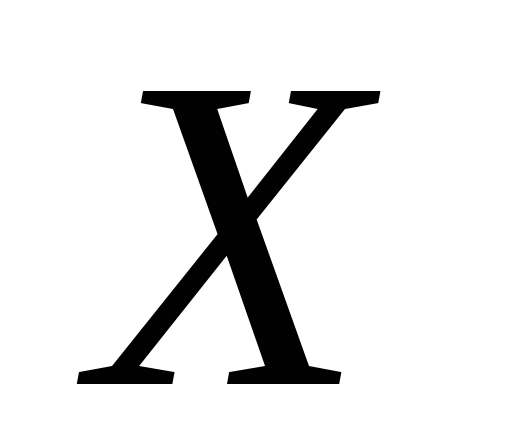 ,
таких, что
,
таких, что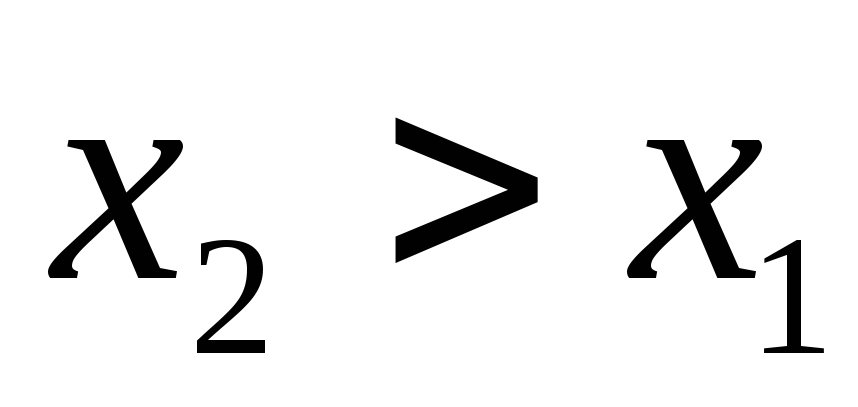 ,
выполнено неравенство
,
выполнено неравенство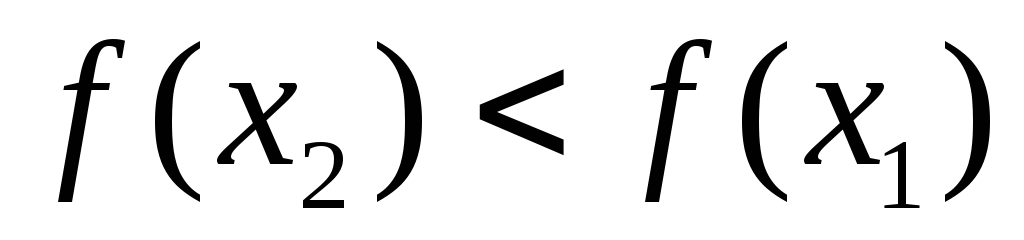 .
.
|
| Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке. О монотонности функции можно судить по ее графику. Например, функция, график которой изображен на рисунке 2.2, возрастает при всех |
рис. 2.2 | рис. 2.3 |
значениях 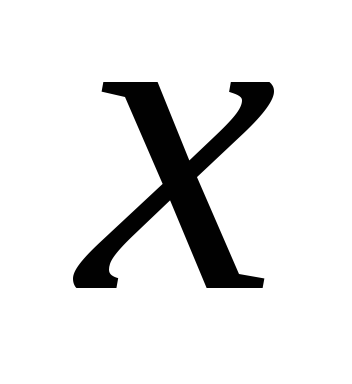 .
Функция, график которой изображен на
рисунке 2.3 убывает на
.
Функция, график которой изображен на
рисунке 2.3 убывает на и возрастает на промежутке
и возрастает на промежутке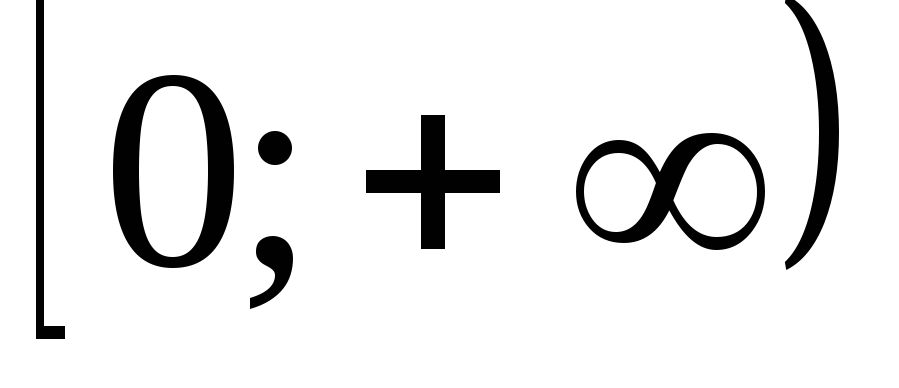 .
.
Четные и нечетные функции
Определение
2.6. Функция 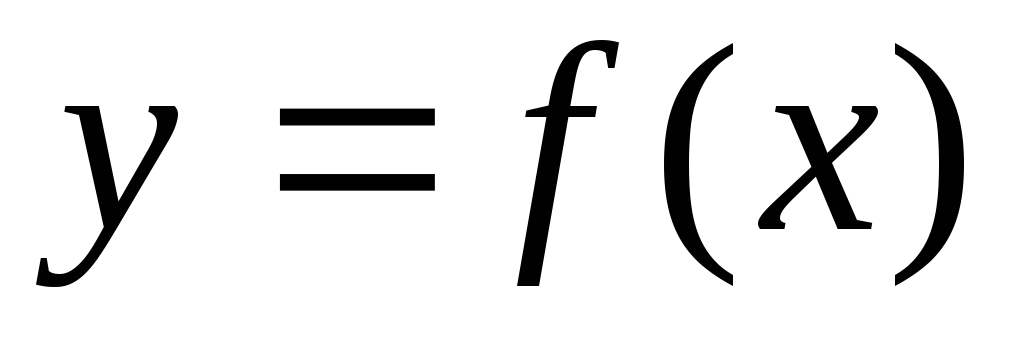 называетсячетной,
если она обладает следующими двумя
свойствами: 1) область определения этой функции
симметрична относительно начала
координат (то есть если
точка
называетсячетной,
если она обладает следующими двумя
свойствами: 1) область определения этой функции
симметрична относительно начала
координат (то есть если
точка  принадлежит области определения, то и
точка
принадлежит области определения, то и
точка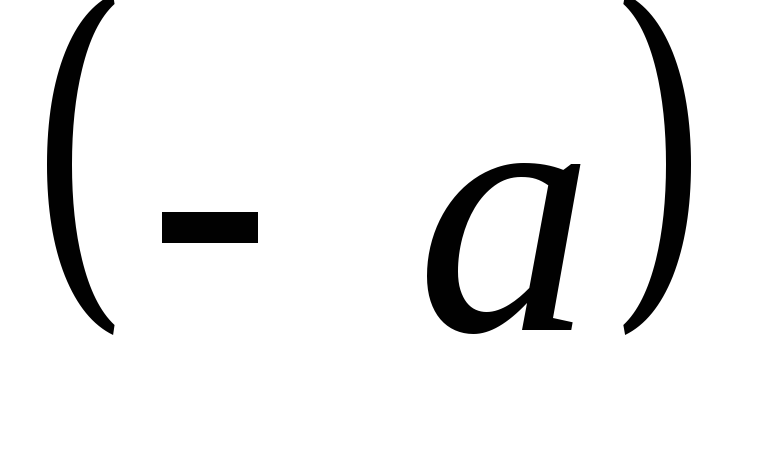 также принадлежит области определения); 2) для любого значения
также принадлежит области определения); 2) для любого значения 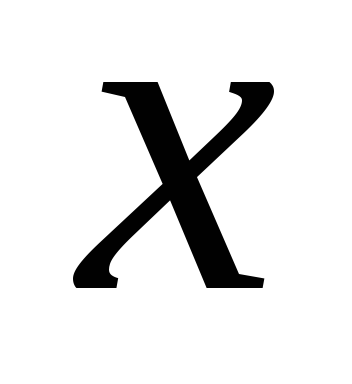 ,
принадлежащего области определения
этой функции, выполняется равенство
,
принадлежащего области определения
этой функции, выполняется равенство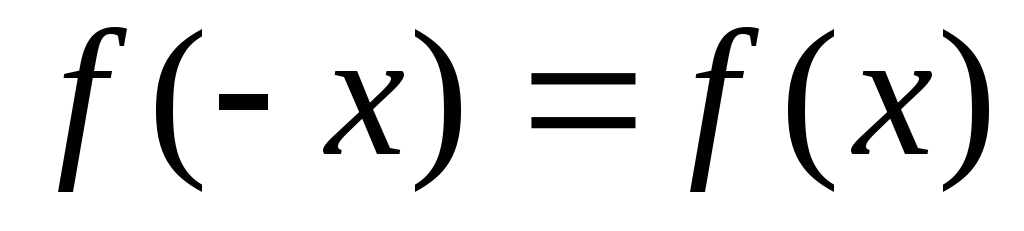 .
.
Определение
2.7. Функция  называетсянечетной,
если она обладает следующими двумя
свойствами: 1) область определения этой функции
симметрична относительно начала
координат; 2) для любого значения
называетсянечетной,
если она обладает следующими двумя
свойствами: 1) область определения этой функции
симметрична относительно начала
координат; 2) для любого значения  ,
принадлежащего области определения
этой функции, выполняется равенство
,
принадлежащего области определения
этой функции, выполняется равенство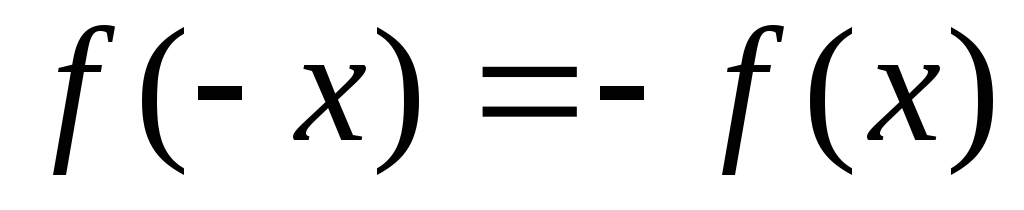 .
.
Замечание 2.1. График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
|
| График четной
функции Например, каждая из функций
|
рис. 2.4 | рис. 2.5 |
не является ни четной, ни нечетной. Такие функции называют функциями общего вида.
studfile.net
Функции и способы задания функций
Определение функции
Существуют множество определений для понятия «функция».
Одними из классических определений понятия «функция» считаются определения на базе соответствий. Приведем ряд таких определений.
Определение 1
Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функцией.
Определение 2
Пусть даны два непустых множества $X$ и $Y$. Соответствие $f$, которое каждому $x\in X$ сопоставляет один и только один $y\in Y$ Называется функцией ($f:X → Y$).
Определение 3
Пусть $M$ и $N$ — два произвольных числовых множества. Говорят, что на $M$ определена функция $f$, принимающая значения из $N$, если каждому элементу $x\in X$ поставлен в соответствие один и только один элемент из $N$.
Следующее определение дается через понятие переменной величины. Переменной величиной называется величина, которая в данном исследовании принимает различные числовые значения.
Определение 4
Пусть $M$ — множество значений переменной величины $x$. Тогда, сели каждому значению $x\in M$ соответствует одно определенное значение другой переменной величины $y$ есть функция величины $x$, определенной на множестве $M$.
Далее рассмотрим теоретико-множественные определения.
Определение 5
Пусть $X$ и $Y$ — некоторые числовые множества. Функцией называется множество $f$ упорядоченных пар чисел $(x,\ y)$ таких, что $x\in X$, $y\in Y$ и каждое $x$ входит в одну и только одну пару этого множества, а каждое $y$ входит, по крайней мере, в одну пару [15].
Определение 6
Всякое множество $f=\{\left(x,\ y\right)\}$ упорядоченных пар $\left(x,\ y\right)$ таких, что для любых пар $\left(x’,\ y’\right)\in f$ и $\left(x»,\ y»\right)\in f$ из условия $y’≠ y»$ следует, что $x’≠x»$ называется функцией или отображением [7].
Определение 7
Функция $f:X → Y$ — это множество $f$ упорядоченных пар $\left(x,\ y\right)\in X\times Y$, таких, что для любого элемента $x\in X$ существует единственный элемент $y\in Y$ такой, что $\left(x,\ y\right)\in f$, то есть функция — кортеж объектов $\left(f,\ X,\ Y\right)$.
В этих определениях
$x$ — независимая переменная.
$y$ — зависимая переменная.
Все возможные значения переменной $x$ называется областью определения функции, а все возможные значения переменной $y$ называется областью значения функции.
Далее будем рассматривать три способа для задания функций: аналитический, табличный и графический.
Аналитический способ задания функции
Для этого способа нам понадобится понятие аналитического выражения.
Определение 8
Аналитическим выражением называется произведение всех возможных математических операций над какими-либо числами и переменными.
Аналитическим способом задания функции и является её задание с помощью аналитического выражения.
Пример 1
$y=x^2+7x-3$, $y=\frac{x+5}{x+2}$, $y=cos5x$.
Приведем далее преимущества и недостатки данного способа:
Плюсы:
- С помощью формул мы можем определить значение функции для любого определенного значения переменной $x$;
- Функции, заданные таким способом можно изучать с помощью аппарата математического анализа.
Минусы:
- Малая наглядность.
- Иногда приходится производить очень громоздкие вычисления.
Табличный способ задания функции
Данный способ задания состоит в том, что для нескольких значений независимой переменной выписываются значения зависимой переменной. Все это вносится в таблицу.
Пример 2

Рисунок 1.
Плюс: Для любого значения независимой переменной $x$, которая внесена в таблицу, сразу узнается соответствующее значение функции $y$.
Минусы:
- Чаще всего, нет полного задания функции;
- Малая наглядность.
Графический способ задания функции
Введем понятие графика функции:
Определение 9
Графиком функции $f(x)$ называется множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Задание графика с помощью такого изображения его в декартовой системе координат называется графическим способом.
Пример 3

Рисунок 2.
Пример задачи
Пример 4
Дан аналитический вид функции $y=x^2$. Привести табличный и графический способы задания этой же функции.
Решение.
Сначала приведем табличный способ. Так как при возведении в четную степень любого числа получим неотрицательное значение, то получим следующую таблицу:

Рисунок 3.
Это и есть табличное задание.
Перейдем теперь к заданию в виде графика. Для этого отметим в декартовой системе координат точки из таблицы выше. Получим:

Рисунок 4.
spravochnick.ru
Способы задания функций
Существуют следующие способы задания функции y = f(x):
- Явный аналитический способ по формуле вида y = f(x).
- Интервальный.
- Параметрический: x = x(t), y = y(t).
- Неявный, как решение уравнения F(x, y) = 0.
- В виде ряда, составленного из известных функций.
- Табличный.
- Графический.
Явный аналитический способ задания функции
При явном способе, значение функции определяется по формуле, представляющем собой уравнение y = f(x). В левой части этого уравнения стоит зависимая переменная y, а в правой – выражение, составленное из независимой переменной x, постоянных, известных функций и операций сложения, вычитания, умножения и деления. Известными функциями являются элементарные функции и специальные функции, значения которых можно вычислить, используя средства вычислительной техники.
Вот несколько примеров явного задания функции с независимой переменной x и зависимой переменной y:
;
;
.
Интервальный способ задания функции
При интервальном способе задания функции, область определения разбивается на несколько интервалов, и функция задается отдельно для каждого интервала.
Вот несколько примеров интервального способа задания функции:
Параметрический способ задания функции
При параметрическом способе, вводится новая переменная, которую называют параметром. Далее задают значения x и y как функции от параметра, используя явный способ задания:
(1)
Вот примеры параметрического способа задания функции, используя параметр t:
Преимущество параметрического способа заключается в том, что одну и ту же функцию можно задать бесконечным числом способов. Например, функцию можно задать так:
А можно и так:
Такая свобода выбора, в некоторых случаях, позволяет применять этот способ для решения уравнений (см. «Дифференциальные уравнения, не содержащие одну из переменных»). Суть применения заключается в том, что мы подставляем в уравнение вместо переменных x и y две функции и . Затем задаем одну из них по собственному усмотрению, чтобы из получившегося уравнения можно было определить другую.
Также этот способ применяется для упрощения расчетов. Например, зависимость координат точек эллипса с полуосями a и b можно представить так:
.
В параметрическом виде этой зависимости можно придать более простую форму:
.
Уравнения (1) – это не единственный способ параметрического задания функции. Можно вводить не один, а несколько параметров, связав их дополнительными уравнениями. Например можно ввести два параметра и . Тогда задание функции будет выглядеть так:
Здесь появляется дополнительное уравнение , связывающее параметры. Если число параметров равно n, то должно быть n – 1 дополнительных уравнений.
Пример применения нескольких параметров изложен на странице «Дифференциальное уравнение Якоби». Там решение ищется в следующем виде:
(2) .
В результате получается система уравнений. Чтобы ее решить, вводят четвертый параметр t. После решения системы получается три уравнения, связывающие четыре параметра и .
Неявный способ задания функции
При неявном способе, значения функции определяется из решения уравнения .
Например, уравнение эллипса имеет вид:
(3) .
Это простое уравнение. Если мы рассматриваем только верхнюю часть эллипса, , то можно выразить переменную y как функцию от x явным способом:
(4) .
Но даже если можно свести (3) к явному способу задания функции (4), последней формулой не всегда удобно пользоваться. Например, чтобы найти производную , удобно дифференцировать уравнение (3), а не (4):
;
.
Задание функции рядом
Исключительно важным способом задания функции является ее представление в виде ряда, составленного из известных функций. Этот способ позволяет исследовать функцию математическими методами и вычислять ее значения для прикладных задач.
Самым распространенным представлением является задание функции с помощью степенного ряда. При этом используется ряд функций:
.
Также применяется ряд и с отрицательными степенями:
.
Например, функция синус имеет следующее разложение:
(5) .
Подобные разложения широко применяются в вычислительной технике, поскольку они позволяют свести вычисления к арифметическим операциям.
В качестве иллюстрации, вычислим значение синуса от 30°, используя разложение (5).
Переводим градусы в радианы:
.
Подставляем в (5):
.
В математике, на ряду со степенными рядами, широко применяются разложения в тригонометрические ряды по функциям и , а также по другим специальным функциям. С помощью рядов можно производить приближенные вычисления интегралов, уравнений (дифференциальных, интегральных, в частных производных) и исследовать их решения.
Табличный способ задания функции
При табличном способе задания функции мы имеем таблицу, которая содержит значения независимой переменной x и соответствующие им значения зависимой переменной y. Независимая и зависимая переменные могут иметь разные обозначения, но мы здесь используем x и y. Чтобы определить значение функции при заданном значении x, мы по таблице, находим значение x, наиболее близкое к нашему. После этого определяем соответствующее значение зависимой переменной y.
Для более точного определения значения функции, мы считаем, что функция между двумя соседними значениями x линейна, то есть имеет следующий вид:
.
Здесь – значения функции, найденные из таблицы, при соответствующих им значениях аргументов .
Рассмотрим пример. Пусть нам нужно найти значение функции при . Из таблицы находим:
.
Тогда
.
Точное значение:
.
Из этого примера видно, что применение линейной аппроксимации привело к повышению точности в определении значения функции.
Табличный способ применяется в прикладных науках. До развития вычислительной техники, он широко применялся в инженерных и других расчетах. Сейчас табличный способ применяется в статистике и экспериментальных науках для сбора и анализа экспериментальных данных.
Графический способ задания функции
При графическом способе, значение функции определяется из графика, по оси абсцисс которого откладываются значения независимой переменной, а по оси ординат – зависимой.
Графический способ дает наглядное представление о поведении функции. Результаты исследования функции часто иллюстрируют ее графиком. Из графика можно определить приближенное значение функции. Это позволяет использовать графический способ в прикладных и инженерных расчетах.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
определение , способы задания, график Содержание
85
§ 7. Числовая функция: определение , способы задания, график 70
6.1. Определение числовой функции 70
7.1. Сужение функции 72
7.2. Способы задания функции 73
7.3. Явно или неявно заданные функции 73
7.4. Параметрически заданные функции 75
7.5. График функции 77
7.6. Примеры построения графиков функций 78
7.7. Упражнения для самостоятельной работы 83
Вопросы для самопроверки 85
Глоссарий 85
Определение числовой функции
Определение числовой функции |
Переменная величина yназываетсячисловой функциейпеременной величиныx, если каждому возможному числовому значению величиныxставится в соответствие по какому-нибудь правилу или закону единственное числовое значение величиныy. |
Обозначения: 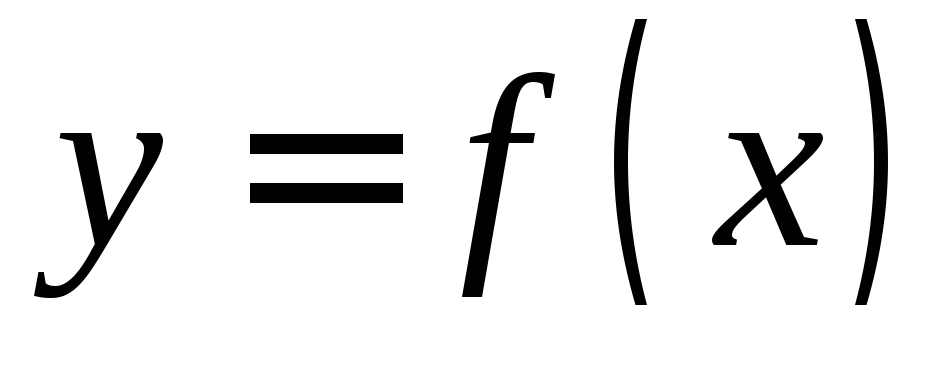 или
или или
или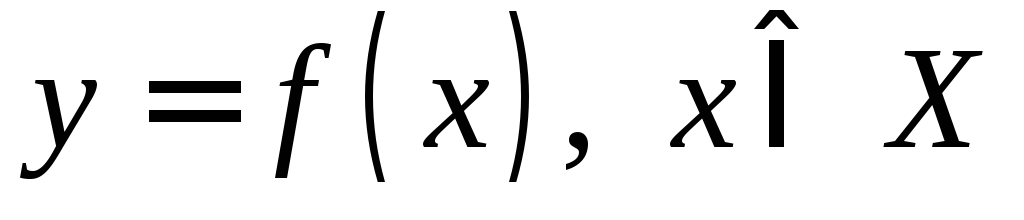 или
или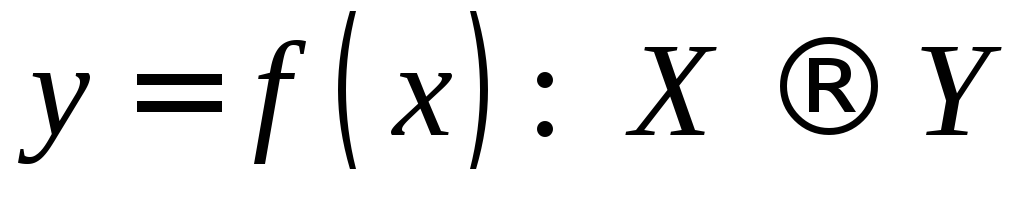 или
или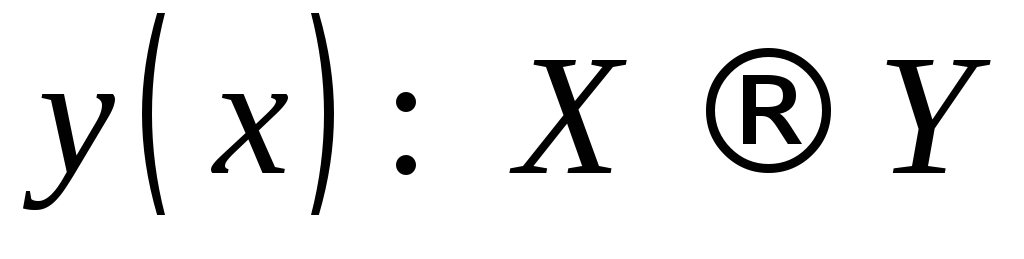 .
.
где x— это независимая переменная, или аргумент;y— это зависимая переменная, или функция.
Если обозначить через
X– множество числовых значений, которые может принимать переменнаяx,
Y– множество числовых значений, которые принимает переменнаяy,
то
функциональная зависимость между
переменными xиyздесь задает отображение числового
множестваXна числовое
множествоY, при котором
каждому элементу  ставится в соответствие единственный
элемент множестваY(рис. 40).
ставится в соответствие единственный
элемент множестваY(рис. 40).
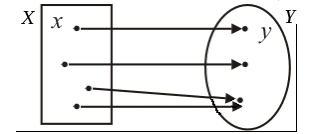
Рис. 40
В отличие
от более общего определения функции
как отображения множеств, состоящих из
элементов любой природы, числовая
функция задает отображение множества X, элементами которого
являются числа, на множествоY,
элементами которого тоже являются
числа. Кроме того, далее будем считать,
что множествоY — это есть множество значений функции,
так что отображение является сюръекцией.
является сюръекцией.
МножествоXзадания функции и множествоYзначений функции для числовых функций традиционно называютобластью определения функции(ООФ)иобластью значений функции(ОЗФ).
Значение функции в точке
Если задано отображение множеств
функцией  ,
то элементы множествXиYназываются точками.
Символом
,
то элементы множествXиYназываются точками.
Символом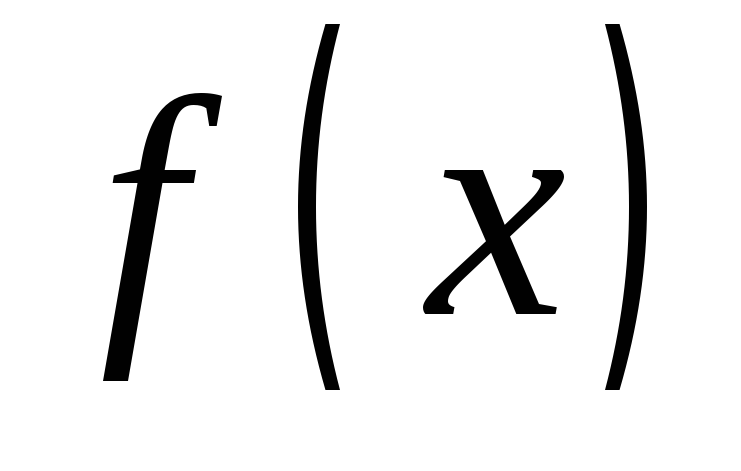 обозначается при этом как сама функция,
так и элемент
обозначается при этом как сама функция,
так и элемент ,
соответствующий элементуx при этой функциональной зависимости.
,
соответствующий элементуx при этой функциональной зависимости.
Если x0— это фиксированное значение аргументаx, то значение функции в точкеx0обозначается следующими символами:
 или
или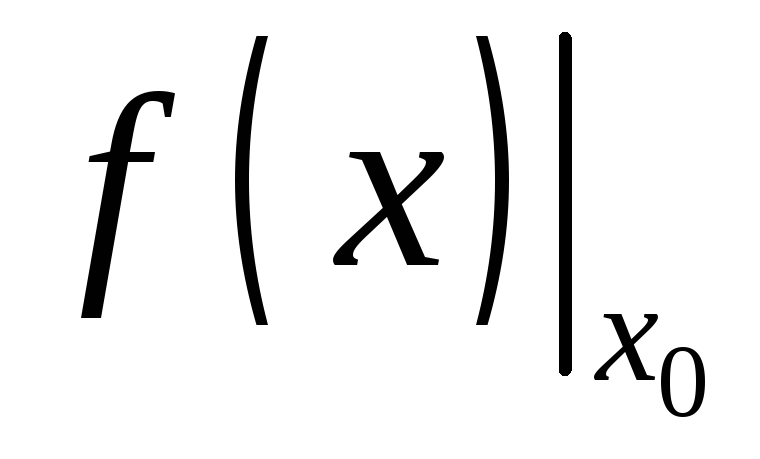 или
или  или
или 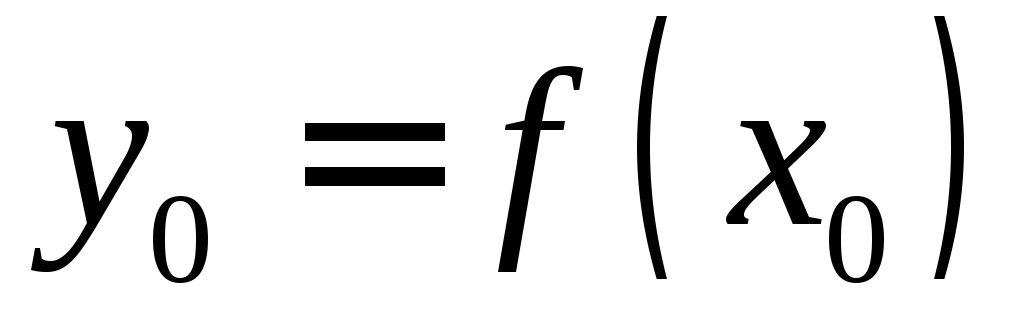 .
.
Например, 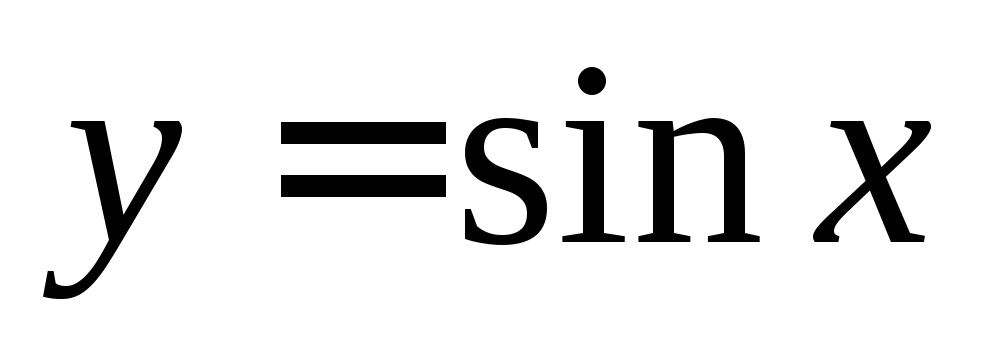
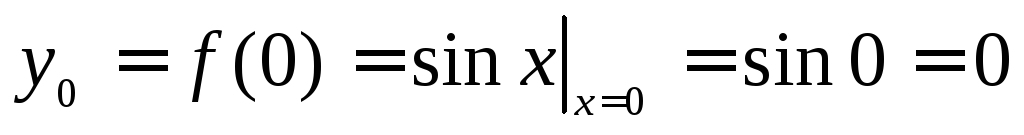 ;
;
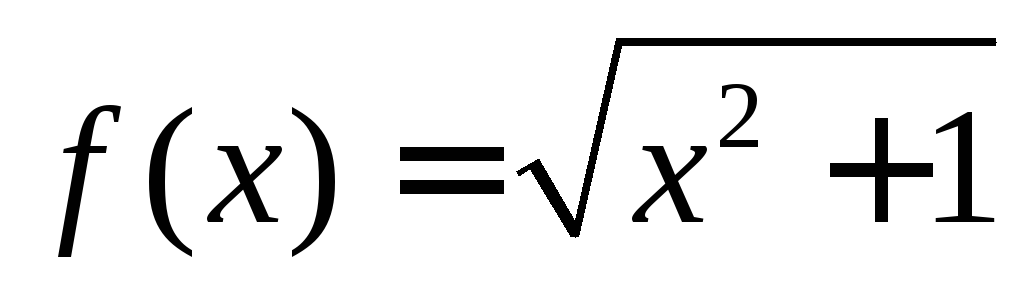
 ,
,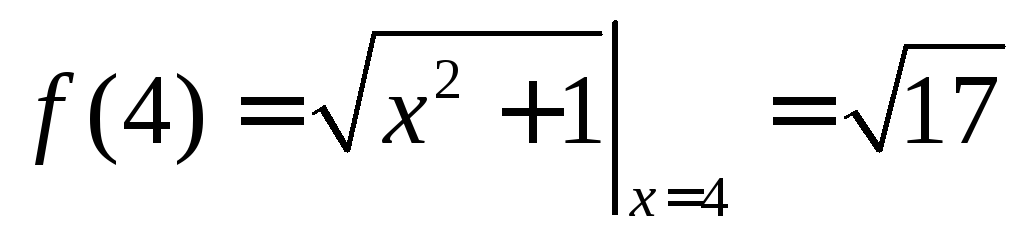 .
.
Сужение функции
Если есть функция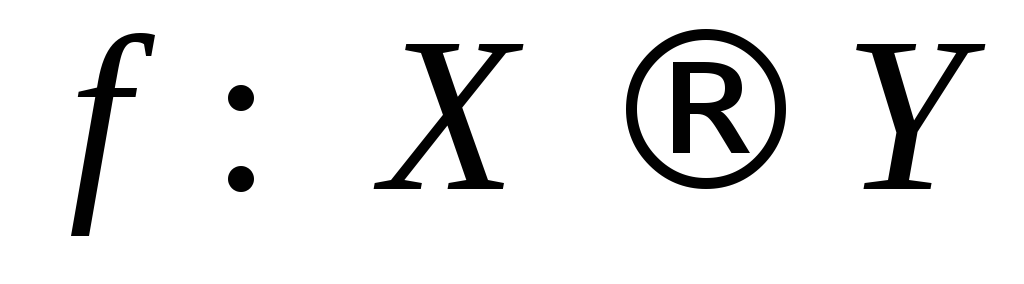 и рассматривается некоторое подмножествоЕ множестваХ, то отображение
и рассматривается некоторое подмножествоЕ множестваХ, то отображение называетсясужением
функции f на множество Е.
называетсясужением
функции f на множество Е.
Пример 1 (сужение функций)
1) 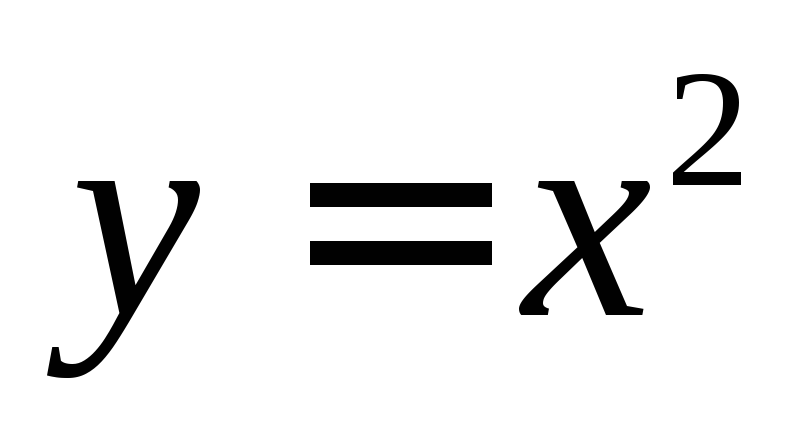 ,
,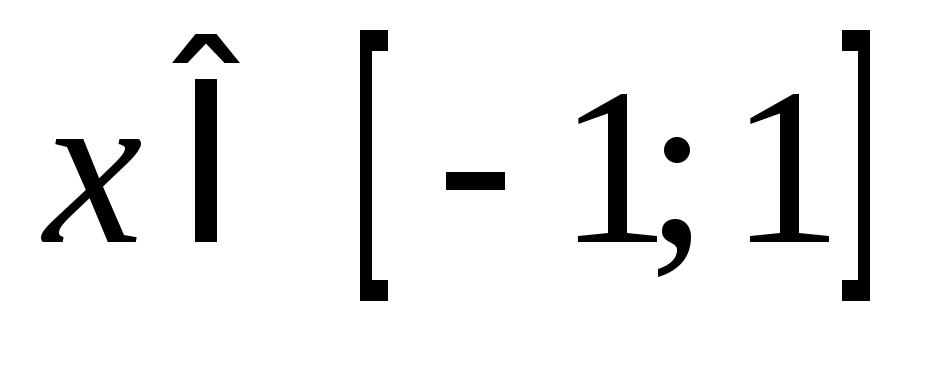 — это есть
сужение функции
— это есть
сужение функции ,
,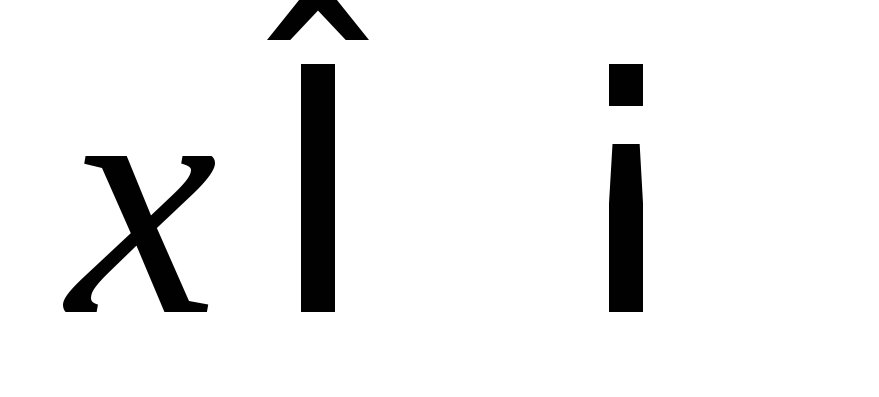 на множество
на множество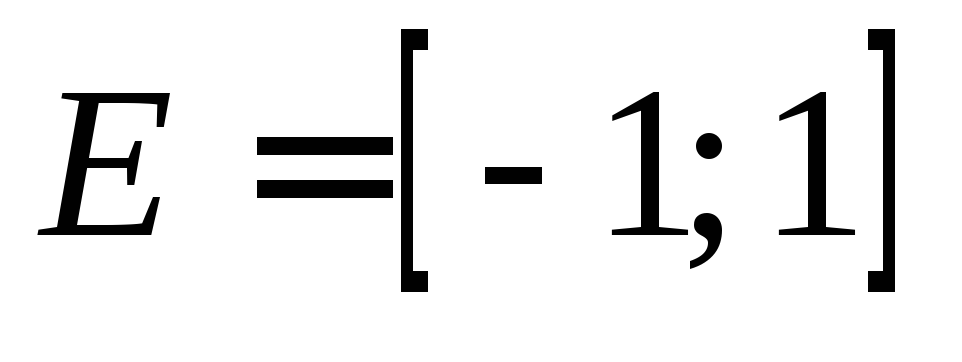 ;
;
2) любая
последовательность  есть сужение функции
есть сужение функции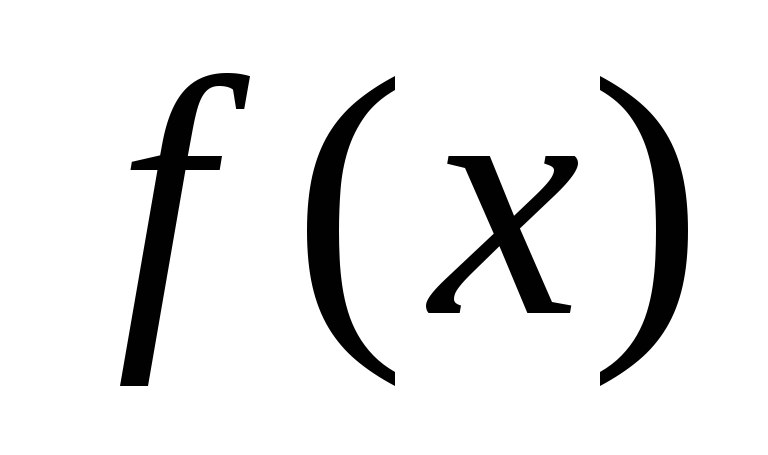 на множество натуральных чисел
на множество натуральных чисел ; например,
; например,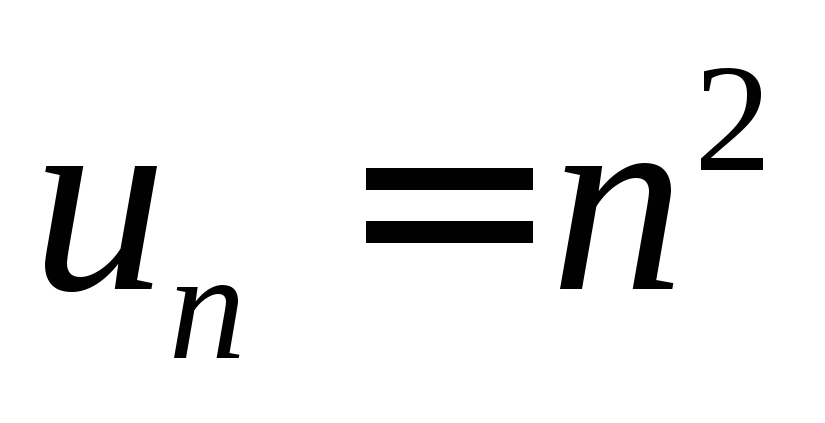 – это есть сужение функции
– это есть сужение функции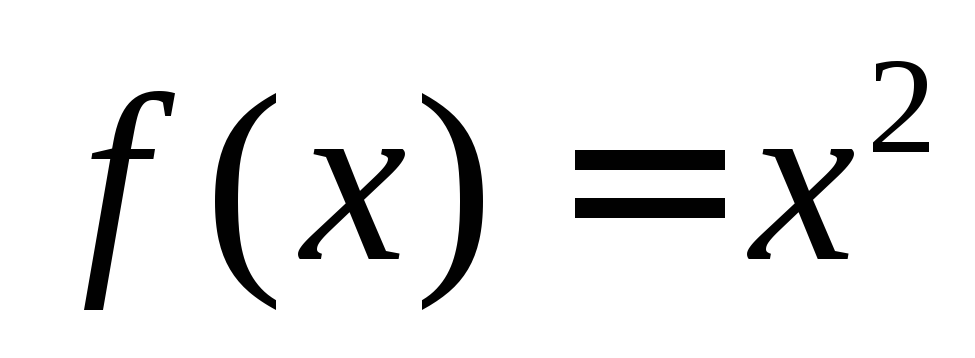 ,
,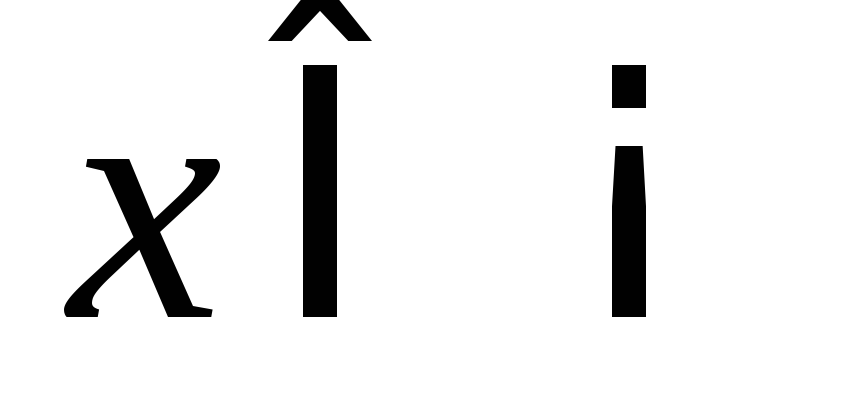 на множество
на множество .
.
Наряду с понятием сужения функции существует и понятие расширения функции.
Пример 2 (расширение функций)
1) 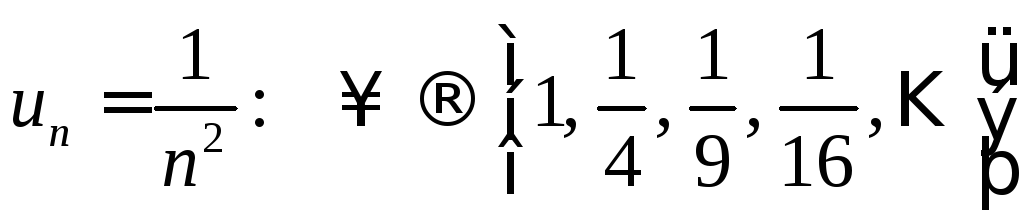 ;
от
этой функции можно перейти к её расширению
на множество
;
от
этой функции можно перейти к её расширению
на множество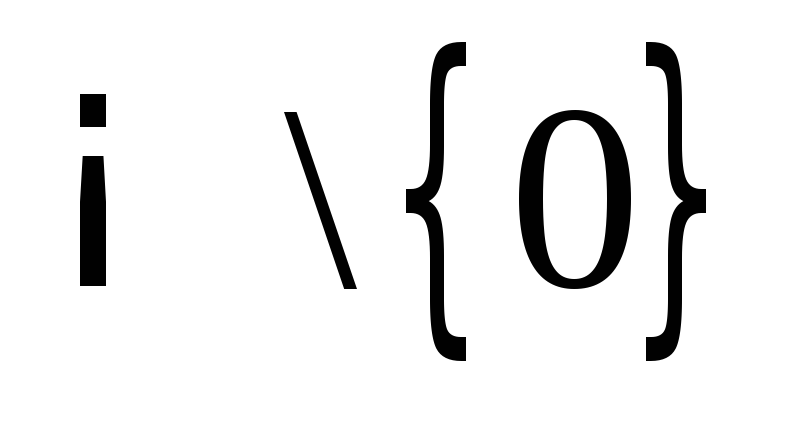 :
: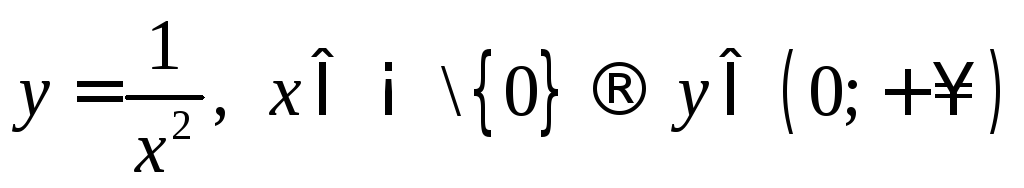 ;
;
2) от функции 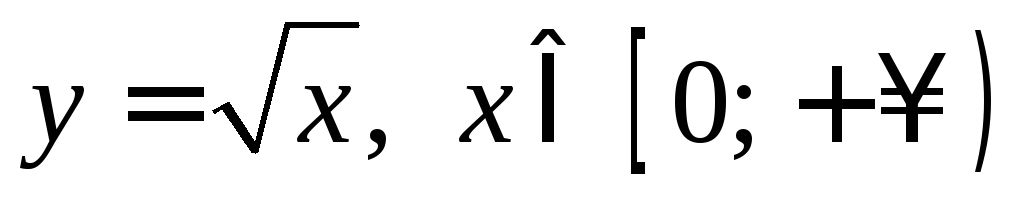 можно перейти к её расширению на множество
можно перейти к её расширению на множество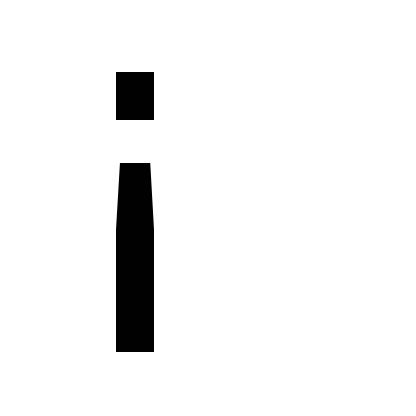 ,
если рассматривать её значения на
множестве комплексных чисел, где возможно
извлечение корня квадратного из
отрицательного числа.
,
если рассматривать её значения на
множестве комплексных чисел, где возможно
извлечение корня квадратного из
отрицательного числа.
Способы задания функции
1.Аналитический способ задания функции — функция задается математической формулой, связывающей аргумент и функцию. По этой формуле для каждого возможного значения аргумента можно вычислить соответствующее значение функции. При этом нужно различать:
явное задание функции,
неявное задание функции,
параметрическое задание функции.
2.Табличный способ задания функции— используется для функций, заданных на дискретном конечном множестве значений аргумента; записывается обычно в виде следующей таблицы:
x | x1 | x2 | … | xn |
y | y1 | y2 | … | yn |
3.Графический способ задания функции— задается множество точек координатной плоскости, координаты которых являются соответствующими друг другу значениями аргумента и функции.
4.Описательный
способ задания функции– функциональная зависимость описывается
словами. Например,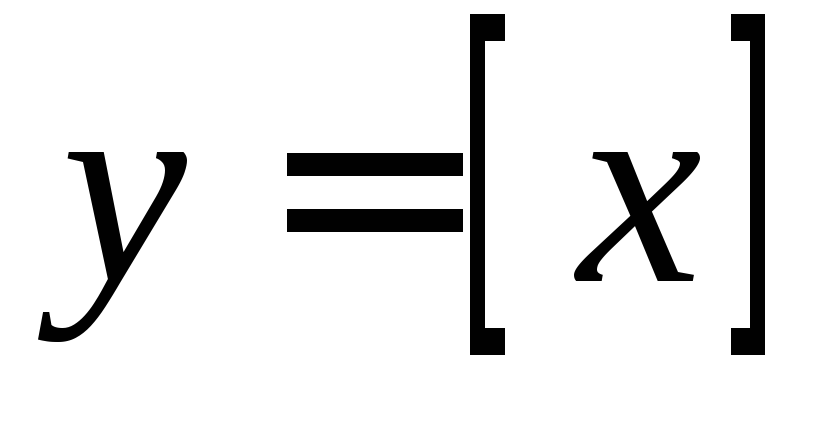 ,
где
,
где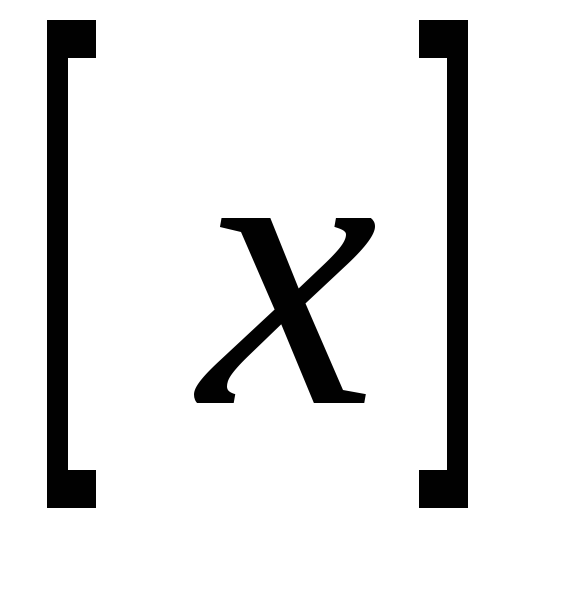 — этоцелая
часть x, которая
определяется как наибольшее целое
число, не превышающееx.
— этоцелая
часть x, которая
определяется как наибольшее целое
число, не превышающееx.
studfile.net
§4. Функция одной переменной 1. Понятие функции и способы ее задания
19
Пара
чисел х и у называется упорядоченной,
если указано, какое из этих чисел
считается первым, а какое — вторым.
(х;у) Определение4.1 Пусть
Х и У – некоторые числовые множества.
Функцией называется множество f
упорядоченных пар чисел (х;у) таких, что
х 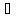 Х, у
Х, у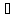 У и каждое х входит в одну и только одну
пару этого множества, а каждое у входит,
по крайней мере, в одну пару. При этом
говорят, что числу х поставлено в
соответствие число у, и пишут у=f(x).
Число у называется значение функции f
в точке х. Переменную у называют зависимой
переменной, а переменную х – независимой
(аргументом), множество Х – областью
определения (существования х) функции,
а множество У – множеством значений
функции.
У и каждое х входит в одну и только одну
пару этого множества, а каждое у входит,
по крайней мере, в одну пару. При этом
говорят, что числу х поставлено в
соответствие число у, и пишут у=f(x).
Число у называется значение функции f
в точке х. Переменную у называют зависимой
переменной, а переменную х – независимой
(аргументом), множество Х – областью
определения (существования х) функции,
а множество У – множеством значений
функции.
Вместо
термина «функция» употребляют еще
равнозначный термин «отображение», а
вместо записи y=f(x)
пишут f:
x 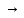 у и говорят, что отображениеf
отображает число х в число у, или число
у является образом числа х при отображении
f.
у и говорят, что отображениеf
отображает число х в число у, или число
у является образом числа х при отображении
f.
Пусть
на некотором множестве Х определена
функция f(x),
тогда значение этой функции, соответствующее
некоторому значению аргумента хо,
обозначается уо=f(xo).
Для нахождения значения у по данному
значению х 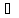 Х надо произвести над этим значением х
определенную систему операцийf.
Таким образом, если функция задана, то
можно определить множество ее значений
У={y}.
Х надо произвести над этим значением х
определенную систему операцийf.
Таким образом, если функция задана, то
можно определить множество ее значений
У={y}.
Область
определения функции (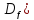 может состоять из одного или нескольких
промежутков, из отдельных точек и других
множеств. Множество ее значений (
может состоять из одного или нескольких
промежутков, из отдельных точек и других
множеств. Множество ее значений (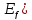 определяется законом соответствия.
определяется законом соответствия.
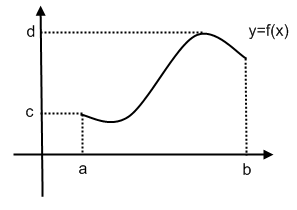
y=f(x), 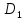 =[a;b],
=[a;b], [c;d]
[c;d]
т.е.
аргумент х изменяется от a
до b
a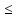 х
х 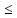 b,а
функция у изменяется от с до d
(c
b,а
функция у изменяется от с до d
(c 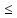 y
y 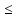 d)
d)
Может оказаться, что область значения функции состоит из одного какого-нибудь числа С (геометрически из одной точки на оси Оу), т.е. каждому значению х, взятому из области определения функции, соответствует только одно число С. В этом случае функция постоянна f(x) = c = const
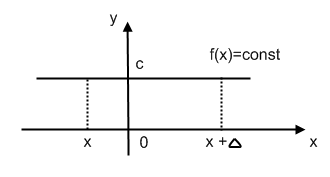
Способы задания функции
Аналитический
Этот способ состоит в том, что зависимость между переменными величинами определяется с помощью формулы, указывающей, какие действия можно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента. Примеры:
y=x3 + 7 задает функцию, область определения которой – числовая прямая (-
 ;
+
;
+ )
и такая же область значений;
)
и такая же область значений;у=задает функцию,
 = [-1; 1],
= [-1; 1],
1-x2≥0 1-y2=x2
X=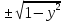
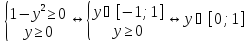
y=n!
 =
{1, 2, 3, … , n, …}= N,
=
{1, 2, 3, … , n, …}= N, ={1!,
2!, 3!, … , N!, …}
={1!,
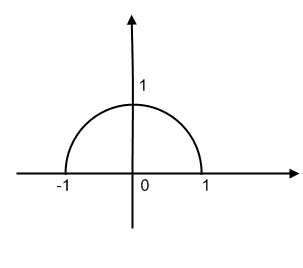
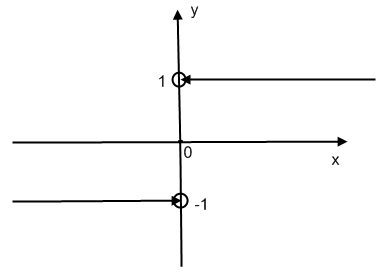
2!, 3!, … , N!, …}y = sgn x =
 =
{-1, 0, 1}
=
{-1, 0, 1}
[signum]
Функция Дирака у=

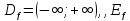 =
{0, 1}
=
{0, 1}
Эту функцию изобразить графически невозможно.
Табличный
x | 0 | 0,1 | 0,2 | 3 | 0,6 |
y | -1 | 10 | 1 | -2 | -8 |
Поставим
в соответствие каждому х, записанному
в первой строке таблицы, число у, стоящее
во второй строке под ними, числом х и
будем говорить, что полученная функция
задана таблицей.  = {0; 0,1; 0,2; 3; 0,6],
= {0; 0,1; 0,2; 3; 0,6],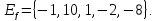 С помощью таблицы можно задать функцию
только при конечном числе значений
аргумента
С помощью таблицы можно задать функцию
только при конечном числе значений
аргумента
Графический
Графиком функции у=f(x) называется множество точек плоскости, прямоугольные координаты которых удовлетворяют уравнению у=f(x). Функция у=f(x) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определить значения функции только приближенно, т.к. построение графика и нахождение на нем значений функции связано с погрешностями.
2. у=
4.
y
= sgn x = 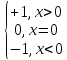
2. Элементарные функции, их классификация
Функция
у=f(x),
заданная на множестве Х, называется
элементарной, если ее можно задать одной
формулой вида у=f(x)
так, что ее значение элементарных
операций («+», «-», « »,
«
»,
« »,
возведение в степень, извлечение корня,
логарифмирование, вычисление значений
тригонометрических и обратных
тригонометрических функций), причем
число операций, сами операции и порядок
их выполнения не зависит от значения
аргумента х.
»,
возведение в степень, извлечение корня,
логарифмирование, вычисление значений
тригонометрических и обратных
тригонометрических функций), причем
число операций, сами операции и порядок
их выполнения не зависит от значения
аргумента х.
К классу элементарных функций относятся прежде всего все основные элементарные функции, а также функции, полученные из них при помощи конечного числа элементарных операций.
Например, элементарной функции y=lg(3x2-8) при х=6 равно2. Это значение найдено при помощи 4-х операций.
Примеры неэлементарных функций:
y=n! Количество операций, необходимое для определения значений 1-й функции, неограниченно возрастает с увеличением n.
у=

Она определена на всей числовой прямой 2-мя формулами и не может быть задана одной формулой с ограниченным числом элементарных действий.
Таким образом, если функция неэлементарная, то число операций над аргументом, либо сами операции, либо то и другое изменяются в зависимости от изменения аргумента.
Имеет место следующая классификация элементарных функций.
Функция вида Р(х)=аохm+a1xm-1+…+am-1x+am, где m
 ,
m
,
m ;
a0,
a1,…
, am–
любые целые числа (а0
;
a0,
a1,…
, am–
любые целые числа (а0 0)
– коэффициенты
0)
– коэффициенты
Называется рациональной функцией или алгебраическим многочленом степени m. Многочлен 1-й степени называется линейной функцией.
Функция, представляющая собой отношение 2-х целых рациональных функций
R(x)=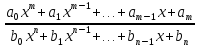 ,
называется дробно-рациональной функцией
,
называется дробно-рациональной функцией
Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.
Функция, полученная с помощью конечного арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющиеся рациональной, называется иррациональной.
Всякая функция, не являющаяся рациональной или иррациональной, называется трансцендентной функцией, например f(x)=sin x + x
3. Виды функций
Монотонные функции
Функция
f(x)
называется возрастающей (убывающей) на
некотором множестве Х, если для любой
пары чисел х1 и х2,
принадлежащих этому множеству х1 < х2 =>
f(х1)
< f(х2)
(f(х1)
> f(х2)),
т.е. большому значению аргумента
соответствует большое значение функции.
Для любых х1 и х2 х1 < х2 =>
f(х1) 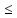 f(х2)
(f(х1)
f(х2)
(f(х1) 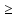 f(х2))
– неубывающая (невозрастающая)
f(х2))
– неубывающая (невозрастающая)
Функция f(x) называется кусочно-монотонной на данном множестве, если это множество можно разбить на конечное число подмножеств, в каждом из которых функция изменяется монотонно.
Ограниченные функции
Функция
y=f(x)
называется ограниченной сверху (снизу)
на некотором множестве Х, если существует
такое число М (m),
что f(x)≤
М (f(x)
≥ m)
для любых х из этого множества. Функция
называется ограниченной на некотором
множестве Х, если она ограничена сверху
и снизу, т.е. если существует М и m
для любых x X
m≤f(x)≤
М
X
m≤f(x)≤
М  |f(x)|
≤ max
{m,M}
|f(x)|
≤ max
{m,M}
Если таких чисел m и М не существует, то функция называется неограниченной
Пример: 
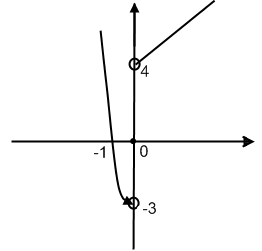
 =>
на (
=>
на ( )
функция кусочно-монотонная, ограничена
снизу и ограничена сверху, т.е. -3<y<
)
функция кусочно-монотонная, ограничена
снизу и ограничена сверху, т.е. -3<y<
Четные и нечетные функции
Функция называется четной (нечетной), если
симметрична относительно начала координат
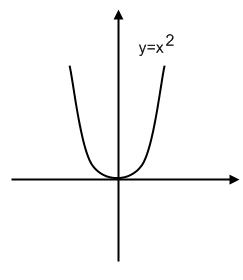

График четной функции симметричен относительно оси Оу, нечетной – относительно начала координат.
Любую функцию f(x), заданную на симметричном относительно начала координат множестве, можно представить в виде суммы четной и нечетной функций на этом множестве. Это следует из того, что
f(x)
= 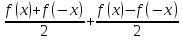
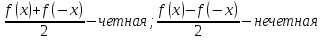
Например,
5х = 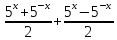
Периодические функции
Функция
f(x)
называется периодической, если существует
такое число T>0,
что для любого х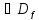
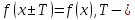 период
функцииf(x)
период
функцииf(x)
Отсюда
следует, что  ,
где с =const
,
где с =const
Числа 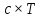 также являются периодами функции. Если
число х
также являются периодами функции. Если
число х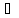
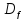 => числа (х+
=> числа (х+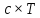 )
)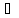
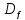 .
Это значит, что если функция периодическая,
то областью определения ее будет
неограниченное множество действительных
чисел, т.е. какое бы большое числоN>0
ни взяли, в
.
Это значит, что если функция периодическая,
то областью определения ее будет
неограниченное множество действительных
чисел, т.е. какое бы большое числоN>0
ни взяли, в 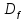 найдется число |x+k
найдется число |x+k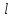 |>
N
при достаточно больших k.
|>
N
при достаточно больших k.
Наименьший положительный период функции f(x), если он существует, определяется минимальным периодом.
Если периодичная функция f(x) определена на всей числовой прямой, за исключением, может быть, изолированных точек, то для получения графика функции f(x) достаточно построить его в каком-либо сегменте [x0, x0+T]. Из сегмента удалены точки, где функция f(x) не определена, поэтому во всех сегментах [x0+сТ, x0+(с+1)T] графики функций f(x) в силу ее периодичности будут одинаковыми.
Например,
y=tg
x
определена для любого x Для
получения графика этой функции достаточно
построить его на интервале (-
Для
получения графика этой функции достаточно
построить его на интервале (- 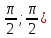
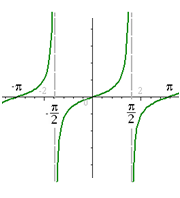
Сложная функция
Функция называется сложной, если ее аргумент в свою очередь является функцией другой переменной.
Если
на некотором множестве Х определена
функция z= со множеством значений
со множеством значений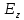 ,
а на множестве
,
а на множестве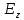 — функция у=f(z),
то функция у=f[
— функция у=f(z),
то функция у=f[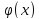 ]
называется сложной функцией от х
[суперпозицией функций
]
называется сложной функцией от х
[суперпозицией функций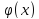 иf(z)],
а переменная z
– промежуточной переменной сложной
функции.
иf(z)],
а переменная z
– промежуточной переменной сложной
функции.
Обратная функция
Пусть
Х и У – некоторые множества и пусть
задана функция f,
т.е. множество пар чисел (х,у) (х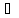 Х, у
Х, у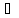 У),
в котором любое число х входит в одну и
только одну пару, а любое число у – по
крайней мере в одну пару. Если в любой
паре этого множества числа х и у поменять
местами, то получим множество пар чисел
(х;у), которое называется обратной
функцией
У),
в котором любое число х входит в одну и
только одну пару, а любое число у – по
крайней мере в одну пару. Если в любой
паре этого множества числа х и у поменять
местами, то получим множество пар чисел
(х;у), которое называется обратной
функцией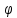 к функцииf.
Обратная функция х=
к функцииf.
Обратная функция х=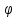 (у).
(у).
Обратная
функция не всегда является функцией,
т.к. каждое число у может входить не
только в одну, но и в несколько пар.
Например, для функции y=x
обратная функция х=у однозначна (любое
число у входит в одну пару), для функции
y=x2 обратная
функция х=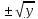 двузначна (любое число у входит в 2 пары),
а обратная функция х=arcsin
y
для функции y=sin
x
многозначна, т.к. любое число у входит
в бесконечное число пар.
двузначна (любое число у входит в 2 пары),
а обратная функция х=arcsin
y
для функции y=sin
x
многозначна, т.к. любое число у входит
в бесконечное число пар.
Из
определения следует, что если обратная
функция однозначна, т.е является функцией
в обычном смысле, то множество значений
У функции f
служит областью определения обратной
функции 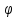 .
Пусть, например, функцияy=f(x)
определена на [a;b],
.
Пусть, например, функцияy=f(x)
определена на [a;b], 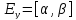 и любое
и любое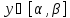 соответствует ровно одномуx
соответствует ровно одномуx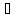 [a;b],
тогда по определению на
[a;b],
тогда по определению на 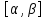 определена однозначная обратная функция
х=
определена однозначная обратная функция
х=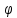 (у),
(у),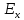 =[a;b].
=[a;b].
Таким
образом, функция y=f(x)
и обратная функция х= (у)
имеют один и тот же график, например,
у=5 х и х=
(у)
имеют один и тот же график, например,
у=5 х и х= у. Если оси Ох и Оу поменять местами, для
чего следует повернуть в пространстве
плоскость Оху вокруг своей биссектрисыI
координатного угла на 1800,
то любое положение графика обратной
функции х=
у. Если оси Ох и Оу поменять местами, для
чего следует повернуть в пространстве
плоскость Оху вокруг своей биссектрисыI
координатного угла на 1800,
то любое положение графика обратной
функции х=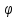 (у)
является графиком функции у=
(у)
является графиком функции у=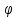 (х).
(х).
Теорема 4.1 (существование обратной функции)
Если
функция y=f(x)
возрастает (убывает) на множестве Х={х},
то на соответствующем множестве У={y}
существует однозначная обратная функция
х=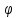 (у),
также возрастающая (убывающая).
(у),
также возрастающая (убывающая).
studfile.net
Явно или неявно заданные функции
Если формула, связывающая аргумент x и функциюy, имеет вид
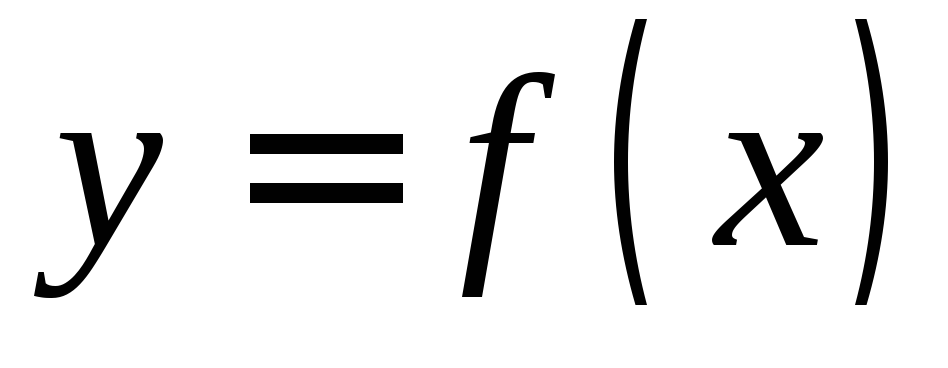 ,
,
то переменнаяy называетсяявно заданной функцией переменной x.
Например, 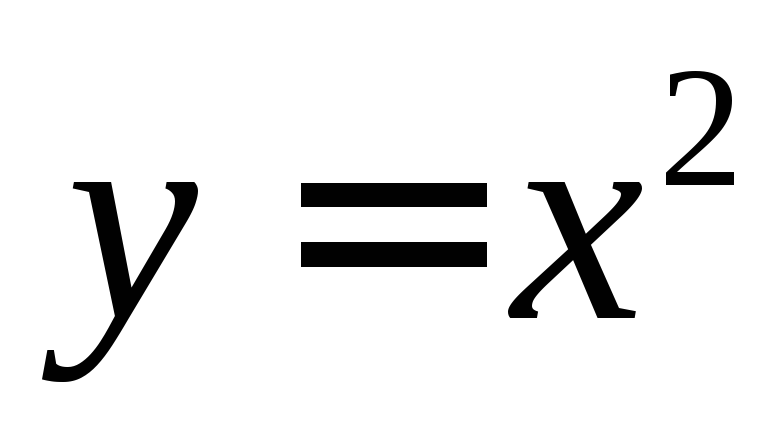 ,
, .
.
Если формула, связывающая аргументxи функциюу, записана в виде уравнения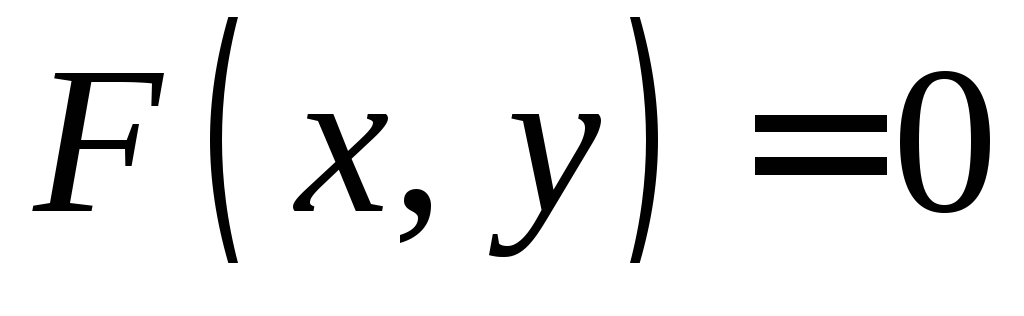 ,
то определяемая из этого уравнения
переменная
,
то определяемая из этого уравнения
переменная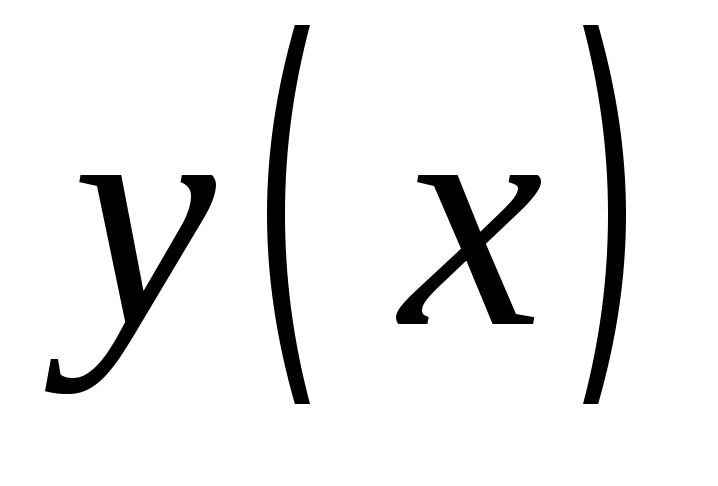 называетсяфункцией,
заданной неявно.
называетсяфункцией,
заданной неявно.
Пример 3 (неявно заданные функции)
1) Уравнение 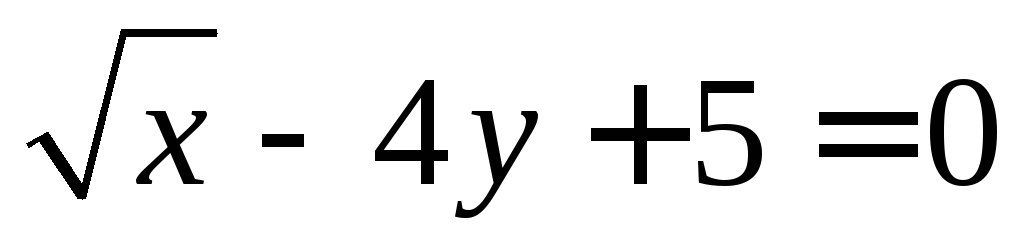 задает неявно функцию
задает неявно функцию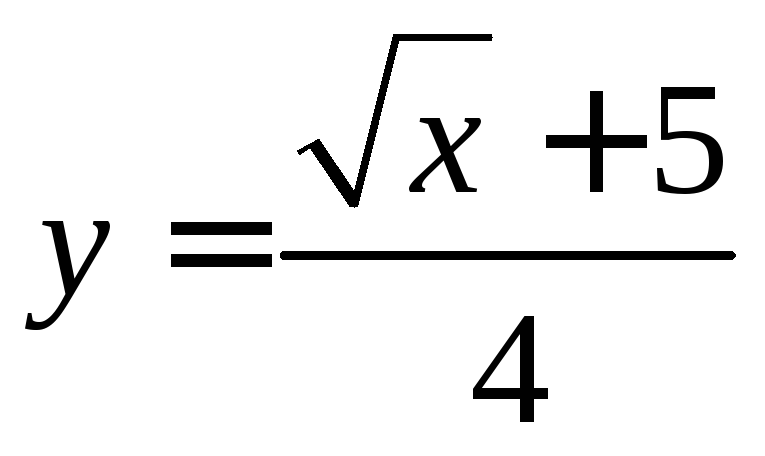 ;
;
2) уравнение  задает неявно функцию
задает неявно функцию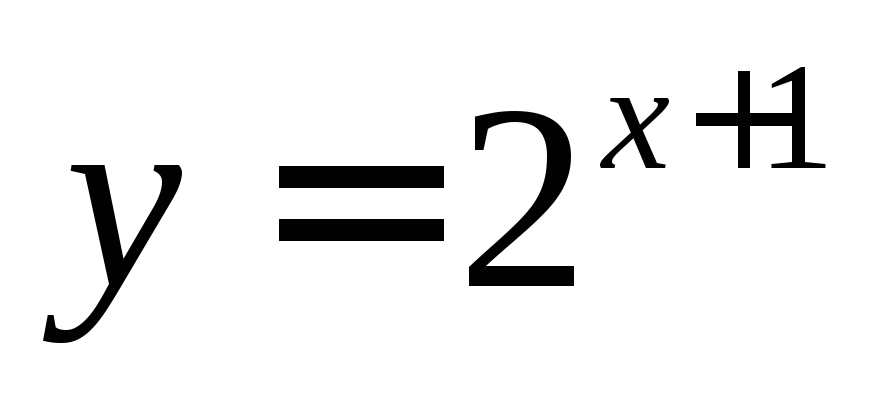 ;
;
3) уравнение  задает неявно две функции;
задает неявно две функции;
4) уравнение 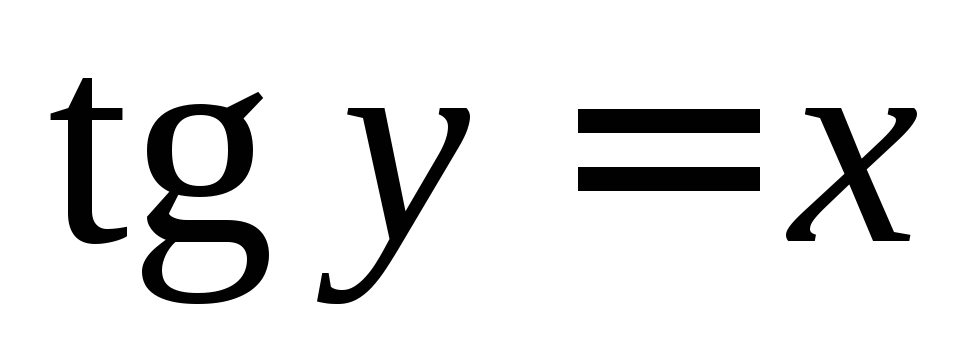 задает неявно бесконечное множество
функций
задает неявно бесконечное множество
функций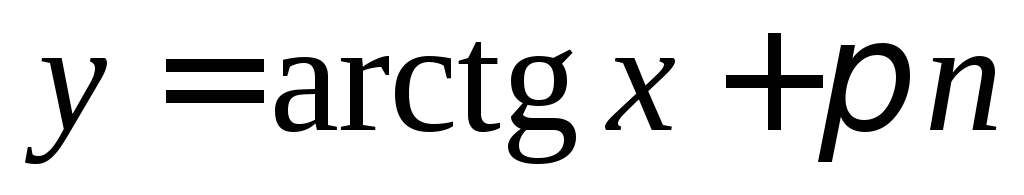 ,
,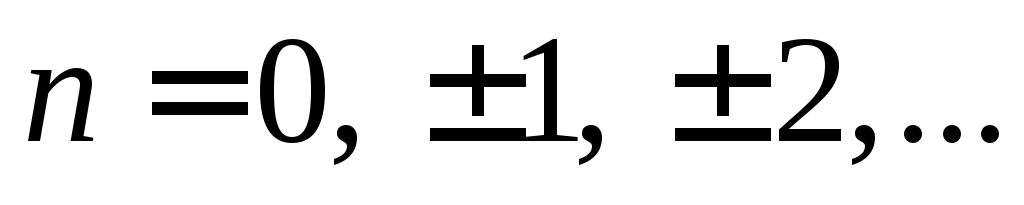 .
.
Из
примеров видно, что если уравнение 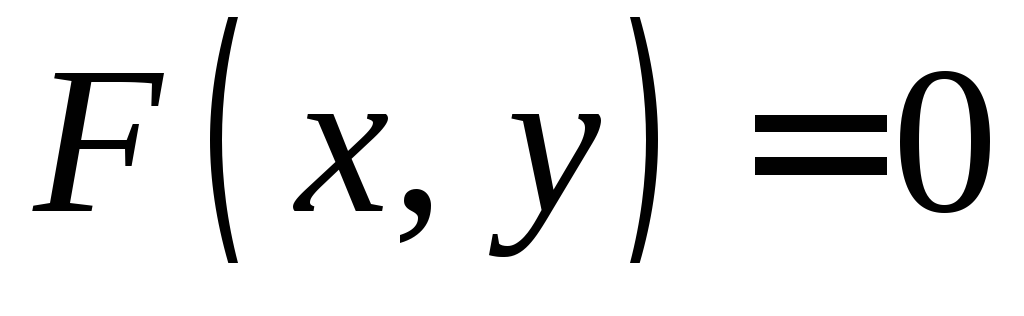 удается решить относительноу, то
осуществляется переход от неявно
заданной функции к ее явному заданию
удается решить относительноу, то
осуществляется переход от неявно
заданной функции к ее явному заданию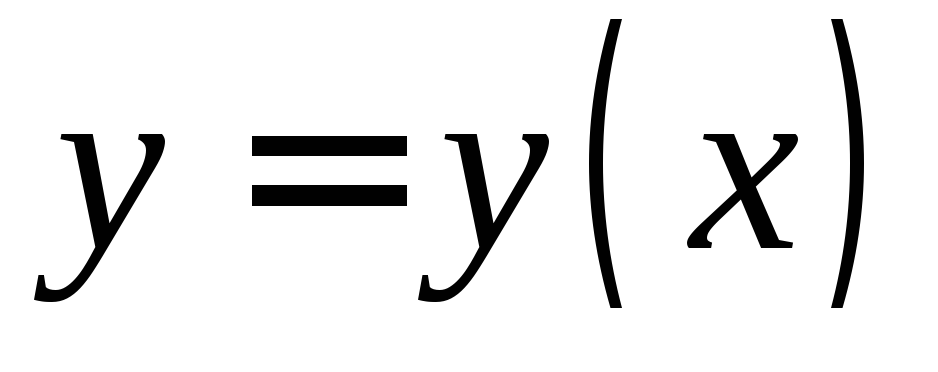 .
При этом часто получается многозначная
функция, которую всегда можно рассматривать
как совокупность однозначных функций
(совокупность однозначных ветвей
многозначной функции).
.
При этом часто получается многозначная
функция, которую всегда можно рассматривать
как совокупность однозначных функций
(совокупность однозначных ветвей
многозначной функции).
Например, 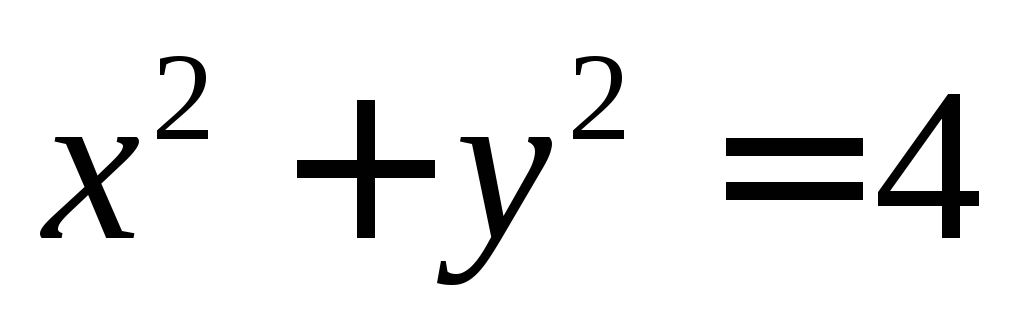
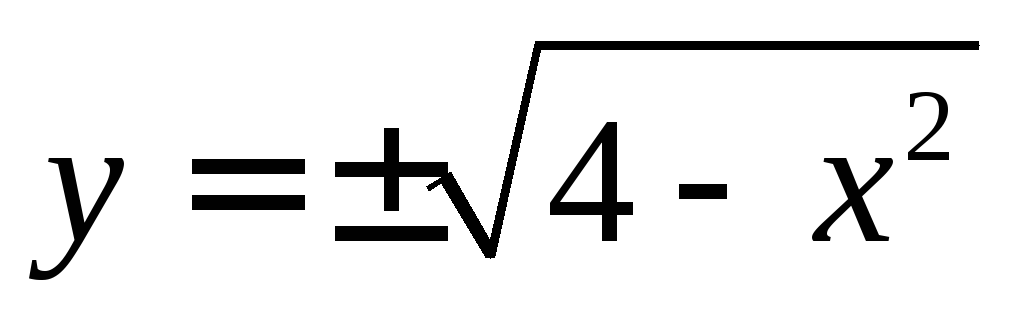
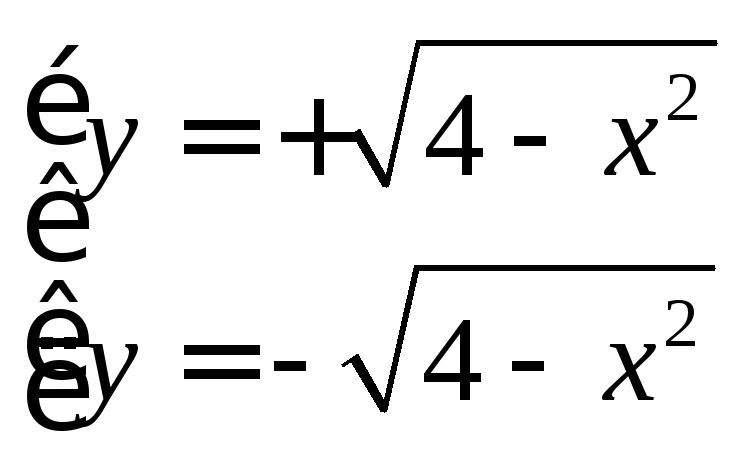 ;
;
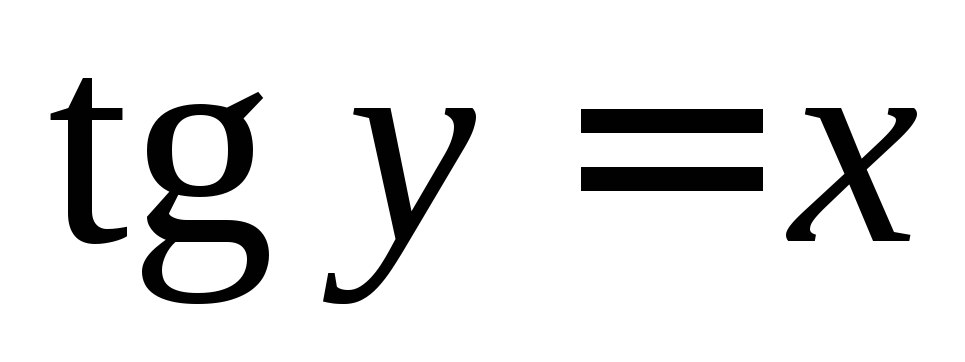
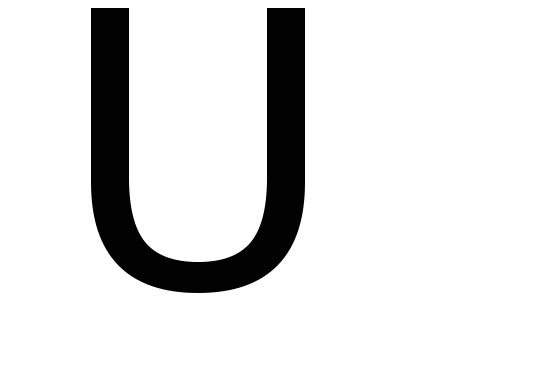
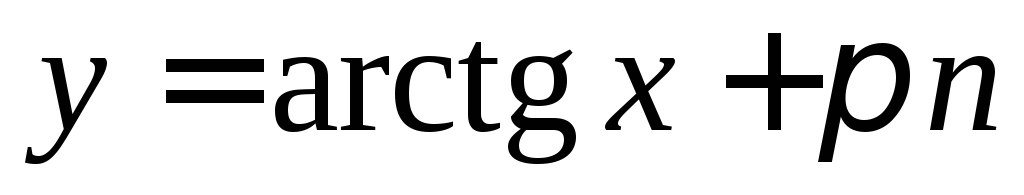 ,
,
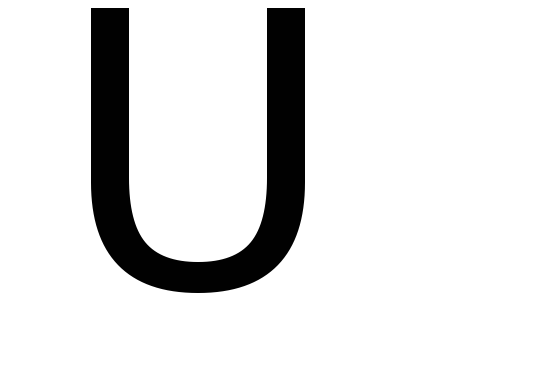
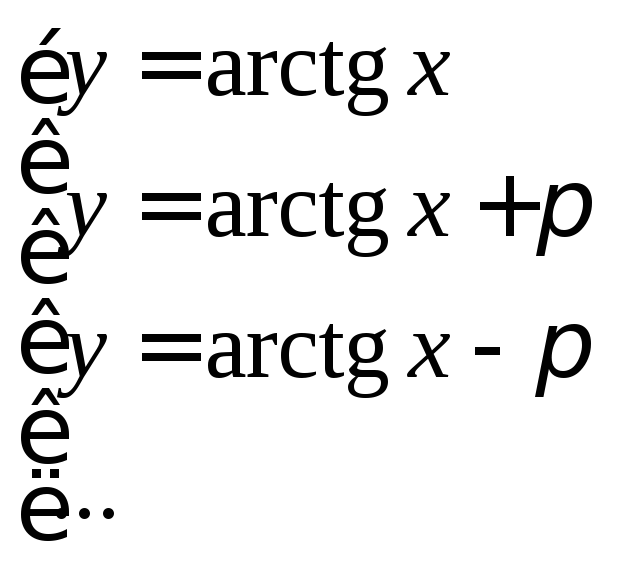
Однако на практике
решить уравнение 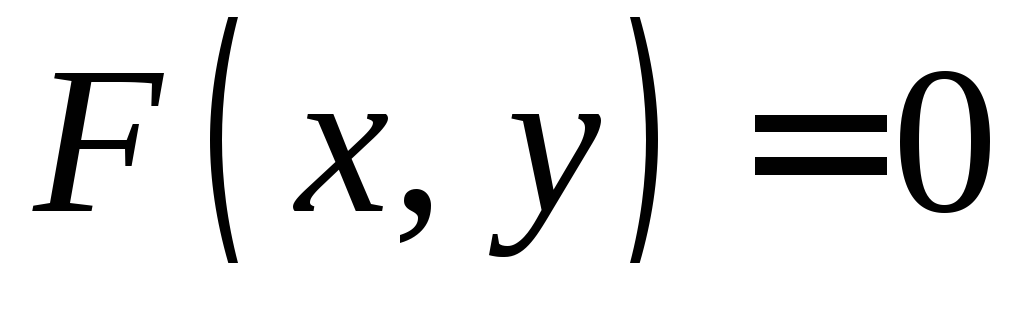 относительно переменнойуполучается
далеко не всегда или это решение
получается слишком громоздким. Например,
уравнение
относительно переменнойуполучается
далеко не всегда или это решение
получается слишком громоздким. Например,
уравнение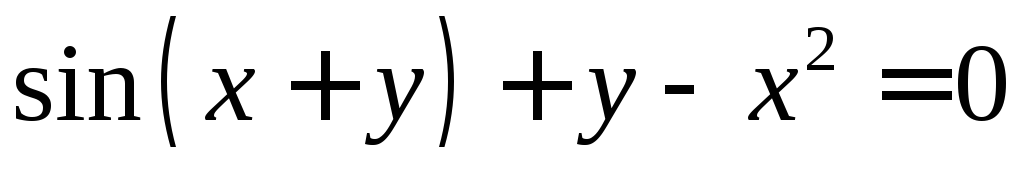 нельзя решить относительноy.
Поэтому в этих случаях приходится
работать с функциями, имеющими только
неявное задание.
нельзя решить относительноy.
Поэтому в этих случаях приходится
работать с функциями, имеющими только
неявное задание.
Замечание (к неявному заданию функций)
В
уравнении 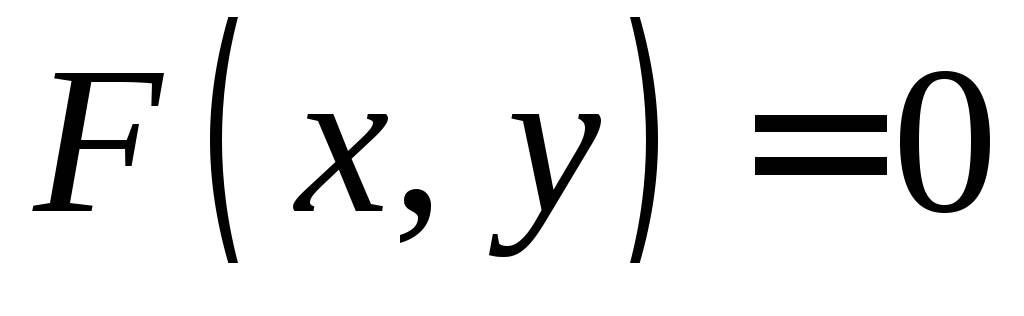 переменныеx и y входят
равноправно, поэтому можно считать, что
это уравнение задает неявно функцию
переменныеx и y входят
равноправно, поэтому можно считать, что
это уравнение задает неявно функцию 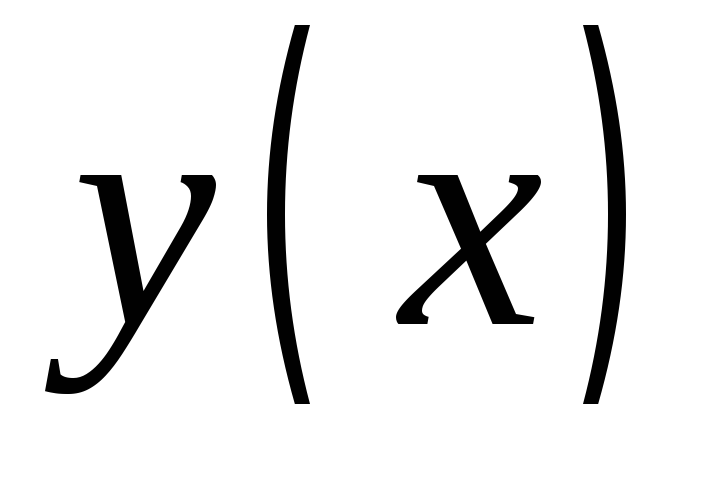 или функцию
или функцию .
.
Например, 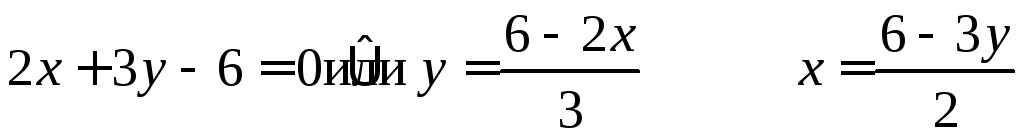 .
.
Параметрически заданные функции
Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
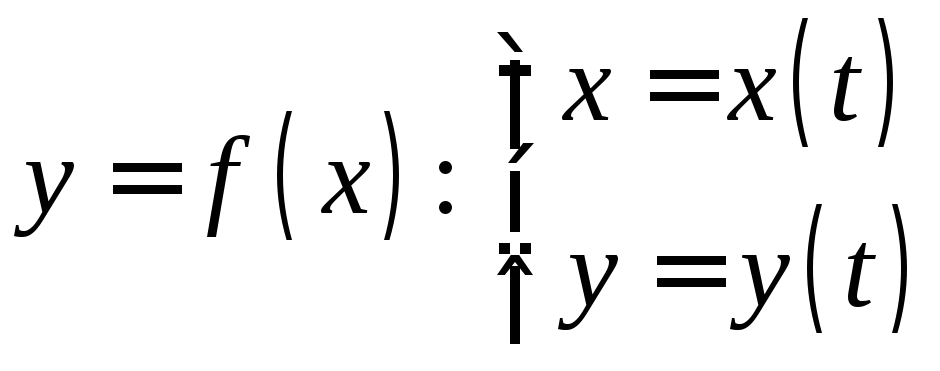 ,
где
,
где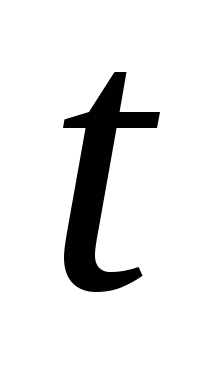 – это параметр,
– это параметр,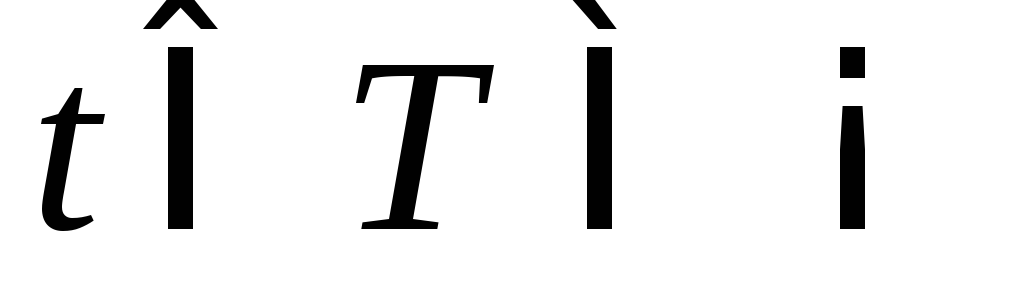 .
.
В этом случае функция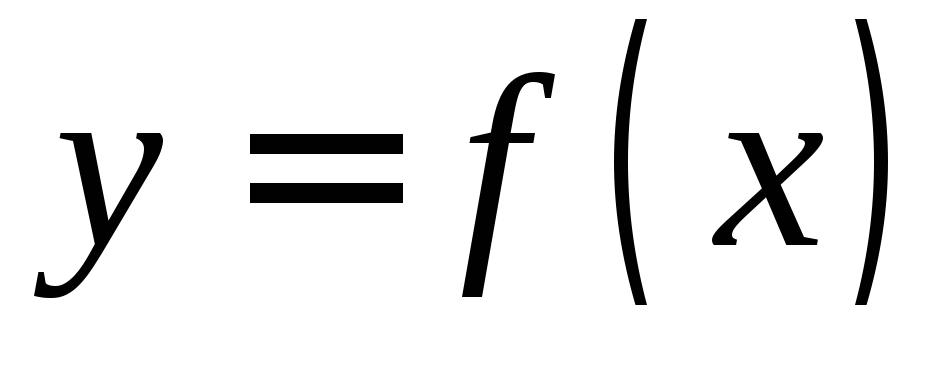 называетсяфункцией,
заданной параметрически.
называетсяфункцией,
заданной параметрически.
Например, в механике при описании движения точки по некоторой траектории задаются абсцисса и ордината движущейся точки как функции времени t (рис. 41).
От параметрически заданной функции можно перейти к явной или неявной форме её задания, если удаётся исключить параметр t.
Пример 4 (параметрически заданные функции)
1.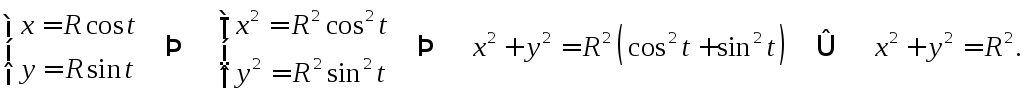
Таким образом,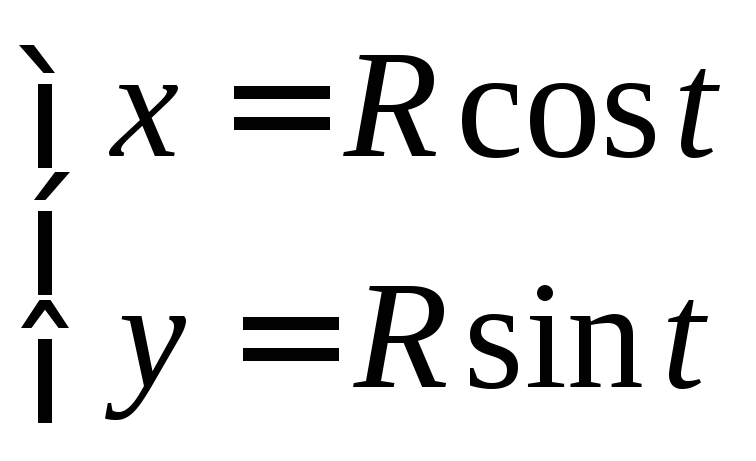 — это естьпараметрические
уравнения окружности радиуса R с центром
в начале координати, следовательно, задают две функции
— это естьпараметрические
уравнения окружности радиуса R с центром
в начале координати, следовательно, задают две функции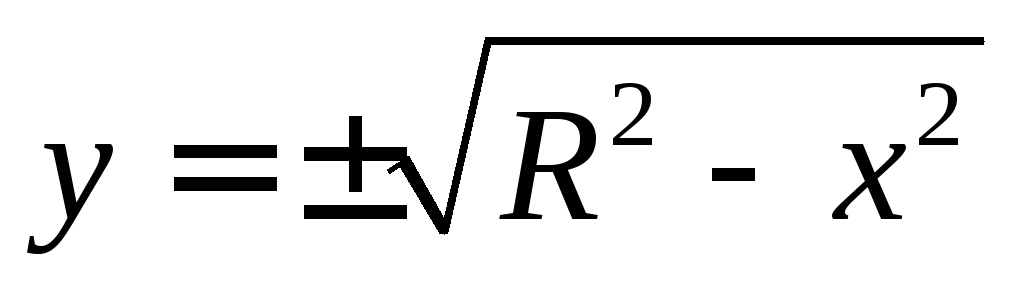 ,
, :
:
| на верхней полуокружности на нижней полуокружности |
2.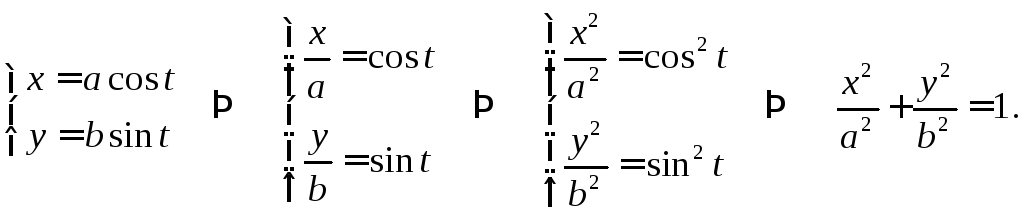
Таким образом, — это естьпараметрические
уравнения эллипса с полуосями a и b и с
центром в начале координат,
они задают две функции:
— это естьпараметрические
уравнения эллипса с полуосями a и b и с
центром в начале координат,
они задают две функции:
x | на верхней половине эллипса на нижней половине эллипса |
3.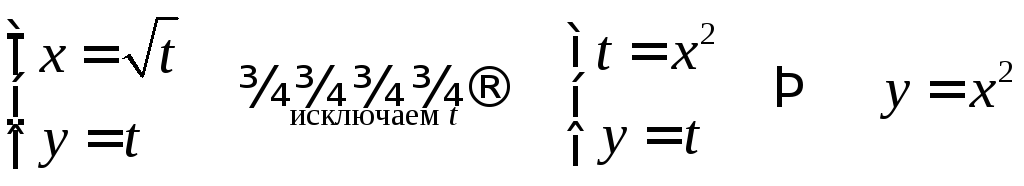 — уравнение параболы;
— уравнение параболы;
| уравнение той же параболы. |
Из последнего примера хорошо видно, что для одной и той же функции можно записать несколько вариантов параметрических уравнений, вводя по-разному параметр.
Выполнить исключение параметра из параметрических уравнений не всегда возможно, поэтому нужно уметь работать и с функциями, имеющими только параметрические задания.
График функции
Графиком
функции называется множество точек
называется множество точек координатной плоскости, координаты
которых есть соответствующие друг другу
значения аргумента и функции (рис. 42).
координатной плоскости, координаты
которых есть соответствующие друг другу
значения аргумента и функции (рис. 42).
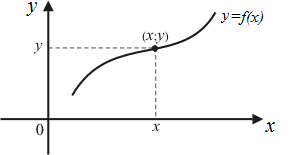
Рис. 42
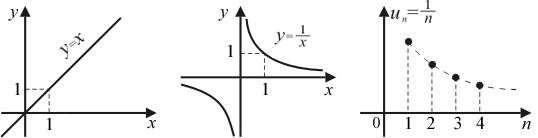
Графиком функции может быть линия или несколько линий или дискретное множество точек (рис.43).
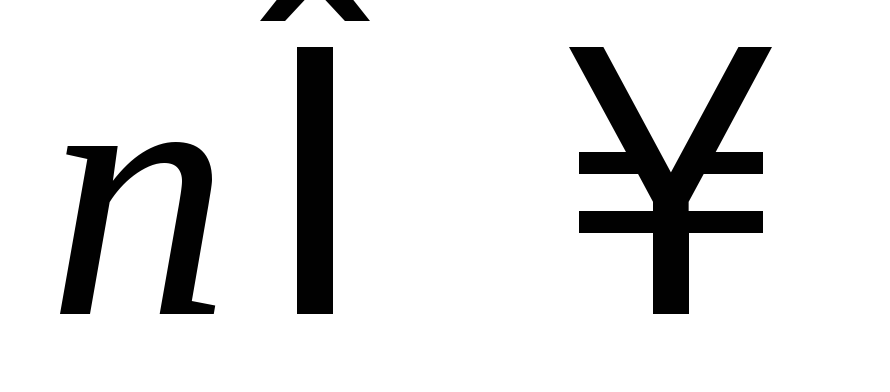




0
0
Рис. 43
График функциональной зависимости может строиться не только в системе декартовых прямоугольных координат XOY, но и в других координатных системах.
Например, в полярной системе координат функцияy = xзаписывается в виде = и имеет графикомспираль Архимеда(рис. 44).
Рис. 44 | Здесь
показана часть спирали при |
По
умолчанию график функции 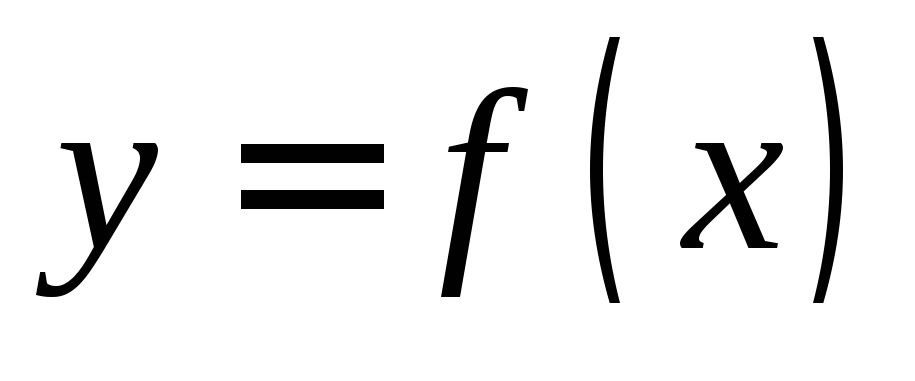 строится в системе прямоугольных
декартовых координатXOY.
строится в системе прямоугольных
декартовых координатXOY.
studfile.net
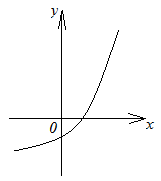
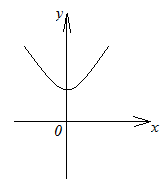

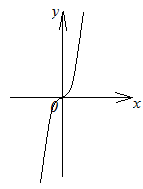
 изображен на рисунке 2.4. График нечетной
функции
изображен на рисунке 2.4. График нечетной
функции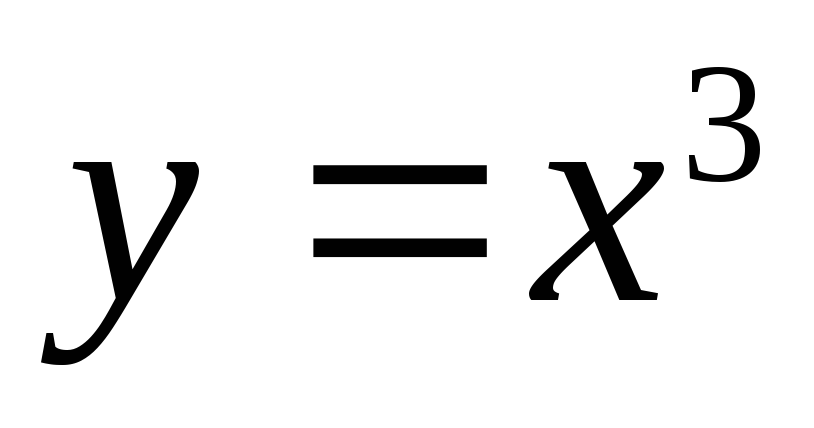 изображен на рисунке 2.5. Заметим, что
не всякая функция является четной или
нечетной.
изображен на рисунке 2.5. Заметим, что
не всякая функция является четной или
нечетной. ,
,  ,
,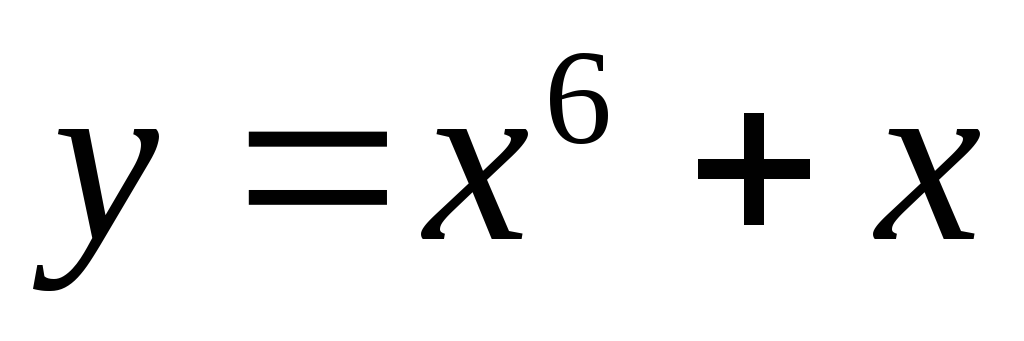
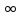 ;
+
;
+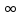 )
и такая же область значений;
)
и такая же область значений;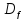 = [-1; 1],
= [-1; 1],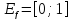
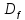 =
{1, 2, 3, … , n, …}= N,
=
{1, 2, 3, … , n, …}= N,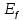 ={1!,
2!, 3!, … , N!, …}
={1!,
2!, 3!, … , N!, …}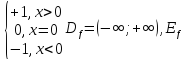 =
{-1, 0, 1}
=
{-1, 0, 1}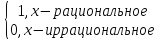
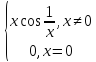
 ,
m
,
m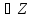 ;
a0,
a1,…
, am–
любые целые числа (а0
;
a0,
a1,…
, am–
любые целые числа (а0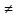 0)
– коэффициенты
0)
– коэффициенты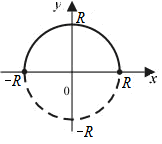
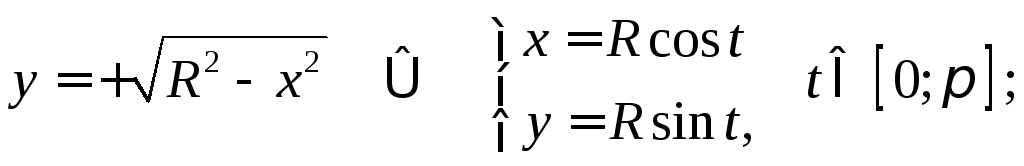
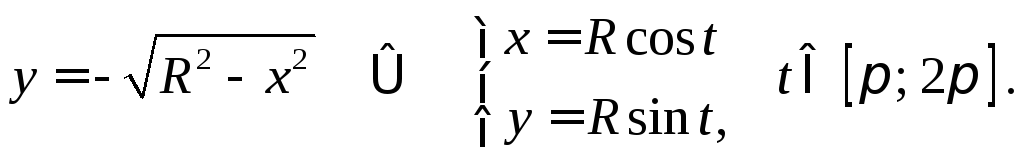

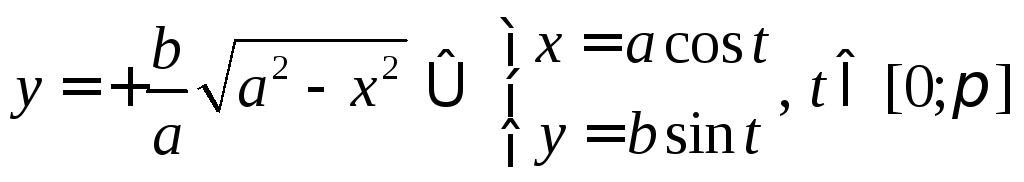 ;
;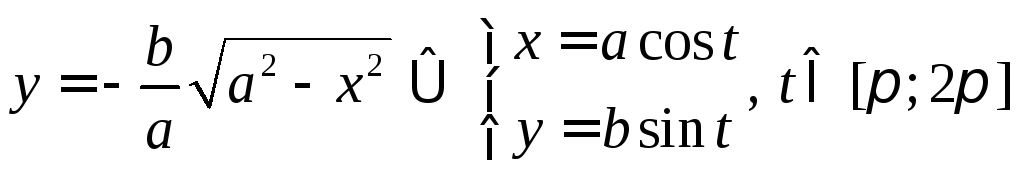 .
.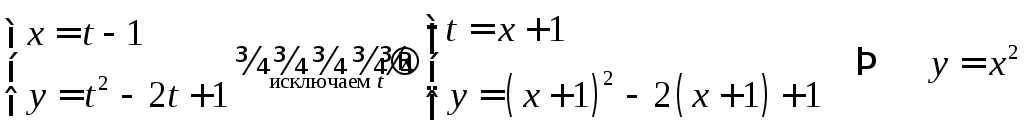 —
—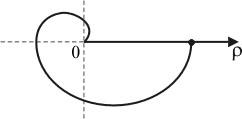

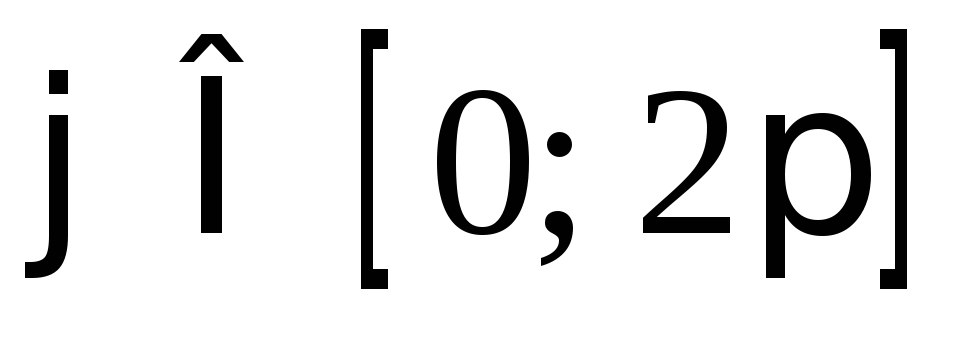 (первый завиток спирали Архимеда). В
общем случае спираль Архимеда задается
уравнением
= aφ.
(первый завиток спирали Архимеда). В
общем случае спираль Архимеда задается
уравнением
= aφ.