Теорема Фалеса ℹ️ формулировка и доказательство, применение в геометрии, решение задач, интересные факты об обобщенной теореме

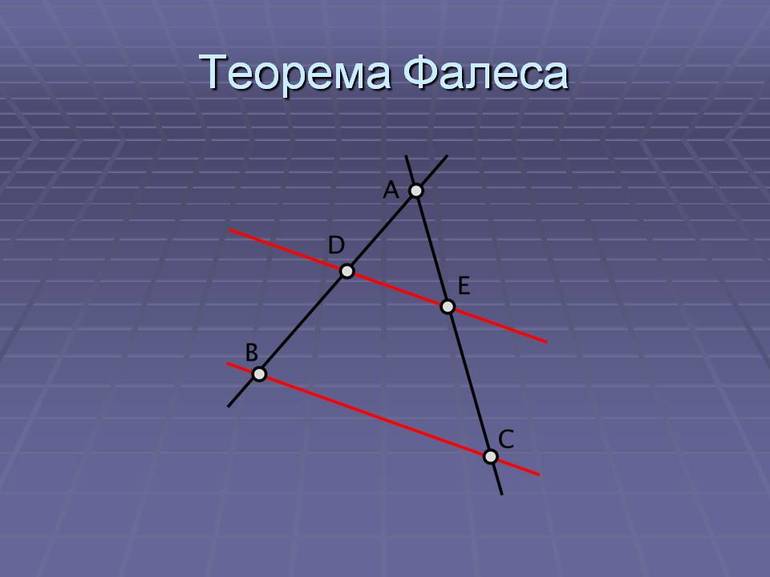
Краткое описание

Фалес хорошо известен в истории как талантливый геометр. Именно этому человеку многие учёные приписывают открытие и доказательство многих теорем. Фалес смог разработать весьма интересный способ определения точного расстояния от берега до видимого невооружённым взглядом водного транспорта. Некоторые историки склонны полагать, что именно для этих целей учёный использовал признак некоего сходства прямоугольных треугольников. Современные последователи великого математика высоко ценят все его достижения, что он смог вывести и доказать многочисленные теоремы, законы.

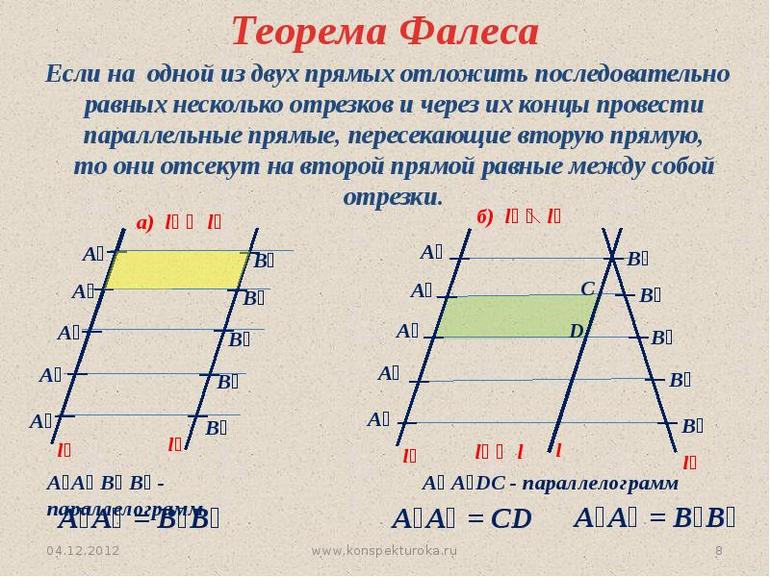
Наиболее логическое доказательство правильности предположений на основании единых положений, принятых за проверенные истины, было изобретено именно греками. Сегодня историкам трудно сказать, что именно в научном перечне принадлежит Фалесу. Конечно, благодаря этому талантливому человеку Греция обрела не только философа и математика, но и естествоиспытателя.

Перед изучением теоремы обязательно нужно понять, что параллелограмм — это самый обычный четырёхугольник, у которого все противоположные стороны попарно параллельны. А вот трапеция является специфическим четырёхугольником, у которого две стороны параллельны друг другу, а две другие стороны обладают противоположными характеристиками. Изучение этой темы состоит из нескольких частей, так как первым делом нужно ознакомиться с теорией, а только потом можно приступать к решению задач.

Основные понятия

Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.

Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии. А это значит, что все линии, которые параллельны одной прямой, являются параллельными между собой. Математики полагают, что итоговый угол между параллельными линиями приравнивается 0. Но это утверждение актуально только в том случае, если у отрезков одинаковые направления и они расположены под углом 180 градусов.

В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю

Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи. В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.

Научное пояснение значений

Если постараться поочерёдно отложить сразу несколько одинаковых отрезков только на одной из двух прямых линий, а потом провести прямые через конечные точки, которые смогут пересечь вторую прямую, то именно на второй прямой они смогут отсечь равные отрезки. Развёрнутая формулировка этой темы в геометрии носит название теоремы о пропорциональных геометрических отрезках. В качестве наглядного примера следует ознакомиться с этой формулой: S1S2/N1В2 = S2S3/N2N3 = S1S3/N1N3.

Важные нюансы:

• Востребованная теорема греческого математика является частным случаем закона о пропорциональных отрезках, так как идентичные отрезки можно считать пропорциональными с элементарным коэффициентом ровности, который равняется единице.
• В изучаемой теореме нет каких-либо ограничений и требований на взаимное расположение всех секущих. Это связано с тем, что она верна как для пересекающихся прямых, так и для параллельных линий. На итоговый результат совершенно не влияет то, где находятся отрезки на секущих.

Для изучения всех нюансов этой темы необходимо рассмотреть вариант, который демонстрирует ситуацию с несвязанными парами отрезков. К примеру: существующий угол пересекает прямые LL1 || ВВ1 || СС1 || КК1 и при этом LB = СК. Через точки L и С проводят прямую линию, которая будет расположена параллельно другой стороне сформированного угла LB2В1L1 и СК2К1С1. Свойства параллелограмма тоже имеют свои особенности:

1. LB2 = L1В1.
2. СК2 = С1К1.

Треугольники ? JSS2 и ? СКК2 равны. Они построены на основании второго признака равенства геометрических фигур. Если целью задачи является безусловное доказательство при параллельных прямых, тогда нужно выполнить несколько несложных действий. Следует провести прямую SC. Углы SCK и JSC равны как внутренние накрест лежащие при прямых СК и JS, а также секущей SC. А вот углы JCS и CSK равны как внутренние накрест проложенные линии при параллельных прямых JC и SK, секущий SC. Тогда по второму признаку равенства треугольников геометрические фигуры JSC и KCS равны. Из этого вытекает, что JC = SK и JS = СК.

Ключевые особенности теоремы

Когда учащийся попробует на одной из двух прямых линий отложить разные отрезки, а потом через их концы провести параллельные линии, которые будут пересекать вторую прямую, то в итоге на второй прямой они обязательно отсекут идентичные между собой отрезки. Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.

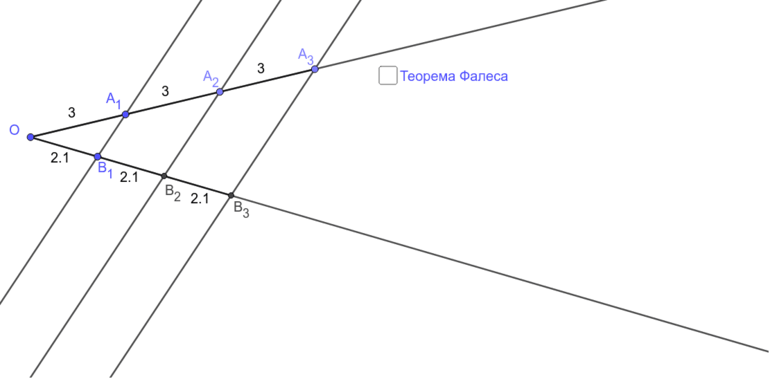
Записи с идеями Фалеса не удалось сохранить до наших дней, из-за чего историкам приходится восстанавливать информацию из разных источников. Специалистам удалось доказать, что математик из Греции вывел 7 теорем для геометрии. Основное правило гласит, что если параллельные линии, у которых пересекаются стороны угла, отсекают только на одной его стороне равные отрезки, то аналогичная ситуация происходит и на другой его стороне.

Наглядное доказательство

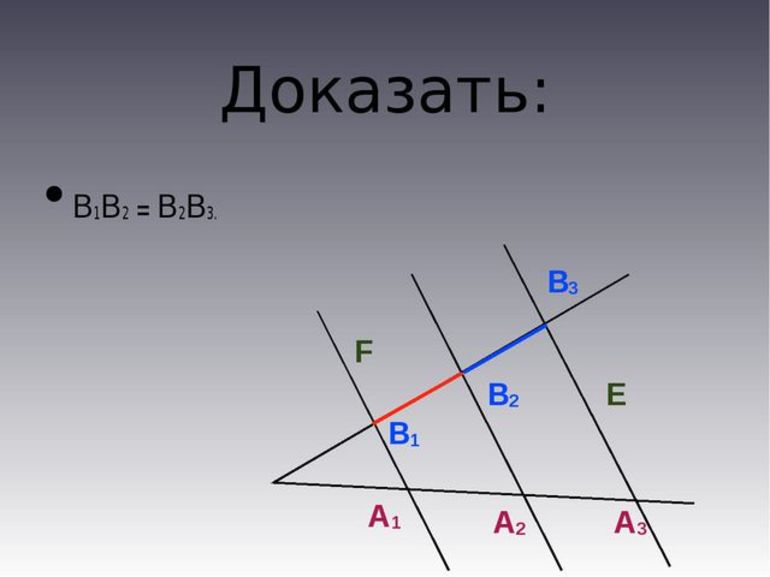
В качестве примера можно взять точки Н1, Н2 и Н3, которые служат для обозначения пересечения используемых параллельных отрезков только с одной стороны угла. А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.

? Т1В2В1 = ? Т2В2В3 — это утверждение актуально только по отношению ко второму признаку равенства треугольников. Можно понять, что Т1В2 = В2Т2, < Т1В2В1 = < Т2В2В3 (как вертикальные треугольники). < В1Т1В2 = < = В3Т2В2 (как внутренние накрест лежащие треугольники при прямых линиях В1Т1 и Т2В3, а также секущем отрезке Т1Т2). Из установленного равенства треугольников получается, что В1В2 = В2В3. На этом можно считать, что теорема в геометрии полностью доказана. Если всё сделано правильно, то в итоге должна получиться следующая формула: (АВ = ВТ, АА1 || ВВ1 ||ТТ1) А1В1 = В1Т1.

Интересные нюансы из истории

Обобщение теоремы позволило современным математикам понять пропорциональность конкретного отрезка. Действующее правило гласит, что параллельные прямые, которые пересекают стороны угла, отсекают пропорциональные отрезки. Формула выглядит следующим образом: АА1 || ВВ1 || ТТ1 → АВ ВС = А1В1/В1Т1.

Применение обобщённой теоремы имеет несколько интересных исторических фактов:

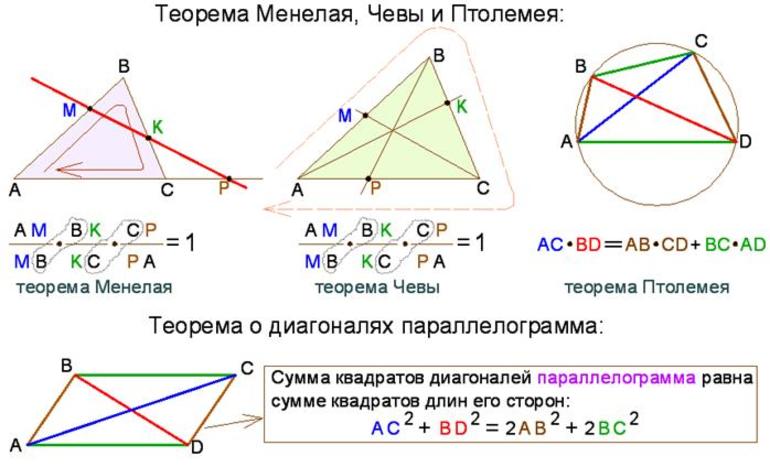
1. За пределами русской литературы широко распространённой теоремой известного математика Фалеса принято называть раздел евклидовой геометрии. Утверждение касается того, что сформированный угол, который базируется на определённом диаметре окружности, является прямым. Доказательство этой удивительной теоремы действительно приписывают Фалесу, так как этому есть письменное доказательство, которое удалось сберечь.
2. Теоремы Менелая, Фалеса и Чевы используются в первую очередь тогда, когда в условиях задачи были даны соотношения между отрезками. Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок.
3. В морской отрасли активно используется теорема при построении навигации. Она применяется в качества основного правила о том, что столкновение кораблей, которые движутся по волнам с одинаковой скоростью, неизбежно, если сохранится ранее заданный курс движения.
4. Известная в Аргентине группа представила песню, которая посвящена теореме. В представленном клипе для этой песни было приведено доказательство для прямой теоремы используемых пропорциональных отрезков.
5. Все азы геометрии Фалес постигал на территории Древнего Египта.

Теорему талантливого учёного из Греции активно изучают в 8 классе на уроках геометрии.

Вариации и обобщения

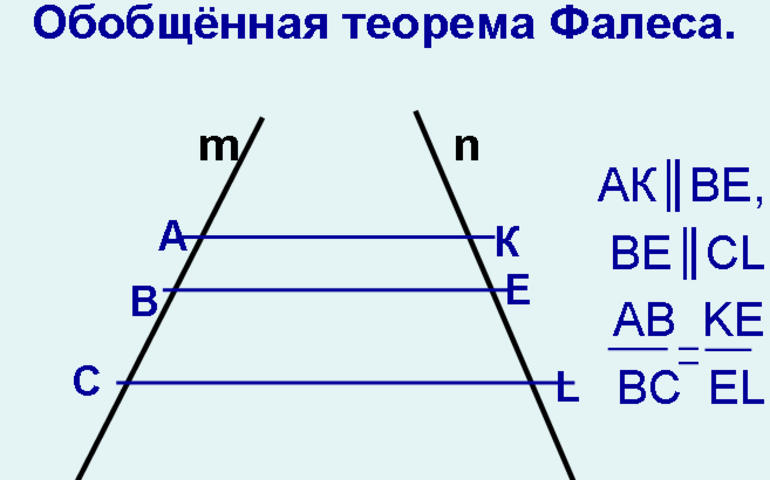
Используемая в геометрии теорема Фалеса с доказательством имеет много нюансов, которые нужно учитывать тем, кто решил изучить эту тему. Если абсолютно идентичные отрезки начинаются от вершины треугольника, то и обратная форма теоремы будет уместной. Для пересекающихся линий предназначена следующая формулировка: если 2 линии пересекают ближайшие прямые, отсекая при этом равные между собой отрезки начиная от самой верхней части, то такие прямые считаются параллельными. Эти нюансы часто не учитывают учащиеся, из-за чего допускают грубые ошибки.

Максимального сходства отрезков на обеих секущих линиях нужно требовать в том случае, если секущие являются параллельными. В противном случае утверждение становится неактуальным. Учащимся нелишним будет узнать следующий закон: L является математическим соответствием между двумя точками прямых линий w и q. Тогда элементарное множество прямых D L (D) будет множеством касательных к некоторому коническому сечению. В приведённой Фалесом теореме в роли конического сечения будет выступать удалённая точка, которая максимально соответствует направлению параллельных линий.

Огромные заслуги талантливого математика

В своё время Фалес Милетский был главным основателем Ионийской школы. Неоценимой заслугой этого человека было создание многофункциональной научной геометрии. Великий учёный специфического египетского искусства измерения смог самостоятельно создать полезную для человечества дедуктивную геометрию.

Благодаря целеустремлённости Фалеса все доступные в то время знания были оперативно переведены в научную категорию. Математик смог донести результаты своих наблюдений до того уровня, который подходит для учеников школ, указав при этом на определённый комплекс понятий. Доказанная талантливым и наблюдательным Фалесом теорема играет одну из самых важных ролей в геометрии. Она была хорошо известна не только в Древнем Египте, но и в других крупных странах. Актуальность и многогранность теоремы позволяет специалистам ежедневно строить новые здания, дороги и другие конструкции.

Фалес смог при помощи обычного посоха и тени установить габариты египетской пирамиды. Для этого он в обычный ясный день закрепил свой массивный посох на том участке, на котором заканчивалась тень от величественного сооружения. Он весь день прождал того момента, когда итоговая длина имеющейся тени от посоха максимально сравнялась с его высотой, после он измерил длину тени.

Благодаря этому он смог доказать всем, что длина одной тени имеет прямое отношение к другой тени, а вот сама высота посоха прямо пропорциональна высоте пирамиды. Эти соображения учёного поразили могущественного фараона по имени Амасис.

nauka.club

Теорема Фалеса — это… Что такое Теорема Фалеса?

Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.

Теорема Фалеса — одна из теорем планиметрии.

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

Доказательство в случае секущих  

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Также существует обобщённая теорема Фалеса:

Параллельные прямые отсекают на секущих пропорциональные отрезки:

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что следует, что прямые .

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Вариации и обобщения

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть  — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни^[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.

Интересные факты

• Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Литература

• Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

dic.academic.ru

Теорема Фалеса. Подобие треугольников. Видеоурок. Геометрия 7 Класс

На этом уроке мы рассмотрим определение подобных фигур – фигур, которые в быту мы называем похожими. Кроме того, рассмотрим теорему Фалеса, которую мы будем использовать в качестве инструмента для доказательства различных теорем.

До сих пор мы говорили о равенстве: фигуры равны, если при наложении они совмещаются, т. е. у них совпадают и форма, и размеры.

Иногда нас могут интересовать только размеры фигур без учета их формы. Для этого мы ввели такую характеристику, как площадь. Если у фигур площади равны (такие фигуры называются равновеликие), то они занимают одну и ту же (по размерам) часть плоскости, при этом форма фигур нас не интересует (см. рис. 1).

Рис. 1. Фигуры с равными площадями

Но чаще всего нас будет интересовать совпадение фигур по форме без учета размеров. Почему так? Монеткой в руке можно полностью закрыть Луну. И монета, и Луна имеют форму круга, но радиус монеты несколько сантиметров, а Луны – больше тысячи километров.

На видимые размеры объектов влияют не только их реальные размеры, но и расстояние до этих объектов. Если изобразить два объекта, то без указания масштаба нельзя будет понять, одинаковые ли у них размеры. А вот форма объекта от расстояния до него и введенного масштаба не зависит: форма Луны не изменится от того, приблизимся мы к ней или удалимся от нее.

У фигур с одинаковой формой много общих свойств, поэтому, изучив одну из них, мы получим результат для всех объектов такой формы.

Теперь нужно определиться, что такое «одинаковая форма». Если поле нужно разделить между пятью людьми, то никто не будет бегать по полю с линейками. Поле нарисуют на бумаге, разделят сначала его и только потом – настоящее поле. Очень часто большую фигуру-оригинал заменяют меньшей, но такой же формы. Поле, план квартиры, карта города, схема кинотеатра и т. д. – это примеры соответствия: если наша цель – выбор места, то схема зала эквивалентна самому залу.

В геометрии соответствие называется подобием. Значение этого слова нам известно: два объекты подобны, если они похожи. Но что такое похожесть с точки зрения геометрии?

Дети рисуют дом. На каком из рисунков получилось похоже (см. рис. 2)? На третьем.

Рис. 2. Рисунки домов

Мы уже говорили об этом, когда изучали пропорции: их размеры пропорциональны. Итак, для похожести требуется выполнение двух условий: одинаковая форма и пропорциональность размеров.

Поскольку мы выделяем различные по форме классы фигур (треугольники, четырехугольники, окружности и т. д.), то, очевидно, что можно говорить только о подобии внутри одного класса: подобные треугольники, подобные четырехугольники, подобные окружности и т. д.

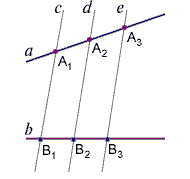
Пропорциональность размеров говорит о том, что если один из подобных объектов увеличить (или уменьшить) в несколько раз, то он совпадет с другим. Тогда понятно, что все окружности подобны, т. к. они задаются всего одним параметром – радиусом. Действительно, возьмем любые две окружности с радиусами 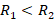. Совместим их центры (см. рис. 3). Если увеличить радиус первой окружности

interneturok.ru

Фалес Милетский, или о том, как важно знать подобие треугольников и теорему Фалеса.

Эта гробница мала, но слава над ней необъятна.
В ней перед тобою сокрыт многоразумный Фалес.

Надпись на гробнице Фалеса Милетского
 

Представьте себе такую картину. 600 г. до н.э. Египет. Перед вами огромнейшая египетская пирамида. Чтобы удивить фараона и остаться у него в фаворитах вам нужно измерить высоту этой пирамиды. В  распоряжении у вас… ничего. Можно пасть в отчаяние, а можно поступить, как Фалес Милетский: использовать теорему подобия треугольников. Да, оказывается, все достаточно просто. Фалес Милетский подождал пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая соответственно, была равна тени, отбрасываемой пирамидой.  

Кто же такой этот Фалес Милетский? Человек, который обрел славу одного из «семи мудрецов» древности? Фалес Милетский – древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Годы его жизни были установлены только приблизительно: 625-645 гг до н.э.

Среди доказательств знания Фалесом астрономии можно привести следующий пример. 28 мая 585 г до н.э. предсказание Милетским солнечного затмения помогло прекратить длившуюся уже 6 лет войну между Лидией и Мидией. Это явление настолько испугало мидян, что они согласились на невыгодные для себя условия заключения мира с лидийцами.

Довольно широко известна легенда, которая характеризует Фалеса как находчивого человека. Фалесу часто приходилось слышать нелестные отзывы о его бедности. Однажды он решил доказать то, что и философы могут при желании жить в достатке. Еще зимой Фалес по наблюдению за звездами определил, что летом будет хороший урожай маслин. Тогда же он нанял маслодавильни в Милете и на Хиосе. Это обошлось ему довольно дешево, так как зимой спрос на них практически отсутствует. Когда же маслины дали богатый урожай, свои маслодавильни Фалес начал сдавать внаем. Собранное большое количество денег таким методом расценивалось как доказательство того, что философы могут зарабатывать своим умом, но их призвание выше таких земных проблем. Эта легенда, кстати, повторялась самим Аристотелем.

Что же касается геометрии, то многое из его «открытий» было позаимствовано у египтян. И все же этот перенос знаний в Грецию считается одной из основных заслуг Фалеса Милетского.

Достижениями Фалеса считаются формулировка и доказательство следующих теорем:

• вертикальные углы равны;
• равными треугольниками признаются те, у которых сторона и два прилегающих угла соответственно равны;
• углы при основании равнобедренного треугольника равны;
• диаметр делит круг пополам;
• вписанный угол, опирающийся на диаметр, является прямым.

Именем Фалеса названа еще одна теорема, которая полезна при решении геометрических задач. Существует ее обобщенный и частный вид, обратная теорема, формулировки также могут немного отличаться в зависимости от источника, но смысл их всех остается одним. Рассмотрим эту теорему.

Если параллельные прямые пересекают стороны угла и отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Допустим, точки А₁, А₂, А₃ – точки пересечения параллельных прямых с одной из сторон угла, а В₁, В₂, В₃ – точки пересечения параллельных прямых с другой стороной угла. Необходимо доказать, что если А₁А₂ = А₂А₃, то и В₁В₂ = В₂В₃.

Через точку В₂ проведем прямую, параллельную прямой А₁А₂. Обозначим новую прямую С₁С₂. Рассмотрим параллелограммы A₁C₁B₂A₂ и A₂B₂C₂A₃.

Свойства параллелограмма позволяют нам утверждать, что A1A2 = C₁B₂ и A₂A₃ = B₂C₂.  А так как по нашему условию А₁А₂ = А₂А₃, то и C₁B₂ = В₂С₂.

И, наконец, рассмотрим треугольники Δ C₁B₂B₁ и Δ C₂B₂B₃.

C₁B₂ = B₂C₂ (доказано выше).

<C₁B₂B₁ и <C₂B₂B₃ вертикальные, т.е. равны.
<B₁C₁B₂ и <B₃C₂B₂ внутренние накрестлежащие.

А это значит, что Δ C₁B₂B₁ и Δ C₂B₂B₃ будут равны по второму признаку равенства треугольников (по стороне и прилегающим углам).

Таким образом, теорема Фалеса доказана.

Использование данной теоремы значительно облегчит и ускорит решение геометрических задач. Успехов в освоении этой занимательной науки математики!

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Теорема Фалеса — Википедия

Материал из Википедии — свободной энциклопедии

Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.

Теорема Фалеса — теорема планиметрии о параллельных и секущих.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Формулировки

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Более общая формулировка, также называемая теорема о пропорциональных отрезках

Параллельные прямые отсекают на секущих пропорциональные отрезки:

A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}

Замечания

• В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

• Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Доказательство в случае параллельных прямых

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Вариации и обобщения

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }, следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }.

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.

Лемма Соллертинского

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers^[es] представила песню, посвящённую теореме^[1].

Литература

• Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

См. также

wikipedia.green

Теорема Фалеса — Википедия. Что такое Теорема Фалеса

Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.

Теорема Фалеса — теорема планиметрии о параллельных и секущих.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Формулировки

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Более общая формулировка, также называемая теорема о пропорциональных отрезках

Параллельные прямые отсекают на секущих пропорциональные отрезки:

A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}

Замечания

• В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

• Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Доказательство в случае параллельных прямых

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Вариации и обобщения

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

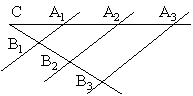В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }, следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }.

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.

Лемма Соллертинского

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers^[es] представила песню, посвящённую теореме^[1].

Литература

• Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

См. также

wiki.sc

Теорема Фалеса | Треугольники

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых. Кроме того, существует еще и обобщенная теорема Фалеса.

Теорема Фалеса.

Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

 

∠COD

   

Замечание.

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых.

Теорема.

Если параллельные прямые пересекают две данные прямые и отсекают на одной прямой равные отрезки, то они отсекают равные отрезки и на другой прямой.

 

a и b — прямые

   

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса).

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

 

   

 

Теорема Фалеса и ее модификации применяется в том числе, и в задачах на построение (в частности, для деления отрезка на n равных частей и при построении четвертого пропорционального отрезка).

Четырехугольники

www.treugolniki.ru