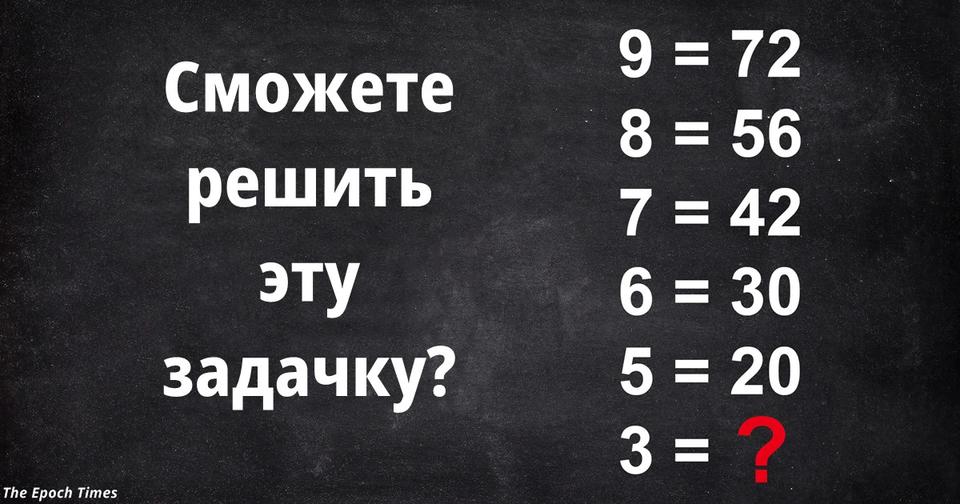«Математическая культура мышления хороша тем, что, образно говоря, вправляет мозги»
НИУ ВШЭ активно сотрудничает с академическими институтами, которые открывают в университете базовые кафедры и направляют лучших специалистов для преподавания и научной работы. Новостная служба портала расспросила заместителей директора Математического института имени В.А. Стеклова РАН — академика РАН Льва Беклемишева и Сергея Горчинского о развитии математики в современном мире, о возможностях карьеры для выпускников математических факультетов и об особенностях работы ученых со студентами.
О математике
Лев Дмитриевич, Сергей Олегович, какое место сегодня занимает математика среди других наук? Можно ли считать ее не только наукой, но и искусством?
Лев Беклемишев: По этому вопросу есть разные точки зрения даже в среде профессионалов. Я представитель специфической области математики — математической логики, в которой важны гуманитарные аспекты.
А традиционные области связаны прежде всего с физикой. Академик Владимир Арнольд считал, что математика — это часть физики, которая не требует затрат на экспериментальные установки. У разных областей математики — разное происхождение: геометрия исходно считалась наукой об измерении земли, а теория вероятностей «математизировалась» только на рубеже XIX-XX веков.
Что касается элементов искусства, то они есть в каждой науке, и, конечно, в математике они тоже есть. Полезные теоремы — это красивые теоремы, а некрасивые скорее всего лишены ценности. Математики часто приходят к своим научным результатам интуитивно, и обыденное представление о математике как о человеке, главное достоинство которого — умение быстро считать, довольно далеко от реальности. Конечно, математики живут в мире своих образов, но это не мешает им ориентироваться в действительности.
Сергей Горчинский: Мы с Львом Дмитриевичем занимаемся разной математикой, я специализируюсь на алгебраической и арифметической геометрии, но с ним полностью согласен.
Искусство оперирует категориями «красиво» и «некрасиво», а наука — «доказано или не доказано». В свое время я решил заниматься математикой, потому что это единственный вид деятельности человека, где существует объективная правда. В физических или химических экспериментах многое зависит от условий, поэтому там все не настолько однозначно, как в математике с ее «дважды два четыре».
Почему, на ваш взгляд, математику называют царицей наук?
Л.Б.: Потому что еще в античности и в средние века научное знание складывалось как знание математическое, и язык математики был языком науки. И сегодня всем очевидно, что ни одной наукой, в которой нуждается общество, невозможно заниматься, не умея математически строго рассуждать и тем более не умея использовать минимальный математический аппарат.
Если же абстрагироваться от формул, то математическая культура мышления хороша тем, что, образно говоря, вправляет мозги, учит логически мыслить.
С.Г.
: Продолжу аллегорию: есть люди, которым хорошо вправили мозги математикой, а есть те, которым просто не повезло с учителями.
Чем объяснить традиционное противопоставление гуманитариев и математиков? Они мыслят по-разному?
Л.Б.: Да, по-разному. Даже у коллег-математиков есть разные типы математического мышления — кто-то лучше мыслит пространственными структурами, а кто-то склонен комбинировать разные элементы и строить конструкции невообразимой сложности. Есть вычислители, у которых сильно развита интуиция. При этом математическое мышление очень помогает вне зависимости от того, какой именно наукой человек занимается.
Среди математиков немало гуманитарно образованных людей, и, например, Владимир Успенский — ученик Андрея Колмогорова, основатель отделения теоретической и прикладной лингвистики в МГУ, в такой же степени гуманитарий, как и математик. Академик Андрей Зализняк, знаменитый лингвист, обладал ярко выраженным математическим строем мысли, но занялся изучением языка и достиг там необыкновенных высот.
Другой вопрос, что порог вхождения в математике выше, чем в гуманитарных науках.
С.Г.: На мой взгляд, любимый многими историк Натан Эйдельман — совсем не гуманитарий, потому что у него строгие, логические, понятные тексты.
Насколько широк спектр математических исследований сегодня? Бывает ли так, что ученые, работающие в одной области математики, не разбираются в том, чем занимаются их коллеги в другой области?
Л.Б.: К сожалению, бывает. Но есть ученые универсального типа, интересы которых покрывают если не всю математику, то очень многое, как, например, Андрей Колмогоров или Владимир Арнольд. Это представители старшего поколения, и их становится все меньше.
В начале XX века математика разрасталась в разные стороны, а с 1970-80-х годов преобладающей тенденцией стало объединение. Именно тогда стали развиваться новые приложения математики в физике, алгебраическая геометрия и другие направления, связанные со многими областями математики сразу.
Эта тенденция сохраняется и сегодня.
О сотрудничестве с ВШЭ
В чем вы видите необходимость сотрудничества МИАН с университетами?
Для нас вузы — это прежде всего источник кадров, и мы считаем, что лучшие студенты, выпускники, аспиранты, молодые ученые должны приходить именно к нам. Кадры в математике решают все. Традиционно большинство наших сотрудников оканчивали мехмат МГУ, и многие формы сотрудничества были ориентированы на него. Мехмат по-прежнему остается нашей основной базой, откуда к нам приходили и приходят новые сотрудники. Но когда появился новый, современный факультет математики в Вышке, и туда пошли хорошие школьники, которые потом стали хорошими студентами, мы не могли оставаться в стороне.
Как организовано взаимодействие МИАН с Вышкой?
Очень естественно. Наши сотрудники вовлечены в жизнь факультета математики, мы преподаем и ведем исследования, участвуем в его развитии, в обсуждении самых разных вопросов.
Более демократичного ученого совета, чем на этом факультете, я ни разу в своей жизни не встречал. На его заседаниях все равны, невзирая на должности и звания, и кадровые вопросы, вопросы распределения нагрузки всегда вызывают бурные обсуждения.
На факультете математики открыта базовая кафедра МИАН, которую возглавляет академик РАН Виктор Васильев. Но кафедра в данном случае — условное понятие. На факультете вообще нет кафедр в привычном понимании этого слова, когда небольшой коллектив кафедры как бы живет на отдельной территории, определяет свои традиционные курсы и мало взаимодействует с другими кафедрами. На факультете математики действует другой принцип, согласно которому все преподаватели должны взаимодействовать друг с другом, участвовать в совместной деятельности и не делиться на группы по специальностям.
Студенты факультета математики составляют значительную долю тех, кто занимается в Научно-образовательном центре МИАН. В этом году у меня один аспирант из ВШЭ пишет диссертацию, два четверокурсника — дипломы, несколько студентов младших курсов — курсовые работы.
С.Г.: Мы сотрудничаем не только с факультетом математики, но и с другими подразделениями Вышки. Лично я не занимаю преподавательскую должность (хотя это не мешает мне брать студентов и аспирантов), являюсь научным сотрудником Международной лаборатории зеркальной симметрии и автоморфных форм. А примерно десять лет назад начинал работать в Международной лаборатории алгебраической геометрии и ее приложений, созданной на мегагрант по 220-му постановлению под руководством Федора Богомолова. В этих лабораториях и другие наши коллеги по институту работают в качестве совместителей.
Открытие Международной лаборатории алгебраической геометрии и ее приложений было для нас очень полезным, мы сразу начали организовывать совместные конференции, это стало очень удобным. Они в основном проходили в здании МИАН, а участников из других городов и стран размещали в гостинице Вышки на улице Вавилова. Другим важным фактором стала возможность привлекать в лабораторию студентов-стажеров и доплачивать им за работу.
Что можете сказать о студентах Высшей школы экономики?
Л.Б.: Когда они занимаются математикой, у них горят глаза, и таких студентов всегда приятно учить.
О работе и о зарплате
Чем занимаются и как зарабатывают на жизнь математики в современной России? Какие варианты научной карьеры возможны и предпочтительны?
Л.Б.: Идеальная карьера для тех, кто хочет специализироваться на теоретической математике, — научные исследования. Можно спокойно заниматься любимым делом в академическом институте, иногда преподавать. Если математик совсем не преподает, это не очень хорошо на нем отражается.
Старт карьеры математика — защита кандидатской диссертации. За некоторое время до защиты, когда он находится в определенной среде, ему становится понятно, что это за среда, в каком институте она существует, какие исследования там и по соседству ведутся, с кем ему хочется работать. В последнее время проблем с нехваткой рабочих мест для таких людей в Москве нет.
Есть наш институт, Институт проблем передачи информации — на стыке математики с другими науками; физические институты, где также востребованы математики, Институт теоретической физики в Черноголовке, Физический институт РАН, где математика более прикладная.
Другой вариант — когда человеку интересно работать со школьниками, развивать олимпиадное движение, например. Это благородная деятельность, и те, кто ею занимается, часто сами сильные математики. Они понимают, что такое настоящая математика, просто свои усилия направляют на другое.
И, конечно, есть традиционная траектория — пойти преподавать в вуз. Современный университетский преподаватель должен сочетать в себе и учителя, способного объяснить студентам сложные вещи, и самостоятельно работающего ученого. Научные публикации теперь считаются одним из ключевых требований к вузовским преподавателям.
К сожалению, молодых и не только молодых преподавателей часто перегружают педагогической работой. При таком количестве аудиторных часов, как это принято в некоторых вузах, совершенно невозможно продуктивно заниматься наукой — этим наши университеты невыгодно отличаются от западных.
С.Г.: Есть и другие карьерные возможности — за рамками преподавания и науки, и их выбирают порядка 90% выпускников. Прежде всего это сфера ИТ, самая массовая профессия для профессиональных математиков — программист. Вторая сфера, где много математики, — банковская, третья — страхование. Есть много примеров, когда люди профессионально занимаются финансовой математикой, начинают торговать на биржах, создают свои компании и нанимают сотрудников-математиков.
А за рубеж математики часто уезжают?
Л.Б.: Для продолжения образования, для работы в академическом секторе — да, потому что рынок такого рода мест с хорошей зарплатой за рубежом шире, чем в России. Но есть и противоположные примеры, когда обладатели степени PhD, постдоки возвращаются в Россию. Я сам долго работал в разных странах, самый длительный период в Нидерландах, в Утрехте, где у меня была постоянная позиция, но 15 лет назад вернулся в Россию.
Разницу в зарплате ощутили?
Когда я уехал на первый постдок в 1998 году, как раз перед кризисом, разница в моей зарплате была примерно в тридцать раз.
Сейчас разница намного меньше, ситуация в МИАН в последние 10-15 лет улучшилась кардинально. То же можно сказать и про некоторые другие места. Высшая школа экономики с ее факультетом математики стала одним из первых массовых вузов, где преподавателям математики стали серьезно платить. Высокая зарплата прежде всего обусловлена надбавками за публикации в ведущих международных журналах.
С.Г.: В нашем институте тоже есть система надбавок, она непростая, привязана к разным показателям результативности, учитывается любая полезная для института деятельность, и критерии мы обсуждаем на ученом совете. Положение майского указа президента о зарплатах ученых, которые должны быть не ниже удвоенной средней зарплаты по региону, мы выполняем, средний показатель публикуется каждый год в отчете директора.
Вообще зарплата ученого в академическом институте складывается из многих мелких «ручейков» — помимо постоянной части и надбавок, есть разнообразные гранты, и человек может одновременно работать в нескольких проектах.
Так что если ты активен, то можешь заниматься любимым делом и при этом хорошо зарабатывать.
Л.Б.: В общественном сознании есть стереотип, что ученый должен быть бедным. Сейчас это далеко не всегда так — во всяком случае, если ученый демонстрирует результаты в своей работе. Но важно понимать, что такое относительное благополучие характерно для элитных учреждений в Москве. В регионах уровень зарплат ученых и преподавателей вузов далеко не такой высокий.
О Математическом институте имени В.А. Стеклова
Расскажите вкратце об истории МИАН. Когда он был создан? Каковы основные вехи его развития?
История МИАН отсчитывается с 1921 года, когда в Санкт-Петербурге был открыт Физико-математический институт Академии наук. В 1934 году Академия переехала в Москву, и институт был разделен на две части — МИАН и ФИАН. Позже от нашего института отпочковались другие, причем они больше и по размерам, и очень значимы. Среди них — Институт прикладной математики имени М.
В. Келдыша, который начинался как отдел МИАН и сыграл ключевую роль в космической программе. Некоторые из создателей ядерного оружия тоже работали у нас. Уже в постсоветские годы МИАН был одной из первых точек в России, где в начале 1990-х появился интернет.
Сегодня МИАН — лучший, элитарный математический институт страны. Его славу составляют ученые, портреты наших великих предшественников размещены в галерее на девятом этаже. В библиотеке, помимо книг по математике, много интересных архивных материалов. Сохранился шкаф, принадлежавший Пафнутию Львовичу Чебышеву — одному из великих русских математиков.
Мы не только ведем исследования, но и преподаем как в ведущих вузах Москвы, так и в научно-образовательном центре (НОЦ), созданном при МИАН. Там по вечерам проводятся бесплатные спецкурсы и учебные семинары для студентов любых вузов по разным разделам математики. Если студент сдает экзамены (это необязательно), мы сообщаем об этом в его университет, и там ему результат засчитывают.
Для студентов это хорошая подпитка курсами по современным направлениям математики от людей, ею профессионально занимающихся, а для нас важно, что ребята начинают знакомиться с МИАН, привыкают к его атмосфере.
В институте есть лаборатория популяризации и пропаганды математики, возглавляемая Николаем Андреевым. Один из ее самых успешных проектов — книга «Математическая составляющая», где доступно рассказывается о роли математики в крупнейших достижениях цивилизации, о математической «начинке» привычных вещей. Недавно вышло второе издание этой книги.
Сколько человек работает в институте? Много ли молодых исследователей?
Коллектив МИАН — порядка 120 ученых, в том числе более 30 членов РАН. Примерно треть — молодые ученые.
Возрастной состав института отражает недавнюю историю математической науки в нашей страны. У нас много сотрудников старше 70 лет, потом провал — представителей моего поколения, тех, кому сейчас 45-55 лет, немного, в «голодные» 1990-е они чаще уезжали за рубеж.
А молодежи до 35 лет довольно много. В год к нам приходят 4-5 человек, и мы, конечно, начинаем примечать их задолго до того, как принимаем на работу. В последние годы мы налаживаем институт постдоков — молодых сотрудников, принимаемых на ограниченное время, на 2-3 года. Это позволяет нам получше присмотреться к человеку, а для самого человека это дает шанс начать свою карьеру как ученого.
Есть ли среди сотрудников выпускники Вышки, работающие на полную ставку?
Пока нет, все-таки факультет математики в Вышке начал работать в 2007 году, и защиты кандидатских диссертаций его первых выпускников только начинаются. Но многие работают у нас как совместители, по грантам, по срочным контрактам, и мы тоже считаем их своими сотрудниками.
Математика: модель реальности — или реальность сама по себе?
Автор фото, Getty Images
Подпись к фото,Реальна ли математика?
Представьте себе Нептун.
Почему именно Нептун? Да потому, что увидеть его невооруженным взглядом просто невозможно.
Даже в хороший телескоп его едва разглядишь: восьмая планета Солнечной системы, удаленная от Земли на 4,3 млрд километров, выглядит в небе крошечной белой точкой.
Именно поэтому с древних времен наше воображение поражают планеты, расположенные ближе к Земле — такие как Венера или Марс, — ведь они так ярко сияют по ночам.
А о существовании Нептуна мы узнали лишь в XIX веке.
Тем не менее, его открытие было важным вдвойне.
Уран и Нептун
Дело было не просто в том, что мы нашли нового соседа по космосу.
«Нептун открыл новую страницу в изучении Солнечной системы, потому что его обнаружили, не рассматривая небеса невооруженным глазом или с помощью телескопа», — утверждает астрофизик Космической научной лаборатории Малларда при Университетском колледже Лондона Люси Грин.
Нептун нашли благодаря математике.
Автор фото, NASA
Подпись к фото,Нептун открыли не с помощью наблюдений, а благодаря математическим вычислениям
В XIX веке закон всемирного тяготения Ньютона был уже глубоко осмыслен, и благодаря ему можно было рассчитать орбиты планет, вращающихся вокруг Солнца.
Всех известных планет, за исключением Урана, орбита которого почему-то не совпала с расчетами.
В те времена Уран считался самой удаленной от Солнца планетой, и некоторые ученые даже предположили, что на таком большом удалении ньютоновские законы могут не действовать.
Однако другие ученые полностью полагались на математику, которая подсказывала им, что поблизости от Урана должно находиться крупное небесное тело, которое и влияет на его орбиту.
«Они вычислили, что, как и где должно происходить, а потом направили телескоп в то место, которое подсказала математика, — и новая планета была обнаружена», — объясняет Грин.
Автор фото, Getty Images
Подпись к фото,Астроному догадались о существовании еще одной планеты благодаря отклонению орбиты Урана
Открытие Нептуна стало неопровержимым историческим доказательством того, что математика — это не выдумка, а реальность.
Именно это и заинтересовало слушателя программы Би-би-си CrowdScience из Перу Серхио Хуаркайо.
«От Галилея, который мог назвать скорость шара, который катится вниз по склону, и до, к примеру, бозона Хиггса, существование которого было предсказано математическим путем — до того, как сама частица была обнаружена, — эта способность предсказывать существование вещей, которые никто не видел, кажется мне потрясающей», — написал Серхио.
«Что такое математика: модель, описание, метафора реальности — или сама реальность?»
Серхио не единственный, кто задается этим вопросом.
Философы размышляют над ним уже тысячи лет, и он продолжает служить поводом для глубоких разногласий.
Не бывает отрицательного торта
Почти никто не сомневается в том, что человечество занялось математикой из чисто практических соображений: людям нужно было вести счет и делать измерения. С этого и начнем.
Возьмем, к примеру, торт.
Автор фото, Getty Images
Подпись к фото,Торт или есть — или его нет…
Математика много чего может рассказать о торте: какого он размера, сколько весит, как и на сколько частей его можно разделить. Это все очень осязаемые вещи.
Но тот же торт может продемонстрировать, что математика способна зайти куда дальше, чем реальность.
Если съесть треть торта, от него останутся две трети.
Пока что все просто. Если съесть еще одну треть, а потом — еще одну, то от торта не останется ничего.
«Так мы описываем пределы мышления древних людей, — поясняет автор книг по математике Алекс Беллос. — Они применяли практическую математику для измерения и счета, но они понятия не имели об отрицательных числах».
Автор фото, Getty Images
Подпись к фото,Изобретние денег позволилол наглядно представить концепцию отрицательных чисел
Если ваше представление о реальности включает лишь предметы, которые можно измерить или сосчитать, то вам трудно представить что-то меньше нуля.
О долгах и отрицательных числах
Как только вы съели торт до последней крошки, он закончился: отрицательного торта не бывает.
И все же, по словам Беллоса, существует область, в которой вы оперируете отрицательными числами, и это кажется вам вполне естественным.
Он имеет в виду деньги: «Может быть, у вас есть деньги, а может — вы кому-то должны. И первое практическое применение отрицательных чисел произошло в контексте бухгалтерии и долгов».
Если вы должны кому-то 5 долларов, а я дам вам эту сумму, то у вас останется 0 долларов. Это та реальность, в которую нас вводят отрицательные числа.
Сегодня невозможно представить математику без отрицательных чисел, и дело не только в долгах.
Пока что мы не выходили за рамки реальности. Но когда начинаешь играть с отрицательными числами, происходят странные вещи.
Невероятная загадка
Если помножить отрицательные числа друга на друга, получается положительный результат.
-1 x -1 = 1, и вот тут нас подстерегает настоящая загадка.
Если в уравнении есть и положительные, и отрицательные числа, то в какой-то момент несложно получить такой результат:
Подпись к фото,Это математическое уравнение может поставить в тупик
«Тут возникает законный вопрос: что это за чертовщина? Как найти число, которое при возведении в квадрат дает -1!», — восклицает Беллос.
«Это точно не положительное число, потому что, когда их возводишь в квадрат, результат всегда положительный. Но это не может быть и отрицательное число — ровно по той же причине», — объясняет он.
«Когда люди впервые с этим столкнулись, они решили, что это абсурд. Однако со временем математики стали говорить: да, абсурд, но его можно использовать в работе — ответ получается верный. Так что пусть философы осмысляют, как такое возможно, — а нам, математикам, нужны ответы. Если это необъяснимое число помогает найти ответ, то и ладно».
Тут-то мы и расстаемся с реальностью. Но математика продолжает служить для ее объяснения.
Мнимые числа
«Квадратный корень из -1 называется мнимым числом. Это ужасное название, потому что оно как бы говорит нам, что до сих пор математика была реальной — и вдруг стала воображаемой», — говорит Беллос.
«Но математика была воображаемой с самого начала. Мы можем рассуждать о трех тортах — однако видим лишь сами торты, мы не видим «три», «три» — это абстракция», — подчеркивает Беллос.
Автор фото, Getty Images
Подпись к фото,Существует слово «три» и цифра 3, однако само число 3 — абстракция, как и все другие числа
«То же самое — с мнимыми числами. Это кажется безумием, но когда начинаешь понимать их роль, то все выглядит очень логично. А для описания языком математики таких явлений, как гармонические колебания, лучше всего подходит совокупность вещественных и мнимых чисел. Такая совокупность называется комплексным числом», — продолжает он.
В наши дня квадратный корень из -1 (его принято обозначать буквой i) столь же реален, как и само число -1, уверены математики. Даже если нам так же сложно представить i, как нашим далеким предкам было трудно понять, как чего-то может быть -1.
Не волнуйтесь
Если вы запутались, не переживайте, просто читайте дальше — и все станет ясно. Честное слово.
Комплексные числа позволяют решать некоторые уравнения, для которых не существует решений в действительных числах.
Эти числа чрезвычайно полезны для понимания реальности и служат отличным инструментом для описания и понимания практически любых процессов, связанных с колебаниями и волнами.
Их широко используют в электронике, радарах, при медицинском сканировании. Они также помогают понять поведение субатомных частиц.
Но как нечто, существующее лишь в мире математических грез, может при этом быть столь полезным в реальном мире?
Некоторые, вроде венгерского физика Юджина Вигнера, считали это практически чудом.
В 1960 году Вигнер написал фундаментальную статью о комплексных числах под названием «Непостижимая эффективность математики в естественных науках».
Автор фото, Getty Images
Подпись к фото,Если математика — это иснтрумент, помогающий нам понять реальность, почему мы удивляемся, когда это происходит?
Непостижимая эффективность
Но если математика изначально была придумана людьми именно для описания реальности, то кажется совершенно логичным, что она и выполняет эту функцию. Что же в этом необъяснимого?
Давайте обратимся к человеку, который работает на стыке математики с философией — Эленор Нокс занимается философией физики.
«Мы действительно изобрели математику для понимания физических систем, и было бы логично, если бы она выполняла только эту задачу. Но математика стала развиваться по иному пути», — объясняет Нокс.
«Нередко математики решают какие-то абстрактные задачи просто потому, что им это интересно — и только потом выясняется, что именно эти вычисления были необходимы для совершения какого-то важного открытия в физике», — говорит она.
В качестве примера Нокс приводит неевклидову геометрию — совокупность теорий, которыми многие математики увлекались в конце XIX века просто в силу того, что это было им интересно.
«Считалось, что весь наш мир можно описать с помощью евклидовой геометрии — той самой, которую учат в школе. Например, там есть теорема, доказывающая, что сумма углов треугольника равняется 180 градусам».
Математики 1800-х годов не собирались опровергать евклидову геометрию. Они просто вели исследования — и обнаружили интересные математические структуры.
Автор фото, Getty Images
Подпись к фото,Неевклидова геометрия позволила нам увидеть формы, которые раньше возникали лишь в головах у математиков
«Когда уже в XX веке Альберту Эйнштейну понадобилось описать законы пространства-времени в рамках теории относительности, на помощь ему пришла именно неевклидова геометрия. Без нее у него бы просто ничего не получилось», — говорит Нокс.
«Сегодня мы считаем, что мир имеет именно такую геометрическую структуру, которая когда-то считалась странной и непонятной. При этом никто из математиков, которые начинали над ней работать, не мог предсказать это конкретное открытие», — заключает философ.
Такого рода примеры заставляют нас думать, что отношения математики с реальностью если не волшебны, то по крайней мере поразительны.
Основополагающая реальность
По мере развития современной физики нам, простым смертным, все сложнее понимать сложную математику и ту странную реальность, которую она описывает.
Но, быть может, в этом нет ничего удивительного. Ведь нет никаких причин считать, что повседневная реальность, данная нам в ощущении, — это и есть основополагающая реальность Вселенной.
Удивительно, но с помощью математики, кажется, можно исследовать гораздо больше, чем позволяют наши органы чувств.
Наступит ли тот момент, когда в поиске основополагающей реальности математика достигнет предела в своей способности описывать эту реальность?
«XX век дал нам две наиболее успешные физические теории: теорию квантовой механики (описывающую поведение сверхмалых частиц на атомном и субатомном уровне) и теорию относительности, — говорит Нокс.
— При этом оказалось, что совместить математику этих двух теорий — невероятно сложная задача».
Автор фото, Getty Images
Подпись к фото,Математика дает нам возможность заглянуть намного дальше, чем позволяют наши органы чувств
«У нас нет непротиворечивой модели, которая помогла бы понять, как две эти теории могут сосуществовать в одном мире и описывать одну и ту же реальность, — продолжает эксперт. — Приходится иметь дело с невероятно сложными концепциями, не имея в настоящий момент возможности подтвердить свои умозаключения экспериментально».
Как мы уже видели, многое начиналось с идеи, которая ждала своего практического применения. Но, быть может, мы уже достигли предела?
«Сегодня можно сказать, что до сих пор нам очень и очень везло с тем, как математика описывала нашу Вселенную, — говорит Нокс. — Однако есть и другая точка зрения — что математика способна описывать лишь отдельные элементы этого мира, но не весь его целиком».
«Или что понять мир в полном объеме вообще очень трудно. Или что эта математика слишком сложна для нас и нам с ней не справиться. Или что мы до сих пор ее так и не поняли, но рано или поздно поймем», — продолжает она.
Большая разница
Быть может, не стоит удивляться тому, что иногда чертовски трудно увязать законы математики с законами физической реальности. В конце концов, это ведь не разные вещи.
Как сказал в свое время Эйнштейн, «чем больше математические законы привязаны к реальности, тем менее они надежны; а чем более они надежны — тем дальше они от реальности».
Автор фото, Getty Images
Подпись к фото,1 + 1 = 2, и это не подлежит сомнению…
«У математики есть такое свойство: она либо совершенно верна, либо абсолютно ошибочна, — поясняет Нокс. — Если я докажу что-то математическим путем, уже никто не сможет это оспорить».
«С физическими законами дело обстоит иначе, и в этом их кардинальное отличие.
Мы часто ошибались с законами. Законы Ньютона прекрасны, изящны и применимы во многих конкретных случаях, но они не содержат окончательной истины. И нет никаких сомнений — в будущем докажут, что и законы Эйнштейна тоже приблизительны», — предсказывает философ.
Открытие или изобретение?
Откуда взялась математика?
Это большой вопрос для самих математиков.
Автор фото, Getty Images
Подпись к фото,У древних египтян была даже богиня математики Сешат
«Я по-настоящему верю, что открываю новые концепции и изобретаю пути размышления над ними, — утверждает Юджиния Ченг из Чикагского института искусств. — Когда я провожу абстрактные исследования, мне кажется, что я брожу по абстрактным джунглям в поисках разных вещей — а потом придумываю способ рассказать о них и подвести под них свою теорию, чтобы привести свои мысли в порядок и доступно их объяснить».
Ченг работает в области теории категоризации (иногда ее еще называют «математикой математики»), задача которой — навести мосты между различными областями математики.
Что есть реальность?
Трудно представить себе что-то еще более абстрактное, поэтому мы спросили Ченг, считает ли она, что та математика, которую она изучает, имеет отношение к реальности?
«Когда люди спрашивают меня о реальности, я хочу задать им ответный вопрос: а что такое реальность вообще? — говорит она. — То, что мы называем реальностью, — это галлюцинации, которые мы считаем реальными лишь на том основании, что воспринимаем их одинаково».
«Люди говорят, что числа не реальны, поскольку их нельзя потрогать. Но при этом есть немало вполне реальных вещей, которые нельзя потрогать — например, голод», — объясняет Ченг.
Автор фото, Getty Images
Подпись к фото,Абстракция — это не обязательно что-то нереальное
«Вот почему я предпочитаю говорить о конкретных вещах — тех, что можно пощупать, с которыми можно взаимодействовать непосредственно, — и об абстрактных вещах, которыми мы оперируем в нашем сознании».
«Математика — вещь абстрактная, но абстрактная идея может быть столь же реальной, как что угодно».
А что реально?
С одной стороны, можно утверждать, что математика — это реальность.
Возьмите, к примеру, биологию, которая основана на химии — которая, в свою очередь, руководствуется законами физики — и… мы приходим к числам.
Или представьте голубое небо, цвет которого объясняется длиной волн отраженного света — и… все это тоже числа.
Автор фото, Getty Images
Подпись к фото,Числа окружают нас повсюду
Кажется, если копнуть физическую реальность поглубже — в любом случае упрешься в математику.
Однако математика не в состоянии поведать нам ничего существенного о таких самых важных в жизни вещах как любовь, мораль или даже голод.
Так что из всех по-настоящему больших вопросов мы можем с определенной уверенностью ответить только на один: наверное, мы так и не найдем окончательного ответа на вопрос, заданный перуанцем Серхио Хуаркайа.
Но поискать ответ все равно стоило.
Каково быть слабым в математике / Хабр
Я, как учитель математики нередко разочаровываюсь в учениках. Они прогуливают. Они ленятся. Они плачут, словно младенцы, если у них отнять калькуляторы. Но хуже всего то, чего они
не делают. Не задают вопросов. Не записывают. Не исправляют тесты, даже если это может повысить их общий балл. Разве их не волнуют их неудачи в учебе?
Существует много объяснений такого поведения: лень, равнодушие, отвлекающие внешкольные факторы и т.д. Но если спросите меня, то я назову более глубокую причину: незнание математики заставляет чувствовать себя глупо. А это неприятно.
Это трудно понять, если вы никогда не испытывали подобное. К счастью, у меня такой опыт есть (хотя тогда нечему было радоваться). Мой рассказ о математической безграмотности. Возможно что-то вам будет знакомо.
В колледж я поступал математически подкованным, на выпускном экзамене я набрал самый высокий балл.
Казалось, что математика мне дается совсем легко. Но потом я столкнулся с топологией.
Уроки по топологии проходила в формате семинаров, где студенты учили друг друга. Дважды за семестр каждый из нас должен быть подготовить лекцию, дать домашнее задание и оценить его.
Мое непонимание предмета приходило спокойно, постепенно. Я читал лекции одноклассников, смутно понимая только половину из написанного. Я заучивал основные моменты, но не понимал сути предмета, надеясь, что когда-нибудь отрывочные знания примут форму чего-то целого. Но я ничего не делал для этого. Не задавал вопросов, потому что боялся показаться глупым. В итоге все становилось только хуже, проблески понимания угасали, становилось неинтересно. Я понял, что совсем запутался.
В итоге я сделал то, что делают большинство студентов. Я положился на человека, который разбирался в предмете лучше меня. Это была моя девушка (учащаяся в том же классе). Все, что она объясняла мне, я просто записывал своими словами, не вникая в суть, из-за чего знания не задерживались надолго в моей голове.
Я винил всех вокруг в своих неудачах. Свою девушку, которая уговорила меня выбрать этот курс. Преподавателя, который сидел на занятиях в стороне и посмеивался над нашей некомпетентностью. Зачем вообще нужна эта топология? Когда все оправдания закончились, я сказал себе: я ненавижу этот класс! Я ненавижу топологию!
Я ненавижу математику!
Мой первый опыт в качестве лектора в классе был положительным, несмотря на то, что знания предмета почти не было. Но погружаясь в материал, понимал, что вторая лекция не будет такой легкой прогулкой.
Я постоянно ленился, часто жалуясь на сложность предмета. Но вскоре понял, что дело не просто в лени. Сталкиваясь с тем, что я не понимал, я сталкивался со своими сомнениями и тревогами. А постоянное откладывание отодвигает эти неприятные чувства.
Поскольку день второй лекции приближался, я начал паниковать. Я позвонил отцу, человеку с доброй душой. Не помогло. Я позвонил сестре, учителю математики, с которой всегда было весело.
Я потел, пока поднимался в лифте к нему в кабинет. Самое страшное было то, что я восхищался им. Большинство математиков мирового класса относились к общению со студентами как к обременительному акту благотворительности. Он же был другим: проницательным, трудолюбивым, искренним. Я стучал в дверь кабинета, чтобы сказать ему, что потерпел неудачу.
Он был благосклонен ко мне, предложил несколько идей и помог с презентацией, чтобы я мог показать хоть что-то на предстоящей лекции. Я умолял не задавать вопросов по материалу на уроке, по сути просил его не делать свою работу. И он нехотя согласился.
Я провел вторую лекцию и попытался забыть ее как можно быстрее.
Оглядываясь назад, я понимаю, что был идеальным примером плохого студента, продемонстрировав все симптомы:
- Запутался в материале
- Боялся задавать вопросы
- Стеснялся принимать помощь преподавателя
- Вместо этого изводил друзей
- Копировал чужие домашние работы
- Оправдывался, обвиняя других
- Медлил
- Боялся провала на публике
- Боялся осуждения преподавателя
- Чувствовал себя идиотом
- Не желал признавать ничего из вышеперечисленного
Удивительно, насколько трудно писать об этом даже сейчас.
Математические неудачи так же, как и романтические, запоминаются надолго.
Я рассказал эту историю, чтобы показать, что проблема не в отсутствии «природного ума», наоборот, подобные неудачи происходят при сочетании множества причин: излишней тревожности, низкой мотивации, пробелов в знании предмета и т.д. Сложнее всего избежать неудач в моменты, когда требуется обнажить свои недостатки.
Незнание топологии не делает меня глупым. Это делает меня слабым в топологии. Эту разницу очень важно понимать. В конце концов, я благодарен за полученный опыт.
«Зачем нам математика? Чтобы принимать рациональные решения» — профессор РАН Сергей Попов
Профессор РАН, специалист в области астрофизики компактных объектов (нейтронных звезд, черных дыр) Сергей Попов уверен, что математика способна эффективно описать окружающий мир.
Как именно математика описывает мир?
По этому поводу есть разные точки зрения. Одна состоит в том, что математика — это язык.
И мы можем описывать мир на языке математики. Другая говорит, что структура мира непосредственно является математикой. Математика не случайна, мы не придумываем математические истины, а открываем точно так же, как новые виды животных. Все остальное находится где-то в середине этих крайностей. Математика как язык, наверное, ближе большинству ученых, они стихийно отнесли бы себя к этому флангу. На другом краю есть всякие известные люди, например космолог Макс Тегмарк, его книжка «Наша математическая вселенная» переводилась на русский.
Я специально не обращаю внимания на религиозные аспекты, но, если мы о них вспомним, тогда, наверное, люди окажутся ближе к Тегмарку. Известные слова Галилея о том, что книга природы написана на языке математики, как бы подразумевают вопрос: кем написана? Для Галилея, очевидно, вопроса здесь не было, точно так же, как и для Ньютона. Метафора XVII века «Бог как великий часовщик» описывает создателя творящим все по определенным математическим законам. Однако, я думаю, подавляющее большинство современных ученых во время работы действуют в другой парадигме.
И тогда мы снова возвращаемся к названным двум крайностям. Я думаю, что действительно математика — это способ понимания мира, рассказывания самому себе об этом мире.
И здесь существенно договориться о том, что мы подразумеваем под словом «понимание».
Понимание бывает разным. Можно выделить разные его уровни. Первый этап — уложить у себя в голове некую картину. Второй этап — быть способным рассказать об этом другим. Третий этап — уметь применять. И четвертый — уметь развивать. Все это — четко отделяющиеся друг от друга этапы. Например, мифологическое сознание по сути не дает возможности развивать, влиять на понимание. Поэтому магия не работает, а техника — вполне. Именно техника стала бурно развиваться, когда вышла за рамки более или менее простого опыта. Скажем, как строить прочный мост? Вот некая гильдия мостостроителей десять поколений строила мосты. Половина упала, зато они в итоге научились строить без всяких формул, выработали некий метод, традицию.
Но если вы вырабатываете формулы, то вы можете строить совершенно удивительные мосты, которые не падают никогда.
В некотором смысле аналогией математики, на мой взгляд, является литература. Литература — это тоже вымышленный мир, но не романы Донцовой и даже не боевая научная фантастика, а доведенные до предельного накала страстей и эмоций события. Скажем, абсурдистская литература находится в поиске языка для описания реальности. Это постоянно развивающаяся надстройка над языком: поэтические образы, цитаты, отсылки к героям — они важны, потому что помогают описывать мир. Эффективность математики похожа на эффективность литературы. Есть литературные персонажи, которые оказались настолько показательны, что их в некотором смысле и ученые не рассматривают как вымысел. Самый яркий, наверное, пример — это царь Эдип из трагедии Софокла. Можно поискать и другие. Поэзия в этом смысле еще более похожа на математику: придумывает метафоры, тропы, обогащает наш словарь не в смысле слов, а в смысле тех кирпичиков, из которых мы можем создавать у себя в голове описание мира.
Математика тоже создает описание мира, которое на первом этапе позволяет именно укладывать в голове. Существенно, что математика работает при этом как потрясающий инструмент, который помогает не только объяснить, но и развивать. Удивительное свойство математики состоит в том, что манипуляция с символами на бумаге дает ответ, существует ли или возможно ли в природе нечто реальное.
Математика восхищает тем, что формулой можно описать реальность, творить ее, как писатель делает это словом. Но если архетип вписывается в стратегию формулы, то как быть с многомерностью зависящего от случайных переменных творчества?
Не будем мельчить: представим, что мы приходим к условным древним грекам, говорим по-древнегречески и переводим на древнегреческий постмодернистский роман с его потоками сознания, вложенными планами, метапрозой и интертекстуальностью. Это примерно то же, как прийти к древним математикам с концепцией многомерности пространства. Вспомним «Поминки по Финнегану»: Джойс описывает такие штуки, которые — и это очень важно — до этого, например, считались принципиально невозможными.
Просто не знали, как к этому подступиться. То же самое происходит в математике. Только здесь это будет не экспериментальный словотворческий роман с мотивом уробороса, бесконечного возвращения, а какое-нибудь сравнение двух бесконечных множеств: вот у нас есть одна бесконечность и другая бесконечность — какая из них больше? И если интуитивно они равны, то нам понадобится придумать новый язык, чтобы показать разницу. Здесь нам важна преемственность, соответствие предыдущего новому, то есть новое, как правило, объемлет предыдущее. В многоплановых постмодернистских романах отдельные кусочки выглядят как нормальные рассказы, а все вместе сплетается в какую-то новую интересную сеть.
Математика показала свою совершенно поразительную эффективность как метод познания того, что мы называем реальным миром, то есть мир внешних объектов. При этом она способна делать это на разных наречиях. Возьмите «Математические начала натуральной философии» Ньютона — там формул почти нет, зато картинок очень много, геометрических рисунков, которые объясняют его идеи.
В «Физике» Аристотеля вообще формул нет, если я правильно помню.
Любопытно, что вы сравниваете математику и литературу, когда традиционная культура их противопоставляет.
Математика, как и литература, открывает нам больше возможностей, чем мы реально встречаем в своей жизни. И важно, с одной стороны, не переоценивать математику (не все, что посчитали — это формально правильно с точки зрения математики, и не все это обязательно обнаружится в нашем мире), а с другой — важно пытаться выяснять, что же из математических конструкций подходит для описания реальных явлений и, наоборот, как для описания реальных явлений привлечь математические конструкции.
Иногда теория опережает практику. Например, мир античастиц был открыт именно благодаря анализу уравнений.
Математика, как и литература, развивается не сама по себе. Последняя естественно связана с тем, что происходит в обществе. Иногда немножко опережает, чаще немножко отстает.
То же самое происходит во взаимоотношениях математики с естественными и другими науками. Так это было у Эйнштейна. Общая теория относительности — тензорная теория, но Эйнштейн как следует тензорами вначале не владел, ему не приходило в голову, что их можно использовать. Ему друг-математик Марсель Гроссман объяснил, что эти математические структуры подходят для описания его теории. До этого все остальные фундаментальные физические теории не использовали такой язык в принципе. То же самое происходит, на мой взгляд, во взаимоотношениях «искусство и жизнь». То есть надо было быть Пикассо, чтобы догадаться, что весь этот кошмар бомбардировки Герники нужно было изобразить именно такими методами. Сравните с «Последним днем Помпеи», например. И там и там кошмар, и там и там что-то валится с небес, и там и там смерть, но воспринимается это по-разному. Пикассо нашел совершенно новый метод описания. В математике это бывает так же продуктивно, как и в искусстве. В обоих случаях мы видим прогресс, движение вперед и преемственность.
И этот новый метод, во-первых, лучше и точнее описывает уже известные явления, а во-вторых, позволяет описать и принципиально новые явления. И вот это существенно. Математика и правда открывает новые сущности. Иногда теория просто опережает практику. Например, мир античастиц был открыт именно благодаря анализу уравнений. Поль Дирак вначале записал уравнение, где появился позитрон, потом позитрон был открыт, ну а потом открылся и весь мир античастиц. И такие примеры не единичны, по крайней мере в науке.
Насколько просто математика дается математикам?
Это, кстати, большая проблема, сейчас в меньшей степени, но раньше она реально ломала жизни. Если в школе ты хорошо решаешь задачки, то поступай на мехмат. А там вообще про другое. Даже я не смог бы заниматься именно математикой, у меня не так мозг устроен. Современная профессиональная математика совсем не похожа на школьное о ней представление. Это некий внутренний мир; хочется сказать «формальный», но это слово у нас немножко не тот смысл приобрело.
Математик может вообще не думать о том, как будет применяться результат его работы. Это точно так же, как разница между художниками и дизайнерами. Художник может не думать, подойдет ли его картина для принта на футболке, впишется ли его скульптура в интерьер. И большая часть математиков поступает так же. Большой секрет математики в том, что ученые десятилетия назад что-то разработали, а придумать, к чему это применить, смогли только сейчас. Сейчас, с ростом информатизации всего вокруг, математические методы становятся очень востребованными. И мы многое можем делать не потому, что компьютеры стали мощнее, а потому, что люди используют совершенно новые алгоритмы работы с информацией, и это помогает быстро обрабатывать очень большие объемы данных.
Фундаментальной математикой занимаются люди с очень особым стилем мышления. Особо интересующиеся могут почитать книжку «О науке» Анри Пуанкаре. Это выдающийся математик конца XIX — начала ХХ века, почти наш современник. Многое из того, что сейчас является передовыми областями исследования, например теория хаоса, возникало в работах Пуанкаре.
Так вот, в своих работах он как раз пытался описать, как он думает. Это довольно редкий пример, когда математик очень высокого уровня пробует это сделать, и у него получается показать работу своей мысли.
Как именно работают математики?
Математику можно было бы назвать идеальной профессией для удаленной работы, но сложность в том, что, как и всем теоретикам, математикам очень нужно общение. У них должна быть возможность думать в изоляции, но должна быть и возможность встречаться с другими, обмениваться идеями. Наверное, с зумами, скайпами, со всем остальным это проще стало делать, но надо иногда физически вместе стоять у доски, с бумажками — как-то по-другому контакт устанавливается.
Человечество сейчас разумным образом решило, что в наши дни у него есть возможность относительно много по сравнению с прошлыми эпохами тратить ресурсов на разработку того, что не демонстрирует быстрого применения, но общая практика показывает, что в итоге это все себя оправдывает.
Тем более что как в анекдоте: «Математика очень дешевая наука — нужны только карандаши, бумага и ластики».
Если есть желание организовать систему улиц или по уже известным улицам проложить транспортные маршруты — это, безусловно, математическая задача.
Для математики всегда была важна внутренняя логика развития. В этом смысле она так до сих пор и строит этот свой большой мир, а отдельные его кусочки оказываются полезны для чего-то. Представьте, что у нас были бы какие-то люди, занимающиеся фундаментальной медициной, которые придумывали бы такие странные методы, что они потом подошли бы для лечения инопланетян. Вот прилетели инопланетяне: «У нас авария, есть пострадавший». — «О, да-да, мы, кстати, тут придумали такую штуку — на Земле она никому не нужна, а вот вам-то, значит, для вот этого третьего щупальца очень подойдет». И хоп — она правда подошла. Вот математика работает таким же поразительным образом. Придумываются вещи, которые не были ранее востребованы и, казалось бы, никогда не понадобятся.
Это называют непостижимой эффективностью математики. Просто теоретические выкладки вдруг оказываются реальностью, о чем математики и не подозревали, пока их создавали.
Есть ли у математики какие-то свойства, которые, скажем, ученым известны, а обычным людям непонятны, недоступны, они просто о них не знают, но были бы полезны в повседневной жизни? Может ли математика вообще быть полезной нам каждый день, кроме как считать сдачу в магазине?
Какие-то простые ноу-хау, безусловно, есть. Скажем, простой алгоритм выбора более быстрой очереди в кассу супермаркета. Есть замечательный анекдот о пользе математики. Продавщица всех обманывает, обвешивает. Человек кладет на весы огромную связку бананов и спрашивает: «Сколько весит?» «Пять килограммов», — отвечает та, преувеличивая. Он делит связку пополам, кладет одну часть на весы, спрашивает: «Сколько весит?» Та отвечает: «Три». — «О! Значит, я возьму оставшиеся два».
Есть старая, если не ошибаюсь, Ломоносова, фраза: «Математику изучать надобно, поскольку она в порядок ум приводит».
Она не теряет свою актуальность, потому что в некотором смысле простые математические занятия похожи на занятия спортом. Упражнения в спортзале развивают определенные группы мышц, а математические навыки позволяют, я бы сказал, принимать более рациональные решения.
Связаны ли как-то математика и организация городской среды?
Безусловно, да. Если есть желание организовать систему улиц или по уже известным улицам проложить транспортные маршруты — это, безусловно, математическая задача. И люди давно их начали решать. Точно так же, как другой часто встречающийся пример: составление расписаний. Это тоже математическая задача на оптимизацию: у вас есть много всего, есть определенные требования.
Вообще говоря, мы живем в мире, где очень много всего происходит в соответствии с законами математики. Каждое здание вокруг нас строится не просто по художественному эскизу архитектора, оно потребовало инженерных расчетов. Все сконструированные и сооруженные объекты их требуют: машины, эскалаторы, светофоры, дороги.
Все больше попыток использовать математику в экономике, теорию игр используют в прикладной политике, так сказать. Скажем, математические задачи лежат в основе организации системы выборов или определения победителей в разного рода премиях. В некоторых системах выбор кандидатов осуществляется часто по очень сложным алгоритмам. Математика используется при распределении ограниченного числа ресурсов, например выдаче грантов. Скажем, у вас есть 11 мест, 164 заявки на них, и вам нужно, не потратив всю жизнь на это, как-то честно и разумно провести конкурс. Для этого тоже разрабатываются математические методы.
Собственно, не надо и в политику далеко ходить. Вот самая простая ситуация в рабочем коллективе: вы решаете, куда всем вместе пойти. Кто-то говорит, что никуда не хочет идти, кто-то предлагает просто погулять, а кто-то активно тащит всех прыгать с парашютом. Так вот, математически количество очень активных сторонников определенной точки зрения, требующееся, чтобы сдвинуть всех остальных, невелико, порядка 10%.
Вся эпидемиология основана на математическом анализе. Появилось очень много работ, анализирующих распространение ковида в тех или иных странах, и накладывание этого на размеры городов, устройство их транспортных и инженерных сетей. Все это показывает, как математика реагирует на внешние запросы.
Что касается российской математической школы или российских математиков — насколько они впереди планеты всей?
Мы узнаем выдающихся математиков, когда им уже лет пятьдесят-шестьдесят и все основные результаты они получили раньше. Вообще российская наука продолжает существовать в неправильной парадигме: мы очень печалимся, что у нас люди уезжают. Но это нормальный процесс. Печалиться надо, что к нам не приезжают другие. То есть речь не о том, чтобы, воспитав ученого, не дать ему уехать, а если он уехал, то его вернуть. Это всегда проигрышная стратегия. Важно, чтобы у нас был приток мозгов. Все-таки там, где математика хорошо развивается, не только есть свои школы, но есть и свободное общение.
Мне кажется, у нас этого существенно не хватает. Во всех науках, математика не исключение.
16 мая Политехнический музей приглашает детей и их родителей на встречу «100 вопросов ученому» с астрофизиком Сергеем Поповым. Для участия нужна регистрация.
Фото: из личного архива Сергея Попова
О непостижимой (не)эффективности преподавания математики
Сеятель знанья на ниву народную!
Почву ты, что ли, находишь бесплодную,
Худы ль твои семена?
Робок ли сердцем ты? слаб ли ты силами?
Труд награждается всходами хилыми,
Доброго мало зерна!
Н. А. Некрасов
Александр ШеньМатематика — один из самых объемных школьных предметов (по общему числу часов). Экзамен по математике требуется для самых разных вузов, курсы математики в вузах обязательны для студентов многих специальностей и т. д. Но и преподаватели, и учащиеся жалуются, что большая часть их труда уходит впустую — и это во многих странах.
Иногда это объясняют «бесплодной почвой» — мол, когда математику изучали избранные, дело шло неплохо, а когда началось всеобщее (и весьма) среднее образование, тут-то всё и рухнуло, потому что способности к изучению математики встречаются редко. Конечно, доля истины в этом есть — способности разных людей могут отличаться очень сильно. Но, скажем, отбор в гимназиях был не только и не столько по математическим способностям, сколько по социальным факторам — и далеко не все выпускники гимназий успешно и с удовольствием изучали математику1.
При этом школьный курс математики, в общем-то, довольно прост. Много лет назад, едучи в метро, я увидел школьника, причем скорее гопника, чем ботаника (как теперь говорят), который вертел в руках модный тогда кубик Рубика — и быстро и ловко его собрал.
• Построение курса. Готовая математическая теория строится (излагается) как здание: каждый следующий результат опирается на предыдущие и служит надежной основой для последующих. Возникает иллюзия, что можно так и преподавать: изложить что-то, проверить, что это усвоено, и затем на это опираться. Хотя на самом деле обучение и изучение скорее напоминает перекрытие реки: первые брошенные камни уходят без следа под воду, а часть из них уносится потоком, но постепенно русло заполняется и наконец возникает (должна возникать) плотина, надежно удерживающая воду.
• Учебные программы. Часто начинают с обсуждения «программы» курса математики4. Это хорошо согласуется с идеей построения математического знания начиная с фундамента. Потом, «утвердив» такую программу, пишут учебники. Потом их «внедряют» — при этом выясняется, что школьники мало что понимают, и начинается процесс упрощения и вырождения учебников при сохранении декларированной программы
Составив программу (в школе или вузе), начинают по ней преподавать в соответствии с «учебным планом». При этом преподаватели обнаруживают (или не обнаруживают — так тоже бывает), что школьники или студенты ничего не понимают, отчасти потому, что не разобрались в предыдущих курсах, отчасти потому, что слишком быстро. Но план уже утвержден — и водитель локомотива, под присмотром диспетчера, старается соблюдать расписание, хотя вагоны давно отцепились.
• При составлении программы часто стараются прийти кратчайшим путем к тому, что должно в нее войти. Зачем элементарная геометрия, если (как писал Дьёдонне) можно с помощью нескольких строк векторной алгебры доказать то, для чего раньше нужны были леса из треугольников? Но смысл обучения математике не в том, чтобы проговорить доказательство каких-то признанных необходимыми фактов, а в том, чтобы научить рассуждать (решать задачи — в том числе и сложные для решающего). Поход может быть трудным с непривычки, но какой смысл ехать вместо этого на такси от старта до финиша? Может быть, это имел в виду Евклид (и не понял Дьёдонне), когда (согласно легенде) говорил, что «в математике нет царского пути».
• Для успешного преподавания нужно, чтобы изучаемое было понятным, посильным и интересным. Математические доказательства должны восприниматься как убедительные рассуждения о чем-то реальном, а не как произвольный материал для заучивания.
Решение задач — как выяснение истины, а не загадочные действия по образцу. Когда-то, будучи в гостях у своего товарища в Англии, я спросил его сына, что они проходят в школе. «Сложение и вычитание». — «А знаешь, сколько будет 100 минус 1?» Вопрос этот оказался трудным, и я решил спросить иначе: «Сколько будет сдачи, если платить фунт, а товар стоит пенс?» — «99 пенсов, но при чем тут это?» — был немедленный ответ.
И. М. Гельфанд любил рассказывать, как работяги в вечерней школе, не умевшие сравнить 2/3 и 1/2, ни секунды не колебались в ответе на вопрос «Что лучше: две бутылки на троих или одна на двоих?». Впрочем, когда мой коллега по моей просьбе задал подобный вопрос своим детям (видимо, не имевшим достаточного опыта), только один из троих ответил правильно. (Интересно, что одна из ответивших сказала, что «для этого надо сравнить по величине дроби», но не смогла этого правильно сделать.)
Не смог сейчас найти, в какой книге я это читал, но помню примерно такую историю. Рассказчик вспоминает, как в школе учитель добивался ответа от его соученика, задавая всё более простые вопросы, и наконец спросил: куда покатится шар, если положить его на наклонную плоскость — вверх или вниз? Растерянный ученик сказал, что вверх, — и учитель дал волю гневу.
Когда всё утихло, рассказчик спросил товарища удивленно: «Зачем ты так, неужели ты не знаешь, куда покатится шар?» — «Настоящий шар, конечно, вниз — но кто его знает, как там у вас…»
Преподаватели возмущаются, когда на вопрос об определении модуля школьники отвечают «число без знака». Но уж лучше пусть они так отвечают, чем заучивают определение из учебника (|a| равно a при a ≥ 0 и –a при a a | при a
В свое время этот вопрос был в заданиях ВЗМШ (Всесоюзной заочной математической школы, организованной по инициативе И. М. Гельфанда), и было много неверных ответов. Там же было замечено, что школьник может более или менее уверенно решать уравнения, но затрудниться в ответе на вопрос о том, какое число заменено звездочкой в уравнении x3 + *|x| — 5 = 0, если x = 1 является его корнем.
Давным-давно, на студенческих каникулах, я разговаривал с какими-то далекими от математики студентами (чуть ли не военного вуза).
Они спрашивали, к чему вообще математика — и были озадачены, когда выяснилось, что я могу регулярно у них выигрывать в игру «ним».
Сложный для изучения материал приходится упрощать. Как писал Н. Г. Чернышевский, «Наука сурова и незаманчива в своем настоящем виде; она не привлечет толпы. Наука требует от своих адептов очень много приготовительных познаний и, что еще реже встречается в большинстве — привычки к серьезному мышлению. Поэтому, чтоб проникнуть в массу, наука должна сложить с себя форму науки. Ее крепкое зерно должно быть перемолото в муку и разведено водою для того, чтоб стать пищею вкусною и удобоваримою»6. Но что будет, если приготовленное по рецепту Чернышевского пойло (может, и удобоваримое, но всё же едва ли вкусное) впихивать годами?
• Плохое «локальное качество» учебников. Помню, как в начале перестройки телевидение передавало выступление учителя математики Виктора Фёдоровича Шаталова — при полном восторженном зале.
Среди прочего он рассказал придуманное им доказательство теоремы о равенстве сумм противоположных сторон в описанном четырехугольнике. Состояло оно в том, что на рисунке он пометил четыре пары равных отрезков буквами (кажется, они образовывали какое-то слово7) и торжествующе сказал: «Видите, противоположные стороны вместе дают эти четыре буквы!» — сорвав аплодисменты. Я удивился: разве не ровно это написано в учебнике? Оказалось, что нет — там были равенства отрезков, обозначенных своими концами, и чтобы понять, о чем речь, надо было переводить взгляд с рисунка на текст и обратно несколько раз.
Когда я был школьником 7-го класса математической школы (№ 2), на нас решили попробовать (тогда экспериментальный) учебник геометрии Колмогорова с соавторами, и одно обсуждение я запомнил. Там было определение луча AB как множества точек, лежащих по ту же сторону от A, что и B, а после этого давалась задача: сколько лучей возникает, если на прямой есть три точки A, B, С? После этого начался спор с участием школьников и нашей замечательной учительницы, Галины Алексеевны Чувахиной (Биллим).
Одни говорили, что лучей шесть — каждая точка дает два луча. Другие возражали: в определении говорится о «луче AB» — но два из шести лучей нельзя так назвать (нет второй точки), остаются только четыре. И все так и остались в некотором замешательстве (едва ли предусмотренном авторами учебника), а через некоторое время эксперимент свернули.
Конечно, хорошо, когда учебники пишут профессиональные математики, там будет меньше ляпов (хотя всякое бывает, особенно когда их начинают дорабатывать «практики»). Но если эти математики не имеют многолетнего опыта преподавания, причем не в специальных математических классах, а в «массовой школе» (а так практически всегда и бывает), то у них могут быть самые неожиданные идеи о том, что и как можно объяснить школьникам (ср. определение вектора по Колмогорову как геометрического преобразования) и какой текст школьники и учителя смогут понять, а какой — нет.
• Наука «педагогика» с разговорами о «навыках» и «компетенциях». Думаю, что каждый, кто заполнял всякие таблицы с указанием, какие компетенции вырабатывает такой-то раздел курса, или какие компетенции проверяет такая-то задача, понимают, о каком бреде идет речь.
Циничная поговорка «кто умеет — делает, кто не умеет — учит, как делать» часто дополняется: «…а кто и этого не умеет — идет в методисты и учит, как учить»8. Один из (лучших, на мой взгляд) московских учителей математики рассказывал, как к нему на урок пришел проверяющий «методист» и остался недоволен: дескать, «урок не обучающий» (что бы это ни значило).
• Существующая ситуация часто оказывается плохим для всех, но устойчивым равновесием. Преподаватели заинтересованы, чтобы на их занятия ходили, слушали и это бы помогало сдать экзамен. Студенты заинтересованы, чтобы можно было, проявив некоторую усидчивость, подготовиться к экзамену и получить хорошую оценку. Поэтому на экзамене даются задачи заранее известных типов, а на занятиях разбираются образцы решений задач, похожих на экзаменационные — несмотря на бессмысленность этой ситуации для всех участников, никто не заинтересован от нее отклоняться. Это видно и на уровне ЕГЭ, где каждый год даются задачи одних и тех же пронумерованных типов, и выпускаются пособия, так и называющиеся: «Как решать задачу номер 14».
В свое время аналогичный эффект проявлялся во «вступительной математике» — вспомним все эти «алгебраические, тригонометрические и показательные уравнения и неравенства», которые были на всех вступительных экзаменах и составляли предмет постоянной дрессировки как в школе, так и у репетиторов. При этом наиболее квалифицированные репетиторы могли за сравнительно небольшое время (и за немалые деньги) сильно помочь абитуриенту повысить шансы сдать экзамен в какой-нибудь не очень сложный вуз (сдать, так и не узнав, что означает эта странная буква «x» в «решаемых» им уравнениях). Было даже специальное учение об «ОДЗ», открывавшее ритуал решения уравнения («область допустимых значений»).
Этот эффект не ограничивается школьными задачами и плохими преподавателями. На мехмате упражнения по дифференциальным уравнениям у нас в группе вел замечательный математик, но они, как и во всех других группах, состояли в решении уравнений разных типов: на одном занятии — с разделяющимися переменными, на другом — еще какие-то и т.
п. Наконец, пришло время контрольной. Преподаватель сказал, что на ней будут уравнения таких-то и таких-то типов, и я в ужасе спросил: «Но хоть скажут, какого типа какое?» — и только после этого понял, как глупо выгляжу.
• Органы управления образованием. Желая как-то контролировать подведомственные школы, они заинтересованы в показателях успешности преподавания. Часто говорят, что эти показатели (тот же ОГЭ/ЕГЭ) показывают не то, что надо, но проблема более серьезная и редко отмечаемая. Почти любой (минимально разумный) тест (контрольная работа) будет сильно коррелировать с реальными успехами школьников, если вопросы для них неожиданные. Но когда заранее известный тест используют как критерий успешности школы и школьника, оптимальная стратегия подготовки к нему будет далека от осмысленного обучения (см. выше о репетиторах).
• Идея «математики для пользователей». Большая часть изучающих математику в будущем не будут математиками, и у них нет ни времени, ни желания, ни сил, ни (часто) способностей, чтобы изучать математику долго и тщательно.
Поэтому (говорят многие) нужно научить их «применять математику», оставив подробности (точные определения, доказательства и т. п.) для более профессиональной подготовки. Возьмем курс математики для математиков, выбросим из него доказательства и определения и научим оставшимся рецептам. Примерно так и выглядит курс высшей математики «для ВТУЗов» (или undergraduate calculus в английском варианте). Между тем это нелепо как раз с точки зрения будущего использования: трудно себе представить, чтобы будущему программисту или финансовому аналитику пришлось искать предел по правилу Лопиталя (а как раз умение понимать математический язык и проводить рассуждения корректно могло бы и пригодиться).
Александр Шень, математик, ст. науч. сотр. Института проблем передачи
информации РАН (Москва), науч. сотр. LIRMM CNRS (Франция, Монпелье)
1 Лев Толстой вспоминает в автобиографической повести «Юность»: «На экзамен математики я пришел раньше обыкновенного.
Я знал предмет порядочно, но было два вопроса из алгебры, которые я как-то утаил от учителя и которые мне были совершенно неизвестны. Это были, как теперь помню: теории сочетаний и бином Ньютона». Дальше он рассказывает, что один из вопросов (бином Ньютона) ему успел рассказать знакомый, который хорошо разбирался в математике, но ему попался второй («О ужас! это была теория сочетаний!»), и он чудом спасся от позора и отлично сдал экзамен, поменявшись билетом с товарищем по несчастью, у которого как раз был бином Ньютона. Остается гадать, что понял Толстой в биноме Ньютона, если сочетания вызывали у него ужас.
2 Ср. высказывание Колмогорова: «Надо думать, что даже у совсем хороших математиков сложность системы знакомого им родного языка превосходит и по сложности строения, и по объему всё, что они усваивают как математики» (письмо В. А. Успенскому, 5 марта 1962 года, приведенное в: Успенский В. А. Колмогоров как центр моего мира. Труды по нематематике, том 5, М.
, 2018, с. 100. Другое высказывание Колмогорова (доклад «Автоматы и жизнь» // Колмогоров А. Н. Математика — наука и профессия. Библиотечка «Квант», вып. 88, с. 52–53): «Слаломист, преодолевая дистанцию, в течение десяти секунд воспринимает и перерабатывает значительно большую информацию, чем при других, казалось бы, более интеллектуальных видах деятельности, во всяком случае больше, чем математик пропускает через свою голову за сорок секунд напряженной работы мысли».
3 Заранее прошу прощения, если я что-то запомнил неправильно: я старался ничего не придумывать, рассказывая разные байки, но мог перепутать.
4 При этом приводятся аргументы «нельзя же не знать, что…». То обстоятельство, что это всё равно мало кто знает, хотя это и есть в программе, деликатно обходится.
5 Учебник геометрии А. В. Погорелова начинался как две небольшие брошюры, в которых автор старался, и довольно остроумно, предложить способ построения геометрии, который мог бы восприниматься и на уровне первого знакомства, и как (почти) строгое изложение для знатоков.
В массовом учебнике от этого остались какие-то странные развалины. См. Погорелов А. В. Элементарная геометрия. Планиметрия. М.: Наука, 1969; Стереометрия. М.: Наука, 1970. Учебник геометрии вышел в 1982 году (еще как «учебное пособие») и переиздавался несколько десятилетий, с постоянными изменениями, в том числе и после смерти автора — при этом из выходных данных нельзя понять, кто эти изменения вносил.
6 Чернышевский Н. Г. О поэзии. Сочинение Аристотеля. Перевел, изложил и объяснил Б. Ордынский. Собрание сочинений в 15 томах, том 2. Гослитиздат, 1949, с. 273.
7 Сейчас проверил: в Интернете есть эта передача, youtu.be/aQj4eBlcGtg?t=2451, и образованное четырьмя буквами слово — ВЕРА.
8 Или, хуже того, идет в органы управления образованием и проверяет заполнение всех этих бумаг.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
См. также:
Страх математики и радость открытия
А.
Коняев: У нас в гостях Андрей Юрьевич Окуньков, математик и Филдсовский лауреат. Андрей Юрьевич, за что вы получили Филдсовскую премию, и что это такое?
А. Окуньков: Вообще это не премия, это медаль. Денежная премия есть, но она небольшая, 15 тысяч канадских долларов. Был такой канадский математик Джон Филдс, и решили создать медаль, которую многие сравнивают с Нобелевской премией. В отличие от Нобелевской премии, которую дают каждый год (а по математике вообще не дают), и несколько человек ее делят, Филдсовскую дают раз в четыре года. Ну, и у нас есть еще что-то вроде Олимпийских игр — Международный конгресс математиков. Вот я, собственно, пришел в майке следующего Конгресса, теорему Пифагора на мне можно узреть.
А. Коняев: Вы же Филдсовскую премию в один год получили с Перельманом, но он не приехал?
А. Окуньков: Да, я ему очень благодарен, что он не приехал. Я его совсем не знаю, но что он не приехал и забрал внимание всех людей, мне было очень приятно.
А. Коняев: Вы имеет в виду, что он не приехал и не забрал внимание?
А. Окуньков: Наоборот, что он не приехал, и все внимание из-за этого переключилось на него. Мне больше понравилось так.
А. Коняев: Просто как обычно жизнь устроена — есть люди, которые занимаются математикой, но про большинство из них никто ничего не знает. Обычно в публичное поле прорываются с помощью каких-то премий, и публичность тех, кто получает Филдсовскую медаль, резко возрастает сразу. Забавно, что вам это не понравилось.
А. Окуньков: Не то что не понравилось, это для меня лишняя работа, потому что надо быть послом математики, где-то что-то делать и так далее.
А. Коняев: Хорошо. Самый простой вопрос (но и самый сложный и самый непонятный, потому что, когда мы говорим о математике, это всегда сложно): математику все изучают в школе, но изучают ли они ту самую математику, которой занимаются профессиональные математики? Что такое математика — искусство, наука?
А.
Окуньков: Это, конечно, наука. Человек может подходить даже к науке как к искусству, есть люди, которые в цветах что-то видят, или что-то с нотами ассоциируют, но это особенности психики конкретного человека. Математика — это, конечно, во-первых, наука, во-вторых — «самонаучная» наука, потому что все остальные науки свои знания выражают терминами математики.
А. Коняев: То есть математика – самая главная наука?
А. Окуньков: Если угодно. Ну, не то что главная… Знаете, есть выражение, что математика царица наук. Это подразумевает что-то антропоморфное, подчинение, субординацию. Просто математика необходима всем остальным наукам для банального выражения их собственного знания, это очевидно.
А. Коняев: А другие люди скажут, что математика — это филология, потому что мы оперируем словами, языком.
А. Окуньков: Так можно сказать, что компьютеры — тоже филология… Давайте поговорим про камень или другой предмет. Вот есть телефон, и вот он упал.
Что, собственно говоря, произошло?
А. Коняев: Физик скажет, что изменились его координаты, он подвинулся.
А. Окуньков: Физик должен сказать какую-то математику. Древние, еще до Галилея, говорили, что положение телефона на столе – это его естественное положение. Я его поднял, отпустил, и он вернулся в свое естественное положение. Во многих областях знаний люди до сих пор, на самом деле, так рассуждают. Потом люди стали задавать вопросы: а сколько времени ему потребуется для того, чтобы он вернулся в естественное положение? Это был довольно прикладной вопрос, потому что людей интересовало, по какой траектории предмет пролетит. Были потрясающие теории после открытия книгопечатания, что предмет летит сначала прямо, потом резко вниз… И разработали какой-то механизм, математический язык, чтобы понять, как объект летит, по какой траектории, сколько времени занимает полет. Это тот этап математики, который использовали до Ньютона.
Потом пришел Ньютон — или Гук — и сказал, что есть закон всемирного тяготения: любому предмету в природе, согласно действующим на него силам, предписано, какое ускорение он будет испытывать в данную минуту времени.
То есть закон всемирного тяготения говорит, что любой предмет испытывает некоторое ускорение, и есть простое уравнение — его можно решить, увидеть все эти параболы и прочее. Следующее поколение физиков много лет использовало язык вот такого рода дифференциальных уравнений. Потом люди стали думать дальше. Почему земля притягивает телефон? Что это значит? Тогда появился Эйнштейн. Что нам Эйнштейн говорит? Мне кажется, что телефон вот тут лежит. Но если подумать — вот мы тут с вами тихонечко сидим за столом, а ведь вся Земля в этом время крутится вокруг своей оси, вокруг Солнца, а само Солнце крутится с гигантской скоростью вокруг центра Галактики. И выходит, что все мы куда-то летим. Так что же говорит Эйнштейн? Что таких вещей как покой в принципе нет. То есть в каких-то координатах это покой, а в каких-то координатах это движется. Все предметы, которые находятся в состоянии физического покоя, на самом деле движутся сообразно кратчайшей траектории.
Притяжение меняет понятие близости, оно искривляет пространство, поэтому наш телефон вместо того, чтобы лететь параллельно столу вокруг Солнца, падает на стол.
А следующий вопрос еще более интересный — почему он на столе-то останавливается? Для объяснения этого потребовалась третья математика. Он останавливается, потому что испытывает не только гравитационную силу, он испытывает электромагнитные силы относительно всех остальных атомов, которые вокруг него имеются. И вот когда он совсем приблизился к столу, надо уже говорить о тех атомах и электронах, которые имеются в телефоне, имеются в столе, как они между собой взаимодействуют. Это уже совсем сложная математика пошла.
А. Коняев: Забавно, что вы используете фигуру Эйнштейна, а не Римана, который, собственно, придумал всю эту историю. Вот мы говорим про Эйнштейна — это начало ХХ века, 1915 год, у него первая лекция. И есть Бернхард Риман, который пришел к своему учителю Гауссу в 60-е годы XIX века, и рассказал ему, что придумал отдельную математику. А Эйнштейну Давид Гильберт в Гёттингене сказал, что те уравнения, которые выписывает Эйнштейн, – не те уравнения, которые выписывал до него Ньютон, и они требуют более сложной математики, и рассказал про математику Римана, сказал, «я как раз передоказывал Римана, пользуйся».
Первое уравнении Эйнштейна написал Гильберт — Эйнштейн же несколько раз делал доклад, сначала у него было неправильное уравнение, а потом Гильберт выписал правильное уравнение, Эйнштейн сказал «клево», и вот это уравнение назвали уравнением Эйнштейна. Так и работает наука, тут главное вовремя подсуетиться. Просто математики очень много. А хочется встать на позицию и сказать, что вот есть математика, она первична, она язык.
А. Окуньков: Ну, она не язык, она в каком-то смысле более настоящая, реальная. Возвращаясь к компьютерным аналогиям — они понятнее, — вот есть процессор. Квантовый процессор, биологический, и прочее. Что такое процессор? Это какая-то штука, которая приближенно осуществляет некоторую математическую вещь. Но и в этом смысле математика незыблема, а разные физические процессы можно рассматривать как процессор, который какие-то вещи — математические сущности — постепенно реализует.
Я математикой стал заниматься после того, как из армии вернулся, я не то что на олимпиады какие-то ходил.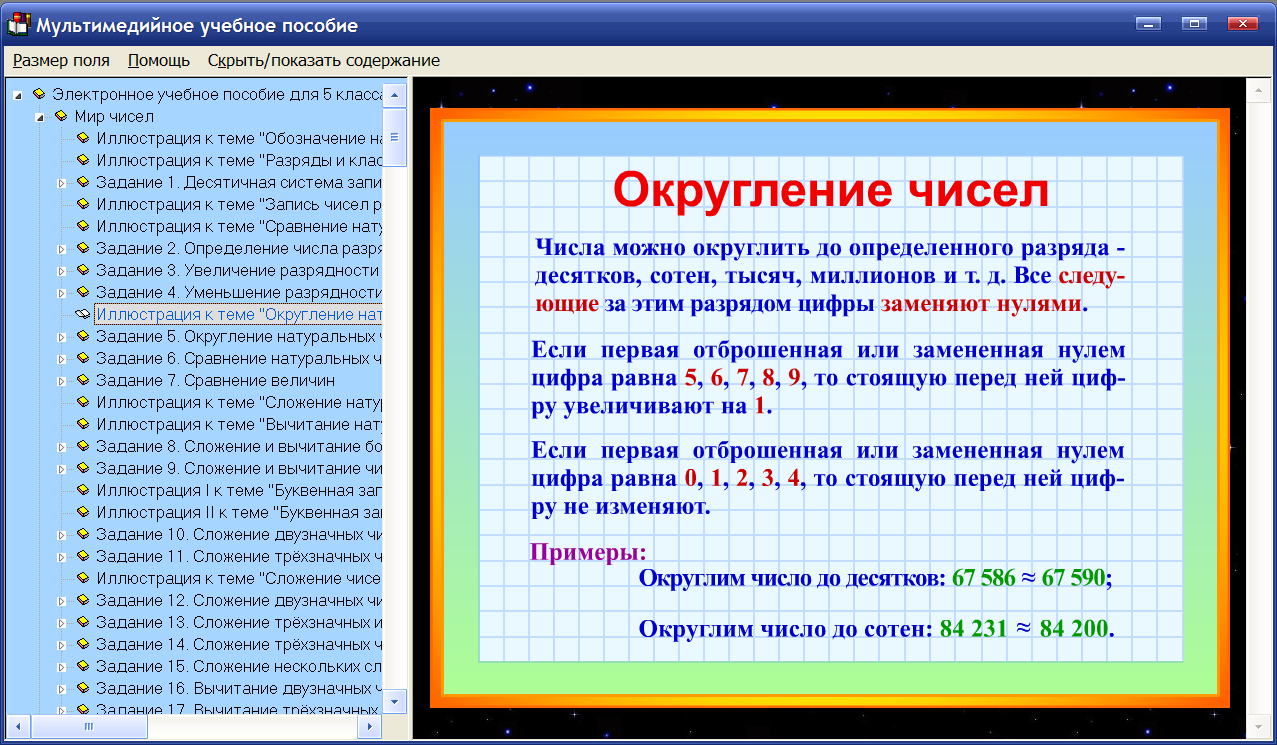
Я ходил, но не по математике. В школе была атмосфера дополнительных знаний, учебники были неплохие, дополнительный материал, какие-то кружки.
А. Коняев: Есть ощущение, что, когда говорят про математику в школе, это чаще всего некий набор навыков плюс некий набор утверждений.
А. Окуньков: Школа — это очень сложно. Я учу студентов в университете, все равно это тоже очень сложно.
А. Коняев: Мы не пытаемся придумать школьное образование. Вот у меня есть подруга, ей 37 лет, и когда у нее стресс, ей снится, что она пишет контрольную по математике.
А. Окуньков: У меня тоже был стресс, связанный с математикой в школе. Мы хулиганили, я сломал циркуль, я не знал, что делать. У нас был сосед, он работал на заводе и смог выточить нужные детали, приделал циркулю «искусственный сустав». Это было таким главным кошмаром по математике.
А. Коняев: Да, есть люди, которые прошли школу и вышли со страхом математики, Всемирная организация здравоохранения даже признает такую форму расстройства — mathematical anxiety.
То есть люди сидят и боятся математики. И это удивительно, потому что хочется сказать, что тот набор идей — потому что математика это все-таки про идеи, про объекты, между которыми сложные отношения, — люди в нем разбираются, и видно, как одна область перетекает в другую. А в школе тебе говорят: научись складывать, есть еще квадратное уравнение, еще буквы какие-то написаны, есть дискриминант, треугольник. Поэтому хочется спросить: когда человек закончил школу, как ему объяснить, как настоящая математика выглядит?
А. Окуньков: Школьное образование – сложная вещь, потому что, действительно, если придумывать одно образование для всех, это сложно. Но вот я учился, закончил школу в 1986 году, мне казалось, что у нас было бесконечное число ресурсов: популярные издания, пятое, десятое… Сейчас только лучше стало, сейчас столько всяких книг о математике.
А. Коняев: Это называется когнитивное искажение. У меня тоже была хорошая школа по математике, но это вторая.
Первая, в которой я учился, там все понятно было. Было понятно, что люди, которые ходят на уроки математики, не будут интересоваться математикой, не надо им это вообще. А вот вторая школа — да, были ресурсы и все.
А. Окуньков: Ну даже если говорить не только о школе — пошел я в ближайший книжный магазин, и меня многое там интеллектуально привлекло, в том числе и книги по математике.
А. Коняев: Хорошо, тогда так попробуем. К нам приходил тренер по боксу, он говорил, что после 30 уже бесполезно заниматься боксом профессионально. А вот если человек в 35 лет решил заинтересоваться математикой, есть у него еще варианты, или он уже бесконечно отстал?
А. Окуньков: Вы знаете, мы тут решили с женой бороться с «ковидными» мозгами — нам 50 лет с хвостиком, — решили заняться японским языком. Я несколько раз в жизни пытался начать, вот сейчас серьезно занимаемся, тяжело очень, но я думаю, что все-таки выучить сможем.
А. Коняев: То есть и с математикой можно?
А.
Окуньков: Да, наверное, можно. Ведь математика — это тоже целый мир, в ней можно много всяких разных вещей найти. Что-то, что человеку нравится, что человека интересует, найти какое-то счастье в познании или занятии этим . Я, знаете, всегда студентам говорю — не переживайте на тему того, что вы не первые доказали какую-то теорему, а вы решили какой-то там простой пример из книжки. Радость открытия всегда одна и та же. Что-то вы поняли — и это прекрасно. Я всегда своим аспирантам говорю, что если вы что-то осознали, даже если кто-то до вас это уже опубликовал, это все равно радость огромная.
По-моему, Колмогоров говорил, что занятие математикой требует очень много свободного времени. Что это означает? Мне кажется, что в математике очень много времени нужно для того, чтобы подумать о чем-то, потом понять. И при этом можно мыть посуду, куда-то идти… Вот на это нужно время. И то же самое, иногда надо, чтобы человек сказал самое главное, замолчал, и все люди потом подумали.
А.
Коняев: Вот эта идея про «подумать» очень любопытная, у Колмогорова же было расписание, когда он жил на даче, у него работа занимала два часа, а все остальное время… Он час поработал, а дальше он ушел в лес на три часа.
А. Окуньков: Есть много знаменитых историй о том, как к математику пришла грандиозная идея, когда он заносил ногу для того, чтобы зайти в какой-то дилижанс, или еще что-то. Очень редко было, что я писал-писал-писал — и вот сошлось.
А. Коняев: А как у вас происходит этот процесс — «подумать»? Вы видите цифры или уравнения?
А. Окуньков: На самом деле с ковидом это очень сильно поменялось. Когда в карантине мы сидели… В анекдотах про Ландау говорят, что он думал, лежа на диване — я тоже решил так попробовать, нормально получается. Но нужен перед глазами листок бумаги, чтобы какие-то линии нарисовать и все прочее. А вообще я очень любил, когда мы жили в Москве на Новой Лесной, ходить в сквер кидать баскетбольный мяч, а когда мы жили в Принстоне, у нас свое кольцо было баскетбольное.
Вы кидаете мяч и думаете, входите в какую-то механику.
А. Коняев: А музыку вы слушаете?
А. Окуньков: Нет, может, кому-то это и помогает, меня это отвлекает, это вообще очень интересно, как у нас в мозге обрабатывается математика. Удивительно, что все математические идеи — да и музыкальные тоже, насколько я понимаю, — в развитии человека, а он существует примерно два миллиона лет, появились относительно недавно (Андрей Юрьевич, очевидно, имеет в виду представителей рода Homo, появившихся на Земле даже более двух миллионов лет назад, — прим. ред.). Они в мозге наложились на какие-то другие центры — не то что у нас есть специальный центр для математики в голове. Может быть, поэтому у всех нас проработка математической информации на разные нейронные куски замкнута, и мне лично музыка мешает. Хотя нет, знаете, мне музыка помогает, если это только музыка — если я сижу на концерте, я начинаю думать о математике.
Т. Каргинов: А во сне вы видите свою работу?
А.
Окуньков: Нет. Но один раз меня начали мучить кошмары относительно той задачи, которую я пытался решить.
А. Коняев: Как выглядели эти кошмары?
А. Окуньков: Я чуть ли не матричным элементом оказался в этой матрице. Меня это так напугало тогда, я решил над этой задачей больше не думать.
А. Коняев: А математические объекты математические реальны? Они существуют?
А. Окуньков: Конечно, реально. Но что значит «существуют»? Я уже говорил, что физики разных времен математику под то, о чем они говорят, подводят по-разному. И самые обыденные вещи на самом деле оказываются чем-то иным. Воздух состоит из молекул, молекулы состоят из атомов, атомы имеют свое строение, и так далее. Поэтому все, что мы воспринимаем, это некоторое композитное восприятие. Вся информация, которую мозг воспринимает как происходящее вокруг нас, — это некоторые состояния нашего мозга, вызванные сигналами, которые он получает извне.
А.
Коняев: И они довольно ограничены. У нас, к примеру, всего четыре вкуса, и все многообразие вкусов мы формируем из этих четырех.
А. Окуньков: Это понятно. Я к тому, что любой предмет для нас состоит из каких-то других предметов, которые состоят из более сложных вещей, и в конце концов, когда мы уже дойдем до микромира, там все квантовое. И всегда люди спрашивают — что в основе всего? Мы не знаем. Мы знаем только математические модели, и они построены на своей логике, они не противоречивы, описывают физическую реальность, и они более реальны в некотором смысле, чем сама реальность.
А. Коняев: Просто когда мы смотрим на стакан, мы держим его, мы можем его пощупать. Если ты человеку начинаешь отвечать на вопрос, реален ли стакан и что значит его пощупать, это звучит как издевательство — конечно, реален, я сейчас возьму и кину в тебя этот стакан, и поспорь с его реальностью! Реальность стакана, летящего тебе в лоб, очень сложно ставить под сомнение и задавать вопрос, он реален, или летит в меня абстракция.
Проблема состоит в том, что если всерьез рассматривать вопрос существования, то мы начинаем двигаться куда-то вниз и приходим к тому, что стакан — понятно, а существуют ли кварки, или существует ли черная дыра?
А. Окуньков: Ну, собственно, когда мы дойдем до частиц типа протонов… Они же ни в каком месте не находятся, они — некоторая вероятностная сущность, она флуктуирована. Факт в том, что стакан имеет определенную форму, и это на самом деле выражение некоторого математического факта, сродни тому, что все люди принимают случайные решения, но общество в целом действует очень предсказуемо. То же самое атомы, из которых состоит стакан, — они как-то случайно там болтаются, но в целом стакан имеет определенную форму и никуда не девается в нашем представлении.
Т. Каргинов: А можно ли с помощью формул доказать или опровергнуть существование бога?
А. Окуньков: Это какой-то средневековый вопрос. Смешно, кстати, что до сих пор думают, что в Средневековье люди думали, что земля плоская.
На самом деле еще Блаженный Августин на первой странице своей книги пишет слова, что что-то так же очевидно как то, что Земля круглая.
А. Коняев: Ответ нет! Если ты предполагаешь, что есть бог, то он точно знает математику лучше, чем ты, он всесилен и понимает все, что есть, всю реальность. Давай возьмем наше представление о случайности — мы подкидываем монетку и не знаем, как она упадет. Мы для описания этого факта придумываем теорию вероятности. Говорим о том, что с вероятностью, равной одному, упадет, или с вероятностью, равной одному, не упадет. Бог же как всесильное существо либо должен точно знать, как монетка упадет, то есть он должен понимать все происходящее вокруг, либо для него не должно существовать вероятности по другим причинам, например, для него совершенно неважно как упадет монетка, потому что наш мир разделяется на мир, где монетка упала орлом, и мир, где упала решкой. И бог все эти миры видит, для него траектория объекта такая, ветвящаяся во времени и пространстве, и он обозревает ее сразу.
Т. Каргинов: Помнишь, у братьев Стругацких, по-моему, был такой рассказ, называется «Миллион лет до нашей эры» (Тимур имеет в виду рассказ «За миллиард лет до конца света», — прим. ред.), там была история математика, он доказал какую-то формулу, которая должна была изменить вообще все, и якобы мироздание начало им подкидывать всякие сложные штуки…
А. Коняев: «Вселенский гомеостаз» это называлось. Видишь, когда пытаешься женить бога и математику, так себе получается.
А. Окуньков: Согласно воззрениям квантовой теории поля, наш мир «пробует» все мыслимые пути, это так. Все на свете происходит всеми немыслимыми способами, а то, что мы видим, — просто усреднение из этого всего.
А. Коняев: В квантовой механике, квантовой теории поля если ты считаешь какие-то траектории, ты должен поступить так: взять две точки, нарисовать все-все-все возможные траектории, дальше что-то по ним посчитать, и у тебя получится усредненная настоящая траектория.
А. Окуньков: Вот я к вам шел с Белорусского вокзала, и с точки зрения квантовой механики я не весь целый к вам шел, а все-все частицы которые меня составляют летели по всему миру. Все вносили свой вклад, но немножко разными фазами, потому что все эти фазы сократились кроме очень маленькой окрестности от Белорусского вокзала до сюда, как вот вы меня на геолокации видели. Мир так устроен, так и есть.
Т. Каргинов: Я так понимаю, это все это тесно связано с понятием времени?
А. Коняев: У математиков нет проблем с понятием времени. Есть у физиков.
Т. Каргинов: Как математики видят время?
А. Коняев: Просто параметр, t. Он есть, и не является чем-то сверхъестественным. Это же главная проблема… Вернемся к Эйнштейну, Риману. Эйнштейн взял хорошую математику, но она настолько клевая, что с точки зрения физики возникает много вопросов. Например, ты можешь двигаться по траектории, которая обращает время, как в сериале Dark.
Там так было, что ты двигался, двигался, потом встретил кого-то, родил кого-то, а этот кто-то оказался твоей мамой. Приходится добавлять какие-то утверждения, приходится говорить — пусть здесь работает принцип причинности. Это означает, что если у тебя есть физический процесс, нельзя математику поменять и сделать замену, чтобы причины и следствия поменялись местами. Если у тебя есть причина и следствие, то должно быть направление, должно быть время. И начинаются вопросы: куда смотрит стрелка времени, почему время движется вперед, а не назад, почему оно должно в одном направлении двигаться. Вот физики этим занимаются. А у математиков — t, просто t.
А. Окуньков: Математиков сильно волнует, что такое пространство. Это только кажется, что оно очевидно существует, но если вернуться к тому, что оно, по теории Эйнштейна, есть динамическая вещь… С чего мы начали: Эйнштейн говорит, что пространство —живое, оно в принципе может меняться, но никто не сказал, что оно должно быть таким, как мы его представляем.
Ну вот представьте его как лист бумаги — но почему, собственно говоря, оно не может выглядеть как упаковочная штука с огромным числом пузырей? Собственно, если мы очень сильно приблизим бумагу, то увидим, что она и есть дырявая…
А. Коняев: Основной вклад Римана был как раз в том, что он предложил некую математику для описания пространства, он считал, что пространство играет важную роль. При Ньютоне считалось, что пространство ни в чем не участвует — оно есть, и все события внутри него разворачиваются, а Риман считал, что пространство должно во всем участвовать. И вот он придумал уравнения… Понятно, что не бывает так, что его идея была единственная, до него никто не догадался. Разумеется, у него был хороший учитель, и много кому это в голову приходило, но в целом его математика и дала эту идею, что гравитацию нужно описывать в терминах окружающего пространства, что оно у тебя колеблется, гнется в каком-то многомерном смысле, и вот это уже и есть гравитация.
Т.
Каргинов: Надо родиться такими, как вы, нужен определенный склад ума, чтобы заниматься математикой, это очень сложно. И Андрей когда мне что-то рассказывает про математику, всегда говорит и про физику. Химия еще не дошла.
А. Окуньков: Почему же, некоторые части физики уже считаются химией. Структура молекулы, например.
Т. Каргинов: Скажите, пожалуйста, я так понимаю, все математики очень много сталкиваются с провалами?
А. Коняев: Провал — это когда пришла вечером хорошая идея (а вечером всегда плохие идеи приходят), проверил с утра — и она не получилась.
А. Окуньков: Вот это, кстати, хороший совет — если пришла хорошая идея вечером, никогда не проверяй ее вечером.
А. Коняев: Да. Вечером такой сидишь, тебе приходит хорошая идея — у тебя есть задача, ты не понимаешь, как решать, и вот приходит идея. Нельзя проверять ее вечером, ты накосячишь. Ты оставляешь ее до утра, и с вероятностью 90% находишь косяк.
А. Окуньков: Почему это специфично для математиков, разве для инженеров не так?
А. Коняев: Для большинства людей так часто ошибаться — это что-то не то.
А. Окуньков: Любой творческий процесс с этим сопряжен.
А. Коняев: Да, это важно, любой творческий процесс! Это проблема, с которой сталкиваются студенты последнего курса.
А. Окуньков: А у вас такого никогда не было? Пишешь вечером, кажется, нормально, а утром оказывается, что ерунда. При чем здесь математика?
А. Коняев: Я говорю про другое. Есть студенты, которые учатся на мехмате, последний курс. У них до этого была математика какая — они ходили на пары, им давали задачи, они их решали, у задач были ответы. Потом они начинают заниматься научной работой. Им дали задачу, что-то у них получилось, а потом перестало получаться. И это важная часть жизни, но я знаю множество историй, когда у людей перестало получаться, и они такие: все, я пойду работать в Google.
А потом человек всю жизнь страдает.
А. Окуньков: Опять же, мне кажется, это не настолько специфично для математиков, поскольку у меня обе дочки физикой занимаются. Там, бывает, месяцами что-то делаешь, и не работает.
А. Коняев: И как человек с этим справляется?
А. Окуньков: Это вопрос любой деятельности. А как вот мореплаватели отправлялись в далекие страны, и там вообще ничего не находили? Математикам в этом смысле, я считаю, легче, потому что мы практически не зависим от аппаратов. Или зависим в негативном смысле — иногда люди считают на компьютере, у них не сходится, они думают, что решают неправильно. А это компьютер считает неправильно.
Т. Каргинов: Я недавно на самолете летел, и на зоне досмотра одному парню сказали выложить все электронное. Он из рюкзака выложил ноутбук, телефон и огромный калькулятор. Я еще подумал — кто возит калькуляторы с собой…
А. Коняев: Я слышал историю, что стояли математики в аэропорту, потом прибежала охрана, скрутила одного из них и увела.
Дело было вот в чем. В алгебраической геометрии есть такая штука, называется «раздутие» — по-английски это будет blow-up, похоже на слово «взрыв». «Плоскость» на английском — plane, как «самолет». И один математик объяснял другому, как делать трехточечное раздутие на плоскости — three point blow-up on a plane. И охрана среагировала.
А. Окуньков: Да, в математике множество простых слов означают что-то совершенно другое…
А. Каргинов: А вот такой вопрос… В книге Замятина «Мы» люди живут в антиутопичном мире, устроенном математиками. У меня вопрос такой: можно ли доверять математикам устройство мира?
А. Коняев: Я бы не доверил. Во-первых, среди математиков много консерваторов. Когда в XIX веке Виктория стала королевой Викторией, это было серьезным геополитическим испытанием для Европы, и среди прочего, например, в Германии, которая все еще не была совсем единым государством, начался откат от либеральных идей. В Геттингенском университете, который был центром европейской математики до 1937 года, пока фашисты всех не разогнали, получилось, что Риман и Гаусс были консерваторами, а какое-то количество тех, с кем они работали, были либералами.
Их уволили, это совершенно не помешало им дальше заниматься математикой, но обозначило эту историю.
А. Окуньков: Я немного вступлюсь за математиков. Поскольку я в математику пришел позже, учился, в армии послужил, а также по роду своей деятельности с физиками много общаюсь, с другими учеными. Мне как раз кажется, что математики в принципе, во-первых, незлобивы, во-вторых, математик ничего не прячет, делится знаниями со всеми на свете. В смысле доступности и демократичности — это потрясающе, я бы сказал. Вся математика в интернете в открытом доступе, за исключением старых книг, за которые издатели хотят с вас денег.
Т. Каргинов: Скажите, а эта наука везде одинакова? Или есть направления, там, китайская математика и так далее?
А. Окуньков: Есть школы, разные школы и законы. Школы в основном связаны с тем, что где-то был сильный ученый в какой-то области, и его ученики составили некоторую школу.
Т. Каргинов: В российской математике есть школы?
А.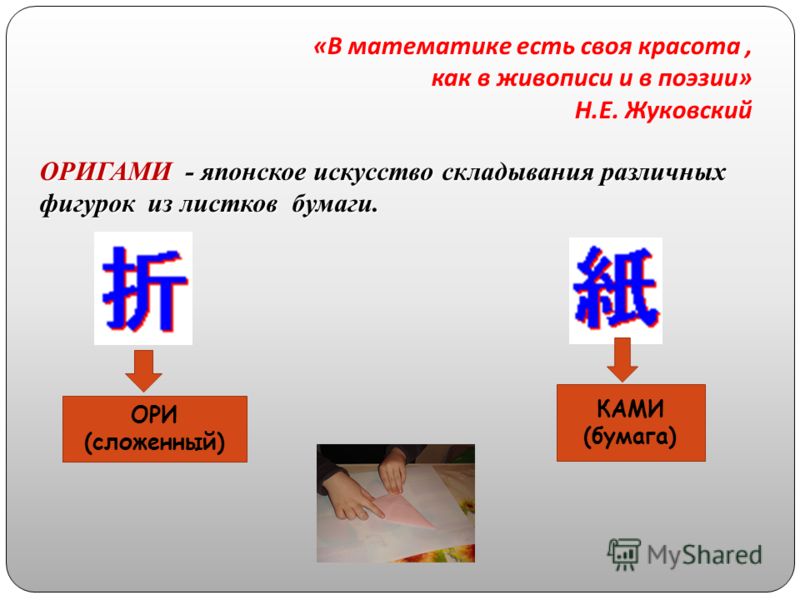
Окуньков: Конечно есть. У нас есть свои школы, сильнее в каких-то отраслях математики, слабее в других.
Т. Каргинов: Вы себя отождествляете с российскими математиками?
А. Окуньков: Да, конечно.
Т. Каргинов: Что это значит, быть российским математиком?
А. Окуньков: Это некоторый взгляд на то, что важно, что красиво, чем и как стоит заниматься.
Т. Каргинов: То есть в российской математике – это такая культурная форма?
А. Окуньков: В любой стране это культурная форма!
А. Коняев: То есть можно быть российским математиком, если тебя зовут Сунь Ван Хо, и ты живешь в Индии? Но ты учился здесь и будешь хорошим российским математиком?
А. Окуньков: Да, наверное.
А. Коняев: То есть это такая культурная общность, не обязательно, чтобы математики жили на территории России, чтобы быть российскими.
А. Окуньков: Территориальность – это даже смешно сейчас, уже последние полтора года все со всеми по Zoom общаются, но и до этого, собственно говоря, это не так уж было и важно.
Т. Каргинов: Я слышал, в Питере будет международный конгресс. Что происходит там? Что вы там делаете?
А. Окуньков: Замечательно, что у математиков есть такой объединяющий конгресс, который пытается в себя вобрать всю математику. Это замечательно, потому что математика едина, гораздо более едина, чем какая-либо другая дисциплина. Даже в смысле математической физики. Одна и та же математика может описывать много разных физических сущностей. Тот факт, что сообщество старается собраться и обсудить, что произошло за четыре года, это великолепно. Там есть некая обязательная программа, которую формирует специальный комитет — он заседает, решает, кого позвать. Это от Международного союза идет, там есть пленарные докладчики и секционные докладчики.
Т. Каргинов: В стендапе есть такое понятие — comedy buddy, это человек, с которым ты придумываешь шутки, а вот в математике есть что-то подобное?
А. Окуньков: Это в математике совершенно необходимо.
У меня может быть несколько таких людей. Давид Каждан такой человек, он приедет в Петербург и будет пленарным докладчиком. Ему можно рассказать любую математику, и он отреагирует. (Давид Каждан — израильский, в прошлом советский и американский математик. Член Национальной академии наук США и Израильской академии наук, лауреат премии Израиля и премии Шао, — прим. ред.)
Т. Каргинов: Я почему-то думал, что это сугубо индивидуальный процесс.
А. Окуньков: Нет, это как раз очень важно, сказать — это мне напоминает то-то, а не пробовал ли ты делать это. Когда люди сами о чем-то думают, они часто попадают, образно, в такую комнату, из которой не видят выхода, и ходят по ней, ходят… А этот человек скажет — вот тут занавеска, можно выйти.
А. Коняев: Это важная часть любой конференции. Самое интересное — это не доклады, которые очень важны, но потом люди расходятся, между собой о чем-то разговаривают, и это самая важная часть. Еще надо обязательно куда-нибудь сходить, выпить пива или вина, тоже помогает.
Т. Каргинов: Час пролетел очень незаметно. Почему у меня не было таких лекций!
Известный математик о проблемах преподавания в школе — Реальное время
Математик с мировым именем о проблемах преподавания царицы наук в России
В российских школах образовалась огромная пропасть в преподавании математики. Если в обычных учебных заведениях «не учат буквально ничему», то в «крутых» — куют будущих победителей международных олимпиад. «Есть и середина, например, добротные кадетские классы или классы хороших православных гимназий, где школьники знают математику получше, чем «в среднем по больнице», — утверждает знаменитый математик, профессор Московского физико-технического института и популярный блогер Алексей Савватеев. В интервью «Реальному времени» популяризатор рассказал о причинах образовательного кризиса, лучших школах математики в стране и о том, как царица наук может доказать существование Абсолютной Истины или Бога.
— Алексей, большинство людей никогда не пользуется в жизни или на работе знаниями из старших классов школы и вуза. Вы считаете, что всем нужно изучать синусы, производные, интегралы? Если да, то зачем?
— «Учитель! А разве мне пригодится вся эта ваша математика?» — «Нет, она пригодится только умным детям!» В этом анекдоте — вся суть дела. Подобно тому, как стихи Бродского для грубого невежи звучат как абракадабра, а у ценителя вызовут самые высокие резонансы в душе, так и все математические конструкции окажутся полезными только для людей тонкого чутья, ума и интеллекта.
Математика не учит тому, как ее использовать — это каждый должен научиться делать сам. И это правильно — иначе бы она метала бисер перед известно кем.
— Насколько велика разница между преподаванием математики по программам элитных гимназий и обычных школ? Какие школьные учебники по математике вы можете порекомендовать?
— Учебников, кроме Пчёлко и Киселева, я никаких рекомендовать не хочу: «самое лучшее вино — это вино выдержанное», и вышеназванные книги проверены многими поколениями школьников.
Из современных книг, как мне кажется, каждый, вооружившись теми знаниями, которые содержатся в Киселеве, найдет себе материал по вкусу.
Что же касается преподавания в школах, то, боюсь, ни один человек «извне» не способен даже представить себе ту пропасть, которая сформировалась в этом месте. Здесь просто нет никакого сравнения.
В обычных школах не учат буквально ничему, а в крутых школах куют будущих победителей международных олимпиад. Это даже не небо и земля, это свежий ветер и полный вакуум. Есть и середина — например, добротные кадетские классы или классы хороших православных гимназий, где школьники знают математику получше, чем «в среднем по больнице». Видел сам и свидетельствую об этом.
Фото: vk.com/alexei_savvateevЧто же касается преподавания в школах, то, боюсь, ни один человек «извне» не способен даже представить себе ту пропасть, которая сформировалась в этом месте. Здесь просто нет никакого сравнения
— Почему образовалась такая пропасть?
— Господь всех создал очень-очень разными, с разными в том числе и способностями к математике.
Пропасть была всегда, но она расширяется по мере смены советского «курса на уравниловку» курсом на «социальный дарвинизм», как бы ни относиться к последнему. Люди, способные к математике, получают при «социальном дарвинизме» больше шансов, возможностей и свободы. СССР был страной работяг, «диктатурой пролетариата», а на деле — диктатурой серости и послушности. Нынче все-таки другие времена.
— В одном интервью вы несколько раз говорили про вдохновение, которое сопровождает изучение математики. Этот момент сложно понять людям, кому математика кажется невыносимо тяжелым предметом. Вы считаете, что каждого человека можно вдохновить на изучение математики, или с рождения нужен специфический склад ума?
— Если честно, то, конечно, не каждого. Математикой «ушиблено» около 5 процентов населения, из них только каждый пятый (уже 1 процент остался!) это осознает. Еще каждый десятый (одно промилле в итоге) решает развивать свои знания. Примерно так.
— Получается, что наша система образования рассчитана максимум на 5% людей? А что делать 95%, которым не повезло получить математический склад ума? Бесполезно тратить время над тем, что они не могут понять?
— Я бы не хотел вдаваться в эти философствования.
Ни один из этих 95% не жалуется на отсутствие знаний по математике. Люди, наоборот, даже рады ничего не делать для понимания предмета. Будут ли эти 95% хорошо знать математику — не так важно, как то, будут ли ее знать на отлично оставшиеся 5%. Над чем я изо всех сил и работаю в России.
— В каких школах России самые сильные преподаватели по математике?
— Это хорошо известный список — московские школы №179, 2, 57; питерская №239; челябинский 31-й лицей; РЕМШ в Адыгее; одна из школ Кургана; я не огласил и половины списка. Ярославль, Калуга, Ижевск, Иркутск, Новосибирск, Киров имеют первоклассные школы и первоклассных учителей. Я прошу прощения у всех, кого я не упомянул.
Хороших школ и ярчайших учителей — многие сотни, если не тысячи, по стране. Кроме того, в России живут и творят свои шедевры, навскидку, около 500 выдающихся задачных композиторов (часто это те же преподаватели, но не всегда). Россия богата талантами, как никакая страна в мире — и это не фашизм, а простая констатация факта!
Фото: vk.
com/alexei_savvateevМатематикой «ушиблено» около 5 процентов населения, из них только каждый пятый (уже 1 процент остался!) это осознает. Еще каждый десятый (одно промилле в итоге) решает развивать свои знания. Примерно так«Только ограничение информационного потока может вывести ребенка на орбиту успеха»
— Чтобы вы посоветовали родителям из глубинки, где нет выдающихся школ, или тем родителям, у кого нет возможности отдать своего ребенка в такую школу? Как можно помочь ребенку развить интеллект, получить хорошее образование, если нет больших денег?
— Вы спрашиваете про деньги, и сразу ясно, что вы «не в теме». Это в блатных (а на деле — отстойных) заведениях для поступления нужны деньги. Все хорошие математические школы отбирают строго по собеседованиям. Любой талантливый школьник, даже из самой бедной семьи, без труда поступит в такую школу, его даже еще раньше распознают по результатам всяких интернет-конкурсов.
Заочные конкурсы, интернет-олимпиады, онлайн-кружки — вот путь наверх. Лучше вместе с родителями их проходить. Для детей из младших классов есть matznanie.ru, для средних и старших — много всего, например, мой YouTube-канал, а также мои 100 уроков математики, из которых 20 уже сняты в суперкачестве фондом «Дети и Наука».
— Детям сложно справиться с информационным потоком в Сети, который отвлекает от обучения и распыляет внимание. Получается, если не давать ребенку смартфон и не позволять сидеть в соцсетях, скорее всего, он будет намного умнее остальных детей в классе?
— Не скорее всего, а наверняка. С вероятностью 1. Конечно, если у ребенка при этом есть математические способности от рождения. Мой старший сын — отличный тому пример: у него нет смартфона, он участвует в финалах всероссийских олимпиад как по математике, так и по информатике. Однако и для остальных моих детей (а у меня их пятеро) я придерживаюсь тактики ограничения времени онлайн. Даже если в математику они не пойдут.
Есть одно главное, что родитель должен сегодня понять: только ограничение информационного потока может вывести ребенка на орбиту успеха. Точка.
— Расскажите о роли математики в современной науке. Она остается царицей всех наук?
— Она не просто остается Царицей. Она именно сегодня ею становится в полной мере — после того, как во всех других областях знания был осознан неточный, приблизительный характер любых делаемых утверждений. Даже в физике! На разных масштабах и уровнях применяются совершенно разные модели, и «универсальной физической картины мира» скорее нет, чем она есть. Я уже не говорю о науках пограничных между естественными и гуманитарными, таких как экономика и социология, да и во многом даже биология. Там вообще точное знание если порой и добывается, то такая ситуация — очень большая редкость.
Все науки, осознавая абсолютность математического знания, пытаются равняться на него и переходить на «математические рельсы», но математика дарит им всем ровно столько, сколько им всем положил Господь.
И лишь для одной науки у Него нет границ щедрости: для Царицы всех наук, Его главной любимицы — Математики!
Есть одно главное, что родитель должен сегодня понять: только ограничение информационного потока может вывести ребенка на орбиту успеха. Точка«В математике есть целый ряд видимых «проявлений» Бога»
— Математика может доказать, что Бог есть?
— Концепция строгого доказательства вообще присутствует только в математике. Бог математику создал, поэтому он сам выше нее — и тем самым выше любых строгих доказательств. Никаким законам Господь Бог не подчиняется, напротив, это именно Он сочиняет законы и для математики, и для любых других наук. Данным богословским вопросом добрую половину жизни интересовался один из величайших ученых — Исаак Ньютон.
В математике есть целый ряд видимых «проявлений» Бога (но, конечно, как объяснено выше, доказательством Бытия Божьего ни одно из них не является).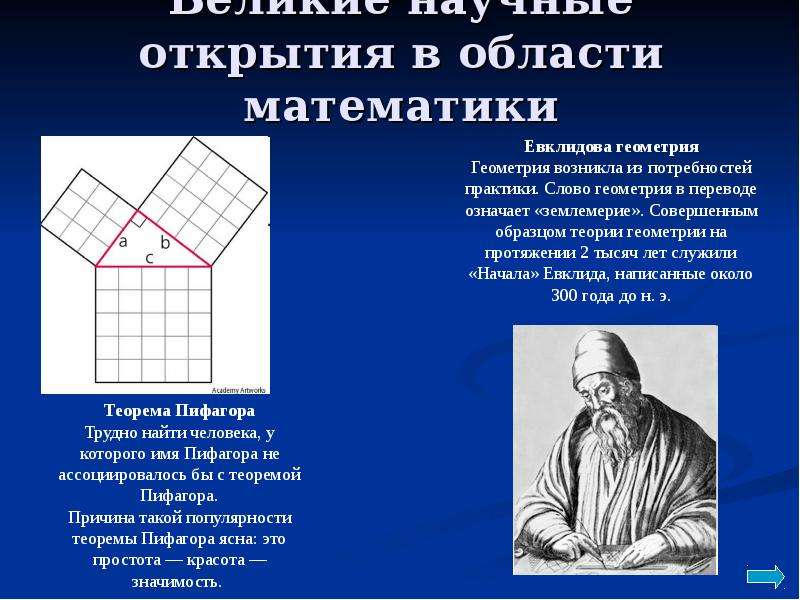
Первое указание на Него — это «актуальная бесконечность», а также тот факт, что мы вообще умеем с ней «работать». Мы можем просуммировать бесконечный ряд. Мощный компьютер может просуммировать только триллион триллионов слагаемых. А ум математика может сказать, чему равна сумма бесконечного ряда (в определенных случаях). Ум математика говорит, что 1+1/2+1/4+1/8+1/16+… равно в точности 2. Не меньше и не больше. Это проявление чего-то такого, чего нет в материальном мире, где все по определению конечно.
Далее идет идеальный образ. Переход через бесконечность — это лишь одно из проявлений идеализации чего-то. Миллиард слагаемых мы заменяем на бесконечность, и нам часто становится легче найти их полную сумму. Таких идеализаций очень много в математике. Математика дает такие сильнейшие методы, как дифференциальное и интегральное исчисление, которые на выходе дают решения конкретных практических задач.
Вы решаете задачу в идеализации, возвращаетесь к реальной задаче — и «идеальное», а в жизни приближенное решение вас полностью устраивает! Если нарисовать окружность на доске, то она не будет идеальной, но каждый школьник видит за этим рисунком идеальную окружность.
Платоновские образы — это и есть Бог, точнее, Его присутствие в математике.
Далее идет теорема Гёделя о неполноте, грубо говоря, повествующая о том, что в любой непротиворечивой теории, построенной на аксиомах, есть утверждение, которое в ней истинно, но не доказуемо ее средствами. Это математическая теорема. Это непосредственное, прямое указание на Бога, положившего нам «границы постижимого».
Фото: vk.com/alexei_savvateevУченый может быть как агностиком, так и верующим в Бога. А вот агрессивный атеизм с научным подходом несовместим «от слова совсем»
И последнее. В математике есть системы линейных дифференциальных уравнений, в которых скорость изменения любого параметра в любой момент является линейной комбинацией всех участвующих в постановке задачи параметров. Мы умеем решать такие уравнения еще со времен Ньютона. А вот если дифференциальные уравнения нелинейны, то мы не просто не умеем их решать, мы часто не можем дать даже приближенного прогноза поведения решения ни на какой разумный период времени.
Почему прогноз погоды с математической точки зрения невозможен на семь дней вперед и далее? Потому что системы дифференциальных уравнений, которые используются для прогноза погоды, непредсказуемы принципиально. В них заложена такая неприятная вещь, как локальная неустойчивость.
Если, например, вы выйдете на улицу и глубоко выдохнете, то этим вы можете инициировать совершенно другой сценарий развития климата. Это такой эффект бабочки. Это свойство практически всех процессов, которые описывают реальные вещи — течение жидкости, перемещение газа, многое другое. Возникает прочное ощущение, что Господь прямо сказал нам, ученым: «А дальше я вас не пускаю! Да, вы можете написать эти уравнения, но я вам не разрешаю их решать с той точностью, с которой вы хотите».
Имеющий уши — да слышит. А кто не понял ничего из только что сказанного и продолжает твердить, подобно барану, что Бога нет и «наука это доказала», то что тут можно поделать? Только руками развести. Как говорится, «насильно в мир иной не затащишь», как умрут — так все сразу и узнают.
И заодно по шапке как следует получат за свое невежество!
— А кто такой атеист, по-вашему? Среди ученых их много?
— Надо различать атеистов и агностиков. Атеист — это такой сектант, который сам себя убедил в отсутствии Бога и со всеми играет в игру «Вы меня не переубедите». Естественно, никто его и не переубедит, даже если ему Бога, сошедшего с Небес, покажут. Он скажет, что это галлюцинация была. Агностик же говорит так: «Я Бога не видел, следовательно, утверждать о Его наличии или отсутствии не берусь». Это вполне себе «научная» позиция, имеющая право на существование и уважение (в отличие от атеистической).
Ученый может быть как агностиком, так и верующим в Бога. А вот агрессивный атеизм с научным подходом несовместим «от слова совсем». Впрочем, настоящий ученый редко бывает даже и агностиком, ибо из любой глубокой науки Бог просто «выпирает». Не замечать Его — это особое искусство, но все-таки данное явление встречается в ученом мире.
— Есть ли открытия в математике в последние годы, о которых стоит узнать широкому кругу наших читателей?
— Здесь все зависит от того, что понимать под «последними годами».
Если лет 30, то это и Великая теорема Ферма, и «развязывание узлов» Васильевым, Гусаровым и Концевичем, и доказательство Перельмана великой гипотезы Пуанкаре. В самые последние годы если и был прогресс, то его трудно изложить простым языком. Даже я ничего там не понимаю!
Матвей Антропов
Справка
Алексей Савватеев — доктор физико-математических наук, популяризатор математики, проректор университета Дмитрия Пожарского, профессор Московского физико-технического института, научный руководитель Кавказского математического центра, ведущий научный сотрудник ЦЭМИ РАН, разработчик, вдохновитель и лектор курса «100 уроков математики», автор книги «Математика для гуманитариев. Живые лекции».
ОбществоОбразованиеКакие математические концепции необходимы для понимания уроков физики на уровне колледжа? | Образование
Физику часто рассматривают как эзотерическую, сложную область, но большая часть физики очень проста и описывает, как происходят вещи в повседневной жизни.
Вам не нужно быть математическим гением, чтобы изучать физику, но вам необходимо знать основы, а на уроках физики в колледже часто используются математический анализ и алгебра.
Алгебра
Если вы не освоили алгебру, то вы не сможете освоить исчисление, которое является обязательным условием физики.Алгебра учит основам абстрактного математического мышления, и после того, как учащиеся освоят основные уравнения алгебры, они узнают о концепциях, имеющих прямое отношение к физике. Линейная алгебра, например, играет ключевую роль в физике, потому что этот тип алгебры требует, чтобы учащиеся отображали трехмерные пространства.
Геометрия и тригонометрия
Свойства объекта, такие как его площадь или объем, могут влиять на то, как он взаимодействует с окружающей средой. Например, знание того, как определить основные свойства геометрических фигур, может помочь вам сделать выводы, относящиеся к физике.Аналитическая геометрия, сочетающая алгебру и геометрию, также может помочь вам освоить физику, потому что помогает решать алгебраические задачи, касающиеся физических объектов.
Исчисление
Исчисление поможет вам решить многие физические уравнения. Вы начнете с исчисления с одной переменной, а затем перейдете к исчислению с несколькими переменными. Последнее чрезвычайно важно для физики, потому что вы будете работать с производными по направлению и подобными понятиями в трехмерном пространстве. Этот процесс может подготовить вас к решению сложных физических уравнений, а математическое мышление, которое вы приобретете в исчислении, поможет натренировать ваш разум, чтобы думать как физик.
Вероятность и статистика
Вероятность и статистика играют ключевую роль в квантовой механике. Из квантовой механики вы узнаете, что материя и энергия — это и частицы, и волны, и будете делать предсказания о поведении объекта на основе этих знаний. Этот тип физики исследует физические явления, происходящие на микроуровне, и опирается на вероятностные формулы, чтобы делать выводы о крошечных частицах.
Дифференциальные уравнения
Дифференциальные уравнения являются краеугольным камнем многих известных физических теорий.
Чтобы понять дифференциальные уравнения, вам понадобятся базовые знания в области исчисления. Когда вы начнете заниматься физикой, вы, скорее всего, выучите такие уравнения, как уравнение гармонического осциллятора. Хотя вам не нужно проходить отдельный курс по дифференциальным уравнениям, вам понадобятся и алгебра, и исчисление, чтобы освоить дифференциальные концепции.
Ссылки
Биография писателя
Ван Томпсон — адвокат и писатель. Бывший инструктор по боевым искусствам, он имеет степень бакалавра музыки и информатики Вестчестерского университета и доктора юридических наук Университета штата Джорджия.Он является лауреатом многочисленных писательских наград, в том числе премии CALI Legal Writing Award 2009.
Какую математику мне следует выучить, чтобы открыть собственный бизнес? | Образование
Владение собственным бизнесом может дать вам свободу следовать своим творческим увлечениям и возможность внести что-то новое в свою область. Однако это не освободит вас от изучения базовой математики.
Даже если ваш бизнес не имеет ничего общего с математикой, вам придется освоить базовую арифметику, а некоторые виды бизнеса требуют математических знаний более высокого уровня.
Арифметика
Арифметика является частью повседневной жизни владельца бизнеса. Вам нужно будет уметь складывать, делить, вычитать и умножать числа, чтобы рассчитать свой заработок, предоставлять клиентам оценки и платить своим сотрудникам. Базовые арифметические навыки также помогут вам заполнить налоги, особенно если вы имеете право на многочисленные вычеты и кредиты. Арифметика также поможет вам рассчитать свои расходы, определить процентные платежи и сбалансировать бюджет вашего бизнеса.
Геометрия
Геометрия обязательна для владельцев творческих профессий, таких как дизайн интерьера, строительство, искусство и архитектура. Вам нужно будет рассчитать площадь помещения, если вы хотите уложить полы, объем и периметр художественных проектов и количество расходных материалов, таких как краска, которые вам понадобятся.
Алгебра
Решение для переменной может помочь вам решить множество бизнес-уравнений. Например, если вы хотите определить, сколько акций нужно продать, чтобы достичь определенного числа, вам может помочь алгебра.Графические функции также могут помочь вам спланировать будущее вашего бизнеса, а идентификация функций может помочь вам определить их диапазоны.
Исчисление
Не всем владельцам бизнеса нужны вычисления, но если вы работаете в области науки, техники или математики, вам, вероятно, понадобятся вычисления. Это особенно верно, если вы планируете предоставлять научные услуги, а не просто работать с людьми, предлагающими эти услуги. Расчет также может помочь вам понять документы и бизнес-планы ваших клиентов.Например, если инженер представляет вам предложение, исчисление может помочь вам определить его осуществимость. Расчет также может помочь вам сделать экономические прогнозы.
Курсы бизнес-математики
Если вам нужно освежить свои математические навыки, вы можете рассмотреть возможность прохождения курса математики для владельцев бизнеса.
Ваш местный колледж, скорее всего, предлагает вводные курсы по алгебре, математическому анализу и геометрии. Некоторые школы даже предлагают математические курсы специально для владельцев бизнеса. Например, Universal Class предлагает онлайн-курс по бизнес-математике.
Ссылки
Биография писателя
Ван Томпсон — адвокат и писатель. Бывший инструктор по боевым искусствам, он имеет степень бакалавра музыки и информатики Вестчестерского университета и доктора юридических наук Университета штата Джорджия. Он является лауреатом многочисленных писательских наград, в том числе премии CALI Legal Writing Award 2009.
Виды математики
Виды математики
Вы видите что-нибудь в этом последнем предложении, что кажется вам, возможно, неверным? Я делаю. Это слово «просто». Если бы письменная форма языка была просто символическим представлением языка, изучение его не должно было бы быть таким трудным — настолько трудным, что многие люди никогда не достигнут мастерства. Разговорный язык — это система, которая развивалась вместе с нашим видом в течение трех миллионов лет и достигла кульминации, как мы думаем, около 100 000 лет назад, и в значительной степени характерна для Homo sapiens .С другой стороны, письменный язык — это система, которую наши предки изобрели где-то около 10 000 лет до н. э. С когнитивной точки зрения письменный язык и разговорный язык — совершенно разные процессы.
Я полагаю, что то же самое справедливо и для математики, по крайней мере, для тех частей математики, которые непосредственно связаны с реальным миром, в котором мы живем, и непосредственно абстрагированы от него (в частности, числа, элементарная арифметика и основные идеи геометрии и тригонометрии).
Исследования неоднократно демонстрировали, что, когда люди оказываются в ситуации, когда им необходимы базовые математические навыки в повседневной жизни, они довольно быстро овладевают ими и быстро начинают бегло говорить.
В одном из таких исследований, проведенном в начале 1990-х годов, трое исследователей, Терезинья Нуньес из Лондонского университета, Англия, и Аналучия Диас Шлиманн и Дэвид Уильям Каррахер из Федерального университета Пернамбуку в Ресифи, Бразилия, вышли на уличные рынки Ресифи с магнитофоном, изображая из себя обычных покупателей на рынке.Их целевыми субъектами были маленькие дети в возрасте от 8 до 14 лет, которые присматривали за своими родителями. киосков, пока последние отсутствовали. В каждом прилавке исследователи предлагали молодым владельцам прилавков транзакции, предназначенные для проверки различных арифметических навыков.
Работая полностью в уме, без бумаги и карандаша, не говоря уже о ручном калькуляторе, маленькие дети получали правильный ответ в 98% случаев.
Но выдавать себя за клиентов было лишь первым этапом исследования, проведенного Нуньес и ее коллегами.Примерно через неделю после того, как они «проверили» детей в своих киосках, они посетили испытуемых в их домах и попросили каждого из них пройти карандашно-бумажный тест, который включал точно такие же арифметические задачи, которые были предложены им в контекст покупок за неделю до этого. Следователи постарались провести этот второй тест как можно менее угрожающе. Он включал в себя как простые арифметические вопросы, представленные в письменной форме, так и словесные задачи, представленные в виде торговых операций того же типа, что дети выполняли в своих киосках.Испытуемым были предоставлены бумага и карандаш, и их попросили написать свой ответ и любую работу, которую они хотели записать. Их также попросили произнести свои рассуждения вслух по ходу дела.
Хотя арифметика детей была практически безошибочной, когда они были у своих рыночных прилавков (чуть более 98 % правильных ответов), в среднем они набрали только 74 %, когда им предлагались словесные задачи, требующие той же арифметики, и ошеломляюще низкие 37 %, когда те же самые задачи были представлены им в виде простого символьного арифметического теста.
Исследователи отметили, что методы, которые дети применяли — с большим успехом — на уличном рынке, отличались от тех, которым их учили (и до сих пор учат) в школе. Скорее, на рынке они применяли методы, которые освоили, работая вместе со своими родителями и друзьями. Ясно, что «уличная математика», как Нуньес и ее коллеги назвали умственную деятельность, которую они наблюдали на рынке, сильно отличалась от символической системы символов, с которой дети сталкивались в школе.
Если вы хотите подробно ознакомиться с методами, которыми дети пользовались на рынке, и изучить ошибки, которые они допускали при выполнении расчетов с помощью бумаги и карандаша, прочтите книгу Уличная математика и школьная математика (обучение в Doing: Social, Cognitive and Computational Perspectives), которую Нуньес и ее коллеги написали о своем исследовании.
Описание аналогичного исследования, проведенного в США, на этот раз среди ориентированных на цену взрослых покупателей супермаркетов, с аналогичными результатами, было дано Джин Лэйв в ее книге «Познание на практике: разум, математика и культура в повседневной жизни».
Обучение в действии).
Я резюмировал оба исследования в своей более поздней книге «Математический инстинкт».
Хотя мы еще не понимаем, как человеческий мозг выполняет математические операции, будь то мысленно в реальной среде, такой как уличный рынок или супермаркет, или символически, используя бумагу и карандаш, кажется довольно ясным, что эти два вида деятельности находятся на одном уровне. по крайней мере так же отличаются друг от друга, как письменный и разговорный языки. Написанная символическая математика не является «просто» физически представленной версией умственной деятельности, которую Нуньес и др. назвали «уличной математикой».
В то время как современные технологии означают, что овладение навыками точного счета в уме сегодня уже не так важно, как раньше, общепризнано, что хорошее понимание числа и количества — то, что часто называют арифметикой или количественной грамотностью — абсолютно необходимо для человек должен быть полноценным членом современного общества.
Признание этого факта привело к созданию ряда учебников, предназначенных для обучения людей этому важному навыку.
Но подождите минутку. Не кажется ли вам что-то странным в этом развитии событий? Мы не используем книги, чтобы учить маленьких детей понимать и говорить на своем родном языке — это вызов «Уловке 22», если таковой когда-либо существовал; скорее, мы позволяем им улавливать его в той среде, в которой они его подвергают. Мы также не учим людей читать и писать ноты для того, чтобы они наслаждались музыкой, пели, играли на музыкальном инструменте или даже создавали музыку; вместо этого мы знакомим их с музыкой и позволяем им развивать навыки пения и игры на практике.Почему же тогда нужно хотя бы на минуту поверить, что предоставление ребенку учебника по математике приведет к арифметике — к тому, что он станет компетентным в том, что я предпочитаю называть «повседневной математикой»?
На самом деле, я не думаю, что мы верим, что такой подход сработает. (Конечно, учитывая различия между людьми, любой подход, вероятно, сработает для некоторых, но исследования Нуньеса и др.
, Лаве и других показывают, что все, кроме ничтожного меньшинства людей, становятся опытными в уличной математике, когда поместить в реальную среду, где это важно для них и в которой они подвергаются этому.) Скорее, мы пишем книги, потому что это доминирующая технология записи математических знаний и их широкого распространения. Ведь до недавнего времени это была наша только техника для тех целей.
Подход, основанный на учебниках, работал (для многих людей) в те дни, когда у (многих) людей была достаточная мотивация, чтобы приложить огромные усилия, необходимые для того, чтобы заставить его работать, о чем свидетельствует огромное влияние книги Леонардо Liber abaci на западную цивилизацию. после его появления в 1202 г.Но это явно не работает в сегодняшних западных обществах.
И я оставляю в стороне вопрос о том, как мы измеряем, достиг ли человек желаемого уровня навыков в повседневной математике. Если метод оценки состоит в том, чтобы дать им письменный тест, то дети-владельцы киосков в Ресифи будут классифицированы как не умеющие считать, а это явно не так!
На мой взгляд, сегодня технологии и более глубокое понимание того, как люди учатся, предоставляют нам ряд альтернатив для обучения и оценки навыков повседневной математики, некоторые из которых основаны на компьютере, другие ориентированы на физическую активность, а некоторые используют и то, и другое.
Но изучение этих альтернатив не является целью данного эссе. Я обращусь к этому захватывающему будущему в более поздней колонке. Скорее, моя текущая точка зрения состоит в том, что нам необходимо признать фундаментальный факт, что письменная, символическая математика не является «просто» письменной версией умственной деятельности, которую я называю «повседневной математикой». (Не то чтобы я был первым, кто использовал этот термин, и ни в коем случае не единственным, кто его использовал.) Действительно, с когнитивной точки зрения, я вообще не думаю, что символическая математика является вариантом повседневной математики; Я считаю, что это совсем другая умственная деятельность.(Я прожил достаточно долго, чтобы сожалеть о том, что сказал поколениям студентов колледжа, что математика — это просто «формализованный здравый смысл». Обычная математика такова, но символическая математика — определенно нет.)
Такое признание не означает, что символическая математика не важна. Боже мой, наше нынешнее общество во многом зависит от него! Само наше выживание требует постоянного притока людей с разной степенью владения символической математикой, вплоть до полноценного эксперта.
Но, объединяя два совершенно разных вида умственной деятельности под общим термином «(базовая) математика» и молчаливо считая один из них просто письменной версией другого, я считаю, что мы стреляем себе в обе ноги, когда дело доходит до обучения тому или иному виду. .
Угол Девлина обновляется в начале каждого месяца.
Математик Кит Девлин (email: [email protected]) является исполнительный директор Центра изучения языка и информации Стэнфордского университета и Математик в выпуске выходного дня NPR.Последняя книга Девлина, Раскрытие преступлений с помощью математики: ЦИФРЫ ЗА NUMB3RS, книга-компаньон к хиту телевизионный криминальный сериал NUMB3RS, и написана в соавторстве с профессором Гэри Лорденом из Калифорнийского технологического института, ведущим консультантом по математике в этой серии. Он был опубликован в прошлом месяце Plume.
Какая математика имеет значение?
Немногие вопросы образования вызывают такую решительную поддержку со стороны политических и деловых лидеров, как призыв к более высоким стандартам в математике.
Идея требовать, чтобы учащиеся изучали математику в течение большего количества лет — и более сложной математики — в старшей школе, продолжает набирать обороты, в основном благодаря убеждению, что учащимся потребуются более сильные навыки, чтобы конкурировать в экономике завтрашнего дня.
Но что, если завтрашняя экономика потребует чего-то меньшего?
Поскольку штаты повышают академические требования, некоторые исследователи и эксперты по труду говорят, что стремление к более тщательному изучению математики на самом деле не соответствует навыкам, которые требуются работодателям, даже во многих высокооплачиваемых областях.
Во многих хорошо оплачиваемых и востребованных профессиях, требующих некоторой математики, необходимый уровень редко превышает содержание 9-го или 10-го класса, утверждают некоторые наблюдатели. По их словам, свободное владение сложными математическими темами менее важно, чем умение решать проблемы и применять математику к различным задачам.
Посещение продвинутых курсов, таких как Алгебра 2, дает очевидные преимущества, соглашаются эксперты по труду и исследователи в области образования.
Исследования показывают, что учащиеся, изучающие математику в средней школе, с большей вероятностью преуспеют в колледже и получат более высокооплачиваемую работу.
Но если главной целью старшей школы является подготовка учащихся к работе, то, по мнению некоторых, необходимо переосмыслить требования к более жестким учебным программам и курсовым работам. Они также говорят, что создание курсов, в которых больший упор делается на реальную или «прикладную» математику, а не просто на повышение академических требований, может не только улучшить рабочие навыки студентов, но и их энтузиазм по этому предмету.
Неправильный образ мыслей?
«У нас сложился образ мышления «колледж для всех», — говорит Джеймс Э.Розенбаум, профессор социологии, образования и социальной политики в Северо-Западном университете в Эванстоне, штат Иллинойс, изучавший связь между школой и работой. Когда люди предполагают, что школы уделяют больше внимания математике, чем «прикладной математике», говорит он, «это звучит так, как будто мы отказываемся от возможности».
«Мир изменился. Работодателям нужно больше навыков», — говорит Розенбаум. «Педагоги предполагают, что эти навыки означают «колледж». Я думаю, что [будущим работникам] нужны хорошие, твердые навыки 10-го класса.
В середине 1990-х годов Розенбаум провел опрос работодателей, нанимавших работников самых разных офисных и производственных профессий, на предмет навыков, которые они считали наиболее важными. Он сосредоточился на рабочих местах начального уровня, которые давали возможность продвижения по службе, но не требовали высшего образования.
Из 51 опрошенного работодателя 35 заявили, что от работников требуется знание относительно базовой математики, например, как выполнять простые арифметические действия и складывать дроби, хотя для некоторых профессий требуются знания алгебры и тригонометрии.Некоторые менеджеры, однако, сказали, что им было трудно найти работников даже с базовыми математическими способностями.
[Гендель] подвергает сомнению предположение, выдвинутое многими политиками, о том, что изучение более сложной математики сделает учащихся более привлекательными.
Необходимость относительно базовой математики была также очевидна в исследовании, проведенном Майклом Дж. Генделем, профессором социологии Северо-восточного университета в Бостоне, в рамках доклада, который он завершает.В прошлом году Handel опросила 2300 сотрудников из самых разных профессий. Среди них были «высшие белые воротнички», такие как менеджеры и техники; служащие «белого воротничка», такие как продавцы; и ряд рабочих и обслуживающего персонала, таких как фабричные работники и работники общественного питания.
В рамках специального анализа, проведенного для Education Week , Гендель обнаружил, что, хотя 94 % работников этих профессий сообщили, что используют какую-либо математику на работе, только 22 % заявили, что используют более сложную математику, чем сложение, вычитание. , умножение или деление.Только 19 процентов сказали, что они использовали математику, достигающую уровня Алгебры 1, и 9 процентов использовали Алгебру 2.
Подавляющее большинство рабочих, напротив, сказали, что они использовали более простую математику, такую как дроби, умножение и деление.
Даже среди высокопоставленных белых воротничков, таких как менеджеры, только 30 процентов сказали, что они использовали Алгебру 1 на работе, и только 14 процентов сказали, что использовали Алгебру 2. Многие из этих рабочих мест, отмечает Гендель, вероятно, Согласно федеральным прогнозам труда, к 2014 году она станет одной из самых быстрорастущих профессий в стране.
Гендель подчеркивает, что он не утверждает, что учащиеся должны «меньше заниматься математикой» или что им не следует стремиться к углубленному изучению предмета. Но он подвергает сомнению предположение, выдвинутое многими политиками, о том, что изучение продвинутой математики сделает студентов более привлекательными или более полезными для работодателей на рынке труда в будущем.
«Эти результаты должны смягчить некоторые из наиболее преувеличенных и, возможно, более эмоциональных заявлений о предполагаемом несоответствии между школой и работой», — говорит Гендель.
Он говорит, что надеется, что его исследование поможет «привнести нотку реализма» в дебаты о математических навыках, необходимых на работе.
Высокооплачиваемые работники
В то же время Гендель и другие согласны с тем, что прохождение продвинутых математических курсов, таких как Алгебра 2, имеет явные преимущества, помогая студентам добиться успеха в колледже и получить хорошую работу.
Согласно исследованию, опубликованному Энтони П.Карневале и Донна М. Дерошерс для Службы тестирования образования, некоммерческой организации, расположенной в Принстоне, штат Нью-Джерси.
«Те, кто получают лучшую работу, больше всего занимаются математикой», — пишут авторы, добавляя: «Очевидно, что алгебра 2 — это пороговый курс математики, который выбирают люди, которые в конечном итоге получают хорошую работу в верхней половине доходов. распределение.»
Чем больше у вас знаний по математике, тем больше у вас возможностей для решения проблем, которые вам понадобятся позже.
Джеймс Рубильо,
Исследования показывают, что лишь небольшая часть рабочих — менее 5 процентов — широко используют алгебру 2, тригонометрию, исчисление или даже геометрию на работе, обнаружили Карневале и Дерошерс. Однако этот факт не обязательно означает, что школам лучше снизить требования по высшей математике. По словам авторов, эти занятия также помогают учащимся развивать превосходные навыки математического мышления.
«Чем больше у вас знаний по математике, тем больше возможностей для решения задач, которые вам понадобятся позже», — говорит Джеймс Рубильо, исполнительный директор Национального совета учителей математики, профессиональной ассоциации, насчитывающей 100 000 членов в Рестоне, штат Вирджиния. , «Вы получаете комфорт и уверенность, когда сталкиваетесь со сложными вычислениями».
Это мнение разделяет Курт В. Берглунд, который в прошлом году устроился инженером-разработчиком программного обеспечения в Microsoft Corp.
По его словам, его работа часто требует переключения между математикой, которую он изучал в старшей школе, и более продвинутыми принципами.
Берглунд, 25 лет, говорит, что он часто полагается на линейную алгебру при разработке трехмерного программного обеспечения. Он должен быть знаком с задачами с несколькими переменными и исчислением при чтении исследований в области дизайна. И он использует процесс, аналогичный «доказательствам» из геометрии, пытаясь писать более качественные программные коды.
«Вы смотрите на свой код и задаетесь вопросом, будет ли это работать всегда?» — говорит Берглунд. — Ты как бы рассуждаешь в своей голове.
Иногда, по его словам, он обращается к своим учебникам по математике в колледже, когда ему нужно освежить понятие.«На самом деле я бы хотел, чтобы моя математика была сильнее», — говорит он. «Вы определенно используете всю палитру».
Джон Д. Краман, старший политический аналитик в Achieve, некоммерческой организации в Вашингтоне, которая выступает за высокие академические стандарты, говорит, что школы могут требовать сильных программ по математике, но при этом гибких.
Achieve, созданная губернаторами и бизнес-лидерами, поддерживает, чтобы все учащиеся проходили основные курсы математики в средней школе, что даст им материал, эквивалентный алгебре 2, даже если они не изучают курс с таким точным названием, говорит Краман. .
Школы не должны просто разрешать учащимся отказываться от более сложных математических курсов, учитывая образовательные и профессиональные преимущества посещения этих курсов, добавил он.
«В итоге вы получите ужасно несправедливую систему, — говорит он, — которая рискует «детями из бедных школ получить плохую математику».
За последнее десятилетие требования штата по математике неуклонно повышались. По данным Комиссии по образованию штатов, в настоящее время в 24 штатах учащиеся должны пройти три года по математике до окончания средней школы.Только в двух штатах — Алабаме и Южной Каролине — требуется четыре года математики, хотя 10 других штатов и округ Колумбия постепенно вводят это требование, по данным ECS из Денвера.
Ищу математику для работы
В то время как большинство штатов избегают предписывать конкретный учебный план по математике в средней школе, количество более подробных предписаний увеличивается. Всего три года назад в трех штатах — Арканзасе, Индиане и Техасе — поэтапно ввели требования к учащимся пройти курс «Алгебра 2» перед выпуском из средней школы, если учащиеся не запрашивали специального разрешения не делать этого.По данным ECS, сегодня семь штатов продвигаются к внедрению требований по алгебре 2.
По мере того, как эти выпускные требования возрастают, политики должны прилагать больше усилий, говорят некоторые наблюдатели, чтобы дополнять традиционные продвинутые курсы другими математическими вариантами для учащихся, такими как занятия, в которых особое внимание уделяется прикладным навыкам и навыкам на рабочем месте.
Чтобы поддерживать интерес учащихся к математике и карьере, связанной с математикой, не менее важно показать им, что делает предмет актуальным.
Такие курсы могут быть не менее сложными с академической точки зрения, но также могут представлять математику менее абстрактно — подход, который, в свою очередь, будет поддерживать больший интерес учащихся к математике и к школе в целом, говорят Карневале и Дерошерс.
Rubillo из организации учителей математики считает, что учащимся четвертого года обучения в старших классах будет полезно больше «альтернативных» курсов математики, которые объединяют математику с уроками бизнеса, личных финансов, компьютеров и других предметов.По словам Рубильо, бывшего учителя математики в местном колледже, изучение математики на четвертом году обучения в старшей школе имеет решающее значение, потому что учащимся, потерявшим связь с предметом, с большей вероятностью потребуется коррекционная работа при поступлении в двух- или четырехгодичный колледж.
Однако создание таких курсов создает очевидные проблемы для школ.
Школьные округа уже изо всех сил пытаются найти достаточно учителей, квалифицированных для преподавания математики, особенно продвинутых курсов. По словам Рубильо, найти учителей с подготовкой, необходимой для совмещения математики с бизнесом и другими специализированными областями, будет особенно сложно.По его словам, в школах также не хватает учебников и других ресурсов, которые помогли бы учителям проводить эти уроки.
Многие работодатели, работающие в технических областях, «крайне разочарованы» тем, что средние школы не включают прикладную математику и решение задач в математические занятия, говорит Марк МакКаллох, консультант Siemens Building Technology, подразделения всемирной инженерной и электронной компании, базирующейся в Швейцария.
Посещение таких предметов, как алгебра 2, имеет решающее значение для студентов, планирующих карьеру в инженерных областях, говорит МакКаллох, бывший директор средней школы, который также является президентом компании All Student Can Learn, предоставляющей образовательные услуги в Дайере, штат Индиана.
, что способствует повышению квалификации рабочей силы.
Но для того, чтобы поддерживать энтузиазм студентов в отношении математики и связанных с математикой профессий, не менее важно показать им, что делает этот предмет актуальным в различных профессиональных областях, говорит он. Маккалох утверждает, что акцент на реальных приложениях особенно силен в начальной школе, когда многие учащиеся изучают такие предметы, как математика и деньги, но от средней к старшей школе он постепенно исчезает.
«Когда дело доходит до старших классов, учителя математики занимаются исключительно теоретической деятельностью, — говорит он.«Когда ученик спрашивает: «Где я могу увидеть, как это применяется, где бы я мог использовать многочлен?», учителя смотрят на них так: «Вы должны это выучить. Это хорошая основа». Они не могут сказать вам, что это для скорости реакции в химии, или вы увидите это, когда будете комбинировать химические вещества».
Описание теста по математике | АКТ
Раздел математики предназначен для оценки математических навыков, которые учащиеся обычно приобретают на курсах, изучаемых до начала 12 класса.
Большинство вопросов самодостаточны. Некоторые вопросы могут входить в набор из нескольких вопросов (например, каждый об одном и том же графике или диаграмме).
Охваченный материал подчеркивает основные области содержания, которые являются предпосылками для успешной работы на курсах начального уровня по математике в колледже.Знание основных формул и вычислительные навыки предполагаются в качестве основы для решения задач, но запоминание сложных формул и обширные вычисления не требуются.
Примечание: Вы можете использовать калькулятор в разделе математики.
См. www.act.org/calculator-policy.html для получения подробной информации о запрещенных моделях и функциях.
Использование говорящих калькуляторов должно быть предварительно одобрено ACT.
Содержимое, на которое распространяется тест ACT по математике
Для раздела математики сообщается девять баллов: балл за раздел в целом и восемь баллов в отчетной категории, основанные на конкретных математических знаниях и навыках.Приблизительный процент раздела, посвященного каждой категории отчетности:
Подготовка к высшей математике (57–60%)
Эта категория охватывает новейшую математику, которую изучают учащиеся, начиная с того момента, когда учащиеся начинают использовать алгебру как общий способ выражения и решения уравнений.
Эта категория делится на пять подкатегорий.
- Число и количество (7–10%)
Продемонстрировать знание действительных и комплексных систем счисления. Студенты будут понимать и рассуждать о числовых величинах во многих формах, включая целые и рациональные показатели, а также векторы и матрицы.
Решите, нарисуйте и смоделируйте несколько типов выражений. Студенты будут использовать множество различных типов уравнений, включая, помимо прочего, линейные, полиномиальные, радикальные и экспоненциальные отношения. Студент будет находить решения систем уравнений, даже если они представлены простыми матрицами, и применять свои знания в приложениях.
Вопросы этой категории проверяют знание определения функций, обозначений, представлений и приложений. Вопросы могут включать, помимо прочего, линейные, радикальные, кусочные, полиномиальные и логарифмические функции. Студенты будут манипулировать и переводить функции, а также находить и применять важные функции графиков.
Давать определение и применять знания о формах и твердых телах, такие как соотношения конгруэнтности и подобия или измерения площади поверхности и объема. Понимать состав объектов и находить пропущенные значения в треугольниках, кругах и других фигурах, в том числе с помощью тригонометрических соотношений и уравнений конических сечений.
- Статистика и вероятность (8–12%)
Описывать центр и разброс распределений, применять и анализировать методы сбора данных, понимать и моделировать взаимосвязи в двумерных данных и вычислять вероятности, включая соответствующие выборочные пространства.
Интеграция основных навыков (40–43%)
Эта категория посвящена измерению того, насколько хорошо вы можете обобщать и применять свои знания и навыки для решения более сложных задач.Вопросы просят вас обратиться к таким понятиям, как ставки и проценты; пропорциональные отношения; площадь, площадь поверхности и объем; средний и медианный; и выражать числа по-разному.
Решать нестандартные задачи, предполагающие объединение навыков в цепочки шагов; применение навыков в различных контекстах; понимание связей; и демонстрация беглости.
Моделирование
В этой категории представлены все вопросы, связанные с созданием, интерпретацией, пониманием, оценкой и улучшением моделей.Каждый вопрос также учитывается в других соответствующих категориях отчетности, указанных выше. Эта категория является общей мерой того, насколько хорошо вы используете навыки моделирования по математическим темам.
См.
примеров вопросов и советы по тестированию.
Какие математические навыки нужны спортивному статистику? | Работа
Есть и другие способы заниматься профессиональным спортом, кроме того, чтобы быть спортсменом.На самом деле, ваши математические способности могут просто помочь вам нанять. Спортивные команды и спортивные вещатели проявляют большой интерес к статистике как к способу анализа игры и ее игроков, так и к предоставлению статистики общественности. Как спортивный статистик, вы должны обладать значительными математическими навыками и, вероятно, иметь как минимум степень бакалавра в области статистики.
Ментальная арифметика
Статистики должны уметь складывать, вычитать, умножать и делить числа в уме, когда того требует ситуация.Они должны уметь мысленно записывать ключевые игровые показатели в периоды быстрых действий. Это особенно верно во время продолжительной игры, как это иногда бывает в хоккее или баскетболе.
Статистика
Как следует из названия, статистики должны быть экспертами в области статистического мышления и статистических расчетов. К ним относятся дифференциальное и интегральное исчисление, вероятность, моделирование и статистический метод. Прохождение курсов по алгебре в рамках вашей степени также укрепит ваше понимание статистического метода.
Навыки работы с компьютером
Статистики часто используют компьютеры для обработки своих чисел и создания новых взглядов на спортивные игры или индивидуальную карьеру. Поэтому полезны глубокие знания вычислительной техники, равно как и интерес к новым приложениям и программному обеспечению, которые расширяют возможности манипулирования статистикой. Некоторые статистики пишут свои собственные программы для выполнения определенных расчетов.
Сбор и анализ данных
Спортивные статистики должны хорошо разбираться в методологии данных.
Опросы по сбору данных, организация данных, интерпретация и обобщение — все это ключевые навыки. Поскольку спортивные статистики, в частности, делятся своими выводами с широким кругом неспециалистов, они должны быть особенно квалифицированы в представлении данных для непрофессиональной аудитории.
Информация о зарплате статистиков за 2016 год
Средняя годовая зарплата статистиков в 2016 году составила 80 500 долларов США, согласно данным Бюро статистики труда США. На нижнем уровне статистики получали зарплату 25-го процентиля в размере 60 760 долларов, что означает, что 75 процентов зарабатывали больше этой суммы.Зарплата 75-го процентиля составляет 104 420 долларов, что означает, что 25 процентов зарабатывают больше. В 2016 году в США статистиками работало 37 200 человек.
Требования к математике для получения степени психолога
Если у вас есть хоть малейшее беспокойство по поводу математики, вам может быть интересно, участвуют ли числа в онлайн-программе бакалавриата по психологии.
Одна из причин, по которой требование по математике может стать неожиданностью, заключается в том, что психология так часто ассоциируется с качественными вещами, такими как эмоции и чувства.Многие психологи и специалисты в области психического здоровья разговаривают один на один с клиентами в клинических, медицинских и образовательных учреждениях, и эта близость кажется полной противоположностью холодным, твердым цифрам.
Будьте уверены, вы можете найти варианты карьеры психолога и программу бакалавриата по психологии, которая не потребует овладения продвинутой математикой.
Математика и психология: как они связаны?
Когда мы взглянем на психологию в целом, вы увидите, насколько важна математика для изучения разума и поведения.Например, с помощью количественных (на основе чисел) исследований мы можем выявлять закономерности, находить связи и делать открытия. Изучение различных аспектов или характеристик населения может установить ожидания или исходные данные, которые могут оказаться полезными на практике.
Тем не менее, возможно, вам будет легче узнать, что психологи, заинтересованные в более обширных профессиональных или научных исследованиях, обычно продолжают обучение в магистратуре или докторантуре. программа. Здесь вы найдете более продвинутые исследования по количественному анализу, статистическим методам в исследованиях, дизайну опросов и другим курсам, связанным с математикой.Среди подразделов психологии вы даже найдете такие, которые специализируются на математике. Новые области, такие как нейромаркетинг и искусственный интеллект, также выигрывают от количественных аспектов психологии.
Какие уроки математики я бы выбрал на бакалавриате по психологии?
Большинство программ бакалавриата по психологии требуют математики, но это не должно удерживать вас от получения онлайн-степени по психологии.
Даже если количественные вещи — например, статистические методы в исследованиях — не нужны для вашего идеального положения, глубокое понимание данных — их сбор, анализ и интерпретация — будет невероятно полезным.
Вот почему статистика является обычным требованием в аккредитованных программах бакалавриата по психологии. Национальный университет предлагает три онлайн-степени по этой дисциплине:
Класс вероятности и статистики требуется во всех из них. Базовое понимание алгебры полезно для этого и других занятий, связанных с исследованиями. На самом деле, чтобы настроить вас на успех в статистике, National предпочитает, чтобы вы сначала прошли Алгебру I и Алгебру 2. (Также может быть достаточно проходного балла на вступительном тесте.) Чтобы вы чувствовали себя более уверенно при посещении этих вводных математических занятий в National, вы должны знать, что вы не получите буквенную или процентную оценку — вам нужно только пройти.
Бакалавр искусств в области психологии также требует курса психологических исследований. Помимо описания дизайна опросов и экспериментов, вы узнаете, что делать с результатами и как выявлять проблемы с вашими данными.
Степень бакалавра в области интегративной психологии является альтернативой традиционной научной степени бакалавра по психологии, поскольку она больше фокусируется на состоянии и опыте человека.
Математическое требование для этой степени останавливается на вероятности и статистике.Вместо этого эта степень онлайн-психологии фокусируется на качественных исследованиях и анализе: это означает изучение через наблюдение и опыт, а не путем обработки чисел.
Бакалавр спортивной психологии фокусируется на производительности и мотивации, а также не требует каких-либо официальных курсов математических / количественных исследований, кроме статистики.
В поисках помощи при математическом беспокойстве
Мы используем здесь термин «математическая тревога» как общий термин для описания дискомфорта, связанного с числами и уравнениями.Многие, многие люди сказали бы, что они не математические волшебники, так что не чувствуйте себя одинокими или обескураженными.
Вот несколько советов, которые помогут повысить вашу уверенность в математике:
- Изучите словарный запас, чтобы вам было удобнее пользоваться терминами в тексте.
- Не беспокойтесь о запоминании формул; в реальном мире вы всегда сможете найти их.
- Задавайте вопросы в классе (или в частном порядке вне класса).
- Математика изучается на практике.
- Найдите дополнительные учебные ресурсы (либо печатные руководства, либо онлайн-занятия).
- Воспользуйтесь преимуществами обучающих программ на месте или в Интернете.
- Попробуйте позитивный внутренний диалог; это может помочь изменить ваше давнее мнение о том, что вы «плохо разбираетесь в математике».
Наконец, если вы изучаете психологию онлайн в Национальном университете, вы можете напомнить себе, что каждый курс длится всего четыре недели. Через месяц вы перейдете к новой теме!
В современном мире, управляемом данными, математика и психология могут быть более связаны, чем когда-либо. Тем не менее, вы можете преуспеть в этой области без исключительно сильных математических навыков.Изучите нашу страницу программы психологии, чтобы найти вариант степени, который лучше всего соответствует вашим карьерным целям.