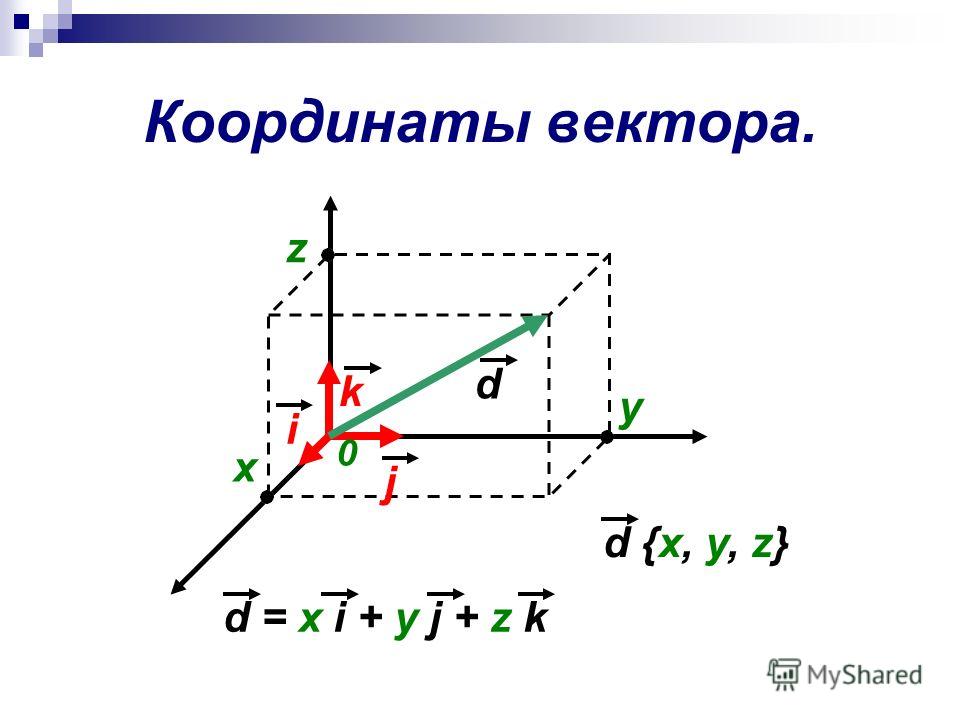
Координаты вектора — презентация онлайн
1. Тема 5. Координаты и векторы
ХI. Координаты вектора• https://youtu.be/m-N_6l3v6sA
у
p xi y j
x и y — координаты вектора p
3i
2 j
i
и
OA 2;1
b
b 3; 2
A
1
j
О
p x; y
a
i 1
х
0 0 i 0 j
0 0;0
j координатные векторы
a x1 i y1 j = b x2 i y2 j
x1 x2 , y1 y2
координаты равных векторов соответственно равны
10. КАЖДАЯ КООРДИНАТА СУММЫ
ДВУХ ВЕКТОРОВ ИЛИ БОЛЕЕ ВЕКТОРОВ
РАВНА СУММЕ СООТВЕТСТВУЮЩИХ
КООРДИНАТ ЭТИХ ВЕКТОРОВ
a x1; y1
b x2 ; y2
a x1 i y1 j
b x2 i y2 j
a b x1 i y1 j x2 i y2 j ( x1 x2 )i ( y1 y2 ) j
a b x1 x2 ; y1 y2
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
20. КАЖДАЯ КООРДИНАТА РАЗНОСТИ
ДВУХ ВЕКТОРОВ РАВНА
РАЗНОСТИ СООТВЕТСТВУЮЩИХ КООРДИНАТ
ЭТИХ ВЕКТОРОВ
a x1; y1
b x2 ; y2
a x1 i y1 j
b x2 i y2 j
a b x1 i y1 j x2 i y2 j ( x1 x2 )i ( y1 y2 ) j
a b x1 x2 ; y1 y2
UROKIMATEMATIKI.
 RU
RU30. КАЖДАЯ КООРДИНАТА ПРОИЗВЕДЕНИЯ
ВЕКТОРА НА ЧИСЛО РАВНА
ПРОИЗВЕДЕНИЮ СООТВЕТСТВУЮЩЕЙ
КООРДИНАТЫ ВЕКТОРА НА ЭТО ЧИСЛО
a x; y
ka
a xi y j
k a kxi ky j
k a kx; ky
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
a 1; 2
30:
1
p 2a b c
3
b 0;3
c 2;3
2a 2; 4
1
b 0; 1
3
1
p 2a b c
3
10: 2 0 2; 4 1 3
p 0; 2
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
7. Тема 5. Координаты и векторы
ХII. Метод координат в пространстве.Координаты вектора
https://infourok.ru/videouroki/1467
Определение
Векторы называются компланарными, если при
откладывании их из одной и той же точки они будут лежать
в одной плоскости.
Определение
z
1
0
1
x
1
y
z
1
0
1
x
1
y
z
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1
Определить:
координаты векторов:
B
5
P
T
C
3
O
2
A
D
M
К
x
y
z
Задача.

Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
Решение:
х = ОА = 2;
B
5
P
T
C
O
2
у = ОD = 3; z = ОB = 5
A
D
M
К
x
y
z
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
5
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
D
M
К
y
z
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
х = ОА = 2; у = ОD = 3; z = 0
5
D
M
К
x
y
z
Задача.

Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
х = ОА = 2; у = ОD = 3; z = 0
5
D
M
К
x
y
z
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
х = ОА = 2; у = ОD = 3; z = 0
5
D
M
К
x
y
z
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
х = ОА = 2; у = ОD = 3; z = 0
5
D
M
К
x
y
z
Задача.
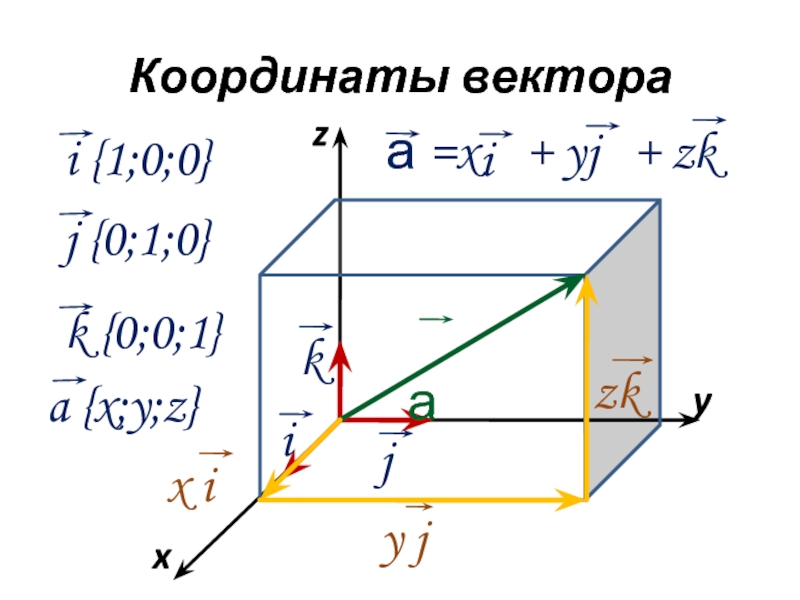
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
B
P
T
C
O
Решение:
х = ОА = 2; у = ОD = 3; z = ОB = 5
2
A
z = МК = -1; х = ОА = 2; у = ОD = 3
5
D
M
К
x
y
Нулевой вектор
z
y
х
нулевой вектор равен: ноль, умноженный на вектор и, плюс ноль,
умноженный на вектор джи, плюс ноль, умноженный на вектор ка),
то все координаты нулевого вектора равны кулю.
Координаты равных векторов
соответственно равны.
т. е. если векторы
то
х₁ = х₂, у₁ = у₂, z₁ = z₂
Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
Рассмотрим правила,
позволяющие по координатам данных векторов
найти координаты их суммы, разности и
произведения вектора на данное число
Складываются соответствующие координаты
Каждая координата разности двух векторов
равна разности соответствующих
координат этих векторов.

Вычитаются соответствующие координаты
Каждая координата произведения
вектора на число равна произведению
соответствующей координаты вектора на
это число.
Умножается число на координату
Рассмотренные правила позволяют находить координаты любого вектора,
представленного в виде алгебраической суммы данных векторов,
координаты которых известны
Задача 1.
Дано:
Найти:
Решение:
х=2+0–2=0
у = –4 –1 + 3 = –2
z=0+2+1=3
Задача 2.
Дано:
Векторы i j k — единичные векторы,
Следовательно координаты векторов в их линейном
разложении есть коэффициенты при единичных
векторах
Решение:
26. Тема 5. Координаты и векторы
ХIII. Метод координат в пространстве.Связь между координатами векторов и координатами точек
https://infourok.ru/videouroki/1478
Два ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых
Вектор, конец которого совпадает с данной точкой,
а начало – с началом координат,
z
1
радиус-вектор
0
1
x
1
y
Координаты любой точки равны соответствующим
координатам её радиус-вектора
Доказательство:
z
B
C(x, y, z)
0
A
x
D
y
Координаты любой точки равны соответствующим
координатам её радиус-вектора
Доказательство:
z
B
C(x, y, z)
0
A
x
D
y
Координаты любой точки равны соответствующим
координатам её радиус-вектора
Доказательство:
z
B
C(x, y, z)
0
A
x
D
y
Каждая координата вектора равна разности
соответствующих координат его конца и начала
Доказательство:
C (x2; y2; z2)
D (x1; y1; z1)
С (x2; y2; z2)
D(x1; y1; z1)
A
Задача 1.

Дано:
А (2; –3; 0)
B (7; –12; 18)
C (–8; 0; 5)
Найти:
координаты
Решение:
Задача 2.
Дано:
Найти:
координаты векторов, противоположных данным
векторам
Решение:
⇒
Задача 3.
Дано:
ОА = 4, ОВ = 9, ОС = 2
z
C (0; 0; 2)
Найти:
координаты
Решение:
O
x
A (4; 0; 0)
В y
(0; 9; 0)
Часть 2 — Векторные и тензорные операции. Ранги тензоров / Хабр
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота.

- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Несказанно рад, что читателям понравилась
предыдущая статья. Сразу сделаю оговорку — просто рассказать о таком ёмком понятии как тензор не получится — велик объем информации. Могу обещать, что к концу цикла мозаика сложится.
А в прошлый раз мы остановились на том, что рассмотрев представление вектора в косоугольном базисе, и определив, что он представляется двумя разными (ковариантными и контравариантными) наборами координат, получили общие выражения для скалярного произведения, учитывающие изменение метрики пространства.
Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором >своих компонент и правилом преобразования компонент при смене базиса.
Скалярное произведение — это хорошо. Но как же быть с остальными операциями? Как они связываются с геометрией пространства и представимы ли в тензорном виде? Разумеется представимы, ведь векторы — это… тензоры! И скаляры — это тоже тензоры. Привычные нам математические объекты лишь частные примеры более общего понятия, коим является тензор.
Вот об этом мы и поговорим под катом.
1. Геометрический смысл метрического тензора
Рис. 1. Соотношения в трехгранном угле, образованном базисом
Рассмотрим произвольный базис
Вычислим объем параллелепипеда, натянутого на базис так, как это принято в стереометрии
где
S— площадь основания параллелепипеда;
h — высота, проведенная к данному основанию.
Площадь основания вычисляется тривиально — как модуль векторного произведения
С определением высоты придется повозится. Если бы мы знали угол
, то легко нашли бы высоту
Угол
связан с линейными и двугранными углами трехгранного угла
– первая теорема косинусов для трехгранного угла. Из нее выражаем косинус двугранного угла
Квадрат синуса необходимого нам угла выражаем через полученный косинус
Выполняем последовательные подстановки от (6) до (2), не забывая возвести в квадрат площадь
Sи высоту
h. Выкладки достаточно громоздкие и для их выполнения можно воспользоваться СКА (Maple или Mathematica) и получить квадрат объема параллелепипеда
Теперь вычислим определитель метрического тензора. Им называется определитель матрицы, которая составлена из компонентов тензора. Входящие в нее скалярные произведения векторов базиса выпишем в явном виде
Вычислив его, получим тот же результат, что и для квадрата объема
Таким образом, утверждение (1) верно. Соответственно, объем параллелепипеда, натянутого на базис можно получить извлечением корня из определителя метрического тензора
Соответственно, объем параллелепипеда, натянутого на базис можно получить извлечением корня из определителя метрического тензора
где
для краткости обозначим значение определителя.
Корень (7) часто встречается в литературе по ОТО и альтернативным теориям гравитации типа РТГ. Эта величина имеет фундаментальное значение и пригодится нам чуть позже.
2. Тензорное произведение векторов. Диада. Ранг тензора. Свертка
Обратим внимание на выражение скалятного произведения
Величину
называют
тензорным произведением двух векторовили
диадой. Тензорным это произведение названо потому что перемножаются тензоры и на выходе получается тензор, в данном случае второго ранга,
.
Ранг тензора — это количество его индексов. Вектор, внезапно, тоже является тензором, только первого ранга. Да это и понятно — ведь вектор, как геометрическая сущность, не зависит от системы координат, в которой его рассматривают. От выбора системы координат зависят лишь его компоненты.
От выбора системы координат зависят лишь его компоненты.
Тензор второго ранга (8), разумеется, представлен матрицей своих компонент
Используя (8) можно переписать скалярное произведение в виде
это тоже тензорное произведение, называемое
сверткойиз-за того, что приводит к уменьшению ранга результирующего тензора. Все индексы в (10) «немые», по ним производится двойное суммирование компонент метрического тензора и диады и на выходе получатся число
c.
Внимательный читатель скажет, что на выходе должен получится тензор. Так тензор и получается — скаляр, это тоже тензор. Нулевого ранга, так как не имеет индексов и не подлежит преобразованию при смене базиса. Скалярное произведение инвариантно относительно смены базиса, ибо ни длина участвующих в нем векторов ни угол между ними от смены базиса не меняются. Значит скаляр — это тензор нулевого ранга.
Но не любое число есть скаляр. Скаляр — это длина вектора, скалярное произведение векторов, масса материального тела, абсолютная температура и прочие величины, не зависящие от системы координат. Компонента вектора уже не является скаляром — она меняется при смене базиса.
Компонента вектора уже не является скаляром — она меняется при смене базиса.
О ранге тензоров и типе из компонент мы поговорим чуть позже, а пока перейдем к следующему животрепещущему вопросу.
3. Векторное произведение. Тензор Леви-Чивиты
Вернемся к нашим векторам и выполним их векторное умножение
За неимением других вариантов, аккуратно раскроем скобки, помня о некоммутативности операции
Разумеется мы хорошо учились в университете и знаем, что векторное произведение вектора самого на себя равно нулю. Но мы не будем сильно спешить с упрощением, ибо кроме этого, несомненно приятного факта, мы видим ещё одну вешь — компоненты диады (9). Но кроме упрощения связанного с нулевым произведением коллинеарных векторов мы больше ничего не наблюдаем. Мы работаем с произвольным базисом в чистом виде.
Применим хитрость — умножим вектор скалярно на первый вектор базиса учтя теперь, что произведения
Коэффициенты в квадратных скобках — смешанные произведения векторов. Если векторы компланарны (лежат в одной плоскости) то такое произведение равно нулю. То есть, если в смешанном произведении повторяется хотя бы один вектор, оно равно нулю. Значит у нас остается только два слагаемых из девяти, в которых не повторяются векторы при смешанном умножении
Если векторы компланарны (лежат в одной плоскости) то такое произведение равно нулю. То есть, если в смешанном произведении повторяется хотя бы один вектор, оно равно нулю. Значит у нас остается только два слагаемых из девяти, в которых не повторяются векторы при смешанном умножении
Так, а теперь вспоминаем, что
— ковариантная компонента вектора
. Ну и наконец переставим векторы в векторном произведении первого слагаемого, добавив минус как и положено по правилу векторного произведения
Аналогичным образом выделяем остальные компоненты
Выражения (11) — (13) очень напоминают формулы для расчета проекций векторного произведения из курса векторной алгебры, с точностью до множителя со смешанным произведением. Но мы-то работаем не в декартовом базисе, естественно ожидать некоторое отличие. Кстати, а что это за множитель? Ведь смешанное произведение векторов имеет геометрический смысл… Это же… объем параллелепипеда, натянутого на векторы в нем участвующие. А объем параллелепипеда, натянутого на базис это ведь корень из определителя метрического тензора! То есть
А объем параллелепипеда, натянутого на базис это ведь корень из определителя метрического тензора! То есть
Вот она и всплыла на поверхность, метрика используемого пространства. Таким образом, можно построить некий тензор, свертка исходных векторов с которым дает ковариантный вектор, являющийся результатом векторного произведения. Более того, этот тензор связан с метрическим тензором. Таковой тензор третьего ранга носит имя итальянского математика Леви-Чивиты.
Не трудно увидеть, что компоненты тензора Леви-Чивиты определяются соотношением
Их будет 27, но большинство из них, а именно 21 равны нулю. Это те компоненты, индексы которых повторяются хотя бы один раз. Ненулевых компоненты только шесть, они соответствуют не повторяющимся индексам. По модулю они равны
, но три из них положительны, другие три отрицательны. В формулах (11) — (13) мы переставили векторы местами и добавили минусы, чтобы сделать коэффициенты при диадах положительными а сами формулы похожими на привычные нам по курсу векторной алгебры.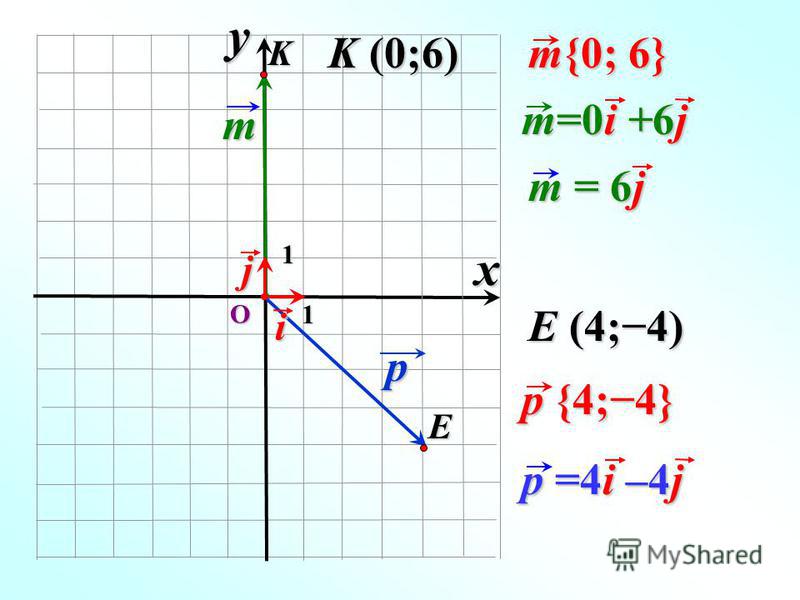 Теперь вернем всё на свои места
Теперь вернем всё на свои места
Знак смешанных произведений зависит от порядка индексов: в наборах (1,2,3), (2,3,1), (3,1,2) они положительны, в наборах (1,3,2), (2,1,3) и (3,2,1) — отрицательны. Известно, что если векторы заданы в правой системе координат, то их смешанное произведение будет положительно, если они образуют правую тройку векторов. В первых слагаемых (16) — (18) фигурируют правые тройки векторов базиса. Во вторых слагаемых, в смешанном произведении участвуют те же векторы, но взятые как левая тройка.
Как определить, какую тройку дают базисные векторы? Очень просто, ведь они упорядочены, им присвоены номера 1, 2, 3. Если мы соблюдаем порядок следования векторов, мы получаем тройку, соответствующую используемой системе координат, то есть (1,2,3) — правая тройка.
А если первым мы берем вектор 2? То за ним должен следовать вектор 3, по порядку. А какой следующий? А следующий вектор 1, начинаем всё сначала, но не нарушая порядка следования векторов, то есть и (2,3,1) — правая тройка, ну и (3,1,2) — тоже правая тройка. Говоря языком комбинаторики — базисные векторы в упорядоченной тройке образуют четную перестановку (то есть не нарушающую порядок следования элементов). Если порядок следовая векторов в тройке обратный принятому, то их перестановка будет нечетной. Таким образом перестановки (3,2,1), (2,1,3), (1,3,2) — нечетные, а тройки векторов — левые.
Говоря языком комбинаторики — базисные векторы в упорядоченной тройке образуют четную перестановку (то есть не нарушающую порядок следования элементов). Если порядок следовая векторов в тройке обратный принятому, то их перестановка будет нечетной. Таким образом перестановки (3,2,1), (2,1,3), (1,3,2) — нечетные, а тройки векторов — левые.
Используя всё вышесказанное, введем функцию
и, на основании (14) и (19) наконец выпишем тензор Леви-Чивиты
для правой системы координат
для левой системы координат.
После этого можно выписать выражение для векторного произведения в тензорном виде
Таким образом — векторное произведение, это свертка диады тензором Леви-Чивиты, дающая на выходе
ковектор— то есть вектор, заданный ковариантными компонентами.
4. Смешанное (векторно-скалярное) произведение векторов
Вооружившись полученными знаниями рассмотрим теперь такую операцию
Не оперируя векторами, попробуем сразу записать её в тензорном виде. Во-первых, скалярное произведение коммутативно, поэтому
Во-первых, скалярное произведение коммутативно, поэтому
А теперь вспомним, что скалярное произведение можно расписать как тензорное
произведение ковектора на вектор
Векторное произведение, исходя из (21)как раз и дает ковектор, а значит
То есть, окончательно, смешанное произведение в тензорной форме
где снова участвует тензор Леви-Чивиты.
Выражение (22) можно было получить оперируя векторами, выйдя опять на определение тензора Леви-Чивиты, но, как видно, рациональнее использовать тензорную запись.
5. Ранг тензора. Ковариантные и контравариантные компоненты
Итак, в процессе разбора векторных операций мы пришли к выводу, что тензоры — это математические объекты, обобщающие свойства и операции над многими, известными нам математическими объектами. Тензорами являются и скаляры и векторы. Различаются они рангом и количеством ковариантных и контравариантных компонент. Ранг равен общему числу индексов тензора, а обозначается он парой целых чисел в скобках (
p, q), где
p— число контравариантных индексов,
q — число ковариантных индексов. Говорят что тензор —
Говорят что тензор —
-раз контравариантный и
q-раз ковариантный, ранга
p+q.
- Тензор ранга (0,0) — это скаляр, величина, значение которой может быть выражено одним числом, со значением инвариантным относительно смены системы координат. У скаляра нет индексов, и он вообще не преобразуется при смене базиса. Но, повторимся, не всякое число есть скаляр. Так например, компонент вектора или тензора не есть скаляр, ибо он изменяется при смене базиса.
- Тензор ранга (1,0) — вектор. Для вектора естественно контравариантное представление, для вычисления скалярного произведения векторов требуется их свертка с метрическим тензором.
Преобразование компонент вектора производится путем применения к нему линейного оператора, по сути умножением матрицы преобразования на столбец, содержащий компоненты вектора, что в тензорной форме выглядит как
- Тензор ранга (0,1) — ковектор. Если в рассматриваемом пространстве определен невырожденный метрический тензор
то вектор и ковектор — это два разных представления одного и того же геометрического объекта — вектора. В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором
В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором
где контрвариантный метрический тензор, компоненты которого — матрица,
обратная матрице компонент тензора .Для скалярного умножения ковектора на вектор не нужно использовать метрический тензор, оно производится прямой сверткой с вектором.
Преобразование компонент ковектора так же производится путем применения к нему линейного оператора, но в отличие от вектора, производится умножение строки, содержащей компоненты ковектора на матрицу преобразования координат - Тензор ранга (0,2) — билинейная форма, примером которой может служить дважды ковариантный метрический тензор gij. Компоненты метрического тензора преобразуются путем двукратного применения к нему линейного оператора преобразования координат, что соответствует умножению транспонированной матрицы преобразования на матрицу метрического тензора и последующему умножению результата на матрицу преобразования
- Тензор ранга (2,0) — примером может служить диада (8).
 Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
операторов, преобразующих исходные векторы. - Тензор ранга (1,1) — линейный оператор. Примером может служить матрица поворота или любого другого преобразования координат векторов и ковекторов. Вообще, применение линейного оператора сводится к операции матричного умножения
где — результат преобразования; — исходный вектор; — компоненты матрицы линейного оператора. Рассмотрим процесс преобразования линейного оператора. Пусть S матрица перехода от одно базиса к другому. Тогда, при смене базиса преобразуются оба вектора — и аргумент и результат
Подставляя (24) в (23) получаем
откуда, умножая слева на матрицу получаем
где — компоненты матрицы . С другой стороны, для векторов в новом базисе справедливо
С другой стороны, для векторов в новом базисе справедливо
сравнивая (25) и (26), получаем выражение преобразования линейного оператора
Все перечисленные объекты обладают общностью свойств: имеют набор компонент и правило преобразования при смене базиса.
Выводы
Подведем некоторые итоги.
Во-первых, мы выяснили, что векторные операции могут быть сведены к тензорным соотношениям, что избавляет нас от неудобства каждый раз выводить формулы для них при использовании экзотической системы координат или увеличении размерности пространства. Соотношения останутся прежними, изменится только внутренность тензоров, связанных с геометрией пространства и выбором положительного направления вращения в нем. Учитывая, что многие уравнения физики, математики и механики оперируют векторными величинами, использование тензоров позволяет записать уравнения лишь однажды. Кроме того, тензорная запись компактна — это упрощает проведение выкладок.
Во-вторых, мы понимаем, что многие математические объекты — скаляры, векторы, билинейные формы, линейные операторы — всё это частные случаи тензоров, а значит их свойства могут быть обобщены под могучим крылом своего более сложного собрата-тензора.
В дальнейшем мы увидим, как тензорная запись позволяет подходить к весьма прозаичным вопросам с общих позиций, облегчая жизнь исследователю.
Продолжение следует…
Разложение вектора по базису » Аналитическая геометрия f(x)dx.Ru
п.2. Разложение вектора по базису.
Определение. Пусть – произвольный вектор, – произвольная система векторов. Если выполняется равенство
, (1)
то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительно базиса .
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и – базис . Возьмем произвольный вектор . Так как оба вектора и коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что и тем самым мы получили разложение вектора по базису векторного пространства .
Возьмем произвольный вектор . Так как оба вектора и коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что и тем самым мы получили разложение вектора по базису векторного пространства .
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и , где . Тогда и используя закон дистрибутивности, получаем:
.
Так как , то из последнего равенства следует, что , ч.т.д.
2) Пусть теперь Р произвольная плоскость и – базис . Пусть произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую , на которой лежит вектор . Через конец вектора проведем прямую параллельную вектору и прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма , и , , – базис , – базис .
См. ниже рис. 3. По правилу параллелограмма , и , , – базис , – базис .
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что
и . Отсюда получаем:
и возможность разложения по базису доказана.
рис.3.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства : и . Получаем равенство
, откуда следует . Если , то , а т.к. , то и коэффициенты разложения равны: , . Пусть теперь . Тогда , где . По теореме о коллинеарности двух векторов отсюда следует, что . Получили противоречие условию теоремы. Следовательно, и , ч.т.д.
3) Пусть – базис и пусть произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора и вектор от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость и плоскость ; далее через конец вектора проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
Эти 6 плоскостей высекают параллелепипед:
рис.4.
По правилу сложения векторов получаем равенство:
. (1)
По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично, и , где . Теперь, подставляя эти равенства в (1), получаем:
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и . Тогда
. (3)
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
. (4)
Из равенства (4) следует, что вектор раскладывается по базису , т.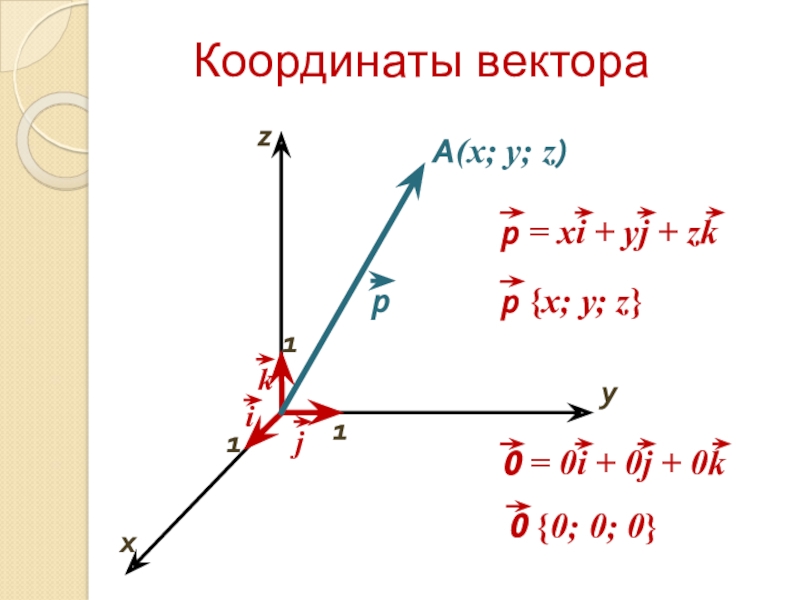 е. вектор лежит в плоскости векторов и, следовательно, векторы компланарные, что противоречит условию.
е. вектор лежит в плоскости векторов и, следовательно, векторы компланарные, что противоречит условию.
б) Остается случай , т.е. . Тогда из равенства (3) получаем или
. (5)
Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что и , ч.т.д.
Теорема доказана.
Возможно найдутся ответы здесь:
Экспресс вектор в полярной форме
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Умножение векторов – Гипертекст по физике
Обсуждение
умножение скаляра на вектор
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным.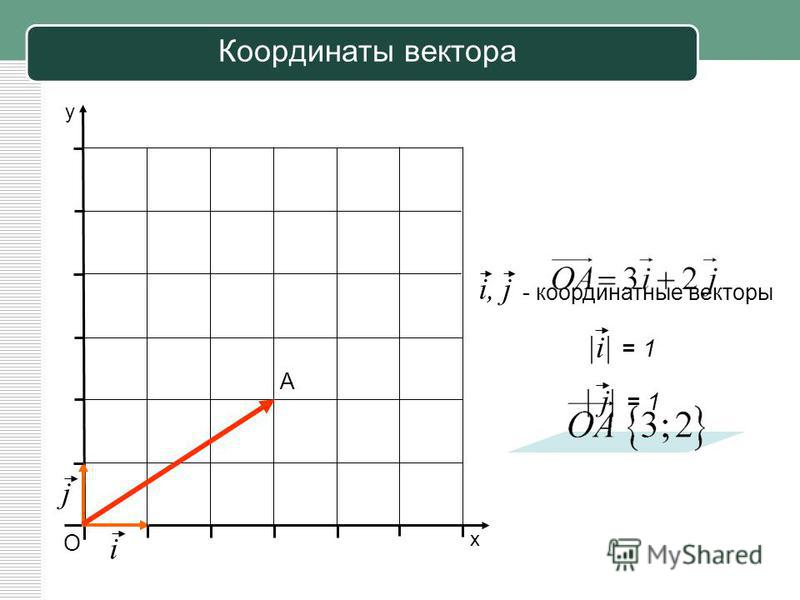 Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, полярный форм-вектор…
Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, полярный форм-вектор…
r = r r̂ + θ θ̂
умножить на скаляр и будет…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр является дистрибутивным.
a ( A + B ) = a A + a B
Следовательно, прямоугольный форм-вектор…
r = x х + y х
умножить на скаляр и будет…
a r = ax î + a ĵ
скалярный продукт
Геометрически скалярное произведение двух векторов равно единице, умноженной на проекцию второго на первый.
Символ, используемый для обозначения этой операции, представляет собой небольшую точку средней высоты (·), откуда и произошло название «точечный продукт». Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
A · B = AB cos θ
Скалярный продукт является распределительным…
А · ( В + С ) = А · В + А · С
33и коммутативный…
А · Б = Б · А
Поскольку проекция вектора на самого себя оставляет его величину неизменной, скалярное произведение любого вектора на самого себя есть квадрат величины этого вектора.
A · A = AA cos 0° = A 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора с самим собой равно единице. Кроме того, поскольку вектор не имеет перпендикулярной к себе проекции, скалярное произведение любого единичного вектора на любой другой равно нулю.
х · х = х · х = k̂ · k̂ = 0(s 1)(0)
х · х = х · k̂ = k̂ · х ) = 9°0035 3 = 0(1)(1)
Используя эти знания, мы можем вывести формулу скалярного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, но он состоит в основном из членов, равных нулю.
Полученный продукт выглядит так, как будто это будет ужасный беспорядок, но он состоит в основном из членов, равных нулю.
| А · В = | ( A x î + + ĵ + ĵ + A Z K ) · ( b x î + b y ĵ + B z k̂ ) | |||||||||||
| А · В = | А x î | · | В x î | + | А x î | · | Б у х | + | А x î | · | B z k̂ | |
| + | А и х | · | В x î | + | А и х | · | Б у х | + | А и х | · | B z k̂ | |
| + | A z k̂ | · | В x î | + | A z k̂ | · | Б у х | + | A z k̂ | · | B z k̂ | |
| А · В = | A x B x + A y B y + A z 7 B z | | ||||||||||
Таким образом, скалярное произведение двух векторов равно сумме произведений их параллельных компонентов. Отсюда мы можем вывести теорему Пифагора для трех измерений.
Отсюда мы можем вывести теорему Пифагора для трех измерений.
A · A · A = AA = AA = AA COS 0 ° = A x A x + A Y + A Z A Z
A 2 2 = A x 2 + 3 Y
перекрестное произведение
Геометрически перекрестное произведение двух векторов есть площадь параллелограмма между ними.
Символ, используемый для обозначения этой операции, представляет собой большой диагональный крест (×), откуда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как векторное произведение .
A × B = AB sin θ n̂
Вектор n̂ (n hat) представляет собой единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Перекрестное произведение является распределительным…
A × ( B + C ) = ( A × B ) + ( A × 3 C
, но не коммутативный…
A × B = − B × A
Изменение порядка перекрестного умножения на противоположное меняет направление произведения.
Поскольку два одинаковых вектора образуют вырожденный параллелограмм без площади, векторное произведение любого вектора на себя равно нулю…
А × А = 0
Применение этого следствия к единичным векторам означает, что векторное произведение любого единичного вектора с самим собой равно нулю.
х × х = х х х = k̂ × k̂ ° = 0 0 (1) (0)
Следует отметить, что векторное произведение любого единичного вектора на любой другой будет иметь модуль, равный единице. (В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение 90 584, а не 90 585 коммутативно, порядок операций важен.
(В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение 90 584, а не 90 585 коммутативно, порядок операций важен.
- Держите правую руку горизонтально, большой палец должен быть перпендикулярен остальным. Ни в коем случае не сгибайте большой палец.
- Укажите пальцем в направлении первого вектора.
- Расположите ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
- Теперь ваш большой палец указывает в направлении векторного произведения.
Правосторонняя система координат , которая является обычной системой координат, используемой в физике и математике, представляет собой систему, в которой любое циклическое произведение трех координатных осей положительно, а любое антициклическое произведение отрицательно. Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическому и положительному. Любой продукт, который движется в противоположном направлении, является антициклическим и отрицательным.
Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическому и положительному. Любой продукт, который движется в противоположном направлении, является антициклическим и отрицательным.
| Перекрестное произведение циклической пары единичных векторов равно положительному . | Перекрестное произведение антициклической пары единичных векторов равно отрицательному . |
Используя эти знания, мы можем вывести формулу векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто он будет ужасным беспорядком, и это так!
A × B = ( A x î +
y ĵ + A Z K ) × ( B x î + B y × + B z k̂ )
Произведение двух трехчленов состоит из девяти членов.
| А × В | = | А x î | × | В x î | + | А x î | × | Б у х | + | А x î | × | B z k̂ |
| + | А и х | × | В x î | + | А и х | × | Б у х | + | А и х | × | B z k̂ | |
| + | A z k̂ | × | В x î | + | A z k̂ | × | Б у х | + | A z k̂ | × | B z k̂ |
Три из них равны нулю.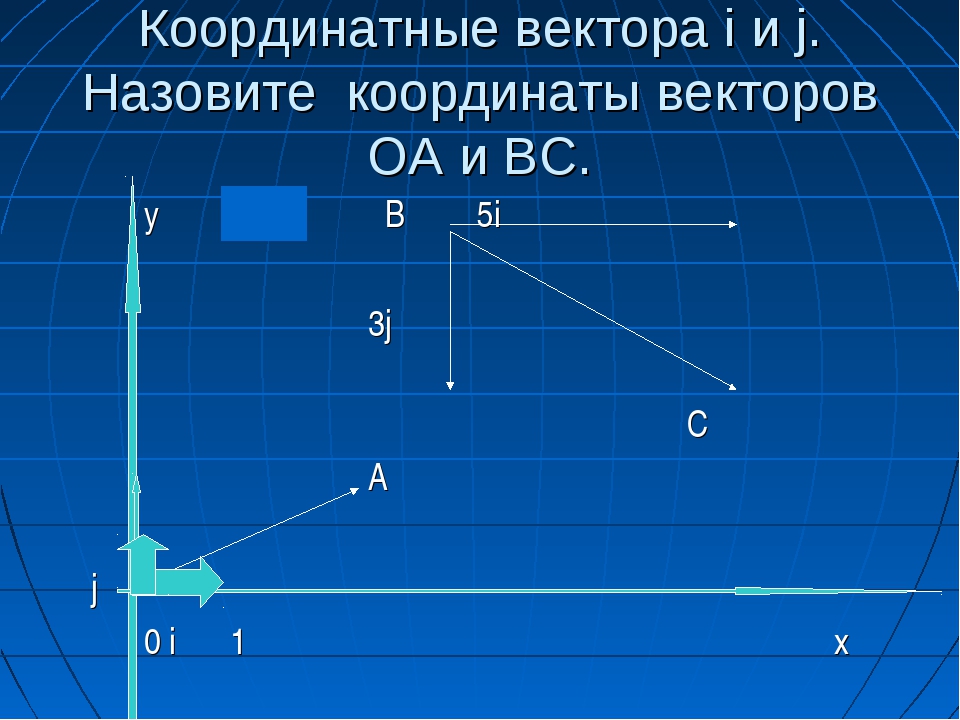 Устраните их.
Устраните их.
| А × В | = | A x B y k̂ | − | А х В z х |
| − | A y B x k̂ | + | А у Б з х | |
| + | А z В х х | − | A z B y î |
Сгруппировать термины по единичному вектору и фактору.
A × B = ( A Y B Z — A Z B Z ) î
Есть более простой способ написать это.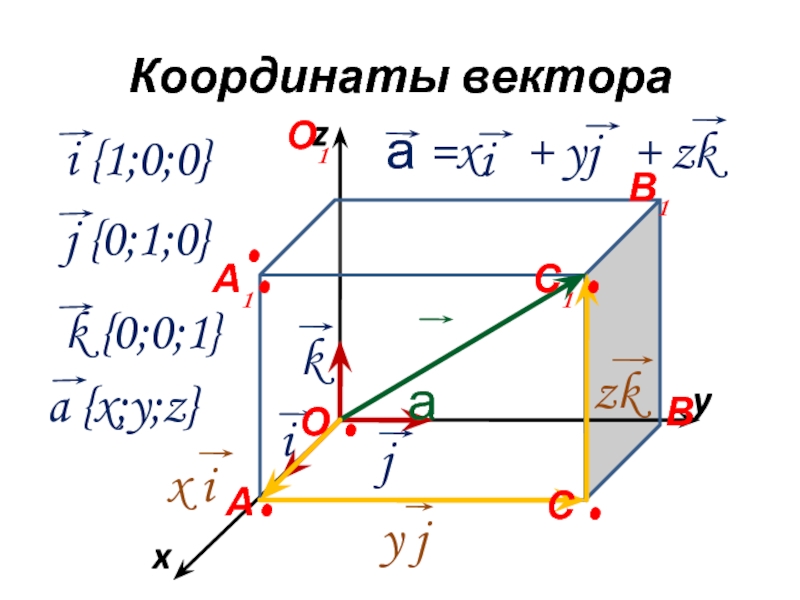 Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов — это определитель матрицы, первая строка которой — единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор.Символически…
Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов — это определитель матрицы, первая строка которой — единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор.Символически…
| А × В = | î | — | к̂ |
| А x | А г | А з | |
| Б x | Б г | Б г |
Расширение определителя 3×3 по его первой строке — это первый шаг.Это дает нам три определителя 2×2.
| А × В = | А г | А з | î — | А x | А з | х + | А x | А г | к̂ |
| Б г | Б г | Б x | Б г | Б x | Б г |
Эти определители 2×2 можно быстро найти. Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители.
Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители.
A × B = ( A Y B Z — A Z B Z ) î
Положение и смещение
Положение и смещениеПоложение и перемещение
Многие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей.
которые находятся в движении.Движение – это правило, а не исключение. Физические законы, управляющие движением
этих объектов
универсальны, т.е. все объекты движутся по одним и тем же правилам,
и одна из целей этого класса состоит в том, чтобы понять эти правила.
Когда объект движется, его позиция изменяется как функция времени.
Положение объекта
дано относительно некоторой согласованной точки отсчета.Недостаточно просто
укажите расстояние от
ориентир. Мы также должны указать направление . Расстояние скаляр количество, это число, указанное в каких-то единицах . Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает.Единичный вектор — это направление
показатель. Это безразмерный вектор с величиной 1, используемый для указания
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, д = смещение.
Таким образом, хотя d = расстояние, д = смещение.
Ссылки:
Скаляры и векторы
(Пожалуйста, изучите!)
Направление вектора
Позиция
Удобный способ указать позицию объекта с помощью системы координат . Мы выбираем фиксированную точку, называемую началом координат . и три направленные линии, которые проходят через начало координат и перпендикулярны друг другу. Эти линии называются координатными осями трехмерной прямоугольной (декартовой) системы координат и помечены оси x, y и z. Три числа с единицами определяют положение точка P. Эти числа представляют собой координаты x, y и z точки P. Координаты точки P на на диаграмме справа (а, б, в).
Координаты точки P
являются компонентами вектора положения. Единичный вектор
указание в направлении x имеет x-компоненту 1 и y- и z-компоненты
нуль. Обозначается i . Точно так же единичный вектор
, указывающий в направлении y, обозначается j , а единичный вектор
направление в направлении z обозначается как k .Единичные векторы
являются указателями поворота.
Обозначается i . Точно так же единичный вектор
, указывающий в направлении y, обозначается j , а единичный вектор
направление в направлении z обозначается как k .Единичные векторы
являются указателями поворота.
Компоненты любого вектора в сумме образуют
сам вектор.
Вектор положения точки P с координатами (a, b, c)
может быть записано с точки зрения его компонентов как
г = а и + б j +
с к .
Величина вектора положения равна его длине r. Это
зависит от выбора начала системы координат.Это
— прямолинейное расстояние P от начала координат.
Ниже приведено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на рисунке!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры. )
)
Чтобы получить наилучший вид, измените окно просмотра, перетащив мышь и
увеличить или уменьшить масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления векторов компонентов.
Пример:
Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат.
Рабочий объем
Изменение положения называется смещением . На приведенной ниже диаграмме показано позиции P 1 и P 2 игрока в два разных момента времени.
Стрелка, указывающая от P 1 к P 2 , является вектор смещения .
Его величина — прямая расстояние между P 1 и P 2 .
Компоненты смещения
вектор из P 1 в
P 2 (x 2 — x 1 ) вдоль оси x, (y 2 —
y 1 ) по оси Y.
Вектор смещения d от P 1 до P 2 может
можно записать как d = (x 2 — x 1 ) i + (y 2 -у 1 ) у .
Водоизмещение d составляет (x 2 — x 1 ) штук в
направление x плюс (y 2 — y 1 ) единицы измерения в направлении y.
Величина смещения
d = ((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 ) ½ .Этот
следует из
пифагорейский
теорема.
Расстояние между двумя точками P 1 с координатами (x 1 ,
у 1 ,
z 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) равно
d =
((х 2 — х 1 ) 2 + (у 2 — у 1 ) 2 + (z 2 — z1) 2 )½ .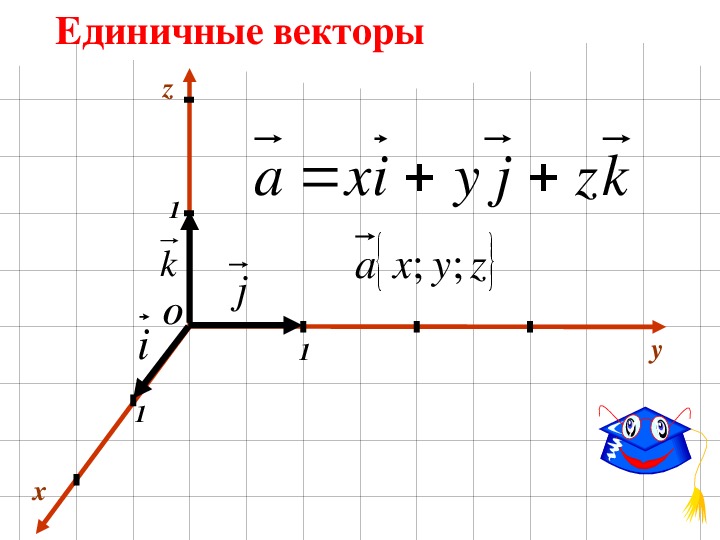
- Расстояние d является величиной вектора смещения d .
- Направление вектора смещения d – направленный отрезок прямой от P 1 к P 2 .
- Мы называем этот направленный отрезок геометрической или графической представление вектора d .
- Мы рисуем стрелку на P 2 , чтобы указать что сегмент линии начинается с P 1 и заканчивается на P 2 .
Тройка действительных чисел d x = (x 2 — x 1 ), d y = (y 2 — y 1 ), d z = (z 2 — z 1 ) называются декартовыми компонентами числа d .
Ссылка: Расстояние и смещение (Пожалуйста, изучите!)
Проблема:
Футбольный защитник бежит 15. 0 м
прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние.
0 м
прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние.
Решение:
Проблема:
Во время движения по прямому межгосударственному шоссе вы обратите внимание, что указатель мили показывает 260.Вы путешествуете, пока не достигнете 150-мильного отметку, а затем вернитесь к отметке 175 миль. Что величина вашего результирующего смещения от 260-мильной отметки?
Решение:
- Рассуждение:
Результирующее смещение представляет собой вектор d , сумму двух векторов д 1 и d 2 , которые указывают в противоположных направлениях. - Детали расчета:
Результирующее смещение представляет собой вектор d , сумму двух векторов д 1 и d 2 , которые указывают в противоположных направлениях.
Проблема:
Кончик лопасти вертолета 5,00 м от центра вращения. За один оборот лезвия вычислить вектор смещения и общее расстояние, пройденное наконечником лезвия.
Решение:
- Рассуждение:
После одного оборота наконечник возвращается в исходное положение. Вектор его смещения d = 0. - Детали расчета:
Общее пройденное расстояние кончик равен окружности окружности радиусом r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное совет 31.42 м.
Вектор смещения имеет одинаковую величину и направление независимо от выбор начала координат системы координат. Величина и направление
вектор смещения, однако, зависит от системы отсчета , в которой
система координат закреплена и находится в состоянии покоя.
Пример:
Автомобиль двинулся вперед расстояние 6 м, пока ребенок переместился с заднего сиденья на переднее сидеть на расстоянии 1 м.
- Использование автомобиля в качестве системы отсчета и привязка системы координат в машине водоизмещение ребенка d (автомобиль) = (1 м) i .
- Использование дороги в качестве системы отсчета и привязка системы координат на дороге перемещение ребенка d (дорога) = (6 м) i + (1 м) i = (7 м) i .
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings. COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.ТЕГИ}}
{{$элемент}}
{{l10n_strings.ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}
COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.ТЕГИ}}
{{$элемент}}
{{l10n_strings.ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings. АВТОР}}
АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Единичный вектор — формула, определение, пример, задачи
Векторы — это геометрические объекты, имеющие величину и направление.Векторы имеют начальную точку и конечную точку, которая представляет конечное положение точки. К векторам можно применять различные арифметические операции, такие как сложение, вычитание и умножение. Вектор, величина которого равна 1, называется единичным вектором. Например, вектор v = (1,3) не является единичным, поскольку его модуль не равен 1, т. е. |v| = √(1 2 +3 2 ) ≠ 1,
Например, вектор v = (1,3) не является единичным, поскольку его модуль не равен 1, т. е. |v| = √(1 2 +3 2 ) ≠ 1,
Любой вектор может стать единичным вектором, если мы разделим его на величину того же заданного вектора.а. Длина единичных векторов равна 1. Единичные векторы обычно используются для обозначения направления вектора.
Единичный вектор имеет то же направление, что и заданный вектор, но имеет модуль, равный одной единице; Для вектора А; единичный вектор; \(\шляпа{A}\) и \(\vec{A} = (1/|A|)\шляпа{A}\)
Величина вектора: Величина векторной формулы дает числовое значение для данного вектора. Вектор имеет как направление, так и величину. Величина векторной формулы суммирует отдельные измерения вектора по осям x, y и z.k обычно – это единичные векторы вдоль оси x, оси y и оси z соответственно. Каждый вектор, существующий в трехмерном пространстве, может быть выражен как линейная комбинация этих единичных векторов.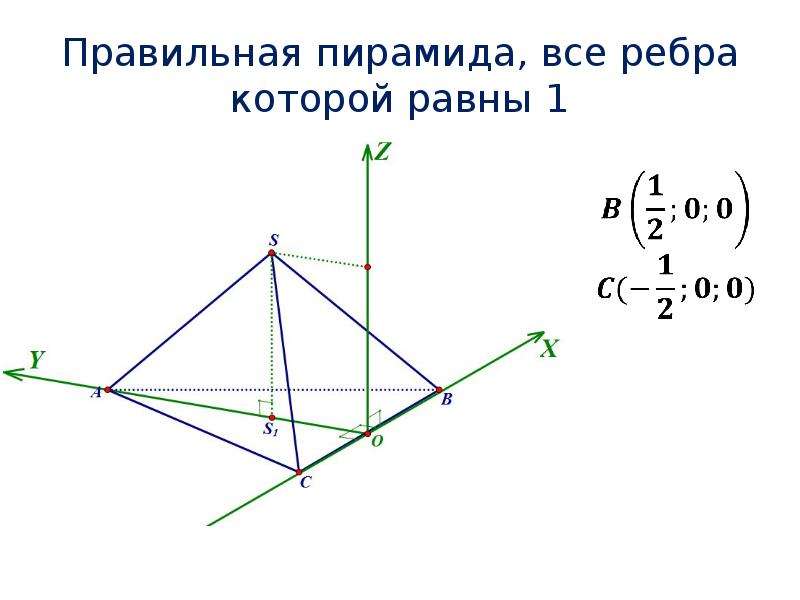 Скалярное произведение двух единичных векторов всегда является скалярной величиной. С другой стороны, перекрестное произведение двух заданных единичных векторов дает третий вектор, перпендикулярный (ортогональный) к ним обоим.
Скалярное произведение двух единичных векторов всегда является скалярной величиной. С другой стороны, перекрестное произведение двух заданных единичных векторов дает третий вектор, перпендикулярный (ортогональный) к ним обоим.
Нормальный вектор блока:
«Вектор нормали» — это вектор, перпендикулярный поверхности в определенной точке.Его также называют «нормальным» к поверхности, содержащей вектор. Единичный вектор, полученный после нормализации вектора нормали, является единичным вектором нормали, также известным как «единичная нормаль». Для этого разделим ненулевой вектор нормали на его векторную норму.
Формула единичного вектора
Поскольку векторы имеют как величину (значение), так и направление, они показаны стрелкой \(\hat{a}\) и обозначают единичный вектор. Если мы хотим найти единичный вектор любого вектора, мы делим его на величину вектора.к
Формула модуля вектора:
| → a|= √ (x 2 + y 2 + z 2 )
Единичный вектор = вектор/величина вектора
Выше приведена формула единичного вектора.
Как найти единичный вектор?
Чтобы найти единичный вектор с тем же направлением, что и заданный вектор, просто разделите вектор на его величину. Например, рассмотрим вектор v = (1,4), величина которого равна |v|.
Электромагнетизм имеет дело с электрическими и магнитными силами. Здесь векторы пригодятся для представления и выполнения вычислений с участием этих сил. В повседневной жизни векторы могут представлять скорость самолета или поезда, где необходимы как скорость, так и направление движения.
Свойства векторов
Свойства векторов помогают получить подробное представление о векторах, а также выполнить многочисленные вычисления с использованием векторов. Здесь перечислены некоторые важные свойства векторов.
- \(\vec A . \vec B = \vec B. \vec A \)
- \( \vec A \times \vec B\neq \vec B \times \vec A \)
- \(\шляпа i .\шляпа i =\шляпа j.\шляпа j = \шляпа k.\шляпа k = 1 \)
- \(\шляпа i .
 \шляпа j =\шляпа j.\шляпа k = \шляпа k.\шляпа i = 0 \)
\шляпа j =\шляпа j.\шляпа k = \шляпа k.\шляпа i = 0 \) - \(\шляпа i \times \шляпа i =\шляпа j\times \шляпа j = \шляпа k\times \шляпа k = 0 \)
- \(\hat i \times \hat j = \hat k~;~ \hat j\times \hat k = \hat i~;~ \hat k\times \hat i = \hat j \)
- \(\hat j \times \hat i = -\hat k~;~ \hat k \times \hat j = -\hat i~;~ \hat i \times \hat k = -\hat j \)
- Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.
- Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.
Похожие темы:
Важные замечания по единичным векторам:
- Скалярное произведение ортогональных единичных векторов всегда равно нулю.
- Перекрестное произведение параллельных единичных векторов всегда равно нулю.
- Два или более единичных вектора коллинеарны, если их векторное произведение равно нулю.

- Норма вектора — это действительное неотрицательное значение, представляющее его величину.
Часто задаваемые вопросы по Unit Vector
Что такое единичный вектор в математике?
Вектор, величина которого равна 1, является единичным вектором. Он также известен как вектор направления, поскольку обычно используется для обозначения направления вектора. Векторы \(\hat i\), \(\hat j\), \(\hat k\) являются единичными векторами вдоль оси x, оси y и оси z соответственно.
Как найти единичный вектор с тем же направлением, что и заданный вектор?
Чтобы найти единичный вектор с тем же направлением, что и заданный вектор, мы делим вектор на его величину. Например, рассмотрим вектор v = (1, 4), величина которого равна |v|. Если мы разделим каждую компоненту вектора v на |v| мы получим единичный вектор \(\шляпа v\), который находится в том же направлении, что и v.
Для чего используется единичный вектор?
Единичные векторы используются только для указания направления вектора. Единичные векторы существуют как в двух, так и в трехмерных плоскостях. Каждый вектор имеет единичный вектор в виде своих компонентов. Единичные векторы вектора направлены вдоль осей.
Единичные векторы существуют как в двух, так и в трехмерных плоскостях. Каждый вектор имеет единичный вектор в виде своих компонентов. Единичные векторы вектора направлены вдоль осей.
Что такое формула единичного вектора?
Единичный вектор \(\hat{A}\) получается делением вектора \(\longrightarrow A\) на его величину \(|\mathrm{A}|\). Единичный вектор имеет те же координаты направления, что и заданный вектор. \(\шляпа{А}=\фракция{А}{\середина А}\)
Что такое нормальный единичный вектор?
Единичный вектор нормали к двумерной кривой — это вектор с величиной 1, перпендикулярный кривой в некоторой точке.Обычно вы ищете функцию, которая дает вам все возможные единичные векторы нормалей данной кривой, а не только один вектор.
Как найти единичный вектор, перпендикулярный двум векторам?
В результате перекрестного произведения двух непараллельных векторов получается вектор, перпендикулярный им обоим. Итак, для заданных двух векторов \(\vec{x}\) и \(\vec{y}\) мы знаем, что \(\vec{x} \times \vec{y}\) будет вектор, перпендикулярный обоим \(\vec{x} \& \vec{y}\). Далее мы находим единичный вектор этого результирующего вектора, чтобы получить единичный вектор, перпендикулярный двум заданным векторам.
Далее мы находим единичный вектор этого результирующего вектора, чтобы получить единичный вектор, перпендикулярный двум заданным векторам.
Когда два вектора считаются параллельными?
Два или более вектора параллельны, если они движутся в одном направлении. Кроме того, векторное произведение параллельных векторов всегда равно нулю.
| Пример | Значение | Латекс |
|---|---|---|
| $P$ | Точки и позиции обозначаются прописными курсивными буквами. | \$П\$ |
| $(4, 5, -2)$ | Координаты позиции задаются в виде кортежа, поэтому $P$ находится в точке $(4, 5, -2)$ — это то же самое, что сказать, что $P$ имеет координаты $x = 4$, $y = 5$, $ г = -2$. Обратите внимание на отличие от векторных компонентов с помощью квадратных скобок. 2}$. 2}$. | \$\|\boldsymbol{v}\|\$, \$v\$ |
| $\шляпа{\boldsymbol{v}}$ | В единичных векторах используется верхняя шляпа, поэтому $\hat{\boldsymbol{v}} = \frac{\boldsymbol{v}}{\|\boldsymbol{v}\|}$. | \$\шляпа{\boldsymbol{v}}\$ |
| $\шляпа{\boldsymbol{\imath}}$, $\шляпа{\boldsymbol{\jmath}}$, $\шляпа{\boldsymbol{k}}$ | декартовы базисные векторы, поэтому мы пишем $\boldsymbol{v} = 3\hat{\boldsymbol{\imath}} + \hat{\boldsymbol{\jmath}} + 7\hat{\boldsymbol{k}}$. | \$\шляпа{\boldsymbol{\imath}}\$, \$\шляпа{\boldsymbol{\jmath}}\$, \$\шляпа{\boldsymbol{k}}\$ |
| $[3, 1, 7]$ | Компоненты вектора используют квадратные скобки, поэтому мы пишем $[\boldsymbol{v}]_R = [3, 1, 7] = 3\hat{\boldsymbol{\imath}} + \hat{\boldsymbol{\jmath}} + 7\шляпа{\boldsymbol{k}}$.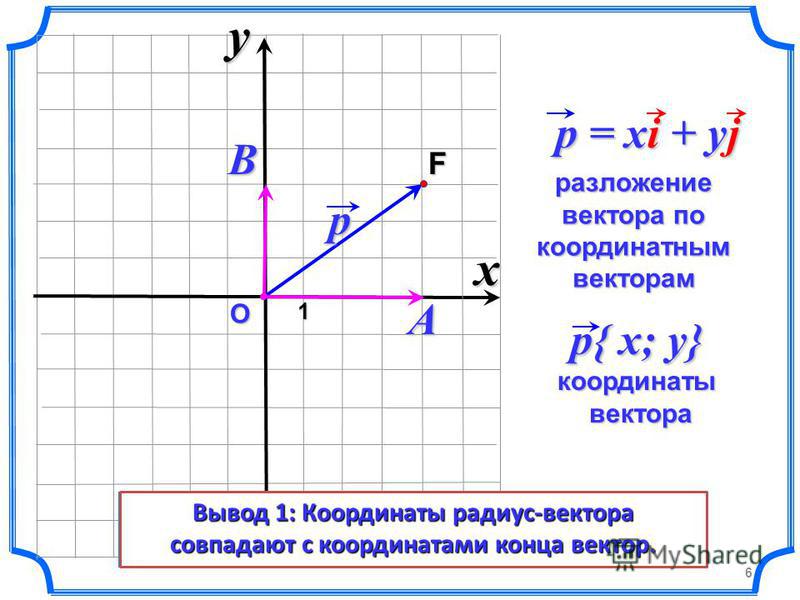 Если базис ясен, то будем писать $\boldsymbol{v} = [3, 1, 7]$. Если базис ясен, то будем писать $\boldsymbol{v} = [3, 1, 7]$. | \$[3, 1, 7]\$ |
| $[\boldsymbol{v}]_R$ | Компоненты вектора в базисе $R$. Стандартные имена базиса: $R$ для прямоугольного (декартова), $P$ для полярного, $C$ для цилиндрического, $S$ для сферического. | \$[\boldsymbol{v}]_R\$ |
| $v_x, v_y, v_z$ | Компоненты вектора выделены нежирным шрифтом с нижними индексами, поэтому $\boldsymbol{v} = [v_x, v_y, v_z] = v_x\,\hat{\boldsymbol{\imath}} + v_y\,\hat{\boldsymbol{\ jmath}} + v_z\,\hat{\boldsymbol{k}}$. | \$v_x, v_y, v_z\$ |
| $v$ против $v_x$ | Величина (положительная) — это простая буква $v$, а знаковый компонент — $v_x$. | \$v\$ против \$v_x\$ |
| $\шляпа{\boldsymbol{e}}_r, \шляпа{\boldsymbol{e}}_\theta$ | Полярные базисные векторы.Может быть, нам следует изменить это на $\hat{\boldsymbol{r}}, \hat{\boldsymbol\theta}$? | \$\шляпа{е}_r\$, \$\шляпа{е}_\тета\$ |
| $\boldsymbol{r}$, $\boldsymbol{r}_P$, $\boldsymbol{r}_{OP}$, $\overrightarrow{OP}$ | Вектор положения точки $P$ из начала координат $O$. Происхождением и/или точкой можно пренебречь, если это очевидно из контекста. | \$\boldsymbol{r}\$, \$\boldsymbol{r}_P\$, \$\boldsymbol{r}_{OP}\$, \$\overrightarrow{OP}\$ |
| $\boldsymbol{\rm A}$ | Матрицы выделены прямым (римским) жирным шрифтом. 2\$ 2\$ |
Что такое единичный вектор вектора i j k? — Ответы на все
Что такое единичный вектор вектора i j k?
Объяснение: Чтобы определить единичный вектор, разделите заданный вектор на его модуль. Величина вектора определяется выражением √(i)2+(j)2+(k)2 , где i,j и k — компоненты вектора. √(2)2+(−1)2+(1)2=√6 .
Какова формула вектора?
Величина вектора →PQ — это расстояние между начальной точкой P и конечной точкой Q .В символах величина →PQ записывается как | →ПК | . Если заданы координаты начальной и конечной точек вектора, можно использовать формулу расстояния, чтобы найти его величину.
Является ли I J K единичным вектором?
Декартовы координаты Когда единичный вектор в пространстве выражается в декартовой системе счисления как линейная комбинация i, j, k, три его скалярных компонента могут называться направляющими косинусами. Значение каждой компоненты равно косинусу угла, образованного единичным вектором с соответствующим базисным вектором.
Объясняется ли единичный вектор I Ja?
Нет, их сумма имеет величину √2, поэтому очевидно, что это не единичный вектор.
Какова формула вектора АВ?
Мы можем использовать скалярное произведение, чтобы найти угол между двумя векторами, благодаря следующей формуле: a·b = |a| | б | cosq, где q — угол между a и b.
Что такое вектор положения в математике?
В геометрии вектор положения или вектор положения, также известный как вектор положения или вектор радиуса, представляет собой евклидов вектор, представляющий положение точки P в пространстве относительно произвольного исходного положения O.Обычно обозначается x, r или s, он соответствует отрезку прямой от O до P.
Всегда ли единичный вектор равен 1?
Поскольку единичный вектор по определению имеет величину 1, поэтому, если вам нужен единичный вектор в направлении A, вам нужно разделить его на величину.
Является ли векторная сумма единичного вектора i и Ja?
Нет, их сумма имеет величину √2, поэтому очевидно, что это не единичный вектор. Но если мы умножим сумму на 1/√2, она станет единичным вектором.
Но если мы умножим сумму на 1/√2, она станет единичным вектором.
Что такое единичный вектор?
Вектор – это величина, которая имеет как величину, так и направление.Вектор, величина которого равна 1, является единичным вектором. Любой вектор может стать единичным вектором, если его разделить на величину данного вектора. …
Что такое формула векторов?
Вектор — это объект, который имеет как величину, так и направление. Вектор обычно представлен стрелкой, направление которой совпадает с направлением величины, а длина пропорциональна величине величины. Векторные величины часто представляются масштабированными векторными диаграммами.
Что такое вектор и его формула?
Вектор – это величина, которая имеет как величину, так и направление.Например, вектор v = (1,3) не является единичным, поскольку его модуль не равен 1, т. е. |v| = √(12+32) ≠ 1. Любой вектор может стать единичным вектором, если его разделить на величину данного вектора.
Как выглядит вектор положения?
Вектор положения, прямая линия, один конец которой прикреплен к телу, а другой конец прикреплен к движущейся точке и используется для описания положения точки относительно тела. По мере перемещения точки вектор положения будет изменяться по длине или по направлению, или по длине и по направлению одновременно.
Чему равно скалярное произведение единичного вектора i и i?
Скалярное произведение между единичным вектором и самим собой также легко вычислить. Учитывая, что все векторы имеют длину один, скалярные произведения равны i⋅i=j⋅j=k⋅k=1.
Какова формула результирующего вектора?
R = A + B. Векторы в противоположном направлении вычитаются друг из друга, чтобы получить результирующий вектор. Здесь вектор B противоположен по направлению вектору A, а R — результирующий вектор.
Что такое векторное уравнение прямой?
В общем, векторное уравнение — это любая функция, которая принимает любую одну или несколько переменных и возвращает вектор.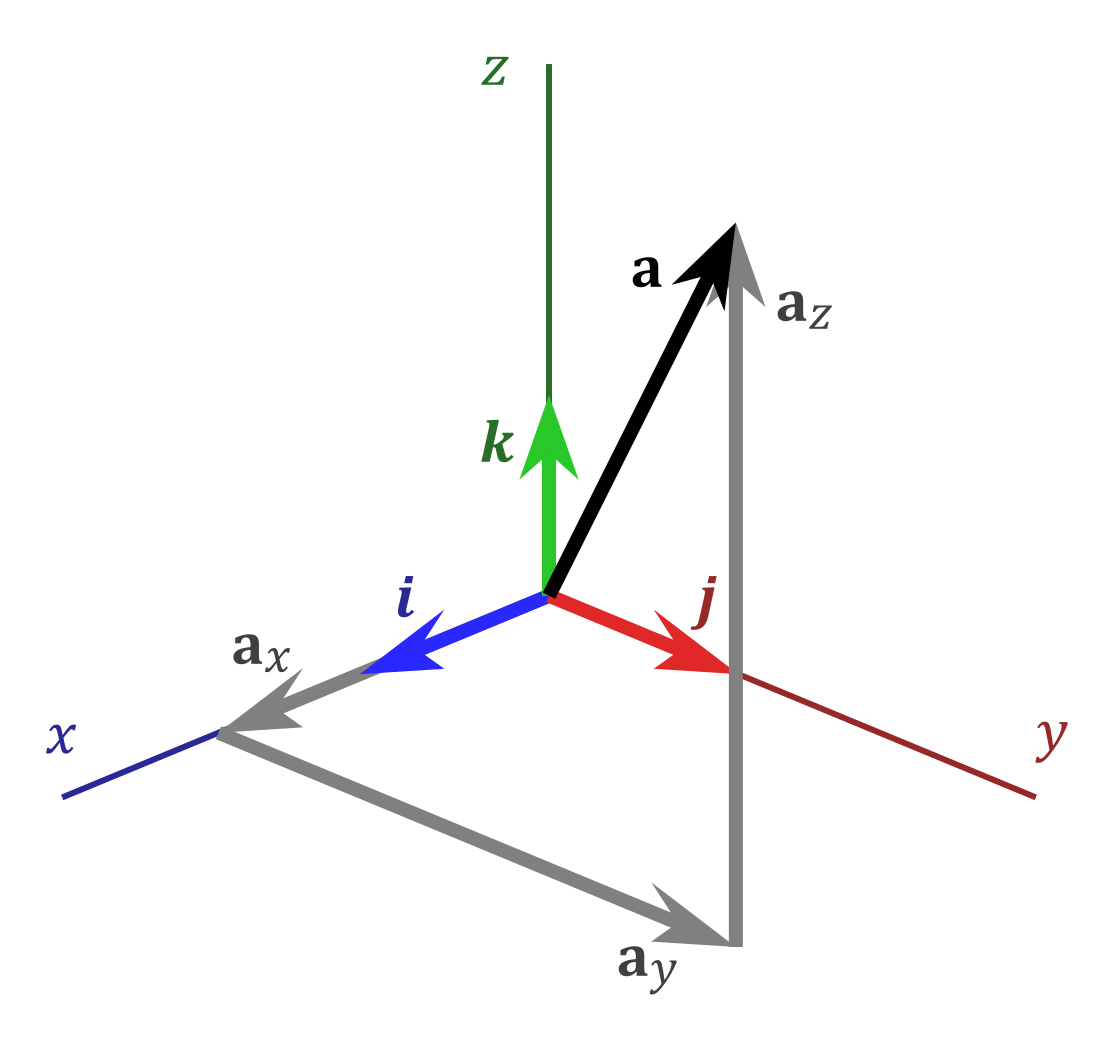 Векторное уравнение линии — это уравнение, определяющее вектор положения каждой точки на линии. Это работает как для прямых линий, так и для кривых.
Векторное уравнение линии — это уравнение, определяющее вектор положения каждой точки на линии. Это работает как для прямых линий, так и для кривых.
Что показывает вектор положения?
Какова формула позиции?
Обычное применение производных — это взаимосвязь между скоростью, скоростью и ускорением.В этих задачах вам обычно дается уравнение положения в форме «x=» или «s(t) = s(t)= s(t)=», которое говорит вам о расстоянии объекта от некоторой контрольной точки.
.
 В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором
В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных С другой стороны, для векторов в новом базисе справедливо
С другой стороны, для векторов в новом базисе справедливо
 \шляпа j =\шляпа j.\шляпа k = \шляпа k.\шляпа i = 0 \)
\шляпа j =\шляпа j.\шляпа k = \шляпа k.\шляпа i = 0 \)