Виды треугольников (прямоугольные, тупоугольные, остроугольные)
Тип урока: получение новых знаний (частично поисково — исследовательский)
Цель: сформировать представление обучающихся о разных видах треугольников;
Задачи:
образовательные:
- добиться осмысленности понятий: прямой, тупой, острый, развернутый угол; прямоугольный, тупоугольный, остроугольный треугольник: добиться умения выделять углы треугольника в заданных фигурах; выделять треугольники в заданных фигурах.
развивающие:
- способствовать развитию у обучающихся интуиции
и воображения; внимания, наблюдательности и
вооружать логическим методом, — основным методом,
с помощью которого обосновывается истинность
или ложность утверждений; помочь обучающимся
осознать социальную, практическую и личностную
значимость данного учебного материала,
обеспечить развитие умения ставить цель и
формулировать задачи, планировать свою
деятельность.

- реализовать право каждого ученика на полноценное личностное развитие, на основе качественного и индивидуализированного обучения.
воспитательные:
- способствовать развитию математического языка (его основным диалектам, алгебраическому и геометрическому) на котором говорит современная наука, интереса к предмету математика, создавать положительный образ математики у обучающихся.
Планируемые предметные результаты:
- умение различать треугольники: остроугольный, прямоугольный, тупоугольный: умение, выделять треугольники в заданных фигурах; развивать навыки выделения соответственных элементов в треугольниках, нахождение треугольников всех видов.
Планируемые метапредметные результаты:
- личностные: положительное отношение к учению, понимание необходимости сотрудничества с учителем, готовности к взаимодействию с ним и дружескому взаимопониманию, понимание необходимости товарищеского сотрудничества с одноклассниками, готовности к взаимодействию и взаимопониманию;
- регулятивные: умение определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий, планировать свои действия, оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки;
- познавательные: умение ориентироваться в своей системе знаний, отличать полученное новое, от уже известного с помощью учителя, добывать новые знания, находить ответы на вопросы учителя, используя учебник, свой жизненный опыт и информацию, полученную на уроке;
- коммуникативные: умение с достаточной
полнотой и точностью выражать свои мысли,
слушать и понимать речь других, учиться работать
в паре, формулировать собственное мнение.

Ход урока
I. Организационный момент.
— Итак, друзья, внимание –
Развивать и волю, и смекалку.
Садитесь правильно, начинаем наш урок.
Есть у математики молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы важную закалку.
Учится с тобою молодёжь
— Соберитесь и ответьте мне, какие качества нам необходимо включить в работу, чтобы для всех этот урок стал полезным?
— Внимание.
— Старание.
— Хорошее настроение.
— Покажите смайликами ваше настроение?
- Зеленый — отличное,
- синий – не очень,
- красный — плохое.
Древнегреческий поэт Нивей утверждал, что
математику нельзя изучать, наблюдая, как это
делает сосед.
— Почему он так говорил?
(ответы детей)
— Поэтому, каждый из вас должен работать на уроке в полную силу, слушать друг – друга внимательно, дополнять, выполнять все задания, а не смотреть, как работает сосед.
Оценивать себя вы будете по “Рабочей карте урока”. Она есть у каждого из вас на парте. Сюда вы будете вносить свою отметку за каждый этап урока.
В конце урока подведете итог своей работы и выставите себе средний балл за урок, то есть за усвоение темы.
Кто знает, как работать с “Рабочей картой урока”, покажите смайликом?
Да – зеленый, не уверен — синий, нет – красный.
Рабочая карта урока
(с/о – самооценка, о/т – оценка товарища)
| Работа с классом с/о |
Работа по рисунку в учебнике с/о |
Работа в паре.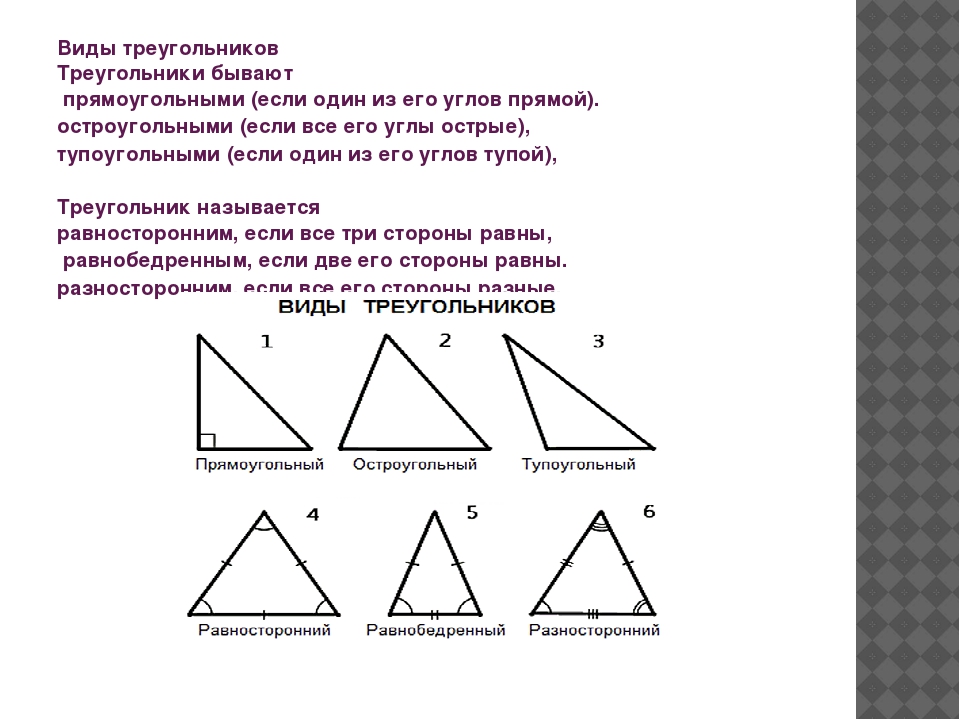 “Собери пару” о/т |
Самостоятельная работа (дифференцированная) с/о |
диктант. (графический) с/о |
Итог. с/о |
II. Актуализация опорных знаний.
— ребята, повторим, то, что уже знаем?
— откройте тетради и начнем работать со мной.
— в тетрадях, отметим три точки, не лежащие на одной прямой, точку А, точку В и точку С и соединим их отрезками.
— вы изобразили фигуру у себя, а я заранее на
доске.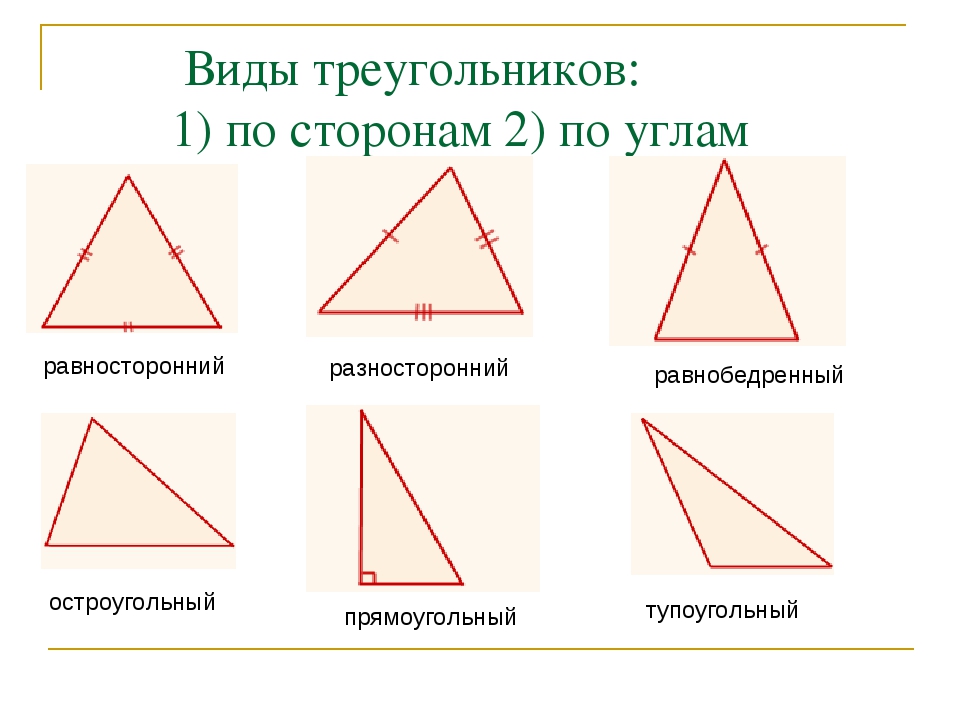
— посмотрите, какая фигура у меня получилась и проверьте себя.
— какую фигуру мы получили? (треугольник)
— почему эта фигура так называется? (три угла, три вершины, три стороны)
— Приведите примеры, где встречаются треугольники в нашей повседневной жизни? (примеры детей)
1. Треугольник — ударный музыкальный инструмент в виде металлического прута, изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
2. Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
3. Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы
4. Треугольники в конструкции мостов.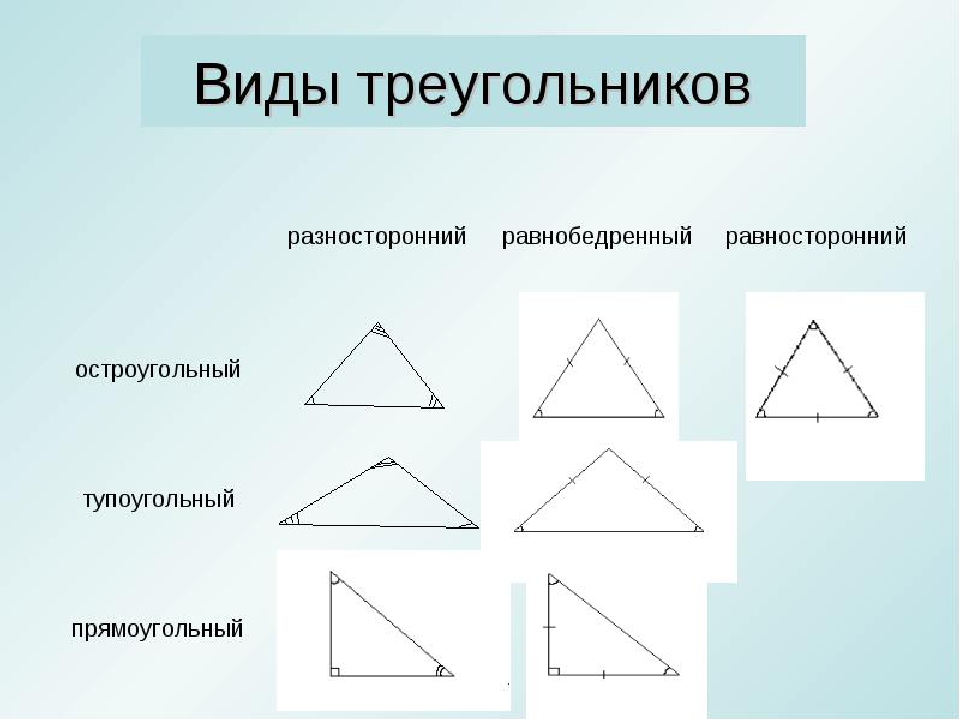
5. Высоковольтные линии электропередачи.
6. Треугольники делают конструкции надежными.
7. Настенные часы в виде треугольника
8. Детская игрушка пирамидка.
9. Детские спасательные круги в идее треугольника.
10. Женские украшения.
— посмотрите на наш треугольник.
— прочитайте, как называется построенный треугольник? ( ВСА, СВА ) и т. д.
— назовите углы этого треугольника? угол ( ВСА, СВА, АСВ).
— можно его назвать просто, угол А, угол В, угол С.
— вспомните, какие углы вы знаете? (острый, тупой, прямой,)
— посмотрите на слайд и скажите.
— какие вы видите углы?
— покажите прямой угол.
— как можно это проверить? (с помощью треугольника, угольника)
— выйди к доске и проверь.
— покажите тупой угол.
— как можно это проверить?
— выйди к доске и проверь.
— покажите острый угол.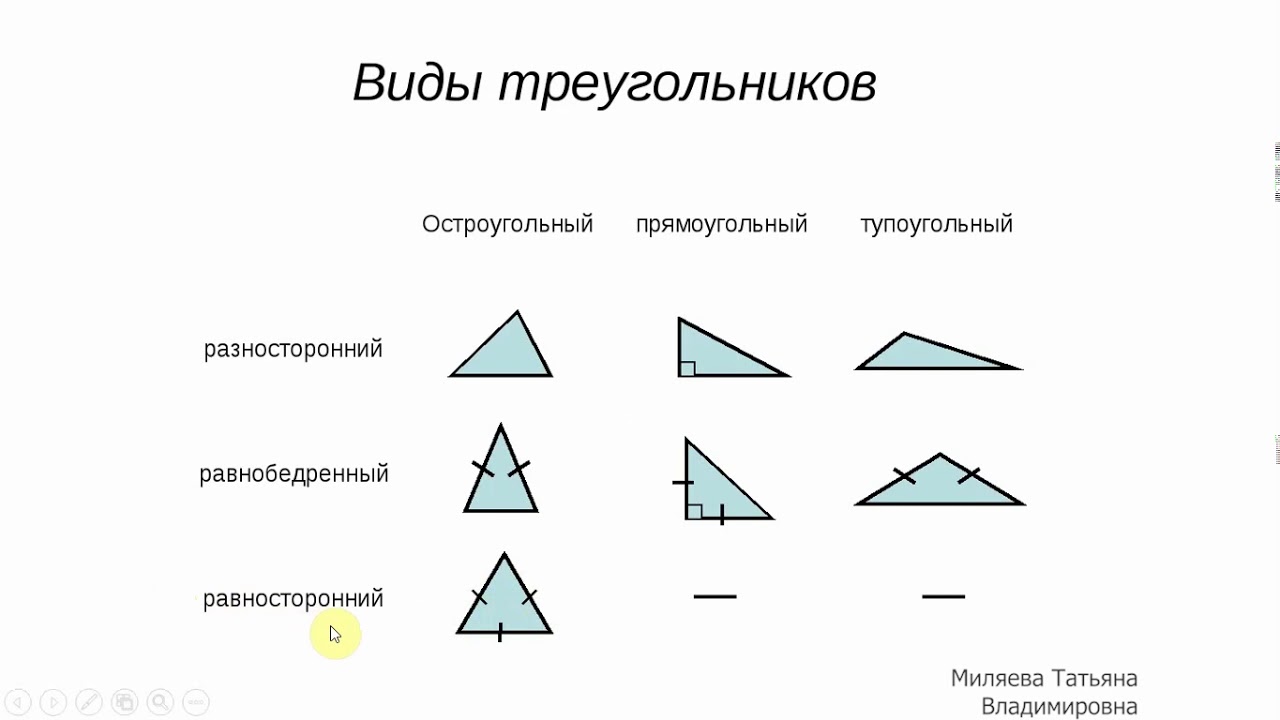
— как можно это проверить?
— выйди к доске и проверь.
— а как называется вот этот угол, кто знает? (развернутый)
— на что он похож? (на веер)
— правильно.
— встаньте и покажите мне развернутый угол, с помощь рук.
— Что мы сейчас с вами повторили? (острые, тупые, прямые, развернутые углы)
— оцените свою работу в рабочей карте.
III. Формирование новых знаний.
— подошло время узнать тему нашего урока.
— перед вами ребус, прочитав ребус, вы узнаете тему нашего урока.
Замените букву и на е, в первой цифре.
Виды КОВ.
— как называется тема нашего урока?
Тема урока “Виды треугольник”.
— ребята, давайте поставим цель урок,
— продолжите фразу.
— что мы должны узнать в ходе урока?
— чему научимся?
— что попробуем выполнить?
Мы узнаем – какие виды треугольников бывают?
Мы научимся — различать разные виды треугольников?
Мы попробуем применить на практике наши знания
в самостоятельной работе.
— давайте с вами узнаем, какие виды треугольников бывают?
— как вы думаете, кто нам может помочь в этом? (учитель, учебник)
— правильно, с помощью учебника мы узнаем на уроке, какие виды треугольников бывают?
Учитель:
“Если бы треугольники создали себе бога, он был бы с тремя сторонами”, — сказал известный французский философ Шарль Монтескьё.
2. Работа по учебнику.
Откройте стр 4 учебника математика часть № 2
— Какие треугольники вы видите на рисунке, назовите их?
треугольник АВС, треугольник ДЕК, треугольник МТО.
— есть ли среди них треугольник с прямым углом? (да)
— назовите его? ДЕК
— назовите угол, который у него прямой? Е
— как вы определили, что угол Е, у него прямой?
— давайте проверим?
— и так в треугольнике Е, прямой.
— как можно назвать этот треугольник? (прямоугольный)
(да – это прямоугольный треугольник)
— посмотрите и скажите, два других угла в этом треугольнике, какие? (острые)
— почему вы так решили?
— давайте проверим?
— посмотрите и скажите, есть ли среди этих треугольников треугольник с тупым углом? (да)
— назовите его? ТОМ
— какой угол у него тупой? (О)
— давайте проверим?
— какие два других угла в треугольнике ТОМ? (острые)
— давайте проверим.
— как мы можем назвать этот треугольник? (тупоугольный)
(да – это тупоугольный треугольник)
— а остался ли у нас еще треугольник?
— назовите его? АВС
— посмотрите и скажите, какие у него углы? (все острые)
— давайте проверим.
— как же мы, можем его назвать? (остроугольный)
— сделайте вывод, какие бывают треугольники в зависимости от их углов?
(тупоугольные, остроугольные, прямоугольные)
— давайте узнаем, совпадает ли наш вывод с выводом в учебнике.
— прочитайте вывод в учебнике.
(читают вывод в учебнике стр 4)
— совпадает ли наш вывод с выводом учебника? (да)
— какие треугольники называются прямоугольными – есть прямой угол, остроугольными – есть острый угол, тупоугольными – есть тупой угол.
— покажите смайликами, как вы поняли этот материал?
— значит, первую цель мы с вами достигли.
— мы узнали, какие виды треугольников бывают?
— а теперь, мы с вами должны закрепить
изученный материал, научится различать
треугольники на практике по видам.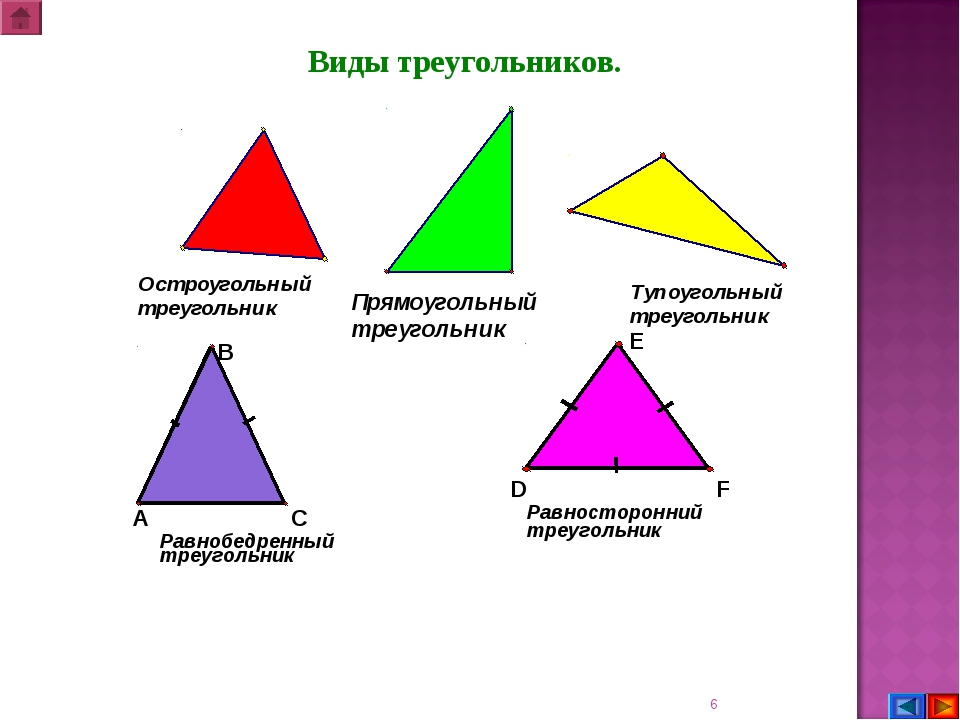
— посмотрите на странице 4 № 8.
— прочитайте задание.
— что нужно сделать в этом задании?
— выпишите сначала остроугольные, затем прямоугольные, а потом тупоугольные треугольники.
(самостоятельно выполняют работу)
Проверьте себя по слайду и поставьте отметку в карту.
- Остроугольный – 6, 1
- Прямоугольный – 7, 4.
- Тупоугольный – 2. 3, 5.
— отодвиньте учебник.
— Скажите, чему мы учились, работая с упражнением № 8 ?
— мы учились – различать виды треугольников
3. Первичное закрепление. (фронтальная работа)
Физкультминутка.
“Полет – это математика”, — писал советский летчик Валерий Чкалов
Давайте попробуем, умеет ли ваша мысль летать, и проверим ваше внимание?
— встаньте ребята, когда я вам показываю
тупоугольный треугольник – поднимите руки так,
как будь-то, вы тянитесь к солнышку, когда я вам
показываю остроугольный треугольник –
поставьте ноги на ширину плеч, когда я вам покажу
прямоугольный треугольник – вы вытяните руки
вперед.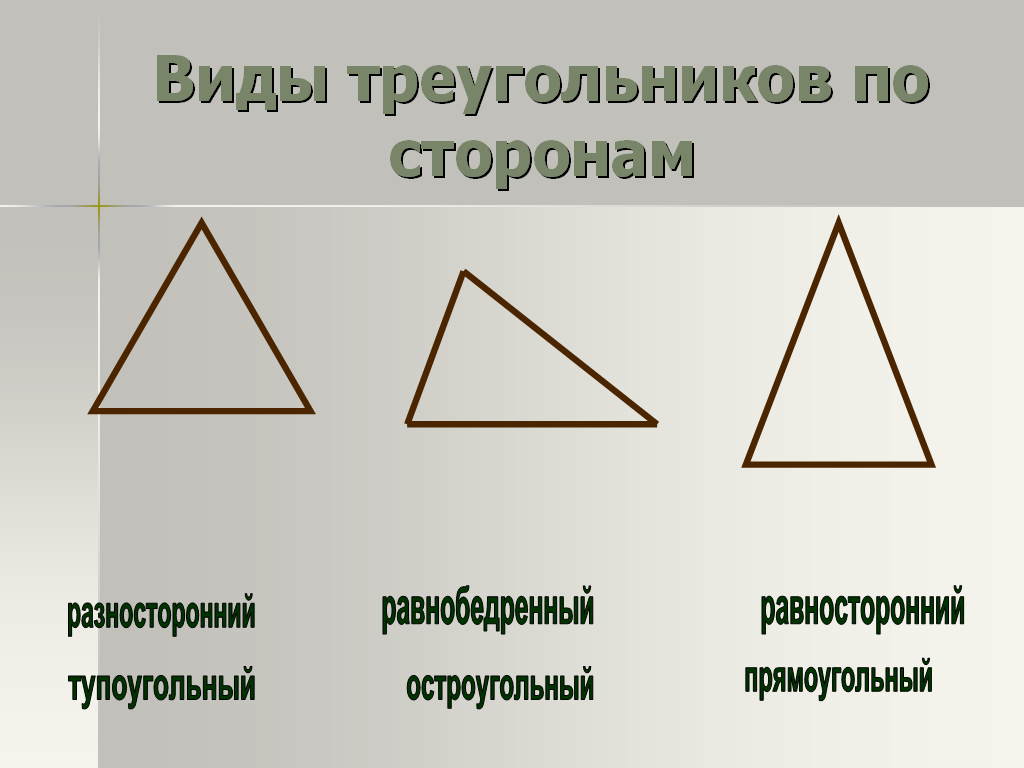
(показываю не путая детей, так как новый материал)
— мы с вами отдохнули и повторили, что, продолжите фразу?
— Повторили — виды треугольников
Оцените свой ответ в таблице самостоятельно.
4. Работа в парах. (вторичное закрепление)
“Величие человека — в его способности мыслить”, — писал великий французский ученый, математик Блез Паскаль.
Давайте же с вами помыслим, работая в парах.
— Возьмите карточку с видами треугольников.
(соедините треугольник и объясните своему товарищу, почему именно этот треугольник называется тупоугольным, прямоугольным, остроугольным, работайте в парах по очереди, вспомните принципы работы в парах).
ВИДЫ ТРЕУГОЛЬНИКОВ
| Треугольник | Вид треугольника |
| Остроугольный | |
| Тупоугольный | |
| Прямоугольный |
— проверьте полученный результат по слайду.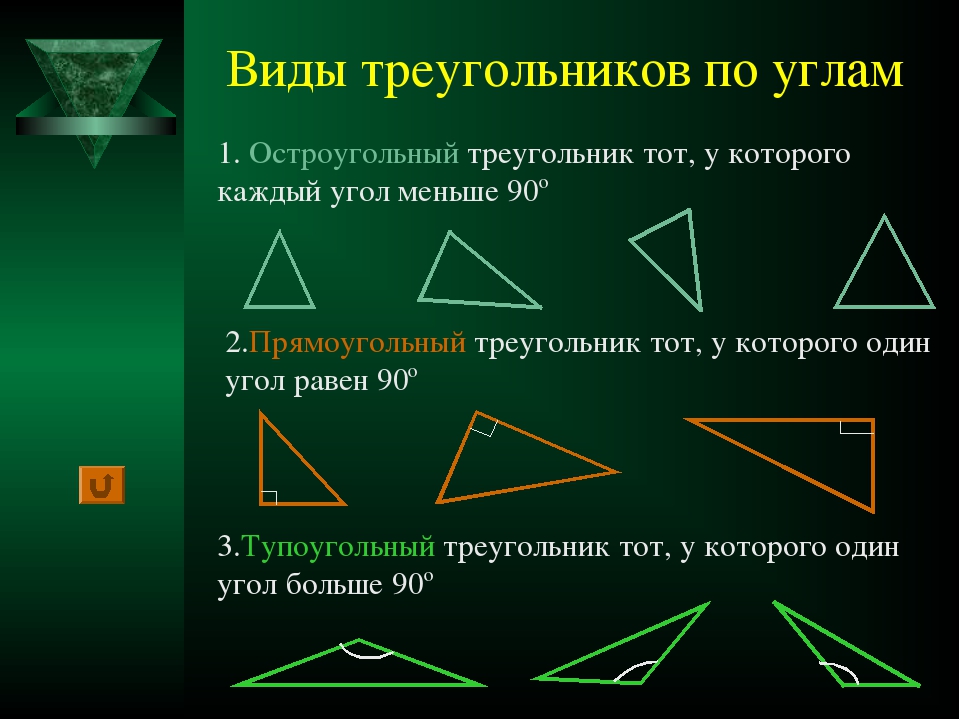
— проверьте свою работу, поменяйтесь картами со своим товарищем и поставьте ему отметку.
— оцените работу в паре, было ли вам комфортно, понимал ли вас, товарищ?
Смайликом: отлично, не очень, плохо.
III. Закрепление изученного материала.
(самостоятельная работа)
Математика уступает свои крепости лишь сильным и смелым.
Писал о людях известный математик Андрей Григорьевич Конфорович.
Поднимите руку, кто считает себя сильным?
Перед вами Самостоятельная работа. Выберите себе уровень по силам. Если вы взяли сильный уровень, а почувствовали, что не справляетесь, можете поменять уровень в процессе работы, на тот который вам доступен.
(у каждого варианта 3 уровня, А, Б, С.)
- А – уровень слабый на “3”,
- Б – уровень средний на “4”,
- В – уровень сильный на “5”.
У первого варианта свои уровни, у второго
варианта свои уровни.
Ответы записывайте внизу. У вас при выполнении задания правильно получится имя мальчика или девочки.
Дифференцированная самостоятельная работа.
Самостоятельная работа
Вариант № 1
| Уровень А (слабый) | Уровень Б (средний) | Уровень В (сильный) | |||||||||
| 1. Определи, какой это вид
треугольника?
А) остроугольный И) прямоугольный М) тупоугольный |
1. Дострой треугольник до
логического завершения, определи, какой вид
треугольника у тебя получился?
А) прямоугольный Ю) тупоугольный Н) остроугольный |
1. Дострой по данным вершинам
треугольник, определи вид получившегося
треугольника? Дострой по данным вершинам
треугольник, определи вид получившегося
треугольника?
О) прямоугольный В) остроугольный Е) тупоугольный |
|||||||||
| 2. определи сколько треугольников
на рисунке?
Р) 3 , Б) 2, К) 6 . |
2. Определи сколько треугольников
на рисунке?
М) 4 Л) 6 Н) 5 |
2. Определи сколько треугольников
на рисунке?
К) 3, Д) 4, Л) 5. |
|||||||||
| 3. Может ли в треугольнике быть
два тупых угла? К) да, Л) не знаю, А) нет. |
3. Может ли быть в треугольнике
два тупых угла. Г) да, Я) нет, В) не знаю. |
3. Может ли в треугольнике быть
один угол прямой, другой угол тупой, а третий
острый? М) да, Я) нет, Ф) не знаю. |
|||||||||
| ОТВЕТ: | и | р | а | ОТВЕТ: | ю | л | я | ОТВЕТ: | о | л | я |
Самостоятельная работа
Вариант № 2
| Уровень А (слабый) | Уровень Б (средний) | Уровень В (сильный) | |||||||||
1. Определи, какой это вид
треугольника? Определи, какой это вид
треугольника?
А) тупоугольный Ю) остроугольный В) прямоугольный |
1. Дострой треугольник до
логического завершения, определи, какой вид
треугольника у тебя получился?
К ) тупоугольный М) тупоугольный Я) прямоугольный |
1. Дострой по данным вершинам
треугольник до логического завершения, определи,
какой вид треугольника получился? З) остроугольный Р) тупоугольный М) прямоугольный |
|||||||||
| 2. Определи, сколько
треугольников на рисунке?
И) 4 , Д) 1, Р) 3. |
2. Определи, сколько
треугольников на рисунке?
Н) 5, Г) 4, Д) 3. |
2. Определи, сколько
треугольников на рисунке?
А) 7 Б) 8 В) 10 |
|||||||||
| 3. Может ли в треугольнике быть
три острых угла? А) да Г) не знаю Е) нет. |
3. Может ли в треугольнике быть
два прямых угла? У) да, С) не знаю, А) нет. |
3. Может ли быть в треугольнике
один угол тупой, другой угол прямой, а третий угол
острый? Я) нет, М) да, Т) не знаю. |
|||||||||
| ОТВЕТ: | Ю | Р | А | ОТВЕТ: | Я | Н | А | ОТВЕТ: | Р | А | Я |
— посмотрите на слайд.
— проверьте свои ответы.
Поставьте себе в таблицу отметку, за эту работу.
IV. Подведение итога урока.
— вспомните, какие цели мы ставили на уроке?
— продолжите фразу.
- Мы узнали — какие виды треугольников бывают?
- Мы научились — различать разные виды треугольников?
- Мы применили — на практике знания в самостоятельной работе.
— какие качества вам помогли сегодня на уроке?
— Внимание.
— Старание.
— Хорошее настроение.
— давайте поставим отметку себе за урок.
— Покажите смайликами ваше настроение в конце урока?
- Зеленый — отличное,
- синий – не очень,
- красный — плохое.
V. Домашнее задание. (деференцированное с учетом способностей детей)
— учитель комментирует данное задание, перед
тем как его дать, каждое упражнение.
— запишите домашнее задание.
Д/З стр 4, № 12 или если вам тяжело выполнить задание, то сочините сказку о треугольниках, стр 5 № 15 (1 строка)
Приложение 1
Приложение 2
Равнобедренный остроугольный треугольник рисунок. Какие есть треугольники
Треугольник (с точки зрения пространства Эвклида) – это такая геометрическая фигура, которая образована тремя отрезками, соединяющими три точки, не лежащими на одной прямой. Три точки, которые образовали треугольник, называются его вершинами, а отрезки соединяющие вершины называются сторонами треугольника. Какие есть треугольники?
Равные треугольники
Существует три признака равенства треугольников. Какие треугольники называются равными? Это те, у которых:
- равны две стороны и угол между этими сторонами;
- равна одна сторона и два прилежащие к ней угла;
- равны все три стороны.
У прямоугольных треугольников существуют следующие признаки равенства:
- по острому углу и гипотенузе;
- по острому углу и катету;
- по двум катетам;
- по гипотенузе и катету.

Какие бывают треугольники
По числу равных сторон треугольник может быть:
- Равносторонним. Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей.
- Неравносторонним. Треугольник, не имеющий равных сторон.
- Равнобедренным. Это треугольник с двумя равными сторонами. Две одинаковые стороны – боковые, а третья сторона – основание. В таком треугольнике совпадают биссектриса, медиана и высота, если их опустить на основание.
По величине углов треугольник может быть:
- Тупоугольным — когда один из углов имеет величину более 90 градусов, то есть когда он тупой.
- Остроугольным – если все три угла в треугольнике острые, то есть они имеют величину менее 90 градусов.
- Какой треугольник называется прямоугольным? Это такой, у которого есть один прямой угол равный 90 градусов. Катетами в нем будут назваться две стороны, которыми образован этот угол, а гипотенузой – противолежащая прямому углу сторона.

Основные свойства треугольников
- Против меньшей стороны всегда лежит меньший угол, а больший угол всегда лежит против большей стороны.
- Равные углы всегда лежат против равных сторон, а против разных сторон всегда лежат разные углы. В частности, в равностороннем треугольнике все углы имеют одинаковое значение.
- В любом треугольнике сумма углов равняется 180 градусов.
- Внешний угол можно получить, если у треугольника продолжить одну из его сторон. Величина внешнего угла будет равняться сумме не смежных с ним внутренних углов.
- Сторона треугольника больше, чем разность его двух других сторон, но меньше, чем их сумма.
В пространственной геометрии Лобачевского сумма углов треугольника будет всегда меньше, чем 180 градусов. На сфере это значение больше 180 градусов. Разность между 180 градусов и суммой углов треугольника называется дефектом.
Предмет: математика
Класс: 3 класс
Учебник: «Математика» 2 часть.
Тема: Виды треугольников
Тип урока: открытие новых знаний
Цель: Научить определять виды треугольников по измерениям длин их сторон.
Задачи :
1)Актуализировать знания о геометрических фигурах — прямоугольник, квадрат, треугольник.
2)Актуализировать сложение и вычитание трёхзначных чисел, деление двузначного числа на однозначное, двузначное и круглое; умножение двузначного на однозначное число.
3)Ввести термины: равнобедренный, равносторонний, разносторонний треугольник.
Ход урока
1.Мотивация к учебной деятельности
Посмотрите, скажите, что это такое?
(пирамида)
Скажите, из чего она состоит? (из частей, уровней …)
Можно ли эту пирамиду сравнить с нашим знанием? (да)
Каждый день вы строите всё новые и новые пирамиды, каждый уровень пирамиды- это новое знание, которое вы получаете на уроке. А что будет с пирамидой, если мы уберём синий уровень? (Она разрушиться, станет меньше. )
)
А как из-за чего может разрушиться наша пирамида знаний? (Из-за не выполненного д/з, пропусков уроков, не внимательно слушать учителя.)
Что нужно делать, чтобы наша пирамида становилась прочнее, росла? (Учить уроки, хорошо работать на уроке, выполнять д/з, не прогуливать школу.)
Ребята, вы сказали всё верно. А теперь давайте представим, что наша пирамида отбросила тень. Скажите, на какую геометрическую фигуру тень похожа?
(На треугольник.)
Сегодня мы продолжим работать с такой геометрической фигурой, как треугольник.
2.Актуальзация знаний и фиксация затруднений в проблемной ситуации
С какими геометрическими фигурами вы знакомы? (квадрат, прямоугольник, треугольник).
На доске таблица, заполните её, опираясь на свои знания (у каждого обучающегося карточка с такой таблицей):
Как называются первые две геометрические фигуры? (прямоугольник и квадрат, одним словом это четырёхугольники.)
Скажите, какие виды четырёхугольников вы знаете? Ответить на этот вопрос вам поможет изображение их на слайде.
Названия четырёхугольников появляются после ответов детей.
(ромб, квадрат, прямоугольник, трапеция, параллелограмм — называют их по изображениям на слайде или доске.)
Можете ли вы сказать, что такое прямоугольник, а что такое квадрат?
(Прямоугольник — четырёхугольник, у которого все углы прямые.
Квадрат — это прямоугольник, у которого все стороны равны)
Найдите лишнюю геометрическую фигуру, опираясь на результаты таблицы. (Треугольник).
Хорошо, четырёхугольники все очень разные, а что вы знаете о треугольнике? (Треугольники бывают: остроугольные, тупоугольные, прямоугольные.)
Что вы ещё знаете о треугольнике? (Определение)
Треугольник — это геометрическая фигура, у которой 3 угла, 3 вершины, 3 стороны.
Заполните следующую таблицу, опираясь на свои знания:
(Учитель заполняет таблицу в соответствии ответам детей. В колонках «название» возникают разные мнения, а некоторые дети оставляют их пустыми. )
)
3.Выявление места и причины затруднения.
Какое задание вы выполняли? (Заполни таблицу.)
Где возникло затруднение? (При записи названий треугольников)
Почему возникло затруднение? (Не знаем как они называются)
Какую цель урока нужно поставить? (Узнать, какие ещё есть виды треугольников кроме изученных (тупоугольный, остроугольный, прямоугольный) , научиться определять эти виды у треугольников.)
Какая тема нашего урока? (Виды треугольников)
4.Открытие нового знания.
Давайте вернёмся к таблице.
Впишем размеры сторон треугольников. (Вписывают.)
Хорошо, а сейчас посмотрите и скажите, что вы заметили? (У первого треугольника все стороны равны, у второго 2 стороны равны, а у третьего все стороны разные.)
Верно, а можете ли вы придумать названия этим треугольникам, основываясь на том объяснении, которое вы сейчас дали? (Да)
Как вы назовёте треугольник, у которого все стороны равные? Придумай прилагательное, состоящее из 2х слов: равные стороны. (Равносторонний)
(Равносторонний)
Как назвать треугольник, у которого все стороны различные? (Разносторонний)
Как называется треугольник, у которого 2 стороны равные? (Дети сомневаются, чтобы ответить на этот вопрос они пользуются учебником с.73) (Равнобедренный) А какой ещё треугольник можем назвать равнобедренным? (Равносторонний)
Заполните таблицу самостоятельно, опираясь на новые знания.
А можем ли сейчас дать определение видам треугольников? (Да)
Равносторонний — треугольник, у которого все три стороны равны.
Равнобедренный — треугольник, у которого равны хотя бы две стороны. Равнобедренным треугольником является и равносторонний треугольник.
Разносторонний — треугольник, у которого все стороны разные.
Проверьте свои определения с.73 -учебник. (Проверяют.)
Верно ли вы составили определения? (Да.)
5.Первичное закрепление с проговариванием во внешней речи
Выполните задание из учебника с.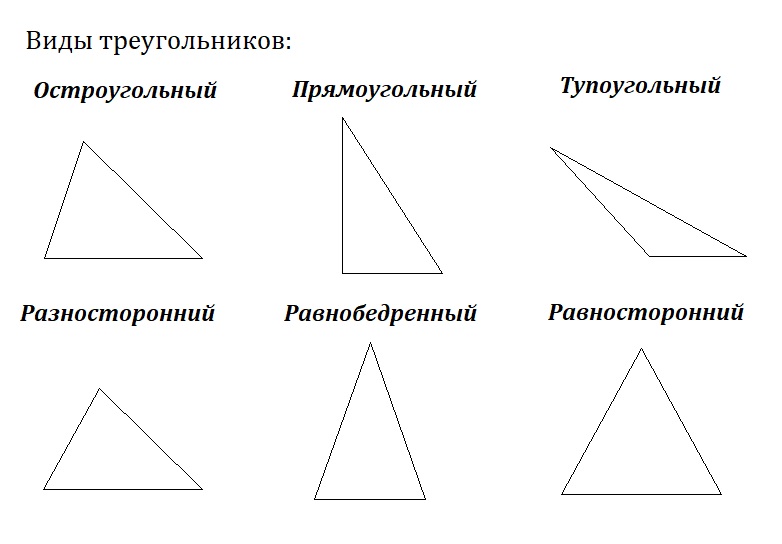 74 (под?)
74 (под?)
1)Разносторонние: 2,3,5
2)Равнобедренные: 1, 4 , 6, 7
(Учащиеся записывают в тетради. По очереди говорят ответы, аргументируя. Образец фиксируется на доске).
6.Самостоятельная работа с самопроверкой по эталону.
Выполнение задания самостоятельно. По окончанию работы — самопроверка по образцу (на доске или на индивидуальных карточках).
№1.Заполни таблицу , схематично изобрази треугольники.
№2.Выпиши номера:
1)Разносторонних треугольников.
2)Равнобедренных, из выписанных номеров подчеркни номера равносторонних треугольников.
Эталон:
Задание №1:
Задание №2:
1)Разносторонние треугольники: 2,3,4
2)Равнобедренные треугольники (подчеркнут номер равностороннего треугольника): 1, 5
7.Включение в систему знаний и повторение
На песке мальчик нарисовал треугольники и зашифровал слова, найди значения выражений, записанные в треугольниках. Сначала решай те, которые записаны в разносторонних треугольниках, а потом в равнобедренных треугольниках. И отгадаешь зашифрованные слова.
Сначала решай те, которые записаны в разносторонних треугольниках, а потом в равнобедренных треугольниках. И отгадаешь зашифрованные слова.
Подсказка: Запиши числа в порядке возрастания и слова у тебя получатся.
Карточка:
Решение:
Ответ: Виды треугольников
8.Рефлексия учебной деятельности.
Нарисуй соответственно пирамиду знаний, состоящую из 7 уровней. Каждый уровень — это ответ на вопрос.
Ответьте на вопросы:
1)Ребята, что такое вы записали «виды треугольников»? (Тему нашего урока)
2)Какова была наша цель? (Узнать, как называются все 3 вида треугольников, научиться определять эти виды по измерениям длин сторон.)
3)Какие виды треугольников вы узнали? (разносторонний, равнобедренный, равносторонний)
4) А почему они так называются?
( Равносторонний — треугольник, у которого все стороны равны.
Равнобедренный — треугольник, у которого хотя бы две стороны равны, в том числе и равносторонний треугольник, потому что у него есть две равные стороны. )
)
Разносторонний — треугольник, у которого все стороны разные.)
5) Научились схематично изображать все виды треугольников? (Да, на самостоятельной работе.)
6) Какие открытия вы сегодня сделали? (Новые виды треугольников, их названия.)
7) Ребята, а вы сможете определить вид треугольника по его измерениям? (Да) Я вам сейчас буду говорить измерения, а вы поднимать вверх карточку с названием вида треугольника (карточки выданы дополнительно- по 3 карточки.)
1. 2см, 3см,5 см.- разносторонний
2. 4см, 4см, 2 см — равнобедренный
3.6см, 6см,6см — равносторонний, равнобедренный
Поднимите руки, кто сегодня достиг вершины этого знания? (Поднимают)
А поднимите руки, кому не хватило 1, 2 уровней. (Поднимают.)
(Учитель анализирует «пирамиды знаний у детей, делает выводы — какой уровень западает и на следующем уроке начинает актуализацию знаний с этого.)
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.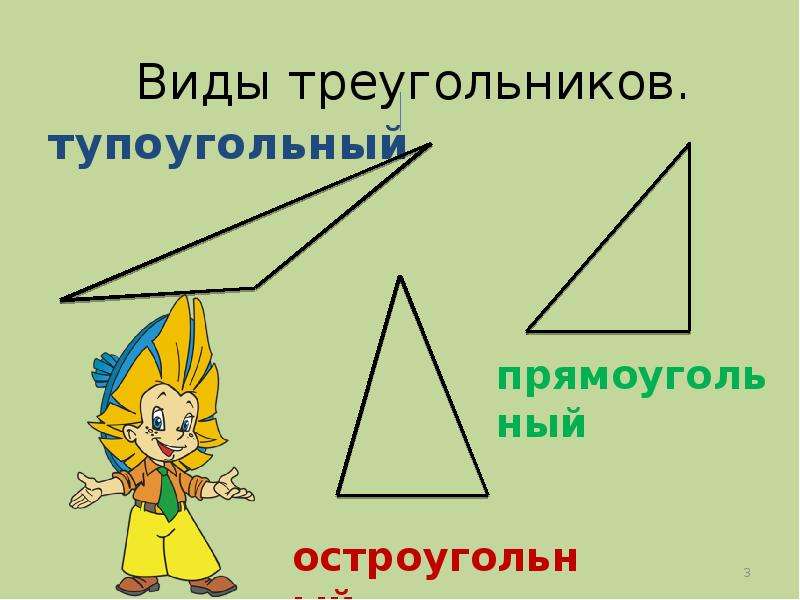
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
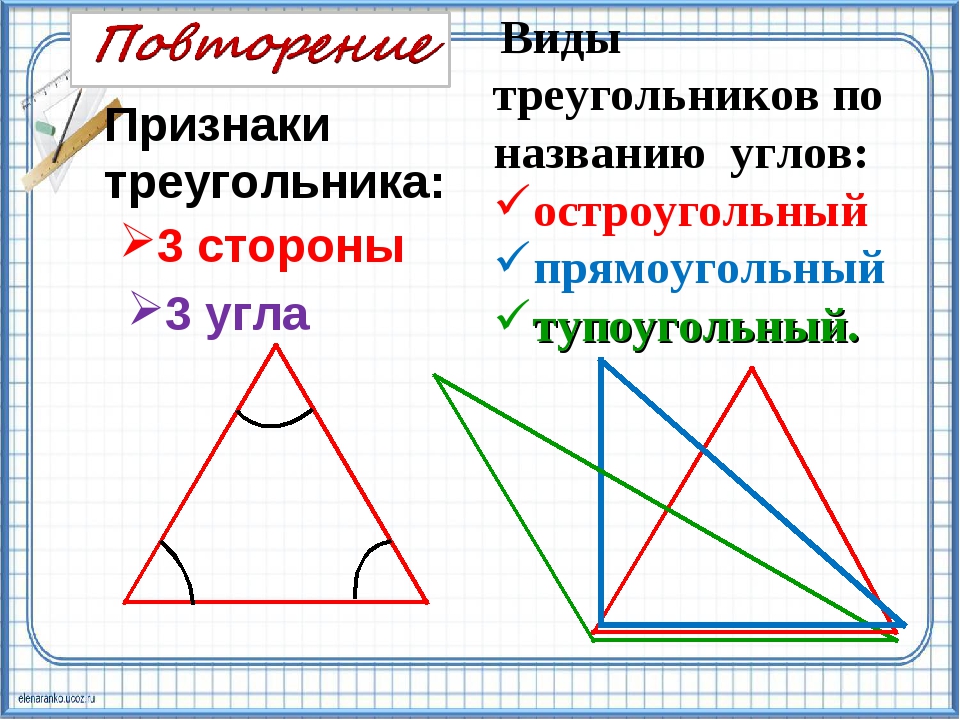
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис.
9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.
 : Просвещение, 2012.
: Просвещение, 2012. - Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.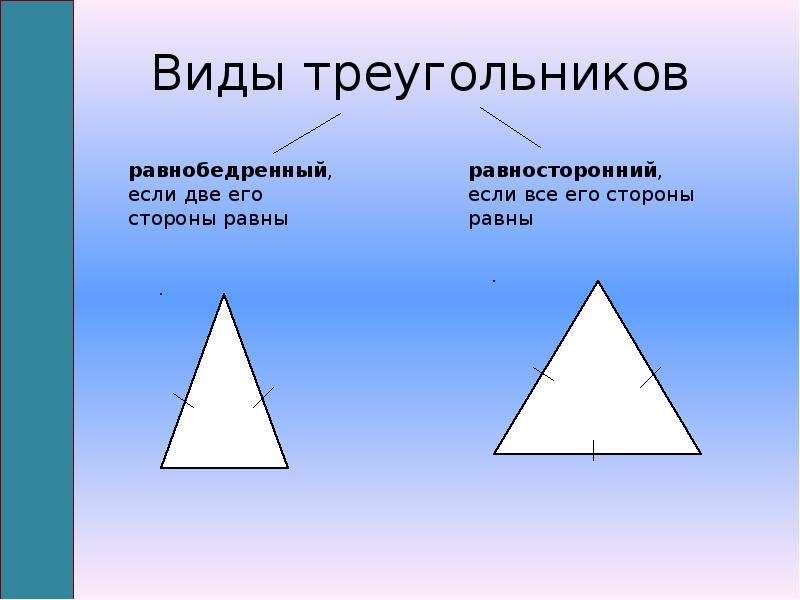
3. Составьте задание по теме урока для своих товарищей.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.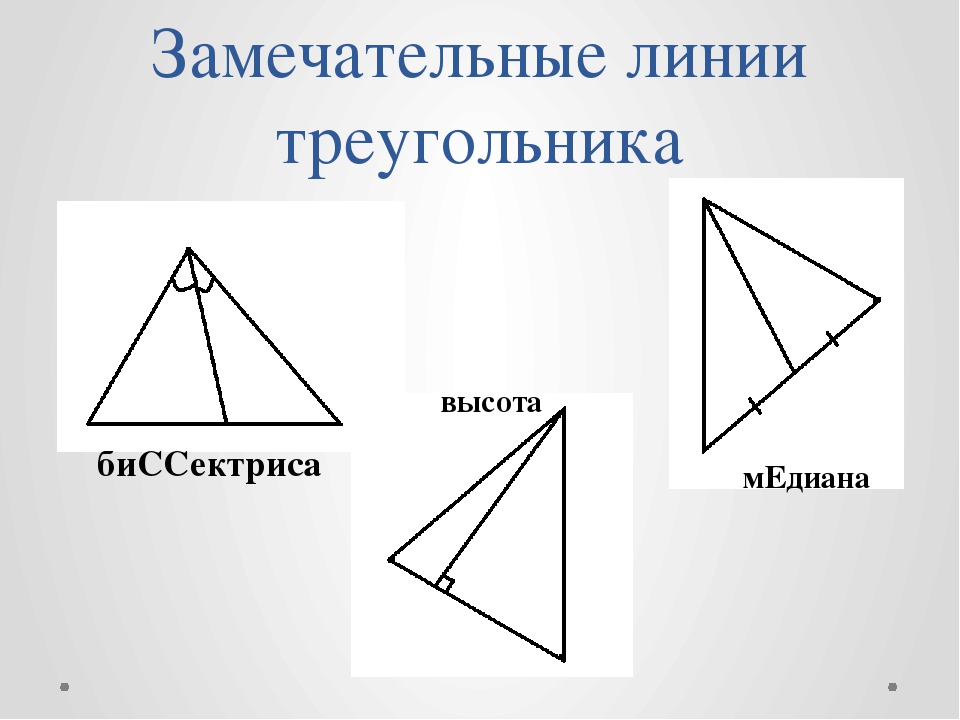
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис.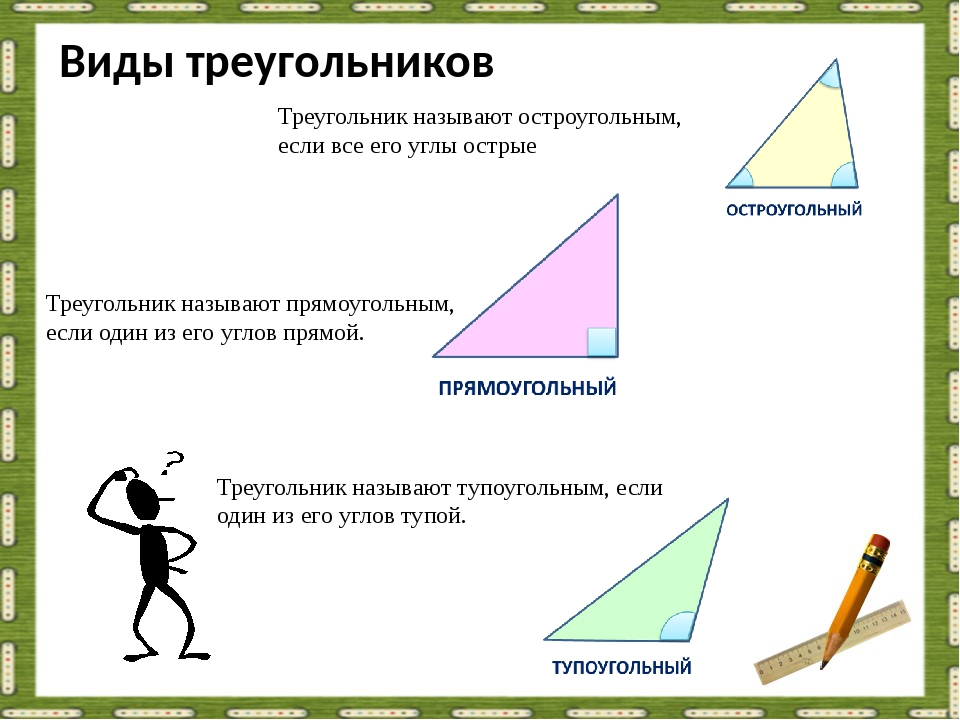 8).
8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.
 И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012. - М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Задачи:
1. Познакомить учащихся с разными видами треугольников в зависимости от вида углов (прямоугольный, остроугольный, тупоугольный). Учиться находить на чертежах треугольники и их виды. Закреплять основные геометрические понятия и их свойства: прямая линия, отрезок, луч, угол.
2. Развитие мышления, воображения, математической речи.
3. Воспитание внимания, активности.
Ход урока
I. Организационный момент.
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем два квадрата,
А на них огромный круг.
А потом ещё кружочки,
Треугольник колпачок.
Вот и вышел очень — очень
Развесёлый Чудачок.
II. Объявление темы урока.
Сегодня на уроке мы с вами совершим путешествие по городу Геометрии и побываем в микрорайоне Треугольники (т.е. познакомимся с разными видами треугольников в зависимости от их углов, будем учиться находить эти треугольники на чертежах.) Проведём урок в форме “игры-соревнования” по командам.
1 команда — “Отрезок”.
2 команда — “Луч”.
3 команда — “Угол”.
А гости будут представлять жюри.
Жюри нас по пути направит
И без вниманья не оставит. (Оценивать по баллам 5,4,3,…).
А на чём же мы будем путешествовать по городу Геометрии? Вспомните, какие виды пассажирского транспорта есть в городе? Нас очень много, какой же мы выберем? (Автобус).
Автобус. Чётко, кратко. Начинается посадка.
Усаживаемся поудобнее и начнём наше путешествие. Капитаны команд получите билеты.
Но билеты эти непростые, а билеты — “задания”.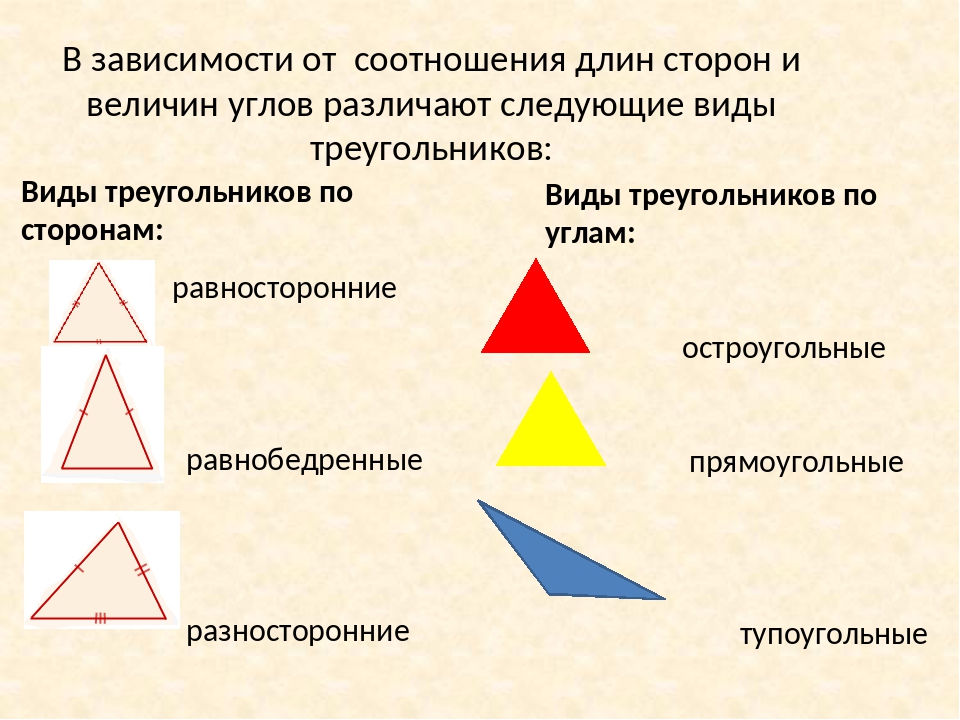
III. Повторение пройденного материала.
Первая остановка “ Повторяй-ка”.
Вопрос всем командам.
Найти на чертеже прямую линию и назвать её свойства.
Без конца и края линия прямая!
Хоть сто лет по ней иди,
Не найдёшь конца пути!
- Прямая не имеет ни начала, ни конца — она бесконечна, поэтому её измерить нельзя.
Начинаем наше соревнование.
Защита названий своих команд.
(Все команды читают первые вопросы и обсуждают. По очереди капитаны команд зачитывают вопросы, 1 команда читает 1 вопрос).
1. Показать на чертеже отрезок. Что называется отрезком. Назвать его свойства.
- Часть прямой, ограниченная двумя точками, называется отрезком. У отрезка есть начало и конец, потому его можно измерить при помощи линейки.
(2 команда читает 1 вопрос).
1. Показать на чертеже луч. Что называется лучом. Назвать его свойства.
- Если отметить точку и из неё провести часть
прямой, то получится изображение луча.
 Точка, из
которой проведена часть прямой, называется
началом луча.
Точка, из
которой проведена часть прямой, называется
началом луча.
Конца у луча нет, поэтому его измерить нельзя.
(3 команда читает 1 вопрос).
1 .Показать на чертеже угол. Что называется углом. Назвать его свойства.
- Проведя из одной точки два луча, получается геометрическая фигура, которая называется углом. У угла есть вершина, а сами лучи называются сторонами угла. Углы измеряются в градусах с помощью транспортира.
Физкультминутка (под музыку).
IV. Подготовка к изучению нового материала.
Вторая остановка “Сказочная”.
На прогулке Карандаш встретил разные углы. Хотел с ними поздороваться, да забыл, как зовут каждого из них. Придётся Карандашу помочь.
(Углы уч-ся проверяют с помощью модели прямого угла).
Задание командам. Прочитайте вопросы №2, обсудите.
1 команда читает 2 вопрос.
2. Найти прямой угол, дать определение.
- Угол величиной 90°называется прямым углом.

2 команда читает 2 вопрос.
2. Найти острый угол, дать определение.
- Угол меньше прямого, называется острым.
3 команда читает 2 вопрос.
2. Найти тупой угол, дать определение.
Угол больше прямого, называется тупым.
В микрорайоне, где любил гулять Карандаш, все углы отличались от других жителей тем, что гуляли всегда втроём, пили чай втроём, ходили в кино втроём. И Карандаш никак не мог понять, что за геометрическую фигуру вместе составляют три угла?
А подсказкой вам будет стихотворение.
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три!
О свойствах какой фигуры говорится?
- О треугольнике.
Какая же фигура называется треугольником?
- Треугольник — это геометрическая фигура, у которой три вершины, три угла, три стороны.
(Уч-ся показывают на чертеже треугольник,
называют вершины, углы и стороны).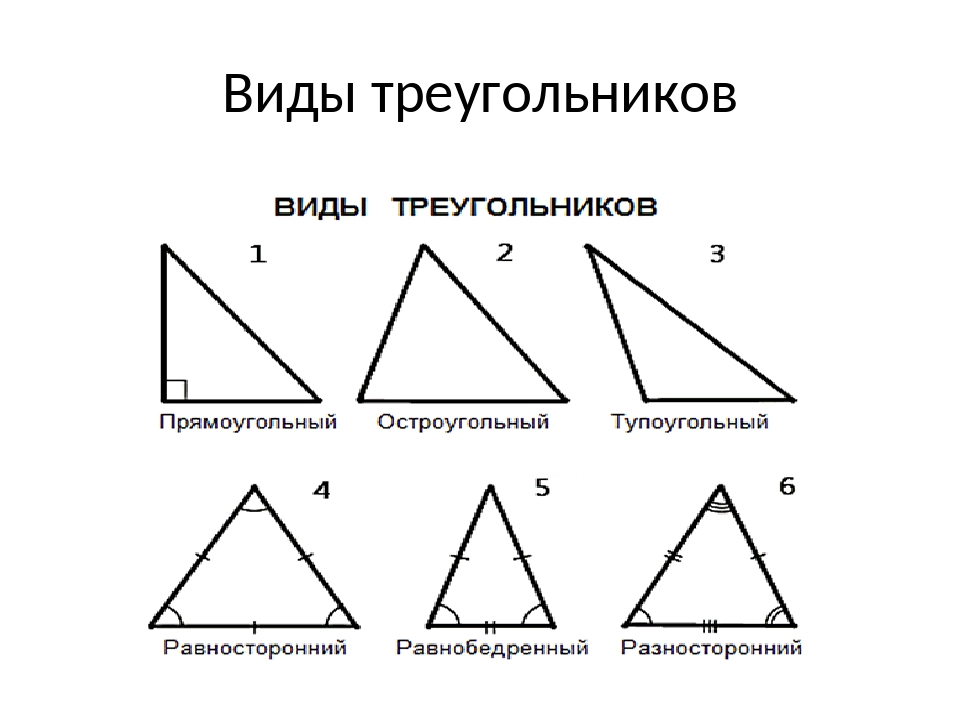
Вершины: А, В, С (точки)
Углы: ВАС, АВС, ВСА.
Стороны: АВ, ВС, СА (отрезки).
V. Физкультминутка:
8 раз ногою топнем,
9 раз руками хлопнем,
мы присядем 10 раз,
и наклонимся 6 раз,
мы подпрыгнем ровно
столько (показ треугольника)
Ай, да, счёт! Игра и только!
VI. Изучение нового материала.
Скоро углы подружились и стали неразлучны.
И теперь микрорайон мы будем так и называть: микрорайон Треугольники.
Третья остановка “Знайка”.
А как зовут эти треугольники?
Давайте дадим им имена. И попробуем сами сформулировать определение.
2. Найди треугольники разных видов
1 команда найдет и покажет тупоугольные треугольники.
2 команда найдёт и покажет прямоугольные треугольники.
3 команда найдёт и покажет остроугольные треугольники.
VIII. Следующая остановка “Соображай-ка”.
Задание всем командам.
Переложив 6 палочек, составьте из фонаря 4 равных треугольника.
Какие по виду углов получились треугольники? (Остроугольные).
IX. Итог урока.
В каком же микрорайоне мы с вами побывали?
С какими видами треугольников познакомились?
Определение вида треугольника. Треугольник
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.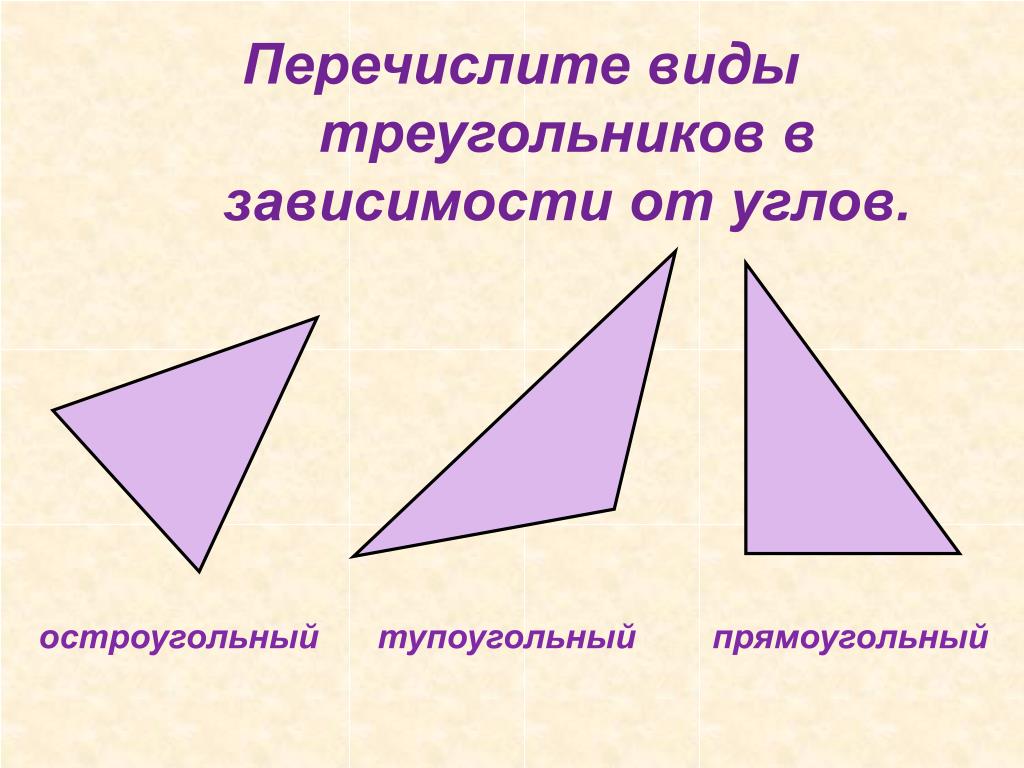
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Треугольник — определение и общие понятия
Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми.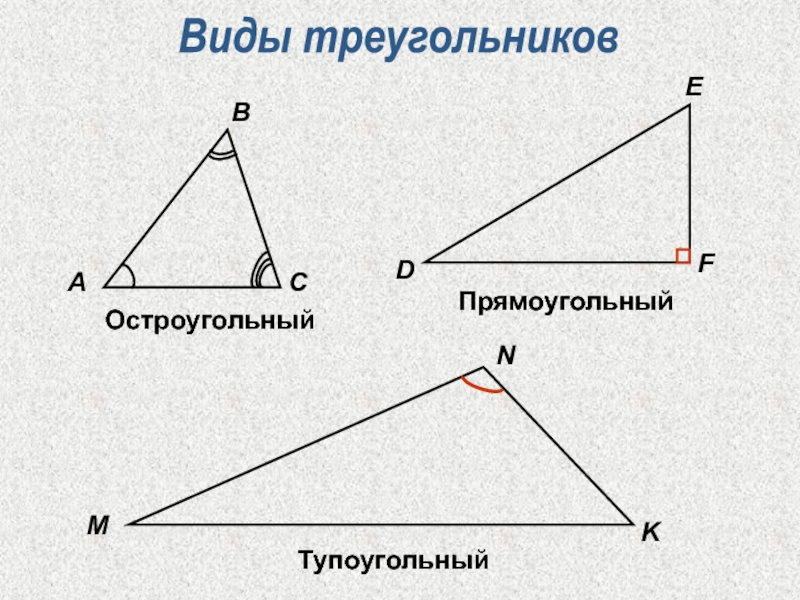 Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.
Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.
Виды треугольников
Согласно величины, углов треугольников, они делятся на такие разновидности, как:
Прямоугольные;
Остроугольные;
Тупоугольные.
К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.
Остроугольные треугольники – это те, у которых все его углы острые.
А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.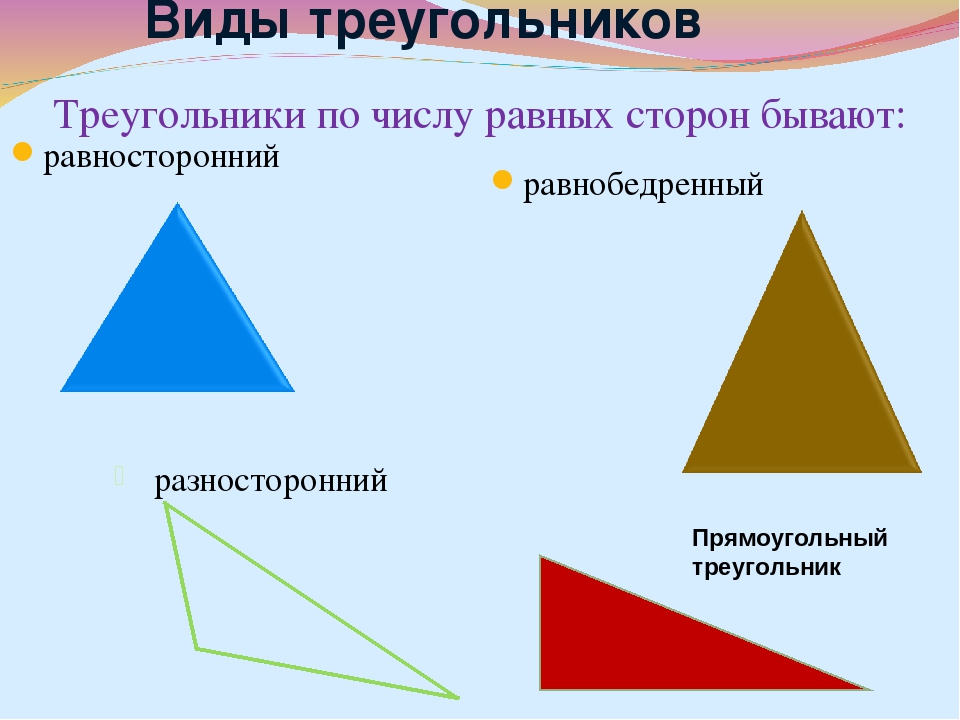
Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:
Равнобедренные;
Равносторонние;
Разносторонние.
Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?
Основные свойства треугольников
Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.
В любом треугольнике:
Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:
1. a b – c;
2. b a – c;
3. c a – b.
Задание
В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:
1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?
Признаки равности треугольников
I признак
II признак
III признак
Высота, биссектриса и медиана треугольника
Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.
Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.
Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.
Историческая справка
Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности.
Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.
В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».
Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.
Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.
А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.
Задание: А какие теории о Бермудском треугольнике слышали вы?
А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.
Домашнее задание
Решите кроссворд на заданную тему
Вопросы к кроссворду:
1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.
Вопросы к теме треугольников:
1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.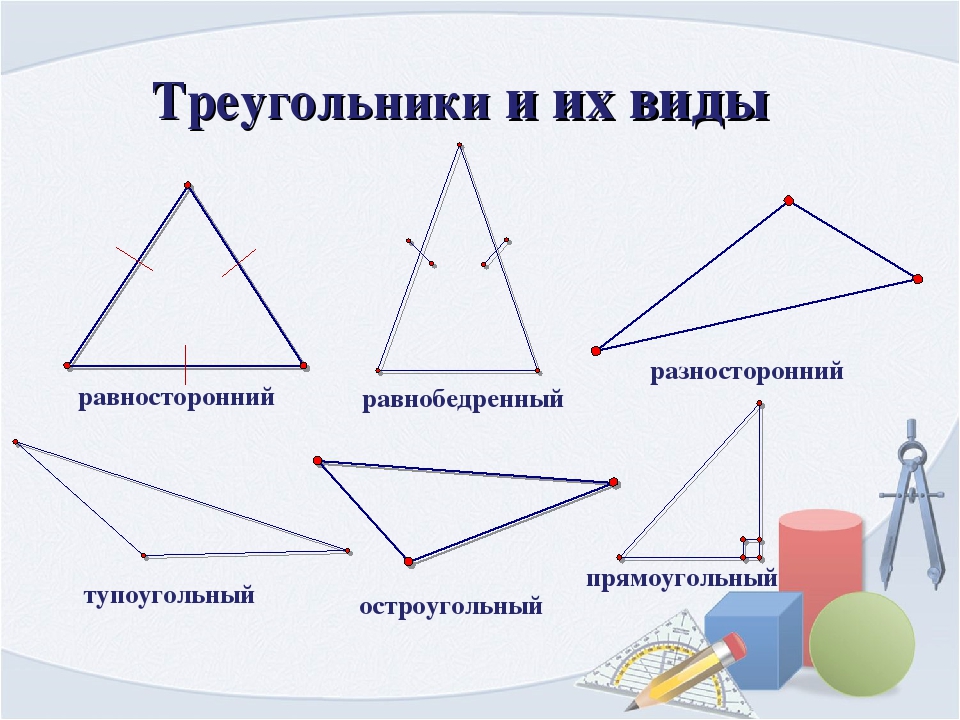
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис.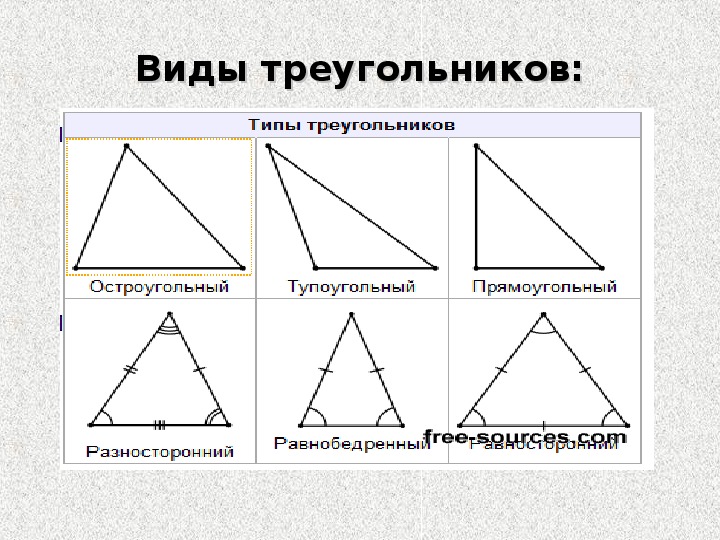 4. Остроугольный треугольник
4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис.
9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис.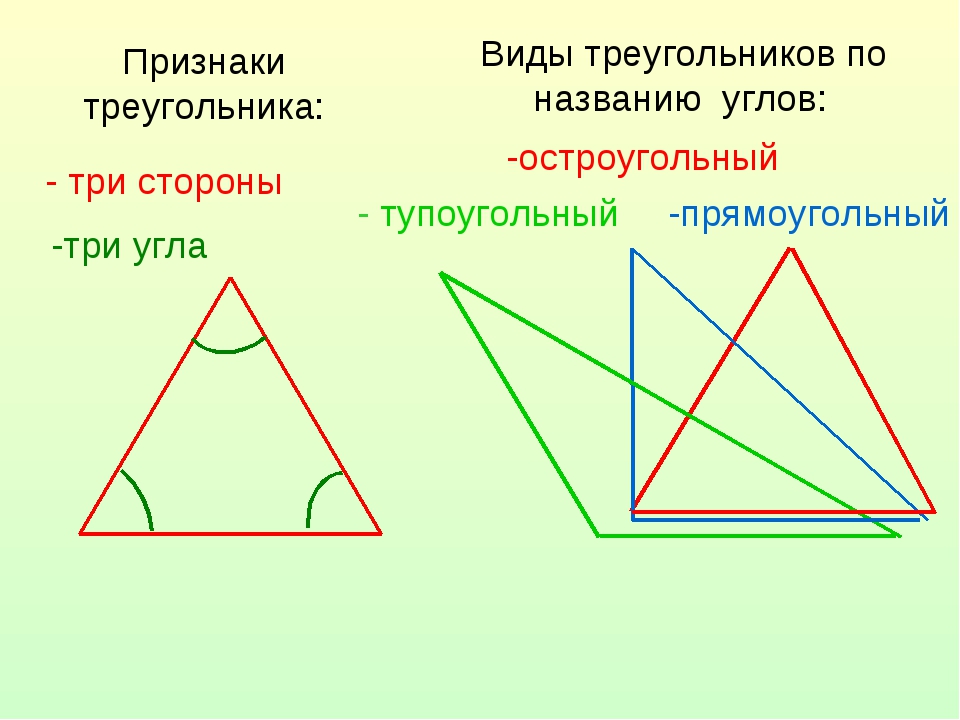 12).
12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.
 : Просвещение, 2012.
: Просвещение, 2012. - Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Треугольник (с точки зрения пространства Эвклида) – это такая геометрическая фигура, которая образована тремя отрезками, соединяющими три точки, не лежащими на одной прямой. Три точки, которые образовали треугольник, называются его вершинами, а отрезки соединяющие вершины называются сторонами треугольника. Какие есть треугольники?
Равные треугольники
Существует три признака равенства треугольников. Какие треугольники называются равными? Это те, у которых:
- равны две стороны и угол между этими сторонами;
- равна одна сторона и два прилежащие к ней угла;
- равны все три стороны.
У прямоугольных треугольников существуют следующие признаки равенства:
- по острому углу и гипотенузе;
- по острому углу и катету;
- по двум катетам;
- по гипотенузе и катету.
Какие бывают треугольники
По числу равных сторон треугольник может быть:
- Равносторонним.
 Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей.
Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей. - Неравносторонним. Треугольник, не имеющий равных сторон.
- Равнобедренным. Это треугольник с двумя равными сторонами. Две одинаковые стороны – боковые, а третья сторона – основание. В таком треугольнике совпадают биссектриса, медиана и высота, если их опустить на основание.
По величине углов треугольник может быть:
- Тупоугольным — когда один из углов имеет величину более 90 градусов, то есть когда он тупой.
- Остроугольным – если все три угла в треугольнике острые, то есть они имеют величину менее 90 градусов.
- Какой треугольник называется прямоугольным? Это такой, у которого есть один прямой угол равный 90 градусов. Катетами в нем будут назваться две стороны, которыми образован этот угол, а гипотенузой – противолежащая прямому углу сторона.
Основные свойства треугольников
- Против меньшей стороны всегда лежит меньший угол, а больший угол всегда лежит против большей стороны.

- Равные углы всегда лежат против равных сторон, а против разных сторон всегда лежат разные углы. В частности, в равностороннем треугольнике все углы имеют одинаковое значение.
- В любом треугольнике сумма углов равняется 180 градусов.
- Внешний угол можно получить, если у треугольника продолжить одну из его сторон. Величина внешнего угла будет равняться сумме не смежных с ним внутренних углов.
- Сторона треугольника больше, чем разность его двух других сторон, но меньше, чем их сумма.
В пространственной геометрии Лобачевского сумма углов треугольника будет всегда меньше, чем 180 градусов. На сфере это значение больше 180 градусов. Разность между 180 градусов и суммой углов треугольника называется дефектом.
Треугольник — это выпуклый многоугольник с наименьшим числом углов и сторон. Треугольник образуется замкнутой ломаной , состоящей из трёх звеньев, и той частью плоскости, которая находится внутри ломаной.
В тексте треугольники обозначаются символом Δ и тремя прописными латинскими буквами, стоящими при вершинах — ΔABC :
В треугольнике ABC точки A , B и C — это вершины треугольника , отрезки AB , BC и CA — стороны треугольника .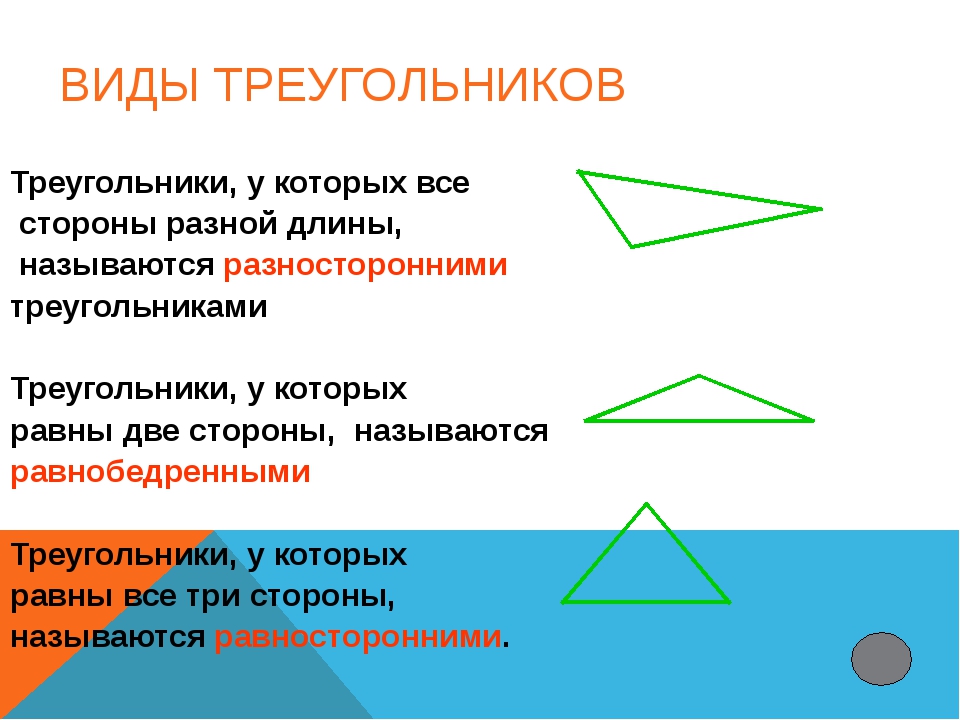 Углы, образованные сторонами треугольника, называются углами треугольника .
Углы, образованные сторонами треугольника, называются углами треугольника .
Нижнюю сторону треугольника обычно называют основанием . В треугольнике ABC сторона AC — основание.
Виды треугольников
Треугольники различаются между собой, во-первых, по характеру углов, во-вторых, по характеру сторон.
По характеру углов треугольник называется:
- Остроугольным , если все его углы являются острыми.
- Прямоугольным , если один угол прямой. В прямоугольном треугольнике стороны, образующие прямой угол, называются катетами , а сторона, лежащая напротив прямого угла — гипотенузой .
- Тупоугольным , если один из его углов тупой.
По характеру сторон треугольник называется:
- Разносторонним , если все его стороны имеют различную длину.
- Равнобедренным , если две его стороны равны между собой. Равные стороны называются боковыми сторонами , а третья сторона — основанием .
 В равнобедренных треугольниках углы при основании равны.
В равнобедренных треугольниках углы при основании равны. - Равносторонним , если все три его стороны равны между собой. В равносторонних треугольниках все три угла равны.
Равные стороны стороны на чертежах отмечаются одинаковым количеством чёрточек.
Урок математики на тему «Виды треугольников» (4 класс)
Проект урока
Школа: №124
Класс: 4в
Учитель: Ермилова С.А.
Предмет: математика по программе Моро М. И. Бантовой, Бельтюковой, по учебнику математика М. И. Моро 4класс.
Тема урока: Виды треугольников.
Тип урока: открытие нового знания.
Учебная задача: Исследовать тему «Виды треугольников»
Цели урока:
1.Образовательные:
-Познакомить детей с понятиями «остроугольный, тупоугольный, прямоугольный треугольник».
-Учащиеся узнают о разнообразии треугольников и установят зависимость между видом угла и названием треугольника.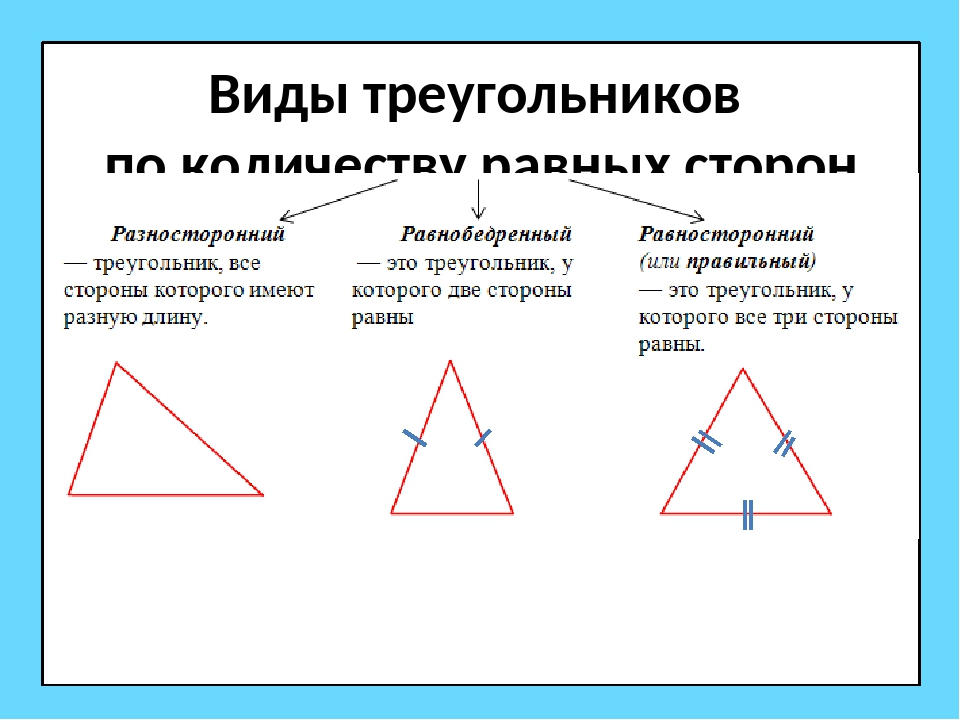
— Продолжить работу над совершенствованием навыка устного счета.
2.Развивающие:
— Развивать познавательную мотивацию учащихся с помощью исследовательских методов обучения при изучении видов треугольников.
-В ходе исследования, учащиеся должны выявить зависимость между видом угла и видом треугольника.
— Через дифференцированный подход, учащиеся определят границу своих знаний в определении вида треугольника и нахождении площади прямоугольного треугольника
3. Воспитывающие:
— Осознание детьми практического применения полученных знаний на практике.
— Формирование навыка учебного сотрудничества при работе в парах.
Оборудование:
-учебник М.И. Моро (Математика 4кл. 2часть)
-компьютер
-мультимедиа проектор
-презентация Power Point
-индивидуальные чертежные инструменты
План урока
1.Орг. момент (1мин.)
2. Устный счет (5мин.)
3. Работа над новым материалом (10мин. )
)
Создание проблемной ситуации
Постановка темы и цели урока
Поиск решения
4. Первичное закрепление (7мин.)
5. Физ.минутка (1мин.)
6. Работа над пройденным материалом (7мин.)
7. Домашнее задание (1мин.)
8. Итоги урока (2мин.)
9. Рефлексия (1мин.)
Деятельность учителя1.Орг. момент
Сегодня к нам на урок пришли гости. Повернитесь, подарите им свои улыбки, чтобы в классе стало тепло и уютно. Присаживайтесь.
Эпиграфом к уроку я взяла слова А. С. Пушкина: «Вдохновение нужно в геометрии, как в поэзии» Как Вы понимаете эти слова?
Итак, чему будет посвящен сегодняшний урок?
Первым в мире человеком, собравшим все знания по геометрии был др.греч. ученый Евклид. Он записал все свои исследования и знания, накопленные другими людьми, в 13 книгах «Началах». 1-я книга- о треугольниках; 2-ое «Начало»- о многоугольниках; 3-я- об окружностях.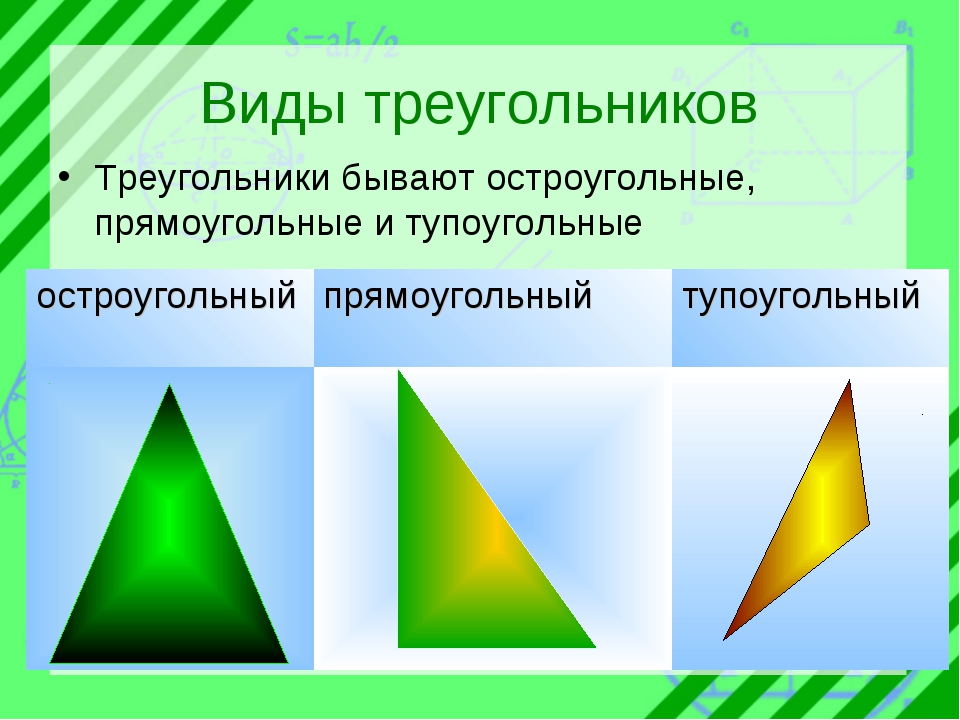 А с каким из « Начал» Евклида мы познакомимся сегодня, узнаете, выполнив задание.
А с каким из « Начал» Евклида мы познакомимся сегодня, узнаете, выполнив задание.
2. Устный счет (Слайд№2)
Найдите значение данных выражений и угадайте зашифрованное слово
Проверьте свою работу (Слайд№3)
3.Актуализация знаний. Создание проблемной ситуации.
Материал со страниц, какой книги Евклида мы будем разбирать?
Что такое треугольник?
Охарактеризуйте каждый треугольник (Слайд№4)
Какой признак положен в основу данной классификации?
А как еще можно назвать каждый из этих треугольников?
Вы хотите это узнать? А зачем вам это нужно?
Б) Постановка темы и цели урока.
Тогда сформулируйте тему урока.
Да, мы продолжим исследовать тему «Виды треугольников»
В) Поиск решения.(Слайд№5)
Чем отличаются данные треугольники?
Как же можно назвать данные треугольники?
Подумайте, посоветуйтесь друг с другом и пользуясь словами «Прямой, острый, тупой и словом угол» составьте три сложных слова, которые могли бы выразить существенный признак этих треугольников.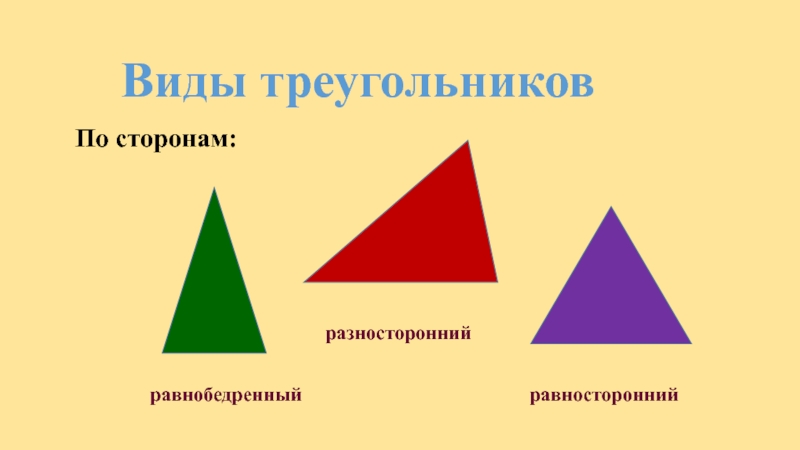
Какие слова вы составили?
Сделайте вывод, какие треугольники называются остроугольные, прямоугольные и тупоугольными.
Г) Воспроизведение нового материала.
Итак, какой вопрос у вас возник в начале урока?
Теперь вы можете на него ответить?
Сравните открытые нами знания с выводом в учебнике на стр.10.
4.Первичное закрепление.
Найдите №42. Прочитайте задание. Что нас просят сделать?
Предлагаю сначала определить вид треугольника на глаз, а затем проверить себя при помощи угольника.
Прочитайте задание №43.
Что нужно сделать?
Я предлагаю 1 ряду построить остроугольный треугольник, 2 ряду прямоугольный, а 3- тупоугольный.
Но прежде, чем строить расскажите мне план ваших действий.
Взаимопроверка.
5.Физ. минутка.
Если я показываю остроугольный треугольник, вы 3раза подпрыгиваете на месте.Прямоуг.-3раза прогибаетесь назад.Тупоугольн.-3раза наклоняетесь вперед.
6.Работа над пройденным материалом. (Слайд№6)
Прочитайте задание.
Выполните его. Проверьте. Назовите треугольники, которые у вас получились.
Предлагаю поработать с данными треугольниками самостоятельно.
Прочитайте 1 задание. Его нужно выполнить всем.
Ко 2 заданию у вас на столах есть карточки с пошаговой помощью. Старайтесь пользоваться минимальным числом подсказок или использовать их в качестве самопроверки.
3 задание дополнительное по желанию.
Проверка. (Слайд №7)
7. Домашнее задание.
Стр. 11 на полях найдите фигуру ТМКР. Посчитайте сколько треугольников в данной фигуре. Выпишите названия всех остроугольных, прямоугольных и тупоугольных треугольников. №46 стр10.
8.Итоги урока.
Итоги урока я предлагаю провести при помощи графического диктанта. Определите истинность высказывания.
1.Если в треугольнике один из углов прямой, то треугольник прямоугольный.
2.Если в треугольнике есть острый угол, то треугольник остроугольный.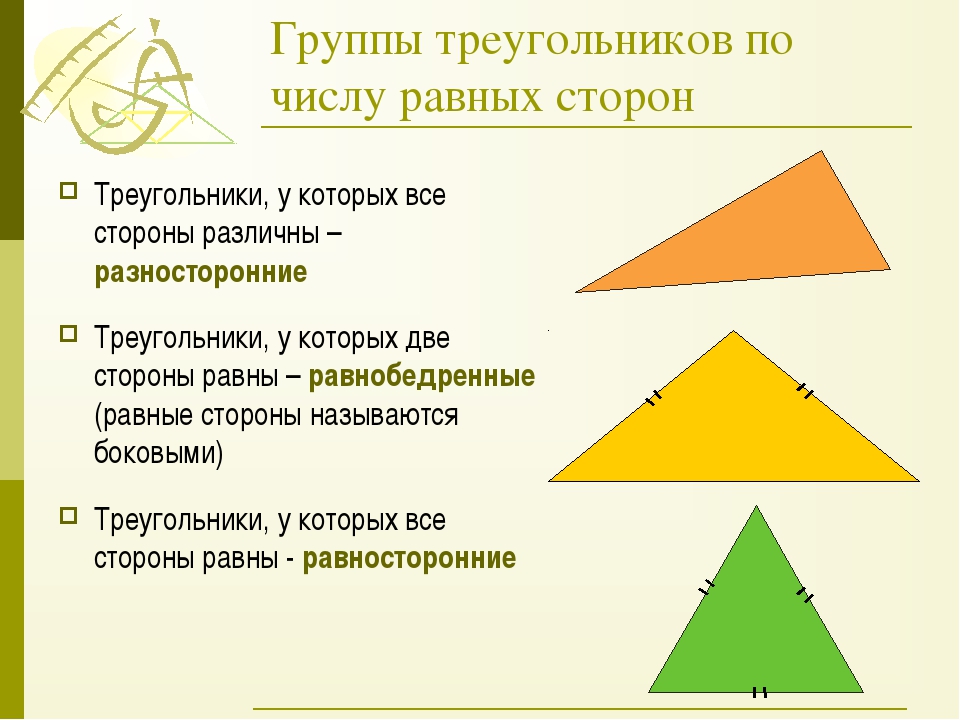
3.Не верно, что в тупоугольном треугольнике все углы тупые.
4. Если в треугольнике все углы острые, то треугольник остроугольный.
5.Если в треугольнике АВС угол В –тупой, то углы А и С будут острыми.
6.Если в прямоугольнике провести две диагонали, то они разделят прямоугольник на 4 треугольника.
Проверка.
Итак , какая учебная задача была поставлена перед нами?
Ответьте на этот вопрос.
Какой признак положен в основу данной классификации?
9.Рефлексия.
Вам понравился урок? Кто считает, что хорошо работал на уроке, поднимите зеленый треугольник; кто может работать лучше — красный. Спасибо.
Все ли вопросы, интересующие нас, мы рассмотрели?
Деятельность учащихся
Вдохновение – это творчество, нужно в геометрии, чтобы представить и изобразить фигуру, выбрать из множества решений одно.
Геометрии.
Самопроверка
Материал со страниц 1-ой книги о треугольниках.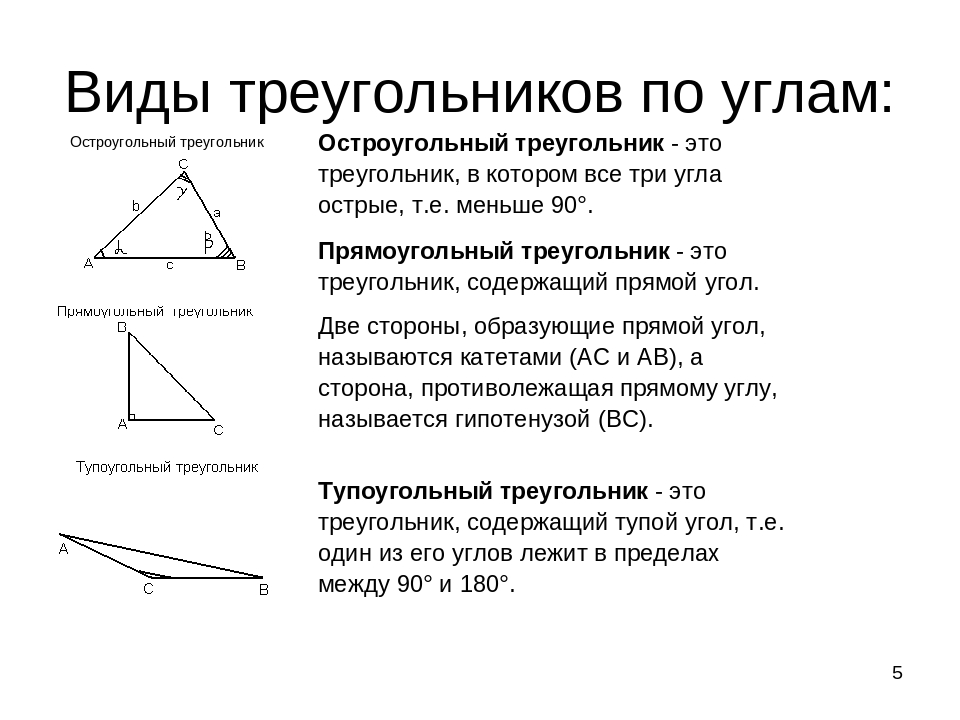
Геометрическая фигура, состоящая из 3 вершин, 3 углов, 3 сторон.
1.-разносторонний, т.к. все стороны разной длины
2- равносторонний, т.к. все стороны одинаковой длины
3- равнобедренный, т.к. две стороны равны
Длины сторон.
Не знаем
Да! Интересно, пригодится в дальнейшем при изучении геометрии.
Виды треугольников.
1- Один угол прямой, а остальные острые.
2- Все углы острые.
3- Один угол тупой, а остальные острые.
Видами углов
Прямоугольный, остроугольный, тупоугольный.
Остроуг. –это треугольник у которого все углы острые и т.д.
Какие бывают треугольники?
Да, остроугольные, прямоугольные и тупоугольные.
Один ребенок читает вслух. Дети повторяют задание.
Характеризуют треугольники.
Дети читают (один вслух)
Построить треугольники.
1.Поставить точку и обозначить ее буквой.
2. Из этой точки провести два отрезка, чтобы они образовали прямой, острый или тупой угол. Обозначить концы отрезков буквами.
Обозначить концы отрезков буквами.
3. Соединить полученные точки.
Построить прямоугольник.
Истинное высказывание.
Ложное высказывание.
Истинное
Истинное
Истинное
Ложное
Исследовать какие бывают треугольники.
Мы знали, что треугольники бывают разносторонние, равносторонние и равнобедренные.
Мы узнали, что треугольники еще бывают остроугольные, прямоугольные и тупоугольные.
Вид угла
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о сумме углов треугольника:
Сумма углов треугольника равна 180 градусов.
Из теоремы следует, что если в треугольнике один из углов является прямым или тупым, то сумма двух других углов данного треугольника не больше 90 градусов, а следовательно, каждый из них острый.
По
величине углов выделяют следующие виды треугольников.
Определение:
Остроугольный треугольник — это треугольник, у которого все три угла острые.
Определение:
Тупоугольный треугольник — это треугольник, у которого один из углов тупой.
Определение:
Прямоугольный треугольник — это треугольник, у которого один из его углов является прямым.
Нужно знать, что стороны прямоугольного треугольника имеют специальные названия.
Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Если взять прямоугольный лист бумаги и разрезать его, получим:
Получим две модели прямоугольного треугольника.
Пример.
Доказать, что угол с вершиной на окружности, опирающийся на диаметр, — прямой.
Для начала соединим точку В
с точкой О, которая является центром нашей окружности. Так как отрезки ОА, ОВ и
ОС равны как радиусы окружности, то треугольники АОВ и ВОС являются
равнобедренными. А значит, у них углы при основаниях равны. Обозначим градусные
меры этих углов m и n. Тогда ∠АОВ=2n, так как он является внешним углом треугольника
ВОС, смежным с ∠ВОС. А нам известно, что внешний угол
треугольника равен сумме двух внутренних, не смежных с ним.
Так как отрезки ОА, ОВ и
ОС равны как радиусы окружности, то треугольники АОВ и ВОС являются
равнобедренными. А значит, у них углы при основаниях равны. Обозначим градусные
меры этих углов m и n. Тогда ∠АОВ=2n, так как он является внешним углом треугольника
ВОС, смежным с ∠ВОС. А нам известно, что внешний угол
треугольника равен сумме двух внутренних, не смежных с ним.
А так как сумма углов треугольника равна 180 градусов, то:
Что и требовалось доказать.
Пример.
Доказать, что если в равнобедренном треугольнике АВС один из углов равен 60 градусов, то он равносторонний.
Если ∠А при основании равнобедренного треугольника АВС равен 60 градусов, то и второй ∠С при основании равен 60 градусам. Получаем:
Следовательно, треугольник АВС равносторонний.
Пусть ∠В при вершине равнобедренного треугольника АВС равен 60 градусам. Тогда получим:
А так как углы А и С-
углы при основании равнобедренного треугольника, то они равны между собой и
равны 60 градусам. А следовательно, и в этом случае
треугольник АВС является равносторонним. Что и требовалось доказать.
А следовательно, и в этом случае
треугольник АВС является равносторонним. Что и требовалось доказать.
Пример.
Доказать, что в прямоугольном треугольнике АВС медиана, проведённая к гипотенузе АВ, равна половине гипотенузы.
Отложив ∠2=∠1, получаем:
Треугольник ADC является равнобедренным. А следовательно, отрезок DA=DC.
Так как по условию угол АВС — прямой, то:
Известно, что сумма острых углов прямоугольного треугольника равна 90 градусов, то есть:
Тогда из равенств получаем:
Из этого следует, что ВСD равнобедренный треугольник, у которого стороны DB и DC равны.
Следовательно, СD - медиана и СD равняется половине гипотенузы АВ. Что и требовалось доказать.
Треугольники / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Треугольники
Треугольник — это ломаная линия, которая состоит из трёх звеньев-отрезков.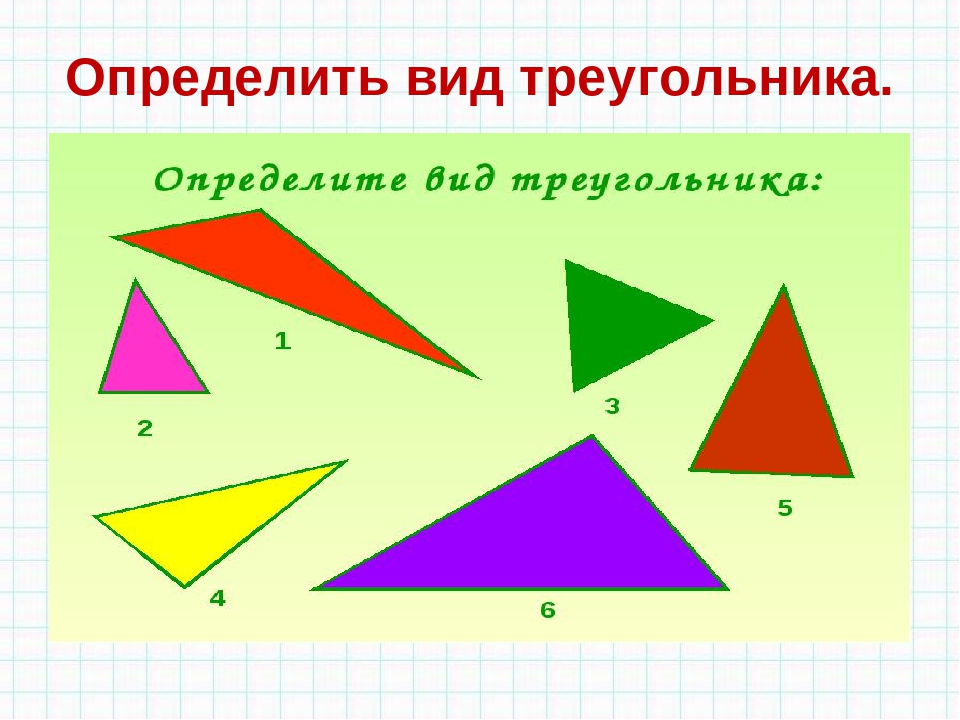
У треугольника три стороны.
У треугольника три вершины.
Бывают треугольники, у которых все стороны равны. Они называются равносторонними.
Бывают треугольники, у которых две стороны равны. Они называются равнобедренными.
Равносторонний треугольник тоже можно отнести к равнобедренным.
А это прямоугольный треугольник.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Круг. Шар. Овал
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
1 класс
Страница 101, Моро, Волкова, Степанова, Учебник, часть 1
Страница 5, Моро, Волкова, Степанова, Учебник, часть 2
Страница 3.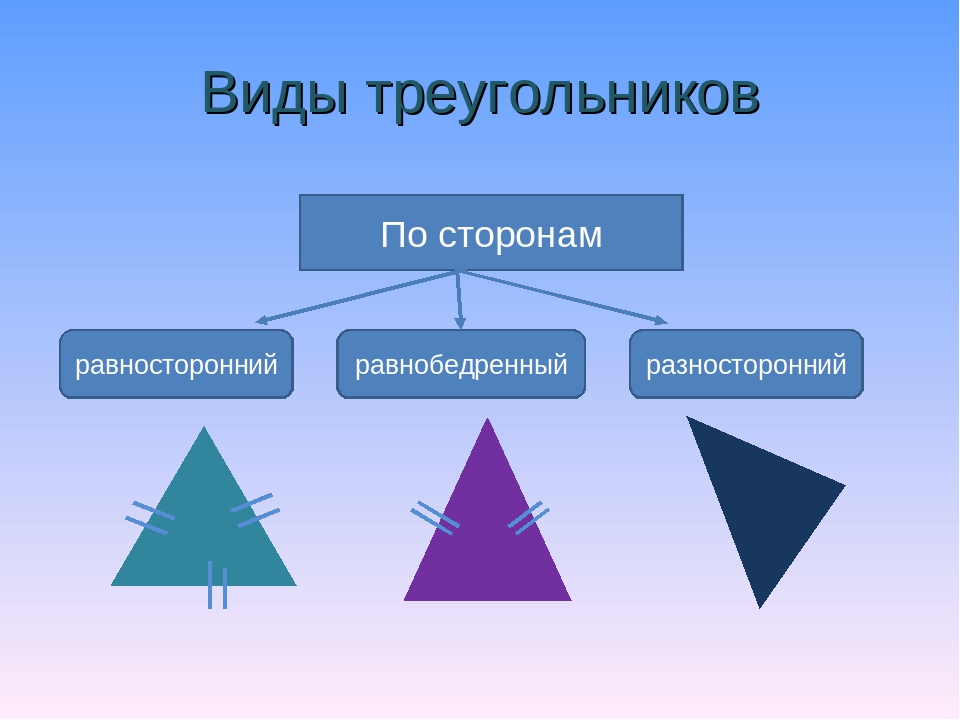 Урок 2,
Петерсон, Учебник, часть 1
Урок 2,
Петерсон, Учебник, часть 1
Страница 7. Урок 4, Петерсон, Учебник, часть 1
Страница 18. Урок 11, Петерсон, Учебник, часть 1
Страница 47. Урок 29, Петерсон, Учебник, часть 1
Страница 3. Урок 2, Петерсон, Учебник, часть 2
Страница 30. Урок 16, Петерсон, Учебник, часть 3
Страница 47. Урок 24, Петерсон, Учебник, часть 3
Страница 71. Урок 36, Петерсон, Учебник, часть 3
2 класс
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 37, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57. Урок 29,
Петерсон, Учебник, часть 1
Урок 29,
Петерсон, Учебник, часть 1
Страница 63. Урок 32, Петерсон, Учебник, часть 1
Страница 83. Урок 34, Петерсон, Учебник, часть 2
Страница 16. Урок 5, Петерсон, Учебник, часть 3
Страница 25. Урок 9, Петерсон, Учебник, часть 3
Страница 63. Урок 23, Петерсон, Учебник, часть 3
3 класс
Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 8. Урок 2,
Петерсон, Учебник, часть 1
Урок 2,
Петерсон, Учебник, часть 1
Страница 25. Урок 8, Петерсон, Учебник, часть 1
4 класс
Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 57. Вариант 2. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
© budu5.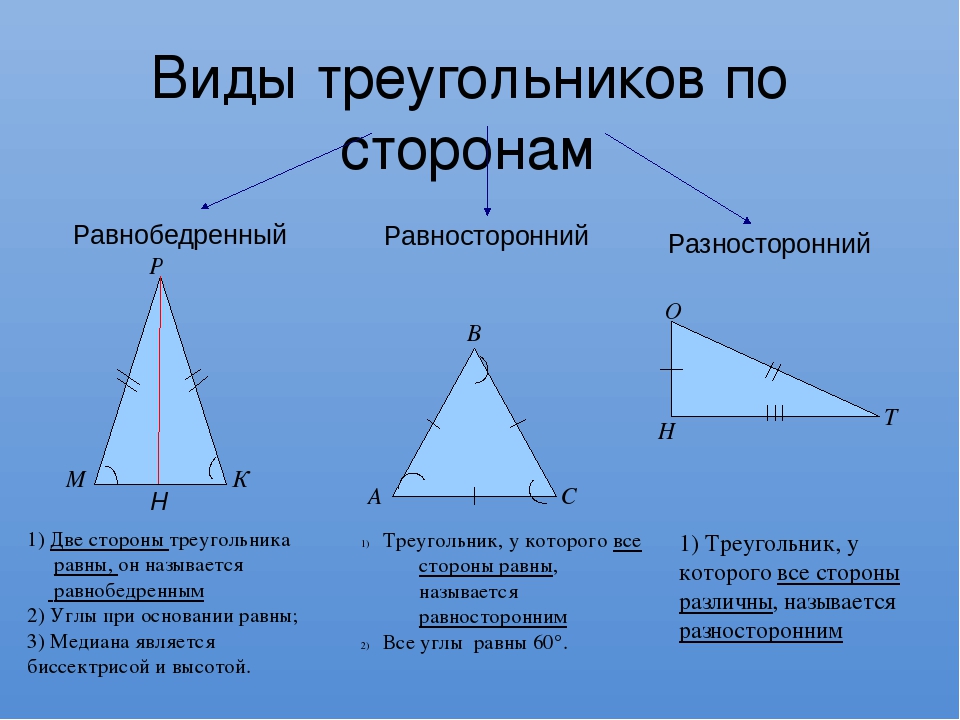 com, 2022
com, 2022
Пользовательское соглашение
Copyright
Свойства треугольников, формулы и примеры
Все свойства треугольников
В любом треугольнике три угла и три стороны.
Сумма углов любого треугольника равна .
Против большего угла треугольника лежит большая сторона.
Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).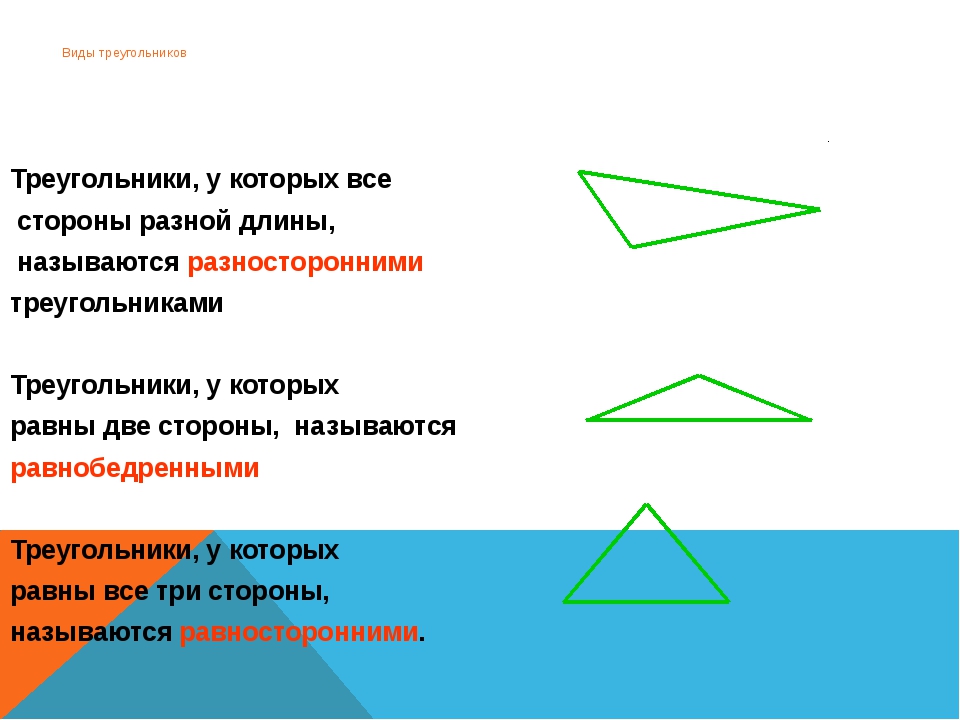
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
I признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Треугольники называются подобными, если их стороны пропорциональны.
Признаки подобия треугольников
- Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Подробнее про теорему косинусов по ссылке.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности (обобщенная теорема синусов):
Подробнее про теорему синусов по ссылке.
Площадь треугольника можно вычислить по формулам
1. Через высоту и основание
2. По двум сторонам и углу между ними
3. По формуле Герона
где – полупериметр треугольника
4. Через радиусы вписанной и описанной окружностей
где – полупериметр треугольника, – радиус вписанной окружности;
– радиус описанной окружности.
Примеры решения задач
Треугольники — Формула, Свойства, Определение, Примеры
Треугольник — это замкнутая фигура с 3 углами, 3 сторонами и 3 вершинами. Треугольник с тремя вершинами говорит P, Q и R представлен как △PQR. Его также называют трехсторонним многоугольником или треугольником. В этом мини-уроке мы изучим все о треугольниках, которые часто встречаются вокруг нас. Если вы обратите внимание на форму вывесок и ваших любимых бутербродов, она образует форму треугольника.
Части треугольника
Треугольник состоит из различных частей.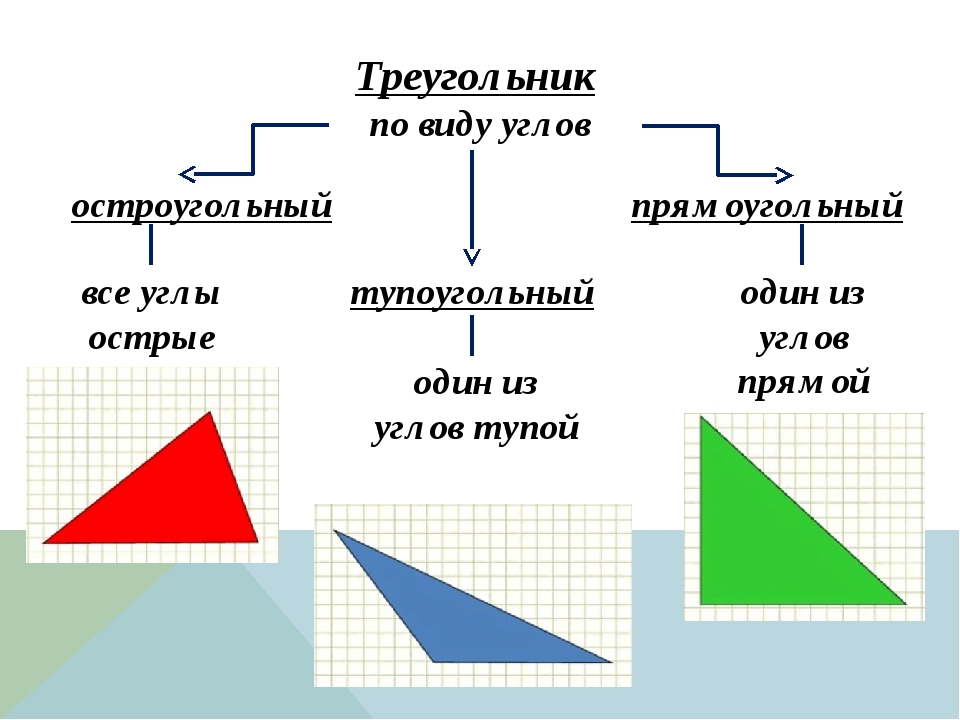 У него 3 угла, 3 стороны, 3 вершины. Давайте изучим концепцию с помощью фигуры треугольника, приведенной ниже. Посмотрите на треугольник PQR.
У него 3 угла, 3 стороны, 3 вершины. Давайте изучим концепцию с помощью фигуры треугольника, приведенной ниже. Посмотрите на треугольник PQR.
На изображении выше:
- Три угла: ∠PQR, ∠QRP и ∠RPQ.
- Три стороны: сторона PQ, сторона QR и сторона RP.
- Три вершины: P, Q и R
Классификация треугольника
В соответствии с двумя основными элементами треугольники можно классифицировать как:
- На основе уголков
- На основании измерения их сторон.
Давайте разберемся в классификации треугольников с помощью таблицы, приведенной ниже. Таблица дает информацию о разнице между 6 различными типами треугольников на основе углов и сторон.
Примечание: Сумма всех углов треугольника равна 180°.
Свойства треугольника
Каждая геометрическая фигура имеет фиксированные свойства для определения соотношения между разными сторонами и углами. В этом разделе мы изучим важные свойства треугольника, перечисленные ниже.
В этом разделе мы изучим важные свойства треугольника, перечисленные ниже.
- Треугольник имеет три стороны, вершины и углы.
- Свойство суммы углов треугольника гласит, что сумма трех внутренних углов треугольника всегда равна 180°. Например, в любом заданном треугольнике PQR угол P + угол Q + угол R = 180°.
- Свойство неравенства треугольника утверждает, что сумма длин двух сторон треугольника больше, чем длина третьей стороны.
- Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон, то есть (Гипотенуза² = Основание² + Высота²).
- Сторона, противоположная большему углу, является самой длинной стороной.
- Свойство внешнего угла треугольника гласит, что внешний угол треугольника всегда равен сумме внутренних противоположных углов.
Формулы треугольника
В геометрии для каждой двумерной формы всегда есть два основных измерения, которые нам нужно выяснить, т.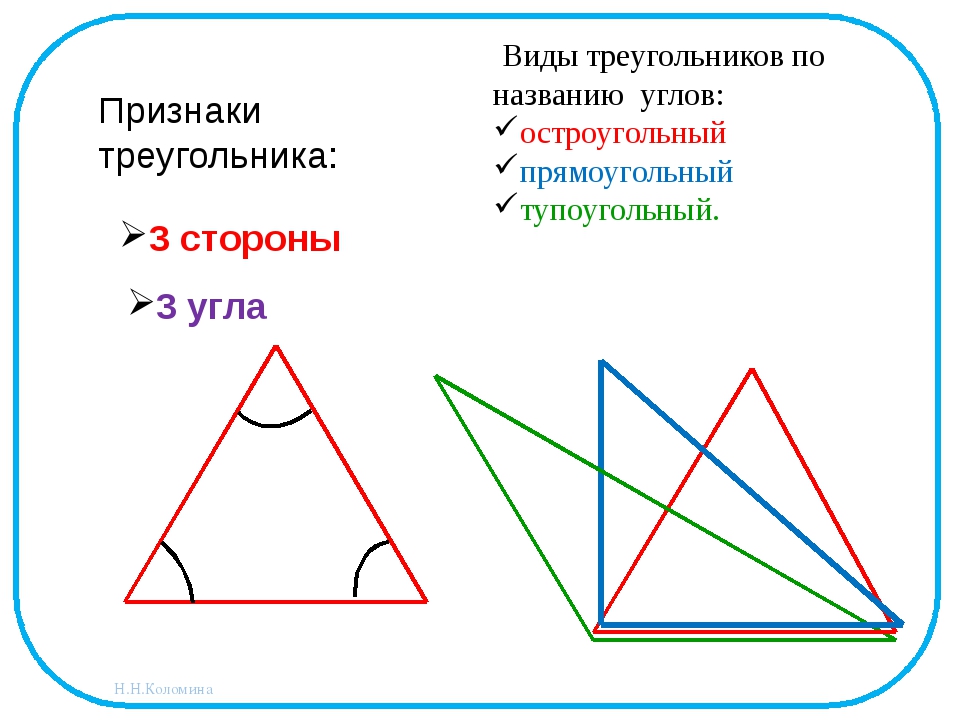 е.е., площадь и периметр этой фигуры. Точно так же треугольник имеет две основные формулы, которые помогают нам определить его площадь и периметр. Рассмотрим формулы подробнее.
е.е., площадь и периметр этой фигуры. Точно так же треугольник имеет две основные формулы, которые помогают нам определить его площадь и периметр. Рассмотрим формулы подробнее.
Периметр треугольника
Периметр треугольника равен сумме всех трех сторон треугольника. Рассмотрим △ABC.
На приведенном выше рисунке три стороны треугольника представлены как AB= c, AC = b и CB = a соответственно.
Периметр треугольника равен сумме всех трех сторон АВ + ВС + СА.
Формула периметра треугольника = a + b + c единиц
Половина периметра треугольника называется полупериметром треугольника. Он дается как (a + b + c)/2 единиц.
Площадь треугольника
Площадь треугольника — это пространство, занимаемое треугольником. Это половина произведения его основания и высоты (высоты). Он всегда измеряется в квадратных единицах, так как является двумерным. Посмотрите на данный треугольник ABC.
Площадь ΔABC = 1/2 × AD × BC квадратных единиц.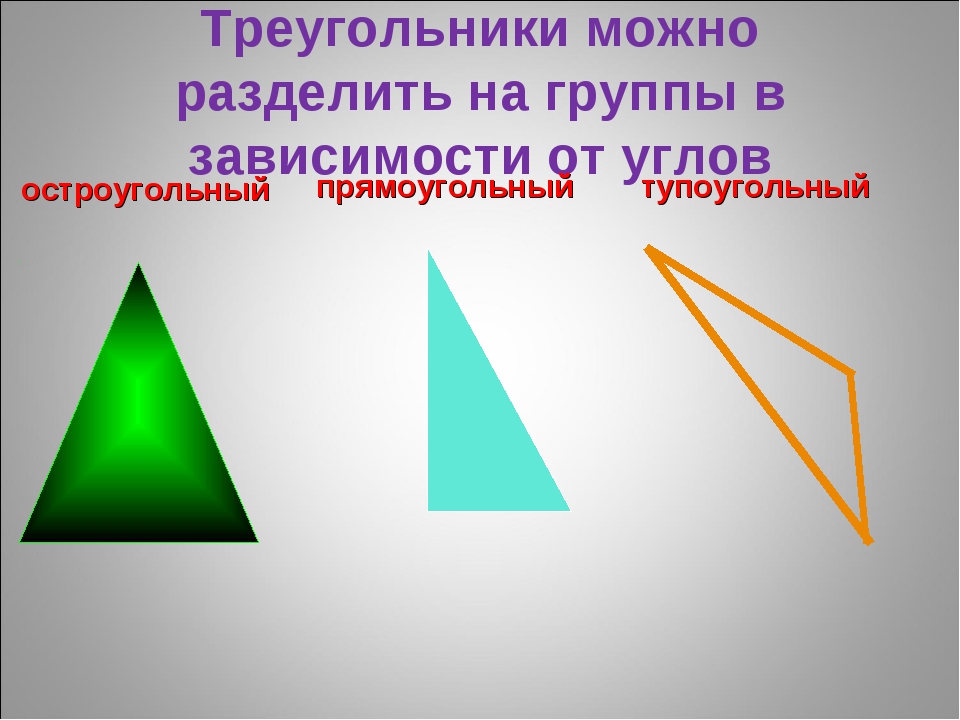
Здесь ВС — основание, а AD — высота треугольника.
Важные примечания о треугольнике
- Треугольник не может иметь измерение или значение всех углов меньше 60°.
- Треугольник — это трехсторонняя замкнутая фигура.
- Существуют две важные формулы, относящиеся к треугольникам, т. е. формула Герона и теорема Пифагора.
- Сумма углов треугольника составляет 180° и определяется как ∠1 + ∠2 + ∠3 = 180°.
☛Похожие статьи о треугольниках
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о треугольниках и темах, связанных с треугольниками.
Часто задаваемые вопросы о Triangle
Что такое треугольник в геометрии?
В геометрии треугольник определяется как двумерная фигура с тремя сторонами, углами и вершинами. Он также считается многоугольником (треугольником).
Каковы две основные формулы треугольника?
Две основные формулы треугольника — это площадь треугольника и периметр треугольника.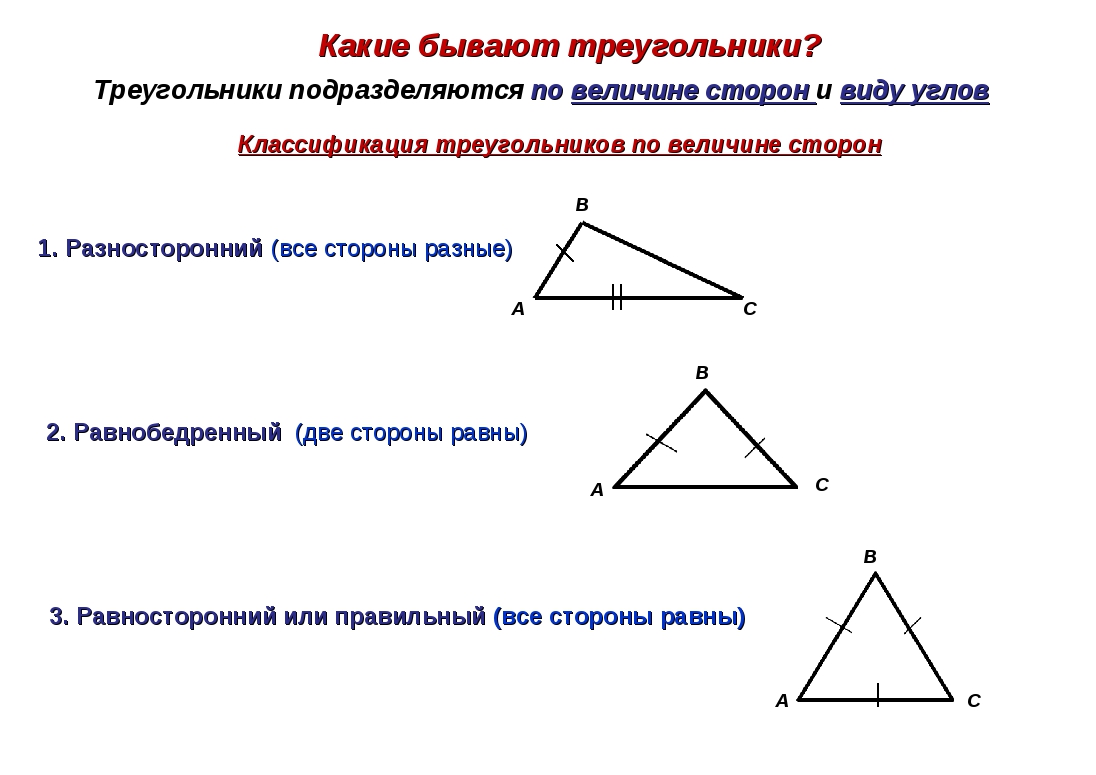 Эти формулы треугольника могут быть математически выражены как;
Эти формулы треугольника могут быть математически выражены как;
Сколько типов треугольников существует в математике?
В основном существует шесть типов треугольников, классифицированных на основе сторон и углов, перечисленных ниже:
Всегда ли равнобедренные треугольники острые?
Нет, равнобедренный треугольник может быть остроугольным, прямоугольным или тупоугольным в зависимости от величины углов, которые он имеет.
Какова площадь разностороннего треугольника?
Площадь разностороннего треугольника используется для нахождения площади, занимаемой разносторонним треугольником внутри его сторон.Площадь разностороннего треугольника равна половине произведения основания на высоту разностороннего треугольника. Таким образом, площадь разностороннего треугольника с основанием «b» и высотой «h» определяется как «1/2 × b × h».
Какая формула используется для нахождения площади прямоугольного треугольника?
Формула, используемая для нахождения площади прямоугольного треугольника с основанием (b) и высотой (h): 1/2 × основание × высота (или) 1/2 × b × h.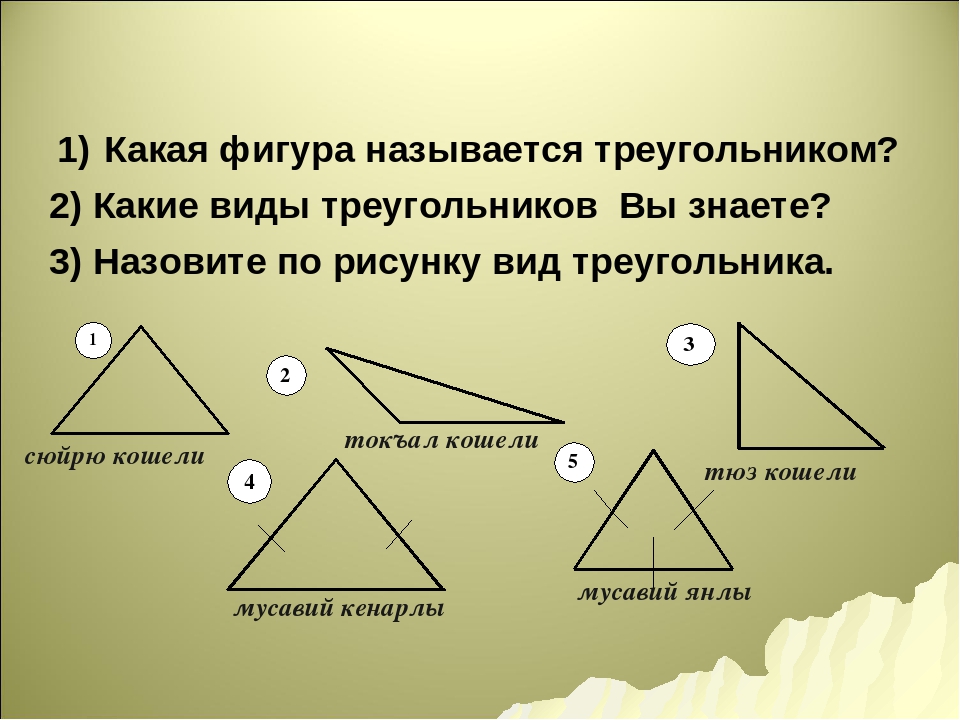
Что такое равносторонний треугольник?
Равносторонний треугольник – это правильный многоугольник (треугольник) с тремя равными сторонами.Равносторонние треугольники также имеют три равных угла, каждый из которых равен 60 градусов и в сумме составляет 180 градусов.
Что такое равнобедренный треугольник?
В треугольнике, если длины только двух сторон равны и мера соответствующих противоположных углов также равна, то треугольник называется равнобедренным.
Чем полезны таблицы треугольников?
Рабочие листыTriangle дают учащимся понимание понятий, основанных на треугольниках. Эти рабочие листы могут включать типы треугольников, классификацию треугольников, отсутствующие углы, свойства треугольников, площадь и периметр треугольников и так далее.
☛Также проверьте:
Что такое прямоугольный треугольник в геометрии?
Прямоугольный треугольник — это треугольник, один из углов которого равен 90 градусов (прямой угол). В геометрии у нас есть три разных имени для всех трех сторон прямоугольного треугольника, которые перечислены ниже:
В геометрии у нас есть три разных имени для всех трех сторон прямоугольного треугольника, которые перечислены ниже:
- Гипотенуза (самая длинная сторона или сторона, противоположная углу 90°)
- Основание
- Перпендикуляр (высота).
Типы треугольников – объяснение и примеры
В геометрии треугольник является наиболее важной формой , определяемой как замкнутая двумерная диаграмма, содержащая 3 стороны, 3 угла и 3 вершины.Проще говоря, треугольник — это многоугольник с 3 сторонами. Слово «треугольник» происходит от латинского слова «triangulus», что означает «треугольный».
В древние времена астрономы разработали метод триангуляции для определения расстояний до далеких звезд. Они измеряют расстояние от двух разных мест, затем измеряют угол, создаваемый смещением или параллаксом, образованным движением наблюдателя между двумя местами. Затем применяли закон синусов для расчета необходимого расстояния.
Египтяне построили пирамиды около 2900 г.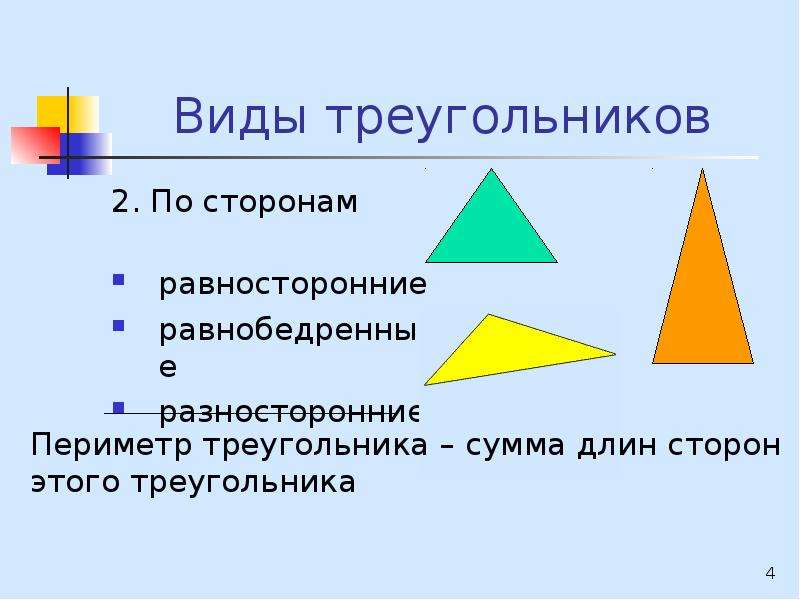 до н.э. Его форма на самом деле представляет собой трехмерную пирамиду с треугольными гранями. Это идеально спроектированная модель, длина и углы которой со всех сторон одинаковы. Милет (624 г. до н.э. – 547 г. до н.э.), греческий математик, перенял египетскую геометрию и был привезен в Грецию.
до н.э. Его форма на самом деле представляет собой трехмерную пирамиду с треугольными гранями. Это идеально спроектированная модель, длина и углы которой со всех сторон одинаковы. Милет (624 г. до н.э. – 547 г. до н.э.), греческий математик, перенял египетскую геометрию и был привезен в Грецию.
Аристарх (310 г. до н.э. – 250 г. до н.э.), греческий математик, использовал описанный выше метод для определения расстояния между Землей и Луной. Эратосфен (276 г. до н.э. — 195 г. до н.э.) снова использовал тот же метод для определения расстояния вокруг поверхности Земли (называемого окружностью).
В этой статье будет обсуждено значение треугольника , различных типов треугольников и их свойства, а также их практическое применение.
Что такое треугольник?
Треугольник — двумерная замкнутая фигура с 3 сторонами. Это многоугольник с тремя углами, тремя вершинами и тремя углами, соединенными вместе, который образует замкнутую диаграмму. Мы используем символ ∆ для обозначения треугольника.
Мы используем символ ∆ для обозначения треугольника.
Фигуры A и B представляют собой треугольники.
Различные типы треугольников
Типы треугольников.
- Остроугольные
- Тупоугольные
- Прямоугольные
Остроугольные
Остроугольные треугольники внутренние углы меньше 90 градусов.
Каждый из углов a, b и c меньше 90 градусов.
Тупоугольный треугольник
Тупоугольный треугольник — это треугольник, в котором один из внутренних углов больше 90 градусов.
Угол a более тупой, а углы b и c острые.
Прямоугольный треугольник
Прямоугольный треугольник — это треугольник, в котором один из углов равен ровно 90 градусам. Гипотенуза – это сторона прямоугольного треугольника с наибольшей длиной.
На приведенном выше рисунке угол a = 90 градусов, а углы b и c являются острыми углами.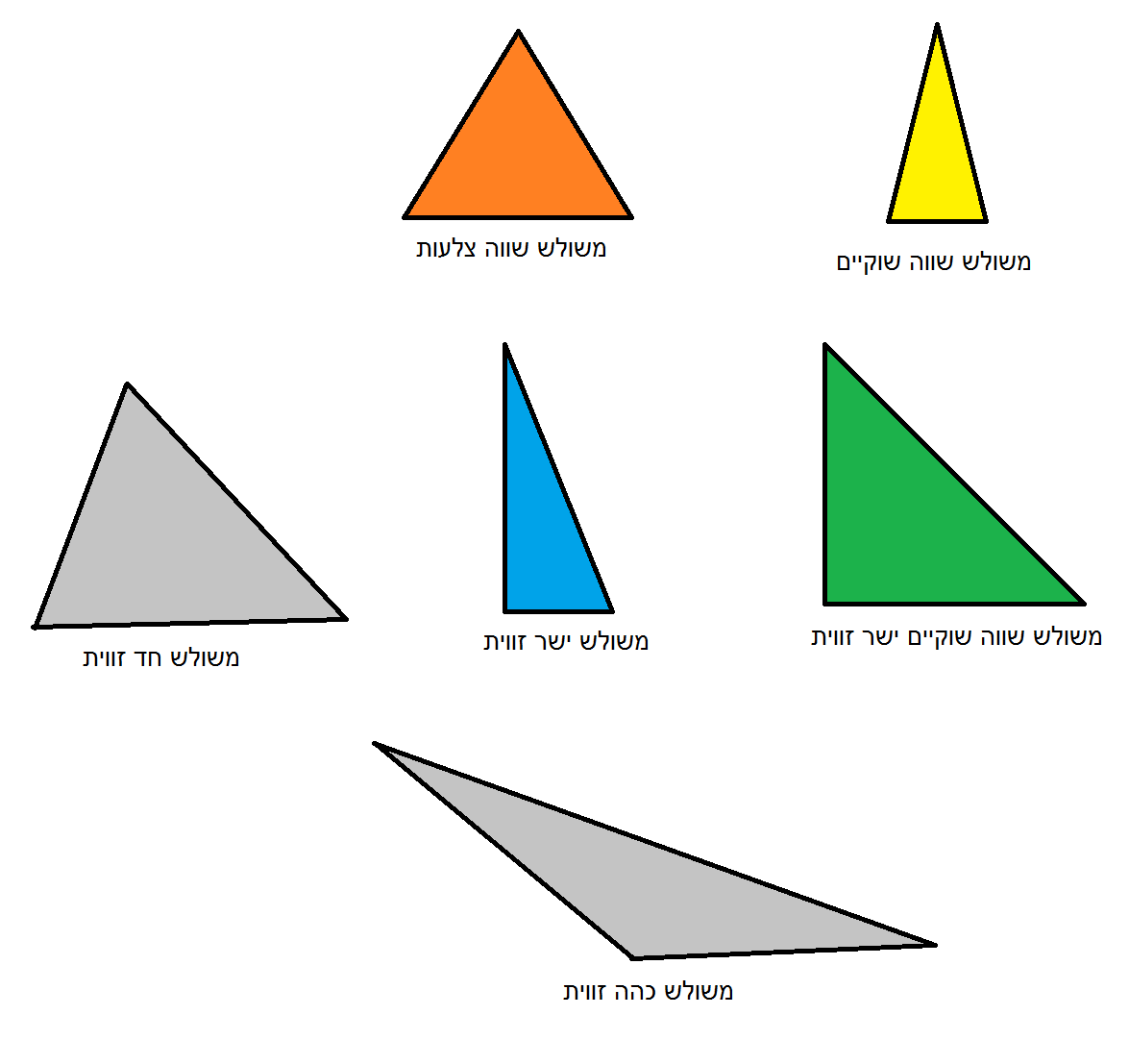
Классификация треугольников по длинам их сторон
Мы можем классифицировать треугольники на 3 типа в зависимости от длин их сторон:
- Разносторонний
- Равнобедренный
- Равносторонний Равнобедренный 3
- Треугольник представляет собой двумерный многоугольник
- Треугольник имеет 3 стороны, 3 угла и 3 вершины.
- Сумма длин любых двух сторон треугольника больше, чем длина оставшейся стороны.
- Сумма длин трех сторон дает периметр треугольника.
- Площадь треугольника равна произведению основания на высоту.
- Дорожные знаки.
 Большинство дорожных знаков отображаются на треугольных конструкциях.
Большинство дорожных знаков отображаются на треугольных конструкциях. - Пирамиды Египта: Пирамиды — древние памятники, построенные египтянами. Пирамиды имеют треугольную форму.
- Ферма: Фермы крыш или мостов изготавливаются треугольной формы, потому что треугольник считается самой прочной формой.
- Бермудский треугольник: Бермудский треугольник представляет собой треугольную область в Атлантическом океане, где считается, что любое судно или самолет, проходящие в этой точке, проглатываются. Считается, что в Бермудском треугольнике таинственным образом исчезли 50 кораблей и 20 самолетов.
- Глобальная система позиционирования (GPS) использует алгоритмы триангуляции для определения долготы и широты объекта.
- Лестница, прислоненная к стене, имеет форму треугольника.
- Эйфелева башня имеет треугольную форму.
- Концепция треугольников вычисляет высоту или высоту высоких объектов, таких как флагштоки, горы, здания и т. д.
- Бутерброды и кусочки пиццы имеют треугольную форму.

Разносторонний треугольник — длины всех сторон различны или не равны.
Равнобедренный треугольник. Свойства равнобедренного треугольника включают треугольник, у которого две стороны равны по длине, а третья не равна.
Равносторонний треугольник. Свойства равностороннего треугольника связаны с треугольником, у которого все три стороны равны по длине.
Остроугольный треугольник – углы треугольника меньше 90°
Тупоугольный треугольник – один угол треугольника больше 90°
Прямоугольный треугольник – один угол треугольника равен 90°
Наличие трех сторон, трех углов и трех вершин.
Все внутренние углы равны 180°.
Третья сторона треугольника меньше суммы двух других сторон.
Полупроизведение основания и высоты дает площадь треугольника.
Сумма всех трех сторон треугольника дает его периметр.
Треугольник имеет 3 медианы, по одной из каждой вершины.
Все медианы сходятся в одной точке.

Центроид треугольника — это точка, где встречаются 3 медианы.
Медиана треугольника делит его на два меньших треугольника.
RHS (прямой угол-гипотенуза-сторона)
- 15 минут веселья в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
0 Равнобедренный треугольник треугольник, у которого две стороны и два угла равны. Равные длины треугольника изображаются дугой с каждой стороны.
На диаграмме выше , длина стороны AB = AC и ∠ ABC =∠ ACB.
Равносторонний треугольник
У равностороннего треугольника все три стороны равны, а также все три внутренних угла равны. В этом случае каждый внутренний угол равностороннего треугольника равен 60 градусам. Равносторонний треугольник иногда называют равноугольным треугольником, потому что все три угла равны.
в равностороннем треугольнике, сторонам ab = до н.э. = AC и ∠ ABC = ∠ ABC = ∠ ACB = ∠ BAC
Обратите внимание, что углы равностороннего треугольника не зависят на длинах сторон.
Разносторонний треугольник
Разносторонний треугольник — это треугольник, в котором все стороны имеют разную меру и все внутренние углы также различны.
Свойства треугольника
Свойства треугольников имеют широкое применение. Многие математики использовали его при решении своих задач. Евклидова геометрия и тригонометрия широко используют свойства треугольников.
Вот несколько основных свойств треугольника:
Примеры работы с различными типами треугольников
Пример 1
Найдите значение угла x в треугольнике ниже.
Решение
Это равнобедренный треугольник, у которого две стороны равны, а также два угла равны.Следовательно,
x = (180° – 70°)/2
x = 110°/2
= 55°
Пример 2
Найдите угол y в прямоугольном треугольнике, показанном ниже.
Решение
Один угол прямоугольного треугольника равен 90°. Итак, мы;
y + 50 + 90 = 180
y = (180 – 140) °
y = 40°
Решение
Это разносторонний треугольник, потому что все стороны и углы имеют разные измерения.Точно так же треугольник можно также классифицировать как тупоугольный треугольник, потому что один угол тупой.
Пример 4
Классифицируйте показанный ниже треугольник.
Решение
Это равнобедренный треугольник. Две стороны равны, и два угла равны по измерению.
Применение треугольников
Давайте рассмотрим некоторые примеры практического применения треугольников:
Треугольники: самая сильная форма
Одной из любимых форм среди архитекторов является треугольник.Треугольник
— самая прочная форма, способная удерживать свою форму, имеющая сильное основание
и обеспечивающая огромную поддержку.
Некоторые из самых известных архитектурных чудес мира, такие как Эйфелева башня
, Великие пирамиды Гизы и пирамида Лувра, опираются на треугольники
для создания красивых и прочных конструкций. Двумя наиболее часто используемыми треугольниками
в архитектуре являются треугольник 30⁰-60⁰-90⁰ и треугольник 45⁰-45⁰-90⁰.
Существует несколько типов треугольников: равносторонний треугольник, который
имеет 3 стороны одинаковой длины, равнобедренный треугольник с двумя равными сторонами и разносторонний треугольник
, у которого нет сторон одинаковой длины.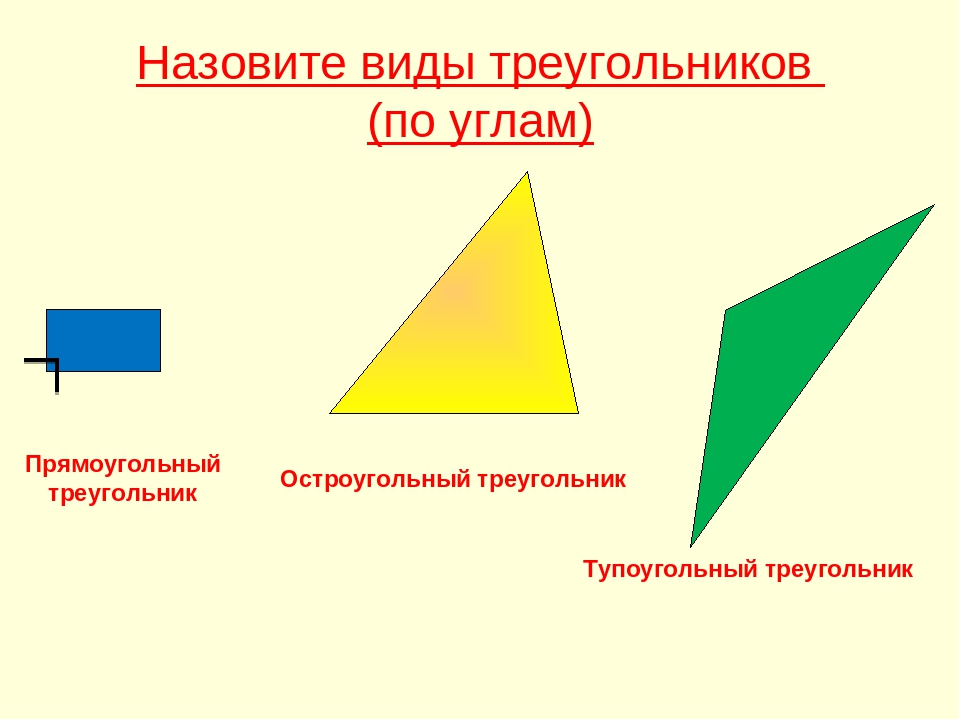 Помимо всех различий
Помимо всех различий
в треугольниках, у них есть некоторое сходство, все они имеют три стороны и чрезвычайно
стабильны. Сравнение того, как другие формы выдерживают давление, доказывает устойчивость треугольников
. Если на одну сторону квадрата надавить, число
в конечном итоге превратится в ромб. Независимо от величины давления, приложенного к треугольнику, он
поглотит давление и останется жестким. Многоугольник — это фигура, состоящая из
прямых линий, а треугольник — единственный многоугольник, который не сдвинется под давлением.
Из-за способности треугольников выдерживать огромное давление, эта форма
часто используется в архитектуре для обеспечения стабильности. Геометрия и архитектура
фундаментально связаны, и, понимая форму треугольника,
архитекторы обеспечивают необходимую поддержку развивающейся структуре. Дома
с А-образной рамой, ферменные мосты и геодезические купола опираются на треугольники для создания прочной конструкции
.
Наименьший многоугольник является самым сильным многоугольником, и количество структур
, зависящих от силы треугольника, доказывает это.Как архитектор-любитель,
, вы можете создавать огромные структуры, используя треугольники. Треугольные опорные балки
можно найти на больших спортивных аренах, мостах и фундаменте вашего дома! Треугольники
— одна удивительная форма!
Сегодня вы можете проверить прочность треугольника, построив собственный ферменный мост
! https://sciencemadefun.net/downloads/Truss%20Bridge_EOTD_May%205th.pdf
Иллюстративная математика
Задача
Ниже приведены изображения четырех треугольников с заданными длинами сторон:
Для каждого треугольника найдите и проведите все оси симметрии.
Комментарий к IM
Разделение треугольников на разносторонние, равнобедренные и равносторонние можно представить себе
с точки зрения линий симметрии. Разносторонний треугольник – это треугольник, у которого нет
линии симметрии, а в равнобедренном треугольнике есть хотя бы одна линия симметрии
а равносторонний треугольник имеет три оси симметрии.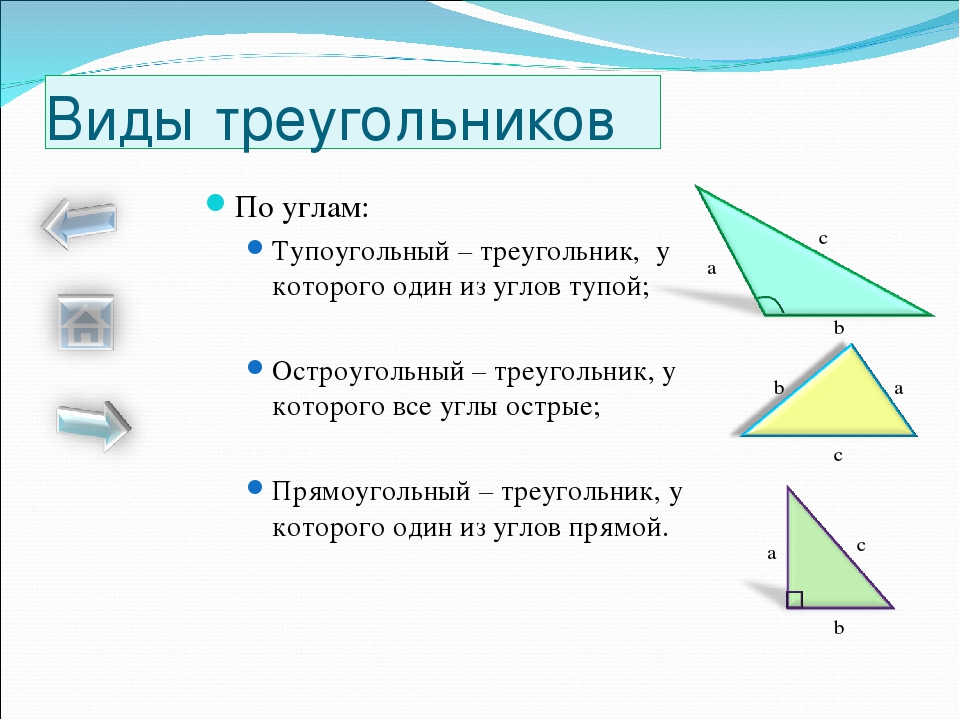 Эта деятельность обеспечивает
учащимся предоставляется возможность узнать эти отличительные черты различных типов треугольников до того, как будет введен технический язык.За
найдя линии симметрии, вырезанные модели четырех треугольников были бы
полезно, так что студенты могут сложить их, чтобы найти линии.
Эта деятельность обеспечивает
учащимся предоставляется возможность узнать эти отличительные черты различных типов треугольников до того, как будет введен технический язык.За
найдя линии симметрии, вырезанные модели четырех треугольников были бы
полезно, так что студенты могут сложить их, чтобы найти линии.
Это задание предназначено для обучения, предоставляя учащимся с возможностью экспериментировать с физическими моделями треугольников, приобретая пространственные интуиция, выполняя размышления. В конце решения было добавлено слово о том, почему для этих треугольников нет других линий симметрии: это было вставлено на случай, если эта тема возникнет в ходе обсуждения в классе, но основное внимание должно быть сосредоточено на определении правильных линий симметрии. .
Решение
Линии симметрии четырех треугольников указаны на рисунке. ниже:
Линия симметрии треугольника должна проходить через одну вершину. Две стороны, встречающиеся в этой вершине, должны быть одинаковой длины, чтобы существовала линия симметрии.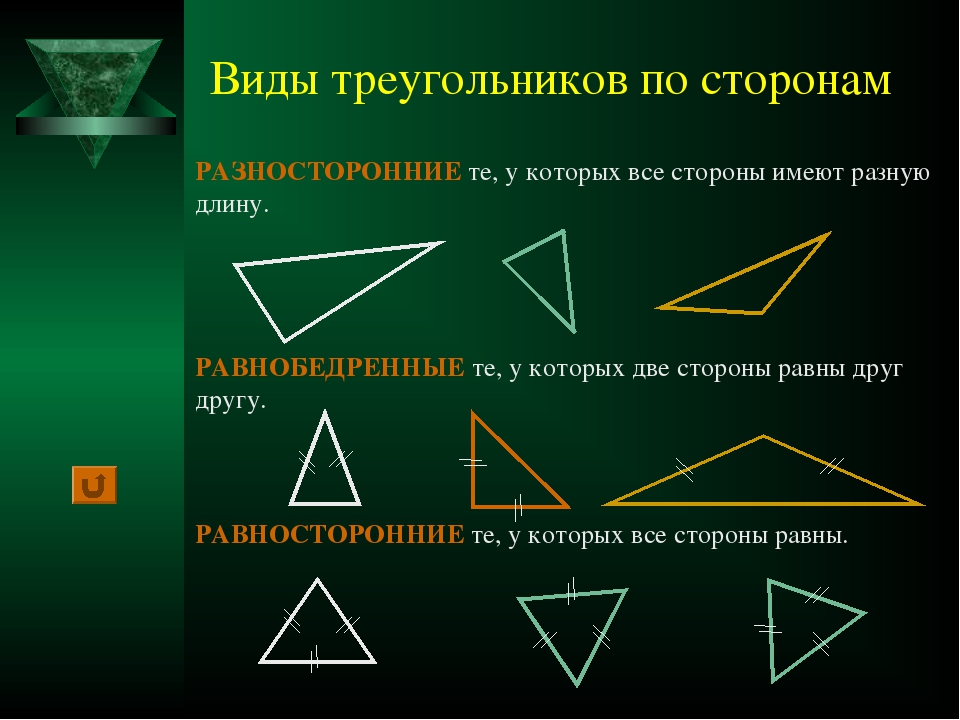 Когда две стороны, сходящиеся в вершине, имеют одинаковую длину, линия симметрии, проходящая через эту вершину, проходит через середину противоположной стороны. Для треугольника с длинами сторон 4, 4, 3 единственная возможность состоит в том, чтобы сложить две стороны длины 4 совмещенными, чтобы линия симметрии проходила через вершину, где встречаются эти две стороны.Для треугольника, все стороны которого имеют длину 3, правильная складка, проходящая через любую вершину, может служить линией симметрии, поэтому возможны три прямые. Треугольник со сторонами 2, 4, 5 не может иметь линий симметрии, так как все стороны различны. Наконец, треугольник со сторонами 3, 5, 5 имеет одну линию симметрии, проходящую через вершину, где встречаются две стороны длины 5.
Когда две стороны, сходящиеся в вершине, имеют одинаковую длину, линия симметрии, проходящая через эту вершину, проходит через середину противоположной стороны. Для треугольника с длинами сторон 4, 4, 3 единственная возможность состоит в том, чтобы сложить две стороны длины 4 совмещенными, чтобы линия симметрии проходила через вершину, где встречаются эти две стороны.Для треугольника, все стороны которого имеют длину 3, правильная складка, проходящая через любую вершину, может служить линией симметрии, поэтому возможны три прямые. Треугольник со сторонами 2, 4, 5 не может иметь линий симметрии, так как все стороны различны. Наконец, треугольник со сторонами 3, 5, 5 имеет одну линию симметрии, проходящую через вершину, где встречаются две стороны длины 5.
Чтобы понять, почему для этих треугольников нет других линий симметрии, заметим, что линия симметрии должна проходить через вершину треугольника: если прямая разрезает треугольник на два многоугольника, но не проходит через вершину, то одна из этих многоугольники — это треугольник, а другой — четырехугольник.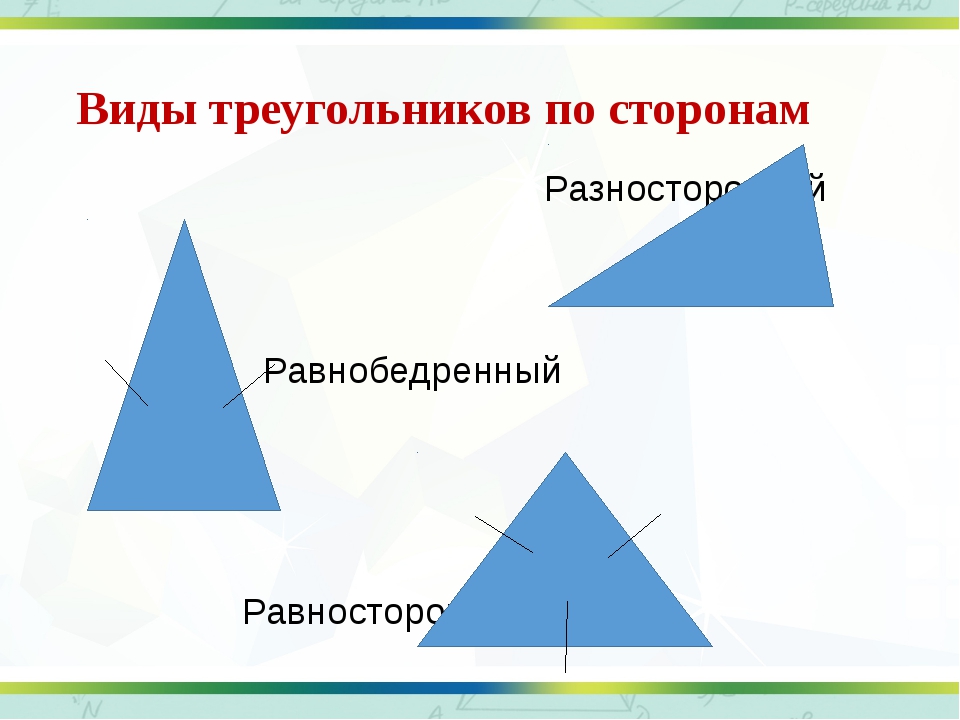 Как только вершина треугольника выбрана, существует только одна возможная линия симметрии треугольника, проходящая через эту вершину, а именно та, которая проходит через середину противоположной стороны.
Как только вершина треугольника выбрана, существует только одна возможная линия симметрии треугольника, проходящая через эту вершину, а именно та, которая проходит через середину противоположной стороны.
Что такое треугольники? – Типы, свойства и пример
Что такое треугольники в геометрии?
Формы и узоры всегда очаровывали нас с незапамятных времен. Жесткость одних и завихрения других часто озадачивают нас, а природа, в которой заключены такие красивые узоры, просто завораживает.Треугольники — одна из тех фигур, которые обладают множеством функций и приложений в нашем мире. Треугольник определяется как замкнутая двумерная фигура с 3 сторонами, 3 углами и 3 вершинами в геометрии. Это тип многоугольника, у которого сумма всех трех углов обычно равна 180°.
Типы треугольников
Поскольку треугольник представляет собой двумерную фигуру, типы треугольников классифицируются на основе их сторон и измерения углов.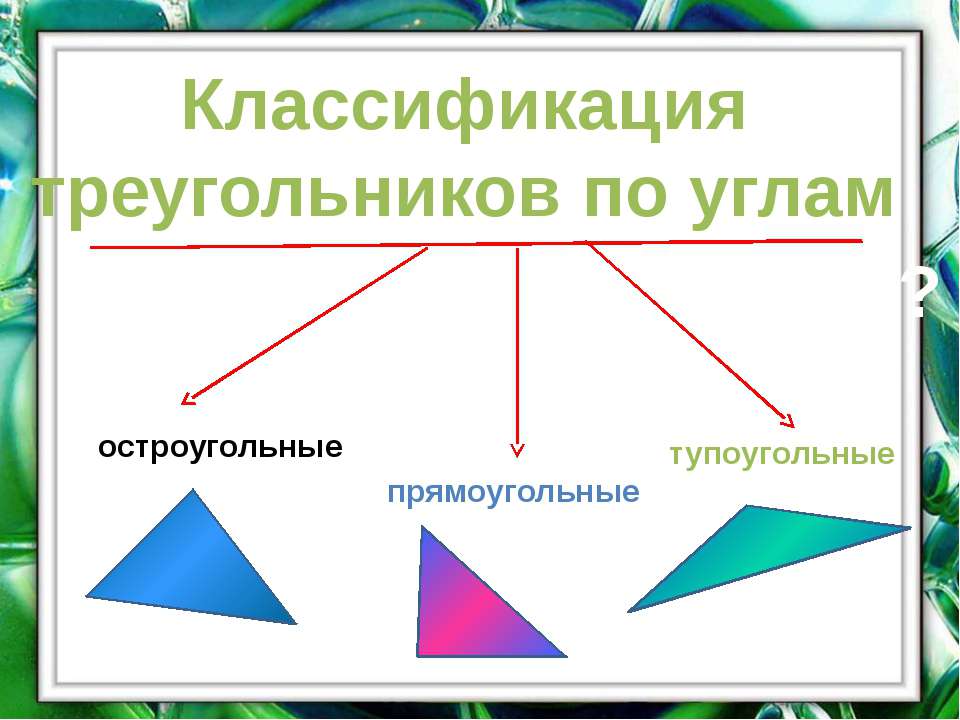
Треугольники подразделяются на три типа в зависимости от длины его сторон:
Треугольник классифицируется на основе углов,
Свойства треугольника
Треугольники подчиняются определенным свойствам и правилам для достижения определенного состояния и решения сложных геометрических задач.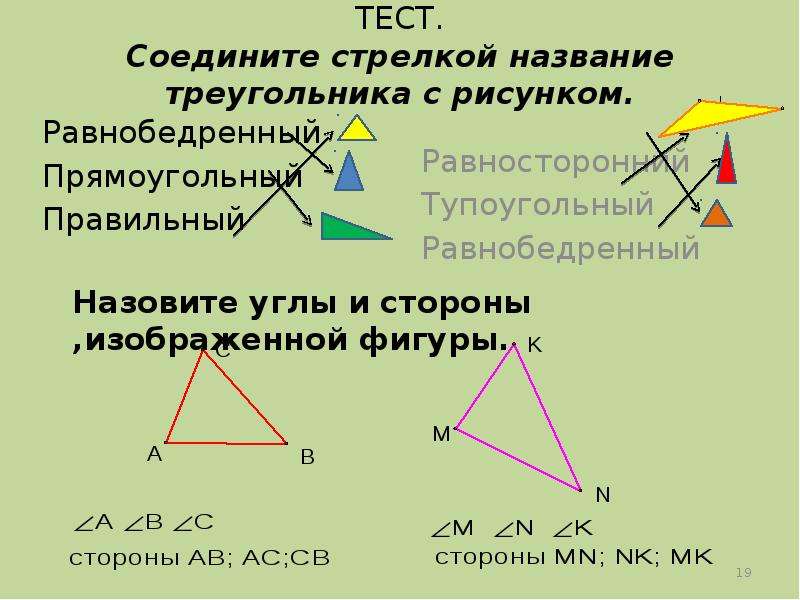 Ниже перечислены некоторые свойства треугольников:
Ниже перечислены некоторые свойства треугольников:
Свойства медианы в треугольнике
Следующие свойства устанавливаются для нахождения медианы треугольника,
Что такое конгруэнтный треугольник?
Когда все три стороны и три угла данного треугольника равны, он называется конгруэнтным треугольником.Он основан на форме и размере треугольника. Объект и его зеркальное отображение обычно называют конгруэнтностью. Два изображения конгруэнтны, если они накладываются друг на друга. В геометрических фигурах одинаковые длины отрезков конгруэнтны, как и угол измерения.
Условия конгруэнтного треугольника устанавливаются как свойство сторон треугольника.
Все три стороны эквивалентны относительно второго треугольника.
Любые две стороны и угол эквивалентны относительно второго треугольника.
Любые два угла и сторона эквивалентны относительно свойства f второго треугольника.
Невключенная сторона и два угла равны соответствующим углам и сторонам другого треугольника.
Гипотенуза со стороной прямоугольного треугольника эквивалентна гипотенузе и стороне прямоугольного треугольника.
Пример конгруэнтного треугольника
На рисунке ΔABC и ΔPQR — конгруэнтные треугольники.Следовательно,
Вершины: вершины A и P, B и Q, C и R равны
Стороны: AB=PQ, QR=BC и AC=PR;
Углы: ∠A = ∠P, ∠B = ∠Q и ∠C = ∠R
[Изображение будет загружено в ближайшее время]
Назовите свойство суммы углов треугольника определяется как сумма всех внутренних углов треугольника равна 180°.
Придумайте теорему для вычисления свойства суммы углов треугольника.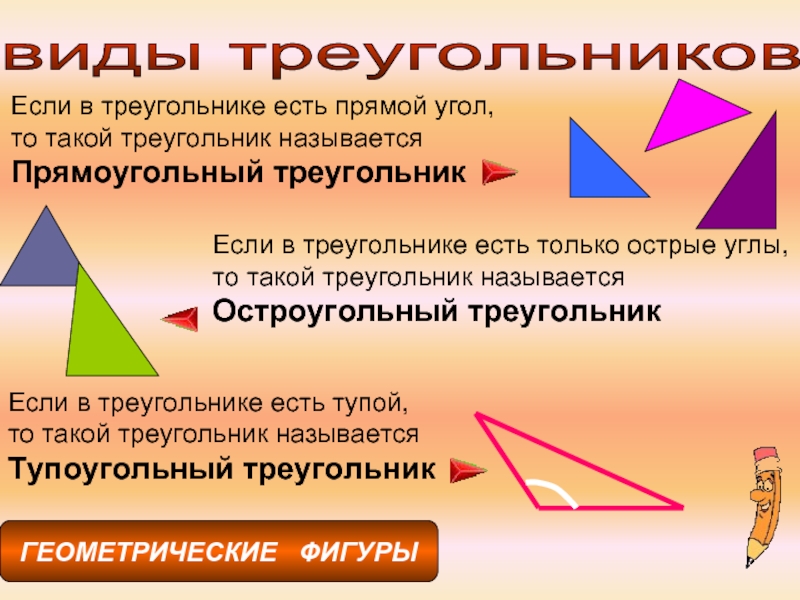
Доказательство:
Возьмем ΔABC, докажем свойство треугольника, нарисовав линию PQ,
[изображение будет загружено в ближайшее время]
Поскольку PQ — прямая,
∠PAB + ∠BAC + ∠ QAC = 180⁰
PQ ll BC и AB, AC — трансверсали
Отсюда ∠QAC = ∠ACB и ∠PAB = ∠CBA — пара противоположных углов
Подставляя ∠QAC и ∠PAB , получаем ∠ACB 5 + ∠BAC + ∠CBA = 180⁰
Следовательно, сумма всех внутренних углов равна 180⁰.
Почему треугольник — сильная форма?
Возможно, вы слышали, что треугольник — это сильная форма. Но почему это?
Почему треугольники — сильная форма
Когда инженеры строят конструкции, они хотят убедиться, что конструкция выдержит вес . Другими словами, они не хотят, чтобы конструкция падала при воздействии на нее силы . Например, мосты должны выдерживать материалы, из которых сделан мост, а также весь транспорт, проходящий по нему. Одной из фигур, которая может очень хорошо выдерживать вес, является треугольник. Но что делает треугольники такими хорошими в этом?
Одной из фигур, которая может очень хорошо выдерживать вес, является треугольник. Но что делает треугольники такими хорошими в этом?
Давайте посмотрим, как треугольник передает силу .
Когда сила ( нагрузка ) приложена к одному из углов треугольника, она распределяется по каждой стороне. Две стороны треугольника сжаты. Другое слово для этого сжатия — сжатие . Третья сторона треугольника вытянута или вытянута вбок. Другое слово для этого растяжения — натяжение .
Когда к верхнему углу треугольника прикладывается направленная вниз нагрузка, стороны треугольника испытывают сжатие, а основание треугольника испытывает растяжение (© Let’s Talk Science, 2020).Как треугольники используются в мостах
Вы часто видите, что треугольники используются для создания мостов. Мосты объединяют несколько треугольников. Они применяют сжатие и растяжение в разных местах.
Мосты часто строятся из нескольких треугольников. Сжатие происходит на внешних сторонах треугольников, а растяжение — на внутренней и нижней сторонах треугольников (© Let’s Talk Science, 2020).
Сжатие происходит на внешних сторонах треугольников, а растяжение — на внутренней и нижней сторонах треугольников (© Let’s Talk Science, 2020).Треугольники можно использовать для изготовления ферм. Фермы используются во многих конструкциях, таких как крыши, мосты и здания. Фермы объединяют горизонтальные и диагональные балки в треугольники. Мосты, в которых используются фермы, называются мостами с фермами .
Спрингтаунский ферменный мост (Источник: Дэниел Кейс [CC BY-SA 3.0] через Викисклад).Существует несколько различных типов ферм, используемых при проектировании мостов. Тип фермы зависит от того, как расположены горизонтальные и диагональные балки.Существует четыре основных типа ферм, используемых для изготовления мостов.
Ферма Уоррена
При этом используются диагональные лучи, которые образуют равносторонних треугольников. Эти треугольники имеют три стороны одинаковой длины.
Ферма Уоррена (красная для сжатия, синяя для растяжения, черная для отсутствия нагрузки) (© Let’s Talk Science, 2020).
Ферма Хау
При этом используются диагональные балки, которые наклоняются вверх к центру моста, пока они не встречаются в прямом равнобедренном треугольнике.У этого типа треугольника две стороны одинаковой длины, а третья сторона разной длины.
Ферма Хоу, показывающая расположение сил (Let’s Talk Science на основе изображения с сайта skyciv.com).Ферма Пратта
При этом используются диагональные балки, которые наклоняются вниз к центру моста, пока они не встречаются в перевернутом равнобедренном треугольнике.
Ферма Пратта, показывающая расположение сил (Let’s Talk Science на основе изображения с сайта skyciv.com).K Ферма
Это более сложный тип фермы, который состоит из треугольников, расположенных спиной к спине и образующих K-образную форму.
Ферма A K с черной буквой K (© Let’s Talk Science, 2020).Знаете ли вы?
Самый длинный мост в Канаде – Мост Конфедерации, длина которого составляет 12,9 км.
Он соединяет Нью-Брансуик и остров Принца Эдуарда.
Как треугольники используются на крышах
Тип фермы, обычно используемый для поддержки крыш, называется фермой King Post. Ферма шкворня имеет горизонтальную балку, называемую анкерной балкой , и вертикальную балку, называемую шкворнем (отсюда и ее название).Есть две стойки, которые соединяют верхнюю часть центральной стойки с балкой, образуя треугольные формы. Эти стойки называются основными стропилами . Внутри этих треугольников добавлены диагональные стойки для соединения основных стропил с центральной стойкой. Эти стойки делают крышу еще прочнее.
Ферма королевского столба (Источник: Джордж Пондерево [CC BY-SA 3.0] через Wikimedia Commons). Изображение — этикетки(1) Королевский пост
(2) Анкерная балка
(3) Основные стропила
(4) Стойки
Эти фермы шкворня затем соединяются вместе с большим количеством балок, образуя прочную и устойчивую конструкцию, которая может поддерживать крышу.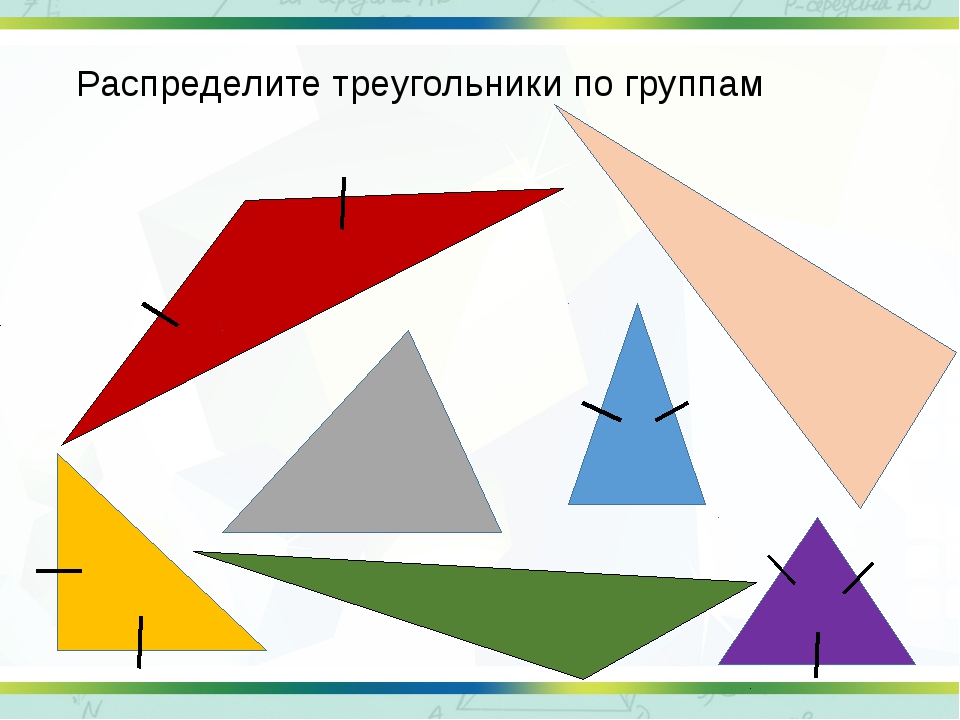
(1) Коньковая балка
(2) Прогоны
(3) Рядовые стропила
Это пример «двойной крыши» с основными и обычными стропилами.
Треугольники являются чрезвычайно важными формами, когда речь идет о технике. От мостов до домов и даже самолетов — использование треугольников в конструкциях всегда будет важно!
Этот самолет Stearman имеет стойки на крыльях, называемые стойками N (Источник: Arpingstone [общественное достояние] через Wikimedia Commons).Геометрические фигуры: характеристики треугольников
В предыдущих постах мы исследовали геометрические фигуры, такие как круг и квадрат. Теперь пришло время лучше узнать треугольник и понять его характеристики.
Треугольник , как следует из его названия, имеет три угла .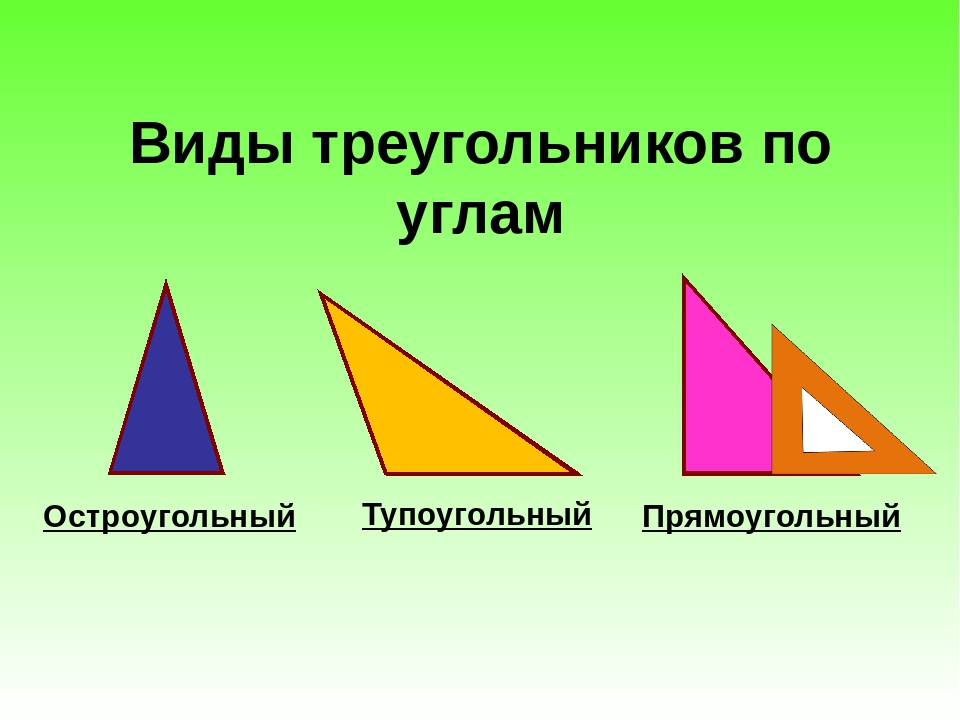 Он также имеет три стороны . Это делает его геометрической формой, образованной наименьшим количеством сторон и углов.
Он также имеет три стороны . Это делает его геометрической формой, образованной наименьшим количеством сторон и углов.
Как видите, существует множество различных типов треугольников, но разница между ними зависит не от их размера или ориентации, а от измерения их углов.Один важный факт заключается в том, что сумма измерений всех трех углов всегда равна 180 º . Это свойство, которым обладает каждый треугольник.
Мы собираемся рассмотреть наиболее важные типы треугольников и их характеристики. Если вам нужно просмотреть типы углов, вы можете взглянуть на предыдущие сообщения.
Классификация треугольников по отношению между их углами: Равносторонний треугольник Название этого треугольника указывает на то, что его три стороны равны в длину.В равносторонних треугольниках все три угла равны; имеют одинаковое измерение.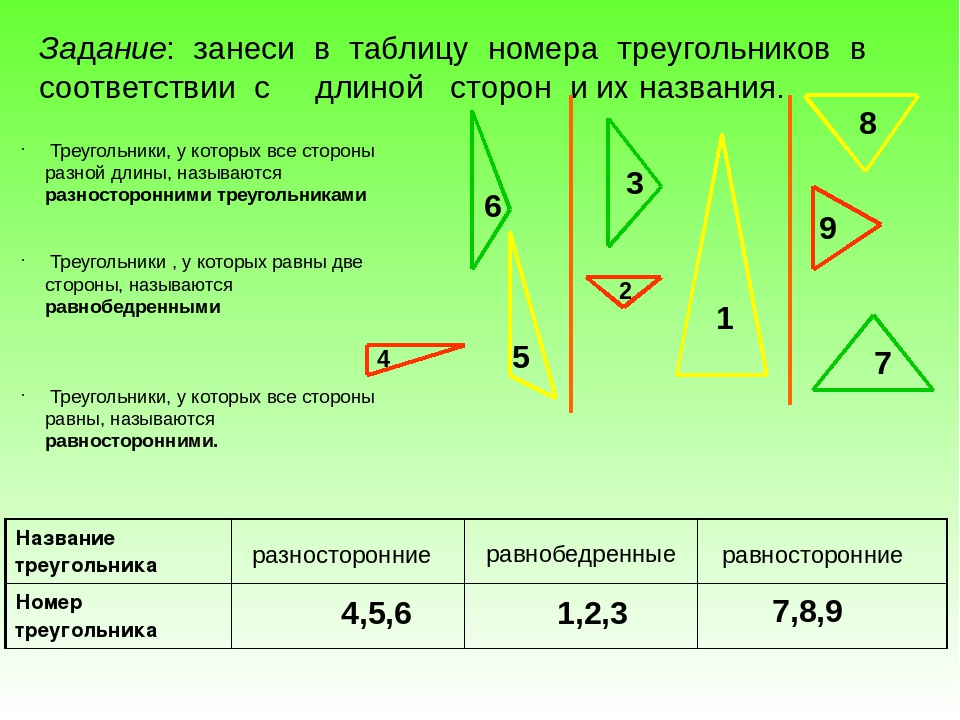 Если мы разделим 180º на количество сторон треугольника, чтобы определить измерения трех углов, мы получим 60º. Каждый из трех углов равностороннего треугольника равен 60º.
Если мы разделим 180º на количество сторон треугольника, чтобы определить измерения трех углов, мы получим 60º. Каждый из трех углов равностороннего треугольника равен 60º.
Этот треугольник противоположен равностороннему треугольнику. В разносторонних треугольниках все углы разные; каждый имеет разные измерения.Благодаря этой характеристике каждая из трех сторон треугольника имеет различных измерений .
Равнобедренный треугольникРавнобедренные треугольники имеют два равных угла и один разный . Таким образом, треугольники имеют две равные стороны и одну различную сторону . Сторона, которая отличается, расположена точно между равными углами.
Классификация треугольников по их типу угла:
Остроугольный треугольник Все углы острого треугольника острые. Равносторонний треугольник также является остроугольным, поскольку все его углы равны 60º. Равнобедренный и разносторонний треугольники также могут быть острыми, если все их углы острые.
Равносторонний треугольник также является остроугольным, поскольку все его углы равны 60º. Равнобедренный и разносторонний треугольники также могут быть острыми, если все их углы острые.
Есть один прямой угол в прямоугольных треугольниках. В таком треугольнике может быть только один прямой угол. Прямой угол равен 90º, а треугольник имеет три угла, которые в сумме дают 180º, поэтому два других угла острые и в сумме дают 90º .Прямоугольный треугольник может быть равнобедренным, если оба его острых угла равны 45º, а если все углы имеют разные измерения, треугольник будет разносторонним.
Тупоугольный треугольник В тупоугольных треугольниках один угол тупой . Два других являются острыми . Если острые углы равны, то тупоугольный треугольник также будет равнобедренным. Если все углы различны, треугольник будет разносторонним.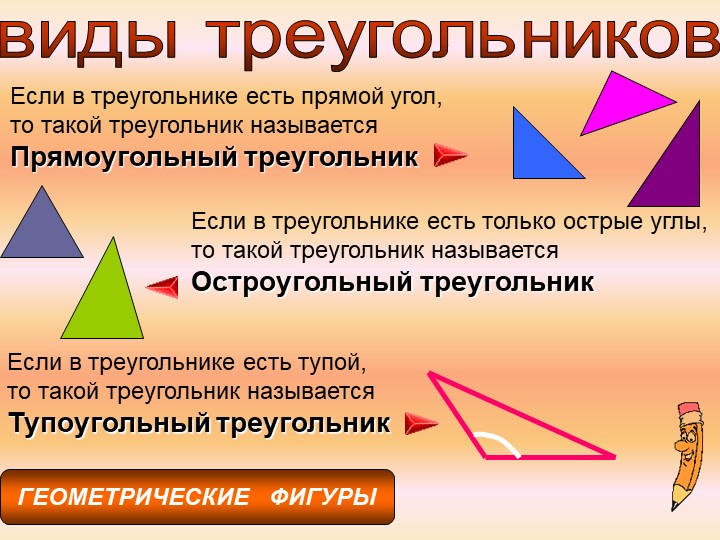
Мы видели, что треугольники — это геометрические фигуры с наименьшим числом углов и сторон.Мы также видели, что существуют разные классификации треугольников в зависимости от измерения их углов, и что внутри этих классификаций разные типы можно комбинировать друг с другом. Например, у нас могут быть разносторонние прямоугольные треугольники или тупоугольные равнобедренные треугольники.
Если вы хотите узнать больше о геометрических фигурах и других математических материалах, зайдите на Smartick и попробуйте его бесплатно.
Подробнее:
Веселье — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.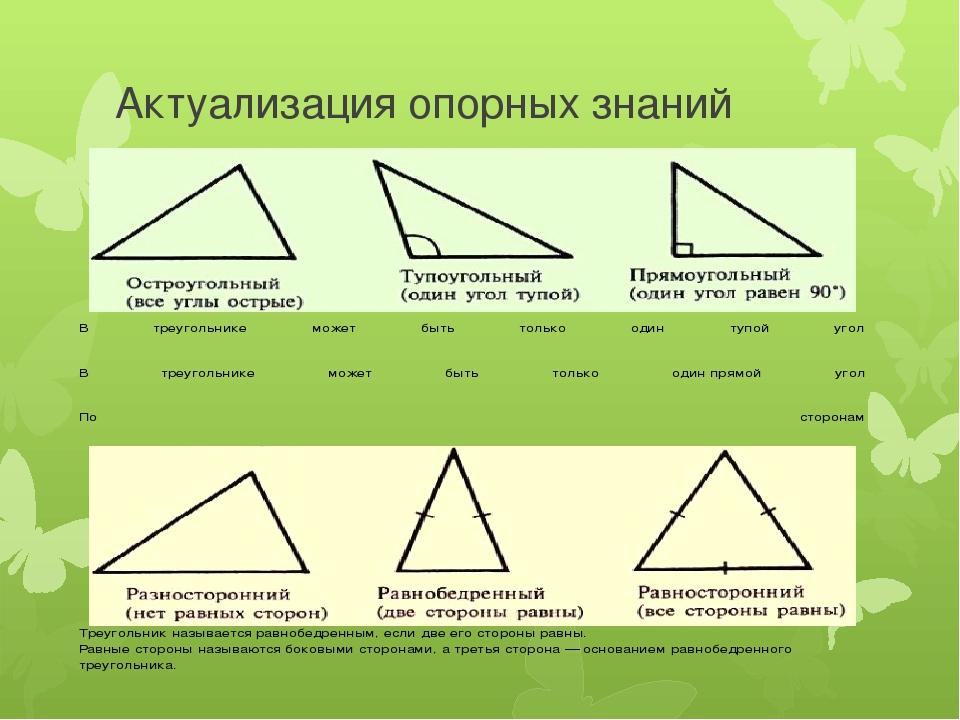

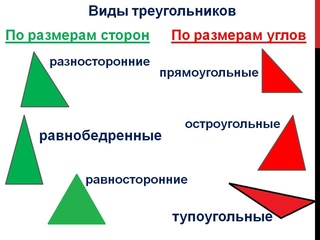
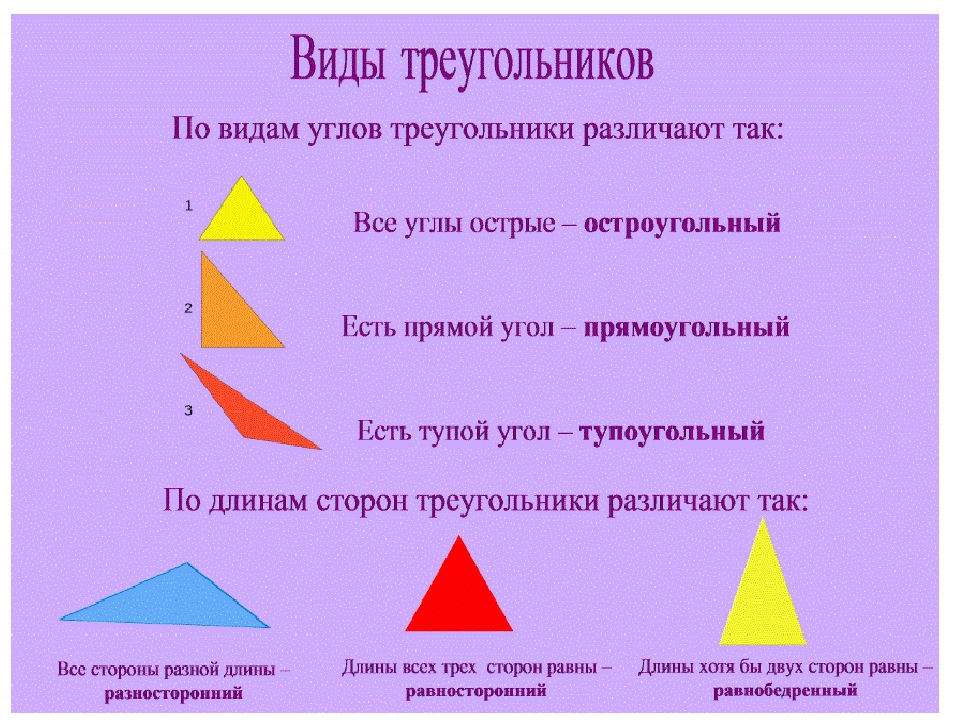

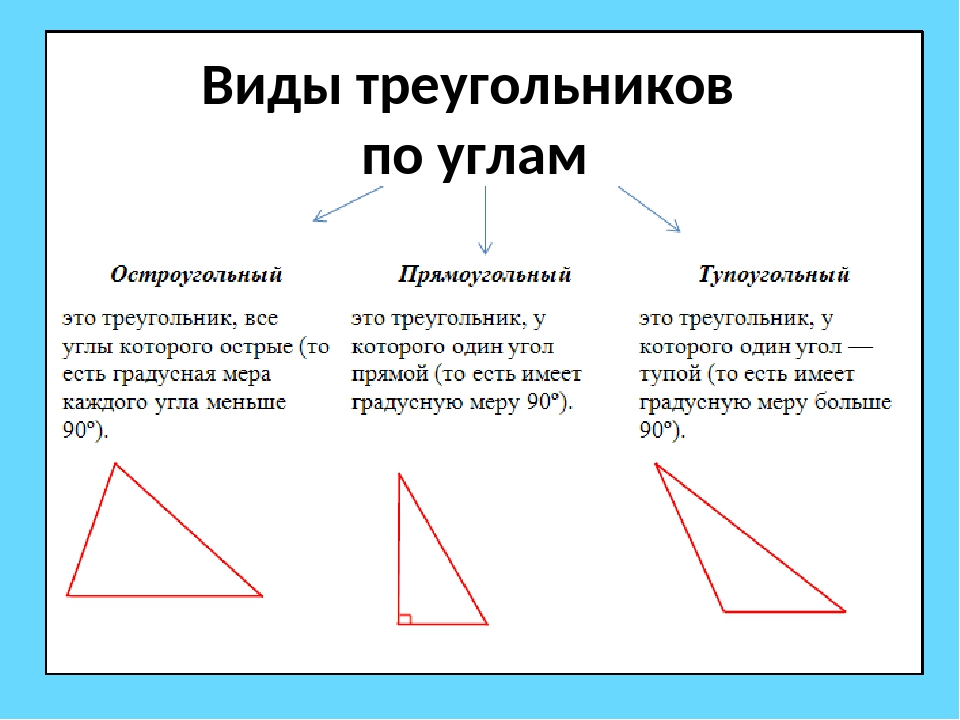
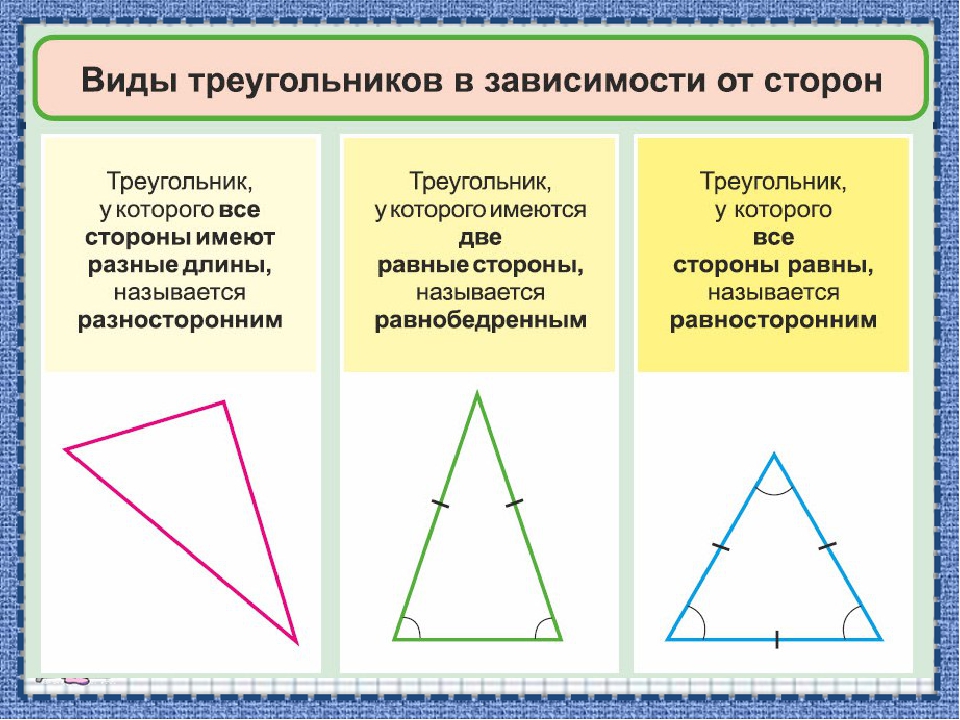
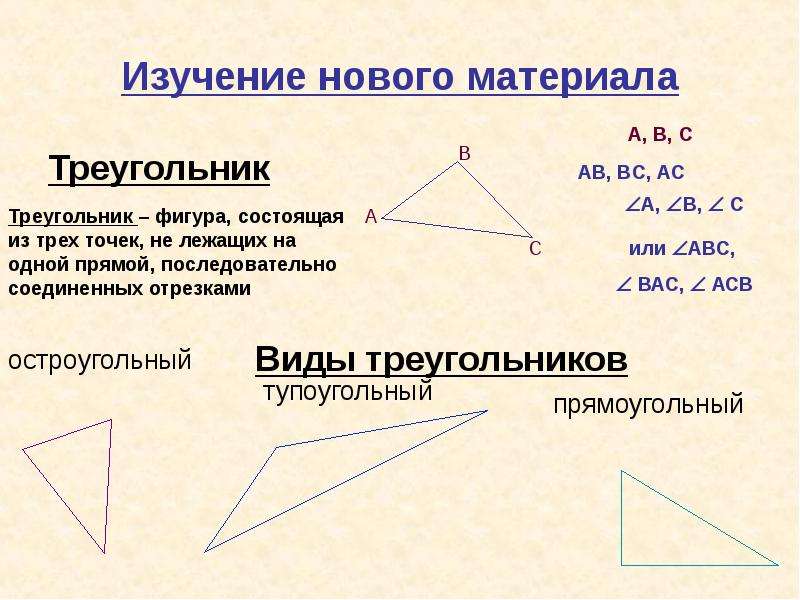 9).
9).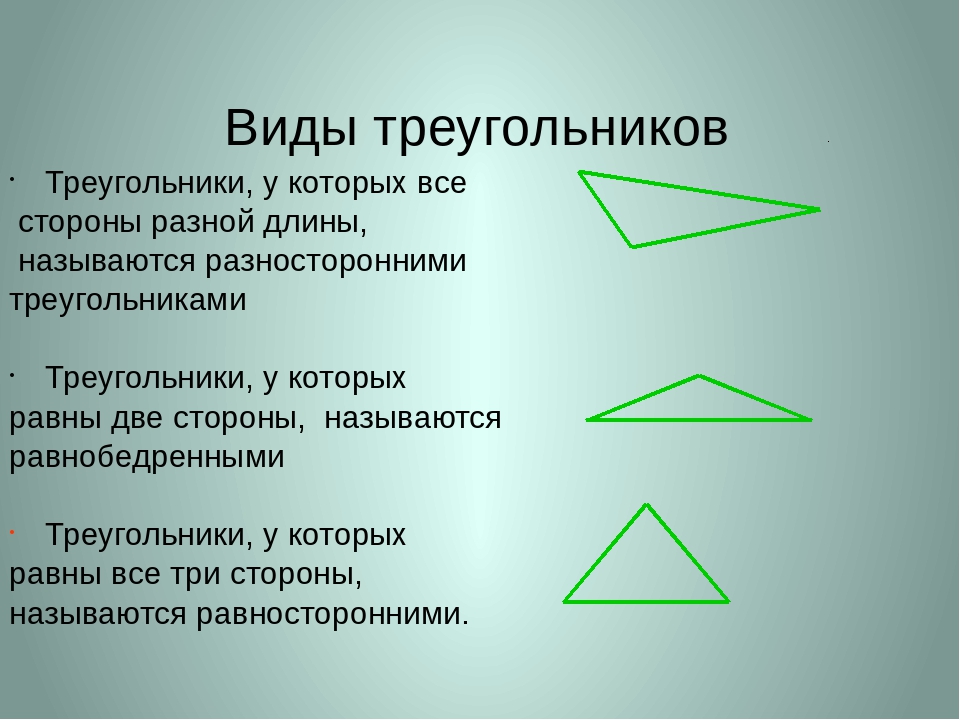 : Просвещение, 2012.
: Просвещение, 2012.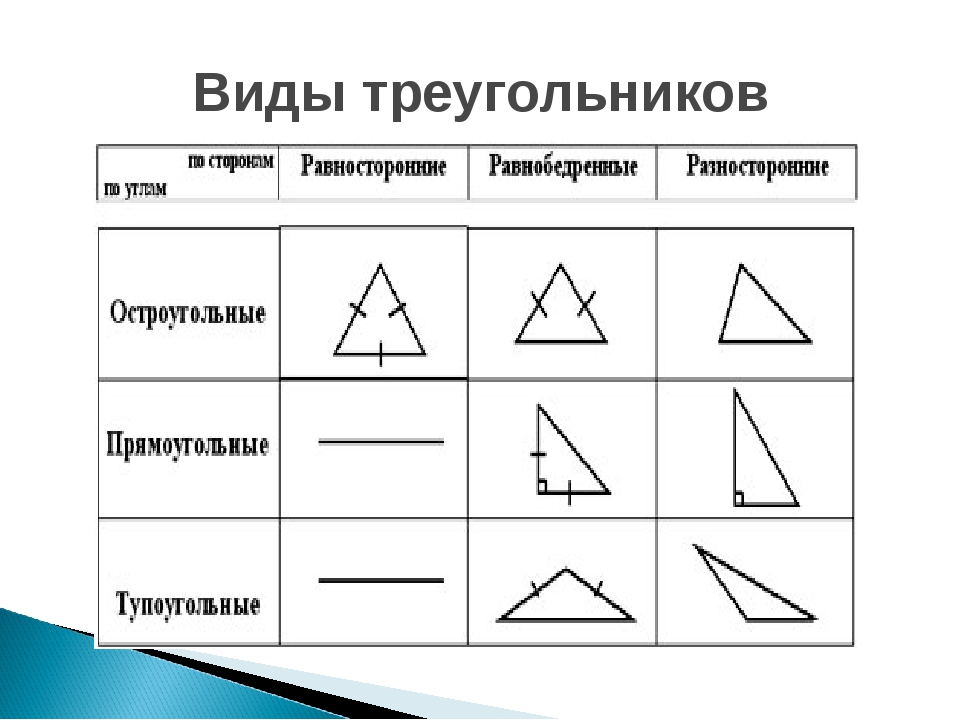 И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.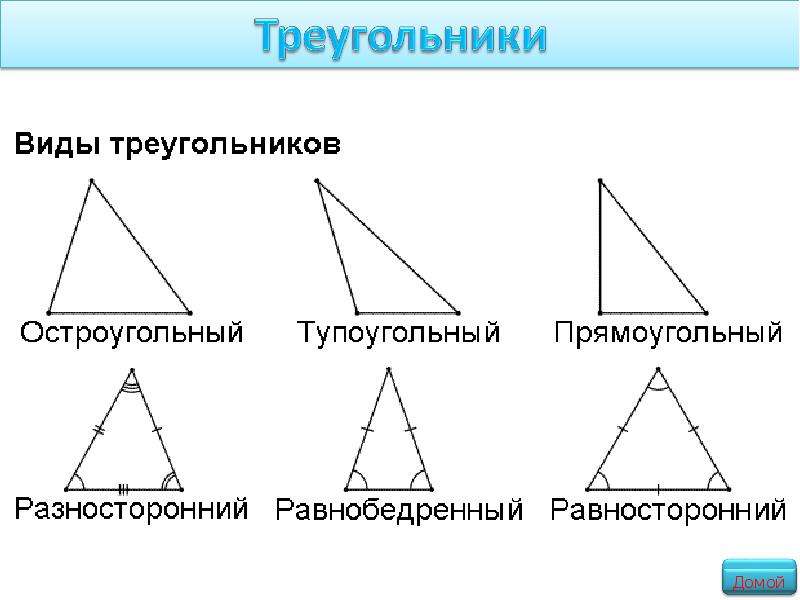
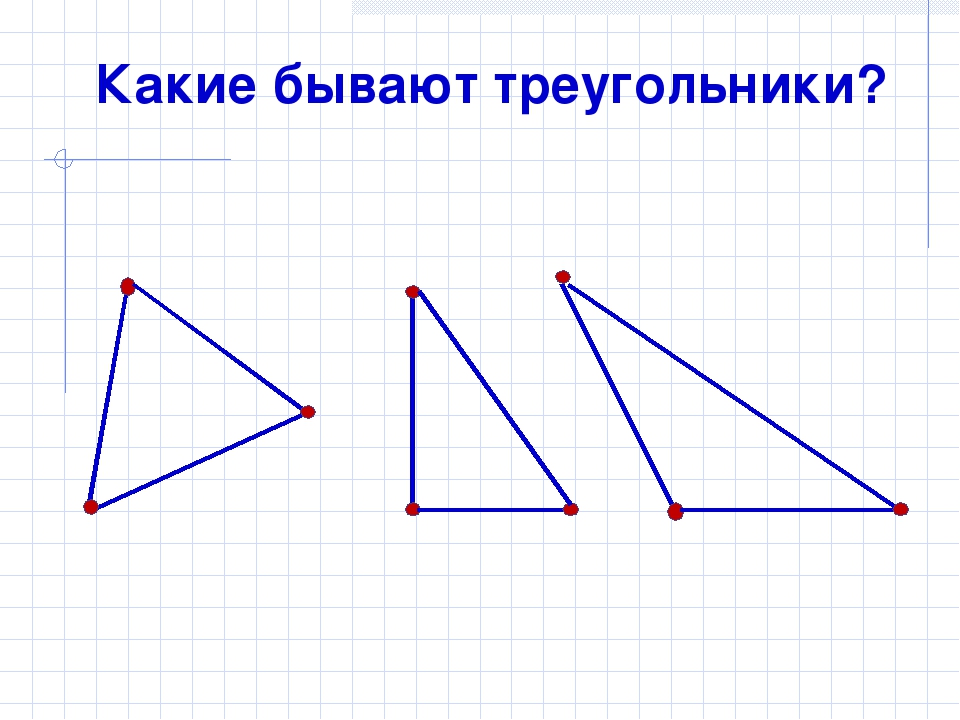 Точка, из
которой проведена часть прямой, называется
началом луча.
Точка, из
которой проведена часть прямой, называется
началом луча.
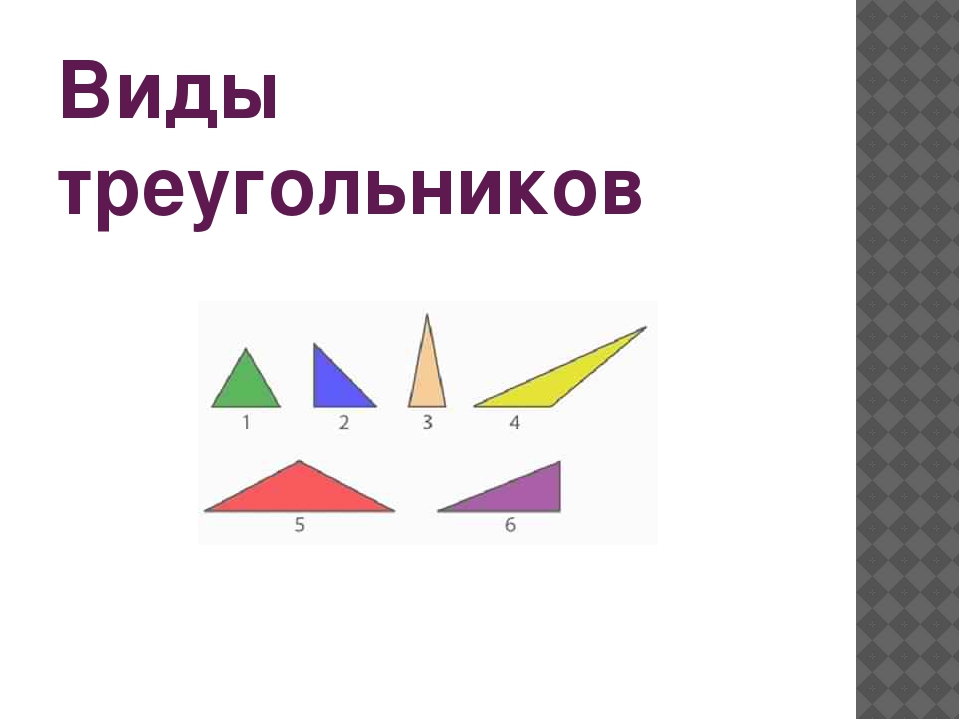 9).
9).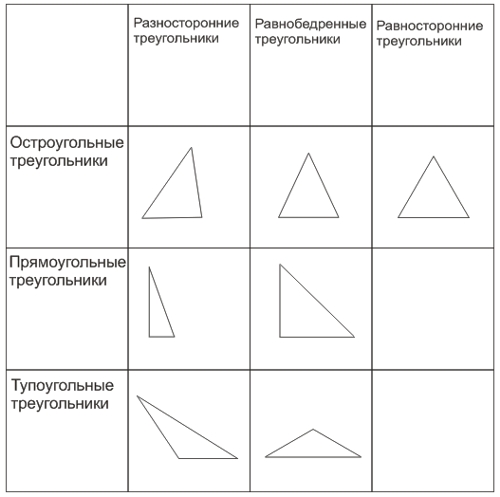 : Просвещение, 2012.
: Просвещение, 2012.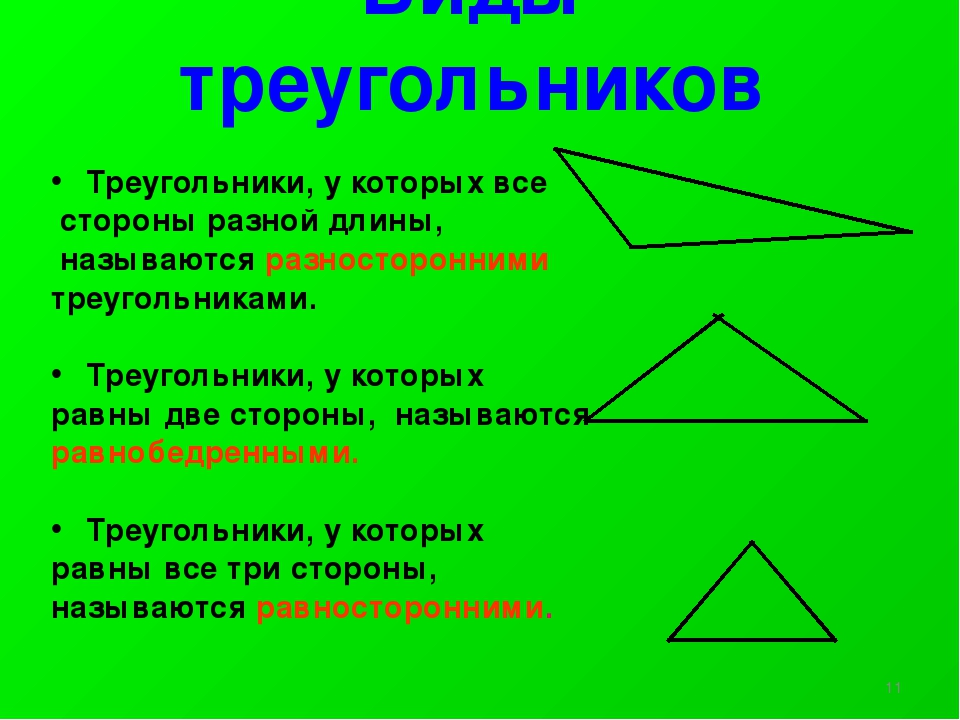 Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей.
Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей.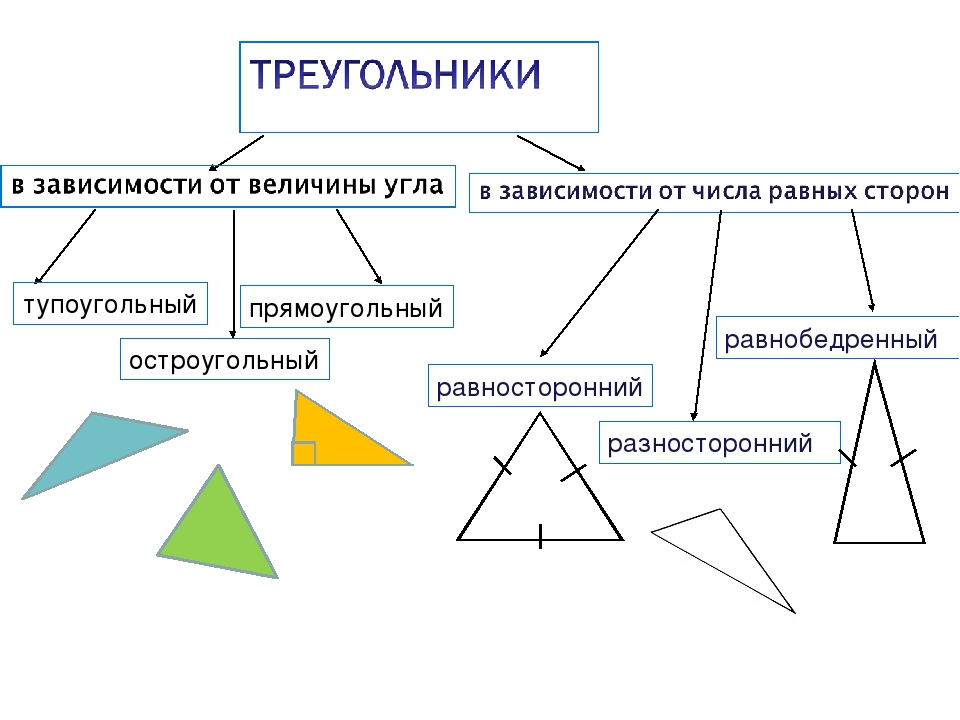
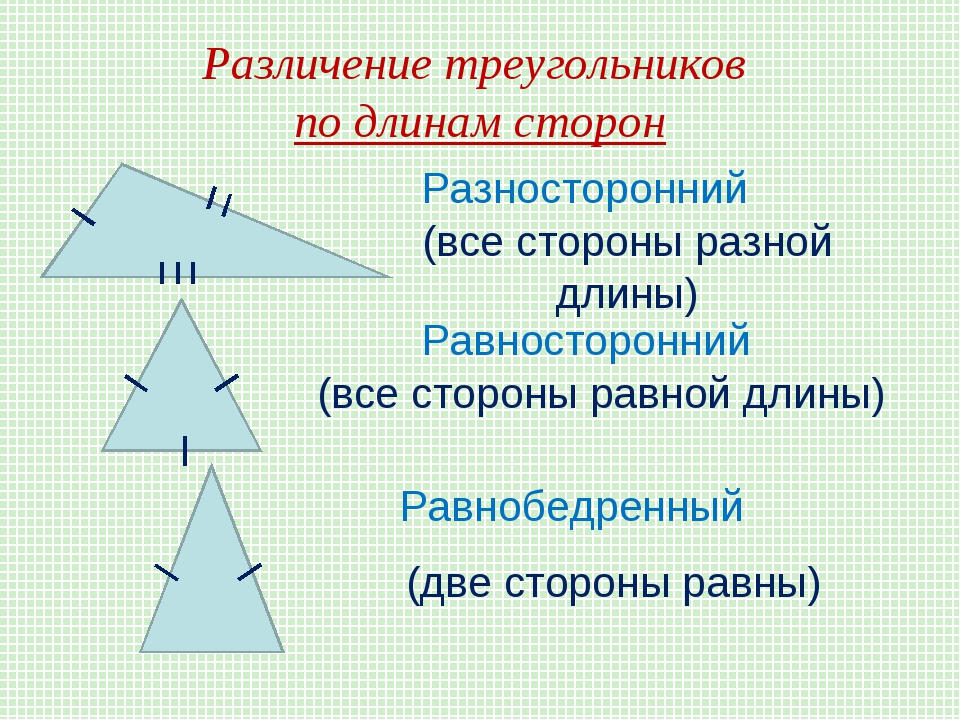 В равнобедренных треугольниках углы при основании равны.
В равнобедренных треугольниках углы при основании равны.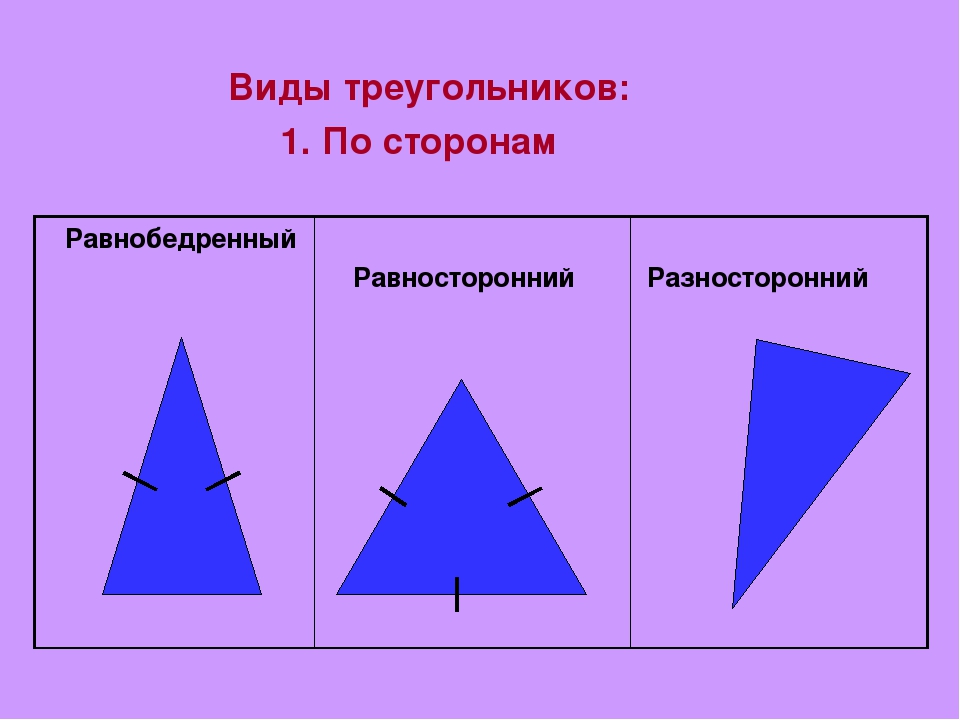 Большинство дорожных знаков отображаются на треугольных конструкциях.
Большинство дорожных знаков отображаются на треугольных конструкциях.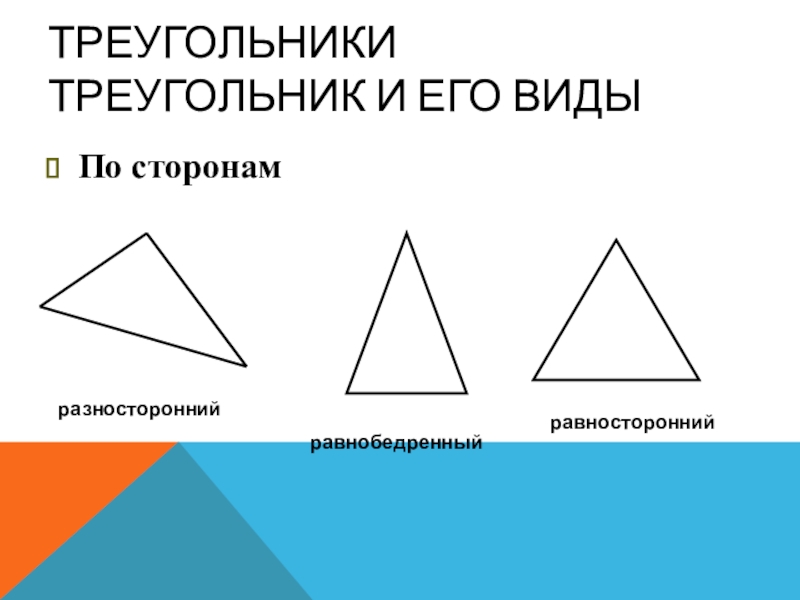

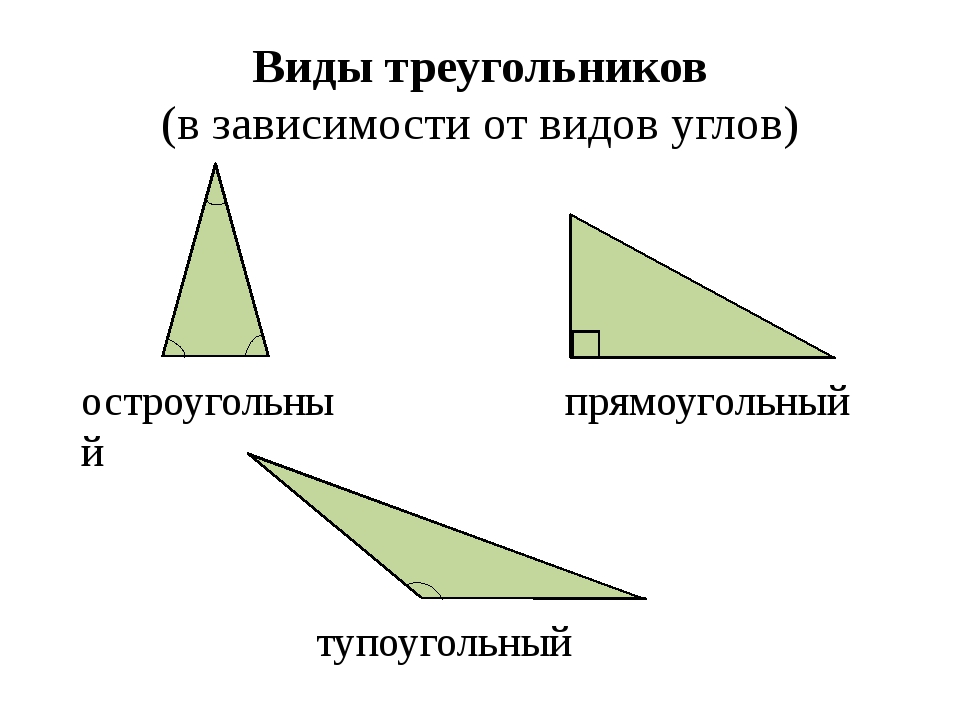 Он соединяет Нью-Брансуик и остров Принца Эдуарда.
Он соединяет Нью-Брансуик и остров Принца Эдуарда.