Иррациональное уравнение — Википедия Переиздание // WIKI 2
Иррациональное уравнение — это уравнение, содержащее неизвестное под знаком корня √ {\displaystyle \surd } или возведённое в степень, которую нельзя свести к целому числу. Простейшим примером иррационального уравнения является уравнение x = 2 {\displaystyle {\sqrt {x}}=2} или x 3 = − 3 {\displaystyle {\sqrt[{3}]{x}}=-3} . Иногда корни могут обозначать в виде рациональных степеней неизвестной, то есть вместо x n {\displaystyle {\sqrt[{n}]{x}}} пишут x 1 n {\displaystyle x^{\frac {1}{n}}} .
Примеры и классификация
Короче сформулировать правило отнесения уравнений к той или иной категории можно так:
- если все степени неизвестной\ых в уравнении принадлежат множеству натуральных чисел N {\displaystyle \mathbb {N} } , то такое уравнение считается алгебраическим.
- если все степени неизвестной\ых в уравнении принадлежат множеству целых чисел Z {\displaystyle \mathbb {Z} } , то такое уравнение называется рациональным.
- если все степени неизвестной\ых в уравнении принадлежат множеству рациональных чисел Q {\displaystyle \mathbb {Q} } , то такое уравнение называется иррациональным.
Образцами более сложных иррациональных уравнений могут послужить такие примеры:
- x + 4 + x + 9 = 5 {\displaystyle {\sqrt {x+4}}+{\sqrt {x+9}}=5} ,
- 7 2 x 2 + 6 3 − 3 x 2 3 = 11 {\displaystyle 7{\sqrt[{3}]{2x^{2}+6}}-3{\sqrt[{3}]{x^{2}}}=11} ,
- x 2 + x − 1 = 10 x + x − 2 11 + 1 {\displaystyle x^{2}+{\sqrt {x-1}}=10x+{\sqrt[{11}]{x-2}}+1}
Связь с алгебраическими уравнениями
Всякое иррациональное уравнение с помощью элементарных алгебраических операций (умножение, деление, возведение в целую степень обеих частей уравнения) может быть сведено к рациональному алгебраическому уравнению. Например, уравнение x 2 + x = 2 {\displaystyle {\sqrt {x^{2}+x}}=2} возведением во вторую степень можно преобразовать к виду x 2 + x = 4 {\displaystyle x^{2}+x=4} , что уже не иррациональное уравнение, но алгебраическое.
При этом следует иметь в виду, что полученное рациональное алгебраическое уравнение может оказаться неэквивалентным исходному иррациональному уравнению, а именно может содержать «лишние» корни, которые не будут корнями исходного иррационального уравнения. Поэтому, найдя корни полученного рационального алгебраического уравнения, необходимо проверить, а будут ли все корни рационального уравнения корнями иррационального уравнения.
Подходы к решению
В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного иррационального уравнения получилось не просто какое-то рациональное алгебраическое уравнение, среди корней которого будут и корни данного иррационального уравнения, а рациональное алгебраическое уравнение образованное из многочленов как можно меньшей степени. Желание получить рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени, вполне естественно, так как нахождение всех корней рационального алгебраического уравнения само по себе может оказаться довольно трудной задачей, решить которую полностью мы можем лишь в весьма ограниченном числе случаев.
Возведение в степень
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному уравнению.
При возведении уравнения в чётную степень получают уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
Заметим, что потеря корней при возведении уравнения в четную степень невозможна, но могут появиться посторонние корни. Рассмотрим пример:
Решим уравнение x 2 + 4 x − 5 = 4 x − 8 {\displaystyle {\sqrt {x^{2}+4x-5}}=4x-8}
Возведём обе части уравнения во вторую степень
( x 2 + 4 x − 5 ) 2 = ( 4 x − 8 ) 2 {\displaystyle ({\sqrt {x^{2}+4x-5}})^{2}=(4x-8)^{2}}
так как мы возводим в чётную степень, то возможно появление посторонних корней, ибо самим процессом возведения мы расширяем область допустимых значений (ОДЗ) для подкоренных выражений.
Так, когда 4 x − 8 {\displaystyle 4x-8} был приравнен к заведомо положительному числу (так как x 2 + 4 x − 5 ⩾ 0 {\displaystyle {\sqrt {x^{2}+4x-5}}\geqslant 0} в силу определения арифметического корня), переменная x {\displaystyle x} не могла принимать значения, которые бы обратили 4 x − 8 {\displaystyle 4x-8} в отрицательные числа, значит 4 x − 8 ⩾ 0 {\displaystyle 4x-8\geqslant 0} или x ⩾ 2 {\displaystyle x\geqslant 2} .
Другими словами в месте с постановкой задачи нам дали ещё и ограничения на значения переменной (ОДЗ) в виде x ⩾ 2 {\displaystyle x\geqslant 2} . Но, после возведения обеих частей в квадрат, мы получаем уравнение
x 2 + 4 x − 5 = 16 x 2 − 64 x + 64 {\displaystyle x^{2}+4x-5=16x^{2}-64x+64} ,
уже в котором область допустимых значений (ОДЗ) переменой x {\displaystyle x} совершенна другая (теперь x {\displaystyle x} может принимать совершенно любые значения, то есть ОДЗ расширилось относительно первоначального уравнения).
Очевидно, что вероятность появления посторонних корней резко выросла просто по факту того, что теперь корнем может стать гораздо больше чисел, а не только те, что x ⩾ 2 {\displaystyle x\geqslant 2} .
Продолжая решать и упрощать x 2 + 4 x − 5 = 16 x 2 − 64 x + 64 {\displaystyle x^{2}+4x-5=16x^{2}-64x+64} мы получим квадратное уравнение:
15 x 2 − 68 x + 69 = 0 {\displaystyle 15x^{2}-68x+69=0} , корнями которого являются
x = 3 {\displaystyle x=3} и x = 23 15 {\displaystyle x={\frac {23}{15}}}
Следует заметить, что x = 3 {\displaystyle x=3} и x = 23 15 {\displaystyle x={\frac {23}{15}}} точно являются корнями уравнения 15 x 2 − 68 x + 69 = 0 {\displaystyle 15x^{2}-68x+69=0} , но ещё не известно являются ли они корнями первоначального x 2 + 4 x − 5 = 4 x − 8 {\displaystyle {\sqrt {x^{2}+4x-5}}=4x-8} уравнения.
Так мы знаем, что корни первоначального уравнения не могут быть меньше 2, а меж тем корень x = 23 15 ≈ 1.533333… {\displaystyle x={\frac {23}{15}}\approx 1.533333…} меньше двух, значит он не может быть корнем первоначального уравнения.
Ответ: x ∈ { 3 } {\displaystyle x\in \{3\}}
Замена системой условий
Использование свойств корней
Введение новых переменных
Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение корень (радикал). При этом уравнение становится рациональным относительно новой переменной.
Пример 1[1]: Решить уравнение 2 x 2 + 3 x + 2 x 2 + 3 x + 9 = 33 , x ∈ R {\displaystyle 2x^{2}+3x+{\sqrt {2x^{2}+3x+9}}=33,x\in \mathbb {R} }
Сделаем замену y = 2 x 2 + 3 x + 9 {\displaystyle y={\sqrt {2x^{2}+3x+9}}} , ясно что при этом мы наложили ограничения на новую переменную в виде y ⩾ 0 {\displaystyle y\geqslant {0}} , так как арифметический корень не может быть отрицательным числом.
После возведения y {\displaystyle y} во вторую степень мы избавимся от знака корня и получим выражение y 2 = 2 x 2 + 3 x + 9 {\displaystyle y^{2}=2x^{2}+3x+9} . Далее, после подстановки y {\displaystyle y} в исходное уравнение, мы получим такое уравнение:
y 2 + y − 42 = 0 {\displaystyle y^{2}+y-42=0} ,
корни которого y = 6 {\displaystyle y=6} и y = − 7 {\displaystyle y=-7} . Но y {\displaystyle y} не может быть отрицательным числом ввиду того как мы определили y {\displaystyle y} через нашу подстановку, поэтому корнем будем считать лишь y = 6 {\displaystyle y=6} . Далее, решая уравнение 2 x 2 + 3 x + 9 = 6 {\displaystyle {\sqrt {2x^{2}+3x+9}}=6} , мы получаем корни x = 3 {\displaystyle x=3} и x = − 4.5 {\displaystyle x=-4.5} .
Ответ: x ∈ { 3 ; − 4.5 } {\displaystyle x\in \{3;-4.5\}}
Пример 2[2]: Решить уравнение x + 28 3 − x − 9 3 = 1 {\displaystyle {\sqrt[{3}]{x+28}}-{\sqrt[{3}]{x-9}}=1}
Сделаем две замены: u = x + 28 3 {\displaystyle u={\sqrt[{3}]{x+28}}} и v = x − 9 3 {\displaystyle v={\sqrt[{3}]{x-9}}} , после их возведения в третью степень получим u 3 = x + 28 {\displaystyle u^{3}=x+28} и v 3 = x − 9 {\displaystyle v^{3}=x-9} . Далее, решив каждое новое уравнение относительно x {\displaystyle x}
x = u 3 − 28 {\displaystyle x=u^{3}-28} и x = v 3 + 9 {\displaystyle x=v^{3}+9} , и после уравнивания этих уравнений, мы получаем уравнение u 3 − 28 = v 3 + 9 {\displaystyle u^{3}-28=v^{3}+9} , но ввиду того, как мы вводили u {\displaystyle u} и v {\displaystyle v} , мы так же имеем уравнение u − v = 1 {\displaystyle u-v=1} , значит у нас появилась система из уравнений:
{ u − v = 1 u 3 − v 3 = 37 {\displaystyle {\begin{cases}u-v=1\\u^{3}-v^{3}=37\end{cases}}}
Решив систему, мы получаем значения v 1 = 3 {\displaystyle v_{1}=3} и v 2 = − 4 {\displaystyle v_{2}=-4} , это значит нам надо решить ещё два уравнения:
x − 9 3 = 3 {\displaystyle {\sqrt[{3}]{x-9}}=3} и x − 9 3 = − 4 {\displaystyle {\sqrt[{3}]{x-9}}=-4} , решения которых x = 36 {\displaystyle x=36} и x = − 55 {\displaystyle x=-55} .
Ответ: x ∈ { 36 ; − 55 } {\displaystyle x\in \{36;-55\}}
Использование области определения
Использование области значений
Тождественное преобразования
Использование производной
Использование мажоранты
Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.
Мажорантой данной функции f ( x ) {\displaystyle f(x)} на заданном промежутке называется такое число A, что либо f ( x ) ⩽ A {\displaystyle f(x)\leqslant {A}} для всех x из данного промежутка, либо f ( x ) ⩾ A {\displaystyle f(x)\geqslant {A}} для всех x из данного промежутка. Основная идея метода состоит в использовании следующих теорем для решения иррациональных уравнений:
Теорема № 1.
Пусть f ( x ) {\displaystyle f(x)} и g ( x ) {\displaystyle g(x)} — некоторые функции, определённые на множестве D {\displaystyle D} . Пусть f ( x ) {\displaystyle f(x)} ограничена на этом множестве числом А сверху, а g ( x ) {\displaystyle g(x)} ограничена на этом множестве тем же числом А, но снизу.
Тогда уравнение f ( x ) = g ( x ) {\displaystyle f(x)=g(x)} равносильно системе:
{ f ( x ) = A g ( x ) = A {\displaystyle {\begin{cases}f(x)=A\\g(x)=A\end{cases}}}
Теорема № 2.
Пусть f ( x ) {\displaystyle f(x)} и g ( x ) {\displaystyle g(x)} — некоторые функции, определённые на множестве D {\displaystyle D} . Пусть f ( x ) {\displaystyle f(x)} и g ( x ) {\displaystyle g(x)} ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f ( x ) + g ( x ) = A + B {\displaystyle f(x)+g(x)=A+B} равносильно системе уравнений:
{ f ( x ) = A g ( x ) = B {\displaystyle {\begin{cases}f(x)=A\\g(x)=B\end{cases}}}
Теорема № 3.
Пусть f ( x ) {\displaystyle f(x)} и g ( x ) {\displaystyle g(x)} — некоторые неотрицательные функции, определённые на множестве D {\displaystyle D} . Пусть f ( x ) {\displaystyle f(x)} ограничена сверху (или снизу) числами А и В соответственно. Тогда уравнение f ( x ) g ( x ) = A B {\displaystyle f(x)g(x)=AB} равносильно системе уравнений (при условии, что A > 0 {\displaystyle A>0} и B > 0 {\displaystyle B>0} ):
{ f ( x ) = A g ( x ) = B {\displaystyle {\begin{cases}f(x)=A\\g(x)=B\end{cases}}}
В этом утверждении особенно важно условие неотрицательности функций f ( x ) {\displaystyle f(x)} и g ( x ) {\displaystyle g(x)} , а также условие положительности
Пример:
Решить уравнение ( x − 2 y + 1 ) 2 + 1 + ( 3 x − y − 2 ) 2 + 25 = 6 {\displaystyle {\sqrt {(x-2y+1)^{2}+1}}+{\sqrt {(3x-y-2)^{2}+25}}=6}
Введём более короткие обозначения: f ( x , y ) = ( x − 2 y + 1 ) 2 + 1 {\displaystyle f(x,y)={\sqrt {(x-2y+1)^{2}+1}}} и g ( x , y ) = ( 3 x − y − 2 ) 2 + 25 {\displaystyle g(x,y)={\sqrt {(3x-y-2)^{2}+25}}} .
Значения f ( x , y ) {\displaystyle f(x,y)} больше или равны 1, так как подкоренное выражение ( x − 2 y + 1 ) 2 + 1 {\displaystyle (x-2y+1)^{2}+1} очевидно ⩾ 1 {\displaystyle \geqslant {1}} . Причём f ( x , y ) = 1 {\displaystyle f(x,y)=1} , только если ( x − 2 y + 1 ) 2 = 0 {\displaystyle (x-2y+1)^{2}=0} . Аналогично, значения g ( x , y ) {\displaystyle g(x,y)} не меньше 5. Значит можно записать f ( x , y ) + g ( x , y ) = 1 + 5 {\displaystyle f(x,y)+g(x,y)=1+5} . Следовательно, используя Теорему № 2:
{ f ( x , y ) = 1 g ( x , y ) = 5 {\displaystyle {\begin{cases}f(x,y)=1\\g(x,y)=5\end{cases}}} или { ( x − 2 y + 1 ) 2 + 1 = 1 ( 3 x − y − 2 ) 2 + 25 = 5 {\displaystyle {\begin{cases}{\sqrt {(x-2y+1)^{2}+1}}=1\\{\sqrt {(3x-y-2)^{2}+25}}=5\end{cases}}}
Возведя оба уравнения в квадрат, получим
{ ( x − 2 y + 1 ) 2 = 0 ( 3 x − y − 2 ) 2 = 0 {\displaystyle {\begin{cases}(x-2y+1)^{2}=0\\(3x-y-2)^{2}=0\end{cases}}} , упрощая далее { x − 2 y + 1 = 0 3 x − y − 2 = 0 {\displaystyle {\begin{cases}x-2y+1=0\\3x-y-2=0\end{cases}}}
Единственное решение этой системы ( 1 ; 1 ) {\displaystyle (1;1)}
Ответ: ( 1 ; 1 ) {\displaystyle (1;1)}
Графический подход
В некоторых случаях построение графика функции позволяет оценить возможные пути решения уравнения, количество корней или их приблизительное значение.
Примечания
Ссылки
 Эта страница в последний раз была отредактирована 20 марта 2020 в 19:50.
Эта страница в последний раз была отредактирована 20 марта 2020 в 19:50.Урок по теме «Иррациональные уравнения»
Цели урока :повторение
обучающая — ввести понятие иррационального уравнения;
— показать способы решения;
развивающая — создание проблемной ситуации при решении иррациональных уравнений
при наличии посторонних корней и выработка умения у учащихся
самостоятельно определять способы решения уравнений;
— развитие алгебраической ,,зоркости,, ;
воспитательная — развитие у учащихся грамотной устной и письменной
математической речи;
— добиться осознанного восприятия темы, заинтересовать поиском
нестандартных решений ( метод ,,пристального взгляда,, )
Дидактическое оснащение урока : интерактивная доска, презентация, учебник ,,Алгебра и начала анализа 10,, под ред Ю.М. Колягин , переносные доски, карточки для индивидуальной работы.
ХОД УРОКА
1. Организационный момент.
Французский писатель Анатоль Франс заметил, что ,,учиться надо весело. Чтобы переваривать знания , надо поглощать их с аппетитом,, Последуем совету писателя : будем на уроке активны, внимательны, будем ,,поглощать,, знания с большим желанием, ведь все новые знания, полученные сегодня, пригодятся нам завтра.
Тема урока : ,,Иррациональные уравнения,, Перед вами стоит задача : научиться решать новый для вас вид уравнений, научиться самостоятельно определять метод их решений.
2. Устный опрос.
Проводится в форме фронтальной работы с классом.
1) Устные упражнения – повторение свойств корней п-ой степени
Слайд 1Найти значение выражения:
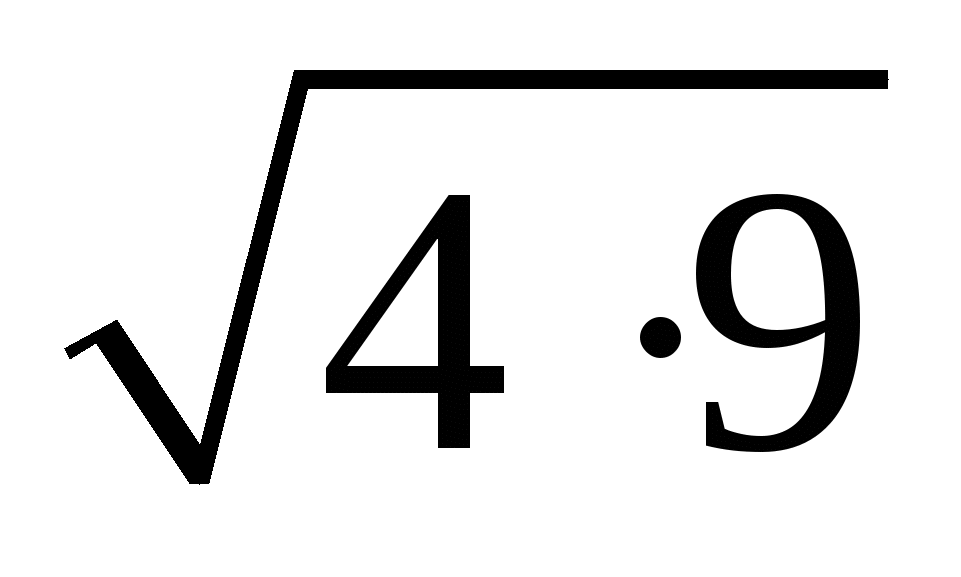 ;
;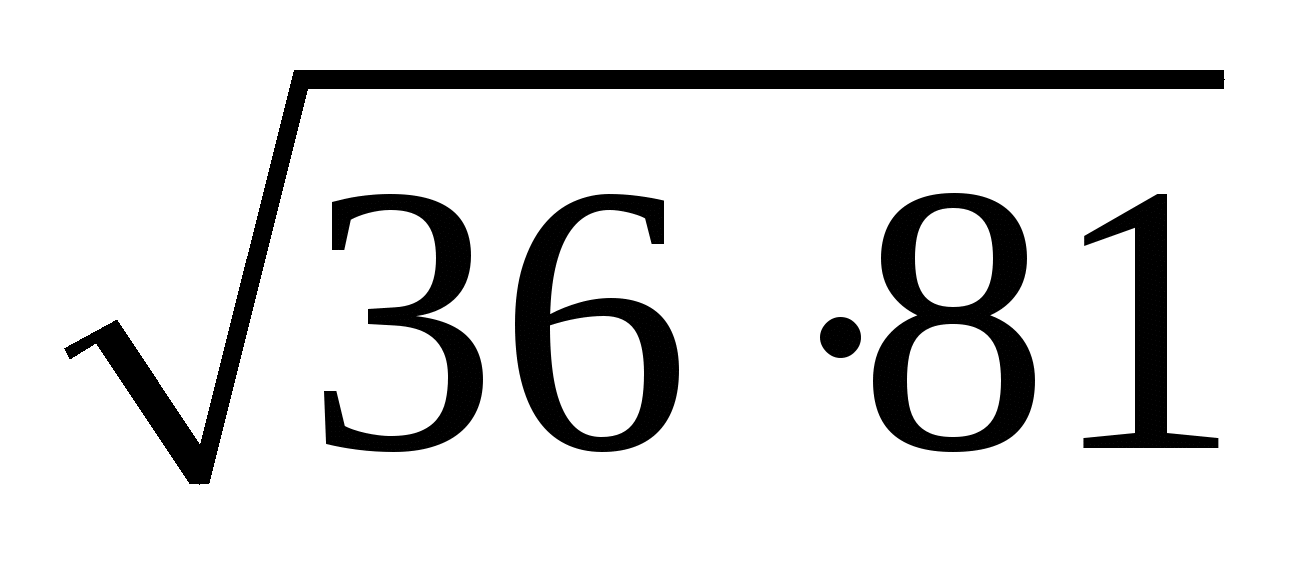 ;
;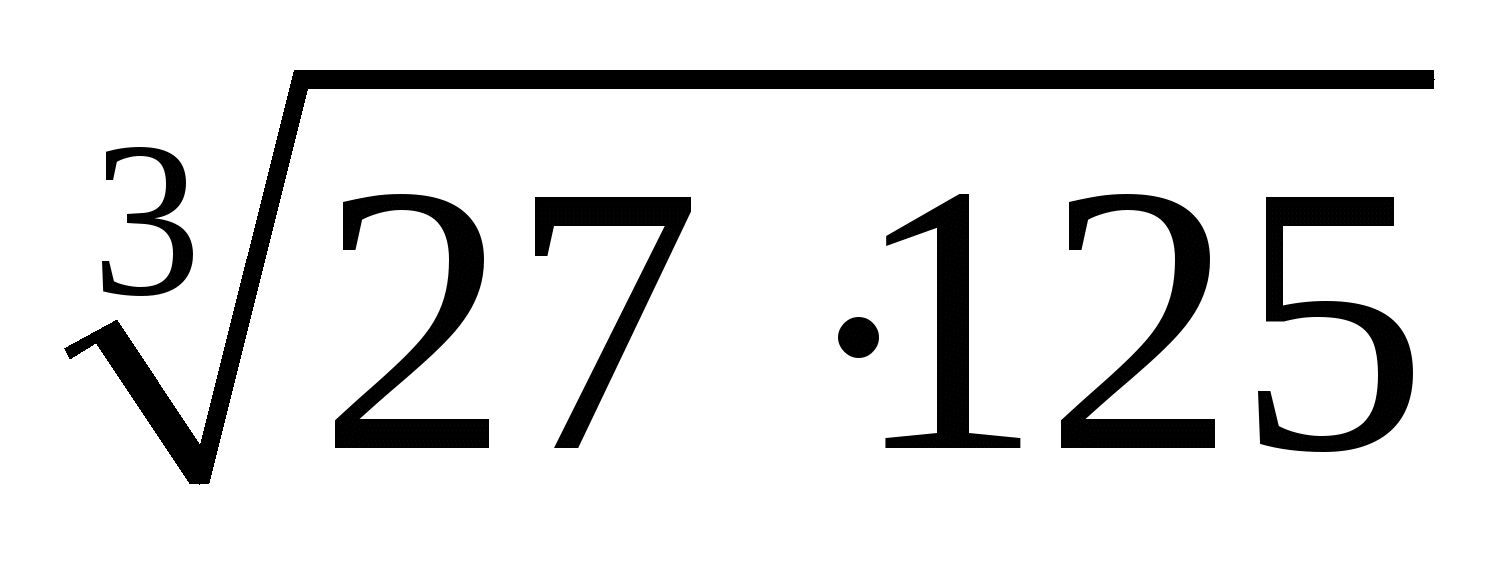 ;
;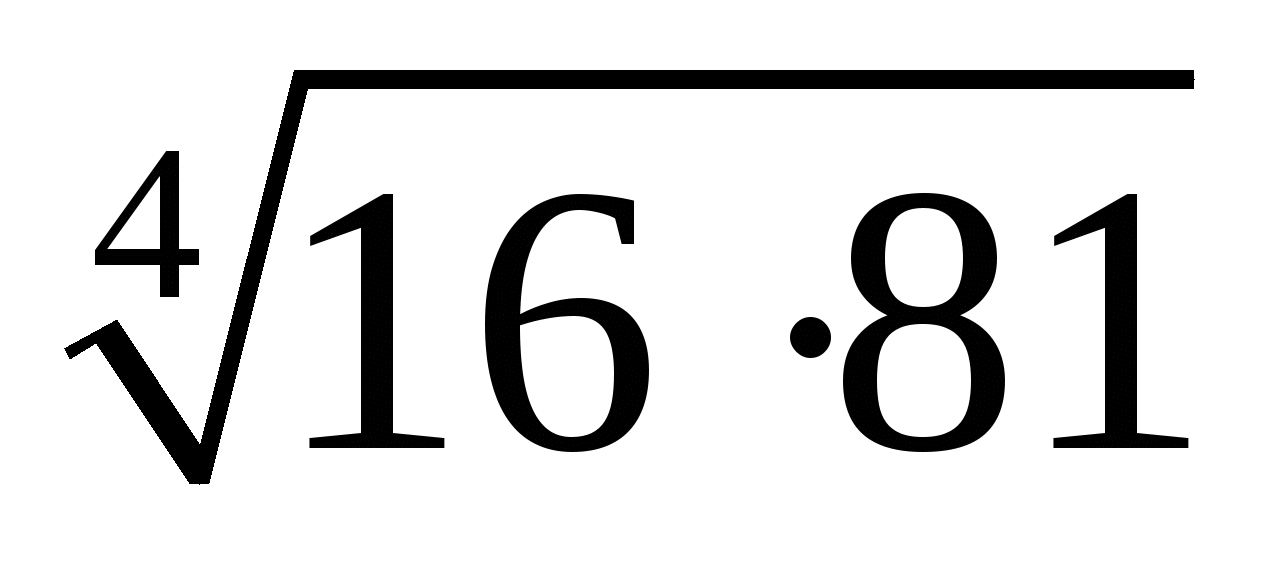 ;
;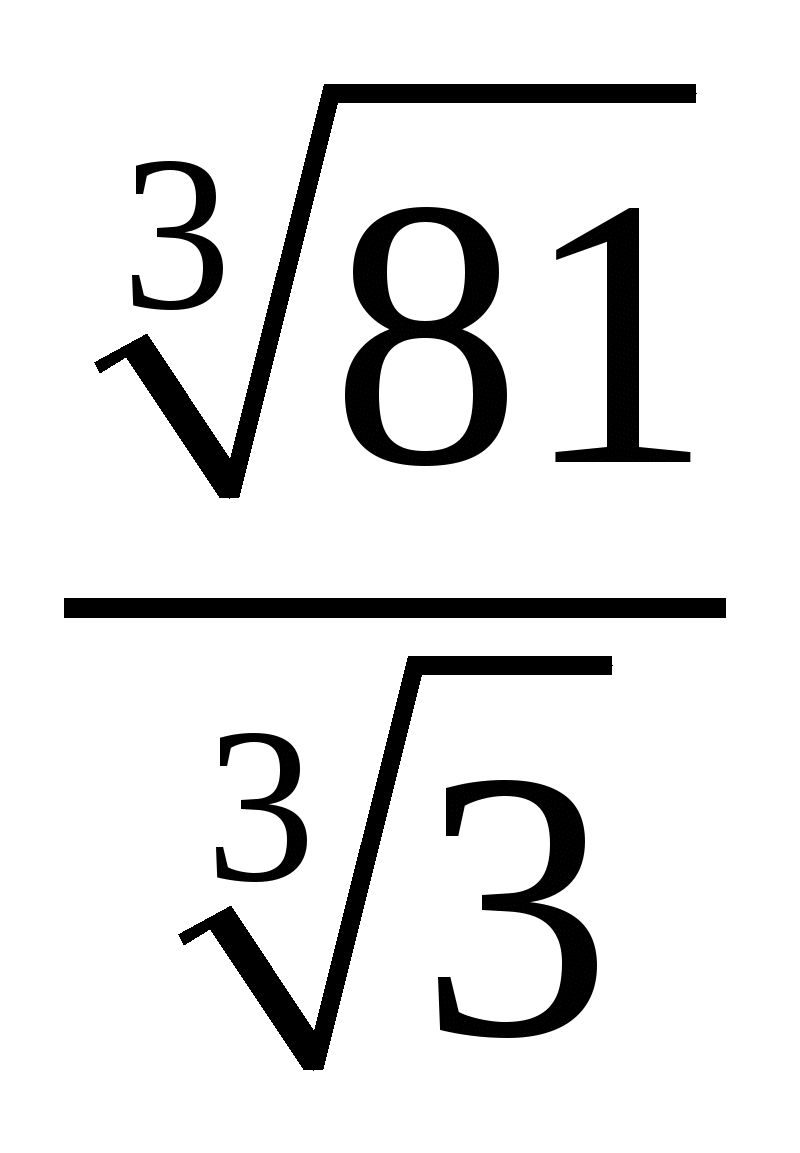 ;
;
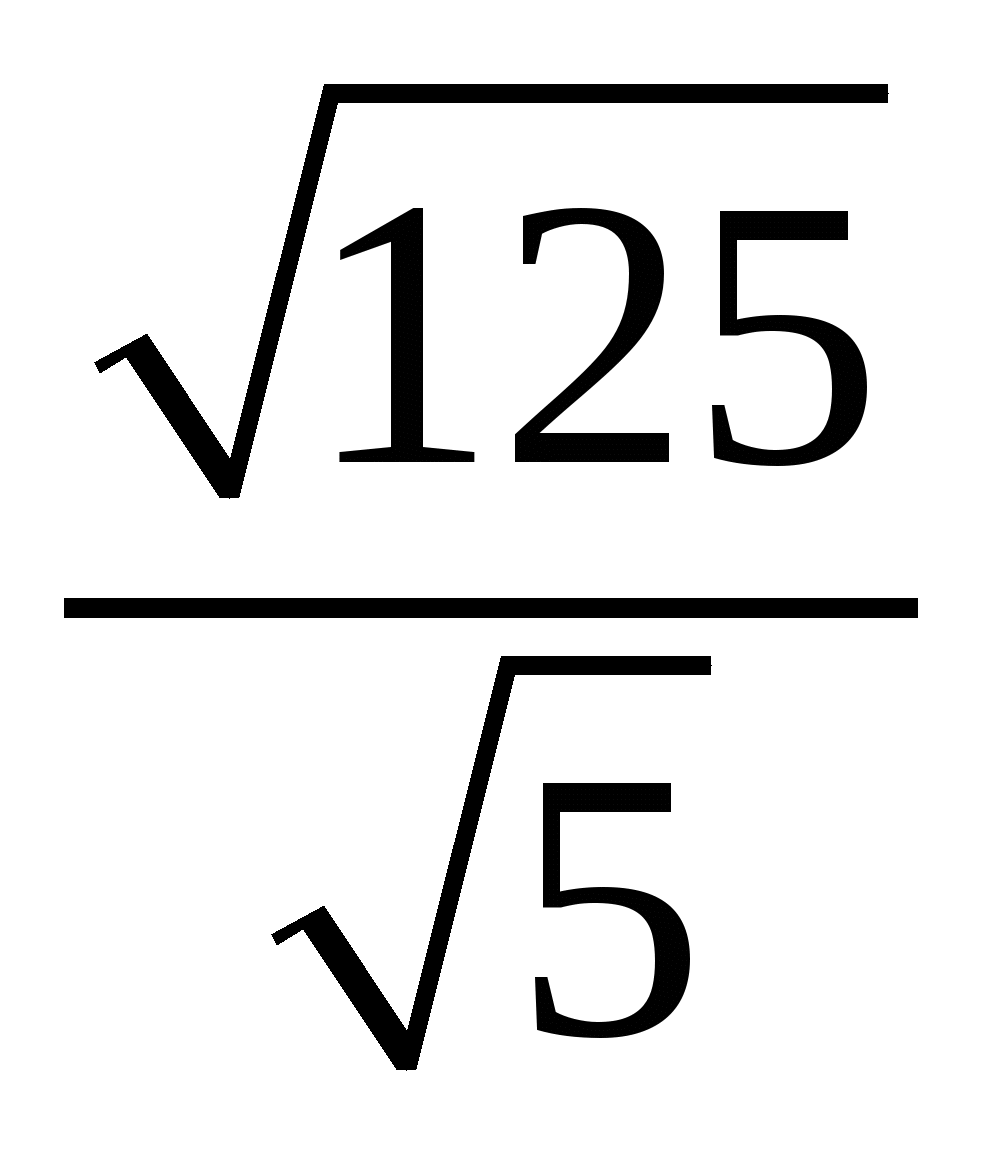 ;
;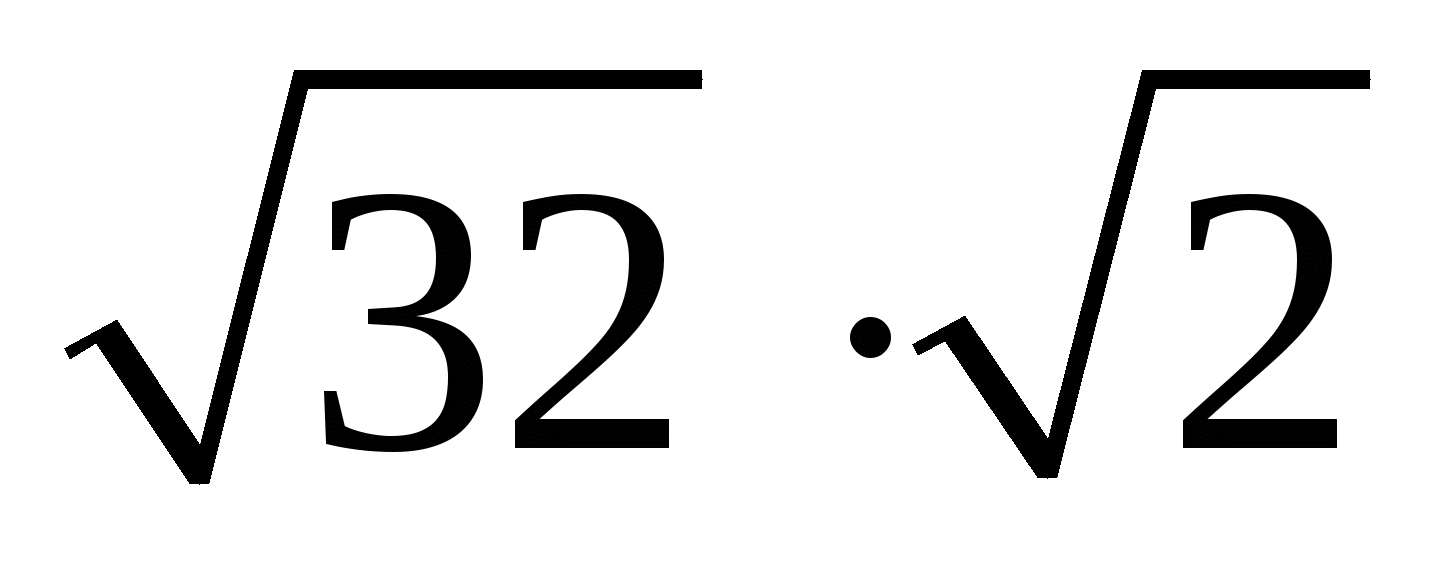 ;
;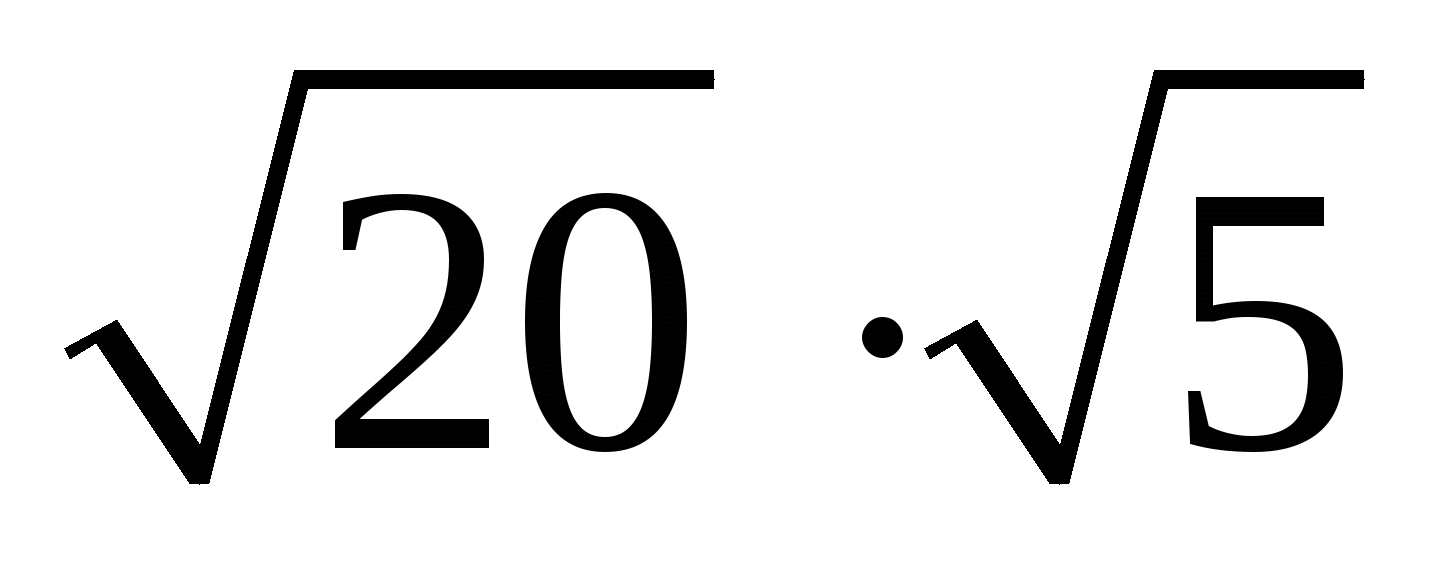 ;
;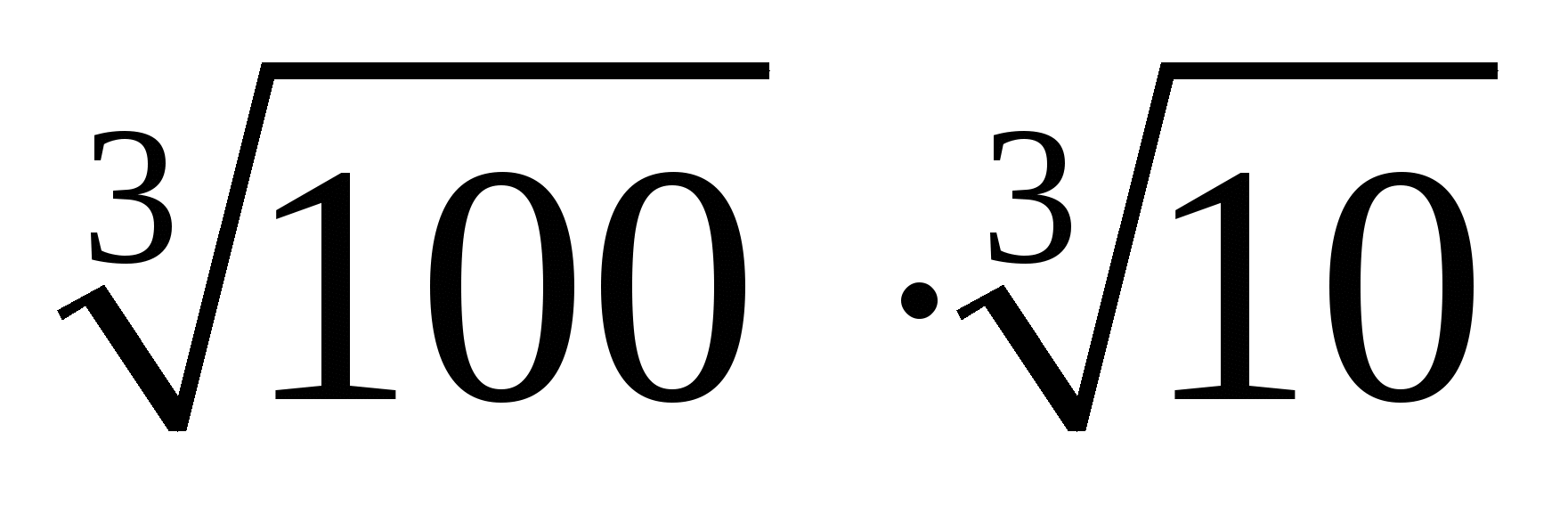 ;
;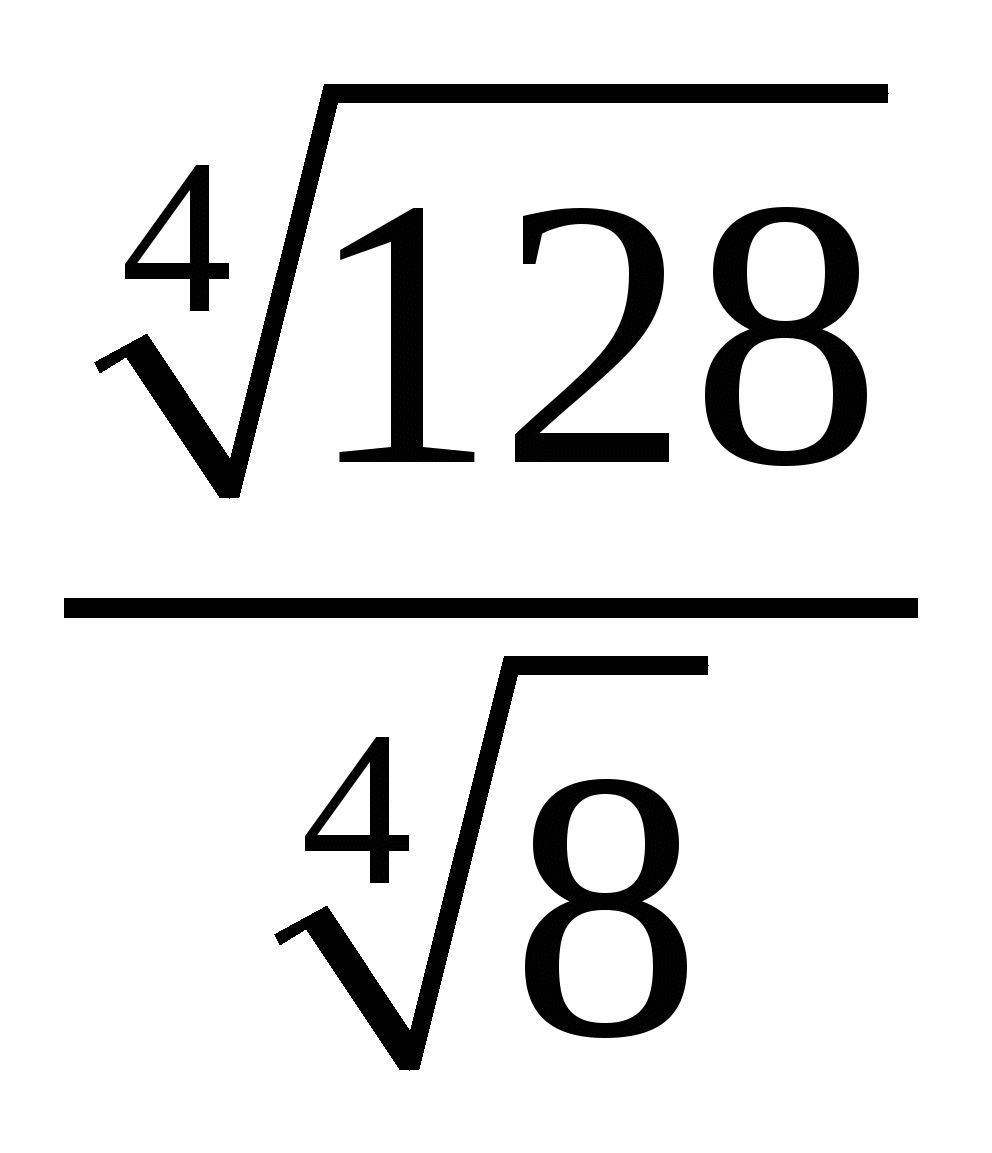
Вынесите множители за знак корня ( х 0, у
0, у 0 ) :
0 ) :
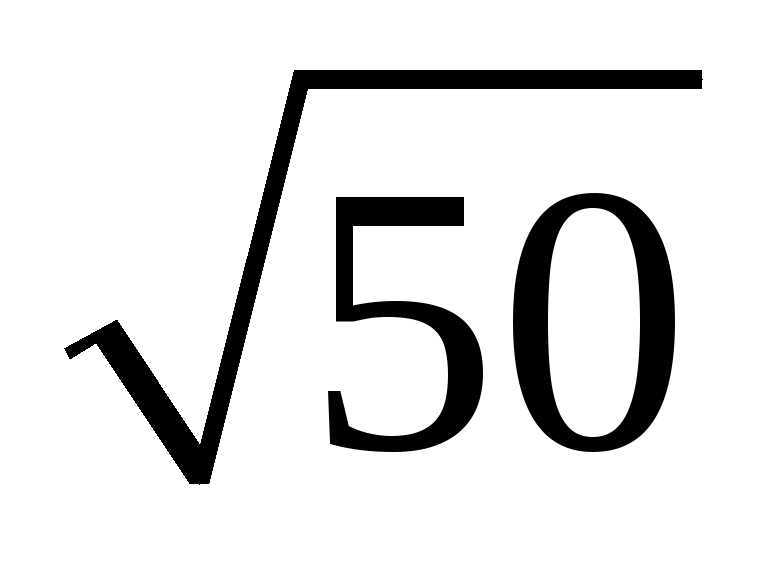 ;
; 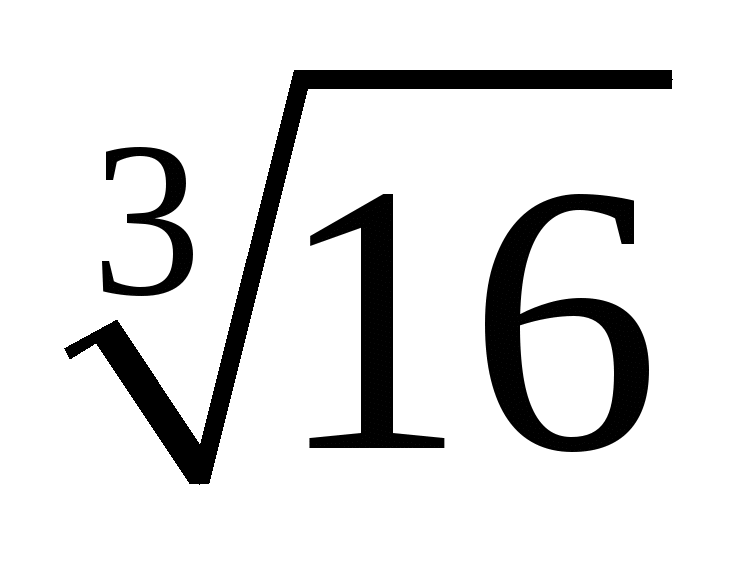 ;
; 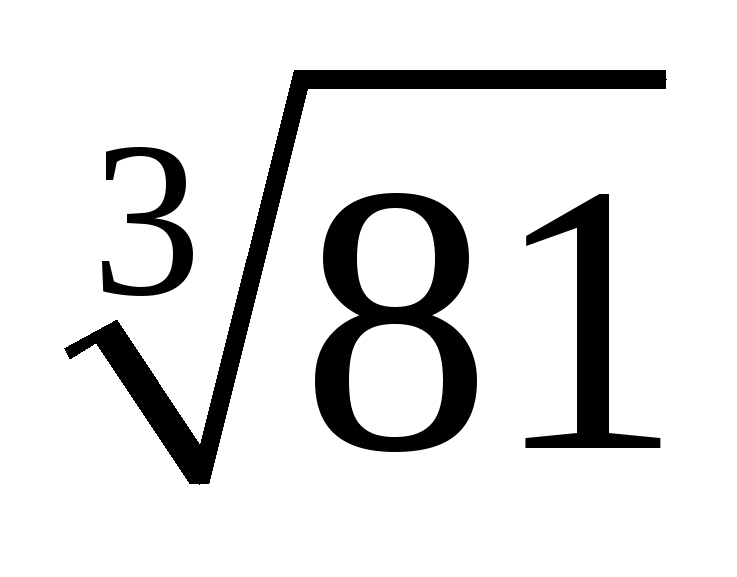 ;
; 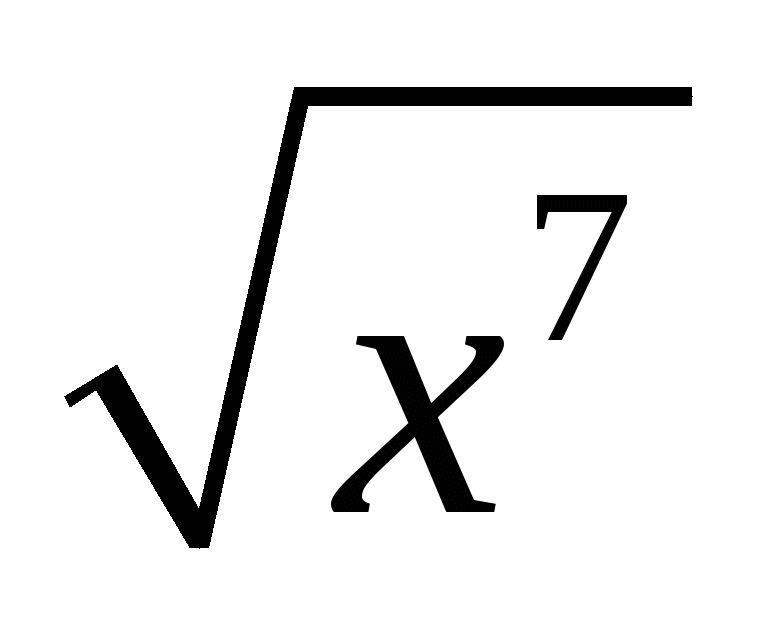 ;
; 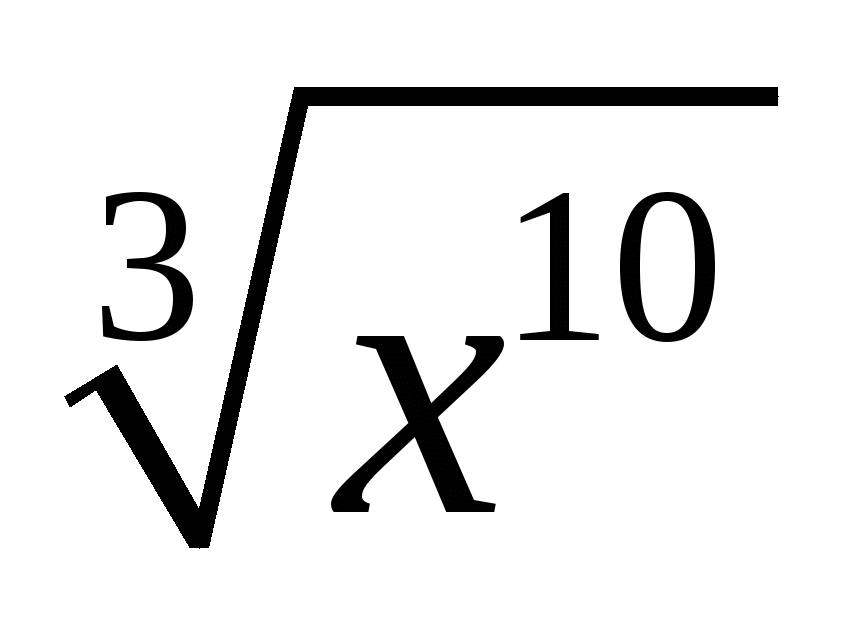
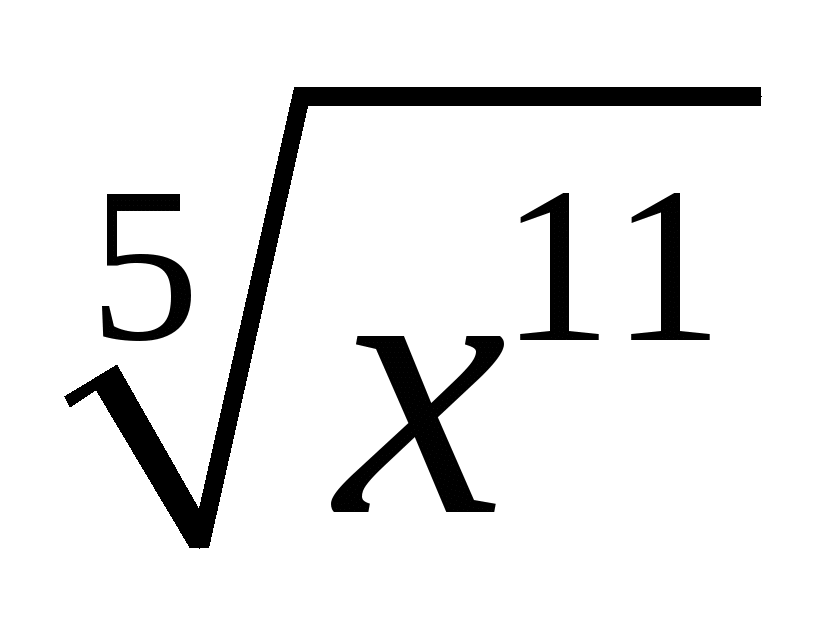 ;
; 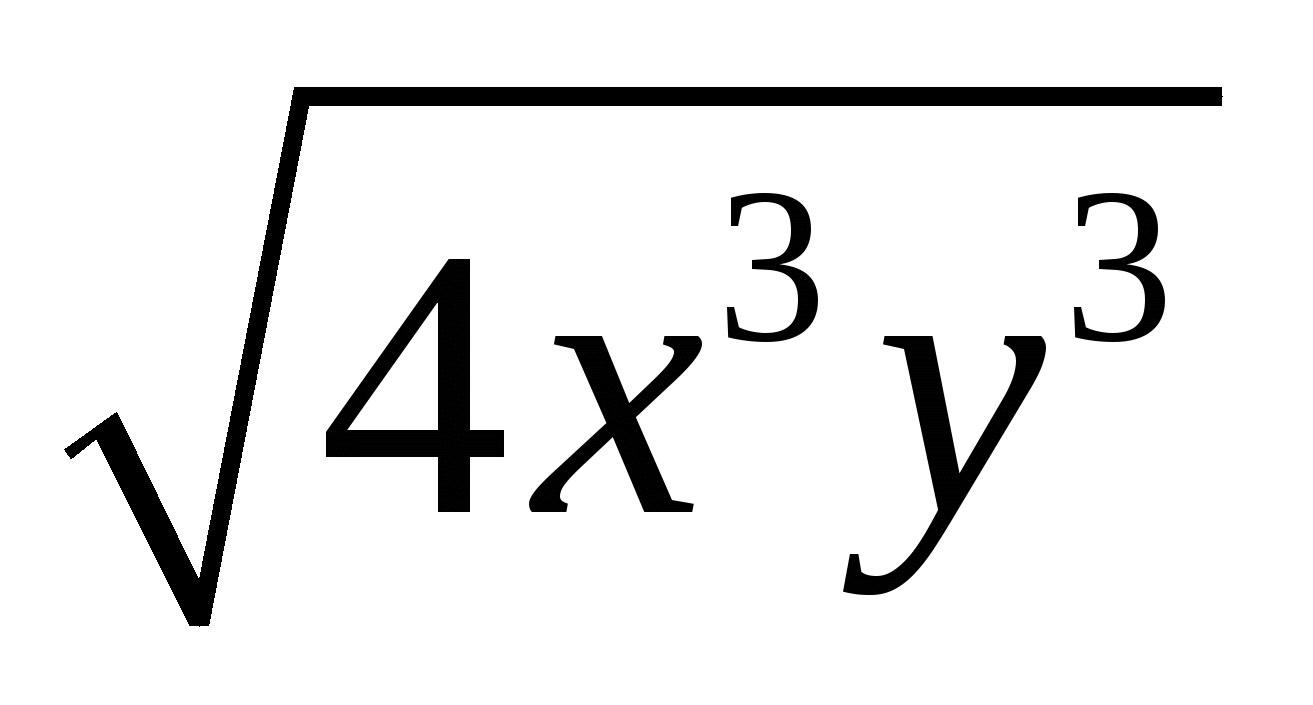 ;
; 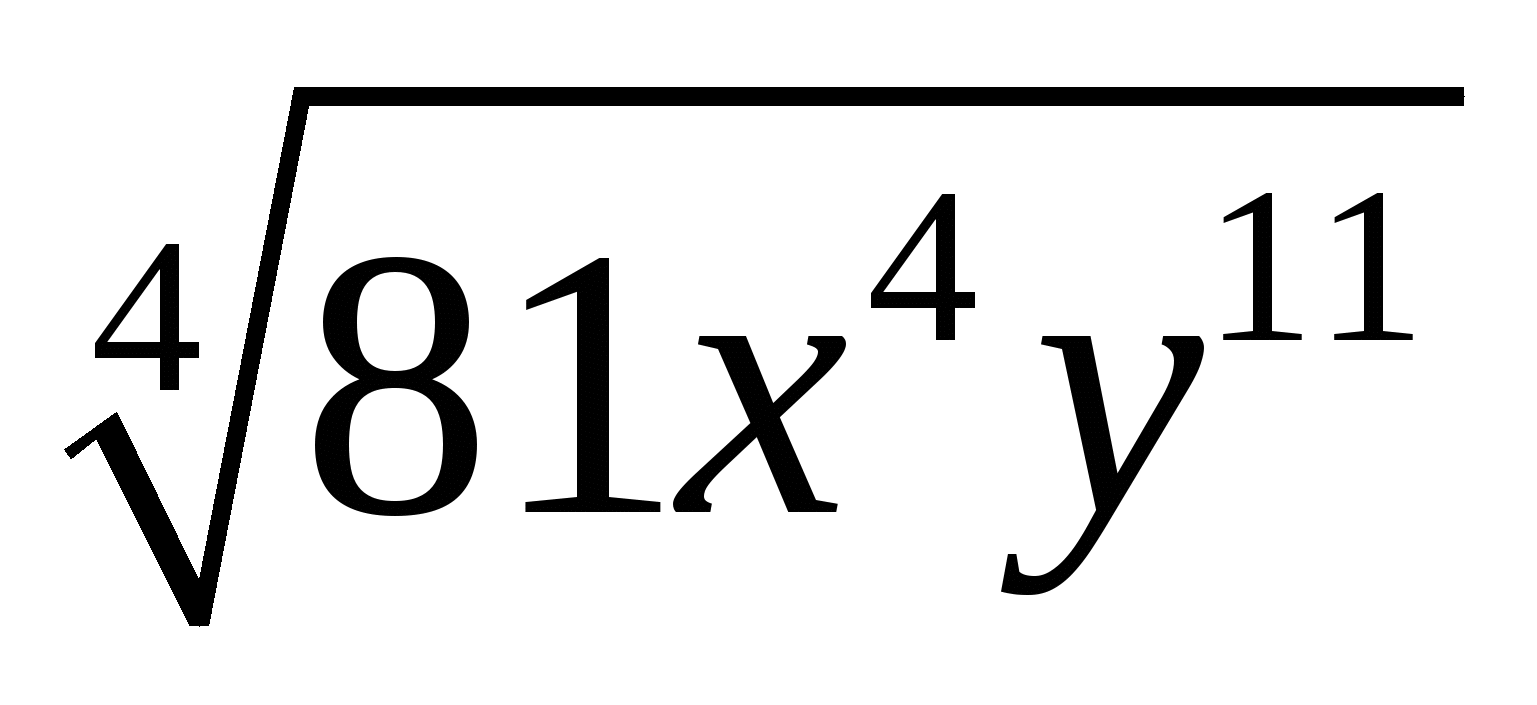 Сслайд 3
Сслайд 3Внесите множитель под знак корня ( х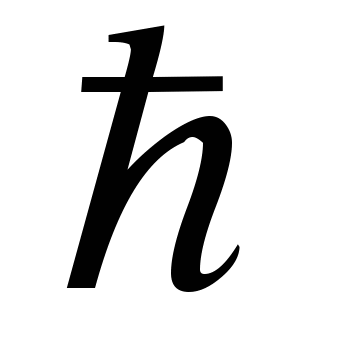 0, у
0, у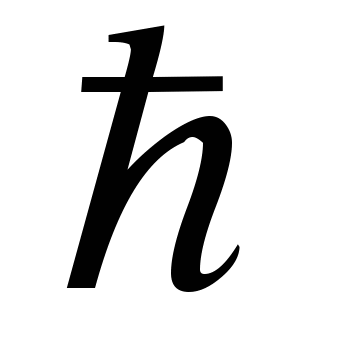 0 ) :
0 ) :
3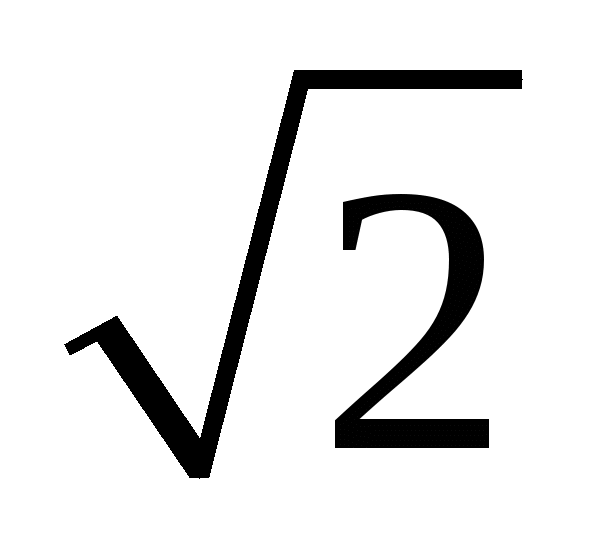 ; 2
; 2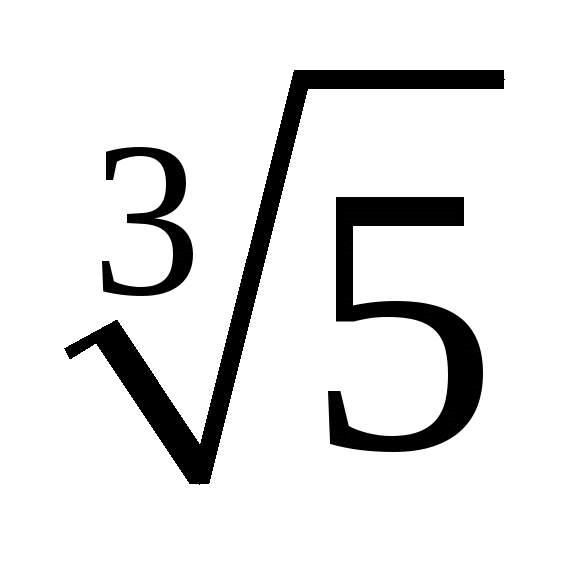
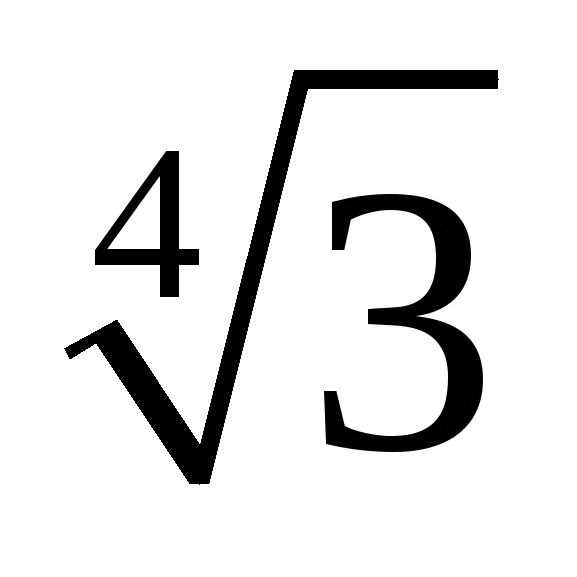 ; 4ху
; 4ху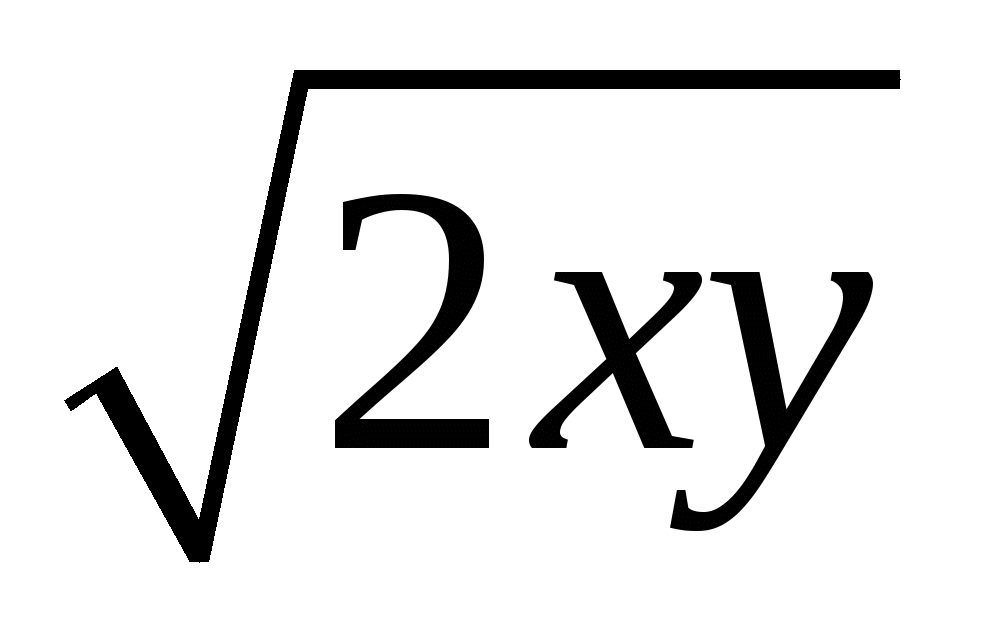 ;
; 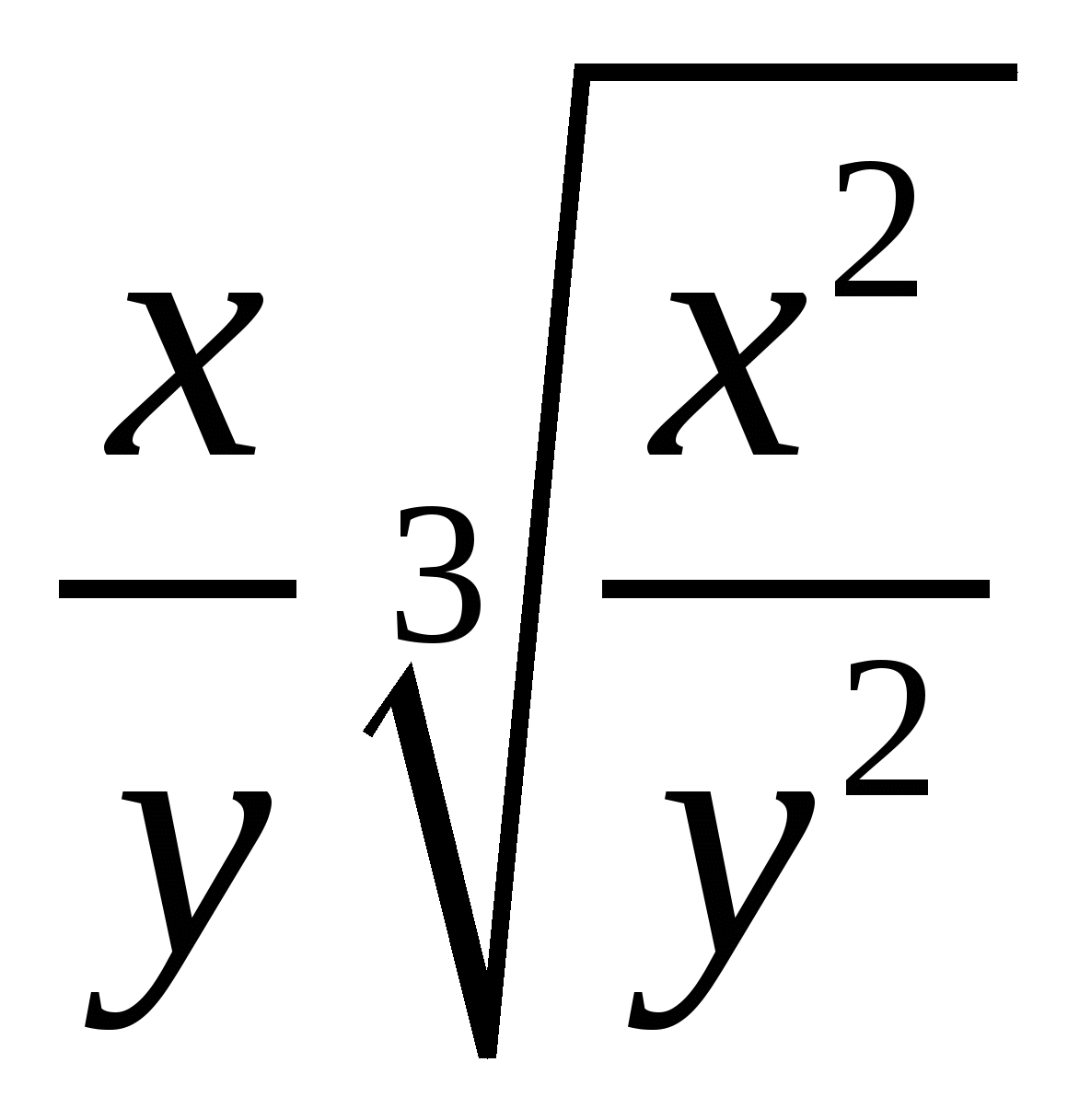 Слайд 4
Слайд 4Как избавиться от иррациональности в знаменателе ?
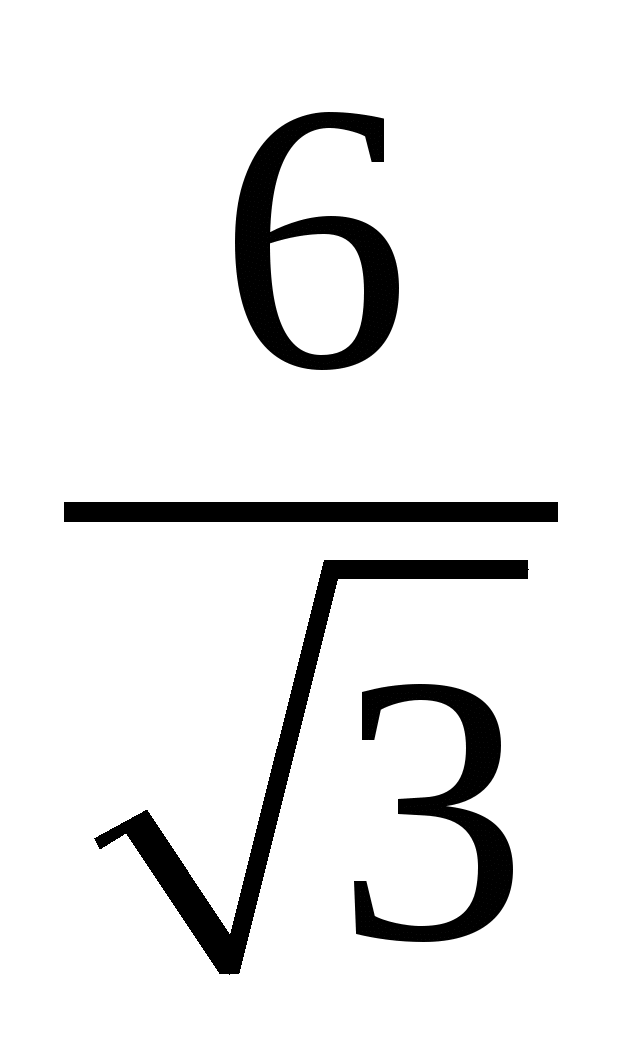 ;
; 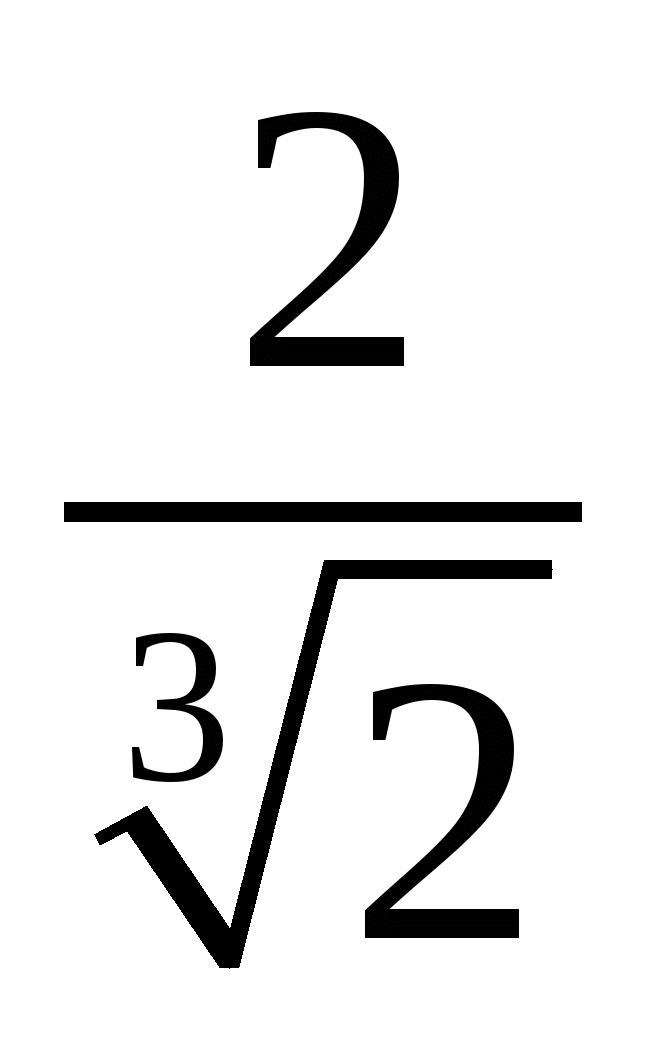 ;
; 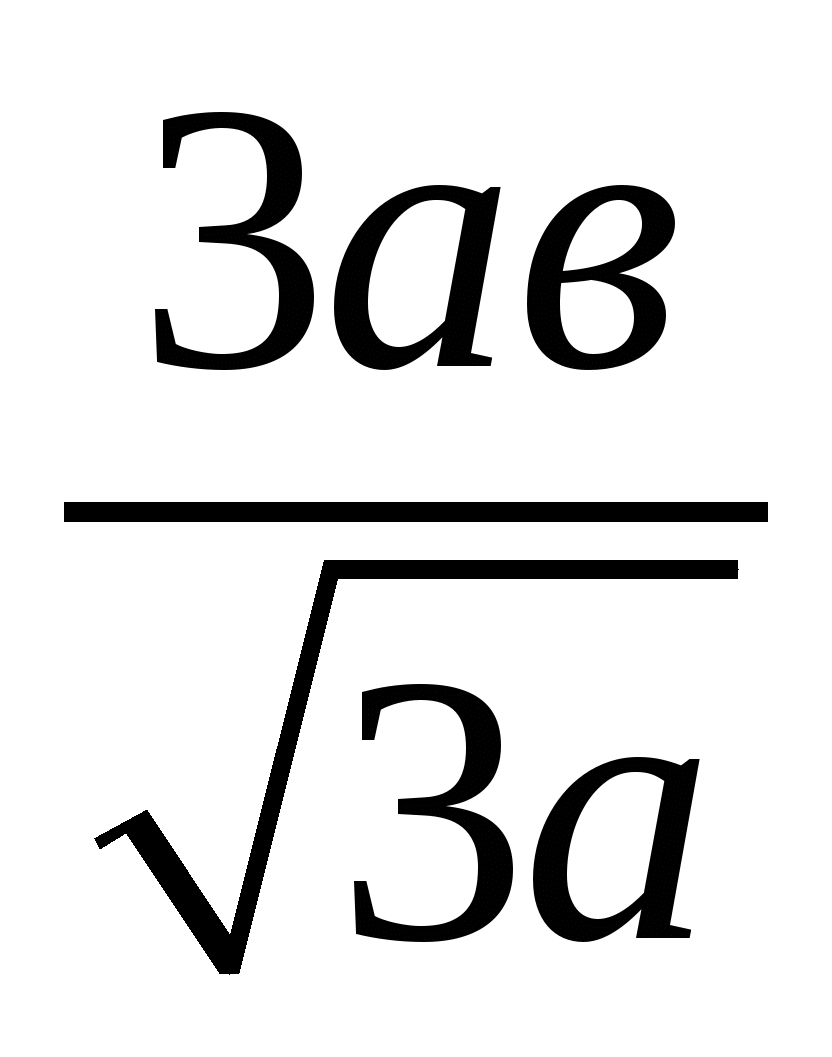
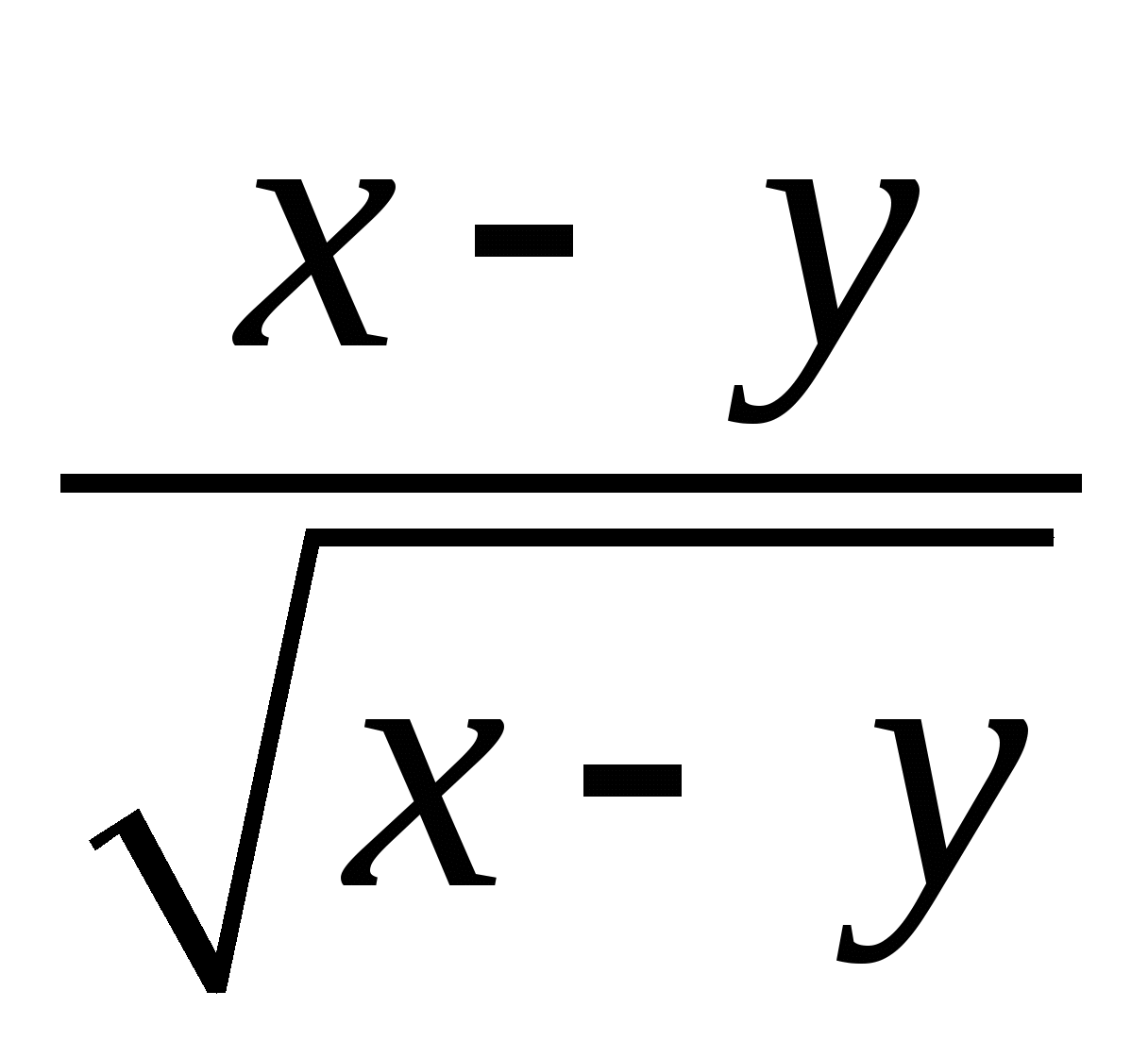 ;
; 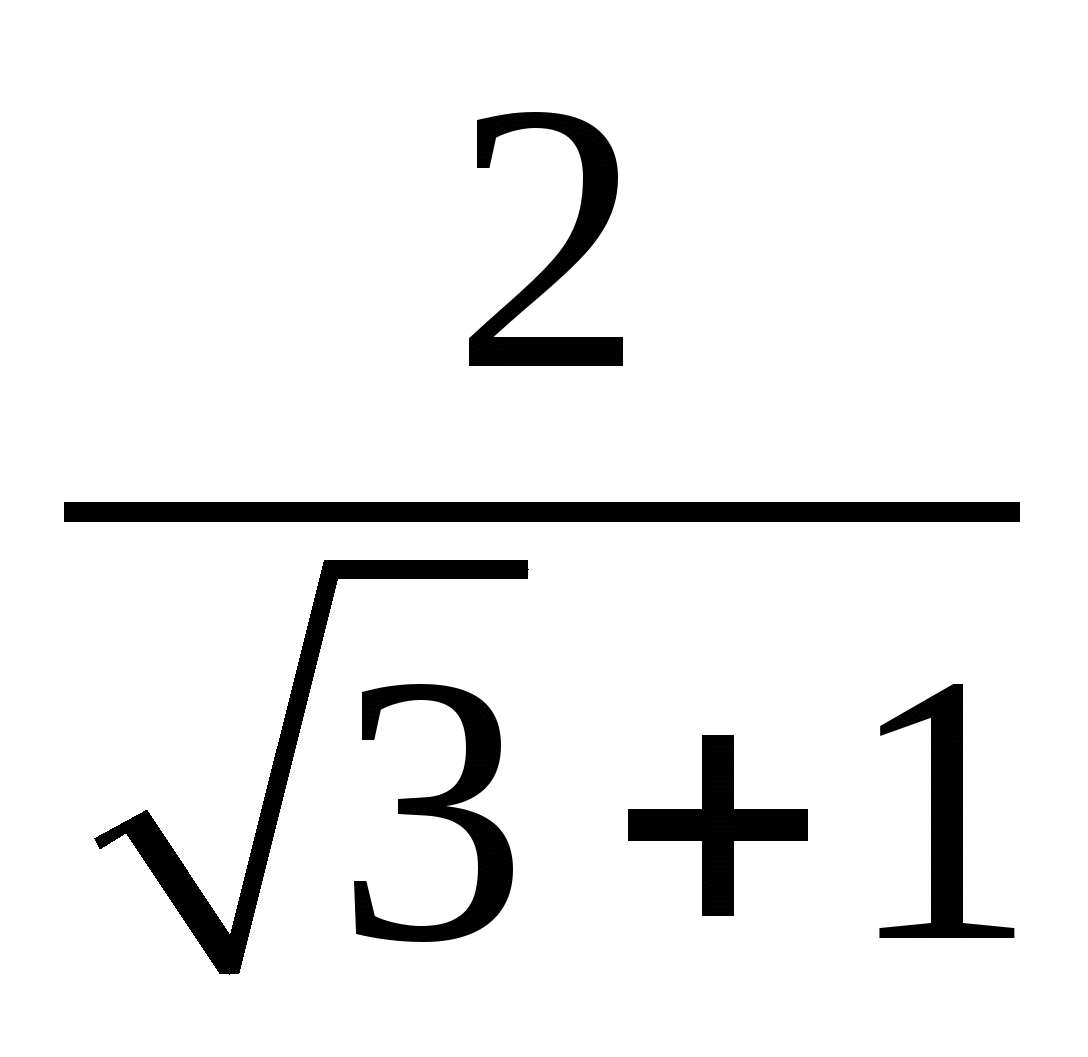 .
.2) Арифметическая разминка .
Задания выполняются учащимися на переносной доске и в тетрадях.( Задание б) — проблемная ситуация : учащиеся должны догадаться и увидеть ,,спрятавшиеся формулы сокращенного умножения под знаками радикалов)
Упростить : а) 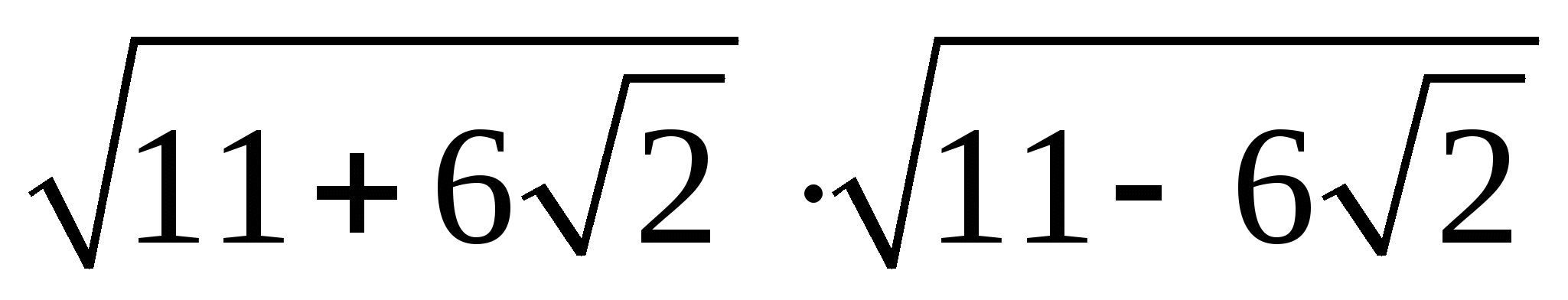 ; б)
; б) 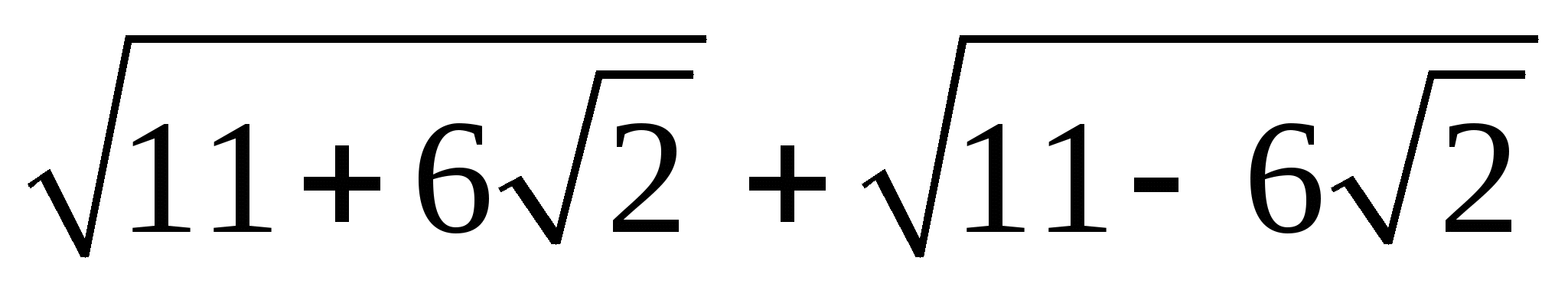 .
.
3. Повторение.
3*Фронтальный опрос — переходный мостик от ранее изученного к новому:
* Что такое уравнение ?
* Что называется корнем уравнения ?
* Какие уравнения называются равносильными ?
* Что значит решить уравнение ?
* Какие виды уравнений вы знаете ?
( на переносной доске написан ряд уравнений – определить их вид )
3х – 2(5х + 4 ) = 17 ; 2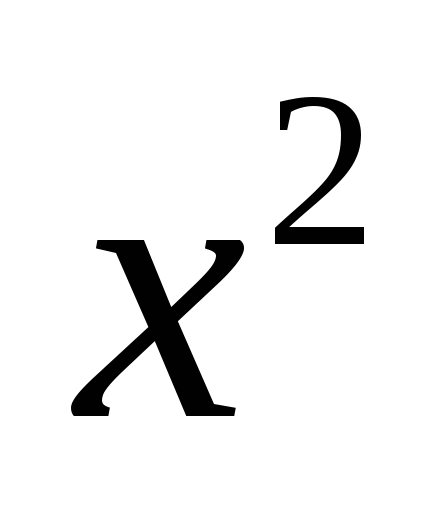 + 5х – 7 = 0 ;
+ 5х – 7 = 0 ; 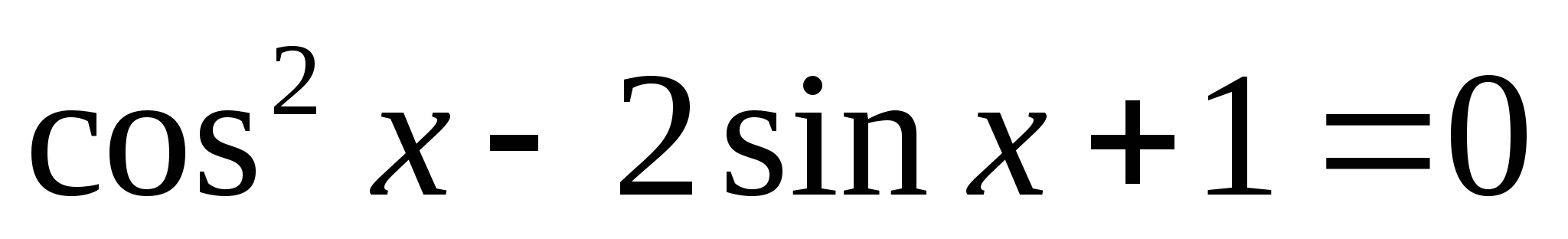 ;
; 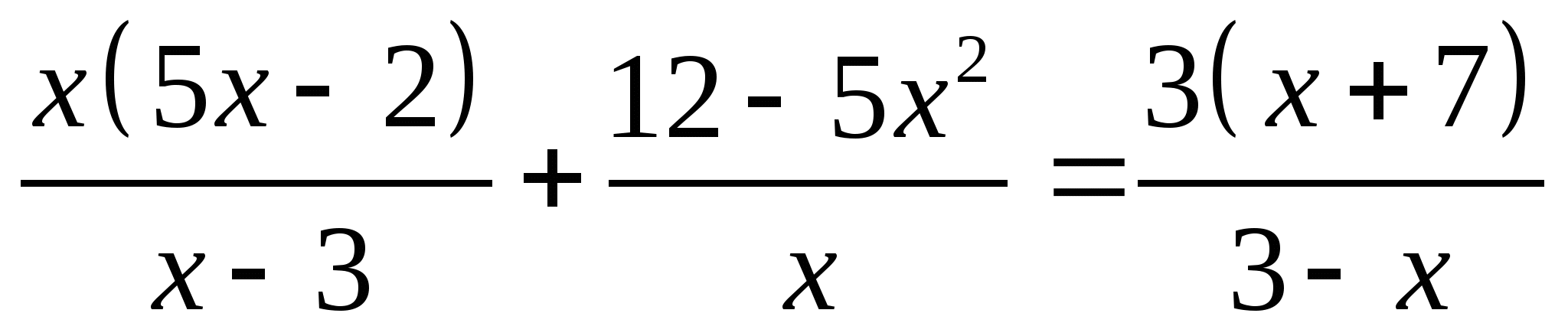 ;
; 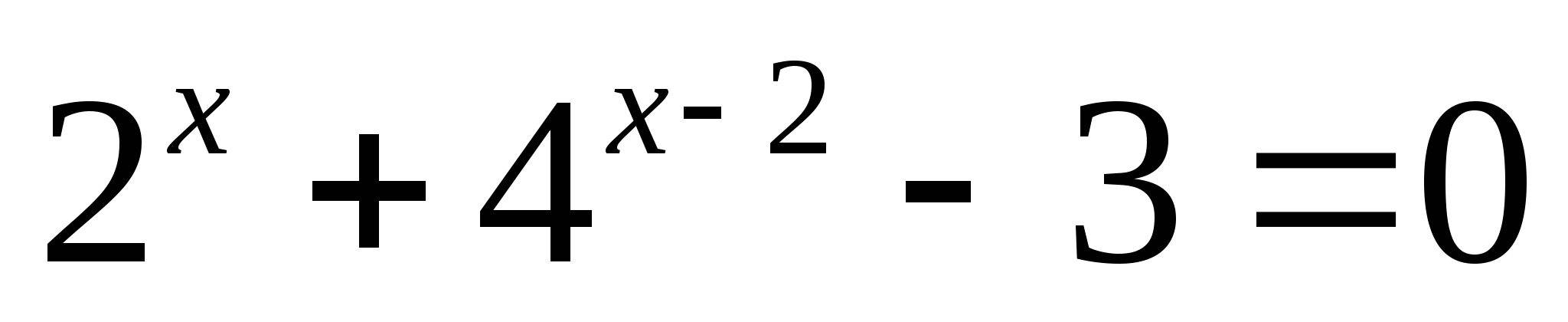 .
.
3** Определение: Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Решение иррационального уравнения
Схема перехода :
 :
: 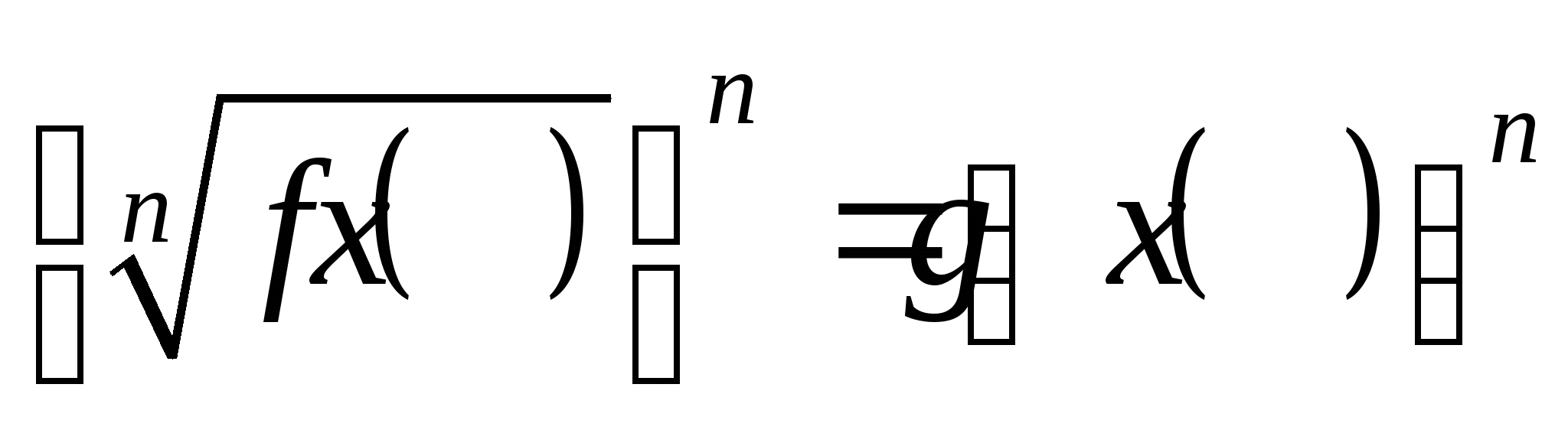
3***Решение иррациональных уравнений. Учитель дает образец оформления решения на доске, учащиеся делают записи в тетрадях. (опорные вопросы , комментарии учителя этапов решения)
1.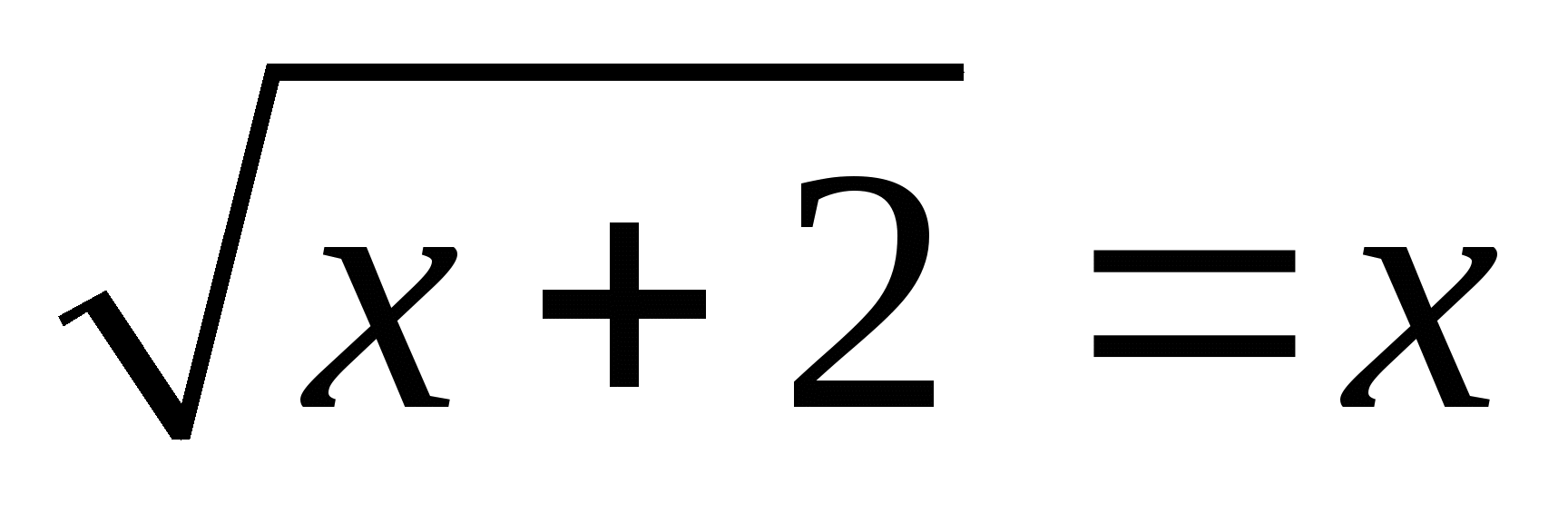 . Ответ: 2. При решении данного уравнения учащиеся самостоятельно должны придти к выводу 1 : При возведении обеих частей уравнения в четную степень возможно появление
. Ответ: 2. При решении данного уравнения учащиеся самостоятельно должны придти к выводу 1 : При возведении обеих частей уравнения в четную степень возможно появление
2. 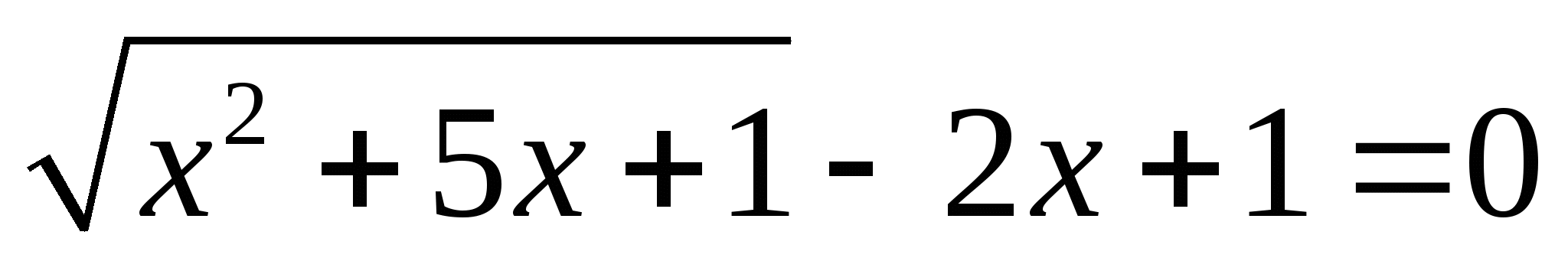 . Ответ : 3.
. Ответ : 3.
3. 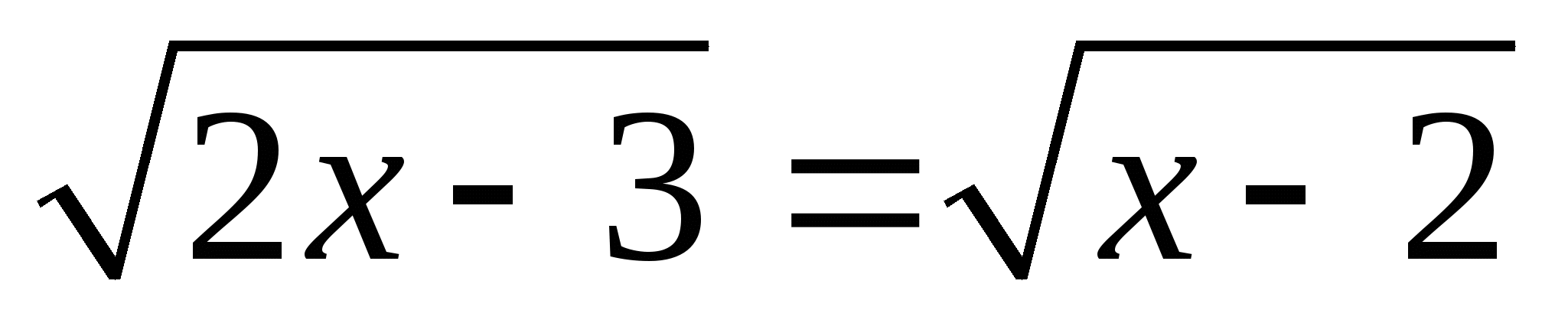 . Ответ : нет решений.
. Ответ : нет решений.
4. 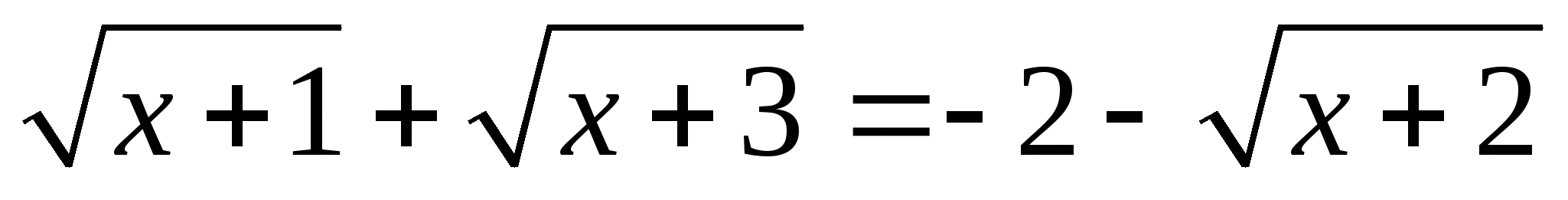 . Ответ : нет корней. ( при решении учитель показывает использование метода монотонности )
. Ответ : нет корней. ( при решении учитель показывает использование метода монотонности )
Иногда рациональнее решать иррациональное уравнение, определив ОДЗ, используя равносильные переходы.
5. 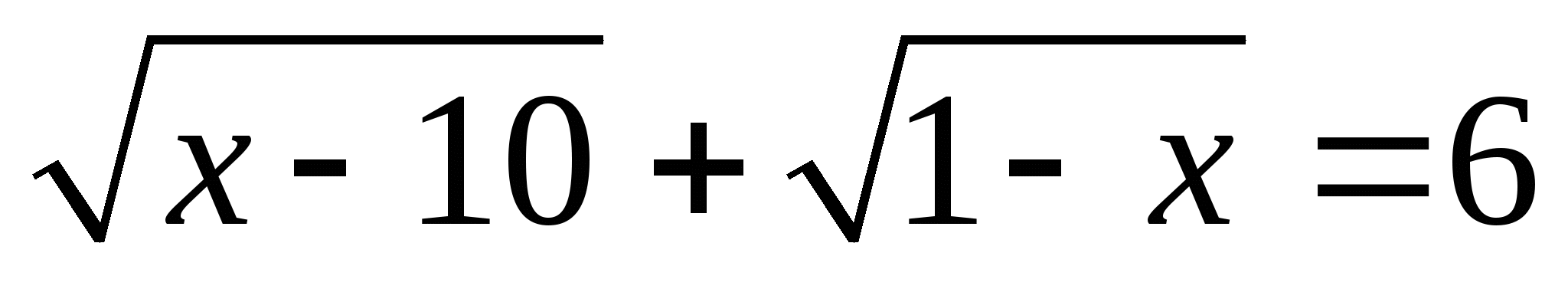 . Ответ : нет корней.
. Ответ : нет корней.
6. 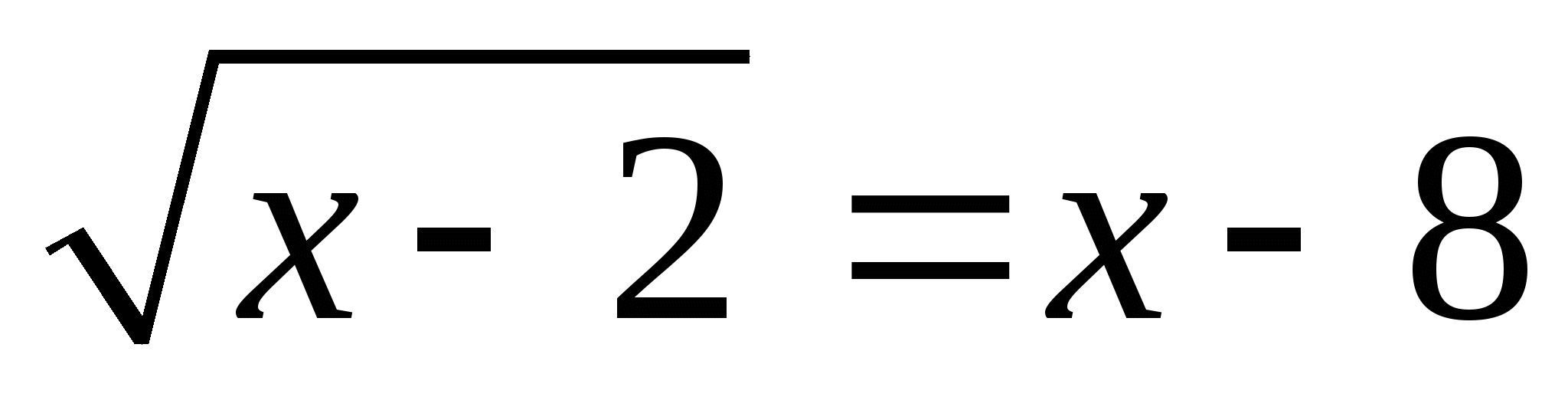 . Ответ: 11.
. Ответ: 11.
7. 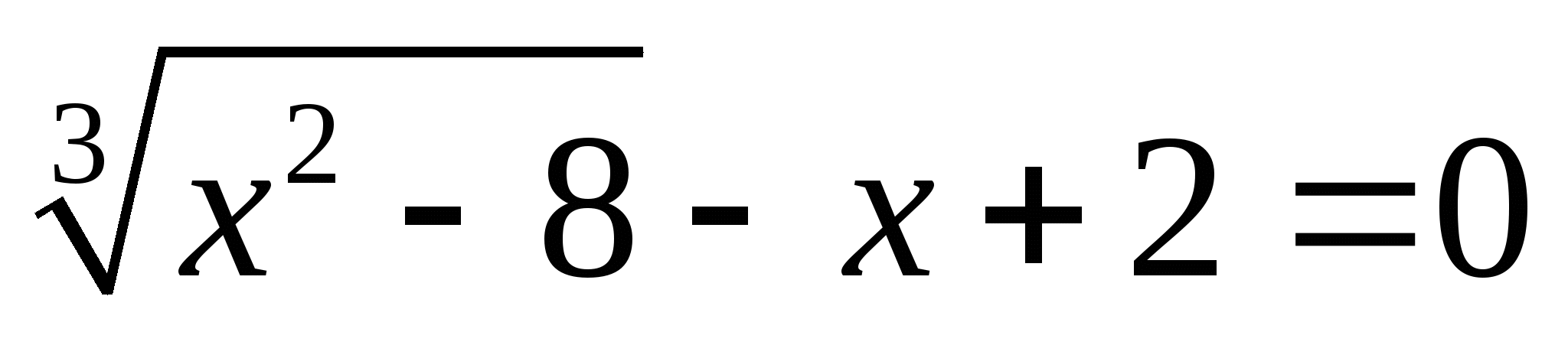 . Ответ : 0 ; 3 ; 4.
. Ответ : 0 ; 3 ; 4.
4.Закрепление повторяемого материала
4* Решение уравнений по тестовым заданиям ЕГЭ
Слайд 5Какие из уравнений являются иррациональными ?
1) 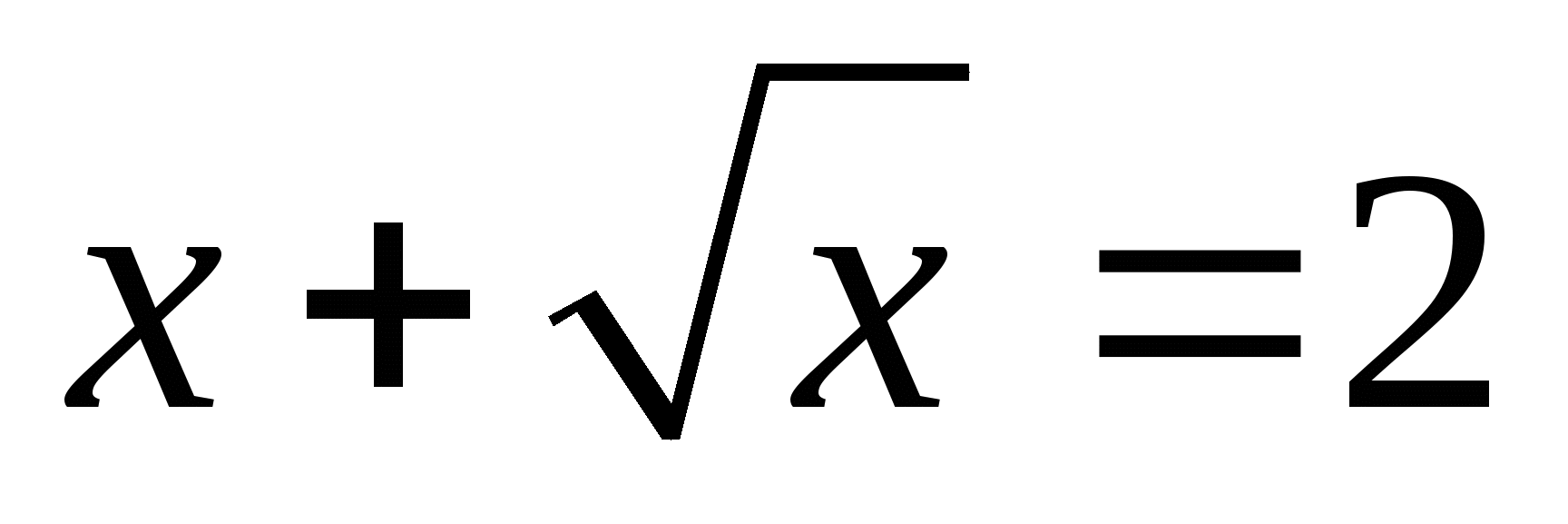 ; 2)
; 2) 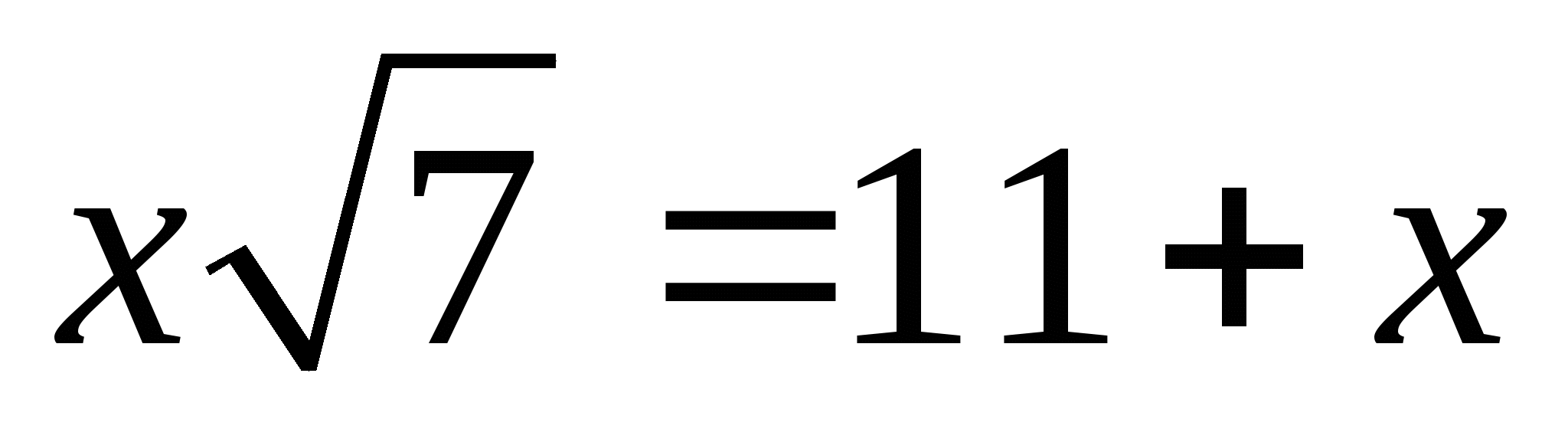 ; 3)
; 3) 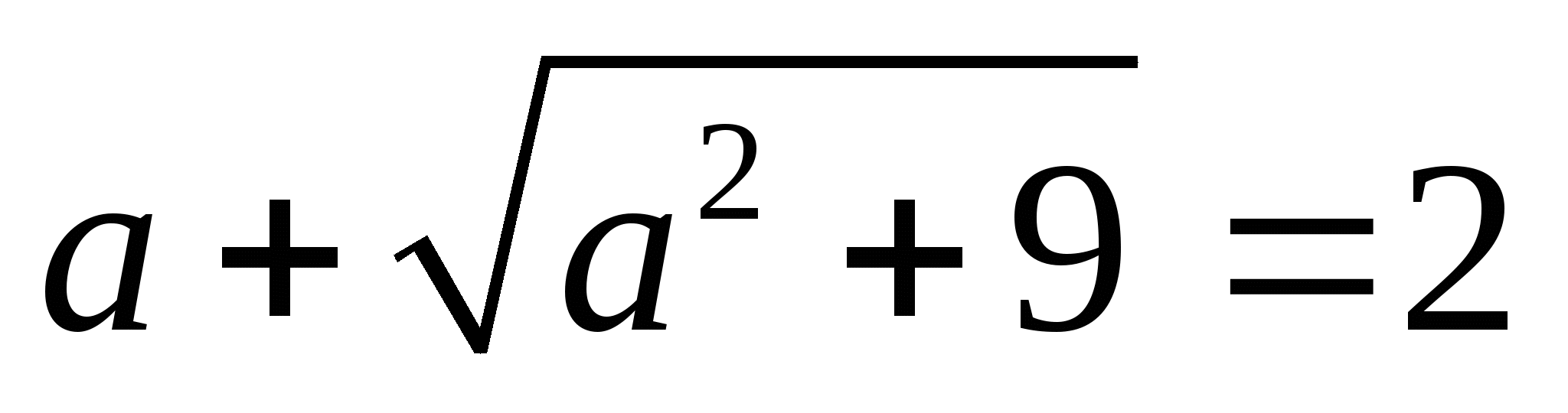 ; 4)
; 4) 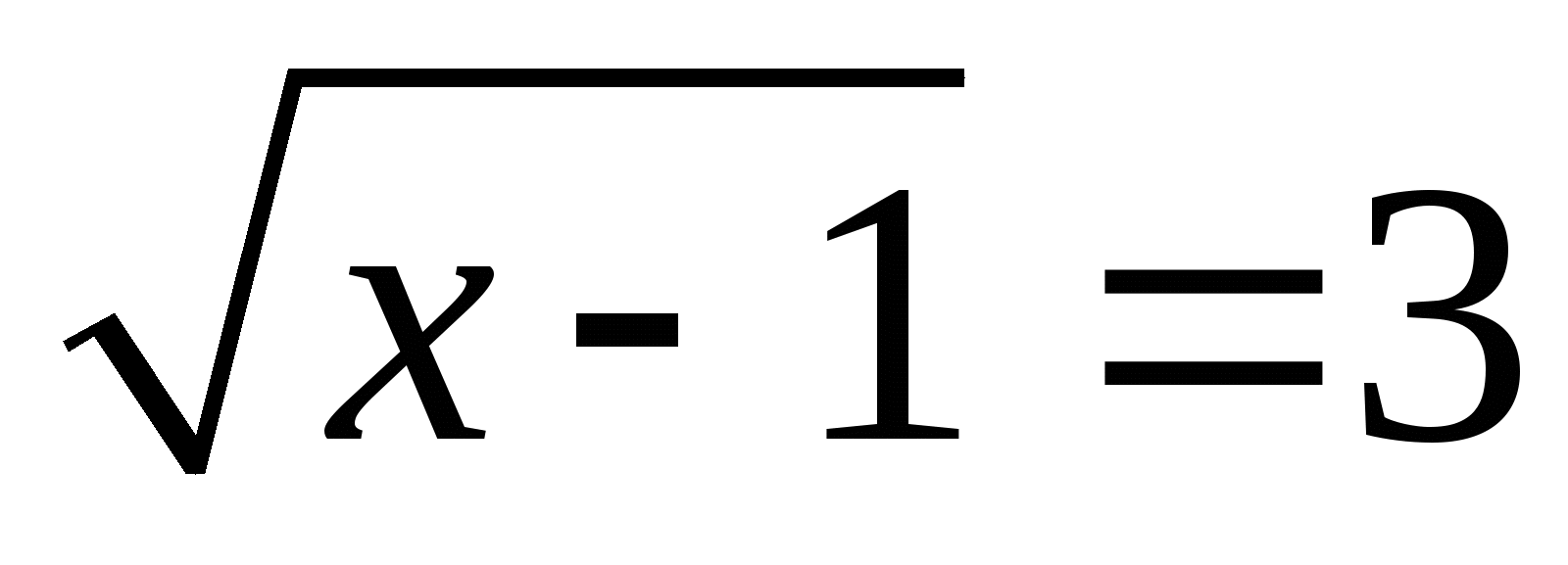 ; 5)
; 5) 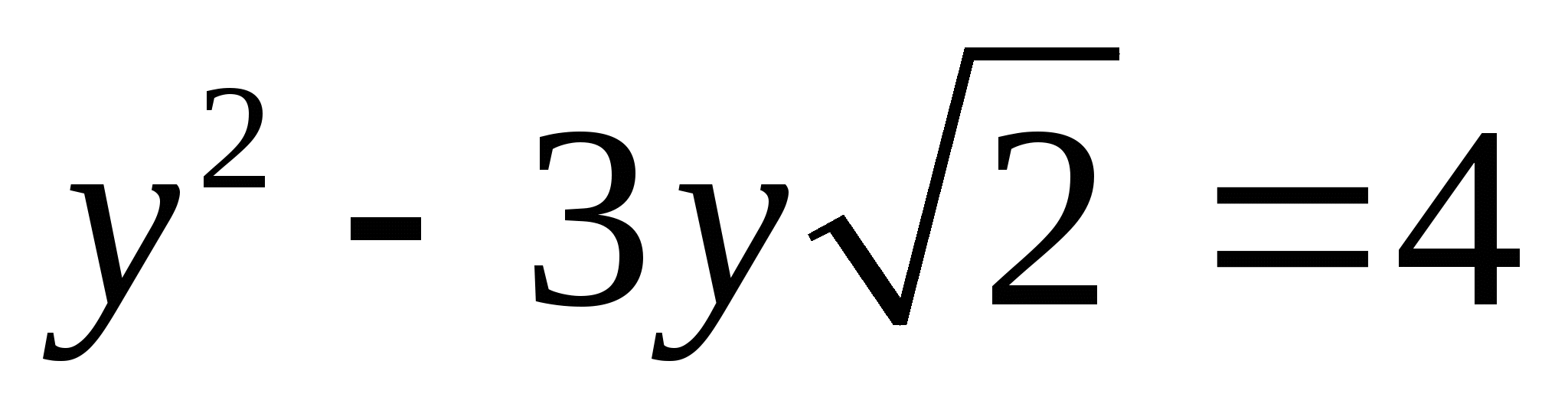 .
.
Является ли число 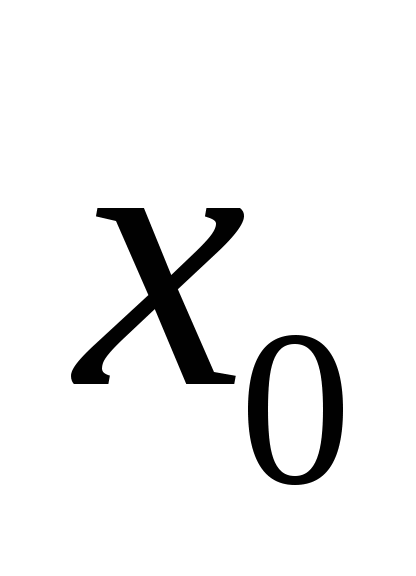 корнем уравнения ?
корнем уравнения ?
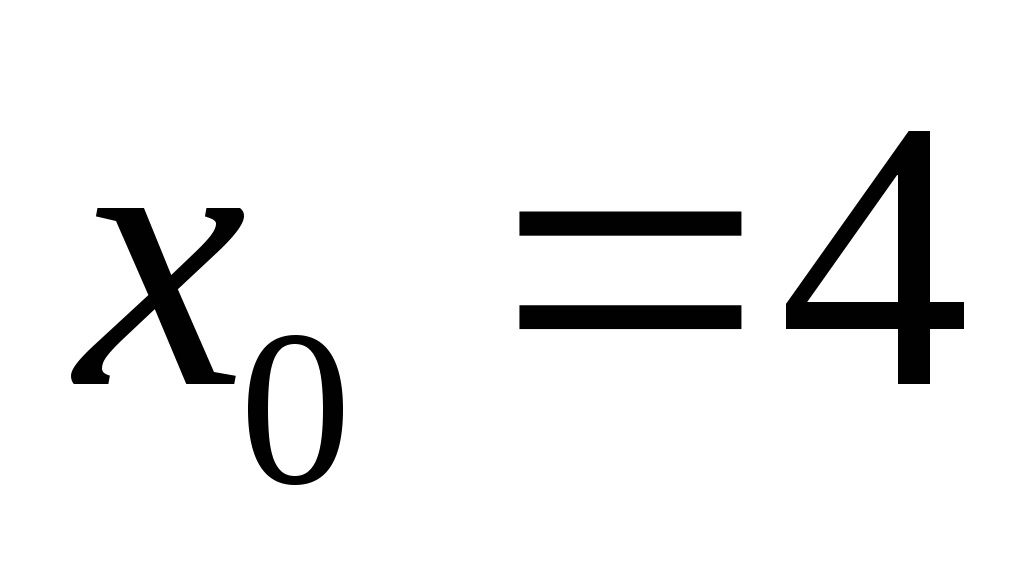
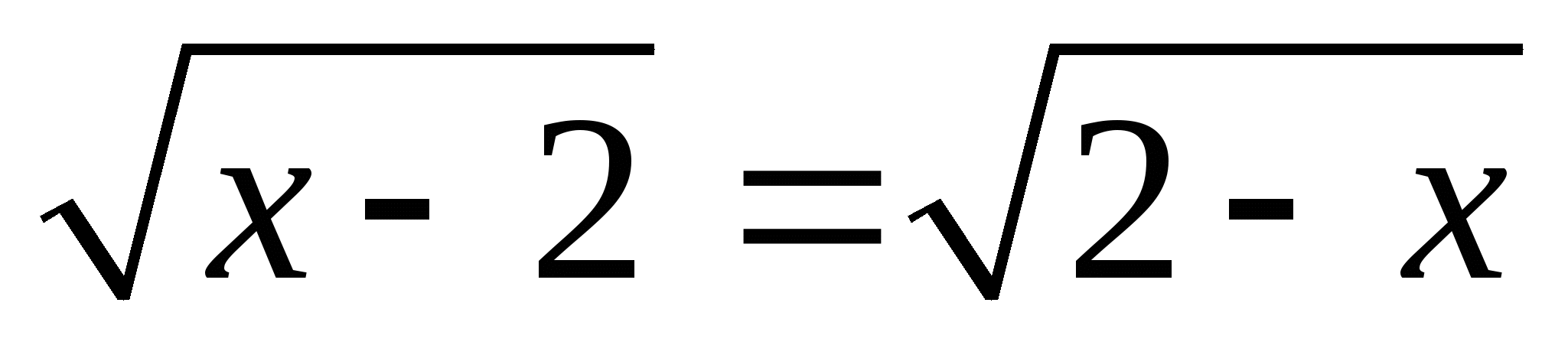 ;
; 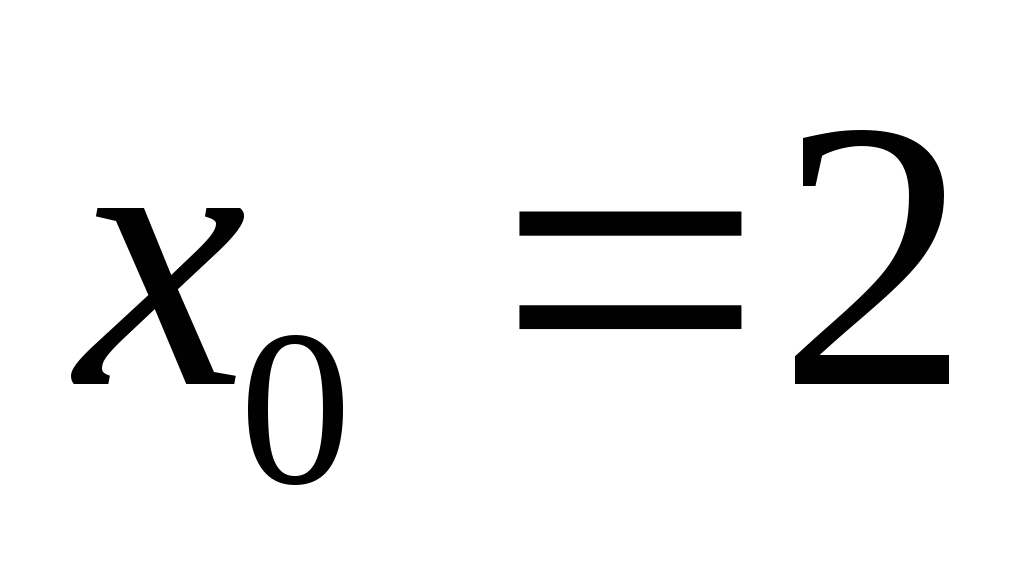
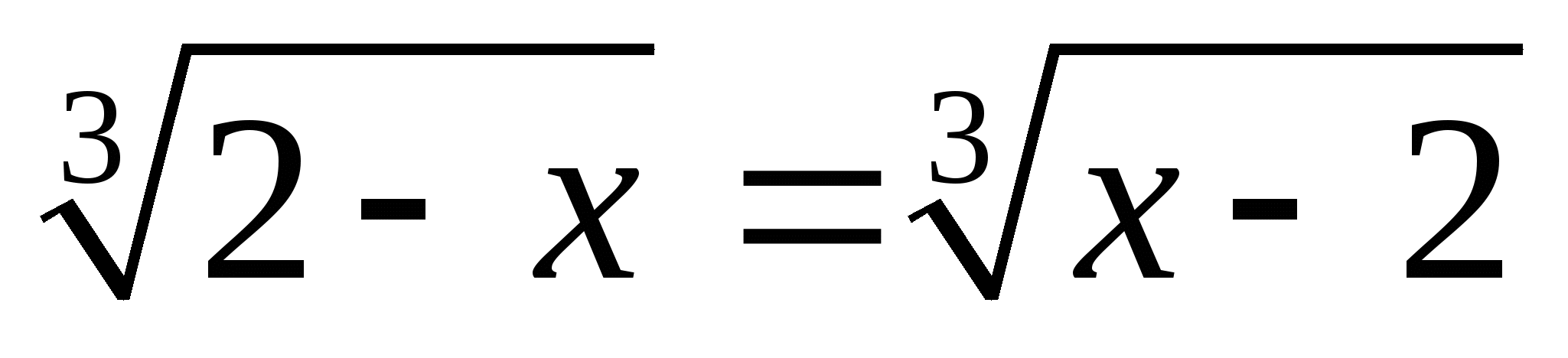 ;
; 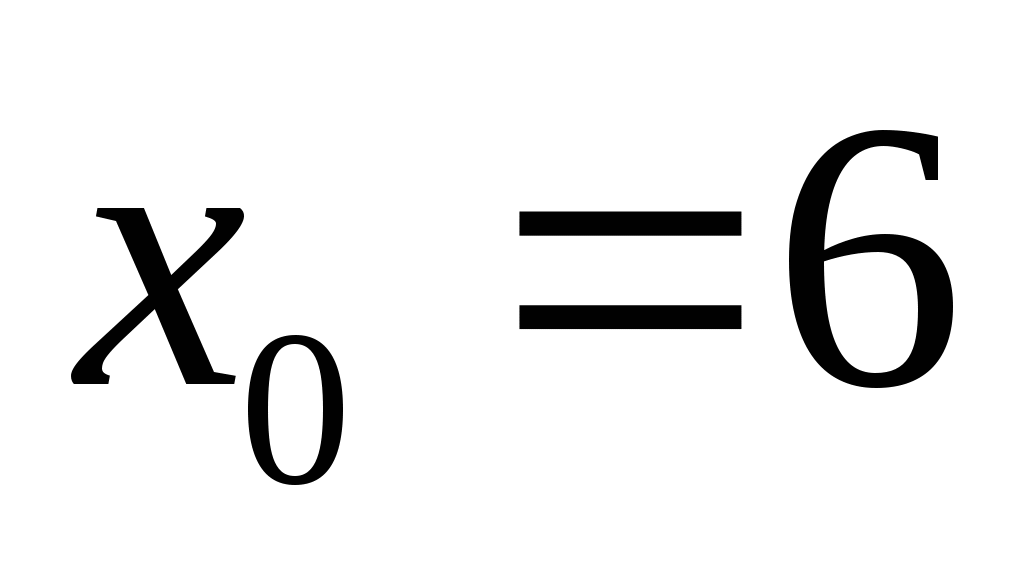
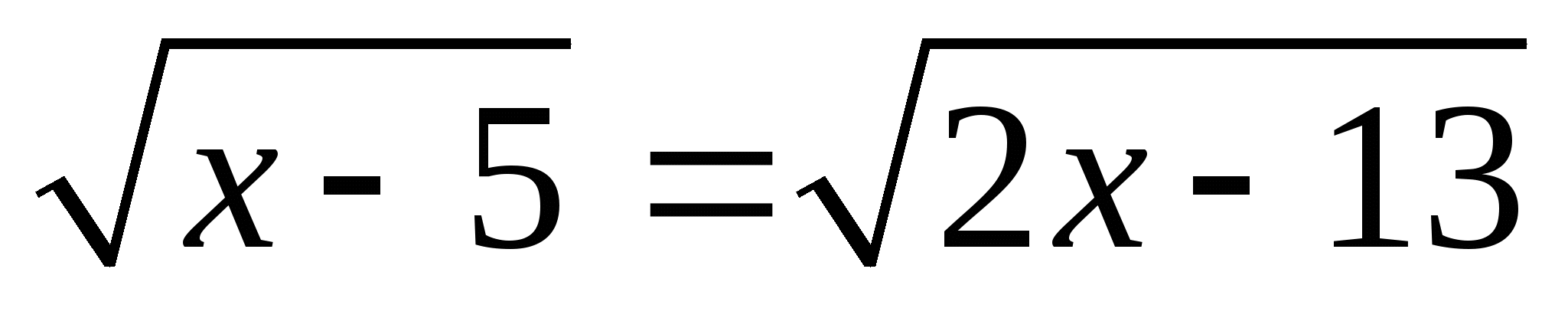 ;
;
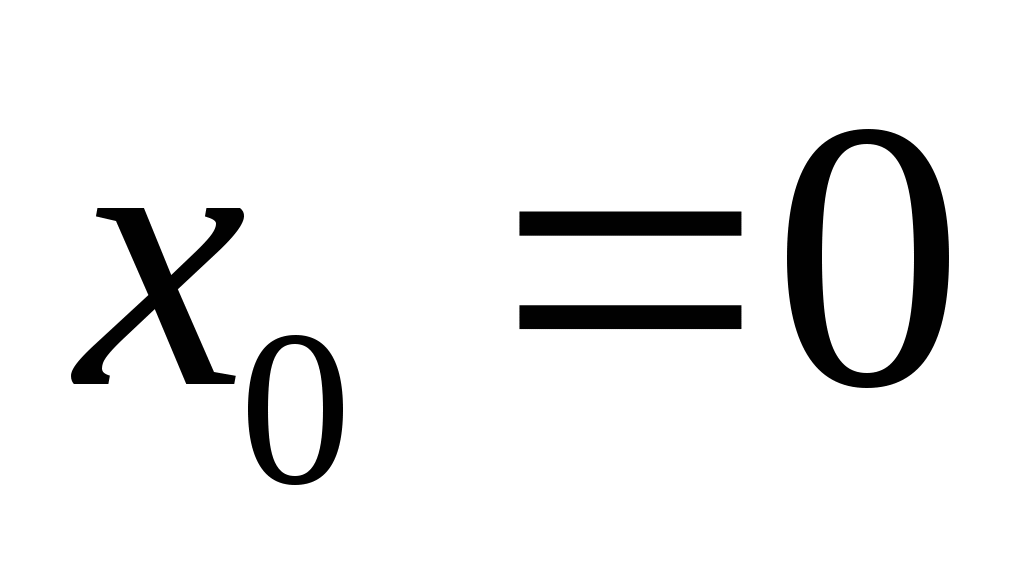
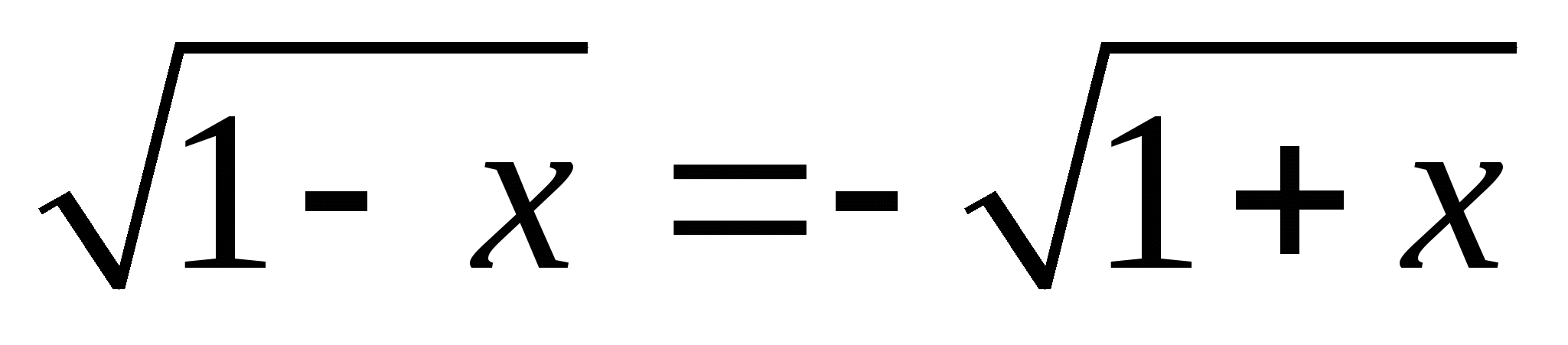
— Основной способ решения иррациональных уравнений ( возведение в степень )
— О чем надо помнить при решении иррациональных уравнений данным способом ? ( о необходимости сделать проверку корней , т.к. появляются посторонние корни)
— Каким еще можно решить способом ? ( найти ОДЗ и осуществить равносильные переходы )
5. Рубрика — это интересно. А ряд иррациональных уравнений можно решить методом ,,пристального взгляда,, суть которого заключается в очевидности корней или их явного отсутствия по причине разногласия с ОДЗ. Например :
Слайд 7*1. 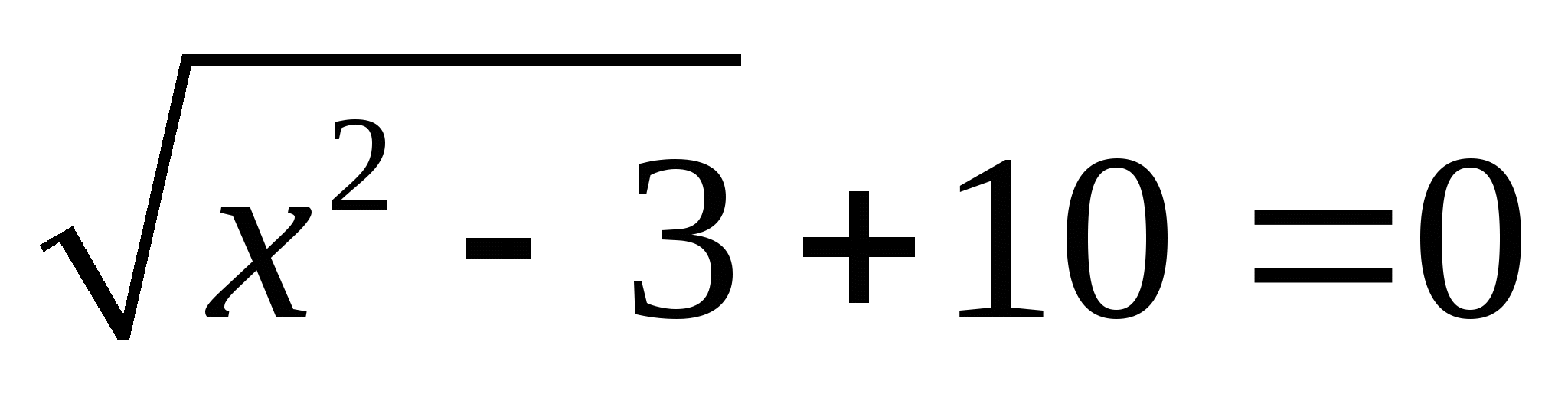 ;
;
2. 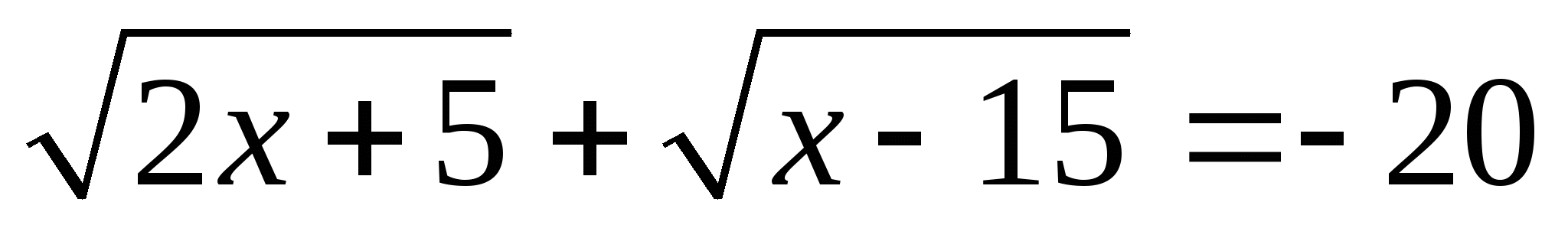 ;
;
3. 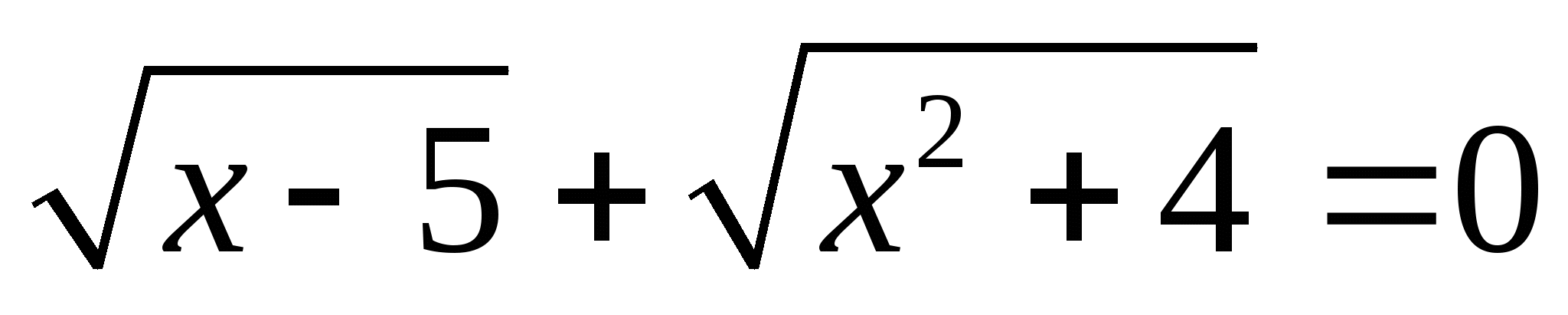 ;
;
4. 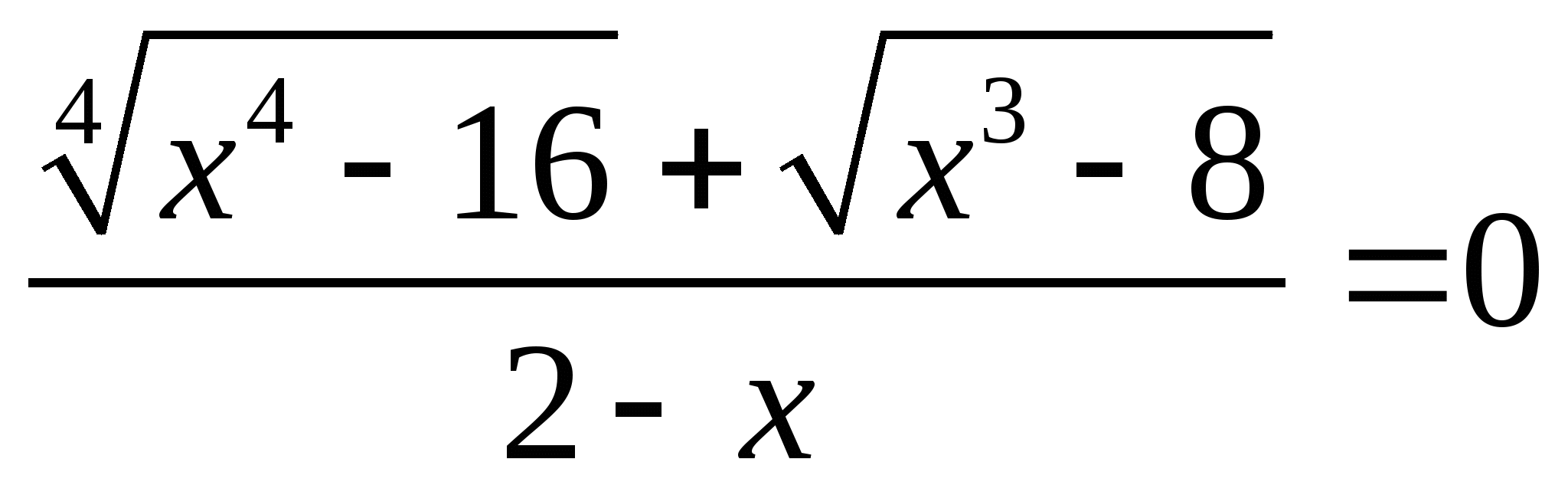 ;
;
5. 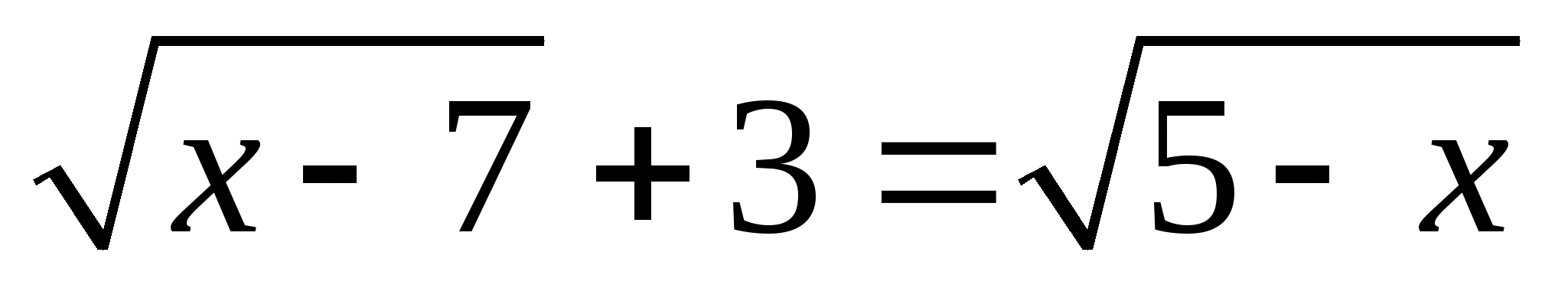 ;
;
Слайд 7
6. 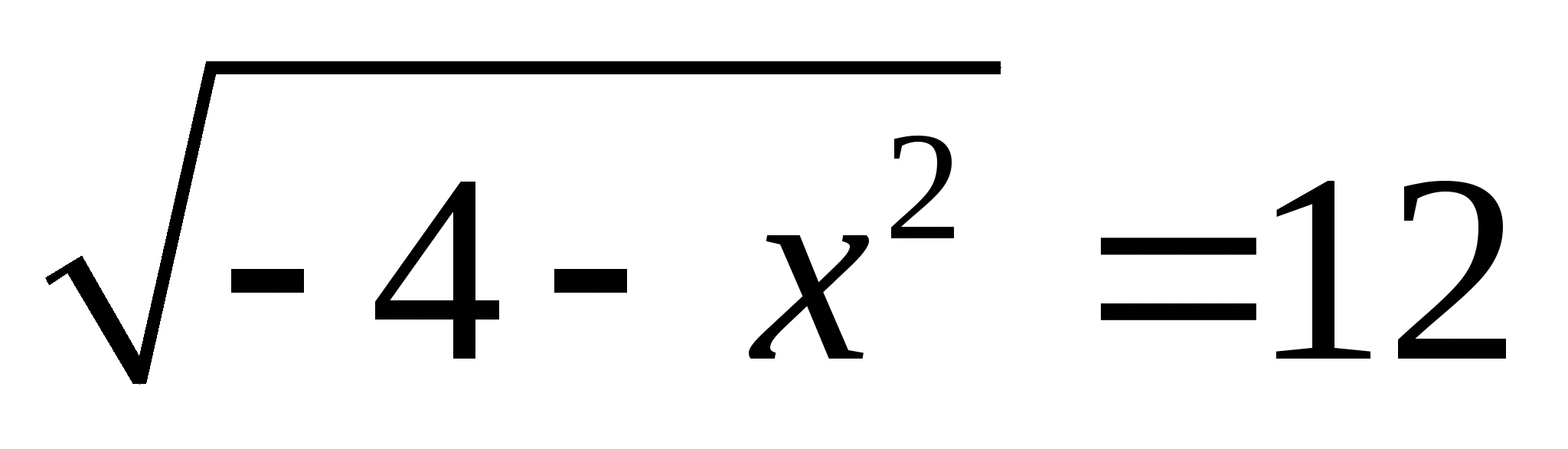 ;
;
7. 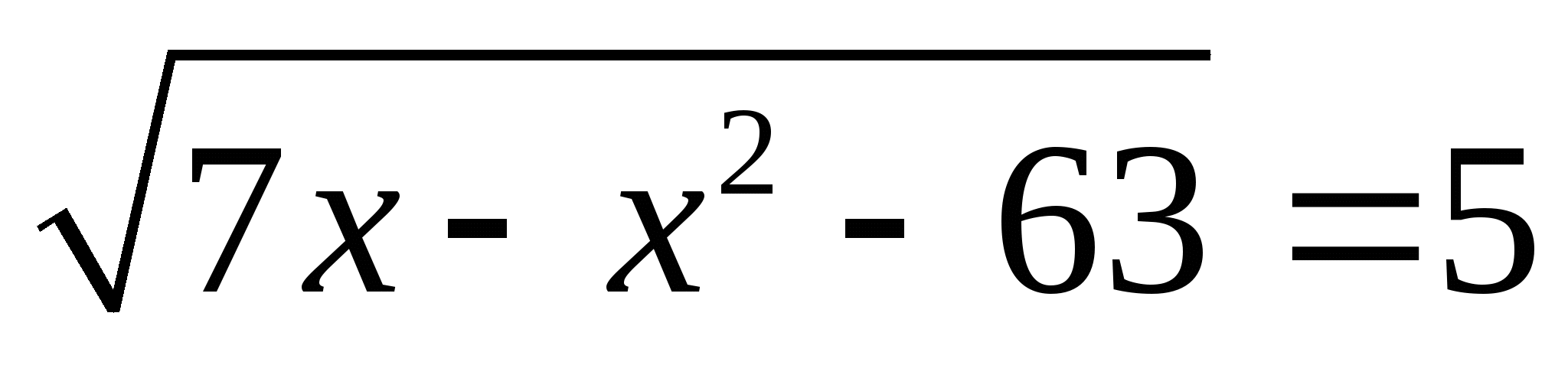 ;
;
8. 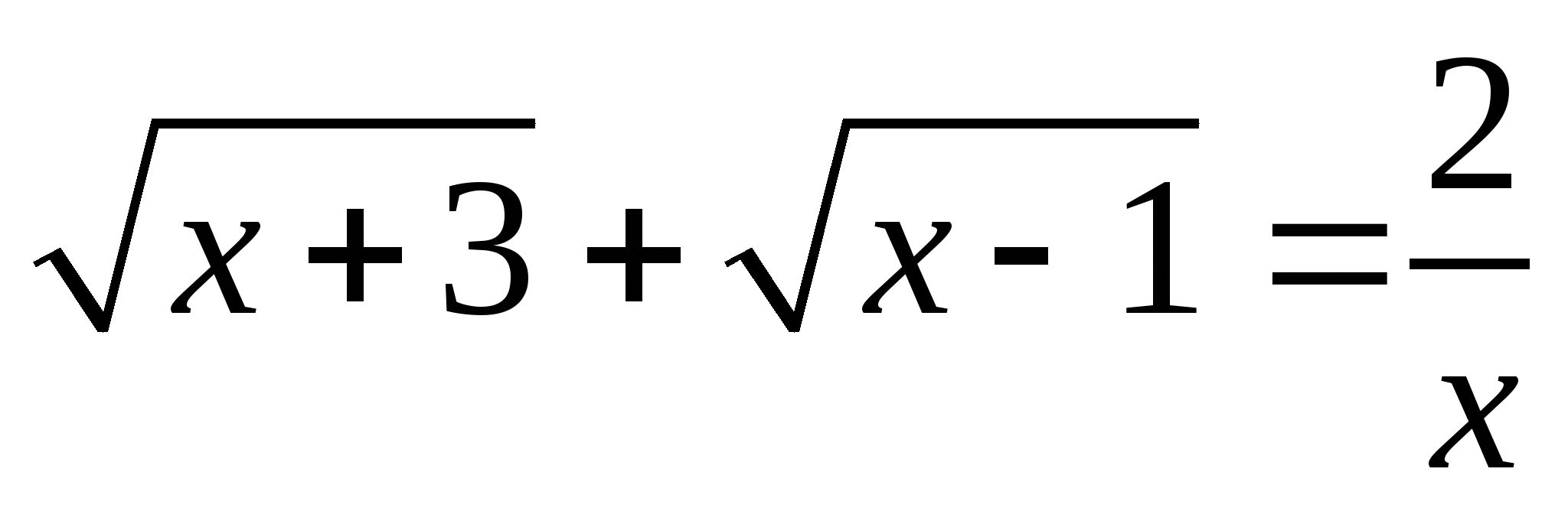 ;
;
9. 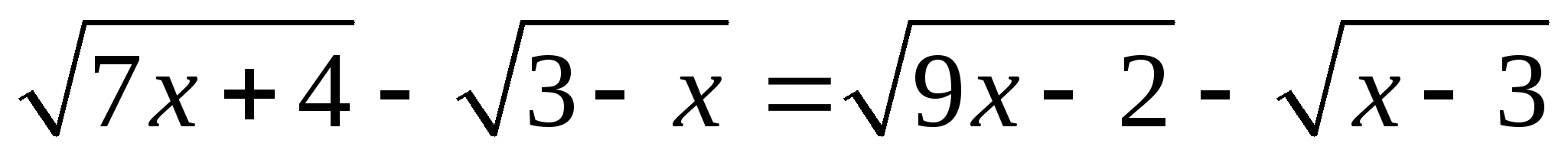 ;
;
10. 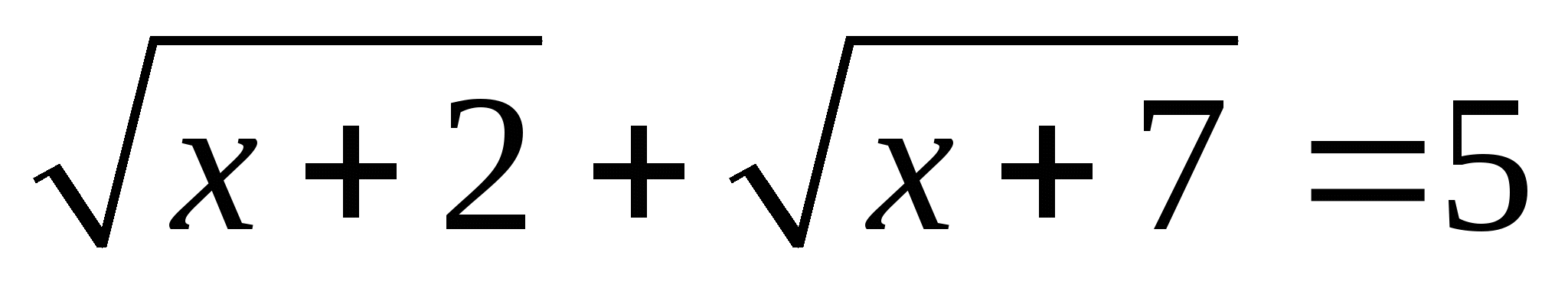 .
.
5* Развиваем алгебраическую зоркость. Задаются решения иррациональных уравнений, в которых допущены ,,стандартные,, ошибки. Найти их.
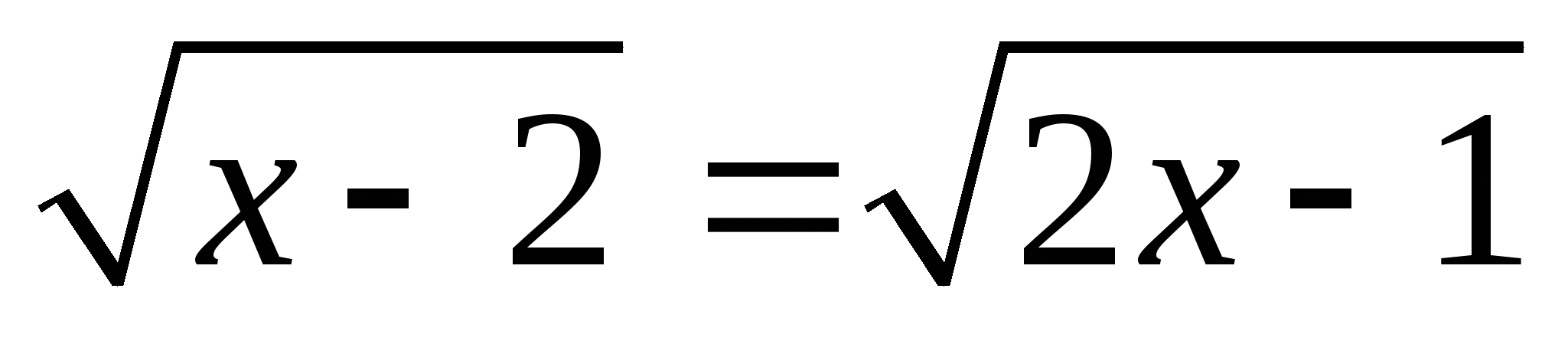
Решение :
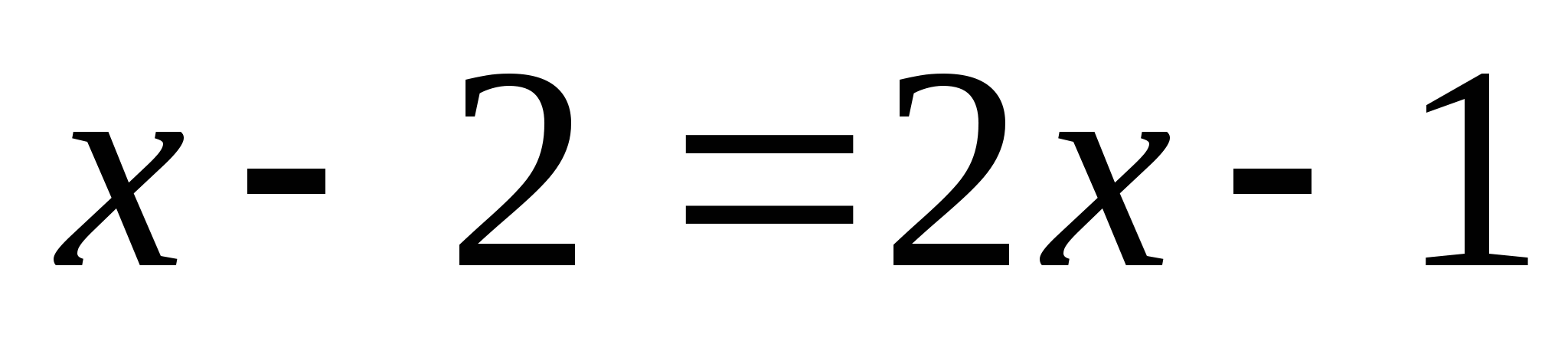
Ответ : 1
Ошибка. Ученик возвел в квадрат формально. На области 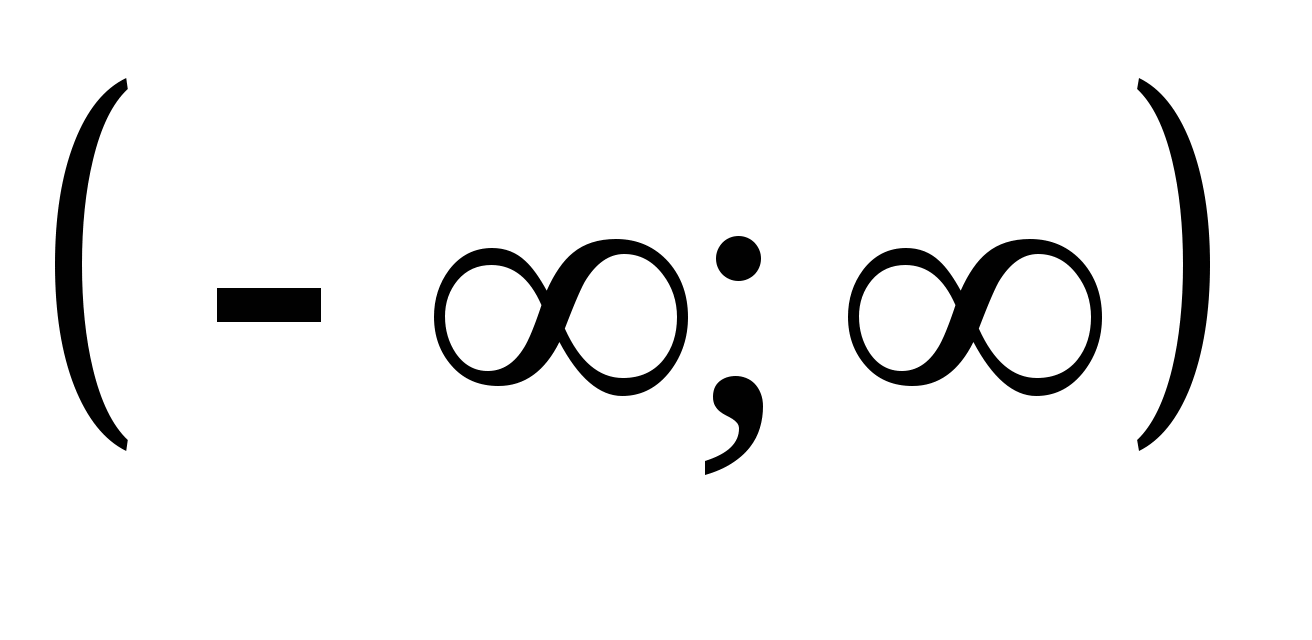 обе части уравнения не определены.
обе части уравнения не определены.
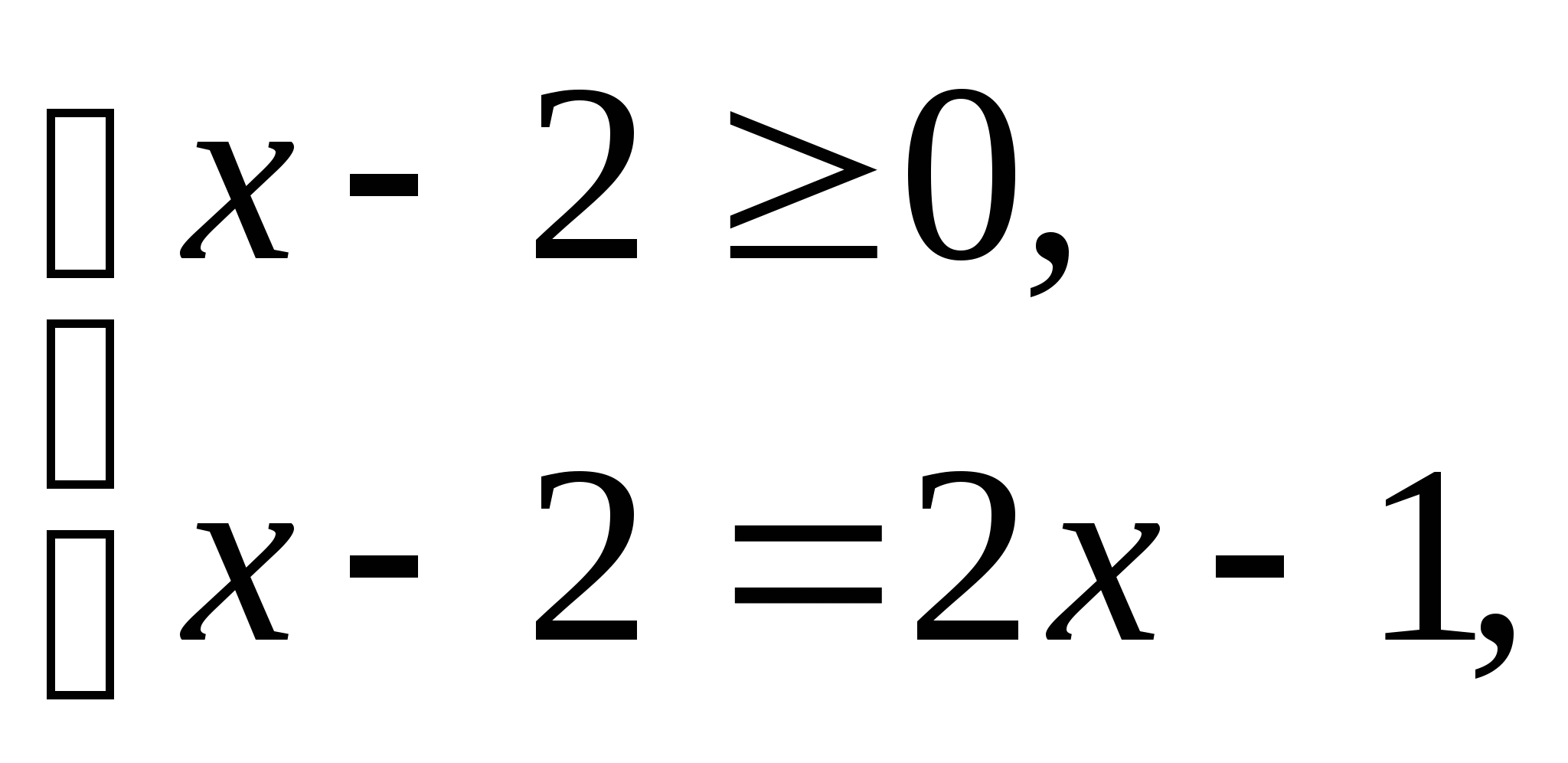
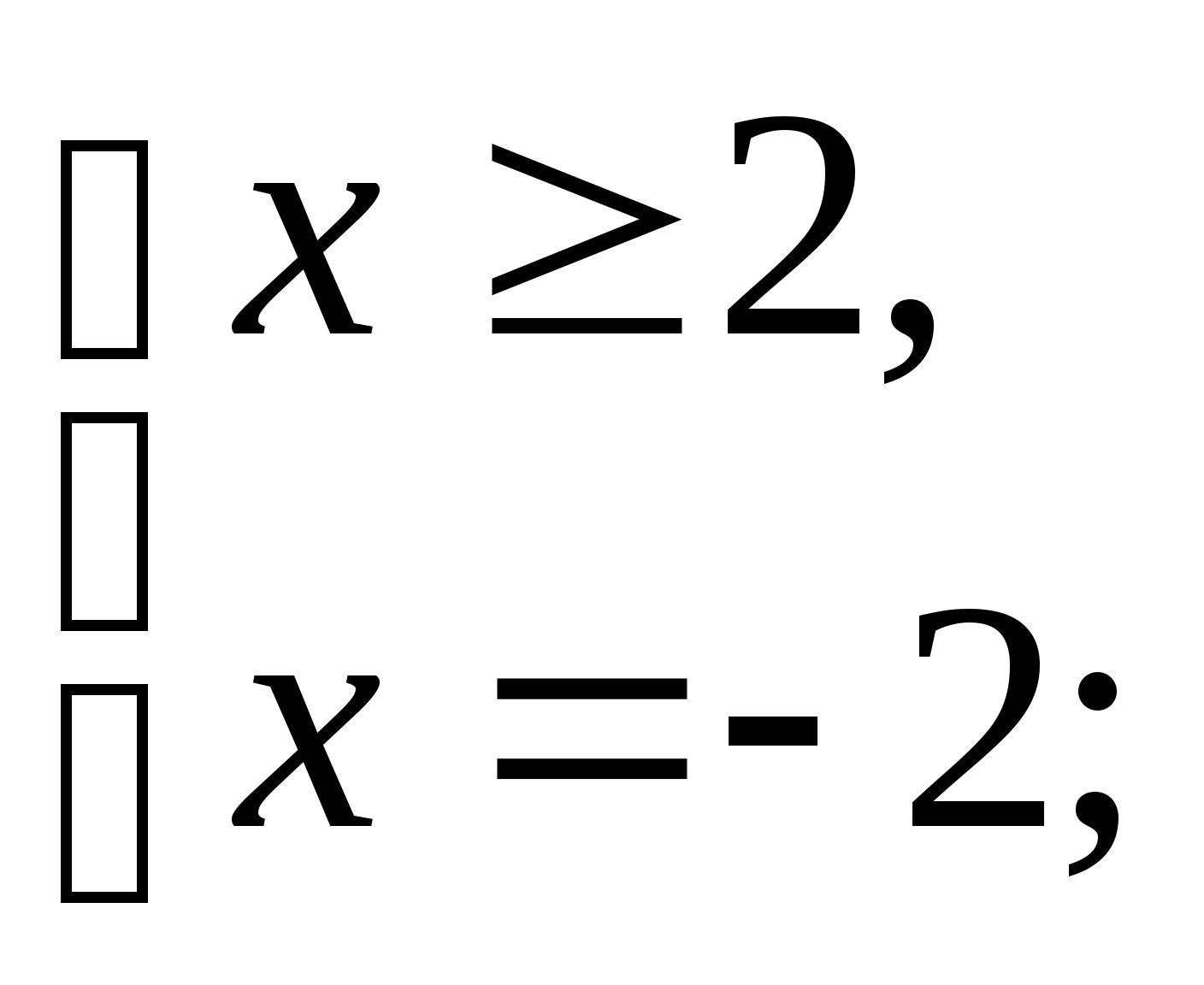
Ответ : нет решений.
2. Решить уравнение :
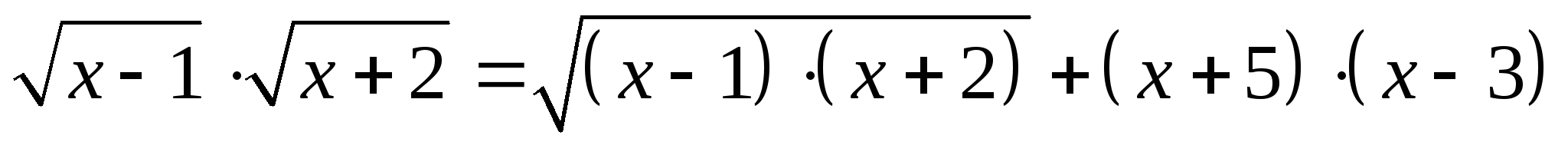
Решение :
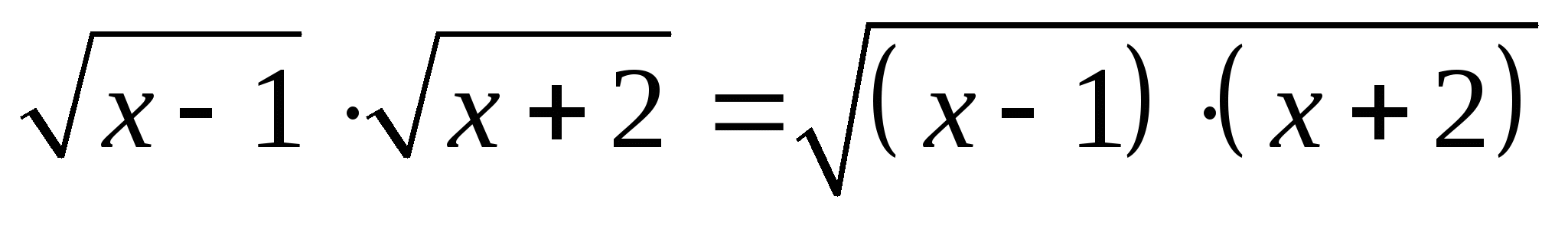 ,
,
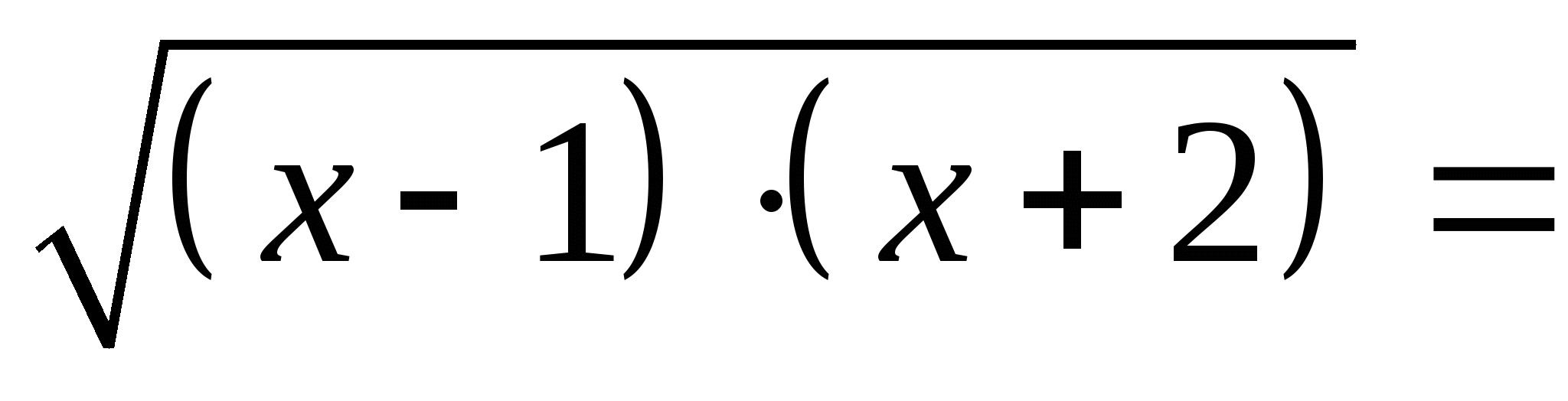
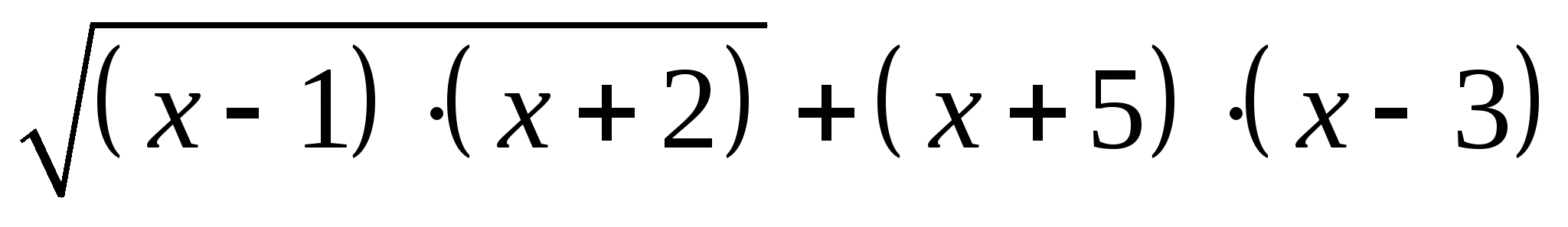 ,
,
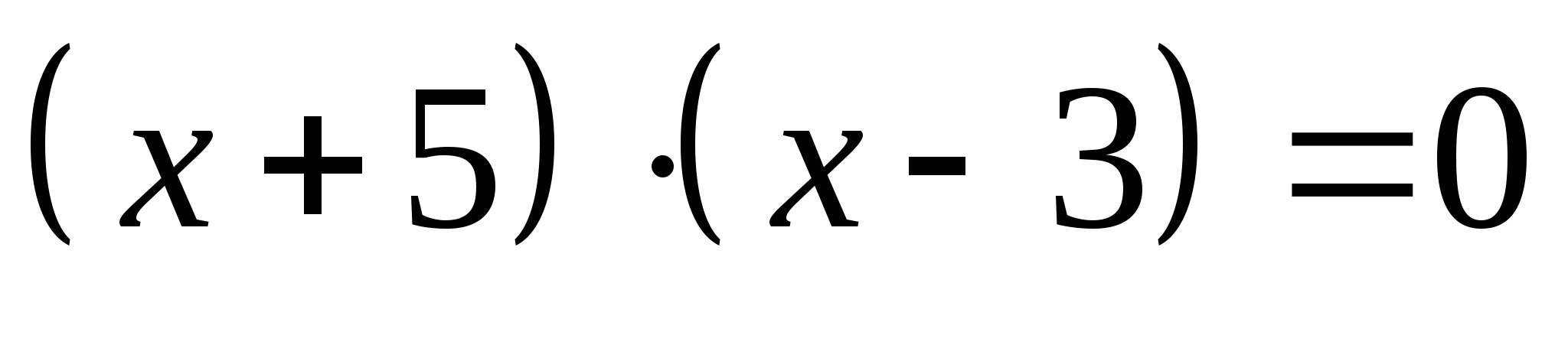 . Ответ : -5 ; 3
. Ответ : -5 ; 3
Ошибка.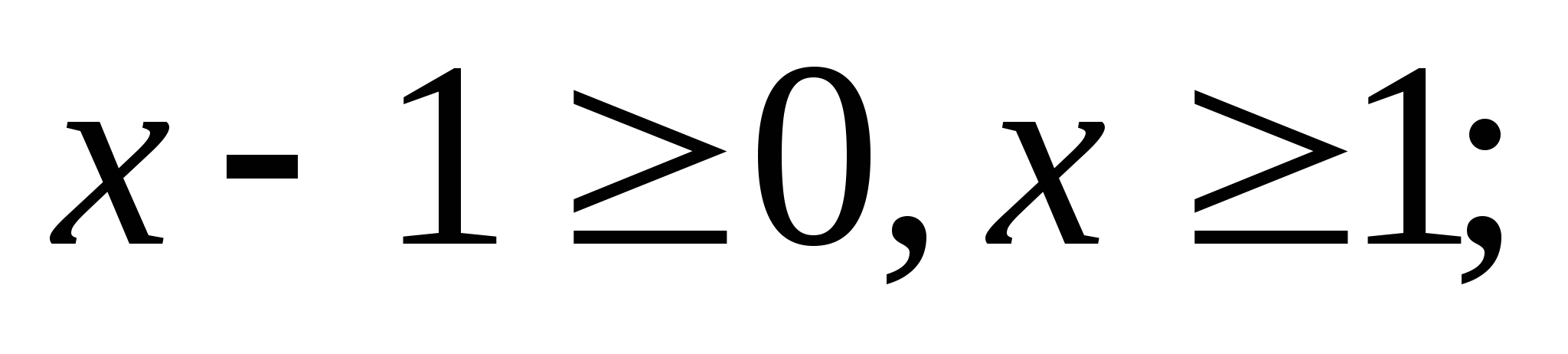
-5 — посторонний корень
Ответ : 3
3. Решить уравнение :
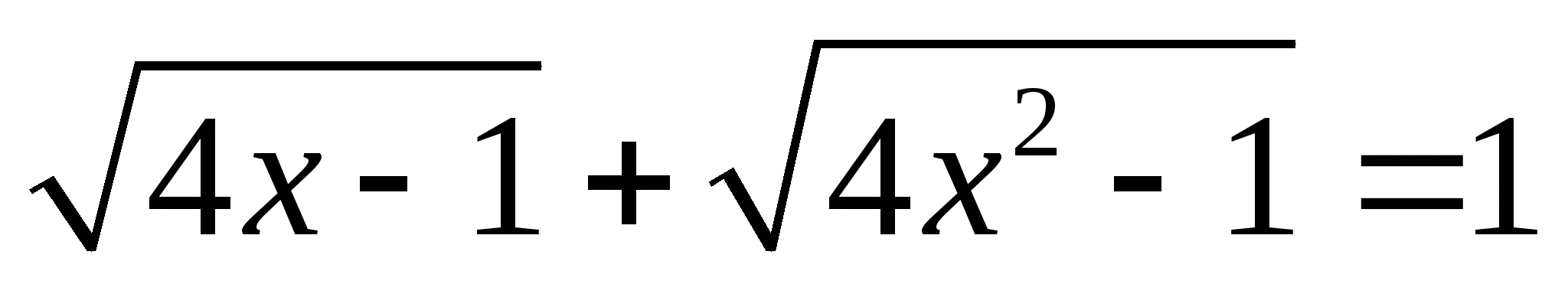
Решение : х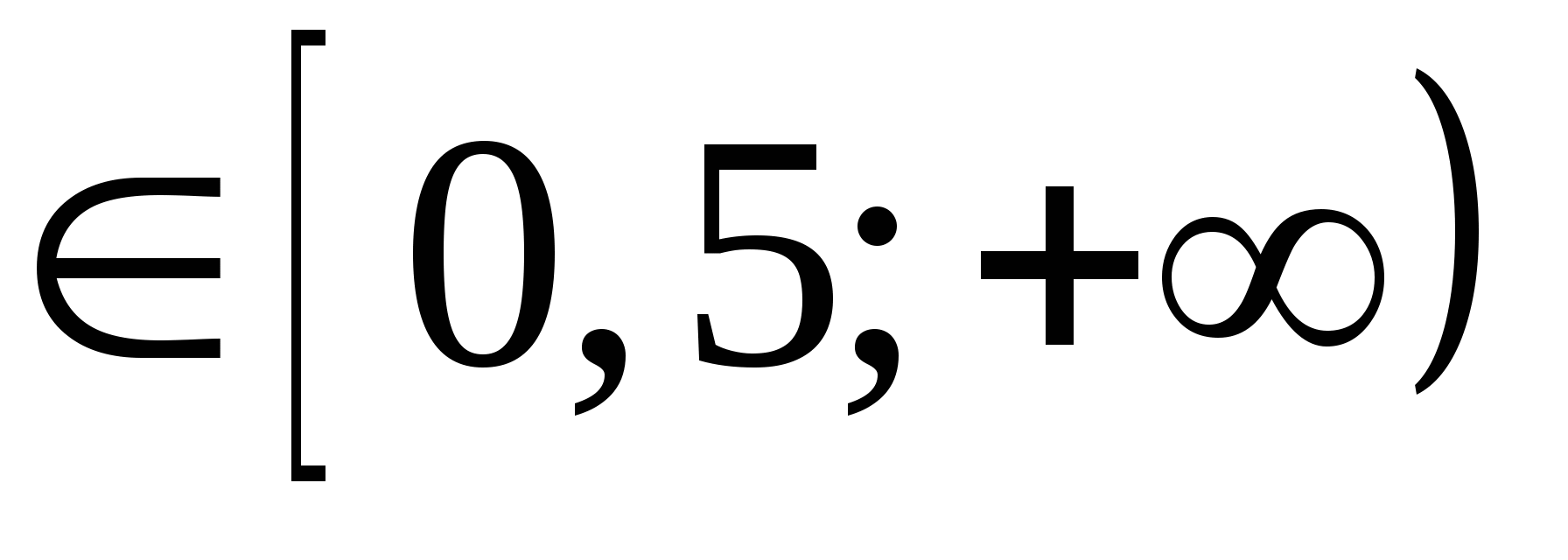
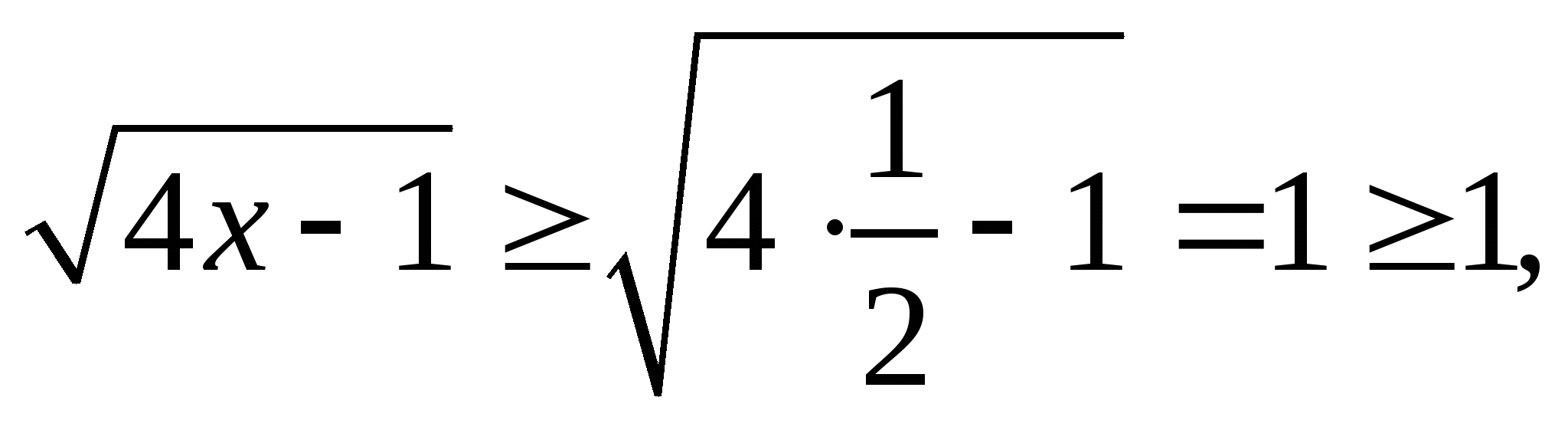
Т.к.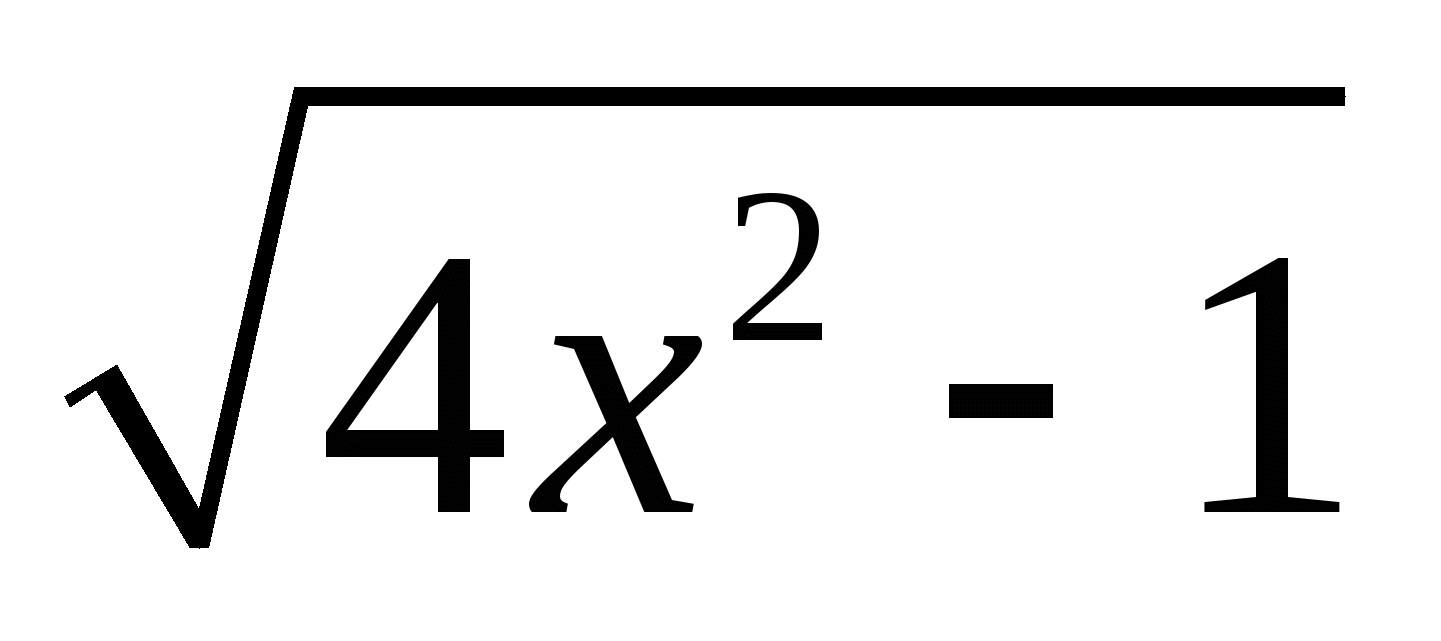 неотрицателен на этом множестве, то уравнение не имеет решений
неотрицателен на этом множестве, то уравнение не имеет решений
Ошибка. Ученик не оценил 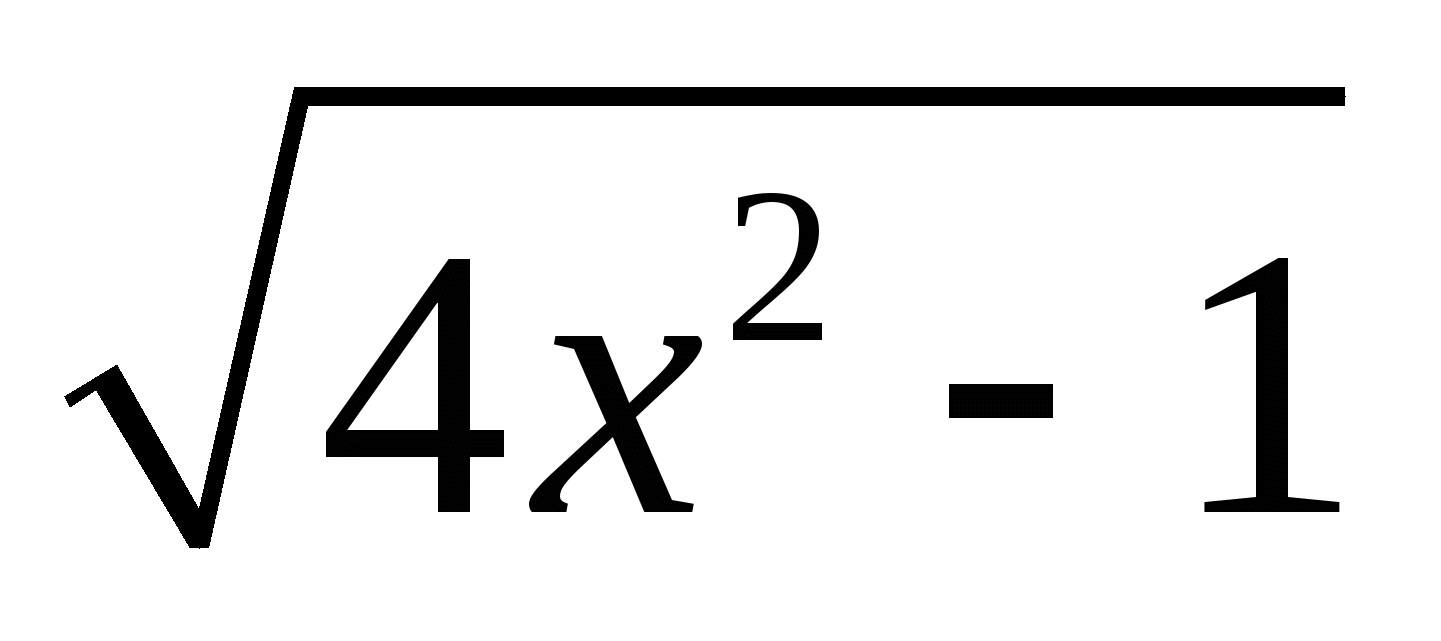 ; при х=0,5
; при х=0,5 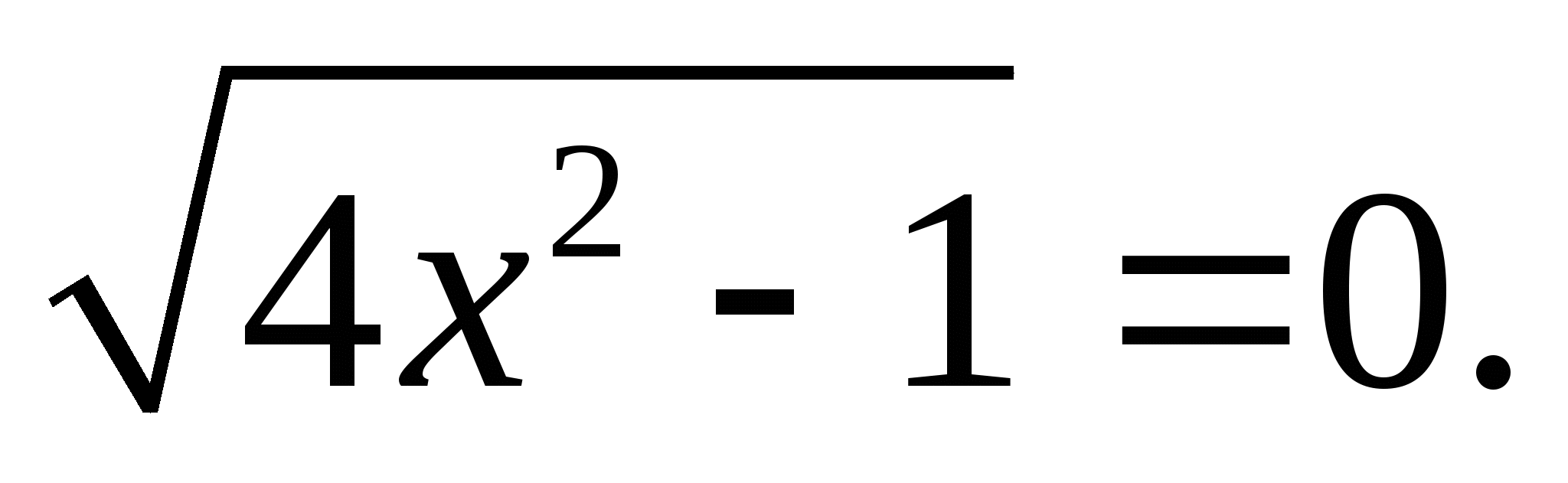
Ответ : 0,5
6. Итоги урока
— Какие уравнения называются иррациональными ? ( уравнения, содержащие неизвестное под знаком корня )
7.Домашнее задание : №№ 418-420 (в.г) ( учитель комментирует каждое задание )
Иррациональное уравнение Википедия
Иррациональное уравнение — это уравнение, содержащее неизвестное под знаком корня √ {\displaystyle \surd } или возведённое в степень, которую нельзя свести к целому числу. Простейшим примером иррационального уравнения является уравнение x = 2 {\displaystyle {\sqrt {x}}=2} или x 3 = − 3 {\displaystyle {\sqrt[{3}]{x}}=-3} . Иногда корни могут обозначать в виде рациональных степеней неизвестной, то есть вместо x n {\displaystyle {\sqrt[{n}]{x}}} пишут x 1 n {\displaystyle x^{\frac {1}{n}}} .
Содержание
- 1 Примеры и классификация
- 2 Связь с алгебраическими уравнениями
- 3 Подходы к решению
- 3.1 Возведение в степень
- 3.2 Замена системой условий
- 3.3 Использование свойств корней
- 3.4 Введение новых переменных
- 3.5 Использование области определения
- 3.6 Использование области значений
- 3.7 Тождественное преобразования
- 3.8 Использование производной
- 3.9 Использование мажоранты
- 3.10 Графический подход
- 4 Примечания
- 5 Ссылки
Примеры и классификация[ | ]
- 3 ( x + 4 ) = x {\displaystyle 3(x+4)=x} — так как переменная x {\displaystyle x} не стоит под знаком корня — это алгебраическое уравнение.
- 3 ( y + z ) 2 = x − π {\displaystyle 3(y+z)^{2}=x-{\sqrt {\pi }}} — так
Урок на тему «Иррациональные уравнения»
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №6
Разработка открытого урока
по алгебре для 8 класса на тему
«Иррациональные уравнения»
Подготовила
учитель математики
Михно Елена Алексеевна
Ст. Новоивановская 2012 г
11.04.2012
Тема: «Иррациональные уравнения»
Цель урока: Обобщить теоретические знания по данной теме
Закрепить основные способы решения иррациональных уравнений и
научиться подбирать свой способ к решению определённого вида уравнения.
Учитель:
Сегодня у нас не совсем обычный урок, к нам пришли гости. Посмотрите на наших гостей, улыбнитесь им, посмотрите друг на друга и тоже улыбнитесь, ведь от улыбки станет всем теплей, поднимется настроение.
открыли тетради и записали тему урока
Посмотрите на доску здесь написаны следующие пословицы.(5 мин)
— Набирайся ума в ученье, храбрости в сраженье.
— Без муки нет науки.
— Была бы охота — заладится всякая работа.
— Математика – гимнастика ума.
Учитель:
Ребята, подумайте и запишите себе в тетрадь, наиболее понравившуюся народную мудрость. Скажите, почему вы записали именно эту пословицу? Чем она вам так понравилась, в чём её смысл?
А мне нравится “ Математика – гимнастика ума”.
Что такое гимнастика?
Выслушав ответы, учитель подводит итог:
Гимнастика – это система упражнений для физического развития человека;
гимнаст – человек ловкий, стройный, сильный, пластичный, красивый.
Также много даёт математика для умственного развития человека — заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует память, внимание, закаляет характер.
Вот и мы сейчас проведём небольшую гимнастику для нашего ума.
Устный счёт. 5 мин
Вычислить:
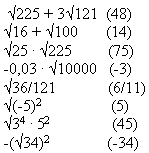
Каждый ответ соответствует некоторому фрагменту пословицы “ Кто хочет много знать, тому мало надо спать”. А как вы понимаете эту пословицу?
Повторение
Работа в группах 5 мин
Сейчас вы должны объединиться в группы по 4 человека и вспомнить, что же мы изучали на прошлых уроках и задать свой вопрос другой группе. Каждая группа должна придумать по 2 вопроса по изученной теме для другой группы. По два раза отвечать одному и тому же человеку от одной команды нельзя. То есть тот, кто отвечал, уже не может задавать вопрос.
Я приготовила вам свои вопросы, часть из их мы уже рассмотрели,
Вопросы к классу 2 мин разобрать
Какие уравнения называются иррациональными?
Какие методы применяются при решении иррациональных уравнений?
Назовите алгоритм решения иррационального уравнения.
Сколько корней может иметь иррациональное уравнение?
Какие равносильные и неравносильные преобразования вы знаете?
Когда необходима проверка корней?
Как решить уравнение, если оно имеет не один, а несколько корней?
Разберёмся с последним вопросом в течение урока
След слайд какие уравнения являются иррациональными? 1 мин (в карточке обвести цифру. Приложение 1)
Является ли число корнем уравнения? 2 мин (в карточке подписать да-нет)
Назовите корни уравнения. 2 мин
Возведите в квадрат выражение. 5 мин (в каточке написать решение)
Решите уравнение и напишите метод, который вы применяли. 10 мин (карточка)
Как же решить уравнение, если оно имеет несколько корней? 5 мин
Посмотрите на решение и сделайте свой вывод как же решать такие уравнения.
Учащиеся предлагают свои выводы по решению таких уравнений.
Вывод: для того, чтобы решить уравнение, в котором не один, а несколько корней нужно избавляться от корней постепенно, применяя равносильные и неравносильные преобразования.
Самостоятельная работа. 10 мин
Итоги урока. 2 мин
Домашнее задание повторить §30 читать §31 №30.19, 30.20, 31.16, 31.17
Что мы сегодня сделали? Чему научились и что закрепили?
Спасибо, и наконец, поднимите руку кто свою работу на уроке оценивает на “5”, “4”, “3”.
Урок понравился? Мне тоже. Вы хорошо поработали, всем спасибо.
Иррациональные числа
Иррациональное число — это действительное число, которое не может быть записано в виде простой дроби.
Нерациональные средства Нерациональные
Давайте посмотрим, что делает число рациональным или иррациональным …
Рациональные числа
A Rational Число может быть записано как Соотношение двух целых чисел (то есть простая дробь).
Пример: 1,5 рационально, потому что его можно записать как отношение 3/2
Пример: 7 является рациональным, потому что его можно записать как соотношение 7/1
Пример 0,333 … (3 повторения) тоже рациональный, потому что его можно записать как отношение 1/3
Иррациональные числа
Но некоторые числа нельзя записать как отношение двух целых чисел…
… их называют Иррациональные числа .
Пример: π (Пи) — известное иррациональное число.
π = 3,1415926535897932384626433832795 … (и более)
Мы не можем записать простой дробью, равной Пи.
Популярное приближение 22 / 7 = 3,1428571428571 … близко, но неточно .
Еще одна подсказка заключается в том, что десятичная дробь продолжается бесконечно без повторения.
Не может быть записано в виде дроби
Это иррационально , потому что не может быть записано как отношение (или дробь),
не потому, что это безумие!
Итак, мы можем определить, является ли это рациональным или иррациональным, попытавшись записать число в виде простой дроби.
Пример: 9,5 можно записать в виде простой дроби, например:
9.5 = 19 2
Значит, это рациональное число (и не иррациональное )
Вот еще несколько примеров:
| Число | В виде фракции | рационально или иррационально? | ||
|---|---|---|---|---|
| 1,75 | 7 4 | Rational | ||
| .001 | 1 1000 | Rational | ||
| √2 (корень квадратный из 2) | ? | Нерационально! |
Квадратный корень из 2
Давайте более внимательно посмотрим на квадратный корень из 2.
| Когда мы рисуем квадрат размером «1», какое расстояние по диагонали? |
Ответ — квадратный корень 2 , что составляет 1.4142135623730950 … (и т. Д.)
Но это не число вроде 3, или пяти третей, или чего-то подобного …
… на самом деле мы не можем записать квадратный корень из 2, используя соотношение двух чисел
… Я объясняю , почему на Is It Irrational? стр.,
… и мы знаем, что это иррациональное число
Известные иррациональные числа
Пи — известное иррациональное число.Люди вычислили Пи с точностью до квадриллиона десятичных знаков, но до сих пор нет никакой закономерности. Первые несколько цифр выглядят так: 3,1415926535897932384626433832795 (и другие …) | ||||||
Число e (число Эйлера) — еще одно известное иррациональное число. Люди также вычислили e с множеством десятичных знаков без какого-либо отображения образца.Первые несколько цифр выглядят так: 2.7182818284590452353602874713527 (и более …) | ||||||
Золотое сечение — иррациональное число. Первые несколько цифр выглядят так: 1.61803398874989484820 … (и многое другое …) | ||||||
Многие квадратные корни, кубические корни и т. Д. Также являются иррациональными числами.Примеры:
|
Но √4 = 2 (рациональное) и √9 = 3 (рациональное) …
… значит, не все корни иррациональны.
Замечание об умножении иррациональных чисел
Взгляните на это:
- π × π = π 2 иррационально
- Но √2 × √2 = 2 является рациональным
Так что будьте осторожны … умножение иррациональных чисел может дать рациональное число!
Интересные факты ….
По-видимому, Гиппас (один из учеников Пифагора ) обнаружил иррациональные числа, пытаясь записать квадратный корень из 2 в виде дроби (предполагается, что с использованием геометрии).Вместо этого он доказал, что квадратный корень из 2 не может быть записан как дробь , поэтому это иррациональное .
Но последователи Пифагора не могли согласиться с существованием иррациональных чисел, и говорят, что Гиппас был утоплен в море в наказание от богов!
,javascript — Тест на иррациональное уравнение
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
- реклама Обратитесь к разработчикам по всему миру
Загрузка…
- Авторизоваться зарегистрироваться
текущее сообщество
Что такое квадратные уравнения? | Живая наука
В математике квадратичный — это тип задачи, в которой переменная умножается сама на себя — операция, известная как возведение в квадрат. Этот язык происходит от того, что площадь квадрата равна его длине стороны, умноженной на себя. Слово «квадратичный» происходит от quadratum , латинского слова «квадрат».
Квадратные уравнения характеризуют большое количество явлений в реальном мире, например, где приземлится ракетный корабль, сколько будет взиматься плата за продукт или сколько времени потребуется человеку, чтобы грести вверх и вниз по реке.Из-за широкого разнообразия приложений квадратичные имеют огромное историческое значение и лежат в основе истории алгебры.
Потоки воды из фонтана образуют параболы. (Изображение предоставлено: Matej Kastelic Shutterstock)Парабола
Математика квадратичности неразрывно связана с U-образной кривой, известной как парабола. Пожалуй, наиболее знакомый пример — это струя воды, бьющая из питьевого фонтана. Есть много других примеров, таких как поперечное сечение спутниковой антенны или кабелей на подвесном мосту.
Парабола была важной формой для многих математиков Древней Греции, таких как Евклид Александрийский (~ 300 г. до н.э.), Архимед Сиракузский (287-212 гг. До н.э.), Аполлоний Пергский (262-190 г. до н.э.) и Папп Александрийский ( 290-350 нашей эры). Эти ученые отметили ряд математических свойств, присущих параболам:
1. Парабола — это набор точек, одинаково удаленных от точки (фокус ) и линии (направляющая ). Правильно названный фокус важен в ряде современных инженерных приложений, так как это точка на параболической тарелке, где отражаются приходящие волны, будь то радиоволны (как в спутниковой тарелке), свет (как в концентрирующей солнечной батарее). или звук (как в параболическом микрофоне).
Каждая точка параболы равноудалена от определенной точки и линии. Все входящие волны отражаются в фокус. (Изображение предоставлено Робертом Кулманом)2. Парабола также образуется путем разрезания конуса, параллельного наклону сторон конуса. Из-за этого параболы находятся в наборе математических кривых, называемых коническими сечениями . Спустя почти 2000 лет после этого открытия Леонардо да Винчи (1452-1519 гг. Н. Э.) В своих исследованиях параболических «горящих зеркал» понял это свойство и разработал компас, который мог рисовать параболы.
Плоскость, пересекающая конус, образует параболу. (Изображение предоставлено Робертом Кулманом)3. Изменения высоты параболы пропорциональны изменениям квадрата ширины этой параболы. Например, если парабола имеет высоту в одну единицу, а в ширину — одну единицу, она будет иметь высоту девять (три в квадрате), а ширина — три. Именно из этого свойства Аполлоний получил слово «парабола» от параболы, греческого слова, означающего «приложение», в том смысле, что ширина «применяется к» (умножается на) самой.Это свойство, которое связывает форму параболы с математическим понятием квадратичного.
Хотя параболы встречаются повсеместно, важно отметить, что они отличаются от других U-образных кривых, таких как подвесная цепь (цепная связь), путь ребенка на качелях (дуга окружности), дуга. от вертикального фонарика, падающего на стену (гипербола) или вершины вида сбоку пружины (синусоида). Эти другие кривые не обладают ранее упомянутыми свойствами парабол.
Для параболы высотой в одну единицу, где она шириной в одну единицу, она будет девять (три в квадрате) высотой, где она будет шириной три единицы. Эта парабола повернута вправо, поэтому она поместится на странице. (Изображение предоставлено Робертом Кулманом)Движение снаряда
Связь между параболами и математикой квадратов имела большое значение в XVI веке нашей эры, когда ученые европейского Возрождения заметили, что снаряды, такие как ядра и минометы, перемещались по параболическим траекториям.Многие известные ученые той эпохи, в том числе Леонардо да Винчи и Галилео Галилей (1564–1642), изучали движение снарядов. По словам Джозефа В. Добена, профессора истории Городского университета Нью-Йорка (CUNY), из-за того, что художники эпохи Возрождения стали одержимы точным отображением реальности в искусстве , Галилей так же стал одержим точным изображением реальности с помощью . математика . В 1638 году Галилей опубликовал первое доказательство того, что равномерное ускорение силы тяжести Земли заставит снаряды двигаться по параболическим траекториям.То, что математику можно было использовать для описания движения, было ключом к прогрессу научной революции.
Графики квадратиков
Примерно в то же время, что и Галилей, французский философ и математик Рене Декарт (1596–1650) опубликовал «Геометрию» (1637), в которой описывалась техника построения графиков алгебраических уравнений в области, называемой аналитической геометрией. Варианты его методов используются и сегодня. Как показано ниже, график квадратного уравнения представляет собой параболу.
График квадратного уравнения образует параболу.Техника построения графиков в том виде, в котором она практикуется сегодня, основана на работах Рене Декарта. (Изображение предоставлено Робертом Кулманом)Древняя квадратичная система: золотое сечение
Чтобы понять метод решения квадратичных решений, который сегодня используют математики, ученые и инженеры, давайте исследуем древнюю математическую задачу: золотое сечение. Кстати, в «Заблуждениях о золотом сечении» (1992) Джордж Марковски, профессор математики в Университете штата Мэн, указал, что историческое значение и эстетическая привлекательность золотого сечения часто преувеличиваются, хотя соотношение кажется верным. часто в теории чисел (параллельно с последовательностью & Фибоначчи), геометрии (например, в икосаэдре) и биологии (например, угол между листьями растения).
Один из методов определения золотого сечения сформулирован следующим образом:
Найдите прямоугольник такой длины и ширины, что когда квадрат срезан с одного конца прямоугольника, оставшийся прямоугольник обрезки будет иметь такую же форму или «соотношение сторон» «как исходный прямоугольник (но повернутый под прямым углом).
Хотя древние греки решали эту проблему с помощью геометрии, мы будем использовать алгебру в том виде, как ее преподают сегодня.
Использование алгебры для определения золотого сечения.(Изображение предоставлено Робертом Кулманом)Чтобы определить, какая длина и ширина дают золотое сечение, мы даем короткой стороне длину 1, а длинной стороне длину x. Поскольку соотношение сторон определяется как отношение длинной стороны к короткой стороне, соотношение сторон для этого прямоугольника равно x / 1 или просто x. Если мы отрежем квадрат от этого прямоугольника, оставшийся обрезок будет иметь длину длинной стороны 1 и длины короткой стороны x — 1. Таким образом, соотношение сторон будет 1 / (x — 1). Понимая, что соотношение сторон для всего прямоугольника и меньшего прямоугольника обрезков должно быть одинаковым, наше уравнение будет x = 1 / (x — 1).
Квадратичная формула
Вот как студенты сегодня должны решать это уравнение. Начните с уравнения:
x = 1 / (x — 1)
Умножьте каждую часть уравнения на выражение x — 1:
x · (x — 1) = 1
Распределите x по выражению x — 1:
x · x — x · 1 = 1
Переменная x, умноженная на себя, записывается как x². Это возведение в квадрат и делает уравнение квадратичным:
x² — x = 1
Теперь мы вычитаем 1 из каждой части уравнения, чтобы получить то, что известно как стандартная форма квадратного уравнения:
x² — x — 1 = 0
Эквивалентно это может быть записано как:
(1) · x² + (-1) · x + (-1) = 0
При сравнении с уравнением a · x² + b · x + c = 0, дает значения a = 1, b = -1 и c = -1.Эти значения используются в формуле квадратного уравнения как
Современная символьная форма квадратного уравнения. (Изображение предоставлено Робертом Кулманом)Символ «±» означает «плюс или минус». По этой причине квадратная формула всегда дает два решения. Подставьте любое из этих значений в уравнение x = 1 / (x — 1), чтобы проверить, совпадают ли при этом обе части уравнения. Это значит, что метод сработал. Обратите внимание, что эти значения также являются местами, в которых график стандартной формы уравнения (y = x² — x — 1) пересекает ось X, где y = 0 (см. График выше).В этом случае положительное значение имеет большее физическое значение, потому что прямоугольник не должен иметь отрицательную ширину.
Древнее вавилонское происхождение
Чтобы дать некоторое представление о том, откуда взялась квадратичная формула и почему она работает, давайте рассмотрим процедуру, использованную на древней вавилонской глиняной табличке, датируемой примерно 1800 годом до нашей эры. (Табличка BM 13901, Британский музей). Согласно Жаку Сезиано в «Введение в историю алгебры» (AMS, 2009) первая задача на этом планшете переводится примерно так:
Я сложил площадь и сторону квадрата, чтобы получить ¾.Какая сторона квадрата?
Задача записана в современных обозначениях как:
x² + x = ¾
Ниже приводится пересказ вавилонских и арабских методов, описанных Сезиано. Сначала мы переведем шаги, которые использовали вавилоняне, но также переведем их на символический язык, который мы используем сегодня в алгебре. Полностью символический язык впервые появился в Европе в 17 веке. Поскольку вавилоняне не знали об отрицательных числах, необходимо записать уравнение в виде x 2 + px = q, где p = 1 и q = ¾.Сравнивая это с современной стандартной формой ax 2 & + bx + c = 0, видно, что p = b / a и q = -c / a.
Древняя вавилонская процедура решения определенного вида квадратичной. Перевод в современные символические обозначения появляется справа. (Изображение предоставлено Робертом Кулманом)Теперь давайте выведем и докажем правильность процедуры, используя геометрические методы, как это делали арабские математики в девятом веке нашей эры. Ниже приводится вариант доказательства, которое появилось в публикации персидского математика Аль-Хваризми «The Сборник по расчетам завершением и балансировкой »в А.Д. 820. Хотя вавилоняне почти наверняка заимствовали свои процедурные методы из геометрии, ни письменные источники, ни доказательства их правильности не появлялись до Золотого века ислама, периода с середины седьмого до середины 13 века, когда мусульмане правил империей, простирающейся от Средней Азии до Северной Африки и Иберии.
Геометрическая демонстрация того, почему древняя вавилонская процедура работает. Вариант этого доказательства впервые был записан в девятом веке нашей эры.D. Аравия и полностью символический язык впервые появились в Европе 17 века нашей эры. (Изображение предоставлено Робертом Кулманом)Если мы «подключим» p = b / a и q = -c / a, формула действительно упростится до современной формы квадратного уравнения, как ее преподают сегодня.
Различные формы квадратичной формулы использовались в Афро-Евразии на протяжении веков. Процедурные версии использовались вавилонянами и египтянами примерно в 19 веке до нашей эры, халдеями в седьмом веке до нашей эры, греками в четвертом веке до нашей эры.К. и индейцы в пятом веке нашей эры. Риторические и синкопированные формы были разработаны арабами в девятом веке нашей эры, а синкопированные и символические формы — европейцами в 11 веке нашей эры. Методы, используемые каждой цивилизацией, развивались по мере того, как отрицательные, иррациональные, мнимые и комплексные числа.
Дополнительные ресурсы
,Что такое иррациональные числа? | Живая наука
Иррациональные числа — это числа, которые нельзя выразить как отношение двух целых чисел. Это противоположно рациональным числам, таким как 2, 7, одна пятая и -13/9, которые могут быть выражены и выражаются как отношение двух целых чисел. В десятичном виде иррациональные числа продолжаются после десятичной точки и никогда не повторяются.
Связано: 9 самых больших чисел в мире
Кто вычислил иррациональные числа?
Греческому математику Гиппасу из Метапонта приписывают открытие иррациональных чисел в V веке до нашей эры.2.)
Легенда гласит, что в награду за его великое открытие Гиппас был брошен в море. Это потому, что он был членом пифагорейцев, квазирелигиозного ордена, которые считали, что «Все есть число» и что Вселенная состоит из целых чисел и их соотношений. Обеспокоенная открытием Гиппаса, группа приговорила его к смертной казни через утопление.
Связано: Фотографии: большие числа, определяющие Вселенную
Позднее страх перед иррациональными числами утих, и в конечном итоге они были включены в математику.Вместе рациональные и иррациональные числа составляют действительных чисел , которые включают любое число на числовой прямой и не имеют мнимого числа i.
Большинство действительных чисел иррациональны. Немецкий математик Георг Кантор окончательно доказал это в XIX веке, показав, что рациональные числа равны , исчисляемым , а действительные числа неисчислимы. Это означает, что реальностей больше, чем рациональных, согласно веб-сайту по истории, математике и другим темам от образовательного карикатуриста Чарльза Фишера Купера.Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные; они составляют все оставшиеся бесчисленные действительные числа.
Известные иррациональные числа:
Квадратный корень из 2
Несмотря на судьбу Гиппаса, √2 — одно из самых известных иррациональных чисел, которое иногда называют постоянной Пифагора, согласно веб-сайту Wolfram MathWorld .
Постоянная Пифагора равна 1.4142135623… (точки указывают, что это продолжается вечно).
Все это может звучать теоретически, но у этого числа есть и очень конкретные приложения. Международные размеры бумаги включают √2. Международная организация по стандартизации (ISO) 216, определение серии размеров бумаги A гласит, что длина листа, разделенная на его ширину, должна быть 1,4142. Таким образом, из листа бумаги формата A1, разделенного пополам по ширине, получится два листа бумаги формата A2. Снова разделите A2 пополам, и получится два листа бумаги A3 и так далее.
Pi
Pi — это отношение длины окружности к ее диаметру. Математики знали о пи еще со времен древних вавилонян, 4000 лет назад.
Пи равно 3,1415926535…
Некоторые супер-фанаты Пи очень гордятся запоминанием как можно большего количества цифр Пи. Суреш Кумар Шарма из Индии установил мировой рекорд в 2015 году, запомнив 70 030 цифр числа Пи, согласно мировому рейтинговому списку Пи .
Phi
Phi также известен как золотое сечение . Его можно найти, взяв палку и разбив ее на две части; если соотношение между этими двумя частями такое же, как соотношение между всей палкой и большим сегментом, считается, что части находятся в золотом сечении.
Фи равно 1,6180339887…
На протяжении веков концепция фи создавалась огромным количеством знаний, например, идея о том, что она олицетворяет совершенную красоту или может быть найдена в природе.Но по большей части это неверно. Фи тесно связан с последовательностью Фибоначчи , еще одним источником многих заблуждений.
e
Основание из натуральных логарифмов называется e в честь его тезки, швейцарского математика 18-го века Леонарда Эйлера.
e равно 2,7182818284…
Наряду с появлением в логарифмах e появляется в уравнениях , включающих комплексные числа и экспоненциальный рост. Так же, как День Пи отмечается 14 марта (3/14), e День отмечается 1 февраля.7 (2/7) или 27 января (27/1), в зависимости от того, какую календарную систему вы используете.
Дополнительные ресурсы:
,