Закон массы: Урок №14. Закон сохранения массы вещества. Химические уравнения – Закон действующих масс — Википедия — Детская игровая комната «Волшебный лес»

Posted on 07.09.202005.02.2020 by alexxlab

Содержание

Закон сохранения массы — Википедия

Закон сохранения массы — закон физики, согласно которому масса физической системы сохраняется при всех природных и искусственных процессах.

В метафизической форме, согласно которой вещество несотворимо и неуничтожимо, этот закон известен с древнейших времён. Позднее появилась количественная формулировка, согласно которой мерой количества вещества является вес (с конца XVII века — масса).

С точки зрения классической механики и химии, сохраняются общая масса закрытой физической системы, равная сумме масс компонентов этой системы (то есть масса считается аддитивной). Этот закон с большой точностью верен в области применимости ньютоновской механики и химии, так как релятивистские поправки в этих случаях пренебрежимо малы.

В современной физике концепция и свойства массы существенно пересмотрены. Масса более не является мерой количества вещества, а закон сохранения массы тесно связан с законом сохранения внутренней энергии системы. В отличие от классической модели, сохраняется масса только изолированной физической системы, то есть при отсутствии энергообмена с внешней средой. Не сохраняется сумма масс компонентов системы (масса неаддитивна). Например, при радиоактивном распаде в изолированной системе, состоящей из вещества и радиации, совокупная масса вещества уменьшается, но масса системы сохраняется, несмотря на то что масса радиации может быть нулевая.

Исторический очерк

Закон сохранения массы исторически понимался как одна из формулировок закона сохранения материи. Одним из первых его сформулировал древнегреческий философ Эмпедокл (V век до н. э.)^[1]:

Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.

Ранее Эмпедокла «принцип сохранения» применялся представителями Милетской школы для формулировки теоретических представлений о первовеществе, основе всего сущего^[2]. Позже аналогичный тезис высказывали Демокрит, Аристотель и Эпикур (в пересказе Лукреция Кара).

Средневековые учёные также не высказывали никаких сомнений в истинности этого закона. Фрэнсис Бэкон в 1620 году провозгласил: «Сумма материи остается всегда постоянной и не может быть увеличена или уменьшена… ни одна мельчайшая её часть не может быть ни одолена всей массой мира, ни разрушена совокупной силой всех агентов, ни вообще как-нибудь уничтожена»^[3].

В ходе развития алхимии, а затем и научной химии, было замечено, что при любых химических превращениях суммарный вес реагентов не меняется. В 1630 году Жан Рэ, химик из Перигора, писал Мерсенну^[4]^[5]^[6]:

Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.

С появлением в трудах Ньютона понятия массы как меры количества вещества, формулировка закона сохранения материи была уточнена: масса есть инвариант, то есть при всех процессах общая масса не уменьшается и не увеличивается (вес, как указал Ньютон, инвариантом не является, поскольку форма Земли далека от идеальной сферы).

В 1673 году опыты Роберта Бойля поставили закон сохранения массы под сомнение — у него при химической реакции с нагреванием вес вещества увеличился. Бойль из этого сделал вывод, что носитель теплоты («флогистон», по тогдашней терминологии) имеет вес; эта гипотеза восстанавливала доверие к сохранению массы. Однако сразу после публикации Бойля французский химик Шерубен д’Орлеан (Chérubin d’Orleans, 1679 год) указал на ошибку Бойля: увеличение веса происходило за счёт воздуха, а в запаянном сосуде вес сохранялся неизменным^[7]. Позднее, в 1755 году об этом писал и М. В. Ломоносов в письме Л. Эйлеру (см. текст в Викитеке):

Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.

Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни.

В дальнейшем, вплоть до создания физики микромира, закон сохранения массы считался истинным и очевидным. Иммануил Кант объявил этот закон постулатом естествознания^[12] (1786). Лавуазье в «Начальном учебнике химии» (1789) привёл точную количественную формулировку закона сохранения массы вещества, однако не объявил его каким-то новым и важным законом, а просто упомянул мимоходом как давно известный и достоверно установленный факт. Для химических реакций Лавуазье сформулировал закон в следующих выражениях^[13]:

Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.

Другими словами, сохраняется масса закрытой физической системы, в которой происходит химическая реакция, а сумма масс всех веществ, вступивших в эту реакцию, равна сумме масс всех продуктов реакции (то есть тоже сохраняется). Масса, таким образом, считается аддитивной.

Современное состояние

В XX веке обнаружились два новых свойства массы.

(M1) Масса физического объекта зависит от его внутренней энергии (см. Эквивалентность массы и энергии). При поглощении внешней энергии масса растёт, при потере — уменьшается. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой. Особенно ощутимо изменение массы при ядерных реакциях. Но даже при химических реакциях, которые сопровождаются выделением (или поглощением) тепла, масса не сохраняется, хотя в этом случае дефект массы ничтожен. Академик Л. Б. Окунь пишет^[14]:

Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:

1) при нагревании железного утюга на 200° его масса возрастает на величину Δm/m≈10−12{\displaystyle \Delta m/m\approx 10^{-12}};
2) при полном превращении некоторого количества льда в воду Δm/m≈3.7⋅10−12{\displaystyle \Delta m/m\approx 3.7\cdot 10^{-12}}.

(M2) Масса не является аддитивной величиной: масса системы не равна сумме масс её составляющих. Примеры неаддитивности:

Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).

Таким образом, при физических процессах, которые сопровождаются распадом или синтезом физических структур, не сохраняется сумма масс составляющих (компонентов) системы, но сохраняется общая масса этой (изолированной) системы:

Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.

Сказанное означает, что в современной физике закон сохранения массы тесно связан с законом сохранения энергии и выполняется с таким же ограничением — надо учитывать обмен системы энергией с внешней средой.

Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один^[15].

Более детально

Чтобы более детально пояснить, почему масса в современной физике оказывается неаддитивной^[16] (масса системы не равна — вообще говоря — сумме масс компонент), следует вначале заметить, что под термином масса в современной физике понимается лоренц-инвариантная величина:

m=E2/c4−p2/c2,{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}},}

где E{\displaystyle E} — энергия, p→{\displaystyle {\vec {p}}} — импульс,c{\displaystyle c} — скорость света. И сразу заметим, что это выражение одинаково легко применимо к точечной бесструктурной («элементарной») частице, так и к любой физической системе, причём в последнем случае энергия и импульс системы вычисляются просто суммированием энергий и импульсов компонент системы (энергия и импульс — аддитивны).

Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.

Кроме того, заметим, что c{\displaystyle c} — универсальная константа, то есть просто число, которое не меняется никогда, поэтому в принципе можно выбрать такую систему единиц измерения, чтобы выполнялось c=1{\displaystyle c=1}, и тогда упомянутая формула будет менее загромождена:

m=E2−p2,{\displaystyle m={\sqrt {E^{2}-p^{2}}},}

как и остальные связанные с нею формулы (и мы ниже будем для краткости использовать именно такую систему единиц).

Рассмотрев уже самый парадоксальный на вид случай нарушения аддитивности массы — случай, когда система нескольких (для простоты ограничимся двумя) безмассовых частиц (например фотонов) может иметь ненулевую массу, легко увидеть механизм, порождающий неаддитивность массы.

Пусть есть два фотона 1 и 2 с противоположными импульсами: p→1=−p→2{\displaystyle {\vec {p}}_{1}=-{\vec {p}}_{2}}. Масса каждого фотона равна нулю, следовательно можно записать:

0=E12−p12,{\displaystyle 0={\sqrt {E_{1}^{2}-p_{1}^{2}}},}

0=E22−p22,{\displaystyle 0={\sqrt {E_{2}^{2}-p_{2}^{2}}},}

то есть энергия каждого фотона равна модулю его импульса. Заметим попутно, что масса равна нулю за счет вычитания под знаком корня ненулевых величин друг из друга.

Рассмотрим теперь систему этих двух фотонов как целое, посчитав её импульс и энергию. Как видим, импульс этой системы равен нулю (импульсы фотонов, сложившись, уничтожились, так как эти фотоны летят в противоположных направлениях)^[17]:

p→=p→1+p→2=0→.{\displaystyle {\vec {p}}={\vec {p}}_{1}+{\vec {p}}_{2}={\vec {0}}.}.

Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:

E=E1+E2.{\displaystyle E=E_{1}+E_{2}.}

Ну и отсюда масса системы:

m=E2−p2=E2−0=E≠0,{\displaystyle m={\sqrt {E^{2}-p^{2}}}={\sqrt {E^{2}-0}}=E\neq 0,}

(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).

В общем случае всё происходит аналогично этому, наиболее отчётливому и простому примеру. Вообще говоря, частицы, образующие систему, не обязательно должны иметь нулевые массы, достаточно, чтобы массы были малы или хотя бы сравнимы с энергиями или импульсами^[18], и эффект будет большим или заметным. Также видно, что точной аддитивности массы нет практически никогда, за исключением лишь достаточно специальных случаев.

Масса и инертность

Отсутствие аддитивности массы, казалось бы, вносит затруднения. Однако они искупаются не только тем, что определённая так (а не иначе, например, не как энергия деленная на квадрат скорости света) масса оказывается лоренц-инвариантной, удобной и формально красивой величиной, но и имеет физический смысл, точно соответствующий обычному классическому пониманию массы как меры инертности.

А именно для системы отсчёта покоя физической системы (то есть той системы отсчета, в которой импульс физической системы ноль) или систем отсчёта, в которых система покоя медленно (по сравнению со скоростью света) движется, упомянутое выше определение массы

m=E2/c4−p2/c2{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}}}

— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).

Это можно конкретно проиллюстрировать, рассмотрев систему, снаружи (для внешних взаимодействий) являющейся обычным твердым телом, а внутри содержащую быстро движущиеся частицы. Например, рассмотрев зеркальный ящик с идеально отражающими стенками, внутри которого — фотоны (электромагнитные волны).

Пусть для простоты и большей четкости эффекта сам ящик (почти) невесом. Тогда, если, как в рассмотренном в параграфе выше примере, суммарный импульс фотонов внутри ящика ноль, то ящик будет в целом неподвижен. При этом он должен под действием внешних сил (например если мы станем его толкать), вести себя как тело с массой, равной суммарной энергии фотонов внутри, деленной на c2{\displaystyle c^{2}}.

Рассмотрим это качественно. Пусть мы толкаем ящик, и он приобрел из-за этого некоторую скорость вправо. Будем для простоты сейчас говорить только об электромагнитных волнах, бегущих строго вправо и влево. Электромагнитная волна, отражающаяся от левой стенки, повысит свою частоту (вследствие эффекта Доплера) и энергию. Волна, отражающаяся от правой стенки, напротив, уменьшит при отражении свои частоту и энергию, однако суммарная энергия увеличится, так как полной компенсации не будет. В итоге тело приобретет кинетическую энергию, равную mv2/2{\displaystyle mv^{2}/2} (если v<<c{\displaystyle v<<c}), что означает, что ящик ведет себя как классическое тело массы m{\displaystyle m}. Тот же результат можно (и даже легче) получить для отражения (отскока) от стенок быстрых релятивистских дискретных частиц (для нерелятивистских тоже, но в этом случае масса просто окажется^[19] суммой масс частиц, находящихся в ящике).

Примечания

↑ Пер. Э. Радлова (см., напр. здесь).
↑ Энциклопедия Кругосвет
↑ Ф. Бэкон, Сочинения, Том 2, Мысль, 1978, стр. 341—342,
↑ Jean Rey, Essais sur la recherche de la cause pour laquelle l’étain et le plomb augmentent de poids quand on les calcine, nouvelle édition revue sur l’exemplaire original et augmentée sur les manuscrits de la Bibliothèque du Roi et des Minimes de Paris, avec des notes, par M. Gobet, Paris, Ruault, 1777, p. 21.
↑ Van Praagh, Gordon. Physical Chemistry, Experimental and Theoretical: An Introductory Text-book. — Cambridge University Press, 1950. — P. 63. — 295 p.
↑ Письмо Жана Рэ
↑ Всемирная история физики, 2007, с. 321—322..
↑ Шубинский В. И. Ломоносов: Всероссийский человек. — М.: Молодая гвардия, 2010. — С. 346-351.. — 471 с. — (Жизнь замечательных людей). — ISBN 978-5-235-03323-8.
↑ Сонин А. С. Несколько эпизодов борьбы с «космополитизмом» в физике. Вестник АН СССР, № 8 (1990), стр. 122—133.
↑ Дмитриев И. С. «Одарован самым счастливым остроумием» (Химические работы М. В. Ломоносова в контексте европейской науки века Просвещения) (неопр.). Дата обращения 19 апреля 2018.
↑ Дорфман Я. Г. Закон сохранения массы при химических реакциях и физические воззрения Ломоносова // Ломоносов М.В. Сборник статей и материалов. — М.-Л.: Издательство АН СССР, 1961. — Т. 5. — С. 182-193.
↑ И. Кант. Метафизические начала естествознания. Соч., том VI, стр. 148.
↑ Лавуазье.
↑ Понятие массы, 1989, с. 519.
↑ 1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553.
↑ Приближенно аддитивной она, конечно же, может быть — в приближении нерелятивистской механики, однако как только в системе имеются движения со скоростями, сравнимыми со скоростью света, аддитивность массы как правило нарушается вполне заметно или даже сильно.
↑ Выбрав (по условию) именно противоположные (и равные по величине) импульсы, мы получили сразу же и удобное для нас обстоятельство: первоначально выбранная система отсчёта тогда сразу оказывается системой, в котором система покоится (это и значит формально, что её импульс равен нулю; да это и интуитивно так). Поэтому энергия нашей физической системы, которую мы посчитаем, как раз и будет сразу её энергией покоя.
↑ В нашей системе единиц c=1{\displaystyle c=1}, для того, чтобы выразить это условие в других (любых) системах единиц надо не забыть умножать или делить на нужные степени c{\displaystyle c}.
↑ В принципе — конечно, лишь приближенно.

Литература

Закон сохранения массы — Википедия

Исторический очерк

Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.

Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.

Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.

Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни.

Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.

Современное состояние

В XX веке обнаружились два новых свойства массы.

Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:
1) при нагревании железного утюга на 200° его масса возрастает на величину Δm/m≈10−12{\displaystyle \Delta m/m\approx 10^{-12}};
2) при полном превращении некоторого количества льда в воду Δm/m≈3.7⋅10−12{\displaystyle \Delta m/m\approx 3.7\cdot 10^{-12}}.

Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).

Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.

Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один^[15].

Более детально

m=E2/c4−p2/c2,{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}},}

Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.

m=E2−p2,{\displaystyle m={\sqrt {E^{2}-p^{2}}},}

0=E12−p12,{\displaystyle 0={\sqrt {E_{1}^{2}-p_{1}^{2}}},}

0=E22−p22,{\displaystyle 0={\sqrt {E_{2}^{2}-p_{2}^{2}}},}

p→=p→1+p→2=0→.{\displaystyle {\vec {p}}={\vec {p}}_{1}+{\vec {p}}_{2}={\vec {0}}.}.

Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:

E=E1+E2.{\displaystyle E=E_{1}+E_{2}.}

Ну и отсюда масса системы:

m=E2−p2=E2−0=E≠0,{\displaystyle m={\sqrt {E^{2}-p^{2}}}={\sqrt {E^{2}-0}}=E\neq 0,}

(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).

Масса и инертность

m=E2/c4−p2/c2{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}}}

— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).

Примечания

↑ Пер. Э. Радлова (см., напр. здесь).
↑ Энциклопедия Кругосвет
↑ Ф. Бэкон, Сочинения, Том 2, Мысль, 1978, стр. 341—342,
↑ Jean Rey, Essais sur la recherche de la cause pour laquelle l’étain et le plomb augmentent de poids quand on les calcine, nouvelle édition revue sur l’exemplaire original et augmentée sur les manuscrits de la Bibliothèque du Roi et des Minimes de Paris, avec des notes, par M. Gobet, Paris, Ruault, 1777, p. 21.
↑ Van Praagh, Gordon. Physical Chemistry, Experimental and Theoretical: An Introductory Text-book. — Cambridge University Press, 1950. — P. 63. — 295 p.
↑ Письмо Жана Рэ
↑ Всемирная история физики, 2007, с. 321—322..
↑ Шубинский В. И. Ломоносов: Всероссийский человек. — М.: Молодая гвардия, 2010. — С. 346-351.. — 471 с. — (Жизнь замечательных людей). — ISBN 978-5-235-03323-8.
↑ Сонин А. С. Несколько эпизодов борьбы с «космополитизмом» в физике. Вестник АН СССР, № 8 (1990), стр. 122—133.
↑ Дмитриев И. С. «Одарован самым счастливым остроумием» (Химические работы М. В. Ломоносова в контексте европейской науки века Просвещения). Проверено 19 апреля 2018.
↑ Дорфман Я. Г. Закон сохранения массы при химических реакциях и физические воззрения Ломоносова // Ломоносов М.В. Сборник статей и материалов. — М.-Л.: Издательство АН СССР, 1961. — Т. 5. — С. 182-193.
↑ И. Кант. Метафизические начала естествознания. Соч., том VI, стр. 148.
↑ Лавуазье.
↑ Понятие массы, 1989, с. 519.
↑ 1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553.
↑ Приближенно аддитивной она, конечно же, может быть — в приближении нерелятивистской механики, однако как только в системе имеются движения со скоростями, сравнимыми со скоростью света, аддитивность массы как правило нарушается вполне заметно или даже сильно.
↑ Выбрав (по условию) именно противоположные (и равные по величине) импульсы, мы получили сразу же и удобное для нас обстоятельство: первоначально выбранная система отсчёта тогда сразу оказывается системой, в котором система покоится (это и значит формально, что её импульс равен нулю; да это и интуитивно так). Поэтому энергия нашей физической системы, которую мы посчитаем, как раз и будет сразу её энергией покоя.
↑ В нашей системе единиц c=1{\displaystyle c=1}, для того, чтобы выразить это условие в других (любых) системах единиц надо не забыть умножать или делить на нужные степени c{\displaystyle c}.
↑ В принципе — конечно, лишь приближенно.

Литература

Закон сохранения массы — Вики

Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.

Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.

В 1673 году опыты Роберта Бойля

Действующих масс закон — это… Что такое Действующих масс закон?

один из основных законов физической химии; устанавливает зависимость скорости химической реакции от концентраций реагирующих веществ и соотношение между концентрациями (или активностями) продуктов реакции и исходных веществ в состоянии химического равновесия. Норвежские учёные К. Гульдберг и П. Вааге, сформулировавшие Д. м. з. в 1864—67, назвали «действующей массой» вещества его количество в единице объёма, т. е. концентрацию, отсюда — наименование закона.

Если в идеальной газовой смеси или идеальном жидком растворе происходит реакция:

аА + а’А’ = bB + b’B’ (1)

(А, А’ и т.д. — вещества, а, а’ и т.д. — стехиометрические коэффициенты), то, согласно Д. м. з., скорость реакции в прямом направлении:

r₊ = k₊ [A] ^a [A’] ^a’ (2)

Здесь [А] — концентрация вещества А и т.д., k₊ — константа скорости реакции (в прямом направлении), k₊ зависит от температуры, а в случае жидкого раствора — также и от давления; последняя зависимость существенна лишь при высоких давлениях. Вид уравнения (2) определяется тем, что необходимым условием элементарного акта реакции является столкновение молекул исходных веществ, т. е. их встреча в некотором малом объёме (порядка размера молекул). Вероятность найти в данный момент в данном малом объёме молекулу А пропорциональна [А]; вероятность найти в нём одновременно а молекул А и а’ молекул А’ по теореме о вероятности сложного события пропорциональна [А] ^a [А’] ^a’. Число столкновений молекул исходных веществ в единичном объёме за единичное время пропорционально этой величине. Определённая доля этих столкновений приводит к реакции. Отсюда вытекает уравнение (2). Мономолекулярные реакции требуют особого рассмотрения.

Скорость реакции (1) в обратном направлении r_— = k_— [B] ^b [B’] ^b’. (3)

Если реакция обратима, т. е. протекает одновременно в противоположных направлениях, то наблюдаемая скорость реакции r = r₊ – r_—. При r₊ = r_— осуществляется химическое равновесие. Тогда, согласно уравнениям (2) и (3),

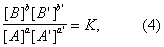
где К = k₊/k_— — константа равновесия. Для газовых реакций обычно применяют равноценное уравнение

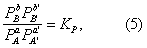
где P_A — парциальное давление вещества А и т.д.

Уравнения (2) и (3) применимы к простой (одностадийной) реакции и к отдельным стадиям сложной реакции, но не к сложной реакции в целом. Уравнения (4) и (5), выражающие Д. м. з. для равновесия, справедливы и в случае сложной реакции.

Общим условием равновесия по отношению к реакции (1), приложимость которого не ограничена идеальными системами, является уравнение

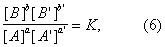в котором [А] — Активность вещества А и т.д. Уравнение (6) выводится из принципов термодинамики. С помощью Д. м. з. для равновесия вычисляют максимально достижимые степени превращения при обратимых реакциях. В число последних входят важные промышленные процессы — синтез аммиака, окисление сернистого газа и многие другие. На основе Д. м. з. для скоростей реакций получают кинетические уравнения, применяемые при расчёте химической аппаратуры.

М. И. Тёмкин.

Действующих масс закон — Большая советская энциклопедия

Де́йствующих масс закон

Один из основных законов физической химии; устанавливает зависимость скорости химической реакции от концентраций реагирующих веществ и соотношение между концентрациями (или активностями) продуктов реакции и исходных веществ в состоянии химического равновесия. Норвежские учёные К. Гульдберг и П. Вааге, сформулировавшие Д. м. з. в 1864—67, назвали «действующей массой» вещества его количество в единице объёма, т. е. концентрацию, отсюда — наименование закона.

Если в идеальной газовой смеси или идеальном жидком растворе происходит реакция:

аА + а’

А’ = bB + b’B’ (1)

r₊ = k₊ [A] ^a [A’] ^a’ (2)

Скорость реакции (1) в обратном направлении r_— = k_— [B] ^b [B’] ^b’. (3)

где К = k₊/k_— — константа равновесия. Для газовых реакций обычно применяют равноценное уравнение

где P_A — парциальное давление вещества А и т.д.

Лит. см. при ст. Кинетика химическая и Термодинамика химическая.

М. И. Тёмкин.

Источник: Большая советская энциклопедия на Gufo.me

Значения в других словарях

ДЕЙСТВУЮЩИХ МАСС ЗАКОН — ДЕЙСТВУЮЩИХ МАСС ЗАКОН: скорость элементарной стадии химической реакции при постоянной температуре пропорциональна концентрациям реагирующих веществ в степенях — равных их стехиометрическим коэффициентам в уравнении этой стадии. Большой энциклопедический словарь
действующих масс закон — ДЕЙСТВУЮЩИХ МАСС ЗАКОН при установившемся хим. равновесии между реагентами и продуктами реакции выполняется равенство , где mi — хим. потенциал i-го компонента системы, ni — eгo стехиометрич. коэф. Химическая энциклопедия

Закон сохранения массы — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Исторический очерк

Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.

Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.

Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.

В СССР на основании этой фразы М. В. Ломоносова объявили автором закона сохранения массы, хотя он никогда не претендовал на такой приоритет и в своём «Обзоре важнейших открытий» данный закон не упоминает. Современные историки подобные претензии считают безосновательными^[8]^[9]. Известный физик и историк науки Я. Г. Дорфман опровергает мнение, что закон сохранения массы был Ломоносовым «выведен на основании опытов с прокаливанием металлов или подвергался им проверке при помощи этих опытов. Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни»^[10].

В дальнейшем, вплоть до создания физики микромира, закон сохранения массы считался истинным и очевидным. Иммануил Кант объявил этот закон постулатом естествознания^[11] (1786). Лавуазье в «Начальном учебнике химии» (1789) привёл точную количественную формулировку закона сохранения массы вещества, однако не объявил его каким-то новым и важным законом, а просто упомянул мимоходом как давно известный и достоверно установленный факт. Для химических реакций Лавуазье сформулировал закон в следующих выражениях^[12]:

Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.

Современное состояние

В XX веке обнаружились два новых свойства массы.

Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:
1) при нагревании железного утюга на 200° его масса возрастает на величину <math>\Delta m / m \approx 10^{-12}</math>;
2) при полном превращении некоторого количества льда в воду <math>\Delta m / m \approx 3.7 \cdot 10^{-12}</math>.

Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).

Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.

Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один^[14].

Более детально

Чтобы более детально пояснить, почему масса в современной физике оказывается неаддитивной^[15] (масса системы не равна — вообще говоря — сумме масс компонент), следует вначале заметить, что под термином масса в современной физике понимается лоренц-инвариантная величина:

где <math>E</math> — энергия, <math>\vec p</math> — импульс,<math>c</math> — скорость света. И сразу заметим, что это выражение одинаково легко применимо к точечной бесструктурной («элементарной») частице, так и к любой физической системе, причём в последнем случае энергия и импульс системы вычисляются просто суммированием энергий и импульсов компонент системы (энергия и импульс — аддитивны).

Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.

Кроме того, заметим, что <math>c</math> — универсальная константа, то есть просто число, которое не меняется никогда, поэтому в принципе можно выбрать такую систему единиц измерения, чтобы выполнялось <math>c = 1</math>, и тогда упомянутая формула будет менее загромождена:

Пусть есть два фотона 1 и 2 с противоположными импульсами: <math>\vec p_1 = — \vec p_2</math>. Масса каждого фотона равна нулю, следовательно можно записать:

<math>\vec p = \vec p_1 + \vec p_2 = \vec 0.</math>.

Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:

Ну и отсюда масса системы:

(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).

В общем случае всё происходит аналогично этому, наиболее отчётливому и простому примеру. Вообще говоря, частицы, образующие систему, не обязательно должны иметь нулевые массы, достаточно, чтобы массы были малы или хотя бы сравнимы с энергиями или импульсами^[17], и эффект будет большим или заметным. Также видно, что точной аддитивности массы нет практически никогда, за исключением лишь достаточно специальных случаев.

Масса и инертность

— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).

Рассмотрим это качественно. Пусть мы толкаем ящик, и он приобрел из-за этого некоторую скорость вправо. Будем для простоты сейчас говорить только об электромагнитных волнах, бегущих строго вправо и влево. Электромагнитная волна, отражающаяся от левой стенки, повысит свою частоту (вследствие эффекта Допплера) и энергию. Волна, отражающаяся от правой стенки, напротив, уменьшит при отражении свои частоту и энергию, однако суммарная энергия увеличится, так как полной компенсации не будет. В итоге тело приобретет кинетическую энергию, равную <math>mv^2/2</math> (если <math>v << c</math>), что означает, что ящик ведет себя как классическое тело массы <math>m</math>. Тот же результат можно (и даже легче) получить для отражения (отскока) от стенок быстрых релятивистских дискретных частиц (для нерелятивистских тоже, но в этом случае масса просто окажется^[18] суммой масс частиц, находящихся в ящике).

Напишите отзыв о статье «Закон сохранения массы»

Примечания

↑ Пер. Э. Радлова (см., напр. [books.google.ru/books?id=eppBExBJLqYC&pg=PA26&lpg=PA26&dq=Ничто+не+может+произойти+из+ничего,+и+никак+не+может+то,+что+есть,+уничтожиться&source=bl&ots=4HlLcJMT_Y&sig=nxVn5rL2CpA_-dGFFHP8t3VrsQg&hl=ru&sa=X&ei=aX7WUoSKK_DV4ATZoYCgDg&ved=0CFkQ6AEwBw#v=onepage&q=Ничто%20не%20может%20произойти%20из%20ничего,%20и%20никак%20не%20может%20то,%20что%20есть,%20уничтожиться&f=false здесь]).
↑ [www.krugosvet.ru/enc/gumanitarnye_nauki/filosofiya/MILETSKAYA_SHKOLA.html Энциклопедия Кругосвет]
↑ Ф. Бэкон, Сочинения, Том 2, Мысль, 1978, стр. 341—342,
↑ Jean Rey, [historyofscience.free.fr/Comite-Lavoisier/f_chap2_lavoisier.html Essais sur la recherche de la cause pour laquelle l’étain et le plomb augmentent de poids quand on les calcine, nouvelle édition revue sur l’exemplaire original et augmentée sur les manuscrits de la Bibliothèque du Roi et des Minimes de Paris, avec des notes], par M. Gobet, Paris, Ruault, 1777, p. 21.
↑ Van Praagh, Gordon. [books.google.ru/books?id=dG83AAAAIAAJ&pg=PA63&lpg=PA63&dq=%22The+heaviness+is+so+closely+linked+to+the+basic+matter+of+the+elements+that,+when+changing+from+one+to+the+other,+they+always+keep+the+same+weight&source=bl&ots=fUYppgq0D5&sig=RqIa7MAOhuLTjYkFwpxHwVTPrvM&hl=ru&sa=X&ei=GKf5VITvEeL5yQOkvYHoBg&ved=0CCUQ6AEwAQ#v=onepage&q=%22The%20heaviness%20is%20so%20closely%20linked%20to%20the%20basic%20matter%20of%20the%20elements%20that%2C%20when%20changing%20from%20one%20to%20the%20other%2C%20they%20always%20keep%20the%20same%20weight&f=false Physical Chemistry, Experimental and Theoretical: An Introductory Text-book]. — Cambridge University Press, 1950. — P. 63. — 295 p.
↑ [historyofscience.free.fr/Lavoisier-Friends/a_chap2_lavoisier.html Письмо Жана Рэ]
↑ Всемирная история физики, 2007, с. 321—322..
↑ Шубинский В. И. Ломоносов: Всероссийский человек. — М.: Молодая гвардия, 2010. — С. 346-351.. — 471 с. — (Жизнь замечательных людей). — ISBN 978-5-235-03323-8.
↑ Сонин А. С. [www.ihst.ru/projects/sohist/papers/son91vr3.htm Несколько эпизодов борьбы с «космополитизмом» в физике.] Вестник АН СССР, № 8 (1990), стр. 122—133.
↑ Дорфман Я.Г. [gidropraktikum.narod.ru/Lomonosov-Dorfman.djvu Закон сохранения массы при химических реакциях и физические воззрения Ломоносова] // Ломоносов М.В. Сборник статей и материалов. — М.-Л.: Издательство АН СССР, 1961. — Т. 5. — С. 182-193.
↑ И. Кант. Метафизические начала естествознания. Соч., том VI, стр. 148.
↑ [him.1september.ru/article.php?ID=200403701 Лавуазье.]
↑ Окунь Л. Б. Понятие массы, указ. соч., стр. 519.
↑ 1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553.
↑ Приближенно аддитивной она, конечно же, может быть — в приближении нерелятивистской механики, однако как только в системе имеются движения со скоростями, сравнимыми со скоростью света, аддитивность массы как правило нарушается вполне заметно или даже сильно.
↑ Выбрав (по условию) именно противоположные (и равные по величине) импульсы, мы получили сразу же и удобное для нас обстоятельство: первоначально выбранная система отсчёта тогда сразу оказывается системой, в котором система покоится (это и значит формально, что её импульс равен нулю; да это и интуитивно так). Поэтому энергия нашей физической системы, которую мы посчитаем, как раз и будет сразу её энергией покоя.
↑ В нашей системе единиц <math>c = 1</math>, для того, чтобы выразить это условие в других (любых) системах единиц надо не забыть умножать или делить на нужные степени <math>c</math>.
↑ В принципе — конечно, лишь приближенно.

Литература

Джеммер М. [eqworld.ipmnet.ru/ru/library/books/Jammer1967ru.djvu Понятие массы в классической и современной физике]. — М.: Прогресс, 1967. — 255 с.
Дорфман Я. Г. Всемирная история физики. С древнейших времён до конца XVIII века. — Изд. 2-е. — М.: КомКнига, 2007. — 352 с. — ISBN 978-5-484-00-938-1.
Окунь Л. Б. [ufn.ru/ufn89/ufn89_7/Russian/r897f.pdf Понятие массы (Масса, энергия, относительность).] Успехи физических наук, № 158 (1989).
Спасский Б. И. [osnovanija.narod.ru/history.html История физики]. — М.: Высшая школа, 1977.
- Том 1: [osnovanija.narod.ru/History/Spas/T1_1.djvu часть 1-я ] [osnovanija.narod.ru/History/Spas/T1_2.djvu часть 2-я]
- Том 2: [osnovanija.narod.ru/History/Spas/T2_1.djvu часть 1-я ] [osnovanija.narod.ru/History/Spas/T2_2.djvu часть 2-я]

Отрывок, характеризующий Закон сохранения массы

Дверь выходила в переднюю заднего хода. В углу сидел старик слуга княжен и вязал чулок. Пьер никогда не был на этой половине, даже не предполагал существования таких покоев. Анна Михайловна спросила у обгонявшей их, с графином на подносе, девушки (назвав ее милой и голубушкой) о здоровье княжен и повлекла Пьера дальше по каменному коридору. Из коридора первая дверь налево вела в жилые комнаты княжен. Горничная, с графином, второпях (как и всё делалось второпях в эту минуту в этом доме) не затворила двери, и Пьер с Анною Михайловной, проходя мимо, невольно заглянули в ту комнату, где, разговаривая, сидели близко друг от друга старшая княжна с князем Васильем. Увидав проходящих, князь Василий сделал нетерпеливое движение и откинулся назад; княжна вскочила и отчаянным жестом изо всей силы хлопнула дверью, затворяя ее.
Жест этот был так не похож на всегдашнее спокойствие княжны, страх, выразившийся на лице князя Василья, был так несвойствен его важности, что Пьер, остановившись, вопросительно, через очки, посмотрел на свою руководительницу.
Анна Михайловна не выразила удивления, она только слегка улыбнулась и вздохнула, как будто показывая, что всего этого она ожидала.
– Soyez homme, mon ami, c’est moi qui veillerai a vos interets, [Будьте мужчиною, друг мой, я же стану блюсти за вашими интересами.] – сказала она в ответ на его взгляд и еще скорее пошла по коридору.
Пьер не понимал, в чем дело, и еще меньше, что значило veiller a vos interets, [блюсти ваши интересы,] но он понимал, что всё это так должно быть. Коридором они вышли в полуосвещенную залу, примыкавшую к приемной графа. Это была одна из тех холодных и роскошных комнат, которые знал Пьер с парадного крыльца. Но и в этой комнате, посередине, стояла пустая ванна и была пролита вода по ковру. Навстречу им вышли на цыпочках, не обращая на них внимания, слуга и причетник с кадилом. Они вошли в знакомую Пьеру приемную с двумя итальянскими окнами, выходом в зимний сад, с большим бюстом и во весь рост портретом Екатерины. Все те же люди, почти в тех же положениях, сидели, перешептываясь, в приемной. Все, смолкнув, оглянулись на вошедшую Анну Михайловну, с ее исплаканным, бледным лицом, и на толстого, большого Пьера, который, опустив голову, покорно следовал за нею.
На лице Анны Михайловны выразилось сознание того, что решительная минута наступила; она, с приемами деловой петербургской дамы, вошла в комнату, не отпуская от себя Пьера, еще смелее, чем утром. Она чувствовала, что так как она ведет за собою того, кого желал видеть умирающий, то прием ее был обеспечен. Быстрым взглядом оглядев всех, бывших в комнате, и заметив графова духовника, она, не то что согнувшись, но сделавшись вдруг меньше ростом, мелкою иноходью подплыла к духовнику и почтительно приняла благословение одного, потом другого духовного лица.
– Слава Богу, что успели, – сказала она духовному лицу, – мы все, родные, так боялись. Вот этот молодой человек – сын графа, – прибавила она тише. – Ужасная минута!
Проговорив эти слова, она подошла к доктору.
– Cher docteur, – сказала она ему, – ce jeune homme est le fils du comte… y a t il de l’espoir? [этот молодой человек – сын графа… Есть ли надежда?]
Доктор молча, быстрым движением возвел кверху глаза и плечи. Анна Михайловна точно таким же движением возвела плечи и глаза, почти закрыв их, вздохнула и отошла от доктора к Пьеру. Она особенно почтительно и нежно грустно обратилась к Пьеру.
– Ayez confiance en Sa misericorde, [Доверьтесь Его милосердию,] – сказала она ему, указав ему диванчик, чтобы сесть подождать ее, сама неслышно направилась к двери, на которую все смотрели, и вслед за чуть слышным звуком этой двери скрылась за нею.
Пьер, решившись во всем повиноваться своей руководительнице, направился к диванчику, который она ему указала. Как только Анна Михайловна скрылась, он заметил, что взгляды всех, бывших в комнате, больше чем с любопытством и с участием устремились на него. Он заметил, что все перешептывались, указывая на него глазами, как будто со страхом и даже с подобострастием. Ему оказывали уважение, какого прежде никогда не оказывали: неизвестная ему дама, которая говорила с духовными лицами, встала с своего места и предложила ему сесть, адъютант поднял уроненную Пьером перчатку и подал ему; доктора почтительно замолкли, когда он проходил мимо их, и посторонились, чтобы дать ему место. Пьер хотел сначала сесть на другое место, чтобы не стеснять даму, хотел сам поднять перчатку и обойти докторов, которые вовсе и не стояли на дороге; но он вдруг почувствовал, что это было бы неприлично, он почувствовал, что он в нынешнюю ночь есть лицо, которое обязано совершить какой то страшный и ожидаемый всеми обряд, и что поэтому он должен был принимать от всех услуги. Он принял молча перчатку от адъютанта, сел на место дамы, положив свои большие руки на симметрично выставленные колени, в наивной позе египетской статуи, и решил про себя, что всё это так именно должно быть и что ему в нынешний вечер, для того чтобы не потеряться и не наделать глупостей, не следует действовать по своим соображениям, а надобно предоставить себя вполне на волю тех, которые руководили им.
Не прошло и двух минут, как князь Василий, в своем кафтане с тремя звездами, величественно, высоко неся голову, вошел в комнату. Он казался похудевшим с утра; глаза его были больше обыкновенного, когда он оглянул комнату и увидал Пьера. Он подошел к нему, взял руку (чего он прежде никогда не делал) и потянул ее книзу, как будто он хотел испытать, крепко ли она держится.
– Courage, courage, mon ami. Il a demande a vous voir. C’est bien… [Не унывать, не унывать, мой друг. Он пожелал вас видеть. Это хорошо…] – и он хотел итти.
Но Пьер почел нужным спросить:
– Как здоровье…
Он замялся, не зная, прилично ли назвать умирающего графом; назвать же отцом ему было совестно.
– Il a eu encore un coup, il y a une demi heure. Еще был удар. Courage, mon аmi… [Полчаса назад у него был еще удар. Не унывать, мой друг…]
Пьер был в таком состоянии неясности мысли, что при слове «удар» ему представился удар какого нибудь тела. Он, недоумевая, посмотрел на князя Василия и уже потом сообразил, что ударом называется болезнь. Князь Василий на ходу сказал несколько слов Лоррену и прошел в дверь на цыпочках. Он не умел ходить на цыпочках и неловко подпрыгивал всем телом. Вслед за ним прошла старшая княжна, потом прошли духовные лица и причетники, люди (прислуга) тоже прошли в дверь. За этою дверью послышалось передвиженье, и наконец, всё с тем же бледным, но твердым в исполнении долга лицом, выбежала Анна Михайловна и, дотронувшись до руки Пьера, сказала:
– La bonte divine est inepuisable. C’est la ceremonie de l’extreme onction qui va commencer. Venez. [Милосердие Божие неисчерпаемо. Соборование сейчас начнется. Пойдемте.]
Пьер прошел в дверь, ступая по мягкому ковру, и заметил, что и адъютант, и незнакомая дама, и еще кто то из прислуги – все прошли за ним, как будто теперь уж не надо было спрашивать разрешения входить в эту комнату.

Пьер хорошо знал эту большую, разделенную колоннами и аркой комнату, всю обитую персидскими коврами. Часть комнаты за колоннами, где с одной стороны стояла высокая красного дерева кровать, под шелковыми занавесами, а с другой – огромный киот с образами, была красно и ярко освещена, как бывают освещены церкви во время вечерней службы. Под освещенными ризами киота стояло длинное вольтеровское кресло, и на кресле, обложенном вверху снежно белыми, не смятыми, видимо, только – что перемененными подушками, укрытая до пояса ярко зеленым одеялом, лежала знакомая Пьеру величественная фигура его отца, графа Безухого, с тою же седою гривой волос, напоминавших льва, над широким лбом и с теми же характерно благородными крупными морщинами на красивом красно желтом лице. Он лежал прямо под образами; обе толстые, большие руки его были выпростаны из под одеяла и лежали на нем. В правую руку, лежавшую ладонью книзу, между большим и указательным пальцами вставлена была восковая свеча, которую, нагибаясь из за кресла, придерживал в ней старый слуга. Над креслом стояли духовные лица в своих величественных блестящих одеждах, с выпростанными на них длинными волосами, с зажженными свечами в руках, и медленно торжественно служили. Немного позади их стояли две младшие княжны, с платком в руках и у глаз, и впереди их старшая, Катишь, с злобным и решительным видом, ни на мгновение не спуская глаз с икон, как будто говорила всем, что не отвечает за себя, если оглянется. Анна Михайловна, с кроткою печалью и всепрощением на лице, и неизвестная дама стояли у двери. Князь Василий стоял с другой стороны двери, близко к креслу, за резным бархатным стулом, который он поворотил к себе спинкой, и, облокотив на нее левую руку со свечой, крестился правою, каждый раз поднимая глаза кверху, когда приставлял персты ко лбу. Лицо его выражало спокойную набожность и преданность воле Божией. «Ежели вы не понимаете этих чувств, то тем хуже для вас», казалось, говорило его лицо.
Сзади его стоял адъютант, доктора и мужская прислуга; как бы в церкви, мужчины и женщины разделились. Всё молчало, крестилось, только слышны были церковное чтение, сдержанное, густое басовое пение и в минуты молчания перестановка ног и вздохи. Анна Михайловна, с тем значительным видом, который показывал, что она знает, что делает, перешла через всю комнату к Пьеру и подала ему свечу. Он зажег ее и, развлеченный наблюдениями над окружающими, стал креститься тою же рукой, в которой была свеча.
Младшая, румяная и смешливая княжна Софи, с родинкою, смотрела на него. Она улыбнулась, спрятала свое лицо в платок и долго не открывала его; но, посмотрев на Пьера, опять засмеялась. Она, видимо, чувствовала себя не в силах глядеть на него без смеха, но не могла удержаться, чтобы не смотреть на него, и во избежание искушений тихо перешла за колонну. В середине службы голоса духовенства вдруг замолкли; духовные лица шопотом сказали что то друг другу; старый слуга, державший руку графа, поднялся и обратился к дамам. Анна Михайловна выступила вперед и, нагнувшись над больным, из за спины пальцем поманила к себе Лоррена. Француз доктор, – стоявший без зажженной свечи, прислонившись к колонне, в той почтительной позе иностранца, которая показывает, что, несмотря на различие веры, он понимает всю важность совершающегося обряда и даже одобряет его, – неслышными шагами человека во всей силе возраста подошел к больному, взял своими белыми тонкими пальцами его свободную руку с зеленого одеяла и, отвернувшись, стал щупать пульс и задумался. Больному дали чего то выпить, зашевелились около него, потом опять расступились по местам, и богослужение возобновилось. Во время этого перерыва Пьер заметил, что князь Василий вышел из за своей спинки стула и, с тем же видом, который показывал, что он знает, что делает, и что тем хуже для других, ежели они не понимают его, не подошел к больному, а, пройдя мимо его, присоединился к старшей княжне и с нею вместе направился в глубь спальни, к высокой кровати под шелковыми занавесами. От кровати и князь и княжна оба скрылись в заднюю дверь, но перед концом службы один за другим возвратились на свои места. Пьер обратил на это обстоятельство не более внимания, как и на все другие, раз навсегда решив в своем уме, что всё, что совершалось перед ним нынешний вечер, было так необходимо нужно.
Звуки церковного пения прекратились, и послышался голос духовного лица, которое почтительно поздравляло больного с принятием таинства. Больной лежал всё так же безжизненно и неподвижно. Вокруг него всё зашевелилось, послышались шаги и шопоты, из которых шопот Анны Михайловны выдавался резче всех.
Пьер слышал, как она сказала:
– Непременно надо перенести на кровать, здесь никак нельзя будет…
Больного так обступили доктора, княжны и слуги, что Пьер уже не видал той красно желтой головы с седою гривой, которая, несмотря на то, что он видел и другие лица, ни на мгновение не выходила у него из вида во всё время службы. Пьер догадался по осторожному движению людей, обступивших кресло, что умирающего поднимали и переносили.
– За мою руку держись, уронишь так, – послышался ему испуганный шопот одного из слуг, – снизу… еще один, – говорили голоса, и тяжелые дыхания и переступанья ногами людей стали торопливее, как будто тяжесть, которую они несли, была сверх сил их.
Несущие, в числе которых была и Анна Михайловна, поровнялись с молодым человеком, и ему на мгновение из за спин и затылков людей показалась высокая, жирная, открытая грудь, тучные плечи больного, приподнятые кверху людьми, державшими его под мышки, и седая курчавая, львиная голова. Голова эта, с необычайно широким лбом и скулами, красивым чувственным ртом и величественным холодным взглядом, была не обезображена близостью смерти. Она была такая же, какою знал ее Пьер назад тому три месяца, когда граф отпускал его в Петербург. Но голова эта беспомощно покачивалась от неровных шагов несущих, и холодный, безучастный взгляд не знал, на чем остановиться.
Прошло несколько минут суетни около высокой кровати; люди, несшие больного, разошлись. Анна Михайловна дотронулась до руки Пьера и сказала ему: «Venez». [Идите.] Пьер вместе с нею подошел к кровати, на которой, в праздничной позе, видимо, имевшей отношение к только что совершенному таинству, был положен больной. Он лежал, высоко опираясь головой на подушки. Руки его были симметрично выложены на зеленом шелковом одеяле ладонями вниз. Когда Пьер подошел, граф глядел прямо на него, но глядел тем взглядом, которого смысл и значение нельзя понять человеку. Или этот взгляд ровно ничего не говорил, как только то, что, покуда есть глаза, надо же глядеть куда нибудь, или он говорил слишком многое. Пьер остановился, не зная, что ему делать, и вопросительно оглянулся на свою руководительницу Анну Михайловну. Анна Михайловна сделала ему торопливый жест глазами, указывая на руку больного и губами посылая ей воздушный поцелуй. Пьер, старательно вытягивая шею, чтоб не зацепить за одеяло, исполнил ее совет и приложился к ширококостной и мясистой руке. Ни рука, ни один мускул лица графа не дрогнули. Пьер опять вопросительно посмотрел на Анну Михайловну, спрашивая теперь, что ему делать. Анна Михайловна глазами указала ему на кресло, стоявшее подле кровати. Пьер покорно стал садиться на кресло, глазами продолжая спрашивать, то ли он сделал, что нужно. Анна Михайловна одобрительно кивнула головой. Пьер принял опять симметрично наивное положение египетской статуи, видимо, соболезнуя о том, что неуклюжее и толстое тело его занимало такое большое пространство, и употребляя все душевные силы, чтобы казаться как можно меньше. Он смотрел на графа. Граф смотрел на то место, где находилось лицо Пьера, в то время как он стоял. Анна Михайловна являла в своем положении сознание трогательной важности этой последней минуты свидания отца с сыном. Это продолжалось две минуты, которые показались Пьеру часом. Вдруг в крупных мускулах и морщинах лица графа появилось содрогание. Содрогание усиливалось, красивый рот покривился (тут только Пьер понял, до какой степени отец его был близок к смерти), из перекривленного рта послышался неясный хриплый звук. Анна Михайловна старательно смотрела в глаза больному и, стараясь угадать, чего было нужно ему, указывала то на Пьера, то на питье, то шопотом вопросительно называла князя Василия, то указывала на одеяло. Глаза и лицо больного выказывали нетерпение. Он сделал усилие, чтобы взглянуть на слугу, который безотходно стоял у изголовья постели.
– На другой бочок перевернуться хотят, – прошептал слуга и поднялся, чтобы переворотить лицом к стене тяжелое тело графа.
Пьер встал, чтобы помочь слуге.
В то время как графа переворачивали, одна рука его беспомощно завалилась назад, и он сделал напрасное усилие, чтобы перетащить ее. Заметил ли граф тот взгляд ужаса, с которым Пьер смотрел на эту безжизненную руку, или какая другая мысль промелькнула в его умирающей голове в эту минуту, но он посмотрел на непослушную руку, на выражение ужаса в лице Пьера, опять на руку, и на лице его явилась так не шедшая к его чертам слабая, страдальческая улыбка, выражавшая как бы насмешку над своим собственным бессилием. Неожиданно, при виде этой улыбки, Пьер почувствовал содрогание в груди, щипанье в носу, и слезы затуманили его зрение. Больного перевернули на бок к стене. Он вздохнул.
– Il est assoupi, [Он задремал,] – сказала Анна Михайловна, заметив приходившую на смену княжну. – Аllons. [Пойдем.]
Пьер вышел.

В приемной никого уже не было, кроме князя Василия и старшей княжны, которые, сидя под портретом Екатерины, о чем то оживленно говорили. Как только они увидали Пьера с его руководительницей, они замолчали. Княжна что то спрятала, как показалось Пьеру, и прошептала:
– Не могу видеть эту женщину.
– Catiche a fait donner du the dans le petit salon, – сказал князь Василий Анне Михайловне. – Allez, ma pauvre Анна Михайловна, prenez quelque сhose, autrement vous ne suffirez pas. [Катишь велела подать чаю в маленькой гостиной. Вы бы пошли, бедная Анна Михайловна, подкрепили себя, а то вас не хватит.]
Пьеру он ничего не сказал, только пожал с чувством его руку пониже плеча. Пьер с Анной Михайловной прошли в petit salon. [маленькую гостиную.]
– II n’y a rien qui restaure, comme une tasse de cet excellent the russe apres une nuit blanche, [Ничто так не восстановляет после бессонной ночи, как чашка этого превосходного русского чаю.] – говорил Лоррен с выражением сдержанной оживленности, отхлебывая из тонкой, без ручки, китайской чашки, стоя в маленькой круглой гостиной перед столом, на котором стоял чайный прибор и холодный ужин. Около стола собрались, чтобы подкрепить свои силы, все бывшие в эту ночь в доме графа Безухого. Пьер хорошо помнил эту маленькую круглую гостиную, с зеркалами и маленькими столиками. Во время балов в доме графа, Пьер, не умевший танцовать, любил сидеть в этой маленькой зеркальной и наблюдать, как дамы в бальных туалетах, брильянтах и жемчугах на голых плечах, проходя через эту комнату, оглядывали себя в ярко освещенные зеркала, несколько раз повторявшие их отражения. Теперь та же комната была едва освещена двумя свечами, и среди ночи на одном маленьком столике беспорядочно стояли чайный прибор и блюда, и разнообразные, непраздничные люди, шопотом переговариваясь, сидели в ней, каждым движением, каждым словом показывая, что никто не забывает и того, что делается теперь и имеет еще совершиться в спальне. Пьер не стал есть, хотя ему и очень хотелось. Он оглянулся вопросительно на свою руководительницу и увидел, что она на цыпочках выходила опять в приемную, где остался князь Василий с старшею княжной. Пьер полагал, что и это было так нужно, и, помедлив немного, пошел за ней. Анна Михайловна стояла подле княжны, и обе они в одно время говорили взволнованным шопотом:

Адиттивность масс системы. Закон сохранения массы

Аддитивность масс системы

Пусть два тела с массами $m_{1} $ и $m_{2} $сталкиваются между собой и соединяются в одно — составное — тело. Примером может служить слипание двух глиняных шаров при столкновении между собой. Другим примером является химическая или ядерная реакция, в которой два атома или ядра соединяются в молекулу или новое ядро. Требуется определить массу составного тела $m$, зная массы $m_{1} $ и $m_{2} $ соединяющихся тел.

Рассмотрим процесс столкновения в какой-либо инерциальной системе отсчета $S$. Обозначим через $v_{1} $ и $v_{2} $ скорости тел до столкновения, а через $v$ — скорость составного тела после столкновения. На основании закона сохранения импульса можно записать:

$m_{1} v_{1} +m_{2} v_{2} =mv$. (1)

Рассмотрим теперь этот же процесс в системе отсчета $S’$, движущейся относительно системы $S$ прямолинейно и равномерно со скоростью $V$.

Согласно принципу относительности закон сохранения импульса справедлив также в системе $S’$ и записывается в виде:

$m_{1} v’_{1} +m_{2} v’_{2} =mv’$. (2)

Ввиду полного равноправия инерциальных систем отсчета массы всех тел в системе $S’$такие же, какими они были в системе $S$. В нерелятивистской физике скорости $v’_{1} ,v’_{2} ,v’$ в системе $S’$связаны с соответствующими скоростями в системе $S$следующими соотношениями:

Поэтому (2) преобразуется в:

или на основании соотношения (1):

Отсюда:

$m=m_{1} +m_{2} $. (3)

Масса составного тела равна сумме масс составляющих тел. Это свойство называется аддитивностью массы.

Закон сохранения массы

Доказательство свойства аддитивности массы может быть обобщено. Нет необходимости предполагать, что сталкиваются только два тела и что после столкновения они соединяются в одно тело. Можно взять, например, произвольную химическую реакцию, в которой реагирует несколько молекул или атомов. Тогда, повторяя рассуждения, мы придем к общему заключению, что сумма масс веществ до реакции равна сумме масс веществ после реакции. Это — закон сохранения массы.

Современный взгляд

В XX веке обнаружились два новых свойства массы:

масса физического объекта зависит от его внутренней энергии;
при поглощении внешней энергии масса растет, при потере — уменьшается.

Закон сохранения массы получен как следствие галилеева принципа относительности. Но галилеев принцип относительности является приближенным предельным случаем эйнштейновского принципа относительности. Законы сохранения массы и энергии, которые в дорелятивистской физике считались двумя независимыми точными законами природы, в релятивистской физике утратили свою независимость и были объединены в единый закон сохранения массы-энергии.

Всякая энергия обладает массой, равной количеству энергии, деленному на квадрат скорости света в вакууме. То обстоятельство, что в химических реакциях не было обнаружено изменение массы вещества, связано с их относительно очень малым энергетическим выходом. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой.

Особенно ощутимо изменение массы при ядерных реакциях. Масса не является аддитивной величиной: масса системы не равна сумме масс ее составляющих. Примеры неаддитивности:

электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею как система;
масса дейтрона, состоящего из одного протона и нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц;
при термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия;
масса протона ($\approx $938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).

Примеры решения задач

Пример 1

Определите массу йодида натрия $NaI$ количеством вещества 1,7 моль.

Дано: $\nu (NaI)$= 1,7 моль.

Найти: $m(NaI)$-?

Решение:

Молярная масса йодида натрия составляет:

$M(NaI)$ = $M(Na)$+$M(I)$= 23 + 127 = 150 г/моль

Определяем массу $NaI$:

\[m(NaI)=\nu (NaI)\cdot M(NaI)=1.7\cdot 150=2553\]

Ответ: $m(NaI)=2553$

Пример 2

Найти приращение кинетической энергии замкнутой системы двух тел с массами $m_{1} $ и $m_{2} $ при их абсолютно неупругом столкновении, если до столкновения тела двигались со скоростями $v_{1} $ и $v_{2} $.

Дано: $m_{1} $,$m_{2} $,$v_{1} $,$v_{2} $.

Найти: $\Delta E_{k} $-?

Решение: Кинетическая энергия тел до столкновения равна:

\[E_{k} =\frac{m_{1} v_{1}^{2} }{2} +\frac{m_{2} v_{2}^{2} }{2} .\]

Кинетическая энергия тел после столкновения равна:

\[E_{k} =\frac{m_{c} v_{c}^{2} }{2} ,\]

где $m_{c} =m_{1} +m_{2} $(масса системы по закону сохранения массы), а

$v_{c} =\frac{m_{1} v_{1} +m_{2} v_{2} }{m_{1} +m_{2} } $(скорость системы по закону сохранения импульса).

Тогда приращение кинетической энергии замкнутой системы равно:

\[\Delta E_{k} =\frac{-m_{1} m_{2} }{m_{1} +m_{2} } \cdot \frac{(v_{1} -v_{2} )^{2} }{2} .\]

Ответ: $\Delta E_{k} =\frac{-m_{1} m_{2} }{m_{1} +m_{2} } \cdot \frac{(v_{1} -v_{2} )^{2} }{2} $

Закон сохранения массы — Википедия

Исторический очерк

Современное состояние

Более детально

Масса и инертность

Примечания

Литература

Закон сохранения массы — Википедия

Исторический очерк

Современное состояние

Более детально

Масса и инертность

Примечания

Литература

Закон сохранения массы — Вики

Действующих масс закон — это… Что такое Действующих масс закон?

Действующих масс закон — Большая советская энциклопедия

Значения в других словарях

Закон сохранения массы — Википедия (с комментариями)

Исторический очерк

Современное состояние

Более детально

Масса и инертность

Напишите отзыв о статье «Закон сохранения массы»

Примечания

Литература

Отрывок, характеризующий Закон сохранения массы

Адиттивность масс системы. Закон сохранения массы

Аддитивность масс системы

Закон сохранения массы

Современный взгляд

Примеры решения задач

Добавить комментарий Отменить ответ