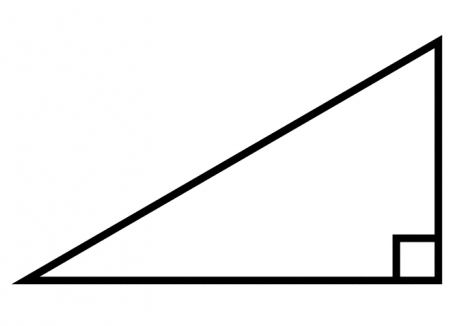
Виды треугольников | Треугольники
В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.
Виды треугольников по углам:
- остроугольные
- прямоугольные
- тупоугольные
Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).
Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Виды треугольников по сторонам:
- равносторонние
- равнобедренные
- разносторонние
Равносторонний треугольник (или правильный треугольник)
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.
Отрезки равной длины на чертеже отмечают равным количеством черточек:
разносторонний треугольник
равносторонний треугольник
равнобедренный треугольник
www.treugolniki.ru
Виды треугольников (по сторонам). Видеоурок. Математика 3 Класс
На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
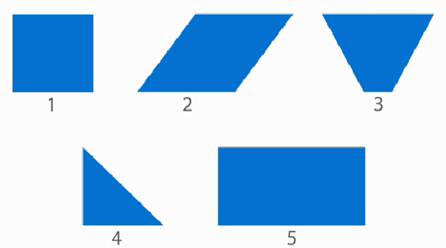
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
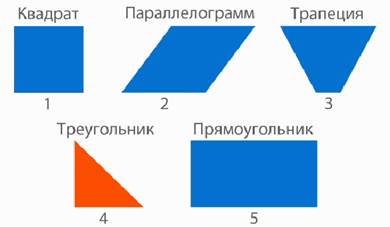
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника, отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
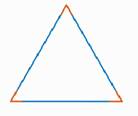
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
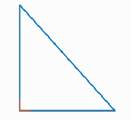
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
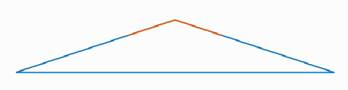
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
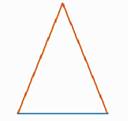
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
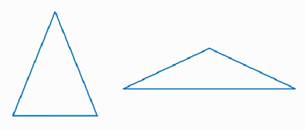
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны. Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
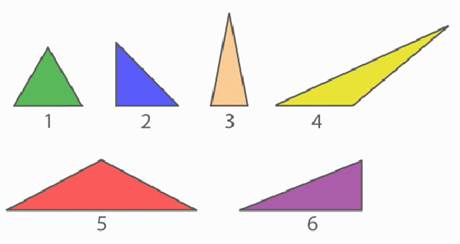
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
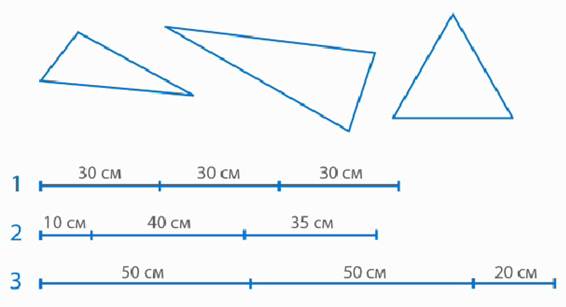
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Nsportal.ru (Источник).
- Prosv.ru (Источник).
- Do.gendocs.ru (Источник).
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …, отрезки – его
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
interneturok.ru
Виды треугольников. Основные факты. Видеоурок. Геометрия 7 Класс
Мы выделили несколько особых видов треугольников: равнобедренные (и их частные случаи – равносторонние) и прямоугольные (см. рис. 1).

Рис. 1. Сверху-вниз: равнобедренный, равносторонний и прямоугольный треугольники
Остановимся подробнее на их свойствах, т. к. они являются удобными инструментами как для изучения других треугольников, так и для изучения многоугольников вообще. Мы уже видели это на конкретном примере, когда выводили формулу площади произвольного треугольника через формулу площади прямоугольного треугольника.
Если у треугольника две стороны равны, то мы его называем равнобедренным. Обычно его ставят на третью сторону, называемую основанием. Равные стороны оказываются по бокам, их называют боковыми.
Если у треугольника равны все три стороны, то его называют равносторонним. Естественно, равносторонний треугольник является равнобедренным, т. е. он обладает и свойствами равнобедренного треугольника, и своими собственными.
Рассмотрим равнобедренный треугольник 
 ,
,  – боковые стороны (см. рис. 2).
– боковые стороны (см. рис. 2).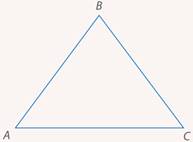
Рис. 2. Равнобедренный треугольник  с основанием
с основанием 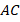 и боковыми сторонами
и боковыми сторонами 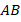 и
и 
Если вырезать такой треугольник из бумаги и согнуть вдоль вертикальной линии, проходящей через точку 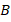 , то образовавшиеся половины совпадут (см. рис. 3).
, то образовавшиеся половины совпадут (см. рис. 3).
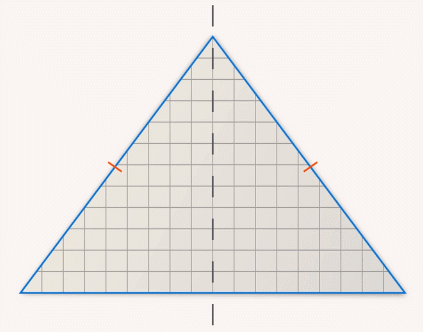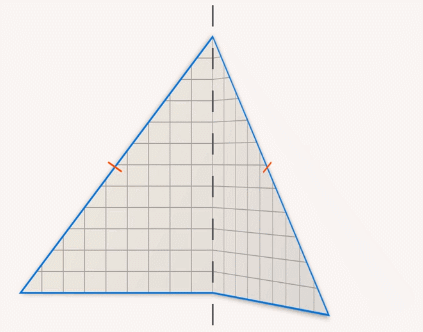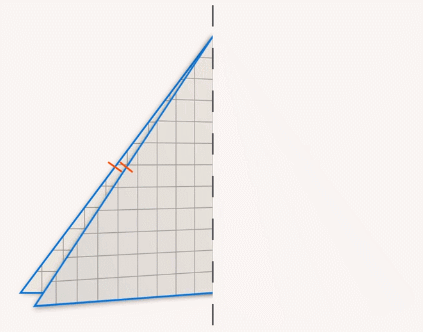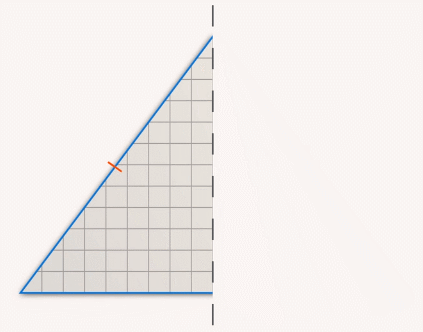
Рис. 3. Бумажный равнобедренный треугольник согнули вдоль вертикальной линии, проходящей через точку 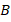
Если разрезать треугольник по линии сгиба и приставить одну из половинок к зеркалу, то мы снова увидим исходный треугольник (см. рис. 4).
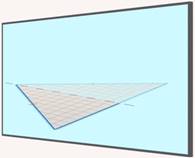
Рис. 4. Половину разрезанного по линии сгиба треугольника приставили к зеркалу
Такое свойство фигуры называется осевой симметрией, т. е. фигура симметрична относительно оси.
Осевая симметрия
Равнобедренный треугольник не единственная фигура, обладающая осью симметрии. Несложно доказать, что у равностороннего треугольника сразу три таких оси (можно рассматривать его как равнобедренный относительно каждой из трех сторон – оснований) (см. рис. 5).
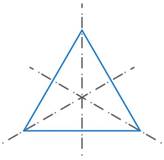
Рис. 5. Равносторонний треугольник имеет три оси симметрии
Из других известных нам фигур: у прямоугольника и ромба есть по две оси симметрии (см. рис. 6), у квадрата – четыре (см. рис. 7), у окружности таких осей бесконечно много (любая прямая, проходящая через центр) (см. рис. 8).
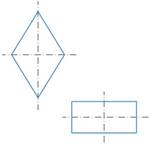
Рис. 6. У прямоугольника и ромба есть две оси симметрии
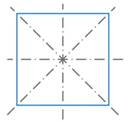
Рис. 7. У квадрата есть четыре оси симметрии

Рис. 8. У окружности бесконечно много осей симметрии
Мы дали интуитивное определение оси симметрии. Сформулируем строгое определение.
Точка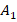 называется симметричной точке
называется симметричной точке 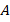 относительно прямой (оси)
относительно прямой (оси) 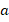 , если
, если  перпендикулярен прямой
перпендикулярен прямой 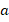 ; если
; если  пересекает прямую
пересекает прямую 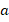 в точке
в точке 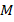 , то
, то  (см. рис. 9).
(см. рис. 9).
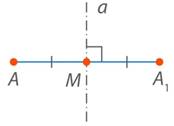
Рис. 9. Точка 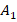 симметрична точке
симметрична точке 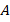 относительно прямой
относительно прямой 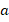
Чтобы доказать симметричность равнобедренного треугольника, докажем сначала несколько важных свойств.
Теорема 1
У равнобедренного треугольника углы при основании равны.
Доказательство
Проведем биссектрису 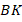 (см. рис. 10).
(см. рис. 10).
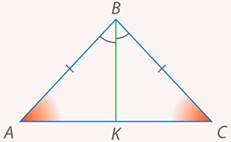
Рис. 10. Равнобедренный треугольник  с проведенной биссектрисой
с проведенной биссектрисой 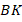
Треугольники 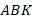 и
и 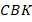 равны по первому признаку:
равны по первому признаку:
 – боковые стороны;
– боковые стороны; – общая;
– общая; , т. к.
, т. к.  – биссектриса.
– биссектриса.
Следовательно,  .
.
Теорема доказана.
Из равенства треугольников 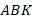 и
и 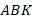 мы получаем еще два факта:
мы получаем еще два факта:
 , т. е.
, т. е.  – середина
– середина  ;
; , а т. к. они еще и смежные (
, а т. к. они еще и смежные ( , следовательно,
, следовательно,  ), значит, они прямые. Т. е. отрезок
), значит, они прямые. Т. е. отрезок  перпендикулярен
перпендикулярен  .
.
Объединим эти два факта в одну теорему.
Теорема 2
Биссектриса в равнобедренном треугольнике, проведенная к основанию, является одновременно медианой и высотой.
Т. е., если мы проводим отрезок 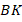 как биссектрису (делим
как биссектрису (делим 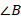 пополам), то он одновременно будет являться и медианой, и высотой (см. рис. 11).
пополам), то он одновременно будет являться и медианой, и высотой (см. рис. 11).
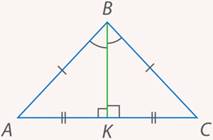
Рис. 11. В равнобедренном треугольнике биссектриса, проведенная к основанию, является и медианой, и высотой
Как вы думаете, если мы начнем строить отрезок 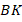 как медиану или высоту, будет ли он сразу являться и всем остальным? Конечно, да. Доказательство тоже очень простое. Попробуйте это сделать самостоятельно, а ознакомиться с доказательствами можно ниже.
как медиану или высоту, будет ли он сразу являться и всем остальным? Конечно, да. Доказательство тоже очень простое. Попробуйте это сделать самостоятельно, а ознакомиться с доказательствами можно ниже.
Доказательство
Теорема 1
Медиана, проведенная к основанию в равнобедренном треугольнике, является биссектрисой и высотой.
Доказательство
Проведем в равнобедренном треугольнике  медиану
медиану 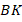 (см. рис. 12).
(см. рис. 12).

Рис. 12. Равнобедренный треугольник  с проведенной медианой
с проведенной медианой 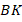
Треугольники 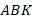 и
и 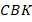 равны по третьему признаку:
равны по третьему признаку:
 – боковые стороны равнобедренного треугольника.
– боковые стороны равнобедренного треугольника. , т. к.
, т. к.  – медиана.
– медиана. – общая.
– общая.
Тогда 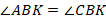 , следовательно,
, следовательно, 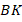 – биссектриса.
– биссектриса.
Аналогично 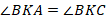 . Учитывая, что они смежные, то
. Учитывая, что они смежные, то 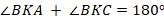 , откуда:
, откуда:  , т. е.
, т. е. 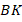 – высота.
– высота.
Теорема доказана.
Теорема 2
Высота, проведенная к основанию в равнобедренном треугольнике, является биссектрисой и медианой.
Доказательство
Если предположить, что высота 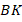 не является биссектрисой, т. е. другая биссектриса, которая обязана быть высотой (по доказанной ранее теореме). Значит, у нас будет две высоты из точки
не является биссектрисой, т. е. другая биссектриса, которая обязана быть высотой (по доказанной ранее теореме). Значит, у нас будет две высоты из точки 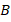 . Но это невозможно, т. к. из точки на прямую можно опустить только один перпендикуляр. Значит,
. Но это невозможно, т. к. из точки на прямую можно опустить только один перпендикуляр. Значит, 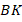 также является биссектрисой, а значит, и медианой.
также является биссектрисой, а значит, и медианой.
Теорема доказана.
С помощью доказанных теорем можно строго доказать, что равнобедренный треугольник обладает осевой симметрией. Причем осью симметрии будет являться высота (она же биссектриса, высота), проведенная из точки 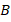 .
.
Рассмотрим произвольную точку 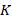 равнобедренного треугольника на боковой стороне (см. рис. 13) (для точек основания проведите доказательство самостоятельно).
равнобедренного треугольника на боковой стороне (см. рис. 13) (для точек основания проведите доказательство самостоятельно).
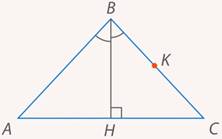
Рис. 13. На боковой стороне равнобедренного треугольника отметили произвольную точку 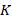
Опустим из точки 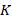 перпендикуляр на высоту
перпендикуляр на высоту  и продлим его до пересечения со второй боковой стороной (точкой
и продлим его до пересечения со второй боковой стороной (точкой 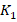 ) (см. рис. 14).
) (см. рис. 14).
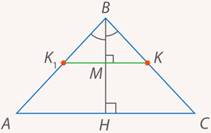
Рис. 14. Из произвольной точки  опустили перпендикуляр и продлили его до пересечения со второй боковой стороной
опустили перпендикуляр и продлили его до пересечения со второй боковой стороной
Наша задача: доказать, что  . Рассмотрим треугольники
. Рассмотрим треугольники  и
и  , в них:
, в них:
 – общая сторона;
– общая сторона; ;
; (т. к.
(т. к.  – биссектриса).
– биссектриса).
Тогда треугольники  и
и  равны по второму признаку равенства. Значит,
равны по второму признаку равенства. Значит,  и равнобедренный треугольник является симметричным относительно оси
и равнобедренный треугольник является симметричным относительно оси  .
.
Теорема доказана.
Итак, если треугольник равнобедренный, то он симметричен. У него равны углы при основании и совпадают три элемента – биссектриса, медиана и высота, проведенные к основанию. Для неравнобедренного треугольника это не так. Это не так уже даже для нашего равнобедренного треугольника, если биссектрису, медиану и высоту проводить из вершины при основании (см. рис. 15).
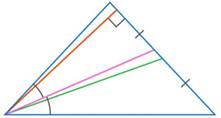
Рис. 15. В равнобедренном треугольнике биссектриса, медиана, высота, проведенные к боковой стороне, не совпадают
А работает ли эта связь в обратную сторону? Т. е. если известно только, что два угла у треугольника равны, можно ли сделать вывод, что и две соответствующие стороны равны, что он равнобедренный? Интуитивно мы понимаем, что это так. Докажем это строго.
Теорема 3.
Если в треугольнике два угла равны, то он равнобедренный.
Доказательство
Пусть в треугольнике  углы
углы  . Опустим высоту
. Опустим высоту  (см. рис. 16).
(см. рис. 16).
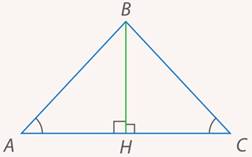
Рис. 16. Треугольник 
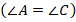 с проведенной высотой
с проведенной высотой 
В треугольниках  и
и 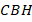 :
:
 – общая;
– общая; ;
; .
.
Тогда треугольники  и
и 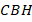 равны по второму признаку равенства (сторона и два угла). Откуда следует, что
равны по второму признаку равенства (сторона и два угла). Откуда следует, что  , т. е. треугольник
, т. е. треугольник  равнобедренный.
равнобедренный.
Теорема доказана.
Полученное утверждение не путаем с определением равнобедренного треугольника: если в треугольнике две стороны равны, то треугольник называется равнобедренным.
А наше утверждение – это признак равнобедренного треугольника: достаточно заметить, что в треугольнике два угла равны, тогда можно утверждать, что он является равнобедренным.
Итак, у равнобедренного треугольника есть такой набор свойств и признаков:
- Если треугольник равнобедренный, то углы при основании равны.
- Если углы при основании равны, то треугольник равнобедренный.
- В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.
Используя такой инструмент, как равнобедренный треугольник и его свойства, мы теперь можем доказать ряд утверждений, которые до этого считали верными без строгого доказательства.
Прежде чем перейти к ранее не доказанным утверждениям, рассмотрим еще один полезный инструмент для доказательства различных фактов, связанных с треугольниками.
Если в треугольнике продолжить одну из сторон, то мы получим угол, смежный с одним из углов треугольника. Такой угол будем называть внешним углом треугольника (см. рис. 17), а углы внутри треугольника – внутренними.
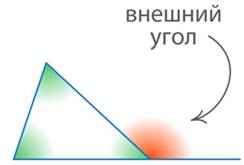
Рис. 17. Внешний угол треугольника
Теорема 4 (о внешнем угле треугольника).
Внешний угол треугольника больше любого внутреннего, не смежного с ним.
На самом деле, мы уже знаем более сильное утверждение о внешнем угле. Сумма углов треугольника равна  , поэтому внешний угол равен сумме двух внутренних, не смежных с ним:
, поэтому внешний угол равен сумме двух внутренних, не смежных с ним:
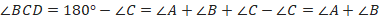
Из этого очевидно следует, что он больше каждого из этих двух внутренних в отдельности.
Но мы не можем использовать для доказательства этой теоремы тот факт, что сумма углов треугольника равна  , т. к. мы его пока формально не доказали. Более того, для того чтобы доказать теорему о сумме углов треугольника, мы будем использовать теорему о внешнем угле. Поэтому доказывать эту теорему мы будем только с использованием уже доказанных нами фактов. Как именно – можно почитать ниже.
, т. к. мы его пока формально не доказали. Более того, для того чтобы доказать теорему о сумме углов треугольника, мы будем использовать теорему о внешнем угле. Поэтому доказывать эту теорему мы будем только с использованием уже доказанных нами фактов. Как именно – можно почитать ниже.
&nbs
interneturok.ru
Треугольники, виды треугольников, свойства треугольников
Понятие треугольника
Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.
Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Определение 1
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Определение 2
Точки в рамках определения 1 называются вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 называются сторонами треугольника.
Треугольник будем обозначать тремя точками его вершин (рис. 1)
Виды треугольников
Треугольники можно разделять на различные виды по углам и по сторонам треугольника. Рассмотрим для начала виды треугольников в различии от их углов.
Определение 4
Треугольник будем называть остроугольным, если все углы в нем менее $90^0$.
Определение 5
Треугольник будем называть тупоугольным, если один из углов в нем более $90^0$.
Определение 6
Треугольник будем называть прямоугольным, если один из углов в нем равен $90^0$.
Все эти виды изображены на рисунке 2.
По сторонам треугольники разделяются на разносторонние, равнобедренные и равносторонние.
Определение 7
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Определение 8
Треугольник будем называть равносторонним, если три его стороны будут равны между собой.
Все эти виды треугольников изображены на рисунке 3.
Свойства треугольников
Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.
Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.
Определение 9
Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.
Определение 10
Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.
Определение 11
Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.
Теорема 1
Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.
Теорема 2
Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.
Теорема 3
Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.
Следующие две теоремы рассматривают свойства для равнобедренных треугольников.
Теорема 4
Углы при основании равнобедренного треугольника будут равными.
Теорема 5
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Замечание 1
Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.
Пример задачи
Пример 1
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.
spravochnick.ru
Виды треугольников. Углы треугольника :: SYL.ru
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает меньше трудностей. Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.
Какая фигура называется треугольником?
Образованная тремя точками и отрезками. Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».
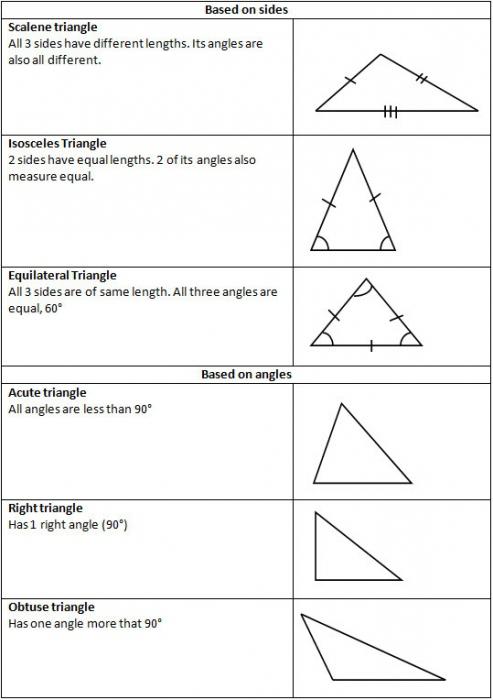
Различия в названиях по углам
Поскольку они могут быть острыми, тупыми и прямыми, то и виды треугольников определяются по этим названиям. Соответственно, групп таких фигур три.
- Первая. Если все углы треугольника острые, то он будет иметь название остроугольного. Все логично.
- Вторая. Один из углов тупой, значит треугольник тупоугольный. Проще некуда.
- Третья. Имеется угол, равный 90 градусам, который называется прямым. Треугольник становится прямоугольным.
Различия в названиях по сторонам
В зависимости от особенностей сторон выделяют такие виды треугольников:
общий случай — разносторонний, в котором все стороны имеют произвольную длину;
равнобедренный, у двух сторон которого имеются одинаковые числовые значения;
равносторонний, длины всех его сторон одинаковые.
Если в задаче не указан конкретный вид треугольника, то нужно чертить произвольный. У которого все углы острые, а стороны имеют разную длину.
Свойства, общие для всех треугольников
- Если сложить все углы треугольника, то получится число, равное 180º. И неважно, какого он вида. Это правило действует всегда.
- Числовое значение любой стороны треугольника меньше, чем сложенные вместе две другие. При этом она же больше, чем их разность.
- Каждый внешний угол имеет значение, которое получается при сложении двух внутренних, не смежных с ним. Причем он всегда больше, чем смежный с ним внутренний.
- Напротив меньшей стороны треугольника всегда лежит самый маленький угол. И наоборот, если сторона большая, то и угол будет самым большим.
Эти свойства справедливы всегда, какие бы виды треугольников ни рассматривались в задачах. Все остальные вытекают из конкретных особенностей.
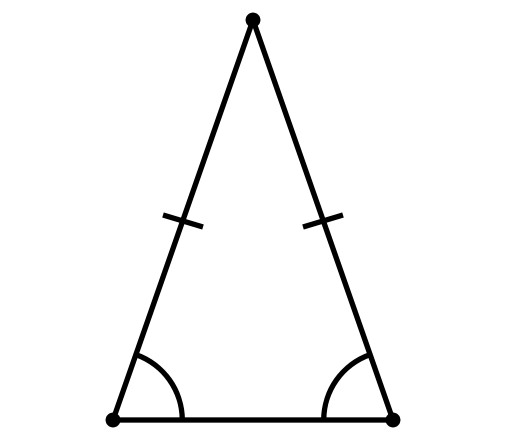
Свойства равнобедренного треугольника
- Углы, которые прилегают к основанию, равны.
- Высота, которая проведена к основанию, является также медианой и биссектрисой.
- Высоты, медианы и биссектрисы, которые построены к боковым сторонам треугольника, соответственно равны друг другу.
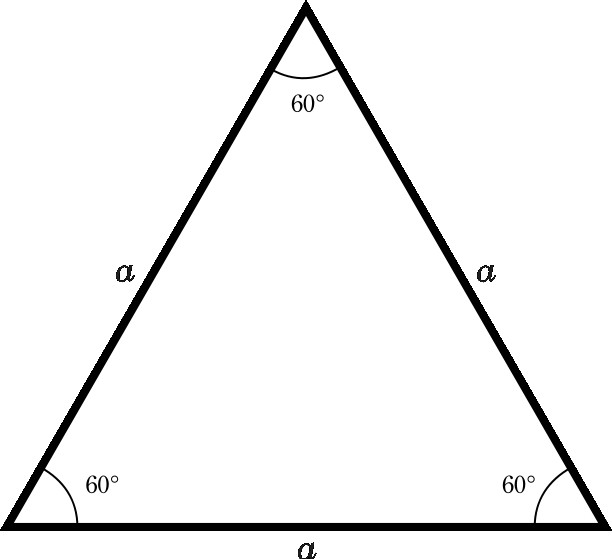
Свойства равностороннего треугольника
Если имеется такая фигура, то будут верны все свойства, описанные немного выше. Потому что равносторонний всегда будет равнобедренным. Но не наоборот, равнобедренный треугольник не обязательно будет равносторонним.
- Все его углы равны друг другу и имеют значение 60º.
- Любая медиана равностороннего треугольника является его высотой и биссектрисой. Причем они все равны друг другу. Для определения их значений существует формула, которая состоит из произведения стороны на квадратный корень из 3, деленного на 2.
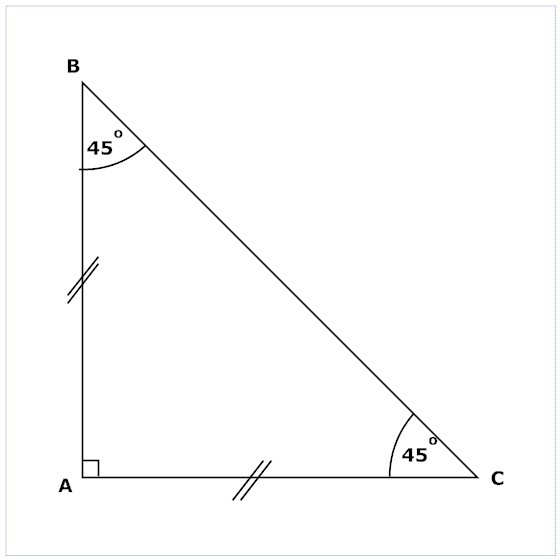
Свойства прямоугольного треугольника
- Два острых угла дают в сумме значение в 90º.
- Длина гипотенузы всегда больше, чем у любого из катетов.
- Числовое значение медианы, проведенной к гипотенузе, равно ее половине.
- Этому же значению равен катет, если он лежит напротив угла в 30º.
- Высота, которая проведена из вершины со значением 90º, имеет определенную математическую зависимость от катетов: 1/н2 = 1/а2 + 1/в2. Здесь: а, в — катеты, н — высота.
Задачи с разными видами треугольников
№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
Решение
Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.
Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.
Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.
№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.
Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.
н = а * √3 / 2, где н — высота, а — сторона.
Подстановка и вычисление дают такой результат: н = 6 √3 (см).
Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.
Ответ: высота равна 6 √3 см.
№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.
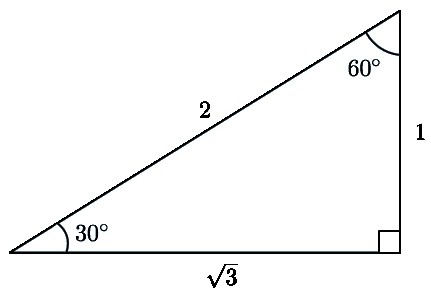
Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Ответ: угол Р равен 60º.
№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.
Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Ответ: углы равны 70º, 70º, 40º.
№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.
Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.
Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.
Ответ: 18º, 45º, 117º
www.syl.ru
Треугольник и его виды
Из всех многоугольников треугольники имеют наименьшее количество углов и сторон.
Треугольники можно различать по виду их углов.
Есди все углы треугольника острые, то его называют остроугольным треугольником (рис. 113, а).
Если один из углов треугольника прямой, то его называют прямоугольным треугольником (рис. 113, б).
Если один из углов треугольника тупой, то его называют тупоугольным треугольником (рис. 113, в).
Говорят, что мы классифицировали треугольники по виду их углов.
Треугольники можно классифицировать не только по виду углов, но и по количеству равных сторон.
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
На рисунке 114, а изображен равнобедренный треугольник ABC, у которого AB = BC. На рисунке равные стороны отмечают равным количеством черточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC − основанием равнобедренного треугольника ABC.
Если стороны треугольника равны, то его называют равносторонним треугольником.
Треугольник, изображенный на рисунке 114, б, − равносторонний, у него MN = NE = EM.
Треугольник, у которого три стороны имеют различную длину, называют разносторонним треугольником.
Треугольники, изображенные на рисунке 113, − разносторонние. Если сторона равностороннего треугольника равна a, то его периметр вычисляют по формуле:
P = 3a
Пример 1. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 2 см, а угол между ними − 50°.
Решение.
С помощью транспортира построим угол A, градусная мера которого 50° (рис. 115). На сторонах этого угла от его вершины с помощью линейки отложим отрезок AB длиной 3 см и отрезок AC длиной 2 см (рис. 116). Соединив отрезком точки B и C, получим искомый треугольник ABC (рис. 117).
Пример 2. С помощью линейки и транспортира постройте треугольник ABC, сторона AB которого равна 2 см, а углы CAB и CBA соответственно равны 40° и 110°.
Решение. С помощью линейки строим отрезок AB длиной 2 см (рис. 118). От луча AB с помощью транспортира откладываем угол с вершиной в точке A, градусная мера которого равна 40°. От луча BA в ту же сторону от прямой AB, в которую был отложен первый угол, откладываем угол с вершиной в точке B, градусная мера которого равна 110°(рис. 119).
Найдя точку C пересечения сторон углов A и B, получаем искомый треугольник ABC (рис. 120).
reshalka.com
Все виды треугольников и их свойства. Виды треугольников, углы и стороны
Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую называют тупоугольной.
Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться. Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.
Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют Их главная особенность — равенство двух сторон и углов при основании.
Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.

Любой вид обладает следующими свойствами:
1) Сумма всех углов равняется 180 градусам.
2) Всегда существует ортоцентр — точка пересечения всех трех высот.
3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.
4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.
Теперь вы познакомились с основным
aqpi.ru
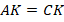 , т. е.
, т. е. 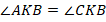 , а т. к. они еще и смежные (
, а т. к. они еще и смежные (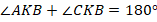 , следовательно,
, следовательно, 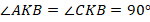 ), значит, они прямые. Т. е. отрезок
), значит, они прямые. Т. е. отрезок 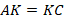 , т. к.
, т. к. 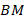 – общая сторона;
– общая сторона; ;
; (т. к.
(т. к.  ;
;