Урок алгебры в 7-м классе по теме «Множества точек на координатной плоскости»

Цели урока:

• формирование умения перейти от алгебраического описания множества точек к геометрическому изображению и наоборот;
• продолжить формирование умений, связанных с работой на координатной плоскости;
• формирование умения мыслить по аналогии, умения наблюдать и делать выводы, умения обобщать.

ХОД УРОКА

I. Оргмомент

II. Актуализация знаний

1. Определить координаты точек.

 

 

2. Построить отрезок LE, если L(–1; 2), Е(4; 5).
Построить прямую РТ, если Р(0; 3), Т(–1; –2)

III. Постановка проблемы

Приготовить пять координатных плоскостей.
Отметьте указанные точки на координатных плоскостях
1) А(3; 1), В(4; –1), С(–5; –2).

 

 

 

2) М(3; –2), N(–4; –2), К(1.5; –2)

 

 

 

3) Р(5; –1), Е(5; 4), F(5;1/2)

 

 

 

 

4) Х(6; 0), У(–3; 0), Z(1; 0)

 

 

 

 

 

5) Q(0; 3), N(0; 5), L(0; –1/2)

 

Посмотрите на чертежи, что можно сказать о расположении точек:
В первом случае?

 

 

В остальных случаях?
Что общего?

 

 

Мы выяснили, что общее в 2–4 рисунках то, что точки лежат на одной прямой.

IV. «Открытие» детьми нового знания

Подумайте, как можно записать множество точек, изображенных на рисунке

 

 

 

Какое условие является общим для этих точек?

 

А как это условие записать на языке алгебры?                        у = 3
(ордината равна 3)
На рис.2 проведите через отмеченные точки                         

у = – 2
прямую, запишите множество этих точек.
Проведите на остальных рисунках через отмеченные точки прямые.
А как бы вы записали на языке алгебры множества точек, изображенных на рисунке 3? 4? 5?                                                                                          
Подумайте, а затем проверим правильность записей.

х = 5
у = 0
х = 0

Что означают эти записи на математическом языке?

 

Множество точек расположенных где? На координатной плоскости

Итак, тема нашего урока:

 

А цель урока?
Учитель еще раз формулирует тему и цель урока, записывает тему на доске.
Изобразите на координатной плоскости множество точек, удовлетворяющих условию:

Записи

У обучающихся                                                     На доске

                        х  =  5
                           х =  – 4

 

 

 

                                у  =  – 4
                                у  =  1

 

 

Проверяем правильность построения и записи.
А теперь давайте попробуем изобразить множество точек, удовлетворяющих условию х > 3.
Как можно это условие прочитать на русском языке?        – точки, большие 3

Чтобы построить точку в координатной плоскости, необходимо, что знать?

 

Прочитайте условие х > 3

 

 

Построим в координатной плоскости прямую х = 3

 

 

 

Где будут располагаться точки, абсцисса которых больше 3?

Покажите несколько таких точек

 

 

 

А множество всех точек удовлетворяющих условию х > 3 можно показать с помощью штриховки

 

 

 

х > 3 задает полуплоскость, расположенную правее прямой х = 3 и все точки этой прямой.

Изобразите множество точек, удовлетворяющих условию у < – 2.

 

 

Проверим правильность построения.

Изобразите множество точек, удовлетворяющих условию у > 1.

 

Проверяем правильность построения.
Постройте множество точек у > 1.
Каким свойством обладают точки этого множества            у них ордината больше 1
А как они должны располагаться относительно                   – выше

прямой у = 1
А точки прямой у = 1 удовлетворяют условию y > 1             нет
А как это показать?                                                                  – не знаем

В этом случае прямая у = 1 изображается пунктиром.

Изобразим множество точек, удовлетворяющих условию у > 1.

 

 

Приглашается ученик к доске.

Изобразите множество точек, удовлетворяющих условию:

а) х < – 4;                                         б) у < 2.

а)

б)

Проверяем правильность построения.

V. Первичное закрепление

На рисунках изображены полуплоскости.

Указать условия, которые им соответствуют.

Предполагаемые ответы:

1) х < 4; 2) у < 5; 3) у > – 3; 4) 2 < х < 5; 5) –5 < у < 2.

Как можно назвать множество точек, изображенных на рисунках 4, 5? (На что они похожи?)

Предполагаемые ответы: полоса.

Изобразите в одной координатной плоскости множества точек, удовлетворяющие условиям: х < 7, х > –2, у < 3, у > –1.

Выделите множество точек, удовлетворяющих одновременно всем этим условиям.
Какую фигуру получили?

VI. Самостоятельная работа с последующей самопроверкой

1.  Опишите на алгебраическом языке множества точек, изображенные на рисунках.

1 вариант                                                                                         2 вариант

1.

 

 

 

 

 

 

 

 

2. Изобразите на координатной плоскости множества точек, удовлетворяющих условию:

а) –2 < х < 1                                                    a) –3 < х < 5
б) 1 < у < 4                                                      б) –1 < у < 5.

Проверяем правильность записей построения.

1.

а) х < 1                                                             a) у < – 2
б) –1 < у < 4                                                      б) – 2 < х < 2.

2.

                                                           

 

 

 

 

 

 

 

 

VII. Повторение

№ 569 (а – г) устно.

VIII. Итог урока

– Над чем мы сегодня работали?
– Что нового узнали?

(Высказывания детей)

IX. Домашнее задание

1. Составить справочную таблицу

2. Составить и решить задания, аналогичные № 564, 569.

urok.1sept.ru

Изображение на плоскости множества точек

Слайд 1

Изображение на плоскости множества точек, заданного неравенством с двумя переменными Выполняла работу: Сурова Ксения

Слайд 2

Цель: 1). Сформировать: — понятие того, что решением неравенства с двумя переменными является множество точек плоскости. — умение изображать на плоскости множество точек, заданных неравенством с двумя переменными. — учить пользоваться алгоритмом. 2). Развивать: умение анализировать предложенную ситуацию; графические навыки. 3). Воспитывать внимательность.

Слайд 3

Ход: 1. Подготовка к восприятию нового материала : у-3х+4=0 . . х 2 +6х-8=0 х 2 +у-16=0 -Что является решением уравнения с двумя переменными? -Можно ли изобразить на координатной плоскости решение уравнения с двумя переменным? Что будет являться решением такого уравнения ?

Слайд 4

2. Изучение нового материала. Каждая линия разбивает координатную плоскость на две части (полуплоскости). 0 х у у-3х+4=0 -4 2-я полуплоскость 1-я полуплоскость Какому условию точки лежащие на прямой?  f ( х;у )=0 (уравнение прямой)  Как вы думаете, а какому условию удовлетворяют точки не лежащие на прямой? Рассматриваем первый рисунок: Возьмём точки А(-4;-1), В(-2;4). С(0;2). Какой полуплоскости принадлежат данные точки? Подставим координаты точек в уравнение прямой и сравним полученные значения с нулём . А(-4;-1) -1-3(-4)+4= -1+12+4=15, 15  0, В(-2;4) 4-3(-2)+4=4+6+4=14, 14 0, С(0;2) 2-3 0+4=6, 6 0. Значение нашего многочлена f ( х;у ) в точках А,В,С принимает значение больше 0.

Слайд 5

Как записать данное условие с помощью математической модели?  у-3х+4  0  . Какой полуплоскости принадлежат точки Д(6;0), Е(0;-6), F (3;-3). Сравним значения многочлена у-3х+4 в этих точках с нулём. Д(6;0) 0-36+4=-18+4=-14, -14  0, Е(0;-6) -6-30+4= -2, -2  0, F (3;-3) -3-3  3+4= -3-9+4, -8  0. Какому условию удовлетворяют точки нижней полуплоскости  у-3х+4  0  Вывод: Точки не лежащие на прямой удовлетворяют неравенству. f ( х;у )  0 или f ( х;у )  0.

Слайд 6

3. Заполнить таблицу. Какому из условий удовлетворяют точки координатной плоскости: А(0;4), В(0;-4),О(0;0), С(-2;-2), Д(5;0), Е(4;8), F (0;-6), К(4;1), М(-2;1), N (8;-2) F ( х;у )=0 F ( х;у )  0 F ( х;у )  0

Слайд 7

Задать неравенством множество точек плоскости на рисунках: х у 0 4 2 у=х 2 -6х+8 у х 0 4 -4 4 -4 х 2 +у 2 =16 Подведём итог: Как же задать множество точек плоскости неравенством? Составил алгоритм своих действий. 1. Строим график функции f ( х;у )=0 2. Берём контрольную точку. 3. Проверяем выполнение неравенства f ( х;у )  0 или f ( х;у )  0

Слайд 8

6 3 0 у х у+2х-6=0 6 3 0 у х у+2х-6=0 4. Задать неравенством точек координатной плоскости В чём отличие этих двух случаев? Вывод: В первом случае точки прямой входят в указанное множество, поэтому данные точки задают множество, удовлетворяющее неравенству f ( х;у )  0, во втором случае точки прямой не являются частью множества указанной полуплоскости, поэтому наше множество задаётся неравенством f ( х;у )  0. И так, если знак неравенства нестрогий, то график уравнения изображаем сплошной линией; если знак неравенства строгий, то график уравнения изображаем пунктиром.

Слайд 9

Самостоятельная работа. Вариант 1 Вариант 2 Отобразить на плоскости множество точек, заданных неравенством: А) у=2х-4  0 (2б) у-х -5  0 В) х 2 +4х+у 2  0 (3б) х 2 =у 2 -4у≤0 Задать множество точек координатной плоскости неравенством: (2б) Изобразить графически решение неравенства (3б ) Как по вашему мнению можно задать данное множество:(Такой же рисунок без штриховки изображен на доске.)Какие линии изображены?(прямая окружность) Прямая разбивает плоскость на две полуплоскости. Какой полуплоскости принадлежит заштрихованная часть и какому условию она удовлетворяет? у+х-4≥0 Окружность разбивает плоскость на две части: внутри окружности и вне её. Нас интересует внутренняя часть. Какому условию она удовлетворяет.( х+у ) 2 +(у-2) 2 -9

Слайд 10

То есть данное множество является результатом пересечения двух множеств. То есть решением системы неравенств: ( х-2) 2 +( y-2) 2 -9 0 И так ми с вами задали некоторое множество системой неравенств. Подведём итог: Составим алгоритм построения множества точек плоскости, заданное системой неравенств: Строим график уравнения f 1 ( х;у )=0 и f 2 ( х;у )=0 Изображаем множество точек удовлетворяющее первому неравенству. Изображаем множество точек удовлетворяющее второму неравенству. Результат – пересечение множеств.

Слайд 11

Спасибо за внимание!!!

nsportal.ru

7. Множества точек на плоскости, задаваемые уравнениями

и неравенствами с двумя переменными

Пусть на плоскости выбрана система координат. Тогда любое уравнение с двумя переменными F(x;y) = 0 задает множество точек на плоскости, а именно множество точекM(x;y), координатыкоторых удовлетворяют этому уравнению.

Например, точка M(– 3; 4) принадлежит множеству, заданному уравнениемx²+y²= 25, а точкаN(1; 6) не принадлежит этому множеству, так как (–3)²+ 4²= 25, а 1²+ 6²≠ 25. В этом легко убедиться, если построить график данного уравнения в декартовой системе координат (рис. 7.1). Геометрическим местом всех точек, принадлежащих этому множеству, является окружностьR= 5 с центром в начале координат.

Рис. 7.1

Если мы рассмотрим множество, заданное в виде неравенства x²+y²< 25, то множеством будут являться все точки, находящиеся внутри этой окружности (рис.7.2). Сама окружность изображена пунктиром, чтобы показать, что точки, принадлежащие самой окружности (границе области) в данном случае на нее не попадают и точка

M(– 3; 4)множествуx²+y²< 25 (области), в чем легко убедится, а точкаN(1; 2){x²+y²< 25}.

Рис. 7.2

Если же x²+y²≤ 25, то здесь уже войдет и граница (сама окружность). Изобразим ее жирной линией (рис. 7.3).

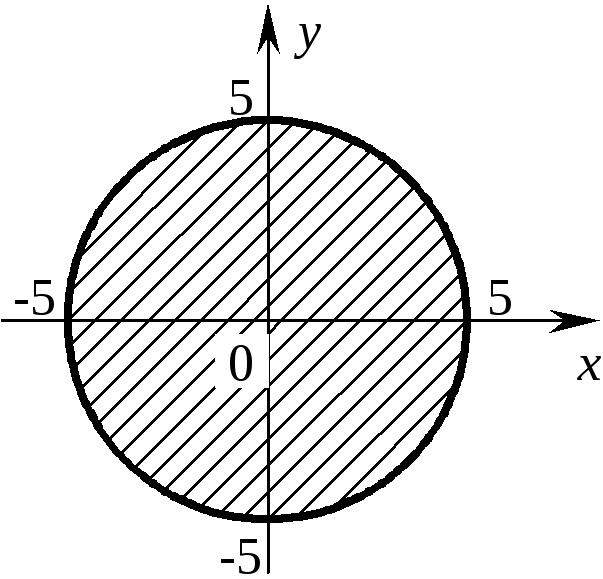
Рис. 7.3

То же касается систем линейных неравенств.

Пример.Построить область допустимых решений системы линейных неравенств.

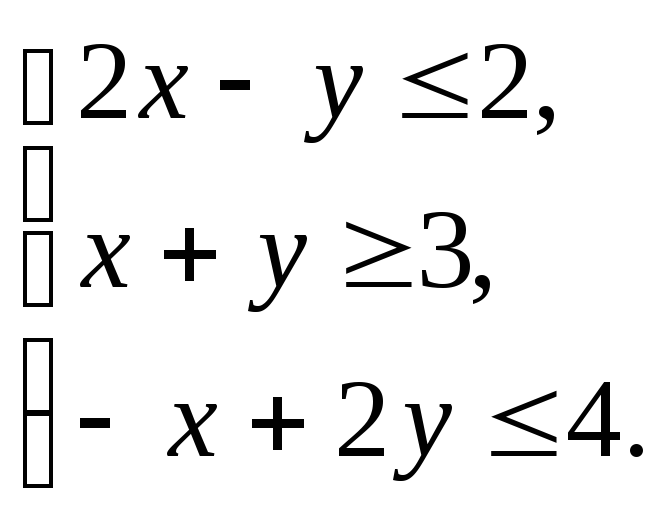
Решение.Нумеруем ограничения задачи

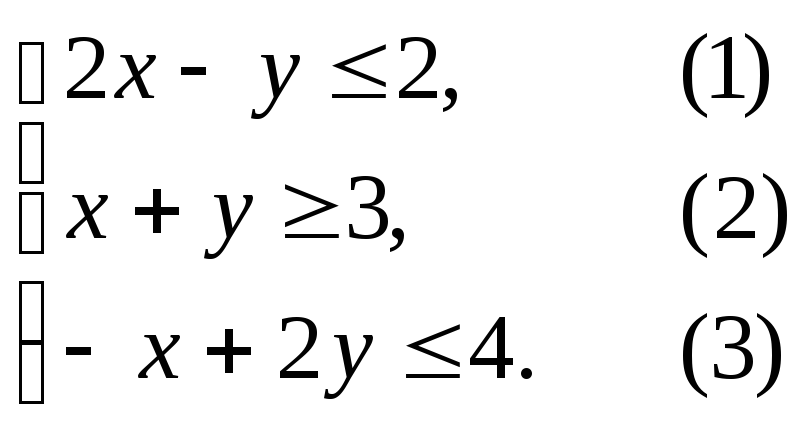
В прямоугольной декартовой системе координат (рис. 7.4) строим прямую 2x – y = 2, соответствующую ограничению (1).

Рис. 7.4

Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решения неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая (1) не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение: 2·0 – 0 < 2. Получаем строгое неравенство 0 < 2. Следовательно, точкаОлежит в полуплоскости решений. Таким образом, стрелки на концах прямой (1) должны быть направлены в полуплоскость, содержащую точкуО.

Аналогично строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и (3).

Находим общую часть полуплоскостей решений. Полученную область допустимых решений отмечаем на рис. 7.4 штриховкой. В этой области находятся все точки M(x;y), в которых выполняются все три неравенства системы. ◄

Задание 3

Решить неравенство (а) и систему неравенств (б).

3.1.а); б)	3.2.а); б)
3.3.а); б)	3.4.а); б)
3.5.а); б)	3.6.а); б)
3.7.а); б)	3.8.а); б)
3.9.а); б)	3.10.а); б)
3.11.а); б)	3.12.а); б)
3.13.а); б)	3.14.а); б)
3.15.а); б)	3.16.а); б)
3.17.а); б)	3.18.а); б)
3.19.а); б)	3.20.а); б)
3.21.а); б)	3.22.а); б)
3.23.а); б)	3.24.а); б)
3.25.а); б)	3.26.а); б)
3.27.а); б)	3.28.а); б)
3.29.а); б)	3.30.а); б)

studfile.net

Задание фигур на координатной плоскости уравнениями и неравенствами

Пусть задано уравнение с двумя переменными F(x; y). Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.

Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.

Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.

Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a)² + (y – b)² = R² – окружность, радиус которой равен R, а центр находится в точке O(a; b).

Пример 1.

Построить график уравнения x² – 9y² = 0.

Решение.

Разложим на множители левую часть уравнения.

(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.

Ответ: рисунок 1.

Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.

Первое уравнение равносильно системе

{f(x) ≥ 0,
{y = f(x) или y = -f(x).

То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.

Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).

Пример 2.

Построить график уравнения |y| = 2 + x.

Решение.

Заданное уравнение равносильно системе

{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.

Строим множество точек.

Ответ: рисунок 2.

Пример 3.

Построить график уравнения |y – x| = 1.

Решение.

Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.

Ответ: рисунок 3.

При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей, основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.

Пример 4.

Построить график уравнения x + |x| + y + |y| = 2.

Решение.

В данном примере знак каждого подмодульного выражения зависит от координатной четверти.

1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:

2x + 2y = 2, а после упрощения x + y = 1.

2) Во второй четверти, где x < 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.

3) В третьей четверти x < 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.

4) В четвертой четверти, при x ≥ 0, а y < 0 получим, что x = 1.

График данного уравнения будем строить по четвертям.

Ответ: рисунок 4.

Пример 5.

Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.

Решение.

Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.

Область	Знак подмодульного выражения	Полученное уравнение после раскрытия модуля
I	x ≥ 1 и y ≥ 1	x + y = 3
II	x < 1 и y ≥ 1	-x + y = 1
III	x < 1 и y < 1	x + y = 1
IV	x ≥ 1 и y < 1	x – y = 1

Ответ: рисунок 5.

На координатной плоскости фигуры могут задаваться и неравенствами.

Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.

Рассмотрим алгоритм построения модели решений неравенства с двумя переменными:

1. Записать уравнение, соответствующее неравенству.
2. Построить график уравнения из пункта 1.
3. Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
4. Изобразить графически множество всех решений неравенства.

Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.

Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.

1) ax + bx + c ≥ 0. Рисунок 6.

2) |x| ≤ a, a > 0. Рисунок 7.

3) x² + y² ≤ a, a > 0. Рисунок 8.

4) y ≥ x². Рисунок 9.

5) xy ≤ 1. Рисунок 10.

Если у  вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь. Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.

 Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Множество точек координатной плоскости, изображенное на рисунке, задаётся системой неравенств

На рис 1 изображены два треугольника они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рис. 2, нарисуйте два треугольника так, чтобы они разбивали плоскость на семь частей.

Master-Margarita

Нам надо повернуть два треугольника так, как это показано на рисунке внизу.

Просто перевернуть длинный треугольник и наложить на более короткий.

Тогда у нас получится, что данные треугольники разбивают плоскость на семь частей.

Maste­r-Mar­garit­a1Всего 1 ответ.

Другие интересные вопросы и ответы

Как изобразить на координатной плоскости множество точек, удовлетворяющих указанным требованиям?

Гость7

Исходя из требований нужно расставить эти точки, либо найти их координаты и указать их на координатной плоскости, если множество имеет какую-либо закономерность, то можно указать его часть, а остальные точки указать в виде правила для множества, это может быть и прогрессия, и множество, которое стремиться к бесконечности и замкнутая фигура внутри осей координат, пример изображения множества точек на плоскости при y=-2

Иван В.4Всего 1 ответ.

Изобразите на координатной плоскости х и у множество решений системы неравенств 2х-3у≥1 х+2у<2

Guest4

Построй по двум точкам эти две прямые
Смотри где их значение больше 1 и меньше или равно двух
Вот и ответ

Вроде я так лет 40 назад решал!!!

Гость2Всего 1 ответ.

Множество точек координатной плоскости, изображенное на рисунке, задаётся системой неравенств

Сергей Чекашкин1

и чо?
нам-то чо?Xthn_13(666)3

Всего 1 ответ.

Почему Преподобный Макарий Египетский на иконах изображается нагим и в шерсти/волосах?

Никвай Башарин3

Согласно Преданию, преподобный был наг и все его тело покрывали волосы, скрывавшие наготу. Так было например и с прп. Марией Египетской и некоторыми другими пустынножителями.

Сергей Сизов1Всего 1 ответ.

ask-homework.ru

«« Красивые множества на плоскости ». П р и м е р. Изобразим на координатной плоскости множество точек, заданное условием у =. Задание фигур на координатной плоскости уравнениями и нераве

Изображение на плоскости множества точек, заданного неравенством с двумя переменными Выполняла работу: Сурова Ксения

Цель: 1). Сформировать: — понятие того, что решением неравенства с двумя переменными является множество точек плоскости. — умение изображать на плоскости множество точек, заданных неравенством с двумя переменными. — учить пользоваться алгоритмом. 2). Развивать: умение анализировать предложенную ситуацию; графические навыки. 3). Воспитывать внимательность.

Ход: 1. Подготовка к восприятию нового материала: у-3х+4=0 . . х 2 +6х-8=0 х 2 +у-16=0 -Что является решением уравнения с двумя переменными? -Можно ли изобразить на координатной плоскости решение уравнения с двумя переменным? Что будет являться решением такого уравнения?

2. Изучение нового материала. Каждая линия разбивает координатную плоскость на две части (полуплоскости). 0 х у у-3х+4=0 -4 2-я полуплоскость 1-я полуплоскость Какому условию точки лежащие на прямой?  f (х;у)=0 (уравнение прямой)  Как вы думаете, а какому условию удовлетворяют точки не лежащие на прямой? Рассматриваем первый рисунок: Возьмём точки А(-4;-1), В(-2;4). С(0;2). Какой полуплоскости принадлежат данные точки? Подставим координаты точек в уравнение прямой и сравним полученные значения с нулём. А(-4;-1) -1-3(-4)+4= -1+12+4=15, 15  0, В(-2;4) 4-3(-2)+4=4+6+4=14, 14 0, С(0;2) 2-3 0+4=6, 6 0. Значение нашего многочлена f (х;у) в точках А,В,С принимает значение больше 0.

Как записать данное условие с помощью математической модели?  у-3х+4  0  . Какой полуплоскости принадлежат точки Д(6;0), Е(0;-6), F (3;-3). Сравним значения многочлена у-3х+4 в этих точках с нулём. Д(6;0) 0-36+4=-18+4=-14, -14  0, Е(0;-6) -6-30+4= -2, -2  0, F (3;-3) -3-3  3+4= -3-9+4, -8  0. Какому условию удовлетворяют точки нижней полуплоскости  у-3х+4  0  Вывод: Точки не лежащие на прямой удовлетворяют неравенству. f (х;у)  0 или f (х;у)  0.

3. Заполнить таблицу. Какому из условий удовлетворяют точки координатной плоскости: А(0;4), В(0;-4),О(0;0), С(-2;-2), Д(5;0), Е(4;8), F (0;-6), К(4;1), М(-2;1), N (8;-2) F (х;у)=0 F (х;у)  0 F (х;у)  0

Задать неравенством множество точек плоскости на рисунках: х у 0 4 2 у=х 2 -6х+8 у х 0 4 -4 4 -4 х 2 +у 2 =16 Подведём итог: Как же задать множество точек плоскости неравенством? Составил алгоритм своих действий. 1. Строим график функции f (х;у)=0 2. Берём контрольную точку. 3. Проверяем выполнение неравенства f (х;у)  0 или f (х;у)  0

6 3 0 у х у+2х-6=0 6 3 0 у х у+2х-6=0 4. Задать неравенством точек координатной плоскости В чём отличие этих двух случаев? Вывод: В первом случае точки прямой входят в указанное множество, поэтому данные точки задают множество, удовлетворяющее неравенству f (х;у)  0, во втором случае точки прямой не являются частью множества указанной полуплоскости, поэтому наше множество задаётся неравенством f (х;у)  0. И так, если знак неравенства нестрогий, то график уравнения изображаем сплошной линией; если знак неравенства строгий, то график уравнения изображаем пунктиром.

Самостоятельная работа. Вариант 1 Вариант 2 Отобразить на плоскости множество точек, заданных неравенством: А) у=2х-4  0 (2б) у-х -5  0 В) х 2 +4х+у 2  0 (3б) х 2 =у 2 -4у≤0 Задать множество точек координатной плоскости неравенством: (2б) Изобразить графически решение неравенства (3б) Как по вашему мнению можно задать данное множество:(Такой же рисунок без штриховки изображен на доске.)Какие линии изображены?(прямая окружность) Прямая разбивает плоскость на две полуплоскости. Какой полуплоскости принадлежит заштрихованная часть и какому условию она удовлетворяет? у+х-4≥0 Окружность разбивает плоскость на две части: внутри окружности и вне её. Нас интересует внутренняя часть. Какому условию она удовлетворяет.(х+у) 2 +(у-2) 2 -9

То есть данное множество является результатом пересечения двух множеств. То есть решением системы неравенств: (х-2) 2 +(y-2) 2 -9 0 И так ми с вами задали некоторое множество системой неравенств. Подведём итог: Составим алгоритм построения множества точек плоскости, заданное системой неравенств: Строим график уравнения f 1 (х;у)=0 и f 2 (х;у)=0 Изображаем множество точек удовлетворяющее первому неравенству. Изображаем множество точек удовлетворяющее второму неравенству. Результат – пересечение множеств.

Спасибо за внимание!!!

«Координатная прямая» — Скала Динозавр. На уроках какого предмета вы встречались с координатной прямой? Что напоминает вам координатная прямая? Что называется координатами точки на плоскости? Что такое координатная прямая? Оренбургский государственный степной заповедник создан в 1989 году. Координаты на прямой и плоскости.

«Прямоугольная система координат» — Две взаимно перпендикулярные прямые, Алгоритм отыскания координаты точки М (x1, y1), заданной в прямоугольной системе координат. Название; Обозначение. Единицей длины. Однозначно определяет положение каждой точки на плоскости. Тема: Прямоугольная система координат на плоскости. Делит плоскость на четыре части.

«Системы координат» — Системы координат. Аффинная (косоугольная) система координат. Мировые линии наблюдателей Риндлера (голубые дуги гипербол) в декартовых координатах. Точка в цилиндрических координатах. Полярная система координат. Прямоугольная (Декартова) система координат. В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве.

«Координатная плоскость с координатами» — Карточка 2. Сколько га вспахал третий? 4. 24 человека за 6 дней пропололи участок клубники. 5. Решите уравнение: 0,9(4у-2)=0,5(3у-4)+4,4. 5.Решите уравнение: 0,2(5у-2)=0,3(2у-1)-0,9. 2.Найдите площадь прямоугольника, ширина которого 5,5м, а длина на 1,5 больше ширины. 2.Три тракториста вспахали 405 га земли.

«Координаты на плоскости» — Отметим на координатной плоскости т.А(3;5), В(-2;8), С(-4;-3), Е(5;-5). Цели: 8,150. Ход урока. Вычислите: Система координат. Через отмеченные точки проведём прямые, параллельные осям. Игра Морской Бой. Х — абсцисса У — ордината. Рене Декарт Готфрид Вильгельм Лейбниц. Постройте треугольник. Алгоритм построения: Построим координатную плоскость.

«Декартовы координаты» — Декарт. Линия времени. Декарт впервые ввёл координатную систему. Определение координат точек. Система географических координат. Гиппарх. Путешествие на остров «Координат». Координатная система нашла свое применение во многих сферах жизнедеятельности человека. Рене Декарт (1596-1650). Определение координат острова.

Всего в теме 19 презентаций

5 -4 -3 -2 -1 0 1 2 3 4 5 6

Как называется прямая, изображенная на рисунке?

Назовите координаты точек

А, В, C, D, О.

А(4), В(-4), С(5,5), D(-1,5), О(0)

Оx – ось абсцисс

Оy — ось ординат

Точка 0 – начало отсчета

3 – абсцисса точки М

4 — ордината точки М

Плоскость, с указанной на ней системой координат, называют координатной.

1kingvape.ru
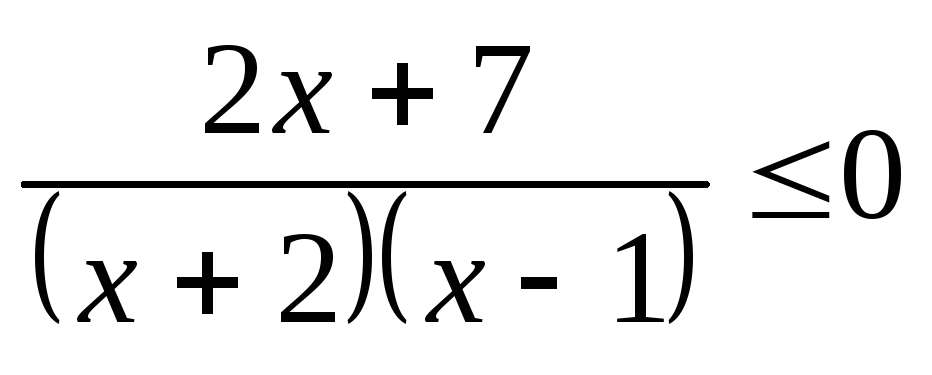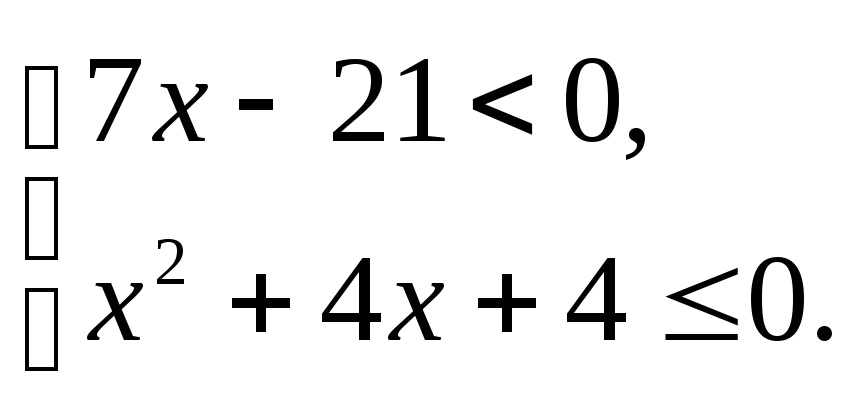
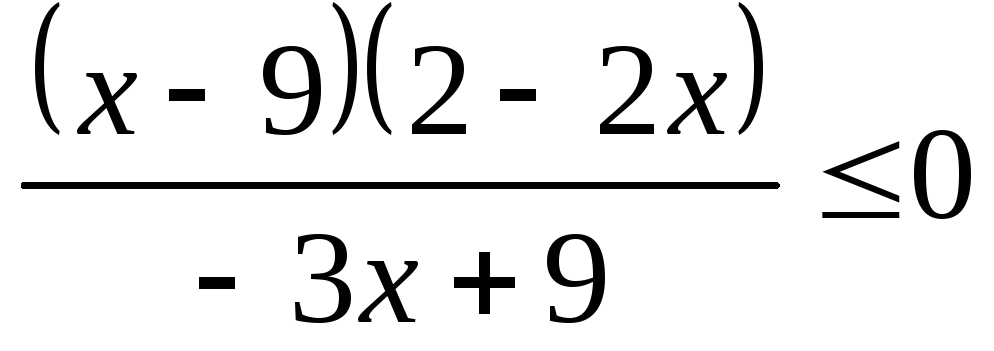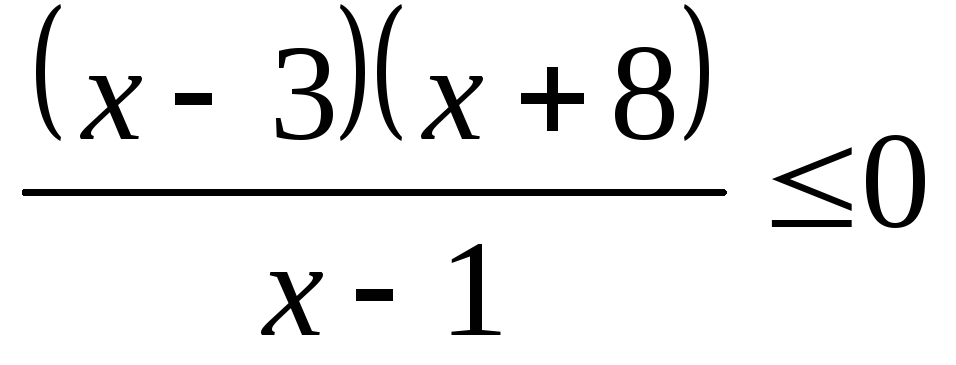
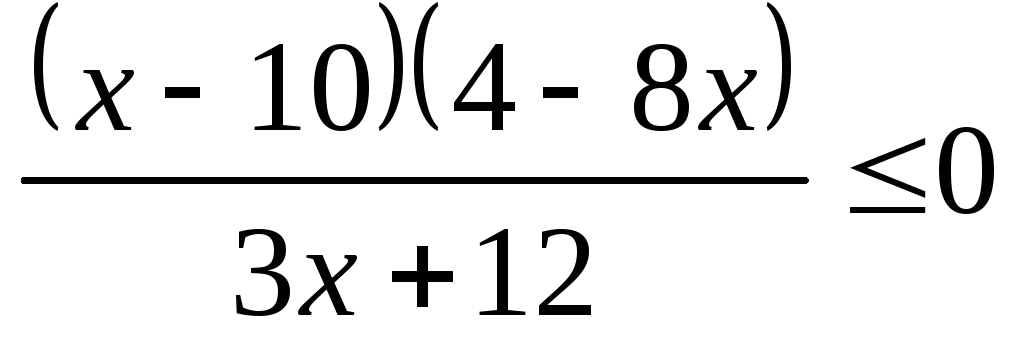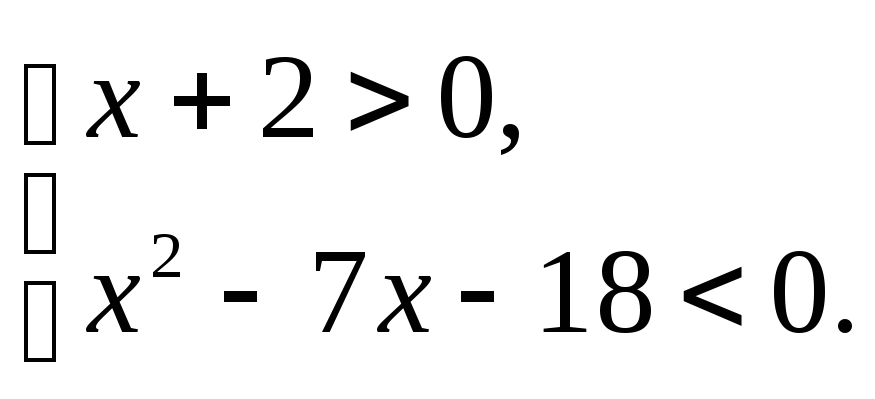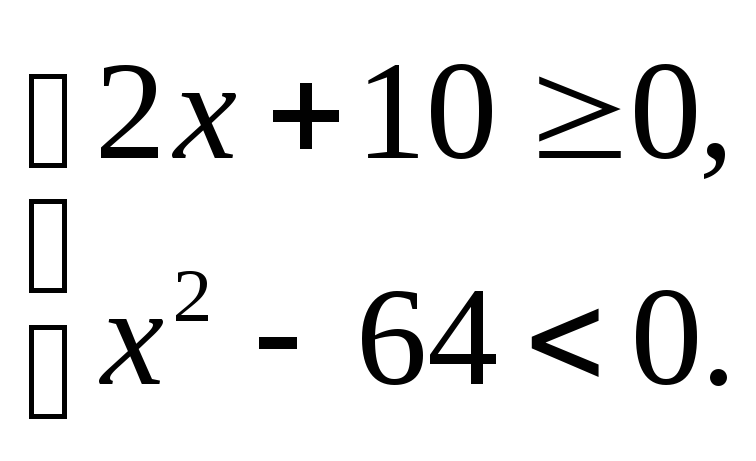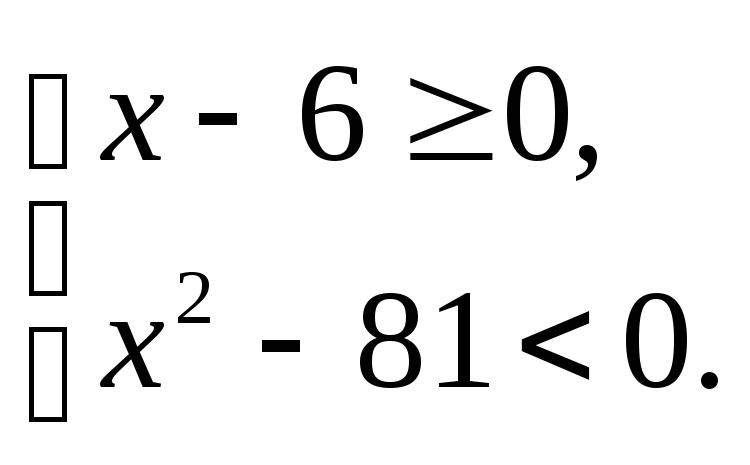