Математическая индукция — это… Что такое Математическая индукция?

Математическая индукция — один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Формулировка
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: .
Допустим, что
Тогда все утверждения нашей последовательности верны. |
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений , , , . Если для любого натурального из того, что истинны все , , , , , следует также истинность , то все утверждения в этой последовательности истинны, то есть . |
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при импликация эквивалентна . Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
История
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида[1]. Современное название метода было введено де Морганом в 1838 году.
Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство.
База, n = 1:
Переход: предположим, что
тогда
- ,
что и требовалось доказать.
Комментарий: верность утверждения в этом доказательстве — то же, что верность равенства
Вариации и обобщения
Примечания
- ↑ Nachum L. Rabinovih Раби Леви бен Гершом и происхождение метода математической индукции = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — В. 6. — С. 237-248.
Литература
Ссылки
- Видео по методу математической индукции
dic.academic.ru
Принцип математической индукции — это… Что такое Принцип математической индукции?
- Принцип математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Принцип локальности
- Принцип максимума (уравнение теплопроводности)
Смотреть что такое «Принцип математической индукции» в других словарях:
Метод математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
ИНДУКЦИИ АКСИОМА — утверждение о справедливости для всех хнек рого предиката Р(х), определенного на множестве всех неотрицательных целых чисел, если выполняются следующие условия: 1) справедливо Р(0),2) для любого х, если верно Р(х), то верно и P(x+1). И. а.… … Математическая энциклопедия
ИНТУИЦИОНИЗМ — (от позднелат. intuitio, от лат. intueor пристально смотрю) направление в обосновании математики и логики, согласно которому конечным критерием приемлемости методов и результатов этих наук является наглядно содержательная интуиция. Вся математика … Философская энциклопедия
Трансфинитные числа — (от Транс… и лат. finitus ограниченный) обобщённые порядковые числа. Определение Т. ч. опирается на понятие вполне упорядоченного множества (см. Упорядоченные и частично упорядоченные множества). Каждое конечное множество можно сделать… … Большая советская энциклопедия
интуиционизм — направление в обосновании математики и логики, согласно которому конечным критерием приемлемости методов и результатов этих наук является наглядно содержательная интуиция. Вся математика должна опираться, согласно И., на интуитивное представление … Словарь терминов логики
СОФИЗМ — (греч. sophisma хитрая уловка, измышление) рассуждение, кажущееся правильным, но содержащее скрытую логическую ошибку и служащее для придания видимости истинности ложному утверждению. С. является особым приемом интеллектуального мошенничества,… … Философская энциклопедия
ТОЖДЕСТВА ПРОБЛЕМЫ — проблемы эквивалентности, проблемы иден тичности, проблемы равенства с л о в (англ. word problems) – задачи нахождения общего метода (алгоритма), позволяющего для произвольной пары элементов к. л. множества, в к ром определено отношение типа… … Философская энциклопедия
Софизм — (от греч. sóphisma уловка, ухищрение, выдумка, головоломка) умозаключение или рассуждение, обосновывающее какую нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Аристотель… … Большая советская энциклопедия
Трансфинитная индукция — способ математических доказательств, обобщающий обычный принцип математической индукции (См. Математическая индукция). См. Трансфинитные числа … Большая советская энциклопедия
Софизм — (от греч. σόφισμα, «мастерство, умение, хитрая выдумка, уловка, мудрость») ложное высказывание, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики … Википедия
dic.academic.ru
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — это… Что такое МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ?
метод доказательства математич. утверждений, основанный на принципе математической индукции: утверждение (х), зависящее от натурального параметра х, считается доказанным, если доказано А(1) и для любого натурального пиз предположения, что верно (п), выведено, что верно также А(n+1).
Доказательство утверждения А(1) составляет первый шаг (или базис) индукции, а доказательство А(n+1)в предположении, что верно (п), наз. индукционным переходом. При этом хназ. параметром индукции, а предположение (п).при доказательстве А(n+1) наз. индуктивным предположением. Принцип М. и. является также основанием для индуктивных определений. Простейшим примером такого определения является определение свойства: «быть словом длины n в данном алфавите

Базис индукции: каждая буква алфавита (*) есть слово длины 1. Индукционный переход: если Е — слово длины п, то каждое слово Еai, где  есть слово длины n+1. Индукция может начинаться с нулевого шага. Часто бывает так, что А(1) и А(n+1) доказываются аналогичными рассуждениями. В таких случаях удобно пользоваться следующей эквивалентной формой принципа М. и. Если для всякого пиз предположения: (х).верно при любом натуральном x<n — следует, что (х).верно также при х=п, то утверждение (х).верно при любом натуральном х. В такой форме принцип М. и. может быть применен для доказательства утверждений (х), в к-рых параметр хпробегает то пли иное множество, вполне упорядоченное по нек-рому трансфинитному типу (трансфинитная индукция). В качестве простых примеров трансфинитной индукции отметим индукцию по параметру, пробегающему множество всех слов в данном алфавите, упорядоченное лексикографически, и индукцию по построению формул в данном логико-математич.
исчислении.
есть слово длины n+1. Индукция может начинаться с нулевого шага. Часто бывает так, что А(1) и А(n+1) доказываются аналогичными рассуждениями. В таких случаях удобно пользоваться следующей эквивалентной формой принципа М. и. Если для всякого пиз предположения: (х).верно при любом натуральном x<n — следует, что (х).верно также при х=п, то утверждение (х).верно при любом натуральном х. В такой форме принцип М. и. может быть применен для доказательства утверждений (х), в к-рых параметр хпробегает то пли иное множество, вполне упорядоченное по нек-рому трансфинитному типу (трансфинитная индукция). В качестве простых примеров трансфинитной индукции отметим индукцию по параметру, пробегающему множество всех слов в данном алфавите, упорядоченное лексикографически, и индукцию по построению формул в данном логико-математич.
исчислении.
Иногда для доказательства нек-рого утверждения А(n) индукцией по пприходится одновременно с (п).доказывать индукцией по пряд других утверждений, без к-рых индукцию для (п).не удается провести. В формальной арифметике можно указать такие утверждения (п), для к-рых в рамках рассматриваемого исчисления индукция не может быть проведена без добавления новых вспомогательных утверждений, зависящих от п(см. [3]). В таких случаях мы имеем дело с доказательством ряда утверждений совместной математической индукцией. Все эти утверждения формально можно объединить в одну конъюнкцию, однако практически такое объединение только усложнило бы рассмотрение, т. к. при этом исчезла бы возможность неформальных осмысленных ссылок на определенные индуктивные предположения.
В нек-рых конкретных математич. исследованиях число понятий и утверждений, определяемых и доказываемых сложной совместной индукцией, исчисляется трехзначной цифрой (см. [4]). В этом случае ввиду наличия в индуктивном доказательстве большого числа перекрестных ссылок на индуктивные предположения, для содержательного (неформального) понимания любого (даже самого простого) определения или утверждения при данном достаточно большом значении параметра индукции читатель должен быть знаком с содержанием всех вводимых совместной индукцией понятий и многих свойств этих понятий для меньших значений параметра индукции. По-видимому, единственным корректным с логич. точки зрения выходом из возникающего здесь логич. круга является аксиоматич. изложение всей рассматриваемой системы понятий. Таким образом, большое число понятий, определяемых совместной индукцией, приводит к необходимости применения аксиоматического метода в индуктивном определении и доказательстве. Это — наглядный пример необходимости аксиоматич. метода для решения конкретных математич. задач, а не только вопросов, относящихся к основаниям математики.
Лит.:[1] Гильберт Д., Б е р н а й с П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., М., 1979; [2] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Ц и н м а н Л. Л., «Матем. сб.», 1968, т. 77, №1, с. 71-104; [4] Адян С. И., Проблема Бернсайда и тождества в группах, М., 1975.
С. И. Адян.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия
dikc.academic.ru
Математика в деталях: how to математическая индукция
Математическая индукция является кошмаром большинства студентов технических профилей. Расписали так, что вы обязательно поймете данный концепт.
Начнем с того, что такое математическая индукция.
Математическая индукция – метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел, согласно Wikipedia. Говоря простыми словами, у нас есть какое-то математическое высказывание о натуральных числах, и мы хотим доказать/опровергнуть его истинность.
Разные источники дают разное определение натуральных чисел. В моем университете один профессор включает ноль во множество N, а по определению другого натуральные числа начинаются с единицы. Дело вкуса 😉 Но очень важно понять, с каким именно множеством вы работаете. Позже узнаете, почему.
Конечно, если наше математическое высказывание (формула) относится к маленькому множеству чисел, то гораздо легче просто высчитать ответ в уме или ввести данные в Wolfram – на этом всё, пускайте титры.
Например, вы, убивая время в интернете, где-то прочли, что сумма положительных натуральных чисел от 1 до n, то есть, 1+2+3+...+n, вычисляется по формуле n*(n+1)/2. Допустим, у вас проблемы с доверием, и вы хотите проверить, работает ли эта формула на самом деле, или это просто часть всемирного заговора?
Эту формулу можно применить к маленьким множествам, так как вы можете легко вычислить сумму чисел от 1 до 10, от 1 до 20, от 1 до 50, а если вас замучила бессонница, то попробуйте посчитать не овечек, а сумму чисел от 1 до 100. Помогает. Иногда.
Потом остается только подставить значения в формулу и сравнить.
Но если мы говорим о множестве с большим количеством элементов или о бесконечном множестве, то именно тут и пригодится индукция.
Проверка высказывания для наименьшего числа – это начало индукции.
Мы начинаем с базиса (база, base case) – нам дано наименьшее число, для которого нужно проверить истинность высказывания. Обычно это 1, но могут быть и другие варианты, которые обязательно указываются в условии. Например, можно начать с 4 или 5. Это не так важно. Но иногда этот базис не указывается эксплицитно. В этом случае вы начинаете с наименьшего числа вашего множества. Поэтому важно знать, с чего начать. Уточните, включается ноль в N или нет. В примерах в этой статье множество натуральных чисел начинается с единицы.
Затем мы утверждаем, что выражение истинно для любого n>=1. Мы не знаем этого наверняка, конечно. Но мы предполагаем, что если утверждение истинно для любого n, то оно будет верно и для n+1. Это называется шагом индукции. А так как n – это любое число из множества N, то мы можем проверить математическое высказывание для очень-очень-очень больших чисел.
Итак, вернёмся к нашей формуле вычисления суммы чисел от 1 до n.
Начало индукции: проверяем, верна ли формула для n=1: n*(n+1)/2=> 1*(1+1)/2=1*(2)/2=1
Так как сумма чисел от 1 до 1 равна 1, то высказывание истинно для n=1.
Затем мы утверждаем, что математическое высказывание истинно для любого n>=1. То есть 1+2+3+...+n = n*(n+1)/2.
Переходим к шагу индукции – если высказывание верно для n, то оно истинно и для n + 1. 1+2+3+...+n + (n+1) = (n+1)(n+1 + 1)/2.
Левая часть уравнения – это сумма чисел от 1 до n+1. Мы заменили все n в правой части на n+1, так как мы больше не рассматриваем n, а доказываем, что высказывание истинно именно для n+1.
Если вы помните, то сумма чисел от 1 до n вычисляется по формуле n*(n+1)/2. Поэтому часть выражения справа (а именно 1+2+3+...+n) можно заменить на n*(n+1)/2.
У нас остается n*(n+1)/2 + (n+1) = (n+1)(n+1 + 1)/2. Нам нужно доказать или опровергнуть равенство этих двух выражений.
Всё, что происходит дальше – это чистая алгебра. Нам надо всего лишь упростить эти выражения, так как немного трудно что-либо сказать об их равенстве, просто посмотрев на них. Даже если вы своими эльфийскими глазами можете рассмотреть, чему равны обе части, с вас всё равно потребуют формальное доказательство.
Немного упрощаем правую сторону:
n*(n+1)/2 + (n+1) = (n+1)(n+2)/2
Затем раскрываем скобки справа (умножаем n*(n+1)) и слева (умножаем (n+1)(n+2)). Получается (n^2 +n)/2 + (n+1) = (n^2 +3*n + 2)/2
Умножаем обе части уравнения на 2, чтобы избавиться от знаменателя:
(n^2 +n) + 2*(n+1) = (n^2 +3*n + 2)
Раскрываем скобки и упрощаем:
n^2 +n + 2*n+2 = n^2 +3*n + 2
Так как n + 2*n в левой части можно записать в виде 3*n, упрощаем левую часть:
n^2 +3*n+2 = n^2 +3*n + 2
Мы получаем идентичные выражения справа и слева, что означает, что истинность выражения доказана.
Многие из тривиальных алгебраических преобразований сверху можно пропустить, если вы сильны в математике. Но иногда формулы довольно громоздкие, поэтому я бы рекомендовала подробно описывать каждый вычислительный шаг. Так гораздо легче предотвратить и найти ошибки, если таковые имеются( а они очень часто имеются).
Рассмотрим другой пример. Попробуем доказать, что 1 + 3 + 5 + 7 + · · · + (2n − 1) = n^2. Эта формула описывает сумму нечетных чисел, начиная с 1.
1. Начинаем с базиса. Проверяем, истинно ли высказывание для n=1:
n^2 = 1^2 = 1
Сумма нечетных чисел от 1 до 1 равна 1, что действительно так. Чудеса!
2. Затем утверждаем, что выражение истинно для какого-то n>=1, то есть 1 + 3 + 5 + 7 + · · · + (2n − 1) = n^2.
3. Утверждаем, что если высказывание истинно для n, то оно также верно для n+1 (шаг индукции).
Проверяем для n+1:
1 + 3 + 5 + 7 + · · · + (2n − 1) + (2*(n+1)´-1) = (n+1)^2
(2*(n+1)´-1) – это следующее после (2n − 1) нечетное число.В данном случае прибавить n+1 к выражению слева нельзя, как мы это сделали в предыдущем примере, так как если n=999, то n+1 = 1000, что не является нечетным числом. Нам-то нужны исключительно нечетные. А они представлены именно формулой (2n − 1). Иногда в задаче указан определенный паттерн, который нужно учесть, составляя формулы для правой и левой части уравнения.
Можно упростить (2*(n+1)´-1) и получить (2n+1).
1 + 3 + 5 + 7 + · · · + (2n − 1) +(2n+1) = (n+1)^2
Но мы еще не закончили вычисления!
В правой части заменяем 1 + 3 + 5 + 7 + · · · + (2n − 1) на n^2, так как мы именно это взяли за основу в пункте 2. Раскрываем скобки в правой части. Наконец нам понадобилась одна из формул сокращённого умножения, вау!
Подставляем:
n^2 + (2n+1) = n^2 + 2n + 1
Отбрасываем скобки в правой части:
n^2 + 2n+1 = n^2 + 2n + 1
Правая и левая часть уравнения совпадают. Значит, математическое высказывание истинно.
Математическую индукцию еще сравнивают с эффектом домино. Если косточки домино выстроены в ряд, и какая-то упадёт, приложившись к следующей и опрокинув её, то та, в свою очередь, опрокинет следующую, и за ней последуют все остальные. А если мы опрокинем первую косточку, то упадёт весь ряд.
В индукции, если высказывание истинно для натурального числа, с которого мы начинаем, например, 8, то оно истинно для 9. Если оно истинно для 9, то оно верно для 10. И так далее. До бесконечности. Это мы и пытаемся доказать. Есть задачи, которые имею несколько базисов. Например, вам надо проверить какое-то высказывание для n=4, n=5, n=6 в начале индукции. Попадаются и задачи, где база дана в рекурсивной форме.
Потренируйтесь на других примерах. Основным скилом для решения подобных задач является умение находить паттерны. Вы также должны понимать, что именно вы хотите доказать? Что описывает формула? Очень важно знать и уметь применять некоторые формулы, которые помогут вам упростить выражения. Например, те же самые формулы сокращённого умножения. Они очень часто встречаются в математической индукции. Очень многие допускают ошибки именно в конце, когда надо подключить свои знания алгебры.
Помните, что математическая индукция применяется только к высказываниям с натуральными числам. Ваш n не может равняться -10 или 8.5. Дискриминация по отношению к действительным и комплексным числам? Вполне может быть.
Для чего же это всё?
Во-первых, решая подобные задачи, вы развиваете логику и алгоритмическое мышление, что играет не последнюю роль в программировании. Вы учитесь распознавать всякого рода паттерны.
Во-вторых, если вы внимательнее посмотрите на принцип математической индукции, вы заметите, что это чистейшая рекурсия. Предполагаю, что вы знакомы с рекурсией, если вы хотя бы немного программируете. Есть base case – условие завершения алгоритма. Также есть правило перехода. И чтобы проверить высказывание для n, нужно решить что-то для n-1, а потом с помощью алгебры дойти до n.
Рекурсию можно или любить, или люто ненавидеть. Но если ее понять и правильно использовать, она может сделать код элегантнее.
Нравится математика? О чем бы вы хотели почитать?
proglib.io
Математическая индукция — Википедия
Материал из Википедии — свободной энциклопедии
Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Формулировка
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: P1,P2,…,Pn,Pn+1,…{\displaystyle P_{1},P_{2},\ldots ,P_{n},P_{n+1},\ldots }.
Допустим, что
Тогда все утверждения нашей последовательности верны. |
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }. Если для любого натурального n{\displaystyle n} из того, что истинны все P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }, Pn−1{\displaystyle P_{n-1}}, следует также истинность Pn{\displaystyle P_{n}}, то все утверждения в этой последовательности истинны, то есть (∀n∈N)((∀i∈{1;…;n−1})Pi⟶Pn)⟶(∀n∈N)Pn{\displaystyle (\forall n\in {\mathbb {N} }){\Big (}(\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}{\Big )}\longrightarrow (\forall n\in {\mathbb {N} })P_{n}}. |
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при n=1{\displaystyle n=1} импликация (∀i∈{1;…;n−1})Pi⟶Pn{\displaystyle (\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}} эквивалентна P1{\displaystyle P_{1}}. Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
История
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида[1]. Современное название метода было введено де Морганом в 1838 году.
Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
- 1+q+q2+⋯+qn=1−qn+11−q.{\displaystyle 1+q+q^{2}+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
Доказательство. Индукция по n.
База, n = 1:
- 1+q=(1−q)(1+q)1−q=1−q1+11−q.{\displaystyle 1+q={\frac {(1-q)(1+q)}{1-q}}={\frac {1-q^{1+1}}{1-q}}.}
Переход: предположим, что
- 1+q+⋯+qn=1−qn+11−q,{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}},}
тогда
- 1+q+⋯+qn+qn+1=1−qn+11−q+qn+1={\displaystyle 1+q+\cdots +q^{n}+q^{n+1}={\frac {1-q^{n+1}}{1-q}}+q^{n+1}=}
- =1−qn+1+(1−q)qn+11−q=1−qn+1+qn+1−q(n+1)+11−q=1−q(n+1)+11−q{\displaystyle ={\frac {1-q^{n+1}+(1-q)q^{n+1}}{1-q}}={\frac {1-q^{n+1}+q^{n+1}-q^{(n+1)+1}}{1-q}}={\frac {1-q^{(n+1)+1}}{1-q}}},
что и требовалось доказать.
Комментарий: истинность утверждения Pn{\displaystyle P_{n}} в этом доказательстве — то же, что истинность равенства
- 1+q+⋯+qn=1−qn+11−q.{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
Вариации и обобщения
Примечания
- ↑ Nachum L. Rabinovih. Раби Леви бен Гершом и происхождение метода математической индукции = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — Вып. 6. — С. 237-248.
Литература
Ссылки
- Видео по методу математической индукции
wikipedia.green
Знакомство с методом математической индукции — Викиучебник
- Авторы исходного текста: Т. Шульман и А. В. Ворожцов. Дополнено А. Беркович. Журнал Потенциал
Что такое принцип математической индукции?[править]
Вообразим очередь, где первой стоит женщина, за ней снова женщина, а за ней снова женщина. Верно ли, что все стоящие в очереди — женщины?
Конечно, верно! Раз первые три человека в очереди — женщины, то, скорее всего, это очередь за косметикой, или за чем-нибудь таким, в чём нуждаются и разбираются исключительно женщины, и мужчин в этой очереди нет.
Пусть подобные рассуждения иногда оправдывают себя на практике, они не являются математически строгими и никак не связаны с методом математической индукции, о котором мы сегодня хотим поговорить.
Рассмотрим два утверждения:
- Первый человек в очереди есть женщина.
- За женщиной в очереди может стоять только женщина.
Из этих двух утверждений строго следует, что в очереди стоят только женщины. Мы можем последовательными шагами показать что любой человек в очереди — женщина.
Вот строгая формулировка принципа математической индукции:
Пусть имеется последовательность утверждений Y1,Y2,Y3,…{\displaystyle Y_{1},Y_{2},Y_{3},\ldots } И пусть первое утверждение Y1{\displaystyle Y_{1}} верно, и мы умеем доказывать, что из верности утверждения Yk{\displaystyle Y_{k}} следует верность Yk+1{\displaystyle Y_{k+1}}. Тогда все утверждения в этой последовательности верны.
Верность этого метода доказательства вытекает из так называемой аксиомы индукции, пятой из аксиом Пеано, которые определяют натуральные числа. Рассмотрение аксиом Пеано выходит за рамки этой статьи.
Заметим, что аксиому индукции можно заменить на аксиому существования минимума, и доказать аксиому индукции как теорему.
Также в скобках заметим, что существует принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений Y1,Y2,Y3,…{\displaystyle Y_{1},Y_{2},Y_{3},\ldots }. И пусть мы умеем доказывать первое из них, а так же то, что из верности утверждений Y1,Y2,Y3,…,Yk{\displaystyle Y_{1},Y_{2},Y_{3},\ldots ,Y_{k}} следует верность Yk+1{\displaystyle Y_{k+1}}. Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также может быть доказан при помощи математической индукции. Верно и обратное: принцип математической индукции можно доказать, предполагая принцип полной математической индукции. Так что в аксиомах Пеано можно выбрать в качестве одной из аксиом как аксиому существования минимума, как принцип полной математической индукции, так и принцип математической индукции. Какое из этих трёх утверждений брать за теорему, а какую за аксиомы — дело вкуса. Доказательство эквивалентности этих утверждений смотри в приложении B
Ханойские башни[править]
Есть три стержня и n{\displaystyle n} колец разного размера. Класть можно только кольцо меньшего размера на кольцо большего размера или кольцо любого размера на пустой стержень. Можно ли переместить пирамидку с одного стержня на другой? Можно или нельзя?
- Пирамидку, в которой только одно кольцо n=1{\displaystyle n=1}, переместить можно (очевидно).
- Предположим, что мы умеем перемещать пирамидки с числом колец n⩽K{\displaystyle n\leqslant K}.
- Попробуем научиться перемещать пирамидку с n=K+1{\displaystyle n=K+1} . Пирамидку из K{\displaystyle K} колец, лежащих на самом большом K+1{\displaystyle K+1}-м кольце, мы можем согласно предположению переместить на любой стержень. Сделаем это, переместим её на третий стержень. Неподвижное K+1{\displaystyle K+1}-е кольцо не будет нам мешать провести алгоритм перемещения, так как оно самое большое. После перемещения K{\displaystyle K} колец переместим оставшееся K+1{\displaystyle K+1}-е кольцо на второй стержень. Мы можем это сделать, так как второй стержень пустой. Теперь обратим внимание, тот факт, что второй стержень не пустой, не мешает нам класть на него любые кольца, так как имеющееся на нём кольцо самое большое (любое кольцо можно положить на большее, а значит и самое большое по условию задачи). И затем опять применим известный нам по предположению алгоритм перемещения K{\displaystyle K} колец и переместим их на второй стержень, стержень с лежащим внизу K+1{\displaystyle K+1}-м кольцом. Таким образом, если мы умеем перемещать пирамидки с K{\displaystyle K} кольцами, то умеем перемещать пирамидки и с K+1{\displaystyle K+1} кольцом.
- Следовательно утверждение верно для всех случаев, то есть для всех n{\displaystyle n}.
Заметим, что всё решение было разбито на четыре этапа:
- [БАЗА] Показываем, что доказываемое утверждение верно для некоторых простейших частных случаев (в нашей задачке это был случай n=1{\displaystyle n=1})
- [ПРЕДПОЛОЖЕНИЕ] Предполагаем, что утверждение доказано для первых K{\displaystyle K} случаев.
- [ШАГ] В этом предположении доказываем утверждение для случая n=K+1{\displaystyle n=K+1}.
- [ВЫВОД] Утверждение верно для всех случаев, то есть для всех n{\displaystyle n}.
Решение задач по данной схеме и называется методом математической индукции .
Ясно, что методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.
В задаче «Ханойские башни» роль переменной индукции играло количество колец в пирамидке.
Пересечение прямых[править]
Докажите, что любые n{\displaystyle n} прямых, расположенных на одной плоскости, никакие две из которых не параллельны, и никакие три не пересекаются в одной точке, пересекаются ровно в n(n−1)2{\displaystyle {\frac {n(n-1)}{2}}} точках.
Решение:
[БАЗА] В простейшем случае, когда прямых две, известно, что они непараллельны, а значит пересекаются как минимум в одной точке. Они не могут пересекаться в более чем одной точке, так как согласно аксиомам Евклидовой геометрии (а именно, следствие из аксиомы «через две точки можно провести прямую и только одну»), если бы были хотя бы две точки пересечения у двух прямых, то эти прямые совпадали бы, то есть мы бы имели одну прямую, а не две. Имеем, что должно быть не менее одной (включительно) и не более одной (включительно) точек пересечения, а значит точка пересечения одна и утверждение верно.
[ПРЕДПОЛОЖЕНИЕ] Предположим, что оно верно для k{\displaystyle k} прямых, то есть что любые k{\displaystyle k} прямых, никакие две из которых не параллельны, и никакие три не пересекаются в одной точке, пересекаются ровно в k(k−1)2{\displaystyle {\frac {k(k-1)}{2}}} точках.
[ШАГ] Попробуем доказать его для k+1{\displaystyle k+1} прямых. По предположению, 1{\displaystyle 1}-я, 2{\displaystyle 2}-я, …, k{\displaystyle k}-я прямая пересекаются в k(k−1)2{\displaystyle {\frac {k(k-1)}{2}}} точках. Рассмотрим k+1{\displaystyle k+1}-ю прямую и одну из прямых, обозначим её i{\displaystyle i} из списка 1{\displaystyle 1}-я, 2{\displaystyle 2}-я, …, k{\displaystyle k}-я прямая. Как мы уже доказали в [БАЗЕ] любые две прямые, удовлетворяющие условиям задачи, пресекаются ровно в одной точке, а значит и прямые k+1{\displaystyle k+1} и i{\displaystyle i} пересекаются в одной точке. Вспомним, что i{\displaystyle i} обозначает любую прямую из списка 1{\displaystyle 1}-я, 2{\displaystyle 2}-я, …, k{\displaystyle k}. Отсюда k+1{\displaystyle k+1}-я прямая пересекается с каждой из этих k{\displaystyle k} прямых ровно в одной точке.
Рассмотрим список из k+1{\displaystyle k+1} прямых и их точек пересечения. Уберём прямую k+1{\displaystyle k+1} вместе с её точками пересечения. Останется k{\displaystyle k} прямых удовлетворяющих [ШАГУ]. Значит количество точек пересечения у этих k{\displaystyle k} прямых равняется k(k−1)2{\displaystyle {\frac {k(k-1)}{2}}}. Как было показано выше, количество точек пересечения, которое мы убрали вместе с прямой k+1{\displaystyle k+1}, равняется k{\displaystyle k}.
Следовательно, количество точек пересечения всех k+1{\displaystyle k+1} прямых есть k(k−1)2+k=k2+k2=(k+1)k2{\displaystyle {\frac {k(k-1)}{2}}+k={\frac {k^{2}+k}{2}}={\frac {(k+1)k}{2}}}.
То есть для k+1{\displaystyle k+1} прямых утверждение доказано.
[ВЫВОД] Утверждение верно для любого количества прямых.
Разрезание квадрата[править]

Из квадрата клетчатой бумаги размером 2n×2n{\displaystyle 2^{n}\times 2^{n}} вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на «уголки» из трёх клеток.
Решение:
[БАЗА] Для n=1{\displaystyle n=1} получим квадрат размером 2×2{\displaystyle 2\times 2}. Вырежем, скажем, правый верхний квадрат. Останется три квадрата, представляющие собой «уголки». Утверждение верно.
[ПРЕДПОЛОЖЕНИЕ] Пусть это уже доказано для квадратов со стороной 2k{\displaystyle 2^{k}} с вырезанной одной клеткой. Докажем для квадратов 2k+1×2k+1{\displaystyle 2^{k+1}\times 2^{k+1}}.
[ШАГ] Разбиваем квадрат 2k+1×2k+1{\displaystyle 2^{k+1}\times 2^{k+1}} на четыре квадрата 2k×2k{\displaystyle 2^{k}\times 2^{k}} и вырезаем из каждой недырявой части угловую клетку так, чтобы вырезанные клетки образовали уголок:

[ВЫВОД] Таким образом, получаем четыре квадрата, в каждом из которых вырезано по одной клетке, и по предположению индукции их мы можем замостить уголками. Замощение квадрата 2k+1×2k+1{\displaystyle 2^{k+1}\times 2^{k+1}} будет состоять из замощения четырёх квадратов 2k×2k{\displaystyle 2^{k}\times 2^{k}} c вырезанной одной клеткой по середине. Что и требовалось доказать.
Интуиция[править]
Возможно, вы, прочитав решение, скажете себе, что вы всё поняли, но сами бы такую задачу решить не смогли. На вопрос «почему?» вы скажите: что-то непонятно, почему нужно было делить квадрат 2k+1×2k+1{\displaystyle 2^{k+1}\times 2^{k+1}} на четыре части.
В большинстве учебников вопросу интуиции в решении задач не уделяется внимание вообще. Даётся просто формально правильное решение. Отчасти это объясняется экономией места, отчасти тем, что это не являются частью решения, отчасти тем, что у каждого своя интуиция и не сильно понятно что именно нужно описывать, отчасти тем, что достаточно просто перерешать большое количество задач, как у вас появится интуиция. Не споря с этими утверждениями, я всё же решил, что в некоторых относительно трудных случаях я буду писать пару слов о том, почему нужно сделать то или иное действие. В подсказках к решению задач вы часто также будете находить то действие или тот факт, которое нужно было найти «интуитивно», как здесь деление квадрата на четыре части.
В этом примере интуиция могла бы быть такой. Возьмём квадрат 2k+1×2k+1{\displaystyle 2^{k+1}\times 2^{k+1}}. Нам нужно применить к нему метод математической индукции, а значит нам надо «найти» в нём квадрат 2k×2k{\displaystyle 2^{k}\times 2^{k}}. Допустим, это будет центр большего квадрата. Меньший квадрат без одной клетки мы можем вымостить «угольником». Но что сделать с оставшимися 2k+1×2k+1−2k×2k=22k+2−22k=22k(22−1)=3⋅22k{\displaystyle 2^{k+1}\times 2^{k+1}-2^{k}\times 2^{k}=2^{2k+2}-2^{2k}=2^{2k}(2^{2}-1)=3\cdot 2^{2k}} квадратиками (плюс вырезанный квадратик из меньшего квадрата). Но постойте, 3⋅22k{\displaystyle 3\cdot 2^{2k}} — это количество клеток в ещё трёх квадратах! Мы взяли один квадрат, а из оставшихся клеток можно сделать ещё три одинаковых квадрата! Нужно только подумать о том, чтобы эти клетки располагались в форме квадрата (у нас они располагаются «полосами»), а также о том, чтобы «вырезанные» клетки каждого меньшего квадрата не были разбросаны как попало.
Упражнение. Допустим, сторона квадрата будет 3n×3n{\displaystyle 3^{n}\times 3^{n}}. Попытайтесь «интуитивно» понять, почему застелить его «уголками» не получится. Пройдитесь по доказательству в случае квадрата 2n×2n{\displaystyle 2^{n}\times 2^{n}} и найдите место, где доказательство «падает». Постройте контр-пример.
Попробуйте решить самостоятельно следующие геометрические задачи:
Геометрические задачи[править]
Три острых угла[править]
Задача 1.1. Докажите, что при каждом натуральном n{\displaystyle n}, начиная с 3{\displaystyle 3}, существует выпуклый n{\displaystyle n}-угольник, имеющий ровно три острых угла.
Подсказка [1].
Раскраска плоскости[править]
Задача 1.2. Плоскость разделена на части n{\displaystyle n} прямыми. Докажите, что эти части можно раскрасить в два цвета так, что соседние куски будут раскрашены в разные цвета.
Подсказка [2].
Сумма углов n{\displaystyle n}-угольника.[править]
Задача 1.3. Докажите что сумма углов выпуклого n{\displaystyle n}-угольника равна (n−2)⋅180∘{\displaystyle (n-2)\cdot 180^{\circ }}, (или (n−2)π{\displaystyle (n-2)\pi } радиан). В частности для треугольника получаем (3−2)⋅180∘=180∘{\displaystyle (3-2)\cdot 180^{\circ }=180^{\circ }}, а для четырехугольника — (4−2)⋅180∘=360∘{\displaystyle (4-2)\cdot 180^{\circ }=360^{\circ }}
Подсказка [3].
Число кусочков[править]
Задача 1.4. Чему равно количество кусочков, на которые n{\displaystyle n} прямых (не проходящих через одну точку) делят плоскость на части? Одна прямая — на две части, две — на четыре. А пятнадцать прямых?
Подсказка [4]
Доказательства тождеств[править]
Есть целый ряд тождеств, которые удобно доказывать ММИ, к примеру:
Пример 2.1. Если x⩾0{\displaystyle x\geqslant 0}, c⩾0{\displaystyle c\geqslant 0}, то
(x+c)n=xn+O(xn−1){\displaystyle (x+c)^{n}=x^{n}+O(x^{n-1})}, где O(xn−1){\displaystyle O(x^{n-1})} обозначает полином степени не большей чем n−1{\displaystyle n-1}.
Разъяснение
Приведём несколько примеров для разъяснения смысла знака O(xn−1){\displaystyle O(x^{n-1})}. Воспользуемся формулами сокращённого умножения.
(x+c)1=x+c=x+O(x1−1)=x+O(x0){\displaystyle (x+c)^{1}=x+c=x+O(x^{1-1})=x+O(x^{0})}, где O(x0){\displaystyle O(x^{0})} обозначает «полином степени не большей чем 0{\displaystyle 0}», то есть O(x0){\displaystyle O(x^{0})} обозначает скаляр (число). В данном случае O(x0)=c{\displaystyle O(x^{0})=c}, так как c{\displaystyle c} — число, не зависимое от x{\displaystyle x}.
(x+c)2=x2+2xc+c2=x2+((2c)x+c2x0)=x2+O(x1){\displaystyle (x+c)^{2}=x^{2}+2xc+c^{2}=x^{2}+((2c)x+c^{2}x^{0})=x^{2}+O(x^{1})}
(x+c)3=x3+3x2c+3xc2+c3=x3+(3cx2+3c2x+c3+x0)=x3+O(x2){\displaystyle (x+c)^{3}=x^{3}+3x^{2}c+3xc^{2}+c^{3}=x^{3}+(3cx^{2}+3c^{2}x+c^{3}+x^{0})=x^{3}+O(x^{2})}
Докажем три тождества, которые мы тут же используем в доказательстве ниже.
a⋅O(xk)=O(xk){\displaystyle a\cdot O(x^{k})=O(x^{k})}. (1)
В самом деле, слева у нас «полином степени не большей чем k{\displaystyle k}», умноженный на скаляр (число) a{\displaystyle a}. Мы можем перемножить все его коэффициенты на a{\displaystyle a}, от этого степень полинома не изменится, он останется «полиномом степени не большей чем k{\displaystyle k}», а это и есть выражение справа.
x⋅O(xk−1)=O(xk){\displaystyle x\cdot O(x^{k-1})=O(x^{k})}. (2)
В самом деле, если умножим x{\displaystyle x} на «полином степени не большей чем k−1{\displaystyle k-1}», то есть у такого полинома существует ненулевой коэффициент при xk−1{\displaystyle x^{k-1}} и для всех s⩾k{\displaystyle s\geqslant k} степени при xs{\displaystyle x^{s}} равны нулю, то у нас будет ненулевой коэффициент при x⋅xk−1=xk{\displaystyle x\cdot x^{k-1}=x^{k}}, и для всех s⩾k{\displaystyle s\geqslant k} степени при
ru.wikibooks.org

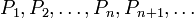
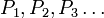 . Допустим, что
. Допустим, что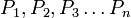 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)

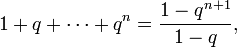
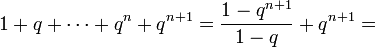
 ,
,
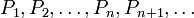
 . Допустим, что
. Допустим, что , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)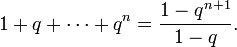
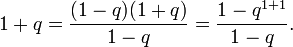
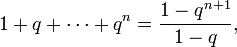
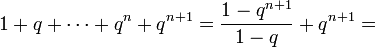
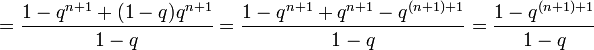 ,
,