{2}} = \frac{1}{2 a} \operatorname{ln}\left|{\frac{- a + x}{a + x}}\right| + C$$

Интеграл от единицы, деленной на разницу x в квадрате минус a в квадрате равен натуральному логарифму от модуля деления x-a на x + a и весь этот логарифм делен на произведение 2a

$$\int \operatorname{ln}\left(x\right)\,dx = x \operatorname{ln}\left(x\right) — x + C$$

Интеграл от натуральной логарифической функции равен произведению x на натуральный логарифм и минус переменная x

$$\int \frac{dx}{x \operatorname{ln}\left(x\right)} = \operatorname{ln}\left(\operatorname{ln}\left(x\right)\right) + C$$

Integral от единицы, деленной на произведение x на натуральный логарифм равняется логарифму от логарифма от x — по сути получается такая сложная функция

$$\int \operatorname{log}_{b}\left(x\right)\,dx = x \operatorname{log}_{b}\left(x\right) — \operatorname{log}_{b}\left(e\right) + C$$

Интеграл от логарифма от x по основанию b равен произведению x на логарифм от x по основанию b минус логарифм от экспоненты по основанию b

$$\int e^{x}\,dx = e^{x} + C$$

Значение интеграла от экспоненты в степени x равно самой экспоненте от x плюс константа C

$$\int a^{x}\,dx = \frac{a^{x}}{\operatorname{ln}\left(a\right)} + C$$

Интеграл от числа a в степени x равняется a в степени x, деленное на натуральный логарифм от a

$$\int \frac{dx}{\sqrt{a^{2} — x^{2}}} = \operatorname{arcsin}\left(\frac{x}{a}\right) + C$$

Интегральное выражение от 1 деленного на корень квадратный из разницы a в квадрате минус x в квадрате равняется арксинусу от деления x на a

$$\int \frac{- dx}{\sqrt{a^{2} — x^{2}}} = \operatorname{arccos}\left(\frac{x}{a}\right) + C$$

Этот же интеграл, но со знаком минус равен арккосинусу от деления x на a

$$\int \frac{dx}{x \sqrt{x^{2} — a^{2}}} = \frac{1}{a} \operatorname{arcsec} \frac{\left|x\right|}{a} + C$$

$$\int \frac{dx}{\sqrt{x^{2} \pm a^{2}}} = \operatorname{ln}\left| x + \sqrt{x^{2} \pm a^{2}}\right| + C$$

$$\int \operatorname{sin}\left(x\right)\,dx = — \operatorname{cos}\left(x\right) + C$$

Интеграл от функции синус от x равен минус косинусу от того же x

$$\int \operatorname{cos}\left(x\right)\,dx = \operatorname{sin}\left(x\right) + C$$

Интеграл от функции косинус от x равен синусу от x

$$\int \operatorname{tg}\left(x\right)\,dx = \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + C$$

Интегральное от тангенса от x равно одной второй от логарифма от суммы тангенса в квадрате от x плюс один

$$\int \frac{dx}{\operatorname{tg}\left(x\right)} = — \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{tg}\left(x\right)\right) + C$$

$$\int \frac{dx}{\operatorname{cos}\left(x\right)} = — \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) -1\right) + \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) + 1\right) + C$$

$$\int \frac{dx}{\operatorname{sin}\left(x\right)} = \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) -1\right) — \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) + 1\right) + C$$

$$\int \frac{dx}{\operatorname{cos}^{2}\left(x\right)} = \frac{\operatorname{sin}\left(x\right)}{\operatorname{cos}\left(x\right)} + C$$

интегралиус от 1 деленной на косинус в квадрате от x равен синусу от x, деленному на косинус от x

$$\int \frac{dx}{\operatorname{sin}^{2}\left(x\right)} = — \frac{\operatorname{cos}\left(x\right)}{\operatorname{sin}\left(x\right)} + C$$

интегрализэ от единицы, деленной на синус в квадрате от x равен минус косинусу от x, деленному на синус от x

$$\int \frac{\operatorname{tg}\left(x\right)}{\operatorname{cos}\left(x\right)}\,dx = \frac{1}{\operatorname{cos}\left(x\right)} + C$$

$$\int \frac{dx}{\operatorname{sin}\left(x\right) \operatorname{tg}\left(x\right)} = \frac{1}{\operatorname{sin}\left(x\right)} + C$$

$$\int \operatorname{sin}^{2}\left(x\right)\,dx = \frac{1}{2} x — \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$

$$\int \operatorname{cos}^{2}\left(x\right)\,dx = \frac{1}{2} x + \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$

$$\int \operatorname{arctg}\left(x\right)\,dx = x \operatorname{arctg}\left(x\right) — \frac{1}{2} \operatorname{ln}\left(x^{2} + 1\right) + C$$

$$\int \operatorname{sin}^{n} \left(x\right)\,dx = — \frac{\operatorname{sin}^{n-1}\left(x\right)*x*\operatorname{cos}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{sin}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$

$$\int \operatorname{cos}^{n} \left(x\right)\,dx = \frac{\operatorname{cos}^{n-1}\left(x\right)*x*\operatorname{sin}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{cos}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$

$$\int \operatorname{sh}\left(x\right)\,dx = \operatorname{ch}\left(x\right) + C$$

Интеграл от гипорболического синуса от x равен гиперболическому косинусу от x

$$\int \operatorname{ch}\left(x\right)\,dx = \operatorname{sh}\left(x\right) + C$$

Интеграл от гипорболического косинуса от x равен гиперболическому синусу от x

$$\int \frac{dx}{\operatorname{ch}^{2}\left(x\right)} = \frac{2 \operatorname{th}\left(\frac{x}{2}\right)}{\operatorname{th}^{2}\left(\frac{x}{2}\right) + 1} + C$$

$$\int \frac{dx}{\operatorname{sh}^{2}\left(x\right)} = — \frac{1}{2} \operatorname{th}\left(\frac{x}{2}\right) — \frac{1}{2 \operatorname{th}\left(\frac{x}{2}\right)} + C$$

$$\int \operatorname{th}\left(x\right)\,dx = x — \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + C$$

$$\int \frac{dx}{\operatorname{sh}\left(x\right)} = \operatorname{ln}\left(\operatorname{th} \frac{x}{2}\right) + C$$

$$\int \frac{dx}{\operatorname{ch}\left(x\right)} = \operatorname{arctg}\left(\operatorname{sh}\left(x\right)\right) + C$$

$$\int \frac{dx}{\operatorname{th}\left(x\right)} = x — \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{th}\left(x\right)\right) + C$$

Калькулятор интегралов онлайн

Оператор	Описание
Простейшие математические операции
+ — * / ()	Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . x
Тригонометрические функции
sin(x)	Синус от x: sin(x)
cos(x)	Косинус от x: cos(x)
tg(x)	Тангенс от x: tan(x)
ctg(x)	Котангенс от x: 1/tan(x)
arcsin(x)	Арксинус от x: arcsin(x)
arccos(x)	Арккосинус от x: arccos(x)
arctan(x)	Арктангенс от x: arctan(x)
arcctg(x)	Арккотангенс от x: \pi/2 — arctan(x)
Некоторые константы
e	Число Эйлера e: \e
π	Число π: \pi

калькулятор интегралов — калькулятор первообразных

Калькулятор интегралов — это онлайн-инструмент, который вычисляет первообразную функции. Он работает как калькулятор определенного интеграла, а также как калькулятор неопределенного интеграла и позволяет мгновенно вычислить интегральное значение.

Если вы изучаете исчисление, вы можете иметь представление о том, насколько сложны интегралы и производные. Что ж, отбросьте свои заботы, потому что калькулятор интеграции здесь, чтобы облегчить вам жизнь. Вы можете оценить интеграл, только поместив функцию в наш инструмент.

Теперь мы обсудим определение интеграла, как использовать интегральный калькулятор с пошаговыми инструкциями, как решать интегралы с помощью интегрального решателя и многое другое.

Что такое интегральное?

Интеграл является обратной производной. Он такой же, как и первообразная. Его можно использовать для определения площади под кривой. Вот стандартное определение интеграла
Википедия.

«В математике интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим.”

С интервалом [a, b] действительной прямой и действительной переменной x определенный интеграл заданной функции f может быть выражен как:

Как правило, есть два типа интегралов.

Oпределенный интеграл онлайн : если интегралы определяются с использованием нижнего и верхнего пределов, они называются определенными интегралами. Стандартный вид определенных интегралов может быть представлен как:

Hеопределенный интеграл онлайн : если не определены нижний или верхний предел, предел указывается постоянной интегрирования. Эти типы интегралов называются неопределенными интегралами, потому что для них нет ограничений.

Стандартная форма неопределенных интегралов:

∫ f (x) dx

Как  работает интеграл онлайн?

Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл.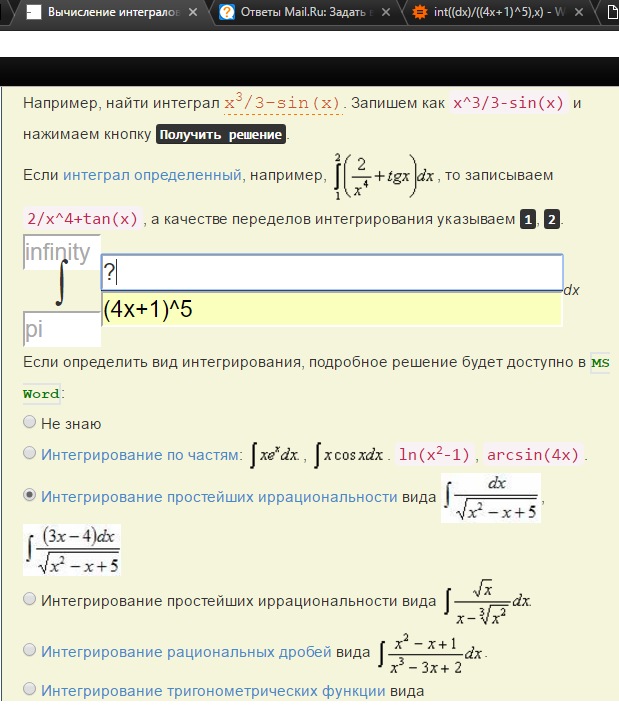 Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.

Кроме того, калькулятор интегральных вычислений дает ощущение простоты в расчетах интегрирования, только принимая функцию от пользователя. Вам не нужно ничего делать, кроме как вводить данные, и этот итерационный калькулятор интегралов делает все это самостоятельно, причем в кратчайшие сроки.

Чтобы использовать этот калькулятор линейного интеграла, выполните следующие действия:

Введите свое значение в данное поле ввода.
Нажмите кнопку «Рассчитать», чтобы получить интеграл.
Используйте кнопку Reset, чтобы ввести новое значение.
Калькулятор интеграции по частям даст вам полностью оцененную интегральную функцию, которую можно в дальнейшем использовать в различных областях. Как упоминалось выше, интегрирование является обратной функцией производных. Если вам нужно решить производную, воспользуйтесь нашим калькулятором производной.

Как вычислить интеграл?

Теперь, когда вы знаете, что такое интегралы и как использовать приведенную выше производную интегрального калькулятора для решения интеграла, вы также можете узнать, как решать интегралы вручную. Это может как-то раздражать тех, кто только начинает с интегралов.

Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять. Кроме того, вы можете подготовить тему к экзаменам, используя приведенное ниже руководство.

Чтобы вычислить интегралы, выполните следующие действия:

Определите и запишите функцию F (x).
Возьмем первообразную функции F (x).
Вычислите значения верхнего предела F (a) и нижнего предела F (b).
Вычислите разницу верхнего предела F (a) и нижнего предела F (b).
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.

Пример — Определенный интеграл
Для функции f (x) = x — 1 найти определенный интеграл, если интервал равен [2, 8].

Решение:

Шаг 1: Определите и запишите функцию F (x).

F (x) = x — 1, интервал = [2, 8]

Шаг 2: Возьмите первообразную функции F (x).

F (x) = ∫ (x − 1) dx = (x2 / 2) — x

Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).

As, a = 1 и b = 10,

F (а) = F (1) = (22/2) — 2 = 0

F (б) = F (10) = (82/2) — 8 = 24

Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).

F (б) — F (а) = 24-0 = 24

Этот метод можно использовать для вычисления определенных интегралов, имеющих пределы. Вы можете использовать калькулятор двойного интеграла выше, если не хотите заниматься интегральными вычислениями.

Пример — интеграл тригонометрической функции
Для функции f (x) = sin (x) найдите определенный интеграл, если интервал равен [0, 2π].

Решение:

Шаг 1: Определите и запишите функцию F (x).

F (x) = sin (x), интервал = [0, 2π]

Шаг 2: Возьмите первообразную функции F (x).

F (x) = ∫ sin (x) dx = cos (x)

Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).

As, a = 0 и b = 2π,

F (а) = F (0) = cos (0) = 0

F (b) = F (2π) = cos (2π) = 0

Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).

F (б) — F (а) = 0 — 0 = 0

Наряду с ручным расчетом вы также можете использовать наш калькулятор тригонометрической подстановки выше, чтобы решить тригонометрический интеграл за доли секунды.

FAQs

Что такое вычисление интегралов?

Интегральное вычисление обращает функцию производной, беря первообразную этой функции. Он используется для определения площади под кривой. Интегральные вычисления могут быть определенными, если есть верхний и нижний пределы. Если интервалов нет, используется интегральная константа C, и этот тип функции называется неопределенным интегралом.

Какая производная от интеграла?

Если мы возьмем производную интеграла, оба они будут компенсировать друг друга, потому что производная и интеграл являются обратными функциями друг к другу. Согласно основной теореме исчисления, интеграл — это то же самое, что и первообразная.

Кто отец интеграции?

Готфрид Вильгельм Лейбниц и Исаак Ньютон независимо предложили правила интеграции в конце 17 века. Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.

Что такое интеграл от 1?

Интеграл от 1 равен x или x + c, потому что если мы добавим интегральную константу. Это можно выразить как диагональная линия, лежащая в 1-м и 3-м квадрантах графика.

∫ 1 dx = x + C

Какой интеграл от sin 2x?

Интеграл от sin 2x можно вычислить методом подстановки. Это будет неопределенный интеграл из-за отсутствия интервала или верхнего и нижнего пределов. Вот интеграл от sin 2x.

∫ sin (2x) dx = — (1/2) cos (2x) + C

Интегральный (первообразный) калькулятор

с шагами

Этот онлайн-калькулятор попытается найти неопределенный интеграл (первообразную) заданной функции с указанными шагами.

Введите функцию:

Интегрировать относительно: autoxtuvwyzabcdfghklmnopqrs

Пожалуйста, пишите без каких-либо различий, таких как `dx`,` dy` и т. Д.

Определенный интеграл см. В калькуляторе определенного интеграла.

Некоторые интегралы могут занять некоторое время. Потерпи!

Если интеграл не рассчитывался или потребовалось много времени, напишите об этом в комментариях. Алгоритм будет улучшен.

Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.{2} \ right)} dx}} = \ color {red} {\ int {\ frac {\ cos {\ left (u \ right)}} {2} du}} $$

Применить постоянное кратное rule $$$ \ int cf {\ left (u \ right)} \, du = c \ int f {\ left (u \ right)} \, du $$$ с $$$ c = \ frac {1 } {2} $$$ и $$$ f {\ left (u \ right)} = \ cos {\ left (u \ right)} $$$:

$$ \ color {красный} {\ int { \ frac {\ cos {\ left (u \ right)}} {2} du}} = \ color {red} {\ left (\ frac {\ int {\ cos {\ left (u \ right)} du} } {2} \ right)} $$

Интеграл косинуса равен $$$ \ int {\ cos {\ left (u \ right)} du} = \ sin {\ left (u \ right)} $$$ :

$$ \ frac {\ color {red} {\ int {\ cos {\ left (u \ right)} du}}} {2} = \ frac {\ color {red} {\ sin {\ left (u \ right)}}} {2} $$

Напомним, что $$$ u = x ^ {2} $$$:

$$ \ frac {\ sin {\ left (\ color {red} {u} \ right)}} {2} = \ frac {\ sin {\ left (\ color {red} {x ^ {2}} \ right)}} {2} $$

Следовательно,

$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} $$

Добавьте постоянную интегрирования:

$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} + C $$

Ответ: $$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} + C $$$

Интегральный калькулятор

| Лучший калькулятор интеграции

Определение интегрального калькулятора

Калькулятор интегралов — это математический инструмент, который упрощает вычисление интегралов. Онлайн-калькулятор интегралов — это быстрый и надежный способ решения различных интегральных запросов. онлайн-калькулятор интеграции и его процесс отличается от обратного производный калькулятор, поскольку эти два являются основными концепциями исчисления.

Ковариация, помимо математического интеграла, определяется таким же образом. Ознакомьтесь с примерами ковариационного уравнения и расчета.

Что такое интеграция?

Интеграция находит дифференциал уравнение математических интегралов.Интегральная функция дифференцирует и вычисляет площадь под кривой графика.

Определение интеграла помогает найти площадь, центральную точку, объем и т. Д. Онлайн-калькулятор интеграции определяет интеграл, чтобы найти площадь под кривой следующим образом:

Где,

F (x) — функция, а

А — площадь под кривой.

Связанные: Что такое дисперсия и способы ее расчета.

Что такое интеграция в калькуляторе интеграции?

Интегральное выражение — это интеграл уравнение или формула интегрирования, она обозначается как функция f (x). В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.

Связанный: Узнайте, как вычислить логарифм и как найти антилогарифм числа?

Как калькулятор интегралов работает с интегральной записью?

Для интегрального уравнения

∫ 2x dx

∫ — это интегральный символ, а 2x — это функция, которую мы хотим интегрировать.

В этом интегральном уравнении dx — это дифференциал переменной x. Он подчеркивает, что переменная интеграции — x.Dx показывает направление по оси x, а dy показывает направление по оси y.

Интегральный символ и интегральные правила используются калькулятором интегралов для быстрого получения результатов. Узнайте больше о научных обозначениях и их расчетах здесь.

Как рассчитать интеграл?

Мы можем вычислить функцию, выполнив несколько простых шагов. Сначала разделите область на кусочки и сложите ширину этих частей на Δx. Тогда ответ будет неточным. (см. рисунок 1)

Если мы сделаем Δx намного меньшей шириной и сложим все эти маленькие кусочки, тогда точность ответа станет лучше. (см. рисунок 2)

Если ширина срезов приближается к нулю, то ответ приближается к истинному или фактическому результату. Итак,

Теперь мы говорим, что dx означает, что срезы Δx приближаются к нулю по ширине.

Обратите внимание, что интеграл является обратной производной

Узнайте, как найти и вычислить значение уклона, прежде чем решать интегральное уравнение.

Вычисляет ли калькулятор интегралов определенный интеграл и неопределенный интеграл?

Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения с помощью в поле ввода. Определенный интеграл имеет как начальное, так и конечное значение. Вычислительные интегралы функции f (x) представляют площадь под кривой от x = a до x = b.

Неопределенный интеграл не имеет верхнего и нижнего пределов функции f (x).Неопределенный интеграл также известен как первообразная.

Узнайте, как найти предел функции здесь.

Попробуйте калькулятор квадратной формулы и калькулятор формулы расстояния, чтобы узнать о различных математических формулах, используемых для решения различных математических уравнений.

Как вычислить двойные интегралы?

Одна из трудностей при вычислении двойных интегралов состоит в том, чтобы определить пределы интегрирования. Пределы интегрирования как порядок dxdydxdy требуются для определения пределов интегрирования для эквивалентного интегрального порядка dydxdydx.

Сложность вычисления двойных интегралов заключается в определении пределов интегрирования. Пределы интегрирования как порядка dxdydxdy определяют пределы интегрирования для интегрального порядка dydxdydx.

Узнайте разницу между средним и средним значением. Также узнайте, как рассчитать с использованием среднего калькулятор и калькулятор средней точки.

Есть ли в интегральном калькуляторе шаги?

Наш калькулятор интегрального исчисления предоставляет вам пошаговые инструкции, чтобы вы могли увидеть, как рассчитывается ваш запрос.Вы можете расширить свои знания и понимание, глядя на пошаговый ответ.

Этот интегральный решатель очень эффективен для сложных проблем интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.

Используйте калькулятор площади трапеции и калькулятор площади прямоугольника, чтобы еще больше укрепить свои математические концепции, связанные с площадью и поверхностью.

Как найти лучший интегральный калькулятор?

Calculatored имеет лучший калькулятор частичных интегралов с точки зрения точности, скорости и результатов.Методы калькулятора для интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете искать вычисленные или найти наш онлайн-калькулятор интегралов в Google.

Как пользоваться калькулятором интегралов с шагом?

Для простых примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что вам нужно сделать, это выполнить следующие шаги:

Шаг №1: Заполните интегральное уравнение, которое вы хотите решить.

Шаг № 2: Выберите переменную как X или Y.

Шаг № 3: Введите значение верхней границы.

Шаг №4: Введите значение нижней границы.

Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».

После того, как вы выполните вышеуказанные шаги и нажмете кнопку «Рассчитать», онлайн-калькулятор интеграции с шагами немедленно решит интеграл по частям. Вы увидите результаты Antiderivative, Integral Steps, Parsing Tree и график результата.

Вы также можете заполнить примеры интегральных примеров для решения интегралов на практике.Мы надеемся, что вы найдете полезную информацию об интегралах и их вычислениях.

Вы также можете использовать другие наши бесплатные калькуляторы, такие как Standard Калькулятор отклонений и калькулятор перекрестных произведений бесплатно.

Пожалуйста, поделитесь своими ценными отзывами ниже. Удачи в обучении и расчетах. Ваше здоровье!

Интегральный калькулятор (первообразный калькулятор) Пошаговый

Первообразный калькулятор

Интегральный калькулятор — это онлайн-инструмент, который вычисляет первообразную функции.Он работает как вычислитель определенного интеграла, а также как калькулятор неопределенного интеграла и позволяет мгновенно вычислить интегральное значение.

Калькулятор линейного интегрирования показывает все шаги, необходимые для вычисления интегралов. Он выполняет интегрирование функции по частям и решает интегралы двумя разными методами.

---

Что такое интеграл?

Интеграл является обратной производной. Его можно использовать для определения площади под кривой.

Его можно определить как:

“ Интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция — дифференцирование (взятие производных). ”

---

Как вычислять интегралы?

Возможно, вы захотите узнать, как решать интегралы вручную.Это может как-то раздражать тех, кто только начинает с интегралов. Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять.

Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.

Пример — Определенный интеграл

Для функции f (x) = x — 1, найдите определенный интеграл, если интервал равен [1, 10].

Решение:

Шаг 1: Определите и запишите функцию F (x).

F (x) = x — 1

Интервал = [1, 10]

Шаг 2: Возьмите первообразную функции и добавьте константу.

= ∫ (x − 1) dx = (x ² /2) — x + C

Шаг 3: Рассчитайте значения верхнего предела F (a) и нижний предел F (б).

As, a = 1 и b = 10 ,

F (a) = F (1) = ( 1 ² / 2) — 1 = -0.5

F (b) = F (10) = ( 10 ² / 2) — 10 = 40

Вычислите разницу между верхним пределом F (a) и нижним пределом F (b).

F (b) — F (a) = 40 — (-0,5) = 40,5

Вы можете использовать калькулятор двойного интеграла выше, если вы не хотите заниматься интегральными вычислениями .

Пример — интеграл от тригонометрической функции

Для функции f (x) = sin (x) , найдите определенный интеграл, если интервал равен [0, 2π].

Решение:

Шаг 1: Запишите функцию.

F (x) = sin (x)

Интервал = [0, 2π]

Шаг 2: Возьмите первообразную функции и добавьте константу C .

= ∫ sin ( x ) dx 25 cos x ) + C

Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).

As, a = 0 и b = 2π ,

F (a) = F (0) = cos (0) = 0

F (b ) = F (2π) = cos (2π) = 0

Шаг 4: Вычислите разницу между верхним пределом F (a) и нижним пределом F (b).

F (b) — F (a) = 0 — 0 = 0

Используйте интегральный решатель выше, чтобы решить тригонометрический интеграл за доли секунды.

Интегральный калькулятор

— Примеры, онлайн-калькулятор интегралов

Калькулятор интегралов

используется для интегрирования функции, которая может быть в форме определенного или неопределенного интеграла. Интегрирование — одна из самых фундаментальных операций исчисления. Это процесс объединения бесконечно малых данных для нахождения целого.

Что такое интегральный калькулятор?

Калькулятор интегралов — это онлайн-инструмент, который помогает найти значение заданного определенного или неопределенного интеграла. Интеграция — это процесс, обратный дифференциации. Таким образом, когда мы интегрируем функцию, мы, по сути, определяем ее первообразную. Чтобы использовать этот калькулятор интегралов , введите значения в указанные поля ввода.

Калькулятор интегралов

Как пользоваться калькулятором интегралов?

Чтобы найти интегральное значение с помощью онлайн-калькулятора интегралов, выполните следующие действия:

• Шаг 1: Откройте онлайн-калькулятор интегралов Cuemath.
• Шаг 2: Выберите определенный или неопределенный интеграл из раскрывающегося списка и введите значения в поля ввода.
• Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти значение интеграла для заданной функции.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести другие значения.

Как работает интегральный калькулятор?

Интеграцию можно определить как процесс определения площади под кривой.Есть два типа интегралов, а именно определенные интегралы и неопределенные интегралы. Ниже приведены различные методы, которые можно использовать для интеграции заданной функции:

• Метод разложения — Используя этот метод, мы можем разбить данную функцию на сумму и разность меньших функций, интегральное значение которых известно. Данная функция может быть алгебраической, тригонометрической, экспоненциальной или их комбинацией.
• Интегрирование заменой — В этом методе мы заменяем переменную интегрирования другой переменной.Это помогает упростить процесс решения интеграла.
• Интегрирование по частным дробям — Предположим, что наше подынтегральное выражение выражено в форме неправильной рациональной функции. Мы можем использовать концепцию частичных дробей, чтобы преобразовать нашу подынтегральную функцию в правильную рациональную функцию. Наконец, мы можем интегрировать это, чтобы получить ответ.
• Интегрирование по частям — Предположим, что наше подынтегральное выражение имеет форму ∫f (x) g (x) dx. Чтобы решить эту задачу с помощью интегрирования по частям, применим формулу: ∫f (x).g (x) dx = f (x) ∫g (x) dx — ∫ [f ′ (x) ∫ g (x) dx] dx.

Существует множество формул для решения специальных интегралов.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. {3} + x + 7) dx \) и проверьте его с помощью калькулятора интегралов.{2} + x} dx \)

☛ Математические калькуляторы:

Калькулятор процентного изменения

— Онлайн-калькулятор процентного изменения

Percent Change Calculator — это онлайн-инструмент, который помогает рассчитать процент увеличения или уменьшения в процентах от одного числа к другому. Процентное изменение используется для обозначения степени изменения, проявляемого величиной за период времени.

Что такое калькулятор процентного изменения?

Калькулятор процентного изменения

помогает вычислить процентное изменение одного числа на другое.Он используется для расчета степени увеличения или уменьшения количества за определенный период времени. Для использования калькулятора

процентного изменения введите значения в указанные поля ввода.

Калькулятор процентного изменения

Как пользоваться калькулятором процентного изменения?

Следуйте инструкциям ниже, чтобы найти процентное изменение с помощью калькулятора процентного изменения:

• Шаг 1 : Зайдите в онлайн-калькулятор процентного изменения Cuemath.
• Шаг 2: Введите начальное и конечное значения в поля ввода.
• Шаг 3 : Щелкните « Calculate », чтобы найти процентное изменение.
• Шаг 4 : Щелкните « Reset », чтобы очистить поля и ввести новые значения.

Как работает калькулятор процентного изменения?

Процентное изменение можно применить к любому количеству. Процентное изменение может быть как положительным, так и отрицательным значением.Положительное значение указывает на то, что количество увеличилось с течением времени. Точно так же отрицательное значение показывает, что количество уменьшилось за данный период времени. Концепция процентного изменения широко используется в сфере финансов. Банки используют процентное изменение для отслеживания цены ценной бумаги. Кроме того, процентное изменение также используется для сравнения цен различных валют. Шаги для расчета процентного изменения между старым значением и новым значением следующие:

1. Вычтите начальное значение количества из его окончательного значения.
2. Разделите значение, полученное на шаге 1, на исходное значение.
3. Умножьте результат на 100, чтобы получить процентное изменение.

Процентное изменение рассчитывается по формуле:

Процентное изменение = ((Конечное значение — Начальное значение) / начальное значение) × 100

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенные примеры процентного изменения

Пример 1: Найдите процентное изменение, если 70 увеличится до 150, и проверьте его с помощью калькулятора процентов.

Решение:

Дано: начальное значение = 70, конечное значение = 150

Процентное изменение = ((Конечное значение — Начальное значение) / начальное значение) × 100

= ((150 — 70) / 70) × 100

= (80/70) × 100

= 1. 142 × 100%

= 114,28%

Поскольку ответ положительный, это процентное увеличение.

Пример 2: Найдите процентное изменение, если количество идет от 90 до 20, и проверьте его с помощью калькулятора процентов.

Решение:

Дано: начальное значение = 90, конечное значение = 20

Процентное изменение = ((Конечное значение — Начальное значение) / начальное значение) × 100

= ((20 — 90) / 90) × 100

= (-70 / 90) × 100

= -0.7778 × 100

= -77,78%

Поскольку ответ отрицательный, это процентное уменьшение.

Точно так же вы можете попробовать калькулятор процентного изменения, чтобы найти процентное изменение для следующих значений.

• Начальное значение = 180, Конечное значение = 250
• Начальное значение = 120, Конечное значение = 100

☛ Математические калькуляторы:

Калькулятор округления

— Примеры, Онлайн-калькулятор округления

Калькулятор округления округляет число до ближайшего выбранного значения разряда. Округление чисел — это процесс, с помощью которого число можно упростить, преобразовав его в значение, к которому оно было изначально ближе.

Что такое калькулятор округления?

Калькулятор округления

— это онлайн-инструмент, который помогает округлить целое число до ближайших десятков, сотен, тысяч, десяти тысяч, сотен тысяч или миллионов разрядов. Округление числа помогает упростить вычисления за счет корректировки значений цифр. Чтобы использовать этот калькулятор округления , введите значение в поле ввода.

Калькулятор округления

* Используйте только 8 цифр.

Как пользоваться калькулятором округления?

Следуйте инструкциям ниже, чтобы использовать калькулятор округления для округления числа.

• Step 1 : Откройте онлайн-калькулятор округления Cuemath.
• Шаг 2 : Введите число в поле ввода калькулятора округления и выберите ближайшее значение места округления из раскрывающегося списка.
• Шаг 3 : Нажмите кнопку «Рассчитать» , чтобы найти значение округления в зависимости от требований.
• Шаг 4 : Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор округления?

Перед округлением значения необходимо соблюдать определенные правила. Они перечислены ниже:

• Правило 1: Любая ненулевая цифра в числе считается значащей.
• Правило 2: Любой ноль, который появляется между ненулевыми цифрами, также считается значимым.
• Правило 3: Предположим, у нас есть целое число. Ноль, помещенный справа от ненулевой цифры, имеет значение.
• Правило 4: Если мы округляем цифру, которая меньше 5, то следующая за ней цифра остается неизменной.
• Правило 5: Если мы округляем цифру, которая больше или равна 5, то следующая за ней цифра увеличивается на 1.
• Правило 6: Предположим, мы округляем цифру с более высоким разрядным значением (сотни, тысячи и т. Д.), Тогда цифры с более низким разрядным значением игнорируются.

При округлении числа получается менее точное значение. Однако это может быть полезно при выполнении расчетов, когда нам нужна оценка.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенные примеры на калькуляторе округления

Пример 1: Округлите 568 до ближайших десятков и проверьте это с помощью калькулятора округления.

Решение:

Чтобы округлить 568 до ближайших десятков, мы видим, что цифра на разряде единиц равна 8, что больше 5.

Следовательно, мы увеличиваем цифру десятков на 1 и заменяем цифру единиц на 0.

Таким образом, 568 становится 570.

Пример 2: Округлите 568 до ближайших сотен и проверьте это с помощью калькулятора округления.

Решение:

Чтобы округлить 568 до ближайших десятков, мы видим, что цифра в разряде сотен равна 5.

Увеличиваем это значение на 1 и игнорируем младшие цифры.

Таким образом, 568 становится 600.

Теперь вы можете использовать калькулятор округления и округлить следующие числа:

• 601 с точностью до сотни
• 189 с точностью до десятков
• 5271 до ближайших

☛ Математические калькуляторы:

Калькулятор интегралов

— первообразные, определенные, неопределенные интегралы

Онлайн-калькулятор интегралов поможет вам оценить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления.Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы.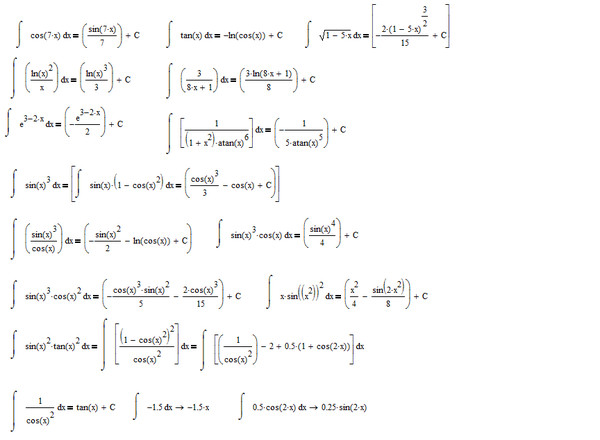 Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интеграции:

• Определенные интегралы
• Неопределенные интегралы (первообразные)

Вычисление интеграла довольно сложно решить вручную, так как оно включает в себя различные сложные формулы интегрирования. Итак, рассмотрим онлайн-программу расчета интегралов, которая решает простые и сложные функции интегралов и показывает вам пошаговые вычисления.

Итак, пришло время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читайте дальше!

Что такое интегральный?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, возникающие при объединении бесконечных данных. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

• Процесс нахождения интегралов, называемый интегрированием
• Интегрируемая функция называется подынтегральным выражением
• В интегральном представлении ∫3xdx, ∫ — символ интеграла, 3x — функция, которую нужно интегрировать, а dx — дифференциал переменной x

Где f (x) — функция, а A — площадь под кривой.Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Ну а теперь поговорим о типах интегралов:

Типы интегралов:

В принципе, есть два типа интегралов:

• Неопределенные интегралы
• Определенные интегралы

Неопределенные интегралы:

Неопределенный интеграл функции принимает первообразную другой функции. Взятие первообразной функции — самый простой способ обозначить неопределенные интегралы символами. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами.Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш онлайн-калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

• ∫1 dx = x + c
• ∫x ⁿ dx = x ^{n + 1} / n + 1 + c
• ∫a dx = ax + c
• ∫ (1 / x) dx = lnx + c
• ∫ a ^x dx = a ^x / lna + c
• ∫ e ^x dx = e ^x + c
• ∫ sinx dx = -cosx + c
• ∫ cosx dx = sinx + c
• ∫ tanx dx = — ln | cos x | + c
• ∫ cosec ² x dx = -cot x + c
• ∫ сек ² x dx = tan x + c
• ∫ cotx dx = ln | sinx | + c
• ∫ (secx) (tanx) dx = secx + c
• ∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

• ∫ 1 / (1-x ² ) ^1/2 dx = sin ^-1 x + c
• ∫ 1 / (1 + x ² ) ^1/2 dx = cos ^-1 x + c
• ∫ 1 / (1 + x ² ) dx = tan ^-1 x + c
• ∫ 1 / | x | (x ² — 1) ^1/2 dx = cos ^-1 x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную — очень сложная задача. Просто введите функцию в предназначенное для этого поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решить интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, по которым нужно рассчитывать интегралы:

• Определить функцию f (x)
• Возьмем первообразную функции
• Вычислить верхний и нижний предел функции
• Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решает первообразную заданной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x ³ + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫x ⁿ dx = x ^{n + 1} / n + 1 + c

∫ x ³ + 5x + 6 dx = x ^{3 + 1} /3 + 1 + 5 x ^{1 + 1} /1 + 1 + 6x + c

Шаг 2:

∫ x ³ + 5x + 6 dx = x ⁴ /4 + 5 x ² /2 + 6x + c

Шаг 3:

∫ x ³ + 5x + 6 dx = x ⁴ + 10x ² + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интегральные функции шаг за шагом, используя формулу интегрирования. 1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интеграции по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Рассчитайте верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) — f (б) = 1 — 0

ф (а) — ф (б) = 1

Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Входы:

• Сначала введите уравнение, которое вы хотите интегрировать
• Затем выберите зависимую переменную, участвующую в уравнении
• Выберите определенный или неопределенный интеграл на вкладке
• Если вы выбрали конкретную опцию, то вы должны ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле
• Когда закончите, пора нажать на кнопку расчета

Выходы:

Интегральный вычислитель показывает:

• Определенный интеграл
• Неопределенный интеграл
• Полные пошаговые вычисления

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл — это числовое значение, равное площади под графиком некоторой функции для некоторого интервала. Это может быть график новой функции, производная которой является исходной функцией (неопределенный интеграл). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления интегралов.Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и получите мгновенные результаты.

Что такое двойной интеграл?

Двойные интегралы — это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко вычисляет интеграл любой заданной функции шаг за шагом.

Артикул:

Из авторизованного источника Википедии: Общее представление об интегралах и их типах

С сайта mathisfun: График интегрирования и подынтегрального выражения, интегральная запись

Из истоков математики.com: Формулы от базового до продвинутого уровня для интеграции

С сайта toppr.com: повседневное использование интеграции в исчислении

Другие языки: Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 計算, 적분 계산기, Integrály Kalkulačka, Calculadora De Integral, Calculate Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integretrall,. Lommeregner, Integral Kalkulator, Integralni Kalkulator, คำนวณ อิน ทิ ก รั, Integrale Rekenmachine.