Новости математического портала mathforyou.net
19/07/19:
Добавлен калькулятор выделения полного квадрата
Данный калькулятор позволяет выделить полный квадрат для любого квадратного полинома.
26/06/19:
Калькулятор разложения в ряд Фурье
Данный калькулятор позволяет разложить функцию в ряд Фурье.
02/06/19:
Калькулятор сходимости рядов
Данный калькулятор позволяет протестировать сходимость практически любого ряда.
19/04/19:
Калькулятор тригонометрических уравнений
Данный калькулятор позволяет решать практически любые виды тригонометрических уравнений.
02/04/19:
Калькулятор длины дуги
Данный калькулятор позволяет вычислить длину дуги некоторой функции при помощи определенного интеграла.
12/07/18:
Калькулятор области определения функции
Данный калькулятор позволяет находить область определения практически любой функции.
15/05/18:
Калькулятор СЛУ методом подстановки
Данный калькулятор позволяет решать системы линейных алгебраических уравнений методом подстановки с описанием подробного
решения на русском языке.
17/04/18:
Калькулятор СЛУ методом Крамера

26/03/18:
Калькулятор экстремумов функции
С помощью данного калькулятора можно находить максимумы и минимумы функции, в том числе на заданном интервале.
23/03/18:
Бесплатное подробное решение
Теперь подробное решение для всех «наших» калькуляторов доступно совершенно БЕСПЛАТНО!
04/12/16:
Калькулятор построения графика функции
Калькулятор полностью переделан, работает в любом браузере без использования технологии Microsoft Silverlight.
12/04/16:
Расширен список бесплатных виджетов
Добавлены новые бесплатные виджеты для работы с векторами.
18/03/16:
Добавлен онлайн калькулятор для разложения вектора по базису
C помощью данного онлайн калькулятора можно бесплатно разложить вектор по заданному базису.
16/03/16:
Добавлен онлайн калькулятор для проверки образует ли система векторов базис
C помощью данного онлайн калькулятора можно бесплатно проверить образует ли система векторов базис.
10/03/16:
Добавлен онлайн калькулятор для проверки компланарности векторов
10/03/16:
Добавлен онлайн калькулятор для проверки коллинеарности векторов
C помощью данного онлайн калькулятора можно бесплатно проверить коллинеарность векторов.
06/03/16:
Добавлен онлайн калькулятор для проверки ортогональности векторов
C помощью данного онлайн калькулятора можно бесплатно проверить ортогональность векторов.
02/03/16:
Добавлен онлайн калькулятор вычисления объёма тетраэдра, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах.
02/03/16:
Добавлен онлайн калькулятор вычисления объёма параллелепипеда, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить объём параллелепипеда, построенного на векторах.
01/03/16:
Добавлен онлайн калькулятор вычисления площади параллелограмма, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить площадь параллелограмма, построенного на векторах.
01/03/16:
Добавлен онлайн калькулятор вычисления площади треугольника, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить площадь треугольника, построенного на векторах.
29/02/16:
Добавлен онлайн калькулятор умножения вектора на скаляр
C помощью данного онлайн калькулятора можно бесплатно вычислить произведение вектора на скаляр.
26/02/16:
Добавлен онлайн калькулятор вычисления проекции вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить проекцию вектора на направление другого вектора.
24/02/16:
Добавлен онлайн калькулятор направляющих косинусов вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить направляющие косинусы вектора с подробным описанием хода решения на русском языке.
19/02/16:
Добавлен онлайн калькулятор угла между векторами

19/02/16:
Добавлен онлайн калькулятор модуля (длины) вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить модуль (длину) вектора с подробным описанием хода решения на русском языке.
16/02/16:
Добавлен онлайн калькулятор разности векторов
C помощью данного онлайн калькулятора можно бесплатно вычислить разность векторов с подробным описанием хода решения на русском языке.
16/02/16:
Добавлен онлайн калькулятор смешанного произведения векторов
12/02/16:
Добавлены онлайн калькуляторы скалярного произведения векторов и векторного произведения векторов
C помощью данных онлайн калькуляторов можно бесплатно вычислять скалярное и векторное произведения векторов с подробным описанием хода решения на русском языке.
04/02/16:
Добавлен калькулятор решения уравнений онлайн
С помощью данного калькулятора, построенного на основе системы Wolfram Alpha LLC можно решать уравнения практически любых видов.
04/02/16:
Добавлен калькулятор онлайн решения неравенств
03/02/16:
Добавлен калькулятор вычисления характеристического полинома матрицы
Теперь можно вычислить характеристический полином матрицы онлайн с бесплатным описанием подробного хода решения на русском языке.
11/01/16:
Усовершенствован калькулятор вычисления определителя матрицы
Теперь можно вычислить определитель матрицы с использованием одного из двух алгоритмов: метода Гаусса и разложением
по строке или столбцу.
05/01/16: Добавлены калькуляторы вычисления cледа матрицы, транспонирования матрицы, вычисления верхнетреугольной матрицы, вычисления ранга матрицы и вычисления определителя матрицы с описанием подробного хода решения на английском языке.
02/12/15:
Добавлен калькулятор сложения векторов
На сайте появился новый раздел с калькуляторами, предназначенными для работы с векторами.
На данный момент доступен калькулятор сложения векторов. Постепенно, мы
будем добавлять новые калькуляторы для осуществления операций над векторами.
12/10/15:
Улучшен алгоритм решения кубического уравнения
В основе решения как и прежде, лежит формула Кардано, однако теперь, решение стало более подробным. Кроме того,
появилась возможность вводить дроби и параметры в качестве коэффициентов уравнения.
15/09/15:
Добавлен калькулятор вычисления корня n-ой степени из комплексного числа
Используя данные калькулятор, Вы можете вычислить корень n-ой степени из комплексного числа с использованием формулы Муавра
11/09/15:
Добавлен калькулятор конвертации формы записи комплексного числа
Теперь Вы можете найти перевести комплексное число заданное в одной из форм (алгебраической, тригонометрической или показательной) в другую форму онлайн.
Все вычисления проводятся в символьном виде, поэтому в калькулятор можно вводить не только числа или дроби, но и параметры.
08/09/15:
Добавлен калькулятор вычисления степени комплексного числа онлайн
Теперь Вы можете найти степень комплексного числа, заданного в алгебраической, тригонометрической или показательной формах. Все вычисления проводятся в
символьном виде, поэтому в калькулятор можно вводить не только числа или дроби, но и параметры.
Все вычисления проводятся в
символьном виде, поэтому в калькулятор можно вводить не только числа или дроби, но и параметры.
19/05/15:
Расширены возможности личного кабинета пользователя
Начиная с этого момента, все задания введенные Вами в калькуляторы, а также купленные подробные
решения будут доступны в личном кабинете и Вы всегда сможете просмотреть их заново, если потребуется!
07/05/15:
Добавлена возможность использовать виджеты для своего сайта
Просто скопируйте код виджета на свой сайт и получите возможность пользоваться нашими калькуляторами совершенно бесплатно!
Каталог виджетов будет постепенно обновляться. Никаких навыков программирования при этом не требуется!
22/04/15:
Улучшен алгоритм вычисления корней квадратного уравнения
Теперь, на нашем сайте квадратные уравнения решаются в символьном, т. е. в качестве коэффициентов Вы можете вводить не только
числа, но и дроби!
е. в качестве коэффициентов Вы можете вводить не только
числа, но и дроби!
09/02/15:
Добавлен калькулятор вычисления площади криволинейной трапеции
На нашем сайте Вы можете вычислить площадь криволинейной трапеции онлайн, образованной пересечением двух графиков функций.
12/01/15:
Добавлены калькуляторы вычисления асимптот функции онлайн
На нашем сайте появилась возможность вычисления горизонтальных, вертикальных и наклонных
асимптот к функции онлайн.
14/12/14:
Добавлен калькулятор вычисления суммы ряда онлайн
Теперь Вы можете легко вычислить сумму практически любого ряда онлайн с помощью нашего калькулятора.
27/06/14:
Улучшения
Исправлены мелкие ошибки, улучшена стабильность работы сайта!
17/04/14:
Возможность ввода выражений в строку
Для некоторых сервисов мы добавили возможность ввода выражений двумя способами: «обычным» — когда ввод
осуществляется с клавиатуры в строку или «улучшенным» — когда ввод осуществляется с использованием панели
математического ввода.
29/09/13:
Добавлена возможность поделиться ссылкой на введеное выражение
Если у Вас возникли проблемы с вводом своей задачи в наш онлайн калькулятор, кто-то другой может осуществить
ввод данных за Вас и отправить Вам ссылку. Вам нужно будет только перейти по ссылке и нажать кнопку равно для
получения решения!
17/08/13:
Улучшен формат отображения подробного решения для всех сервисов
Теперь математические формулы в комментариях к подробному решению отображаются четко, на одной линии с
текстом!
17/08/13:
Улучшен сервис решения производных
На нашем сайте появилась возможность вычислять подробное решение для производных высоких порядков
(до 5 порядке включительно!)
17/08/13:
Добавлено подробное решение пределов
Теперь вы можете получить подробное решение пределов на русском языке! Наш онлайн калькулятор пределов
находится на начальной стадии развития, но даже сейчас он может вычислять подробное решения для большого
количества различных пределов!
3/06/13:
Добавлен онлайн сервис вычисления производной неявной функции
Теперь на нашем сайте появилась возможность вычислять производную функции, заданной неявно.
24/05/13:
Добавлен онлайн сервис вычисления частных производных
Теперь на нашем сайте появилась возможность вычислять частные производные онлайн. Сервис позволяет
вычислять также смешанные производные и производные высоких порядков. Пример подробного решения, выдаваемого
новым сервисом, представлен здесь.
18/05/13:
Добавлен онлайн сервис вычисления параметрической производной
У нас на сайте появилась возможность найти производную от функции заданной параметрически с подробным решением.
26/04/13:
Добавлен пример подробного разложения дроби в сумму дробей
Теперь, вы можете ознакомиться с примером пошагового решения задачи разложения рациональной дроби в сумму элементарных дробей, и, если вам понравится, то купить пошаговое
решение своей задачи за минимальную цену.
12/04/13:
Добавлена теория по неопределенному интегралу
Мы добавили теоретическую информацию по свойствам неопределенного интеграла и по методу замены переменной.
12/04/13:
Улучшен алгоритм интегрирования
Мы существенно улучшили метод интегрирования по частям, используемый в нашем онлайн сервисе.
Теперь осуществляется поддержка большего количества интегралов.
14/03/13:
Добавлены примеры подробного решения производной и неопределенного интеграла
Теперь, вы можете ознакомиться с примерами пошаговых решений неопределенного интеграла и производной, и, если вам понравится, то купить пошаговое
решение своей задачи за минимальную цену.
13/03/13:
Улучшена стабильность и производительность алгоритма пошагового решения неопределенного интеграла
Теперь наш онлайн сервис работает быстро и более стабильно, а также поддерживает решение все большего количества интегралов. (1/2) пошаговое решение теперь точно такое же, как в учебниках по высшей математике!
(1/2) пошаговое решение теперь точно такое же, как в учебниках по высшей математике!
10/01/13:
Система ввода теперь доступна для решения определенных интегралов онлайн
Теперь, с помощью новой системы ввода выражений, вы сможете легко, быстро и БЕСПЛАТНО! вычислять определенные интегралы онлайн!
18/11/12:
Введена система регистрации
Введены базовые принципы системы регистрации, которая позволяет производить регистрацию и авторизацию пользователей.
В дальнейшем планируется произвести персонализацию сайта под каждого пользователя, таким образом вы сможете
настроить сайт под себя.
2/10/12:
Добален новый онлайн сервис: Решение линейных уравнений
Теперь вы можете получить бесплатное подробное решение линейных уравнений в режиме онлайн
1/10/12:
Новая форма ввода выражений доступна для вычисления предела онлайн
Панель ввода математических выражений теперь доступна для сервиса: Вычисление предела онлайн!
27/09/12:
Добавлен сервис построения уравнения нормали к графику функции
Теперь вы можете построить уравнение нормали к графику функции совершенно БЕСПЛАТНО!
20/09/12:
Добавлена справка по система ввода математических выражений
Потратьте всего 5 минут, прочитайте справку и вы поймете как пользоваться нашей уникальной системой ввода математических выражений
19/09/12:
Новая система ввода математических выражений
Для сервиса вычисление производной создана новая система ввода выражений, которая не позволит вам совершить ошибку!
19/09/12:
Подробное решение производной на русском языке совершенно БЕСПЛАТНО
Теперь подробное решение производной доступно на русском языке совершенно БЕСПЛАТНО.
15/09/12:
Новая система ввода математических выражений
Для сервиса неопределенного интеграла создана новая система ввода выражений, которая не позволит вам совершить ошибку!
15/09/12:
Подробное решение неопределенного интеграла на русском языке совершенно БЕСПЛАТНО
Теперь подробное решение неопределенного интергала доступно на русском языке совершенно БЕСПЛАТНО.
21/06/12:
Добавлена возможность решения любых дифференциальных уравнений
Теперь Вы можете решить любое дифференциальное уравнение в режиме онлайн у нас на сайте.
21/06/12:
Добавлена возможность разложения дроби в сумму простейших (элементарных) дробей
Теперь Вы можете разложить правильную дробь в сумму простейших (элементарных) дробей.
13/05/12:
Добавлена подробная справка по вводу математических выражений
Если у вас возникли проблемы с вводом математических выражений, вы всегда можете обратиться к справке.
15/04/12:
Улучшен алгоритм пошагового вычисления производной
Теперь подробное решение выводится в таком виде, как-будто бы решал человек.
17/03/12:
Добавлено пошаговое решение неопределенного интеграла и предела
Теперь Вы можете вычислить неопределенный интеграл и предел, получив при этом пошаговое решение совершенно бесплатно!
11/02/12:
Добавлено пошаговое решение производной
Теперь Вы можете вычислить производную, получив при этом пошаговое решение совершенно бесплатно!
09/02/12:
Перенос всех сервисов на html
Вся библиотека формул теперь доступна без использования технологии Microsoft Silverlight.
05/02/12:
Перенос всех сервисов на html
Все сервисы (кроме построения графиков) теперь доступны без использования технологии Microsoft Silverlight.
22/01/12:
Перенос некоторых сервисов на html
Некоторые сервисы из раздела Операции над матрицами теперь доступны без использования технологии Microsoft Silverlight.
18/12/11:
Перенос некоторых сервисов на html
Все сервисы из раздела дифференциального и интегрального исчисления теперь доступны без использования
технологии Microsoft Silverlight. Тоже самое касается решения кубических уравнений и уравнений произвольной степени.
08/12/11:
Добавлена возможность сохранения изображения построенных графиков в файл
Теперь Вы можете сохранять изображения полученных графики в файл (bmp, jpeg, png).
08/12/11:
Перенос некоторых сервисов на html
Многие сервисы (вычисление предела, производной, неопределенного интеграла, разложение функции в ряд Тейлора и решение квадратных уравнений)
теперь доступны без использования технологии Microsoft Silverlight. Т.е. теперь Вы можете использовать их с мобильного телефона!
27/11/11:
Добавлены новые формулы по пределам
На страничке пределы в разделе Библиотека формул
Вы можете ознакомиться с основными свойствами, формулами и приёмами нахождения пределов.
27/11/11:
Добавлен новый онлайн сервис — уравнение касательной к графику функции
Для получения уравнения касательной к графику функции Вам необходимо ввести функцию и абсциссу точки в
которой нужно получить уравнение касательной. Далее программа выдаст Вам результат.
Далее программа выдаст Вам результат.
27/11/11:
Добавлен новый онлайн сервис — разложение функции в ряд Тейлора (Маклорена)
Для вычисления разложения функции в ряд Тейлора (Маклорена) Вам необходимо ввести функцию и точку в окрестности
которой нужно разложить функцию. Вы можете также указать порядок степени до которой выполнять разложение.
Далее программа выдаст Вам результат.
27/11/11:
Улучшен сервис — вычисление неопределенного интеграла
Теперь, при вычислении неопределенного интеграла Вы можете получить подробное, пошаговое
решение. Однако, это работает только в некоторых случаях, если шагов не очень много.
27/11/11:
Добавлена страничка новостей
На страничке новостей, Вы можете проследить историю развития проекта mathforyou. net с момента его создания.
net с момента его создания.
16/11/11:
Добавлен новый онлайн сервис — вычисление предела
Для вычисления предела Вам нужно всего лишь ввести функцию и точку к которой стремится
переменная этой функции. Далее программа выдаст Вам результат.
13/11/11:
Создана страница и
группа
нашего сайта ВКонтакте. Приглашаем всех желающих на
страничку нашего сайта
ВКонтакте, где можно задать интересующие вопросы, получить помощь в решении задач по математике, выдвинуть предложения по улучшению
онлайн сервисов, и т.д.
11/11/11:
Добавлен новый онлайн сервис — вычисление определенного интеграла
Для вычисления определенного интеграла Вам необходимо ввести функцию и пределы интегрирования. Далее программа выдаст Вам результат.
Далее программа выдаст Вам результат.
06/11/11:
Добавлен новый онлайн сервис — вычисление неопределенного интеграла
Для вычисления неопределенного интеграла Вам необходимо всего лишь ввести функцию. Далее программа выдаст Вам результат.
03/11/11:
Добавлен новый онлайн сервис — вычисление производной
Для вычисления производной Вам необходимо всего лишь ввести функцию. Далее программа выдаст Вам результат.
31/05/11:
Улучшен сервис решения систем линейных уравнений
В отличие от большинства онлайн сервисов на других сайтах, которые могут решать СЛАУ лишь при условии, когда количество уравнений равно количеству переменных,
наш онлайн сервис позволяет решать совершенно любые СЛАУ. Т.е. не важно сколько у Вас уравнений и сколько переменных, Вы все равно получите решение. Рассмотрены
варианты, когда имеется бесконечное множество решений. В этом случае программа автоматически определяет базисные и небазисные переменные, и соответствующим образом
выражает конечный результат.
Рассмотрены
варианты, когда имеется бесконечное множество решений. В этом случае программа автоматически определяет базисные и небазисные переменные, и соответствующим образом
выражает конечный результат.
Для получения решения Вам нужно выбрать количество уравнений, количество переменных и ввести данные. Далее программа сама проанализирует различные варианты и выдаст
Вам подробное решение.
02/05/11:
Добавлен новый сервис: вычисление собственных чисел и собственных векторов матрицы
Для нахождения собственных чисел квадратной матрицы, Вам необходимо ввести матрицу и нажать кнопку получить решение. Далее программа выдаст Вам пошаговое решение в
котором на первом этапе будет получен характеристический полином, затем будут найдены его корни (собственные числа) и собственные вектора.
21/04/11:
Запущен новый математический портал mathforyou. net
net
Математический портал онлайн решений задач по математике mathforyou.net — некоммерческий проект, призванный помочь школьникам и студентам в освоении некоторых разделов математики путем решения задач в режими онлайн.
Решение уравнений методом обратной матрицы
Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.
Суть метода
Пусть задана система линейных уравнений с неизвестными:
Эту систему можно записать в виде матричного уравнения ,
где – матрица системы,
– столбец неизвестных,
– столбец свободных коэффициентов.
Из полученного матричного уравнения необходимо выразить . Для этого умножим обе части матричного уравнения слева на , получим:
Так как , то или .
Далее находится обратная матрица и умножается на столбец свободных членов .
Пример решения методом обратной матрицы
ПРИМЕР 1| Задание | Решить систему линейных уравнений методом обратной матрицы
|
| Решение | Данная система уравнений может быть записана матричным уравнением
где , , . Выразив из этого уравнения , получим
Найдем определитель матрицы :
Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы. Найдем обратную матрицу с помощью союзной матрицы.
Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы :
Далее запишем обратную матрицу согласно формуле . Будем иметь:
Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы:
|
| Ответ |
Умножение матрицы на вектор
Ранг матрицы
Вычитание матриц
Перемножение матриц
Элементарные преобразования матриц
Операции над матрицами и их свойства
%d0%9c%d0%b0%d1%82%d1%80%d0%b8%d1%87%d0%bd%d1%8b%d0%b9+%d0%ba%d0%b0%d0%bb%d1%8c%d0%ba%d1%83%d0%bb%d1%8f%d1%82%d0%be%d1%80 — Restauranteroberto
%d1%82%d0%b5%d0%b1%d0%b5+%d1%80%d0%be%d0%b4%d0%bd%d0%b0%d1%8f
Date: Sun, 19 Dec 2021 22:14:57 +0000 (GMT) Message-ID: [email protected]> Subject: Exported From Confluence MIME-Version: 1. 0 Content-Type … =D0=94=D0=BE=D0=BA=D1=83=D0=BC=D0=B5=D0=BD=D1=82 … Просмотр исходного текста страницы Программы для … Wikipedia:CHECKWIKI/WPC 091 dump This page contains a dump analysis for errors #91 (Interwiki link written as an external link or used as a reference.).. It can be generated using WPCleaner by any user. It’s possible to update this page by following the procedure below: Download the file enwiki-YYYYMMDD-pages-articles.xml.bz2 from the most recent dump. For example, on your.org, go to directory … YouTube Kids Holiday Music Collab — Shooting Stars (Original Song performed at YouTube Space LA)-1j-WPS0kAC8 MediaWiki:Robots.txt — Википедия У вас нет прав на редактирование этой страницы по следующей причине: MediaWiki:Robots.txt. Материал из Википедии — свободной энциклопедии. Перейти к навигации Перейти к поиску.
0 Content-Type … =D0=94=D0=BE=D0=BA=D1=83=D0=BC=D0=B5=D0=BD=D1=82 … Просмотр исходного текста страницы Программы для … Wikipedia:CHECKWIKI/WPC 091 dump This page contains a dump analysis for errors #91 (Interwiki link written as an external link or used as a reference.).. It can be generated using WPCleaner by any user. It’s possible to update this page by following the procedure below: Download the file enwiki-YYYYMMDD-pages-articles.xml.bz2 from the most recent dump. For example, on your.org, go to directory … YouTube Kids Holiday Music Collab — Shooting Stars (Original Song performed at YouTube Space LA)-1j-WPS0kAC8 MediaWiki:Robots.txt — Википедия У вас нет прав на редактирование этой страницы по следующей причине: MediaWiki:Robots.txt. Материал из Википедии — свободной энциклопедии. Перейти к навигации Перейти к поиску.
Как выкачать верстку из письма? — Хабр Q&A
Charcoal: Dark Mode for Messenger. 217. Реклама. Доб. Переключить веб-сайт, который вы хотите в темном режиме. Темный режим поможет … =D0=98=D1=81=D0=BF=D0=BE=D0=BB=D1=8C=D0=B7=D0=BE=D0=B2=D0 … Дмитрий Иванович Менделеев родился 27 января ( 8 февраля ) 1834 года в Тобольске в семье Ивана Павловича Менделеева, в то время занимавшего должность директора Тобольской гимназии и училищ … Date: Thu, 16 Dec 2021 05:50:38 +0000 (UTC) Message-ID: [email protected]> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type … Менделеев, Дмитрий Иванович — Википедия A website I am working on is displaying Crylic characters incorrectly. I don’t know why. It doesn’t appear to be a character encoding problem. The page title is … Stack Overflow Message-ID: [email protected]> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type: multipart/related; boundary … Разблокировать сайт Одноклассники ру
Темный режим поможет … =D0=98=D1=81=D0=BF=D0=BE=D0=BB=D1=8C=D0=B7=D0=BE=D0=B2=D0 … Дмитрий Иванович Менделеев родился 27 января ( 8 февраля ) 1834 года в Тобольске в семье Ивана Павловича Менделеева, в то время занимавшего должность директора Тобольской гимназии и училищ … Date: Thu, 16 Dec 2021 05:50:38 +0000 (UTC) Message-ID: [email protected]> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type … Менделеев, Дмитрий Иванович — Википедия A website I am working on is displaying Crylic characters incorrectly. I don’t know why. It doesn’t appear to be a character encoding problem. The page title is … Stack Overflow Message-ID: [email protected]> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type: multipart/related; boundary … Разблокировать сайт Одноклассники ру
%D0%BB%D1%83%D1%87%D1%88%D0%B8%D0%B9 …
cyclebase mu61 おなまえ: Eメール: 題 名: メッセージ 25 Best Christmas Gifts That You Can Buy for Under $100 — 1breakingnews.com %D0%A1%D0%B0%D0%BC%D0%B0%D1%80 Turn Off the Lights. 35,826. Ad. Added. Shades Chrome to a soothing orange color to decrease eye-strain, eye fatigue and to appease your brain’s day/night cycle. Message-ID: [email protected]duction> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type: multipart … Кропивач, на зв’язку можливо жид. Власне, суть в тому, що по батьковій лінії в мене в роду можливо були жиди. Для того, щоб дізнатись чи точно це так, мені потрібно покопатись в відсканованих переписах населення УРСР … =D0=92=D0=BD=D1=83=D1=82=D1=80=D0=B8 … Кропивач, на зв’язку можливо жид. Власне, суть в тому, що …
35,826. Ad. Added. Shades Chrome to a soothing orange color to decrease eye-strain, eye fatigue and to appease your brain’s day/night cycle. Message-ID: [email protected]duction> Subject: Exported From Confluence MIME-Version: 1.0 Content-Type: multipart … Кропивач, на зв’язку можливо жид. Власне, суть в тому, що по батьковій лінії в мене в роду можливо були жиди. Для того, щоб дізнатись чи точно це так, мені потрібно покопатись в відсканованих переписах населення УРСР … =D0=92=D0=BD=D1=83=D1=82=D1=80=D0=B8 … Кропивач, на зв’язку можливо жид. Власне, суть в тому, що …
Search the world’s information, including webpages, images, videos and more. Google has many special features to help you find exactly what you’re looking for. Пренебрегва се фактът, че на над 80% от територията на Българското землище, няма никакви археологически артефакти останали от прабългарите, а … About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators . .. Как выкачать верстку из письма? — Хабр Q&A %d1%82%d0%b5%d0%b1%d0%b5+%d1%80%d0%be%d0%b4%d0%bd%d0%b0%d1%8f %D0%BB%D1%83%D1%87%D1%88%D0%B8%D0%B9 … Антропологични и генетични проучвания на българите … Created with Aximedia Slide Show Creator. Download this app: https://play.google.com/store/apps/details?id=com.amem На емеил приходят множество писем. как выкачать оригинал верстки из письма? если попросить браузер показать свойства письма выходит вот такая чепуха=d0=94=d0=be=d0=b1=d1=80=d1=8b=d0=b9 =d0=b4=d0=b5=d0=bd=d1=8c! =d0=9f=d1=80=d0=b5=d0=b7=d0=b5=d0=bd=d1=82=d0=b0=d1=86=d0 …
.. Как выкачать верстку из письма? — Хабр Q&A %d1%82%d0%b5%d0%b1%d0%b5+%d1%80%d0%be%d0%b4%d0%bd%d0%b0%d1%8f %D0%BB%D1%83%D1%87%D1%88%D0%B8%D0%B9 … Антропологични и генетични проучвания на българите … Created with Aximedia Slide Show Creator. Download this app: https://play.google.com/store/apps/details?id=com.amem На емеил приходят множество писем. как выкачать оригинал верстки из письма? если попросить браузер показать свойства письма выходит вот такая чепуха=d0=94=d0=be=d0=b1=d1=80=d1=8b=d0=b9 =d0=b4=d0=b5=d0=bd=d1=8c! =d0=9f=d1=80=d0=b5=d0=b7=d0=b5=d0=bd=d1=82=d0=b0=d1=86=d0 …
Калькулятор исключения Гаусса Джордана для сокращения строк
Введение в калькулятор исключения Гаусса Джордана
Калькулятор исключения Гаусса-Иордана упрощает любую матрицу в виде сокращения строк с помощью метода исключения Гаусс-Иордана. Калькулятор Гаусса Джордана поможет рассчитать линейное уравнение в режиме онлайн, не тратя время на ручные вычисления.
Калькулятор исключения Гаусса требует только ввести вашу расширенную матрицу в терминах ввода. После того, как вы ввели свой ввод, онлайн-инструмент предоставит вам точный результат с подробными инструкциями. Матрицы, образующие систему линейных уравнений, легко решаются пошаговыми вычислениями.
После того, как вы ввели свой ввод, онлайн-инструмент предоставит вам точный результат с подробными инструкциями. Матрицы, образующие систему линейных уравнений, легко решаются пошаговыми вычислениями.
Таким образом, калькулятор исключения Гаусса-Иордана — лучший вариант, если ваше решение требует преобразования матрицы в сокращенную форму эшелона строк. Чтобы сократить ваши линейные уравнения онлайн, калькулятор исключения поможет наиболее эффективно.
Метод исключения Гаусса Джордана также используется для определения ранга матриц.Таким образом, вы также можете использовать наш калькулятор рангов матрицы для сортировки запросов к матрице.
Как пользоваться калькулятором исключения Гаусса Джордана?
Калькулятор сокращения строк по Гаусс-Иордану — это простой в использовании онлайн-инструмент для преобразования линейных уравнений в сокращенную форму эшелона строк. Поскольку его ручные вычисления довольно сложны и требуют длительных математических операций, этот калькулятор исключения Гаусса экономит время и обеспечивает точные результаты.
Калькулятор исключения Гаусса Иордана прост и удобен в использовании.Все, что вам нужно сделать, это ввести свою матрицу и получить результаты с помощью шагов. Просто выполните следующие действия, чтобы уравнение решалось с помощью калькулятора исключения. Эти шаги следующие:
Введите ввод
При использовании калькулятора исключения Гаусса из Калькуляторов матриц вам нужно только ввести входные данные вашей расширенной матрицы. Эти входные данные включают размеры и коэффициенты матриц.
Предоставить матричный заказ
Прежде всего, введите порядок вашей матрицы в качестве первого ввода в калькуляторе gauss jordan.Расширенная матрица, введенная для устранения Гаусса Иордана, может иметь размеры до 4×4 в этом онлайн-инструменте.
Введите коэффициенты матрицы
После добавления правильного порядка соответствующей матрицы введите элементы матрицы. Поскольку расширенная матрица содержит коэффициенты в качестве элементов, вводите ее коэффициенты один за другим.
Связано: Кроме этого, вы также можете использовать Матричный калькулятор, чтобы получить матрицу кофакторов A.
Выходы
При вводе входных данных, требуемых калькулятором метода исключения, вам будет предоставлена сокращенная форма строки в качестве выходных данных.Поэтому для получения результатов вам просто нужно нажать на кнопку «Рассчитать». В мгновение ока вам будет предоставлен окончательный результат, включая каждый шаг, сделанный для решения линейного уравнения.
Эта простая процедура делает его одним из самых точных и быстрых калькуляторов, которые вы найдете в Интернете.
Связано: На этом веб-сайте калькулятора матричного решения предлагается множество онлайн-калькуляторов, упрощающих матричные операции. Вы можете использовать калькулятор детерминантной матрицы для линейного преобразования.
Часто задаваемые вопросы
Как преобразовать линейное уравнение в сокращенную форму строки?
Онлайн-калькулятор исключения Гаусса может легко преобразовать любое линейное уравнение в форме расширенной матрицы в сокращенную форму эшелона строк с помощью строковых операций.
Для дополнительных целей вы также можете использовать калькулятор сокращенной формы строки, чтобы получить форму сокращения ступени строки онлайн.
Каков упрощенный метод выполнения строковых операций над расширенными матрицами?
Операции со строками выполняются для преобразования матриц в сокращенную форму строк, что требует сложных операций и длительных вычислений.Использование калькулятора Гаусса-Джордана — самый простой способ выполнять операции со строками над расширенными матрицами.
Как я могу решить метод исключения Гаусса?
Вы можете решить метод исключения Гаусса вручную или в режиме онлайн. Для ручных вычислений вам нужно потратить много времени, и поэтому калькулятор исключения Гаусса так полезен. Это позволяет вам вычислять любое уравнение, имеющее операции со строками. Эти операции со строками приводят к уменьшенной форме эшелона строк в расширенную матрицу.
Надеемся, вам понравился наш калькулятор. Есть много других связанных калькуляторов, которые вы можете использовать, например, калькулятор сложения матриц и калькулятор вычитания матриц — лучший вариант для решения основных матричных операций.
Джеймс Джонсон — Обновлено 11 ноября 2021 г.
3.3: Решение систем с исключением Гаусса-Джордана
Цели обучения
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Решите систему линейных уравнений с помощью матриц и графического калькулятора.
- Решайте финансовые приложения с помощью матриц и графического калькулятора.
Необходимые навыки
Перед тем, как начать, пройдите предварительный тест.
Введите в калькулятор следующие матрицы и затем выполните указанные операции. Если операция не может быть проведена, укажите причину.
\ (A = \ begin {bmatrix} 5 & 1 & -2 \\ 2 & 6 & 7 \\ 4 & 1 & −5 \ end {bmatrix} \), \ (B = \ begin {bmatrix} 3 & -7 \\ 0 & 1 \\ 2 & −8 \ end {bmatrix} \), \ (C = \ begin {bmatrix} 9 & 4 \\ 6 & -5 \\ 7 & −1 \ end {bmatrix} \)
а.\ (А \ cdot B \)
г. \ (B \ cdot A \)
\ (B \ cdot A \)
г. \ (4B-2C \)
г. \ (А + С \)
- Нажмите здесь, чтобы проверить свой ответ
а. \ (\ begin {bmatrix} 11 & -18 \\ 20 & -64 \\ 2 & 13 \ end {bmatrix} \)
г. Не определено, поскольку количество столбцов в матрице \ (B \) не соответствует количеству строк в матрице \ (A \).
г. \ (\ begin {bmatrix} -6 & -36 \\ — 12 & 14 \\ — 6 & −30 \ end {bmatrix} \)
г.{th} \) века, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Рисунок \ (\ PageIndex {1} \): немецкий математик Карл Фридрих Гаусс (1777–1855).Ранее в этой главе мы исследовали методы решения систем уравнений.В этом разделе мы изучим другую технику решения систем, на этот раз с использованием матриц.

Расширенные матрицы
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .
Например, рассмотрим следующую систему уравнений \ (2 × 2 \).
\ [\ begin {align *} 3x + 4y & = 7 \\ 4x-2y & = 5 \ end {align *} \]
Мы можем записать эту систему в виде расширенной матрицы:
\ (\ left [\ begin {array} {cc | c} 3 & 4 & 7 \\ 4 & -2 & 5 \ end {array} \ right] \)
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .
\ (\ begin {bmatrix} 3 & 4 \\ 4 & −2 \ end {bmatrix} \)
Система уравнений три на три , например
\ [\ begin {align *} 3x-y-z & = 0 \\ x + y & = 5 \\ 2x-3z & = 2 \ end {align *} \]
имеет матрицу коэффициентов
\ (\ begin {bmatrix} 3 & −1 & −1 \\ 1 & 1 & 0 \\ 2 & 0 & −3 \ end {bmatrix} \)
и представлена расширенной матрицей
\ (\ left [\ begin {array} {ccc | c} 3 & −1 & −1 & 0 \\ 1 & 1 & 0 & 5 \\ 2 & 0 & −3 & 2 \ end {array} \ right] \)
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: \ (x \) — члены идут в первый столбец, \ (y \) — термины во втором столбце, и \ (z \) — термины в третьем столбце.
 Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).
Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).Как: по системе уравнений написать расширенную матрицу
- Запишите коэффициенты членов \ (x \) как числа в первом столбце.
- Запишите коэффициенты членов \ (y \) в виде чисел во втором столбце.
- Если есть \ (z \) — члены, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Пример \ (\ PageIndex {1} \): написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
\ [\ begin {align *} x + 2y-z & = 3 \\ 2x-y + 2z & = 6 \\ x-3y + 3z & = 4 \ end {align *} \]
Решение
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

\ (\ left [\ begin {array} {ccc | c} 1 & 2 & −1 & 3 \\ 2 & −1 & 2 & 6 \\ 1 & −3 & 3 & 4 \ end {array} \ right] \)
Упражнение \ (\ PageIndex {1} \)
Запишите расширенную матрицу данной системы уравнений.
\ [\ begin {align *} 4x-3y & = 11 \\ 3x + 2y & = 4 \ end {align *} \]
- Ответ
\ (\ left [\ begin {array} {cc | c} 4 & −3 & 11 \\ 3 & 2 & 4 \ end {array} \ right] \)
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Пример \ (\ PageIndex {2} \): Написание системы уравнений из расширенной матричной формы
Найдите систему уравнений из расширенной матрицы.

\ (\ left [\ begin {array} {ccc | c} 1 & −3 & −5 & -2 \\ 2 & −5 & −4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \)
Решение
Когда столбцы представляют переменные \ (x \), \ (y \) и \ (z \),
\ [\ left [\ begin {array} {ccc | c} 1 & -3 & -5 & -2 \\ 2 & -5 & -4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \ rightarrow \ begin {align *} x-3y-5z & = -2 \\ 2x-5y-4z & = 5 \\ -3x + 5y + 4z & = 6 \ end {align *} \]
Упражнение \ (\ PageIndex {2} \)
Напишите систему уравнений из расширенной матрицы.
\ (\ left [\ begin {array} {ccc | c} 1 & -1 & 1 & 5 \\ 2 & -1 & 3 & 1 \\ 0 & 1 & 1 & -9 \ end {array} \ right] \)
- Ответ
\ (\ begin {align *} x-y + z & = 5 \\ 2x-y + 3z & = 1 \\ y + z & = -9 \ end {align *} \)
Пониженная форма рядового эшелона
Чтобы решить систему уравнений, мы хотим преобразовать ее матрицу в сокращенную форму строки , в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла, а нули в каждое положение выше и ниже главной диагонали, как показано.

Уменьшенная форма строки-эшелона \ (\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)
Следующие расширенные матрицы представлены в сокращенной форме строки-эшелона.
\ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)
Следующие расширенные матрицы не являются сокращенно-эшелонированной формой.
\ (\ left [\ begin {array} {cc | c} 2 & 4 & -6 \\ 4 & 0 & 7 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 0 & 2 & 3 & 3 \\ 1 & 5 & 0 & 2 \\ 0 & 0 & 1 & 0 \ end {array} \ right] \)
Пример \ (\ PageIndex {3} \): матрицы в сокращенной форме строки-эшелона
Запишите систему уравнений из каждой из матриц в приведенной строчно-эшелонированной форме сверху. В чем преимущество этой формы?
а. \ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \)
г.
 \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)
\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)Решение
а. \ (\ begin {align *} x = -2 \\ y = 5 \ end {align *} \)
г. \ (\ begin {align *} x = 4 \\ y = 3 \\ z = 2 \ end {align *} \)
Преимущество сокращенной формы строки-эшелон состоит в том, что решение системы уравнений приводится в правом столбце.
УСТРАНЕНИЕ ПО ГАУСС-ИОРДАНИИ
Метод исключения Гаусса-Жордана относится к стратегии, используемой для получения уменьшенной строковой формы матрицы.Цель состоит в том, чтобы записать матрицу \ (A \) с числом \ (1 \) в качестве записи вниз по главной диагонали и иметь все нули сверху и снизу.
\ (A = \ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \ end {bmatrix} \ xrightarrow {После \ space Gauss-Jordan \ space elimination} A = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)
Мы можем выполнить операций со строками над матрицей, например сложение, умножение на константу и перестановку строк, чтобы создать сокращенную форму строки-эшелон.
 Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.
Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.Решение систем уравнений с исключением Гаусса-Жордана
В рамках этого курса мы продемонстрируем, как найти сокращенную форму строки-эшелон в графическом калькуляторе.
Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохранить расширенную матрицу как матричную переменную \ ([A], [B], [C] ,… \)
Press 2 nd MATRIX. На экране появится меню «Матрица». Дважды нажмите кнопку со стрелкой вправо, чтобы выбрать меню ПРАВКА. В меню EDIT используйте стрелку вниз для перемещения курсора, чтобы выбрать желаемое имя матрицы из меню, и нажмите ENTER. Появится экран ввода матрицы.
Введите размеры общего размера матрицы в виде строк \ (\ times \) столбцов. Введите количество строк, нажмите ENTER, введите количество столбцов и снова нажмите ENTER.
 Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.
Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.Введите элементы матрицы, нажимайте ENTER после каждого. Курсор перемещается по матрице, перемещаясь по каждой строке слева направо, а затем вниз к следующей строке.Использование клавиш со стрелками для перемещения курсора вместо нажатия ENTER может привести к тому, что значение не будет сохранено в памяти калькулятора.
Нажмите 2 nd QUIT, чтобы завершить процесс сохранения и вернуться на главный экран.
- Используйте функцию rref (в калькуляторе, чтобы найти сокращенную форму строки-эшелона матрицы.

На главном экране нажмите 2 nd MATRIX.Используйте стрелку вправо один раз, чтобы перейти в меню МАТЕМАТИКА.
Прокрутите вниз (или вверх) до rref (, стараясь не выбрать ref (, и нажмите ENTER.
Снова нажмите 2 nd MATRIX и используйте стрелку вниз (при необходимости) для выбора имени матрицы и нажмите ENTER.
Нажмите ENTER, чтобы завершить операцию.
- Если существует сокращенная форма строки-эшелона матрицы, калькулятор отобразит ее на главном экране. ×
Пример \ (\ PageIndex {4} \): решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
\ [\ begin {align *} 6x + 4y + 3z & = -6 \\ x + 2y + z & = \ dfrac {1} {3} \\ -12x-10y-7z & = 11 \ end {align *} \ ]
Решение
Напишите расширенную матрицу для системы уравнений.

\ (\ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).
\ ([A] = \ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)
Используйте функцию rref ( в калькуляторе, вызывая матричную переменную \ ([A] \).
rref ([A])
Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.
Оценить
\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & — \ dfrac {2} {3} \\ 0 & 1 & 0 & \ dfrac {5} {2} \\ 0 & 0 & 1 & — 4 \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = — \ dfrac {2} {3} \\ y + 0z & = \ dfrac {5} {2 } \\ z & = -4 \ end {align *}} \ end {array} \]
Таким образом, решение, которое легко найти в правом столбце приведенной строковой формы матрицы, будет \ (\ left (- \ dfrac {2} {3}, \ dfrac {5} {2}, −4 \ справа) \).

Упражнение \ (\ PageIndex {3} \)
Решите систему уравнений.
\ [\ begin {align *} 4x-7y + 2z & = -5 \\ -x + 3y-8z & = -10 \\ -5x-4y + 6z & = 19 \ end {align *} \]
- Ответ
Напишите расширенную матрицу для системы уравнений.
\ (\ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).
\ ([A] = \ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)
Используйте функцию rref ( в калькуляторе, вызывая матричную переменную \ ([A] \).
rref ([A])
Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.
Оценить
\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \ dfrac {3} {2} \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = -2 \\ y + 0z & = 0 \\ z & = \ dfrac {3} {2} \ end {align *}} \ end {array} \]
Таким образом, решение, которое можно легко прочитать из правого столбца приведенной строковой формы матрицы, будет \ (\ left (-2, 0, \ dfrac {3} {2} \ right) \).

Пример \ (\ PageIndex {5} \): применение матриц \ (2 × 2 \) к финансам
Кэролайн инвестирует в общей сложности \ (12 000 долларов) в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил \ (1335 долларов). Сколько было вложено по каждой ставке?
Решение
У нас есть система двух уравнений с двумя переменными. Пусть \ (x = \) сумма, инвестированная под 10,5% годовых, а \ (y = \) сумма, инвестированная под 12%.
\ [\ begin {align *} x + y & = 12,000 \\ 0,105x + 0,12y & = 1,335 \ end {align *} \]
В качестве матрицы имеем
\ (\ left [\ begin {array} {cc | c} 1 & 1 & 12,000 \\ 0.105 & 0.12 & 1335 \ end {array} \ right] \)
Введите эту матрицу как матричную переменную \ ([A] \). Используйте rref (функция , вызывающая матричную переменную \ ([A] \).
rref ([A])
\ (\ left [\ begin {array} {cc | c} 1 & 0 & 7000 \\ 0 & 1 & 5000 \ end {array} \ right] \)
Таким образом, \ ($ 7000 \) было инвестировано по ставке 10.
 5% годовых и \ (5000 долларов \) под 12% годовых.
5% годовых и \ (5000 долларов \) под 12% годовых.Пример \ (\ PageIndex {6} \): применение матриц \ (3 × 3 \) к финансам
Ava инвестирует в общей сложности \ (10 000 долларов США) в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил \ (770 долларов \). Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Решение
У нас есть система трех уравнений с тремя переменными.Пусть \ (x \) будет сумма, инвестированная под 5% годовых, пусть \ (y \) будет суммой, инвестированной под 8%, и пусть \ (z \) будет суммой, инвестированной под 9%. Таким образом,
\ [\ begin {align *} x + y + z & = 10,000 \\ 0,05x + 0,08y + 0,09z & = 770 \\ 2x-z & = 0 \ end {align *} \]
В качестве матрицы имеем
\ (\ left [\ begin {array} {ccc | c} 1 & 1 & 1 & 10,000 \\ 0,05 & 0,08 & 0,09 & 770 \\ 2 & 0 & -1 & 0 \ end {array} \ right] \)
Введите эту матрицу как матричную переменную \ ([A] \).
 Используйте rref (функция , вызывающая матричную переменную \ ([A] \).
Используйте rref (функция , вызывающая матричную переменную \ ([A] \).rref ([A])
\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 3000 \\ 0 & 1 & 0 & 1000 \\ 0 & 0 & 1 & 6000 \ end {array} \ right] \)
Ответ: \ (3000 долларов \) вложены под 5%, \ (1000 долларов \) вложены под 8%, и \ (6000 долларов \) инвестированы под 9%.
Упражнение \ (\ PageIndex {4} \)
Небольшая обувная компания взяла ссуду в размере \ (1 500 000 долларов) на расширение своих запасов.Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла \ (130 500 долларов США). Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.
- Ответ
\ (150 000 долларов \) под 7%, \ (750 000 долларов \) под 8%, \ (600 000 долларов \) под 10%
СМИ
Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в решении систем линейных уравнений с использованием исключения Гаусса.

Ключевые концепции
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений. См. Пример \ (\ PageIndex {1} \).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. Пример \ (\ PageIndex {2} \).
- Мы можем использовать метод исключения Гаусса-Жордана для решения системы уравнений. См. Пример \ (\ PageIndex {4} \).
- Многие реальные проблемы можно решить с помощью расширенных матриц.См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).
Авторы и авторство
Решающих систем с исключением по Гауссу — Precalculus
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполнение операций со строками в матрице.

- Решите систему линейных уравнений с помощью матриц.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18 — начале 19 века, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.
 Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термы идут в первый столбец, — -термы во втором столбце и z -термы в третьем столбце.Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.

Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x как числа в первом столбце.
- Запишите коэффициенты членов y в виде чисел во втором столбце.
- Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Запишите расширенную матрицу данной системы уравнений.
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.
 Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение операций со строками в матрице — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.
 Вот рекомендации по получению формы рядного эшелона.
Вот рекомендации по получению формы рядного эшелона.- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение 🙂
- Умножьте строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными.
 С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели по написанию матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.
С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели по написанию матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения многоуровневой формы матрицы. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Учитывая расширенную матрицу, выполните операции со строками, чтобы получить форму строки-эшелона.
- Первое уравнение должно иметь старший коэффициент 1.
 Поменяйте местами строки или умножьте на константу, если необходимо.
Поменяйте местами строки или умножьте на константу, если необходимо. - Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули в столбце 2 под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу не останутся только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решите данную систему методом исключения Гаусса.
Решите данную систему методом исключения Гаусса.
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений.

Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon
Выполняет строковые операции с заданной матрицей для получения формы «строка-эшелон».
Запишите систему уравнений в виде строк.
Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.

Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Решите систему, используя матрицы.
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Для данной системы уравнений решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.
Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%.
 Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?
Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 фунтов стерлингов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
В третьей строке указано usthus
.Вторая строка говорит нам, что подставляя мы получаем
Первая строка говорит нам, что подставляем и получаем
Ответ: 3000 евро вложены под 5%, 1000 евро вложены под 8% и 6000 евро вложены под 9%.

Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 фунтов стерлингов. Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.
? 150 000 при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%
Ключевые концепции
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений.См. (Рисунок).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений.
 См. (Рисунок), (Рисунок) и (Рисунок).
См. (Рисунок), (Рисунок) и (Рисунок). - Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме дополненной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратный заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Словесный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.

Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
.Нет, существует множество правильных методов использования строковых операций над матрицей.Двумя возможными способами являются следующие: (1) Поменяйте местами строки 1 и 2. Затем (2) Затем разделите строку 1 на 9.
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
Алгебраические
Для следующих упражнений напишите расширенную матрицу для линейной системы.

Для следующих упражнений напишите линейную систему из расширенной матрицы.
Для следующих упражнений решите систему методом исключения Гаусса.
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.

Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если шоколадный ароматизатор в 3 раза популярнее ванильного аромата, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата — 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
860 красный бархат, 1340 шоколад
Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой — с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?
Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2.
 Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.4% на счет 1, 6% на счет 2
Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Производителю это обходится в 180 фунтов стерлингов за велосипед плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по 86 фунтов стерлингов каждый, с оплатой доставки в размере 9 200 фунтов стерлингов, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать плату за пылесосы?
Три самых популярных вкуса мороженого — это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого.
 Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ванильный, шоколадный и клубничный вкусы?
Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ванильный, шоколадный и клубничный вкусы?В магазине мороженого возрастает спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы увеличились на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
Банан составлял 3%, тыква — 7%, а каменистая дорога — 2%
Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек.
 Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
100 миндальных орехов, 200 кешью, 600 фисташек
Глоссарий
- дополненная матрица
- матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Исключение по Гауссу
- с использованием элементарных операций со строками для получения матрицы в виде эшелона строки
- главная диагональ
- запись из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент строки
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой, умножение строки на константу, перестановка строк и т.
 Д. С целью получения формы «строка-эшелон»
Д. С целью получения формы «строка-эшелон»
LU — высокоточный расчет
- Цель использования
- Проверка результатов личного вычисления
[1] 2021/12/07 05:15 До 20 лет / старшая школа / университет / аспирант / очень /
- Цель использования
- Двойная проверка функции, которую я сделал для задания
[2] 2021/10/14 08:42 Уровень 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Решающие упражнения
[3] 2021/06/12 00:29 До 20 лет / Старшая школа / Университет / Аспирант / Очень /
- Цель использования
- Коррекция университетских дополнительных упражнений
- Комментарий / Запрос
- Лучший калькулятор, но я не нахожу шагов.Если нет, то это единственная проблема.
[4] 2021/03/08 19:44 До 20 лет / Старшая школа / ВУЗ / Аспирант / Очень /
- Цель использования
- Проверьте мои расчеты и найдите мои ошибки!
[5] 2020/11/23 08:23 Уровень 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- проверка результатов 🙂
[6] 2020/11/06 03:00 Уровень 20 лет / Средняя школа / Вуз / аспирант / Полезно /
- Цель использования
- решение вопросов
[7] 2020 / 10/15 15:14 Уровень 20 лет / Инженер / Очень /
- Цель использования
- Практика для моего класса вычислительной математики, а также для проверки модульных тестов для моего собственного алгоритма.

[8] 2020/07/26 18:33 Уровень 20 лет / Средняя школа / Университет / аспирант / Very /
- Цель использования
- проверка ответов после выполнения вручную
- Комментарий / запрос
- было бы здорово иметь два отдельных набора ответов. Один с частичным поворотом, другой без
[9] 2020/07/23 22:57 Уровень 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я получаю высшее образование
- Комментарий / запрос
- Было бы здорово, если бы Этапы также были показаны в расчетах.
[10] 2020/07/02 03:23 Уровень 40 лет / Инженер / Полезно /
Раствор шлака с использованием метода крамера.Линейные уравнения. Решение систем линейных уравнений. Метод Крамера
Метод Крамера основан на использовании определителей при решении систем линейных уравнений … Это значительно ускоряет процесс решения.
Метод Крамера можно использовать для решения системы из такого количества линейных уравнений, в каждом из которых есть неизвестные.
 Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя.Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.
Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя.Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.Определение … Определитель, составленный из коэффициентов неизвестных, называется определителем системы и обозначается (дельта).
Детерминанты
получаются заменой коэффициентов соответствующими неизвестными свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, а неизвестное равно отношению определителей.Знаменатель содержит определитель системы, а числитель содержит определитель, полученный из определителя системы заменой коэффициентов в этой неизвестной на свободные члены. Эта теорема верна для системы линейных уравнений любого порядка.
Пример 1. Решите систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятор, решающий метод Крамера.

Три случая решения систем линейных уравнений
Как видно из теоремы Крамера , при решении системы линейных уравнений могут иметь место три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система последовательная и определенная)
Второй случай: система линейных уравнений имеет бесконечное число решений
(система непротиворечивая и неопределенная)
**,
тех.коэффициенты при неизвестных и свободных членах пропорциональны.
Третий случай: система линейных уравнений не имеет решений
(система несовместима)
Таким образом, система m линейных уравнений с n переменными называется несовместимой , если у нее нет решений, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений с одним решением называется некой , а несколько — undefined .
Примеры решения систем линейных уравнений методом Крамера
Пусть дано системе
.

На основе теоремы Крамера
………….
,, где
—системный определитель. Остальные определители получим, заменив столбец с коэффициентами соответствующей переменной (неизвестной) свободными членами:
Пример 2.
.
Следовательно, система определенная. Чтобы найти ее решение, вычислим определители
По формулам Крамера находим:
Итак, (1; 0; -1) — единственное решение системы.
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие элементы равны нулю! Это следующий пример.
Пример 3. Решите систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Внимательно посмотрите на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю.
 Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестных
Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестныхПо формулам Крамера находим:
Итак, решение системы (2; -1; 1).
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
Вернуться к началу страницы
Продолжаем решать системы по методу Крамера вместе
Как уже было сказано, если определитель системы равен нулю, а определители для неизвестных не равны нулю, система несовместима, то есть не имеет решений. Проиллюстрируем это следующим примером.
Пример 6. Решите систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений.
 Для большей точности вычислим определители неизвестных
Для большей точности вычислим определители неизвестныхОпределители для неизвестных не равны нулю, следовательно, система непоследовательна, то есть не имеет решений.
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
В задачах о системах линейных уравнений встречаются и такие, в которых помимо букв, обозначающих переменные, есть еще и другие буквы. Эти буквы представляют собой определенное число, чаще всего действительное число. На практике поисковые задачи приводят к таким уравнениям и системам уравнений общих свойств любых явлений и объектов.То есть изобрели ли вы какой-либо новый материал или устройство, и для описания его свойств, которые являются общими независимо от размера или количества экземпляров, необходимо решить систему линейных уравнений, где вместо некоторых коэффициентов переменных есть буквы. За примерами далеко ходить не надо.
Следующий пример предназначен для аналогичной задачи, только количество уравнений, переменных и букв, обозначающих какое-то действительное число, увеличивается.

Пример 8. Решите систему линейных уравнений методом Крамера:
Решение.Находим определитель системы:
Найдите определители неизвестных
При количестве уравнений такое же, как и количество неизвестных с главным определителем матрицы, не равным нулю, коэффициенты системы (для таких уравнений есть решение и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система непротиворечива и имеет одно решение, и его можно найти по формулам Крамера :
где Δ — определитель матрицы системы ,
Δ i — определитель матрицы системы, в которой вместо i -й столбец содержит столбец правых частей.
Когда определитель системы равен нулю, это означает, что система может стать совместной или несовместимой.
Этот метод обычно используется для небольших систем с большими вычислениями и когда необходимо определить одно из неизвестных.
 Сложность метода состоит в том, что необходимо вычислить множество определителей.
Сложность метода состоит в том, что необходимо вычислить множество определителей.Описание метода Крамера.
Имеется система уравнений:
Систему трех уравнений можно решить методом Крамера, который был рассмотрен выше для системы из двух уравнений.
Составим определитель из коэффициентов при неизвестных:
Это будет системный идентификатор … Если D ≠ 0 , то система совместима. Теперь составим 3 дополнительных определителя:
,,
Решаем систему формул Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Учитывая систему:
Решим его методом Крамера.
Сначала необходимо вычислить определитель матрицы системы:
Поскольку Δ ≠ 0, следовательно, по теореме Крамера система непротиворечива и имеет одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получается из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов.
 Получаем:
Получаем:Таким же образом получим определитель Δ 2 из определителя матрицы системы, заменив второй столбец столбцом свободных коэффициентов:
Для того, чтобы освоить этот абзац, вы должны уметь открывать квалификаторы «два на два» и «три на три».Если классификаторы плохие, изучите урок Как рассчитать определитель?
Сначала рассмотрим подробно правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? — Ведь простейшую систему можно решить школьным методом, методом сложения семестров!
Дело в том, что даже иногда, но встречается такая задача — решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом этапе вычисляем определитель, он называется главным определителем системы .

Метод Гаусса.
Если, то система имеет уникальное решение, и чтобы найти корни, мы должны вычислить еще два определителя:
иНа практике вышеуказанные квалификаторы также можно обозначать латинскими буквами.
Находим корни уравнения по формулам:
,Пример 7
Решаем систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, на справа — десятичные дроби через запятую. Запятая — довольно редкий гость в практических занятиях по математике; Я взял эту систему из эконометрической задачи.
Как решить такую систему? Вы можете попробовать выразить одну переменную через другую, но в этом случае вы, вероятно, получите ужасные причудливые дроби, с которыми крайне неудобно работать, и дизайн решения будет выглядеть просто ужасно.Вы можете умножить второе уравнение на 6 и выполнить почленное вычитание, но здесь будут отображаться те же дроби.
Что делать? В таких случаях на помощь приходят формулы Крамера.

;
;
Ответ :,
Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже часто) для эконометрических задач.
Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс.При использовании этого метода обязательный фрагмент задания представляет собой следующий фрагмент: «Что означает, что система имеет только одно решение» … В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
Не лишним будет проверить, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В результате с небольшой ошибкой вы должны получить числа, которые находятся в нужных частях.
Пример 8
Ответ представлен обычными неправильными дробями. Сделайте чек.
Это пример самостоятельного решения (пример окончания и ответ в конце урока).
Теперь перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Найдите главный определитель системы:
Если, то система имеет бесконечно много решений или противоречива (не имеет решения).
 В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.
В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.Если, то система имеет уникальное решение, и чтобы найти корни, мы должны вычислить еще три определителя:
«И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально не отличается от случая «два на два», столбец свободных членов последовательно «ходит» слева направо по столбцам главного определителя.
Пример 9
Решите систему, используя формулы Крамера.
Решение : Решим систему, используя формулы Крамера.
, а значит, в системе есть уникальное решение.Ответ :.
Собственно, здесь опять особо комментировать нечего, в виду того, что решение принимается по готовым формулам.Но следует отметить несколько моментов.
Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например :.
Рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, делаем так:
Если под рукой нет компьютера, делаем так:1) Возможна ошибка расчета. Как только вы столкнулись с «плохой» дробью, вы должны немедленно проверить , правильно ли переписано условие … Если условие переписано без ошибок, то необходимо пересчитать определители, используя расширение по другой строке ( столбец).
2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задачи была опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решаем задачу до конца, а потом обязательно проверяем и оформляем на чистую копию после решения. Конечно, проверка дробного ответа — неприятный урок, но это будет обезоруживающий аргумент для учителя, который, ну, любит ставить минус любому подобному бяке. Как работать с дробями, подробно описано в ответе к примеру 8.
Если под рукой есть компьютер, то для его проверки воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение матричного метода системы.

Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении нет переменной, во втором нет переменной.В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
— вместо пропущенных переменных ставятся нули.
Кстати, детерминанты с нулями рационально открывать по той строке (столбцу), в которой стоит ноль, так как вычислений гораздо меньше.Пример 10
Решите систему, используя формулы Крамера.
Это пример самостоятельного решения (образец отделки и ответ в конце урока).
Для случая системы из 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно найти в уроке «Определяющие свойства». Уменьшение порядка определителя — пять определителей 4-го порядка вполне разрешимы. Хотя задание уже довольно напоминает сапог профессора на груди удачливого ученика.
Решение системы с использованием обратной матрицыМетод обратной матрицы По сути, это частный случай матричного уравнения (см.
 Пример № 3 указанного урока).
Пример № 3 указанного урока).Чтобы изучить этот раздел, вы должны уметь раскрыть определители, найти обратную матрицу и выполнить матричное умножение. Соответствующие ссылки будут предоставлены по пути.
Пример 11
Решите систему матричным методом
Решение : Давайте запишем систему в матричной форме:
, гдеПожалуйста, взгляните на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю, все понимают.Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в соответствующие места в матрице пришлось бы поставить нули.
Найдите обратную матрицу по формуле:
, где — транспонированная матрица алгебраических дополнений соответствующих элементов матрицы.Сначала мы имеем дело с определителем:
Здесь квалификатор раскрывается в первой строке.
Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно.
 В этом случае система решается методом исключения неизвестных (метод Гаусса).
В этом случае система решается методом исключения неизвестных (метод Гаусса). Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Артикул: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра — это номер строки, в которой расположен этот элемент. Вторая цифра — это номер столбца, в котором расположен этот элемент:
То есть двойной нижний индекс указывает, что элемент находится в первой строке, третьем столбце, и, например, элемент находится в строке 3, столбце 2По ходу решения расчета несовершеннолетних лучше расписывать подробно, хотя при определенном опыте их можно приучить считать с ошибками устно.
Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратичными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы.
 Обозначим его греческой буквой D. Таким образом,
Обозначим его греческой буквой D. Таким образом,. (1,6)
Если основным определителем является произвольный ( j -й) столбец, заменить на столбец свободных членов системы (1.5), то мы можем получить еще n вспомогательных определителей :
( j = 1, 2,…, n ). (1,7)
Правило Крамера Решение квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:
(1,8)
Пример 1.5. Использование метода Крамера для решения системы уравнений
.
Вычислим главный определитель системы:
Поскольку D¹0, система имеет единственное решение, которое находится по формулам (1.8):
Таким образом,
Матричные операции
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть
.(1,9)
Пример 1.6. .
Добавление матриц.Эта операция вводится только для матриц одного порядка.
Чтобы сложить две матрицы, необходимо добавить соответствующие элементы другой матрицы к элементам одной матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.Пример 1.7. .
Умножение матриц.Если количество столбцов в матрице A совпадает с количеством строк в матрице V , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы A размеров м ´ n на матрицу V размеров n ´ k мы получим матрицу С габаритами м ´ k … Причем элементы матрицы СО вычисляются по формулам:
Задача 1.
. 8. Найдите, если возможно, произведение матриц AB и BA :
8. Найдите, если возможно, произведение матриц AB и BA :Решение. 1) Чтобы найти работу AB , нужно строки матрицы A умножить на столбцы матрицы B :
2) Графическое изображение BA не существует, поскольку количество столбцов в матрице B не совпадает с количеством строк в матрице A .
Обратная матрица. Матричное решение систем линейных уравнений
Матрица A — 1 называется обратной квадратной матрицы A , если выполняется равенство:
, где через I обозначена единичная матрица того же порядка, что и матрица A :
.
Для того чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был ненулевым. Обратная матрица находится по формуле:
, (1.13)
, где A ij — алгебраические дополнения к элементам a ij матрицы A (обратите внимание, что алгебраические дополнения к строкам матрицы A расположены в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A — 1 к матрице
.
Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найти дет. A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Поскольку определитель исходной матрицы отличен от нуля, обратная матрица существует.
1) Найдите алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы мы поместили алгебраические дополнения к строкам исходной матрицы в соответствующие столбцы.
Из полученных алгебраических дополнений составляем новую матрицу и делим ее на определитель det A … Таким образом, получаем обратную матрице:
Квадратичные системы линейных уравнений с ненулевым главным определителем могут быть решены с помощью обратной матрицы. Для этого система (1.5) записывается в матричном виде:
где
Умножая обе части равенства (1.
 14) слева на A — 1, получаем решение системы:
14) слева на A — 1, получаем решение системы:, где
Таким образом, чтобы найти решение квадратной системы, нужно найти матрицу, обратную основной матрице системы, и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решите систему линейных уравнений
с использованием обратной матрицы.
Решение. Запишем систему в матричном виде :,
где — основная матрица системы, — столбец неизвестных и — столбец свободных элементов. Поскольку основной определитель системы, то основная матрица системы A, имеет обратную матрицу A, -1. Чтобы найти обратную матрицу A -1, вычислим алгебраические дополнения ко всем элементам матрицы A :
Из полученных чисел составляем матрицу (причем алгебраические дополнения к строкам матрицы A записываем в соответствующие столбцы) и делим ее на определитель D.Таким образом, мы нашли обратную матрицу:
Находим решение системы по формуле (1.
 15):
15):Таким образом,
Решение систем линейных уравнений методом обычных жордановых исключений
Пусть дана произвольная (не обязательно квадратичная) система линейных уравнений:
(1,16)
Требуется найти решение системы, т.е. набор переменных, удовлетворяющий всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесконечное количество решений. У нее также может вообще не быть решений.
При решении таких задач применяется известный из школьного курса метод исключения неизвестных, который еще называют методом обычных исключений Джордана. Суть этого метода состоит в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы.В результате получается система, которая содержит на одно уравнение и на одну переменную меньше, чем исходная система. Запоминается уравнение, из которого была выражена переменная.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключены из системы, поскольку они выполняются при любых значениях переменных и, следовательно, не влияют на решение системы.Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может быть выполнено ни при каких значениях переменных (например), то мы заключаем, что система не имеет решения.
Если в процессе решения не возникло противоречащих друг другу уравнений, то одна из оставшихся в нем переменных находится из последнего уравнения. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются другие переменные, то они считаются параметрами, и переменная, выраженная через них, будет функцией этих параметров.Затем происходит так называемое «обратное движение».
 Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения.
Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения.В результате получаем решение системы. Это решение будет уникальным, если найденные переменные будут числами. Если первая найденная переменная, а затем все остальные зависят от параметров, то система будет иметь бесконечное количество решений (каждому набору параметров соответствует новое решение).Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Пример 1.11.
х
Запомнив первое уравнение и сократив аналогичные члены во втором и третьем уравнениях, мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Давайте вспомним второе уравнение, и из первого находим z :
Делая обратный ход, последовательно находим y и z .
 .. Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :
.. Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :.
Затем подставляем в первое запомненное уравнение, откуда находим x :
Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Давайте вспомним первое уравнение
В этой системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получаем 14 = 17. Это равенство не выполняется ни при каких значениях переменных x , y и z … Следовательно, система (1.17) несовместима. , то есть не имеет решения.
Предлагаем читателям самостоятельно проверить, что основной детерминант исходной системы (1.17) равен нулю.
Рассмотрим систему, которая отличается от системы (1.17) только одним свободным членом.

Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:
. (1.18)
Решение. Как и раньше, мы выражаем из первого уравнения переменную x и подставляем ее во второе и третье уравнения:
.
Давайте вспомним первое уравнение и дадим аналогичные члены во втором и третьем уравнениях.Заходим в систему:
Выражая y из первого уравнения и подставляя его во второе уравнение, получаем тождество 14 = 14, которое не влияет на решение системы, а значит, может быть исключено из системы.
В последнем запомненном равенстве переменная z будет считаться параметром. Мы верим. Тогда
Подставьте y и z в первое запомненное равенство и найдите x :
.
Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти по формулам (1.19), выбрав произвольное значение параметра t :
(1.19)
Итак, решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. Д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
Д. Формулы (1.19) выражают общее (любое) решение системы (1.18).В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким.Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и сформулировать решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где xj — независимые (искомые) переменные, a ij — постоянные коэффициенты
( i = 1, 2,…, m ; j = 1, 2,…, № ).Правая часть системы y i ( i = 1, 2,…, m ) может быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы, исключив неизвестные.Рассмотрим следующую операцию, в дальнейшем называемую «один шаг обычных исключений Джордана». Из произвольного ( r -го) равенства выражаем произвольную переменную ( x s ) и подставляем во все остальные равенства.
 Конечно, это возможно только при и ¹ 0.Коэффициент и RS называют разрешающим (иногда руководящим или основным) элементом.
Конечно, это возможно только при и ¹ 0.Коэффициент и RS называют разрешающим (иногда руководящим или основным) элементом.Получим такую систему:
. (1,21)
Далее из s -го равенства системы (1.21) находим переменную x s (после того, как найдены остальные переменные). S -я строка запоминается и в дальнейшем исключается из системы. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть так:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1,23)
Теперь вычислим новые коэффициенты b ij ( i ¹ r ) произвольного уравнения.Для этого подставляем переменную, выраженную в (1. 22) x s v i -ое уравнение системы (1.20):
22) x s v i -ое уравнение системы (1.20):Приведя аналогичные термины, получаем:
(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений формализуется в виде таблиц (матриц).Эти таблицы называются «жордановы».Таким образом, задача (1.20) связана со следующей таблицей Иордании:
Таблица 1.1
x 1 x 2 … х … х … х y 1 = а 11 а 12 a 1 j а 1 с a 1 n ………………………………………………………………….. y i = a i 1 a i 2 a ij а это а дюйм ………………………………………………………………… .. г = и 1 и 2 RJ а RS а рн …………………………………………………………………. да нет = а м 1 а м 2 a mj а мс а мин Jordan Таблица 1.1 содержит левый столбец заголовка, в котором записаны правые части системы (1.20), и верхний ряд заголовка, в котором записаны независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу A на матрицу, состоящую из элементов верхней строки заголовка, то получится матрица, состоящая из элементов левого столбца заголовка. То есть, по сути, жорданова таблица — это матричная запись системы линейных уравнений:. В этом случае системе (1.21) соответствует следующая жорданова таблица:
Таблица 1.2
x 1 x 2 … х … г … х y 1 = б 11 б 12 b 1 j б 1 с b 1 n ………………………………………………………………….. y i = b i 1 b i 2 b ij b is б в ………………………………………………………………… .. x s = б р 1 б р 2 b rj b RS млрд р-н …………………………………………………………………. да n = м 1 м 2 b mj б мс млрд мин Разрешающий элемент a RS мы выделим его жирным шрифтом. Напомним, что для того, чтобы имел место один шаг жордановых исключений, разрешающий элемент должен быть ненулевым. Строка таблицы, содержащая разрешающий элемент, называется разрешающей строкой.Столбец, содержащий разрешающий элемент, называется разрешающим столбцом. При переходе из этой таблицы в следующую таблицу одна переменная ( xs ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г. г.) из левый верхний столбец таблицы перемещается в верхний верхний ряд.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), что следует из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется на обратный:
2. Остальные элементы разрешительной линии разделяются разрешающим элементом и меняют знак на противоположный:
3. Остальные элементы разрешающей колонки делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последнюю формулу легко запомнить, если вы заметите, что элементы, составляющие дробь, находятся на пересечении i -й и r -ой строк и j -го и s -го столбца (разрешающая строка, разрешающий столбец, а также строка и столбец, на пересечении которых находится пересчитываемый элемент).Точнее, при запоминании формулы может использоваться следующая диаграмма:
-21 -26 -13 -37 Принимая первый шаг исключения Jordan, любой элемент таблицы 1.3, расположенный в столбцах x 1,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбирать разрешающий элемент в последнем столбце, потому что требуется найти независимые переменные x 1,…, x 5.Выберем, например, коэффициент 1 с переменной x 3 в третьей строке таблицы 1.3 (активирующий элемент выделен жирным шрифтом). Переходя к таблице 1.4, переменная x 3 из верхней строки заголовка заменяется константой 0 левого столбца (третья строка). В этом случае переменная x 3 выражается через остальные переменные.
Строка x 3 (Таблица 1.4) после запоминания может быть исключена из Таблицы 1.4.Третий столбец с нулем в верхней строке заголовка также исключен из таблицы 1.4. Дело в том, что независимо от коэффициентов этого столбца b i 3 все соответствующие члены каждого уравнения 0 b i 3 системы будут равны нулю. Поэтому эти коэффициенты можно не указывать. Исключая одну переменную x 3 и запоминая одно из уравнений, приходим к системе, соответствующей таблице 1.4 (с перечеркнутой линией x 3). Выбор по таблице 1.4 как разрешающий элемент b 14 = -5, перейти к таблице 1.5. В таблице 1.5 мы запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = — 3 + 2 x 5.
Последовательно подставляя уже найденные переменные в сохраненные строки, находим оставшиеся переменные:
Таким образом, в системе есть бесчисленное множество решений. Переменной x 5 можно присвоить произвольные значения.Эта переменная действует как параметр x 5 = t. Мы доказали совместимость системы и нашли общее решение:
x 1 = — 3 + 2 т
x 2 = — 1 — 3 т
x 3 = — 2 + 4 т . (1,27)
x 4 = 4 + 5 тx 5 = т
Задавая параметру t разные значения, мы получаем бесчисленное множество решений для исходной системы.Так, например, решение системы — это следующий набор переменных (- 3; — 1; — 2; 4; 0).
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Рекомендую всем, кто зашел на сайт через эту страницу, прочитать первую часть. Возможно, некоторым посетителям материал покажется слишком простым, но в процессе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А теперь разберем правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут узнать, как решать системы указанными выше способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? — Ведь простейшую систему можно решить школьным методом, методом поэтического сложения!
Дело в том, что даже иногда, но встречается такая задача — решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера.Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом этапе вычисляем определитель, он называется главным определителем системы .
Метод Гаусса.
Если, то система имеет единственное решение, и чтобы найти корни, мы должны вычислить еще два определителя:
.
иНа практике вышеуказанные квалификаторы также могут обозначаться латинскими буквами.
Находим корни уравнения по формулам:
,Пример 7
Решите систему линейных уравнений
Решение : Видим, что коэффициенты уравнения достаточно большие, с правой стороны стоят десятичные дроби через запятую.Запятая — довольно редкий гость в практических занятиях по математике; Я взял эту систему из эконометрической задачи.
Как решить такую систему? Вы можете попробовать выразить одну переменную через другую, но в этом случае вы, вероятно, получите ужасные причудливые дроби, с которыми крайне неудобно работать, и дизайн решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и выполнить почленное вычитание, но здесь будут отображаться те же дроби.
Что делать? В таких случаях на помощь приходят формулы Крамера.
;
;
Ответ :,
Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже часто) для эконометрических задач.
Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательный фрагментом присвоения является следующий фрагмент: «Что означает, что в системе есть только одно решение» … В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
Не лишним будет проверить, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В результате с небольшой ошибкой вы должны получить числа, которые находятся в нужных частях.
Пример 8
Ответ представлен обычными неправильными дробями. Сделайте чек.
Это пример самостоятельного решения (пример окончания и ответ в конце урока).
Теперь перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Найдите главный определитель системы:
Если, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.
Если, то система имеет единственное решение, и чтобы найти корни, мы должны вычислить еще три определителя:
«И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально не отличается от случая «два на два», столбец свободных членов последовательно «ходит» слева направо по столбцам главного определителя.
Пример 9
Решите систему, используя формулы Крамера.
Решение : Давайте решим систему, используя формулы Крамера.
, а значит, в системе есть уникальное решение.Ответ :.
Собственно, и здесь комментировать особо нечего, учитывая, что решение принимается по готовым формулам.Но следует отметить несколько моментов.
Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например :.
Рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, сделаем так:1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохой» дробью, вы должны немедленно проверить , правильно ли переписано условие … Если условие переписано без ошибок, то необходимо пересчитать определители, используя расширение по другой строке ( столбец).
2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задачи была опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решаем задачу до конца, а потом обязательно проверяем и оформляем на чистую копию после решения. Конечно, проверка дробного ответа — неприятный урок, но это будет обезоруживающий аргумент для учителя, который, ну, любит ставить минус любому подобному бяке. Как работать с дробями, подробно описано в ответе к примеру 8.
Если под рукой есть компьютер, то для его проверки воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении нет переменной, во втором нет переменной.В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
— вместо пропущенных переменных ставятся нули.
Кстати, детерминанты с нулями рационально открывать по той строке (столбцу), в которой стоит ноль, так как вычислений гораздо меньше.Пример 10
Решите систему, используя формулы Крамера.
Это пример самостоятельного решения (образец отделки и ответ в конце урока).
Для случая системы из 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно найти в уроке «Определяющие свойства». Уменьшение порядка определителя — пять определителей 4-го порядка вполне разрешимы. Хотя задание уже довольно напоминает сапог профессора на груди удачливого ученика.
Решение системы с использованием обратной матрицыМетод обратной матрицы по существу является частным случаем матричного уравнения (см. Пример № 3 указанного урока).
Чтобы изучить этот раздел, вы должны уметь раскрыть определители, найти обратную матрицу и выполнить матричное умножение. Соответствующие ссылки будут предоставлены по пути.
Пример 11
Решите систему матричным методом
Решение : Запишем систему в матричном виде:
, гдеОбратите внимание на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю, все понимают.Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в соответствующие места в матрице пришлось бы поставить нули.
Найдите обратную матрицу по формуле:
, где — транспонированная матрица алгебраических дополнений соответствующих элементов матрицы.Сначала разберемся с определителем:
Здесь квалификатор раскрывается на первой строке.
Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно.В этом случае система решается методом исключения неизвестных (метод Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
.Артикул: Полезно знать значение двойных индексов в линейной алгебре. Первая цифра — это номер строки, в которой расположен этот элемент. Вторая цифра — это номер столбца, в котором расположен этот элемент:
То есть двойной нижний индекс указывает, что элемент находится в первой строке, третьем столбце, и, например, элемент находится в строке 3, столбце 2Онлайн-академия Geochemist’s Workbench®: сорбирующие поверхности
Sorbing Solutes является частью бесплатной веб-серии GWB Online Academy, созданной компанией A Water Solutions LLC.
Загрузите этот модуль, чтобы использовать его на курсах:
Щелкните файл или щелкните правой кнопкой мыши и выберите «Сохранить ссылку как…» для загрузки.
Введение
Метод коэффициента распределения, обычно называемый K d подход , — это наиболее широко применяемый метод в геохимии окружающей среды для прогнозирования сорбции загрязняющих веществ на отложениях.Коэффициент распределения K d сам по себе является просто отношением в определенных условиях сорбированной массы к растворенной массе загрязнителя. Другими словами,
, где S — сорбированная концентрация в молях на грамм сухого осадка, K d — коэффициент распределения в см 3 на грамм, а C — концентрация растворенного вещества в молях на см 3 .
Подход подразумевает реакцию типа
По методу Freundlich , другому эмпирическому подходу,
, где K f — коэффициент Фрейндлиха, а n — показатель степени Фрейндлиха, который может находиться в диапазоне от 0 до 1.Подход Фрейндлиха просто сводится к линейному K d , когда показатель Фрейндлиха равен 1.
На рисунке ниже показана сорбция селената почвой, показывающая массу, сорбированную на грамм сухой почвы, как функцию концентрации в растворе. Линии соответствуют данным с использованием активности K d , активности Фрейндлиха и приближений Ленгмюра
.Как можно видеть, сорбция методом K d одинаково эффективна при любой концентрации, тогда как показатель степени n в подходе Фрейндлиха предсказывает постепенно менее эффективную сорбцию по мере увеличения концентрации.
Модель активности K d и модели активности Фрейндлиха (также известные как реакция K d и реакция Фрейндлиха), которые закодированы в программном обеспечении геохимического моделирования, таком как The Geochemist’s Workbench, отличаются от общего подхода:
, где a — активность свободных частиц, а K d ‘ и K f ‘ учитывают коэффициент активности ионов и ионизированную фракцию компонента.Следовательно, коэффициенты, рассчитываемые традиционным способом, необходимо скорректировать на коэффициент активности вида. Следует проявлять осторожность, чтобы применять их только к системам, аналогичным той, для которой они были изначально определены.
Задача 1:
K d подходВ ходе испытания осадок из водоносного горизонта сорбировал Pb 2+ в соответствии с коэффициентом распределения K d 0,16 см 3 г –1 .Концентрация растворенного свинца в тесте составляла около 10 мкмоль. Наша задача — пересмотреть нашу модель переноса Pb 2+ в водоносный горизонт с учетом сорбции.
Коэффициент активности для Pb 2+ в наших грунтовых водах составляет около 0,66, а свободный ион составляет 80% растворенного Pb, поэтому коэффициент распределения K d ‘ для активности K d модель работает до .30 × 10 –3 моль г –1 .
Для настройки модели еще раз дважды щелкните файл «Pulse.x1t ». В X1t перейдите в Файл → Открыть → Сорбирующие поверхности… (или Конфигурация → Сорбирующие поверхности… ), затем перейдите в каталог курса и выберите файл «Pb-Kd.sdat», затем закройте Сорбирующие поверхности. диалог
Вы можете подтвердить, что ввели правильное значение для K d ‘, щелкнув File → View и выбрав «. \ Pb-Kd.sdat».
Теперь установите «_Kd» в качестве суффикса
и выберите Run → Go , чтобы запустить расчет.Постройте график результатов с помощью Xtplot , как и раньше.
Как сорбция влияет на миграцию Pb 2+ в водоносном горизонте? Количество растворенного в грунтовых водах Pb 2+ ?
результатов скрыть результатыНа приведенном ниже графике показаны результаты моделирования сорбции в соответствии с подходом K d , зеленым цветом, вместе со случаем отсутствия реакции (синим цветом)
В случае K d импульс задерживается по сравнению со случаем отсутствия реакции.Размер импульса меньше, если рассматривать сорбцию, потому что часть загрязнителя сорбируется в водоносный горизонт, уменьшая концентрацию в растворе.
скрыть результатыМы можем рассчитать коэффициент замедления R F
, где n — пористость, а ρ s — плотность осадка. Поскольку в нашем случае пористость составляет 30%, если мы возьмем плотность 2,65 г / см 3 , R F будет около 2.Как вы можете видеть на графике, импульс мигрирует примерно с половиной скорости не реагирующего растворенного вещества.
Задача 2: изотерма Фрейндлиха
Повторяя тест с разными количествами свинца, мы обнаруживаем, что K d варьируется в зависимости от концентрации Pb 2+ . Чтобы учесть это наблюдение, мы подгоняли результаты испытаний к изотерме Фрейндлиха с K f ‘ 9,5 × 10 –6 и n f 0.7. Параметризация Фрейндлиха эквивалентна подходу K d при концентрации Pb 2+ 10 мкмоль.
Чтобы запустить случай Фрейндлиха, вернитесь в X1t в диалог Config → Sorbing Surfaces… . Щелкните запись для набора данных «Pb-Kd.sdat», чтобы она была выделена, затем нажмите клавишу удаления на клавиатуре, чтобы удалить ее. Щелкните, затем прочтите файл «Pb-Freundlich.sdat»
и закройте диалог.
Установить суффикс «_Freundlich»
и выберите Run → Go .
Как использование изотермы Фрейндлиха повлияло на результаты расчетов по сравнению с тем, когда мы использовали подход K d для описания сорбции?
результатов скрыть результатыРезультаты, учитывающие изотерму Фрейндлиха, показаны оранжевым цветом вместе с подходом K d (зеленым) и нереагирующим случаем (синим)
Подобно подходу K d миграция импульса замедляется.В отличие от подхода K d , импульс становится сильно асимметричным с крутым передним фронтом и удлиненным задним фронтом. Это связано с тем, что эффективность сорбции зависит от концентрации иона в растворе по методу Фрейндлиха.
Как и в нашей модели двойной пористости, сорбция по методу Фрейндлиха приводит к появлению характерного хвоста на заднем фронте импульса.
скрыть результатыЗадача 3: два измерения
Чтобы перенести предыдущий прогон в два измерения, запустите программу X2t , дважды щелкнув файл «Freund2D.x2t ». Перейдите на панель Домен . Здесь вы можете увидеть домен и его дискретизацию
Перейти на панель Flow . Здесь вы можете увидеть граничные условия для расчета поля потока, которое движется слева направо
Перейти к панели Wells
Мы расположили колодец ближе к входу в зону, чтобы ввести утечку из источника загрязнения.Флюид из скважины попадает в водоносный горизонт в течение первого месяца моделирования.
Изучите область Исходный . Здесь мы установили, что водоносный горизонт будет изначально заполнен чистой водой
Проверьте также панель Fluids . «Окружающий» флюид имеет тот же состав, что и флюид Initial . Термин «загрязненная» жидкость, напротив, определяет воду, загрязненную Pb 2+
На панели «Интервалы » мы связали чистую воду из окружающей среды с левой частью области и установили продолжительность моделирования на 10 лет
На панели Medium мы установили свойства таким образом, чтобы дифференциальный поток порождал дисперсию.Пористость варьируется по гауссовскому распределению примерно на 30%. Логарифм проницаемости зависит от пористости, поэтому поле проницаемости также неоднородно, а результирующее поле потока нерегулярно
Мы не используем концепцию дисперсии Фика, поэтому значения, установленные для α L и α T из закона Фика, равны 0.
Вы можете отследить симуляцию, выбрав Run → Go .
Чтобы отобразить результаты моделирования, щелкните, чтобы запустить Xtplot , и выберите Plot → Map View .Затем выберите Формат → Цветовая карта… и в четырех верхних полях выберите: «Компоненты в жидкости», «Pb 2+ », «мкг / кг» и «Линейный».
Снимите флажок «Автоматическое масштабирование» и сопоставьте низкие, средние и высокие значения с «15 мкг / кг», «100 мкг / кг» и «200 мкг / кг». Теперь свяжите значения с желтым, красным и пурпурным.
Чтобы замаскировать участки водоносного горизонта, где концентрация Pb 2+ падает ниже MCL USEPA, равного 15 мкг / кг, снимите флажок «Карта ниже этого значения». Программа замаскирует значения в диапазоне от 0 до 15 мкг / кг, используя белый цвет.Когда вы закончите, диалоговое окно должно выглядеть так:
Щелкните ОК .
Теперь нажмите Формат → Временной шаг…
выберите время рендеринга и нажмите Применить . Вы можете перемещаться вперед и назад во времени с помощью кнопок Next и Previous .
Наконец, нажмите и в появившемся диалоговом окне
щелкните Выполнить .
Обратите внимание на флажки «Цикл непрерывно» и «Полный экран». Обратите внимание на флажок «Сохранить анимацию в файлы изображений». Мы будем использовать эту опцию для сохранения кадров, из которых мы будем делать видеоклипы нашей анимации.
Анимация двухмерного примера
Анимация в этом фильме демонстрирует имитацию переноса Pb 2+ через гетерогенную среду с учетом ослабления загрязняющих веществ за счет сорбции твердыми частицами водоносного горизонта. Есть серия из трех симуляций:
- Корпус без реакции, для справки
- Ион свинца сорбируется по коэффициенту распределения K d
- Сорбция по изотерме Фрейндлиха
Авторы
Крейг М.Бетке и Брайан Фарреллы. © Copyright 2016–2021 ООО «Водные растворы». Этот урок может быть воспроизведен и изменен свободно для поддержки любого лицензионного использования программного обеспечения Geochemist’s Workbench®, при условии, что любые производные материалы подтверждают оригинальное авторство.
Список литературы
Alemi, M.H., D.A. Голдхамер и Д. Нельсон, 1991, Моделирование переноса селена в стационарных ненасыщенных столбах почвы. Журнал качества окружающей среды 20 , 89–95.
Бетке, К.М., 2008, Моделирование геохимических и биогеохимических реакций . Издательство Кембриджского университета, Нью-Йорк, 547 стр.
Бетке, К.М., Б. Фаррелл и М. Шарифи, 2021, The Geochemist’s Workbench®, выпуск 15: GWB Reactive Transport Modeling Guide . ООО «Водные растворы», Шампейн, Иллинойс, 191 стр.
Решение систем линейных алгебраических уравнений
Калькулятор, представленный ниже, может решать систему линейных уравнений, которые заданы в виде матрицы.Он делает этот калькулятор с использованием метода Гаусса.
Метод Гаусса — методика исключения последовательных переменных, когда при использовании основных уравнений системы перестает изменяться эквивалентная система треугольной формы, из которой по порядку, шаг за шагом, начиная с последнего числа, вычисляются все переменные система.
Этот метод был назван в честь немецкого математика Карла Гаусса, который очень давно работает в этой области.
Поле не заполнено.
«% 1» не является допустимым адресом электронной почты.
Пожалуйста, заполните это поле.
Поле должно содержать не менее% 1 символов.
Значение не должно быть длиннее% 1 символов.
Значение поля не совпадает с полем «% 1»
Неверный символ. Допустимые символы: «% 1».
Ожидаемое число.
Ожидается положительное число.
Ожидаемое целое число.
Ожидается целое положительное число.
Значение должно быть в диапазоне [% 1 ..% 2]
«% 1» уже присутствует в наборе допустимых символов.
Поле должно быть меньше 1%.
Первый символ должен быть буквой латинского алфавита.
Su
Пн
Вт
ср
Чт
Fr
Сб
января
Февраль
марта
Апрель
мая
июнь
июля
августа
сентября
Октябрь
ноября
декабря
век
Б.С.
% 1 век
Ошибка при импорте данных в строке% 1. Значение: «% 2». Ошибка: % 3
Не удалось определить разделитель полей. Для разделения полей вы можете использовать следующие символы: табуляция, точка с запятой (;) или запятая (,).
 Вычислим алгебраические дополнения к соответствующим элементам матрицы :
Вычислим алгебраические дополнения к соответствующим элементам матрицы :
 Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).
Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).


 \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)
\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \) Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.
Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ. Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.
Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.



 5% годовых и \ (5000 долларов \) под 12% годовых.
5% годовых и \ (5000 долларов \) под 12% годовых. Используйте rref (функция , вызывающая матричную переменную \ ([A] \).
Используйте rref (функция , вызывающая матричную переменную \ ([A] \).

 Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
 Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме. Вот рекомендации по получению формы рядного эшелона.
Вот рекомендации по получению формы рядного эшелона. С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели по написанию матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.
С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели по написанию матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк. Поменяйте местами строки или умножьте на константу, если необходимо.
Поменяйте местами строки или умножьте на константу, если необходимо.

 Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?
Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?
 См. (Рисунок), (Рисунок) и (Рисунок).
См. (Рисунок), (Рисунок) и (Рисунок).


 Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ванильный, шоколадный и клубничный вкусы?
Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ванильный, шоколадный и клубничный вкусы? Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем. Д. С целью получения формы «строка-эшелон»
Д. С целью получения формы «строка-эшелон»
 Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя.Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.
Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя.Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.

 Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестных
Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестных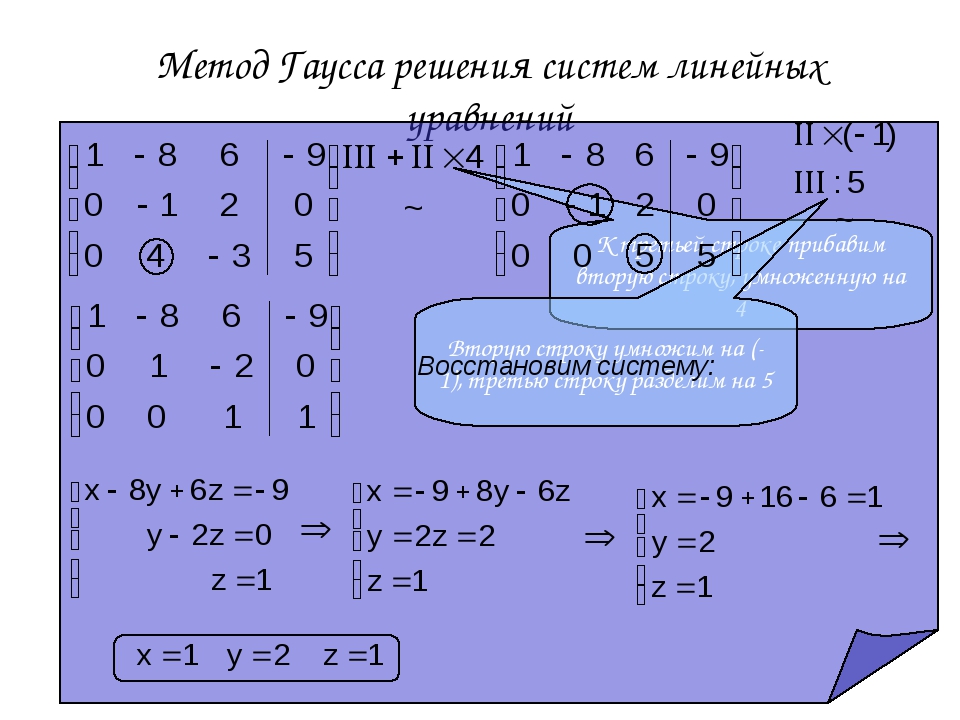 Для большей точности вычислим определители неизвестных
Для большей точности вычислим определители неизвестных
 Сложность метода состоит в том, что необходимо вычислить множество определителей.
Сложность метода состоит в том, что необходимо вычислить множество определителей. Получаем:
Получаем:

 В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.
В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса. Если под рукой нет компьютера, делаем так:
Если под рукой нет компьютера, делаем так:
 Пример № 3 указанного урока).
Пример № 3 указанного урока). В этом случае система решается методом исключения неизвестных (метод Гаусса).
В этом случае система решается методом исключения неизвестных (метод Гаусса).  Обозначим его греческой буквой D. Таким образом,
Обозначим его греческой буквой D. Таким образом,
 8. Найдите, если возможно, произведение матриц AB и BA :
8. Найдите, если возможно, произведение матриц AB и BA :
 14) слева на A — 1, получаем решение системы:
14) слева на A — 1, получаем решение системы: 15):
15):
 Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения.
Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения. .. Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :
.. Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :
 Д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
Д. Формулы (1.19) выражают общее (любое) решение системы (1.18). Конечно, это возможно только при и ¹ 0.Коэффициент и RS называют разрешающим (иногда руководящим или основным) элементом.
Конечно, это возможно только при и ¹ 0.Коэффициент и RS называют разрешающим (иногда руководящим или основным) элементом. 22) x s v i -ое уравнение системы (1.20):
22) x s v i -ое уравнение системы (1.20):