Площадь фигуры ограниченной кривыми в прямоугольных координатах
Площадь фигуры между двумя кривыми в прямоугольных координатах определяется интегралом
от разницы кривых, где одна из них всегда принимает не меньшие значения чем другая , а также кривые непрерывны.
Пределы интегрирования — прямые x1=a, x2=b — ограничивают фигуру (a<b чаще всего это точки пересечения заданных кривых).
Данный цикл задач в первую очередь подойдет студентам мех-мата Львовского национального университета имени Ивана Франко для прохождения практикума из математического анализа.
Студенты других Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П.
Пример 2.81 (2397). Найти площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах ax=y2, ay=x2,(a>0).
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
На графике они будут иметь следующий вид
Площадь между кривыми и нужно найти. Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций y1(x)=y2(x):
Как видите таким условием есть условие равенства функций.
Из последнего уравнения получим две точки x1=0, x2=a.
Дальше, когда Вы не видите графика функций необходимо установить какая из кривых принимает большие значения. Это нужно лишь для того, чтобы с первого раза получить положительное значение площади фигуры.
Выбираем произвольную точку из отрезка интегрирования [0;a] и убеждаемся в правильности неравенства , то есть проверяем которая из кривых принимает большее значения .
Как отмечалось выше, это нужно для того, чтобы после интегрирования получить положительную площадь фигуры между кривыми.
Вычисляем площадь фигуры, которая ограничена заданными кривыми интегрированиям:
Здесь мы имели достаточно простые функции, поэтому возведя их к табличным интегралам найти площадь достаточно легко. Следующие примеры будут содержать все более тяжелые функции, для интегрирования которых нужно применять знание практически всех формул интегрирования.

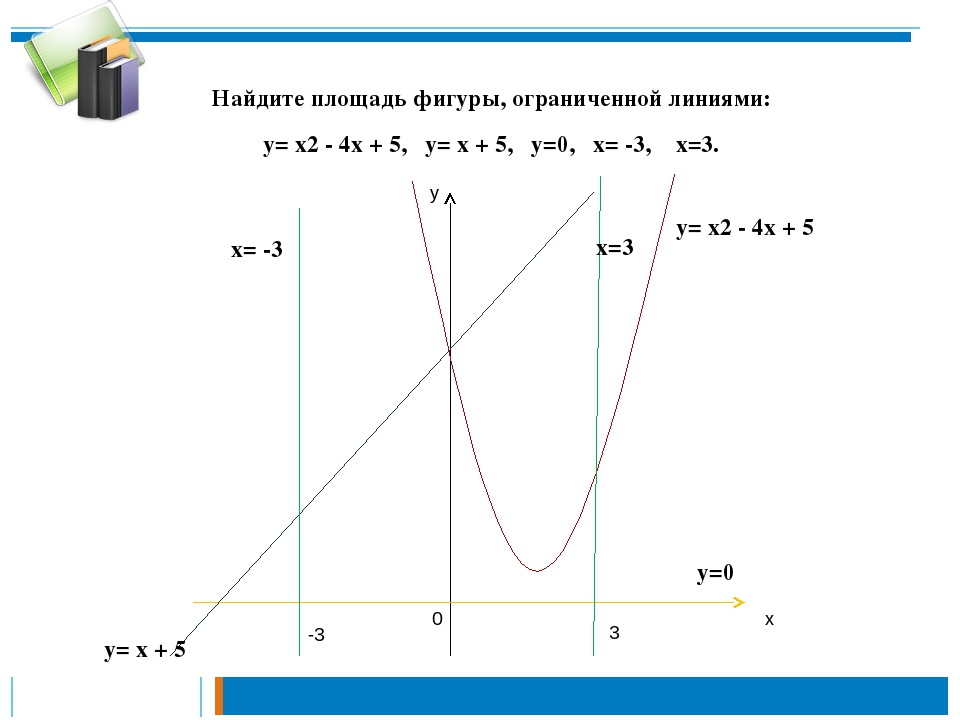
Пример 2.82 (2398) Вычислить площадь фигуры, ограниченной кривыми y=x2, x+y=2.
Вычисление: По методике записываем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x2, y2(x)=2-x.
Здесь функции выразить достаточно просто.
Вычислим пределы интегрирования, приравняв между собой функции y1(x)=y2(x):
x2=2-x.
Переносим переменные по одну сторону от знака равенства и решаем квадратное уравнение
x2+x-2=0;
(x+2)(x-1)=0.
Следовательно, корни уравнения x1=-2, x2=1.
Подстановкой любой точки из промежутка [-2;1], например x=0 в функции убеждаемся, что выполняется неравенство
, поэтому .
Площадь фигуры вычисляем интегрированием разницы кривых в найденных пределах:
Площадь равна S=4,5 квадратных единиц.
По физическому содержанию площадь фигуры равна разнице площадей двух криволинейных трапеций.
 Первая отвечает за верхний график y2(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y2(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.
Первая отвечает за верхний график y2(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y2(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.
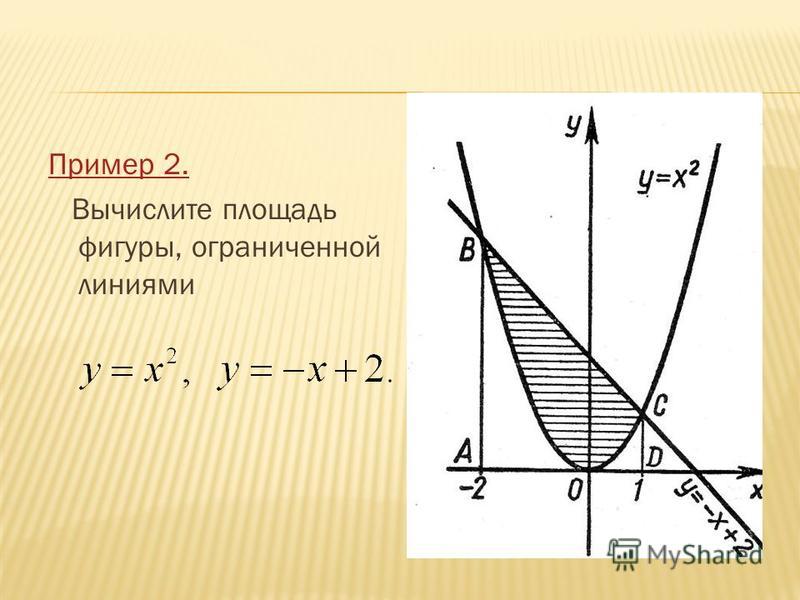
Пример 2.83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x2, x+y=0.
Вычисление: Запишем уравнение кривых, которые ограничивают искомую фигуру:
y1(x)=-x, y2(x)=2x-x2
Из условия равенства функций y1(x)=y2(x) найдем пределы интегрирования:
2x-x2=-x;
x2-3x=0;
x (x-3) =0.
Следовательно, x1=0, x2=3.
Подстановкой единицы видим, что на промежутке [0;3] исполняется неравенство
, то есть .
Находим площадь фигуры ограниченной заданными кривыми:
Под интегралом простая квадратичная функция, поэтому само интегрирование не сложно.
Следующие функции будут более сложными в плане интегрирования, однако используя табличные интегралы площадь найти удается.

Пример 2.84 (2400) Найти площадь фигуры, ограниченной кривыми y=2x, y=2, x=0.
Вычисление: Запишем подынтегральные функции:
y1(x)=2x, y2(x)=2, а также прямую x1=0 (ограничивает фигуру по оси абсцисс).
Найдем вторую границу интегрирования из условия равенства функций y
2x=2, 2x=21, отсюда имеем вторую точку x1=1.
На промежутке [0;1] исполняется неравенство , поэтому .
График степенной функции и прямой приведен ниже.
Площадь фигуры, которая ограничена кривыми равна интегралу:
При интегрировании получим логарифм.
На калькуляторах можете проверить, что площадь положительна.
Пример 2.85 (2401) Вычислить площадь фигуры, ограниченной кривыми y=x, y=x+sin2x, .
Вычисление: Запишем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x, y2(x)=x+sin2x.
Дальше пределы интегрирования:
x1=0, x2=Pi (это известно нам по условию).
На промежутке справедливо неравенство
, поэтому .
Если бы существовала дополнительная точка пересечения, то площадь была бы равна сумме двух интегралов.
Площадь фигуры вычисляем интегрированием: квадрат синуса под интегралом понижаем и выражаем с помощью косинуса двойного угла, а дальше за классической формулой интегрирования
Площадь равна Pi/2, что приблизительно равно 1,5708.
Пример 2.86 (2402) Найти площадь фигуры, ограниченной кривыми
Вычисление: Переписываем функции
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций из условия y1(x)=y2(x):
Поскольку функция парная
то найдем половину площади и результат умножим на двойку.
Из условия находим
что пределы равны плюс, минус бесконечности.
Чтобы легко представить, что мы интегрируем наведем график подынтегральных функций
Учитывая четность функции интегрировать будем от 0 к бесконечности , а полученное значение умножим на двойку.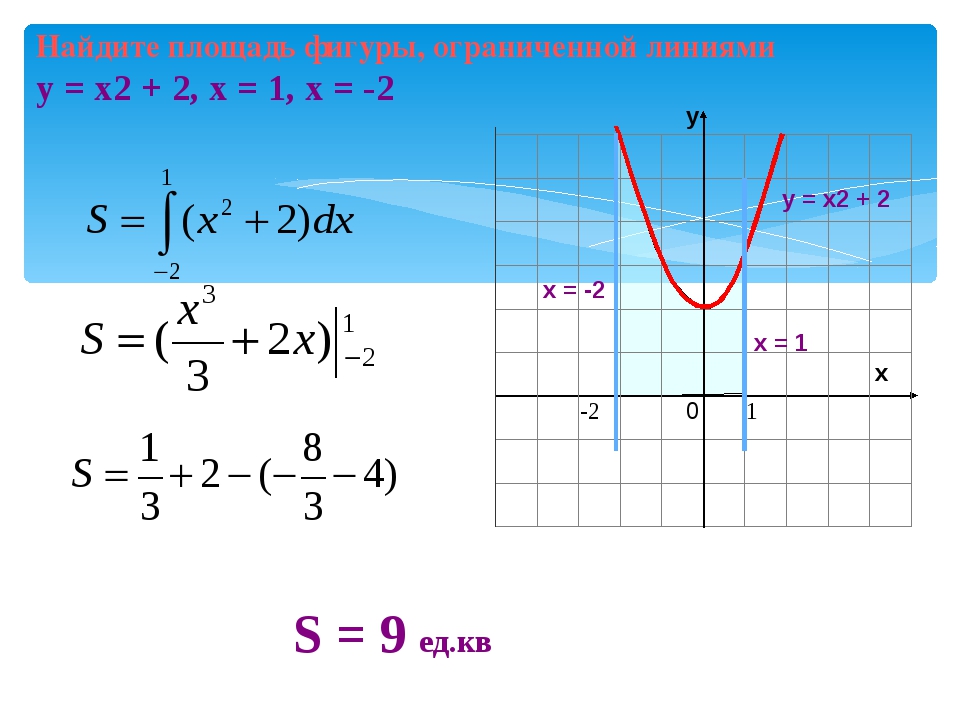
Получим несвойственный интеграл первого рода (детальнее о нем в части ІІІ).
Площадь фигуры вычисляем через предел интеграла:
В результате интегрирования получим арктангенс, который в предельном случае стремится к Pi/2.
Конечная формула достаточно компактна и удобна для расчетов, хотя с таким типом интегралов Вы знакомитесь впервые.
Пример 2.87 (2403) Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Все Вы должны знать, что такой формулой задается уравнение эллипса.
Так как оси эллипса в канонической системе координат являются его осями симметрии, то эти оси делят эллипс на 4 равные части. Поэтому будем рассматривать часть эллипса, который находится в первом квадранте канонической (прямоугольной) системы координат.
Выражаем уравнение функции, которая ограничивает искомую площадь (четверть эллипса):
Запишем пределы интегрирования: из аналитической геометрии известно, что четверть эллипса ограничена прямыми x1=0, x2=a.
Для вычисления площади эллипса в самом интеграле необходимо выполнить замену переменных, что в свою очередь ведет к изменению пределов интегрирование. При этом придем к квадрату косинуса, который понижаем через косинус двойного угла.
В конце манипуляций приходим к табличным интегралам, которые легко интегрируем и подставляем пределы:
Получили классическую формулу площади эллипса S=Pi*a*b .
Видим, если эллипс вырождается в круг при (a=b=R), тогда формула площади круга S=Pi*R2.
Пример 2.88 (2404) Вычислить площадь фигуры, ограниченной кривыми y2=x2(a2-x2).
Вычисление: Так как все переменные в заданном уравнении входят в квадратах, то оси прямоугольной системы координат являются осями симметрии фигуры, которая ограничена этой линией, потому эти оси делят заданную фигуру на 4 равных части. Достаточно рассмотреть часть фигуры, которая заходиться в первом квадранте прямоугольной системы координат.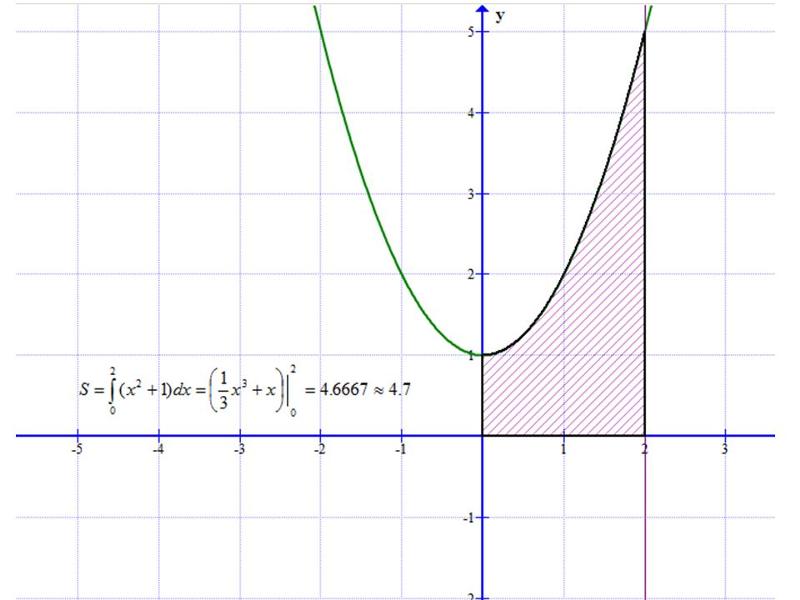
Построим график функции, которая ограничивает искомую площадь четвертины фигуры:
График неизвестной фигуры подобен на крылья бабочки.
При y=0 имеем два корня уравнения x1=0 и x2=a.
Площадь фигуры равна 4 умножить на интеграл с найденными пределами.
Во время интегрирования выполняем замену переменных и пределов интегрирования
Это позволяет перейти к показательной функции, которая легко интегрируется.
Всегда помните, что замена переменных под интегралом ведет к изменению пределов интегрирования.
Пример 2.89 Найти площадь фигуры, ограниченную линиями
Вычисление: Запишем графику функций, которые ограничивают искомую площадь фигуры:
Определим пределы интегрирования из условия y1(x)=y2(x):
отсюда x1=0 и x2=1.
Между функциями справедлива зависимость на [0;1], поэтому .
График функций, что анализируем следующий
Площадь фигуры через определенный интеграл равна 1/3 (сравните 2.
 81 при a=1) :
81 при a=1) :
Пример 2.90 Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Вычислим пределы интегрирования из условия равенства функций y1(x)=y2(x):
Из биквадратного уравнения получим значение точек пересечения:
x1=-1 и x2=1.
Сами же функции в прямоугольных координатах будут иметь вид
Интегрированием находим площадь фигуры (смотри рисунок и образец 2.89) :
Первый интеграл даст арктангенс, запомните хорошо эту формулу.
Пример 2.91 Вычислить площадь фигуры, ограниченной кривыми y=ex, y=e-x,x=1.
Вычисление: Из условия, которое Вы из-за повторяемости должны выучить y1(x)=y2(x) находим точки пересечения кривых:
ex=e-x,x=-x, 2x=0, следовательно, x1=0.
x2=1 (известно за условием).
График функций следующий
Экспоненту интегрировать не трудно, а площадь фигуры выражается формулой (смотри рисунок и образец 2.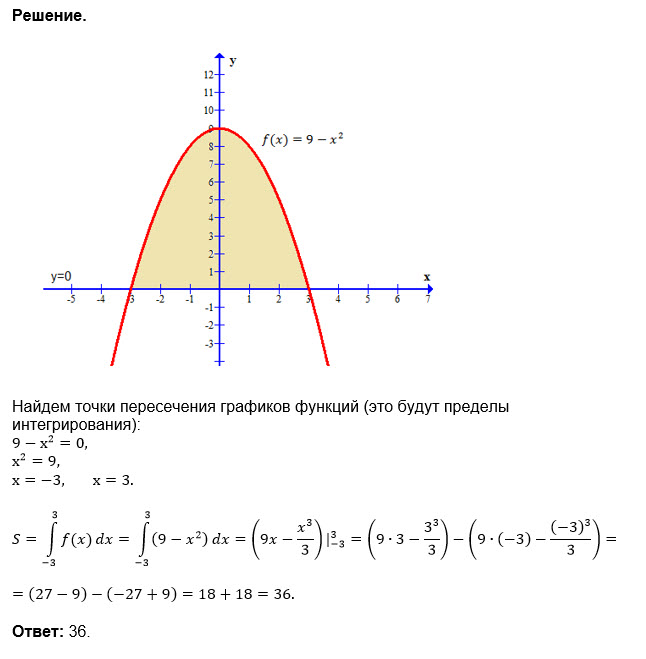 84) :
84) :
Пример 2.92 Найти площадь фигуры, ограниченной кривыми y=ln(x), y=ln2(x).
Вычисление: Пределы интегрирования из условия равенства функций y=ln(x), y=ln2(x) равны x1=1 и x2=e.
Интегрированием логарифмов находим площадь фигуры (смотри рисунок):
Здесь надо проинтегрировать по частям, положив ln(x) =u, (ln2(x)=u) и dx=dv. Попробуйте промежуточные действия провести самостоятельно.
Пример 2.93 Вычислить площадь фигуры, ограниченной кривыми
y=ln(x), y=ln(a), y=ln(b), x=0, где 0<a<b.
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
x (y) =ey (то есть обратная функция к заданной функции y(x)=ln(x)) .
Такой прием применяют, когда пределы интегрирования параллельны оси Оx, то есть y=const.
Запишем пределы интегрирования:
y1=ln(a), y2=ln(b) (берем из начального условия).
График искомой фигуры следующий
Площадь фигуры, которая ограничена заданными кривыми:
Пример 2.94 Найти площадь фигуры, ограниченной кривыми
Вычисление: Пределы интегрирования в формуле площади находим из условия y1(x)=y2(x):
ln(x)/(4x)=x*ln(x).
Упростив на логарифм (если он больше нуля), получим
1=4x2; 4x2-1=0, x1=1/2.
Из условия на логарифм (=0) получим
ln(x) =0; x2=1.
ОДЗ: x>0.
График фигуры в прямоугольных координатах следующий
Площадь фигуры между кривыми (на [0,5;1]) находим интегрированием:
для вычисления интегралов используем метод замены переменных
Вычисление не так просты, поэтому с превращениями попробуйте разобраться самостоятельно.
Пример 2.95 Вычислить площадь фигуры, ограниченной кривыми y=arcsin(x), y=arccos(x), y=0.
Вычисление: Находим точки пересечения кривых из равенства x1(y)=x2(y):
sin(x)=cos(y), отсюда y1=0 (известно за условием) и y1=Pi/4 (образец 2. 93).
93).
На графике это выглядит следующим образом
Учитывая справедливость неравенства вычисляем площадь фигуры:
Думаю, что с такими заданиями на экзамене или модулях Вы справитесь.
Пример 2.96 Найти площадь фигуры, ограниченной кривыми y=tg(x), y=2/3*cos(x), x=0.
Вычисление: Найдем пределы интегрирования, то есть абсциссы точек пересечения заданных функций y1(x)=y2(x):
tg(x)=2/3*cos(x), отсюда
(вторая точка известна за условием).
Кривые на плоскости имеют вид
Площадь фигуры, которая ограничена заданными кривыми () равна интегралу:
Пример 2.97 (2400) Вычислить площадь фигуры, ограниченной кривыми y=|ln(x)|, y=0, x=0,1; x=10.
Вычисление: Выписываем пределы интегрирования x1=0,1; x2=10 из начального условия.
Как строить модуль от логарифма Вы, по-видимому, еще не забыли
Площадь фигуры равна сумме двух интегралов, причем первый берем со знаком минус ():
Во время интегрирования использовали интегрирование частями.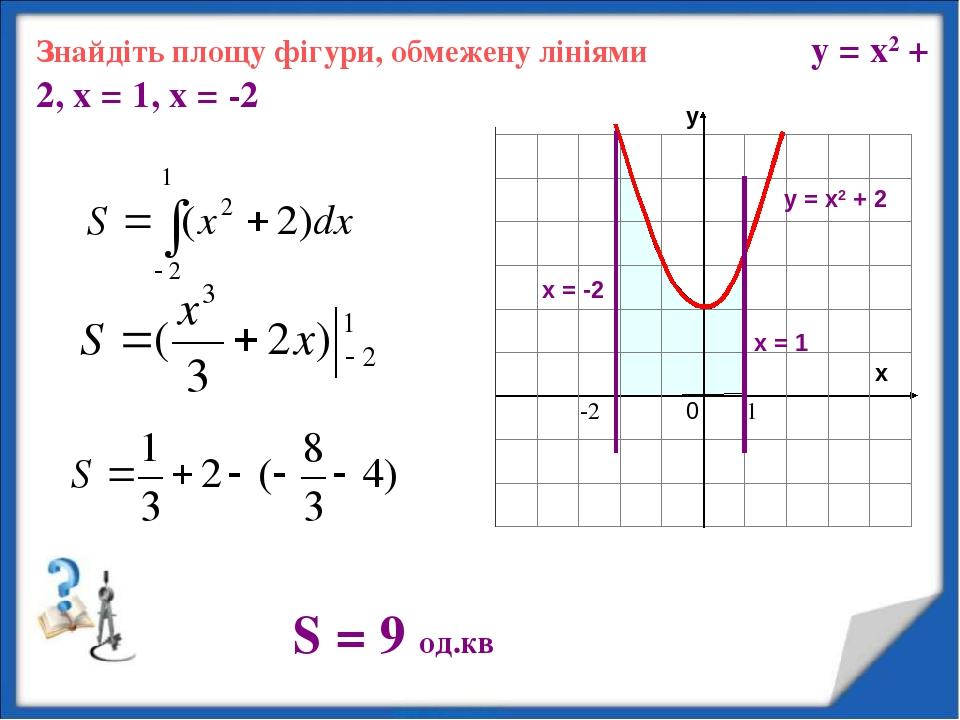
Пример 2.98 (2400) Найти площадь фигуры, ограниченной кривыми y=(x+1)2, x=sin(Pi*y), y=0 .
Вычисление: Построим график функций, которые ограничивают искомую площадь фигуры:
(здесь взяли обратную функцию к заданной y1(x)=(x+1)2), x2=sin(Pi*y).
Выпишем пределы интегрирования:
y1=0; y2=1 (известно за условием).
График функций приведен ниже
Неизвестную площадь фигуры вычисляем интегрированием ():
Пример 2.99 Вычислить площадь фигуры, ограниченной кривыми y=sin(x), y=cos(x), y=0
Вычисление: Из рисунку видно, что площадь S лучше разбить на две части: S=S1+S2.
Запишем уравнение функций, которые ограничивают искомую площадь фигуры:
Интегрируем синус и косинус функции и находим площадь.
Второй вариант заключается в интегрировании разницы обратных функций по y.
Пример 2407 Найти площадь фигуры, ограниченной кривыми (циссоида Диокла) x=2a (a>0).
Вычисление: Поскольку график функции симметричен относительно оси Ox, то будем рассматривать половину площади фигуры (над осью Ox) и результат умножим на 2.
В точке x=2a функция не определена, поэтому будем иметь интеграл второго рода (детальнее смотрите часть ІІІ), он совпадает и, следовательно, площадь будет выражена числом.
Запишем пределы интегрирования:
x1=0 (потому что ) x2=2a (за условием).
График функций следующий
Площадь фигуры, что ограниченна заданной кривой находится достаточно непростым интегрированием
Здесь пришлось трижды выполнять замену переменных, чтобы прийти к правильному ответу.
Еще раз внимательно разберите интеграл.
Пример 2408 Вычислить площадь фигуры, ограниченной кривыми (трактриса), y=0.
Вычисление: Трактриса — кривая, по которой двигается объект, когда его тянуть по горизонтальной плоскости за бечевку фиксированной длины, если направление движения тягача является ортогональным к начальному положению бечевки и скорость тягача бесконечно малая величина. 2). Получается такой своеобразный «лепесток», площадь которого нам и предстоит вычислить.
2). Получается такой своеобразный «лепесток», площадь которого нам и предстоит вычислить.
Наша задача имеет точное решение. А именно, площадь S указанной фигуры следующая:
Однако мы будем использовать несколько иной подход.
Рис. 1. Вычисление области фигуры, ограниченной двумя кривыми
Метод, который описывается далее и применяется нами для вычисления площади фигуры, имеет отношение к теории вероятностей и математической статистике(обычно такой подход называют методами Монте-Карло).
При вычислении площади фигуры мы будем исходить из следующих соображений. Во-первых, замечаем, что область ограниченная кривыми, полностью попадает в единичный квадрат с левой нижней вершиной в точке начала координат и правой верхней вершиной в точке с единичными координатами. Если мы случайным образом выберем точку внутри этого квадрата, то она с некоторой вероятностью попадает в область, что ограничена кривыми (то есть попадает внутрь «лепестка»).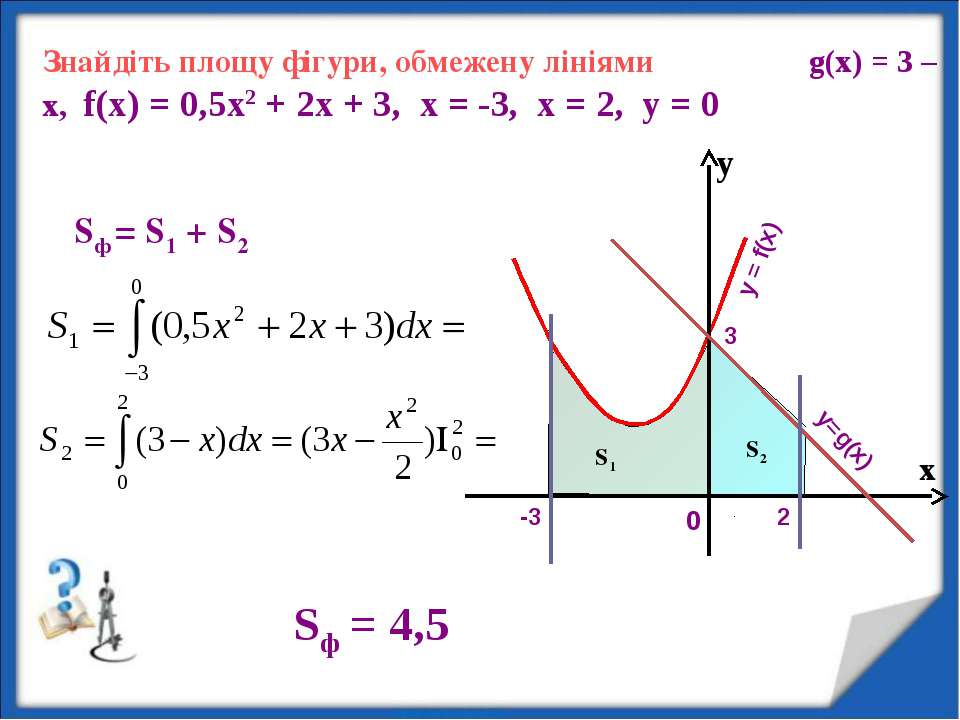
Теория вероятностей утверждает, что эта самая вероятность равна отношению площадей «лепестка» и квадрата. У квадрата с единичной стороной площадь равна единице. Поэтому площадь «лепестка»(которую нам необходимо вычислить) равняется вероятности, с которой случайным образом выбранная точка попадает внутрь «лепестка». Это будет «во вторых».
В третьих, если взять очень много случайных точек, равномерно распределенных по квадрату, и вычислить отношение количества точек внутри «лепестка» к общему количеству точек, в идеале получим оценку, близкую к вероятности попадания случайно выбранной точки внутрь «лепестка».
Мы всю эту процедуру немного модифицируем и поступим следующим образом. Вместо того чтобы генерировать случайны точки, покроем весь квадрат равноотстоящими узловыми точками. Посчитаем, сколько их попало внутрь «лепестка»(то есть области, ограниченной кривыми), и поделим на общее количество точек. Это и будет результат.
Программный код, в котором реализован такой подход, представлен ниже:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Количество равных интервалов, на которые
# делятся стороны единичного квадрата
n = 500
# "Цена деления" - расстояние между соседними точками
dz = 1 / n;
# Количество точек, которые попадают внутрь области
pts = 0
# Начальное значение индекса, определяющего столбец точек
i = 0
# Внешний оператор цикла. Перебираем столбцы точек
while i = x**2:
# Еще одна точка внутри области
pts += 1
# Значение второго индекса увеличиваем на единицу
j += 1
# Значение первого индекса увеличиваем на единицу
i += 1
# Вычисляем площадь фигуры
S = pts / (n + 1) ** 2
# Отображаем результат
print("Площадь фигуры: " + str(S))
Перебираем столбцы точек
while i = x**2:
# Еще одна точка внутри области
pts += 1
# Значение второго индекса увеличиваем на единицу
j += 1
# Значение первого индекса увеличиваем на единицу
i += 1
# Вычисляем площадь фигуры
S = pts / (n + 1) ** 2
# Отображаем результат
print("Площадь фигуры: " + str(S))
Результат, который приведен ниже, достаточно близок к точному решению:
Чтобы понять логику вычислений, имеет смысл мысленно представить, как мы разбиваем каждую из сторон квадрата на определенное количество интервалов. Количество этих интервалов записывается в переменную n(то есть значение 500).
Границу интервалов будем называть узловыми точками. Через каждую узловую точку на сторонах квадрата проводим горизонтальные и вертикальные линии. Точки пересечений этих линий — это именно те точки, которые нам нужны. Каждую такую точку можно «идентифицировать» с помощью двух индексов.
Первый индекс определяет узловую точку по горизонтали, а второй — узловую точку по вертикали. На пересечении линий, проходящих через эти узловых точки, находится «идентифицируемая» точка внутри квадрата.
Если мы зафиксируем первый индекс, и будем брать разные значения для второго индекса, то все соответствующие точки будут находится на одной вертикальной прямой. Про такие точки будем говорить, что они находятся в одном столбце. Если зафиксировать второй индекс и брать разные значения первого индекса, то все соответствующие точки будут находиться на одной горизонтальной прямой. Про такие точки можем говорить, что они формируют ряд точек.
В каждому ряду и в каждом столбце размещено ровно n + 1 точек ( если учитывать и те точки, что находятся на координатных осях).
Расстояние (по горизонтали или по вертикали) между двумя соседними узловыми точками равняется, очевидно, единице, деленной на количество интервалов, на которые разбивалась каждая из сторон квадрата: такая «цена деления» записывается в переменную dz(значение 1/n). 2 = x**2. Кстати, вместо инструкции y = x**2 вполне законно можно было использовать выражение x ** 2 . Такого типа выражения в Python допустимы.
2 = x**2. Кстати, вместо инструкции y = x**2 вполне законно можно было использовать выражение x ** 2 . Такого типа выражения в Python допустимы.
Начальное значение индекса i , определяющего столбец точек, должно быть нулевым (нулевой индекс соответствует точке на координатной оси). Через первый индекс, напомним, «нумеруются» столбцы точек. Когда запускается внешний оператор цикла, в нем проверяется условие i
В теле оператора цикла командой x = dz * i вычисляется координата х (вдоль горизонтальной оси — абсцисса) для точек, находящихся в данном столбце (столбец, напомним, определяется значением индекса i ). Также поскольку далее мы планируем перебирать точки в столбце, командой j = О устанавливаем начальное ну левое значение для второго индекса, (определяющего положение внутренних точек). После этого выполняется второй, внутренний оператор цикла. В нем проверяется условие j
В теле внутреннего оператора цикла командой y = dz * j вычисляется координата у для точки в столбце (координата вдоль вертикальной оси-ордината).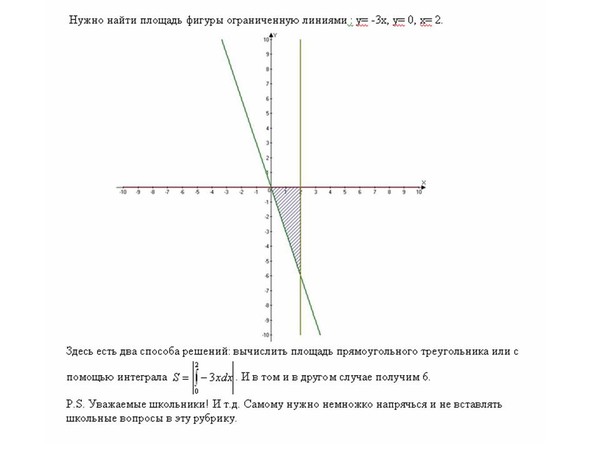 2 точек). Поэтому если мы поделим одно значение на другое, получим площадь «лепестка». Соответствующее значение вычисляется командой S = рts / (n + 1) ** 2. Наконец, командой print отображаем результат.
2 точек). Поэтому если мы поделим одно значение на другое, получим площадь «лепестка». Соответствующее значение вычисляется командой S = рts / (n + 1) ** 2. Наконец, командой print отображаем результат.
Интересное видео в тему:
b {f \ left (x \ right) dx} = F \ left (b \ right) — F \ left (a \ right), \], где \ (F \ left (x \ right) \) — любая первообразная от \ (f \ left (x \ right). \)
Рисунок 1.Мы можем расширить понятие площади под кривой и рассмотреть площадь области между двумя кривыми.
Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) — две непрерывные функции и \ (f \ left (x \ right) \ ge g \ left (x \ right) \) на отрезке \ (\ left [{a, b} \ right], \), то область между кривыми \ (y = f \ left (x \ right) \) и \ (y = g \ left (x \ right) \) в этом интервале равно
\ [A = \ int \ limits_a ^ b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}.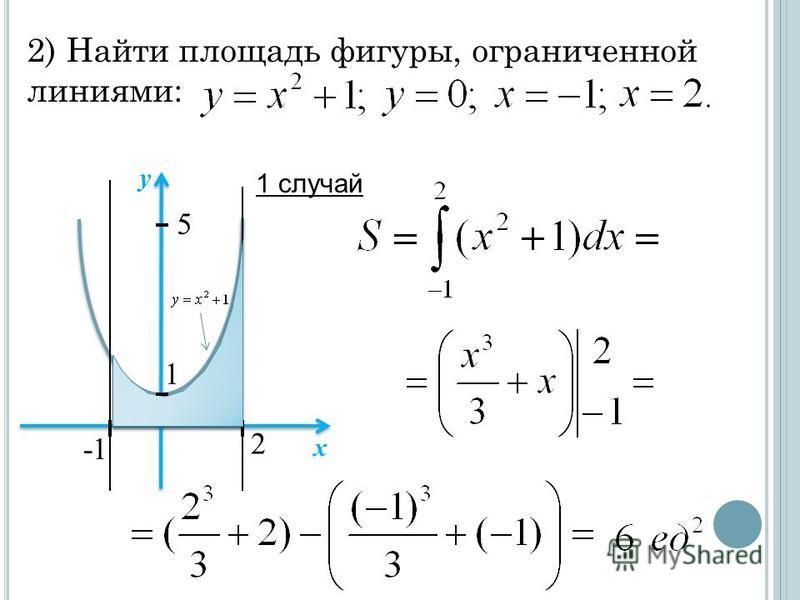 b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx} = F \ left (b \ right) — G \ left (b \ right) — F \ влево (а \ вправо) + G \ влево (а \ вправо), \]
b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx} = F \ left (b \ right) — G \ left (b \ right) — F \ влево (а \ вправо) + G \ влево (а \ вправо), \]
, где \ (F \ left (x \ right) \) и \ (G \ left (x \ right) \) — первообразные функций \ (f \ left (x \ right) \) и \ (g \ left (x \ right), \) соответственно.
Обратите внимание, что эта область всегда будет неотрицательной как \ (f \ left (x \ right) — g \ left (x \ right) \ ge 0 \) для всех \ (x \ in \ left [{a, b } \ right]. \)
Если есть точки пересечения, мы должны разбить интервал на несколько подынтервалов и определить, какая кривая больше на каждом подынтервале.\ prime \ left (t \ right), \) \ (y \ left (t \ right) \) здесь предполагается непрерывными на интервале \ (\ left [{a, b} \ right]. \) Кроме того то есть функция \ (x \ left (t \ right), \) должна быть монотонной на этом интервале.
Рис. 5. Если \ (x = x \ left (t \ right), \) \ (y = y \ left (t \ right), \) \ (0 \ le t \ le T \) являются параметрическими уравнениями гладкая кусочно замкнутая кривая \ (C \), пересекаемая против часовой стрелки и ограничивающая область слева (рис. \ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}.2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)
\ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}.2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)
Пример 3
Найдите координату точки \ (a \), которая разделяет область под корневой функцией \ (y = \ sqrt {x} \) на интервале \ (\ left [{0,4} \ right] \) на равные части.
Пример 4
Область ограничена вертикальными линиями \ (x = t \), \ (x = t + \ frac {\ pi} {2} \), осью \ (x — \) и кривой \ (y = a + \ cos x, \) где \ (a \ ge 1. \) Определите значение \ (t \), при котором область имеет наибольшую площадь.{t + \ frac {\ pi} {2}} = a \ left ({t + \ frac {\ pi} {2}} \ right) + \ sin \ left ({t + \ frac {\ pi} { 2}} \ right) — at — \ sin t = \ cancel {at} + \ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi} {2}} \ right) — \ cancel {at} — \ sin t = \ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi} {2}} \ right) — \ грех т. \]
Использование тождества разницы синусов
\ [\ sin \ alpha — \ sin \ beta = 2 \ cos \ frac {{\ alpha + \ beta}} {2} \ sin \ frac {{\ alpha — \ beta}} {2}, \]
получаем
\ [A = \ frac {{a \ pi}} {2} + 2 \ cos \ frac {{t + \ frac {\ pi} {2} + t}} {2} \ sin \ frac {{\ cancel {t} + \ frac {\ pi} {2} — \ cancel {t}}} {2} = \ frac {{a \ pi}} {2} + 2 \ cos \ left ({t + \ frac {\ pi} {4}} \ right) \ sin \ frac {\ pi} {4} = \ frac {{a \ pi}} {2} + 2 \ cos \ left ({t + \ frac {\ pi } {4}} \ right) \ cdot \ frac {{\ sqrt 2}} {2} = \ frac {{a \ pi}} {2} + \ sqrt 2 \ cos \ left ({t + \ frac { \ pi} {4}} \ right). \]
\]
Область имеет наибольшую площадь, когда \ (\ cos \ left ({t + \ frac {\ pi} {4}} \ right) = -1. \)
Решая это уравнение, находим
\ [\ cos \ left ({t + \ frac {\ pi} {4}} \ right) = — 1, \; \; \ Rightarrow t + \ frac {\ pi} {4} = \ pi + 2 \ pi n, \; \; \ Rightarrow t = \ frac {{3 \ pi}} {4} + 2 \ pi n, \, n \ in \ mathbb {Z}. \]
См. Другие проблемы на странице 2.
Площадь
Площадь области, ограниченной графиком функции, осью x и двумя вертикальными границами, может быть определена непосредственно путем вычисления определенного интеграла.Если f (x ) ≥ 0 на [ a, b ], то площадь ( A ) области, лежащей ниже графика f (x ), выше оси x и между строками x = a и x = b — этоРисунок 1 Нахождение площади под неотрицательной функцией.
Если f (x ) ≤ 0 на [ a, b ], то область ( A ) области, лежащей над графиком f (x ), ниже оси x , а между строками x = a и x = b равно
Рисунок 2 Нахождение области над отрицательной функцией.
Если f (x ) ≥ 0 на [ a, c ] и f (x ) ≤ 0 на [ c, b ], то площадь ( A ) области, ограниченной График f (x ), ось x и линии x = a и x = b будут определяться следующими определенными интегралами:
Рисунок 3 Площадь, ограниченная функцией, знак которой меняется.
Обратите внимание, что в этой ситуации необходимо определить все точки, в которых график f (x ) пересекает ось x и знак f (x ) на каждом соответствующем интервале.
Для некоторых задач, требующих области областей, ограниченных графиками двух или более функций, необходимо определить положение каждого графика относительно графиков других функций области. Возможно, потребуется найти точки пересечения графиков, чтобы определить пределы интегрирования.Например, если f (x ) ≥ g ( x ) на [ a, b ], то площадь ( A ) области между графиками f (x ) и g ( x ), а линии x = a и x = b —
Рисунок 4 Область между двумя функциями.
Обратите внимание, что аналогичное обсуждение может быть проведено для областей, определенных графиками функций y , оси y и линий y = a и y = b .
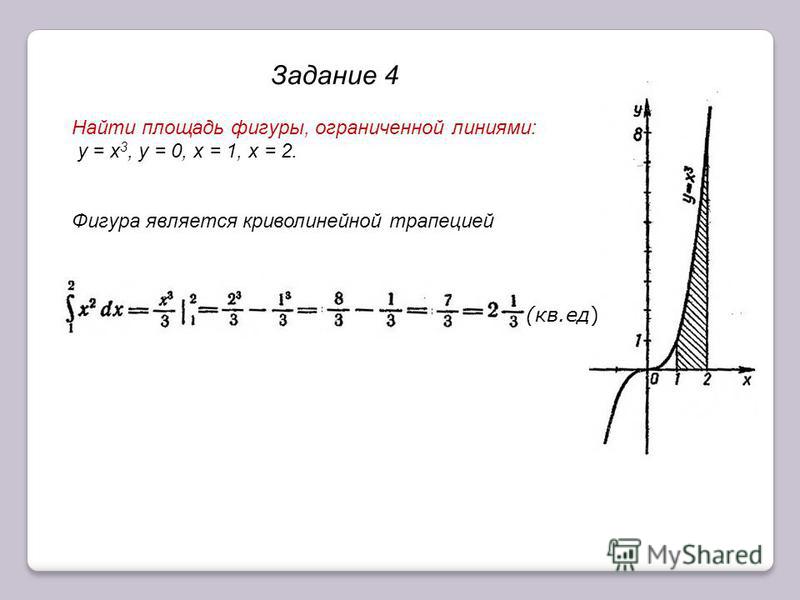
Пример 1: Найдите площадь области, ограниченной x = x 2 , осью x , x = –2 и x = 3.
Поскольку f (x ) ≥ 0 на [–2,3], площадь ( A ) равна
Пример 2: Найдите площадь области, ограниченной x = x 3 + x 2 -6 x и осью x .
Установив y = 0, чтобы определить, где график пересекает ось x , вы обнаружите, что
Поскольку f ( x ) ≥ 0 на [–3,0] и f ( x ) ≤ 0 на [0,2] (см. Рисунок 5), площадь ( A ) регион
Рисунок 5 Диаграмма для примера 2. 2 и линией y = x.2, y = 0 и x = 1 о следующем …
2 и линией y = x.2, y = 0 и x = 1 о следующем …
Эрик К.
задано • 14.02.19a) ось x
b) прямая y = -3
c) прямая x = 3
Дуг К. ответил • 16.02.19
Репетитор по математике с репутацией, делающий сложные концепции понятными
Вот URL-адрес графиков Desmos, упомянутых в видео:
https: // www.desmos.com/calculator/ip98mthmkg
Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
Mathway | Популярные задачи
| 1 | Найдите производную — d / dx | натуральное бревно x | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | e ^ x | |
| 4 | Оценить интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (x) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оценить интеграл | интеграл e ^ x относительно x | |
| 11 | Оценить интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оценить интеграл | интеграл квадратного корня из x относительно x | |
| 13 | Найдите производную — d / dx | cos (x) ^ 2 | |
| 14 | Оценить интеграл | интеграл от 1 / x относительно x | |
| 15 | Оценить интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оценить интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оценить интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оценить интеграл | интеграл от 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оценить интеграл | интеграл 2x по отношению к x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оценить интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное полено 2х | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оценить интеграл | интеграл от e ^ (3x) относительно x | |
| 41 | Оценить интеграл | интеграл от cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оценить интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оценить интеграл | интеграл от tan (x) ^ 2 относительно x | |
| 50 | Оценить интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оценить интеграл | интеграл от x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оценить интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оценить интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оценить интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оценить интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | e ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оценить интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | arcsin (x) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оценить интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное полено 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найти производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оценить интеграл | интеграл cos (x) относительно x | |
| 81 | Оценить интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найти производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оценить интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 относительно x | |
| 84 | Оценить интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (х) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5х | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оценить интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оценить интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | Корень четвертой степени из 4x ^ 4 + 4 (16) | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оценить интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оценить интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
4а.
 Объем Solid of Revolution путем интеграции (дисковый метод)
Объем Solid of Revolution путем интеграции (дисковый метод)М. Борна
Токарный станок
Многие твердые предметы, особенно сделанные на токарном станке , имеют круглое поперечное сечение и изогнутые стороны. На этой странице мы видим, как с помощью интеграции найти тома таких объектов.
Предметы, изготовленные на токарном станке …
Пример 1
Рассмотрим область, ограниченную прямой y = 3x, осью x и x = 1:
График `y = 3x` с заштрихованной областью под» кривой «от` x = 0` до `x = 1`.
Когда заштрихованная область поворачивается на 360 ° вокруг оси «x», создается объем.
Получившееся твердое тело представляет собой конус:
Область под кривой `y = 3x` от` x = 0` до `x = 1`, повернутой вокруг оси` x`, показывая типичный диск.
Дисковый метод для поиска томов
Чтобы найти этот объем, мы могли бы взять срезы (темно-зеленый диск , показанный выше, является типичным срезом), каждый шириной `dx` и радиусом` y`:
Типичный диск, показанный с его размерами, радиусом `= y` и« высотой »` = dx`. 3` (Проверяет ОК.2] dx`
3` (Проверяет ОК.2] dx`
На следующем общем графике y_2 выше y_1. Нижний и верхний пределы области, которая должна быть повернута, обозначены вертикальными линиями в точках «x = a» и «x = b».
Площадь, ограниченная кривыми y_1 и y_2 и линиями x = a и x = b, включая типичный прямоугольник .xyab`y_2`
`y_1`
Площадь, ограниченная кривыми `y_1` и` y_2` и линиями `x = a` и` x = b`.
Когда мы вращаем такую фигуру вокруг оси и делаем срезы, в результате получается шайба формы (с круглым отверстием посередине).2` (нижняя кривая), `y = x + 1` (линия вверху) и` x = 0`, показывая типичный прямоугольник.
Нижний предел интегрирования равен «x = 0» (поскольку в вопросе указано «x ≥ 0»).
Затем нам нужно найти место пересечения кривых, чтобы мы знали верхний предел интегрирования.
Приравнивая 2 выражения и решая:
2 x 2 = x + 1
2 x 2 — x — 1 = 0
(2 x + 1) ( x -1) = 0
x = 1 (поскольку нам нужно учитывать только x ≥ 0.
3`
`~~ 8.2 = 4` в квадранте I, повернутом вокруг оси `y`.
Ответ
Мы понимаем, что это эллипс. Вопрос говорит нам, что интересующая нас область находится только в первом квадранте.
Эллипс x 2 + 4 y 2 = 4, показывающий участок, ограниченный кривой, x = 0, x = 2 и ось x .
Из диаграммы видно, что пределы ограниченной области равны y = 0 и y = 1.3`
Приложения
1. Объем винной бочки
Винная бочка имеет радиус в верхней части 30 см и радиус в середине 40 см. Высота бочки 1 м. Каков объем бочки (в л), если предположить, что форма сторон параболическая?
Ответ
Положим бочку набок, чтобы облегчить алгебру:
Парабола с вершиной в точке `(0, 40)` и проходящая через `(50, 30)`.
Нам нужно найти уравнение параболы с вершиной в точке `(0, 40)` и проходящей через `(50, 30)`.2) / (250) + 40`
Нам нужно найти объем бочки, который образуется, когда мы вращаем эту параболу между x = -50 и x = 50 вокруг оси x .2ч.
Интересно, что Архимед (тот, кто, как известно, выпрыгнул из своей ванны и побежал по улице с криком «Эврика! Я понял») использовал этот подход, чтобы найти объемы сфер около 200 г. до н.э. Этот метод был почти забыт до начала 1700-х годов, когда исчисление было разработано Ньютоном и Лейбницем.
Мы видим, как решить проблему, используя оба подхода.
Объем историческим методом:
Ответ
Поскольку дыня симметрична, мы можем вычислить объем одной половины дыни, а затем удвоить наш ответ.3` или `9.161 \» L «`. Это примерно то же самое, что мы получили, нарезав арбуз и увеличив объем ломтиков.
[См. Также Архимед и площадь параболического сегмента.]
Глава 8 Применение Integral.pmd
% PDF-1.3 % 250 0 объект >>>] / ON [301 0 R] / Order [] / RBGroups [] >> / OCGs [301 0 R] >> / Pages 242 0 R / Type / Catalog >> эндобдж 251 0 объект > / Шрифт >>> / Поля 238 0 R >> эндобдж 247 0 объект > поток приложение / pdf
 pmd
pmd
 Перебираем столбцы точек
while i = x**2:
# Еще одна точка внутри области
pts += 1
# Значение второго индекса увеличиваем на единицу
j += 1
# Значение первого индекса увеличиваем на единицу
i += 1
# Вычисляем площадь фигуры
S = pts / (n + 1) ** 2
# Отображаем результат
print("Площадь фигуры: " + str(S))
Перебираем столбцы точек
while i = x**2:
# Еще одна точка внутри области
pts += 1
# Значение второго индекса увеличиваем на единицу
j += 1
# Значение первого индекса увеличиваем на единицу
i += 1
# Вычисляем площадь фигуры
S = pts / (n + 1) ** 2
# Отображаем результат
print("Площадь фигуры: " + str(S))

 3`
3` 2) / (250) + 40`
2) / (250) + 40`