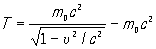Кинетическая энергия — Википедия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

История понятия

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы»^[5].

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}},

при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m}.

Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}

Здесь  M{\displaystyle \ M} — масса тела,  v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[6].

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса

[7]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («

плотность кинетической энергии турбулентности»^[7], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (p^=−jℏ∇{\displaystyle {\hat {p}}=-j\hbar \nabla },  j{\displaystyle \ j} — мнимая единица):

T^=p^22m=−ℏ22mΔ{\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }

где ℏ{\displaystyle \hbar } — редуцированная постоянная Планка, ∇{\displaystyle \nabla } — оператор набла, Δ{\displaystyle \Delta } — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[8].

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как

T=mc21−v2/c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}

где  m{\displaystyle \ m} — масса покоя,  v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта,  c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде  F→=m⋅d(v→/1−v2/c2)/dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).

При скоростях, много меньших скорости света (v≪c{\displaystyle v\ll c}) имеем 1−v2/c2≈1−v2/2c2{\displaystyle {\sqrt {1-v^{2}/c^{2}}}\approx 1-v^{2}/2c^{2}} и выражение для  T{\displaystyle \ T} переходит в классическую формулу  T=1/2⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[9][10].

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также

Примечания

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ ^{1 2} Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
3. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
4. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
5. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
6. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
7. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
8. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
9. ↑ Айзерман, 1980, с. 54.
10. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)

Литература

wikipedia.bio

•Работа, так же как и кинетическая энергия, измеряется в джоулях.

Скорость совершения работы (передачи энергии) называется мощность.

•Мощность есть работа, совершаемая в

единицу времени.

• Мгновенная мощность

или

•Средняя мощность

•Мощность измеряется в ваттах: 1 Вт = 1 Дж/с.

Консервативные силы и системы

•Кроме контактных взаимодействий, наблюдаются взаимодействия между телами, удаленными друг от друга. Подобное взаимодействие осуществляется посредством физических полей (особая форма материи).

•Каждое тело создает вокруг себя поле, которое проявляет себя именно воздействием на другие тела.

Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и конечного положения тела, называются консервативными.

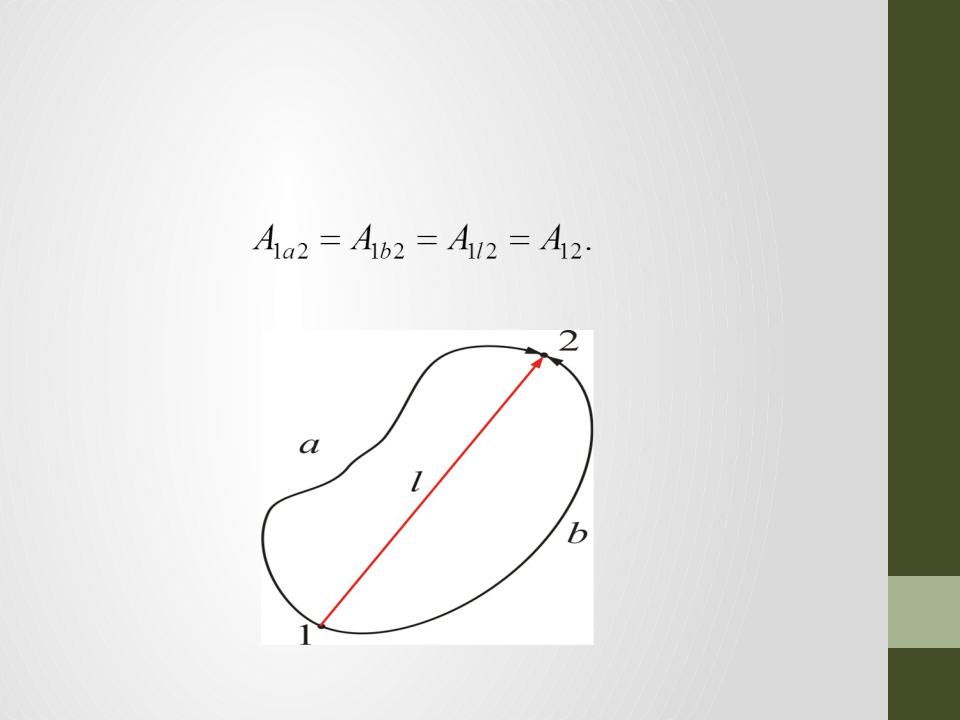
•Обозначим:

•A – работа консервативных сил, по перемещению тела из точки 1 в точку 2.

•Изменение направления движения на противоположное вызывает изменение знака работы консервативных сил. Отсюда следует, что работа консервативных сил вдоль замкнутой кривой равна нулю:

•Интеграл по замкнутому контуру S называется циркуляцией вектора .

Следовательно, если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна.

Консервативные силы: сила тяжести, электростатические силы, силы центрального стационарного поля.

Неконсервативные силы: силы трения, силы

•Консервативная система – такая, внутренние силы которой только консервативные, внешние – консервативны и стационарны. Пример консервативных сил – гравитационные силы.

•Работа по подъему тела массы m на высоту h равна

• С другой стороны,

где α – угол между силой и направлением

перемещения.

Таким образом, из примера видно, что

работа не зависит от формы пути, значит,

силы консервативны, а поле этих сил

потенциально.

Потенциальная энергия

•Если на систему материальных тел действуют консервативные силы, то можно ввести понятие

потенциальной энергии.

Работа, совершаемая консервативными силами при изменении конфигурации системы, то есть при изменении положения тел относительно системы отсчета, не зависит от того, как было осуществлено это изменение.

•Работа определяется только начальной и конечной конфигурациями системы.

•Здесь потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат всех тел системы в поле консервативных сил.

•Итак, K определяется скоростью движения тел системы,

•а U – их взаимным расположением.

• Из следует, что работа консервативных сил равна убыли потенциальной энергии:

•Нет единого выражения для U.

•В разных случаях она определяется по- разному.

Потенциальная энергия при гравитационном взаимодействии

•Работа тела при падении или

•Условились считать, что на поверхности Земли

тогда

•Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга, потенциальную энергию можно найти по формуле

•

•Потенциальная энергия тела массой m, находящегося на высоте h над поверхностью Земли: P(h)=mgh. Потенциальная кривая в этом случае: P=P(h) — прямая линия, проходящая через начало координат , тангенс угла наклона которой к оси h: tgα=mg. Значит, чем больше масса тела, тем больше α.

studfile.net

Кинетическая энергия — Википедия. Что такое Кинетическая энергия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[2]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[3]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

История понятия

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы»^[4].

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}},

при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m}.

Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}

Здесь  M{\displaystyle \ M} — масса тела,  v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[5].

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[6]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[6], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (p^=−jℏ∇{\displaystyle {\hat {p}}=-j\hbar \nabla },  j{\displaystyle \ j} — мнимая единица):

T^=p^22m=−ℏ22mΔ{\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }

где ℏ{\displaystyle \hbar } — редуцированная постоянная Планка, ∇{\displaystyle \nabla } — оператор набла, Δ{\displaystyle \Delta } — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[7].

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как

T=mc21−v2/c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}

где  m{\displaystyle \ m} — масса,  v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта,  c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде  F→=m⋅d(v→/1−v2/c2)/dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).

Выражение для  T{\displaystyle \ T} можно переписать в форме T=mv2/(1−v2/c2+1−v2/c2).{\displaystyle T=mv^{2}/(1-v^{2}/c^{2}+{\sqrt {1-v^{2}/c^{2}}}).} При малых скоростях (v≪c{\displaystyle v\ll c}) оно переходит в классическую формулу  T=1/2⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[8][9].

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[10]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также

Примечания

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
3. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
4. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
5. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
6. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
7. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
8. ↑ Айзерман, 1980, с. 54.
9. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)
10. ↑ Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.

Литература

wiki.sc

Кинетическая энергия — это… Что такое Кинетическая энергия?



Кинетическая энергия

        энергия механической системы, зависящая от скоростей движения её точек. К. э. Т материальной точки измеряется половиной произведения массы m этой точки на квадрат её скорости υ, т. е. Т = ¹/₂mυ². К. э. механической системы равна арифметической сумме К. э. всех её точек: Т = Σ¹/₂m_kυ²_k. Выражение К. э. системы можно ещё представить в виде Т = ¹/₂Mυ_c² + T_c, где М — масса всей системы, υ_c — скорость центра масс, T_c — К. э. системы в её движении вокруг центра масс. К. э. твёрдого тела, движущегося поступательно, вычисляется так же, как К. э. точки, имеющей массу, равную массе всего тела. Формулы для вычисления К. э. тела, вращающегося вокруг неподвижной оси, см. в ст. Вращательное движение.          Изменение К. э. системы при её перемещении из положения (конфигурации) 1 в положение 2 происходит под действием приложенных к системе внешних и внутренних сил и равно сумме работ . Это равенство выражает теорему об изменении К. э., с помощью которой решаются многие задачи динамики.

         При скоростях, близких к скорости света, К. э. материальной точки

        

        ,

         где m₀ — масса покоящейся точки, с — скорость света в вакууме (m₀с² — энергия покоящейся точки). При малых скоростях (υ) последнее соотношение переходит в обычную формулу ¹/₂mυ². См. также Энергия, Энергии сохранения закон.

        

         С. М. Тарг.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Кинетическая теория газов
• Кинетические методы анализа

Смотреть что такое «Кинетическая энергия» в других словарях:

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, энергия, которой обладает движущийся предмет. Получает ее, начав двигаться. Зависит от массы ( ) предмета и его скорости (v), согласно равенству: К. э. = 1/2mv2. При ударе преобразуется в другую форму энергии, такую как… …   Научно-технический энциклопедический словарь

• Кинетическая энергия — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, механическая энергия системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2 от mv2. В сумме с… …   Иллюстрированный энциклопедический словарь

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механич. системы, зависящая от скоростей её точек. К. э. Т матер. точки равна: T=mv2/2, где m масса этой точки, v её скорость. К. э. механич. системы равна сумме К. э. всех её точек: T=Smkv2k/2. Выражение К. э. системы можно ещё… …   Физическая энциклопедия

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механической системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2mv2 …   Большой Энциклопедический словарь

• кинетическая энергия — ▲ энергия ↑ скорость, масса (материи) < > потенциальная энергия кинетическая энергия энергия, определяемая скоростью тела и его массой. механическая энергия. маховик …   Идеографический словарь русского языка

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механич. системы, зависящая от скоростей её точек. К. э. Т материальной точки измеряется половиной произведения массы т этой точки на квадрат её скорости , т. е. Т . К. э. механич. системы равна арифметич. сумме К …   Физическая энциклопедия

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (энергия движения) запас энергии движущегося тела, превращающийся в другой вид энергии при прекращении движения. Напр. К. Э. пули, попадающей в мишень, превращается в теплоту. При поступательном движении тела его К. Э. равна половине произведения …   Морской словарь

• кинетическая энергия — Энергия, которой обладает движущееся тело; определяется как половина произведения массы на квадрат скорости. Для жидкости обычно говорят о плотности кинетической энергии мере количества энергии движения, которой обладает единица объема жидкости.… …   Справочник технического переводчика

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (см.) механического движения тела или системы тел, зависящая от скоростей их точек. К. э. поступательно движущегося тела равна половине произведения массы тела на квадрат его скорости: К э. системы тел равна сумме К. э. всех тел системы …   Большая политехническая энциклопедия

• КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — сила в движении, действующая сила движения; в отличие от потенциальной энергии силы в покое. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907 …   Словарь иностранных слов русского языка

• Кинетическая энергия — Кинетическая энергия  энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной… …   Википедия

dic.academic.ru

Кинетическая энергия — это… Что такое Кинетическая энергия?

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции тела

 — угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

где:

 — масса объекта;

 — скорость движения объекта в инерциальной системе отсчета;

 — скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

См. также

academic.ru

Кинетическая энергия — WiKi

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

История понятия

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой m{\displaystyle m}  называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}} ,

при этом предполагается, что скорость точки v{\displaystyle v}  всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} ) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m} .

Если F→{\displaystyle {\vec {F}}}  — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} . Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t}  и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t} , причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t} , получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T} .

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T}  остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.} 

Здесь  M{\displaystyle \ M}  — масса тела,  v{\displaystyle \ v}  — скорость центра масс, ω→{\displaystyle {\vec {\omega }}}  и I{\displaystyle I}  — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[6].

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V} . Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}} , то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V}  (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},} 

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z} , означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[7]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘} , vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }} , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},} 

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2}  — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2}  — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[7], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}}  — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}}  — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}}  зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}}  от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[9][10].

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.} 

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}  между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также

Примечания

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ ^{1 2} Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
3. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
4. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
5. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
6. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
7. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
8. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
9. ↑ Айзерман, 1980, с. 54.
10. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)

Литература

ru-wiki.org

Кинетическая энергия — это… Что такое Кинетическая энергия?

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции тела

 — угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

где:

 — масса объекта;

 — скорость движения объекта в инерциальной системе отсчета;

 — скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

См. также

dik.academic.ru