Кинетическая и потенциальная энергии
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от 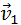 до
до 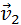 то силы совершили определенную работу A.
то силы совершили определенную работу A.
Работа всех приложенных сил равна работе равнодействующей силы (см. рис. 1.19.1).
|
Рисунок 1.19.1. Работа равнодействующей силы. |
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы 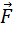 В этом случае векторы силы
В этом случае векторы силы 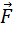 перемещения
перемещения 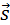 скорости
скорости  и ускорения
и ускорения 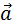 направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
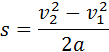
Отсюда следует, что
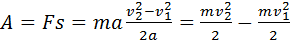
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии и выражается теоремой о кинетической энергии:
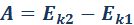
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
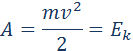
Если тело движется со скоростью  , то для его полной остановки необходимо совершить работу
, то для его полной остановки необходимо совершить работу

В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.
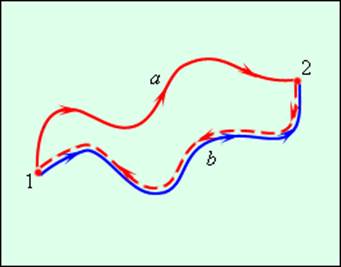
Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рис. 1.19.2.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
|
Рисунок 1.19.2. Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0 |
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести 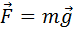 . Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения
. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения 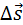 на ось OY, направленную вертикально вверх:
на ось OY, направленную вертикально вверх:
ΔA = Fт Δs cos α = –mgΔs y, |
где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY (рис. 1.19.3), то сила тяжести совершила работу

|
Рисунок 1.19.3. Работа силы тяжести |
Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
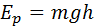
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
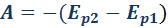
Потенциальная энергия Eр зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
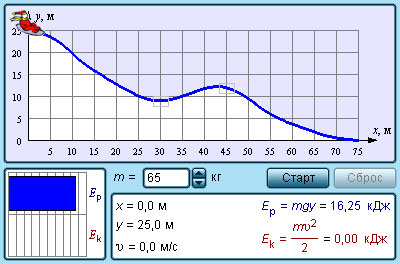 |
Модель. Кинетическая и потенциальная энергия. |
Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготения). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид:
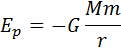
где M – масса Земли, G – гравитационная постоянная.
Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была не деформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком (см 1.18):
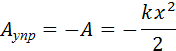
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
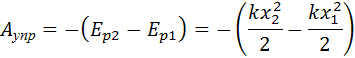
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя.
Результирующая сила. Кинетическая энергия. Работа результирующей силы.
Результирующая сила – это векторная сумма всех сил, действующих на данное тело.
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от 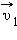 до
до 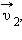 то силы совершили определенную работу A.
то силы совершили определенную работу A.
Работа всех приложенных сил равна работе равнодействующей силы
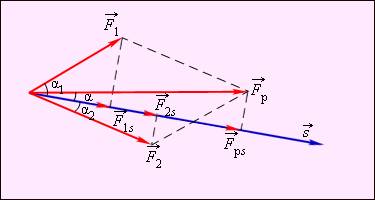
Работа равнодействующей силы. 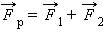
A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы В этом случае векторы силы перемещения скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
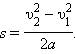
Отсюда следует, что

Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
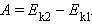
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

Закон сохранения энергии при абсолютно упругом и абсолютно неупругом ударе.
Закон сохранения механической энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Eр2 – Eр1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии:
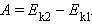
Следовательно
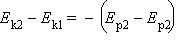
Или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
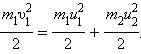
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения.
Физическая кинетика — Википедия
Физи́ческая кине́тика (др.-греч. κίνησις — движение) — микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в различных физических системах (газах, плазме, жидкостях, твёрдых телах) и влияние на них внешних полей
Если известна функция распределения всех частиц системы по их координатам и импульсам в зависимости от времени (в квантовом случае — матрица плотности), то можно вычислить все характеристики неравновесной системы. Вычисление полной функции распределения является практически неразрешимой задачей, но для определения многих свойств физических систем, например, потока энергии или импульса, достаточно знать функцию распределения небольшого числа частиц, а для газов малой плотности — одной частицы.
В кинетике используется существенное различие времён релаксации в неравновесных процессах; например, для газа из частиц или квазичастиц, время свободного пробега значительно больше времени столкновения между частицами. Это позволяет перейти от полного описания неравновесного состояния функцией распределения по всем координатам и импульсам к сокращённому описанию при помощи функции распределения одной частицы по её координатам и импульсам.
Основной метод физической кинетики — решение кинетического уравнения Больцмана для одночастичной функции распределения f(x,p,t){\displaystyle f(x,\;p,\;t)} молекул в фазовом пространстве их координат x{\displaystyle x} и импульсов p{\displaystyle p}. Это уравнение ввёл Больцман в 1872 году
- dfdt=∂f∂t+p→m∂f∂x→+F→∂f∂p→=Stf,{\displaystyle {\frac {df}{dt}}={\frac {\partial f}{\partial t}}+{\frac {\vec {p}}{m}}{\frac {\partial f}{\partial {\vec {x}}}}+{\vec {F}}{\frac {\partial f}{\partial {\vec {p}}}}=\mathrm {St} \,f,}
где St{\displaystyle \mathrm {St} } — интеграл столкновений, определяющий разность числа частиц, приходящих в элемент объёма вследствие прямых столкновений и убывающих из него вследствие обратных столкновений. Для одноатомных молекул или для многоатомных, но без учёта их внутренних степеней свободы[3]
- Stf=∫ω⋅(f′f1′−ff1)dp1dp′dp1′,{\displaystyle \mathrm {St} \,f=\int \omega \cdot (f’f’_{1}-ff_{1})\,dp_{1}dp’dp’_{1},}
где ω{\displaystyle \omega } — вероятность столкновения, связанная с дифференциальным эффективным сечением рассеяния.
- ωdp′dp1′=|v−v1|dσ,{\displaystyle \omega \,dp’dp’_{1}=|v-v_{1}|\,d\sigma ,}
где p{\displaystyle p}, p1{\displaystyle p_{1}} — импульсы молекул до столкновения, v{\displaystyle v}, v1{\displaystyle v_{1}} — соответственно скорости, p′{\displaystyle p’}, p1′{\displaystyle p’_{1}} — их импульсы после столкновения, f{\displaystyle f}, f1{\displaystyle f_{1}} — функции распределения молекул до столкновения, f′{\displaystyle f’}, f1′{\displaystyle f’_{1}} — их функции распределения после столкновения.
Для газа из сложных молекул, обладающих внутренними степенями свободы, их следует учитывать в функции распределения. Например, для двухатомных молекул с собственным моментом вращения M функции распределения будут зависеть также от M{\displaystyle M}.
Из кинетического уравнения следует теорема Больцмана — убывание со временем H{\displaystyle H}-функции Больцмана (среднего логарифма функции распределения) или возрастание энтропии, так как она равна H{\displaystyle H}-функции Больцмана с обратным знаком
Физическая кинетика позволяет получить уравнения баланса для средней плотности вещества, импульса и энергии. Например, для простого газа плотность ρ{\displaystyle \rho }, гидродинамическая скорость V{\displaystyle {\textbf {V}}} и средняя энергия E¯{\displaystyle {\bar {E}}} удовлетворяют уравнениям баланса[5]:
- ∂ρ∂t+div(ρV)=0,{\displaystyle {\frac {\partial \rho }{\partial t}}+\mathrm {div} (\rho {\textbf {V}})=0,} — также известное как уравнение непрерывности
- ∂∂t(ρVα)+∑β∂Παβ∂xβ=0,{\displaystyle {\frac {\partial }{\partial t}}(\rho V_{\alpha })+\sum _{\beta }{\frac {\partial \Pi _{\alpha \beta }}{\partial x_{\beta }}}=0,}
- ∂∂tnE¯+div(q)=0,{\displaystyle {\frac {\partial }{\partial t}}n{\bar {E}}+\mathrm {div} ({\textbf {q}})=0,}
- Παβ=∫mVαVβfdp,{\displaystyle \Pi _{\alpha \beta }=\int mV_{\alpha }V_{\beta }f\,dp,}
где Παβ{\displaystyle \Pi _{\alpha \beta }} — тензор плотности потока импульса, m{\displaystyle m} — масса частиц, n{\displaystyle n} — плотность числа частиц, q=∫EVfdp{\displaystyle {\textbf {q}}=\int E{\textbf {V}}f\,dp} — плотность потока энергии.
Если состояние газа мало отличается от равновесного, то в малых элементах объёма устанавливается распределение, близкое к локально равновесному распределению Максвелла, с температурой, плотностью и гидродинамической скоростью, соответствующими рассматриваемой точке газа. В этом случае неравновесная функция распределения мало отличается от локально равновесной, и решение кинетического уравнения даёт малую поправку к последней, пропорциональную градиентам температуры ∇T{\displaystyle \nabla T} и гидродинамической скорости ∇V{\displaystyle \nabla {\textbf {V}}}, так как Stf0=0{\displaystyle \mathrm {St} \,f_{0}=0}.
С помощью неравновесной функции распределения можно найти поток энергии (в неподвижной жидкости) q=−λ∇T{\displaystyle {\textbf {q}}=-\lambda \nabla T}, где λ{\displaystyle \lambda } — коэффициент теплопроводности, и тензор плотности потока импульса[6]
- Παβ=ρVαVβ+δαβP−σαβ′,{\displaystyle \Pi _{\alpha \beta }=\rho V_{\alpha }V_{\beta }+\delta _{\alpha \beta }P-\sigma ‘_{\alpha \beta },}
где
- σαβ′=η[(∂Vα∂xβ+∂Vβ∂xα)−23δαβdivV]+ζδαβdivV{\displaystyle \sigma ‘_{\alpha \beta }=\eta \left[\left({\frac {\partial V_{\alpha }}{\partial x_{\beta }}}+{\frac {\partial V_{\beta }}{\partial x_{\alpha }}}\right)-{\frac {2}{3}}\delta _{\alpha \beta }\,\mathrm {div} \,{\textbf {V}}\right]+\zeta \delta _{\alpha \beta }\mathrm {div} \,{\textbf {V}}}
— тензор вязких напряжении, η{\displaystyle \eta } — коэффициент сдвиговой вязкости, P{\displaystyle P} — давление. Эти два соотношения известны в механике сплошных сред как закон теплопроводности Фурье и закон вязкости Ньютона. Последнее слагаемое в σαβ′{\displaystyle \sigma ‘_{\alpha \beta }} для газов с внутренними степенями свободы, где ζ{\displaystyle \zeta } — коэффициент «второй», объёмной вязкости, проявляющейся лишь при движениях, в которых divV≠0{\displaystyle \mathrm {div} \,{\textbf {V}}\neq 0}. Для кинетических коэффициентов λ{\displaystyle \lambda }, η{\displaystyle \eta }, ζ{\displaystyle \zeta } получаются выражения через эффективные сечения столкновений, которые, в свою очередь, рассчитываются через константы молекулярных взаимодействий. В многокомпонентной смеси поток какого-либо компонента включает в себя диффузионный поток, пропорциональный градиенту концентрации вещества в смеси с коэффициентом диффузии, и поток за счет термодиффузии (эффект Соре), пропорциональный градиенту температуры с коэффициентом термодиффузии. Поток тепла включает помимо обычного потока за счёт теплопроводности, пропорционального градиенту температуры, дополнительную составляющую, пропорциональную градиентам концентраций компонентов и описывающую диффузионную теплопроводность (эффект Дюфура). Кинетическая теория даёт выражения для этих кинетических коэффициентов через эффективные сечения столкновений, при этом кинетические коэффициенты для перекрёстных явлений вследствие теоремы Онсагера оказываются равными. Эти соотношения являются следствием микроскопической обратимости уравнений движения частиц системы, то есть инвариантности их относительно обращения времени.
Уравнение баланса импульса с учётом выражения для плотности потока импульса через градиент скорости даёт уравнения Навье — Стокса, уравнение баланса энергии с учётом выражения для плотности потока тепла даёт уравнение теплопроводности, уравнение баланса числа частиц определённого сорта с учётом выражения для диффузионного потока даёт уравнение диффузии. Такой гидродинамический подход справедлив, если длина свободного пробега λ{\displaystyle \lambda } значительно меньше характерных размеров областей неоднородности.
Физическая кинетика позволяет исследовать явления переноса в разреженных газах, когда отношение длины свободного пробега λ{\displaystyle \lambda } к характерным размерам задачи L{\displaystyle L} (то есть число Кнудсена λ/L{\displaystyle \lambda /L}) уже не очень мало́ и имеет смысл рассматривать поправки порядка λ/L{\displaystyle \lambda /L} (слабо разреженные газы)[7]. В этом случае кинетика объясняет явления температурного скачка и течения газов вблизи твёрдых поверхностей[8].
Для сильно разреженных газов, когда λ/L≫1{\displaystyle \lambda /L\gg 1}, гидродинамические уравнения и обычное уравнение теплопроводности уже не применимы и для исследования процессов переноса необходимо решать кинетическое уравнение с определёнными граничными условиями на поверхностях, ограничивающих газ. Эти условия выражаются через функцию распределения молекул, рассеянных из-за взаимодействия со стенкой. Рассеянный поток частиц может приходить в тепловое равновесие со стенкой, но в реальных случаях это не достигается. Для сильно разреженных газов роль коэффициента теплопроводности играют коэффициенты теплопередачи[9]. Например, количество тепла Q{\displaystyle Q}, отнесённое к единице площади параллельных пластинок, между которыми находится разреженный газ, равно Q=ϰ(T2−T1)/L{\displaystyle Q=\varkappa (T_{2}-T_{1})/L}, где T1{\displaystyle T_{1}} и T2{\displaystyle T_{2}} — температуры пластинок, L{\displaystyle L} — расстояние между ними, ϰ{\displaystyle \varkappa } — коэффициент теплопередачи.
Теория явлений переноса в плотных газах и жидкостях значительно сложнее, так как для описания неравновесного состояния уже недостаточно одночастичной функции распределения, а нужно учитывать функции распределения более высокого порядка. Частичные функции распределения удовлетворяют цепочке зацепляющихся уравнений (так называемых уравнений Боголюбова или цепочке ББГКИ, то есть уравнений Боголюбова — Борна — Грина — Кирквуда — Ивона). С помощью этих уравнений можно уточнить кинетическое уравнение для газов средней плотности и исследовать для них явления переноса.
Физическая кинетика двухкомпонентной плазмы описывается двумя функциями распределения (для электронов fe{\displaystyle f_{e}}, для ионов fi{\displaystyle f_{i}}), удовлетворяющими системе двух кинетических уравнений (уравнений Власова). На частицы плазмы действуют силы
- Fe=−e(E+v×Bc),Fi=−ZeFe,{\displaystyle F_{e}=-e\left(E+{\frac {v\times B}{c}}\right),\quad F_{i}=-Z_{e}F_{e},}
где Ze{\displaystyle Z_{e}} — заряд иона, E{\displaystyle E} — напряжённость электрического поля, B{\displaystyle B} — магнитная индукция, удовлетворяющие уравнениям Максвелла. Уравнения Максвелла содержат средние плотности тока j{\displaystyle j} и заряда ρ{\displaystyle \rho }, определяемые с помощью функций распределения[10]:
- j=e∫v(Zfi−fe)dp,p=e∫(Zfi−fe)dp.{\displaystyle {\textbf {j}}=e\int {\textbf {v}}(Zf_{i}-f_{e})\,d{\textbf {p}},\quad p=e\int (Zf_{i}-f_{e})\,d{\textbf {p}}.}
Таким образом, кинетические уравнения и уравнения Максвелла образуют связанную систему уравнений Власова — Максвелла, определяющую все неравновесные явления в плазме. Такой подход называется приближением самосогласованного поля. При этом столкновения между электронами учитываются не явно, а лишь через создаваемое ими самосогласованное поле. При учёте столкновений электронов возникает кинетическое уравнение, в котором эффективное сечение столкновений очень медленно убывает с ростом прицельного расстояния, а также становятся существенными столкновения с малой передачей импульса, в интеграле столкновений появляется логарифмическая расходимость. Учёт эффектов экранирования позволяет избежать этой трудности.
Физическая кинетика неравновесных процессов в диэлектриках основана на решении кинетического уравнения Больцмана для фононов решётки[11]. Взаимодействие между фононами вызвано ангармоническими членами гамильтониана решётки относительно смещения атомов из положения равновесия. При простейших столкновениях один фонон распадается на два или происходит слияние двух фононов в один, причём сумма их квазиимпульсов либо сохраняется (нормальные процессы столкновений), либо меняется на вектор обратной решётки (процессы переброса). Конечная теплопроводность возникает при учёте процессов переброса. При низких температурах, когда длина свободного пробега больше размеров образца L{\displaystyle L}, роль длины свободного пробега играет L{\displaystyle L}. Кинетическое уравнение для фононов позволяет исследовать теплопроводность[12] и поглощение звука в диэлектриках[13]. Если длина свободного пробега для нормальных процессов значительно меньше длины свободного пробега для процессов переброса, то система фононов в кристалле при низких температурах подобна обычному газу. Нормальные столкновения устанавливают внутреннее равновесие в каждом элементе объёма газа, которьй может двигаться со скоростью V{\displaystyle V}, мало меняющейся на длине свободного пробега для нормальных столкновений. Поэтому можно построить уравнения гидродинамики фононного газа в диэлектрике[14].
Физическая кинетика металлов основана на решении кинетического уравнения для электронов, взаимодействующих с колебаниями кристаллической решётки. Электроны рассеиваются на колебаниях атомов решётки[15], примесях и дефектах, нарушающих её периодичность, причём возможны как нормальные столкновения, так и процессы переброса[16]. Электрическое сопротивление возникает в результате этих столкновений. Физическая кинетика объясняет термоэлектрические, гальваномагнически и термомагнинтные явления[17], аномальный скин-эффект[18], циклотронный резонанс в высокочастотных полях и другие кинетические эффекты в металлах. Для сверхпроводников она объясняет особенности их высокочастотного поведения.
Физическая кинетика магнитных явлений основана на решении кинетического уравнения для магнонов. Она позволяет вычислить динамическии восприимчивости магнитных систем в переменных полях, изучить кинетику процессов намагничивания.
Физическая кинетика явлений при прохождении быстрых частиц через вещество основана на решении системы кинетических уравнений для быстрых частиц и вторичных частиц, возникающих при столкновениях, например для γ{\displaystyle \gamma }-лучей (фотонов) с учётом различных процессов в среде (фотоэффекта, комптоновского рассеяния, образования пар). В этом случае кинетика позволяет вычислить коэффициенты поглощения и рассеяния быстрых частиц.
Физическая кинетика фазовых переходов первого рода, то есть со скачком энтропии, связана с образованием и ростом зародышей новой фазы. Функция распределения зародышей по их размерам (если зародыши считать макроскопическими образованиями, а процесс роста — медленным) удовлетворяет уравнению Фоккера — Планка[19]:
- ∂f∂t=∂∂α(D∂f∂α−Af),{\displaystyle {\frac {\partial f}{\partial t}}={\frac {\partial }{\partial \alpha }}\left(D{\frac {\partial f}{\partial \alpha }}-Af\right),}
где α{\displaystyle \alpha } — радиус зародыша, D{\displaystyle D} — «коэффициент диффузии зародышей по размерам», A{\displaystyle A} — пропорционально минимальной работе, которую нужно затратить на создание зародыша данного размера. Кинетика фазовых переходов второго рода в наиболее простом приближении основана на уравнении релаксации параметра порядка η{\displaystyle \eta }, характеризующего степень упорядоченности, возникающей при фазовом переходе (уравнение Ландау — Халатникова)[20]:
- ∂η∂t=−γ∂Ω∂η,{\displaystyle {\frac {\partial \eta }{\partial t}}=-\gamma {\frac {\partial \Omega }{\partial \eta }},}
где γ{\displaystyle \gamma } — постоянный коэффициент, Ω{\displaystyle \Omega } — термодинамический потенциал в переменных T{\displaystyle T} и η{\displaystyle \eta }, вблизи точки фазового перехода зависящий от η{\displaystyle \eta }. Для этой зависимости используется разложение по степеням η{\displaystyle \eta } и T−Tc{\displaystyle T-T_{c}}, где Tc{\displaystyle T_{c}} — температура фазового перехода.
Теорию явлений переноса в жидкостях также можно отнести к физической кинетике. Xотя для жидкостей метод кинетических уравнений непригоден, для них возможен более общий подход, основанный на иерархии времён релаксации. Для жидкости время установления равновесия в макроскопически малых (но содержащих ещё большое число молекул) элементарных объёмах значительно меньше, чем время релаксации во всей системе, вследствие чего в малых элементах объёма приближённо устанавливается статистическое равновесие. Поэтому в качестве исходного приближения при решении уравнения Лиувилля можно принять локально равновесное распределение Гиббса с температурой T(x,t){\displaystyle T(x,\;t)}, химическим потенциалом μ(x,t){\displaystyle \mu (x,\;t)} и гидродинамической скоростью V(x,t){\displaystyle V(x,\;t)}, соответствующими рассматриваемой точке жидкости. Например, для однокомпонентной жидкости локально равновесная функция распределения (или матрица плотности) имеет вид
- f=1Zexp(−∫β(x,t)[H~(x)−μ(x,t)n(x)]dx),{\displaystyle f={\frac {1}{Z}}\exp \left(-\int \beta (x,\;t)[{\tilde {H}}(x)-\mu (x,\;t)n(x)]\,dx\right),}
где
- β(x,t)=1kT(x,t),{\displaystyle \beta (x,\;t)={\frac {1}{kT(x,\;t)}},}
- H~(x)=H(x)−p(x)V(x,t)+12mn(x)V2(x,t){\displaystyle {\tilde {H}}(x)=H(x)-p(x)V(x,\;t)+{\frac {1}{2}}mn(x)V^{2}(x,\;t)} — плотность энергии в системе координат, движущейся вместе с элементом жидкости,
- H(x){\displaystyle H(x)} — плотность энергии в неподвижной системе координат,
- p(x){\displaystyle p(x)} — плотность импульса,
- n(x){\displaystyle n(x)} — плотность числа частиц, рассматриваемые как фазовые функции, то есть функции от координат и импульсов всех частиц, например n(x)=∑jNδ(x−xj){\displaystyle n(x)=\sum _{j}^{N}\delta (x-x_{j})}.
Приближённое решение уравнения Лиувилля для состояний, близких к статистически равновесному, позволяет вывести уравнения теплопроводности и Навье — Стокса для жидкости и получить микроскопические выражения для кинетических коэффициентов теплопроводности и вязкости через пространственно-временные корреляционные функции плотностей потоков энергии и импульсов всех частиц системы. Этот же подход возможен и для смеси жидкостей. Подобное решение уравнения Лиувилля есть его частное решение, зависящее от времени лишь через параметры β(x,t){\displaystyle \beta (x,\;t)}, μ(x,t){\displaystyle \mu (x,\;t)}, V(x,t){\displaystyle V(x,\;t)}, соответствующие сокращённому гидродинамическому описанию неравновесного состояния системы, которое справедливо, когда все гидродинамические параметры мало меняются на расстояниях порядка длины свободного пробега (для газов) или длины корреляций потоков энергии или импульса (для жидкостей).
К задачам физической кинетики относится также вычисление обобщённой восприимчивости, выражающей линейную реакцию физической системы на включение внешнего ноля. Её можно выразить через функции Грина с усреднением по состоянию, которое может быть и неравновесным.
В физической кинетике исследуют также кинетические свойства квантовых систем, что требует применения метода матрицы плотности.
- ↑ Лифшиц, Питаевский, 1979, с. 24.
- ↑ Лифшиц, Питаевский, 1979, с. 22.
- ↑ Лифшиц, Питаевский, 1979, с. 23.
- ↑ Лифшиц, Питаевский, 1979, с. 26.
Живая сила (физика) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Живая сила.Жива́я си́ла (лат. Vis viva, нем. lebendige Kraft ) — историческое название кинетической энергии. Впервые название введено Лейбницем[1].
Первоначально наименование «живая сила» было дано Лейбницем для произведения массы тела на квадрат его скорости. Впоследствии Гюстав Кориолис внёс в определение термина поправку, определив его, как произведение половины массы тела на квадрат его скорости[2][3], хотя иногда определение живой силы с множителем «½» встречалось и ранее (например, в статьях Д. Бернулли). В результате термин приобрёл то же содержание, что и современный термин «кинетическая энергия».
Фрагмент статьи Д.Бернулли, опубликованной в 1741 году[4], в котором используется определение живой силы с множителем «½».В аналитической механике восемнадцатого века живая сила, принимаемая равной mv2{\displaystyle mv^{2}}, рассматривалась главным образом только как полезный математический артефакт. Ситуация глубоко изменилась под влиянием индустриализации, связанной с широким применением паровых машин. Тогда возник большой практический интерес к механической работе, производимой двигателями. Исходя из той связи, что существует между механической работой и величиной 12mv2{\displaystyle {\frac {1}{2}}mv^{2}}, Кориолис предложил называть живой силой именно эту величину[5]. Комментируя такой подход, Кориолис писал[6]: «Если ранее наименование живая сила давалось произведению массы на квадрат скорости, то это было потому, что не уделялось внимания работе»[7].
Кинетическая энергия — это… Что такое Кинетическая энергия?
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
История
Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»
Физический смысл
Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:
— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:
Если система замкнута, то есть , то , а величина
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
где:
— масса тела
— скорость центра масс тела
— момент инерции тела
— угловая скорость тела.
Физический смысл работы
Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:
Релятивизм
При скоростях, близких к скорости света, кинетическая энергия любого объекта равна
где:
— масса объекта;
— скорость движения объекта в инерциальной системе отсчета;
— скорость света в вакууме ( — энергия покоя).
Данную формулу можно переписать в следующем виде:
При малых скоростях () последнее соотношение переходит в обычную формулу .
Соотношение кинетической и внутренней энергии
Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.
То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.
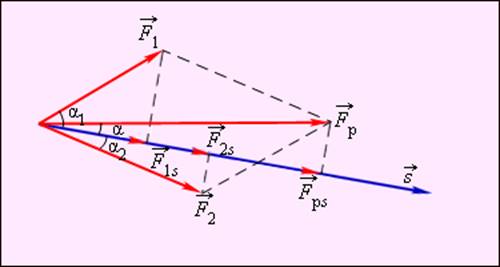
 . A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α
. A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α