Классификация дифференциальных уравнений.
Дифференциальные уравнения первого порядка с разделяющимися переменными – уравнения следующего вида:
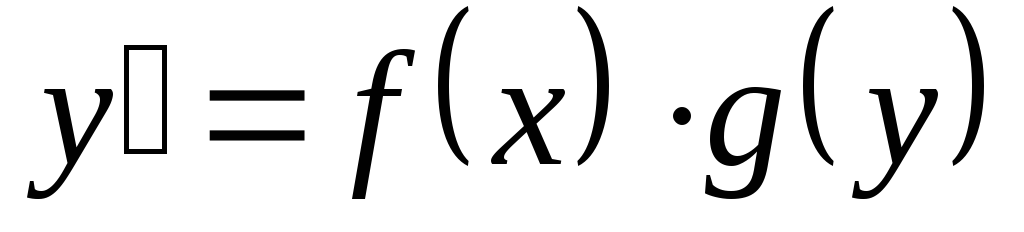 ,
где
,
где 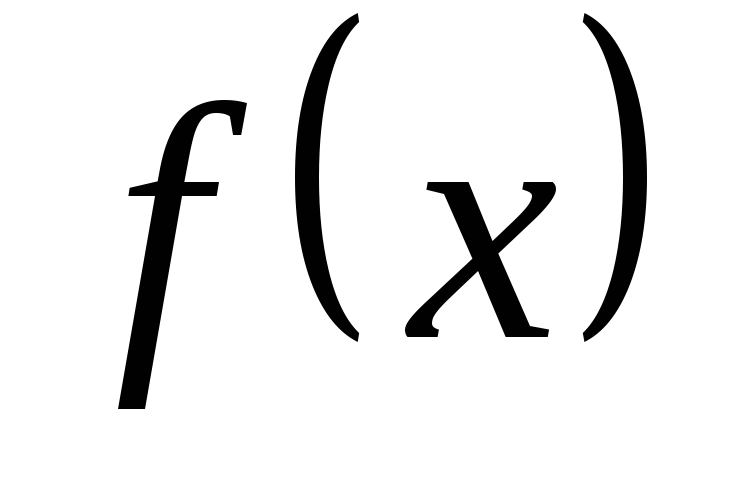 и
и 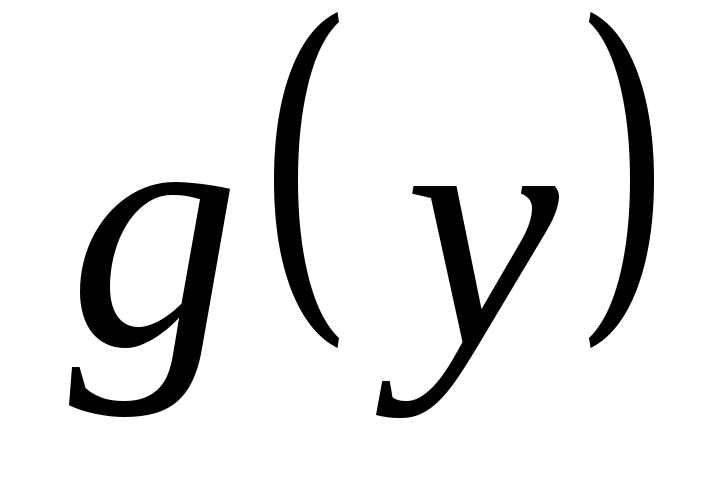 — заданные функции,
— заданные функции,  .
.
Эти уравнения приводятся к виду 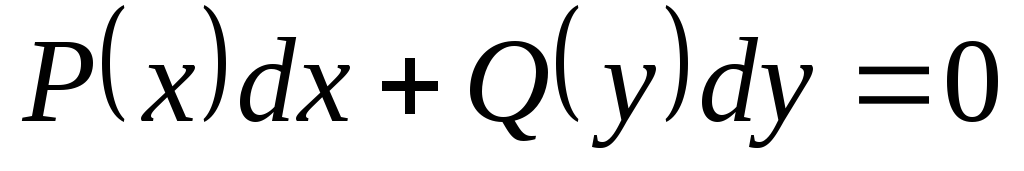 ,
где
,
где 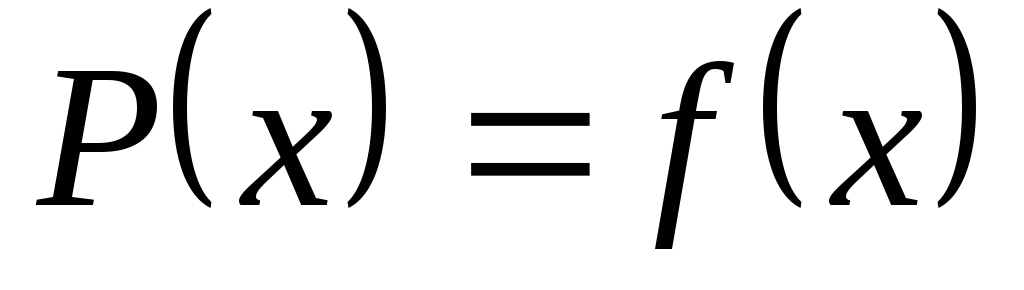 ,
, 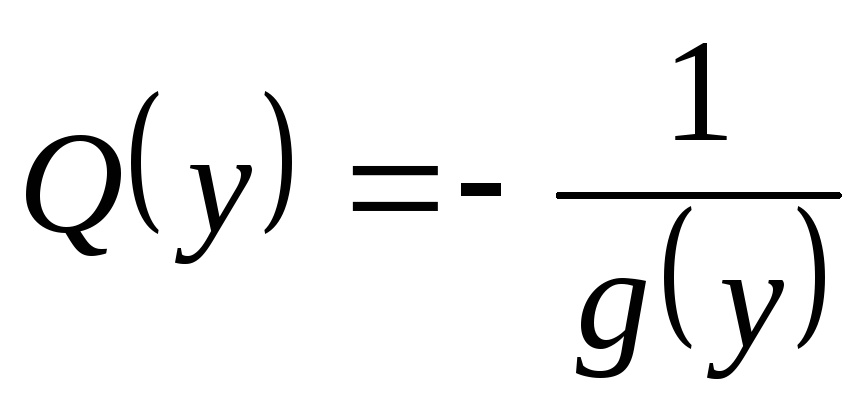
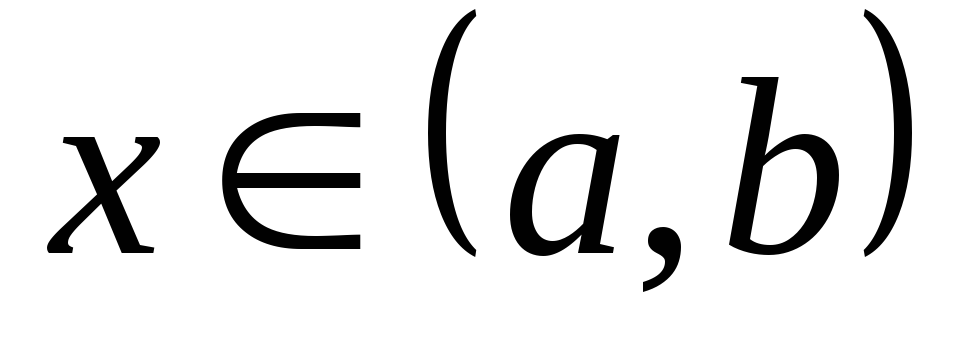 .
. Общий интеграл уравнения 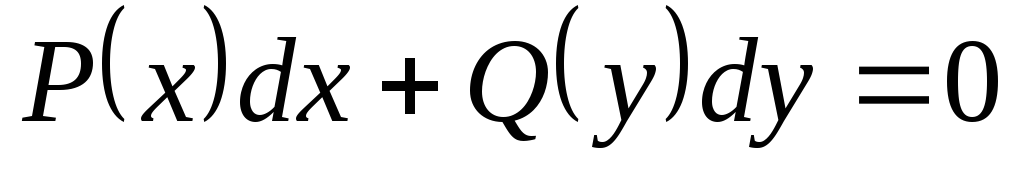 имеет вид
имеет вид 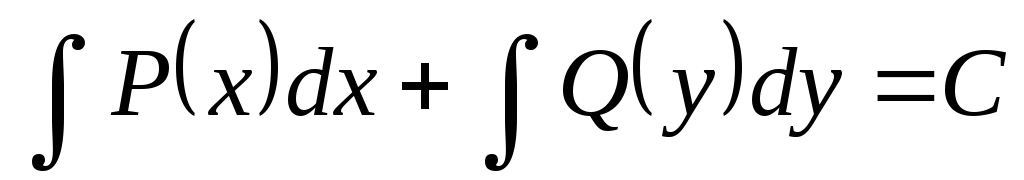 .
.
Пример. Решить дифференциальное
уравнение 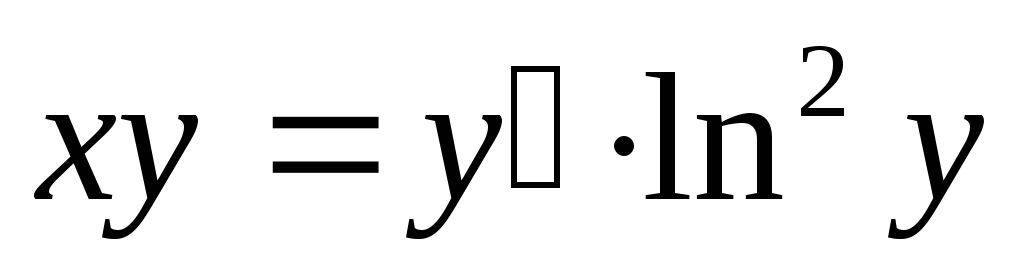
Разделим переменные
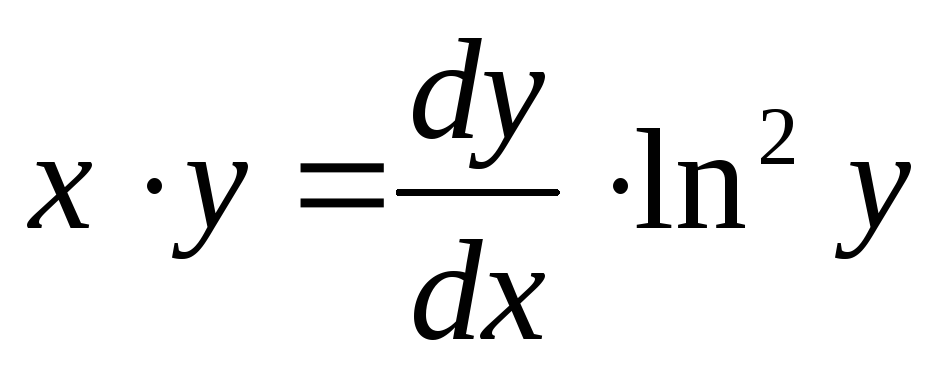

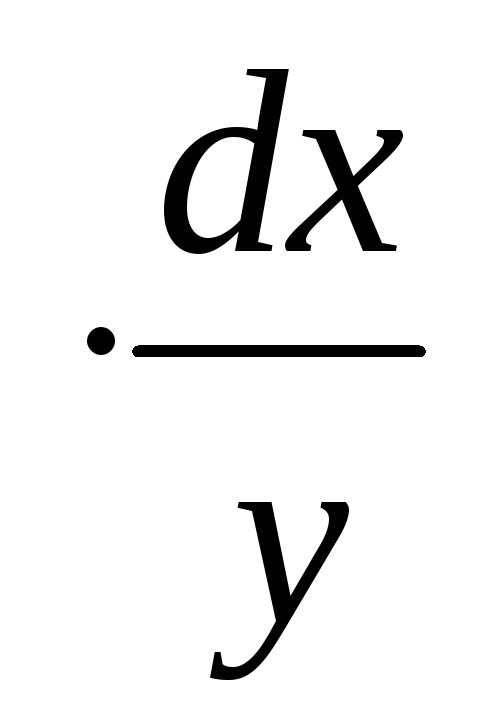 ,
,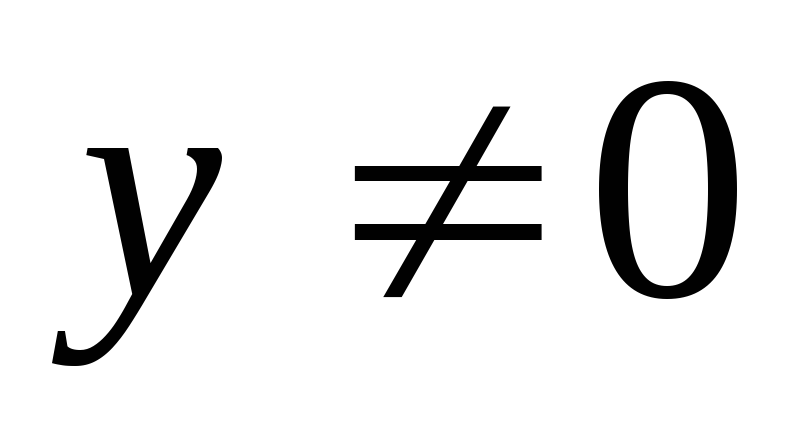
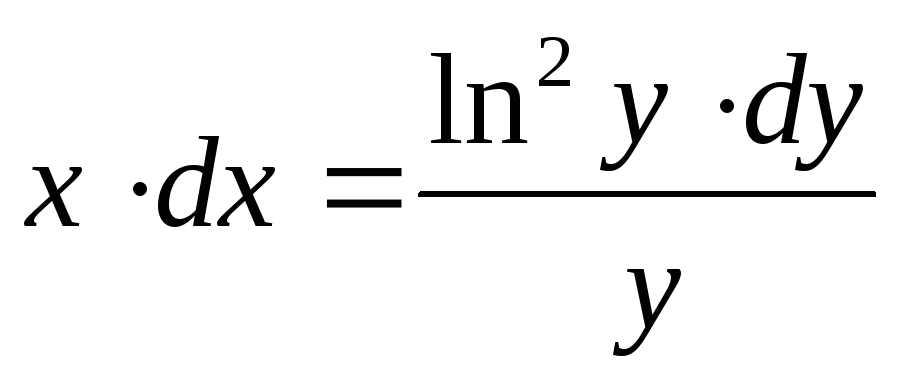
Проинтегрируем уравнение с последующим выражением искомой величины y из равенства:
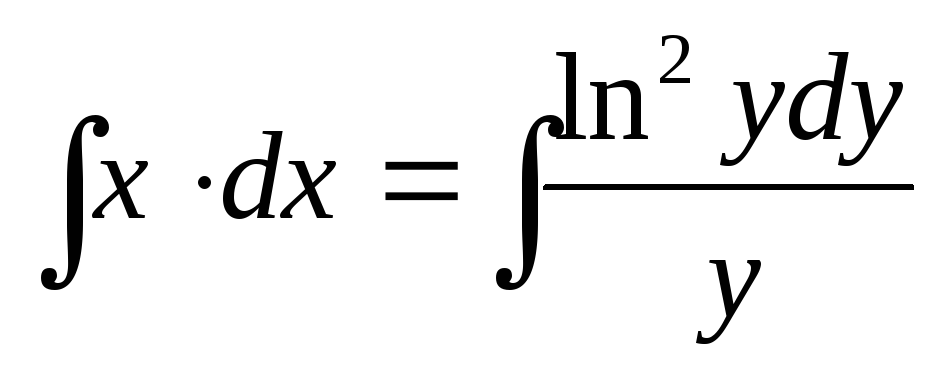 ;
; 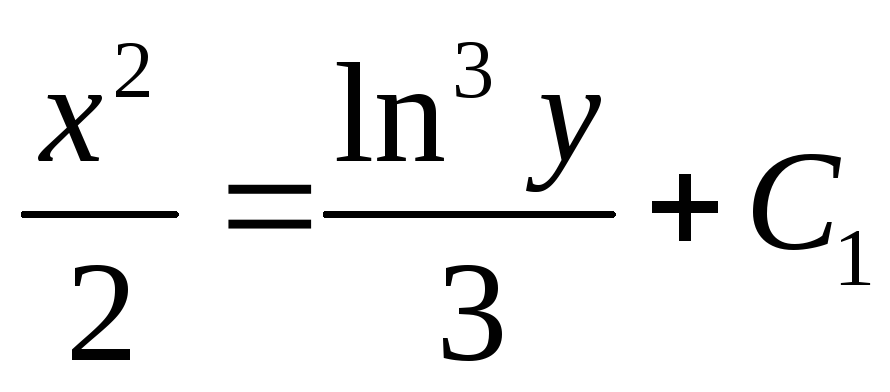 ;
; 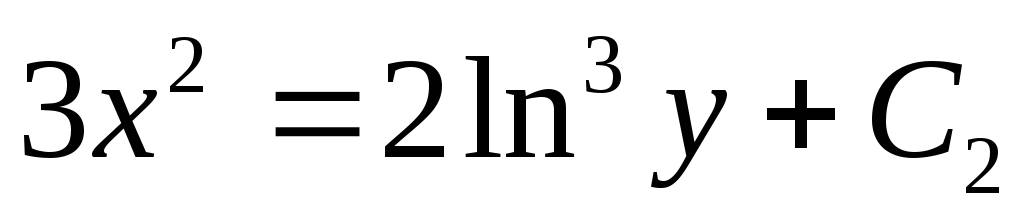
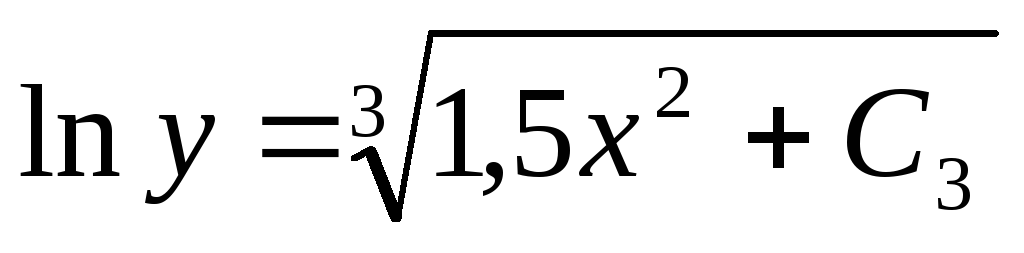
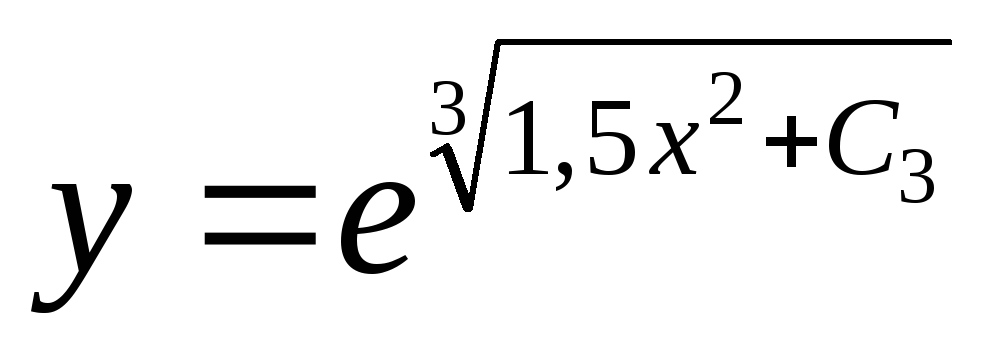 — общее решение дифференциального
уравнения.
— общее решение дифференциального
уравнения.
2. Однородные дифференциальные уравнения первого порядка – это уравнения вида:
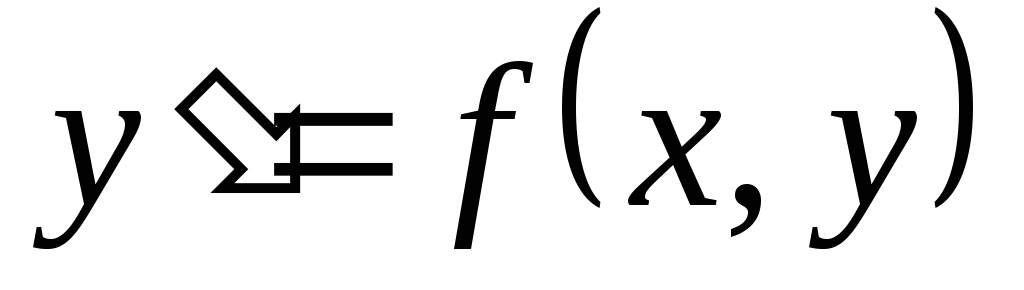
где функция 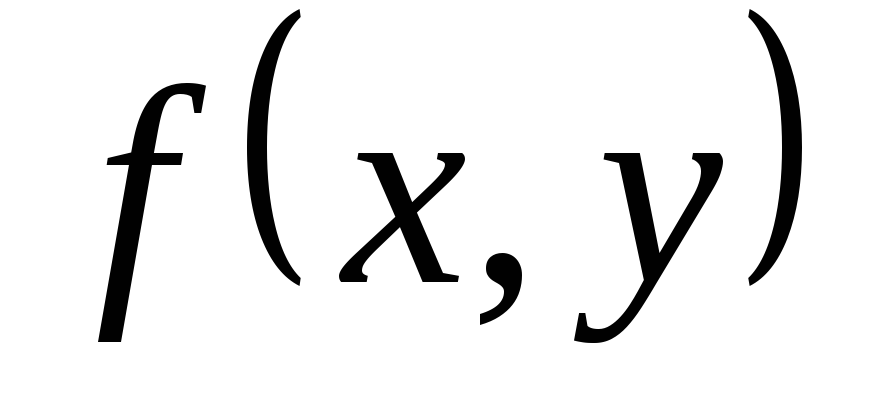 обладает следующим свойством: равенство
обладает следующим свойством: равенство 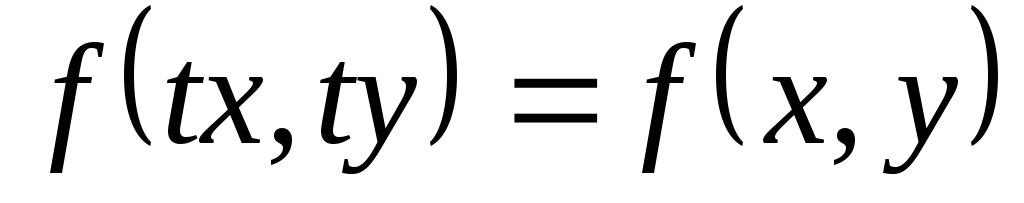 выполняется для произвольного числа
выполняется для произвольного числа 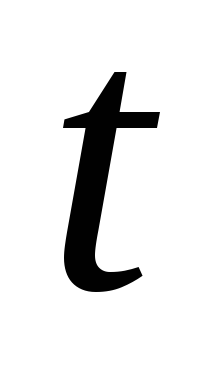 >0.
Для решения однородного дифференциального
уравнения
>0.
Для решения однородного дифференциального
уравнения 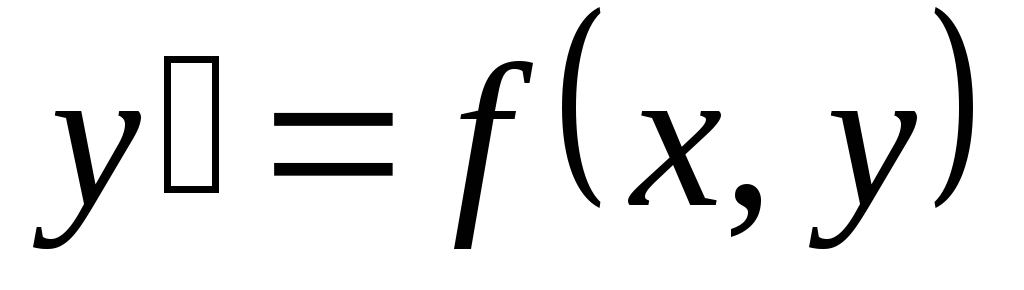 необходимо:
необходимо:
1) свести его к уравнению вида 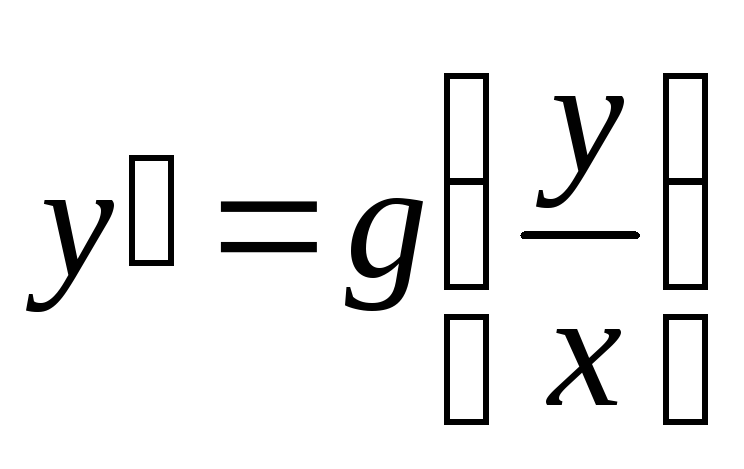 ;
;
2) полученное уравнение свести к
уравнению с разделяющимися переменными,
используя новую переменную 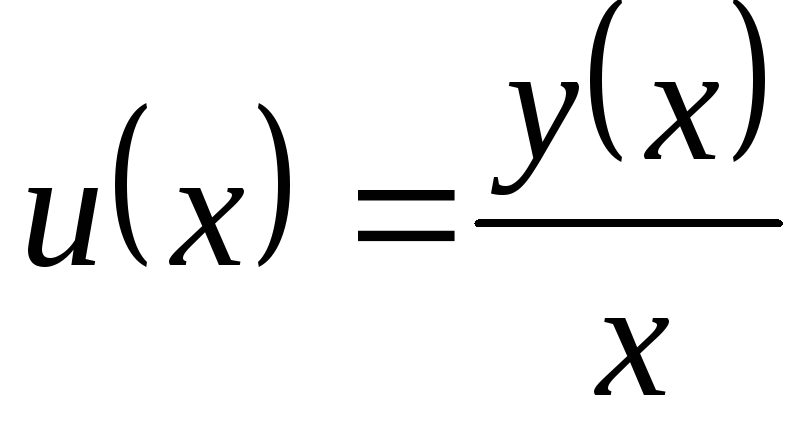
3. Линейные дифференциальные уравнения первого порядка
– это уравнения вида: 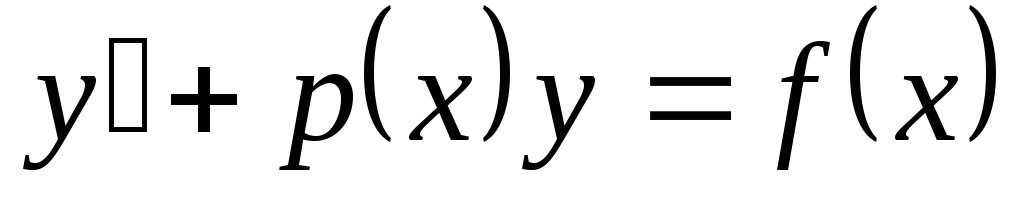 ,
(*)
,
(*)
где 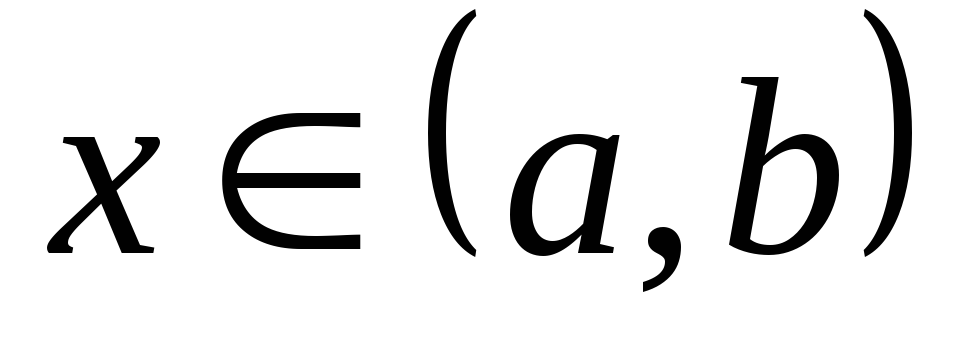 ,
функции р(х) и f(х) непрерывны на
,
функции р(х) и f(х) непрерывны на 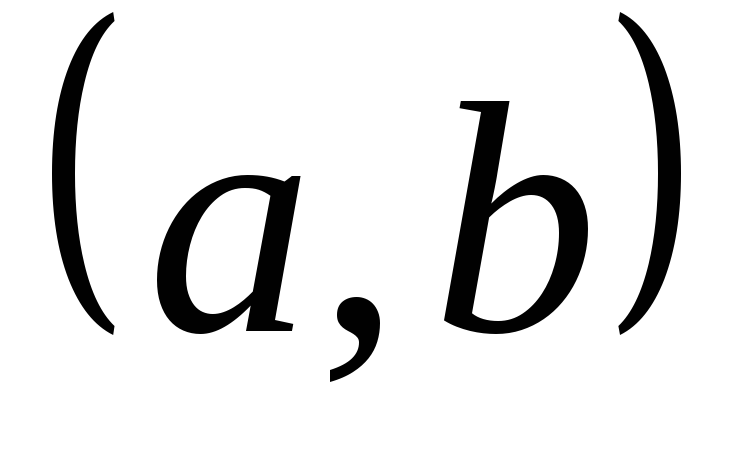 ,
причём
,
причём 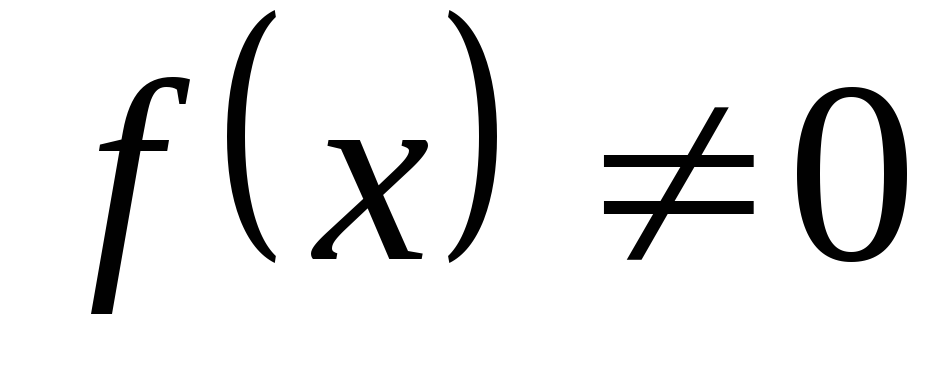 .
Решаются двумя способами. 1) Метод
Бернулли. Искомая функция у(х)представляется в виде у=uv,
откуда, в силу
.
Решаются двумя способами. 1) Метод
Бернулли. Искомая функция у(х)представляется в виде у=uv,
откуда, в силу 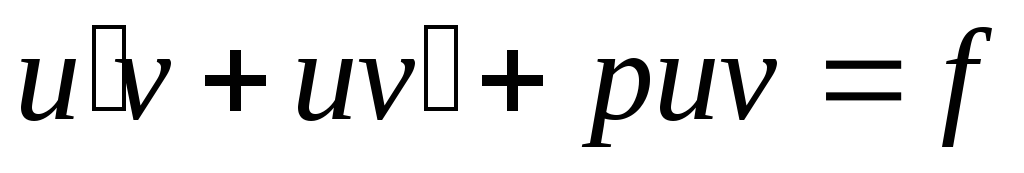 ,
следует два уравнения для нахождения
функций u(x) и v(x):
,
следует два уравнения для нахождения
функций u(x) и v(x): 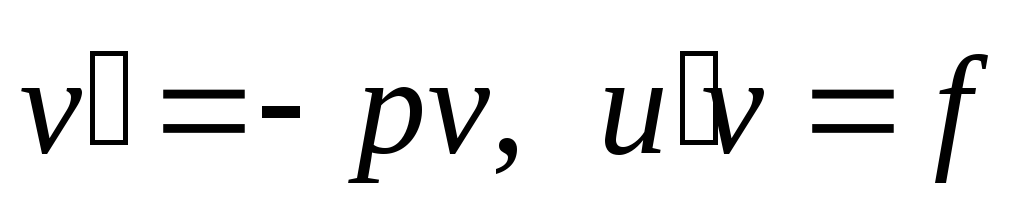 .
Из первого уравнения получаем
.
Из первого уравнения получаем 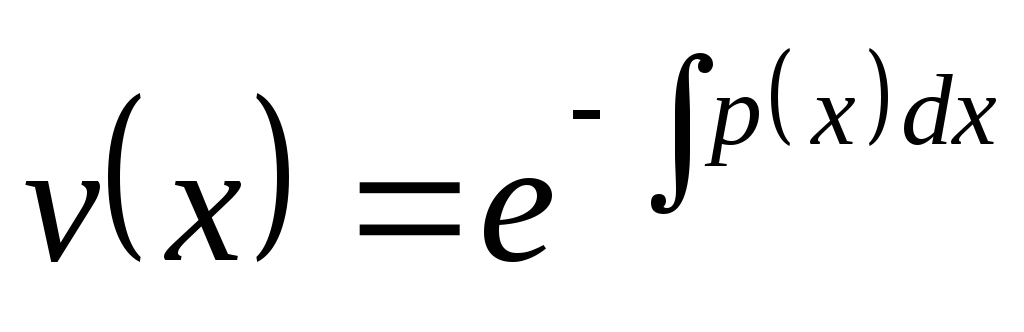
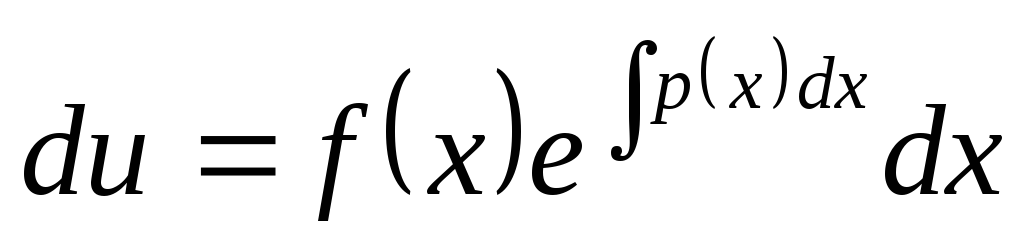 ,
откуда
,
откуда 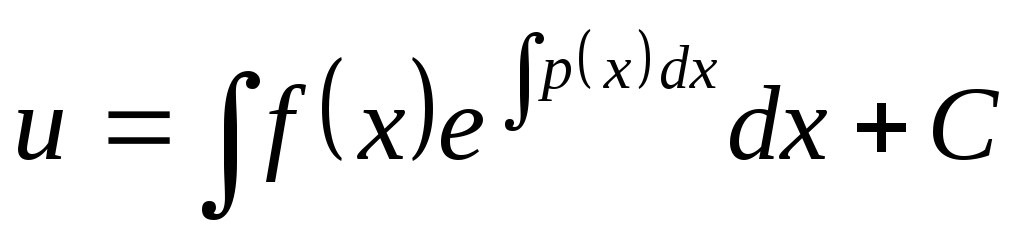 ,
и, таким образом, общее решение уравнения
(*) имеет следующий вид:
,
и, таким образом, общее решение уравнения
(*) имеет следующий вид: 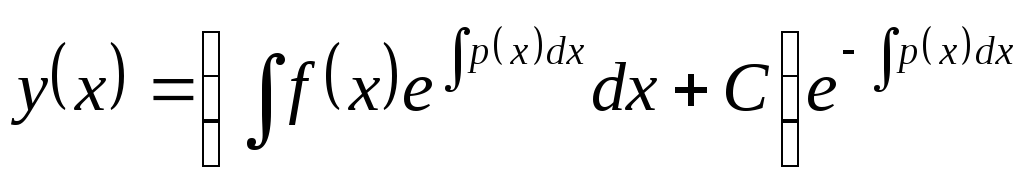 .
.
2) Метод вариации произвольной постоянной
(метод Лагранжа) также состоит из двух
этапов. На первом этапе решения уравнения
(*) находим общее решение уравнения 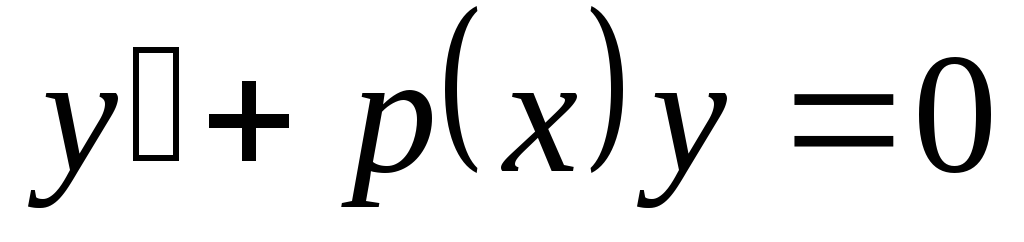 :
: 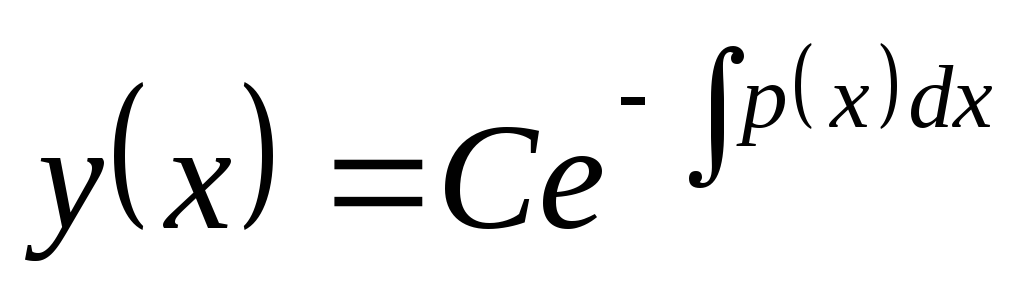 ,
где С – произвольная постоянная. На
втором этапе ищем общее решение уравнения
(*) в виде
,
где С – произвольная постоянная. На
втором этапе ищем общее решение уравнения
(*) в виде 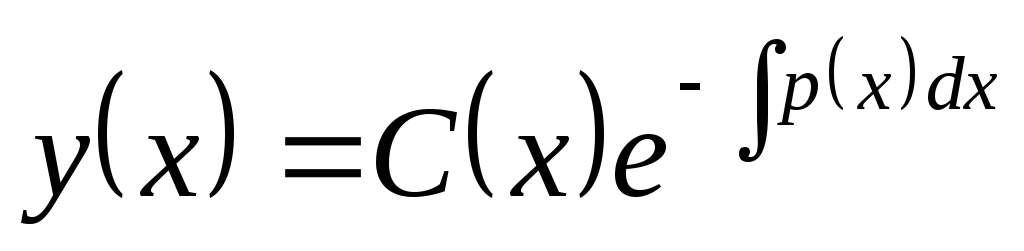
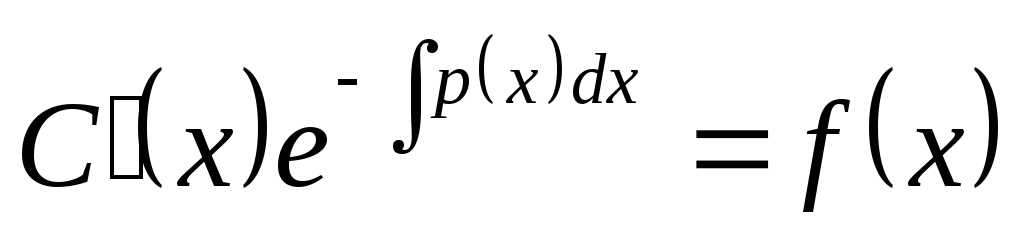 ,
откуда следует
,
откуда следует 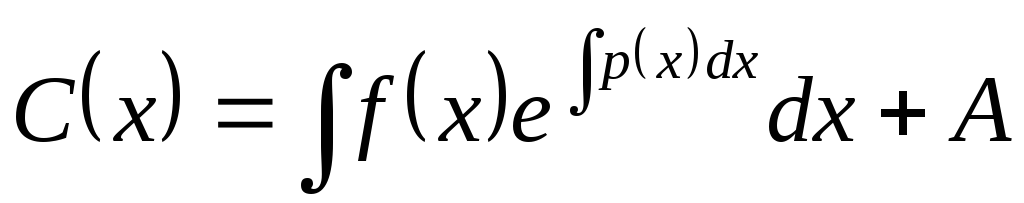 ,
где А – произвольная постоянная, и
,
где А – произвольная постоянная, и 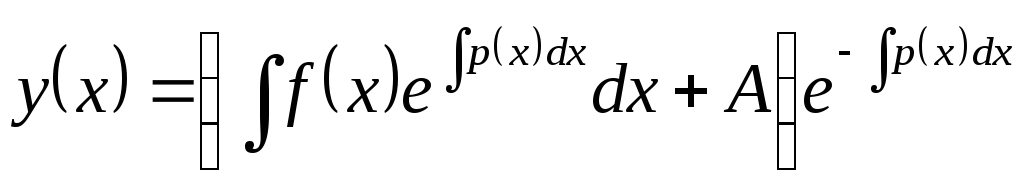 — общее решение уравнения (*).
— общее решение уравнения (*). Пример. Решить дифференциальное
уравнение 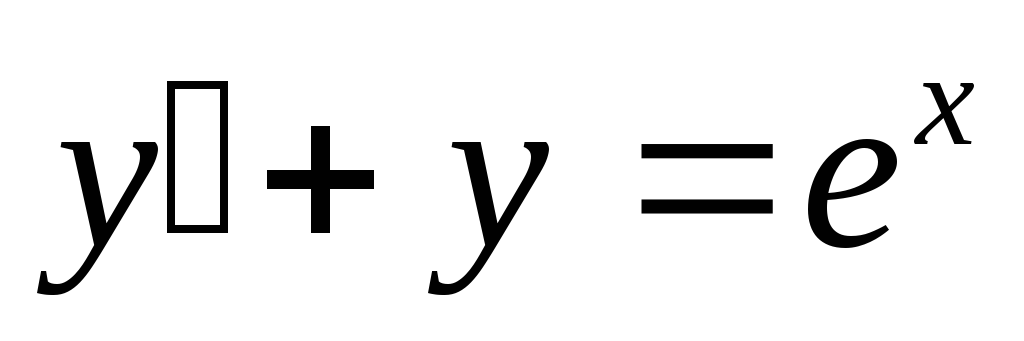
Воспользуемся подстановкой 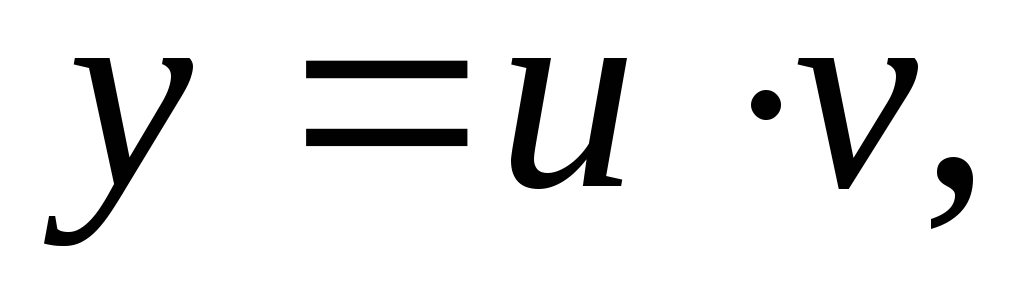
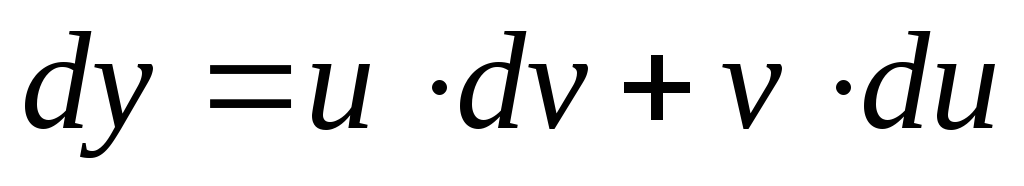
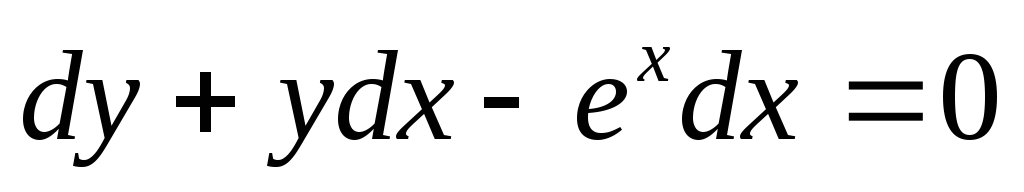
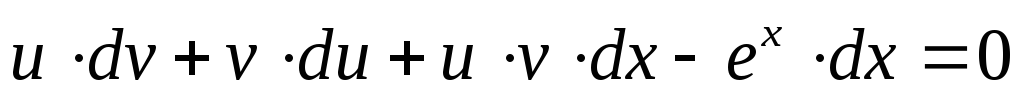 (1)
(1)
Пусть 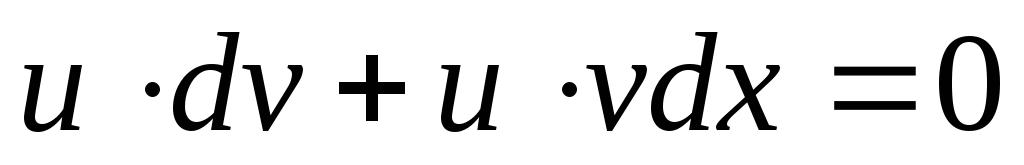 ,
тогда уравнение (1) принимает вид системы:
,
тогда уравнение (1) принимает вид системы:
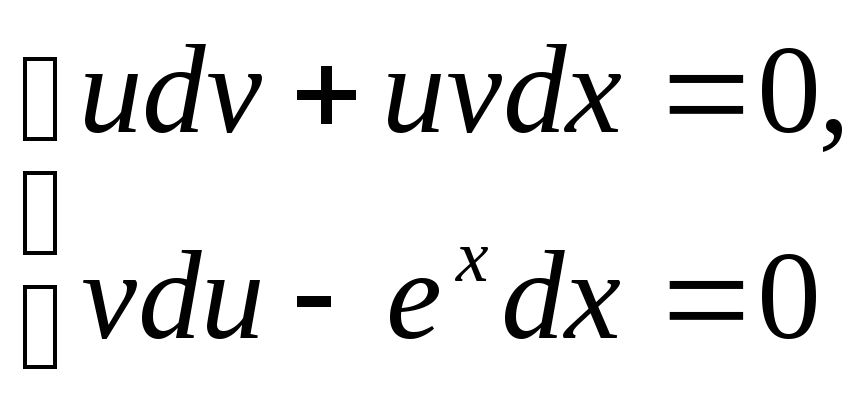

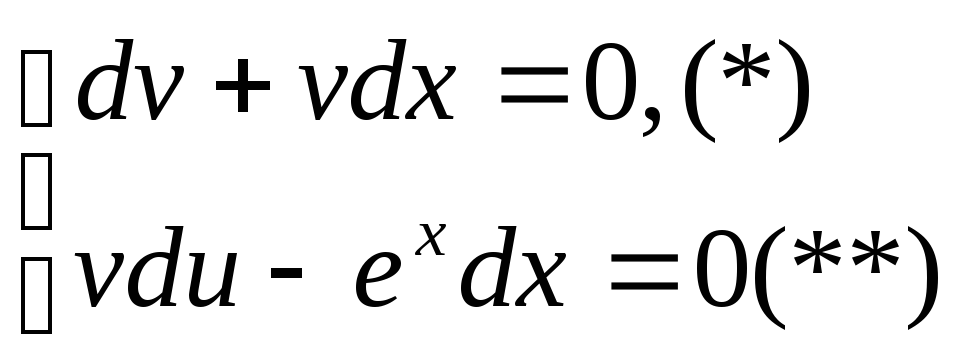

Решим уравнение  как уравнение с разделяющимися переменными
как уравнение с разделяющимися переменными
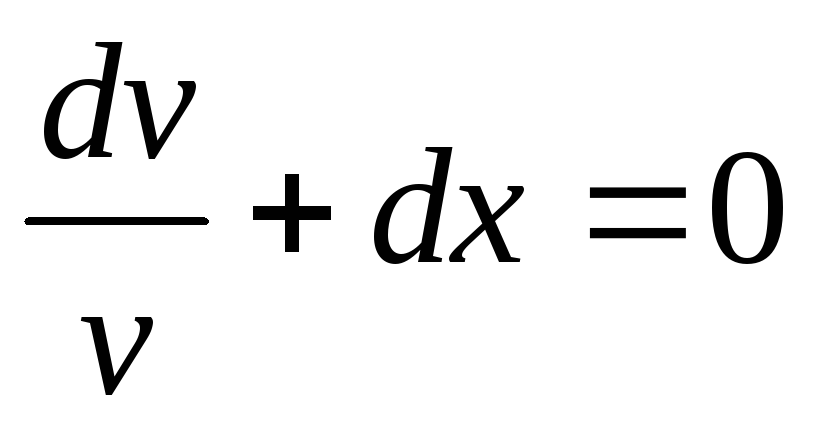
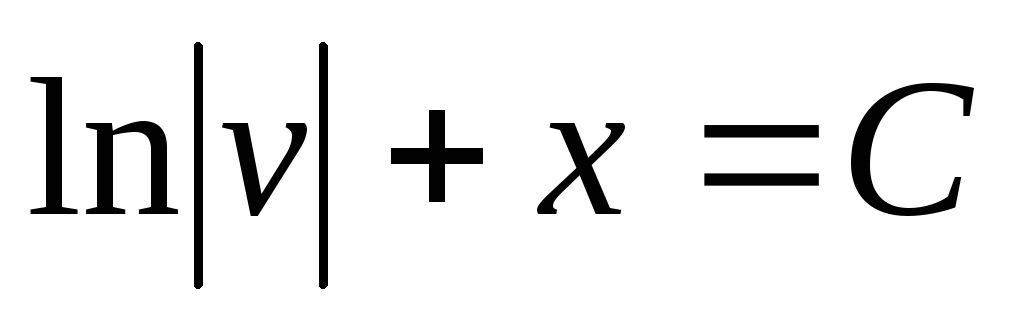 ;
; 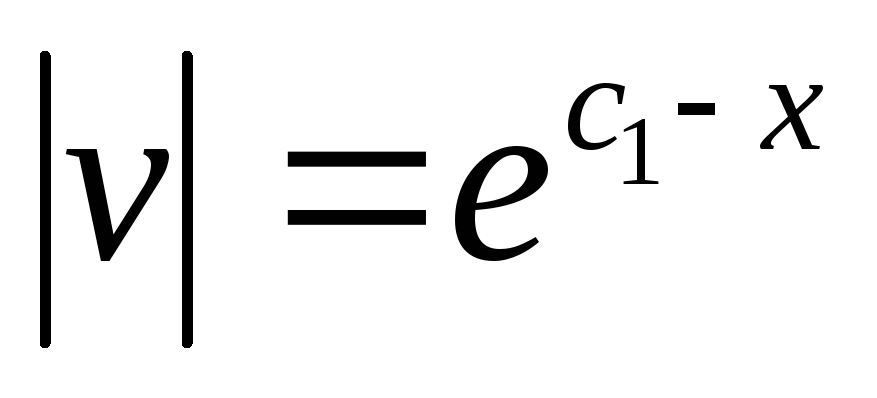 ;
; 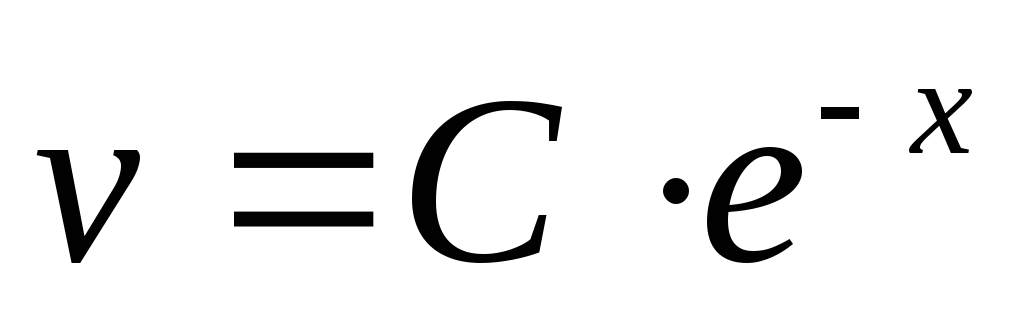
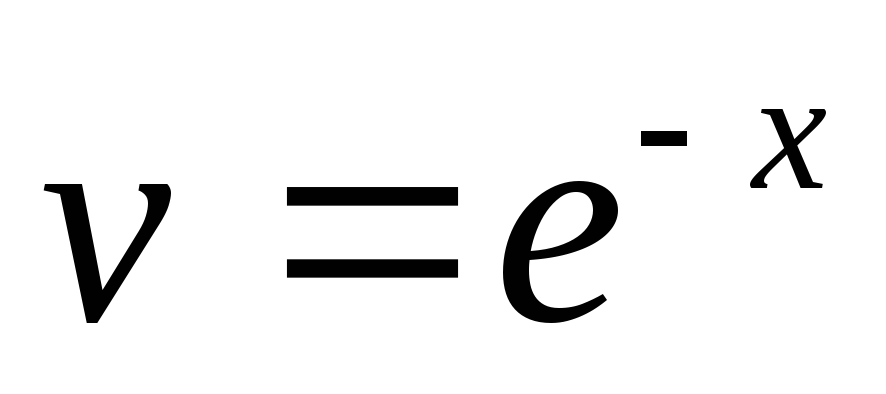 — частное решение.
— частное решение.
Подставляем последнее равенство в  и решим его относительно величины u:
и решим его относительно величины u:
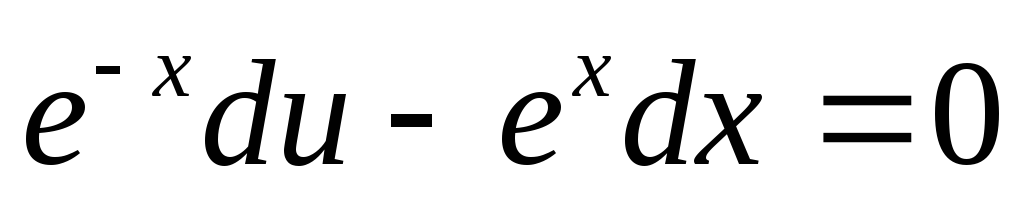

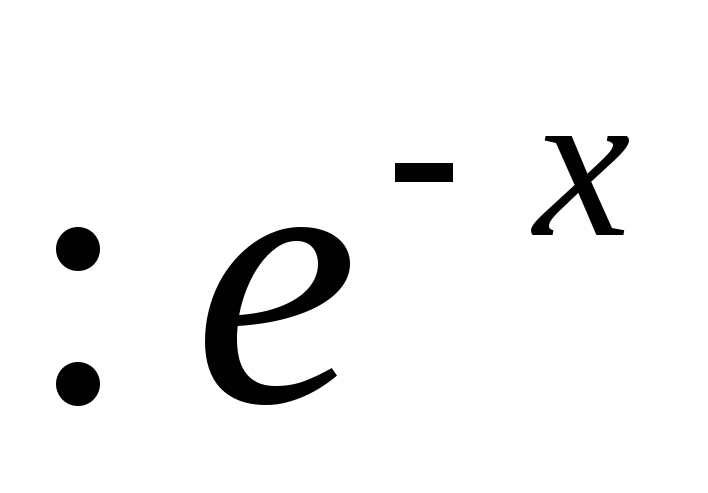 ;
; 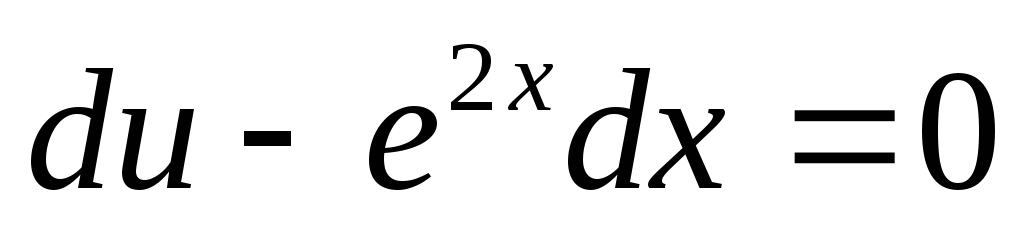
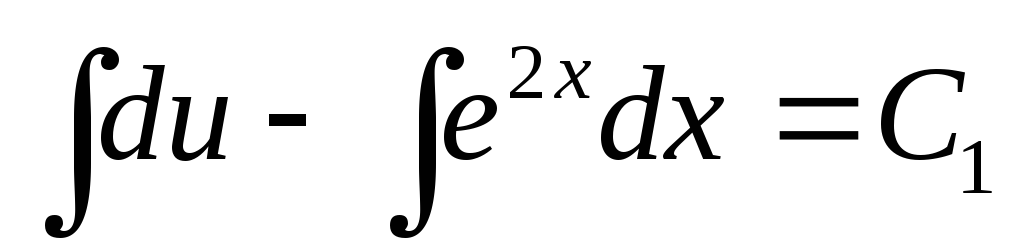
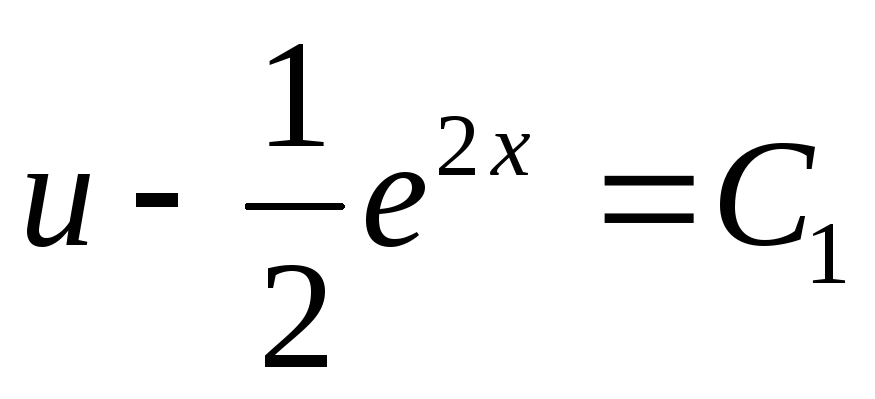 ;
; 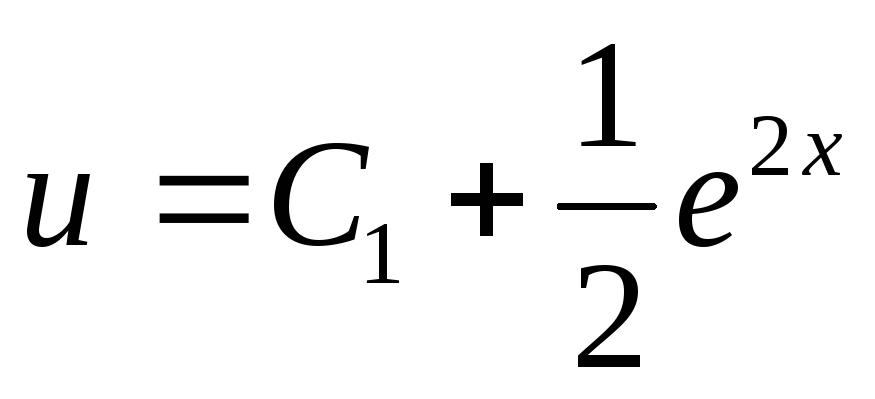
Найдем искомую величину y,
подставив значения u и v в формулу 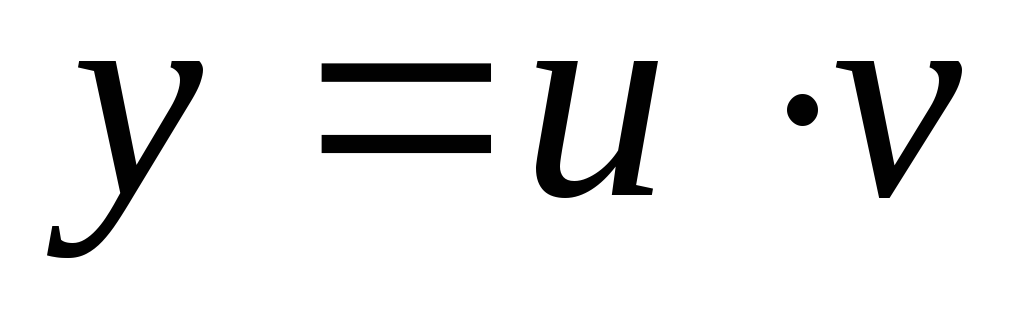
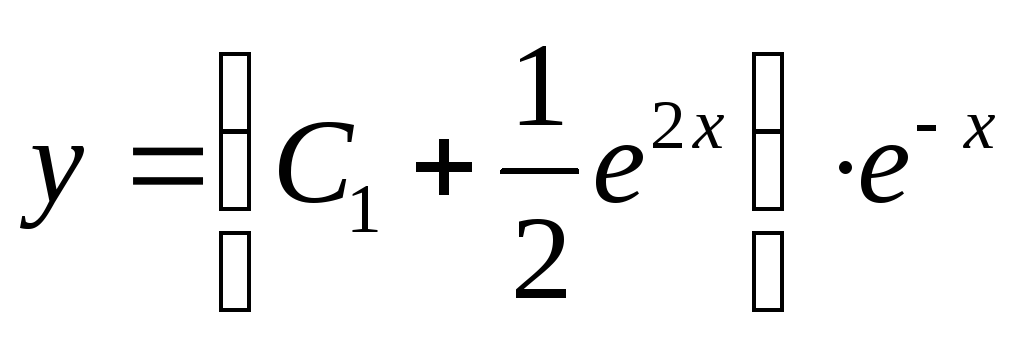 —
общее решение дифференциального
уравнения.
—
общее решение дифференциального
уравнения.
Пример. Найти частное решение
уравнения 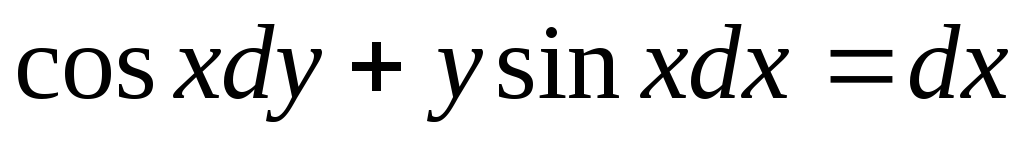 ,
,
если 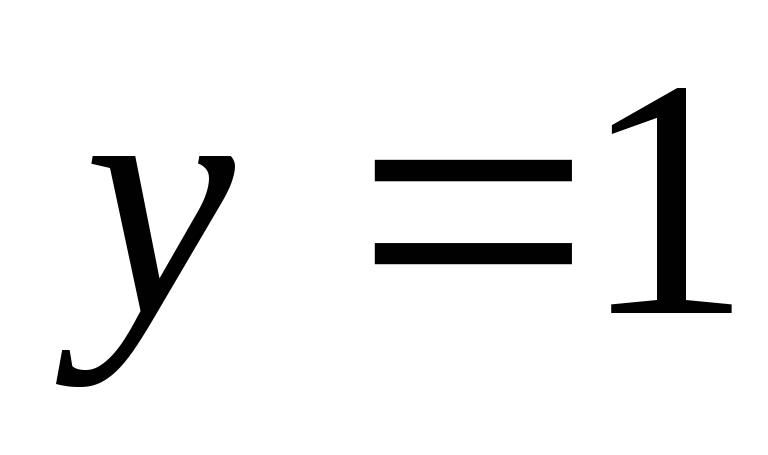 при
при 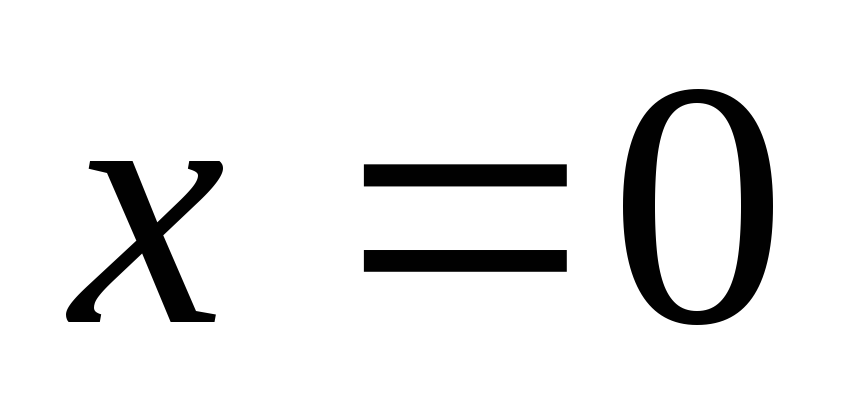 .
.
Разделив все члены данного уравнения
на 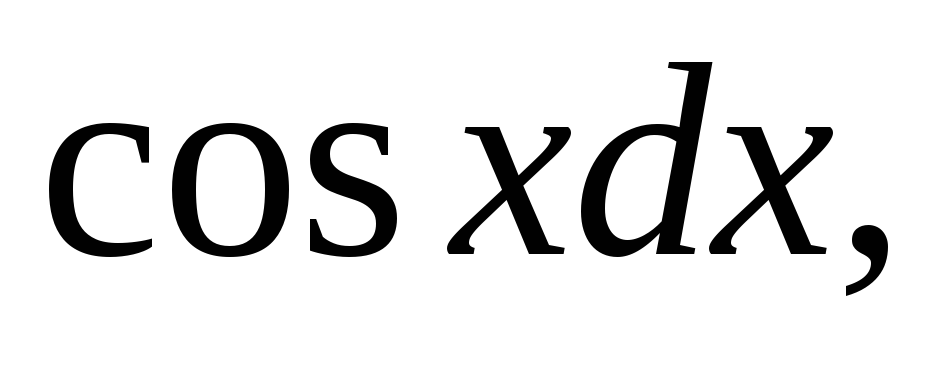 получим уравнение
получим уравнение 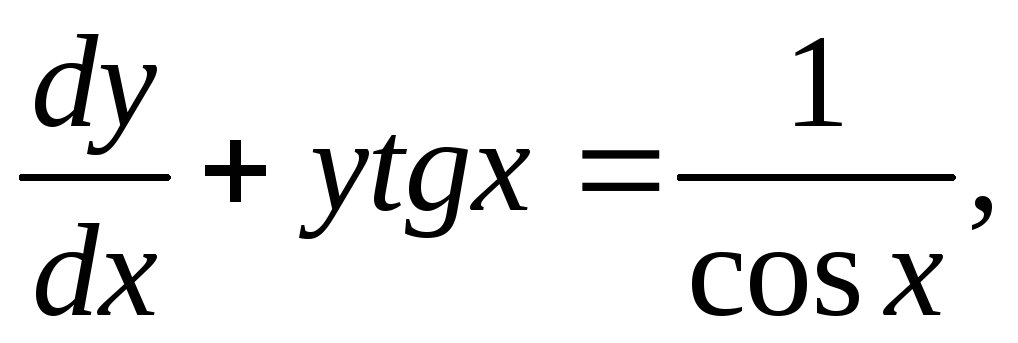 (*)
(*)
которое является линейным. Положим 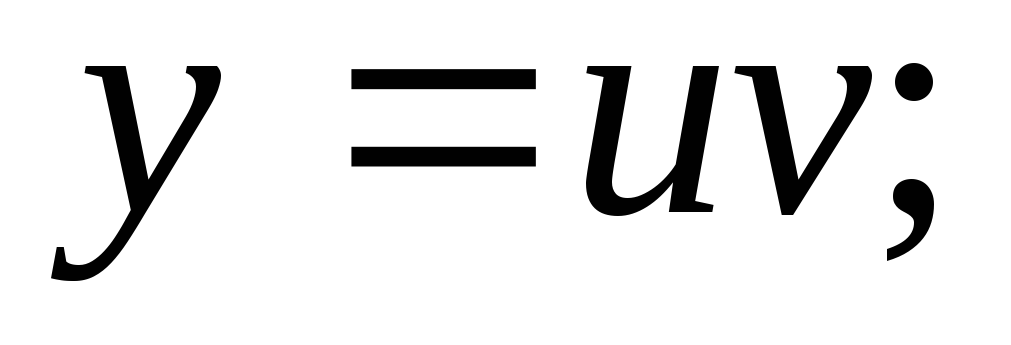 тогда
тогда 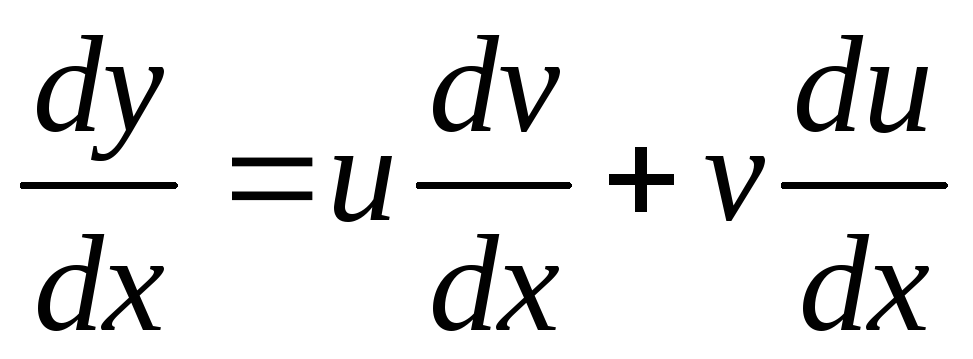 .
Подставив выражения для
.
Подставив выражения для  и
и  в уравнение (*), имеем
в уравнение (*), имеем 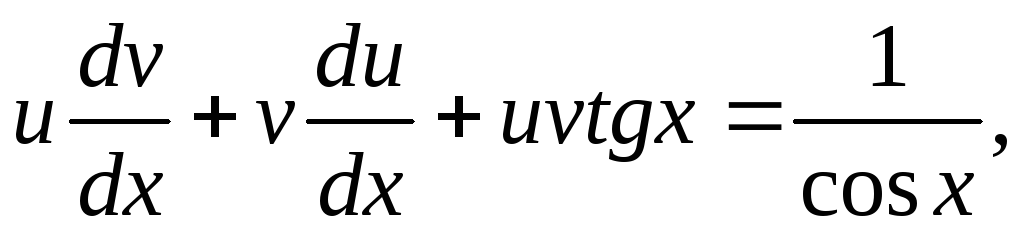 или
или 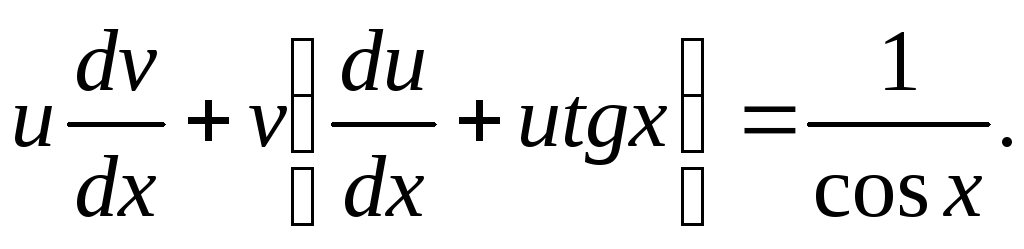 (**)
(**)
Для отыскания u получаем уравнение
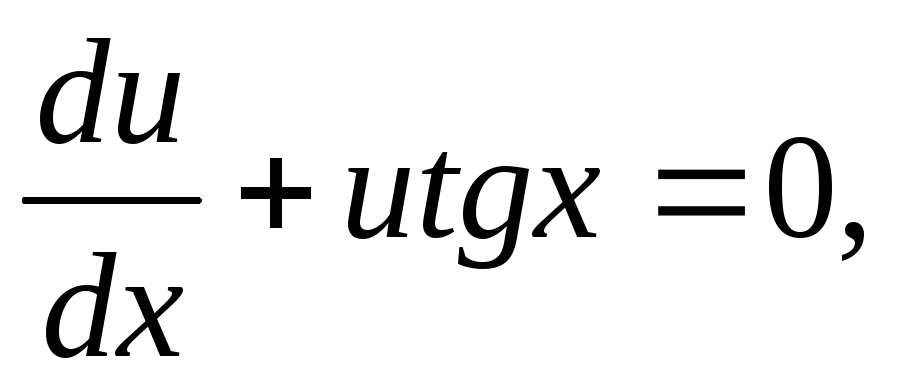 т.е.
т.е. 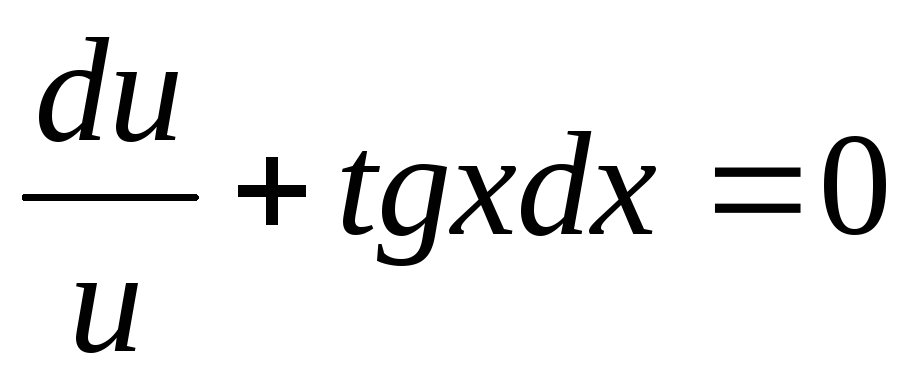 ,
,
откуда 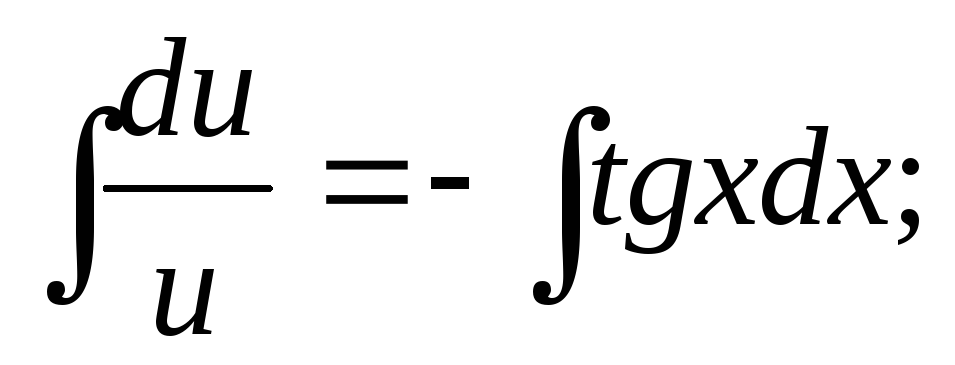
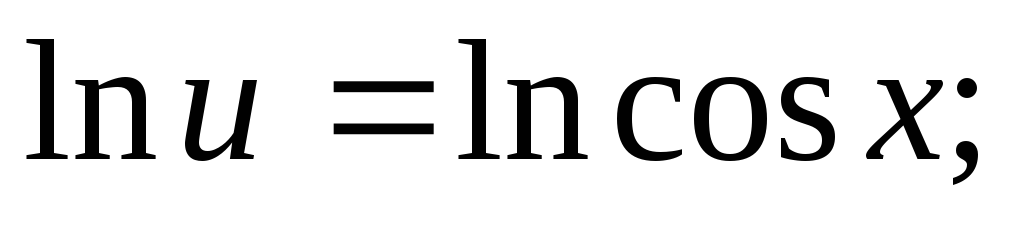
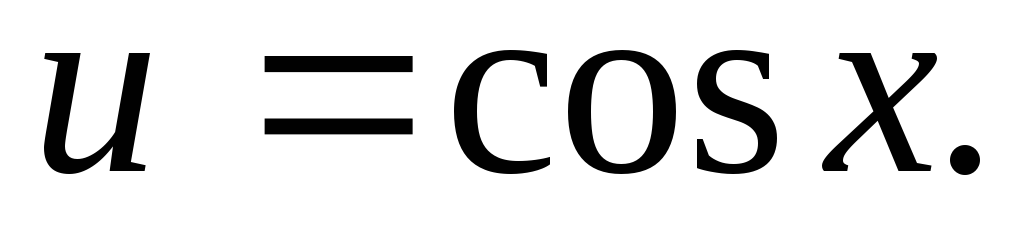
Подставляя выражения для u в уравнение (*), имеем
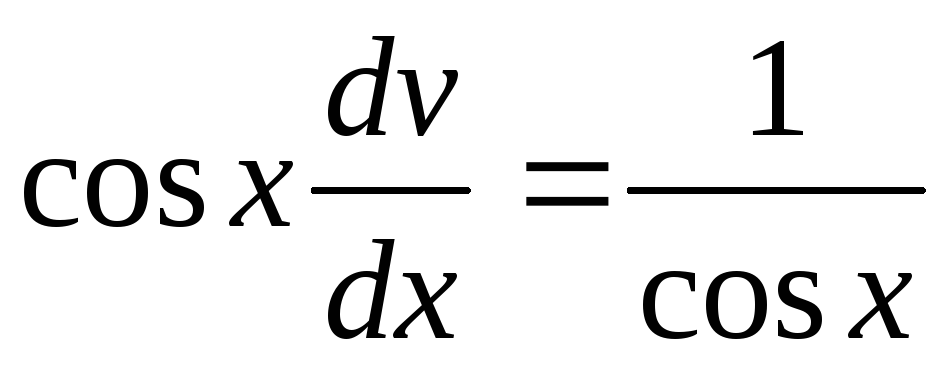 ,
или
,
или 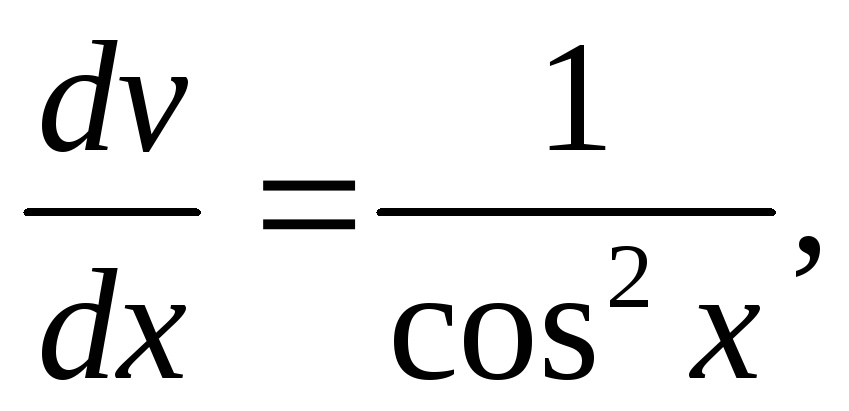 т.е.
т.е. 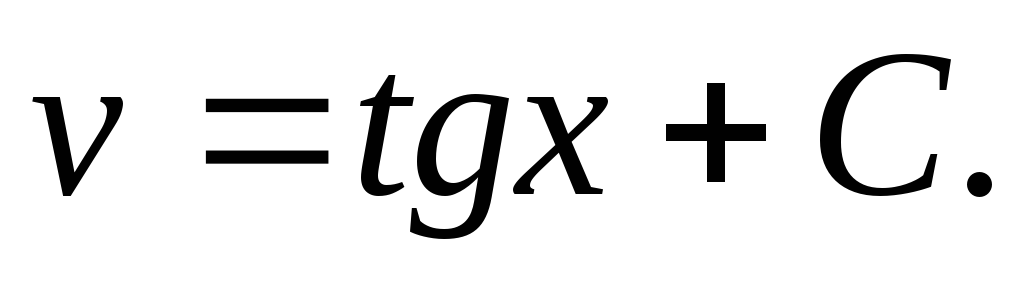
Следовательно, общее решение данного уравнения записывается так:
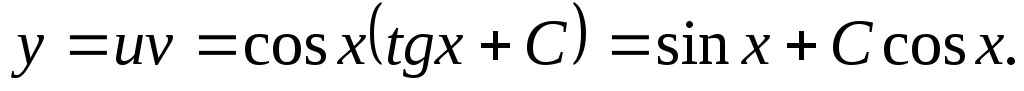
Используя начальные условия 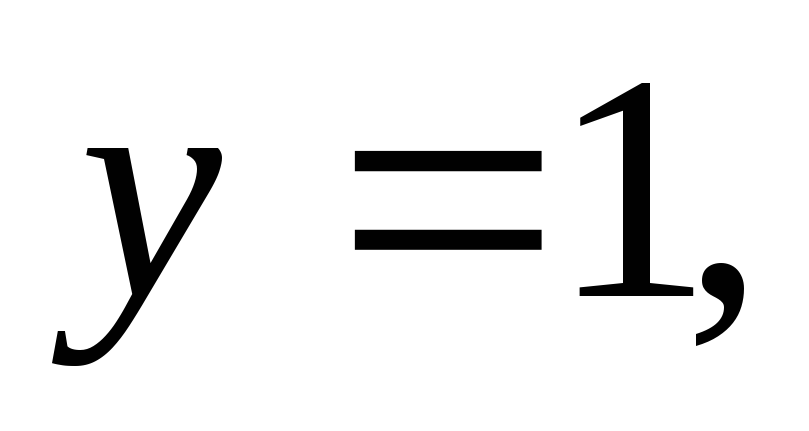
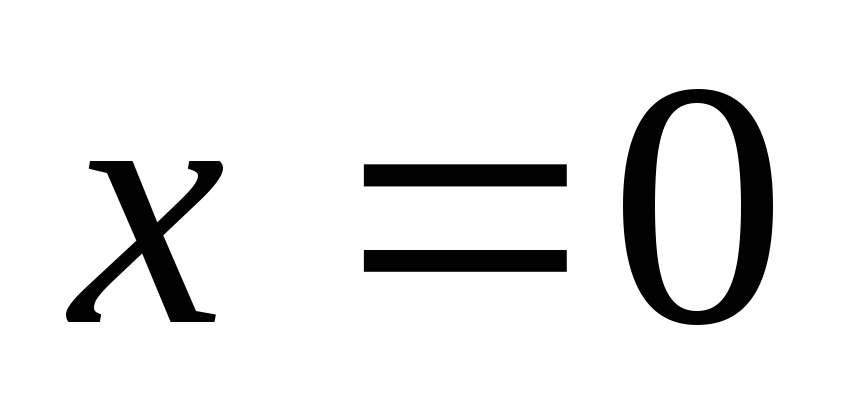 ,
имеем
,
имеем  откуда С=1. Таким образом, искомое частное
решение имеет вид
откуда С=1. Таким образом, искомое частное
решение имеет вид 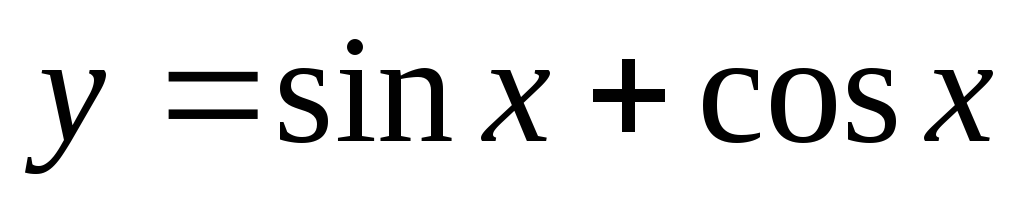 .
.
4. Уравнение Бернулли – это уравнение вида:
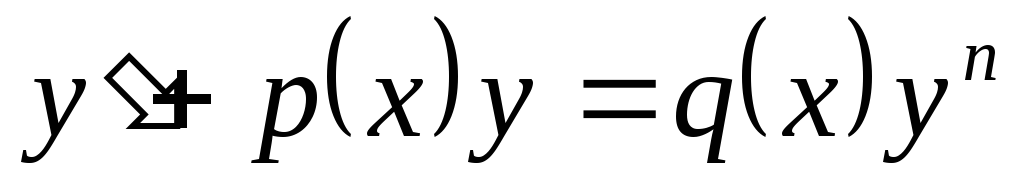 ,
,
где 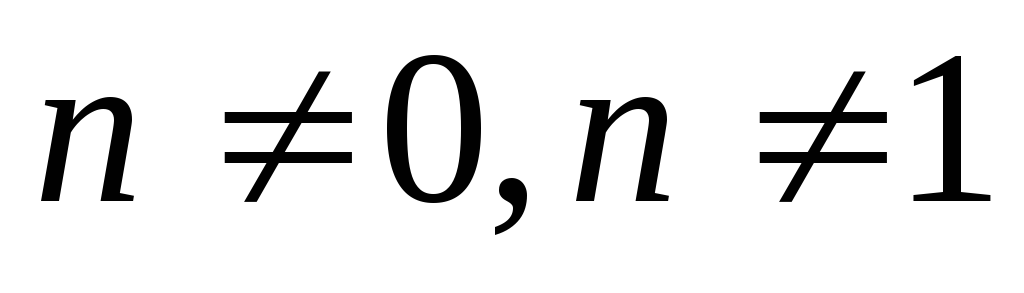 (при
(при 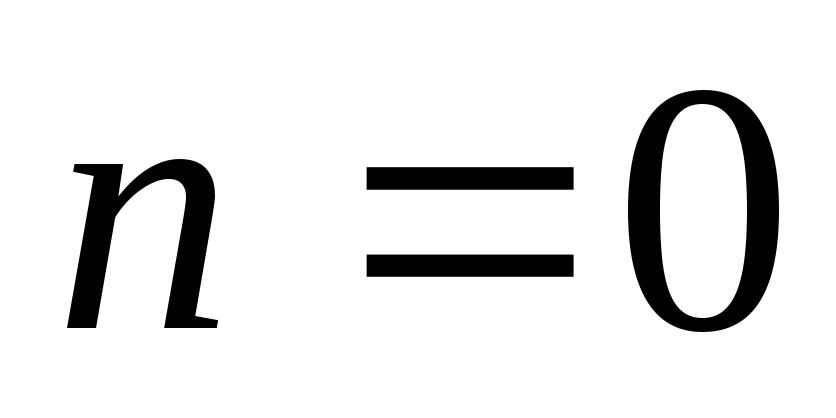 — линейное дифференциальное уравнение,
при
— линейное дифференциальное уравнение,
при 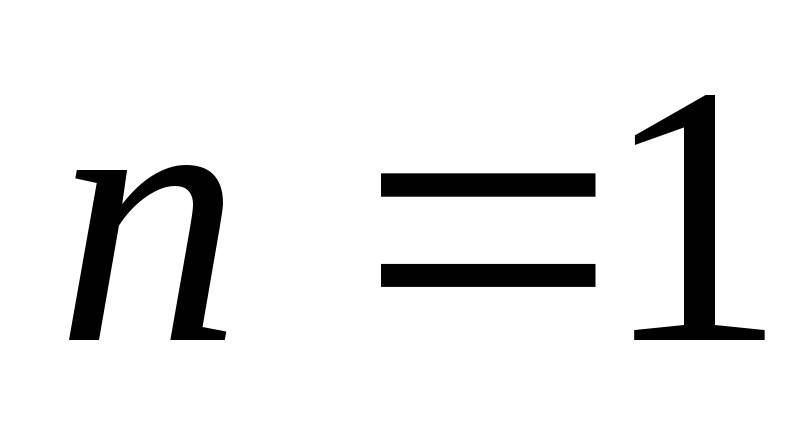 — уравнение с разделяющимися переменными).
Уравнение приводится к линейному
дифференциальному уравнению с помощи
подстановки
— уравнение с разделяющимися переменными).
Уравнение приводится к линейному
дифференциальному уравнению с помощи
подстановки 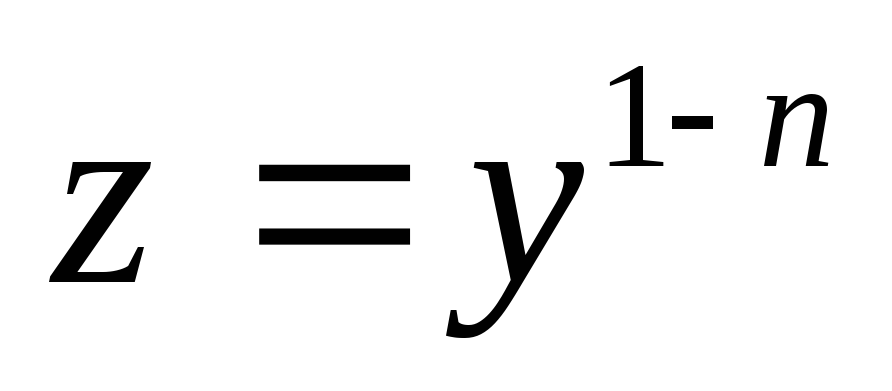 (при
(при 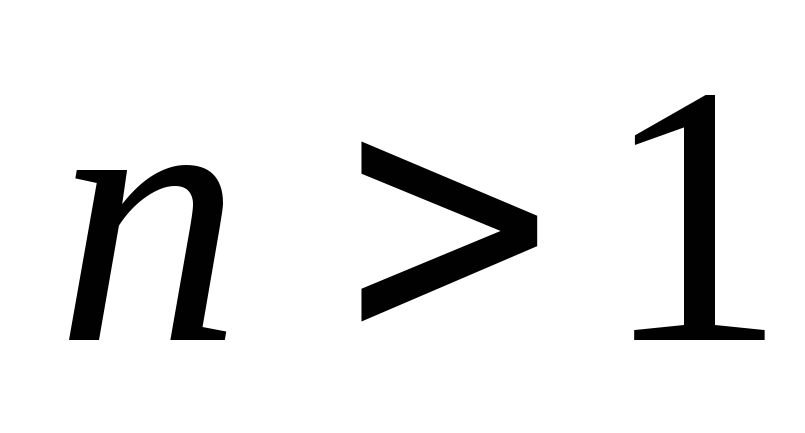 может быть потеряно решение
может быть потеряно решение 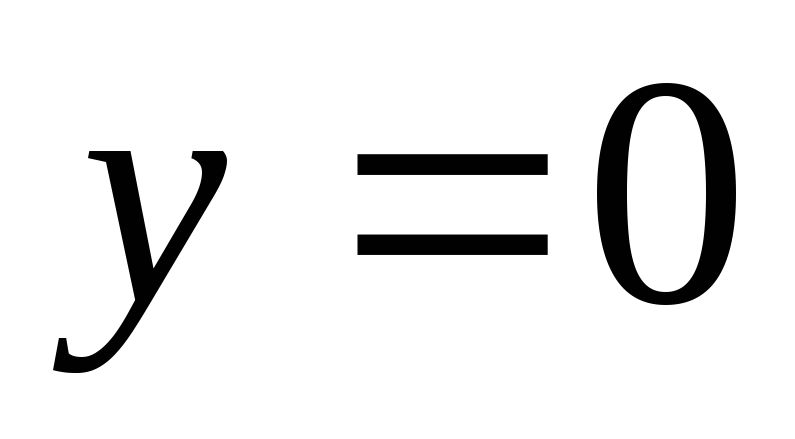 ).
Поэтому оно решается как линейное: либо
методом Бернулли, либо методом Лагранжа.
).
Поэтому оно решается как линейное: либо
методом Бернулли, либо методом Лагранжа.
Пример. Решить дифференциальное
уравнение 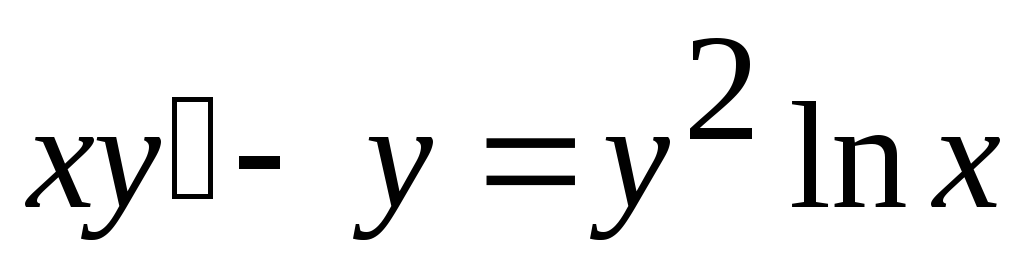
Введем замену z= y1-2 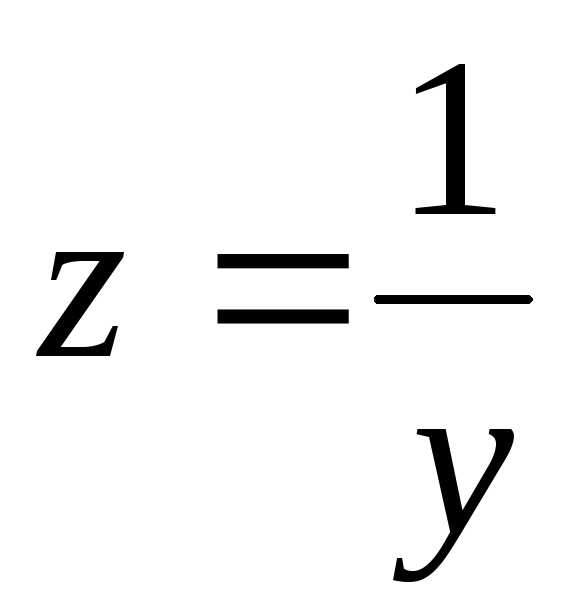 ,
, 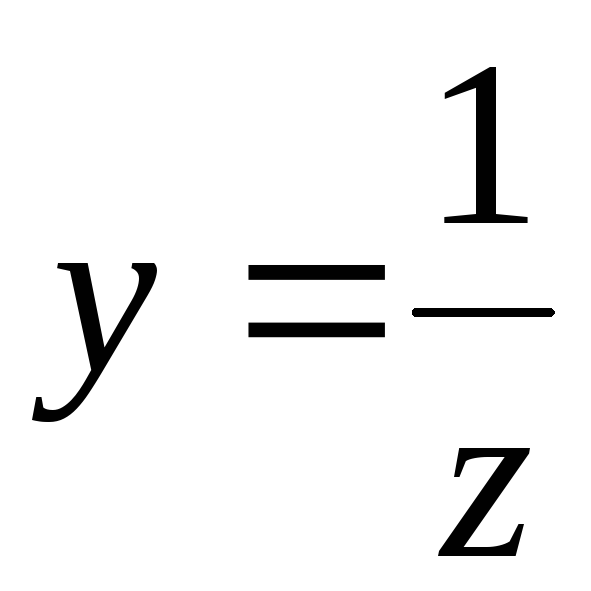 ,
,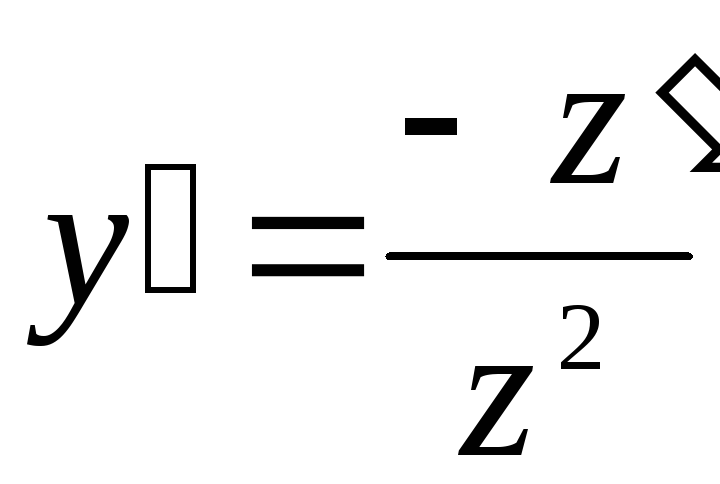 .
.
Подставим эти выражения в уравнение.
Получим 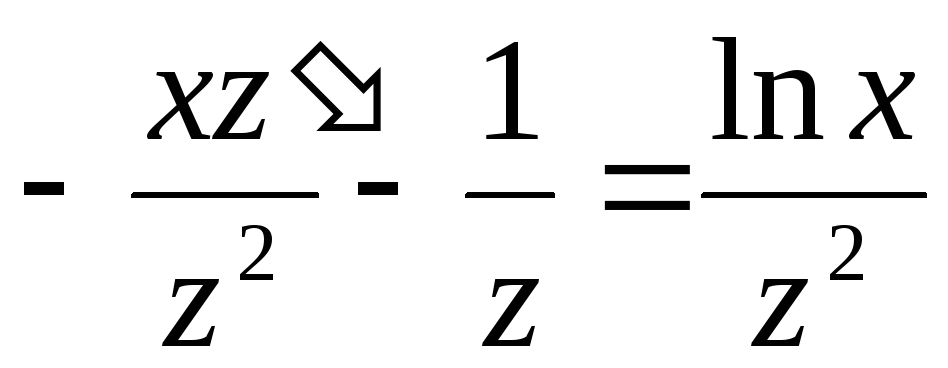 ,
,
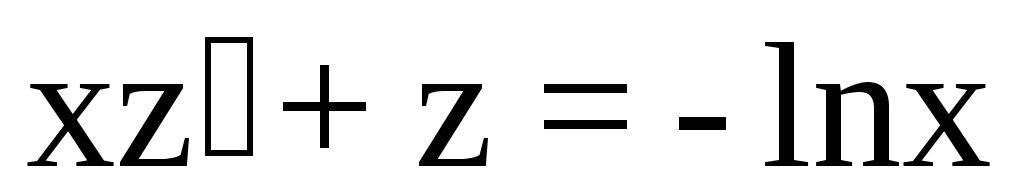 ,
, 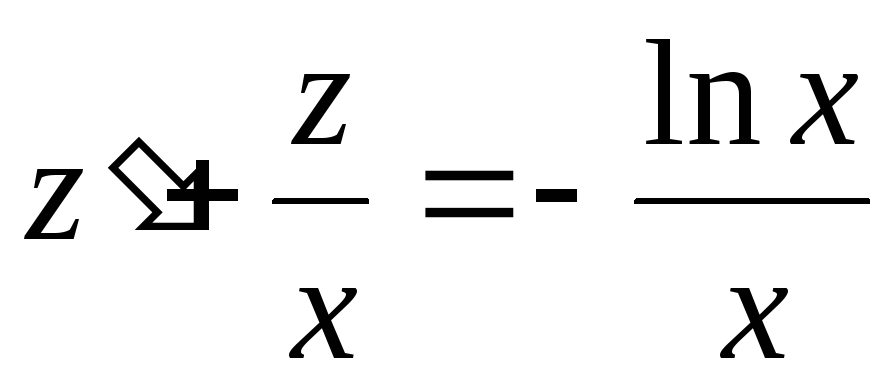
Решим полученное линейное уравнение методом Лагранжа.
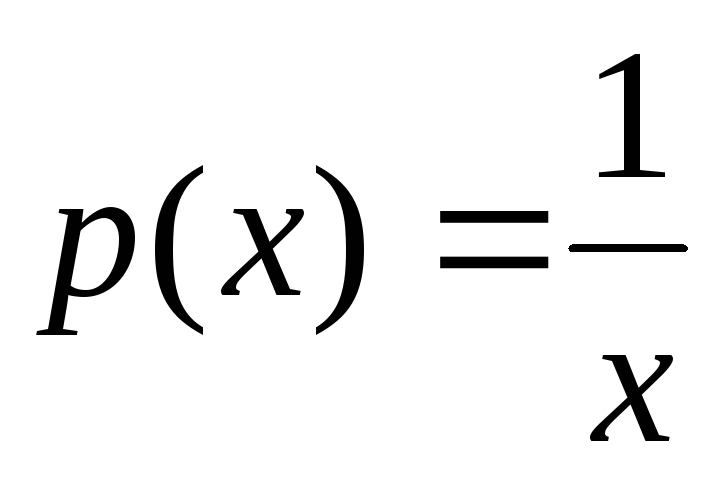
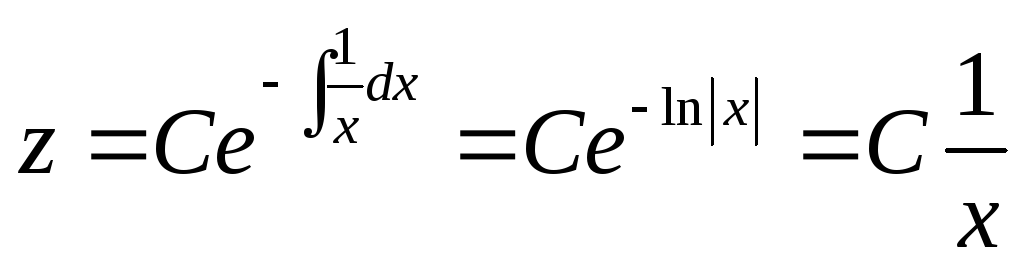
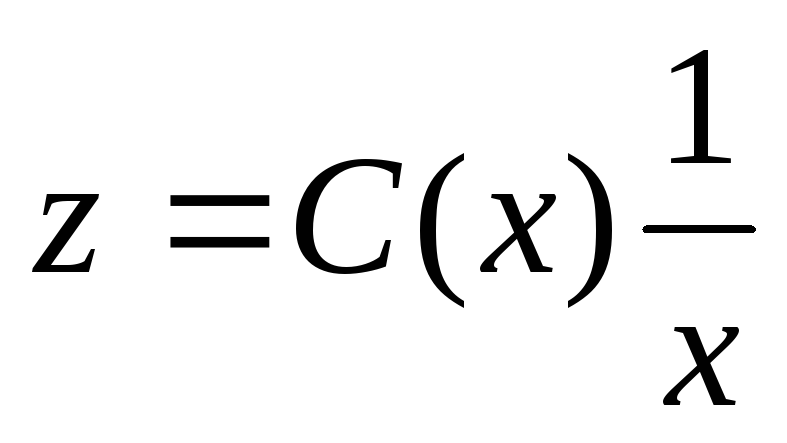 ,
, 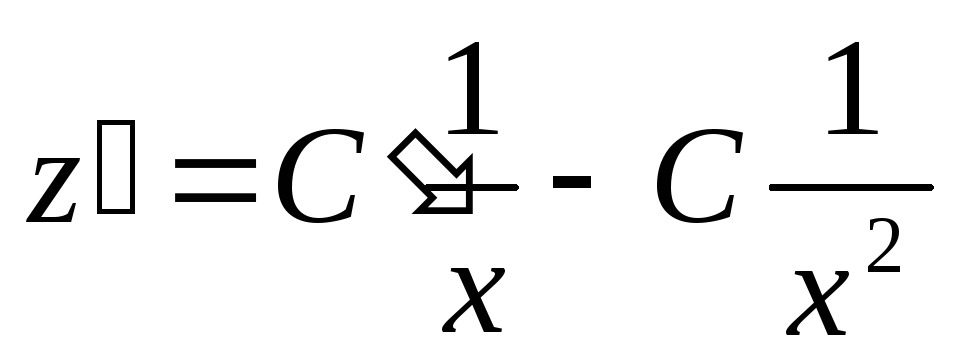
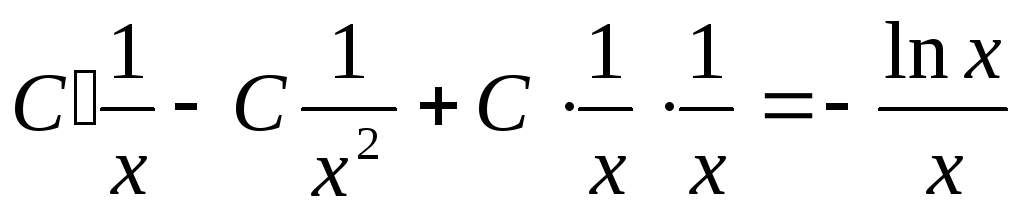 ,
, 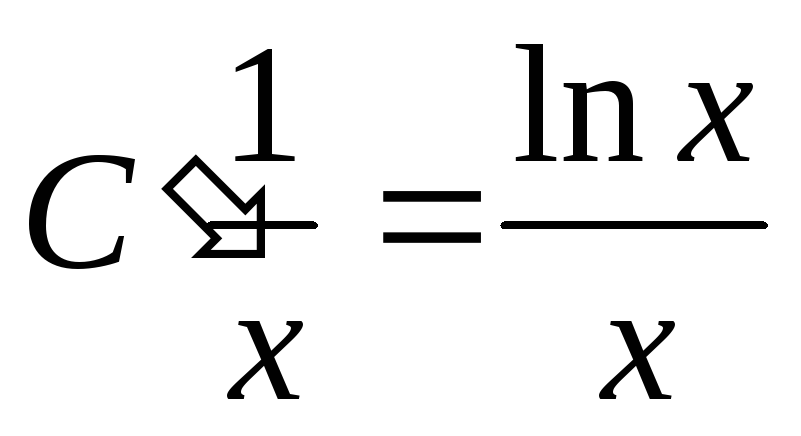 ,
, 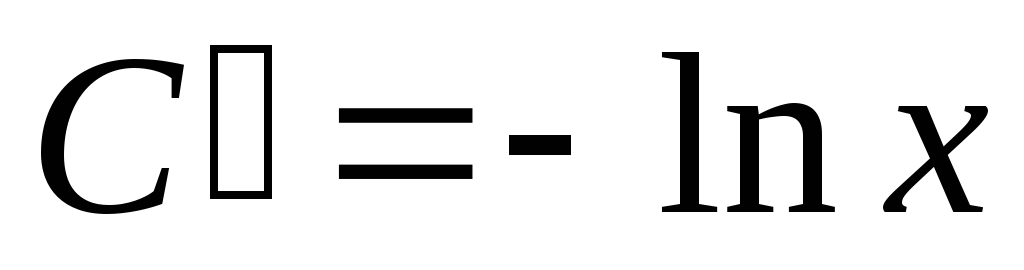
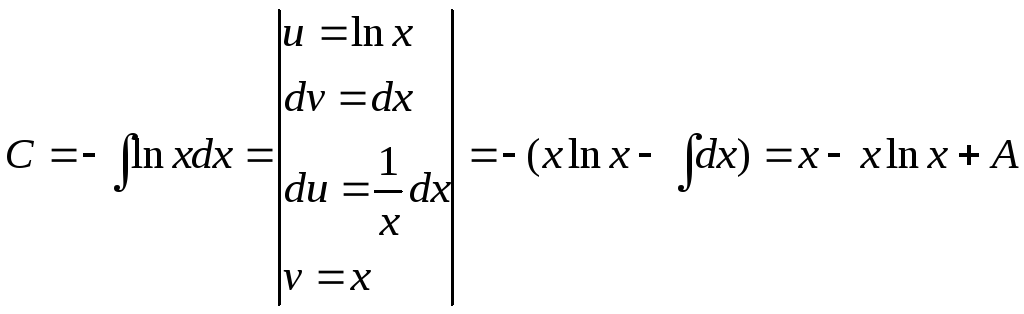
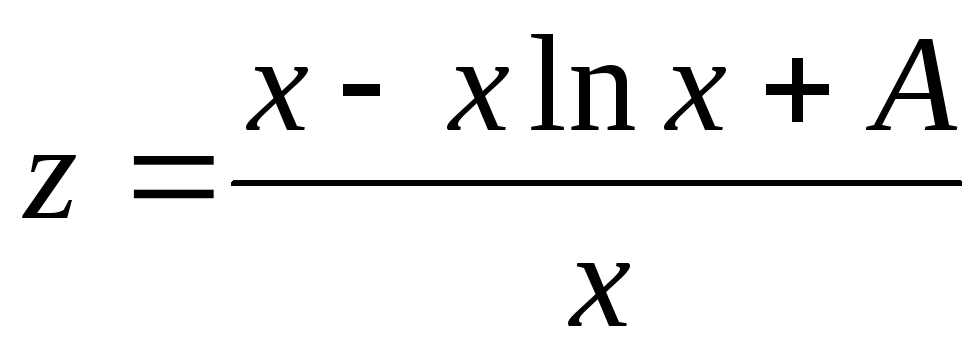
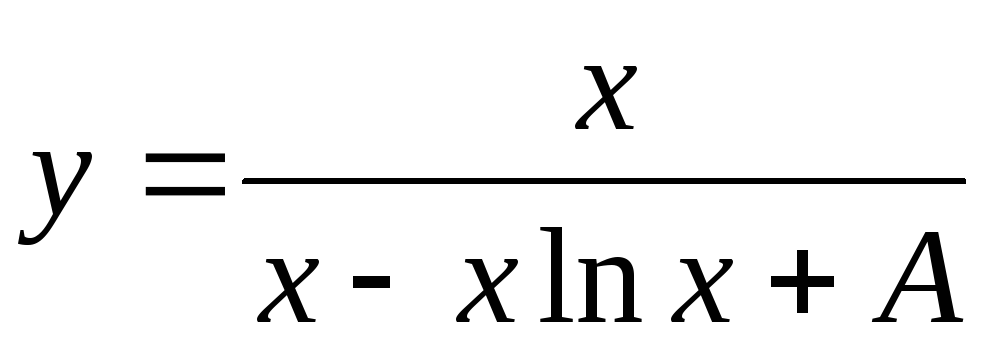 ,
, 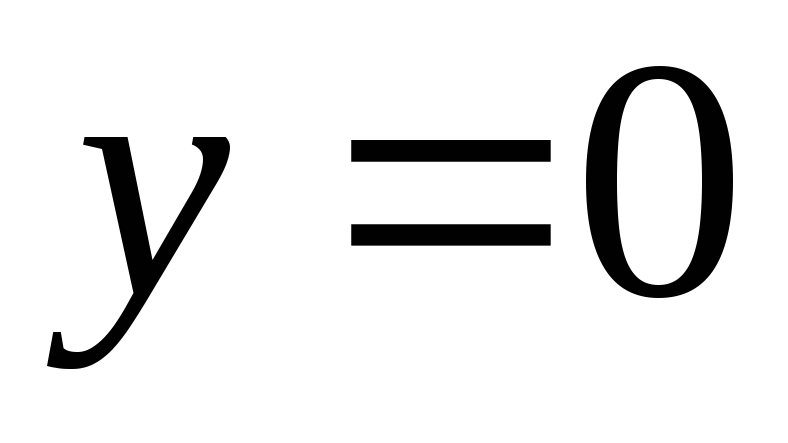 .
.
5.Простейшие дифференциальные уравнения n – го порядка, допускающие понижение порядка методом интегрирования обеих частей уравнения – это уравнения вида:
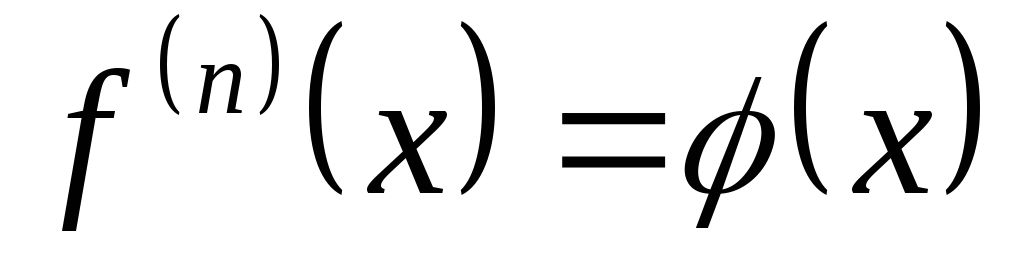 ,
,
где 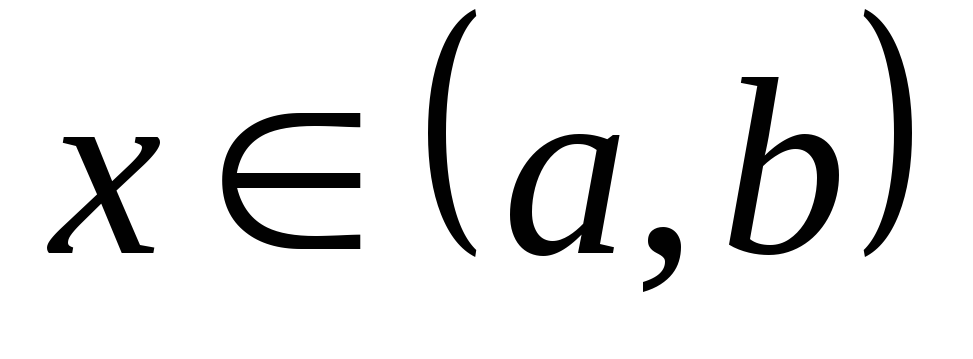 ,
функции
,
функции  (х) и f(х) непрерывны
на
(х) и f(х) непрерывны
на 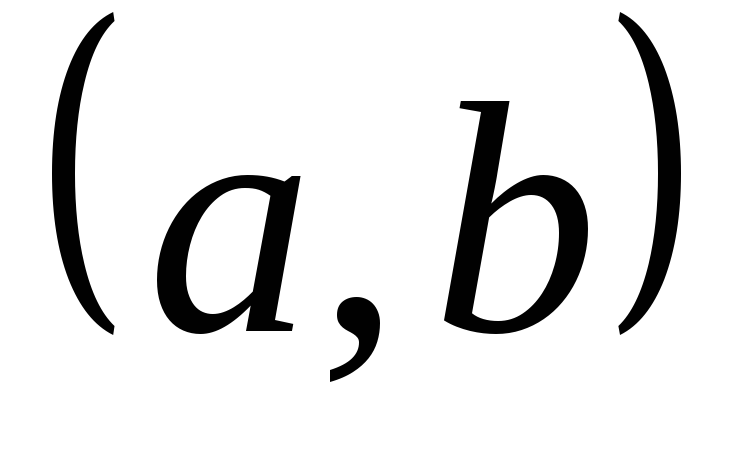 .
.
Пример. Решить уравнение 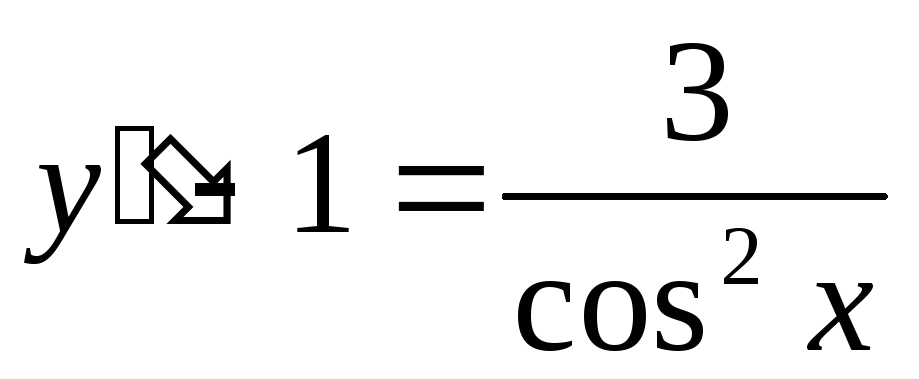
Уравнение является простейшим дифференциальным уравнением 2-го порядка. Понизим порядок уравнения методом интегрирования обеих частей уравнения
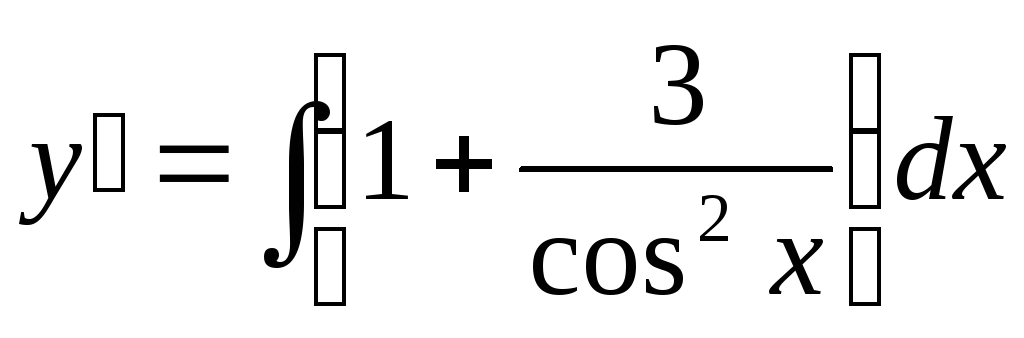 ,
,  =
x + 3tgx + C 1, y
= ∫(x + 3tgx + C 1)dx
=
x + 3tgx + C 1, y
= ∫(x + 3tgx + C 1)dx
y = x 2 – 3ln׀cosx׀ + C1x + C2 – общее решение дифференциального уравнения
6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами – это уравнения вида:
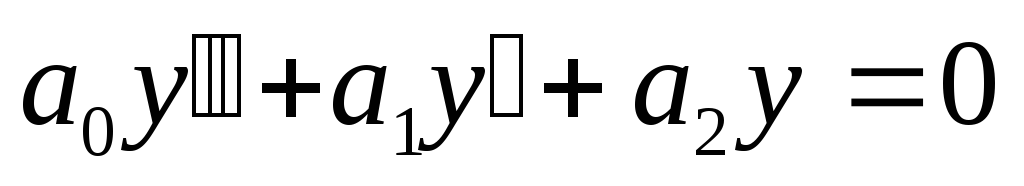 ,
,
где 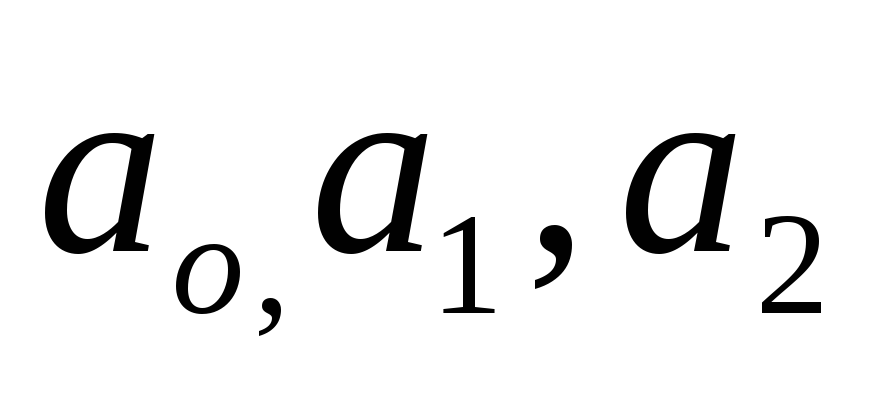 —
постоянные коэффициенты,
—
постоянные коэффициенты, 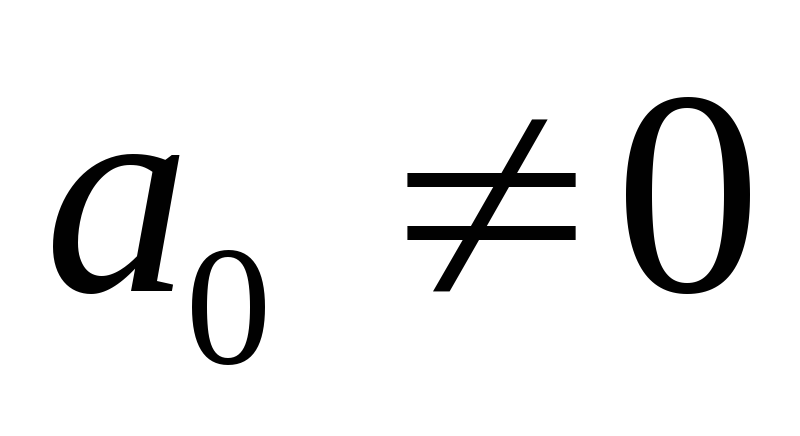
Метод решения. Составляют характеристическое уравнение
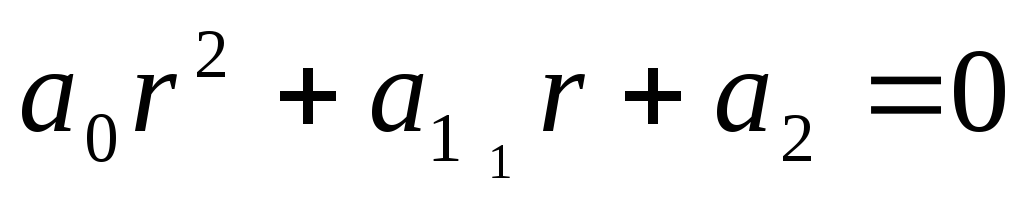 ,
которое получается из дифференциального
уравнения заменой в нем производных
искомой функции y соответствующими степенями r,
причем сама функция у заменяется
единицей.
,
которое получается из дифференциального
уравнения заменой в нем производных
искомой функции y соответствующими степенями r,
причем сама функция у заменяется
единицей.
Тогда общее решение дифференциального уравнения составляется в зависимости от дискриминанта D характеристического уравнения.
Рассмотрим следующие случаи:
а) D>0; два различных
действительных корня
;
тогда 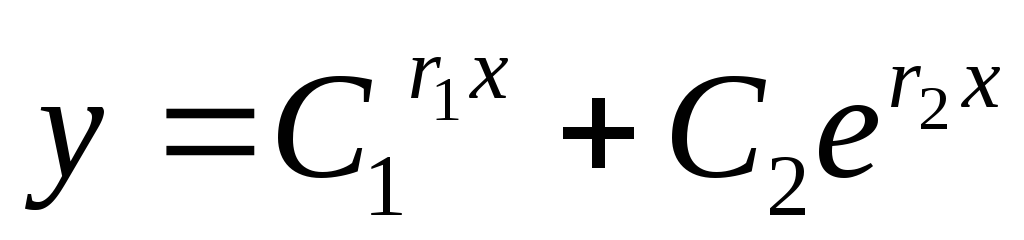 — общее решение дифференциального
уравнения;
— общее решение дифференциального
уравнения;
б) D=0; два равных
действительных корня 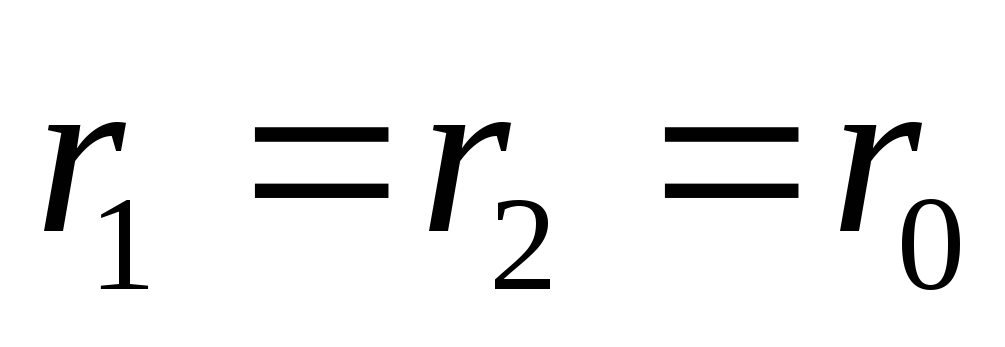 ;
тогда
;
тогда 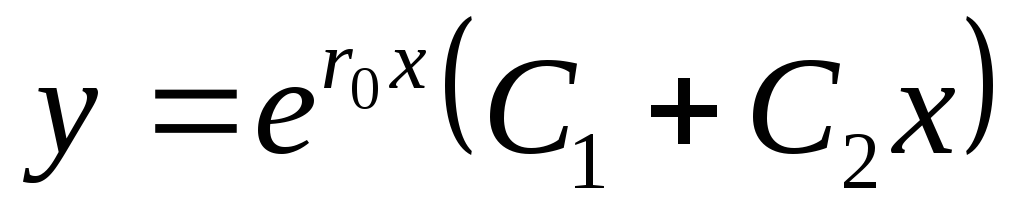 — общее решение дифференциального
уравнения;
— общее решение дифференциального
уравнения;
в) D<0; два различных
комплексных корня: 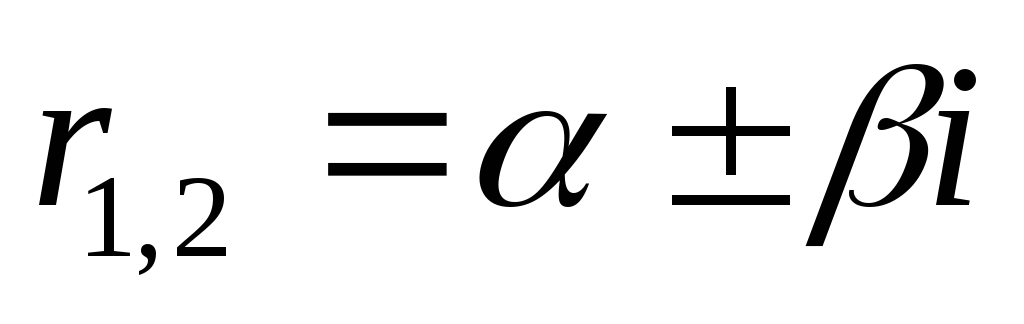 ,
где
,
где 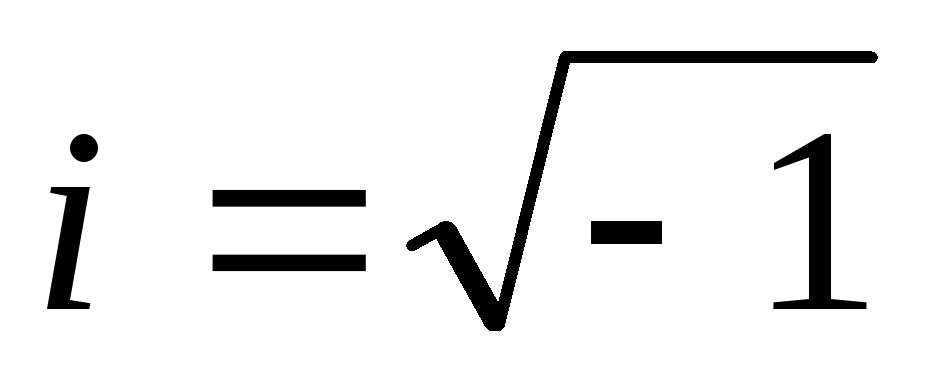 ,
,
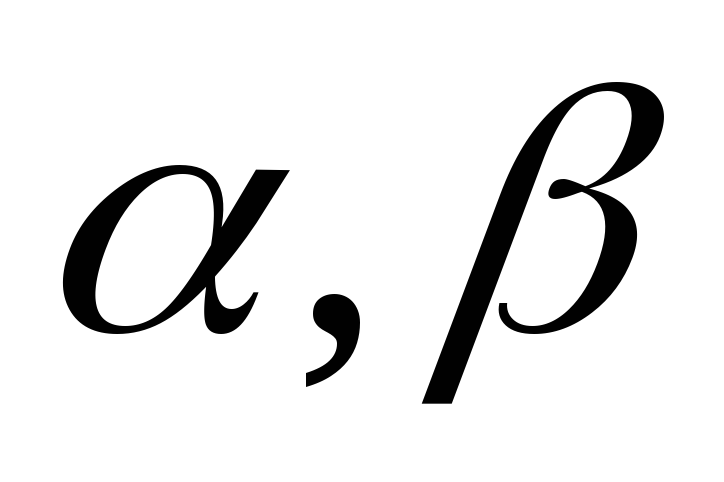 —
действительные числа, причем
—
действительные числа, причем  >0.
>0.
Тогда 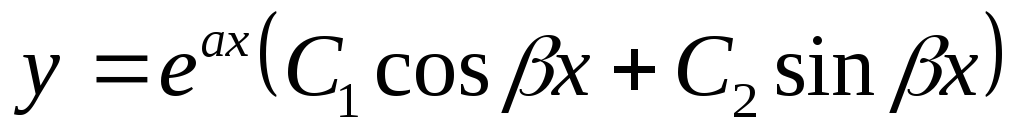 — общее решение дифференциального
уравнения.
— общее решение дифференциального
уравнения.
Пример. Найти частное решение
уравнения 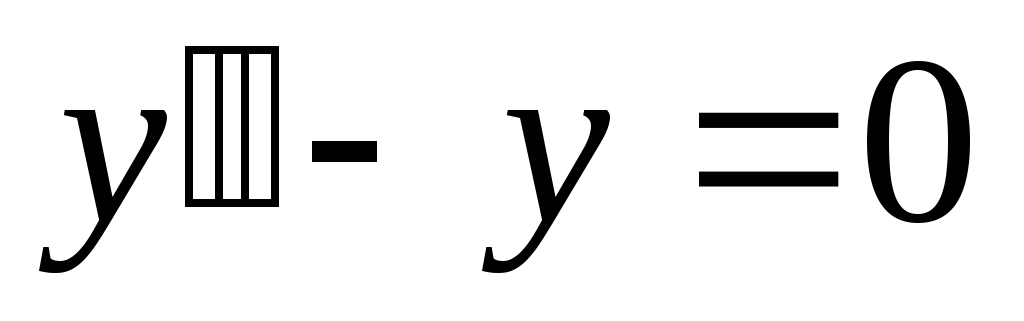 ,
удовлетворяющее начальным условиям
у(0)=0,
,
удовлетворяющее начальным условиям
у(0)=0, 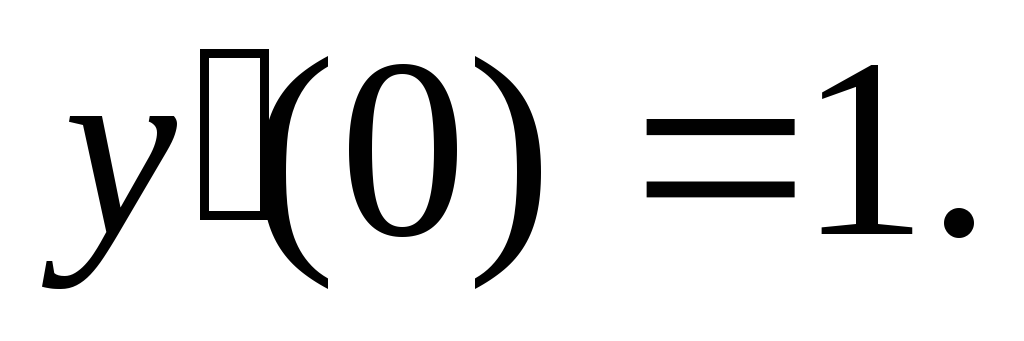
Данная задача с начальными условиями
носит название задачи Коши. Составим
характеристическое уравнение: r2-1=0.
Его решениями являются 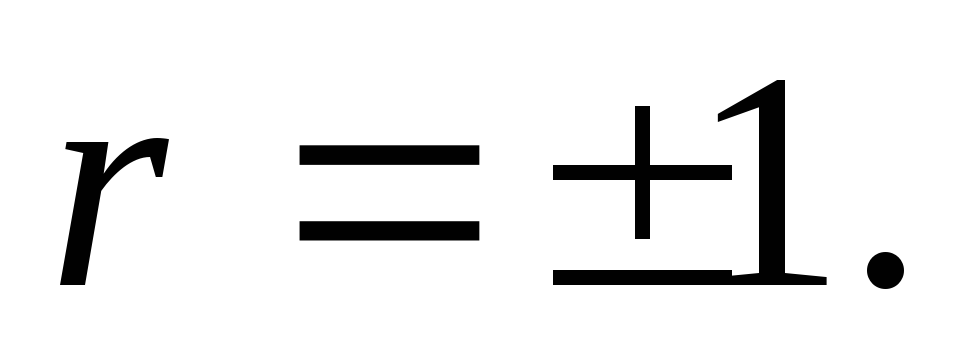 Общее решение уравнения в этом случае
(Д>0) находится по формуле
Общее решение уравнения в этом случае
(Д>0) находится по формуле 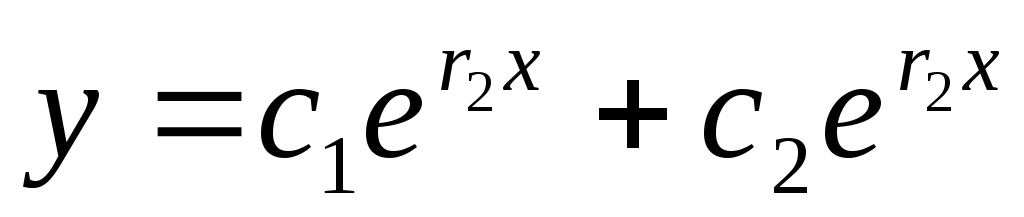 ,
т.е.
,
т.е. 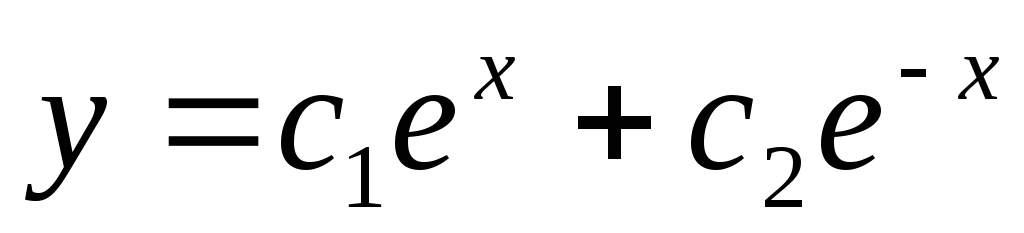 —
общее решение.
—
общее решение.
Найдем 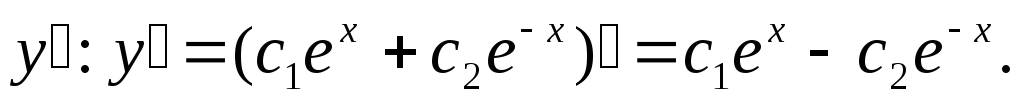
Подставим в уравнения начальные условия:
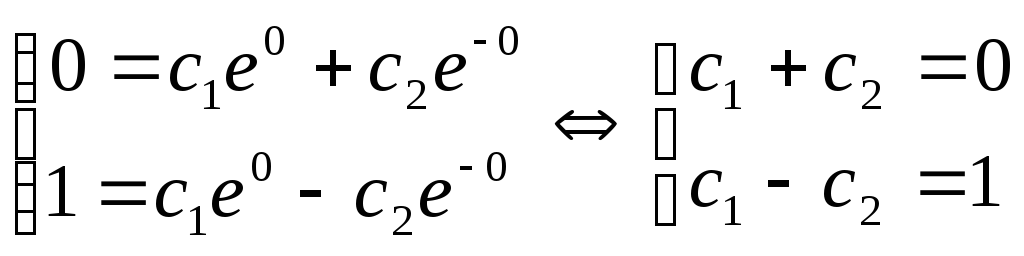
Решая эту систему, получаем 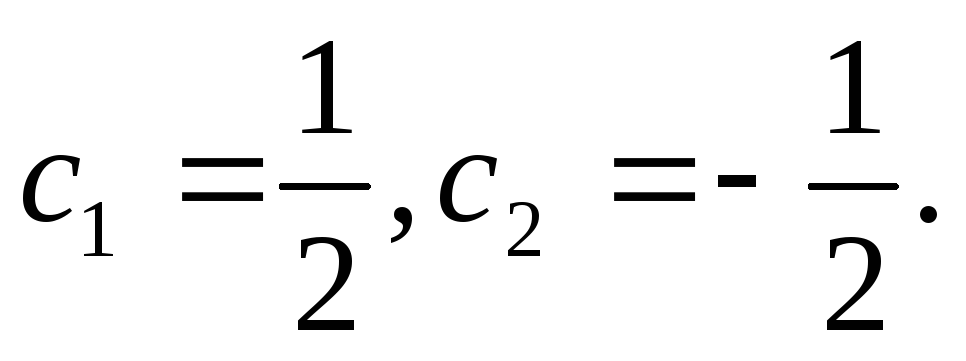 Найденные значения постоянных с1 и с2 подставляем в общее решение
и получаем искомое решение
Найденные значения постоянных с1 и с2 подставляем в общее решение
и получаем искомое решение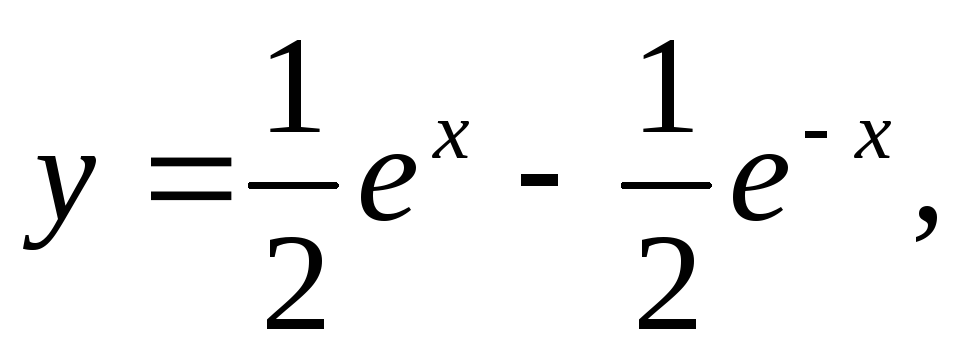 или
или 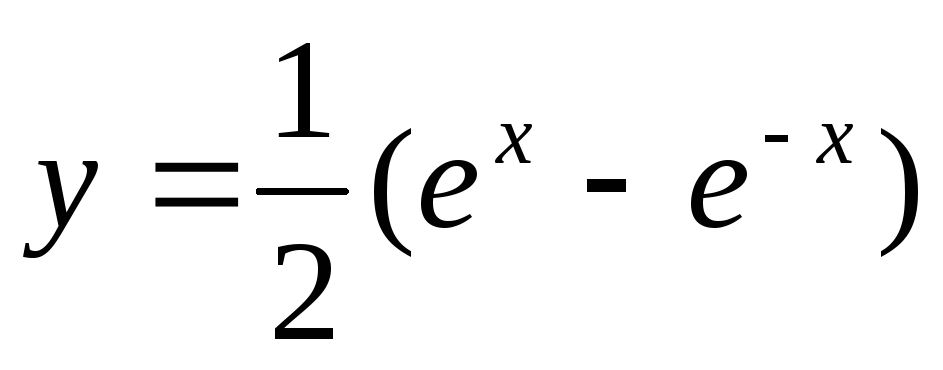
Дифференциальные уравнения Основные понятия
При анализе динамических процессов в различных областях науки и техники часто возникают задачи решения дифференциальных уравнений, которые связывают искомую функцию и её производные различных порядков. Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных.
Дифференциальное уравнение называется
обыкновенным, если оно содержит
искомую функцию от одной переменной,
её производные различных порядков и
независимую переменную. Общий вид
обыкновенного дифференциального
уравнения определяется следующим
выражением: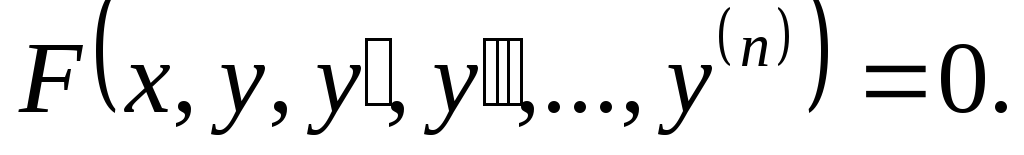 Если в уравнении искомая функция зависит
от нескольких переменных и это уравнение
содержит частные производные, то такое
уравнение называется дифференциальным
уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной,
входящих в уравнение.
Если в уравнении искомая функция зависит
от нескольких переменных и это уравнение
содержит частные производные, то такое
уравнение называется дифференциальным
уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной,
входящих в уравнение.
Пример. Задача нахождения первообразной  — функции, производная которой при каждом
значении
— функции, производная которой при каждом
значении 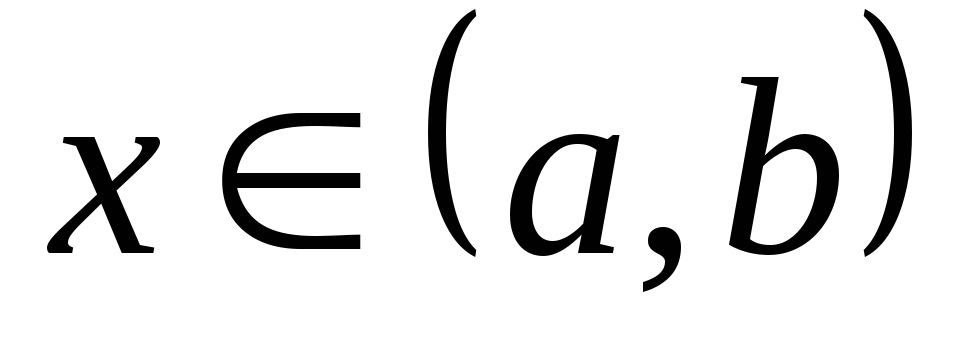 равна заданной функции
равна заданной функции 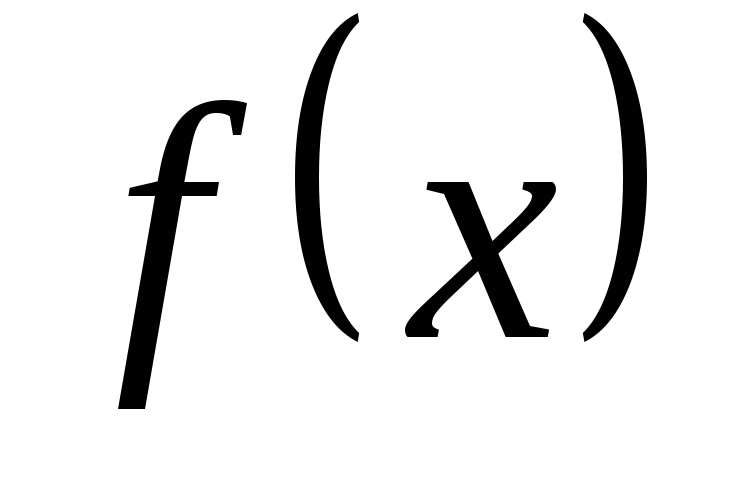 ,
— может быть записана как простейшее
обыкновенное дифференциальное уравнение
первого порядка:
,
— может быть записана как простейшее
обыкновенное дифференциальное уравнение
первого порядка:  .
.
Любая функция 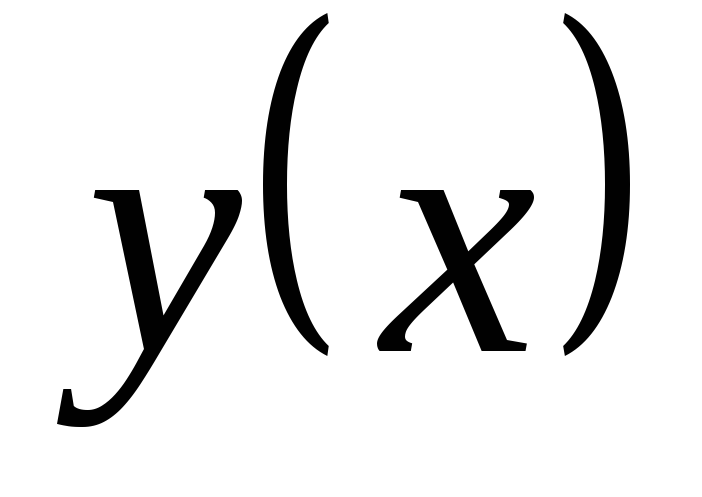 ,
обращающая уравнение
,
обращающая уравнение 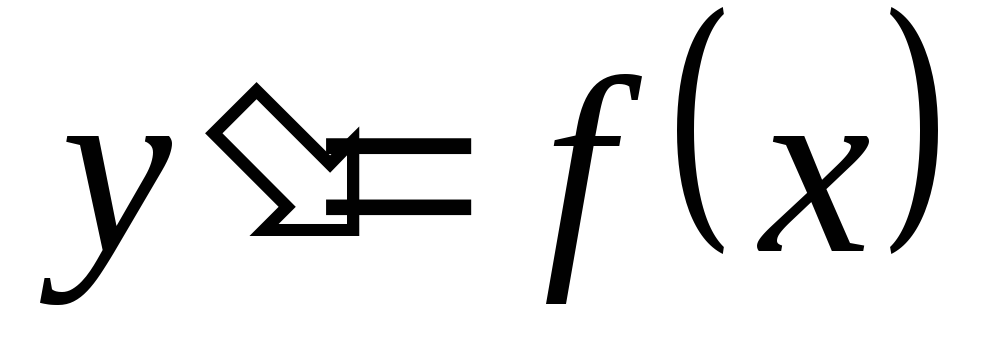 при
при 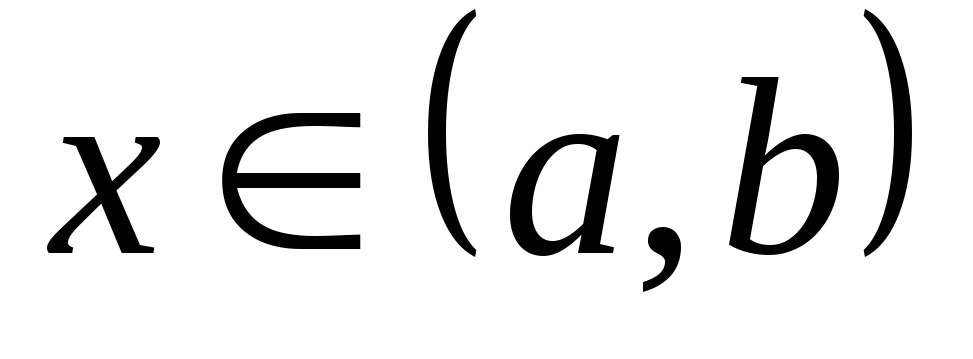 в тождество, может быть выражена с
использованием неопределенного интеграла
в тождество, может быть выражена с
использованием неопределенного интеграла 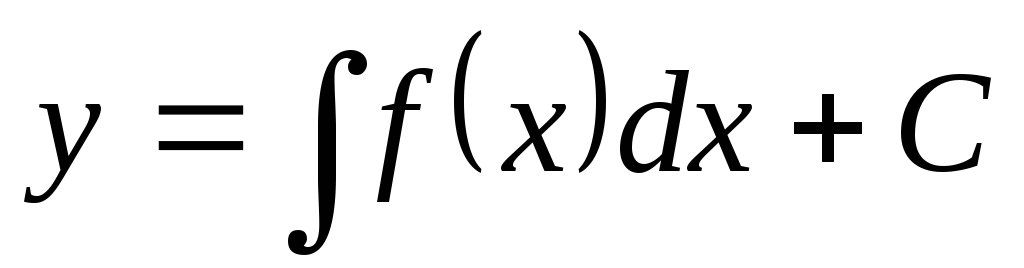 .
Здесь и далее
.
Здесь и далее 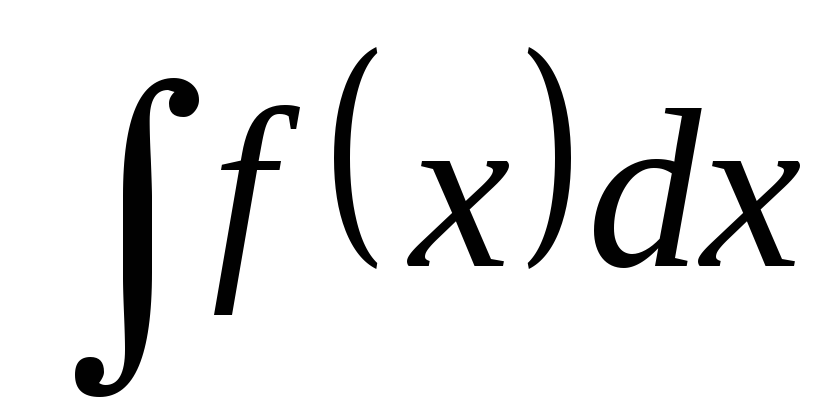 — какая-либо одна из первообразных
функции
— какая-либо одна из первообразных
функции 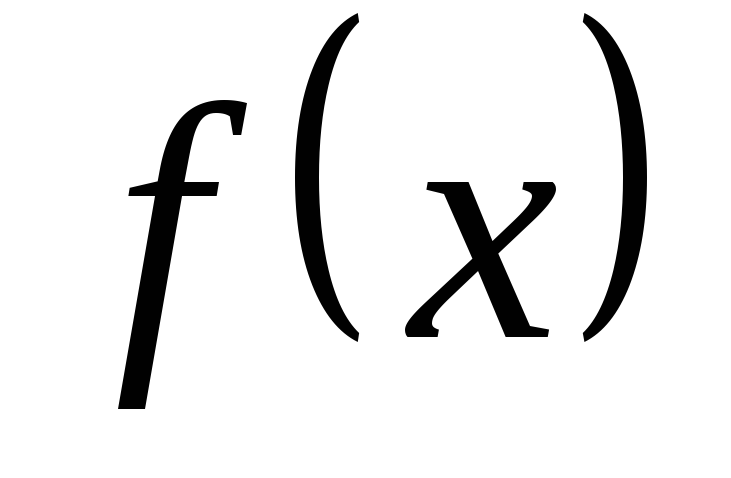 ,
С – произвольная постоянная.
,
С – произвольная постоянная.
Обыкновенным дифференциальным
уравнением первого порядка называется
уравнение вида 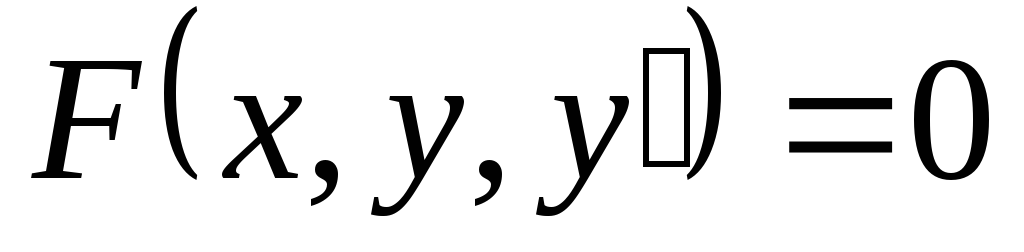 , где F – функция от трех переменных.
, где F – функция от трех переменных.
Уравнение 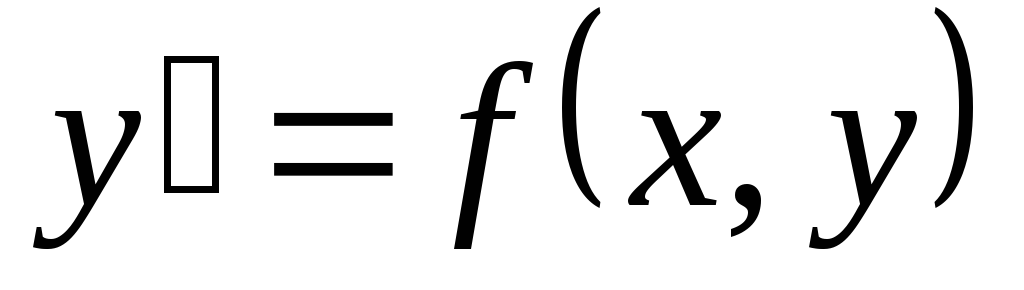 ,
где
,
где 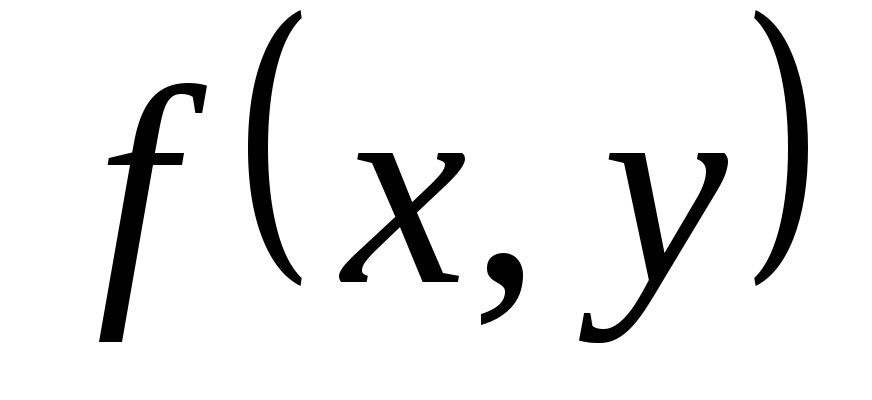 — функция, определённая в некоторой
области D плоскости Оху, называют дифференциальным
уравнением первого порядка, разрешенным
относительно производной. Предполагается,
что функция
— функция, определённая в некоторой
области D плоскости Оху, называют дифференциальным
уравнением первого порядка, разрешенным
относительно производной. Предполагается,
что функция 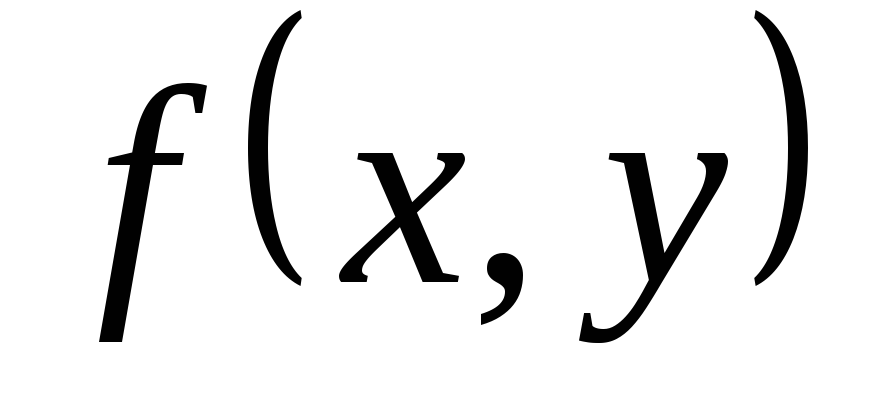 является непрерывной.
является непрерывной.
Решением дифференциального уравнения 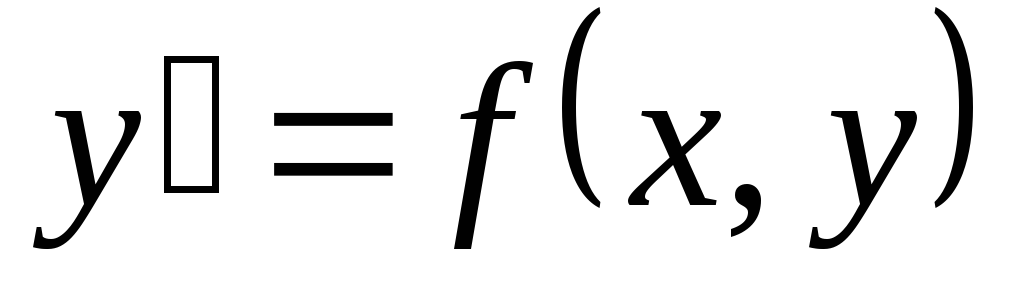 на некотором интервале
на некотором интервале 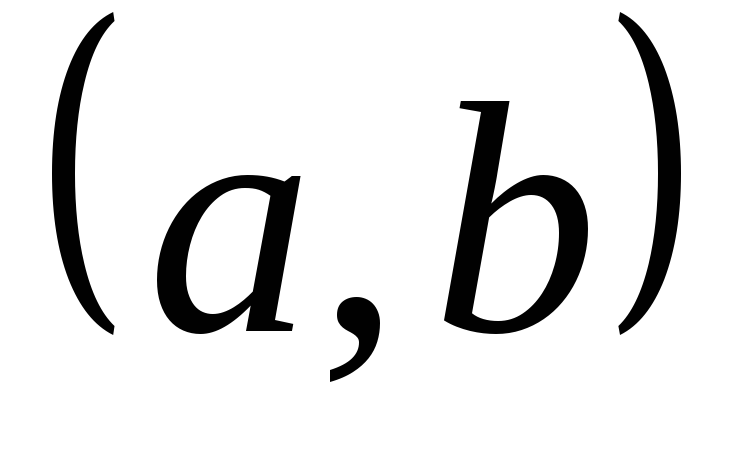 называется функция
называется функция 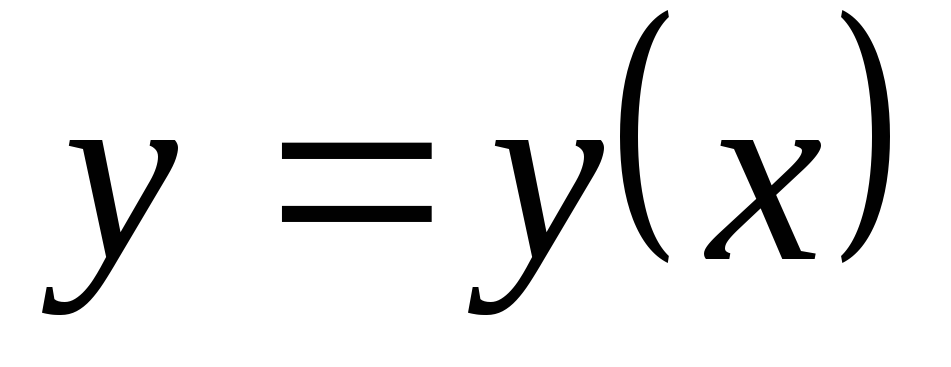 ,
определенная и дифференцируемая на
этом интервале и удовлетворяющая
следующим двум условиям:
,
определенная и дифференцируемая на
этом интервале и удовлетворяющая
следующим двум условиям:
точка
 при
любом
при
любом  ;
; при любом
при любом  .
.
Решить (проинтегрировать)
дифференциальное уравнение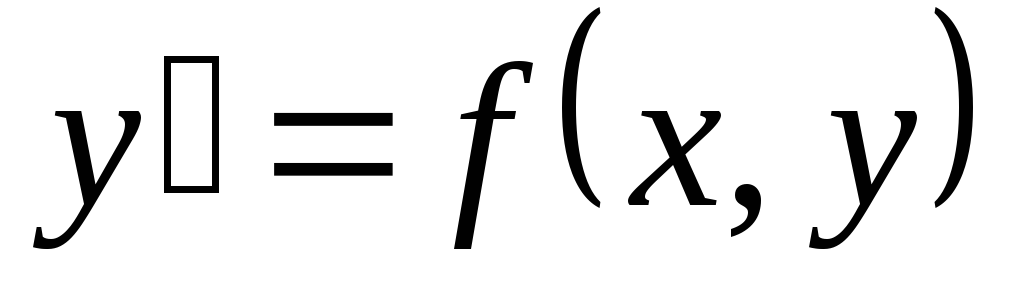 —
—
значит, найти все его решения в заданном
конечном или бесконечном интервале 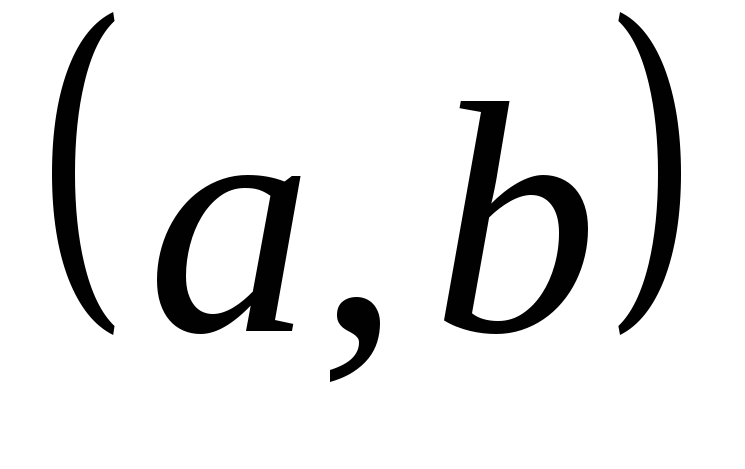 .
.
Интеграл дифференциального уравнения 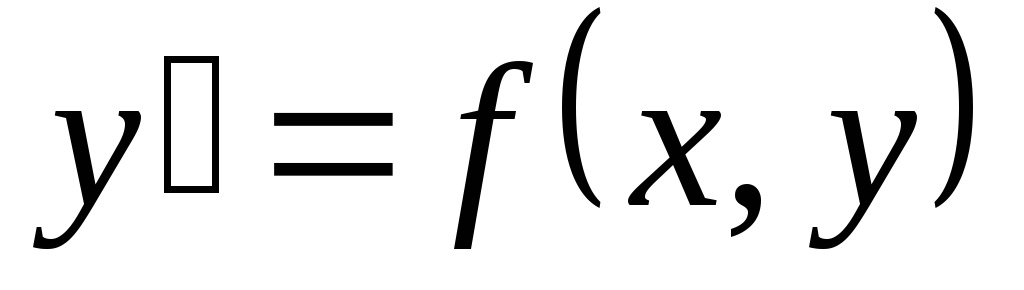 —
решение этого уравнения, заданное в
неявном виде.
—
решение этого уравнения, заданное в
неявном виде.
График решения дифференциального
уравнения 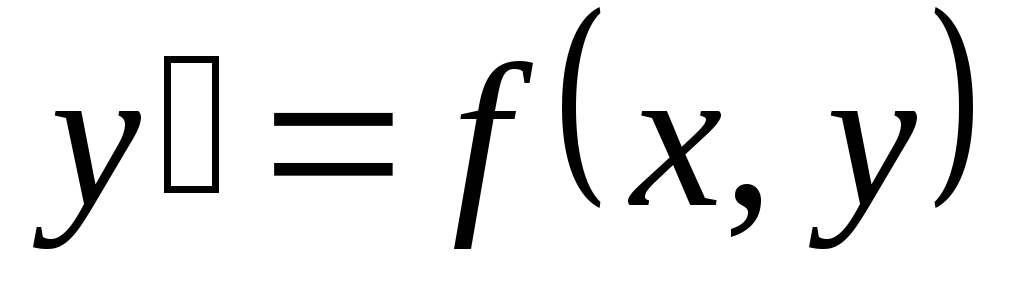 на плоскости Оху называется интегральной кривой.
на плоскости Оху называется интегральной кривой.
Задача Коши при решении дифференциального
уравнения 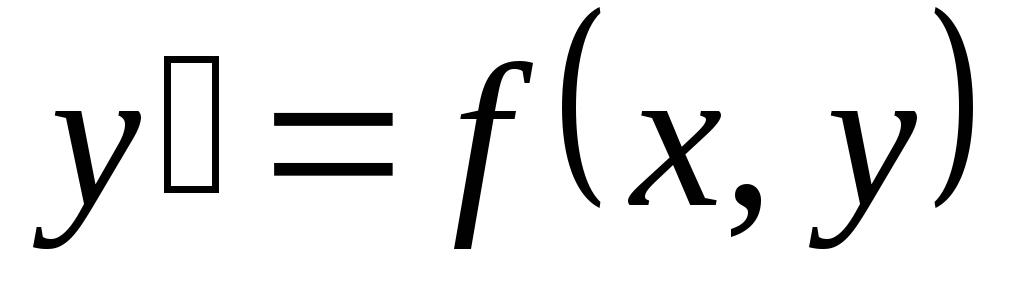 заключается
в следующем: требуется найти его решение,
удовлетворяющее начальному условию
заключается
в следующем: требуется найти его решение,
удовлетворяющее начальному условию 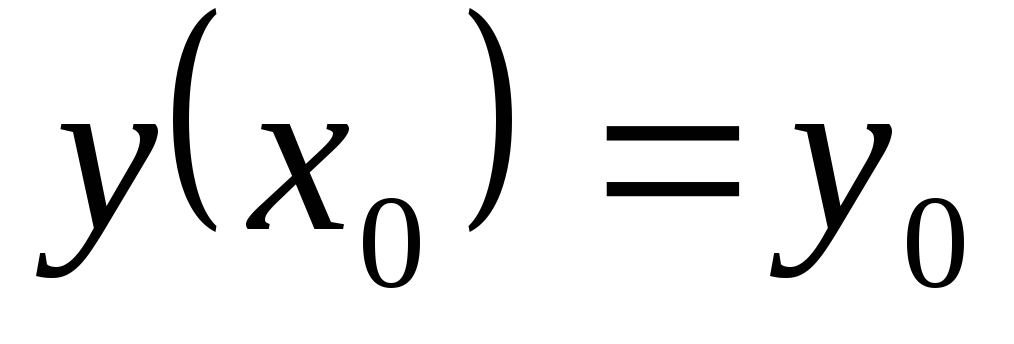 ,
где
,
где 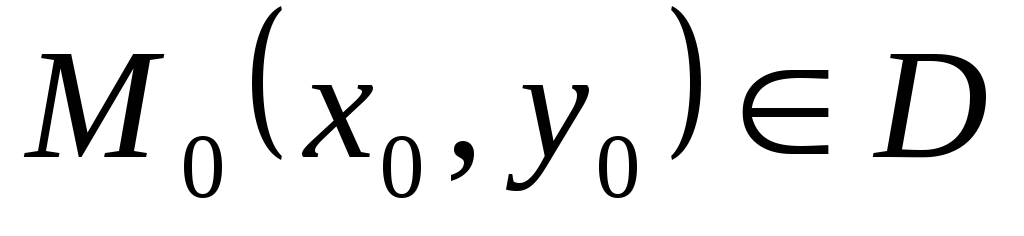 .
.
Пусть задано дифференциальное уравнение 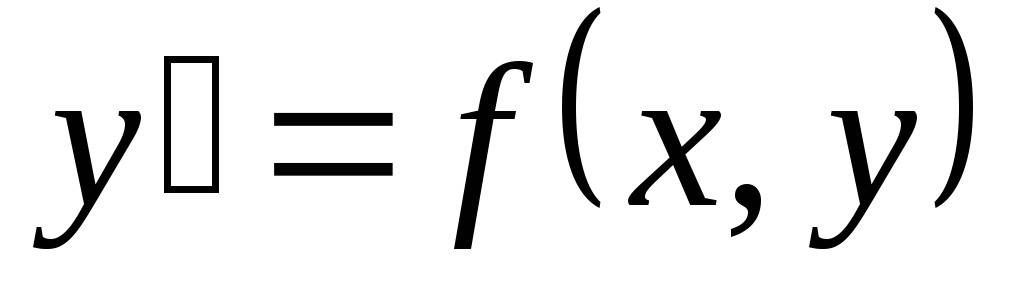 .
Если функция
.
Если функция 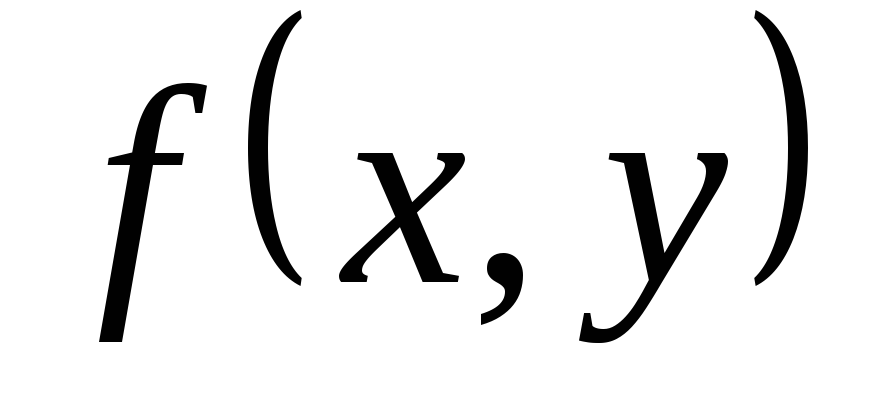 и
её частная производная определены и непрерывны в некоторой
области D, и точка
и
её частная производная определены и непрерывны в некоторой
области D, и точка 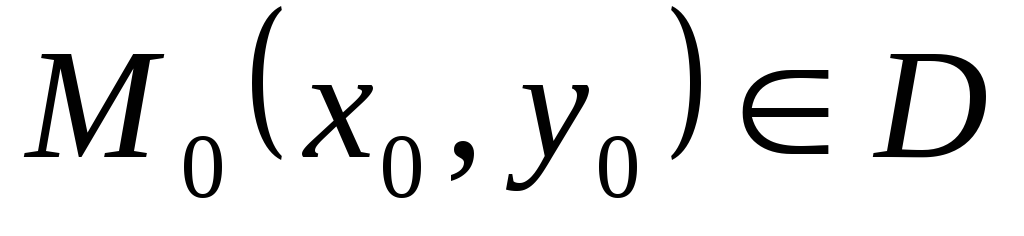 ,то
существует единственное решение
,то
существует единственное решение 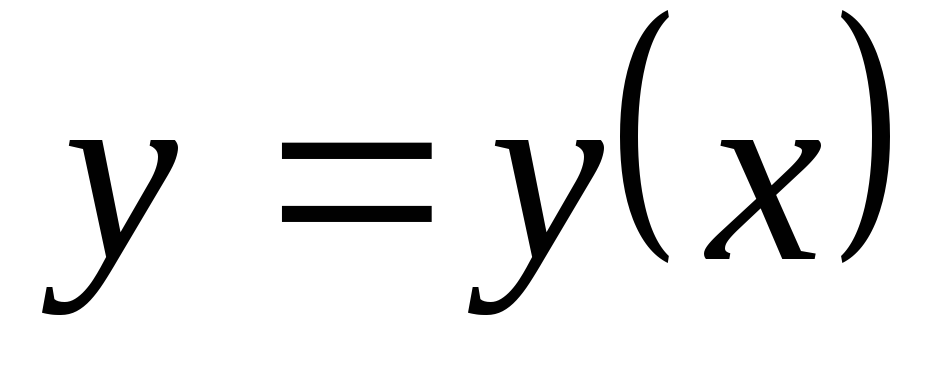 уравнения
уравнения 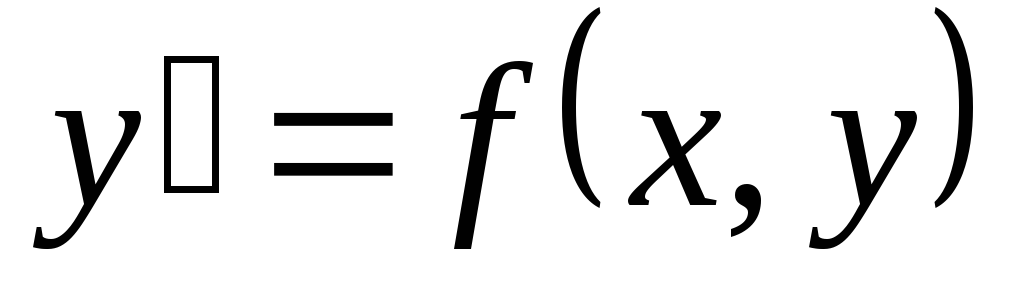 ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию 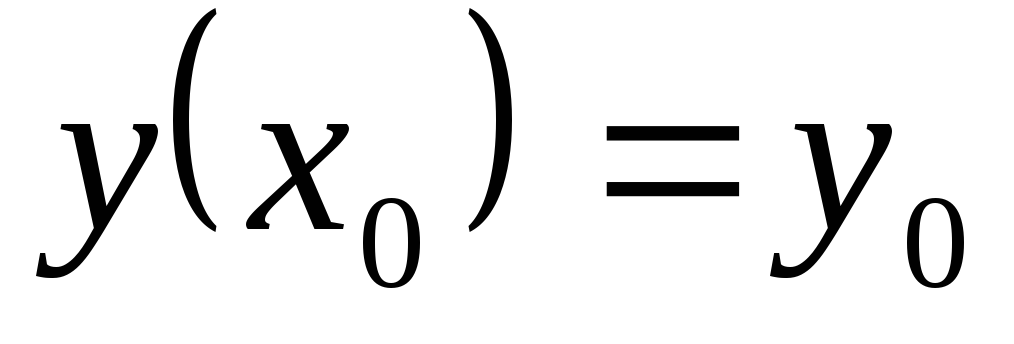 .
.
Общим решением дифференциального
уравнения 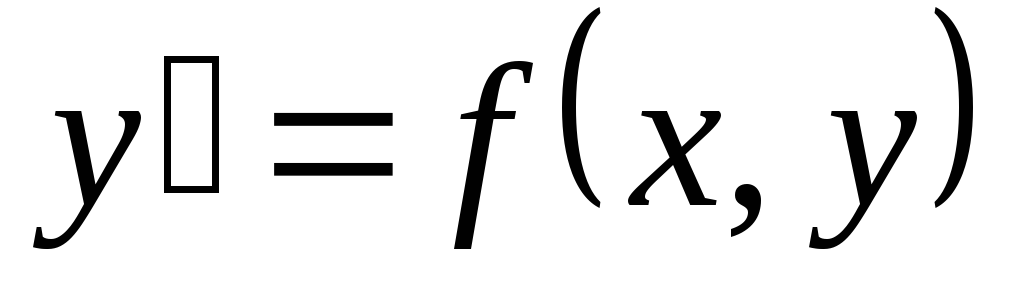 в
некоторой области
в
некоторой области 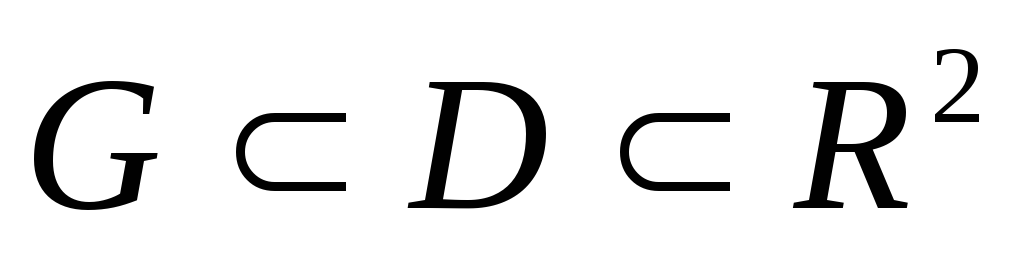 называется
функция
называется
функция 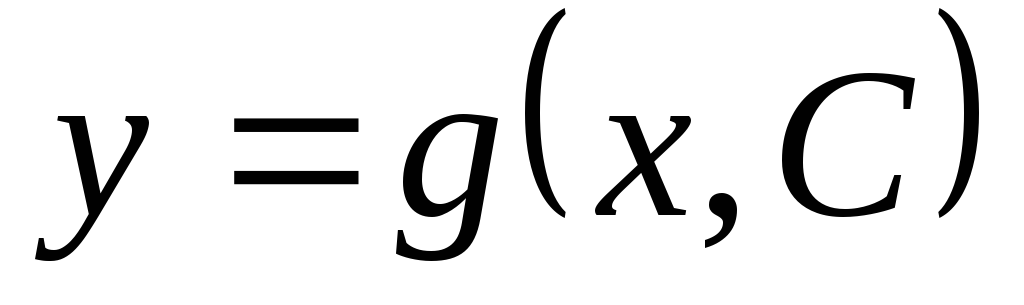 ,зависящая
от переменной х и одной произвольной
постоянной С (параметра), если:
,зависящая
от переменной х и одной произвольной
постоянной С (параметра), если:
 является решением уравнения
является решением уравнения  при любом допустимом значении постоянной
С;
при любом допустимом значении постоянной
С;при любом начальном условии
 ,
удовлетворяющем условию
,
удовлетворяющем условию  ,
существует единственное значение
параметра
,
существует единственное значение
параметра  такое, что функция
такое, что функция  удовлетворяет условию
удовлетворяет условию  .
.
Частным решением дифференциального
уравнения 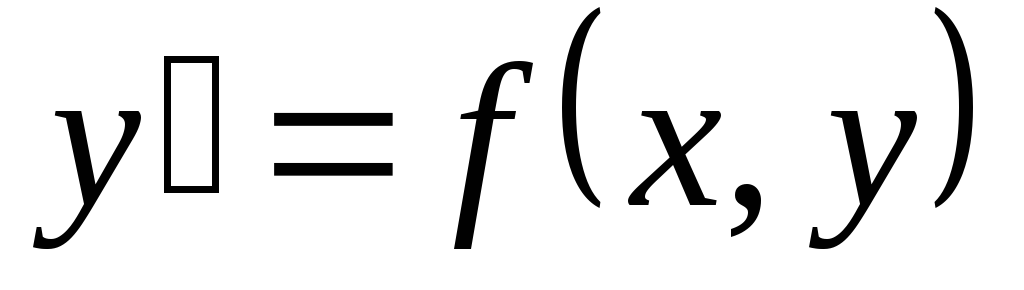 в
некоторой области
в
некоторой области 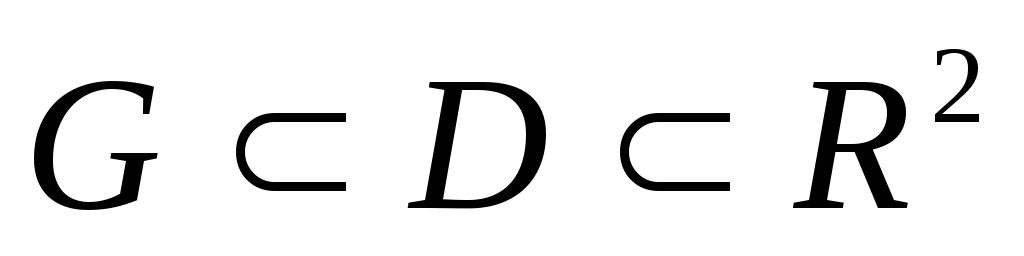 называется функция
называется функция 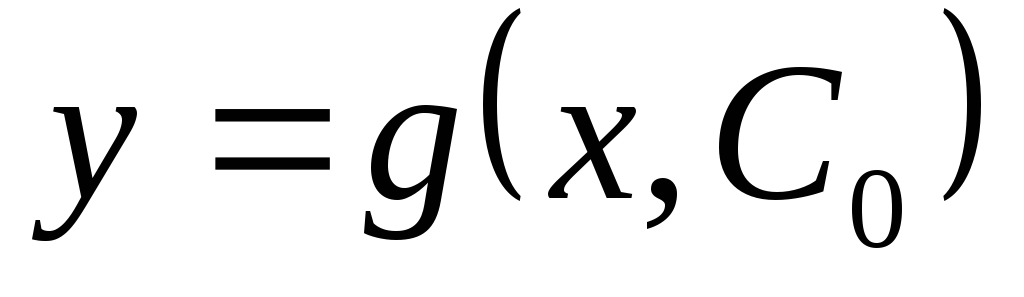 ,
которая получается из общего решения
,
которая получается из общего решения 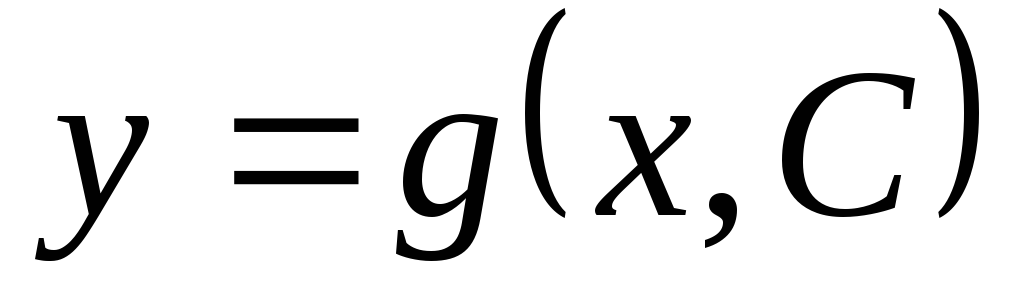 уравнения
уравнения 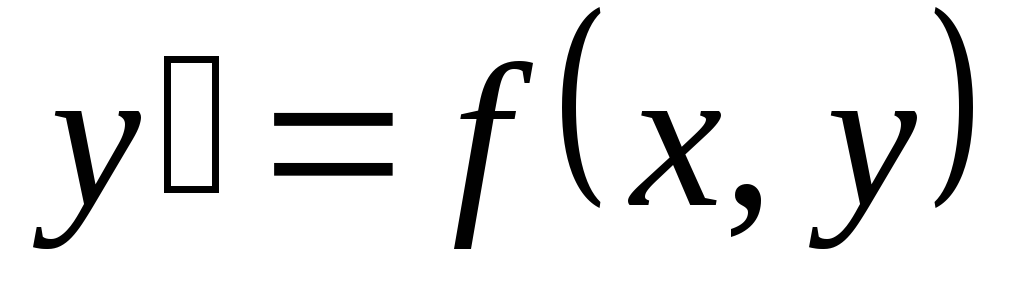 в области G при
конкретном значении произвольной
постоянной
в области G при
конкретном значении произвольной
постоянной 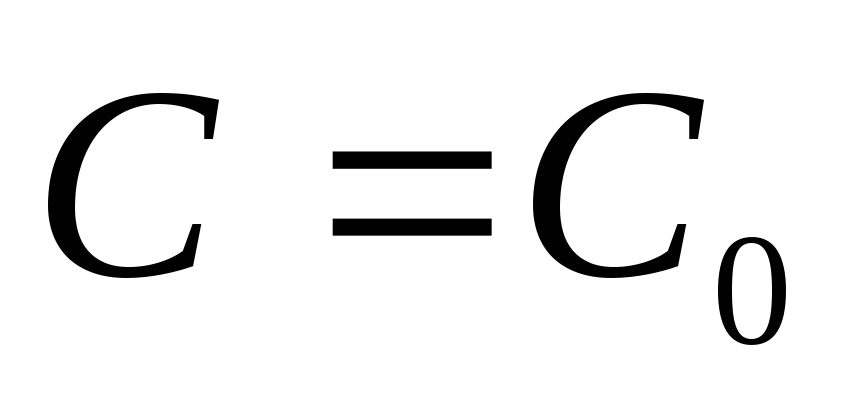 .
.
3. Классификация дифференциальных уравнений в частных производных 2-го порядка
Дифференциальные уравнения в частных производных 2-го порядка не имеют единого метода численного решения. Поэтому следует рассмотреть их классификацию, позволяющую использовать единые методы для численного решения каждого из подтипов этих уравнений.
Общий вид дифференциального уравнения 2-го порядка в частных производных при условии, что искомая функция зависит от двух переменных, можно представить следующим образом:
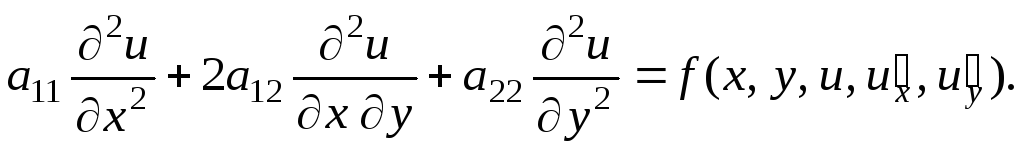
В зависимости от знака величины
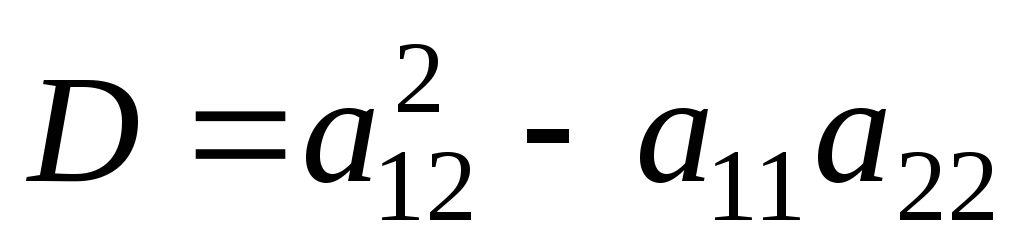 (1.1)
(1.1)
дифференциальные уравнения в частных производных 2-го порядка относят к уравнениям:
при D> 0 –гиперболическоготипа,
при D< 0 –эллиптическоготипа,
при D= 0 –параболическоготипа.
Принадлежность многомерных дифференциальных уравнений в частных производных 2-го порядка к тому или иному типу определяют, руководствуясь следующими правилами.
1. Если в уравнении присутствуют производные 2-го порядка по всем независимым переменным и знаки перед ними одинаковые – то данное уравнение относят к уравнениям эллиптическоготипа, например:
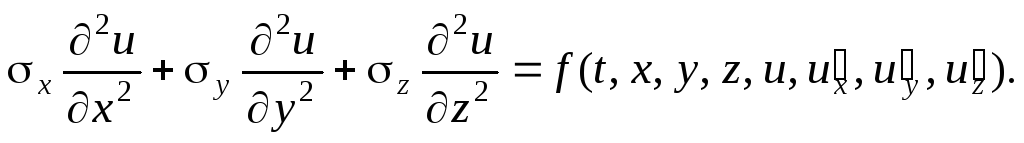
2. Если в уравнении отсутствует производная 2-го порядка хотя бы по одной из независимых переменных – то данное уравнение относят к уравнениям параболическоготипа, например:
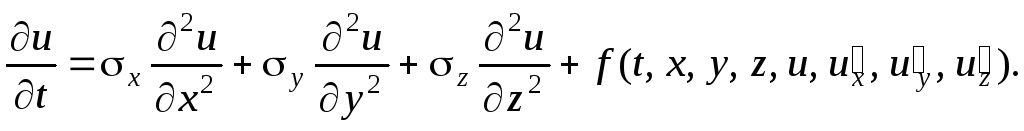
4. Начальные и граничные условия
Для решения дифференциальных уравнений численными методами требуются дополнительные условия. Если искомая функция (концентрация, температура и т.д.) является функцией времени u = f (t), то требуютсяначальные условия, характеризующие значение этой функции в момент времени, принятый за начальный:
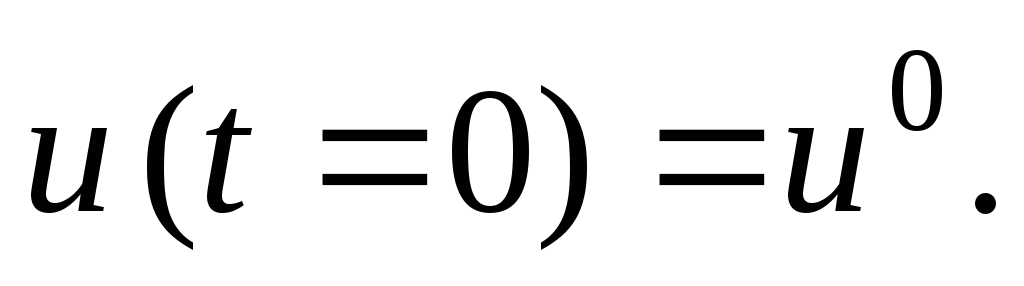
Если искомая функция также является функцией пространственных координат u = f (t, x), то начальные условия характеризуют её распределение в пространстве в начальный момент времени:
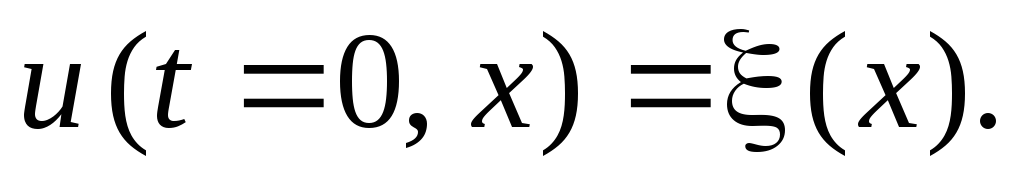
В последнем случае помимо начальных условий, требуются ещё и граничныеусловия, характеризующие значение функцииuна границе изучаемой системы с внешней средой для любого момента времени. Причём если искомая функция является функцией нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них. Количество граничных условий по каждой пространственной координате определяется порядком старшей производной функцииuпо этой координате в дифференциальном уравнении. Например, для решения многомерного уравнения
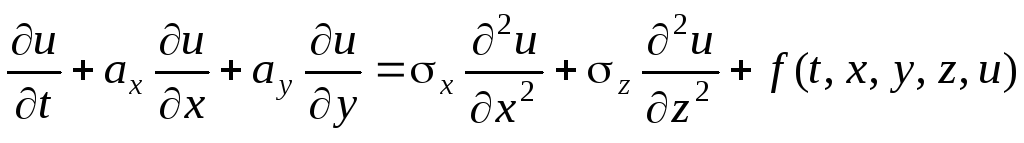
требуются: начальное условие,
2 граничных условия по координате х,
1 граничное условие по координате y,
2 граничных условия по координате z.
5. Классификация граничных условий
В различных физико-химических задачах граничные условия могут быть представлены в разном виде. Рассмотрим классификацию граничных условий на примере уравнения теплового баланса трубчатого реактора с продольным перемешиванием:
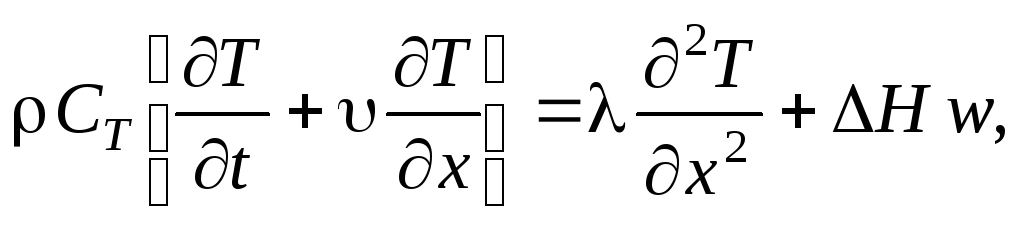
где w– скорость реакции;Hтепловой эффект
реакции;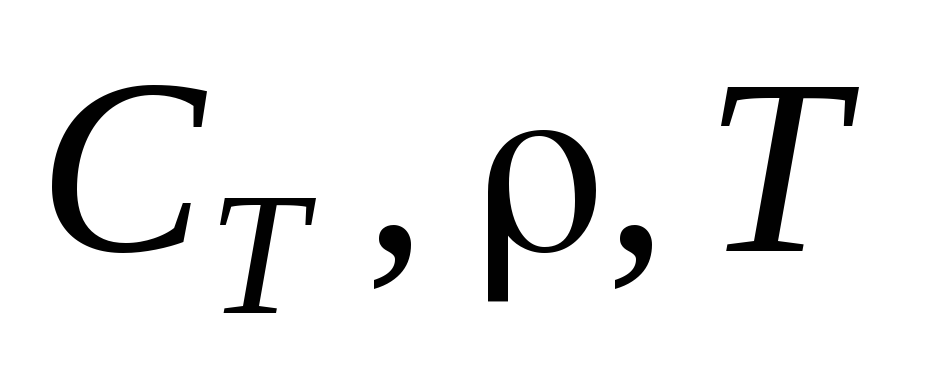 – теплоёмкость, плотность и температура
смеси в реакторе;v–
линейная скорость потока;– коэффициент теплопроводности;х– координата по длине реактора.
– теплоёмкость, плотность и температура
смеси в реакторе;v–
линейная скорость потока;– коэффициент теплопроводности;х– координата по длине реактора.
Начальные условия для данного уравнения характеризуют распределение температуры по длине реактора в начальный момент времени:
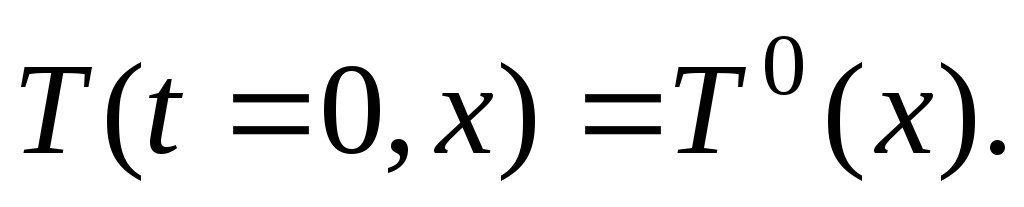
1) Граничные условия 1-го родаопределяют температуры на границах реактора для любого момента времени:
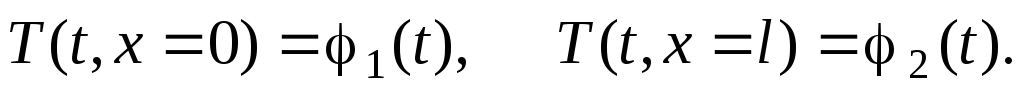
2) Граничные условия 2-го родазадают изменение температуры на границах реактора для любого момента времени:
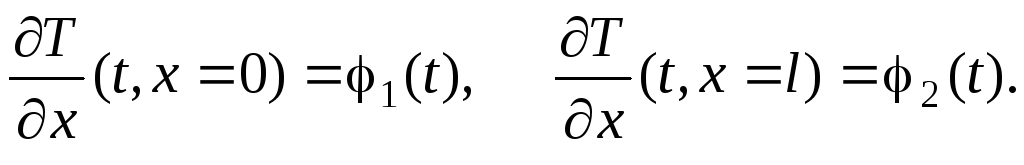
3) Граничные условия 3-го родаопределяют закон свободного теплообмена с окружающей средой на границах реактора для любого момента времени:
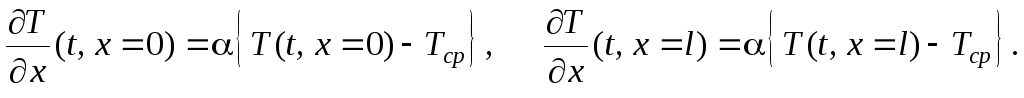
4) Смешанные граничные условия, если при постановке задачи используются граничные условия разных родов, например:
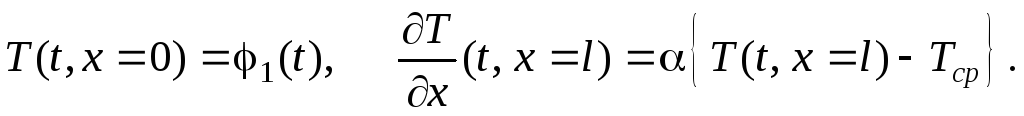
Здесь – коэффициент теплоотдачи;l– длина реактора;Тср– температура окружающей среды.
Тема 1. Классификация дифференциальных уравнений второго порядка в частных производных.
а) Механические колебания пружинного маятника
Схематически представим пружинный маятник с грузом массой m на конце.
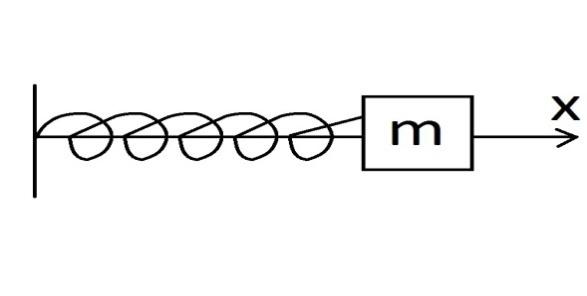
Рис.1
Колебания груза
массой m
совершаются вдоль оси 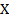 (рис. 1)
(рис. 1)
Если 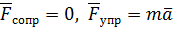 ,
, 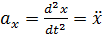 ,
, 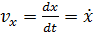 ,
,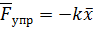 ,
,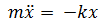 ,тогда
уравнение движения маятника примет вид
,тогда
уравнение движения маятника примет вид
| (1) |
Решение уравнения
(1),если считать что при 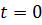 ,
, 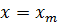 ,
можно представить в виде
,
можно представить в виде
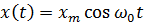 ,
,
где 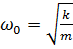 .
.
Пусть 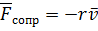 ,
, 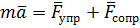 ,
получаем уравнение
,
получаем уравнение
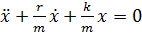 . (1’)
. (1’)
Решение (1’) имеет вид
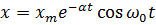 , что указывает
на затухание колебаний.
, что указывает
на затухание колебаний.
б) Электромагнитные колебания в колебательном контуре.


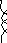 Для
идеального колебательного контура,
Для
идеального колебательного контура,
C

 L
сопротивление которого
L
сопротивление которого ,
напряжение
,
напряжение

Рис.2
на конденсаторе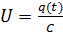 совпадает с э.д.с.
совпадает с э.д.с. индукции
на катушке 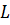 .
.
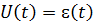 ;
; 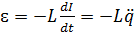 ,
, 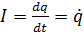 .
.
Получаем уравнение
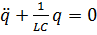 , (2)
, (2)
решение которого имеет вид
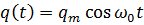 .
.
При 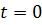 ,
, 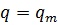 ,
тогда
,
тогда
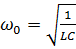 .
.
При 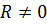
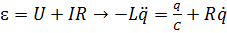 ,
что дает уравнение
,
что дает уравнение
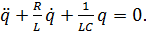 (2’)
(2’)
Как видим, один из процессов переходит в другой при замене величин, указанных в таблице
Маятник |
|
|
|
|
| |
Контур |
|
|
|
|
|
Для упрощения записей ограничимся случаем двух переменных.
Пусть 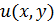 — искомая функция. Ограничиваясь случаем
производных, не выше второй степени
будем считать заданным некий функционал
— искомая функция. Ограничиваясь случаем
производных, не выше второй степени
будем считать заданным некий функционал
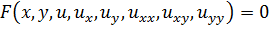 ,
,
где 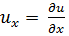 ;
; 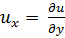 ;
; 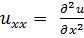 ;
; 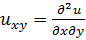 ;
; 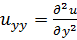 .
.
1.1 Линейное дифференциальное уравнение второго порядка в частных производных.
Введем более простое уравнение:
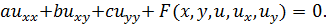 (1.1)
(1.1)
Оно линейно по
старшим производным, если коэффициенты 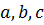
зависят только от
(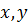 )
и не зависят от
)
и не зависят от 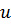 .
.
Введем уравнение
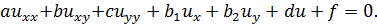 (1.2)
(1.2)
Если 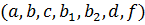 – зависят только от (
– зависят только от (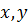 ),
то уравнение (1.2) линейно.
),
то уравнение (1.2) линейно.
Если 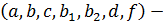 const,
то уравнение называется линейным
дифференциальным уравнением (ДУ) с
постоянными коэффициентами.
const,
то уравнение называется линейным
дифференциальным уравнением (ДУ) с
постоянными коэффициентами.
Если 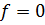 ,
то (1.2) – линейное однородное уравнение.
Нашей дальнейшей целью является упрощение
формы ДУ путем подбора других систем
координат.
,
то (1.2) – линейное однородное уравнение.
Нашей дальнейшей целью является упрощение
формы ДУ путем подбора других систем
координат.
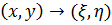 ,
где
,
где 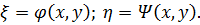
Новые координаты выбираются так, чтобы соответствующий определитель
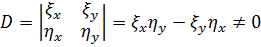 .
.
Лемма 1. При переходе к новой системе координат линейное уравнение остается линейным. Нужно доказать, что (1.1) перейдет в некоторое линейное уравнение:
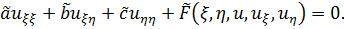 (1.1’)
(1.1’)
1.2 Три типа дифференциальных уравнений второго порядка в частных производных
Для уравнений (1.1),(1.1’) введем некоторую величину, называемую дискриминантом
Для уравнения
(1.1) 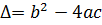 , (1.4)
, (1.4)
Для уравнения
(1.1’) 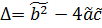 . (1.4’)
. (1.4’)
Лемма 2. При смене системы координат знак 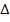 не меняется, если определитель
преобразования
не меняется, если определитель
преобразования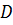 не обращается в ноль:
не обращается в ноль:
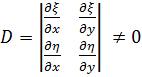 .
.
Если в какой-то
области дискриминант имел определенный
знак, то он сохранит тот же знак в области,
полученной из данной преобразованием
координат,при 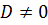 .
.
Будем называть уравнения в той области, где
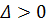 – гиперболическими,
– гиперболическими,
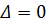 – параболическими,
– параболическими,
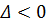 – эллиптическими.
– эллиптическими.
Рассмотрим условия,
когда 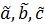 обращаются в ноль.
обращаются в ноль.
1.3 Характеристические уравнения для дифференциальных уравнений второго порядка
Новые координаты приводят к изменению коэффициентов
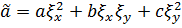 ,
,
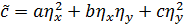 .
.
Лемма 3. Если 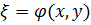 является частным решением уравнения
является частным решением уравнения
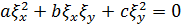 , (1.5)
, (1.5)
то 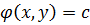 ,
где c
= const
является общим интегралом уравнения:
,
где c
= const
является общим интегралом уравнения:
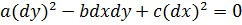 . (1.6)
. (1.6)
Лемма 4. Если  является общим интегралом уравнения
(1.6), то
является общим интегралом уравнения
(1.6), то 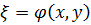 — частное решение (1.5).
— частное решение (1.5).
У
Рис. 3
равнение (1.6) – характеристическое уравнение для (1.1). Зная общий интеграл для характеристического уравнения, можно так подобрать новую переменную ,
где
,
где 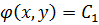 — общий интеграл для (1.6), чтобы
— общий интеграл для (1.6), чтобы 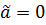 .
.Аналогичным образом, если у нас есть еще один общий интеграл для (1.6),
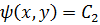 ,то
его примем за новую переменную, чтобы
,то
его примем за новую переменную, чтобы 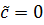 .
.
Для характеристического уравнения
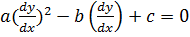 получаем
получаем
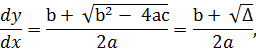
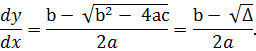
1) Для гиперболических
уравнений (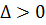 )
существуют 2 решения (2 общих интеграла)
для (1.6).
)
существуют 2 решения (2 общих интеграла)
для (1.6).
Выбираем 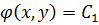 ,
, 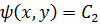 .
.
Тогда можем
обеспечить уничтожаемость 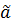 и .
и .
2) Для параболических
уравнений (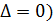 имеется одно решение (один общий интеграл)
для (1.6).
имеется одно решение (один общий интеграл)
для (1.6).
Выберем его за
одну новую переменную 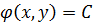 ,
исключается только
,
исключается только 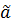 или
или 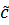 .
.
3) Для эллиптических
уравнений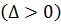 есть два комплексных решения
характеристического уравнения.
есть два комплексных решения
характеристического уравнения.
За новые переменные можно взять их действительную и мнимую части.
1.4 Приведение дифференциальных уравнений второго порядка к каноническому виду
Рассмотрим уравнения гиперболического типа
 для (1.1).
для (1.1).
Сведем его с помощью замены переменных к
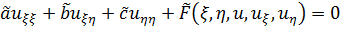 .
.
Так как 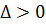 ,
выбираем
,
выбираем 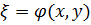 , где
, где 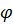 – общий интеграл (1.6).
– общий интеграл (1.6).
Тогда
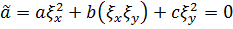
Аналогично
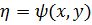 ,
тогда
,
тогда
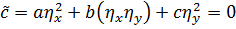
Получаем канонический вид гиперболического уравнения
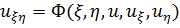 ,
где
,
где 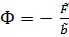 . (1.7)
. (1.7)
Введем еще одну замену:
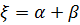 ;
; 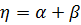 ;
;
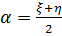 ;
; 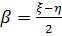 .
.
Посчитаем производные:
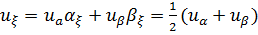 ,
, 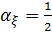 ;
; 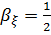 ;
;
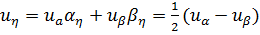 ,
, 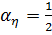 ;
; 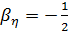 .
.
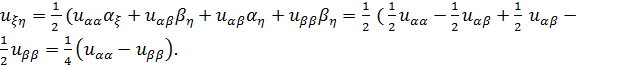
В итоге получаем
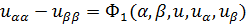 ,
где
,
где 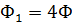 . (1.7’)
. (1.7’)
Уравнения параболического типа (
 ).
).
Поскольку 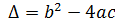 ,
, 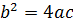 .
.
Характеристическое уравнение имеет одно решение
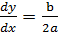 .
.
Пусть 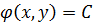 .
Выберем новую переменную
.
Выберем новую переменную 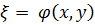 ,
что позволяет обратить коэффициент
,
что позволяет обратить коэффициент  в 0. Вторую переменную берем произвольным
образом
в 0. Вторую переменную берем произвольным
образом
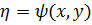 .
.
Подсчитаем 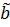 .
.
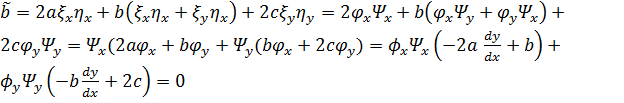 ,
поскольку
,
поскольку 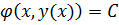 ,
, 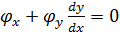 ;
;
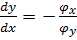 .
В результате получаем
.
В результате получаем
. (1.8)
Это каноническая форма уравнения параболического типа.
3)  Эллиптические
уравнения
Эллиптические
уравнения 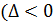 ).
).
В этом случае имеем
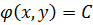 ,
, 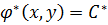 ,
— комплексные общие интегралы. Представим
,
— комплексные общие интегралы. Представим
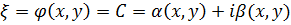
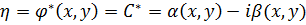
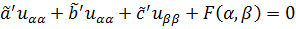 (1.1’’)
(1.1’’)
После замены переменных получаем
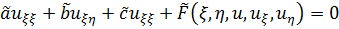 ,
,
где
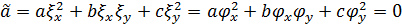 .
.
Совершим еще одну замену переменных
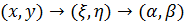 .
.
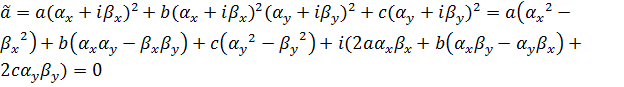 .
.
При второй замене переменных (1.3) переходят в (1.3’)
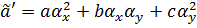 ;
;
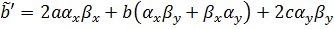 ; (1.3’)
; (1.3’)
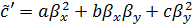 .
.
В итоге получаем 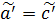 ;
; 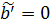 .
.
Каноническая форма эллиптического ДУ имеет вид
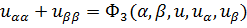 , (1.9)
, (1.9)
где 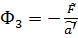 .
.
Каноническая форма для уравнений гиперболического вида принимает вид (1.7) или (1.7’), для уравнений параболического типа – (1.8), для уравнений эллиптического вида – (1.9).
В этих формулах 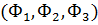 — всевозможные комбинации из
— всевозможные комбинации из 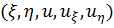 .
.
Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 3-4
Уравнения в частных производных второго порядка Лекция №3-4
Тема: Уравнения в частных производных второго порядка.
Вопросы:
1. Общий вид уравнения второго порядка. Линейные уравнения второго порядка в частных производных. Линейные однородные и линейные неоднородные уравнения.
2. Свойства решений линейного однородного и линейного неоднородного уравнений.
3. Классификация дифференциальных уравнений второго порядка.
4. Приведение линейного уравнения к каноническому виду: гиперболический тип, параболический тип и эллиптический тип.
5. Постановка основных задач для линейных дифференциальных уравнений второго порядка.
Уравнение вида
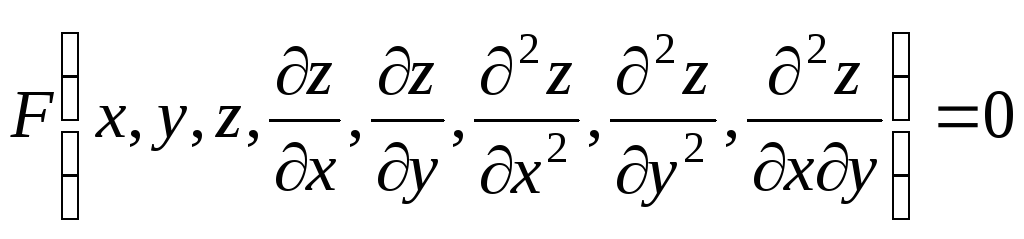 (3.1)
(3.1)
есть дифференциальное уравнение второго порядка с искомой функцией z от двух переменных х и у.
Уравнения математической физики в отличие от уравнений с частными производными второго порядка общего вида (3.1) являются линейными, т.е. линейно зависят от искомой функции и ее частных производных. Например, в случае двух независимых переменных они имеют вид
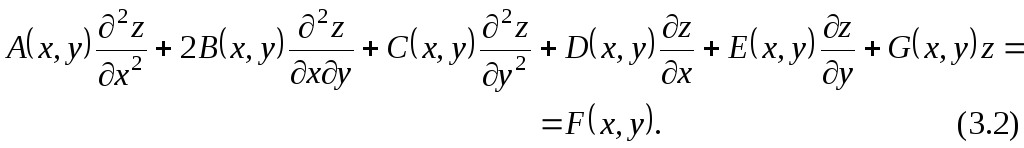
Уравнение (3.2)
называется однородным, если 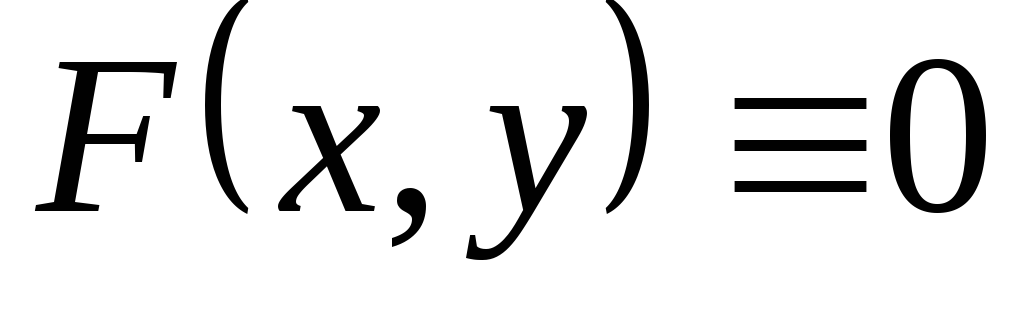 .
Если
.
Если 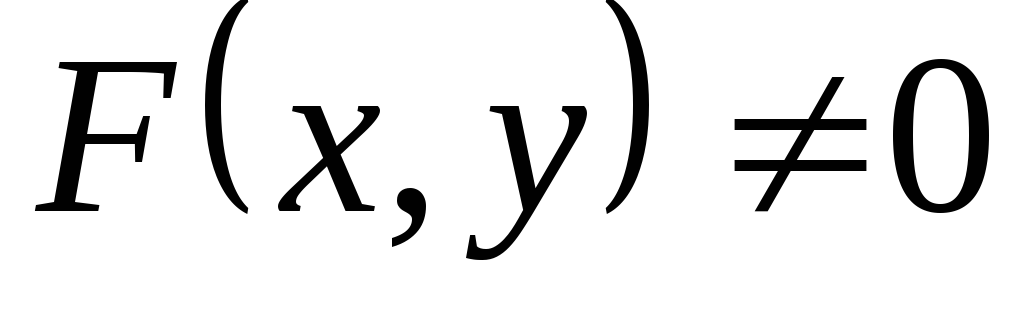 ,
то уравнение (3.2) называется неоднородным.
,
то уравнение (3.2) называется неоднородным.
Обозначим левую
часть уравнения (3.2) через 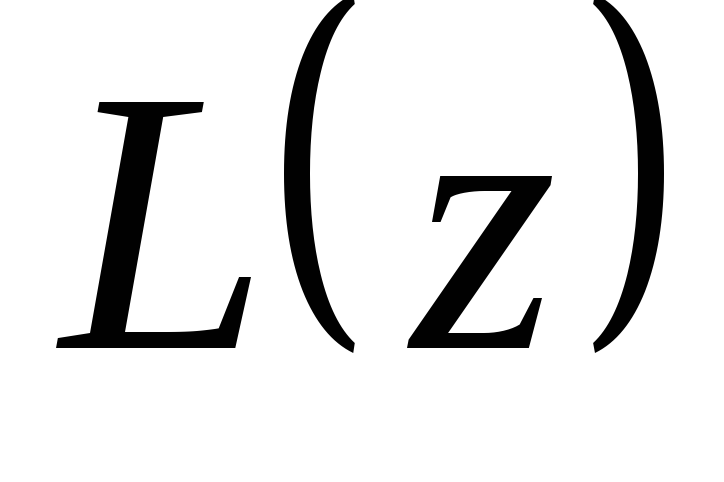 ,
тогда (3.2) можно записать в виде:
,
тогда (3.2) можно записать в виде:
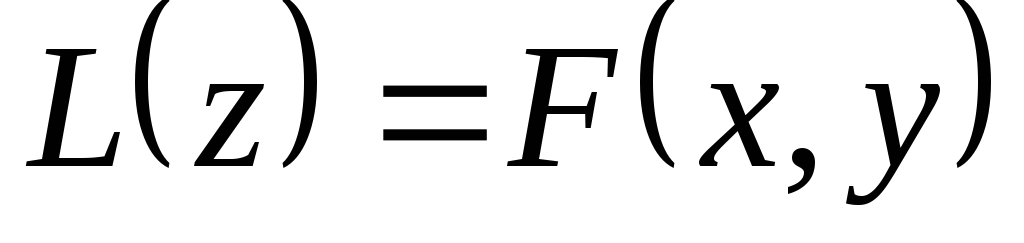 . (3.3)
. (3.3)
Соответствующее однородное уравнение примет вид
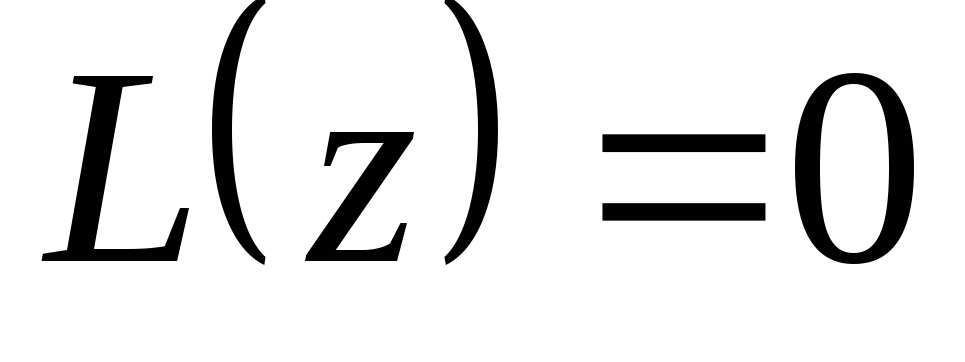 . (3.4)
. (3.4)
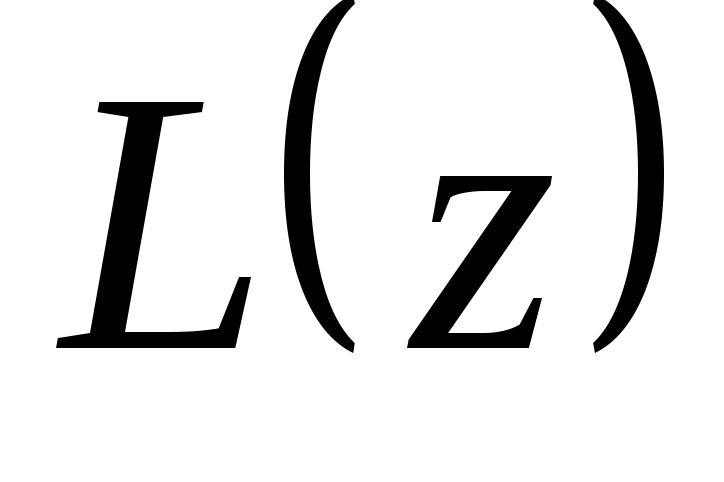 — линейный
дифференциальный оператор. Самостоятельно
проверить свойства линейности оператора
— линейный
дифференциальный оператор. Самостоятельно
проверить свойства линейности оператора 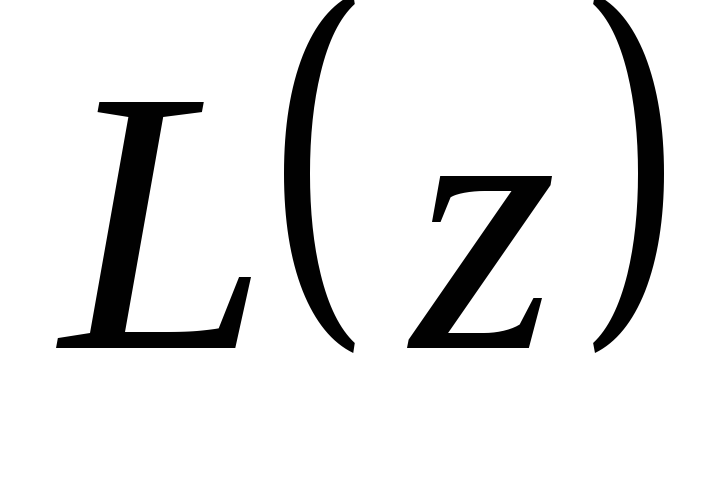 .
.
Из свойств линейности
оператора 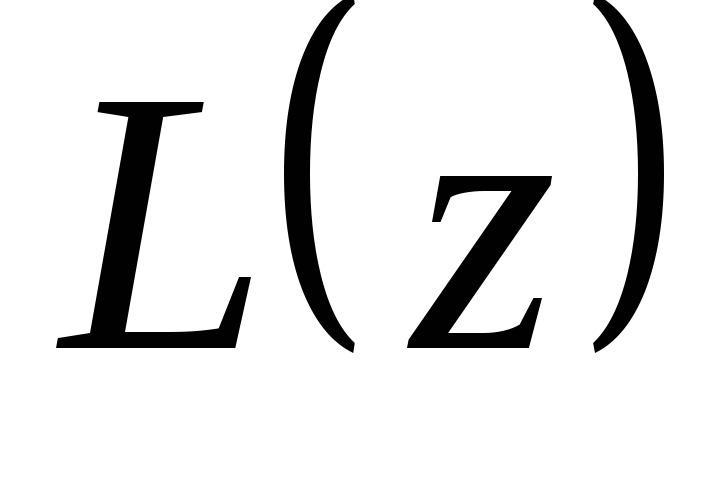 непосредственно вытекают следующие
утверждения:
непосредственно вытекают следующие
утверждения:
Теорема 3.1. Если 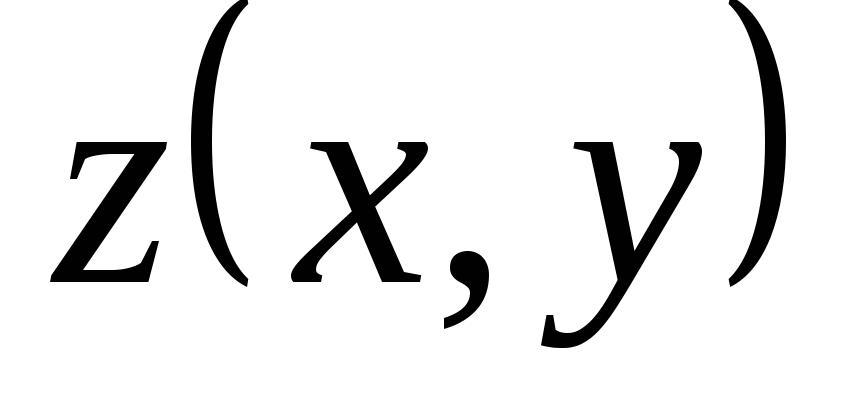 — решение линейного однородного уравнения
(3.4), то функция
— решение линейного однородного уравнения
(3.4), то функция 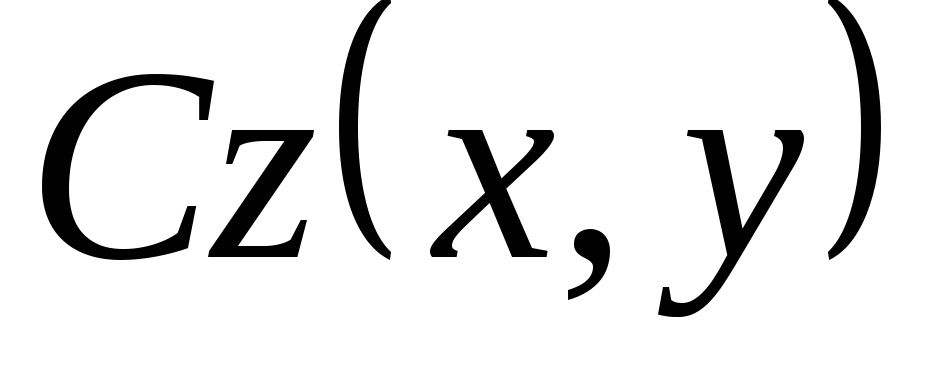 также является решением уравнения
(3.4), где С – произвольная постоянная.
также является решением уравнения
(3.4), где С – произвольная постоянная.
Теорема 3.2. Если 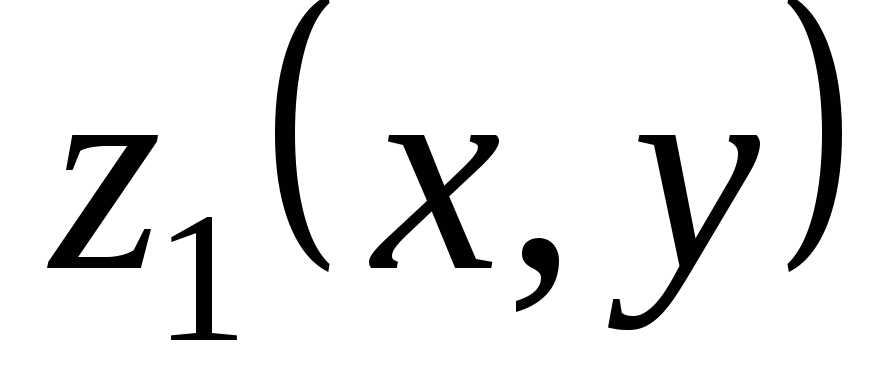 и
и 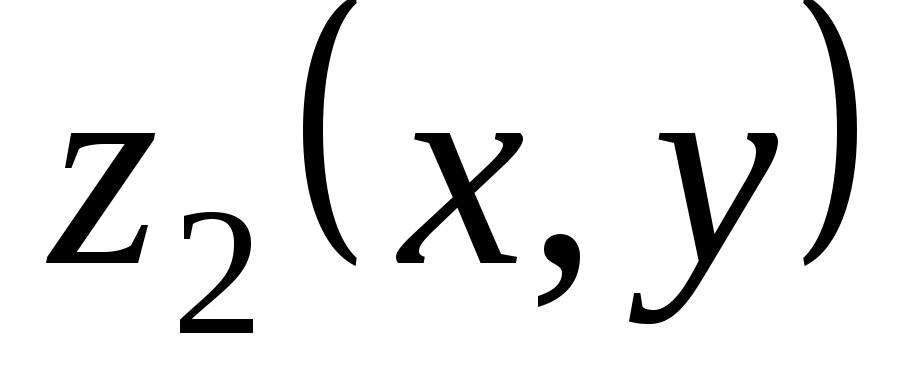 — решения линейного однородного уравнения
(3.4), то сумма
— решения линейного однородного уравнения
(3.4), то сумма 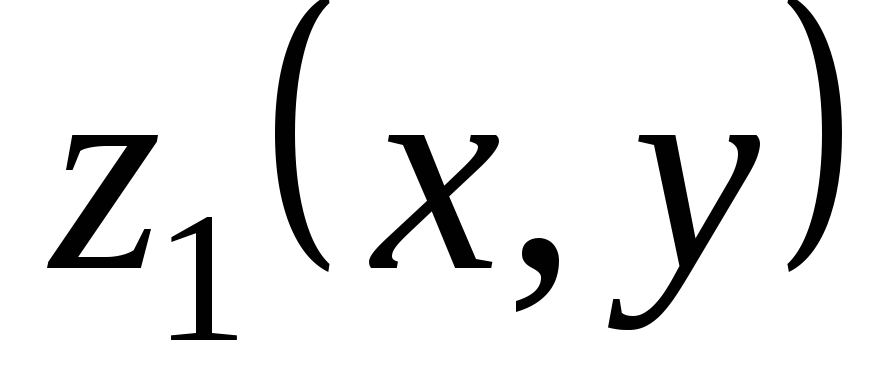 +
+ 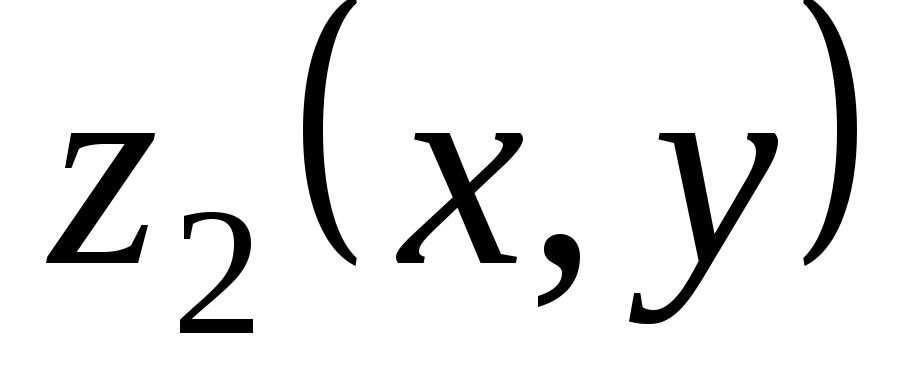 также является решением этого уравнения.
также является решением этого уравнения.
Следствие. Линейная комбинация с произвольными
постоянными коэффициентами k решений уравнения (3.4) 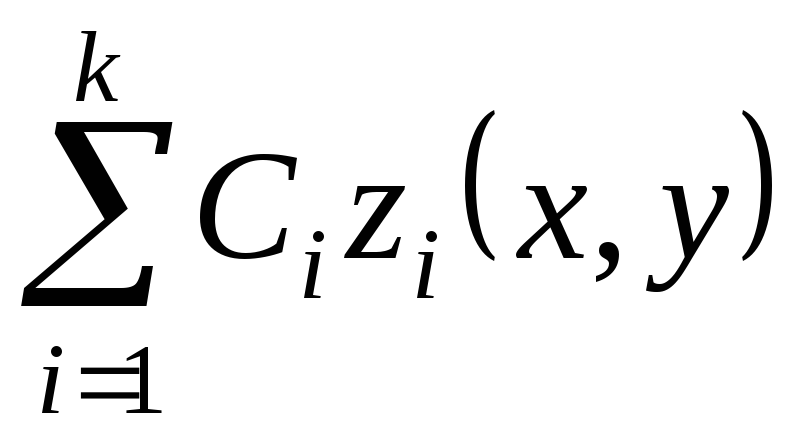 также является решением этого уравнения.
также является решением этого уравнения.
В отличие от обыкновенных линейных однородных дифференциальных уравнений, имеющих конечное число линейно независимых частных решений, линейная комбинация которых дает общее решение этого уравнения, уравнения в частных производных могут иметь бесконечное множество линейно независимых частных решений.
Например. Уравнение
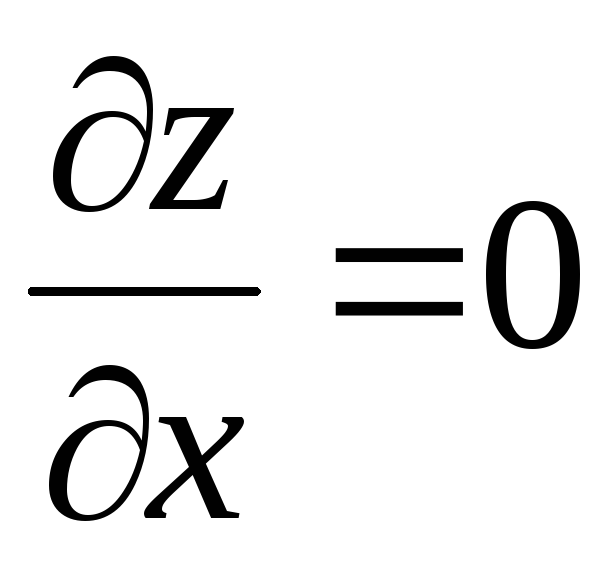
имеет общее решение 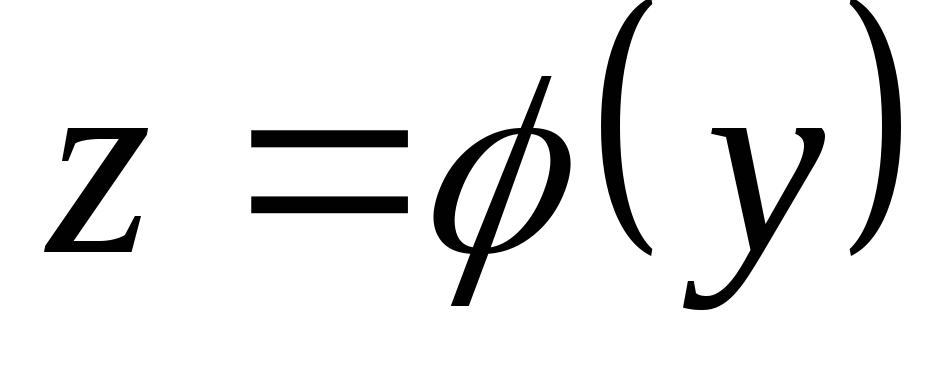 ,
поэтому его решениями будут, например,
функции
,
поэтому его решениями будут, например,
функции 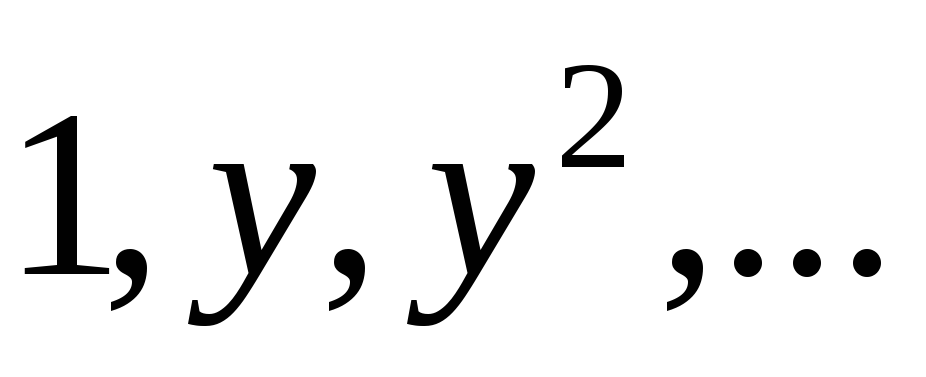 .
.
Для линейного неоднородного
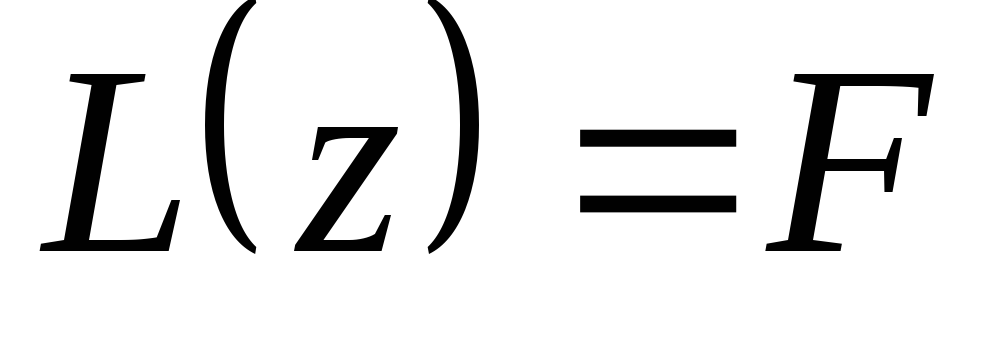 . (3.5)
. (3.5)
уравнения справедливы следующие утверждения:
Теорема 3.3. Если  — решение линейного неоднородного
уравнения (3.5), а
— решение линейного неоднородного
уравнения (3.5), а 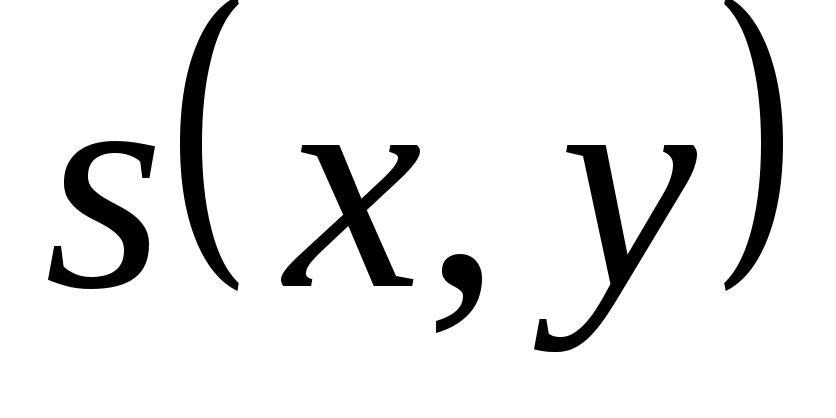 — решение соответствующего однородного
уравнения (3.4), сумма
— решение соответствующего однородного
уравнения (3.4), сумма 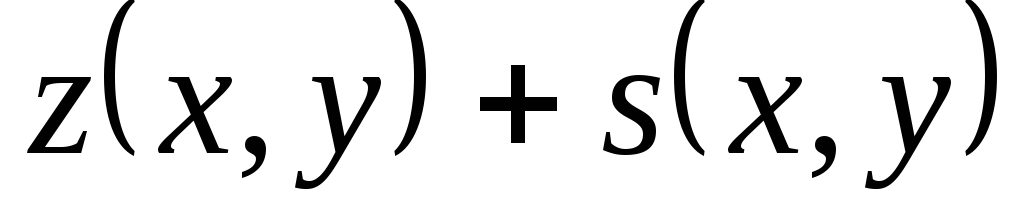 также является решением неоднородного
уравнения (3.5).
также является решением неоднородного
уравнения (3.5).
Теорема 3.4. Если 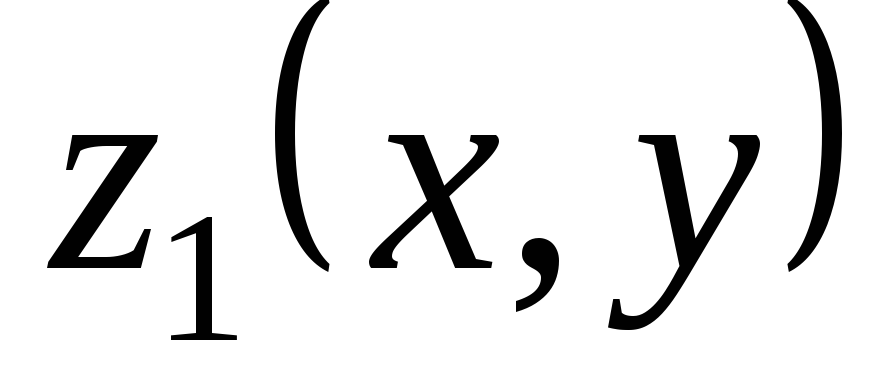 — решение уравнения
— решение уравнения 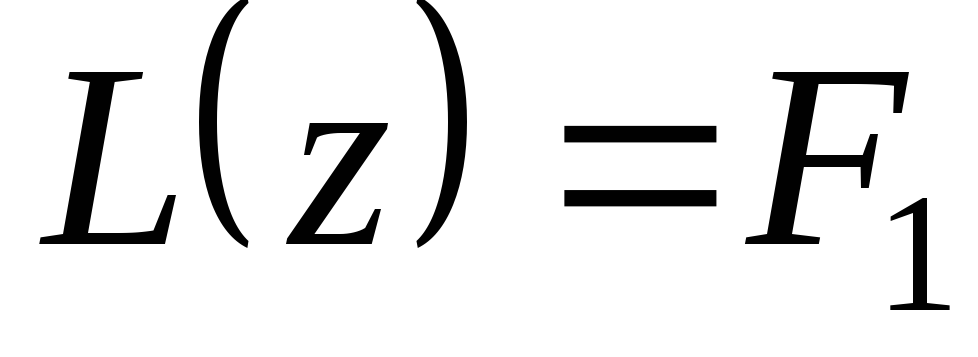 ,
а
,
а 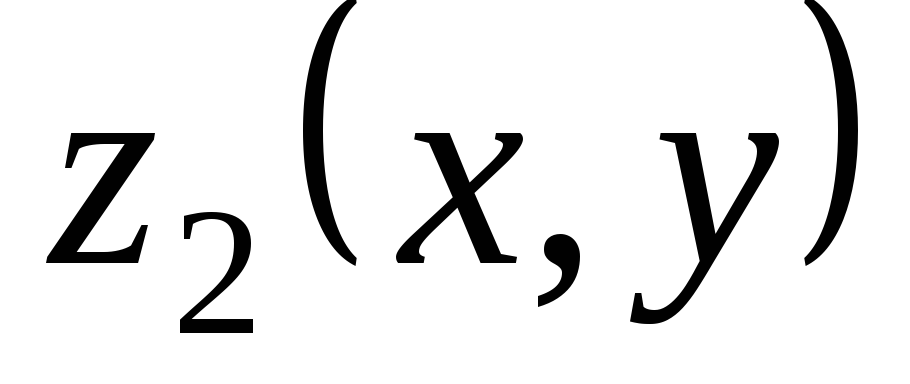 — решения уравнения
— решения уравнения 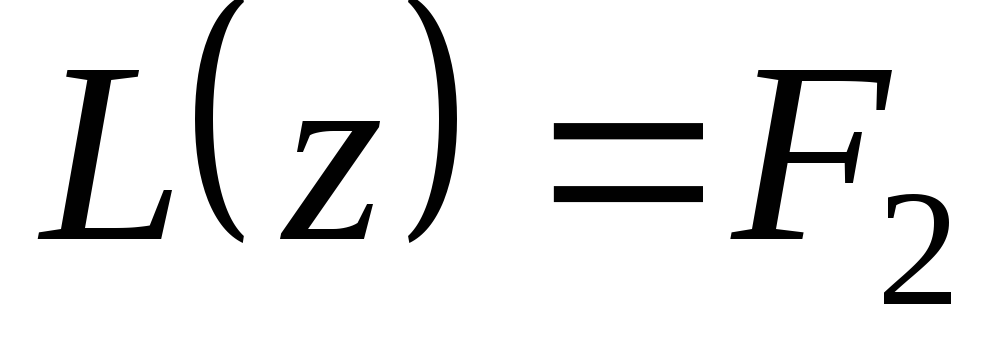 ,
то сумма
,
то сумма 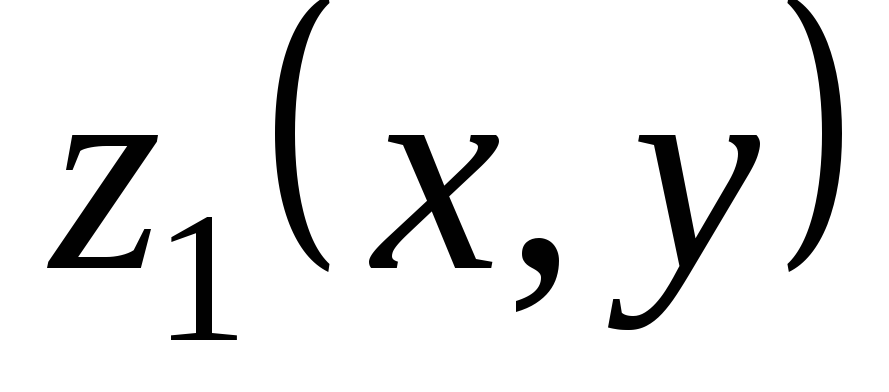 +
+ 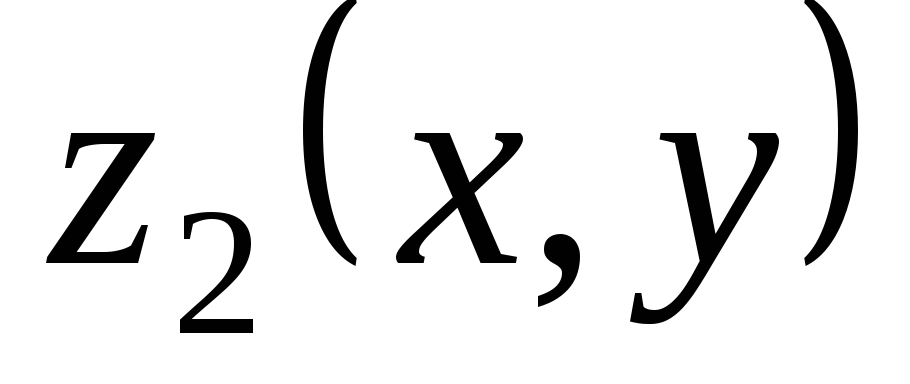 является решением уравнения
является решением уравнения 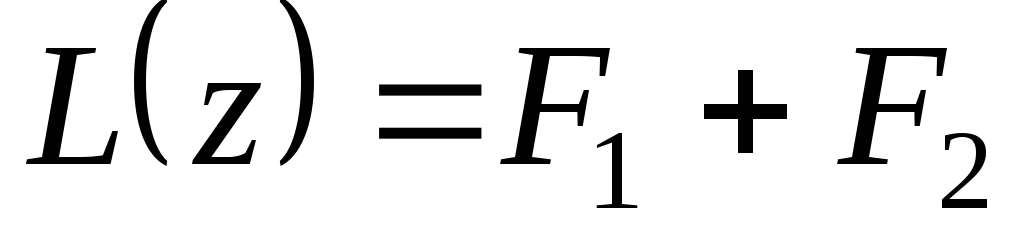 .
.
Рассмотрим классификацию дифференциальных уравнений второго порядка с двумя независимыми переменными.
Определение. Линейное дифференциальное уравнение
второго порядка (3.2) в некоторой области  на плоскости хОу называется
на плоскости хОу называется
гиперболическим в
 ,
если
,
если  в
в  ;
;эллиптическим в
 , если
, если  в
в  ;
;параболическим в
 , если
, если  в
в  .
.
Простейшим из уравнений гиперболического типа является волновое уравнение
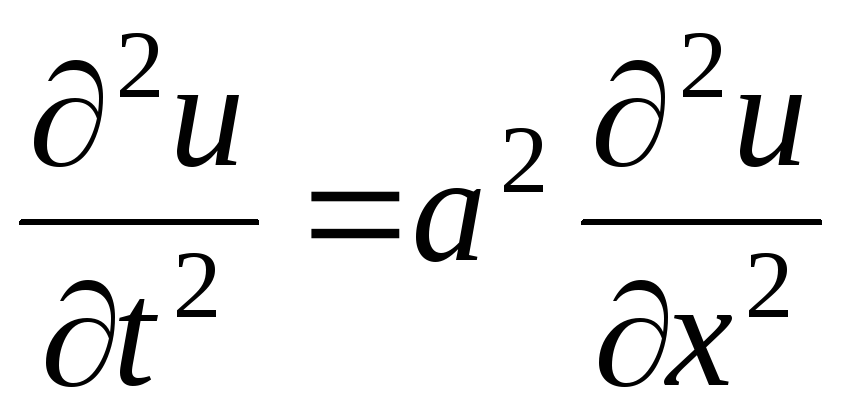 .
.
Оно встречается в задачах, связанных с колебательными процессами.
Простейшим из уравнений эллиптического типа является уравнение Лапласа
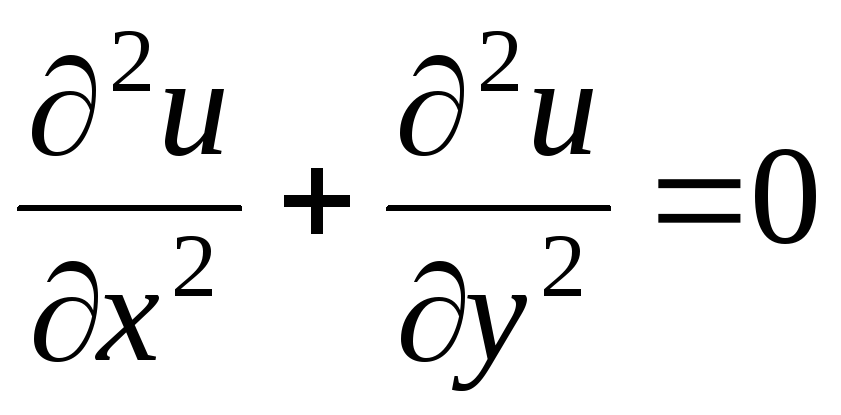 .
.
К интегрированию этого уравнения приходят при изучении стационарных процессов.
Простейшим уравнением параболического типа является уравнение теплопроводности (уравнение Фурье)
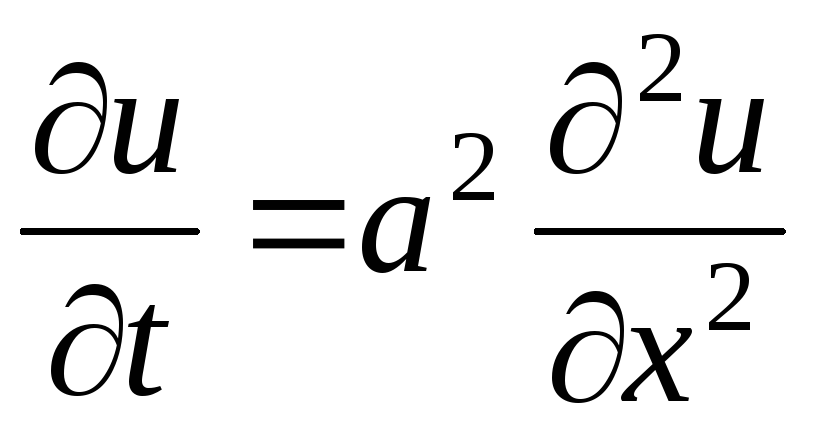 .
.
Оно часто встречается при изучении процессов теплопроводности и диффузии.
Позже мы с вами рассмотрим эти уравнения подробнее.
В курсе математической физики также изучаются волновое уравнение, уравнение Лапласа и уравнение Фурье более общего вида:
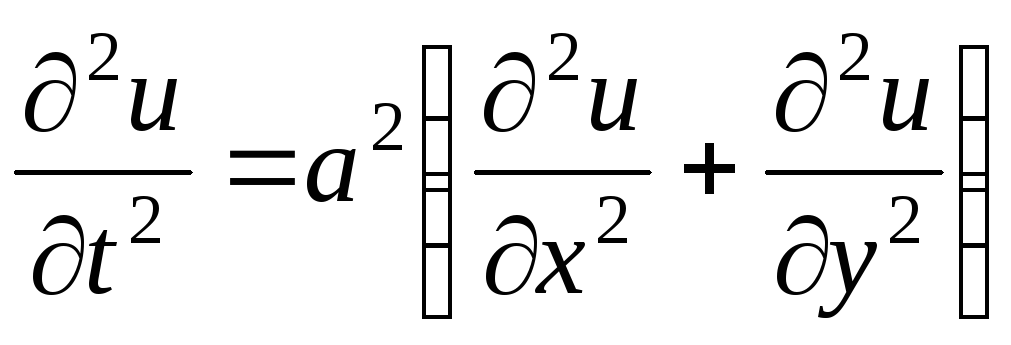 ,
, 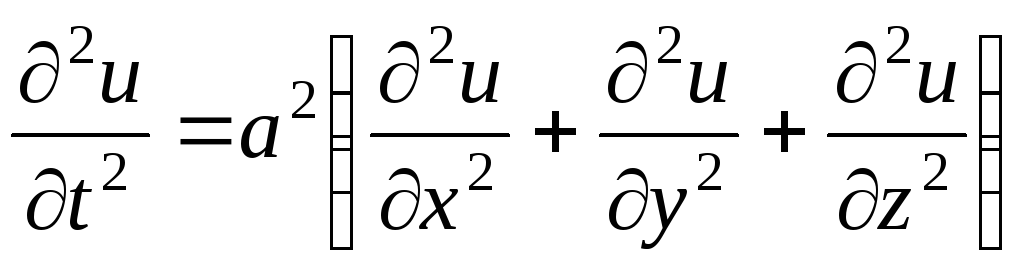 ,
,
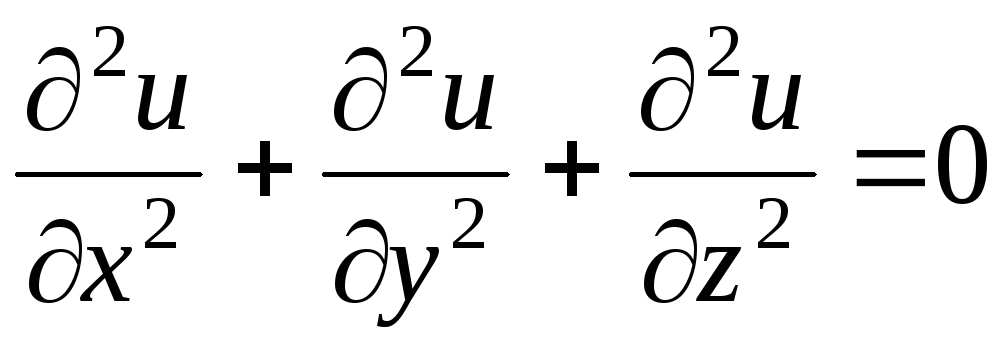 ,
,
, 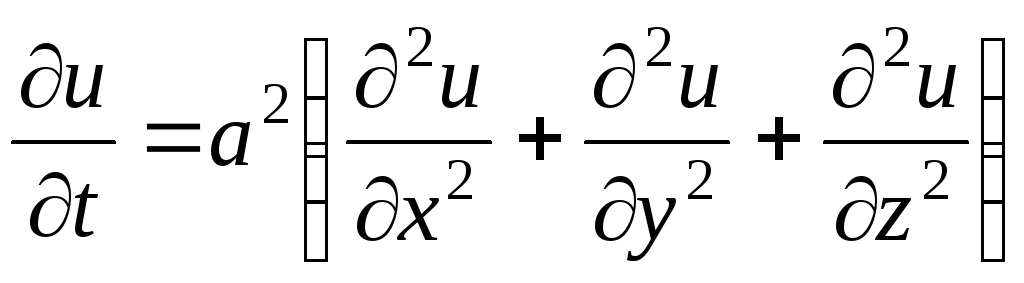 .
.
Приведем уравнение
(3.2) к каноническому виду в достаточно
малой окрестности любой точки, в которой
задано это уравнение. Предположим, что
коэффициенты А, В и С в уравнении (3.2) принадлежат классу 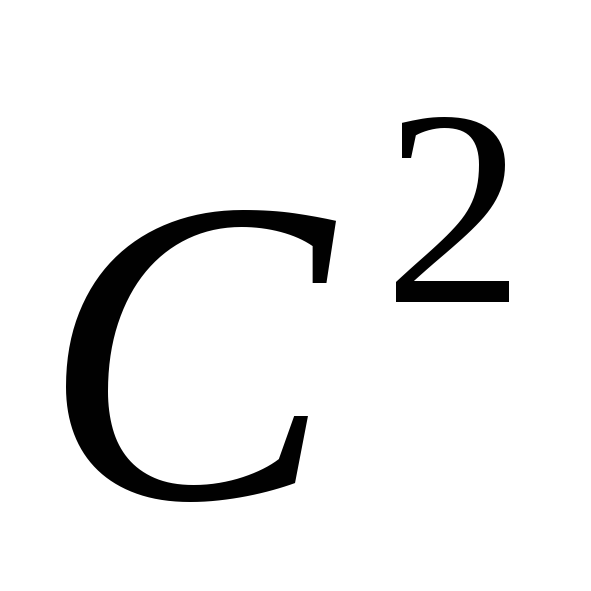 в некоторой окрестности и нигде в ней
не обращаются в нуль одновременно. Для
определенности можно считать, что
в некоторой окрестности и нигде в ней
не обращаются в нуль одновременно. Для
определенности можно считать, что 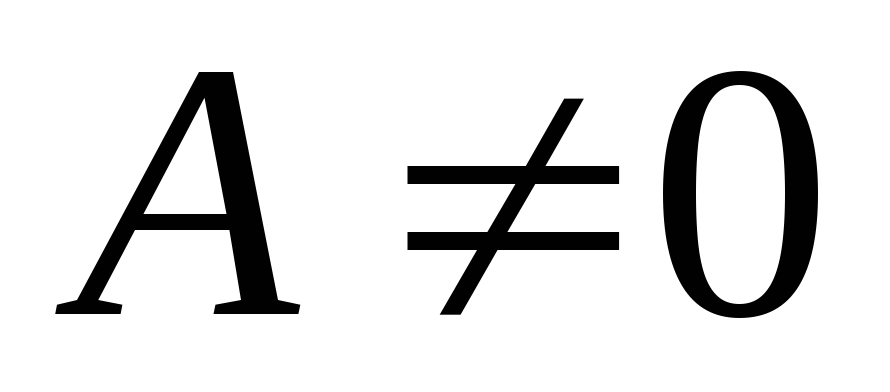 в этой окрестности. Действительно, в
противном случае может оказаться, что
в этой окрестности. Действительно, в
противном случае может оказаться, что 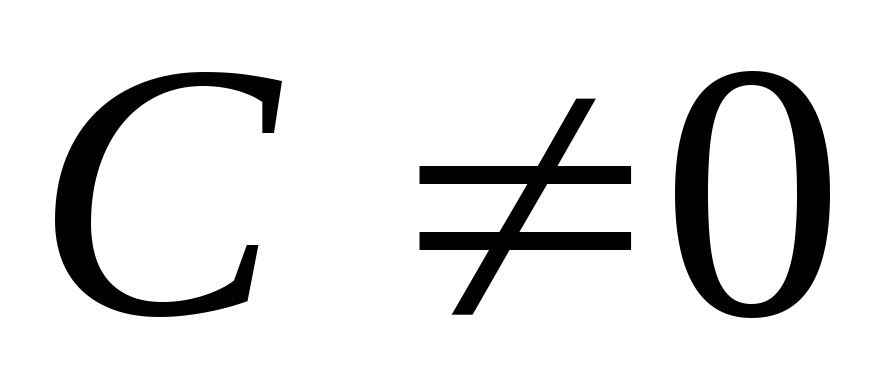 ,
но тогда меняя местами х и у,
получим уравнение у которого
,
но тогда меняя местами х и у,
получим уравнение у которого 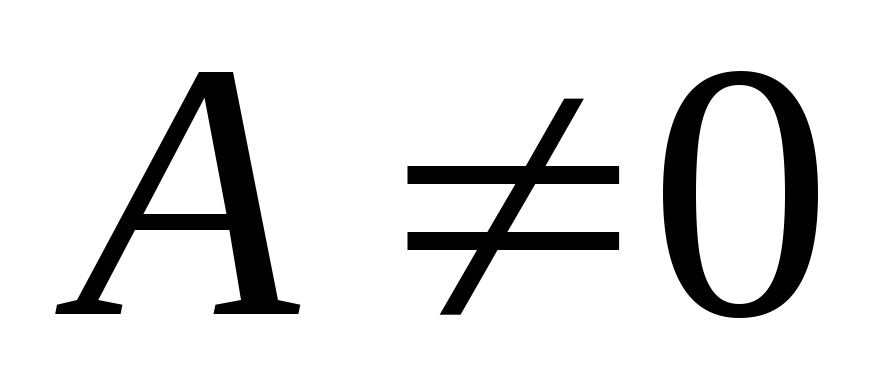 .
Если же А и С обращаются одновременно в нуль в
какой-нибудь точке, то
.
Если же А и С обращаются одновременно в нуль в
какой-нибудь точке, то  в окрестности этой точки. В таком случае
после деления на 2В уравнение (3.2) уже будет иметь канонический
вид:
в окрестности этой точки. В таком случае
после деления на 2В уравнение (3.2) уже будет иметь канонический
вид:
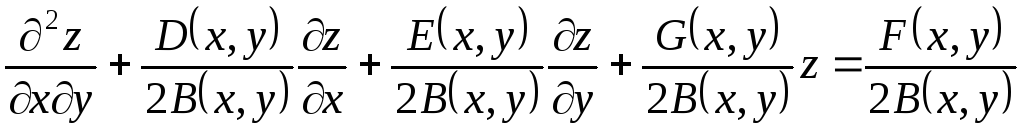 .
.
Перейдем теперь к новым переменным
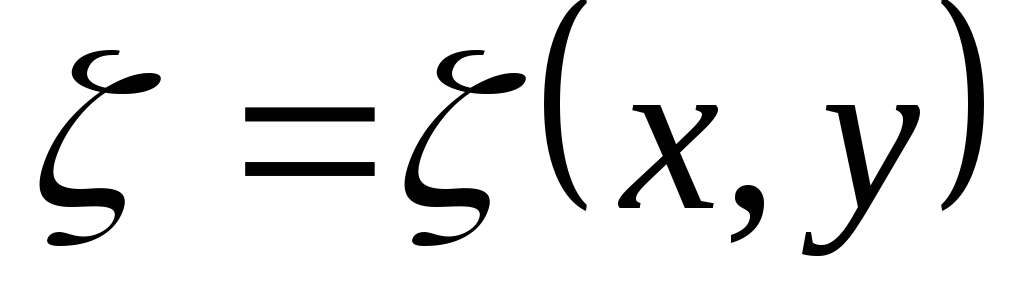 ,
, 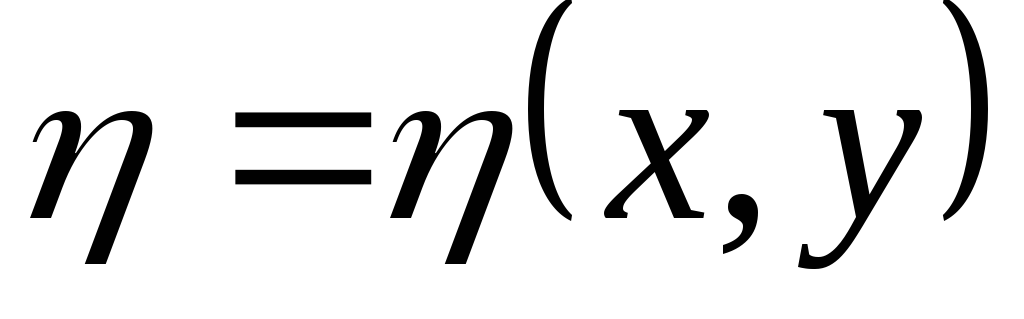
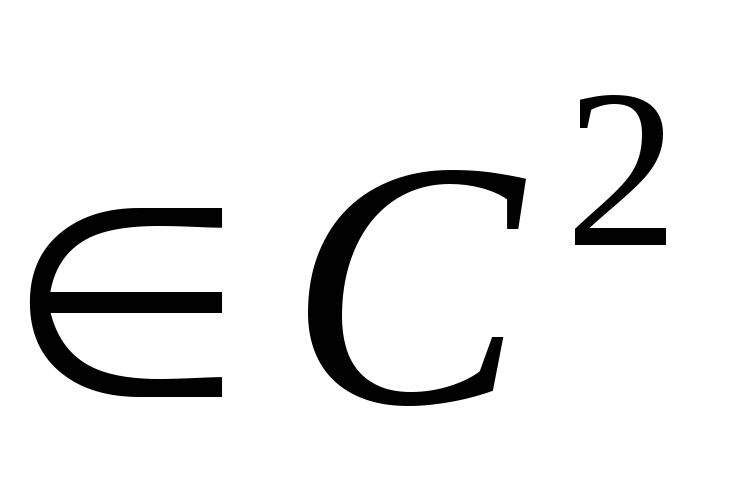 ,
, 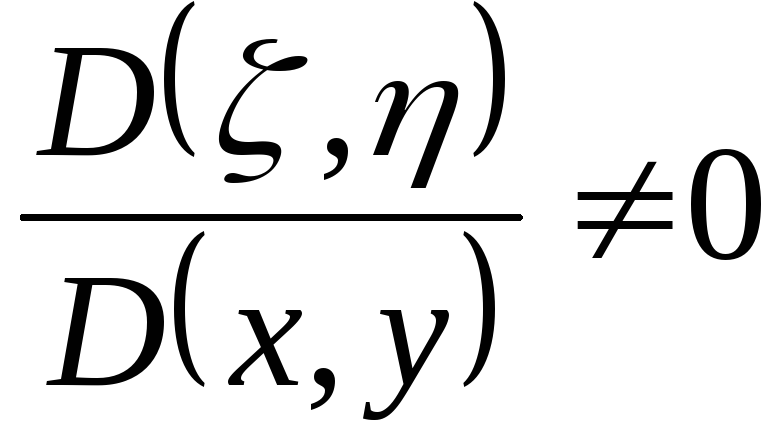 , (3.6)
, (3.6)
тогда
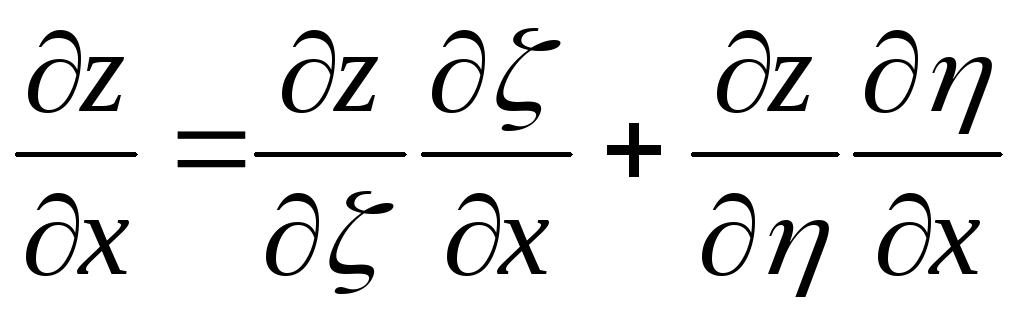 ,
,
 ,
,
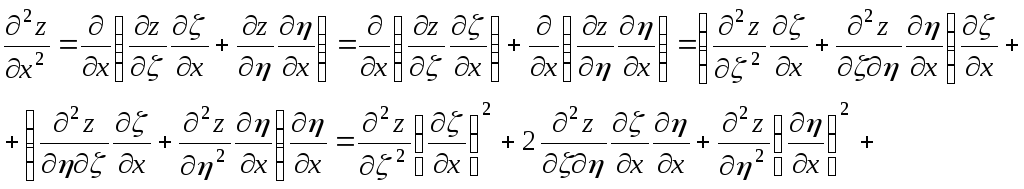
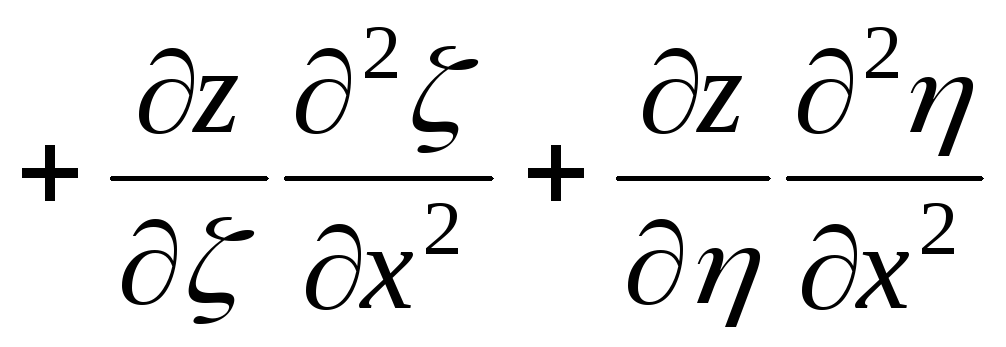 ,
,
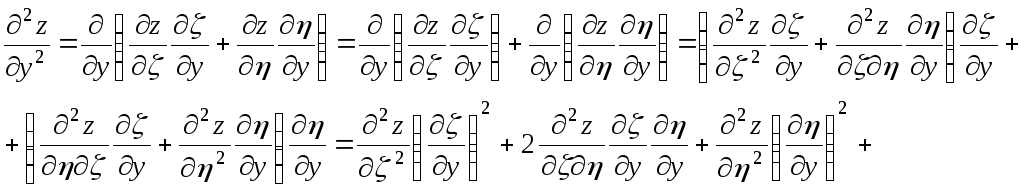
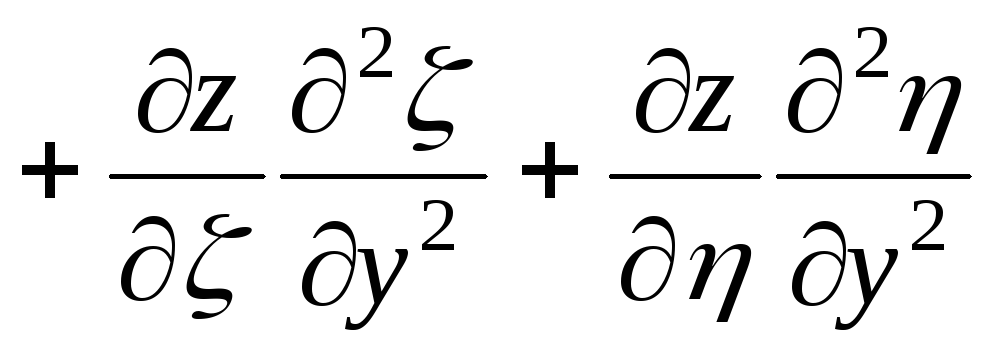 ,
,
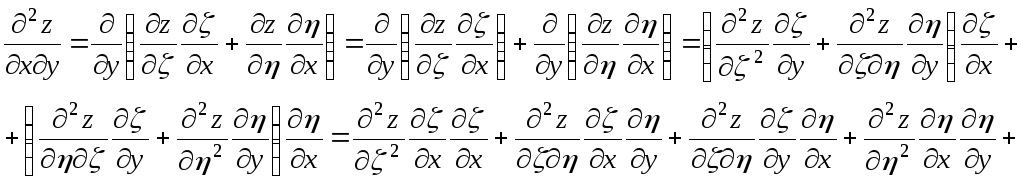
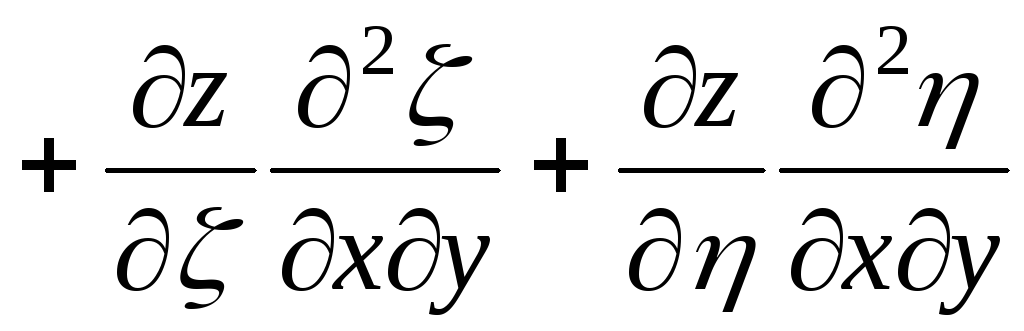 .
.
Поэтому уравнение (3.2) примет вид
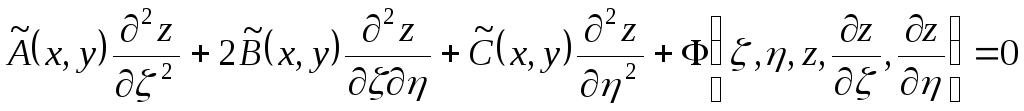 , (*)
, (*)
где
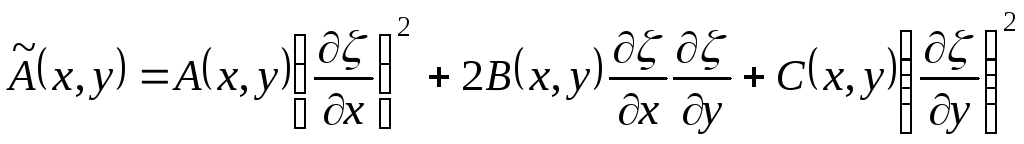 ,
,
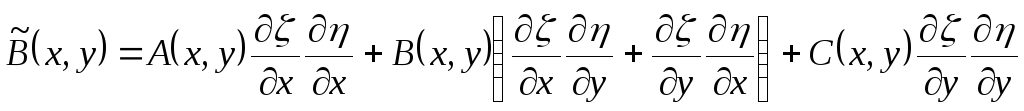 ,
,
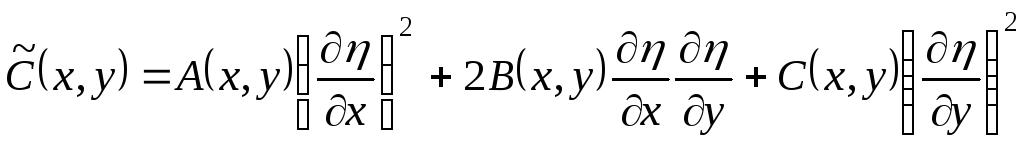 .
.
Потребуем, чтобы
функции  и
и  обращали в нуль коэффициенты
обращали в нуль коэффициенты  и
и 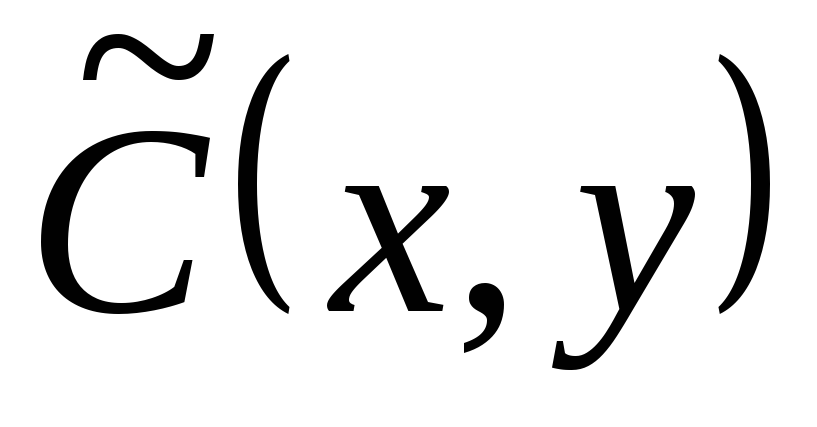 ,
т.е. удовлетворяли уравнениям:
,
т.е. удовлетворяли уравнениям:
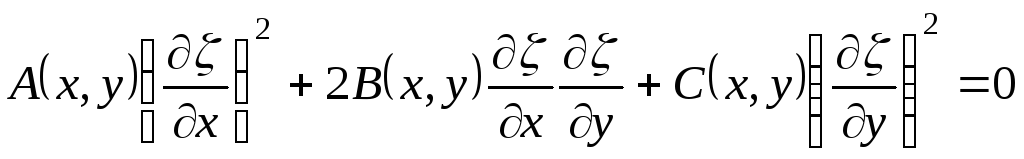 ,
,
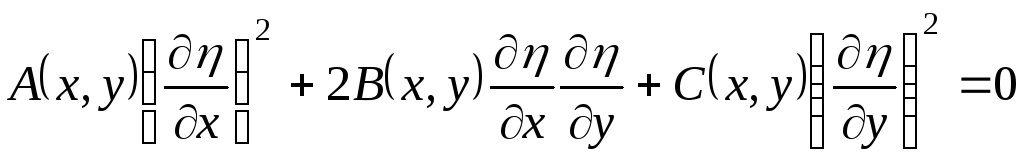 .
.
Так как 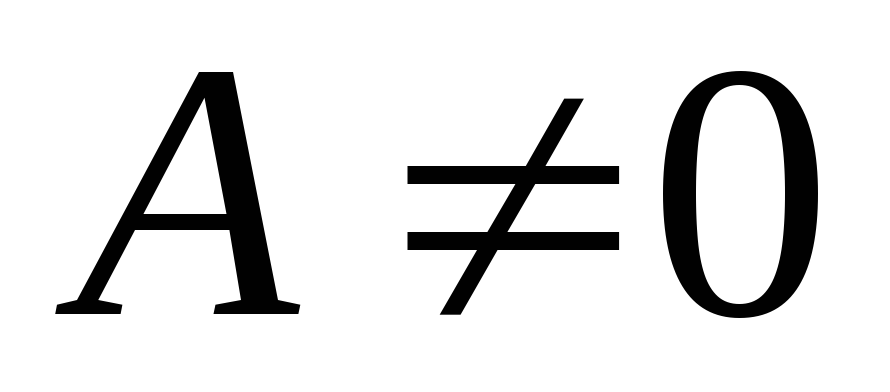 ,
то эти уравнения эквивалентны линейным
уравнениям
,
то эти уравнения эквивалентны линейным
уравнениям
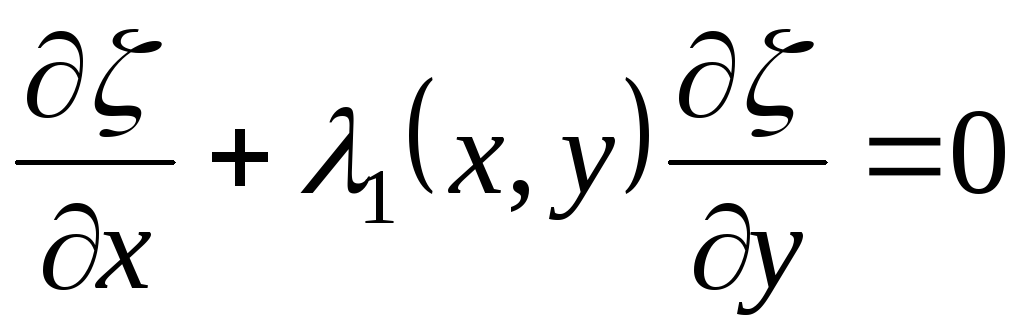 ,
, 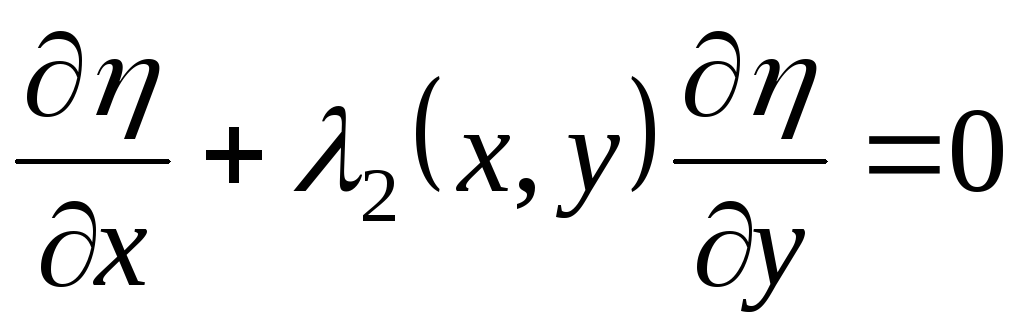 , (3.7)
, (3.7)
где 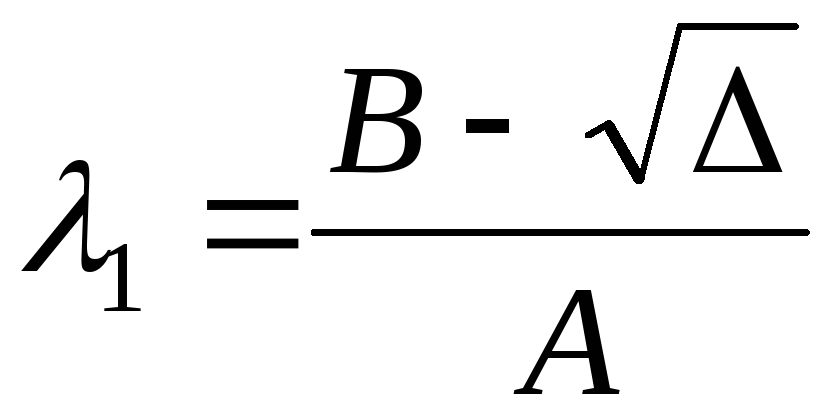 ,
, 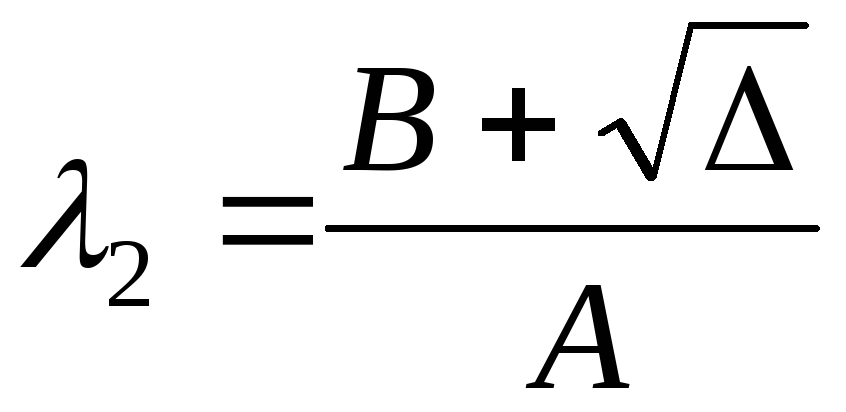 ,
, 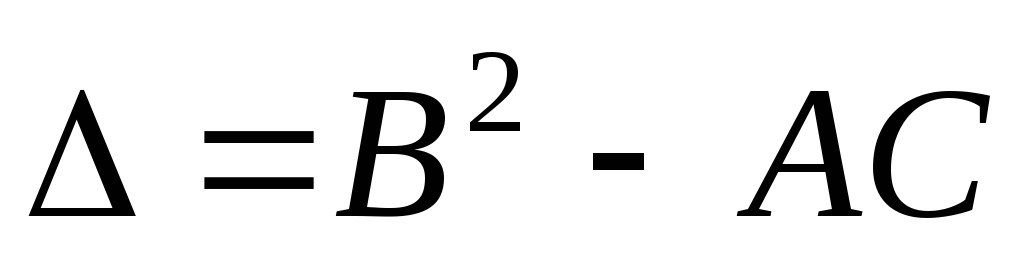 .
.
Как мы с вами
заметили, в зависимости от  возможны три типа уравнений. Рассмотрим
отдельно эти три случая.
возможны три типа уравнений. Рассмотрим
отдельно эти три случая.
Гиперболический тип,
 .
.
В этом случае уравнение (3.2) приводится к каноническому виду:
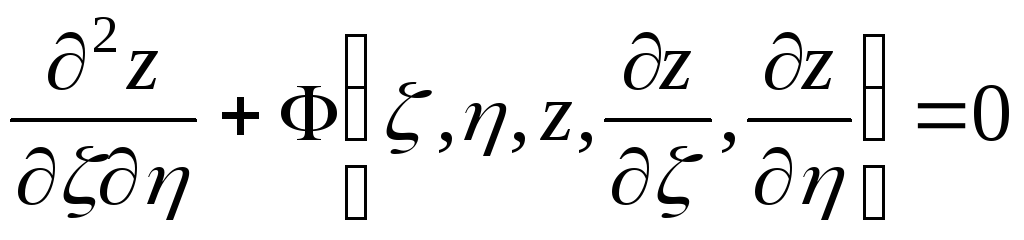 . (3.8)
. (3.8)
Замена переменных  ,
,  приводит уравнение (3.2) к другому,
эквивалентному, каноническому виду:
приводит уравнение (3.2) к другому,
эквивалентному, каноническому виду:
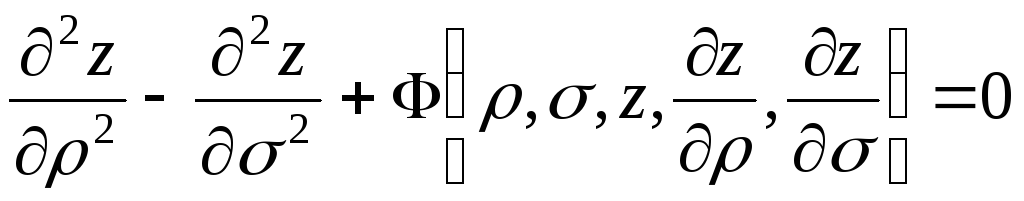 . (3.9)
. (3.9)
Для доказательства
представления (3.8) покажем, что существует,
по крайней мере, одна пара решений  и
и 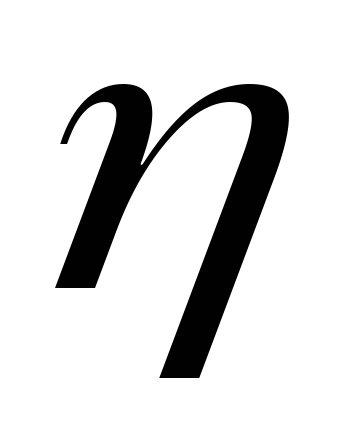 уравнений (3.7), удовлетворяющих условиям
(3.6). Установим сначала связь этих решений
с характеристиками уравнения (3.2).
уравнений (3.7), удовлетворяющих условиям
(3.6). Установим сначала связь этих решений
с характеристиками уравнения (3.2).
Предположим, что
существуют решения уравнений (3.7), такие
что  ,
,  в рассматриваемой окрестности, тогда
кривые
в рассматриваемой окрестности, тогда
кривые
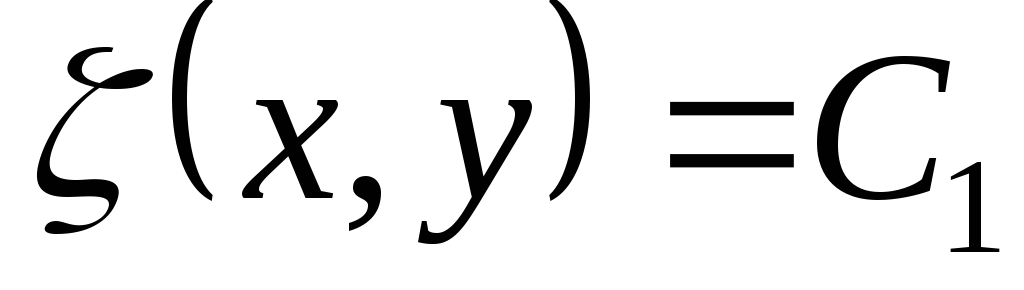 ,
, 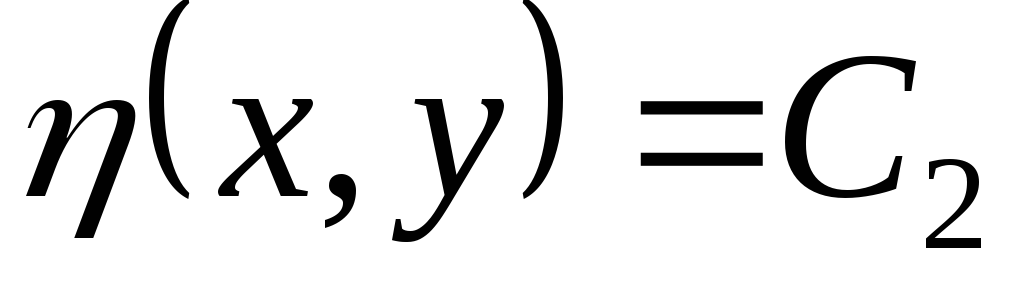
определяют два семейства характеристик уравнения (3.2). Докажем теперь следующее вспомогательное утверждение.
Лемма. Пусть функция 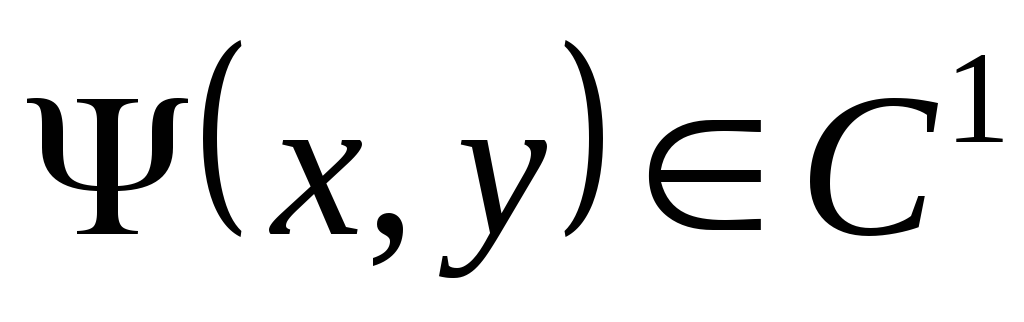 такая, что
такая, что 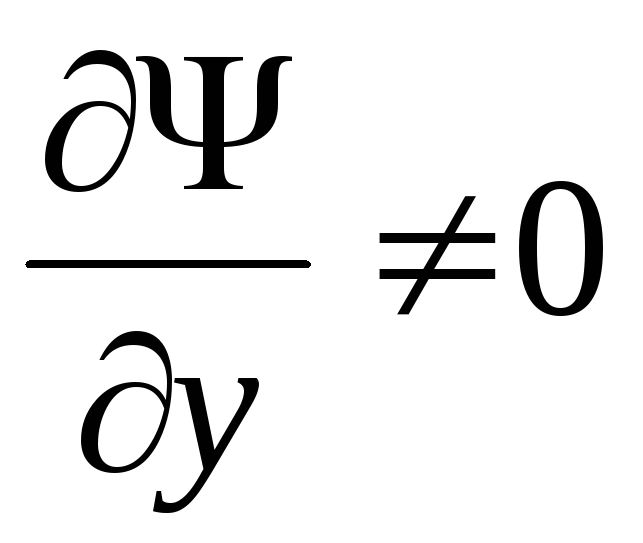 .
Для того, чтобы семейство кривых
.
Для того, чтобы семейство кривых 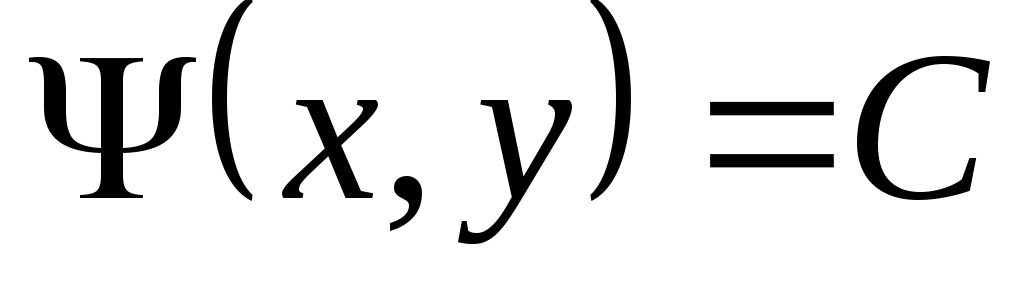 определяло характеристики уравнения
(3.2), необходимо и достаточно, чтобы
выражение
определяло характеристики уравнения
(3.2), необходимо и достаточно, чтобы
выражение 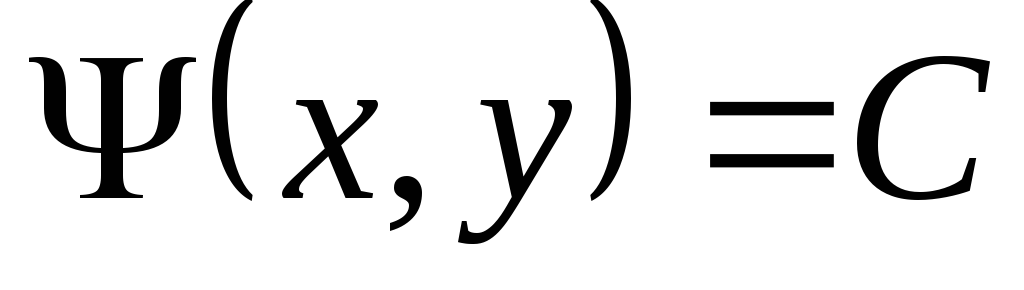 было общим интегралом одного из
обыкновенных дифференциальных уравнений
было общим интегралом одного из
обыкновенных дифференциальных уравнений
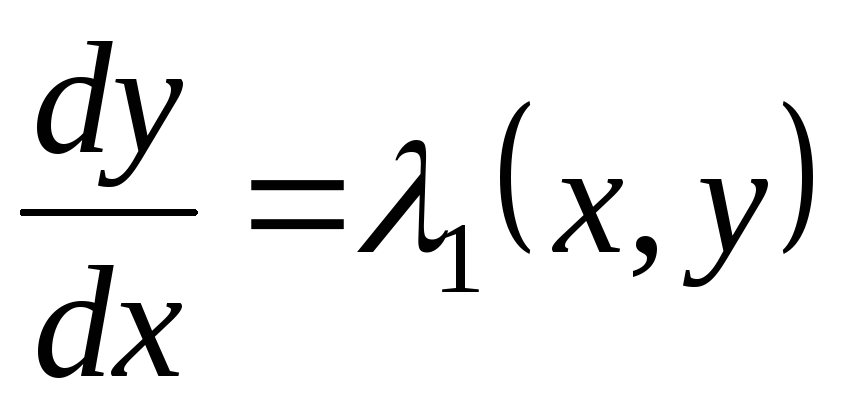 ,
, 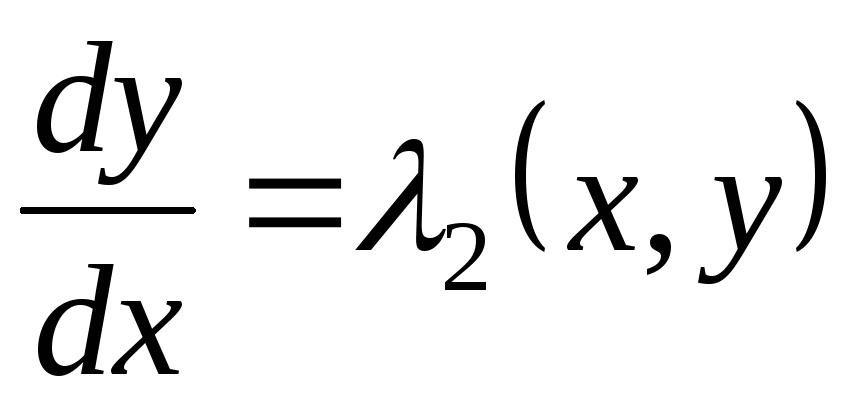 . (3.10)
. (3.10)
Уравнения (3.10) называются дифференциальными уравнениями характеристик уравнения (3.2).
Доказательство. 1. Докажем необходимость. Пусть 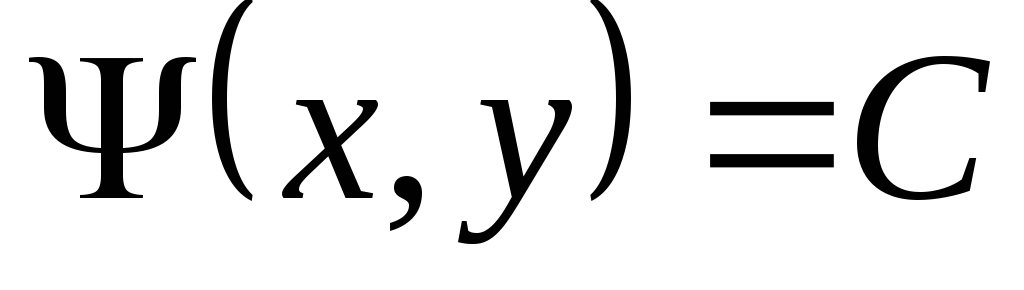 — семейство характеристик уравнения
(3.2). Из условия
— семейство характеристик уравнения
(3.2). Из условия 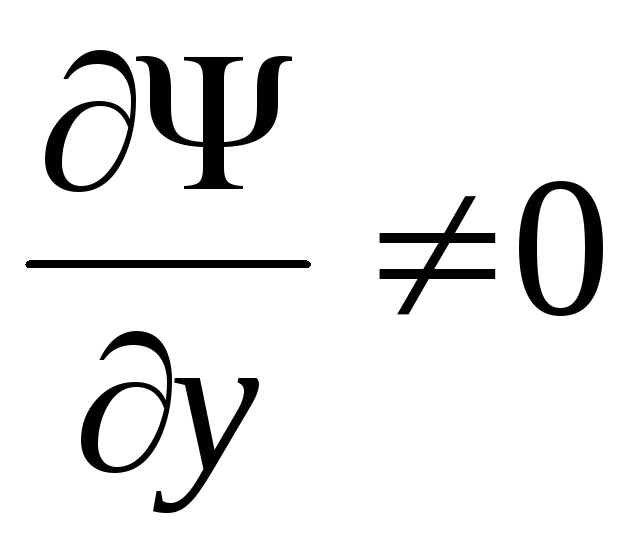 следует, что данное семейство заполняет
некоторую окрестность D,
через каждую точку которой проходит
одна и только одна характеристика. Пусть
следует, что данное семейство заполняет
некоторую окрестность D,
через каждую точку которой проходит
одна и только одна характеристика. Пусть  .
Тогда, если в преобразовании (3.6) взять,
например,
.
Тогда, если в преобразовании (3.6) взять,
например,  ,
то в этой окрестности функция
,
то в этой окрестности функция  будет удовлетворять уравнению
будет удовлетворять уравнению
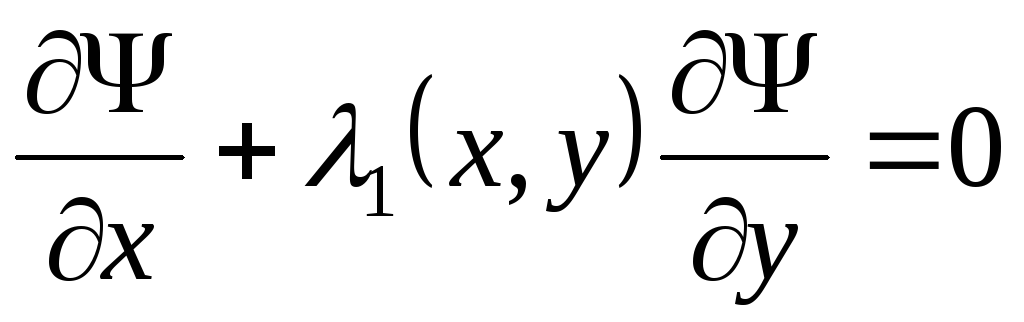 .
.
Так как на каждой характеристике справедливо соотношение
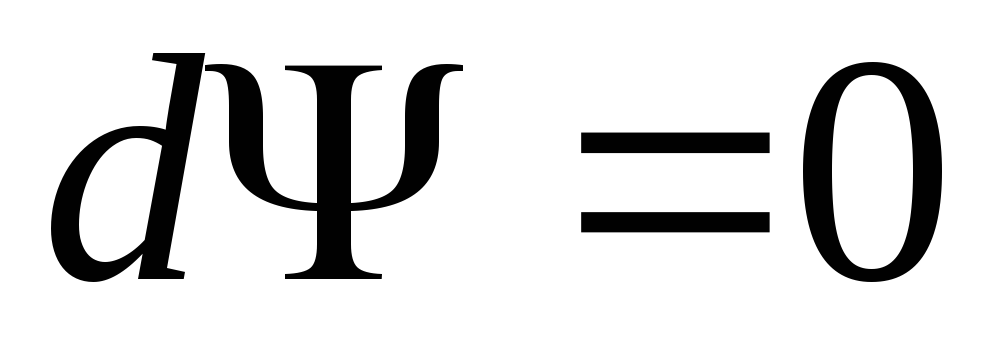 ,
, 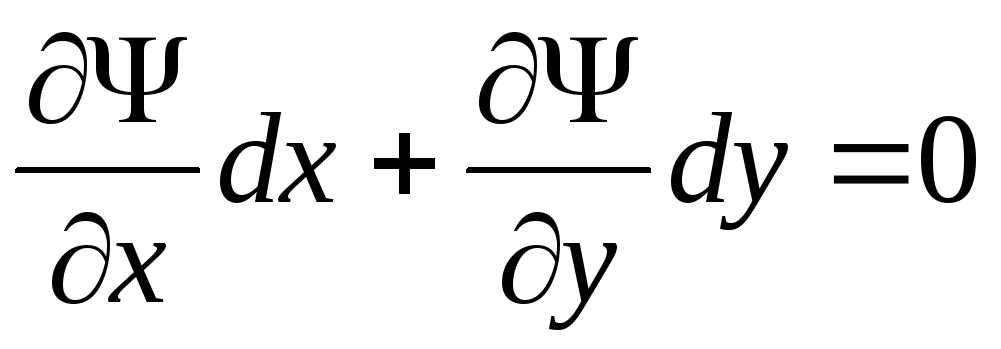 ,
,
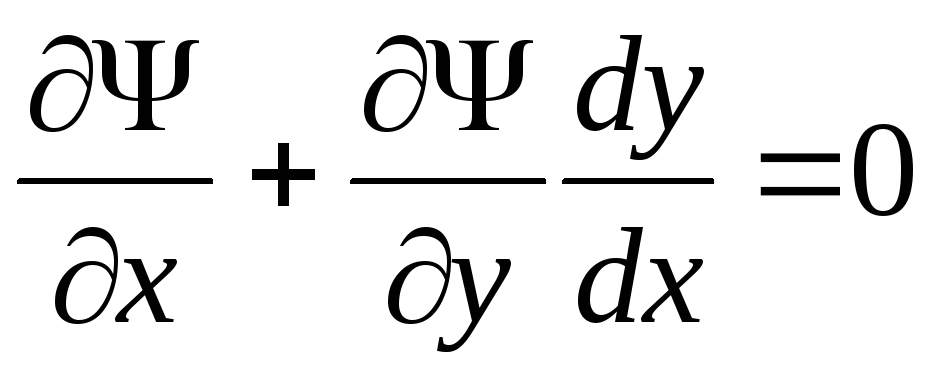 ,
,
то поскольку 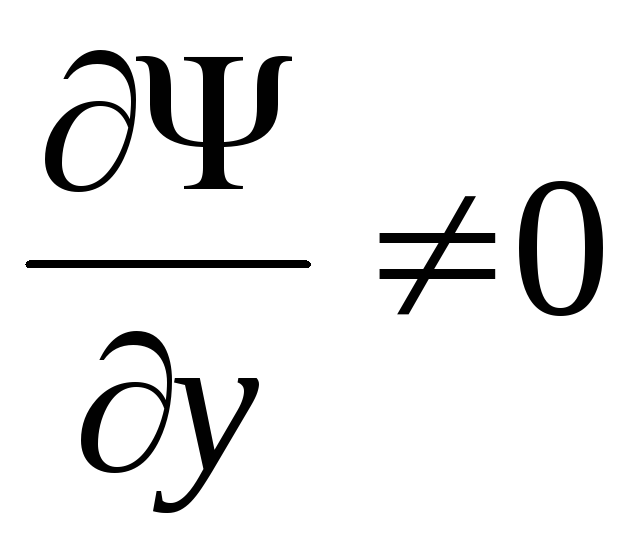 ,
получаем
,
получаем
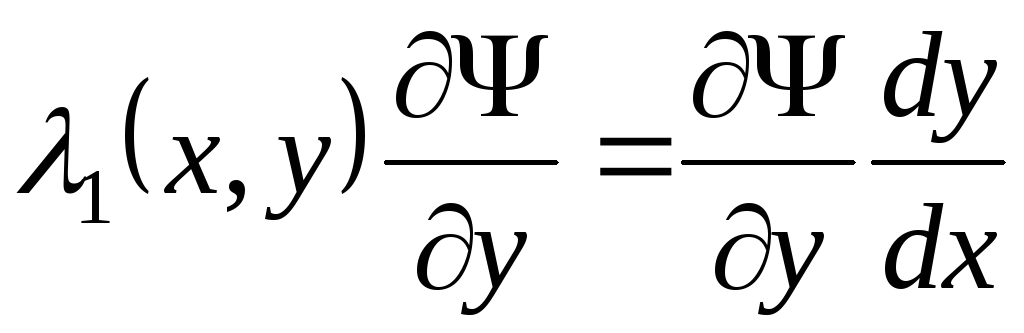 ,
или
,
или 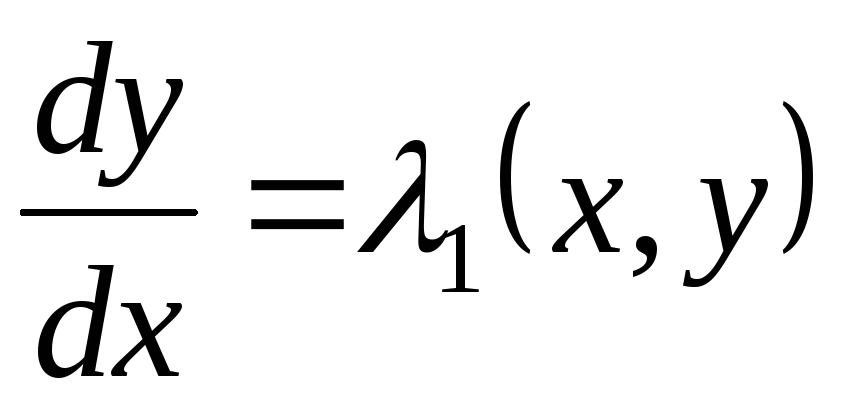 ,
,
т.е. 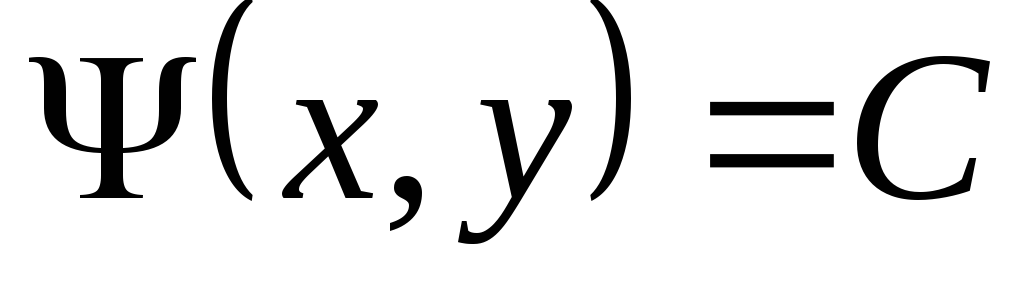 есть общий интеграл первого из уравнений
(3.10). Необходимость доказана.
есть общий интеграл первого из уравнений
(3.10). Необходимость доказана.
2. Докажем
достаточность. Пусть 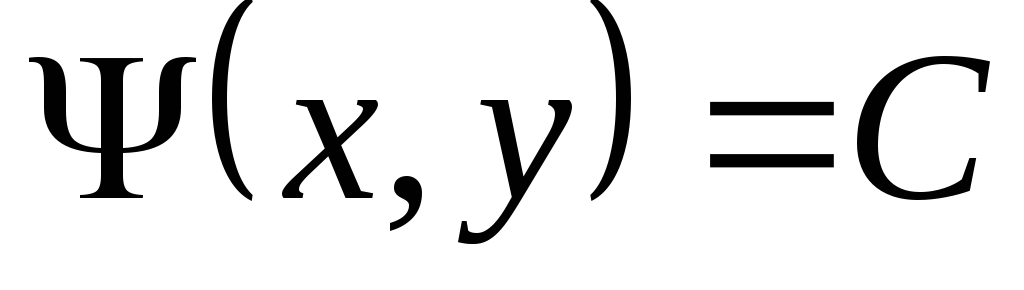 есть общий интеграл одного из уравнений
(3.10), например, первого из них. По
определению это значит, что если функция
есть общий интеграл одного из уравнений
(3.10), например, первого из них. По
определению это значит, что если функция 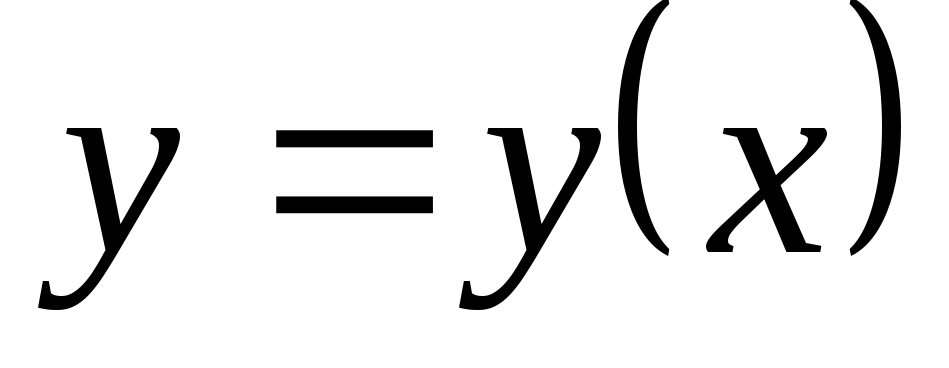 является решением этого уравнения, то
является решением этого уравнения, то
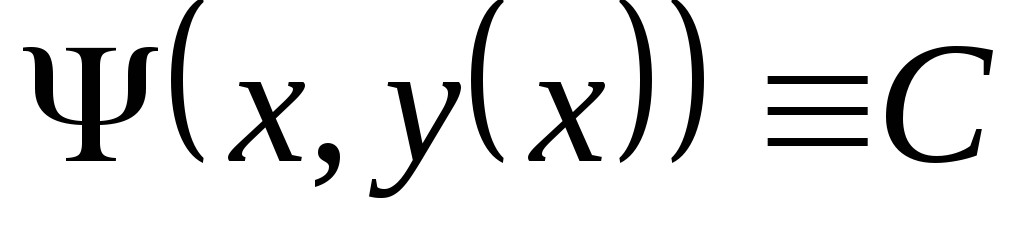 ,
,
поэтому, продифференцировав последнее тождество по х, будем иметь
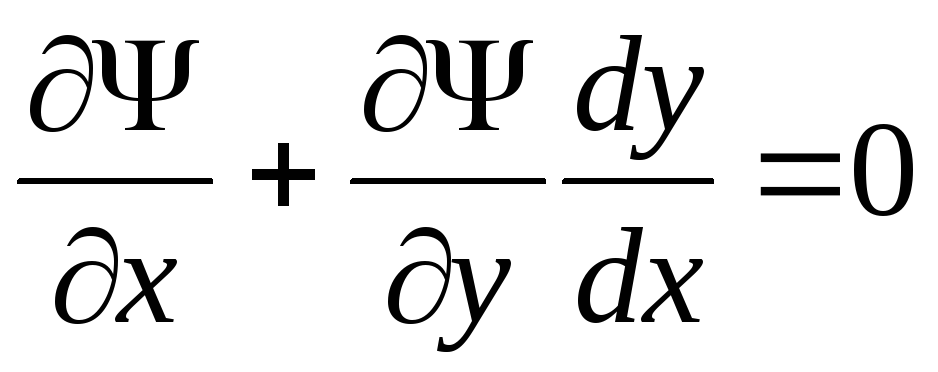 ,
,
и, следовательно,
на каждой линии 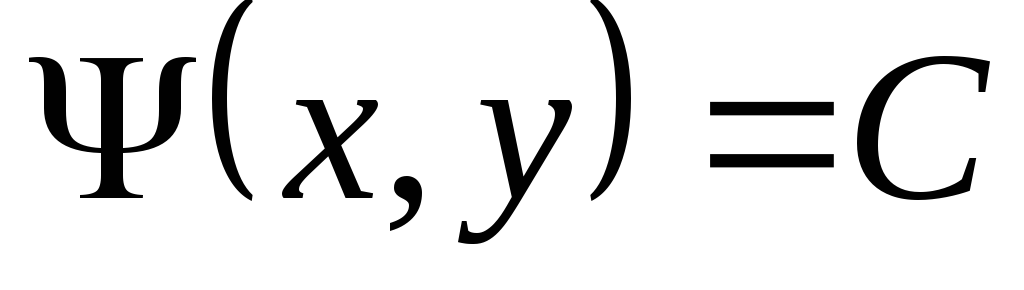 выполняется соотношение
выполняется соотношение
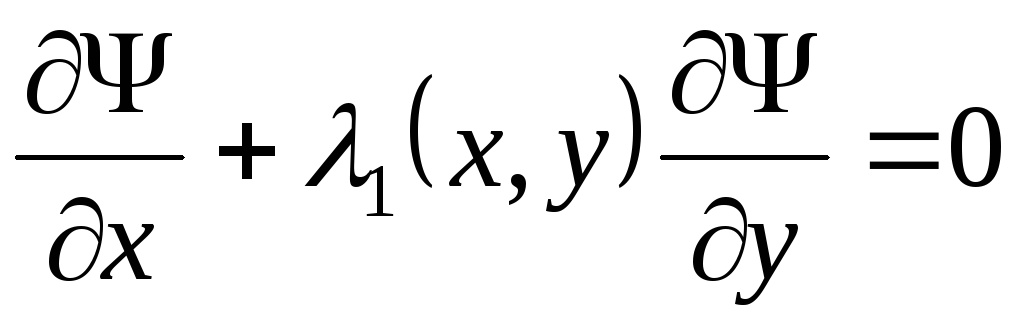 . (3.11)
. (3.11)
Но по теореме
существования и единственности решения
для обыкновенных дифференциальных
уравнений через каждую точку из
рассматриваемой окрестности проходит
одна интегральная кривая 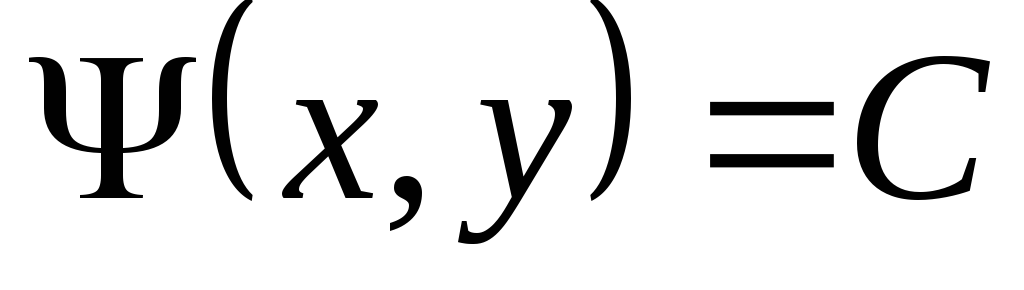 этого уравнения. Поэтому уравнение
(3.11) выполняется во всех точках
рассматриваемой окрестности. А так как
по условию
этого уравнения. Поэтому уравнение
(3.11) выполняется во всех точках
рассматриваемой окрестности. А так как
по условию 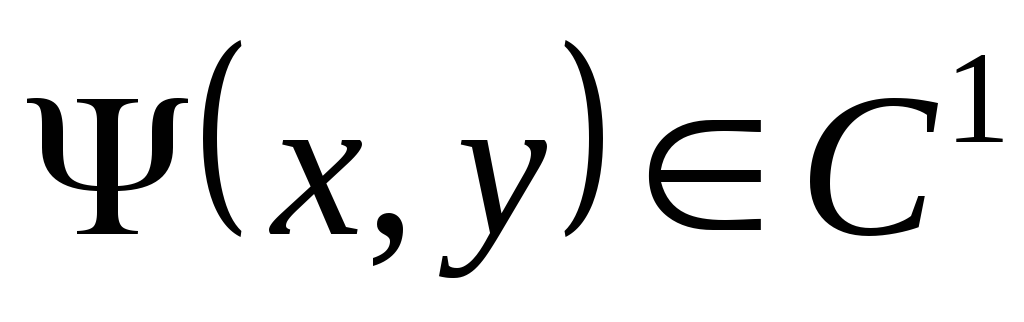 ,
, 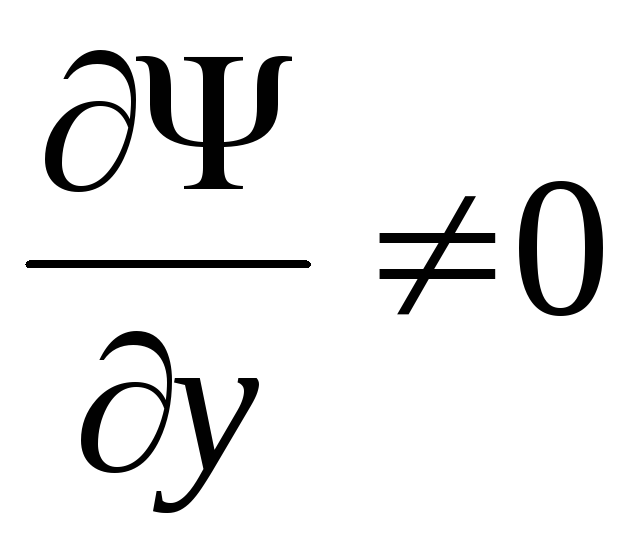 ,
то кривые
,
то кривые 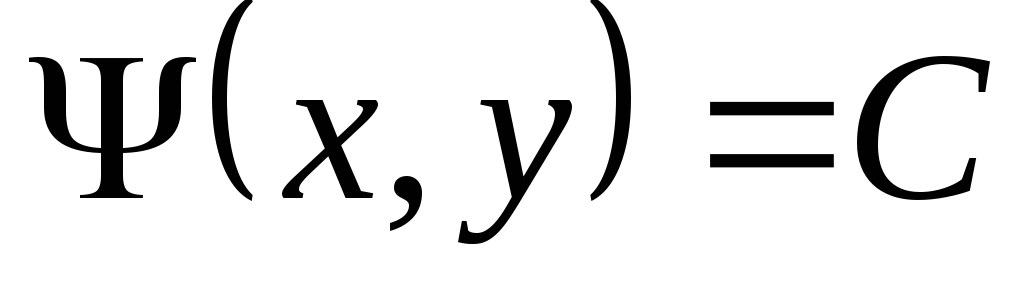 являются характеристиками уравнения
(3.2). Лемма доказана.
являются характеристиками уравнения
(3.2). Лемма доказана.
На основании доказанной леммы общие интегралы уравнений (3.10):
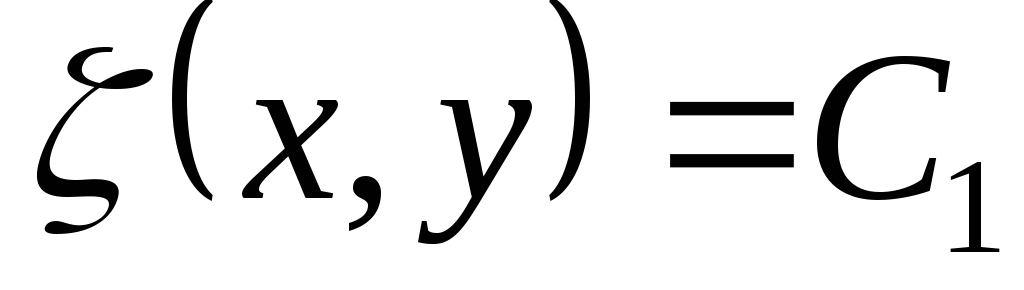 ,
и
,
и 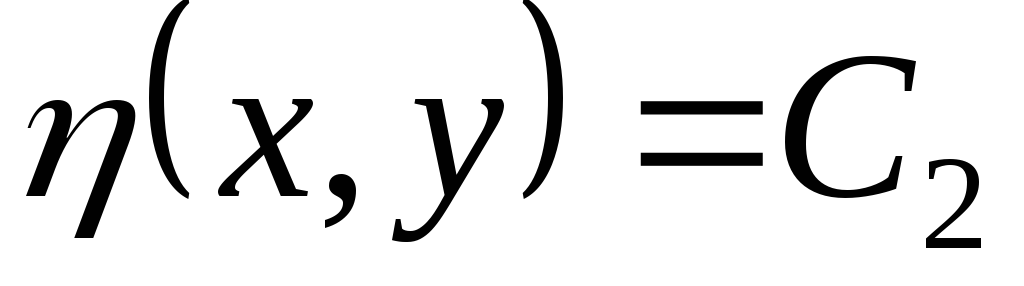
такие, что 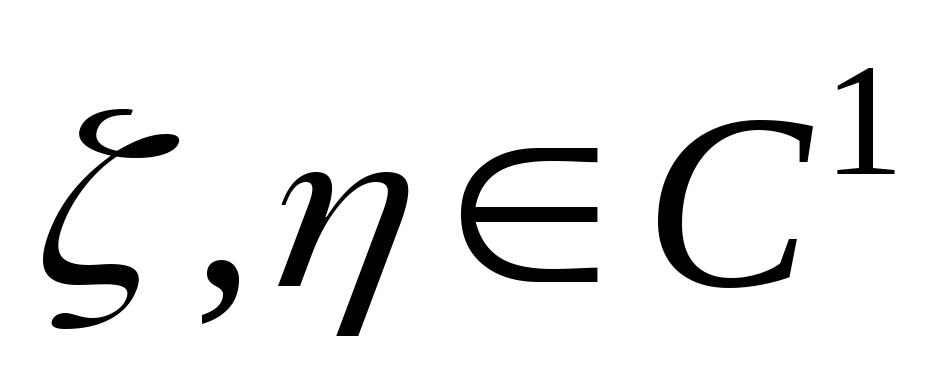 ,
, 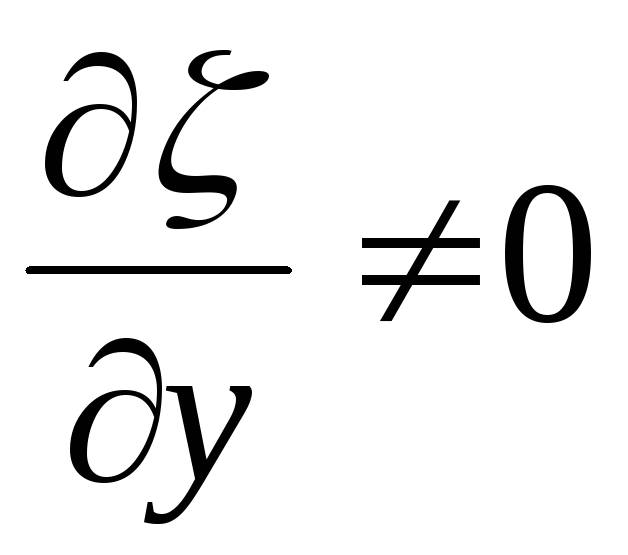 ,
, 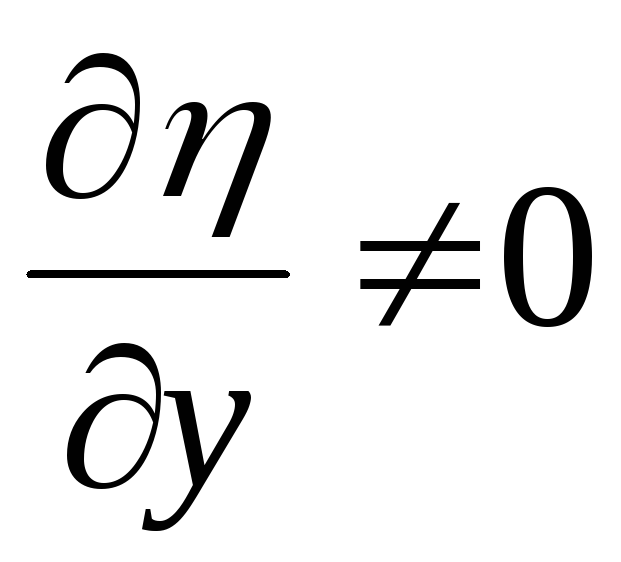 ,
определяют два семейства характеристик
уравнения (3.2). Причем, так как
,
определяют два семейства характеристик
уравнения (3.2). Причем, так как 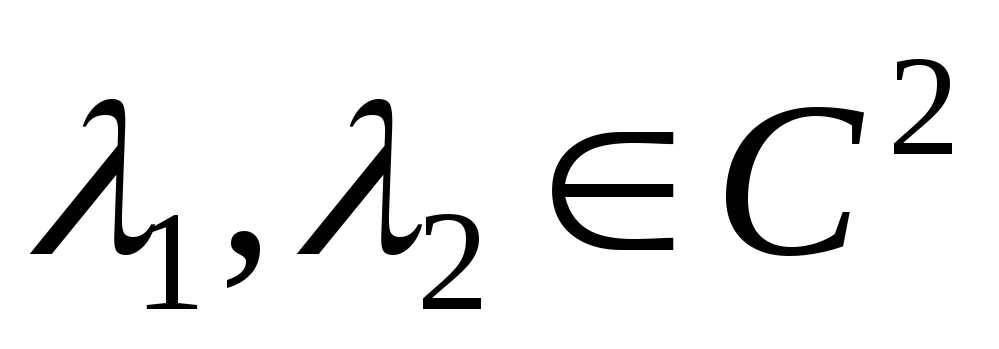 ,
то и
,
то и 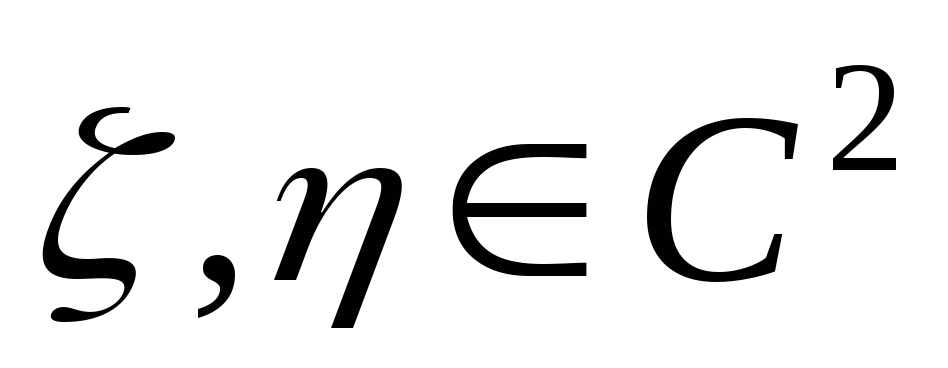 ,
а так же
,
а так же
 .
.
Т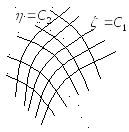 аким
образом, семейства характеристик
аким
образом, семейства характеристик 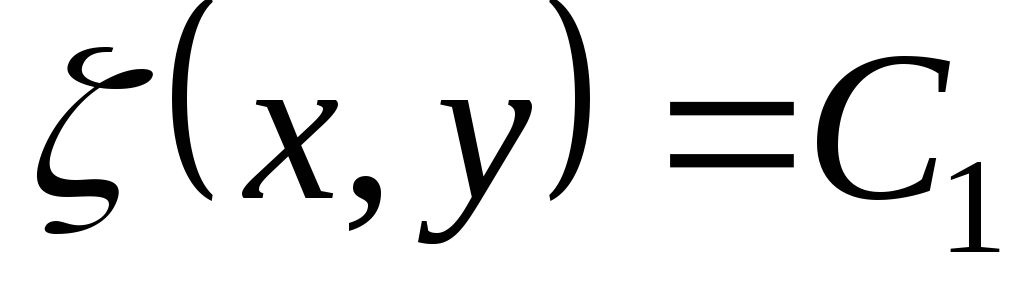 ,
, 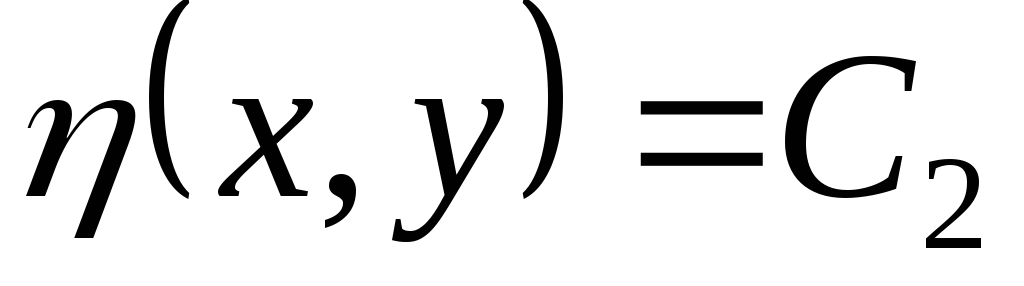 образуют семейства координатных линий
и функции
образуют семейства координатных линий
и функции 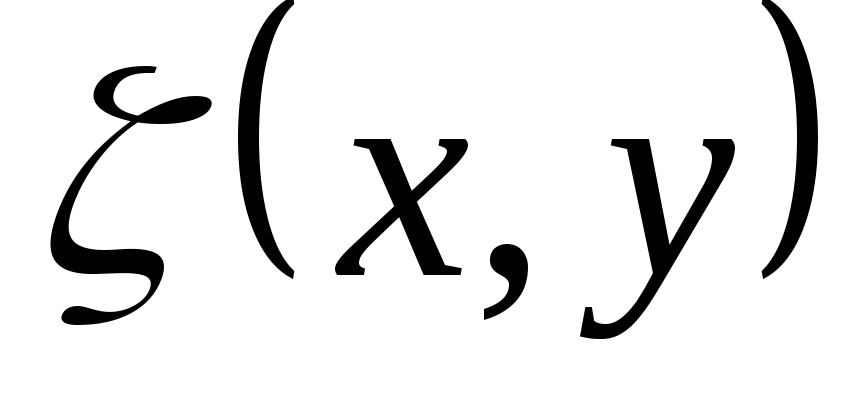 и
и 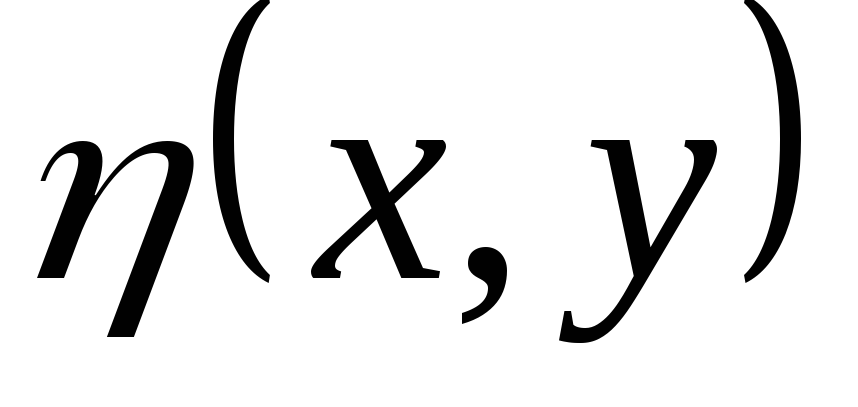 можно принять за новые переменные. При
этом в уравнении (*) коэффициенты
можно принять за новые переменные. При
этом в уравнении (*) коэффициенты 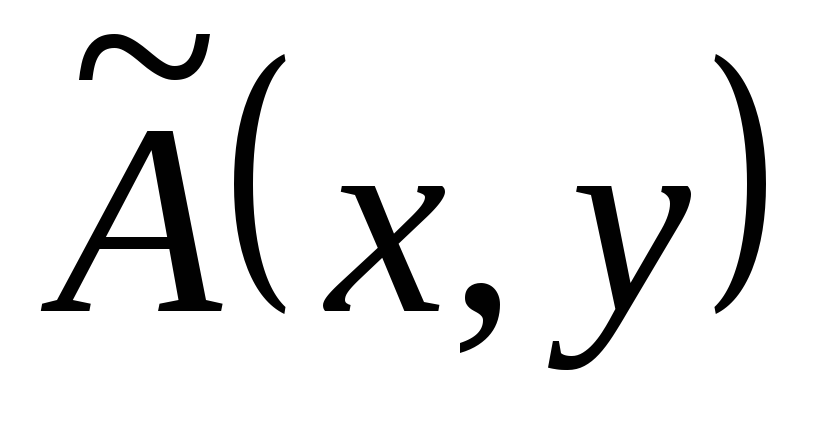 и
и 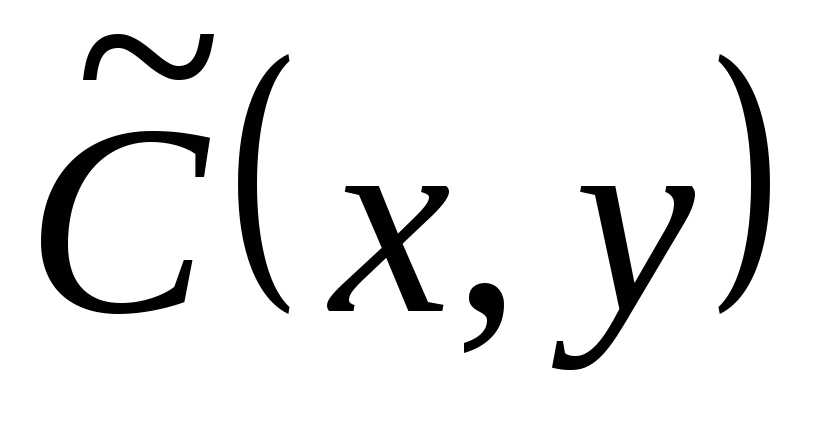 будут равны нулю и
будут равны нулю и
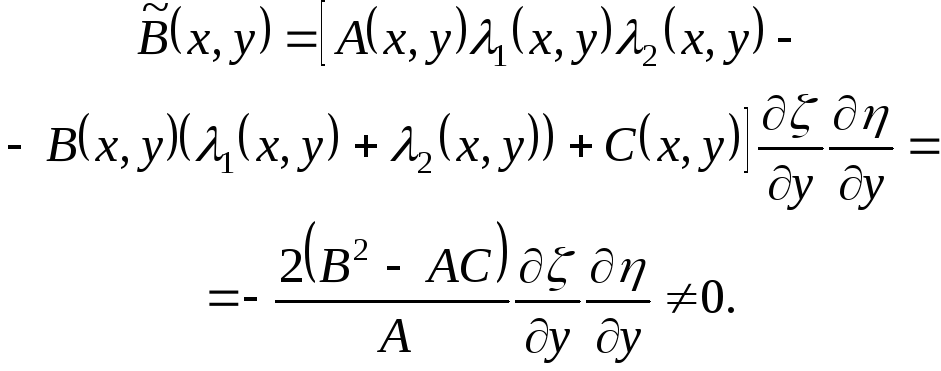
Поэтому, разделив
уравнение (*) на 2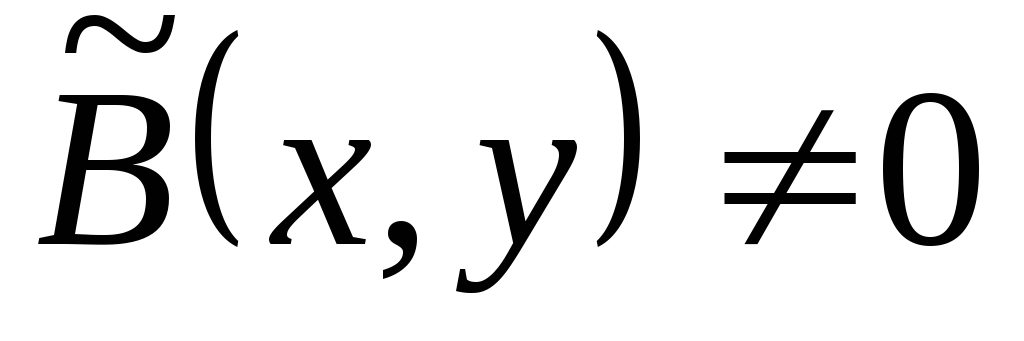 ,
получим уравнение в канонической форме
(3.8).
,
получим уравнение в канонической форме
(3.8).
Параболический тип,
 .
.
Уравнение (3.2) приводится к каноническому виду
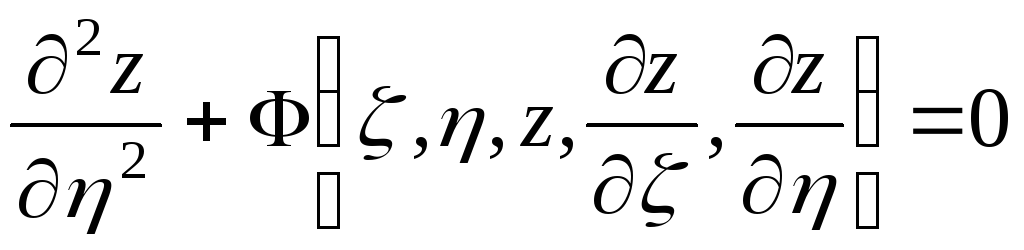 .
.
Так как в некоторой
окрестности  ,
то
,
то 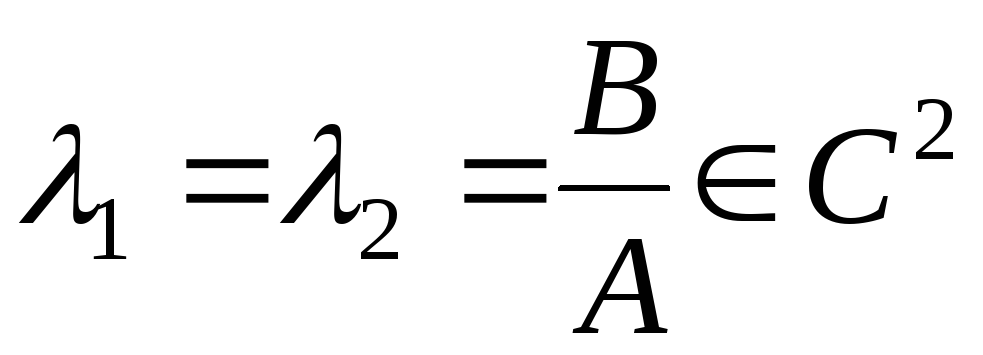 ,
поэтому дифференциальные уравнения
(3.7) совпадают и равны
,
поэтому дифференциальные уравнения
(3.7) совпадают и равны
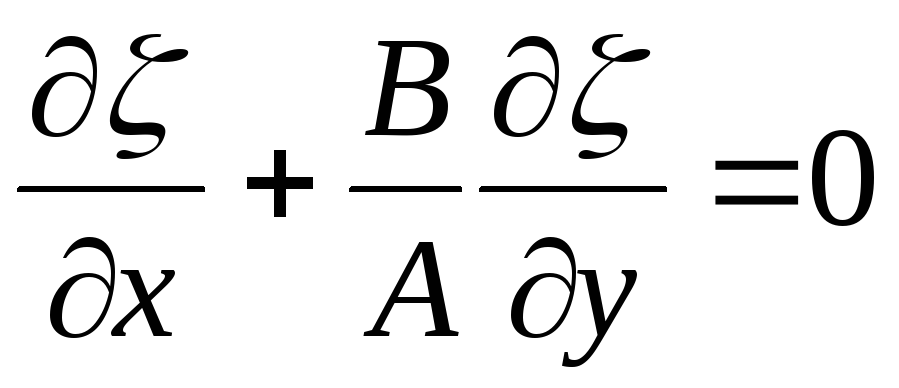 .
.
Следовательно, мы
получили одно семейство характеристик  уравнения (3.2), определяемое в силу леммы,
общим интегралом уравнения
уравнения (3.2), определяемое в силу леммы,
общим интегралом уравнения
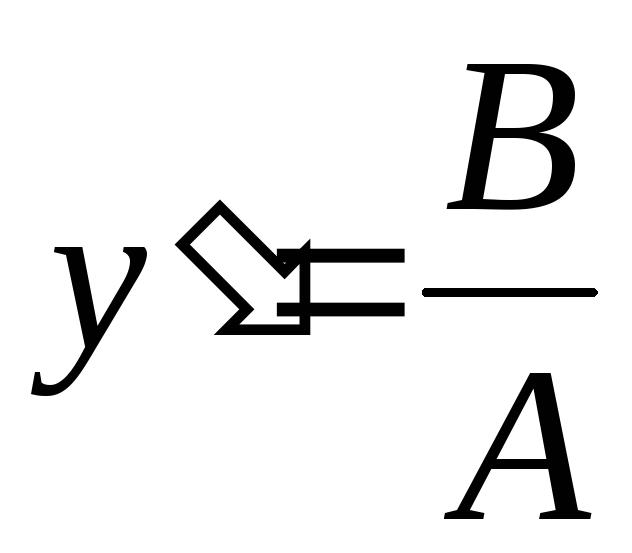 ,
,
таким что 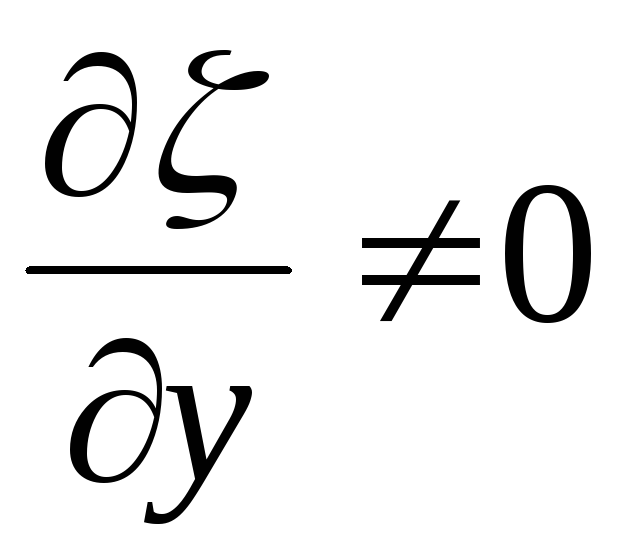 и
и  .
В качестве второго семейства координатных
линий выберем прямые
.
В качестве второго семейства координатных
линий выберем прямые 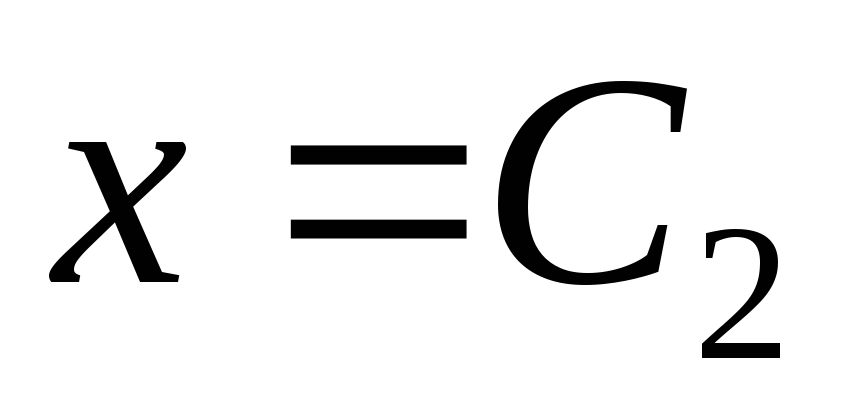 .
В результате замена переменных
.
В результате замена переменных
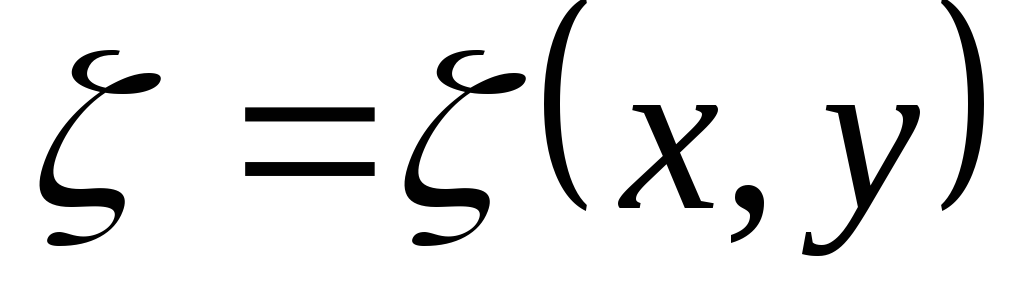 ,
, 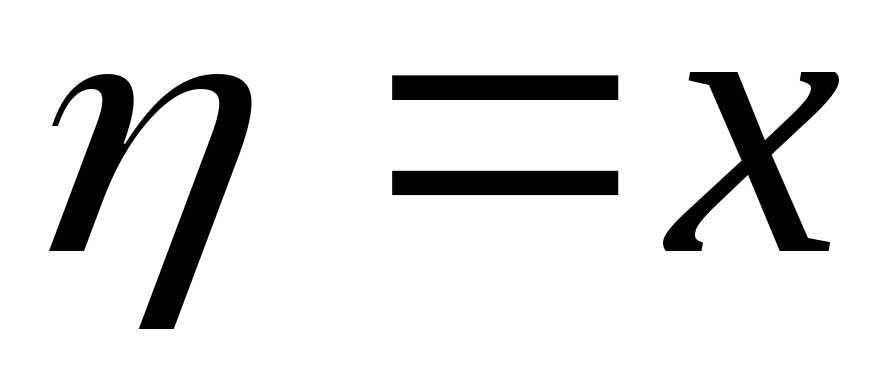 ,
, 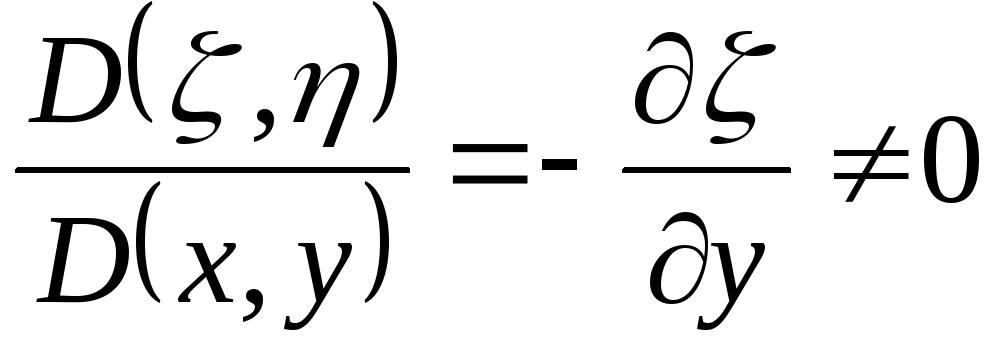
дает
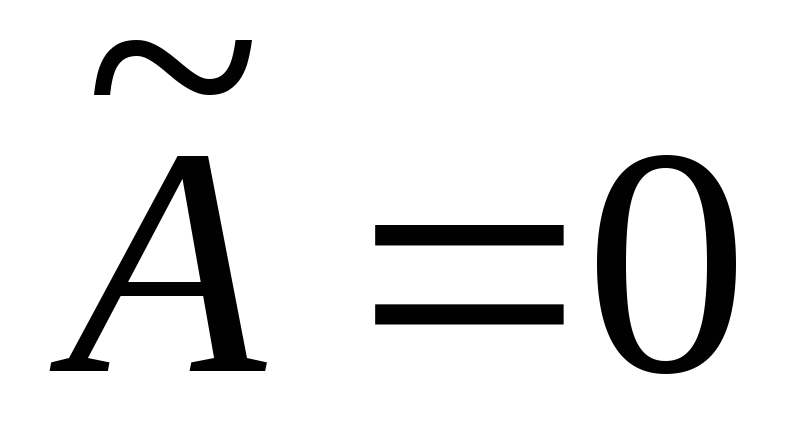 ,
, 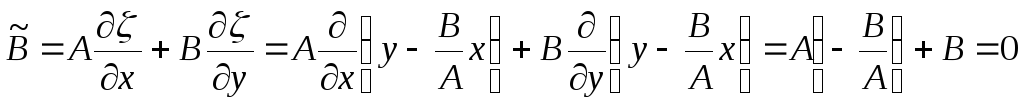 ,
, 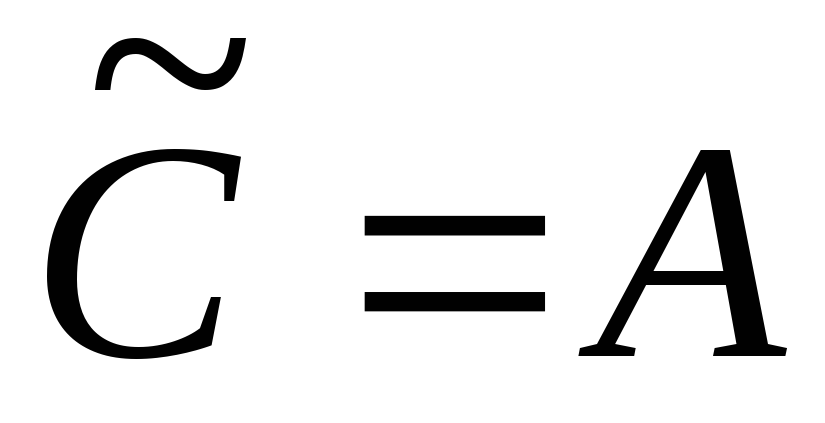 .
.
Разделив уравнение
(*) на коэффициент 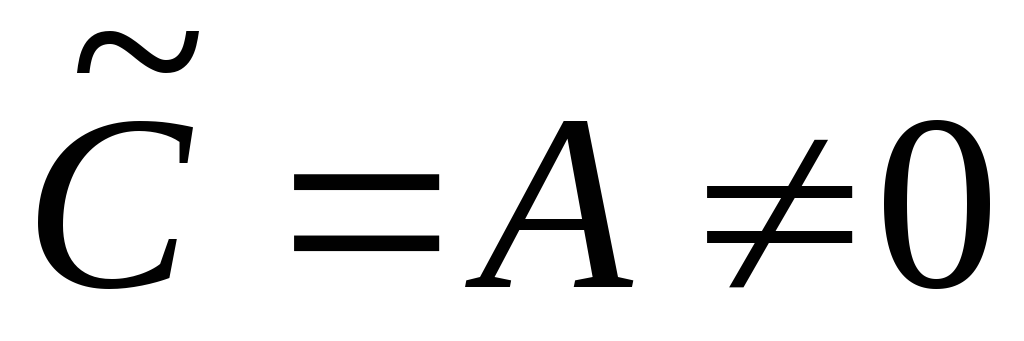 ,
получим уравнение в канонической форме.
,
получим уравнение в канонической форме.
Эллиптический тип,
 .
.
Если коэффициенты А, В и С в уравнении (3.2) – аналитические функции в окрестности некоторой точки. Тогда это уравнение приводится к каноническому виду
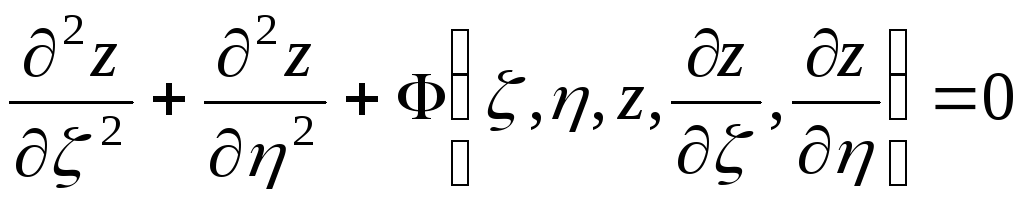 .
.
В этом случае,
коэффициенты 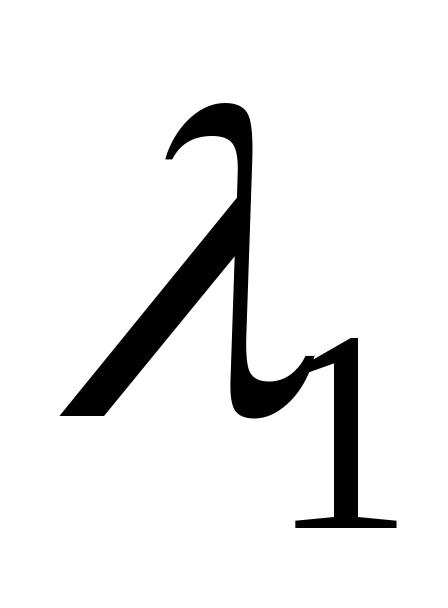 и
и 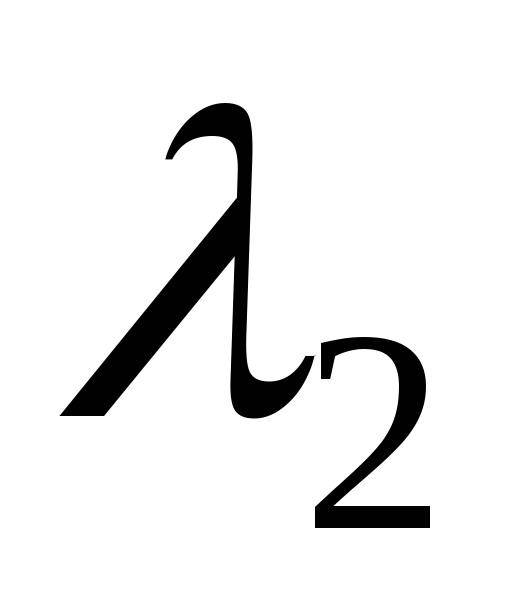 уравнений (3.7) – аналитические функции,
причем при действительных
уравнений (3.7) – аналитические функции,
причем при действительных 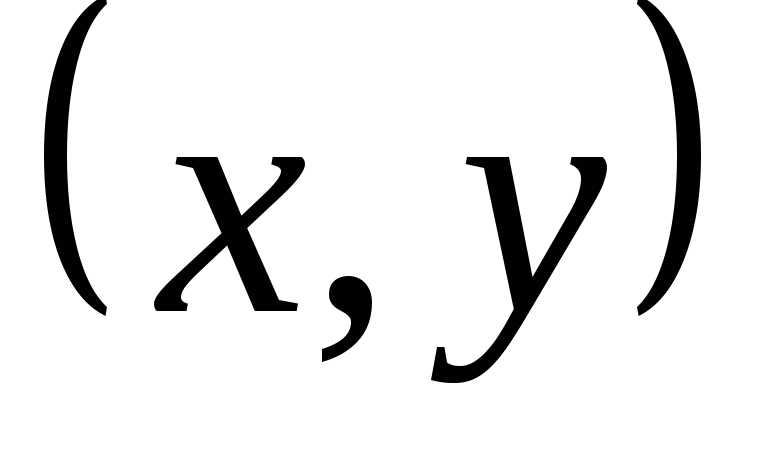 :
: 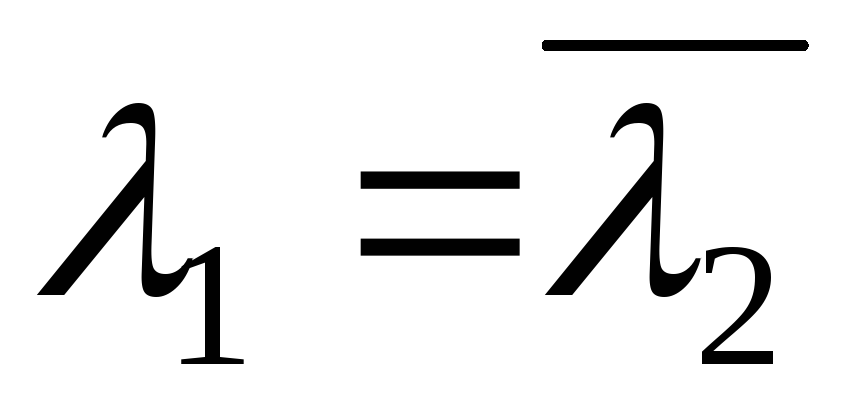 .
Из теоремы Ковалевской следует, что в
достаточно малой окрестности существует
аналитическое решение
.
Из теоремы Ковалевской следует, что в
достаточно малой окрестности существует
аналитическое решение 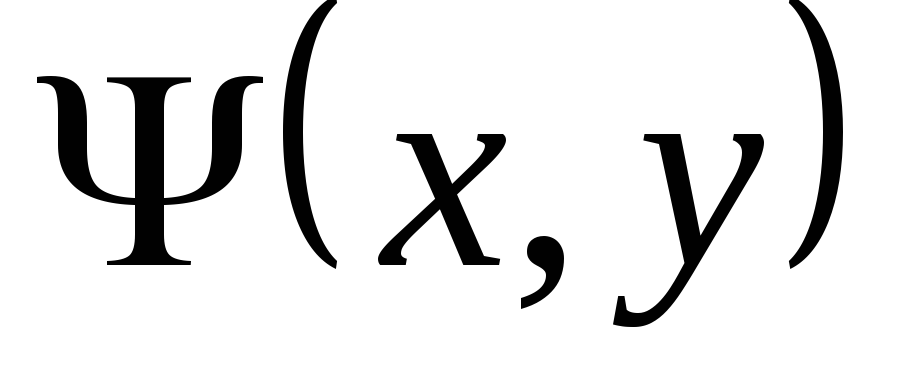 уравнения
уравнения
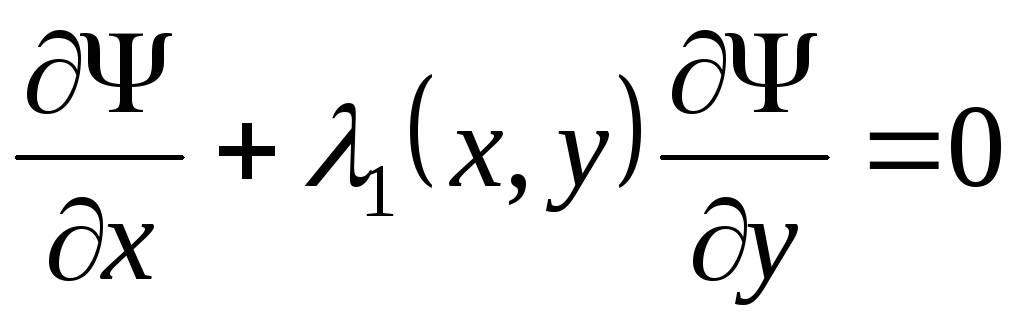 ,
,
удовлетворяющее
условию 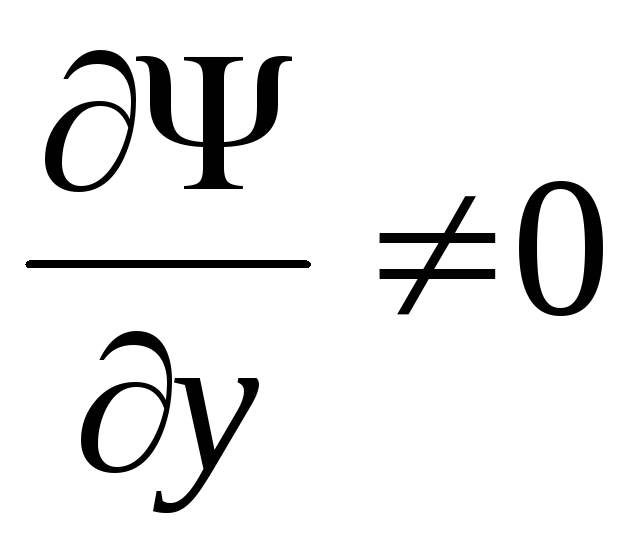 .
Положим теперь
.
Положим теперь
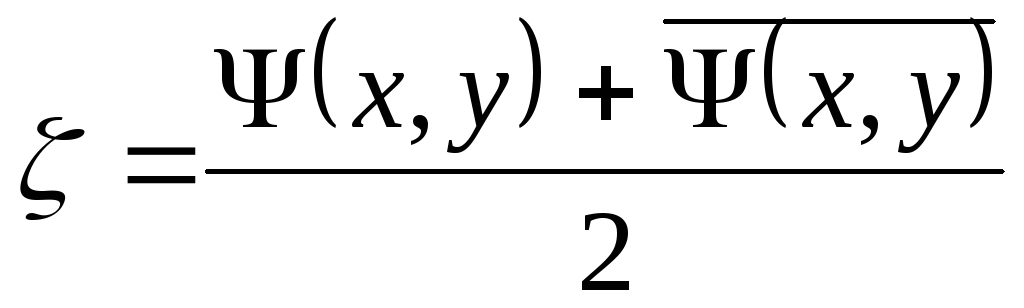 ,
, 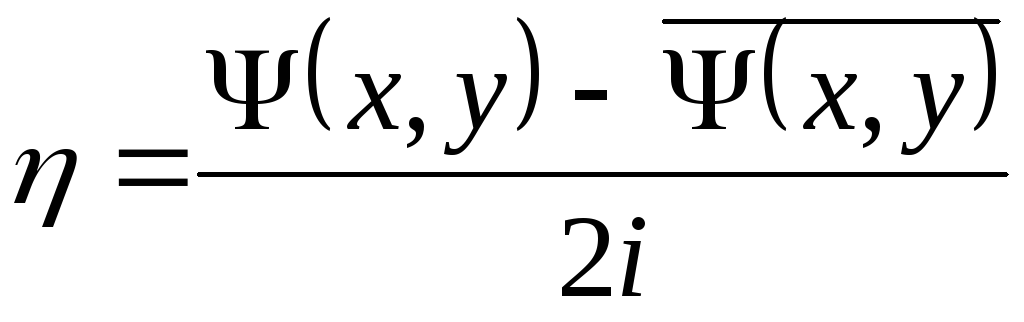 , (3.12)
, (3.12)
где 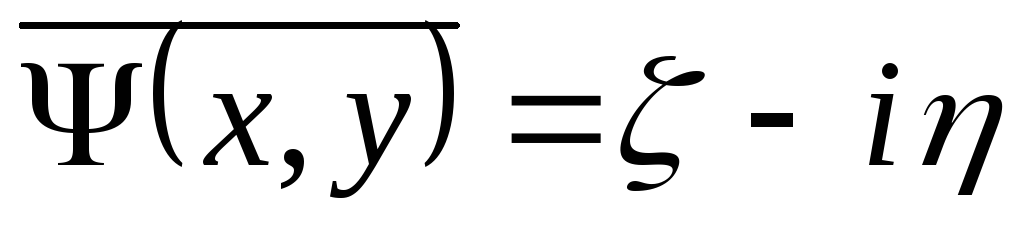 — функция, комплексно сопряженная с
— функция, комплексно сопряженная с 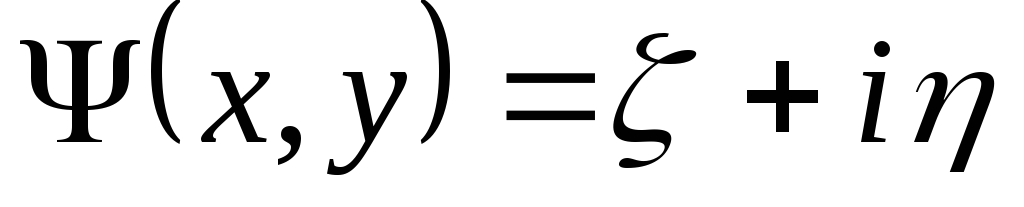 .
Функция удовлетворяет второму уравнению из
(3.7):
.
Функция удовлетворяет второму уравнению из
(3.7):
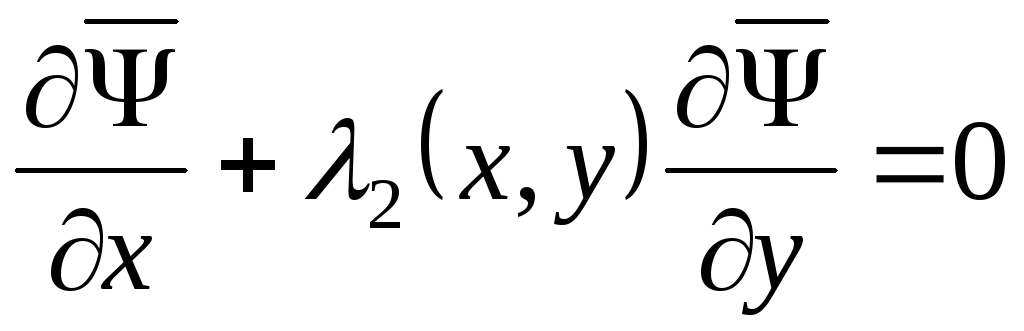 ,
,
так как
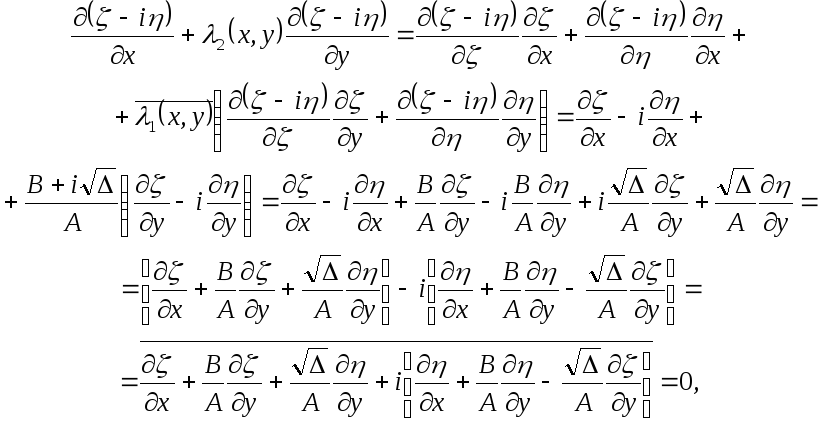
поскольку функция 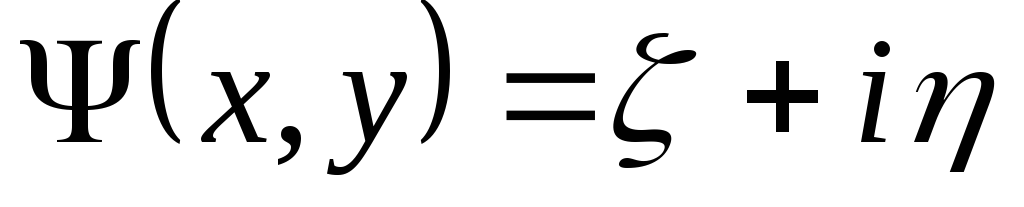 удовлетворяет первому уравнения из
(3.7), т.е.
удовлетворяет первому уравнения из
(3.7), т.е.
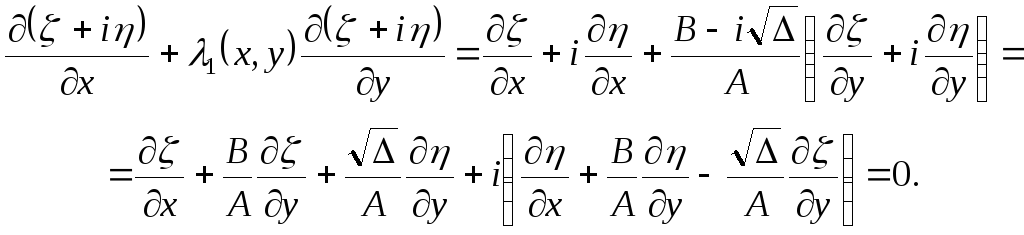
Так как функции 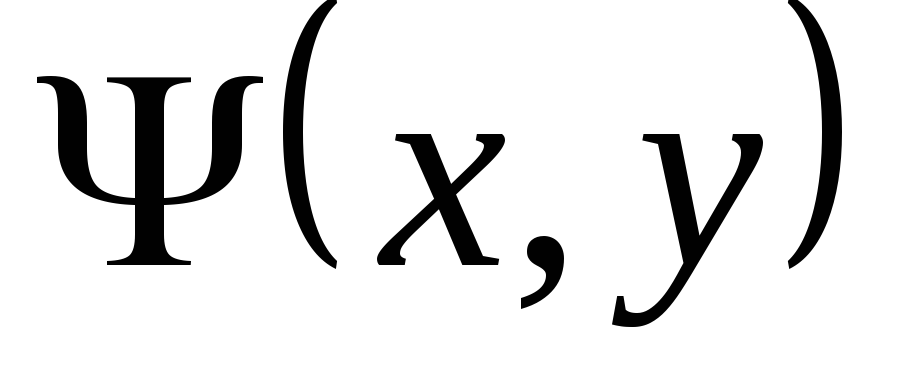 и
и 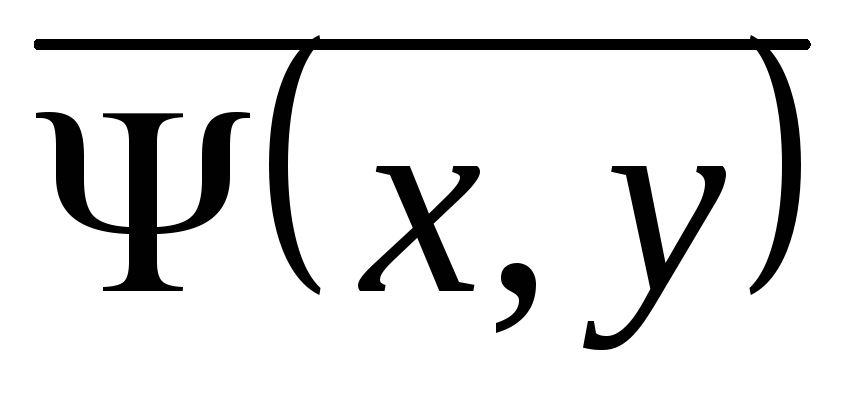 аналитические, то
аналитические, то 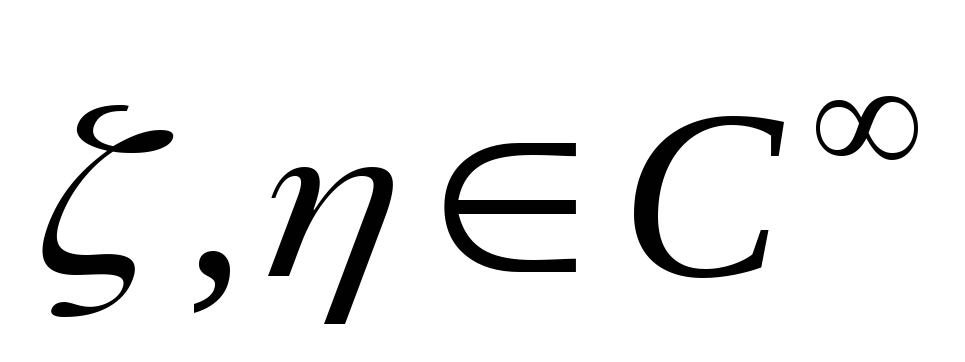 и их якобиан
и их якобиан
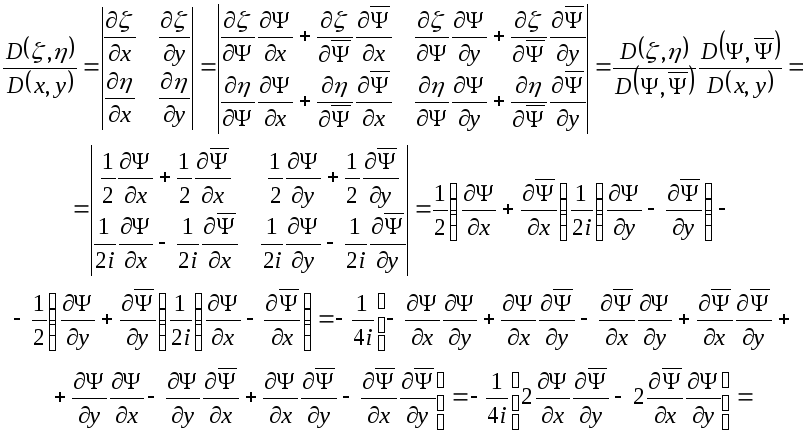
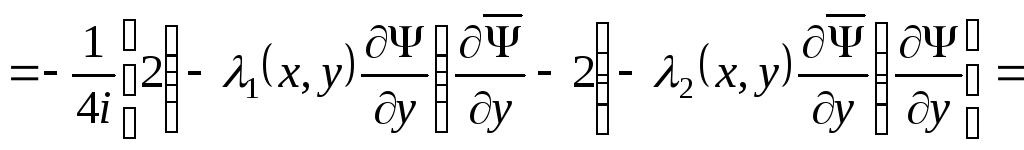
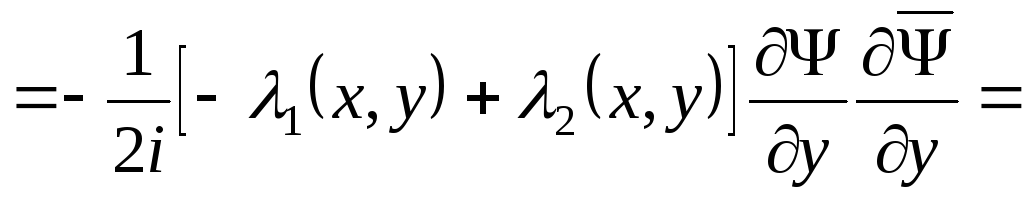
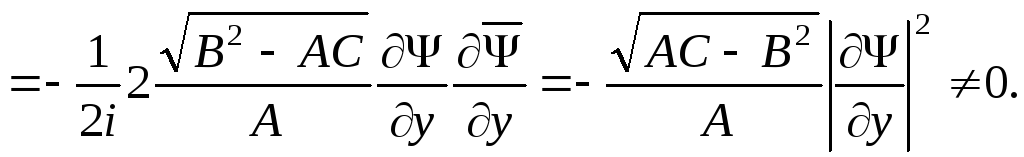
Поэтому функции 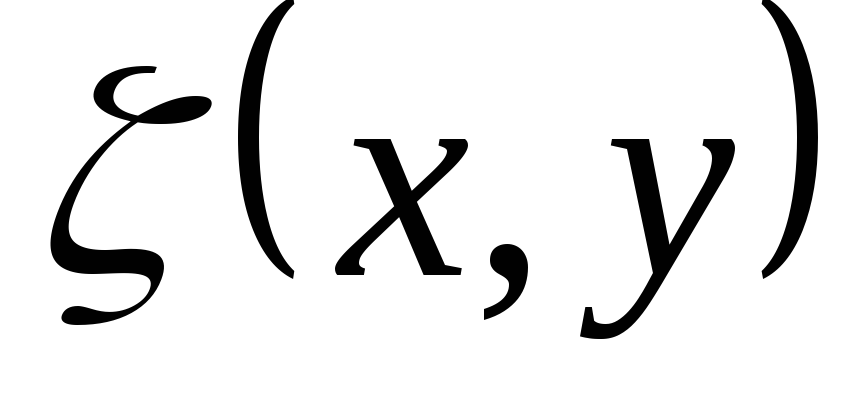 и
и 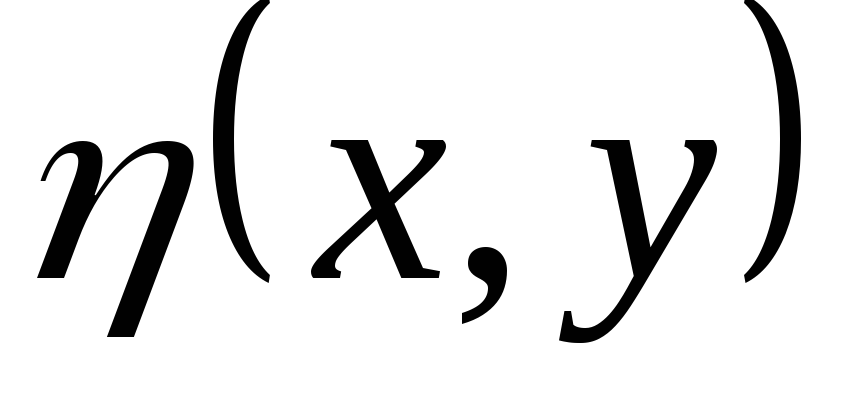 можно взять за новые переменные. По
построению функция
можно взять за новые переменные. По
построению функция  удовлетворяет уравнению
удовлетворяет уравнению
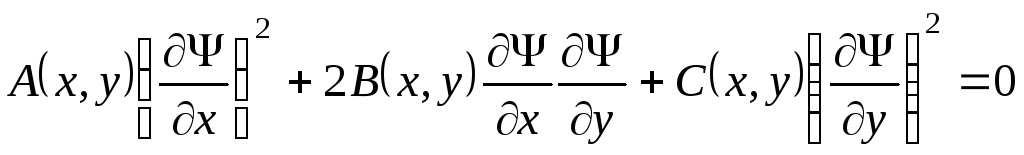 .
.
Выделим действительную и мнимую части и переходя к новым переменным пользуясь формулами (3.12), получим
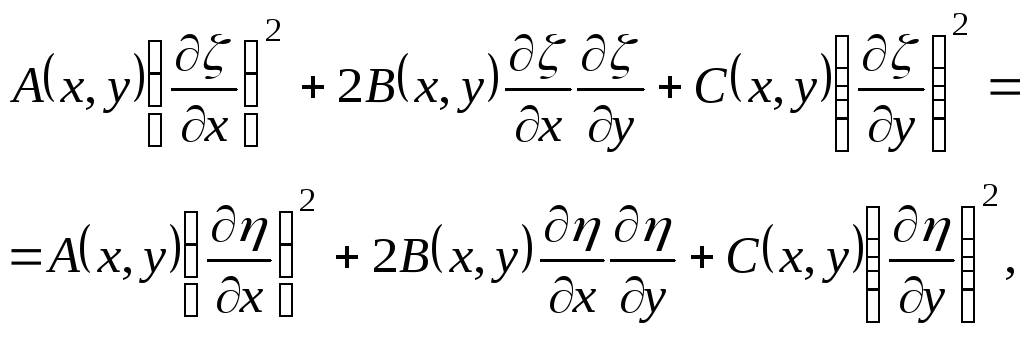 ,
,
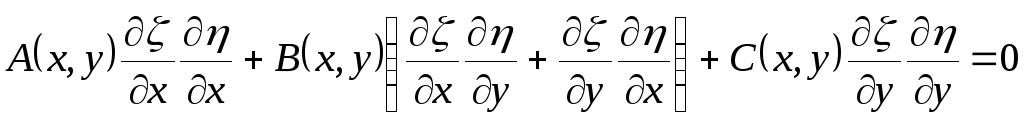 .
.
Учитывая формулы
для коэффициентов 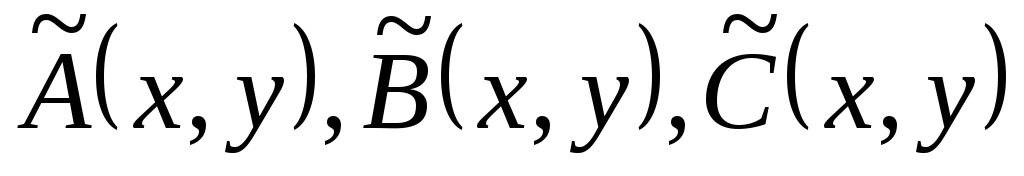 получаем, что
получаем, что 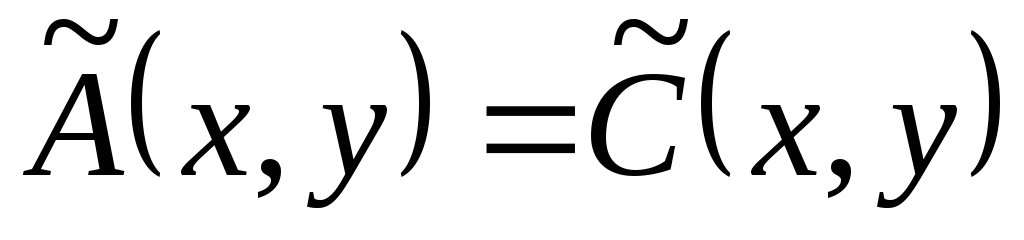 и
и 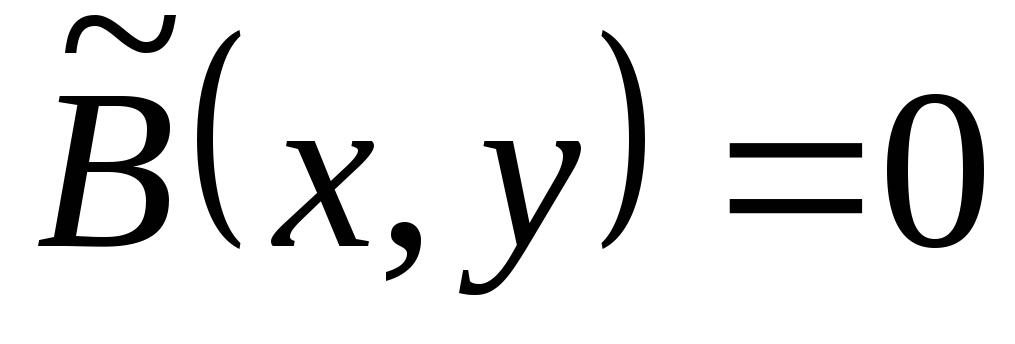 в переменных
в переменных  и
и 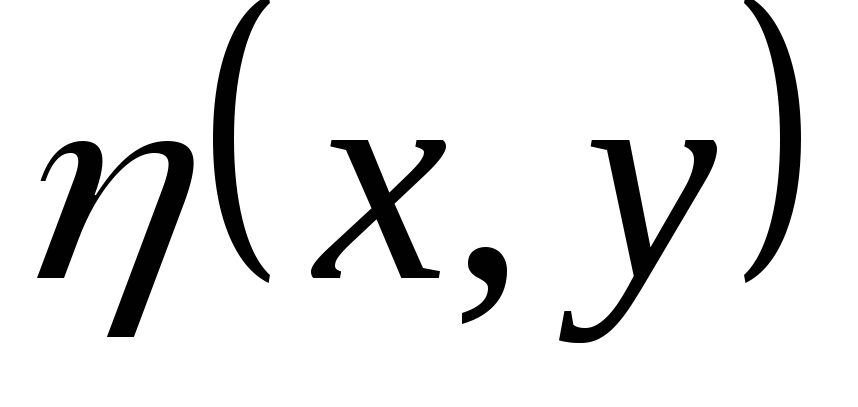 .
Далее, поскольку
.
Далее, поскольку 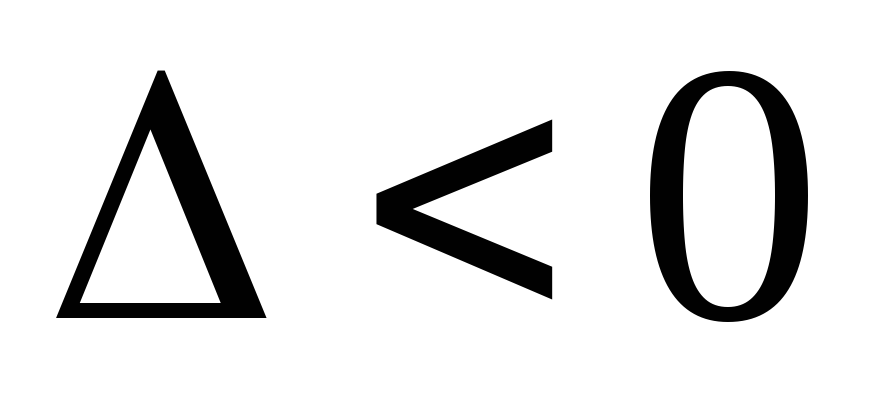 и
и 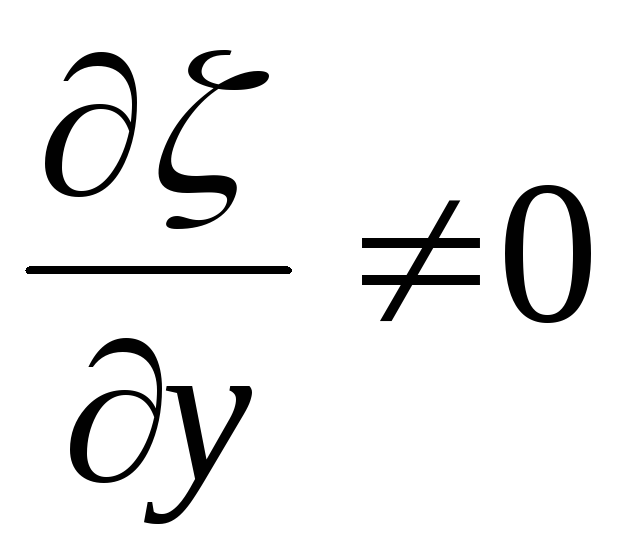 ,
то
,
то 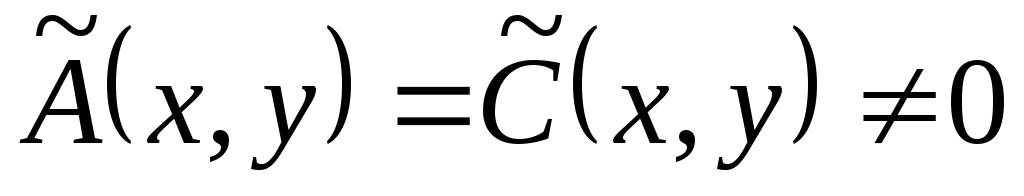 .
Разделив уравнение (*) на
.
Разделив уравнение (*) на 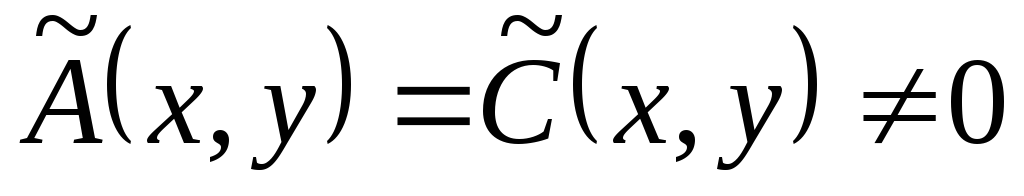 ,
приведем его к каноническому виду
,
приведем его к каноническому виду
 .
.
Постановка основных задач для линейных дифференциальных уравнений второго порядка.
Чтобы полностью
описать тот или иной физический процесс,
необходимо кроме самого уравнения,
описывающего этот процесс, задать
начальное состояние этого процесса
(начальные условия) и режим на границе
той области  ,
в которой происходит этот процесс
(граничные условия). Это связано с
неединственностью решения дифференциальных
уравнений. Так, например, для уравнений
в частных производных решение зависит
от произвольных функций. Поэтому, чтобы
выделить решение, описывающее реальный
физический процесс, необходимо задать
дополнительные условия. Такими
дополнительными условиями и являются
краевые условия (начальные и граничные).
Соответствующая задача называется краевой задачей.
,
в которой происходит этот процесс
(граничные условия). Это связано с
неединственностью решения дифференциальных
уравнений. Так, например, для уравнений
в частных производных решение зависит
от произвольных функций. Поэтому, чтобы
выделить решение, описывающее реальный
физический процесс, необходимо задать
дополнительные условия. Такими
дополнительными условиями и являются
краевые условия (начальные и граничные).
Соответствующая задача называется краевой задачей.
Выделяют три основных типа краевых задач для дифференциальных уравнений:
задача Коши для уравнений гиперболического и параболического типов. Задаются начальные условия, область
 совпадает со всем пространством
совпадает со всем пространством  (п – число независимых переменных),
граничные условия отсутствуют;
(п – число независимых переменных),
граничные условия отсутствуют;краевая задача для уравнений эллиптического типа. Задаются граничные условия на границе области
 ,
начальные условия отсутствуют;
,
начальные условия отсутствуют;смешанная задача для уравнений гиперболического и параболического типов. Задаются и начальные и граничные условия,


 .
.
22
Классификация дифференциальных уравнений
⇐ ПредыдущаяСтр 3 из 6Следующая ⇒
Для вычислителя важно уметь классифицировать дифференциальные уравнения, так как от этого зависит выбор численного метода решения. Дифференциальные уравнения можно классифицировать по нескольким признакам. Рассмотрим наиболее важные из них.
— Обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных.
Если неизвестная функция в дифференциальном уравнении зависит только от одной переменной, то такое дифференциальное уравнение называется обыкновенным дифференциальным уравнением.
Если неизвестная функция в дифференциальном уравнении зависит от нескольких переменной, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Примеры.
Стационарное одномерное течение жидкости в трубе описывается обыкновенным дифференциальным уравнением:
 , (1.1)
, (1.1)
т.к. неизвестная функция u(x) зависит только от одной переменной х.
Стационарное двумерное течение жидкости в трубе описывается дифференциальным уравнением в частных производных:
 . (1.2)
. (1.2)
Здесь неизвестная функция u(x,у) зависит от двух переменных: х,у.
— Порядок
Порядок уравнения равен порядку наивысшей производной, входящей в дифференциальное уравнение.
Например, уравнение (1) – I порядка, уравнение (2) – II порядка. Уравнение II порядка в самом общем случае можно представить в виде:
 (1.3)
(1.3)
Уравнения II порядка классифицируются следующим образом:
а) если В2-4АС=0, то уравнение (1.3) является уравнение параболическим;
б) если В2-4АС<0, то уравнение (1.3) является уравнение эллиптическим;
с) если В2-4АС>0, то уравнение (1.3) является уравнение гиперболическим.
Уравнение II порядка (1.2) является параболическим уравнением (проверьте это, приведя его к виду (1.3) и найдя, чему равно выражение В2-4АС).
Примером эллиптического уравнения является уравнение Пуассона, описывающее стационарное распределение температуры от теплового источника q(x,y) (при q(x,y)>0 в точке (x,y) тепло выделяется, а при q(x,y)<0 — поглощается):
 (1.4)
(1.4)
В качестве примера гиперболического уравнения приведем уравнение колебаний:
 (1.5)
(1.5)
Отметим, что тип уравнения определяется только коэффициентами при вторых производных и никак не зависит ни от коэффициентов при первых производных и при самой функции, ни от свободного члена.
Рассмотрим еще одно уравнение с переменными и коэффициентами:
 (1.6)
(1.6)
Здесь А=x, В=0, C=1, следовательно, В2-4АС=-4х. Этот пример иллюстрирует тот факт, что тип уравнения с переменными и коэффициентами может изменяться от точки к точке: при х<0 уравнение (1.6) является эллиптическим, при х=0 уравнение (1.6) является параболическим, при х>0 уравнение (1.6) гиперболическое.
— Линейность
Линейным называется такое дифференциальное уравнение, в которое зависимая переменная и все ее производные входят линейным образом, в частности, они не умножаются друг на друга, не возводятся в степень, не являются аргументами трансцендентных функций и т.п.
Например, уравнения (1.4)-(1.6) являются линейными, а уравнения (1.1)-(1.2) — нелинейными (объясните, почему). Уравнение (1.3) является линейным, если коэффициенты A, B, C, D, E, F не зависят от неизвестной функции f и ее производных.
Большинство уравнений, описывающих теплофизические явления и процессы, являются нелинейными.
— Однородность
Дифференциальное уравнение называется однородным, если оно не имеет членов, содержащих неизвестную.
Дифференциальное уравнение вида (1.3) является однородным, если его правая часть равна нулю для всех x и y. В противном случае оно является неоднородным.
Например, уравнение (1.5) – однородное, а уравнения (1.1), (1.2), (1.4), (1.6) — неоднородные. Уравнение (1.3) является однородным, если G=0 , и неоднородным, если G¹0.
Аналитически можно решить, как правило, только обыкновенные линейные дифференциальные уравнения (да и то далеко не все) и только некоторые специальные виды дифференциальных уравнений в частных производных. Для всех остальных уравнений, а особенно для уравнений и систем уравнений, описывающих реальные задачи, имеющие практическое приложение, численные методы являются практически единственными методами решения.
Рекомендуемые страницы:
8. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОБЩЕГО ВИДА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Разделяя переменные и интегрируя, получим |
|
∫( y − z)d ( y − z) = −∫dx ( y − z)2 = −2x +C2 . | (8.6) |
Совокупность соотношений (8.5) и (8.6) в общей теории СДУ называется общим интегралом системы.
Ответ: y2 − z2 = C1,
( y − z)2 = −2x +C2. ■
8.3. Задача Коши для нормальной системы
Задача Коши для нормальной системы (8.3), ставится так:
найти решение y1 = y1 (x), y2 = y2 (x),…, yn = yn (x),
удовлетворяющее начальным условиям (условиям Коши)
y | = y0 | , y | 2 | = y0 | ,…, y | n | = y0 | , | (8.7) |
1 | 1 |
| 2 |
| n |
|
|
где x0 , y10 , y20 ,…, yn0 — заданные числа.
Геометрически находится интегральная кривая, проходящая через заданную точку (x0 , y10 , y20 ,…, yn0 ).
8.4. Теорема существования и единственности решения задачи Коши для нормальной системы
Теореме Пикара. Если правые части системы (8.3) непрерывны в некоторой окрестности начальной точки (x0 , y10 , y20 ,…, yn0 ) и имеют непрерывные в этой окрестности частные производные по y1 , y2 , y3 ,…, yn , то система (8.3) имеет единственное решение (8.2),
определенное в некоторой окрестности точки x0 и удовлетворяющее начальным условиям (8.7).
Условия теоремы Пикара, в частности, заведомо выполнены, если правые части нормальной системы есть многочлены относительно
y1 , y2 , y3 ,…, yn , коэффициенты которых непрерывны в окрестности начального значения x0 . При этом начальные значения y10 , y02 , y 03 ,…, y0n можно брать произвольно.
 при
любом
при
любом 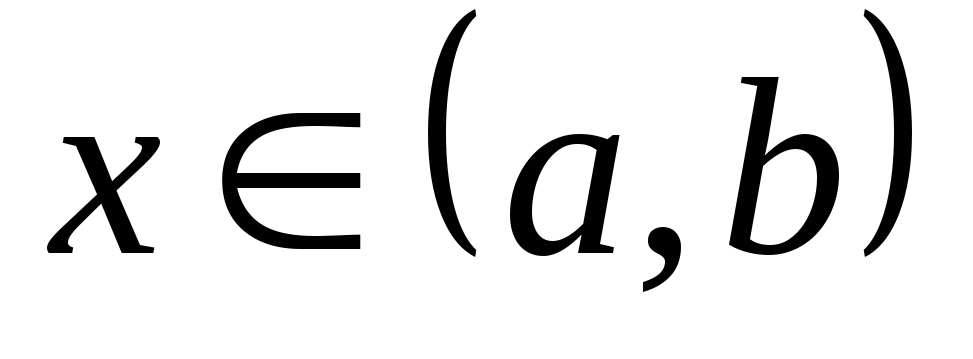 ;
;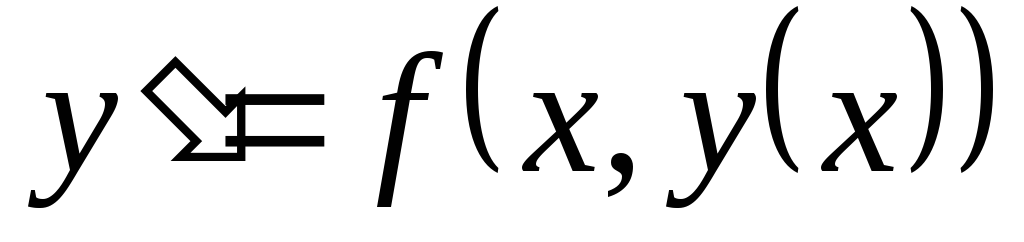 при любом
при любом 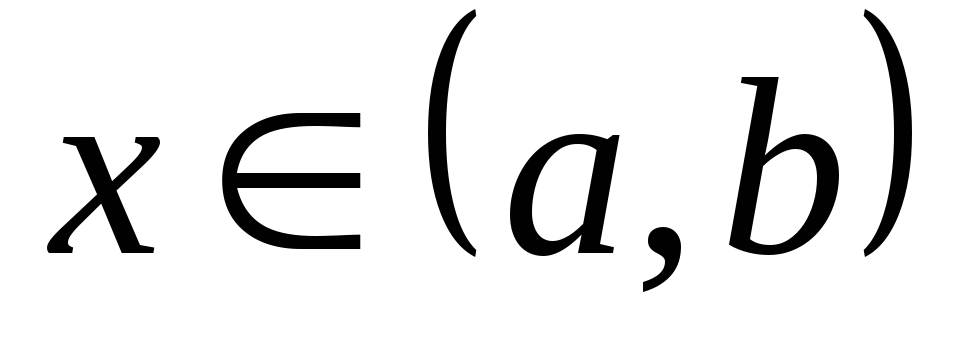 .
.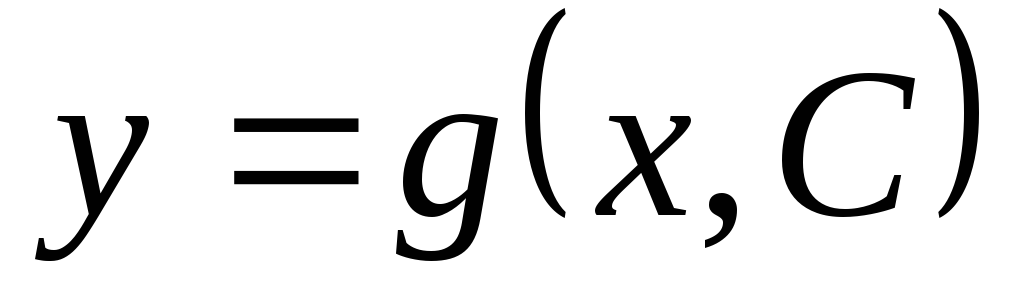 является решением уравнения
является решением уравнения 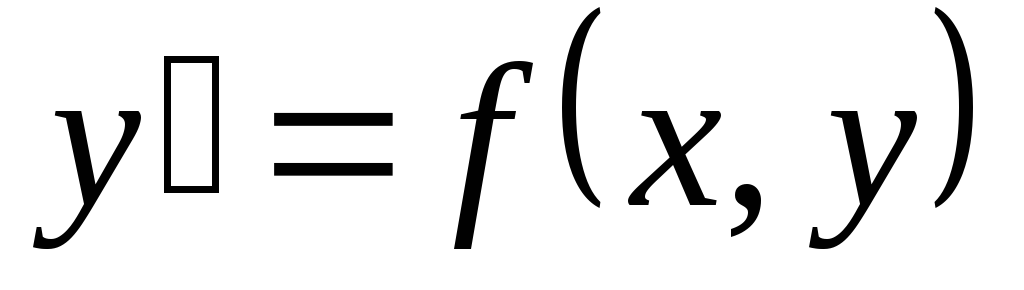 при любом допустимом значении постоянной
С;
при любом допустимом значении постоянной
С;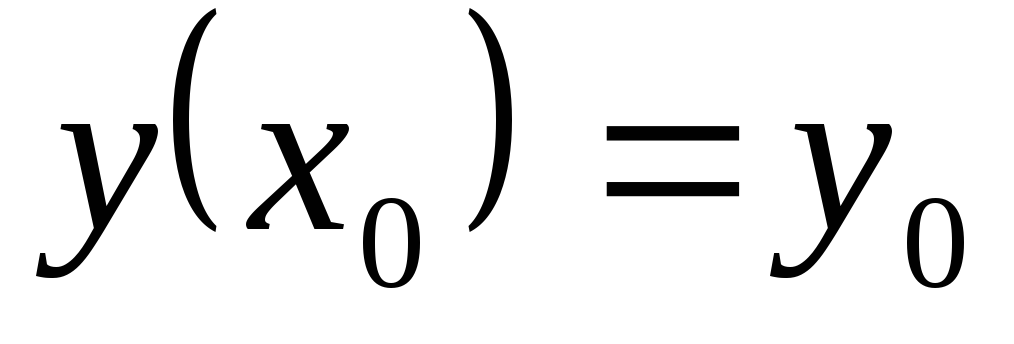 ,
удовлетворяющем условию
,
удовлетворяющем условию 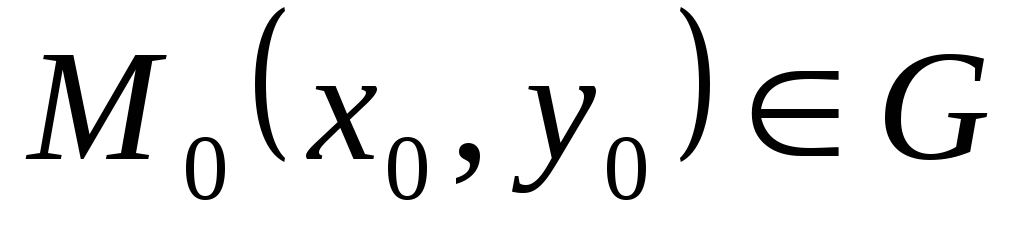 ,
существует единственное значение
параметра
,
существует единственное значение
параметра  такое, что функция
такое, что функция 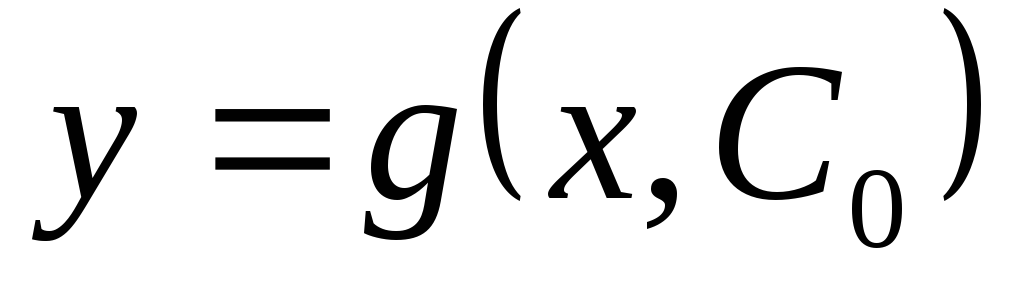 удовлетворяет условию
удовлетворяет условию 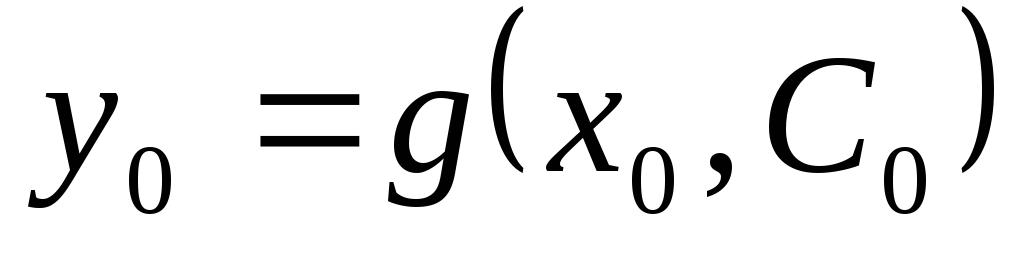 .
.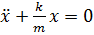 .
.
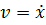
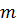
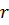
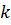
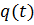
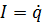
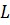
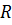

 для (1.1).
для (1.1).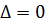 ).
). ,
если
,
если 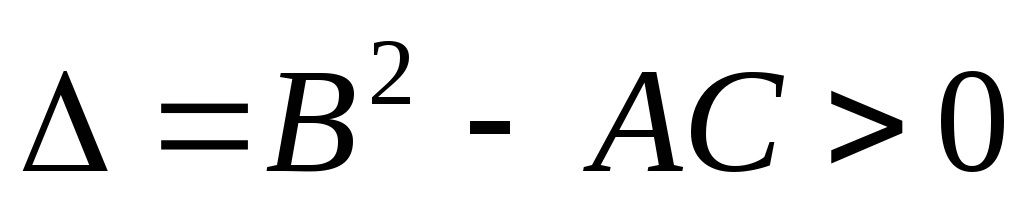 в
в  ;
; , если
, если 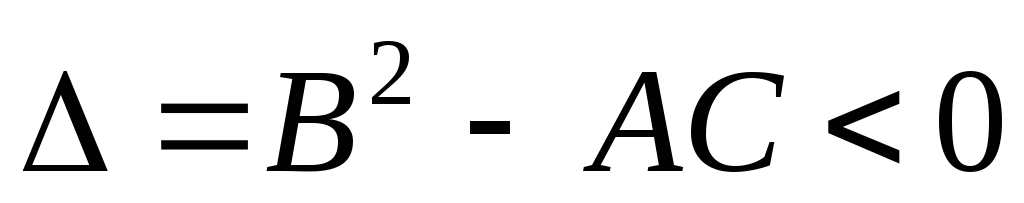 в
в  ;
; , если
, если 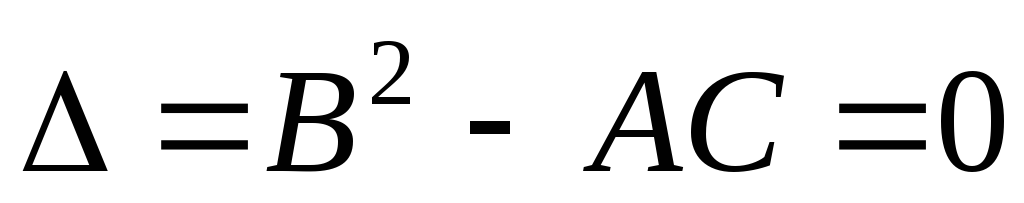 в
в  .
.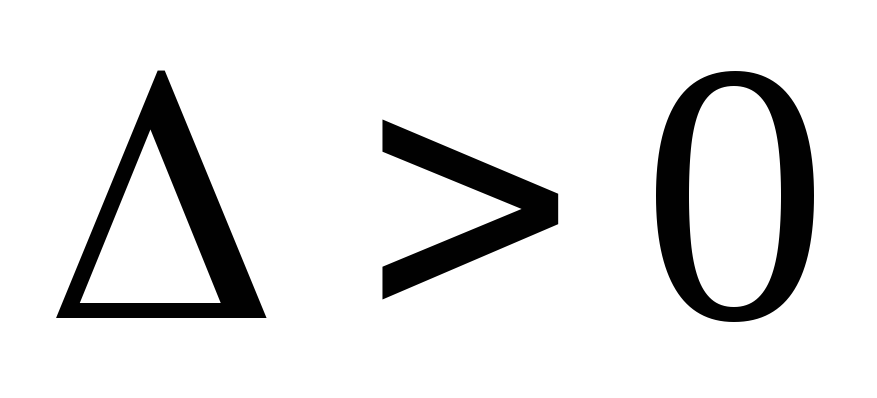 .
.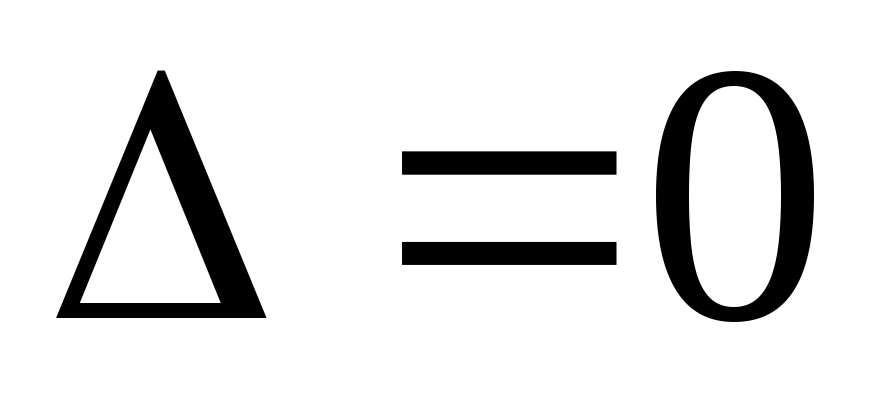 .
.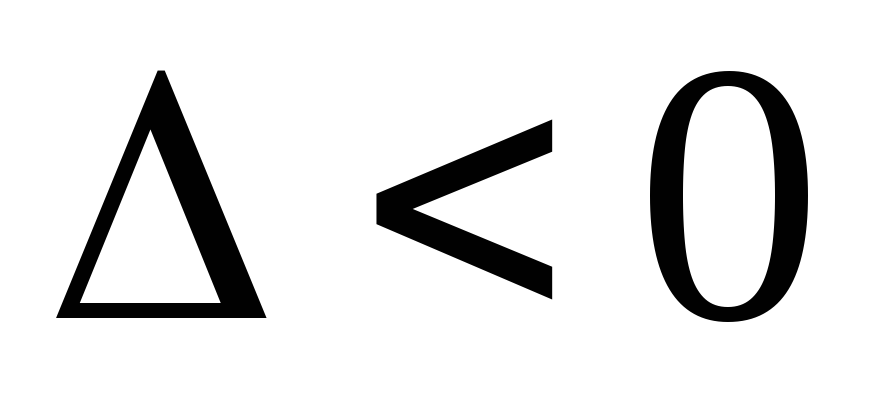 .
. совпадает со всем пространством
совпадает со всем пространством 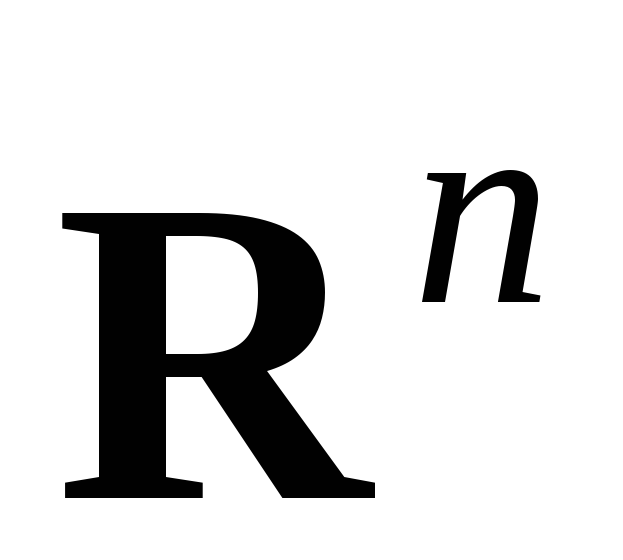 (п – число независимых переменных),
граничные условия отсутствуют;
(п – число независимых переменных),
граничные условия отсутствуют; ,
начальные условия отсутствуют;
,
начальные условия отсутствуют;
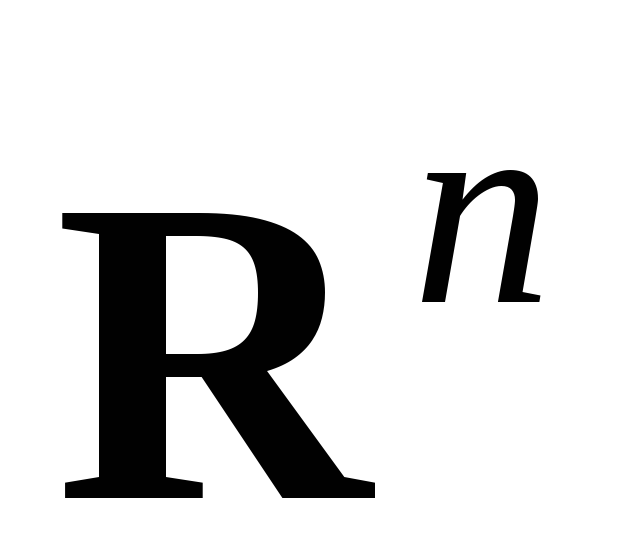 .
.