Химическое уравнение — Википедия

Химическим уравнением (уравнением химической реакции) называют условную запись химической реакции с помощью химических формул, числовых коэффициентов и математических символов.

Уравнение химической реакции даёт качественную и количественную информацию о химической реакции, реагентах и продуктах реакции; его составление основывается на законах стехиометрии, в первую очередь, законе сохранения массы веществ в химических реакциях. Кроме уравнений используются полные и краткие схемы химических реакций — условные записи, дающие представление о природе реагентов и продуктов, то есть качественную информацию о химической реакции.

Титульный лист Tyrocinium Chymicum

В начале не было представления о химических уравнениях, ещё не были известны основные химические законы, но уже в алхимический период развития химии начали обозначать химические элементы символами.

С дальнейшим развитием химии менялись представления о символике химических элементов, ской записи, используя химические формулы. Первым предложил использовать химические уравнения Жан Бегун (Jean Beguin) в 1615 году в одном из первых учебников по химии Tyrocinium Chymicum («Начала химии»)^[1].

Конец XVIII—начало XIX вв. — становление законов стехиометрии. У истоков этих исследований стоял немецкий ученый И. В. Рихтер. В студенческие годы на него большое впечатление произвели слова его учителя — философа И. Канта о том, что в отдельных направлениях естественных наук истинной науки столько, сколько в ней математики. Рихтер посвятил свою диссертацию использованию математики в химии. Не будучи в сущности химиком, Рихтер ввел первые количественные уравнения химических реакций, стал использовать термин

стехиометрия.

Для составления уравнений химических реакций, кроме знания формул реагентов и продуктов реакции, необходимо верно подобрать коэффициенты. Это можно сделать, используя несложные правила^[2]. В левой части уравнения записывают формулы (формулу) веществ, вступивших в реакцию, соединяя их знаком «плюс». В правой части уравнения записывают формулы(формулу) образовавшихся веществ, также соединенных знаком «плюс». Между частями уравнения ставят знак равенства или стрелку. Затем находят коэффициенты — числа, стоящие перед формулами веществ, чтобы число атомов одинаковых элементов в левой и правой частях уравнения было равным.

Для обозначения различных типов реакций используются следующие символы^[3]:

Закон сохранения массы гласит, что количество вещества каждого элемента до реакции равняется количеству вещества каждого элемента после реакции. Таким образом, левая и правая части химического уравнения должны иметь одинаковое количество атомов того или иного элемента. Химическое уравнение должно быть электронейтрально, то есть сумма зарядов в левой и правой части уравнения должна равняться нулю.

Как правило, химические уравнения записываются с наименьшими целочисленными коэффициентами. В случае, если перед химической формулой нет коэффициента, подразумевается что он равен единице. Проверка материального баланса, то есть количества атомов с левой и правой части, может быть следующей: перед самой сложной химической формулой ставится коэффициент 1. Далее расставляются коэффициенты перед формулами таким образом, что бы количество атомов каждого из элементов в левой и правой части уравнения было равно. Если один из коэффициентов — дробный, то следует умножить все коэффициенты на число стоящее в знаменателе дробного коэффициента. Если перед формулой коэффициент 1, то его опускают.

Одним из способов уравнивания количества атомов в химическом уравнении является подбор коэффициентов.

Расстановка коэффициентов в химической реакции горения метана:

1CH₄ + O₂→{\displaystyle \rightarrow } CO₂ + H₂O

Количество атомов углерода с левой и правой сторон одинаково. Следующий элемент, который следует уравнять — водород. Слева 4 атома водорода, справа 2, чтобы уравнять количество атомов водорода следует поставить коэффициент 2 перед водой, в результате:

1CH₄ + O₂→{\displaystyle \rightarrow } CO₂ + 2H₂O

Проверка правильности расстановки коэффициентов в любом химическом уравнении производится подсчетом количества атомов кислорода, если в левой и правой части количество атомов кислорода одинаково, значит коэффициенты расставлены правильно.

1CH₄ + 2O₂→{\displaystyle \rightarrow } CO₂ + 2H₂O

Перед молекулами CH₄ и CO

2 коэффициент 1 опускают.

CH₄ + 2O₂→{\displaystyle \rightarrow } CO₂ + 2H₂O

Для более сложных случаев применяются математический метод уравнивания реакций с помощью составления системы линейных алгебраических уравнений и метод Гарсиа (аналог математического метода Гаусса).

Окислительно-восстановительные реакции[править | править код]

Окислительно-восстановительные реакции — это встречно-параллельные химические реакции, протекающие с изменением степеней окисления атомов, входящих в состав реагирующих веществ, реализующихся путём перераспределения электронов между атомом-окислителем и атомом-восстановителем. Любая окислительно-восстановительная реакция представляет собой единство двух противоположных превращений — окисления и восстановления, происходящих одновременно и без отрыва одного от другого.

При составлении уравнения окислительно-восстановительной реакции необходимо определить восстановитель, окислитель и число отдаваемых и принимаемых электронов. Как правило, коэффициенты подбирают, используя либо метод электронного баланса, либо метод электронно-ионного баланса (иногда последний называют методом полуреакций).

Запись ионных уравнений[править | править код]

Ионные уравнения — это химические уравнения, в которых электролиты записаны в виде диссоциировавших ионов. Ионные уравнения используются для записи реакций замещения и реакций обмена в водных растворах. Пример, реакция обмена, взаимодействие хлорида кальция и нитрата серебра с образованием осадка хлорида серебра:

CaCl₂(ж) + 2AgNO₃(ж) →{\displaystyle \rightarrow } Ca(NO₃)₂(ж) + 2AgCl(тв)

полное ионное уравнение:

Ca²⁺ + 2Cl⁻ + 2Ag⁺ + 2NO₃⁻→{\displaystyle \rightarrow } Ca²⁺ + 2NO₃⁻ + 2AgCl(тв)

• Левицкий М. Язык химиков // Химия и жизнь. — 2000. -№ 1. — С.50-52.
• Кудрявцев А. А. Составление химических уравнений — 4-е издание, перераб. и доп., 1968—359 с.
• Берг Л. Г. Громаков С. Д. Зороацкая И. В. Аверко-Антонович И. Н. Способы подбора коэффициентов в химических уравнениях — Казань: изд-во Казанского ун-та, 1959.- 148 с.
• Леенсон И. А. Чет или нечет — М.: Химия, 1987. — 176 с.

ru.wikipedia.org

Активность (химия) — Википедия

У этого термина существуют и другие значения, см. Активность.

Акти́вность компонентов раствора — эффективная (кажущаяся) концентрация компонентов с учётом различных взаимодействий между ними в растворе, то есть с учётом отклонения поведения системы от модели идеального раствора.

Активность была предложена в 1907 году Льюисом как новая переменная, применение которой вместо концентрации позволяет использовать для описания свойств реальных растворов относительно простые уравнения, полученные для идеальных систем. Альтернативой этому пути является использование более сложных уравнений, учитывающих взаимодействие между частицами (см., например, уравнение Ван-дер-Ваальса).

Активность отличается от общей концентрации на некоторую величину. Отношение активности (a{\displaystyle a}) к общей концентрации вещества в растворе называется коэффициентом активности:

γ=ac{\displaystyle \gamma ={a \over c}}

Коэффициент активности служит мерой отклонения поведения раствора (или компонента раствора) от идеального. Отклонения от идеальности могут быть обусловлены различными химическими и физическими причинами — дипольные взаимодействия, поляризация, образование водородных связей, ассоциация, диссоциация, сольватация и др.^[1]

Исходя из понятия химического потенциала, активность компонента в растворе можно определить как величину, которую нужно подставить в выражения для химического потенциала компонента в идеальном растворе:

dμi=RTd(ln⁡xi){\displaystyle {\text{d}}\mu _{i}=RT\,{\text{d}}\!\left(\ln {x_{i}}\right)}

μi=μi∗+RTln⁡xi{\displaystyle \mu _{i}=\mu _{i}^{*}+RT\ln {x_{i}}}

(где μi∗{\displaystyle \mu _{i}^{*}} — химический потенциал чистого i{\displaystyle i}-го компонента) вместо мольной доли x, для того, чтобы получить действительное значение химического потенциала i{\displaystyle i}-го компонента в реальном растворе:

dμi=RTd(ln⁡ai){\displaystyle {\text{d}}\mu _{i}=RT\,{\text{d}}\!\left(\ln {a_{i}}\right)}

μi=μi0+RTln⁡ai{\displaystyle \mu _{i}=\mu _{i}^{0}+RT\ln {a_{i}}}

где μi0{\displaystyle \mu _{i}^{0}} — стандартный химический потенциал^[2].

Размерность и величина активности зависит от используемого способа выражения концентрации — если ax{\displaystyle a_{x}} (активность при выражении концентрации как мольной доли) величина безразмерная, то ac{\displaystyle a_{c}} и am{\displaystyle a_{m}} (для молярности и моляльности соответственно) — размерные величины, выражаются в моль/л и моль/кг.

В теории дистилляции активность компонента жидкости представляется как давление p{\displaystyle p} пара компонента смеси в сравнении с давлением p0{\displaystyle p^{0}} пара чистого компонента: a=p/p0{\displaystyle a=p/p^{0}}. При этом p=ap0=γ{\displaystyle p=ap^{0}=\gamma }Np0{\displaystyle Np^{0}} , где N – молярная доля компонента в жидкости, γ –коэффициент активности. Концентрационная зависимость активности, построенная при заданной температуре в координатах а-N, носит название диаграммы активности. Известны экспериментально построенные диаграммы активности для ряда двойных систем^[3][4][5].

Коэффициент активности в общем случае может быть как больше, так и меньше единицы (при этом говорят о положительных или отрицательных отклонениях от идеального поведения соответственно, или о положительных и отрицательных отклонениях от закона Рауля). Возможны и знакопеременные отклонения от идеального поведения в одной диаграмме (с изменением в пределах от 0,01 и менее до 10 и более, что отражает сложных характер взаимодействия компонентов в системе). Например, для железа в системе Fe-S при 1300 °C коэффициенты активности изменяется от 0,004 при xFe{\displaystyle x_{Fe}}=0,48 до 1,47 при xFe{\displaystyle x_{Fe}}=0,68^[6]. В некоторых системах концентрационная зависимость активности является причиной существования стабильного состава, по достижении которого состав испаряющейся жидкости не меняется^[7].

Важно отметить, что величина активности и коэффициента активности может быть различной в зависимости от выбора стандартного состояния.

При использовании активности и коэффициента активности важную роль играет выбор стандартного состояния компонента, то есть состояния, в котором μi=μist{\displaystyle \mu _{i}=\mu _{i}^{\mathrm {st} }}

Для растворов взаимно неограниченно растворимых жидкостей в качестве стандартного может быть выбрано состояние чистого компонента (как для растворителя, так и для растворенного вещества):

при xi→1{\displaystyle x_{i}\rightarrow 1} ai→1{\displaystyle a_{i}\rightarrow 1} и γi→1{\displaystyle \gamma _{i}\rightarrow 1}

Иногда такой выбор называют симметричной системой стандартного состояния.

В случае, если рассматривается раствор газа и или твердого вещества в жидкости, мольную долю растворенного вещества нельзя изменять до единицы. Тогда для растворителя — жидкости — стандартное состояние может быть выбрано так же, как показано выше, а для растворенного вещества за стандартное состояние принимают гипотетический раствор с концентрацией, равной единице, но сохраняющий свойства предельно разбавленного раствора. Иначе говоря, это такое состояние, для которого давление пара численно равно константе Генри:

pst=kH{\displaystyle p^{\mathrm {st} }=k_{\mathrm {H} }}

Таким образом, для растворителя и растворенного вещества здесь принимаются разные стандартные состояния — это несимметричная система стандартных состояний.

В системах с ограниченной растворимостью за стандартное может быть принято состояние компонента в насыщенном растворе:

pist=pisat{\displaystyle p_{i}^{\mathrm {st} }=p_{i}^{\mathrm {sat} }}

ai=pipisat{\displaystyle a_{i}={\frac {p_{i}}{p_{i}^{\mathrm {sat} }}}}

γi=aixi{\displaystyle \gamma _{i}={\frac {a_{i}}{x_{i}}}}

В зависимости от исследуемой системы, в качестве стандартного может быть выбрано и другое состояние, например, для серы при исследовании богатых сульфидных расплавов — состояние серы в стехиометрическом сульфиде^[6]. При рассмотрении результатов эксперимента, использовании справочных данных и т. п. следует обязательно указывать, какое именно состояние компонента принято за стандартное.

Экспериментальные методы определения активности компонентов в растворе основаны на изучении какого-либо гетерогенного равновесия в системе. При рассмотрении этих методов следует помнить, что в условиях равновесия химические потенциалы i-го компонента в разных фазах (I и II) равны:

μiI=μiII{\displaystyle \mu _{i}^{\mbox{I}}=\mu _{i}^{\mbox{II}}}

Это соотношение является исходной точкой для вывода расчетных уравнений в некоторых из методов определения активности. Кроме того, активности компонентов в некоторой фазе связаны между собой уравнением:

∑ixid(ln⁡ai)=0{\displaystyle \sum _{i}x_{i}{\text{d}}\!\left(\ln a_{i}\right)=0}

По равновесному давлению пара[править | править код]

В основе этого метода лежит соотношение:

ai=pipist{\displaystyle a_{i}={\frac {p_{i}}{p_{i}^{\mathrm {st} }}}}

где pi{\displaystyle p_{i}} — парциальное давление пара компонента над раствором, а pist{\displaystyle p_{i}^{\mathrm {st} }} — давление пара этого компонента для стандартного состояния (см. выше). Соответственно, если за стандартное состояние принято состояние чистого компонента, то pist=pi0{\displaystyle p_{i}^{st}=p_{i}^{0}}.

Экспериментальные методы определения давления пара компонентов над раствором весьма разнообразны; выбор того или иного из них определяется, в частности, исследуемой системой (водный раствор или иная низкотемпературная система, либо расплавленный металл, шлак, штейн и т. п.).

По повышению температуры кипения раствора[править | править код]

Температура кипения раствора Tb{\displaystyle T_{\mathrm {b} }} выше температуры кипения чистого растворителя Tb0{\displaystyle T_{\mathrm {b} }^{0}}. Данные об изменении температуры кипения раствора могут быть использованы для расчета активности растворителя, в соответствии с уравнением:

ln⁡a1=−ΔHevapRTb0T1ΔTb{\displaystyle \ln a_{1}=-{\frac {\Delta H_{\mathrm {evap} }}{RT_{\mathrm {b} }^{0}T_{1}}}\Delta T_{\mathrm {b} }},

где ΔHevap{\displaystyle \Delta H_{\mathrm {evap} }} — теплота испарения растворителя, в интервале от температуры кипения чистого растворителя до температуры кипения раствора принимаемая постоянной. Индексом «1» обычно обозначается растворитель.

По понижению температуры замерзания раствора[править | править код]

Температура замерзания раствора Tmelt{\displaystyle T_{\mathrm {melt} }} ниже температуры замерзания чистого растворителя Tmelt0{\displaystyle T_{\mathrm {melt} }^{0}}. Соответственно, активность растворителя можно рассчитать, используя зависимость:

ln⁡a1=−ΔHmeltRTmelt0TmeltΔTmelt{\displaystyle \ln a_{1}=-{\frac {\Delta H_{\mathrm {melt} }}{RT_{\mathrm {melt} }^{0}T_{\mathrm {melt} }}}\Delta T_{\mathrm {melt} }},

где ΔHmelt{\displaystyle \Delta H_{\mathrm {melt} }} — теплота плавления растворителя.

По осмотическому давлению раствора[править | править код]

Величина осмотического давления раствора может быть использована для определения активности растворителя в соответствии с соотношением:

ln⁡a1=−πV1¯RT{\displaystyle \ln a_{1}=-{\frac {\pi {\overline {V_{1}}}}{RT}}}

где π{\displaystyle \pi } — осмотическое давление, V1¯{\displaystyle {\overline {V_{1}}}} — парциальный молярный объём растворителя.

По распределению компонента между конденсированными фазами[править | править код]

Активность компонента раствора можно определить, изучая равновесное распределение его между двумя контактирующими конденсированными фазами (различными растворителями, сплавом и шлаком, шлаком и штейном и т. п.), одна из которых — исследуемый раствор, а для другой активность или коэффициент активности уже известны. В общем случае:

aiIaiIst=aiIIaiIIst{\displaystyle {\frac {a_{i}^{\mathrm {I} }}{a_{i}^{\mathrm {I_{st}} }}}={\frac {a_{i}^{\mathrm {II} }}{a_{i}^{\mathrm {II_{st}} }}}}

В частности, если выбор стандартного состояния компонента для фаз таков, что μi0I=μi0II{\displaystyle \mu _{i}^{0_{\mathrm {I} }}=\mu _{i}^{0_{\mathrm {II} }}}, это выражение принимает более простой вид:

aiI=aiII{\displaystyle a_{i}^{\mathrm {I} }=a_{i}^{\mathrm {II} }}

Экспериментально в этом методе определяют равновесные концентрации компонента или коэффициент распределения компонента между растворами.

По равновесию химической реакции с газовой фазой[править | править код]

При исследовании оксидных расплавов активность компонентов часто определяют, используя следующие химические реакции:

MeO+h3=Me+h3O{\displaystyle {\rm {MeO+H_{2}=Me+H_{2}O}}}

MeO+CO=Me+CO2{\displaystyle {\rm {MeO+CO=Me+CO_{2}}}}

Для первой из приведенных реакций константа равновесия имеет вид:

KMeO=ph3O⋅aMeph3⋅aMeO{\displaystyle K_{\mathrm {MeO} }={\frac {p_{\mathrm {H_{2}O} }\cdot a_{\mathrm {Me} }}{p_{\mathrm {H_{2}} }\cdot a_{\mathrm {MeO} }}}}

Если оксидный и металлический расплавы взаимно нерастворимы и восстанавливается индивидуальный оксид, то aMe=1{\displaystyle a_{\mathrm {Me} }=1}, и тогда:

aMeO=1KMeO⋅ph3Oph3{\displaystyle a_{\mathrm {MeO} }={\frac {1}{K_{\mathrm {MeO} }}}\cdot {\frac {p_{\mathrm {H_{2}O} }}{p_{\mathrm {H_{2}} }}}}

Если металл выделяется в виде сплава с другими компонентами или растворяется в фазе-коллекторе, его активность не равна единице и формула принимает вид:

aMeO=1KMeO⋅ph3Oph3⋅aMe{\displaystyle a_{\mathrm {MeO} }={\frac {1}{K_{\mathrm {MeO} }}}\cdot {\frac {p_{\mathrm {H_{2}O} }}{p_{\mathrm {H_{2}} }}}\cdot a_{\mathrm {Me} }}

Активность металла в сплаве здесь должна быть известна из независимых измерений.

Опытным путём в данном методе определяют отношение Ph3OPh3{\displaystyle {\frac {P_{\mathrm {H_{2}O} }}{P_{\mathrm {H_{2}} }}}}.

Кроме того, активность оксидного компонента связана с равновесным давлением кислорода над расплавом, с учётом реакций в газовой фазе, например:

h3+12O2=h3O{\displaystyle {\rm {H_{2}+{\tfrac {1}{2}}O_{2}=H_{2}O}}}

или

CO+12O2=CO2{\displaystyle {\rm {CO+{\tfrac {1}{2}}O_{2}=CO_{2}}}}

Тогда можно показать, что aMeO=PO212(PO2st)12{\displaystyle a_{\mathrm {MeO} }={\frac {P_{\mathrm {O_{2}} }^{\tfrac {1}{2}}}{(P_{\mathrm {O_{2}} }^{\mathrm {st} })^{\tfrac {1}{2}}}}}

Для сульфидных расплавов используют реакцию:

MeS+h3=Me+h3S{\displaystyle {\rm {MeS+H_{2}=Me+H_{2}S}}}

или (значительно реже):

MeS+O2=Me+SO2{\displaystyle {\rm {MeS+O_{2}=Me+SO_{2}}}}

По значению ЭДС гальванического элемента[править | править код]

Электродвижущая сила концентрационной цепи с переносом может быть выражена следующим соотношением:

E=RTnFln⁡a″Mea′Me{\displaystyle E={\frac {RT}{nF}}\ln {\frac {{a»}_{\mathrm {Me} }}{{a’}_{\mathrm {Me} }}}}

Соответственно, такую цепь можно использовать для нахождения активности и коэффициента активности. В некоторых случаях (например, для сложных сульфидных расплавов) побочное взаимодейтсвие электролита с электродами может приводить к невозможности определения активности компонентов по ЭДС цепи, тогда используют концентрационные цепи без переноса. Нахождение активности компонента по ЭДС концентрационной цепи без переноса — один из самых точных способов определения активности^[8] .

1. ↑ Краснов К. С., Воробьев Н. К., Годнев И. Н. и др. Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика: Учеб. для вузов. — 2-е изд., перераб. и доп. — М. : Высш. шк., 1995. — 512 с. — ISBN 5-06-002913-1
2. ↑ Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов/ Под ред. А. Г. Стромберга. — 2-е изд., перераб. и доп. — М.: Высш. шк., 1988. — 496 с.
3. ↑ Девятых Г.Г., Еллиев Ю.Е. Введение в теорию глубокой очистки веществ. — М.: Наука, 1981. — 320 с.
4. ↑ Пазухин В.А., Фишер А.Я. Разделение и рафинирование металлов в вакууме. — М.: Металлургия, 1969. — 204 с.
5. ↑ Иванов В.Е., Папиров И.И., Тихинский Г.Ф., Амоненко В.М. Чистые и сверхчистые металлы (получение методом дистилляции в вакууме). — М.: Металлургия, 1965. — 263 с.
6. ↑ ^{1 2} Вайсбурд С. Е. Физико-химические свойства и особенности строения сульфидных расплавов. — М. : Металлургия, 1996. — 304 с. — ISBN 5-229-00903-9
7. ↑ Кравченко А. И. О временной зависимости состава двойного сплава при его разгонке в вакууме // Известия АН СССР. Серия «Металлы», 1983. — № 3. — С. 61–63.
8. ↑ Лукомский Ю. Я., Гамбург Ю. Д. Физико-химические основы электрохимии. Учебник. — Долгопрудный : Издательский Дом «Интеллект», 2008. — 424 с. — ISBN 978-5-91559-007-5

• Ван-дер-Ваальс И.Д., Констамм Ф. Курс термостатики. Термические равновесия материальных систем. Часть I. Общая термостатика. — М.: ОНТИ — Главная редакция химической литературы, 1936. — 452 с.

ru.wikipedia.org

Коэффициент — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 мая 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 мая 2019; проверки требуют 2 правки.

Коэффицие́нт (от лат. co(cum) «совместно» + efficients «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.^{[B: 1][1]}

Если говорить об идеализации реальных физических систем в виде динамических моделей, зависимости между величинами, определяющими состояние системы, можно выразить в виде тех или иных дифференциальных уравнений, в которые входит некоторое число постоянных параметров, характеризующих систему, — то есть отражающих её свойства; постоянные параметры или их комбинации входят в такие уравнения в виде коэффициентов.^{[B: 2]}.^[2]

Коэффициентами также называют различные величины (как безразмерные, так и имеющие размерность), чаще числа, во многих отраслях точных наук — переводные множители, коэффициенты пропорциональности, константы, модули, стехиометрические коэффициенты.

Например, в выражении

a₁x₁ + a₂x₂ + a₃x₃ + …

a₁ — коэффициент при переменной x₁ и т. д.

В многочлене

P(x) = a_nxⁿ + a_{n − 1}x^{n − 1} + … + a₁x¹ + a₀.

a_i — коэффициент при i-ой степени переменной x.

ru.wikipedia.org

3.2. Активность и коэффициент активности

Несмотря на то, что термодинамика не учитывает процессы, происходящие в реальных растворах, например, притяжение и отталкивание ионов, термодинамические закономерности, выведенные для идеальных растворов, можно применить и для реальных растворов, если заменить концентрации активностями.

Активность (a) -такая концентрация вещества в растворе, при использовании которой свойства данного раствора могут быть описаны теми же уравнениями, что и свойства идеального раствора.

Активность может быть как меньше, так и больше номинальной концентрации вещества в растворе. Активность чистого растворителя, а также растворителя в не слишком концентрированных растворах принимается равной 1. За 1 принимается также активность твёрдого вещества, находящегося в осадке, или жидкости, не смешивающейся с данным раствором. В бесконечно разбавленном растворе активность растворённого вещества совпадает с его концентрацией.

Отношение активности вещества в данном растворе к его концентрации называетсякоэффициентом активности.

Коэффициент активности — это своеобразный поправочный коэффициент, показывающий, насколько реальность отличается от идеала.

3.3. Отклонения от идеальности в растворах сильных электролитов

Особенно заметное отклонение от идеальности имеет место в растворах сильных электролитов. Это отражается, например, на их температурах кипения, плавления, давлении пара над раствором и, что особенно важно для аналитической химии, на величинах констант различных равновесий, протекающих в таких растворах.

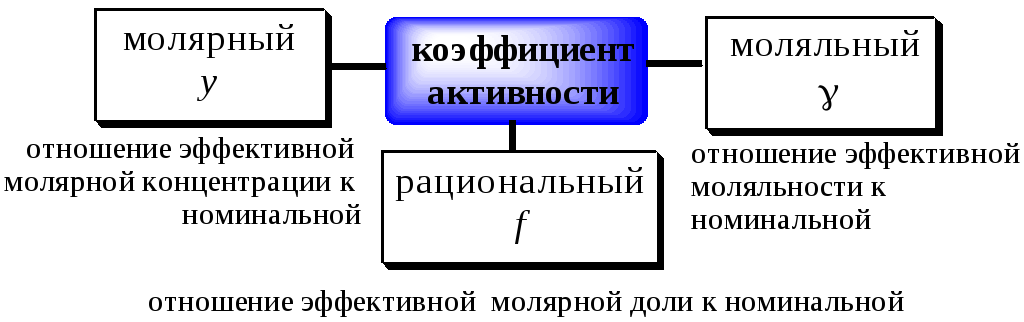
Для характеристики активности электролитов используют:

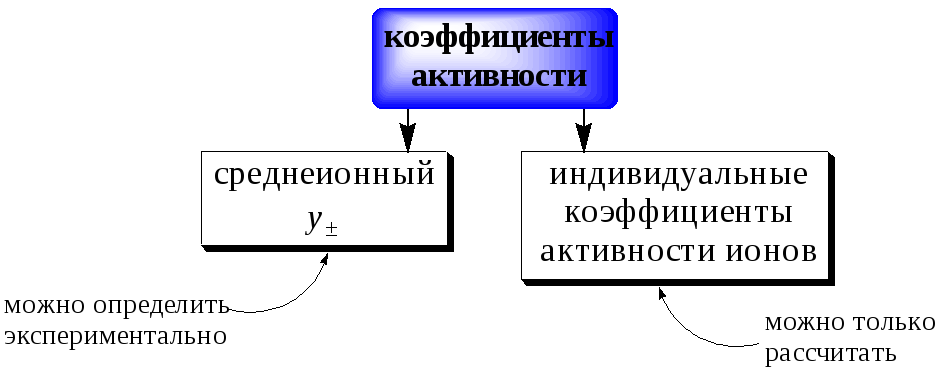
Для электролита A_mB_n:

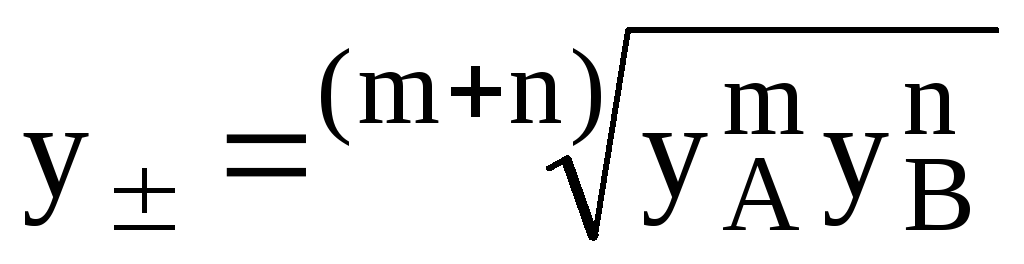
Величина, которая учитывает влияние концентрации (С) и заряда (z) всех ионов, присутствующих в растворе, на активность растворённого вещества, называетсяионной силой (I).

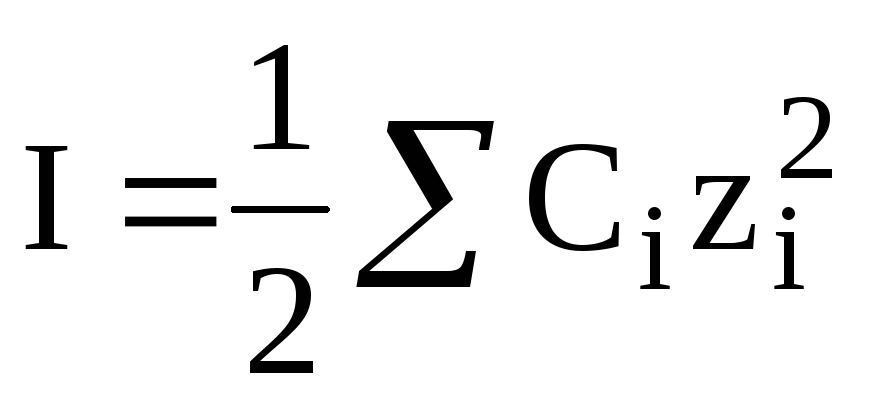
Пример 3.1.В 1,00 л водного раствора содержится 10,3 г NaBr, 14,2 г Na₂SO₄ и 1,7 г NH₃. Чему равна ионная сила такого раствора?

0,100 Моль/л

0,100 Моль/л

С(Na⁺) = 0,300 моль/л, С(Br^—) = 0,100 моль/л, С(SO₄^2-) = 0,100моль/л

I= 0,5[0,300(+1)²+ 0,100(-1)²+ 0,100(-2)²] = 0,400 моль/л

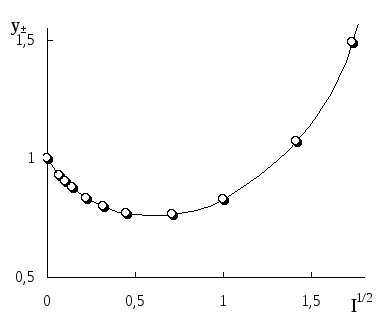
Рис. 3.1. Влияние ионной силы на среднеионный коэффициент активности HCl

На рис. 3.1 показан пример влияния ионной силы на активность электролита (HCl). Аналогичная зависимость коэффициента активности от ионной силы наблюдается также уHClO₄,LiCl,AlCl₃и многих других соединений. У некоторых электролитов (NH₄NO₃,AgNO₃) зависимость коэффициента активности от ионной силы является монотонно убывающей.

Универсального уравнения, с помощью которого можно было бы рассчитать коэффициент активности любого электролита при любой величине ионной силы, не существует. Для описания зависимости коэффициента активности от ионной силы в очень разбавленных растворах (до I< 0,01) можно использоватьпредельный закон Дебая-Хюккеля

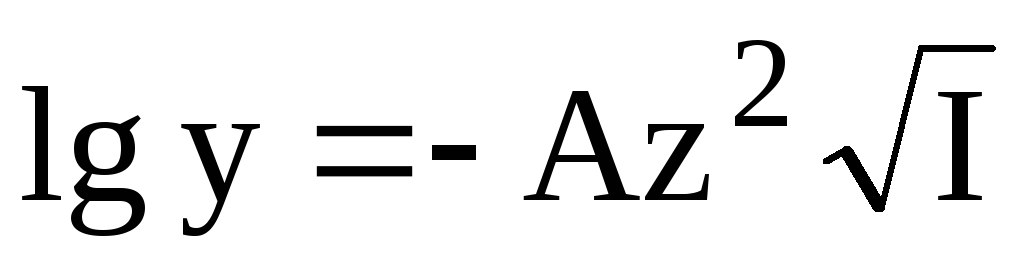
где A — коэффициент, зависящий от температуры и диэлектрической проницаемости среды; для водного раствора (298К) A  0,511.

Данное уравнение было получено голландским физиком П. Дебаем и его учеником Э. Хюккелем исходя из следующих предположений. Каждый ион был представлен в виде точечного заряда (т.е. размер иона не учитывался), окружённого в растворе ионной атмосферой— областью пространства сферической формы и определённого размера, в которой содержание ионов противоположного знака по отношению к данному иону больше, чем вне её. Заряд ионной атмосферы равен по величине и противоположен по знаку заряду создавшего её центрального иона. Между центральным ионом и окружающей его ионной атмосферой существует электростатическое притяжение, которое стремится стабилизировать данный ион. Стабилизация приводит к понижению свободной энергии иона и уменьшению его коэффициента активности. В предельном уравнении Дебая-Хюккеля природа ионов не учитывается. Считается, что при малых значениях ионной силы коэффициент активности иона не зависит от его природы.

При увеличении ионной силы до 0,01 и больше предельный закон начинает давать всё большую и большую погрешность. Это происходит потому, что реальные ионы имеют определённый размер, вследствие чего их нельзя упаковать так плотно, как точечные заряды. При увеличении концентрации ионов происходит уменьшение размеров ионной атмосферы. Так как ионная атмосфера стабилизирует ион и уменьшает его активность, то уменьшение её размера приводит к менее значительному уменьшению коэффициента активности.

Для расчёта коэффициентов активности при ионных силах порядка 0,01 — 0,1 можно использовать расширенное уравнение Дебая-Хюккеля:

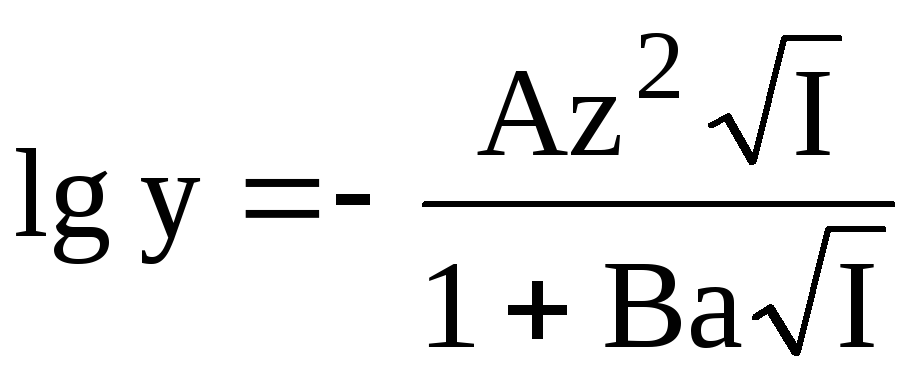
где B  0,328 (T = 298K, a выражено в ), a — эмпирическая константа, характеризующая размеры ионной атмосферы.

При более высоких значениях ионной силы (до 1) количественную оценку коэффициента активности можно проводить по

уравнению Дэвиса.

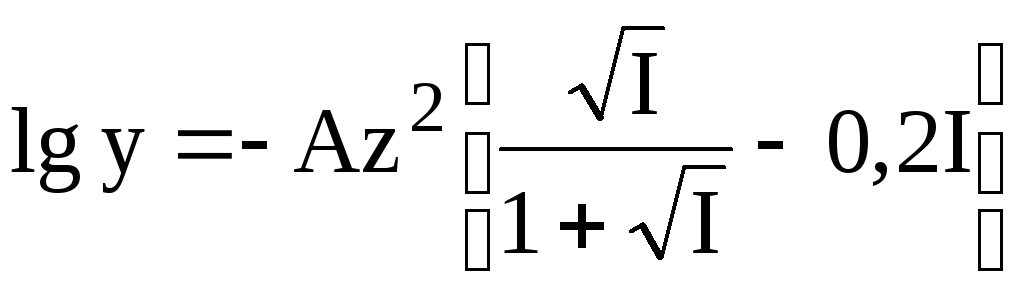
В данном уравнении a принято равным 3,05, поэтому произведение Ba равно 1. Фактор 0,2I учитывает образование ионных пар, изменение диэлектрической проницаемости и т.д.

В ещё более концентрированных растворах начинают сильно проявляться индивидуальные особенности ионов, поэтому уравнения, описывающего экспериментальные данные для таких растворов, нет.У одних электролитов коэффициент активности уменьшается, что может быть обусловлено образованием ионных пар, у других он увеличивается — за счёт уменьшения не принимающих участие в гидратации молекул воды и по другим причинам.

Пример 3.2. Рассчитать коэффициенты активности иона H⁺ при ионной силе 0,010 и 0,10.

При I = 0,010 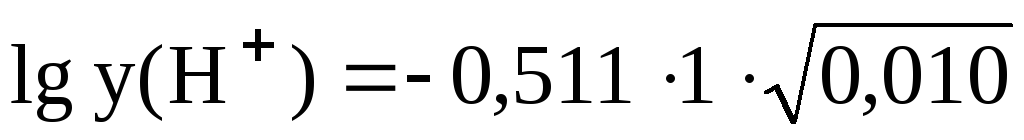= -0,0511;

0,89.

При I = 0,10 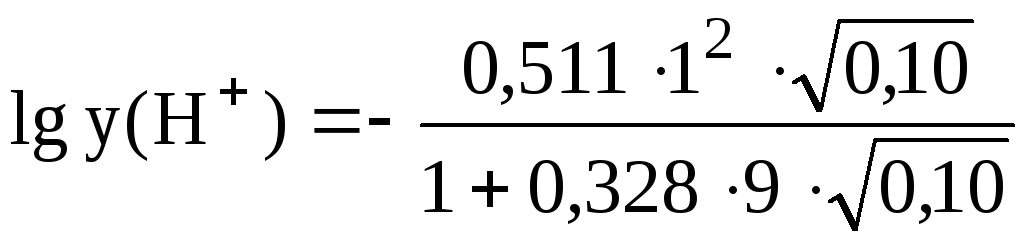=-0,0836,

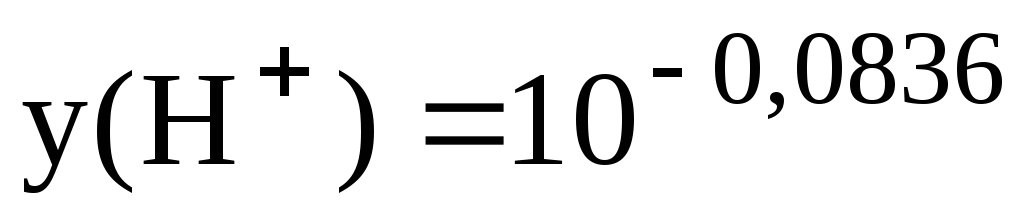= 0,82

studfile.net

Изотонический коэффициент — Википедия

Материал из Википедии — свободной энциклопедии

Изотонический коэффициент (также фактор Вант-Гоффа; обозначается i) — безразмерный параметр, характеризующий поведение вещества в растворе. Он численно равен отношению значения некоторого коллигативного свойства раствора данного вещества к значению того же коллигативного свойства неэлектролита той же концентрации при неизменных прочих параметрах системы:

i=πsolut.πnel. solut.=ΔTbp solut.ΔTbp nel. solut.=ΔTmp solut.ΔTmp nel. solut.=Δpsolut.Δpnel. solut.{\displaystyle i={\frac {\pi _{solut.}}{\pi _{nel.~solut.}}}={\frac {\Delta T_{bp~solut.}}{\Delta T_{bp~nel.~solut.}}}={\frac {\Delta T_{mp~solut.}}{\Delta T_{mp~nel.~solut.}}}={\frac {\Delta p_{solut.}}{\Delta p_{nel.~solut.}}}} ,

где solut. — данный раствор, nel. solut. — раствор неэлектролита той же концентрации, T_bp — температура кипения, а T_mp — температура плавления (замерзания).

Смысл параметра ясен из определения каждого из коллигативных параметров: они зависят от концентрации в растворе частиц растворённого вещества. Неэлектролиты в растворе не диссоциируют, значит, каждая молекула неэлектролита образует в растворе лишь одну частицу. В свою очередь, электролиты в растворе под влиянием сольватации частично или полностью распадаются на ионы, образуя при этом несколько частиц на одну диссоциировавшую молекулу. Соответственно, и коллигативные свойства данного раствора (аддитивные величины) зависят от содержания в нём частиц (ионов) каждого типа из тех, которым принадлежат частицы, образовавшиеся в растворе в результате диссоциации исходной молекулы, — раствор представляется как бы смесью растворов каждого из типов частиц. Например, раствор хлорной извести содержит три типа частиц — катионы кальция, хлорид-анионы и гипохлорит-анионы. Итак, изотонический коэффициент показывает, насколько в растворе электролита больше частиц по сравнению с раствором неэлектролита аналогичной концентрации, и связан со способностью вещества распадаться в растворе на ионы, то есть, со степенью диссоциации. Если формульная единица или молекула содержит n ионов (или атомов при полярных связях, в растворе превращающихся в ионы), количество исходных молекул равно N, а степень диссоциации соединения — α, то количество диссоциировавших молекул равно N·α (при этом образуются N·α·n ионов), а общее количество частиц в растворе равно ((N — N·α) + N·α·n).

Изотонический же коэффициент равен отношению:

i=N−N⋅α+N⋅α⋅nN=N(1−α+α⋅n)N=1+α(n−1){\displaystyle i={\frac {N-N\cdot \alpha +N\cdot \alpha \cdot n}{N}}={\frac {N(1-\alpha +\alpha \cdot n)}{N}}=1+\alpha (n-1)}.

Изотонический коэффициент в растворах сильных электролитов[править | править код]

Поскольку сильные электролиты диссоциируют практически полностью, можно было бы ожидать для них изотонический коэффициент, равный количеству ионов (или поляризованных атомов) в формульной единице (молекуле). Однако в действительности этот коэффициент всегда меньше определённого по формуле. Например, изотонический коэффициент для 0,05-моляльного раствора NaCl равен 1,9 вместо 2,0 (для раствора сульфата магния той же концентрации и вовсе i = 1,3). Это объясняет теория сильных электролитов, разработанная в 1923 году П. Дебаем и Э. Хюккелем: передвижение ионов в растворе затруднено образовавшейся оболочкой сольватации. К тому же, ионы взаимодействуют и между собой: разноимённо заряженные притягиваются, а одноимённо заряженные — отталкиваются; силы взаимного притяжения приводят к образованию групп ионов, перемещающихся по раствору совместно. Такие группы называют ионными ассоциатами или ионными па́рами. Соответственно, раствор ведёт себя так, будто содержит меньше частиц, чем на самом деле, ведь свобода их перемещения ограничена. Наиболее очевиден пример, касающийся электропроводности растворов λ, которая возрастает с разбавлением раствора. Через отношение реальной электропроводности к таковой при бесконечном разбавлении определяют мнимую степень диссоциации сильных электролитов, также обозначаемую через α:

α=λλ∞=nimgndisslv.{\displaystyle \alpha ={\frac {\lambda }{\lambda _{\infty }}}={\frac {n_{img}}{n_{disslv.}}}},

где n_img — мнимое, а n_disslv. — реальное количество частиц в растворе.

Очевидно, что взаимодействие ионов уменьшается с повышением температуры (вследствие возросшего теплового движения частичек), а также с уменьшением их концентрации, то есть, разбавлением раствора, ведь тогда уменьшается вероятность встречи двух частичек. Экстраполируя разбавление в сторону бесконечности, коэффициент i стремится к своему максимальному значению, определяемому по формуле растворённого соединения. Степень диссоциации α, в соответствии с вышеупомянутой формулой зависимости между i и α, одновременно возрастает, приближаясь к единице (1).

Изотонический коэффициент был введён в последней четверти XIX века Я. Х. Вант-Гоффом. В 1901 году он первым получил Нобелевскую премию по химии — за свои заслуги в изучении растворов.

• Еремин В. В., Каргов С. И., Успенская И. А., Кузьменко Н. Е., Лунин В. В. Основы физической химии. Теория и задачи: учеб. пособие для вузов. — М.: Издательство «Экзамен», 2005. — 480 с. — (Серия «Классический университетский учебник»). — ISBN 5-472-00834-4.
• Kokars, V. Vispārīgā ķīmija (1. daļa). Rīga: RTU izdevniecība, 2009. 286 lpp. (латыш.)

ru.wikipedia.org

Активность (химия) — это… Что такое Активность (химия)?

У этого термина существуют и другие значения, см. Активность.

Активность компонентов раствора — эффективная (кажущаяся) концентрация компонентов с учётом различных взаимодействий между ними в растворе, то есть с учётом отклонения поведения системы от модели идеального раствора.

Активность была предложена в 1907 году Льюисом как новая переменная, применение которой вместо концентрации позволяет использовать для описания свойств реальных растворов относительно простые уравнения, полученные для идеальных систем. Альтернативой этому пути является использование более сложных уравнений, учитывающих взаимодействие между частицами (см., например, уравнение Ван-дер-Ваальса).

Активность отличается от общей концентрации на некоторую величину. Отношение активности () к общей концентрации вещества в растворе называется коэффициентом активности:

Коэффициент активности служит мерой отклонения поведения раствора (или компонента раствора) от идеального. Отклонения от идеальности могут быть обусловлены различными химическими и физическими причинами — дипольные взаимодействия, поляризация, образование водородных связей, ассоциация, диссоциация, сольватация и др.^[1]

Исходя из понятия химического потенциала, активность компонента в растворе можно определить как величину, которую нужно подставить в выражения для химического потенциала компонента в идеальном растворе:

(где  — химический потенциал чистого -го компонента) вместо мольной доли x, для того, чтобы получить действительное значение химического потенциала -го компонента в реальном растворе:

где  — стандартный химический потенциал^[2].

Размерность и величина активности зависит от используемого способа выражения концентрации — если (активность при выражении концентрации как мольной доли) величина безразмерная, то и (для молярности и моляльности соответственно) — размерные величины, выражаются в моль/л и моль/кг.

В теории дистилляции активность компонента жидкости представляется как давление пара компонента в сравнении с давлением пара чистого компонента: . При этом , где N – молярная доля компонента в жидкости, γ –коэффициент активности. Концентрационная зависимость активности, построенная при заданной температуре в координатах а-N, носит название диаграммы активности. Известны экспериментально построенные диаграммы активности для ряда двойных систем^[3][4][5].

Коэффициент активности в общем случае может быть как больше, так и меньше единицы (при этом говорят о положительных или отрицательных отклонениях от идеального поведения соответственно, или о положительных и отрицательных отклонениях от закона Рауля). Возможны и знакопеременные отклонения от идеального поведения в одной диаграмме (с изменением в пределах от 0,01 и менее до 10 и более, что отражает сложных характер взаимодействия компонентов в системе). Например, для железа в системе Fe-S при 1300 °C коэффициенты активности изменяется от 0,004 при =0,48 до 1,47 при =0,68^[6]. В некоторых системах концентрационная зависимость активности является причиной существования стабильного состава, по достижении которого состав испаряющейся жидкости не меняется^[7].

Важно отметить, что величина активности и коэффициента активности может быть различной в зависимости от выбора стандартного состояния.

Выбор стандартного состояния

При использовании активности и коэффициента активности важную роль играет выбор стандартного состояния компонента, то есть состояния, в котором

Для растворов взаимно неограниченно растворимых жидкостей в качестве стандартного может быть выбрано состояние чистого компонента (как для растворителя, так и для растворенного вещества):

при и

Иногда такой выбор называют симметричной системой стандартного состояния.

В случае, если рассматривается раствор газа и или твердого вещества в жидкости, мольную долю растворенного вещества нельзя изменять до единицы. Тогда для растворителя — жидкости — стандартное состояние может быть выбрано так же, как показано выше, а для растворенного вещества за стандартное состояние принимают гипотетический раствор с концентрацией, равной единице, но сохраняющий свойства предельно разбавленного раствора. Иначе говоря, это такое состояние, для которого давление пара численно равно константе Генри:

Таким образом, для растворителя и растворенного вещества здесь принимаются разные стандартные состояния — это несимметричная система стандартных состояний.

В системах с ограниченной растворимостью за стандартное может быть принято состояние компонента в насыщенном растворе:

В засимости от исследуемой системы, в качестве стандартного может быть выбрано и другое состояние, например, для серы при исследовании богатых сульфидных расплавов — состояние серы в стехиометрическом сульфиде^[6]. При рассмотрении результатов эксперимента, использовании справочных данных и т. п. следует обязательно указывать, какое именно состояние компонента принято за стандартное.

Методы определения активности

Экспериментальные методы определения активности компонентов в растворе основаны на изучении какого-либо гетерогенного равновесия в системе. При рассмотрении этих методов следует помнить, что в условиях равновесия химические потенциалы i-го компонента в разных фазах (I и II) равны:

Это соотношение является исходной точкой для вывода расчетных уравнений в некоторых из методов определения активности. Кроме того, активности компонентов в некоторой фазе связаны между собой уравнением:

По равновесному давлению пара

В основе этого метода лежит соотношение:

где  — парциальное давление пара компонента над раствором, а  — давление пара этого компонента для стандартного состояния (см. выше). Соответственно, если за стандартное состояние принято состояние чистого компонента, то .

Экспериментальные методы определения давления пара компонентов над раствором весьма разнообразны; выбор того или иного из них определяется, в частности, исследуемой системой (водный раствор или иная низкотемпературная система, либо расплавленный металл, шлак, штейн и т. п.).

По повышению температуры кипения раствора

Температура кипения раствора выше температуры кипения чистого растворителя . Данные об изменении температуры кипения раствора могут быть использованы для расчета активности растворителя, в соответствии с уравнением:

,

где  — теплота испарения растворителя, в интервале от температуры кипения чистого растворителя до температуры кипения раствора принимаемая постоянной. Индексом «1» обычно обозначается растворитель.

По понижению температуры замерзания раствора

Температура замерзания раствора ниже температуры замерзания чистого растворителя . Соответственно, активность растворителя можно рассчитать, используя зависимость:

,

где  — теплота плавления растворителя.

По осмотическому давлению раствора

Величина осмотического давления раствора может быть использована для определения активности растворителя в соответствии с соотношением:

где  — осмотическое давление,  — парциальный молярный объём растворителя.

По распределению компонента между конденсированными фазами

Активность компонента раствора можно определить, изучая равновесное распределение его между двумя контактирующими конденсированными фазами (различными растворителями, сплавом и шлаком, шлаком и штейном и т. п.), одна из которых — исследуемый раствор, а для другой активность или коэффициент активности уже известны. В общем случае:

В частности, если выбор стандартного состояния компонента для фаз таков, что , это выражение принимает более простой вид:

Экспериментально в этом методе определяют равновесные концентрации компонента или коэффициент распределения компонента между растворами.

По равновесию химической реакции с газовой фазой

При исследовании оксидных расплавов активность компонентов часто определяют, используя следующие химические реакции:

MeO + H₂ = Me + H₂O

MeO + CO = Me + CO₂

Для первой из приведенных реакций константа равновесия имеет вид:

Если оксидный и металлический расплавы взаимно нерастворимы и восстанавливается индивидуальный оксид, то , и тогда:

Если металл выделяется в виде сплава с другими компонентами или растворяется в фазе-коллекторе, его активность не равна единице и формула принимает вид:

Активность металла в сплаве здесь должна быть известна из независимых измерений.

Опытным путем в данном методе определяют отношение .

Кроме того, активность оксидного компонента связана с равновесным давлением кислорода над расплавом, с учётом реакций в газовой фазе, например:

или

Тогда можно показать, что

Для сульфидных расплавов используют реакцию:

или (значительно реже):

По значению э. д. с. гальванического элемента

Электродвижущая сила концентрационной цепи с переносом может быть выражена следующим соотношением:

Соответственно, такую цепь можно использовать для нахождения активности и коэффициента активности. В некоторых случаях (например, для сложных сульфидных расплавов) побочное взаимодейтсвие электролита с электродами может приводить к невозможности определения активности компонентов по ЭДС цепи, тогда используют концентрационные цепи без переноса. Нахождение активности компонента по ЭДС концентрационной цепи без переноса — один из самых точных способов определения активности^[8] .

См. также

Примечания

1. ↑ Краснов К. С., Воробьев Н. К., Годнев И. Н. и др. Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика: Учеб. для вузов. — 2-е изд., перераб. и доп. — М. : Высш. шк., 1995. — 512 с. — ISBN 5-06-002913-1
2. ↑ Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов/ Под ред. А. Г. Стромберга. — 2-е изд., перераб. и доп. — М.: Высш. шк., 1988. — 496 с.
3. ↑ Девятых Г.Г., Еллиев Ю.Е. Введение в теорию глубокой очистки веществ. — М.: Наука, 1981. — 320 с.
4. ↑ Пазухин В.А., Фишер А.Я. Разделение и рафинирование металлов в вакууме. — М.: Металлургия, 1969. — 204 с.
5. ↑ Иванов В.Е., Папиров И.И., Тихинский Г.Ф., Амоненко В.М. Чистые и сверхчистые металлы (получение методом дистилляции в вакууме). — М.: Металлургия, 1965. — 263 с.
6. ↑ ^{1 2} Вайсбурд С. Е. Физико-химические свойства и особенности строения сульфидных расплавов. — М. : Металлургия, 1996. — 304 с. — ISBN 5-229-00903-9
7. ↑ Кравченко А. И. О временной зависимости состава двойного сплава при его разгонке в вакууме // Известия АН СССР. Серия «Металлы», 1983. — № 3. — С. 61–63.
8. ↑ Лукомский Ю. Я., Гамбург Ю. Д. Физико-химические основы электрохимии. Учебник. — Долгопрудный : Издательский Дом «Интеллект», 2008. — 424 с. — ISBN 978-5-91559-007-5

Ссылки

dic.academic.ru

Концентрация смеси — Википедия

Концентра́ция или до́ля компонента смеси — величина, количественно характеризующая содержание компонента относительно всей смеси. Терминология ИЮПАК под концентрацией компонента понимает четыре величины: соотношение молярного, или численного количества компонента, его массы, или объёма исключительно к объёму раствора^[1] (типичные единицы измерения — соответственно моль/л, л⁻¹, г/л, и безразмерная величина). Долей компонента ИЮПАК называет безразмерное соотношение одной из трёх однотипных величин — массы, объёма или количества вещества.^[2] Однако в обиходе термин «концентрация» могут применять и для долей, не являющихся объёмными долями, а также к соотношениям, не описанным ИЮПАК. Оба термина могут применяться к любым смесям, включая механические смеси, но наиболее часто применяются к растворам.

Можно выделить несколько типов математического описания: массовая концентрация, молярная концентрация, концентрация частиц и объемная концентрация^[3].

Эти стаканы, содержащие красный краситель, демонстрируют качественные изменения концентрации. Растворы слева более разбавлены, по сравнению с более концентрированными растворами справа.

Массовая доля компонента — отношение массы данного компонента к сумме масс всех компонентов. По рекомендациям ИЮПАК,^[4] обозначается символом w{\displaystyle w}, в русскоязычной литературе чаще встречается обозначение ω{\displaystyle \omega }. Массовая доля — безразмерная величина, как правило выражается в долях единицы или в процентах (для выражения массовой доли в процентах следует умножить указанное выражение на 100 %):

ωB=mBm{\displaystyle \omega _{\mathrm {B} }={\frac {m_{\mathrm {B} }}{m}}}

где:

• ω_B — массовая доля компонента B
• m_B — масса компонента B;
• m{\displaystyle m} — общая масса всех компонентов смеси.

В бинарных растворах часто существует однозначная (функциональная) зависимость между плотностью раствора и его концентрацией (при данной температуре). Это даёт возможность определять на практике концентрации важных растворов с помощью денсиметра (спиртометра, сахариметра, лактометра). Некоторые ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора (спирта, жира в молоке, сахара). Следует учитывать, что для некоторых веществ кривая плотности раствора имеет максимум, в этом случае проводят два измерения: непосредственное, и при небольшом разбавлении раствора.

Часто для выражения концентрации (например, серной кислоты в электролите аккумуляторных батарей) пользуются просто их плотностью. Распространены ареометры (денсиметры, плотномеры), предназначенные для определения концентрации растворов веществ.

Пример: зависимость плотности растворов H₂SO₄ от её массовой доли в водном растворе при 25 °C^{[источник не указан 2829 дней]}

ω, %	5	10	15	20	30	40	50	60	70	80	90	95
ρ H2SO4, г/мл	1,032	1,066	1,102	1,139	1,219	1,303	1,395	1,498	1,611	1,727	1,814	1,834

Объёмная доля компонента — отношение объёма компонента к сумме объёмов компонентов до смешивания. Объёмная доля измеряется в долях единицы или в процентах.

ϕB=VB∑Vi{\displaystyle \phi _{\mathrm {B} }={\frac {V_{\mathrm {B} }}{\sum V_{i}}}},

где:

• ϕB{\displaystyle \phi _{\mathrm {B} }} — объёмная доля компонента B,
• V_B — объём компонента B;
• ∑Vi{\displaystyle \sum V_{i}} — сумма объёмов всех компонентов до смешивания.

При смешивании жидкостей их суммарный объём может уменьшаться, поэтому не следует заменять сумму объёмов компонентов на объём смеси.

Как было указано выше, существуют ареометры, предназначенные для определения концентрации растворов определённых веществ. Такие ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора. Для распространённых растворов этилового спирта, концентрация которых обычно выражается в объёмных процентах, такие ареометры получили название спиртомеров или андрометров.

Молярность (молярная объёмная концентрация)[править | править код]

Молярная концентрация (молярность, мольность^[5]) — количество вещества (число молей) компонента в единице объёма смеси. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л. Также используют выражение «в молярности». Возможно другое обозначение молярной концентрации, которое принято обозначать М. Так, раствор с концентрацией 0,5 моль/л называют 0,5-молярным, записывают «0,5 M».

По рекомендации ИЮПАК, обозначается буквой c{\displaystyle c} или [B]{\displaystyle [B]}, где B — вещество, концентрация которого указывается.^[6]

Примечание: После числа пишут «моль», подобно тому, как после числа пишут «см», «кг» и т. п., не склоняя по падежам.

cB=nBV{\displaystyle {c_{\mathrm {B} }}={\frac {n_{\mathrm {B} }}{V}}},

где:

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)[править | править код]

Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов). Для записи концентрации таких растворов используют сокращения «н» или «N». Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.

c(feq B)=c((1/z) B)=z⋅cB=z⋅nBV=1feq⋅nBV{\displaystyle c(f_{eq}~\mathrm {B} )=c{\big (}(1/z)~\mathrm {B} {\big )}=z\cdot c_{\mathrm {B} }=z\cdot {\frac {n_{\mathrm {B} }}{V}}={\frac {1}{f_{eq}}}\cdot {\frac {n_{\mathrm {B} }}{V}}},

где:

Нормальная концентрация может отличаться в зависимости от реакции, в которой участвует вещество. Например, одномолярный раствор H₂SO₄ будет однонормальным, если он предназначается для реакции со щёлочью с образованием гидросульфата калия KHSO₄, и двухнормальным в реакции с образованием K₂SO₄.

Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы. ИЮПАК рекомендует обозначать мольную долю буквой x{\displaystyle x} (а для газов — y{\displaystyle y})^[7], также в литературе встречаются обозначения χ{\displaystyle \chi }, X{\displaystyle X}.

xB=nB∑ni{\displaystyle x_{\mathrm {B} }={\frac {n_{\mathrm {B} }}{\sum n_{i}}}},

где:

• xB{\displaystyle x_{\mathrm {B} }} — мольная доля компонента B;
• nB{\displaystyle n_{\mathrm {B} }} — количество компонента B, моль;
• ∑ni{\displaystyle \sum n_{i}} — сумма количеств всех компонентов.

Мольная доля может использоваться, например, для количественного описания уровня загрязнений в воздухе, при этом её часто выражают в частях на миллион (ppm — от англ. parts per million). Однако, как и в случае с другими безразмерными величинами, во избежание путаницы, следует указывать величину, к которой относится указанное значение.

Моляльность (молярная весовая концентрация, моляльная концентрация)[править | править код]

Моляльная концентрация (моляльность,^[5] молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя. Измеряется в молях на кг, также распространено выражение в «моляльности». Так, раствор с концентрацией 0,5 моль/кг называют 0,5-мольным.

mB=nBmA{\displaystyle {m_{\mathrm {B} }}={\frac {n_{\mathrm {B} }}{m_{\mathrm {A} }}}},

где:

Следует обратить особое внимание, что, несмотря на сходство названий, молярная концентрация и моляльность — величины различные. Прежде всего, в отличие от молярной концентрации, при выражении концентрации в моляльности расчёт ведут на массу растворителя, а не на объём раствора. Моляльность, в отличие от молярной концентрации, не зависит от температуры.

Массовая концентрация — отношение массы растворённого вещества к объёму раствора. По рекомендации ИЮПАК, обозначается символом γ{\displaystyle \gamma } или ρ{\displaystyle \rho }^[8].

ρB=mBV{\displaystyle \rho _{\mathrm {B} }={\frac {m_{\mathrm {B} }}{V}}}.

где:

• mB{\displaystyle m_{\mathrm {B} }} — масса растворённого вещества;
• V{\displaystyle V} — общий объём раствора;

В аналитической химии используется понятие титр по растворённому или по определяемому веществу (обозначается буквой T{\displaystyle T}).

По рекомендациям ИЮПАК концентрация частиц обозначается буквой C{\displaystyle C}^[9], однако также часто встречается обозначение n{\displaystyle n} (не путать с количеством вещества).

CB=NBV=nB⋅NAV=cB⋅NA{\displaystyle C_{\mathrm {B} }={\frac {N_{\mathrm {B} }}{V}}={\frac {n_{\mathrm {B} }\cdot N_{\mathrm {A} }}{V}}=c_{\mathrm {B} }\cdot N_{\mathrm {A} }},

где:

Весообъёмные (массо-объёмные) проценты[править | править код]

Иногда встречается использование так называемых «весообъёмных процентов»^[10], которые соответствуют массовой концентрации вещества, где единица измерения г/(100 мл) заменена на процент. Этот способ выражения используют, например, в спектрофотометрии, если неизвестна молярная масса вещества или если неизвестен состав смеси, а также по традиции в фармакопейном анализе.^[11] Стоит отметить, что поскольку масса и объём имеют разные размерности, использование процентов для их соотношения формально некорректно. Также международное бюро мер и весов^[12] и ИЮПАК^[13] не рекомендуют добавлять дополнительные метки (например «% (m/m)» для обозначения массовой доли) к единицам измерения.

Другие способы выражения концентрации[править | править код]

Существуют и другие, распространённые в определённых областях знаний или технологиях, методы выражения концентрации. Например, при приготовлении растворов кислот в лабораторной практике часто указывают, сколько объёмных частей воды приходится на одну объёмную часть концентрированной кислоты (например, 1:3). Иногда используют также отношение масс (отношение массы растворённого вещества к массе растворителя) и отношение объёмов (аналогично, отношение объёма растворяемого вещества к объёму растворителя).

Применимость способов выражения концентрации растворов, их свойства[править | править код]

В связи с тем, что моляльность, массовая доля, мольная доля не включают в себя значения объёмов, концентрация таких растворов остаётся неизменной при изменении температуры. Молярность, объёмная доля, титр, нормальность изменяются при изменении температуры, так как при этом изменяется плотность растворов. Именно моляльность используется в формулах повышения температуры кипения и понижения температуры замерзания растворов.

Разные виды выражения концентрации растворов применяются в разных сферах деятельности, в соответствии с удобством применения и приготовления растворов заданных концентраций. Так, титр раствора удобен в аналитической химии для волюмометрии (титриметрического анализа) и т. п.

Формулы перехода от одних выражений концентраций к другим[править | править код]

В зависимости от выбранной формулы погрешность конвертации колеблется от нуля до некоторого знака после запятой.

От массовой доли к молярности[править | править код]

cB=ρ⋅ωBM(B){\displaystyle c_{\mathrm {B} }={\frac {\rho \cdot \omega _{\mathrm {B} }}{M(\mathrm {B} )}}},

где:

• cB{\displaystyle c_{\mathrm {B} }} — молярная концентрация вещества B
• ρ{\displaystyle \rho } — плотность раствора;
• ωB{\displaystyle \omega _{\mathrm {B} }} — массовая доля вещества B;
• M(B){\displaystyle M(\mathrm {B} )} — молярная масса вещества B.

Если плотность раствора выражена в г/мл, а молярная масса в г/моль, то для выражения ответа в моль/л выражение следует домножить на 1000 мл/л. Если массовая доля выражена в процентах, то выражение следует также разделить на 100 %.

От молярной концентрации к нормальной[править | править код]

c((1/z) B)=cB⋅z{\displaystyle {c((1/z)~\mathrm {B} )}={c_{\mathrm {B} }}\cdot {z}},

где:

От массовой доли к титру[править | править код]

T=ρ⋅ω{\displaystyle {T}={\rho }\cdot {\omega }},

где:

• ρ{\displaystyle \rho } — плотность раствора, г/мл;
• ω{\displaystyle \omega } — массовая доля растворённого вещества, в долях от 1;

От молярности к титру[править | править код]

T=cB⋅M{\displaystyle {T}={c_{\mathrm {B} }}\cdot {M}},

где:

• cB{\displaystyle {c_{\mathrm {B} }}} — молярная концентрация;
• M{\displaystyle M} — молярная масса растворённого вещества.

Если молярная концентрация выражена в моль/л, а молярная масса — в г/моль, то для выражения ответа в г/мл его следует разделить на 1000 мл/л.

От моляльности к мольной доле[править | править код]

xB=mBmB+1M(A){\displaystyle x_{\mathrm {B} }={\frac {m_{\mathrm {B} }}{m_{\mathrm {B} }+{\frac {1}{M(\mathrm {A} )}}}}},

где:

• mB{\displaystyle m_{\mathrm {B} }} — моляльность,
• M(A){\displaystyle M(\mathrm {A} )} — молярная масса растворителя.

Если моляльность выражена в моль/кг, а молярная масса растворителя в г/моль, то единицу в формуле следует представить как 1000 г/кг, чтобы слагаемые в знаменателе имели одинаковые единицы измерения.

1. ↑ International Union of Pure and Applied Chemistry. concentration (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — DOI:10.1351/goldbook.C01222.
2. ↑ International Union of Pure and Applied Chemistry. fraction (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — DOI:10.1351/goldbook.F02494.
3. ↑ IUPAC Gold Book internet edition: «concentration».
4. ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — mass fraction, w (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
5. ↑ ^{1 2} Z. Sobecka, W. Choiński, P. Majorek. Dictionary of Chemistry and Chemical Technology: In Six Languages: English / German / Spanish / French / Polish / Russian. — Elsevier, 2013-09-24. — С. 641. — 1334 с. — ISBN 9781483284439.
6. ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — amount concentration, c (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
7. ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — amount fraction, x ( y for gaseous mixtures) (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
8. ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — mass concentration, γ, ρ (англ.). goldbook.iupac.org. Дата обращения 16 декабря 2018.
9. ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — number concentration, C,n (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
10. ↑ Способы приготовления растворов на МедКурс. Ru
11. ↑ Бернштейн И. Я., Каминский Ю. Л. Спектрофотометрический анализ в органической химии. — 2-е изд. — Ленинград: Химия, 1986. — с. 5
12. ↑ The International System of Units (SI) (неопр.). www.bipm.org. Дата обращения 23 декабря 2018.
13. ↑ Quantities, Units and Symbols in Physical Chemistry (неопр.) (недоступная ссылка). www.iupac.org. Дата обращения 23 декабря 2018. Архивировано 20 декабря 2016 года.

ru.wikipedia.org